Как найти стороны ромба 🚩 высота в ромбе 🚩 Образование 🚩 Другое
Допустим, нам известны длины диагоналей ромба. Как найти длину стороны ромба?Так как диагонали ромба (AC, BD) пересекаются под прямым углом и делятся точкой пересечения (O) пополам, то сторона ромба (AB) будет диагональю прямоугольного треугольника (ABO) с катетами, образованными половинками диагоналей ромба (AO, BO). Тогда по теореме Пифагора получается: квадрат длины стороны ромба равняется сумме квадратов половин длин его диагоналей.
|AB|^2=|AO|^2+|BO|^2=(|AC|/2)^2+(|BD|/2)^2.
Соответственно, длина стороны ромба будет равняться корню квадратному из суммы квадратов половинок его диагоналей.
|AB|=√((|AC|/2)^2+(|BD|/2)^2).
Пусть нам известны площадь ромба (ABCD) и его высота (BH), т.е. длина перпендикуляра, опущенного из вершины (B) на сторону (AD) (или ее продолжение). Как определить сторону ромба (AB) в этом случае?
Как видно из рисунка, ромб состоит из двух треугольников (ABD и DBC) площадь каждого из которых равняется половине произведения высоты на основание. Следовательно площадь ромба будет равна произведению высоты на длину стороны. Отсюда получается простая формула для вычисления длины стороны ромбы: нужно его площадь разделить на длину высоты.
|AB|=S/|BH|
Если известна величина угла ромба и длина одной из диагоналей, то нахождение стороны ромба производится аналогично первому случаю, только вместо теоремы Пифагора необходимо использовать тригонометрические соотношения. При этом следует учесть, что диагонали ромба являются одновременно биссектрисами углов, то есть делят их пополам.
Пусть, например, нам известна величина угла BAD и длина выходящей из него диагонали АС. Исходя из тригонометрических зависимостей в прямоугольном треугольнике ABO, получаем, что длина стороны ромба будет равна частному от половины исходящей диагонали на синус половины угла.
В виде формулы эта зависимость будет выглядеть следующим образом:
|AB|= (|AC|/2)/sin(α/2), где α — величина угла BAD.
Аналогично вычисляется длина стороны ромба в случае, когда заданы другие параметры — длина противоположной углу диагонали, соотношение диагоналей и т.д. Для определения стороны ромба достаточно лишь выбрать подходящую тригонометрическую функцию — косинус, тангенс и т.п.
www.kakprosto.ru
Как найти сторону ромба, если знаешь только его площадь?
<a href=»/» rel=»nofollow» title=»15907216:##:1VfA6qt»>[ссылка заблокирована по решению администрации проекта]</a>
Допустим, нам известны длины диагоналей ромба. Как найти длину стороны ромба? Так как диагонали ромба (AC, BD) пересекаются под прямым углом и делятся точкой пересечения (O) пополам, то сторона ромба (AB) будет диагональю прямоугольного треугольника (ABO) с катетами, образованными половинками диагоналей ромба (AO, BO). Тогда по теореме Пифагора получается: квадрат длины стороны ромба равняется сумме квадратов половин длин его диагоналей. |AB|^2=|AO|^2+|BO|^2=(|AC|/2)^2+(|BD|/2)^2. Соответственно, длина стороны ромба будет равняться корню квадратному из суммы квадратов половинок его диагоналей. |AB|=√((|AC|/2)^2+(|BD|/2)^2). Пусть нам известны площадь ромба (ABCD) и его высота (BH), т. е. длина перпендикуляра, опущенного из вершины (B) на сторону (AD) (или ее продолжение). Как определить сторону ромба (AB) в этом случае? Как видно из рисунка, ромб состоит из двух треугольников (ABD и DBC) площадь каждого из которых равняется половине произведения высоты на основание. Следовательно площадь ромба будет равна произведению высоты на длину стороны. Отсюда получается простая формула для вычисления длины стороны ромбы: нужно его площадь разделить на длину высоты. |AB|=S/|BH| Если известна величина угла ромба и длина одной из диагоналей, то нахождение стороны ромба производится аналогично первому случаю, только вместо теоремы Пифагора необходимо использовать тригонометрические соотношения. При этом следует учесть, что диагонали ромба являются одновременно биссектрисами углов, то есть делят их пополам. Пусть, например, нам известна величина угла BAD и длина выходящей из него диагонали АС. Исходя из тригонометрических зависимостей в прямоугольном треугольнике ABO, получаем, что длина стороны ромба будет равна частному от половины исходящей диагонали на синус половины угла. В виде формулы эта зависимость будет выглядеть следующим образом: |AB|= (|AC|/2)/sin(α/2), где α — величина угла BAD. Аналогично вычисляется длина стороны ромба в случае, когда заданы другие параметры — длина противоположной углу диагонали, соотношение диагоналей и т. д. Для определения стороны ромба достаточно лишь выбрать подходящую тригонометрическую функцию — косинус, тангенс и т. п. Подробнее: <a rel=»nofollow» href=»http://www.kakprosto.ru/kak-3743-kak-nayti-storony-romba#ixzz46UEQzvte» target=»_blank»>http://www.kakprosto.ru/kak-3743-kak-nayti-storony-romba#ixzz46UEQzvte</a>
touch.otvet.mail.ru
Ответы@Mail.Ru: Как найти диагональ ромба?
рассмотри треугольник и попробуй найти его стороны, может так не знаю
ПО теореме Пифагора: (d1/2)^2+(d2/2)^2=a^2 6^2+(d2/2)^2=10^2 36+(d2/2)^2=100 (d2/2)^2=100-36=64 (d2/2)=8 d2=16
сумма квадратов диагоналей = сумме квадратов сторон (это свойство) 12^2 + x ^2 = 10^2+10^2+10^2+10^2 откуда x=корень ( 400 — 144)= 16
Задача на теорему Пифагора 1. половина диагонали (меньшей) — 6см. (а) 2. Строна -10 см. (с) 3. Половина другой диагонали — (в) = корень кв. из ( с в квадрате — а в квадрате) в= корень (10*10-6*6) = 8 4. значит вся диагональ — 8*2 =16… вот и все!
Диагонали пересекаются у ромба, и точка их пересечения делит их пополам. Следовательно в прямоугольном треугольнике, у которого гипотенуза равна 10см, один катет 12/2 = 6см, то по тиореме пифагора 10*10 = 6*6+х*х, где х — второй катет, отсюда получаем что х*х = 64, то х = 8, а так как х является половиной искомой диагонали, то вся диагональ равна 2*х=2*8=16см.
по св-ву ромба его диагонали пересекаются под прямым углом и точкой пересечения делятся попалам, те у тебя прямоугольный треугольник с гипотинзой 10 и катетом 6 по т-ме Пифагора получаем другой катет 8 но это 1/2 диагонали те 8*2=16
длина искомой диоганали равна двум квадратным корням из разности -длина стороны в квадрате минус половина известной диоганали в квадрате.
touch.otvet.mail.ru
Найти углы ромба
Свойства ромба:
1. Ромб — частный случай параллелограмма
2. Противоположные стороны — параллельны
3. Все четыре стороны — равны
4. Диагонали пересекаются под прямым углом (90°)
5. Диагонали являются биссектрисами

a — сторона ромба
D — большая диагональd — меньшая диагональ
α — острый угол
β — тупой угол
Формулы косинуса углов через диагональ и сторону:

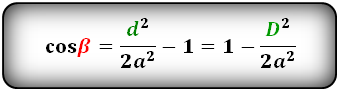
Формулы синуса углов через диагонали :
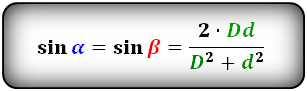
Формулы синуса углов через площадь S и сторону :
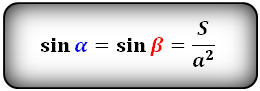
Формулы тангенса половинных углов через диагонали
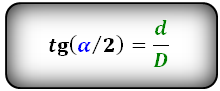
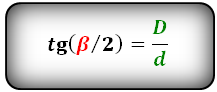
Формулы соотношения острого и тупого углов:
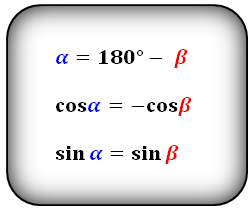
Для определения величины угла в градусах или радианах, используем функции arccos или arcsin или arctg
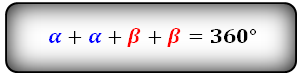
Формулы площади ромба
Формула периметра ромба
Все формулы по геометрии
- Подробности
- Автор: Administrator

www-formula.ru
