Урок алгебры в 9-м классе «Построение графика квадратичной функции, содержащей модуль»
Цели урока:
- Исследование расположения графика квадратичной функции в зависимости от модуля.
- Развитие исследовательских умений и навыков самостоятельной работы.
- Развитие умений анализировать и на основе экспериментальных данных делать выводы.
- Применение графиков функций,содержащих модуль, к решению задач.
Оборудование:
- 20 посадочных мест за ученическими компьютерами, объединенными в локальную сеть
- Компьютер учителя
- Мультимедийный проектор
- Экран
- Карточки с заданиями для работы в группах
- Электронные презентации для устной работы, выполненные в Microsoft Power Point.
- Учебник математики «Алгебра. Функции. Анализ данных.9 класс»Г.В.Дорофеев
- Учебное электронное пособие «Алгебра 7-9» ,серия «Все задачи школьной математики» («Просвещение — Медиа»), содержащее программу-графопостроитель для
План урока.
- Устная работа с использованием электронной презентации
- Практическая работа в группах за компьютерами с использованием программы-графопостроителя для Microsoft Word «НК- График»
- Отчет групп по практической работе. Демонстрация полученных графиков функций на экране .Выводы.
- Решение задач на применение графиков функций с модулем. Работа в группах за компьютерами с использованием «НК- График».
- Отчет групп по решению задач. Демонстрация результатов на экране.
- Подведение итогов урока.
Ход урока.
1. Актуализация знаний
Учитель: Знание свойств функций, умение работать с графиками помогает решать многие задачи, в том числе экзаменационные.
Внимание на экран.
(Демонстрируются слайды презентации с устными заданиями, см. Приложение 1)
2. Практическая работа.
Учитель: Каждая группа получила карточку с заданием. В ходе работы необходимо исследовать расположение графика квадратичной функции в зависимости от модуля. Результатом работы должен стать вывод о поведении графика. При анализе полученных результатов , обратите внимание на следующие моменты:
- Какая часть графика не изменилась?
- Что произошло с оставшейся частью графика?
Начать наше исследование мне хочется словами И.Гете:
«Настоящий ученик умеет выводить известное из неизвестного и этим приближаться к учителю».
(С помощью программы «НК – График» ученики строят графики на компьютерах.)
Карточки с заданиями для групп.
Группа № 1 Построение графика функции вида
Постройте на одной координатной плоскости графики функций
Ответьте на вопросы:
- Какая часть графика осталась без изменений?
- Что произошло с частью графика, расположенной в нижней полуплоскости?
Сформулируйте правило построения графика функции
- Построить график функции y =….
- Часть графика ……………………………………………..оставить без изменения
- Часть графика, расположенную в …………………………………
отобразить в ……………………………………………………….
Группа №2 Построение графика функции вида
Постройте на одной координатной плоскости графики функций
y=
Ответьте на вопросы:
- Какая часть графика осталась без изменений?
- Что произошло с частью графика, расположенной в нижней полуплоскости?
Сформулируйте правило построения графика функции
- Построить функцию………………….
- ……………………………………………………………………….
- ………………………………………………………………………
Группа № 3 Построение графика функции вида y=f()
Постройте на одной координатной плоскости графики функций
y=2x-6x+4
y=2x-6+4
Ответьте на вопросы:
- Какая часть графика осталась без изменений?
- Что произошло с частью графика, расположенной правее оси ОY?
Сформулируйте правило построения графика функции y=f()
- Построить график функции y=…….
- Часть графика, расположенную……………………………..
оставить без изменений и отобразить в …………………………
Группа № 4. Построение графика функции вида y=f()
Постройте на одной координатной плоскости графики функций
y=2x-6x+4
y=2x-6+4
Ответьте на вопросы:
- Какая часть графика осталась без изменений?
- Что произошло с частью графика , расположенной правее оси ОY?
Сформулируйте правило построения графика функции y=f()
- Построить график функции y=…….
- ……………………………………………………………………………
Группа № 5 Построение графика функции вида y=f()
Постройте на одной координатной плоскости графики функций
y=-2x+4x+1
y=-2x+4+1
Ответьте на вопросы:
- Какая часть графика осталась без изменений?
- Что произошло с частью графика , расположенной правее оси ОY?
Сформулируйте правило построения графика функции y=f()
- Построить график функции y=…….
- ……………………………………………………………………
3. Отчет групп.
Учитель: Приступаем к обсуждению результатов.
Группы №1,№2 работали с функцией вида. Результаты работы посмотрим на экране.
(Группы делают вывод о поведении графика, формулируют правило построения графика функции.Примерные результаты работы групп см. в Приложении 2)
Учитель: Группы №3,№4,№5 работали с функцией вида
(Группы №3,№4,№5 аналогично анализируют итоги своей работы)Пример результата работы одной из групп:
4. Применение графиков квадратичной функции с модулем к решению задач.
Учитель: С помощью графиков можно решать уравнения и системы уравнений .
Свободное владение техникой построения графиков помогает решать многие нестандартные задачи и порой являются единственным или наиболее простым средством их решения.
Рассмотрим некоторые такие задания.(Работа по группам за компьютерами.)
Карточки для групп с задачами.
Группа № 1
Используя график функции y= ,решите неравенства f(x)<0, f(x)>
Группа № 2
При каком значении параметра «а» уравнение = а имеет 3 корня? Решите уравнение ,используя графики функций y= и y=a.
Группа №4.
Сколько решений имеет система уравнений? (решите систему графически)
Группа № 3.
Найдите наибольшее целое значение параметра «а» , при котором прямая у=а не имеет общих точек с графиком функции y=2x -6+4
Группа № 5
Найдите наибольшее целое значение параметра «а» при котором уравнение 2x+4+1=а имеет более двух корней (при решении используйте графики функций).
5. Разбор заданий. Отчет групп.
(Результаты работ групп демонстрируются на экране, ученики каждой группы представляют решение своих задач. См. Приложение 3)
Пример решения задачи одной из групп:
6. Итог урока.
Учитель: Сегодня в ходе практической работы мы выявили способы построения графика квадратичной функции, содержащей модуль, увидели красоту этих графиков, научились анализировать и делать выводы. Мы также рассмотрели некоторые задачи на применение графиков функций.
Все группы справились с поставленной задачей.
7. Домашнее задание.
Пункт 2. пример 1, пример 2.
№ 302(в), № 303(б)
* CD- диск «Алгебра 7-9», серия «Все задачи школьной математики» («Просвещение — Медиа») № В08 (раздел «Функции и графики»).
План-конспект урока по алгебре (9 класс) по теме: Построение графиков функций, содержащих знак модуля
Тема: Построение графиков функций, содержащих знак модуля
Цели: Образовательная: обеспечить усвоение темы через осмысление ранее полученных знаний и исследовательскую деятельность учащихся, основываясь на этапах научного познания.
Развивающая: продолжать развитие проблемного мышления для решения познавательных задач; формировать представление о процессе научного познания; продолжить работу по овладению методами научного исследования.
Воспитательная: способствовать воспитанию у школьников культуры исследовательского труда, воспитанию навыков коммуникативного общения.
Формы организации учебной деятельности: фронтальная, групповая, индивидуальная.
Методы обучения: наглядно-иллюстративный, объяснительно-иллюстративный, частично-поисковый, исследовательский.
Оборудование:
- Раздаточный материал
- Мультимедийный комплекс для демонстрации презентации
Эпиграф к уроку:
«Мыслящий ум не чувствует себя счастливым, пока ему не удастся связать воедино разрозненные факты, им наблюдаемые».
Д.Хевеши
Ход урока:
- Организационный момент
Роль функций в жизни нашей неизменна,
Об этом знать должны вы непременно,
Описывать реальные процессы
Нельзя без функций в век науки и прогресса.
Наглядно представляя функций виды
Мы чертим графики, рисуем их эскизы,
И свойства функций так по ним легко читаются!
Что графики в ответ нам улыбаются…
Показ презентации «Графики улыбаются» (Приложение 1)
Вопросы учащимся:
Вы понимаете, что такие графики получаются с использованием не одной функции, а нескольких. Как называются такие функции? (кусочно-заданные функции)
- Проверка домашнего задания
Постройте и прочитайте график функции
Свойства функции:
- ;
- убывает возрастает ;
- функция ограниченная;
- функция непрерывная.
- Фронтальная работа с классом:
- Что называется областью определения функции?
- Какая функция называется возрастающей?
- Какая функция называется убывающей?
- Какая функция называется ограниченной? (функция называется ограниченной снизу, если существует такое число т, при котором для любого значения х из области определения выполняется неравенство ; функция называется ограниченной сверху, если существует такое число М, при котором для любого значения х из области определения выполняется неравенство )
- Что такое наибольшее и наименьшее значения функции? (число т называется наименьшим значением функции, если существует такая точка , что и выполняется неравенство ; число M называется наименьшим значением функции, если существует такая точка , что и выполняется неравенство )
- Что называется областью значения функции? (множество всех значений функции , называется областью значений функции)
- Какая функция называется непрерывной?
- Что такое выпуклость функции? (функцию называют выпуклой вниз (вверх), если соединив любые две точки ее графика, соответствующая часть графика лежит ниже (выше) проведенного отрезка)
А теперь обратим внимание на последние четыре графика функций.
- Знакомы ли вам функции графики, которых изображены на слайде?
- Хотели бы вы научиться строить такие графики?
Построение графиков, содержащих модуль, осуществляется двумя способами:
- На основании определения модуля
Построение графика функции
Приводится пример построения графика функции
Построение графика функции
Приводится пример построения графика функции
- На основании правил геометрического преобразования графиков функций.
Какие геометрические преобразования, можно использовать при построение графиков функций? (параллельный перенос вдоль осей ОХ и ОУ, симметричное отображение относительно осей или точки)
Формулируется цель урока.
На сегодняшнем уроке мы с вами продолжим и усовершенствуем построение графиков функций, содержащих модуль.
Внимание на эпиграф.
Сегодня вам самим придется попробовать себя в роли исследователей, сделать новые открытия.
- Групповая исследовательская работа
Класс делится на 4 группы по 5-7 человек. В каждой группе назначается консультант. Группам раздается задание и правила выполнения исследовательской работы (Приложение 2).
На экране:
Правила работы в группах:
И стину познаем, а не соревнуемся!
Д аем высказаться товарищу!
Е динство цели и задачи!
А ктивность.
Л юбознательность.
Задания группам:
I и III группы
Постройте графики функций:
II и IV группы
Постройте графики функций:
После работы учащиеся выступают перед классом, делают выводы. Полученные выводы обобщаются вместе с учителем. Учащимся раздаются правила (алгоритмы) построения графиков функции, содержащих знак модуля (Приложение 3)
- Самостоятельная работа
Учащимся предлагается выполнить разноуровневую самостоятельную работу, на четыре варианта (Приложение 4)
- Домашнее задание
Постройте графики функций. Сделайте вывод, как построить график функции , с помощью геометрических преобразований графиков.
- Подведение итогов
- Удалось ли нам углубить знания об основных свойствах функций?
- Усовершенствовали ли мы умения исследовать функции и строить графики?
- Рефлексия
Приложение 1
Презентация «ГРАФИКИ УЛЫБАЮТСЯ»
Приложение 2
ИССЛЕДОВАТЕЬСКАЯ РАБОТА
I группа
Постройте графики функций:
План исследования
Задание 1
- Постройте график функции .
Задание 2
- Используя определение модуля, запишите функцию , как кусочно-заданную.
- Постройте ее график.
- Проанализируйте, какое преобразование можно использовать при построении графика не прибегая к определению модуля?
- Сделайте вывод.
Задание 3
- Используя определение модуля, запишите функцию , как кусочно-заданную.
- Постройте ее график.
- Проанализируйте, какое преобразование можно использовать при построении графика не прибегая к определению модуля?
- Сделайте вывод.
ИССЛЕДОВАТЕЬСКАЯ РАБОТА
II группа
Постройте графики функций:
- ;
План исследования
Задание 1
- Постройте график функции .
Задание 2
- Используя определение модуля, запишите функцию , как кусочно-заданную.
- Постройте ее график.
- Проанализируйте, какое преобразование можно использовать при построении графика не прибегая к определению модуля?
- Сделайте вывод.
Задание 3
- Используя определение модуля запишите функцию , как кусочно-заданную.
- Постройте ее график.
- Проанализируйте, какое преобразование можно использовать при построении графика не прибегая к определению модуля?
- Сделайте вывод.
Приложение 3
Построение графика .
Чтобы построить график функции , если известен график функции , нужно оставить на месте ту его часть, где , и симметрично отобразить относительно оси Х другую его часть, где .
Алгоритм построения графика:
- Построить график функции ,
- Часть графика , лежащая над осью ОХ, сохраняется, а часть его, лежащая под осью ОХ, отображается симметрично относительно оси ОХ.
Построение графика .
Чтобы построить график функции , если известен график функции , нужно оставить на месте ту его часть, где , а при отразить построенную часть симметрично относительно оси ОУ.
Алгоритм построения графика:
- Построить график функции ,
- При график сохраняется, а при отражает построенную часть симметрично относительно оси ОУ.
Приложение 4
Самостоятельная работа «Построение графиков, содержащих знак модуля»
1 уровень
- Постройте график функции.
Вариант 1
Вариант 2
- Опишите его свойства.
2 уровень
- Постройте график функции.
Вариант 3
Вариант 4
- Опишите его свойства.
Приложение 4
Рефлексия урока
Ребята, мы с вами очень плодотворно поработали! Молодцы! Мне очень было приятно работать с вами! А вы не могли бы поделиться своими впечатлениями? Ответьте, пожалуйста, на вопросы рефлексии.
- Что вы узнали нового? ______________________________________________________________
- Смогли бы вы объяснить новый материал другу? _______________________
- Над чем вам надо еще поработать в данной теме? ______________________________________________________________
- Какой вопрос сегодняшнего урока был самым трудным? ______________________________________________________________
- Поставьте оценки по пятибалльной шкале за работу на уроке:
а) себе, оценив свою активность на уроке, самостоятельность, правильность выполнения заданий;
б) классу;
в) учителю.
Спасибо!
ГРАФИКИ УРАВНЕНИЙ СОДЕРЖАЩИХ МОДУЛИ
Описание презентации по отдельным слайдам:
1 слайд Описание слайда:
Описание слайда:«Построение графиков содержащих модуль». МОУ «СШ 84 с углубленным изучением английского языка» учитель математики Мамошкина Т.А. Ярославль 2016г.
2 слайд Описание слайда:
Описание слайда:Цели проекта: Изучить различные способы построения графиков с модулями. Овладеть навыками работы с компьютерной программой Advanced Grapher.
3 слайд Описание слайда:
Описание слайда:Задачи проекта: Рассмотреть понятие модуль. Познакомиться с историей происхождения понятия. Рассмотреть различные способы построения графиков с модулем: — с помощью симметрии y=|f(x)|; — по определению |y|=|f(x)|; — с помощью промежутков.
 Описание слайда:
Описание слайда:Модулем действительного числа x называется само это число, если x≥0 и противоположное число, если x<0.
5 слайд Описание слайда:
Описание слайда:Геометрически |x| означает расстояние на координатной прямой от точки, изображающей число x, до начала отсчета.
6 слайд Описание слайда:
Описание слайда:Карл Теодор Вильгельм Вейерштрасс (31 октября 1815 — 19 февраля 1897) Выдающийся немецкий математик, «отец современного анализа»… Готфрид Вильгельм Лейбниц (1 июля 1646 — 14 ноября 1716) немецкий философ, логик, математик, физик…
7 слайд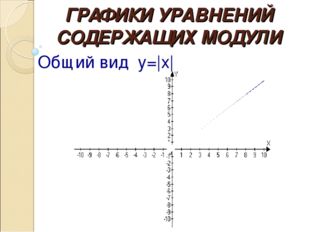 Описание слайда:
Описание слайда:ГРАФИКИ УРАВНЕНИЙ СОДЕРЖАЩИХ МОДУЛИ Общий вид y=|x|
8 слайд Описание слайда:
Описание слайда:ПЕРВЫЙ МЕТОД ПОСТРОЕНИЯ ГРАФИКОВ
9 слайд Описание слайда:
Описание слайда:Построим график функции: Y=|||x|-3|-3|
10 слайд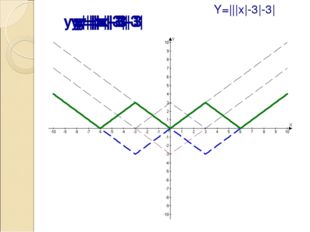 Описание слайда:
Описание слайда:y=|x| y=|x|-3 y=||x|-3| y=||x|-3|-3 y=|||x|-3|-3| Y=|||x|-3|-3|
11 слайд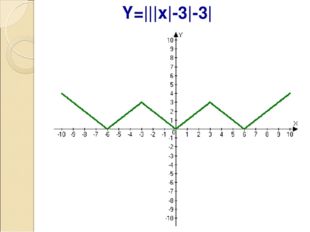 Описание слайда:
Описание слайда:Y=|||x|-3|-3|
12 слайд Описание слайда:
Описание слайда:Рассмотрим еще несколько функции построенных этим методом:
13 слайд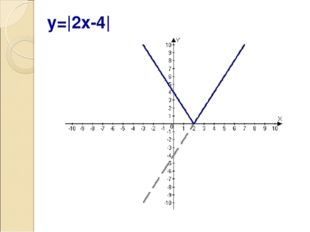 Описание слайда:
Описание слайда:y=|2x-4|
14 слайд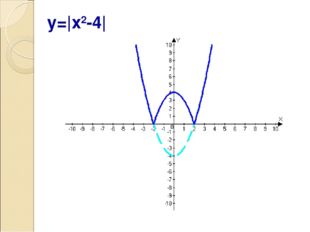 Описание слайда:
Описание слайда:y=|x2-4|
15 слайд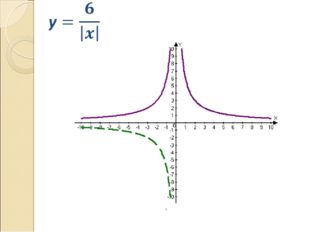 Описание слайда: 16 слайд
Описание слайда: 16 слайд 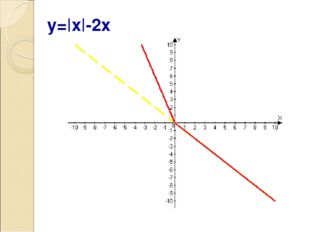 Описание слайда:
Описание слайда:y=|x|-2x
17 слайд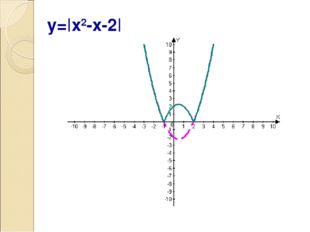 Описание слайда:
Описание слайда:y=|x2-x-2|
18 слайд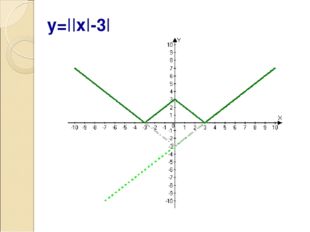 Описание слайда:
Описание слайда:y=||x|-3|
19 слайд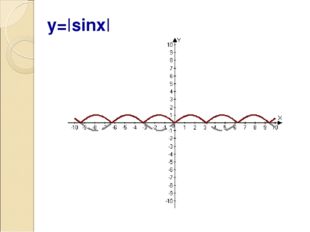 Описание слайда:
Описание слайда:y=|sinx|
20 слайд Описание слайда:
Описание слайда:ВТОРОЙ МЕТОД ПОСТРОЕНИЯ ГРАФИКОВ
21 слайд Описание слайда:
Описание слайда:Построим график функции: |y|=5-|x|
22 слайд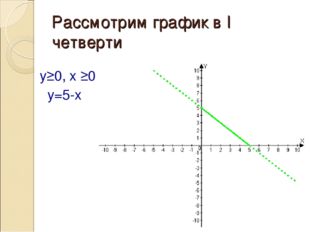 Описание слайда:
Описание слайда:Рассмотрим график в I четверти y≥0, x ≥0 y=5-x
23 слайд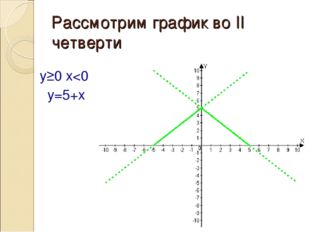 Описание слайда:
Описание слайда:Рассмотрим график вo II четверти y≥0 x<0 y=5+x
24 слайд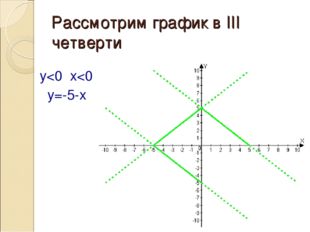 Описание слайда:
Описание слайда:Рассмотрим график в III четверти y<0 x<0 y=-5-x
25 слайд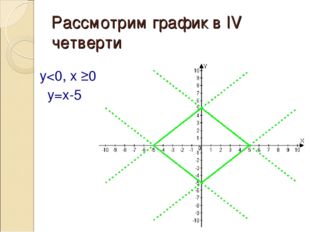 Описание слайда:
Описание слайда:Рассмотрим график в IV четверти y<0, x ≥0 y=x-5
26 слайд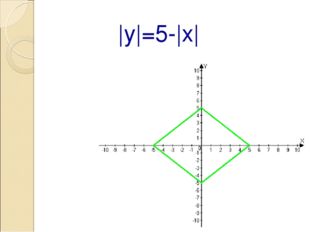 Описание слайда:
Описание слайда:|y|=5-|x|
27 слайд Описание слайда:
Описание слайда:Рассмотрим еще несколько функции построенных этим методом:
28 слайд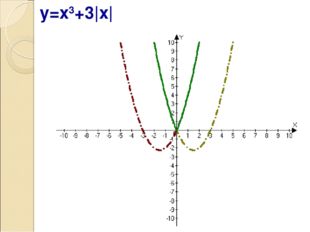 Описание слайда:
Описание слайда:y=x3+3|x|
29 слайд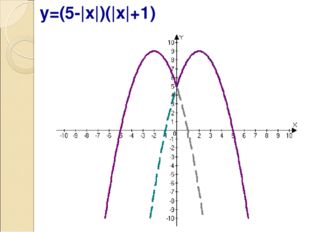 Описание слайда:
Описание слайда:y=(5-|x|)(|x|+1)
30 слайд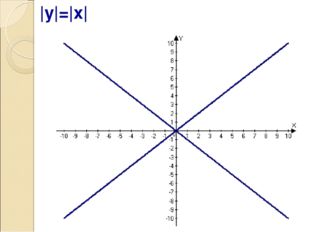 Описание слайда:
Описание слайда:|y|=|x|
31 слайд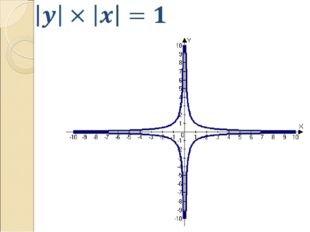 Описание слайда: 32 слайд
Описание слайда: 32 слайд 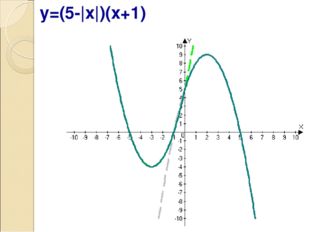 Описание слайда:
Описание слайда:y=(5-|x|)(x+1)
33 слайд Описание слайда:
Описание слайда:|y|-|x|=1
34 слайд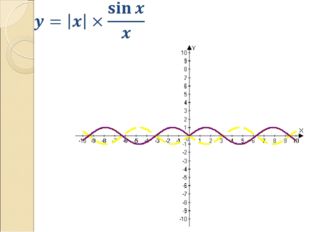 Описание слайда: 35 слайд
Описание слайда: 35 слайд  Описание слайда:
Описание слайда:ТРЕТИЙ МЕТОД ПОСТРОЕНИЯ ГРАФИКОВ
36 слайд Описание слайда:
Описание слайда:Построим график функции y=|x-2|-|x+2|
37 слайд Описание слайда:
Описание слайда:Найти корни выражений, стоящих под знаком модуля; разбить числовую прямую этими корнями на промежутки; построить график на каждом промежутке отдельно.
38 слайд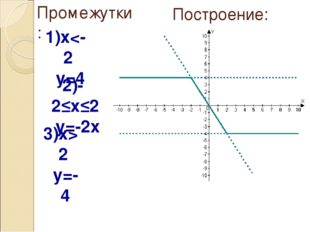 Описание слайда:
Описание слайда:Промежутки: 1)x<-2 y=4 2)-2≤x≤2 y=-2x 3)x>2 y=-4 Построение:
39 слайд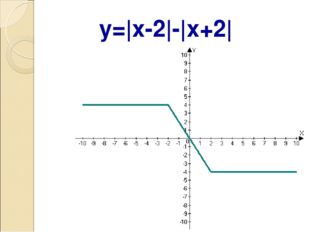 Описание слайда:
Описание слайда:y=|x-2|-|x+2|
40 слайд Описание слайда:
Описание слайда:Рассмотрим еще несколько функции построенных этим методом:
41 слайд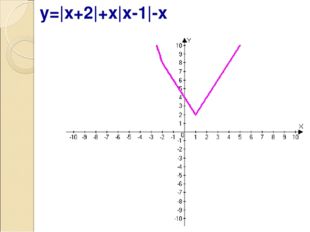 Описание слайда:
Описание слайда:y=|x+2|+x|x-1|-x
42 слайд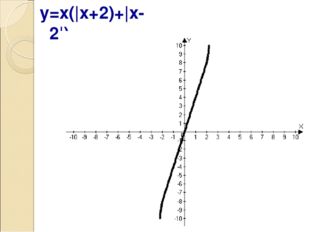 Описание слайда:
Описание слайда:y=x(|x+2)+|x-2|)
43 слайд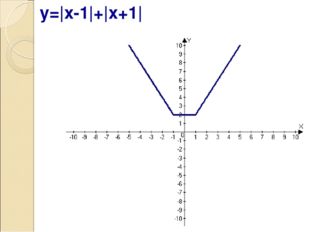 Описание слайда:
Описание слайда:y=|x-1|+|x+1|
44 слайд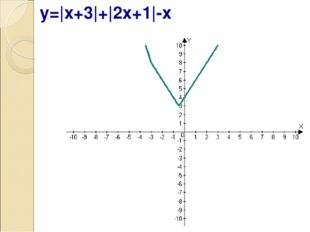 Описание слайда:
Описание слайда:y=|x+3|+|2x+1|-x
45 слайд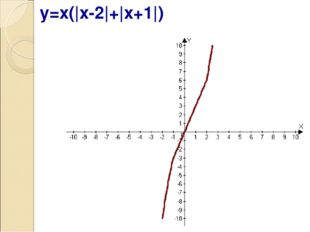 Описание слайда:
Описание слайда:y=x(|x-2|+|x+1|)
46 слайд Описание слайда:
Описание слайда:СПАСИБО ЗА ВНИМАНИЕ

Курс профессиональной переподготовки
Учитель математики

Курс повышения квалификации
Курс повышения квалификации
Найдите материал к любому уроку,
указав свой предмет (категорию), класс, учебник и тему:
Выберите категорию: Все категорииАлгебраАнглийский языкАстрономияБиологияВсеобщая историяГеографияГеометрияДиректору, завучуДоп. образованиеДошкольное образованиеЕстествознаниеИЗО, МХКИностранные языкиИнформатикаИстория РоссииКлассному руководителюКоррекционное обучениеЛитератураЛитературное чтениеЛогопедия, ДефектологияМатематикаМузыкаНачальные классыНемецкий языкОБЖОбществознаниеОкружающий мирПриродоведениеРелигиоведениеРодная литератураРодной языкРусский языкСоциальному педагогуТехнологияУкраинский языкФизикаФизическая культураФилософияФранцузский языкХимияЧерчениеШкольному психологуЭкологияДругое
Выберите класс: Все классыДошкольники1 класс2 класс3 класс4 класс5 класс6 класс7 класс8 класс9 класс10 класс11 класс
Выберите учебник: Все учебники
Выберите тему: Все темы
также Вы можете выбрать тип материала:

Общая информация
Номер материала: ДБ-1124884
Похожие материалы
Вам будут интересны эти курсы:
Оставьте свой комментарийУрок по теме «Построение графиков квадратичной функции с модулем»
Инфоурок › Алгебра ›Презентации›Урок по теме «Построение графиков квадратичной функции с модулем»Описание презентации по отдельным слайдам:
1 слайд Описание слайда:
Описание слайда:Быкасов Андрей Иванович, учитель математики НОУ «Нефтеюганская православная гимназия», г.Нефтеюганск, Тюменская область Урок по теме «Построение графиков квадратичной функции с модулем» Учебник А.Г.Мордкович, базовый уровень, 4-й урок темы «Функция y = ax2 + bx + c, ее свойства и график»
2 слайд Описание слайда:
Описание слайда:Тема : «Построение графиков квадратичной функции с модулем » Цель: обобщить знание свойств квадратичной функции и научить применять свойства квадратичной функции при построении графиков квадратичной функции с модулем Задачи: Выявить степень сформированности у учащихся понятия квадратичной функции, её свойств, особенностей её графика. Создать условия для формирования умения анализировать, сравнивать, классифицировать графики изученных функций. Продолжить развитие умения построения графиков квадратичной функции с модулем, используя программу AGrapher. Формировать умение сотрудничать, работая в группе. Оборудование: проектор, экран, 4 компьютера, программа AGrapher.
3 слайд Описание слайда:
Описание слайда:Этапы урока Организационный Мотивация к учебной деятельности. Актуализация знаний и фиксация затруднения в пробном действии (работа с графиками функций). Выявление места и причины затруднения. Построение проекта выхода из затруднения. Реализация построенного проекта. Самостоятельная работа с самопроверкой по эталону. Включение в систему знаний и повторение. Рефлексия учебной деятельности. Оценивание работы на уроке. Домашнее задание.
4 слайд Описание слайда:
Описание слайда:1. Организационный На перемене дети садятся по группам. Группы формируются на добровольной основе, консультант группы определяется учителем. Каждой группе выдаются листы контроля результатов деятельности. Здравствуйте, ребята! Я рада сегодня вас видеть и очень надеюсь на совместную плодотворную работу. Сегодня мы работаем в группах. В каждой группе мною был назначен консультант, который поможет мне оценить в конце урока каждого из вас. В течение всего урока мы будем накапливать баллы: за каждый правильный, точный и логичный ответ Вы будете получать «+» в таблице, лежащей на вашем столе. Здесь мне будет нужна помощь консультантов. В конце урока мы просуммируем «+» и поставим отметки в зависимости от их количества: более 8 «+»- «5» 6-7 «+»- «4» 4-5 «+»- «3».
5 слайд Описание слайда:
Описание слайда:2. Мотивация к учебной деятельности . Задача этапа: Создать условия для возникновения у ученика внутренней потребности включения в учебную деятельность. Если вы хотите научиться плавать, то смело входите в воду, а если хотите научиться решать задачи, то решайте их! Дьёрдь Пойя Сегодня нам предстоит решение многих задач, вы видите, как можно научится их решению по мнению известного венгерского математика Д.Пойя. Согласны ли вы, что такой подход применим и к нашему уроку?(Да) Для начала предлагаю вспомнить, что мы знаем о функциях.
6 слайд Описание слайда:
Описание слайда:3. Актуализация знаний и фиксация затруднения в пробном действии. 1 группа 2. 1Актуализация знаний и фиксация з1атруднения в пр№1обном действии. 2 группа Постройте графики функций: №1 №2 №3 №4. 3 группа Постройте графики функций: №1. №2. №3. №4. 4 группа №1 №3 №2 №4 За каждое выполненное задание, консультант выставляет «+» в лист контроля (максимум 4 балла) Запишите формулы и названия функций, которые вы видите на графиках.(Каждые 2 правильно записанные формулы оцениваются «+», максимум 4 балла). Постройте графики функций:
7 слайд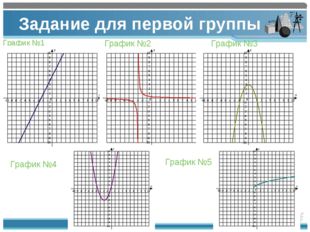 Описание слайда:
Описание слайда:Задание для первой группы График №1 График №2 График №3 График №4 График №5
8 слайд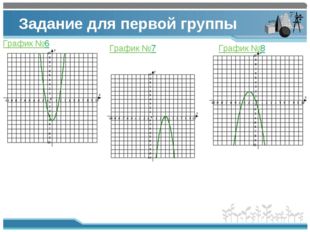 Описание слайда:
Описание слайда:Задание для первой группы График №6 График №7 График №8
9 слайд Описание слайда:
Описание слайда:Проверка 1группа №1 №2 №3 №4 №5 №6 №7 №8 За каждое правильно выполненные 2 задания, консультант выставляет «+» в лист контроля
10 слайд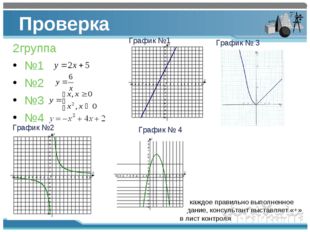 Описание слайда:
Описание слайда:Проверка 2группа №1 №2 №3 №4 График №2 График №1 График № 3 График № 4 За каждое правильно выполненное задание, консультант выставляет «+» в лист контроля
11 слайд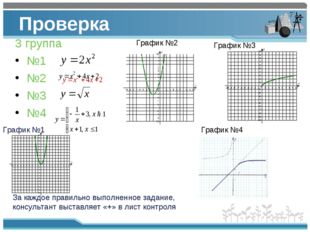 Описание слайда:
Описание слайда:Проверка 3 группа №1 №2 №3 №4 За каждое правильно выполненное задание, консультант выставляет «+» в лист контроля График №1 График №2 График №3 График №4
12 слайд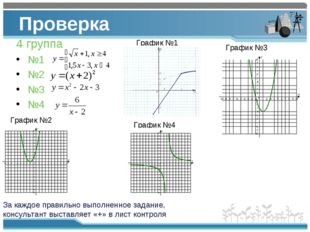 Описание слайда:
Описание слайда:Проверка 4 группа №1 №2 №3 №4 За каждое правильно выполненное задание, консультант выставляет «+» в лист контроля График №1 График №2 График №4 График №3
13 слайд Описание слайда:
Описание слайда:3. Актуализация знаний и фиксация затруднения в пробном действии. Повторим определение модуля Как получаем из функции можно получить функцию ? Постройте графики функций За каждое правильно выполненное задание, консультант выставляет «+» в лист контроля
14 слайд Описание слайда:
Описание слайда:3. Актуализация знаний и фиксация затруднения в пробном действии. 1. Организовать актуализацию изученных способов действий, достаточных для построения нового знания. 2. Зафиксировать актуализированные способы действий в речи. 3. Зафиксировать актуализированные способы действий в знаках (эталонах). Графики каких функций вам знакомы?(линейная, прямой и обратной пропорциональности, квадратичная, у = ) Как по графику определить вид функции и её формулу? (уметь пользоваться правилами параллельных переносов вдоль осей Ох,Оу, уметь определять коэффициенты, оси симметрии и асимптоты) Формулы для каких графиков функций вы не смогли определить? Почему? (последние формулы видим впервые, поэтому не можем определить вид функции и как строить графики) Давайте попробуем сформулировать цель нашего урока. (Научиться строить графики нового вида, научиться узнавать их среди других графиков функций, описывать их свойства.) А я добавлю к вашей цели еще одну: обобщить знание свойств квадратичной функции и научиться применять свойства квадратичной функции в построении графиков с модулем.
15 слайд Описание слайда:
Описание слайда:«Построение графиков квадратичной функции с модулем» Тема урока
16 слайд Описание слайда:
Описание слайда:4.Построение проекта выхода из затруднения. Построим графики квадратичных функций с модулем Выполнив практическую работу, сделаем вывод о свойствах графика и
17 слайд Описание слайда:
Описание слайда:5.Реализация построенного проекта. 1.Организовать построение нового способа на примере, вызвавшем затруднение. 2.Организовать фиксацию нового способа действия в речи и с помощью эталона. 3. Зафиксировать преодоление возникшего ранее затруднения. Каждой группе предлагается построить график одной функции в программе AGrapher, описать её свойства по алгоритму: 1 2
18 слайд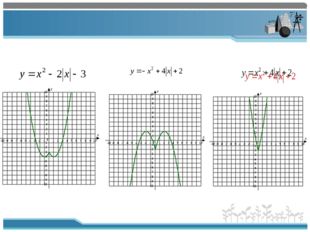 Описание слайда: 19 слайд
Описание слайда: 19 слайд 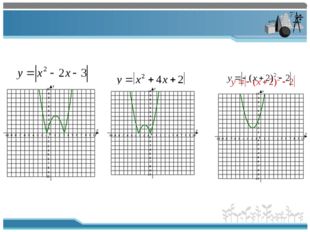 Описание слайда: 20 слайд
Описание слайда: 20 слайд  Описание слайда:
Описание слайда:6.Организовать фиксацию нового способа действия в речи и с помощью эталона. а) Давайте обобщим способы построения графиков функций, в которых выражение, задающее функцию, находится под знаком модуля, в единый алгоритм (строим график функции без модуля, потом часть графика, находящаяся ниже оси Ох, отображается в верхнюю полуплоскость) б) Давайте обобщим способы построения графиков функций, в которых аргумент находится под знаком модуля, в единый алгоритм.(строим график функции без модуля, потом часть графика, находящаяся правее оси Оу, отображается в левую полуплоскость) На основании какого математического понятия мы получаем эти новые способы действия? (На основании определения модуля выражения) Сравним полученный нами алгоритм с эталоном. За каждый правильный ответ, консультант выставляет «+» в лист контроля.
21 слайд Описание слайда:
Описание слайда:6. Алгоритм построения графика квадратичной функции вида (эталон) 1.Строим график функции у = f(х). 2.Часть графика, для которой, значения функции положительны — оставляем без изменения. 3.Часть графика, для которой, значения функции отрицательны – зеркально отображаем в верхнюю полуплоскость.
22 слайд Описание слайда:
Описание слайда:Алгоритм построения графика квадратичной функции вида (эталон) 1.Строим график функции у = f(х). 2.Часть графика, для которой, значения аргумента положительны — оставляем без изменения. 3.Часть графика, для которой, значения аргумента положительны – зеркально отображаем в левую полуплоскость.
23 слайд Описание слайда:
Описание слайда:7. Самостоятельная работа с самопроверкой по эталону. Каждой группе выдается задание на построение графиков функций За правильно выполненное задание, консультант выставляет «+» в лист контроля 1 группа 4 группа 3 группа 2 группа
24 слайд Описание слайда:
Описание слайда:8.Включение в систему знаний и повторение. Как построить график квадратичной функции с модулем.(проговаривают алгоритмы) Графики каких функций мы можем построить с учетом нового знания, полученного сегодня на уроке? (перечисляют функции)
25 слайд Описание слайда:
Описание слайда:8.Включение в систему знаний и повторение. 1 2 3 4 5 Построить графики функций
26 слайд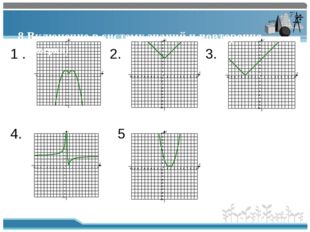 Описание слайда:
Описание слайда:1 . 2. 3. 4. 5. 8.Включение в систему знаний и повторение. (проверка)
27 слайд Описание слайда:
Описание слайда:9. Подведение итогов, рефлексия Просуммируем «+» и поставим отметки в зависимости от их количества: более 8 «+» — «5» 6-7 «+» — «4» 4-5 «+» — «3». 1. Затрудняюсь в построении графика без помощи алгоритма 2. Могу построить строить графики функций с модулями 3. Я все понял и могу объяснить другим В листе контроля укажите, как вы оцениваете свои достижения поставленных целей на этом уроке
28 слайд Описание слайда:
Описание слайда:10. Домашнее задание 3. Я все понял и могу объяснить другим 2. Могу построить строить графики функций с модулями 1. Затрудняюсь в построении графика без помощи алгоритма Выучить определение модуля. Построить графики функций:
29 слайд Описание слайда:
Описание слайда:Самоанализ урока Тема урока. «Построение графиков квадратичной функции с модулем». Цель урока: обобщить знание свойств квадратичной функции и научить применять её свойства в построении графиков квадратичной функции с модулем. Урок четвертый в теме «Функция y = ax2 + bx + c, ее свойства и график». Цель урока реализовывалась через формирование у учащихся умения анализировать графики функций и делать выводы. Урок построен в деятельностной технологии обучения. Обучающиеся знают ряд функций (линейная, обратной пропорциональности, квадратичная, ) умеют определять формулу по графику, умеют строить график, зная формулу. В ходе урока учащиеся углубляют и расширяют знания о функциях. Учатся обобщать полученные знания и применять их в новых ситуациях. Выполняют исследование свойств графиков с модулем на компьютере при помощи программы AGrapher. Задачи урока были выполнены в ходе организации деятельности учащихся через исследование, сравнение, обобщение графиков различных квадратичных функций с модулем. Для решения задач урока использовала различные формы и методы работы, обучающиеся выполняли самостоятельную работу в группах, выступали с выводами, обобщали знания о функциях. На этапах выявления места и причины затруднений и реализации построенного проекта самостоятельная работа способствовала пониманию как строятся графики функций содержащих модуль Задачи урока соответствуют особенностям учебного материала.
30 слайд Описание слайда:
Описание слайда:Самоанализ урока Содержание учебного материала учитывает возрастные особенности обучающихся и способствует формированию у школьников компетенций: учебно-познавательных: обучающиеся формулировали цель урока; выбирали основание для сравнения и обобщения , делали выводы; оценивали свою работу. коммуникативных: приобретали навыки общения, аргументировали свои выводы; выступали с устными комментариями; информационных: извлекали необходимую информацию, работая с программой для построения графиков функций, работали над созданием алгоритма построения графиков квадратичной функции с модулем; Ведущими методами на уроке были частично-поисковый, исследовательский методы. Учащиеся были активны на уроке, работоспособны на всех этапах. Домашняя работа предложена дифференцированно с учетом уровня усвоения материала и самооценки учащегося. Считаю, что все используемые на уроке методы, формы, приемы, средства способствовали достижению цели урока. Цель урока реализована: дети научились строить графики квадратичной функции с модулем и описывать её свойства.

Курс профессиональной переподготовки
Учитель математики

Курс повышения квалификации
Курс повышения квалификации
Найдите материал к любому уроку,
указав свой предмет (категорию), класс, учебник и тему:
Выберите категорию: Все категорииАлгебраАнглийский языкАстрономияБиологияВсеобщая историяГеографияГеометрияДиректору, завучуДоп. образованиеДошкольное образованиеЕстествознаниеИЗО, МХКИностранные языкиИнформатикаИстория РоссииКлассному руководителюКоррекционное обучениеЛитератураЛитературное чтениеЛогопедия, ДефектологияМатематикаМузыкаНачальные классыНемецкий языкОБЖОбществознаниеОкружающий мирПриродоведениеРелигиоведениеРодная литератураРодной языкРусский языкСоциальному педагогуТехнологияУкраинский языкФизикаФизическая культураФилософияФранцузский языкХимияЧерчениеШкольному психологуЭкологияДругое
Выберите класс: Все классыДошкольники1 класс2 класс3 класс4 класс5 класс6 класс7 класс8 класс9 класс10 класс11 класс
Выберите учебник: Все учебники
Выберите тему: Все темы
также Вы можете выбрать тип материала:

Общая информация
Номер материала: ДБ-166951
Похожие материалы
Вам будут интересны эти курсы:
Оставьте свой комментарий