Сечение цилиндра плоскостью | Начертательная геометрия
Сечение цилиндра плоскостью,
Сечение цилиндра плоскостью
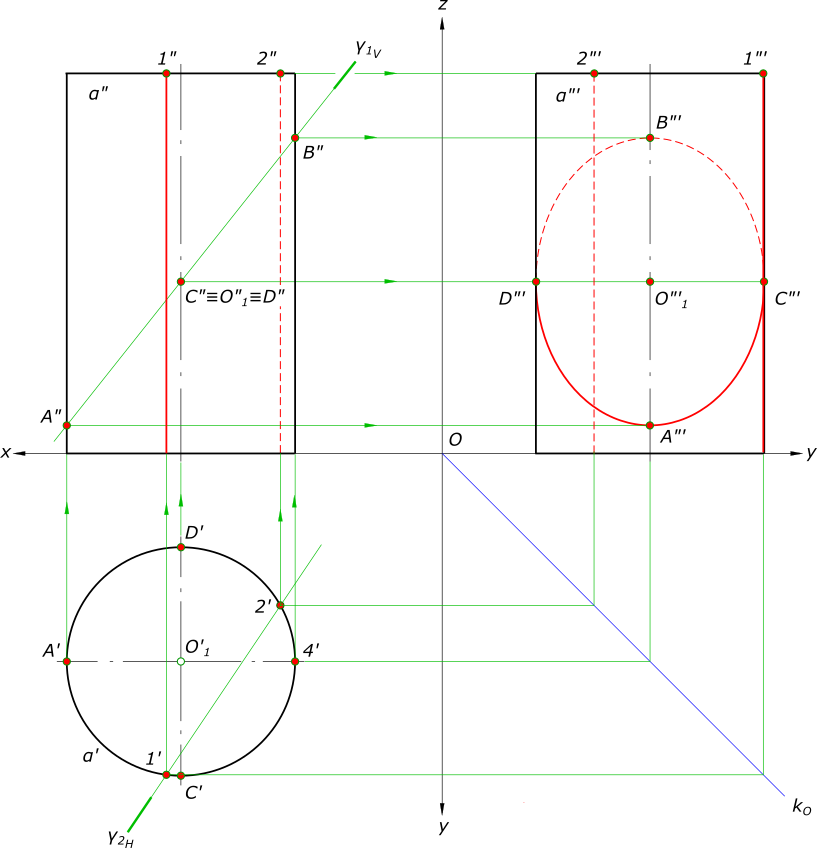
если пересекаются все образующие (Y1), представляет плоскую кривую второго порядка — окружность или эллипс, принадлежащую секущей плоскости. В частом случае, при определенном расположении секущей плоскости (Y2), когда она проходит через две образующие, сечение цилиндра представляет собой прямоугольник
Сечение прямого кругового цилиндра дает — окружность, когда секущая плоскость перпендикулярна к его оси и пересекает все образующие поверхности.
Построение третьей проекции линии сечения цилиндра плоскостью по двум заданным представлено на рисунке. Здесь сечение прямого кругового цилиндра — эллипс с большой осью AB и малой осью CD, когда секущая плоскость не перпендикулярна к его оси и пересекает все образующие поверхности.
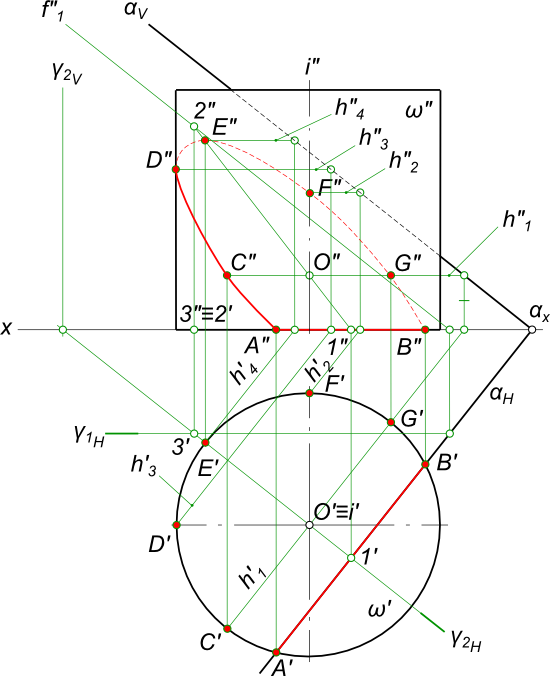
Построим эллиптическое сечение прямого кругового цилиндра ω плоскостью α, занимающей общее положение
Сечение цилиндра плоскостью
Решение задачи на сечение прямого кругового цилиндра плоскостью, в данном случае значительно упрощается потому, образующие цилиндра занимают проецирующее положение: — проекции точек A и B линии пересечения находим без каких-либо дополнительных построений в пересечении окружности основания цилиндра и горизонтального следа αΗ секущей плоскости; — горизонтальные проекции остальных точек линии пересечения находятся на окружности основания цилиндра левее горизонтального следа αΗ. Задавая горизонтальные проекции ряда точек, в том числе и характерных точек кривой линии пересечения — точки D это граница видимости и E это наивысшая, находим их недостающие фронтальные проекции из условия принадлежности плоскости α: — проводим через точки горизонтали плоскости h2, h3, h4 и h5 и в пересечении их с линиями связи точек находим фронтальные проекции C», D», E», F» и G». — проекции A», B», C», D», E», F» и G» соединяем плавной кривой линией и получаем недостающую фронтальную проекцию линии пересечения.
Определение видимости линии пересечения и цилиндра на плоскости проекций выполняем с использованием конкурирующих точек.
+
Развертка усеченного цилиндра построение | МеханикИнфо
Развертка усеченного цилиндра. Построение развертки цилиндра. 4.38/5 (87.50%) проголосовало 8

Проекция цилиндра, срезанного плоскостью, наклонной к плоскости чертежа, по вертикальной плоскости проекции дает прямую линию, на горизонтальной — окружность, на профильной плоскости — замкнутую кривую, эллипс в искаженном виде.
Если представить себе цилиндр, срезанный плоскостью KS (рис. 1, а), параллельной основанию и проходящей через низшую точку наклонного среза 1, то нижняя часть такого цилиндра развернется в прямоугольник A1K1S1B1 (рис. 1, б) с высотой h = BS и основанием А1В1 = πD.

Рис. 1. Развертка усеченного цилиндра:
а — проекция; б — развертка.
Развертка верхней части цилиндра.
Чтобы получить развертку верхней части цилиндра выше плоскости KS, поступают следующим образом. Окружность основания делится на несколько равных частей, в приведенном примере на- восемь равных частей. Точки делений проектируют на вертикальную проекцию и проводят соответствующие образующие цилиндра 11 — 1′; 21 — 2″ и т. д. Затем делят длину развернутой окружности основания на такое же число равных частей, и из точек делений восстанавливают перпендикуляры, которые будут представлять собой те же образующие цилиндра, на которых затем нужно отложить их длины, измеряя одноименные отрезки на вертикальных проекциях (рис. 1, б). Соединив плавной кривой полученные точки, будем иметь развертку боковой поверхности усеченного цилиндра.
Для определения действительной формы поперечного сечения наклонной поверхности цилиндра вводят дополнительную плоскость проекции, параллельную плоскости сечения, на которой форма сечения спроектируется в искаженном виде — в форме эллипса.
Построение сечения цилиндра.
Для построения сечения на дополнительной плоскости проведем линию, параллельную проекции плоскости сечения, и, спроектировав на нее точки 1″ и 5″ с вертикальной проекции, получим большую ось эллипса. Затем из точки 7″ — 3″ на вертикальной проекции проведем линию, перпендикулярную большой оси эллипса, и, отложив на ней вправо и влево от большой оси отрезки 03″ и 07″, равные радиусу основания цилиндра, получим малую ось эллипса 3″ — 7″.
Положение остальных точек 2″, 4″, 6″, 8″ определяется так: на перпендикулярах к большей оси, проведенных из точек 8″ — 2″ и 6″ — 4″ вертикальной проекции, откладываем отрезки m от большей оси эллипса. Плавная кривая, проведенная через полученные восемь точек, будет эллипсом.
Построение эллипса на профильной проекции видно из рис. 1, а.
Для получения полной развертки поверхности цилиндра следует добавить поверхности наклонного сечения и нижнего основания цилиндра, как указано на рис. 1, б.
Непростая задача о площади сечения цилиндра, которая может ввести в заблуждение.
Диаметр основания цилиндра равен 8, а длина его образующей –  . На окружности верхнего основания цилиндра выбраны точки F и D, делящие окружность на две дуги, длины которых относятся как 1:2. Найдите площадь сечения цилиндра плоскостью, проходящей через точки F, D и центр нижнего основания.
. На окружности верхнего основания цилиндра выбраны точки F и D, делящие окружность на две дуги, длины которых относятся как 1:2. Найдите площадь сечения цилиндра плоскостью, проходящей через точки F, D и центр нижнего основания.
На первый взгляд – задача простая. Кажется, что сечение – трапеция, нижнее ее основание – диаметр цилиндра, найти длину верхнего основания вполне можно, также возможно отыскать высоту трапеции и – дело в шляпе. Однако..
Однако надо помнить, что сечение цилиндра наклонной плоскостью – всегда эллипс или его часть!

Сечения цилиндра
Посмотрим на различные сечения цилиндра плоскостями:
Наш случай приблизительно такой:

Сечение цилиндра неосевой плоскостью
И еще нам потребуется знать, какой будет проекция этого сечения на основание цилиндра:

Проекция сечения

Проекция – вид сверху
Все дело в том, что рассчитать непосредственно площадь сечения трудно из-за сложности его формы, поэтому воспользуемся тем, что
Площадь проекции плоской фигуры равна произведению площади этой фигуры на косинус угла между плоскостью фигуры и плоскостью проекции.

Проекция – вид сверху
Определить площадь проекции будет несложно, давайте это сделаем. Проекция будет представлять собой часть полукруга, которую можно разбить на два круговых сектора и треугольник. Нам известно, что длины дуг относятся как 1:2, значит, меньшая дуга имеет градусную меру  , и ей соответствует центральный угол с такой же градусной мерой, который является одним из углов треугольника FDC. Тогда, поскольку треугольник этот – равнобедренный, то два его острых угла равны
, и ей соответствует центральный угол с такой же градусной мерой, который является одним из углов треугольника FDC. Тогда, поскольку треугольник этот – равнобедренный, то два его острых угла равны 
 лежит катет, вдвое меньший гипотенузы). Определим основание треугольника FDC, для этого найдем его половину по теореме Пифагора:
лежит катет, вдвое меньший гипотенузы). Определим основание треугольника FDC, для этого найдем его половину по теореме Пифагора:  , где FC – радиус цилиндра, FC=4,
, где FC – радиус цилиндра, FC=4, 



Площадь треугольника FDC равна половине произведения основания на высоту:

Кроме треугольника FDC в состав площади проекции сечения входят еще два круговых сектора, центральные углы которых равны 30 , то есть площадь каждого из них – 1/12 часть круга, а вместе их площадь – 1/6 часть круга, или
, то есть площадь каждого из них – 1/12 часть круга, а вместе их площадь – 1/6 часть круга, или  . Площадь проекции:
. Площадь проекции:  .
.
Осталось определить  . Сделаем еще рисунок:
. Сделаем еще рисунок:
Найдем высоту сечения, это гипотенуза треугольника KGO, KO:  . В этом выражении нам все известно: KG – это высота
. В этом выражении нам все известно: KG – это высота  – h, а GO – это образующая цилиндра, его высота. Тогда
– h, а GO – это образующая цилиндра, его высота. Тогда

Косинус нужного угла – отношение прилежащего катета к длине гипотенузы:

Сечение. Вид сбоку

Тогда искомая площадь:

Урок геометрии в 11-м классе на тему «Сечение цилиндра плоскостями»
Цели и задачи урока:
- Используя электронный учебник познакомить учащихся с сечением, рассмотреть виды сечений. Сформировать у учащихся умения и навыки построения сечения.
- Развивать: образное мышление, память, речь.
- Воспитывать: интерес к предмету, самостоятельность, аккуратность.
Оборудование: урок проходит в компьютерном классе, с использованием электронного учебника: Уроки геометрии Кирилла и Мефодия 2006г. 11 класс, карточки шаблоны (приложение4), карточки с задачами (приложение3)
Содержание урока:
- Организационный момент (2-3 мин)
- Повторение: (фронтальный опрос 5мин)
- Объяснение нового материала: ввести понятие сечения, рассмотреть виды сечения (презентация в РР 10 мин) (приложение1)
- С помощью электронного учебника сделать вывод (самостоятельная работа 10мин)
- Работа с доской построение сечений: осевое, косое, параллельное его оси, перпендикулярное его оси и решение задач.(8мин)
- Итог урока: тест (проверка знаний 5 мин) (приложение2)
- Домашнее задание: п.53, з.3,4, Постройте сечение цилиндра имеющего форму квадрата. (2 мин)
Ход урока
1. Повторение: проверка усвоения материала
Вопросы:
- Объясните что такое круговой цилиндр (образующая цилиндра, основания и боковая поверхность цилиндра)
- Какой цилиндр называется прямым?
- Что такое радиус цилиндра
- Что такое высота цилиндра
- Что такое ось цилиндра
2. Объяснение нового материала: ввести
понятие сечения, рассмотреть виды сечения (презентация
в РР 15 мин) (приложение1)
3. Электронный учебник: Уроки геометрии
Кирилла и Мефодия 2006г
Расположение в электронном учебнике (адрес)
Выбор урока —> округлые тела —> цилиндр —> содержание урока —> 17,18,19,20.22,28,29,23,34,35.
4. С помощью электронного учебника сделать вывод (самостоятельная работа 10 мин)
Вывод 1:
Теорема: (о сечении цилиндра плоскостью, параллельной основаниям)
Сечение цилиндра плоскостью, параллельной основаниям, есть круг того же радиуса, что основания.
Вывод 2:
Теорема: (о сечении цилиндра плоскостью, перпендикулярной основаниям)
Сечение цилиндра плоскостью, проходящей через его ось или параллельной этой оси, есть прямоугольник.
Вывод 3:
Линия пересечения плоскости с цилиндрической поверхностью — это овал, полученный путем сжатия или растяжения окружности, в математике такая поверхность называется эллипсом. Эллипс имеет центр симметрии и две взаимно перпендикулярные оси симметрии. Отрезки этих осей симметрии, заключенные внутри эллипса, называются большой и малой осями эллипса.
5. Работа с доской построение сечений:
- Осевое, косое, параллельное его оси, перпендикулярное его оси. (4 человека у доски строят сечения),
- Остальные ребята строят на готовых шаблонах все четыре сечения. (приложение4)
- Сильные ребята решают задачи (самостоятельно) на нахождения площади сечения (приложение3)
6. Итог урока: тест (проверка знаний 5 мин) (приложение2)
7. Домашнее задание: п.53, з.3,4, Творческое задание: постройте сечение цилиндра имеющего форму квадрата, как вы думаете, будет называться этот цилиндр?