Ответ: \([-1,5; +∞)\)
Пример 2. Решить неравенство \(\left|3+2x\right|\le \:7\). Система
Решение. \(\left|3+2x\right|\le \:7\) \(—>\) \(3+2x\le \:7\) и \(3+2x\ge \:-7\) или \(-7\le \:3+2x\le \:7\)
\(x\le \:2\) и \(x\ge \:-5\) \(-5\le \:x\le \:2\)
Ответ: [-5;2];
Пример 3. Решить неравенство \(\left|3x-5\right|<\:4\)
Решение: \(-4<3x-5<4\) \(—>\) \(\frac{1}{3}<x<3\)
Ответ: \((\frac{1}{3};3)\);
Пример 4. Решить неравенство \(\left|x-8\right|\ge \:\:3\)
Решение: Совокупность \(\) \(\left[ \begin{gathered} x-8\le \:-3\\ x-8\ge \:3 \\ \end{gathered} \right.\) \(—>\) \(\left[ \begin{gathered} x\le \:5\\ x\ge \:11 \\ \end{gathered} \right.
Ответ: \((+∞;5)⋃ (11;+∞)\)
Больше уроков и заданий по математике вместе с преподавателями нашей онлайн-школы «Альфа». Запишитесь на пробное занятие уже сейчас!
Запишитесь на бесплатное тестирование знаний!
Наши преподаватели
Оставить заявку Репетитор по математикеБелорусский государственный университет
Проведенных занятий:
Дистанционно (Скайп)
Репетитор 5-9 классов. Люблю математику, потому что она логична и красива, она приносит удовольствие и развивает ум, ее нельзя переписать, например, как историю. Хочу, чтобы дети не боялись ее и полюбили, как я. Когда у ребенка начинает получаться, он становится счастливее. Сделать счастливее ваших детей — это моя главная задача!
Люблю математику, потому что она логична и красива, она приносит удовольствие и развивает ум, ее нельзя переписать, например, как историю. Хочу, чтобы дети не боялись ее и полюбили, как я. Когда у ребенка начинает получаться, он становится счастливее. Сделать счастливее ваших детей — это моя главная задача!
Репетитор по математике
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Репетитор 5-9 классов. Решая задачи мы учимся грамотно и четко формулировать мысли, делать верные логические выводы. На своих уроках, в большинстве случаев, я использую методику проблемного изложения материала. На мой взгляд, проблемное обучение лучше всего обеспечивает развитие мыслительных способностей. Я использую все возможности учебного материала для того, чтобы заинтересовать учеников, активизировать самостоятельное мышление.
Решая задачи мы учимся грамотно и четко формулировать мысли, делать верные логические выводы. На своих уроках, в большинстве случаев, я использую методику проблемного изложения материала. На мой взгляд, проблемное обучение лучше всего обеспечивает развитие мыслительных способностей. Я использую все возможности учебного материала для того, чтобы заинтересовать учеников, активизировать самостоятельное мышление.
Благовещенский государственный педагогический институт
Проведенных занятий:Форма обучения:
Дистанционно (Скайп)
 Всегда готова поделиться знаниями! Считаю, что учить наизусть скучные правила необязательно. Главное — понимать что и как, тогда ученик и без скучных заучиваний сможет свободно сформулировать любое правило, а полученные знания будут прочными и навсегда.
Готовлю к ОГЭ и ЕГЭ, мои ученики показывают хорошие и отличные результаты на экзаменах.
На уроках придерживаюсь трех единств: наглядно, понятно, просто.
Всегда готова поделиться знаниями! Считаю, что учить наизусть скучные правила необязательно. Главное — понимать что и как, тогда ученик и без скучных заучиваний сможет свободно сформулировать любое правило, а полученные знания будут прочными и навсегда.
Готовлю к ОГЭ и ЕГЭ, мои ученики показывают хорошие и отличные результаты на экзаменах.
На уроках придерживаюсь трех единств: наглядно, понятно, просто.
Похожие статьи
Записаться на бесплатный урок
Раскрытие модуля, используя его геометрический смысл с примером решения
Раскрытие модуля, используя его геометрический смыслПусть — действительные числа. Тогда выражение имеет геометрический смысл расстояния на числовой прямой от точки с координатой до точки с координатой . Геометрическую интерпретацию модуля как расстояния бывает достаточно удобно использовать при решении некоторых уравнений и неравенств с модулями.
Тогда выражение имеет геометрический смысл расстояния на числовой прямой от точки с координатой до точки с координатой . Геометрическую интерпретацию модуля как расстояния бывает достаточно удобно использовать при решении некоторых уравнений и неравенств с модулями.
Например, решить уравнение геометрически означает найти на числовой прямой все точки , расположенные от точки 3 на расстоянии 1. Представим себе числовую прямую, отметим на ней точку, отвечающую числу 3, и отложим в обе стороны от неё единичные отрезки. Получим две точки, координаты которых и будут искомыми решениями уравнения.
Другой пример. Пусть требуется решить неравенство Это означает, что надо найти на числовой прямой все точки, отстоящие от точки 3 на расстояние, меньшее  Тогда искомые точки образуют интервал с центром в точке 3 длины 2, т.е. . Таким же образом можно решить неравенства и многие другие.
Тогда искомые точки образуют интервал с центром в точке 3 длины 2, т.е. . Таким же образом можно решить неравенства и многие другие.
Рассмотрим теперь более сложный пример.
Пример №273.Решить неравенство
Решение:
Так как , то перенесём все слагаемые в левую часть и разложим её на множители
Решим последнее неравенство, привлекая геометрический смысл модуля. Представим числовую прямую и на ней точки — 1 и 2 .
Решить неравенство означает найти на числовой прямой такие точки , что модуль разности расстояний от до точек — 1 и 2 не меньше 3 . Заметим, что расстояние между этими точками в точности равно 3 . Если точка то сумма расстояний от неё до — 1 и 2 равна 3 , а соответствующая разность расстояний будет меньше 3, т. е. неравенство не выполняется. Если же то модуль разности расстояний от до — 1 и 2 будет равен 3, т.е. неравенство верно. Таким образом, получаем ответ:
е. неравенство не выполняется. Если же то модуль разности расстояний от до — 1 и 2 будет равен 3, т.е. неравенство верно. Таким образом, получаем ответ:
Эта лекция взята со страницы, где размещён подробный курс лекций по предмету математика:
Предмет математика
Эти страницы возможно вам будут полезны:
Уравнения и неравенства содержащие знак модуля с примерами решения
Содержание:
Уравнения и неравенства, содержащие знак модуляОбъяснение и обоснование:
Решать любое уравнение или неравенство, содержащее знак модуля можно одним из трех основных способов: по определению модуля, исходя из геометрического смысла модуля или по общей схеме. Некоторые уравнения или неравенства, содержащие знак модуля, могут быть также решены с использованием специальных соотношений (табл. 15).
В зависимости от выбранного способа решения получаем разные записи решения.
Решите уравнение
I способ (по определению модуля)
Решение:
► 1) Если
(1)
то получаем уравнение
Тогда что удовлетворяет и условию (1).
2) Если
(2)
то получаем уравнение
Тогда что удовлетворяет и условию (2).
Ответ:
Комментарий:
Чтобы раскрыть знак модуля по определению, рассмотрим два случая:
По определению модулем положительного (неотрицательного) числа является само это число, а модулем отрицательного числа является противоположное ему число. Поэтому при а при
В каждом случае решаем полученное уравнение и выясняем, удовлетворяет ли каждый из найденных корней тому условию, при котором мы его находили.
II способ (использование геометрического смысла модуля)
Решение:
► или
или
или
Ответ:
Комментарий:
С геометрической точки зрения — это расстояние от точки 0 до точки По условию уравнения оно равно 6, но расстояние 6 может быть отложено от 0 как вправо (получаем число 6), так и влево (получаем число -6). Таким образом, равенство возможно тогда и только тогда, когда или
Таким образом, равенство возможно тогда и только тогда, когда или
Замечание. При решении уравнения с использованием геометрического смысла модуля знак модуля раскрывается неявно, то есть определение модуля в явном виде не применяется.
Общая схема решения уравнений и неравенств, содержащих знак модуля, — это фактически немного измененный метод интервалов. Поясним содержание этой схемы на примере уравнения с двумя модулями вида
Чтобы решить это уравнение, необходимо раскрыть знаки модулей, а для этого необходимо знать, где функции и будут положительными, а где — отрицательными. То есть фактически мы должны решить неравенства
(1)
(2)
Каждое из этих неравенств мы умеем решать методом интервалов. Перестроим прием решения неравенств методом интервалов таким образом, чтобы он давал возможность одновременно решать каждое из последних неравенств. Как известно, решение неравенства (1) методом интервалов начинается с нахождения его ОДЗ (то есть области определения функции ), а решение неравенства (2) — с нахождения его ОДЗ (то есть области определения функции ). Чтобы начать одновременно решать оба неравенства, необходимо найти общую область определения для функций и то есть найти ОДЗ данного уравнения (это и есть первый из ориентиров необходимой схемы). Чтобы продолжить решение неравенств и методом интервалов, необходимо найти нули функций и то есть найти нули всех подмодульных функций (это и есть второй ориентир). Если далее применить схему метода интервалов одновременно для двух неравенств, необходимо на ОДЗ отметить нули подмодульных функций и разбить ОДЗ на промежутки (это третий ориентир).
Чтобы начать одновременно решать оба неравенства, необходимо найти общую область определения для функций и то есть найти ОДЗ данного уравнения (это и есть первый из ориентиров необходимой схемы). Чтобы продолжить решение неравенств и методом интервалов, необходимо найти нули функций и то есть найти нули всех подмодульных функций (это и есть второй ориентир). Если далее применить схему метода интервалов одновременно для двух неравенств, необходимо на ОДЗ отметить нули подмодульных функций и разбить ОДЗ на промежутки (это третий ориентир).
В каждом из полученных промежутков знаки функций и не могут измениться. Тогда мы можем найти знаки подмодульных функций на каждом промежутке (в любой точке этого промежутка), раскрыть знаки модулей и найти решение данного уравнения в каждом из этих промежутков (это и есть четвертый ориентир общей схемы). Обоснование возможности применения приведенной схемы к решению неравенств, содержащих знак модуля, проводится аналогично.
Примеры решения задач:
Пример №442Решите уравнение
Решение:
► 1. ОДЗ:
2. Нули подмодульных функций:
3. Нули 0 и 2 разбивают ОДЗ на четыре промежутка, в которых подмодульные Рис. 67 функции имеют знаки, показанные на рисунке 67.
4. Находим решения данного уравнения в каждом из промежутков (поскольку знаки подмодульных функций одинаковы на промежутках I и III, удобно для решения объединить эти промежутки). Промежутки I и III: Учитывая знаки подмодульных функций на этих промежутках и определение модуля, получаем, что в этих промежутках данное уравнение равносильно уравнению Отсюда или В рассмотренные промежутки полученные значения не входят, таким образом, в этих промежутках корней нет.
Промежуток II: (Следует обратить внимание на то, чтобы не пропустить значение которое принадлежит ОДЗ.) В этом
промежутке получаем уравнение Отсюда — корень, поскольку принадлежит этому промежутку.
Промежуток IV: (И в этом промежутке необходимо не
забыть значение ) Получаем уравнение Отсюда
— корень, поскольку принадлежит этому промежутку. Объединяя все решения, которые мы получили в каждом промежутке, имеем решение данного уравнения на всей ОДЗ.
Ответ: На рисунке 67 в каждом из промежутков первый знак — это знак функции
а второй — знак функции При выполнении рисунка удобно сначала
отметить на числовой прямой ОДЗ, а потом нули подмодульных функций на ОДЗ.
Проиллюстрируем также получение и использование специальных соотношений, приведенных в таблице 15.
Обоснуем, например, соотношение 5:
Запишем заданное равенство в виде и проанализируем его, опираясь на известные из 6 класса правила действий над числами с одинаковыми и с разными знаками. Чтобы сложить два числа и мы сложили их модули, таким образом, эти числа имеют одинаковые знаки. Если бы эти числа были оба отрицательными, то и их сумма была бы тоже отрицательна, но Тогда получаем, что числа и — оба неотрицательные. Наоборот, если то выполняется Таким образом, действительно уравнение равносильно системе неравенств
Наоборот, если то выполняется Таким образом, действительно уравнение равносильно системе неравенств
Решите уравнение
Решение:
► Поскольку то данное уравнение имеет вид но это равенство может выполняться тогда и только тогда, когда числа и — оба неотрицательные. Таким образом, данное уравнение равносильно системе
Отсюда
Таким образом,
Ответ:
Комментарий:
Если обозначить и то и данное уравнение имеет вид а по соотношению 5 такое уравнение равносильно системе
Заметим, что данное уравнение можно решать и по общей схеме, но тогда решение будет более громоздким.
При решении неравенств, содержащих знак модуля, рассуждения, связанные с раскрытием знаков модулей, полностью аналогичны рассуждениям, которые использовались при решении уравнений, содержащих знак модуля.
Пример №444Решите неравенство
Решение:
► Учитывая геометрический смысл модуля, получаем, что заданное неравенство равносильно неравенству
(1)
Тогда таким образом,
Ответ:
Комментарий:
Неравенство вида (где удобно решать, используя геометрический смысл модуля.
Поскольку заданное неравенство — это неравенство вида а модуль числа — это расстояние на координатной прямой от точки, изображающей данное число, до точки 0, то заданному неравенству удовлетворяют все точки, находящиеся в промежутке Таким образом, Если возникают затруднения с решением двойного неравенства (1), то его заменяют на равносильную систему
Пример №445Решите неравенство (1)
Решение:
► 1. ОДЗ: Тогда то есть таким образом: или
2. Нули подмодульных функций: — не принадлежит ОДЗ) и
3. Нуль 2 разбивает ОДЗ на четыре промежутка, на которых подмодульные функции имеют знаки, показанные на рисунке 68 (на каждом из промежутков первый знак — это знак функции а второй — знак функции
4. Находим решения заданного неравенства в каждом из промежутков (поскольку знаки подмодульных функций являются одинаковыми на промежутках I и II, удобно для решения объединить эти промежутки). Промежутки I и II: Учитывая знаки подмодульных функций в этих промежутках и определение модуля, получаем, что при заданное неравенство равносильно неравенству Тогда то есть Отсюда
В промежутки, которые мы рассмотрели, входят все значения таким образом, в этом случае решением будет
Промежуток III: На этом промежутке получаем неравенство то есть Но при этом значении из промежутка III последнее неравенство обращается в неверное неравенство Таким образом, в промежутке III неравенство (1) решений не имеет.
Промежуток IV: В этом промежутке получаем неравенство то есть Как видим, при любом из IV промежутка неравенство (1) обращается в верное числовое неравенство
Таким образом, решением неравенства (1) в IV промежутке
есть любое число из этого промежутка
Объединяя все решения, полученные в каждом из промежутков, имеем решение данного неравенства на всей ОДЗ: или
Ответ:
Укажем, что для решения некоторых неравенств, содержащих знак модуля, удобно применять также специальные соотношения, приведенные в таблице 15.
Пример №446Решите неравенство
Решение:
► Поскольку и функция монотонно возрастает на множестве неотрицательных чисел, то все разности модулей в неравенстве можно заменить на разности их квадратов (то есть воспользоваться соотношением 4: Получаем неравенство, равносильное заданному
Раскладывая на множители все разности квадратов, имеем:
Далее методом интервалов получаем или (рис. 70).
70).
Ответ: или
Общая схема, предложенная в таблице 15, может быть использована не только при решении уравнений или неравенств, содержащих знак модуля, но и при преобразовании выражений, содержащих знак модуля.
Например, для построения графика функции удобно сначала по общей схеме раскрыть знаки модулей, а уже потом строить график функции
Оформление решения подобного примера может быть таким.
Пример №447Постройте график функции
► 1. Область определения функции: все
2. Нули подмодульных функций: и
3. Отмечаем нули на области определения и разбиваем область определения на промежутки (на рисунке 71 также указаны знаки подмодульных функций в каждом из промежутков).
4. Тогда
Таким образом,
Строим график этой функции (рис. 72).
Уравнения и неравенства с параметрамиРешение уравнений и неравенств с параметрами
Если в запись уравнения или неравенства, кроме переменной и числовых коэффициентов, входят также буквенные коэффициенты — параметры, то при решении таких уравнений можно пользоваться следующим ориентиром.
Любое уравнение или неравенство с параметрами можно решать как обычное уравнение или неравенство до тех пор, пока все преобразования или рассуждения, необходимые для решения, можно выполнить однозначно. Если какое-то преобразование нельзя выполнить однозначно, то решения необходимо разбить на несколько случаев, чтобы в каждом из них ответ через параметры записывался однозначно.
На этапе поиска плана решения уравнения или неравенства с параметрами или в ходе решения часто удобно сопровождать соответствующие рассуждения схемами, по которым легко проследить, в какой момент мы не смогли однозначно выполнить необходимые преобразования, на сколько случаев пришлось разбить решение и чем отличается один случай от другого. Чтобы на таких схемах (или в записях громоздких решений) не потерять какой-то ответ, целесообразно помещать окончательные ответы в прямоугольные рамки. Записывая окончательный ответ, следует учитывать, что ответ должен быть записан для всех возможных значений параметра.
Решите неравенство с переменной
Комментарий:
Заданное неравенство является линейным относительно переменной поэтому используем известный алгоритм решения линейного неравенства:
1) переносим члены с переменной в одну сторону, а без — в другую:
2) выносим в левой части за скобки общий множитель (то есть приводим неравенство к виду ):
Для решения последнего неравенства мы хотели бы разделить обе его части на Но если обе части неравенства разделить на положительное число, то знак неравенства не изменится, а если на отрицательное, то знак неравенства необходимо изменить на противоположный. Кроме того, следует учесть, что на нуль делить нельзя. Следовательно, начиная с этого момента нужно рассмотреть три случая:
Приведенные выше рассуждения можно наглядно записать так:
Решение:
►
Ответ: 1) при 2) при
3) при — любое число.
При решении более сложных уравнений или неравенств следует помнить, что уравнения и неравенства с параметрами чаще всего решают с помощью равносильных преобразований, а все равносильные преобразования уравнений или неравенств выполняют на области допустимых значений (ОДЗ) заданного уравнения или неравенства (то есть на общей области определения для всех функций, которые входят в запись уравнения или неравенства). Поэтому, прежде чем записать ответ, нужно обязательно учесть ОДЗ заданного уравнения или неравенства.
Пример №449Решите уравнение где — переменная.
Комментарий:
Заданные дробные выражения существуют тогда и только тогда, когда знаменатели заданных дробей не равны нулю, следовательно, ОДЗ уравнения:
Умножим обе части заданного уравнения на выражение — общий знаменатель дробей — и получим целое уравнение, которое при условии (то есть на ОДЗ заданного уравнения) равносильно заданному: Из этого уравнения получаем то есть Тогда
Для того чтобы найти значение переменной , хотелось бы разделить обе части последнего уравнения на но при пришлось бы делить на 0, что невозможно. Следовательно, начиная с этого момента нужно рассмотреть два случая.
Следовательно, начиная с этого момента нужно рассмотреть два случая.
Решение в соответствии с приведенными выше рассуждениями можно наглядно записать в виде схемы.
Решение:
► ОДЗ:
Выясним, при каких значениях найденные корни не входят в ОДЗ уравнения, то есть при каких значениях получаем тогда — решений нет. Следовательно, при всех значениях корень не равен 3.
тогда Следовательно, при имеем — посторонний корень (не входит в ОДЗ), то есть при заданное уравнение не имеет корней.
Ответ: 1) при и корней нет; 2) при
Пример №450Решите уравнение относительно переменной л: — а х
Комментарий:
Будем выполнять равносильные преобразования заданного уравнения. Для этого найдем его ОДЗ (знаменатели дробей не равны нулю). Если теперь обе части уравнения умножить на произведение выражений, которые стоят в знаменателях дробей (и которое не равно нулю на ОДЗ уравнения), то получим уравнение равносильное заданному (на ОДЗ заданного). Но последнее уравнение будет квадратным только при потому для его решения следует рассмотреть два случая ( и ).
Но последнее уравнение будет квадратным только при потому для его решения следует рассмотреть два случая ( и ).
Если то для исследования полученного квадратного уравнения нужно рассмотреть еще три случая: — ив каждом из них проверить, входят найденные корни в ОДЗ или нет. При удобно использовать, что значение корня соответствующего квадратного уравнения совпадает с абсциссой вершины параболы
то есть Рассматривая случай следует помнить также предыдущее ограничение:
Поскольку корни уравнения (1) записываются достаточно громоздкими формулами (см. решение), то вместо подстановки полученных корней в ограничение ОДЗ можно подставить «запрещенные» значения в уравнение (1) и выяснить, при каких значениях параметра а мы получим те значения , которые не входят в ОДЗ, а затем проверить полученные значения параметра.
Решение:
► ОДЗ: На этой ОДЗ заданное уравнение равносильно уравнениям:
(1)
1. Если то из уравнения (1) получаем — не входит в ОДЗ, следовательно, при корней нет.
2. Если то уравнение (1) — квадратное. Его дискриминант Рассмотрим три случая:
1) то есть Тогда уравнение (1) имеет одно
значение корня: . Если то корень уравнения (1)
входит в ОДЗ и является корнем заданного уравнения. Если то корень уравнения (1) тоже входит в ОДЗ и является корнем заданного уравнения.
2) то есть следовательно, или
Тогда уравнение (1) не имеет корней.
3) то есть следовательно, но
Тогда уравнение (1) имеет два корня:
(2)
Выясним, при каких значениях а найденные корни не входят в ОДЗ, то есть при каких значениях получаем и Подставляя в уравнение (1) , получаем но при заданное уравнение не имеет корней.
Подставляя в уравнение (1) получаем то есть Тогда (заданное уравнение не имеет корней), или Проверим эти значения
При ОДЗ записывается так: Из формулы корней (2) имеем (входит в ОДЗ) и (не входит в ОДЗ). Следовательно, при заданное уравнение имеет только один корень: При ОДЗ записывается так: а из формулы корней (2) получим: (входит в ОДЗ) и (не входит в ОДЗ). Следовательно, при заданное уравнение имеет только один корень:
Следовательно, при заданное уравнение имеет только один корень:
Таким образом, формулу корней (2) можно использовать, если , только при и
Ответ: 1) если то
2) если то
3) если то 4) если то 5) если то
6) если или то корней нет
Замечание. Чтобы облегчить запись ответа в этом и аналогичных примерах, можно пользоваться таким приемом. Перед записью ответа в сложных или громоздких случаях изобразим ось параметра (а) и отметим на ней все особые значения параметра, которые появились в процессе решения. Под осью параметра (левее от нее) выпишем все полученные решения (кроме решения «корней нет») и напротив каждого ответа отметим, при каких значениях параметра этот ответ можно использовать (рис. 73). После этого ответ записывают для каждого из особых значений параметра и для каждого из полученных промежутков оси параметра. В частности, перед записью ответа в рассмотренном примере, на черновике удобно изобразить такую схему (рис. 73).
73).
Некоторые исследовательские задачи с параметрами удается решить по такой схеме: 1) решить заданное уравнение или неравенство; 2) исследовать полученное решение.
Пример №451Найдите все значения при которых уравнение имеет единственный корень.
Решение:
► ОДЗ: На ОДЗ получаем равносильное уравнение
Тогда или Получаем или Учтем ОДЗ. Для этого выясним, когда при при Тогда при получаем: — посторонний корень; — единственный корень.
При получаем: посторонний корень; —
единственный корень. Также заданное уравнение будет иметь единственный корень, если то есть при (тогда и ).
Ответ:
Комментарий:
Поскольку дробь равна нулю тогда и только тогда, когда ее числитель равен нулю, а знаменатель не равен нулю, то на ОДЗ заданное уравнение равносильно уравнению Дальше учитываем, что произведение равно нулю тогда и только тогда, когда хотя бы один из множителей равен нулю (а второй имеет смысл).
После этого выясним, при каких значениях найденные корни не входят в ОДЗ, то есть приравниваем корни к -7 и находим соответствующие значения . При найденных значениях один из двух полученных корней будет посторонним (), и уравнение будет иметь единственный корень (одно значение корня). Кроме того, заданное уравнение будет иметь единственный корень еще и в том случае, когда два полученных корня ( и ) будут совпадать (и, конечно, будут входить в ОДЗ).
Исследование количества решении уравнении и их системПри решении некоторых задач с параметрами можно пользоваться таким ориентиром: если в задаче с параметрами речь идет о количестве решений уравнения (неравенства или системы), то для анализа заданной ситуации часто удобно использовать графическую иллюстрацию решения.
Наиболее простым соответствующее исследование является в том случае, когда заданное уравнение можно преобразовать к виду поскольку график функции — это прямая, параллельная оси (которая пересекает ось в точке ). Отметим, что, заменяя заданное уравнение на уравнение нужно следить за равносильностью выполненных преобразований, чтобы полученное уравнение имело те же корни, что и заданное, а следовательно, и количество корней у них будет одинаковым. Чтобы определить, сколько корней имеет уравнение достаточно определить, сколько точек пересечения имеет график функции с прямой при различных значениях параметра (Для этого на соответствующем рисунке целесообразно изобразить все характерные положения прямой.)
Отметим, что, заменяя заданное уравнение на уравнение нужно следить за равносильностью выполненных преобразований, чтобы полученное уравнение имело те же корни, что и заданное, а следовательно, и количество корней у них будет одинаковым. Чтобы определить, сколько корней имеет уравнение достаточно определить, сколько точек пересечения имеет график функции с прямой при различных значениях параметра (Для этого на соответствующем рисунке целесообразно изобразить все характерные положения прямой.)
Сколько корней имеет уравнение в зависимости от значения параметра ?
Решение:
► Построим графики функций
Анализируя взаимное размещение полученных графиков, получаем ответ:
1) при уравнение корней не имеет;
2) при уравнение имеет 3 корня;
3) при уравнение имеет 6 корней;
4) при уравнение имеет 4 корня;
5) при уравнение имеет 2 корня.
Комментарий:
Поскольку в этом задании речь идет о количестве решений уравнения, то для анализа заданной ситуации попробуем использовать графическую иллюстрацию решения.
1. Строим график функции (учитывая, что построение может происходить, например, по таким этапам:
2) Строим график функции
3) Анализируем взаимное размещение полученных графиков и записываем ответ (количество корней уравнения равно количеству точек пересечения графика функции с прямой ).
Отметим, что значительное количество исследовательских заданий не удается решить путем непосредственных вычислений (или такие вычисления являются очень громоздкими). Поэтому часто приходится сначала обосновывать какое-то свойство заданного уравнения или неравенства, а затем, пользуясь этим свойством, уже давать ответ на вопрос задачи.
Например, принимая во внимание четность функций, которые входят в запись заданного уравнения, можно использовать такой ориентир.
Если в уравнении функция является четной или нечетной, то вместе с каждым корнем а мы можем указать еще один корень этого уравнения
Пример №453Найдите все значения параметра при которых уравнение (1) имеет единственный корень.
Решение:
► Функция является четной Если — корень уравнения (1), то тоже является корнем этого уравнения. Потому единственный корень у заданного уравнения может быть только тогда, когда то есть Следовательно, единственным корнем заданного уравнения может быть только Если то из уравнения (1) получаем тогда или При уравнения (1) превращается в уравнение Тогда Получаем (тогда то есть ) или (тогда то есть ). Следовательно, при уравнение (1) имеет три корня и условие задачи не выполняется. При уравнение (1) превращается в уравнение Тогда Поскольку то получаем Тогда то есть — единственный корень. Следовательно, удовлетворяет условию задачи.
Ответ:
Комментарий:
Замечаем, что в левой части заданного уравнения стоит четная функция, и используем ориентир, приведенный выше. Действительно, если — корень уравнения то — правильное числовое равенство. Учитывая четность функции имеем Следовательно, — тоже корень уравнения Единственный корень у этого уравнения может быть только тогда, когда корни и совпадают. Тогда
Тогда
Выясним, существуют ли такие значения параметра при которых является корнем уравнения (1). (Это значение и )
Поскольку значение и мы получили из условия, что — корень уравнения (1), то необходимо проверить, на самом ли деле при этих значениях а заданное уравнение будет иметь единственный корень. При решении полученных уравнений целесообразно использовать, что
Использование условий расположения корней квадратного трехчленаИспользование условий расположения корней квадратного трехчлена относительно заданных чисел и
Решение некоторых исследовательских задач с параметрами можно свести к использованию необходимых и достаточных условий расположения корней квадратного трехчлена. Основные из этих условий приведены в таблице 16 (в таблице использованы традиционные обозначения:
Объяснение и обоснование:
Для обоснования указанных условий достаточно воспользоваться тем, что график функции — сплошная (неразрывная) линия. Если такая функция на концах какого-то промежутка принимает значения с разными знаками (то есть соответствующие точки графика находятся в разных полуплоскостях относительно оси ), то внутри этого промежутка есть по крайней мере одна точка, в которой функция равна нулю (рис. 74).
Если такая функция на концах какого-то промежутка принимает значения с разными знаками (то есть соответствующие точки графика находятся в разных полуплоскостях относительно оси ), то внутри этого промежутка есть по крайней мере одна точка, в которой функция равна нулю (рис. 74).
Например, для того чтобы два различных корня квадратного трехчлена при были расположены по разные стороны от заданного числа , достаточно зафиксировать только одно условие: (рис. 75).
Действительно, график квадратичной функции при — парабола, ветки которой направлены вверх. Тогда в случае, когда аргумент стремится к или к (это обозначают обычно так: или функция стремится к следовательно, при или при
Если выполняется условие то с изменением значения аргумента от до квадратичная функция изменяет свой знак с «-» на « + », таким образом, имеет по крайней мере один корень
Точно так же с изменением значения аргумента от до квадратичная функция изменяет свой знак с « + » на «-», следовательно, имеет по крайней мере один корень Но квадратный трехчлен не может иметь более двух корней, значит, при условие необходимое и достаточное для того, чтобы два различных корня квадратного трехчлена были расположены по разные стороны от заданного числа
Аналогичные рассуждения при показывают, что для выполнения этого требования необходимо и достаточно, чтобы Эти два условия можно объединить в одно:
Соответствующее свойство будет обосновано более строго в 11 классе при рассмотрении так называемых непрерывных функций.
Действительно, или Следовательно,
квадратный трехчлен имеет два различных корня, которые расположены по разные стороны от заданного числа тогда и только тогда, когда выполняется условие
Аналогично можно обосновать и другие условия, приведенные в таблице 16.
Заметим, что приведенные условия не обязательно запоминать: для их записи можно пользоваться графиком квадратичной функции (изображенным для нужного расположения корней) и таким ориентиром.
Для того чтобы корни квадратного трехчлена были расположены заданным образом относительно данных чисел и необходимо и достаточно выполнения системы условий, которая включает:
1) знак коэффициента при старшем члене;
2) знаки значений и
3) знак дискриминанта
4) положение абсциссы вершины параболы относительно данных чисел и
Отметим, что для случаев, в которых хотя бы одно из данных чисел расположено между корнями квадратного трехчлена (см.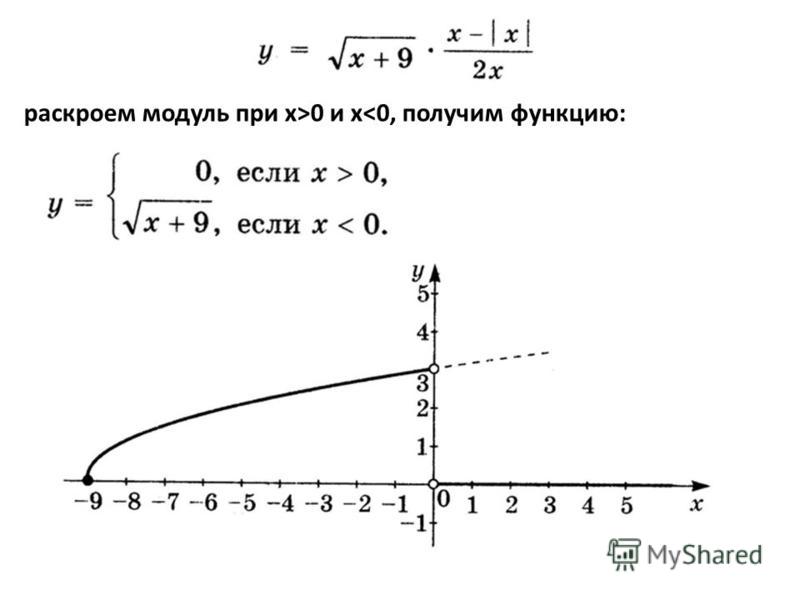 вторую, пятую, шестую и седьмую строки табл. 16), достаточно выполнения первых двух условий этого ориентира, а для других случаев приходится рассматривать все четыре условия. Заметим также, что, записывая каждое из указанных условий, следует выяснить, будет ли выполняться требование задачи в том случае, когда в этом условии будет записан знак нестрогого неравенства.
вторую, пятую, шестую и седьмую строки табл. 16), достаточно выполнения первых двух условий этого ориентира, а для других случаев приходится рассматривать все четыре условия. Заметим также, что, записывая каждое из указанных условий, следует выяснить, будет ли выполняться требование задачи в том случае, когда в этом условии будет записан знак нестрогого неравенства.
Найдите все значения параметра для которых уравнение имеет один корень больше двух, а второй — меньше единицы.
Комментарий:
Поскольку заданное уравнение имеет два различных корня, то оно квадратное (то есть ). Тогда и, чтобы получить ответ на вопрос задачи, достаточно решить совокупность из или Но такой путь решения достаточно громоздкий.
Попробуем воспользоваться условиями расположения корней квадратного трехчлена. Для этого можно непосредственно использовать соответствующие условия, зафиксированные в таблице 16, или получить их с помощью предложенного ориентира. В частности, обозначим и изобразим график квадратичной функции (параболу) в таких положениях, которые удовлетворяют условию задачи (рис. 76, а и б).
В частности, обозначим и изобразим график квадратичной функции (параболу) в таких положениях, которые удовлетворяют условию задачи (рис. 76, а и б).
Для того чтобы корни квадратного трехчлена располагались по разные стороны от чисел 1 и 2, необходимо и достаточно выполнения совокупности условий или Замечаем, что в этих системах знаки и а также и противоположны, поэтому полученную совокупность систем можно заменить одной равносильной системой которая и позволяет получить план решения задачи.
Решение:
► Поскольку заданное уравнение имеет два различных корня, то оно является квадратным (то есть ). Обозначим Как известно, корни квадратного трехчлена будут располагаться по разные стороны от данных чисел 1 и 2 тогда и только тогда, когда выполняется система условий:
Получаем систему
Решаем неравенства (1) и (2) и находим общее решение системы (рис. 77).
Ответ: заданное уравнение имеет один корень больше двух, а второй — меньше единицы при
Сведения из истории:
Напомним, что алгебра — раздел математики, посвященный изучению буквенных выражений и уравнений. Долгое время алгебра была частью науки о числе — арифметики. Значительное количество задач, возникающих в процессе практической деятельности человека, решают одинаковыми способами. Используя вместо чисел буквы, математики научились решать такие задачи в общем виде. Так и образовалась математическая наука — алгебра.
Долгое время алгебра была частью науки о числе — арифметики. Значительное количество задач, возникающих в процессе практической деятельности человека, решают одинаковыми способами. Используя вместо чисел буквы, математики научились решать такие задачи в общем виде. Так и образовалась математическая наука — алгебра.
Исторически зачатки алгебры были известны вавилонянам, египтянам и грекам задолго до нашей эры. Сохранился египетский папирус Ахмеса (XVII в. до н. э.) с решением алгебраических задач. Ученые Вавилона (более 4000 лет назад) умели находить приближенное значение квадратного корня из любого натурального числа, а также решать квадратные уравнения. Это было связано с решением задач на нахождение площадей земельных участков и с развитием астрономии. Однако у вавилонян еще не было понятия отрицательного числа, и поэтому корень квадратного уравнения мог быть только положительным.
Диофант, греческий математик, живший в III в. в Александрии, написал трактат «Арифметика», в котором он уже решал линейные и другие уравнения. В Средние века особенно активно алгебра развивалась в арабских странах и Средней Азии.
В Средние века особенно активно алгебра развивалась в арабских странах и Средней Азии.
Задачи, связанные с квадратными уравнениями, можно найти и в трудах индийских математиков V в. Квадратные уравнения классифицировал в трактате «Алгебра» аль-Хорезми. Он же привел и способы их решения.
В течение многих веков развитие алгебры сильно тормозилось, потому что математикам долго не удавалось ввести в свои исследования удобные обозначения. Поэтому изложение математических работ выглядело громоздко. Только начиная с XVI в. постепенно в математику начали вводить современные обозначения. Символы и т. п. впервые применил французский ученый Рене Декарт (1596-1650). Символ для произвольного числа предложил английский ученый Исаак Ньютон (1643-1727).
Благодаря исследованиям французского математика Франсуа Виета (1540-1603) уравнения второй степени, третьей и четвертой степеней впервые стали рассматривать в буквенных обозначениях. Он ввел буквенные обозначения для неизвестных величин и коэффициентов уравнений. Особенно ценил открытые им формулы, названные впоследствии формулами Виета. Однако Виет признавал только положительные корни. Лишь в XVII в., после работ Г. Декарта, И. Ньютона и других математиков, решение квадратных и других уравнений приобрело современный вид.
Особенно ценил открытые им формулы, названные впоследствии формулами Виета. Однако Виет признавал только положительные корни. Лишь в XVII в., после работ Г. Декарта, И. Ньютона и других математиков, решение квадратных и других уравнений приобрело современный вид.
Идея зависимости величин тоже берет начало от древнегреческой науки. Но греки рассматривали лишь величины, которые имеют «геометрическую» природу, и не ставили вопрос об общем изучении разных зависимостей. Графическое изображение зависимостей между величинами широко использовали Г. Галилей (1564-1642), П. Ферма (1601-1665) и Г. Декарт, который ввел понятие переменной величины. Развитие механики и техники привело к необходимости введения общего понятия функции, что сделал немецкий философ и математик Г. Лейбниц (1646-1716). Большие классы функций изучал в ходе своих исследований И. Ньютон.
В 1718 г. ученик Лейбница, И. Бернулли (1667-1748), дал определение функции, лишенное геометрических образов. Следующий шаг в развитии понятия функции сделал его ученик, член Петербуржской академии наук Л. Ейлер (1707-1783).
Ейлер (1707-1783).
После работ ряда математиков (Ж. Фурье (1768-1830), М. И. Лобачевский, П. Дирихле и др.) было дано следующее определение: «Переменная величина называется функцией переменной величины если каждому значению величины отвечает единственное значение величины ». П. Дирихле (1805-1859)
На современном этапе к словам «каждому значению величины л:» добавляют «принадлежащему некоторому множеству», а вместо переменных величин говорят об элементах этих множеств. Такой подход позволяет рассматривать с единой точки зрения как числовые функции, так и, например, геометрические преобразования и т. п.
Несоизмеримость стороны квадрата и его диагонали была открыта в V в. до н. э. в Древней Греции. Это открытие показало, что для измерения геометрических величин недостаточно рациональных чисел. Поэтому греческие математики отказались от обозначения геометрических величин числами и стали развивать геометрическую алгебру (поэтому и сейчас говорят «квадрат числа», «куб числа» и т. п.).
п.).
Греческий математик Евдокс (IV в. до н. э.) разработал теорию отношений геометрических величин, которая заменяла для древнегреческих математиков современную теорию действительных чисел. В основе теории Евдокса лежит идея о бесконечной делимости отрезков и других фигур.
Р. Декарт ввел произвольно выбранный единичный отрезок, что позволило ему выразить все действия над числами через действия над отрезками. В сущности, он уже работал с положительными действительными числами. Лишь во второй половине XIX в. теория действительных чисел была приведена к теории натуральных чисел.
О понятии действительного числаПервые представления о числах формировались постепенно под влиянием практики. С давних времен числа применялись в ходе счета и измерения величин.
Ответ на вопрос «Сколько элементов содержит данное конечное множество?» всегда выражается или натуральным числом, или числом «нуль». Следовательно, множество
всех неотрицательных чисел обслуживает все потребности счета.
Иначе с измерением величин. Расстояние между двумя пунктами может равняться 3,5 километра, площадь комнаты — 16,45 квадратных метра и т. п.
Исторически положительные действительные числа появились как отношение длин отрезков. С открытием несоизмеримости диагонали единичного квадрата с его стороной стало понятным, что отношение длин отрезков не всегда можно выразить не только натуральным, но и рациональным числом. Чтобы числовое значение каждого отрезка при фиксированной единице измерения было определено, необходимо было ввести новые числа — иррациональные.
Все практические измерения величин имеют только приближенный характер. Их результат с необходимой точностью можно выразить с помощью рациональных дробей или конечных десятичных дробей.
Например, измеряя диагональ квадрата со стороной 1 м с точностью до 1 см, мы выясним, что ее длина приближенно равна м. Измеряя с точностью до 1 мм, получим, что эта длина приближенно равна м.
Однако в математике часто уклоняются от приближенного характера практических измерений. Последовательный теоретический подход к измерению длин отрезков приводит к необходимости рассмотрения бесконечных десятичных дробей. (Именно такими дробями являются числа
Последовательный теоретический подход к измерению длин отрезков приводит к необходимости рассмотрения бесконечных десятичных дробей. (Именно такими дробями являются числа
Отношение длины любого отрезка к длине отрезка, принятого за единицу измерения, всегда можно выразить числом, представленным в виде бесконечной десятичной дроби.
Полная теория действительных чисел достаточно сложна и не входит в программу средней школы. Она обычно рассматривается в курсах математического анализа. Однако с одним из способов ее построения мы ознакомимся в общих чертах.
1. Пусть:
а) каждому действительному числу соответствует (как его запись) бесконечная десятичная дробь:
б) каждая бесконечная десятичная дробь является записью действительного числа.
Но при этом естественно считать десятичную дробь, оканчивающуюся бесконечной последовательностью девяток, только другой записью числа, представленного десятичной дробью, оканчивающей бесконечной последовательностью нулей:
Только исключив из рассмотрения десятичные дроби с девяткой в периоде, получим взаимно однозначное соответствие между множеством действительных чисел и множеством бесконечных десятичных дробей. Число — это целая часть положительного числа а — дробная часть числа Число называют десятичным приближением с точностью до с недостатком, а число называют десятичным приближением с точностью до с избытком для числа
Число — это целая часть положительного числа а — дробная часть числа Число называют десятичным приближением с точностью до с недостатком, а число называют десятичным приближением с точностью до с избытком для числа
Если число отрицательно, то есть то считают, что
и
2. Вводят правило сравнения двух действительных чисел. По определению число меньше числа когда по меньшей мере для одного выполняется неравенство где и — десятичные приближения с точностью до с недостатком для чисел и (Мы воспользовались тем, что правило сравнения конечных десятичных дробей уже известно.)
3. Определяют арифметические действия над действительными числами (при этом также пользуются тем, что эти действия уже определены для конечных десятичных дробей).
Суммой двух действительных чисел и (обозначается ) называют такое действительное число , что для любого выполняются неравенства
В курсах математического анализа доказывается, что такое число существует и оно единственное.
Аналогично произведением двух неотрицательных чисел и называют такое число (обозначают ), что при любом выполняются неравенства
Такое число существует, и оно единственное.
Напомним, что примеры выполнения таким образом определенных действий сложения и умножения действительных чисел было рассмотрено в курсе алгебры 8 класса.
Воспользовавшись тем, что произведение неотрицательных чисел и уже определено, полагают, что для действительных чисел разных знаков а для чисел одинаковых знаков — (как обычно, модулем каждого из чисел и называют число ).
Вычитание определяется как действие, обратное сложению: разностью чисел и называется такое число , что
Деление определяется как действие, обратное умножению: частным называется такое число что
4. Показывают, что неравенства и арифметические операции, определенные выше, сохраняют основные свойства, присущие им во множестве рациональных чисел.
Теория действительного числа была построена сразу в нескольких формах немецкими математиками Р. Дедекиндом (1831-1916), К. Вейерштрассом (1815-1897) и Г. Кантором (1845-1918).
Дедекиндом (1831-1916), К. Вейерштрассом (1815-1897) и Г. Кантором (1845-1918).
Развлечение с модульной арифметикой — лучшее объяснение
Читатель недавно предложил мне написать о модульной арифметике (также известной как «взятие остатка»). Я не особо задумывался над этим, но понял, что модуль по модулю чрезвычайно эффективен: он должен быть в нашем мысленном наборе инструментов рядом со сложением и умножением.
Вместо того, чтобы бить вас по лицу формулами, давайте исследуем идею, которой мы незаметно подвергались в течение многих лет. Есть хорошая статья о модульной арифметике, которая вдохновила этот пост.
Нечетное, четное и тройное
Вскоре после открытия целых чисел (1, 2, 3, 4, 5…) мы поняли, что они делятся на две группы:
- Четное: делится на 2 (0, 2, 4, 6 ..)
- Нечетное: не делится на 2 (1, 3, 5, 7…)
Почему это различие важно? Это начало абстракции — мы замечаем свойств числа (например, четное или нечетное), а не только само число («37»).
Это огромно — это позволяет нам исследовать математику на более глубоком уровне и находить взаимосвязи между типами и числами, а не конкретными.Например, мы можем составить такие правила:
- Четное x Четное = Четное
- Нечетный x Нечетный = Нечетный
- Четное x Нечетное = Четное
Это общие правила — они действуют на уровне собственности. (Интуитивно у меня есть химическая аналогия, что «ровность» — это молекула, которую имеют некоторые числа, и ее нельзя удалить умножением.)
Но четный / нечетный — это очень специфическое свойство: деление на 2. А как насчет числа 3? Как насчет этого:
- «Тринадцать» означает, что число делится на 3 (0, 3, 6, 9…)
- «Throdd» означает, что не делится на на 3 (1, 2, 4, 5, 7, 8…)
Странно, но работоспособно.Вы заметите несколько вещей: есть два типа треддов. Число вроде «4» находится на расстоянии 1 от тройки (остаток 1), а число 5 — от двух (остаток 2).
Быть «тройкой» — это еще одно свойство числа. Возможно, не так быстро, как четный / нечетный, но он есть: мы можем создавать правила вроде «три четверти х три четверти = три четверти» и так далее.
Но это сходит с ума. Мы не можем постоянно придумывать новые слова.
Введите модуль
Операция по модулю (сокращенно «mod» или «%» на многих языках программирования) представляет собой остаток при делении.Например, «5 mod 3 = 2» означает, что 2 — это остаток от деления 5 на 3.
Преобразуя повседневные термины в математические, «четное число» — это число, в котором он равен «0 по модулю 2», то есть его остаток равен 0 при делении на 2. Нечетное число — «1 по модулю 2» (остаток равен 1). .
Почему это круто? Итак, наши «нечетные / четные» правила становятся такими:
- Четный x Четный = 0 x 0 = 0 [четный]
- Нечетный x Нечетный = 1 x 1 = 1 [нечетный]
- Четный x Нечетный = 0 x 1 = 0 [Четный]
Круто, а? Довольно легко решить — мы преобразовали «свойства» в реальные уравнения и обнаружили некоторые новые факты.
Что такое четный x четный x нечетный x нечетный? Ну, это 0 x 0 x 1 x 1 = 0. На самом деле, вы можете увидеть, если будет даже умножено где-нибудь на , весь результат будет нулем … я имею в виду даже :).
Математика часов
Подлость в модульной математике заключается в том, что мы уже использовали ее для отсчета времени — иногда называемой «арифметикой часов».
Например: 7:00 (am / pm не имеет значения). Где будет часовая стрелка через 7 часов?
грн. 7 + 7 = 14, но мы не можем показать «14:00» на часах.Значит, должно быть 2. Мы рассуждаем интуитивно и математически:
- (7 + 7) mod 12 = (14) mod 12 = 2 mod 12 [2 — остаток от деления 14 на 12]
Уравнение «14 по модулю 12 = 2 по модулю 12» означает, что «14 часов» и «2 часа» выглядят одинаково в 12-часовых часах. Это конгруэнтных , обозначенных знаком тройного равенства: 14 ≡ 2 mod 12.
Другой пример: сейчас 8:00. Где будет большая рука через 25 часов?
Вместо того, чтобы прибавлять 25 к 8, вы можете понять, что 25 часов — это просто «1 день + 1 час». Итак, часы закончатся на 1 час вперед, в 9:00.
Итак, часы закончатся на 1 час вперед, в 9:00.
- (8 + 25) по модулю 12 (8) по модулю 12 + (25) по модулю 12 ≡ (8) по модулю 12 + (1) по модулю 12 ≡ 9 по модулю 12
Вы интуитивно преобразовали 25 в 1 и добавили это к 8.
Забавное свойство: математика просто работает
Используя аналогию с часами, мы можем выяснить, работают ли правила модульной арифметики (а они работают).
Сложение / вычитание
Допустим, два раза на наших часах выглядят одинаково («2:00» и «14:00»).Если мы добавим к обоим одинаковые «x» часов, что произойдет?
Ну на часики меняют на столько же! 2:00 + 5 часов ≡ 14:00 + 5 часов — оба покажут 7:00.
Почему? Ну, нас никогда не волновали лишние «12:00», которые таскала с собой 14-я. Мы можем просто добавить 5 к двум остаткам, которые есть у обоих, и они продвинутся одинаково. Для всех совпадающих чисел (2 и 14) сложение и вычитание имеют одинаковый результат.
Умножение
Труднее увидеть, останется ли умножение прежним. Если 14 ≡ 2 (mod 12), можем ли мы умножить обе части и получить тот же результат?
Если 14 ≡ 2 (mod 12), можем ли мы умножить обе части и получить тот же результат?
Давайте посмотрим — что произойдет, если мы умножим на 3?
Ну, 2:00 * 3 ≡ 6:00. Но что такое «14:00» * 3?
Помните, 14 = 12 + 2. Итак, мы можем сказать, что
- 14 * 3 = (12 + 2) * 3 = (12 * 3) + (2 * 3) mod 12
Первую часть (12 * 3) можно игнорировать! «12 часов переполнения», которое несет 14, просто повторяется несколько раз. Но кого это волнует? В любом случае мы игнорируем переполнение.
При умножении имеет значение только остаток, который равен 2 часам для 14:00 и 2:00. Интуитивно вот как я вижу, что умножение не меняет отношения с модульной математикой (вы можете перемножить обе стороны модульного отношения и получить тот же результат). См. Ссылку выше для более строгих доказательств — это мои интуитивно понятные карандашные линии.
Использование модульной арифметики
А теперь самое интересное — чем полезна модульная арифметика?
Простые расчеты времени
Мы делаем это интуитивно, но приятно дать этому название. Ваш рейс прибывает в 15:00. Задерживается на 14 часов. Во сколько он приземлится?
Ваш рейс прибывает в 15:00. Задерживается на 14 часов. Во сколько он приземлится?
Ну, 14 2 mod 12. Я думаю об этом как о «2 часа и переключение между утра и вечера», поэтому я знаю, что это будет «3 + 2 = 5 утра».
Это немного сложнее, чем простой оператор по модулю, но принцип тот же.
Размещение элементов в случайных группах
Предположим, у вас есть люди, которые купили билеты в кино с номером подтверждения. Вы хотите разделить их на 2 группы.
Чем вы занимаетесь? «Шансы здесь, там даже события». Вам не нужно знать, сколько билетов было выписано (первая половина, вторая половина), каждый может мгновенно определить свою группу (без обращения в центральный орган), и схема работает по мере того, как все больше людей покупают билеты.
Нужны 3 группы? Разделите на 3 и возьмите остаток (также известный как мод 3). У вас будут группы «0», «1» и «2».
В программировании взятие по модулю — это то, как вы можете поместить элементы в хеш-таблицу: если ваша таблица имеет N записей, преобразуйте ключ элемента в число, выполните модификацию N и поместите элемент в это ведро (возможно, сохраняя связанный список там). По мере увеличения размера вашей хеш-таблицы вы можете пересчитать модуль для ключей.
По мере увеличения размера вашей хеш-таблицы вы можете пересчитать модуль для ключей.
Выбор случайного предмета
Я использую модуло в реальной жизни. Действительно. У нас есть 4 человека, играющих в игру, и нам нужно выбрать кого-то, кто будет первым. Сыграйте в мини-игру с модом N! Дайте людям номера 0, 1, 2 и 3.
Теперь все говорят: «Раз, два, три, стреляйте!» и выставляет случайное количество пальцев. Сложите их и разделите на 4 — тот, кто получит остаток, ходит первым.(Например: если сумма пальцев равна 11, тот, у кого было «3», ходит первым, поскольку 11 mod 4 = 3).
Это быстро и работает.
Выполнение задач в цикле
Предположим, что задачи должны выполняться по определенному расписанию:
- Задача A выполняется 3 раза в час
- Задача B выполняется 6 раз в час
- Задача C выполняется 1 раз в час
Как сохранить эту информацию и составить расписание? В одну сторону:
- Установить таймер, работающий каждую минуту (значение минут обозначается буквой «n»).

- 3x / час означает каждые 60/3 = 20 минут.Таким образом, задача A запускается всякий раз, когда «n% 20 == 0»
- Задача B запускается всякий раз, когда «n% 10 == 0»
- Задача C запускается всякий раз, когда «n% 60 == 0»
О, вам нужна задача C1, которая выполняется 1 раз в час, но не в то же время, что и задача C? Конечно, пусть он запускается, когда «n mod 60 == 1» (все еще один раз в час, но не то же самое, что и C1).
Мысленно я вижу цикл, который я хочу «поразить» через различные промежутки времени, поэтому вставляю мод. Приятно то, что попадания могут перекрываться независимо друг от друга. В этом отношении это немного похоже на XOR (каждый XOR может быть многоуровневым, но это уже другая статья!).
Аналогично, при программировании вы можете распечатать каждый сотый элемент журнала, выполнив: if (n% 100 == 0) {print…}.
Это очень гибкий и простой способ запускать элементы по расписанию. Фактически, это ответ на проверку работоспособности FizzBuzz. Если в вашем поясе нет операции по модулю, вопрос становится намного сложнее.
Если в вашем поясе нет операции по модулю, вопрос становится намного сложнее.
Поиск свойств номеров
Предположим, я сказал вам это:
Что можно быстро сделать? Что ж, «а» должно быть четным, поскольку оно равно чему-то, что подразумевает умножение на 2.
Если бы я вам еще сказал:
Вы бы не отказались. Не потому, что вы «знаете», что эти два продукта разные, а потому, что один явно четный, а другой — нечетный. Проблема заключается в том, что в обоих случаях a не может быть одним и тем же числом, поскольку свойства не совпадают с .
Такие вещи, как «even», «threeven» и «mod n» являются свойствами, которые являются более общими, чем отдельные числа, и которые мы можем проверить на согласованность. Таким образом, мы можем использовать модуль по модулю, чтобы выяснить, согласуются ли числа, не зная, что это такое!
Если я скажу вам это:
Можно ли решить эти уравнения с целыми числами? Посмотрим:
- 3a + 5b = 8… давайте «mod 3 it»: 0 + 2b ≡ 2 mod 3, или b ≡ 1 mod 3
- 3a + b = 2… давайте «mod 3 it»: 0 + b ≡ 2 mod 3), или b ≡ 2 mod 3
Противоречие, молодцы! B не может быть одновременно «1 mod 3» и «2 mod 3» — это так же абсурдно, как быть четным и нечетным одновременно!
Но есть одна проблема: числа вроде «1. 5 ”не являются ни четными, ни нечетными — они не целые числа! Модульные свойства применяются к целым числам, поэтому мы можем сказать, что b не может быть целым числом .
5 ”не являются ни четными, ни нечетными — они не целые числа! Модульные свойства применяются к целым числам, поэтому мы можем сказать, что b не может быть целым числом .
Потому что на самом деле мы можем решить это уравнение:
- (3a + 5b) — (3a + b) = 8 — 2
- 4b = 6
- б = 1,5
- 3a + 1,5 = 2, поэтому 3a = 0,5 и a = 1/6
Не соблазняйтесь силой по модулю! Знайте его пределы: это применимо к целым числам.
Криптография
Игра с числами имеет очень важное применение в криптографии.Здесь слишком много, чтобы рассказывать о нем, но модуль Diffie-Hellman Key Exchange используется при настройке SSL-соединений для шифрования веб-трафика.
Обычный английский
Гики любят использовать технические слова в обычном контексте. Вы можете услышать: «X совпадает с Y по модулю Z», что примерно означает «игнорирование Z, X и Y одинаковы».
Например:
- b и B идентичны, по модулю капитализации
- iTouch и iPad идентичны, по модулю размера;)
Далее и выше
Странно думать о «полезности» оператора по модулю — это как если бы кто-то спрашивал, почему полезны показатели. В повседневной жизни не очень, но это инструмент, позволяющий понять закономерности в мире и создать свои собственные.
В повседневной жизни не очень, но это инструмент, позволяющий понять закономерности в мире и создать свои собственные.
В общем, я вижу несколько общих вариантов использования:
- Редуктор диапазона: возьмите вход, мод N, и у вас есть число от 0 до N-1.
- Назначение группы: возьмите вход, мод N, и вы пометите его как группу от 0 до N-1. Эта группа может быть согласована любым количеством сторон — например, разные серверы, которые знают N = 20, могут согласовать, к какой группе принадлежит ID = 57.
- Дедуктор свойств: обрабатывайте числа в соответствии с их свойствами (четными, тройными и т. Д.) И вырабатывайте принципы, полученные на уровне свойств.
Я уверен, что упустил еще несколько десятков применений — не стесняйтесь комментировать ниже.Удачной математики!
Другие сообщения этой серии
- Методы сложения чисел от 1 до 100
- Переосмысление арифметики: наглядное руководство
- Quick Insight: интуитивное значение подразделения
- Quick Insight: вычитание отрицательных чисел
- Удивительные узоры в квадратных числах (1, 4, 9, 16…)
- Развлечение с модульной арифметикой
- Учимся считать (как избежать проблемы со столбами)
- Необычное введение в системы счисления
- Еще один взгляд на простые числа
- Интуиция по золотому сечению
- Различные интерпретации числа ноль
модульная арифметика | Britannica
модульная арифметика , иногда называемая арифметикой модуля или арифметика часов , в ее наиболее элементарной форме, арифметика, выполняемая со счетом, который сбрасывается до нуля каждый раз, когда определенное целое число N больше единицы , известный как модуль (mod), был достигнут.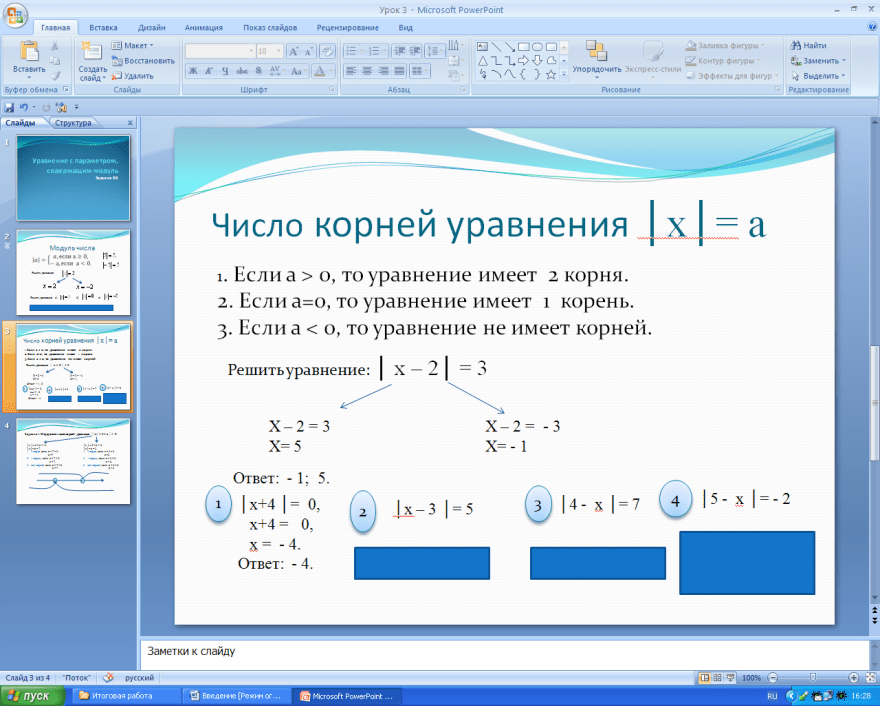 Примерами являются цифровые часы в 24-часовой системе, которые сбрасываются на 0 в полночь ( N = 24), и круговой транспортир с отметкой 360 градусов ( N = 360). Модульная арифметика важна в теории чисел, где она является фундаментальным инструментом при решении диофантовых уравнений (особенно тех, которые ограничиваются целочисленными решениями). Обобщения предмета привели к важным попыткам 19 века доказать последнюю теорему Ферма и к развитию значительных разделов современной алгебры.
Примерами являются цифровые часы в 24-часовой системе, которые сбрасываются на 0 в полночь ( N = 24), и круговой транспортир с отметкой 360 градусов ( N = 360). Модульная арифметика важна в теории чисел, где она является фундаментальным инструментом при решении диофантовых уравнений (особенно тех, которые ограничиваются целочисленными решениями). Обобщения предмета привели к важным попыткам 19 века доказать последнюю теорему Ферма и к развитию значительных разделов современной алгебры.
В модульной арифметике (с модулем N ) единственными числами являются 0, 1, 2,…, N — 1, и они известны как остатки по модулю N . Остатки складываются путем вычисления обычной арифметической суммы, а затем вычитания модуля из суммы столько раз, сколько необходимо для уменьшения суммы до числа M от 0 до N — 1 включительно. M называется суммой чисел по модулю N . Используя обозначения, введенные немецким математиком Карлом Фридрихом Гауссом в 1801 году, можно записать, например, 2 + 4 + 3 + 7 6 (mod 10), где символ ≡ читается как «конгруэнтно. ”
”
Примеры использования модульной арифметики встречаются в древних китайских, индийских и исламских культурах. В частности, они возникают в календарных и астрономических задачах, поскольку они связаны с циклами (искусственными или естественными), но модульная арифметика также встречается в чисто математических задачах. Пример из китайской книги 3-го века нашей эры, Сунь Цзы Sunzi suanjing ( Математическое руководство Мастера Сунь ), спрашивает
У нас есть несколько вещей, но мы не знаем точно, сколько.Если мы посчитаем их по три, у нас останется два. Если считать до пяти, у нас останется три. Если посчитать до семерок, останется две. Сколько всего там вещей?
Это эквивалентно запросу решения одновременных сравнений X 2 (mod 3), X 3 (mod 5) и X 2 (mod 7), одно решение которых is 23. Общее решение таких задач стало известно как китайская теорема об остатках.
Швейцарский математик Леонард Эйлер был пионером современного подхода к конгруэнтности около 1750 года, когда он явно представил идею сравнения по модулю числа N и показал, что эта концепция разделяет целые числа на N классы конгруэнтности или классы вычетов. Два целых числа находятся в одном классе сравнения по модулю N , если их разность делится на N . Например, если N равно 5, то −6 и 4 являются членами одного и того же класса сравнения {…, −6, −1, 4, 9,…}. Поскольку каждый класс сравнения может быть представлен любым из его членов, этот конкретный класс может называться, например, «классом сравнения −6 по модулю 5» или «классом сравнения 4 по модулю 5».
Два целых числа находятся в одном классе сравнения по модулю N , если их разность делится на N . Например, если N равно 5, то −6 и 4 являются членами одного и того же класса сравнения {…, −6, −1, 4, 9,…}. Поскольку каждый класс сравнения может быть представлен любым из его членов, этот конкретный класс может называться, например, «классом сравнения −6 по модулю 5» или «классом сравнения 4 по модулю 5».
В системе Эйлера любые числа N , которые оставляют разные остатки при делении на N , могут представлять классы сравнения по модулю N .Таким образом, одной из возможных систем для арифметики по модулю 5 может быть −2, −1, 0, 1, 2. Добавление классов сравнения по модулю N определяется путем выбора любого элемента из каждого класса, сложения элементов вместе, а затем взятия класс сравнения по модулю N , которому принадлежит сумма в качестве ответа. Эйлер аналогичным образом определил вычитание и умножение классов вычетов. Например, чтобы умножить −3 на 4 (модуль 5), сначала умножьте −3 × 4 = −12; так как −12 3 (mod 5), решение равно −3 × 4 ≡ 3 (mod 5).Эйлер показал, что можно получить тот же результат с любыми двумя элементами из соответствующих классов конгруэнтности.
Например, чтобы умножить −3 на 4 (модуль 5), сначала умножьте −3 × 4 = −12; так как −12 3 (mod 5), решение равно −3 × 4 ≡ 3 (mod 5).Эйлер показал, что можно получить тот же результат с любыми двумя элементами из соответствующих классов конгруэнтности.
Обратите внимание, что когда модуль N не является простым, деление не всегда возможно. Например, 1 ÷ 2 ≡ 3 (mod 5), так как 2 × 3 ≡ 1 (mod 5). Однако уравнение 1 ÷ 2 X (mod 4) не имеет решения, поскольку не существует X такого, что 2 × X ≡ 1 (mod 4). Когда модуль N не является простым, можно разделить класс, представленный как , на класс, представленный как s , тогда и только тогда, когда s и N являются взаимно простыми (то есть, если их Единственным общим множителем является цифра 1).Например, 7 ÷ 4 4 (mod 9), поскольку 4 × 4 ≡ 7 (mod 9) — в этом случае 7 и 9 взаимно просты.
Как использовать оператор% — Real Python
Python поддерживает широкий спектр арифметических операторов, которые вы можете использовать при работе с числами в вашем коде. Одним из этих операторов является оператор по модулю (
Одним из этих операторов является оператор по модулю (% ), который возвращает остаток от деления двух чисел.
Оператор по модулю Python иногда может быть упущен из виду. Но хорошее понимание этого оператора даст вам бесценный инструмент в вашем арсенале инструментов Python.
Математический модуль
Термин по модулю происходит от раздела математики, называемого модульной арифметикой. Модульная арифметика имеет дело с арифметикой целых чисел на круговой числовой строке с фиксированным набором чисел. Все арифметические операции, выполняемые в этой числовой строке, будут повторяться, когда они достигнут определенного числа, называемого модулем .
Классическим примером модульной арифметики являются двенадцатичасовые часы. Двенадцатичасовые часы имеют фиксированный набор значений от 1 до 12.При подсчете двенадцатичасовых часов вы считаете до модуля 12, а затем возвращаетесь к 1. Двенадцатичасовые часы можно классифицировать как «по модулю 12», иногда сокращая до «модуля 12».
Оператор по модулю используется, когда вы хотите сравнить число с модулем и получить эквивалентное число, ограниченное диапазоном модуля.
Например, вы хотите определить, в какое время будет девять часов после 8:00. В двенадцатичасовом формате вы не можете просто прибавить 9 к 8, потому что вы получите 17.Вам нужно взять результат 17 и использовать мод , чтобы получить его эквивалентное значение в двенадцатичасовом контексте:
8 часов + 9 = 17 часов
17 мод 12 = 5
17 mod 12 возвращает 5 . Это означает, что девять часов после 8:00 — это 17:00. Вы определили это, взяв число 17 и применив его к контексту mod 12 .
Теперь, если подумать, 17 и 5 эквивалентны в контексте mod 12 .Если бы вы посмотрели на часовую стрелку в 5:00 и 17:00, она была бы в том же положении. В модульной арифметике есть уравнение, описывающее эту взаимосвязь:
Это уравнение гласит: « a и b равны по модулю n ». Это означает, что
Это означает, что a и b эквивалентны в mod n , поскольку они имеют одинаковый остаток при делении на n . В приведенном выше уравнении n — это модуль для a и b .Используя значения 17 и 5 из предыдущих, уравнение будет выглядеть так:
Это гласит: « 17 и 5 равны по модулю 12 ». 17 и 5 имеют одинаковый остаток, 5 , при делении на 12 . Итак, в mod 12 числа 17 и 5 эквивалентны.
Подтвердить это можно с помощью деления:
17/12 = 1 К 5
5/12 = 0 R 5
Обе операции имеют одинаковый остаток, 5 , поэтому они эквивалентны по модулю 12 .
Теперь это может показаться сложной математикой для оператора Python, но эти знания подготовят вас к использованию оператора по модулю в примерах далее в этом руководстве. В следующем разделе вы познакомитесь с основами использования оператора Python по модулю с числовыми типами
В следующем разделе вы познакомитесь с основами использования оператора Python по модулю с числовыми типами int и float .
Основы операторов Python по модулю
Оператор по модулю, как и другие арифметические операторы, может использоваться с числовыми типами int и float .Как вы увидите позже, его также можно использовать с другими типами, такими как math.fmod () , decimal.Decimal и вашими собственными классами.
Оператор по модулю с
int В большинстве случаев вы будете использовать оператор по модулю с целыми числами. Оператор по модулю, когда он используется с двумя положительными целыми числами, вернет остаток от стандартного евклидова деления:
>>> >>> 15% 4
3
>>> 17% 12
5
>>> 240% 13
6
>>> 10% 16
10
Будьте осторожны! Как и в случае с оператором деления (/), Python вернет ZeroDivisionError , если вы попытаетесь использовать оператор по модулю с делителем 0 :
>>> 22% 0
ZeroDivisionError: целочисленное деление или по модулю нуля
Далее вы познакомитесь с использованием оператора по модулю с плавающей точкой .
Оператор по модулю с поплавком
Подобно int , оператор по модулю, используемый с с плавающей точкой , вернет остаток от деления, но как значение с плавающей запятой :
>>> 12,5% 5,5
1.5
>>> 17,0% 12,0
5.0
Альтернативой использованию числа с плавающей запятой с оператором по модулю является использование math.fmod () для выполнения операций по модулю для значений с плавающей запятой :
>>> импорт математики
>>> математика.fmod (12.5, 5.5)
1.5
>>> math.fmod (8.5, 2.5)
1.0
Официальные документы Python предлагают использовать math.fmod () вместо оператора Python modulo при работе со значениями float , поскольку math.fmod () вычисляет результат операции по модулю. Если вы используете отрицательный операнд, вы можете увидеть разные результаты между math. и  fmod (x, y)
fmod (x, y) x% y . В следующем разделе вы более подробно исследуете использование оператора по модулю с отрицательными операндами.
Как и другие арифметические операторы, оператор по модулю и math.fmod () могут столкнуться с проблемами округления и точности при работе с арифметикой с плавающей запятой:
>>> 13,3% 1,1
0,09999999999999964
>>> импорт математики
>>> math.fmod (13.3, 1.1)
0,09999999999999964
Если для вашего приложения важно поддерживать точность с плавающей запятой, вы можете использовать оператор по модулю с десятичным числом .Десятичный . Вы рассмотрите это позже в этом руководстве.
Оператор по модулю с отрицательным операндом
Все операции по модулю, которые вы видели до этого момента, использовали два положительных операнда и возвращали предсказуемые результаты. Когда вводится отрицательный операнд, все становится сложнее.
Как оказалось, способ, которым компьютеры определяют результат операции по модулю с отрицательным операндом, оставляет неоднозначность относительно того, должен ли остаток принимать знак делимого (делимое число) или знак делителя (число, на которое делится дивиденд). Разные языки программирования обрабатывают это по-разному.
Разные языки программирования обрабатывают это по-разному.
Например, в JavaScript остаток примет знак делимого:
Остаток в этом примере, 2 , положительный, поскольку принимает знак делимого, 8 . В Python и других языках знак делителя примет остаток:
Здесь вы можете видеть, что остаток -1 принимает знак делителя -3 .
Вы можете спросить, почему остаток в JavaScript равен 2 , а остаток в Python равен -1 .Это связано с тем, как разные языки определяют результат операции по модулю. Языки, в которых остаток принимает знак делимого, используют следующее уравнение для определения остатка:
Это уравнение состоит из трех переменных:
-
r— остаток. -
a— дивиденды. -
n— делитель.
trunc () в этом уравнении означает, что используется усеченное деление , которое всегда округляет отрицательное число до нуля. Для получения дополнительных пояснений см. Этапы операции по модулю ниже, используя
Для получения дополнительных пояснений см. Этапы операции по модулю ниже, используя 8 в качестве делимого и -3 в качестве делителя:
r = 8 - (-3 * усечение (8 / -3))
r = 8 - (-3 * усечение (-2,666666666667))
r = 8 - (-3 * -2) # Округление в сторону 0
г = 8 - 6
г = 2
Здесь вы можете увидеть, как такой язык, как JavaScript, получает остаток 2 . Python и другие языки, в которых остаток принимает знак делителя, используют следующее уравнение:
этаж () в этом уравнении означает, что используется разделение этажа .При положительных числах деление этажа вернет тот же результат, что и усеченное деление. Но с отрицательным числом деление по этажам округляет результат в меньшую сторону, в сторону от нуля:
r = 8 - (-3 * этаж (8 / -3))
r = 8 - (-3 * этаж (-2.666666666667))
r = 8 - (-3 * -3) # Округление от 0
г = 8 - 9
г = -1
Здесь вы можете увидеть, что результат: -1 .
Теперь, когда вы понимаете, откуда взялось различие в остатке, вам может быть интересно, почему это важно, если вы используете только Python.Как оказалось, не все операции по модулю в Python одинаковы. В то время как модуль, используемый с типами int и float , принимает знак делителя, другие типы — нет.
Вы можете увидеть пример этого, сравнив результаты 8.0% -3.0 и math.fmod (8.0, -3.0) :
>>> 8,0% -3
-1,0
>>> импорт математики
>>> math.fmod (8.0, -3.0)
2.0
математ.fmod () принимает знак делимого с использованием усеченного деления, тогда как float использует знак делителя. Позже в этом руководстве вы увидите другой тип Python, в котором используется знак делимого, десятичное число . Десятичное число .
Оператор по модулю и
divmod () Python имеет встроенную функцию divmod () , которая внутренне использует оператор по модулю.
divmod () принимает два параметра и возвращает кортеж, содержащий результаты деления по этажу и по модулю с использованием предоставленных параметров.
Ниже приведен пример использования divmod () с 37 и 5 :
>>> divmod (37, 5)
(7, 2)
>>> 37 // 5
7
>>> 37% 5
2
Вы можете видеть, что divmod (37, 5) возвращает кортеж (7, 2) . 7 является результатом разделения этажей на 37 и 5 . 2 является результатом 37 по модулю 5 .
Ниже приведен пример, в котором второй параметр представляет собой отрицательное число. Как обсуждалось в предыдущем разделе, когда оператор по модулю используется с int , остаток примет знак делителя:
>>> divmod (37, -5)
(-8, -3)
>>> 37 // -5
-8
>>> 37% -5
-3 # Результат имеет знак делителя
Теперь, когда у вас была возможность увидеть оператор по модулю, используемый в нескольких сценариях, важно взглянуть на то, как Python определяет приоритет оператора по модулю при использовании с другими арифметическими операторами.
Приоритет оператора по модулю
Как и другие операторы Python, для оператора по модулю существуют особые правила, определяющие его приоритет при оценке выражений. Оператор по модулю (% ) имеет тот же уровень приоритета, что и операторы умножения ( * ), деления (/) и деления по полу ( // ).
Взгляните на пример приоритета оператора по модулю ниже:
>>> >>> 4 * 10% 12 - 9
-5
Операторы умножения и по модулю имеют одинаковый уровень приоритета, поэтому Python будет оценивать их слева направо.Вот шаги для вышеуказанной операции:
-
4 * 10оценивается, в результате получается40% 12 - 9. -
40% 12оценивается, в результате получается4 - 9. -
4–9вычисляется, в результате получается-5.
Если вы хотите переопределить приоритет других операторов, вы можете заключить в круглые скобки операцию, которую вы хотите оценить первой:
>>> >>> 4 * 10% (12-9)
1
В этом примере сначала оценивается (12–9) , затем 4 * 10 и, наконец, 40% 3 , что равно 1 .
Оператор модуля Python на практике
Теперь, когда вы познакомились с основами оператора Python по модулю, вы рассмотрите несколько примеров его использования для решения реальных задач программирования. Иногда бывает сложно определить, когда использовать в коде оператор по модулю. Приведенные ниже примеры дадут вам представление о многих способах его использования.
Как проверить, четное или нечетное число
В этом разделе вы увидите, как использовать оператор по модулю, чтобы определить, является ли число четным или нечетным.Используя оператор по модулю с модулем 2 , вы можете проверить любое число, чтобы увидеть, делится ли оно без остатка на 2 . Если оно делится без остатка, то это четное число.
Взгляните на is_even () , который проверяет, является ли параметр num четным:
def is_even (число):
вернуть число% 2 == 0
Здесь num% 2 будет равно 0 , если num четное, и 1 , если num нечетное. Проверка против
Проверка против 0 вернет логическое значение Истина или Ложь в зависимости от того, является ли num четным.
Проверка на нечетные числа очень похожа. Чтобы проверить нечетное число, вы инвертируете проверку равенства:
def is_odd (число):
вернуть число% 2! = 0
Эта функция вернет Истина , если num% 2 не равно 0 , что означает, что остаток доказывает, что num — нечетное число.Теперь вам может быть интересно, можно ли использовать следующую функцию, чтобы определить, является ли num нечетным числом:
def is_odd (число):
вернуть число% 2 == 1
Ответ на этот вопрос — да и нет. Технически эта функция будет работать так же, как Python вычисляет по модулю с целыми числами. Тем не менее, вам следует избегать сравнения результата операции по модулю с 1 , поскольку не все операции по модулю в Python будут возвращать тот же остаток.
Вы можете понять, почему, на следующих примерах:
>>> >>> -3% 2
1
>>> 3% -2
-1
Во втором примере остаток принимает знак отрицательного делителя и возвращает -1 . В этом случае логическая проверка 3% -2 == 1 вернет False .
Однако, если вы сравните операцию по модулю с 0 , то не имеет значения, какой операнд отрицательный. Результатом всегда будет Истинно , когда это четное число:
>>> -2% 2
0
>>> 2% -2
0
Если вы будете сравнивать операцию Python по модулю с 0 , то у вас не должно возникнуть проблем с проверкой четных и нечетных чисел или любых других кратных чисел в вашем коде.
В следующем разделе вы узнаете, как можно использовать оператор по модулю с циклами для управления потоком вашей программы.
Как запускать код с определенными интервалами в цикле
С помощью оператора Python по модулю вы можете запускать код через определенные промежутки времени внутри цикла. 15}», end = «»)
если индекс% модуля == 0:
Распечатать()
Распечатать()
15}», end = «»)
если индекс% модуля == 0:
Распечатать()
Распечатать()
Этот код определяет split_names_into_rows () , который принимает два параметра. список_имён — это список имен, который следует разбить на строки. Модуль устанавливает модуль для операции, эффективно определяя, сколько имен должно быть в каждой строке. split_names_into_rows () будет перебирать name_list и начинать новую строку после достижения значения модуля .
Прежде чем разбирать функцию более подробно, взгляните на нее в действии:
>>> >>> names = ["Пикард", "Райкер", "Трой", "Крашер", "Ворф", "Дейта", "Ла Форж"]
>>> split_names_into_rows (имена)
---- Пикард ----- ----- Райкер ----- ----- Трой ------
---- Дробилка ---- ----- Worf ------ ----- Данные ------
--- Ла Форж ----
Как видите, список имен разделен на три строки, максимум по три имени в каждой строке. Модуль
Модуль по умолчанию 3 , но вы можете указать любое число:
>>> split_names_into_rows (имена, модуль = 4)
---- Пикард ----- ----- Райкер ----- ----- Трой ------ ---- Крашер ----
----- Ворф ------ ----- Данные ------ --- Ла Форж ----
>>> split_names_into_rows (имена, модуль = 2)
---- Пикард ----- ----- Райкер -----
----- Трой ------ ---- Дробилка ----
----- Worf ------ ----- Данные ------
--- Ла Форж ----
>>> split_names_into_rows (имена, модуль = 1)
---- Пикард -----
----- Райкер -----
----- Трой ------
----Дробилка----
----- Ворф ------
-----Данные------
--- Ла Форж ----
Теперь, когда вы увидели код в действии, вы можете разобрать, что он делает.Во-первых, он использует enumerate () для итерации по name_list , присваивая текущий элемент в списке имени и значению счетчика индексу . Вы можете видеть, что необязательный аргумент start для enumerate () имеет значение 1 . Это означает, что счетчик индекса
Это означает, что счетчик индекса начнется с 1 вместо 0 :
для индекса, имя в перечислении (name_list, start = 1):
Затем внутри цикла функция вызывает print () для вывода name в текущую строку.15 Синтаксис указывает print () выполнить следующие действия:
- Выведите не менее
15символов, даже если строка короче 15 символов. - Выровняйте строку по центру.
- Заполните любое пространство справа или слева от строки символом дефиса (
-).
Теперь, когда имя напечатано в строке, взглянем на основную часть split_names_into_rows () :
, если индекс% модуля == 0:
Распечатать()
Этот код берет индекс текущей итерации и, используя оператор по модулю, сравнивает его с модулем .Если результат равен 0 , то он может запустить код, зависящий от интервала. В этом случае функция вызывает
В этом случае функция вызывает print () , чтобы добавить новую строку, которая начинает новую строку.
Приведенный выше код является только одним примером. Использование шаблона index% modulus == 0 позволяет запускать другой код через определенные промежутки времени в ваших циклах. В следующем разделе вы немного углубитесь в эту концепцию и рассмотрите циклическую итерацию.
Как создать циклическую итерацию
Циклическая итерация описывает тип итерации, которая сбрасывается при достижении определенной точки.Как правило, этот тип итерации используется для ограничения индекса итерации определенным диапазоном.
Вы можете использовать оператор по модулю для создания циклической итерации. Взгляните на пример использования библиотеки turtle для рисования формы:
импортная черепаха
случайный импорт
def draw_with_cyclic_iteration ():
colors = ["зеленый", "голубой", "оранжевый", "фиолетовый", "красный", "желтый", "белый"]
turtle. bgcolor ("gray8") # Hex: # 333333
turtle.pendown ()
turtle.pencolor (random.выбор (цвета)) # Первый цвет случайный
i = 0 # Начальный индекс
в то время как True:
i = (i + 1)% 6 # Обновить индекс
turtle.pensize (i) # Установить размер pensize на i
черепаха вперед (225)
черепаха. правая (170)
# Выберите случайный цвет
если я == 0:
turtle.pencolor (random.choice (цвета))
bgcolor ("gray8") # Hex: # 333333
turtle.pendown ()
turtle.pencolor (random.выбор (цвета)) # Первый цвет случайный
i = 0 # Начальный индекс
в то время как True:
i = (i + 1)% 6 # Обновить индекс
turtle.pensize (i) # Установить размер pensize на i
черепаха вперед (225)
черепаха. правая (170)
# Выберите случайный цвет
если я == 0:
turtle.pencolor (random.choice (цвета))
В приведенном выше коде используется бесконечный цикл для рисования повторяющейся формы звезды. Через каждые шесть итераций он меняет цвет пера. Размер пера увеличивается с каждой итерацией, пока i не будет сброшен обратно на 0 .Если запустить код, то должно получиться примерно следующее:
Важные части этого кода выделены ниже:
импортная черепаха
случайный импорт
def draw_with_cyclic_iteration ():
colors = ["зеленый", "голубой", "оранжевый", "фиолетовый", "красный", "желтый", "белый"]
turtle. bgcolor ("gray8") # Hex: # 333333
turtle.pendown ()
turtle.pencolor (random.choice (цвета))
i = 0 # Начальный индекс
в то время как True:
i = (i + 1)% 6 # Обновить индекс
черепаха.pensize (i) # Установить pensize на i
черепаха вперед (225)
черепаха. правая (170)
# Выберите случайный цвет
если я == 0:
turtle.pencolor (random.choice (цвета))
bgcolor ("gray8") # Hex: # 333333
turtle.pendown ()
turtle.pencolor (random.choice (цвета))
i = 0 # Начальный индекс
в то время как True:
i = (i + 1)% 6 # Обновить индекс
черепаха.pensize (i) # Установить pensize на i
черепаха вперед (225)
черепаха. правая (170)
# Выберите случайный цвет
если я == 0:
turtle.pencolor (random.choice (цвета))
Каждый раз при прохождении цикла, i обновляется на основе результатов (i + 1)% 6 . Это новое значение i используется для увеличения .pensize с каждой итерацией. Как только i достигнет 5 , (i + 1)% 6 будет равно 0 , а i вернется к 0 .
Вы можете увидеть шаги итерации ниже для более ясного понимания:
я = 0: (0 + 1)% 6 = 1
я = 1: (1 + 1)% 6 = 2
я = 2: (2 + 1)% 6 = 3
я = 3: (3 + 1)% 6 = 4
я = 4: (4 + 1)% 6 = 5
i = 5: (5 + 1)% 6 = 0 # Сброс
Когда i сбрасывается обратно на 0 , цвет . меняется на новый случайный цвет, как показано ниже: pencolor
pencolor
, если i == 0:
turtle.pencolor (random.choice (цвета))
Код в этом разделе использует 6 в качестве модуля, но вы можете установить его на любое число, чтобы настроить, сколько раз цикл будет повторяться перед сбросом значения i .
Как преобразовать единицы
В этом разделе вы узнаете, как использовать оператор по модулю для преобразования единиц. В следующих примерах единицы меньшего размера преобразуются в единицы большего размера без использования десятичных знаков. Оператор по модулю используется для определения любого остатка, который может существовать, когда меньшая единица не делится без остатка на большую единицу.
В этом первом примере вы преобразуете дюймы в футы. Оператор по модулю используется для получения оставшихся дюймов, которые неравномерно не делятся на футы.Оператор деления пола ( // ) используется для округления общего количества футов в меньшую сторону:
def convert_inches_to_feet (total_inches):
дюймы = total_inches% 12
футов = total_inches // 12
print (f "{total_inches} дюймов = {футов} футов и {дюймов} дюймов")
Вот пример используемой функции:
>>> >>> convert_inches_to_feet (450)
450 дюймов = 37 футов 6 дюймов
Как видно из выходных данных, 450% 12 возвращает 6 , то есть оставшиеся дюймы, которые не были равномерно разделены на футы. Результатом
Результатом 450 // 12 будет 37 , что представляет собой общее количество футов, на которое дюймы были равномерно разделены.
В следующем примере вы можете пойти немного дальше. convert_minutes_to_days () принимает целое число, total_mins , представляющее количество минут, и выводит период времени в днях, часах и минутах:
def convert_minutes_to_days (total_mins):
дней = total_mins // 1440
extra_minutes = total_mins% 1440
часы = extra_minutes // 60
минут = дополнительные_минуты% 60
print (f "{total_mins} = {days} дней, {часов} часов и {минут} минут")
Разбив это, вы можете увидеть, что функция выполняет следующее:
- Определяет общее количество равномерно делимых дней с
total_mins // 1440, где1440- количество минут в дне - Вычисляет любые оставшиеся
extra_minutesсtotal_mins% 1440 - Использует
extra_minutesдля получения равномерно делимыхчасови любых дополнительныхминут
Вы можете увидеть, как это работает, ниже:
>>> >>> convert_minutes_to_days (1503)
1503 = 1 день, 1 час и 3 минуты
>>> convert_minutes_to_days (3456)
3456 = 2 дня, 9 часов и 36 минут
>>> convert_minutes_to_days (35000)
35000 = 24 дня, 7 часов и 20 минут
Хотя в приведенных выше примерах рассматривается только преобразование дюймов в футы и минут в дни, вы можете использовать любые типы единиц с оператором по модулю, чтобы преобразовать меньшую единицу в большую единицу.
Примечание : Оба приведенных выше примера можно изменить, чтобы использовать divmod () , чтобы сделать код более лаконичным. Если вы помните, divmod () возвращает кортеж, содержащий результаты деления по этажам и по модулю с использованием предоставленных параметров.
Ниже операторы деления по этажам и по модулю были заменены на divmod () :
def convert_inches_to_feet_updated (total_inches):
футы, дюймы = divmod (total_inches, 12)
print (f "{total_inches} дюймов = {футов} футов и {дюймов} дюймов")
Как видите, divmod (total_inches, 12) возвращает кортеж, который распакован в футов и дюймов .
Если вы попробуете эту обновленную функцию, то получите те же результаты, что и раньше:
>>> >>> convert_inches_to_feet (450)
450 дюймов = 37 футов 6 дюймов
>>> convert_inches_to_feet_updated (450)
450 дюймов = 37 футов 6 дюймов
Вы получите тот же результат, но теперь код более лаконичный. Вы также можете обновить
Вы также можете обновить convert_minutes_to_days () :
def convert_minutes_to_days_updated (total_mins):
дней, extra_minutes = divmod (total_mins, 1440)
часы, минуты = divmod (extra_minutes, 60)
print (f "{total_mins} = {days} дней, {часов} часов и {минут} минут")
При использовании divmod () функцию легче читать, чем в предыдущей версии, и она возвращает тот же результат:
>>> convert_minutes_to_days (1503)
1503 = 1 день, 1 час и 3 минуты
>>> convert_minutes_to_days_updated (1503)
1503 = 1 день, 1 час и 3 минуты
Использование divmod () необязательно для всех ситуаций, но здесь имеет смысл, поскольку при расчетах преобразования единиц используется как деление по этажам, так и по модулю.
Теперь, когда вы узнали, как использовать оператор по модулю для преобразования единиц, в следующем разделе вы узнаете, как можно использовать оператор по модулю для проверки простых чисел.
Как определить, является ли число простым числом
В следующем примере вы посмотрите, как можно использовать оператор Python по модулю, чтобы проверить, является ли число простым числом . Простое число - это любое число, которое содержит только два делителя: 1 и само себя. Вот некоторые примеры простых чисел: 2 , 3 , 5 , 7 , 23 , 29 , 59 , 83 и 97 .
Код ниже представляет собой реализацию для определения простоты числа с помощью оператора по модулю:
def check_prime_number (число):
если число <2:
print (f "{число} должно быть больше или равно 2, чтобы быть простым.")
возвращение
факторы = [(1, число)]
я = 2
в то время как я * я <= число:
если num% i == 0:
Factors.append ((i, num // i))
я + = 1
если len (факторы)> 1:
print (f "{число} не простое число. Имеет следующие множители: {факторы}")
еще:
print (f "{num} - простое число")
Имеет следующие множители: {факторы}")
еще:
print (f "{num} - простое число")
Этот код определяет check_prime_number () , который принимает параметр num и проверяет, является ли это простым числом.Если это так, то отображается сообщение о том, что num - простое число. Если это не простое число, отображается сообщение со всеми множителями числа.
Примечание: Приведенный выше код не самый эффективный способ проверки простых чисел. Если вы хотите копнуть глубже, посмотрите Сито Эратосфена и Сито Аткина, где можно найти примеры более эффективных алгоритмов поиска простых чисел.
Прежде чем вы более внимательно посмотрите на функцию, вот результаты с использованием некоторых других чисел:
>>> >>> check_prime_number (44)
44 не простое.Он имеет следующие факторы: [(1, 44), (2, 22), (4, 11)]
>>> check_prime_number (53)
53 - простое число
>>> check_prime_number (115)
115 не простое. Он имеет следующие факторы: [(1, 115), (5, 23)]
>>> check_prime_number (997)
997 - простое число
Он имеет следующие факторы: [(1, 115), (5, 23)]
>>> check_prime_number (997)
997 - простое число
Углубившись в код, вы увидите, что он начинается с проверки, меньше ли num 2 . Простые числа могут быть не более 2 . Если num меньше 2 , то выполнение функции не требуется.Он будет print () сообщение и вернет :
, если число <2:
print (f "{число} должно быть больше или равно 2, чтобы быть простым.")
возвращение
Если num больше 2 , то функция проверяет, является ли num простым числом. Чтобы проверить это, функция выполняет итерацию по всем числам от 2 до квадратного корня из num , чтобы увидеть, делятся ли они на num поровну. Если одно из чисел делится равномерно, значит, был найден множитель, и число не может быть простым числом.
Вот основная часть функции:
факторов = [(1, num)]
я = 2
в то время как я * я <= число:
если num% i == 0:
Factors.append ((i, num // i))
я + = 1
Здесь есть что распаковать, так что давайте рассмотрим это шаг за шагом.
Сначала создается список факторов с начальными факторами (1, num) . Этот список будет использоваться для хранения любых других найденных факторов:
Затем, начиная с 2 , код увеличивает i , пока не достигнет квадратного корня из num .На каждой итерации он сравнивает num с i , чтобы увидеть, делится ли оно без остатка. Коду нужно только проверить квадратный корень из num включительно, потому что он не будет содержать никаких множителей выше этого:
я = 2
в то время как я * я <= число:
если num% i == 0:
Factors.append ((i, num // i))
я + = 1
Вместо того, чтобы пытаться определить квадратный корень из num , функция использует цикл while , чтобы проверить, не является ли i * i <= num . Пока
Пока i * i <= num , цикл не достиг квадратного корня из num .
Внутри цикла while оператор по модулю проверяет, делится ли num без остатка на i :
факторов = [(1, num)]
i = 2 # Начать начальный индекс с 2
в то время как я * я <= число:
если num% i == 0:
Factors.append ((i, num // i))
я + = 1
Если num без остатка делится на i , то i является множителем num , и кортеж множителей добавляется в список множителей .
После завершения цикла и код проверяет, были ли найдены какие-либо дополнительные факторы:
если len (факторы)> 1:
print (f "{число} не простое число. Имеет следующие множители: {факторы}")
еще:
print (f "{num} - простое число")
Если в списке факторов существует более одного кортежа, то num не может быть простым числом. Для непростых чисел коэффициенты распечатываются. Для простых чисел функция выводит сообщение о том, что
Для непростых чисел коэффициенты распечатываются. Для простых чисел функция выводит сообщение о том, что num - простое число.
Как реализовать шифры
Оператор модуля Python может использоваться для создания шифров. Шифр - это тип алгоритма для выполнения шифрования и дешифрования входных данных, обычно текста. В этом разделе вы познакомитесь с двумя шифрами: шифром Цезаря и шифром Виженера .
Цезарь Шифр
Первый шифр, на который вы посмотрите, - это шифр Цезаря, названный в честь Юлия Цезаря, который использовал его для тайной передачи сообщений.Это шифр подстановки, который использует подстановку букв для шифрования строки текста.
Шифр Цезаря работает, взяв зашифровываемую букву и сдвинув ее на определенное количество позиций влево или вправо в алфавите. Какая бы буква ни была в этой позиции, используется как зашифрованный символ. Это же значение сдвига применяется ко всем символам в строке.
Например, если сдвиг был 5 , то A сместился бы на пять букв вверх и стал бы F , B стал бы G и так далее.Ниже вы можете увидеть процесс шифрования текста REALPYTHON со сдвигом 5 :
В результате получается шифр WJFQUDYMTS .
Расшифровка шифра выполняется реверсированием сдвига. Процессы шифрования и дешифрования можно описать следующими выражениями, где char_index - это индекс символа в алфавите:
encrypted_char_index = (char_index + shift)% 26
decrypted_char_index = (char_index - сдвиг)% 26
Этот шифр использует оператор по модулю, чтобы гарантировать, что при сдвиге буквы индекс будет повторяться, если будет достигнут конец алфавита.Теперь, когда вы знаете, как работает этот шифр, взгляните на его реализацию:
строка импорта
def caesar_cipher (текст, сдвиг, расшифровка = ложь):
если не text. isascii () или не text.isalpha ():
поднять ValueError ("Текст должен быть в формате ASCII и не содержать чисел.")
нижний регистр = строка.ascii_lowercase
верхний регистр = строка.ascii_uppercase
результат = ""
если расшифровать:
сдвиг = сдвиг * -1
для символа в тексте:
если char.islower ():
index = lowercase.index (char)
результат + = нижний регистр [(индекс + сдвиг)% 26]
еще:
индекс = верхний регистр.индекс (символ)
результат + = верхний регистр [(индекс + сдвиг)% 26]
вернуть результат
isascii () или не text.isalpha ():
поднять ValueError ("Текст должен быть в формате ASCII и не содержать чисел.")
нижний регистр = строка.ascii_lowercase
верхний регистр = строка.ascii_uppercase
результат = ""
если расшифровать:
сдвиг = сдвиг * -1
для символа в тексте:
если char.islower ():
index = lowercase.index (char)
результат + = нижний регистр [(индекс + сдвиг)% 26]
еще:
индекс = верхний регистр.индекс (символ)
результат + = верхний регистр [(индекс + сдвиг)% 26]
вернуть результат
Этот код определяет функцию под названием caesar_cipher () , которая имеет два обязательных параметра и один необязательный параметр:
-
текст- это текст, который нужно зашифровать или расшифровать. -
сдвиг- количество позиций для сдвига каждой буквы. -
decrypt- логическое значение, устанавливаемое, еслитекстдолжен быть расшифрован.
decrypt включен, чтобы можно было использовать одну функцию для обработки как шифрования, так и дешифрования. Эта реализация может обрабатывать только буквенные символы, поэтому функция сначала проверяет, является ли текст буквенным символом в кодировке ASCII:
def caesar_cipher (text, shift, decrypt = False):
если не text.isascii () или не text.isalpha ():
поднять ValueError ("Текст должен быть в формате ASCII и не содержать чисел.")
Затем функция определяет три переменные для хранения строчных символов ASCII, прописных символов ASCII и результатов шифрования или дешифрования:
нижний регистр = строка.ascii_lowercase # "abcdefghijklmnopqrstuvwxyz"
uppercase = string.ascii_uppercase # "ABCDEFGHIJKLMNOPQRSTUVWXYZ"
результат = ""
Затем, если функция используется для расшифровки текста , она умножает shift на -1 , чтобы сдвинуть назад:
если расшифровать:
сдвиг = сдвиг * -1
Наконец, caesar_cipher () перебирает отдельные символы в тексте и выполняет следующие действия для каждого символа :
- Проверьте, является ли
charстрочными или прописными буквами.
- Получить индекс
charв спискахв нижнем регистреилив верхнем регистреASCII. - Добавьте сдвиг
- Используйте
% 26, чтобы убедиться, что сдвиг вернется к началу алфавита. - Добавить зашифрованный символ к строке результата
После завершения цикла итерации по значению текста возвращается результат :
для символов в тексте:
если char.islower ():
index = lowercase.index (char)
результат + = нижний регистр [(индекс + сдвиг)% 26]
еще:
index = uppercase.index (символ)
результат + = верхний регистр [(индекс + сдвиг)% 26]
вернуть результат
Вот еще раз полный код:
строка импорта
def caesar_cipher (текст, сдвиг, расшифровка = ложь):
если не text. isascii () или не text.isalpha ():
поднять ValueError ("Текст должен быть в формате ASCII и не содержать чисел.")
нижний регистр = строка.ascii_lowercase
прописные буквы = строка.ascii_uppercase
результат = ""
если расшифровать:
сдвиг = сдвиг * -1
для символа в тексте:
если char.islower ():
index = lowercase.index (char)
результат + = нижний регистр [(индекс + сдвиг)% 26]
еще:
index = uppercase.index (символ)
результат + = верхний регистр [(индекс + сдвиг)% 26]
вернуть результат
isascii () или не text.isalpha ():
поднять ValueError ("Текст должен быть в формате ASCII и не содержать чисел.")
нижний регистр = строка.ascii_lowercase
прописные буквы = строка.ascii_uppercase
результат = ""
если расшифровать:
сдвиг = сдвиг * -1
для символа в тексте:
если char.islower ():
index = lowercase.index (char)
результат + = нижний регистр [(индекс + сдвиг)% 26]
еще:
index = uppercase.index (символ)
результат + = верхний регистр [(индекс + сдвиг)% 26]
вернуть результат
Теперь запустите код в Python REPL, используя текст meetMeAtOurHideOutAtTwo со сдвигом 10 :
>>> caesar_cipher ("meetMeAtOurHideOutAtTwo", 10)
woodWoKdYebRsnoYedKdDgy
Зашифрованный результат: woodWoKdYebRsnoYedKdDgy .Используя этот зашифрованный текст, вы можете запустить дешифрование, чтобы получить исходный текст:
>>> caesar_cipher ("woodWoKdYebRsnoYedKdDgy", 10, decrypt = True)
MeetMeAtOurHideOutAtTwo
Шифр Цезаря - забавное занятие для введения в криптографию. Хотя шифр Цезаря редко используется сам по себе, он является основой для более сложных подстановочных шифров. В следующем разделе вы познакомитесь с одним из потомков шифра Цезаря, шифром Виженера.
Хотя шифр Цезаря редко используется сам по себе, он является основой для более сложных подстановочных шифров. В следующем разделе вы познакомитесь с одним из потомков шифра Цезаря, шифром Виженера.
Шифр Виженера
Шифр Виженера представляет собой полиалфавитный замещающий шифр. Для шифрования он использует разные шифры Цезаря для каждой буквы входящего текста. Шифр Виженера использует ключевое слово, чтобы определить, какой шифр Цезаря следует использовать для поиска буквы шифра.
Вы можете увидеть пример процесса шифрования на следующем изображении. В этом примере входной текст REALPYTHON зашифрован с использованием ключевого слова MODULO :
Для каждой буквы входящего текста, REALPYTHON , используется буква из ключевого слова MODULO , чтобы определить, какой столбец шифра Цезаря следует выбрать.Если ключевое слово короче вводимого текста, как в случае с MODULO , то буквы ключевого слова повторяются до тех пор, пока все буквы вводимого текста не будут зашифрованы.
Ниже представлена реализация шифра Виженера. Как вы увидите, оператор по модулю используется в функции дважды:
строка импорта
def vigenere_cipher (текст, ключ, decrypt = False):
если не text.isascii () или не text.isalpha () или не text.isupper ():
Raise ValueError ("Текст должен быть в верхнем регистре ASCII без цифр.")
uppercase = string.ascii_uppercase # "ABCDEFGHIJKLMNOPQRSTUVWXYZ"
результаты = ""
для i, символ в перечислении (текст):
current_key = ключ [i% len (ключ)]
char_index = uppercase.index (символ)
key_index = uppercase.index (текущий_ключ)
если расшифровать:
index = char_index - key_index + 26
еще:
index = char_index + key_index
результаты + = верхний регистр [индекс% 26]
вернуть результаты
Вы могли заметить, что подпись для vigenere_cipher () очень похожа на caesar_cipher () из предыдущего раздела:
def vigenere_cipher (текст, ключ, decrypt = False):
если не текст. isascii () или не text.isalpha () или не text.isupper ():
Raise ValueError ("Текст должен быть в верхнем регистре ASCII без цифр.")
верхний регистр = строка.ascii_uppercase
результаты = ""
isascii () или не text.isalpha () или не text.isupper ():
Raise ValueError ("Текст должен быть в верхнем регистре ASCII без цифр.")
верхний регистр = строка.ascii_uppercase
результаты = ""
Основное отличие состоит в том, что вместо параметра shift , vigenere_cipher () принимает параметр ключа , который является ключевым словом, используемым во время шифрования и дешифрования. Еще одно отличие - добавление text.isupper () . На основе этой реализации vigenere_cipher () может принимать только вводимый текст в верхнем регистре.
Подобно caesar_cipher () , vigenere_cipher () выполняет итерацию по каждой букве входного текста, чтобы зашифровать или расшифровать его:
для i, символ в перечислении (текст):
current_key = ключ [i% len (ключ)]
В приведенном выше коде вы можете увидеть, как функция впервые использовала оператор по модулю:
current_key = ключ [i% len (ключ)]
Здесь значение current_key определяется на основе индекса, возвращенного из i% len (key) . Этот индекс используется для выбора буквы из строки ключа
Этот индекс используется для выбора буквы из строки ключа , например M из MODULO .
Оператор по модулю позволяет использовать ключевое слово любой длины независимо от длины текста , который нужно зашифровать. Как только индекс i , индекс символа, который в настоящее время зашифрован, равен длине ключевого слова, он начнется с начала ключевого слова.
Для каждой буквы входящего текста несколько шагов определяют, как ее зашифровать или расшифровать:
- Определите
char_indexна основе индексаcharвнутрив верхнем регистре. - Определите
key_indexна основе индексаcurrent_keyвнутрив верхнем регистре. - Используйте
char_indexиkey_index, чтобы получить индекс для зашифрованного или дешифрованного символа.
Взгляните на эти шаги в приведенном ниже коде:
char_index = uppercase. index (char)
key_index = uppercase.index (текущий_ключ)
если расшифровать:
index = char_index - key_index + 26
еще:
index = char_index + key_index
index (char)
key_index = uppercase.index (текущий_ключ)
если расшифровать:
index = char_index - key_index + 26
еще:
index = char_index + key_index
Как видите, индексы для расшифровки и шифрования рассчитываются по-разному.Вот почему в этой функции используется расшифровка . Таким образом, вы можете использовать эту функцию как для шифрования, так и для дешифрования.
После определения индекса вы обнаружите, что функция использует второй оператор по модулю:
результаты + = верхний регистр [индекс% 26]
index% 26 гарантирует, что индекс символа не превышает 25 , таким образом гарантируя, что он остается внутри алфавита. С помощью этого индекса зашифрованный или дешифрованный символ выбирается из в верхнем регистре и добавляется к результатам .
Вот еще раз полный код шифра Виженера:
строка импорта
def vigenere_cipher (текст, ключ, decrypt = False):
если не text. isascii () или не text.isalpha () или не text.isupper ():
Raise ValueError ("Текст должен быть в верхнем регистре ASCII без цифр.")
uppercase = string.ascii_uppercase # "ABCDEFGHIJKLMNOPQRSTUVWXYZ"
результаты = ""
для i, символ в перечислении (текст):
current_key = ключ [i% len (ключ)]
char_index = uppercase.index (символ)
key_index = прописные буквы.индекс (текущий_ключ)
если расшифровать:
index = char_index - key_index + 26
еще:
index = char_index + key_index
результаты + = верхний регистр [индекс% 26]
вернуть результаты
isascii () или не text.isalpha () или не text.isupper ():
Raise ValueError ("Текст должен быть в верхнем регистре ASCII без цифр.")
uppercase = string.ascii_uppercase # "ABCDEFGHIJKLMNOPQRSTUVWXYZ"
результаты = ""
для i, символ в перечислении (текст):
current_key = ключ [i% len (ключ)]
char_index = uppercase.index (символ)
key_index = прописные буквы.индекс (текущий_ключ)
если расшифровать:
index = char_index - key_index + 26
еще:
index = char_index + key_index
результаты + = верхний регистр [индекс% 26]
вернуть результаты
Теперь запустите его в Python REPL:
>>> >>> vigenere_cipher (text = "REALPYTHON", key = "MODULO")
DSDFAMFVRH
>>> encrypted = vigenere_cipher (text = "REALPYTHON", key = "MODULO")
>>> печать (в зашифрованном виде)
DSDFAMFVRH
>>> vigenere_cipher (зашифровано, "MODULO", decrypt = True)
РЕАЛПИТОН
Отлично! Теперь у вас есть рабочий шифр Виженера для шифрования текстовых строк.
Расширенное использование оператора модуля Python
В этом последнем разделе вы поднимете свои знания об операторах по модулю на новый уровень, используя их с десятичным числом . Десятичное число . Вы также узнаете, как добавить .__ mod __ () к своим пользовательским классам, чтобы их можно было использовать с оператором по модулю.
Использование оператора модуля Python с десятичным числом
. Десятичное число Ранее в этом руководстве вы видели, как можно использовать оператор по модулю с числовыми типами, такими как int и float , а также с математикой .fmod () . Вы также можете использовать оператор по модулю с Decimal из модуля decimal . Вы используете decimal.Decimal , когда вам нужно дискретное управление точностью арифметических операций с плавающей запятой.
Вот несколько примеров использования целых чисел с десятичным числом , десятичным числом и оператором по модулю:
>>> импортировать десятичный
>>> десятичное. Десятичное (15)% десятичное.Десятичное (4)
Десятичный ('3')
>>> десятичный.Десятичный (240)% десятичный. Десятичный (13)
Десятичный ('6')
Десятичное (15)% десятичное.Десятичное (4)
Десятичный ('3')
>>> десятичный.Десятичный (240)% десятичный. Десятичный (13)
Десятичный ('6')
Вот некоторые числа с плавающей запятой, используемые с десятичным числом . Десятичное число и оператор по модулю:
>>> decimal.Decimal ("12,5")% decimal.Decimal ("5.5")
Десятичный ('1,5')
>>> decimal.Decimal ("13.3")% decimal.Decimal ("1.1")
Десятичный ('0,1')
Все операции по модулю с десятичным числом . Десятичное число возвращают те же результаты, что и другие числовые типы, за исключением случаев, когда один из операндов отрицательный.В отличие от int и float , но как math.fmod () , decimal. Decimal использует знак делимого для результатов.
Взгляните на приведенные ниже примеры, в которых сравниваются результаты использования оператора по модулю со стандартными значениями int и float и с десятичными числами .: Decimal
Decimal
>>> -17% 3
1 # Знак делителя
>>> десятичное.Десятичное (-17)% десятичное.Десятичное (3)
Десятичный (-2) # Знак дивиденда
>>> 17% -3
-1 # Знак делителя
>>> десятичный.Десятичный (17)% десятичный. Десятичный (-3)
Десятичный ("2") # Знак дивиденда
>>> -13,3% 1,1
1.0000000000000004 # Знак делителя
>>> decimal.Decimal ("- 13,3")% decimal.Decimal ("1,1")
Десятичный ("- 0,1") # Знак дивиденда
По сравнению с math.fmod () , десятичное. Десятичное число будет иметь тот же знак, но точность будет другой:
>>> decimal.Decimal ("- 13,3")% decimal.Decimal ("1,1")
Десятичный ("- 0,1")
>>> математика.fmod (-13,3, 1,1)
-0,09999999999999964
Как видно из приведенных выше примеров, работа с десятичным числом , десятичным числом и оператором по модулю аналогична работе с другими числовыми типами. Просто нужно иметь в виду, как он определяет знак результата при работе с отрицательным операндом.
В следующем разделе вы узнаете, как можно переопределить оператор по модулю в своих классах, чтобы настроить его поведение.
Использование оператора Python Modulo с настраиваемыми классами
Модель данных Python позволяет вам переопределить встроенные методы в объекте Python, чтобы настроить его поведение.В этом разделе вы узнаете, как переопределить .__ mod __ () , чтобы вы могли использовать оператор по модулю со своими собственными классами.
В этом примере вы будете работать с классом Студент . Этот класс будет отслеживать количество времени, которое студент учился. Вот начальный Студент класса:
класс Студент:
def __init __ (я, имя):
self.name = имя
self.study_sessions = []
def add_study_sessions (самостоятельно, сеансы):
себя.study_sessions + = сеансы
Класс Student инициализируется параметром name и начинается с пустого списка study_sessions , который будет содержать список целых чисел, представляющих количество минут, изученных за сеанс. Также существует
Также существует .add_study_sessions () , который принимает параметр sessions , который должен быть списком учебных сессий, который нужно добавить к study_sessions .
Теперь, если вы помните из раздела преобразования единиц выше, convert_minutes_to_day () использовал оператор Python по модулю для преобразования total_mins в дни, часы и минуты.Теперь вы реализуете модифицированную версию этого метода, чтобы увидеть, как можно использовать собственный класс с оператором по модулю:
def total_study_time_in_hours (студент, всего_мин.):
часы = total_mins // 60
минут = total_mins% 60
print (f "{student.name} изучил {часы} часы и {минуты} минуты")
Эту функцию можно использовать с классом Студент , чтобы отобразить общее количество часов, которые изучил Студент . В сочетании с классом Student выше код будет выглядеть следующим образом:
класс Студент:
def __init __ (я, имя):
себя. name = имя
self.study_sessions = []
def add_study_sessions (самостоятельно, сеансы):
self.study_sessions + = сеансы
def total_study_time_in_hours (студент, total_mins):
часы = total_mins // 60
минут = total_mins% 60
print (f "{student.name} изучил {часы} часы и {минуты} минуты")
name = имя
self.study_sessions = []
def add_study_sessions (самостоятельно, сеансы):
self.study_sessions + = сеансы
def total_study_time_in_hours (студент, total_mins):
часы = total_mins // 60
минут = total_mins% 60
print (f "{student.name} изучил {часы} часы и {минуты} минуты")
Если вы загрузите этот модуль в Python REPL, то можете использовать его так:
>>> >>> jane = Студент ("Джейн")
>>> jane.add_study_sessions ([120, 30, 56, 260, 130, 25, 75])
>>> total_mins = сумма (джейн.study_sessions)
>>> total_study_time_in_hours (Джейн, total_mins)
Джейн занималась 11 часов 36 минут
Приведенный выше код распечатывает общее количество часов, которые изучала Джейн . Эта версия кода работает, но требует дополнительного шага суммирования study_sessions , чтобы получить total_mins перед вызовом total_study_time_in_hours () .
Вот как можно изменить класс Student , чтобы упростить код:
класс Студент:
def __init __ (я, имя):
себя. name = имя
self.study_sessions = []
def add_study_sessions (самостоятельно, сеансы):
self.study_sessions + = сеансы
def __mod __ (себя, другое):
возвратная сумма (self.study_sessions)% other
def __floordiv __ (я, другой):
возвратная сумма (self.study_sessions) // другое
name = имя
self.study_sessions = []
def add_study_sessions (самостоятельно, сеансы):
self.study_sessions + = сеансы
def __mod __ (себя, другое):
возвратная сумма (self.study_sessions)% other
def __floordiv __ (я, другой):
возвратная сумма (self.study_sessions) // другое
Переопределив .__ mod __ () и .__ floordiv __ () , вы можете использовать экземпляр Student с оператором по модулю. Вычисление суммы () из study_sessions также включен в класс Student .
С этими изменениями вы можете использовать экземпляр Student непосредственно в total_study_time_in_hours () . Поскольку total_mins больше не нужен, вы можете удалить его:
def total_study_time_in_hours (студент):
часы = студент // 60
минут = студент% 60
print (f "{student.name} изучил {часы} часы и {минуты} минуты")
Вот полный код после изменений:
класс Студент:
def __init __ (я, имя):
себя. name = имя
self.study_sessions = []
def add_study_sessions (самостоятельно, сеансы):
self.study_sessions + = сеансы
def __mod __ (себя, другое):
возвратная сумма (self.study_sessions)% other
def __floordiv __ (я, другой):
возвратная сумма (self.study_sessions) // другое
def total_study_time_in_hours (студент):
часы = студент // 60
минут = студент% 60
print (f "{student.name} изучил {часы} часы и {минуты} минуты")
name = имя
self.study_sessions = []
def add_study_sessions (самостоятельно, сеансы):
self.study_sessions + = сеансы
def __mod __ (себя, другое):
возвратная сумма (self.study_sessions)% other
def __floordiv __ (я, другой):
возвратная сумма (self.study_sessions) // другое
def total_study_time_in_hours (студент):
часы = студент // 60
минут = студент% 60
print (f "{student.name} изучил {часы} часы и {минуты} минуты")
Теперь, вызвав код в Python REPL, вы увидите, что он гораздо лаконичнее:
>>> >>> jane = Студент ("Джейн")
>>> Джейн.add_study_sessions ([120, 30, 56, 260, 130, 25, 75])
>>> total_study_time_in_hours (Джейн)
Джейн занималась 11 часов 36 минут
Переопределяя .__ mod __ () , вы позволяете своим пользовательским классам вести себя больше как встроенные числовые типы Python.
Заключение
На первый взгляд, оператор по модулю Python может не привлечь ваше внимание. Тем не менее, как вы видели, в этом скромном операторе есть так много всего. Вы видели множество различных применений оператора по модулю, от проверки четных чисел до шифрования текста.
Тем не менее, как вы видели, в этом скромном операторе есть так много всего. Вы видели множество различных применений оператора по модулю, от проверки четных чисел до шифрования текста.
Из этого руководства вы узнали, как:
- Используйте оператор по модулю с
int,float,math.fmod (),divmod ()иdecimal. Decimal - Вычислить результаты операции по модулю
- Решите реальных проблем с помощью оператора по модулю
- Переопределить
.__ mod __ ()в ваших собственных классах, чтобы использовать их с оператором по модулю
Знания, полученные в этом руководстве, позволяют теперь с большим успехом начать использовать оператор по модулю в собственном коде.Удачного питонинга!
ФункцияMOD
В этой статье описаны синтаксис формулы и использование функции MOD в Microsoft Excel.
Описание
Возвращает остаток от деления числа на делитель. Результат имеет тот же знак, что и делитель.
Синтаксис
MOD (число, делитель)
Аргументы функции MOD имеют следующие аргументы:
Замечания
Если делитель равен 0, MOD возвращает # DIV / 0! значение ошибки.
Функцию MOD можно выразить через функцию INT:
MOD (n, d) = n - d * INT (n / d)
Пример
Скопируйте данные примера из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы формулы отображали результаты, выберите их, нажмите F2, а затем нажмите Enter. При необходимости вы можете настроить ширину столбца, чтобы увидеть все данные.
Формула | Описание | Результат |
|---|---|---|
= МОД (3, 2) | Остаток от 3/2 | 1 |
= МОД (-3, 2) | Остаток -3/2. | 1 |
= МОД (3, -2) | Остаток от 3 / -2. Знак такой же, как у делителя | –1 |
= МОД (-3, -2) | Остаток -3 / -2.Знак такой же, как у делителя | –1 |
2.0 Прогнозные модели - Расчетный параметр LTPP: динамический модуль, сентябрь 2011 г.
2.0 ПРОГНОЗНЫЕ МОДЕЛИ
Было разработано несколько альтернативных прогнозных соотношений для оценки | E * | из более простых свойств материала и объема. Эти прогнозные отношения могут использоваться для заполнения базы данных LTPP с оценкой | E * | ценности. В таблице 1 перечислены прогнозные взаимосвязи, выявленные исследовательской группой. Эти отношения кратко описаны в следующих подразделах.
Эти прогнозные отношения могут использоваться для заполнения базы данных LTPP с оценкой | E * | ценности. В таблице 1 перечислены прогнозные взаимосвязи, выявленные исследовательской группой. Эти отношения кратко описаны в следующих подразделах.
| Номер модели | Модель |
|---|---|
| 1 | Исходное уравнение Витчака (NCHRP 1-37A) (2,11) |
| 2 | Модифицированный Витчак | G * | уравнение (NCHRP 1-40D) (5) |
| 3 | Модель Hirsch (6) |
| 4 | Закон смесей Параллельная модель (7) |
| 5 | Модель ИНС |
| 6 | M R - | E * | модель |
2.
 1 ИСХОДНОЕ УРАВНЕНИЕ ВИТЧАКА (NCHRP 1-37A)
1 ИСХОДНОЕ УРАВНЕНИЕ ВИТЧАКА (NCHRP 1-37A)Андрей и др. переработанный оригинальный Witczak | E * | Уравнение прогнозирования на основе данных 205 смесей с 2750 точками данных. (11) Пересмотренное уравнение выглядит следующим образом:
| (1) |
Где:
| p 200 | = | Процент заполнителя, прошедшего через сито № 200. |
|---|---|---|
| p 4 | = | Процент заполнителя, оставшегося на сите №4. |
| стр 3/8 | = | Процент заполнителя, оставшегося в сите 3 / 8 дюймов - (9,56 мм). |
| p ¾ | = | Процент оставшегося заполнителя в дюйма (19. 01-мм) сито. 01-мм) сито. |
| V a | = | Процент воздушных пустот (по объему смеси). |
| В beff | = | Процент эффективного содержания асфальта (по объему смеси). |
| f | = | Частота нагрузки (герцы). |
| η | = | Вязкость связующего при интересующей температуре (10 6 P (10 5 Па). |
Уравнение Витчака основано на нелинейном регрессионном анализе с использованием обобщенного подхода оптимизации сокращенного градиента в Решателе Microsoft® Excel. Эта модель включает в себя объемные параметры смеси и градацию агрегатов и в настоящее время является одним из двух вариантов анализа уровня 3 с использованием программы NCHRP 1-37A MEPDG. (2) Для вязкостного члена в уравнении 1 программа преобразует все входные данные уровня 2 и 3 в значения регрессии с пересечением-регрессией для значений вязкости и температурной восприимчивости (A-VTS) для формулировки | E * | mastercurve.Кроме того, модель Витчака имеет уравнение (не указано) для преобразования коэффициентов A-VTS из первичных или резервуарных связующих в значения RTFO- и PAV-состаренных связующих.
(2) Для вязкостного члена в уравнении 1 программа преобразует все входные данные уровня 2 и 3 в значения регрессии с пересечением-регрессией для значений вязкости и температурной восприимчивости (A-VTS) для формулировки | E * | mastercurve.Кроме того, модель Витчака имеет уравнение (не указано) для преобразования коэффициентов A-VTS из первичных или резервуарных связующих в значения RTFO- и PAV-состаренных связующих.
Ограничения уравнения Витчака, признанные Бари, включают использование других моделей для перевода используемых в настоящее время | G * | измерение вязкости связующего. (5) Поскольку исходное уравнение прогнозирования Вицчака основано на регрессионном анализе, экстраполяция за пределы базы данных калибровки должна быть ограничена.Бари также упоминает об ограниченном влиянии объема (точности) при сравнении модели с моделью Shell Oil. (5) Другие исследователи также отметили необходимость повышения чувствительности к объемным параметрам, таким как процент пустот в минеральном заполнителе (VMA), процент пустот, заполненных асфальтом (VFA), процент асфальтобетона (AC) и V a . (12)
(12)
2.2 МОДИФИЦИРОВАННОЕ УРАВНЕНИЕ ВИТЧАКА НА ОСНОВЕ |
G * | (НЧРП 1-40Д) (5)Включить связующее | G * | В прогнозной модели Витчак переформулировал модель, включив непосредственно связующую переменную.Обновленная модель выглядит следующим образом:
| (2) |
Где:
| G * | б | = | Динамический модуль сдвига асфальтового вяжущего (фунтов на квадратный дюйм). |
|---|---|---|
| δ б | = | Фазовый угол связующего, связанный с | G * | b (градусы). |
Как и модель NCHRP 1-37A, уравнение 2 основано на нелинейном регрессионном анализе с использованием 346 смесей с 7400 точками данных. Результаты измерений для немодифицированных связующих лучше коррелируют с моделью (R 2 = 0,87) по сравнению с результатами для модифицированных связующих (R 2 = 0,79) в арифметической шкале. В логарифмическом масштабе оба типа связующего имеют R 2 = 0,99. Фазовый угол связки прогнозируется с помощью эмпирического уравнения (R 2 = 0.83). Это уравнение является одним из двух вариантов анализа уровня 3 в самой последней программе MEPDG.
Результаты измерений для немодифицированных связующих лучше коррелируют с моделью (R 2 = 0,87) по сравнению с результатами для модифицированных связующих (R 2 = 0,79) в арифметической шкале. В логарифмическом масштабе оба типа связующего имеют R 2 = 0,99. Фазовый угол связки прогнозируется с помощью эмпирического уравнения (R 2 = 0.83). Это уравнение является одним из двух вариантов анализа уровня 3 в самой последней программе MEPDG.
Поскольку некоторые смеси в этой базе данных не содержат | G * | b данных, правило Кокса-Мерца, использующее поправочные коэффициенты для неньютоновского поведения (см. Уравнения 3–5), используется для расчета | G * | - b из значений A-VTS:
| (3) |
| (4) |
| (5) |
Где:
| f s | = | Частота динамического сдвига. |
|---|---|---|
| δ б | = | Фазовый угол связующего, рассчитанный из уравнения 4 (градусы). |
| η fs, T | = | Вязкость асфальтового вяжущего при определенной частоте нагружения ( f s ) и температуре ( T ), определяемая по уравнению 5 (сантипуаз). |
| T R | = | Температура по шкале Ренкина. |
2.3 МОДЕЛЬ HIRSCH
Christensen et al. изучили четыре различные модели, основанные на параллельной модели закона смесей, и выбрали модель, которая включает модуль связки, VMA и VFA, поскольку она обеспечивает точные результаты в простейшей форме. (6,7) В других, более сложных формах делается попытка включить модуль упругости мастики или толщину пленки, которые трудно измерить. Предлагаемая модель для | E * | оценка представлена в уравнениях 6–8 следующим образом:
Предлагаемая модель для | E * | оценка представлена в уравнениях 6–8 следующим образом:
| (6) |
| (7) |
| (8) |
Где:
| | E * | м | = | Динамический модуль HMA (фунтов на квадратный дюйм). |
|---|---|---|
| P c | = | Совокупный контактный объем. |
| ø | = | Фазовый угол HMA. |
Сильной стороной этой модели является эмпирическое уравнение фазового угла, которое важно для взаимного преобразования | E * | модулю релаксации или податливости ползучести. К недостаткам модели можно отнести отсутствие сильной зависимости от объемных параметров, особенно при низких V, , , и условиях VFA.Также возникают вопросы относительно способности | G * | b Параметр для учета возможных положительных эффектов модификаторов. (7) Следует отметить, что только 206 точек данных использовались для определения коэффициентов в модели Хирша по сравнению с 2750 точками данных для исходной модели Витчака и 7400 точками данных для модифицированной модели Витчака.
К недостаткам модели можно отнести отсутствие сильной зависимости от объемных параметров, особенно при низких V, , , и условиях VFA.Также возникают вопросы относительно способности | G * | b Параметр для учета возможных положительных эффектов модификаторов. (7) Следует отметить, что только 206 точек данных использовались для определения коэффициентов в модели Хирша по сравнению с 2750 точками данных для исходной модели Витчака и 7400 точками данных для модифицированной модели Витчака.
2.4 ЗАКОН СМЕСЕЙ ПАРАЛЛЕЛЬНАЯ МОДЕЛЬ (МОДЕЛЬ АЛЬ-ХАТИБА)
Основываясь на своих выводах по модели Хирша, Аль-Хатиб и др.предлагаем следующую модель: (7)
| (9) |
Где:
| | G * | г | = | Динамический модуль сдвига асфальтового вяжущего в стекловидном состоянии (предполагается, что он составляет 145 000 фунтов на квадратный дюйм (999 050 кПа). |
|---|
Как и модель Хирша, эта формулировка основана на законе смесей для композиционных материалов.В этой модели считается, что различные материальные фазы (заполнитель, асфальтовое вяжущее и воздух) существуют параллельно. Следовательно, эта модель представляет собой более простую интерпретацию модели Хирша. Исследователи отмечают, что их модель устраняет один из основных недостатков модели Хирша (то есть неспособность модели Хирша точно предсказать | E * | смеси при низких частотах и высоких температурах).
К сильным сторонам этой модели можно отнести улучшенное предсказание высокотемпературных и низкочастотных | E * | данные для смесей, используемых в тест-полосках FHWA ускоренной загрузки (ALF).Слабые стороны включают отсутствие проверки модели и тот факт, что исследователи, разработавшие эту модель, сделали это на основе | E * | значения, полученные в результате испытаний при более высоких, чем рекомендованные, амплитудах деформации (200 µε по сравнению с рекомендуемым максимумом 75–150 µε).
2.5 ANN МОДЕЛИ
Исследовательская группа NCSU использовала метод ANN для разработки новых | E * | прогнозные модели. Основное преимущество этого подхода перед статистической регрессией состоит в том, что функциональная форма взаимосвязи не нужна априори.Учитывая, что на | E * | влияет так много переменных, значений и их взаимодействия, метод ИНС фиксирует сложные нелинейные отношения между | E * | и другие смешанные переменные лучше, чем регрессионный анализ.
Техника ИНС использовалась в этом исследовании для разработки нескольких различных моделей. Первая модель - это модель ИНС, которая предсказывает | E * | значения с использованием входных переменных, используемых в модифицированном уравнении Витчака (то есть, динамический модуль упругости связующего и фазовый угол, градация агрегатов и объемные характеристики смеси HMA).Усилия по разработке этой модели ИНС описаны далее в этом отчете. Для обратного вычисления | E * | значения от M R . Во время проекта FHWA DTFH61-05-RA-00108 исследовательская группа NCSU разработала механистический подход для вычисления M R из | E * | HMA. (13,14) Этот подход был успешно проверен с использованием данных измерений для смесей с различными градациями и характеристиками связующего.Проверенные решения затем были применены к доступному | E * | базы данных для оценки значений M R , соответствующих | E * | ценности. Эта база данных была использована для разработки обратного алгоритма, основанного на методе ИНС, который может предсказывать | E * | с M R . Разработка и проверка M R - | E * | ИНС представлены далее в этом отчете. Наконец, метод ИНС был использован для разработки | E * | прогнозная модель, основанная на информации о вязкости связующего.Эта модель ИНС также описана в этом отчете.
Во время проекта FHWA DTFH61-05-RA-00108 исследовательская группа NCSU разработала механистический подход для вычисления M R из | E * | HMA. (13,14) Этот подход был успешно проверен с использованием данных измерений для смесей с различными градациями и характеристиками связующего.Проверенные решения затем были применены к доступному | E * | базы данных для оценки значений M R , соответствующих | E * | ценности. Эта база данных была использована для разработки обратного алгоритма, основанного на методе ИНС, который может предсказывать | E * | с M R . Разработка и проверка M R - | E * | ИНС представлены далее в этом отчете. Наконец, метод ИНС был использован для разработки | E * | прогнозная модель, основанная на информации о вязкости связующего.Эта модель ИНС также описана в этом отчете.
2.6 СВОДКА ВХОДНЫХ ПЕРЕМЕННЫХ
В таблице 2 представлены необходимые входные переменные для каждой прогнозируемой взаимосвязи, описанной ранее. Для моделей, использующих | G * | b , прогнозы возможны только при температурах и частотах, где | G * | b значений. Имея | G * | b только в условиях, используемых в тестировании Superpave ™, недостаточно для генерации | E * | значения в диапазоне условий, обычно необходимых для механистического анализа (14–129.2 ° F (-10–54 ° C)). Например, если у пользователя есть | G * | b только при 147,2 ° F (64 ° C) и 10 радианах в секунду (рад / с), тогда можно предсказать | E * | значение только при 147,2 ° F (64 ° C) и 10 рад / с. Предсказать | E * | при 77 ° F (25 ° C) и 25 рад / с пользователь должен измерить | G * | b при 77 ° F (25 ° C) и 25 рад / с.
Для моделей, использующих | G * | b , прогнозы возможны только при температурах и частотах, где | G * | b значений. Имея | G * | b только в условиях, используемых в тестировании Superpave ™, недостаточно для генерации | E * | значения в диапазоне условий, обычно необходимых для механистического анализа (14–129.2 ° F (-10–54 ° C)). Например, если у пользователя есть | G * | b только при 147,2 ° F (64 ° C) и 10 радианах в секунду (рад / с), тогда можно предсказать | E * | значение только при 147,2 ° F (64 ° C) и 10 рад / с. Предсказать | E * | при 77 ° F (25 ° C) и 25 рад / с пользователь должен измерить | G * | b при 77 ° F (25 ° C) и 25 рад / с.
| Описание переменной | Номер модели | Доступность данных LTPP | ||||||
|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | Специальное исследование дорожного покрытия (SPS) 1 | Общее исследование дорожного покрытия (GPS) 1 | |
| Смесь M R | Х | Есть | Есть | |||||
| | G * | б | Х | Х | Х | Х | Есть 2 | Нет | ||
| σ b | Х | Х | Есть | Нет | ||||
| VMA (в процентах) | Х | Х | Есть | Есть 4 | ||||
| VFA (в процентах) | Х | Есть | Есть 4 | |||||
| Проходящий заполнитель # 200 сито (в процентах) | Х | Х | Х | Есть | Есть | |||
| Агрегат, проходящий через сито №4 (в процентах) | Х | Х | Х | Есть | Есть | |||
| Проходящий заполнитель 3 / 8 -дюймовое сито (в процентах) | Х | Х | Х | Есть | Есть | |||
| Прохождение заполнителя через сито ¾ дюйма (проценты) | Х | Х | Х | Есть | Есть | |||
| V a (по объему смеси ( V смесь )) (в процентах) | Х | Х | Х | Есть | Есть | |||
| Эффективное содержание асфальта (к общему объему смеси) (в процентах) | Х | Х | Х | Есть | Есть 4 | |||
| Частота нагрузки (Гц) | Х | Есть | Нет | |||||
| А-ВТС | Х | Есть 3 | Есть 5 | |||||
1 дюйм = 25. | ||||||||
Предварительный обзор доступной информации в базе данных материалов LTPP показал, что измеренные | G * | b данные доступны только для большинства проектов SPS-9 и только при 10 рад / с при различных температурах. Даже имеющиеся | G * | b данные получены для связующих, выдержанных на разных уровнях (т.е. связующие, выдержанные при RTFO, и связующие, выдержанные на основе PAV). Отсутствие полного | G * | b данные при различных температурах и частотах представляют собой серьезную проблему, потому что все модели, кроме исходного уравнения Витчака, требуют этой информации. (Обратите внимание, что модель M R - | E * | ANN также нуждается в коэффициенте сдвига tT связующего.) В ходе этого проекта исследовательская группа NCSU разработала эмпирические модели, которые позволяют оценить RTFO в возрасте | G * | b значений при различных температурах и частотах из | G * | b значений, полученных при одной частоте и нескольких уровнях температуры и старения.
Даже имеющиеся | G * | b данные получены для связующих, выдержанных на разных уровнях (т.е. связующие, выдержанные при RTFO, и связующие, выдержанные на основе PAV). Отсутствие полного | G * | b данные при различных температурах и частотах представляют собой серьезную проблему, потому что все модели, кроме исходного уравнения Витчака, требуют этой информации. (Обратите внимание, что модель M R - | E * | ANN также нуждается в коэффициенте сдвига tT связующего.) В ходе этого проекта исследовательская группа NCSU разработала эмпирические модели, которые позволяют оценить RTFO в возрасте | G * | b значений при различных температурах и частотах из | G * | b значений, полученных при одной частоте и нескольких уровнях температуры и старения.
Модуль комплексного числа: определение и примеры - видео и стенограмма урока
Нахождение модуля
Обратите внимание, что вектор, представляющий комплексное число a + bi , также является гипотенузой (или самым длинным катетом) прямоугольного треугольника с более короткими сторонами длиной a и b .
Из-за этого есть хорошо известная теорема, которую мы можем использовать, чтобы найти общую формулу для модуля комплексного числа.Эта теорема и есть теорема Пифагора. Теорема Пифагора гласит: «Если прямоугольный треугольник имеет длину сторон a , b и c , где c - гипотенуза или самая длинная сторона, то a 2 + b . 2 = c 2. ''
Если c является модулем комплексного числа, a + bi , то теорема Пифагора дает a 2 + b 2 = c 2.Если извлечь квадратный корень из обеих частей этого уравнения, мы получим следующее:
c = √ ( a 2 + b 2)
Это дает нам общую формулу для модуля комплексного числа a + bi . Поскольку он описывает длину, вы можете видеть, что √ ( a 2 + b 2) даст нам только положительное действительное число или ноль для модуля. Давайте посмотрим на несколько примеров нахождения модуля комплексных чисел.
Давайте посмотрим на несколько примеров нахождения модуля комплексных чисел.
Некоторые примеры
Предположим, что мы хотим найти модуль комплексного числа 3-4 i . Все, что нам нужно сделать, это определить a и b , а затем вставить эти значения в нашу формулу для модуля. В 3 - 4 i , a = 3 и b = -4. Подстановка их в формулу дает следующее:
c = √ ((3) 2 + (-4) 2) = √ (9 + 16) = √ (25) = 5
Мы получаем, что модуль комплексное число 3-4 i равно 5.Эта формула, несомненно, упрощает задачу!
Рассмотрим другой пример. В этом примере мы хотим найти модуль комплексного числа, показанного на графике ниже.
График комплексного числа - точка (2, 7). Это говорит нам, что a = 2 и b = 7, поэтому мы имеем дело с комплексным числом 2 + 7 i . Чтобы найти модуль, мы просто подставляем a = 2 и b = 7 в нашу формулу:
c = √ (22 + 72) = √ (4 + 49) = √ (53) ≈ 7. 28
28
Модуль комплексного числа, показанного на графике, равен √ (53), или приблизительно 7,28. Я думаю, мы уже разбираемся в этом!
Краткое содержание урока
Комплексное число - это число в форме a + bi , где a и b - действительные числа, а i - мнимое число √ (-1) . Мы можем изобразить комплексное число a + bi на комплексной плоскости, нанеся точку ( a , b ) на комплексной плоскости.Это дает модуль комплексного числа.
Если мы проведем отрезок прямой от начала комплексной плоскости до построенного на графике комплексного числа ( a , b ), мы создадим вектор , представляющий комплексное число a + bi . Модуль , c , a + bi - это длина этого направленного отрезка прямой или величина вектора, и его можно найти по следующей формуле:
c = √ ( a 2 + b 2)
Какая изящная концепция! В математике всегда прекрасно, когда все складывается таким образом и обнаруживаются взаимосвязи между концепциями. Давайте уберем эти новообретенные знания в наш набор инструментов для умственной математики для использования в будущем!
Давайте уберем эти новообретенные знания в наш набор инструментов для умственной математики для использования в будущем!
Упрощенное уравнение для модуля Юнга армированного УНТ бетона: AIP Advances: Том 7, № 12
Углеродные нанотрубки (УНТ) получили широкое распространение и признание во всем мире после их изобретения Иидзимой (1991). Эти бесшовные трубы 21 st век 1 1. Hasan et al. , «Расчет прочности на сжатие композита УНТ / цемент», Международный журнал гражданского строительства 9 (3), 223–229 (2011).Обладая чрезвычайно высокими механическими свойствами, находят применение в электронике, биологии, химии и многофункциональных композитах. УНТ представляют собой прокатанные листы графена, обладающие высокой теоретической прочностью, то есть в 100 раз больше, чем у стали, с удельным весом 1/6 и стали, упругой деформацией 12%, модулем Юнга 1 ТПа и пределом прочности при растяжении 200 ГПа. Было обнаружено, что УНТ используются в качестве армирующих волокон, 2 2. Л. Я. Чан, «Механическое определение характеристик бетона, армированного углеродными нанотрубками, с использованием метода конечных элементов.”Значительно улучшая механические свойства любого основного материала. Предел прочности при растяжении и изгибе цементных композитов определялся методом смесей. Модуль Юнга композитов, армированных УНТ, был рассчитан Rouiania et.al. 3 3. Rouiana et al. , «Оценка модуля Юнга композитного бетона, армированного однослойными углеродными нанотрубками», Журнал технических и прикладных наук 3 (6), 504–515 (2008). Материальные отношения из железобетона CNT были 2 2.Л. Ю. Чан, «Механическая характеристика бетона, армированного углеродными нанотрубками, с использованием метода конечных элементов». полученные различными исследователями с учетом нелинейности бетона и межфазного сцепления. Предполагалось, что УНТ равномерно распределены и имеют однонаправленную ориентацию в цементной матрице. Однако Hasan et.al., 1 1.
Л. Я. Чан, «Механическое определение характеристик бетона, армированного углеродными нанотрубками, с использованием метода конечных элементов.”Значительно улучшая механические свойства любого основного материала. Предел прочности при растяжении и изгибе цементных композитов определялся методом смесей. Модуль Юнга композитов, армированных УНТ, был рассчитан Rouiania et.al. 3 3. Rouiana et al. , «Оценка модуля Юнга композитного бетона, армированного однослойными углеродными нанотрубками», Журнал технических и прикладных наук 3 (6), 504–515 (2008). Материальные отношения из железобетона CNT были 2 2.Л. Ю. Чан, «Механическая характеристика бетона, армированного углеродными нанотрубками, с использованием метода конечных элементов». полученные различными исследователями с учетом нелинейности бетона и межфазного сцепления. Предполагалось, что УНТ равномерно распределены и имеют однонаправленную ориентацию в цементной матрице. Однако Hasan et.al., 1 1. Hasan et al. , «Расчет прочности на сжатие композита УНТ / цемент», Международный журнал гражданского строительства 9 (3), 223–229 (2011).предположили случайное распределение нанотрубок в цементе и вывели новый фактор, предложенный для случайной ориентации УНТ в цементной матрице. Было обнаружено, что результаты аналитического моделирования хорошо коррелируют с экспериментами. Ученый предположил функцию распределения для ориентации волокон в композите, и эффективные механические свойства волокон были вычислены на основе их позиционного угла в композите. Также было замечено, что случайная ориентация волокон снижает эффект ориентации волоконного армирования при однонаправленной ориентации.Наконец, 1 1. Hasan et al. , «Расчет прочности на сжатие композита УНТ / цемент», Международный журнал гражданского строительства 9 (3), 223–229 (2011). На основе метода репрезентативного элементарного объема (REV) была получена аналитическая модель для прогнозирования прочности на сжатие композита УНТ / цемент.
Hasan et al. , «Расчет прочности на сжатие композита УНТ / цемент», Международный журнал гражданского строительства 9 (3), 223–229 (2011).предположили случайное распределение нанотрубок в цементе и вывели новый фактор, предложенный для случайной ориентации УНТ в цементной матрице. Было обнаружено, что результаты аналитического моделирования хорошо коррелируют с экспериментами. Ученый предположил функцию распределения для ориентации волокон в композите, и эффективные механические свойства волокон были вычислены на основе их позиционного угла в композите. Также было замечено, что случайная ориентация волокон снижает эффект ориентации волоконного армирования при однонаправленной ориентации.Наконец, 1 1. Hasan et al. , «Расчет прочности на сжатие композита УНТ / цемент», Международный журнал гражданского строительства 9 (3), 223–229 (2011). На основе метода репрезентативного элементарного объема (REV) была получена аналитическая модель для прогнозирования прочности на сжатие композита УНТ / цемент. Немногочисленные аналитические модели 4 4. S. I. Yengejeh et al. , «Углеродные нанотрубки в качестве усиления в композитах: обзор аналитических, численных и экспериментальных подходов», Computational Material Science 136 , 85–101 (2017).https://doi.org/10.1016/j.commatsci.2017.04.023 были основаны на элементарной ячейке с армированием одним волокном. Различные подходы к моделированию были основаны на моделировании методом конечных элементов (МКЭ), рассматривая УНТ как линейный элемент, полый цилиндр и сплошной цилиндр. Также было обнаружено, что координация волокон подчиняется определенному правилу в матрице, армированной УНТ. Mavalizadeh et.al., 4 4. S. I. Yengejeh et al. , «Углеродные нанотрубки в качестве усиления в композитах: обзор аналитических, численных и экспериментальных подходов», Computational Material Science 136 , 85–101 (2017).https://doi.org/10.1016/j.commatsci.2017.04.023, основанный на методе репрезентативного элементарного объема (REV) и МКЭ, выставил объемную долю матрицы в поперечном модуле Юнга и показал, что для полых ОСНТ и При заполнении ОУНТ эффективный модуль Юнга модели уменьшается примерно линейно с увеличением объемной доли матрицы.
Немногочисленные аналитические модели 4 4. S. I. Yengejeh et al. , «Углеродные нанотрубки в качестве усиления в композитах: обзор аналитических, численных и экспериментальных подходов», Computational Material Science 136 , 85–101 (2017).https://doi.org/10.1016/j.commatsci.2017.04.023 были основаны на элементарной ячейке с армированием одним волокном. Различные подходы к моделированию были основаны на моделировании методом конечных элементов (МКЭ), рассматривая УНТ как линейный элемент, полый цилиндр и сплошной цилиндр. Также было обнаружено, что координация волокон подчиняется определенному правилу в матрице, армированной УНТ. Mavalizadeh et.al., 4 4. S. I. Yengejeh et al. , «Углеродные нанотрубки в качестве усиления в композитах: обзор аналитических, численных и экспериментальных подходов», Computational Material Science 136 , 85–101 (2017).https://doi.org/10.1016/j.commatsci.2017.04.023, основанный на методе репрезентативного элементарного объема (REV) и МКЭ, выставил объемную долю матрицы в поперечном модуле Юнга и показал, что для полых ОСНТ и При заполнении ОУНТ эффективный модуль Юнга модели уменьшается примерно линейно с увеличением объемной доли матрицы. Основная проблема 5 5. Р. Надив, «Цемент, армированный нанотрубками WS2: Дисперсия имеет значение», Строительные материалы 98 , 112–118 (2015).https://doi.org/10.1016/j.conbuildmat.2015.08.085 в матрице из армированного бетона УНТ с эффективным диспергированием агломерированных нанотрубок. Было предложено так много методов, включая новый метод WS 2 Наноармированный цемент 5 5. Р. Надив, «Цемент, армированный нанотрубками WS2: Дисперсия имеет значение», Construction and Building Materials 98 , 112–118 (2015) ). https://doi.org/10.1016/j.conbuildmat.2015.08.085, который доказал, что свойства бетона при растяжении, изгибе и разрушении могут быть улучшены с помощью наноматериалов.Также изучает 6 6. B. M. Tyson et al. , «Углеродные нанотрубки и углеродные нановолокна для улучшения механических свойств нанокомпозитных вяжущих материалов», Журнал материалов в гражданском строительстве, 23, (7), 1028–1035 (2011).
Основная проблема 5 5. Р. Надив, «Цемент, армированный нанотрубками WS2: Дисперсия имеет значение», Строительные материалы 98 , 112–118 (2015).https://doi.org/10.1016/j.conbuildmat.2015.08.085 в матрице из армированного бетона УНТ с эффективным диспергированием агломерированных нанотрубок. Было предложено так много методов, включая новый метод WS 2 Наноармированный цемент 5 5. Р. Надив, «Цемент, армированный нанотрубками WS2: Дисперсия имеет значение», Construction and Building Materials 98 , 112–118 (2015) ). https://doi.org/10.1016/j.conbuildmat.2015.08.085, который доказал, что свойства бетона при растяжении, изгибе и разрушении могут быть улучшены с помощью наноматериалов.Также изучает 6 6. B. M. Tyson et al. , «Углеродные нанотрубки и углеродные нановолокна для улучшения механических свойств нанокомпозитных вяжущих материалов», Журнал материалов в гражданском строительстве, 23, (7), 1028–1035 (2011). https://doi.org/10.1061/(asce)mt.1943-5533.0000266 показал, что прочность, пластичность и вязкость разрушения могут быть улучшены путем добавления более низких концентраций либо УНТ, либо углеродных нановолокон (УНВ). Кроме того, переход на фибробетон (FRC) подтверждается тем фактом, что предел прочности на разрыв можно повысить за счет отдельных волокон, а не нескольких кусков стали.Существует множество баз данных по армированию и дисперсии УНТ, где исследователи используют УНТ как одностенные углеродные нанотрубки (ОСНТ), так и многостенные углеродные нанотрубки (МУНТ) в диапазоне от 0,01 до 2%. 8 8. А. М. Рашад, «Влияние углеродных нанотрубок (УНТ) на свойства традиционных вяжущих материалов», Строительные материалы 153 , 81–101 (2017). https://doi.org/10.1016/j.conbuildmat.2017.07.089 Этот низкий процентиль 7 7. Z.Chen et al. , «Композиты на основе цемента со сверхвысокими характеристиками, включающие низкие дозы плазменных углеродных нанотрубок», Материалы и дизайн 108 , 479–487 (2016).
https://doi.org/10.1061/(asce)mt.1943-5533.0000266 показал, что прочность, пластичность и вязкость разрушения могут быть улучшены путем добавления более низких концентраций либо УНТ, либо углеродных нановолокон (УНВ). Кроме того, переход на фибробетон (FRC) подтверждается тем фактом, что предел прочности на разрыв можно повысить за счет отдельных волокон, а не нескольких кусков стали.Существует множество баз данных по армированию и дисперсии УНТ, где исследователи используют УНТ как одностенные углеродные нанотрубки (ОСНТ), так и многостенные углеродные нанотрубки (МУНТ) в диапазоне от 0,01 до 2%. 8 8. А. М. Рашад, «Влияние углеродных нанотрубок (УНТ) на свойства традиционных вяжущих материалов», Строительные материалы 153 , 81–101 (2017). https://doi.org/10.1016/j.conbuildmat.2017.07.089 Этот низкий процентиль 7 7. Z.Chen et al. , «Композиты на основе цемента со сверхвысокими характеристиками, включающие низкие дозы плазменных углеродных нанотрубок», Материалы и дизайн 108 , 479–487 (2016). https://doi.org/10.1016/j.matdes.2016.07.016 достаточно для повышения прочности цементной матрицы на сжатие, растяжение и изгиб. Исследования с использованием макроскопического масштаба 9 9. J. F. Wang et al. , «Многомасштабное моделирование композитов, армированных УНТ и цемента», Компьютерные методы в прикладной механике и технике 309 , 411–433 (2016).https://doi.org/10.1016/j.cma.2016.06.019 рассматривает внедрение УНТ как усиление в соответствующей объемной доле. Матрица была смоделирована различными нелинейными конститутивными моделями для представления конкретных композитов. После всех видов исследований в мезоскопическом масштабе, показывающих структурную морфологию армированных УНТ, в механике сплошной среды было предложено совершенное соединение между УНТ и матрицей. Результаты наноиндентирования показали, что MWCNT могут сильно укрепить матрицу цементного теста в наномасштабе, тем самым увеличивая количество геля C-S-H высокой жесткости и уменьшая пористость.
https://doi.org/10.1016/j.matdes.2016.07.016 достаточно для повышения прочности цементной матрицы на сжатие, растяжение и изгиб. Исследования с использованием макроскопического масштаба 9 9. J. F. Wang et al. , «Многомасштабное моделирование композитов, армированных УНТ и цемента», Компьютерные методы в прикладной механике и технике 309 , 411–433 (2016).https://doi.org/10.1016/j.cma.2016.06.019 рассматривает внедрение УНТ как усиление в соответствующей объемной доле. Матрица была смоделирована различными нелинейными конститутивными моделями для представления конкретных композитов. После всех видов исследований в мезоскопическом масштабе, показывающих структурную морфологию армированных УНТ, в механике сплошной среды было предложено совершенное соединение между УНТ и матрицей. Результаты наноиндентирования показали, что MWCNT могут сильно укрепить матрицу цементного теста в наномасштабе, тем самым увеличивая количество геля C-S-H высокой жесткости и уменьшая пористость. Нанотрубки с модифицированной поверхностью и кристаллы CSH будут обеспечивать высокую прочность связи, приводящую к передаче нагрузки от цементной матрицы к арматуре. Численные исследования 10 10. J. F. Wang et al. , «Многомасштабное моделирование механических свойств и микроструктуры композитов на основе цемента и УНТ. 319 , 393–413 (2017). https://doi.org/10.1016/j.cma.2017.02.026 показал хорошее соответствие между бессеточным методом, экспериментами, а также моделью конечных элементов для случайного распределения с высоким содержанием УНТ.Рамеш-Бабу 11 11. К. Рамеш-Бабу, «Техническое примечание по использованию УНТ в качестве арматуры в железобетонных конструктивных элементах», Материалы конференции AIP 1859 , 020072 (2017). https://doi.org/10.1063/1.49
Нанотрубки с модифицированной поверхностью и кристаллы CSH будут обеспечивать высокую прочность связи, приводящую к передаче нагрузки от цементной матрицы к арматуре. Численные исследования 10 10. J. F. Wang et al. , «Многомасштабное моделирование механических свойств и микроструктуры композитов на основе цемента и УНТ. 319 , 393–413 (2017). https://doi.org/10.1016/j.cma.2017.02.026 показал хорошее соответствие между бессеточным методом, экспериментами, а также моделью конечных элементов для случайного распределения с высоким содержанием УНТ.Рамеш-Бабу 11 11. К. Рамеш-Бабу, «Техническое примечание по использованию УНТ в качестве арматуры в железобетонных конструктивных элементах», Материалы конференции AIP 1859 , 020072 (2017). https://doi.org/10.1063/1.49

 bgcolor ("gray8") # Hex: # 333333
turtle.pendown ()
turtle.pencolor (random.выбор (цвета)) # Первый цвет случайный
i = 0 # Начальный индекс
в то время как True:
i = (i + 1)% 6 # Обновить индекс
turtle.pensize (i) # Установить размер pensize на i
черепаха вперед (225)
черепаха. правая (170)
# Выберите случайный цвет
если я == 0:
turtle.pencolor (random.choice (цвета))
bgcolor ("gray8") # Hex: # 333333
turtle.pendown ()
turtle.pencolor (random.выбор (цвета)) # Первый цвет случайный
i = 0 # Начальный индекс
в то время как True:
i = (i + 1)% 6 # Обновить индекс
turtle.pensize (i) # Установить размер pensize на i
черепаха вперед (225)
черепаха. правая (170)
# Выберите случайный цвет
если я == 0:
turtle.pencolor (random.choice (цвета))
 bgcolor ("gray8") # Hex: # 333333
turtle.pendown ()
turtle.pencolor (random.choice (цвета))
i = 0 # Начальный индекс
в то время как True:
i = (i + 1)% 6 # Обновить индекс
черепаха.pensize (i) # Установить pensize на i
черепаха вперед (225)
черепаха. правая (170)
# Выберите случайный цвет
если я == 0:
turtle.pencolor (random.choice (цвета))
bgcolor ("gray8") # Hex: # 333333
turtle.pendown ()
turtle.pencolor (random.choice (цвета))
i = 0 # Начальный индекс
в то время как True:
i = (i + 1)% 6 # Обновить индекс
черепаха.pensize (i) # Установить pensize на i
черепаха вперед (225)
черепаха. правая (170)
# Выберите случайный цвет
если я == 0:
turtle.pencolor (random.choice (цвета))
 Имеет следующие множители: {факторы}")
еще:
print (f "{num} - простое число")
Имеет следующие множители: {факторы}")
еще:
print (f "{num} - простое число")
 Он имеет следующие факторы: [(1, 115), (5, 23)]
>>> check_prime_number (997)
997 - простое число
Он имеет следующие факторы: [(1, 115), (5, 23)]
>>> check_prime_number (997)
997 - простое число
 isascii () или не text.isalpha ():
поднять ValueError ("Текст должен быть в формате ASCII и не содержать чисел.")
нижний регистр = строка.ascii_lowercase
верхний регистр = строка.ascii_uppercase
результат = ""
если расшифровать:
сдвиг = сдвиг * -1
для символа в тексте:
если char.islower ():
index = lowercase.index (char)
результат + = нижний регистр [(индекс + сдвиг)% 26]
еще:
индекс = верхний регистр.индекс (символ)
результат + = верхний регистр [(индекс + сдвиг)% 26]
вернуть результат
isascii () или не text.isalpha ():
поднять ValueError ("Текст должен быть в формате ASCII и не содержать чисел.")
нижний регистр = строка.ascii_lowercase
верхний регистр = строка.ascii_uppercase
результат = ""
если расшифровать:
сдвиг = сдвиг * -1
для символа в тексте:
если char.islower ():
index = lowercase.index (char)
результат + = нижний регистр [(индекс + сдвиг)% 26]
еще:
индекс = верхний регистр.индекс (символ)
результат + = верхний регистр [(индекс + сдвиг)% 26]
вернуть результат


 isascii () или не text.isalpha ():
поднять ValueError ("Текст должен быть в формате ASCII и не содержать чисел.")
нижний регистр = строка.ascii_lowercase
прописные буквы = строка.ascii_uppercase
результат = ""
если расшифровать:
сдвиг = сдвиг * -1
для символа в тексте:
если char.islower ():
index = lowercase.index (char)
результат + = нижний регистр [(индекс + сдвиг)% 26]
еще:
index = uppercase.index (символ)
результат + = верхний регистр [(индекс + сдвиг)% 26]
вернуть результат
isascii () или не text.isalpha ():
поднять ValueError ("Текст должен быть в формате ASCII и не содержать чисел.")
нижний регистр = строка.ascii_lowercase
прописные буквы = строка.ascii_uppercase
результат = ""
если расшифровать:
сдвиг = сдвиг * -1
для символа в тексте:
если char.islower ():
index = lowercase.index (char)
результат + = нижний регистр [(индекс + сдвиг)% 26]
еще:
index = uppercase.index (символ)
результат + = верхний регистр [(индекс + сдвиг)% 26]
вернуть результат
 isascii () или не text.isalpha () или не text.isupper ():
Raise ValueError ("Текст должен быть в верхнем регистре ASCII без цифр.")
верхний регистр = строка.ascii_uppercase
результаты = ""
isascii () или не text.isalpha () или не text.isupper ():
Raise ValueError ("Текст должен быть в верхнем регистре ASCII без цифр.")
верхний регистр = строка.ascii_uppercase
результаты = ""
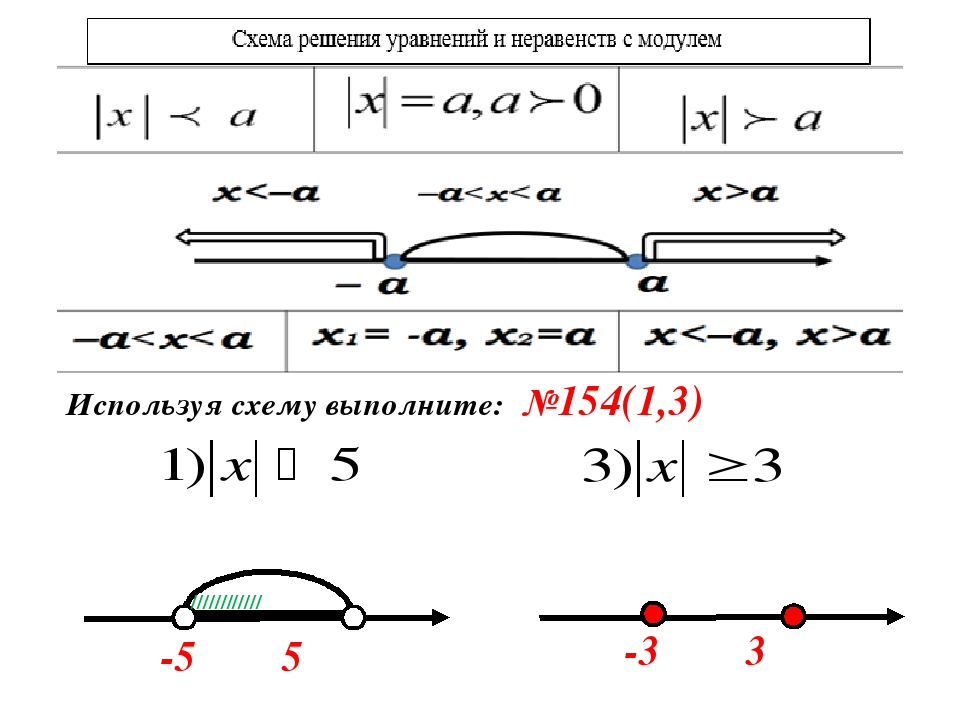 index (char)
key_index = uppercase.index (текущий_ключ)
если расшифровать:
index = char_index - key_index + 26
еще:
index = char_index + key_index
index (char)
key_index = uppercase.index (текущий_ключ)
если расшифровать:
index = char_index - key_index + 26
еще:
index = char_index + key_index
 isascii () или не text.isalpha () или не text.isupper ():
Raise ValueError ("Текст должен быть в верхнем регистре ASCII без цифр.")
uppercase = string.ascii_uppercase # "ABCDEFGHIJKLMNOPQRSTUVWXYZ"
результаты = ""
для i, символ в перечислении (текст):
current_key = ключ [i% len (ключ)]
char_index = uppercase.index (символ)
key_index = прописные буквы.индекс (текущий_ключ)
если расшифровать:
index = char_index - key_index + 26
еще:
index = char_index + key_index
результаты + = верхний регистр [индекс% 26]
вернуть результаты
isascii () или не text.isalpha () или не text.isupper ():
Raise ValueError ("Текст должен быть в верхнем регистре ASCII без цифр.")
uppercase = string.ascii_uppercase # "ABCDEFGHIJKLMNOPQRSTUVWXYZ"
результаты = ""
для i, символ в перечислении (текст):
current_key = ключ [i% len (ключ)]
char_index = uppercase.index (символ)
key_index = прописные буквы.индекс (текущий_ключ)
если расшифровать:
index = char_index - key_index + 26
еще:
index = char_index + key_index
результаты + = верхний регистр [индекс% 26]
вернуть результаты
 Десятичное (15)% десятичное.Десятичное (4)
Десятичный ('3')
>>> десятичный.Десятичный (240)% десятичный. Десятичный (13)
Десятичный ('6')
Десятичное (15)% десятичное.Десятичное (4)
Десятичный ('3')
>>> десятичный.Десятичный (240)% десятичный. Десятичный (13)
Десятичный ('6')
 name = имя
self.study_sessions = []
def add_study_sessions (самостоятельно, сеансы):
self.study_sessions + = сеансы
def total_study_time_in_hours (студент, total_mins):
часы = total_mins // 60
минут = total_mins% 60
print (f "{student.name} изучил {часы} часы и {минуты} минуты")
name = имя
self.study_sessions = []
def add_study_sessions (самостоятельно, сеансы):
self.study_sessions + = сеансы
def total_study_time_in_hours (студент, total_mins):
часы = total_mins // 60
минут = total_mins% 60
print (f "{student.name} изучил {часы} часы и {минуты} минуты")
 name = имя
self.study_sessions = []
def add_study_sessions (самостоятельно, сеансы):
self.study_sessions + = сеансы
def __mod __ (себя, другое):
возвратная сумма (self.study_sessions)% other
def __floordiv __ (я, другой):
возвратная сумма (self.study_sessions) // другое
name = имя
self.study_sessions = []
def add_study_sessions (самостоятельно, сеансы):
self.study_sessions + = сеансы
def __mod __ (себя, другое):
возвратная сумма (self.study_sessions)% other
def __floordiv __ (я, другой):
возвратная сумма (self.study_sessions) // другое
 name = имя
self.study_sessions = []
def add_study_sessions (самостоятельно, сеансы):
self.study_sessions + = сеансы
def __mod __ (себя, другое):
возвратная сумма (self.study_sessions)% other
def __floordiv __ (я, другой):
возвратная сумма (self.study_sessions) // другое
def total_study_time_in_hours (студент):
часы = студент // 60
минут = студент% 60
print (f "{student.name} изучил {часы} часы и {минуты} минуты")
name = имя
self.study_sessions = []
def add_study_sessions (самостоятельно, сеансы):
self.study_sessions + = сеансы
def __mod __ (себя, другое):
возвратная сумма (self.study_sessions)% other
def __floordiv __ (я, другой):
возвратная сумма (self.study_sessions) // другое
def total_study_time_in_hours (студент):
часы = студент // 60
минут = студент% 60
print (f "{student.name} изучил {часы} часы и {минуты} минуты")
 Знак такой же, как у делителя
Знак такой же, как у делителя 4 мм
4 мм