Линейное уравнение с одной переменной (Г.И. Вольфсон). Видеоурок. Алгебра 7 Класс

В каждом автобусе можно разместить 30 школьников. Сколько автобусов потребуется, чтобы перевезти 930 школьников (см. Рис. 1)?

Решение

 

 

Рис. 1. Иллюстрация к задаче

Решим данную задачу с помощью уравнения. Пусть 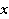 – это искомое число автобусов. В каждый автобус помещается 30 учеников, следовательно, общее количество учеников, которые проедут в искомом числе автобусов, будет равно 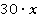. Однако общее количество учеников нам известно – 930, поэтому получили уравнение:

 

Найдём 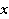, решив данное уравнение:

 

 

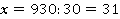
Ответ: 31 автобус.

 

В задаче 1 мы составили уравнение, которое называется линейным уравнением.

Уравнение вида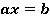

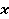, где  – переменная,  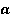и 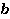 – некоторые числа, называется линейным уравнением с одной переменной.

Число 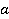 обычно называют коэффициентом, а число  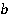– свободным членом. Они могут быть положительными и отрицательными, целыми и нецелыми, и даже нулями. Например:

 

 

 

 

 

 

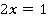
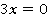
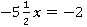
Рассмотрим 2 случая:

1. Коэффициент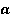

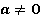 не равен 0 ()

В этом случае обе части линейного уравнения можно разделить на a:

 

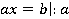
При этом 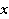 будет равен:

 

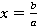
2. Коэффициент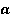

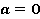 равен 0 ()

В этом случае линейное уравнение принимает вид 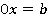. Из этого уравнения и свойства умножения чисел на ноль следует, что, какое бы число мы ни взяли в качестве 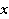, при его подстановке в уравнение  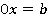получится числовое равенство 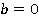. Это равенство верное, когда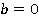 

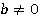, а в остальных случаях при  это равенство неверное.

Следовательно, пр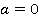и  и 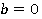любое число является корнем линейного уравнения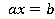, так как при этих условиях подстановка вместо  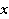любого числа дает верное числовое равенство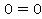

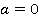 . А при  и 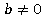 линейное уравнение  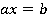не имеет корней, так как при этих условиях подстановка вместо  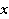любого числа приводит к неверному числовому равенству  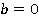(см. Рис. 2).

 

 

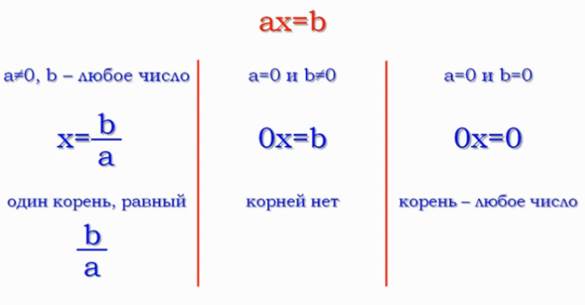
Рис. 2. Решение линейного уравнения с одной переменной

Решите уравнения:

1.  

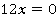
Коэффициент 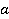 в данном уравнении не равен 0, поэтому корень данного уравнения будет равен:

 

 

2.  

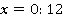
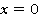
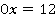
Коэффициент 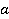 в данном уравнении равен 0, а свободный член  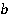не равен нулю, следовательно, у этого уравнения решений нет.

3. 

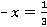
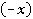 можно представить, как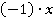

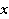. Поэтому  будет равен: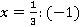

 

 

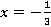
4.

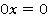
Коэффициент 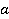 и свободный член  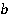в данном уравнении равны 0, поэтому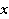

 – это любое число.

5.

 

 

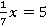
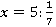
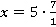
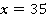
Решите уравнения:

1.

 

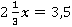
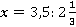
Для удобства выполнения деления переведем 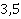 и 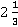 в неправильную дробь.

 

 

 

 

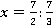
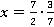
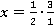
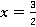
2.  

  

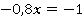
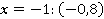
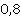 представим в виде обыкновенной дроби.

 

 

 

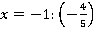
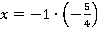
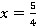
При каких значениях 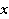 выражение  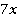равно 0,1?

Решение

Формулировка данной задачи означает, что нам необходимо найти 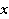 из уравнения .

 

 

 

 

 

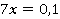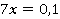
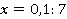
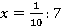
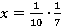
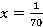
Ответ: .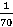

Составьте линейное уравнение, которое имеет корень (-3).

Решение

Общий вид линейного уравнения – это 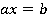. По условию 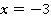, потому необходимо найти такие  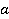и 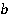, чтобы . Для этого выбираем любое число 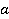, например 2:

 

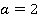
Число 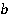 выбираем такое, чтобы равенство  было верным.

 

 

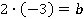
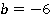
Ответ: .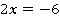

Итоги урока

На этом уроке мы познакомились с понятием линейного уравнения с одной переменной, узнали, как называются составные части таких уравнений. Также мы узнали, сколько решений имеет линейное уравнение с одной переменной, и рассмотрели несколько примеров с решениями.

---

 

Эквивалентные преобразования уравнений

С уравнениями можно производить следующие эквивалентные преобразования.

1. К обеим частям равенства можно прибавлять или вычитать одно и то же число. Например, к каждой части уравнения 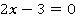 можно прибавить 3, равенство при этом не изменится.

 

 

 

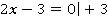
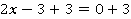
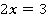
2. Каждую часть уравнения можно домножить или разделить на одно и то же число (не равное нулю). Например, каждую часть уравнения 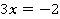 можно домножить на , равенство при этом сохранится.

 

 

 

---

 

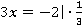
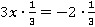
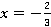
Более сложные примеры

Задача 6

При каких значениях 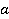 уравнение  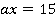имеет корень ?

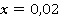Решение

При подстановке 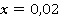 в уравнение  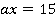должно получиться верное равенство:

 

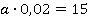
После подстановки 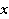 в уравнение  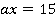мы получили новое линейное уравнение с переменной  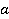и коэффициентом равным 0,02. Решим это уравнение.

 

 

 

 

 

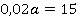
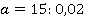
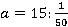
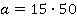
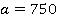
Ответ: .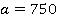

Задача 7

При каких значениях 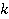 уравнение  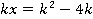имеет: 1. 0 корней; 2. 1 корень; 3. бесконечно много корней?

Решение

Для того чтобы найти 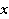 в этом линейном уравнении, необходимо  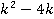разделить на 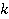. Однако  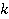может быть равным 0, поэтому рассмотрим два случая.

а) Если 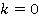, то:

 

 

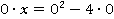
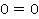
Следовательно, при 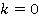: x – это любое число, уравнение имеет бесконечно много решений.

б) Если 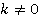, то:

 

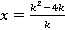
Следовательно, при 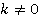: уравнение будет иметь одно решение (один корень).

Ответ: 1. Не существует таких значений 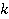, при которых данное уравнение не имеет корней.

2. При

interneturok.ru

Линейное уравнение с двумя переменными и его график. Видеоурок. Алгебра 7 Класс

На данном уроке мы рассмотрим уравнение с двумя переменными, дадим его определение и построим график.

Тема: Линейная функция

Урок: Линейное уравнение с двумя переменными и его график

Мы познакомились с понятиями координатной оси и координатной плоскости.  Мы знаем, что каждая точка плоскости однозначно задает пару чисел (х; у), причем первое число есть абсцисса точки, а второе – ордината.

Мы будем очень часто встречаться с линейным уравнением с двумя переменными, решением которого и есть пара чисел, которую можно представить на координатной плоскости.

Уравнение вида:

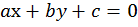, где a, b, с – числа, причем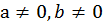

Называется линейным уравнением с двумя переменными х и у. Решением такого уравнения будет любая такая пара чисел х и у, подставив которую в уравнение мы получим верное числовое равенство.

Пара чисел будет изображаться на координатной плоскости в виде точки.

У таких уравнений мы увидим много решений, то есть много пар чисел, и все соответствующие точки будут лежать на одной прямой.

Рассмотрим пример:

Пример 1:

; ; ;

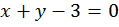
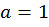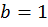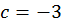Чтобы найти решения данного уравнения нужно подобрать соответствующие пары чисел х и у:

Пусть 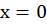, тогда исходное уравнение превращается в уравнение с одной неизвестной:

,

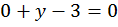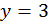
То есть, первая пара чисел, являющаяся решением заданного уравнения (0; 3). Получили точку А(0; 3)

Пусть 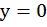. Получим исходное уравнение с одной переменной: 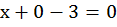, отсюда 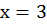, получили точку В(3; 0)

Занесем пары чисел в таблицу:

Построим на графике точки и проведем прямую: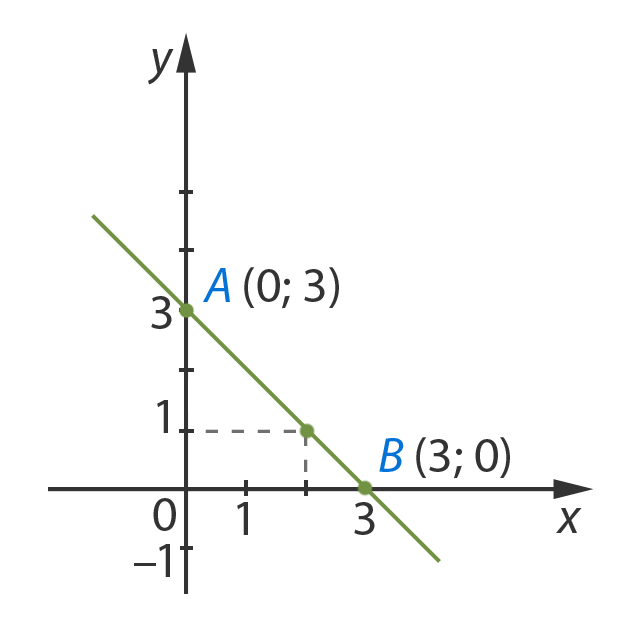

Отметим, что любая точка на данной прямой будет решением заданного уравнения. Проверим – возьмем точку с координатой 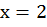 и по графику найдем ее вторую координату. Очевидно, что в этой точке 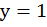. Подставим данную пару чисел в уравнение. Получим 0=0 – верное числовое равенство, значит точка, лежащая на прямой, является решением.

Пока доказать, что любая точка, лежащая на построенной прямой является решением уравнения, мы не можем, поэтому принимаем это за правду и докажем позже.

Пример 2 – построить график уравнения:

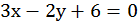
Составим таблицу, нам достаточно для построения прямой двух точек, но возьмем третью для контроля:

В первой колонке мы взяли удобный 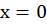, найдем у:

, ,

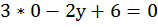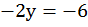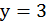
Во втором столбике мы взяли удобный 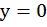, найдем х:

, , ,

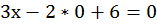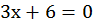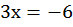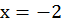
Возьмем для проверки 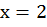 и найдем у:

, ,

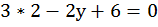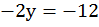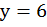
Построим график:

Умножим заданное уравнение на два:

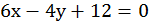
От такого преобразования множество решений не изменится и график останется таким же самым.

Вывод: мы научились решать уравнения с двумя переменными и строить их графики, узнали, что графиком подобного уравнения есть прямая и что любая точка этой прямой является решением уравнения

 

Список рекомендованной литературы

1. Дорофеев Г.В., Суворова С.Б., Бунимович Е.А. и др. Алгебра 7. 6 издание. М.: Просвещение. 2010 г.

2. Мерзляк А.Г., Полонский В.Б., Якир М.С. Алгебра 7. М.: ВЕНТАНА-ГРАФ 

3. Колягин Ю.М., Ткачёва М.В., Фёдорова Н.Е. и др. Алгебра 7 .М.: Просвещение. 2006 г.

 

Рекомендованные ссылки на ресурсы интернет

1. Интернет-портал Nado5.ru (Источник).

2. Портал для семейного просмотра (Источник).

3. Интернет-портал Nado5.ru (Источник).

 

Рекомендованное домашнее задание

Задание 1: Мерзляк А.Г., Полонский В.Б., Якир М.С. Алгебра 7, № 960, ст.210;

Задание 2: Мерзляк А.Г., Полонский В.Б., Якир М.С. Алгебра 7, № 961, ст.210;

Задание 3: Мерзляк А.Г., Полонский В.Б., Якир М.С. Алгебра 7, № 962, ст.210;

interneturok.ru

Алгебра 7-9 классы. 1. Уравнения с одной переменной. Выражения и их преобразования

Алгебра 7-9 классы. 1. Уравнения с одной переменной. Выражения и их преобразования

Подробности

Категория: Алгебра 7-9 классы

 

 

 УРАВНЕНИЯ С ОДНОЙ ПЕРЕМЕННОЙ

 УРАВНЕНИЕ И ЕГО КОРНИ

Решим задачу: «На двух полках 40 книг, причем на верхней полке в 8 раза больше книг, чем на нижней. Сколько книг на нижней полке?»

Обозначим буквой х число книг на нижней полке. Тогда число книг на верхней полке равно Зх. По условию задачи на обеих полках находится 40 книг. Это условие можно записать в виде равенства:

3x + x = 40.

Чтобы найти неизвестное число книг, мы составили равенство, содержащее переменную. Такие равенства называют уравнениями. Переменную в уравнении называют также неизвестным числом или просто неизвестным.

Нам надо найти число, при подстановке которого вместо х в уравнение Зх + х = 40 получается верное равенство. Такое число называют решением уравнения или корнем уравнения. Равенство Зх + х = 40 верно при х = 10. Число 10 — корень уравнения Зх + х = 40.

Определение. Корнем уравнения называется значение переменной, при котором уравнение обращается в верное равенство.

Уравнение Зх + х = 40 имеет один корень. Можно привести примеры уравнений, которые имеют два, три и более корней или вообще не имеют корней.

Так, уравнение (х—4)(х — 5) (х—6)=0 имеет три корня: 4, б и 6. Действительно, каждое из этих чисел обращает в нуль один из множителей произведения (х—4) (х—5)(х—б), а значит, и само произведение. При любом другом значении х ни один из множителей в нуль не обращается, а значит, не обращается в нуль и произведение. Уравнение х + 2 = х не имеет корней, так как при любом значении х левая часть уравнения на 2 больше правой части.

Решить уравнение — значит найти все его корни или доказать, что их нет.

Уравнение х²=4 имеет два корня — числа 2 и —2. Уравнение (х—2) (х+2)=0 также имеет корни 2 и —2. Уравнения, имеющие одни и те же корни, называют равносильными уравнениями. Уравнения, не имеющие корней, также считают равносильными.

Уравнения обладают следующими свойствами:

1)    если к обеим частям уравнения прибавить одно и то же число, то получится уравнение, равносильное данному;

2)    если обе части уравнения умножить или разделить на одно и то же отличное от нуля число, то получится уравнение, равносильное данному.

Рассмотрим уравнение х² — 2 = 7. Прибавив к левой и правой частям этого уравнения число 2, получим уравнение х² = 9. Докажем, что уравнения х² — 2 = 7 и х² = 9 равносильны.

Пусть некоторое значение х является корнем первого уравнения, т. е. при этом значении- х уравнение х²—2 = 7 обращается в верное равенство. Прибавив к обеим частям этого равенства число 2, мы снова получим верное равенство. Значит, при этом значении х второе уравнение также обращается в верное равенство. Мы доказали, что каждый корень первого уравнения является корнем второго уравнения.

Допустим теперь, что некоторое значение х является корнем второго уравнения х² = 9, т. е. обращает его в верное равенство. После вычитания из обеих частей этого равенства числа 2 мы получим верное равенство. Значит, при этом значении х первое уравнение также обращается в верное равенство. Поэтому каждый корень второго уравнения является корнем первого.

Таким образом, уравнения х² — 2 = 7 и х² = 9 имеют одни и те же корни, т. е. являются равносильными.

Подобными рассуждениями устанавливается справедливость обоих свойств уравнений в общем случае.

3) Можно также доказать, что  если в уравнении перенести слагаемое ив одной части в другую, изменив его знак, то получится уравнение, равносильное данному. Например, перенеся в уравнении 5х = 2х + 9 слагаемое 2х с противоположным знаком из правой части уравнения в левую, получим уравнение 5х—2дс=9, ему равносильное.

Перенос слагаемых из одной части уравнения в другую часто применяется при решении уравнений.

 

ЛИНЕЙНОЕ УРАВНЕНИЕ С ОДНОЙ ПЕРЕМЕННОЙ

Каждое из уравнений 5х = — 4,  — 0,2х = 0,  —х= —6,5 имеет вид ах = b где а и b — числа.  В первом уравнении а = 5, b= — 4, во втором а= —0,2, b = 0, в третьем а= — 1, b= —6,5. Такие уравнения называют линейными уравнениями с одной переменной.

Определение. Уравнение вида ах = b, где х — переменная, а и b — числа, называется линейным уравнением с одной переменной.

Число а называется коэффициентом при переменной, а число b — свободным членом.

Рассмотрим линейное уравнение ах = b, в котором коэффициент а не равен нулю. Разделив обе части уравнения на а, получим . Значит, линейное уравнение ах=b в котором а≠ 0, имеет единственный корень

Рассмотрим теперь линейное уравнение ах = b, у которого коэффициент а равен нулю. Если а = 0 и b≠ О, то уравнение ах =b не имеет корней, так как равенство Ox = b, где b≠ 0, не является верным ни при каком x. Если а = 0 и b = О, то любое значение х является корнем уравнения, так как равенство 0х = 0 верно при любом х.

Решение многих уравнений сводится к решению линейных уравнений.

Пример. Решим уравнение

Раскроем скобки:

Перенесем слагаемое —х в левую часть уравнения, а слагаемое 28 в правую, изменив при этом их знаки:

Приведем подобные слагаемые:

Заменяя последовательно одно уравнение другим, равносильным ему, мы получили линейное уравнение, в котором коэффициент при х отличен от нуля. Разделим обе части уравнения на этот коэффициент:

Число —5 является корнем уравнения .

Может случиться, Что при решении уравнения мы придем к линейному уравнению вида 0х=b. В этом случае исходное уравнение либо не имеет корней, либо его корнем является любое число. Например, уравнение сводится к уравнению Ох = 7, и, значит, оно не имеет корней. Уравнение сводится к уравнению 0х = 0, и, значит, любое число является его корнем.

forkettle.ru

Разработка урока в 7 классе на тему «Линейное уравнение с одной переменной»

Технологическая карта урока алгебры в 7 классе по теме:

Автор УМК: Ю.Н. Макарычев, Н.Г. Миндюк, К.И. Нешков, С.Б. Суворова, учебник для 7 класса общеобразовательных учреждений – М.: Просвещение, 2013

Тема урока: Линейное уравнение с одной переменной.

Тип урока: урок комплексного применения знаний и умений (закрепления)

Образовательные цели: отрабатывать навык решения линейных уравнений с одной переменной, основанный на применении свойств равносильности уравнений.

Развивающие цели: способствовать развитию математической речи, оперативной памяти, произвольного внимания, наглядно-действенного мышления; самостоятельного добывания знаний.

Воспитательные цели: воспитывать культуру поведения; обеспечить условия для воспитания аккуратности, культуры общения, ответственного отношения к учению, интереса к изучению математики.

Предметные: понимать алгоритм решения уравнений с помощью свойств равносильности уравнений; уметь решать линейные уравнения с одной переменной;

Личностные: формирование устойчивой мотивации к обучению на основе алгоритма выполнения задачи;

Регулятивные: формулировать познавательную цель на уроке с помощью учителя и строить действия в соответствии с ней; работать по составленному плану; оценивать правильность выполнения действия; вносить коррективы и дополнения в составленные планы.

Коммуникативные: уметь выражать свои мысли в устной форме; уметь слушать и слышать друг друга; выражать готовность к обсуждению разных точек зрения и выработке общей ( групповой ) позиции.

Познавательные: выбирать наиболее эффективные способы решения задачи; структурировать знания; применять методы информационного поиска (с помощью учебника и других средств).

Ресурсы: Алгебра. 7 класс: учебник для общеобразовательных учреждений/, Ю.Н. Макарычев, Н.Г. Миндюк, К.И. Нешков, С.Б. Суворова; под ред. С.А. Теляковского. – М.: Просвещение, 2013.

Формы работы: индивидуальная, фронтальная, групповая, коллективная.

1.Организационный

1 мин

Доброе утро, ребята и уважаемые гости!

Начнем сегодняшний урок со стихов.

Чтобы спорилось нужное дело,

Чтобы в жизни не знать неудач,

В алгебры мир отправимся смело,

В мир уравнений и разных задач.

(Слайд 2)

— А девизом нашего урока будут такие слова:

Думать – коллективно!

Решать – оперативно!

Отвечать — доказательно!

Учиться – старательно! (Слайд 3)

-Ребята, желаю вам следовать этому девизу и хорошего настроения.

Коммуникативные: уметь совместно договариваться о правилах поведения и общения, следовать им; слушать и слышать других

Включаются в ритм урока

Приветствует учащихся, проверяет подготовленность к уроку, организует внимание детей

2.Актуализация знаний. Постановка темы и цели урока

8 мин.

Как вы уже поняли, сегодня на уроке мы отправимся в мир уравнений.

Игра «да» или «нет»

Нужно определить верно ли утверждение. Если неверно, то объяснить. (слайд 4)

1.Уравнение – это выражение, содержащее букву (переменную)? (нет)

2. Корень уравнения — это значение переменной, которое обращает уравнение в верное числовое равенство? (да)

3.Число 5 – это корень уравнения 2х-3=5? (нет)

4.В уравнении 2х-3=5+х число -3 можно перенести в правую часть , а х перенести в левую часть уравнения и получится 2х-х=5-3? (нет)

5. Уравнения вида ах = b, где а и b –некоторые числа, называется линейным уравнением с одной переменной? (да)

6. Не все уравнения являются линейными

1) -2у=4,

2) 6х-3х=2,

3) 5х-5х=0,

4) 5х=5х-7

5) 6(х-1)=4 х+2?

6) х + 3= х? (нет)

Итак, все уравнения являются линейными.

Решите эти уравнения.

Какие трудности возникли при решении?

Что нужно знать и уметь, чтобы не было затруднений?(знать и уметь применять свойства уравнений, уметь решать простые уравнения, упрощать выражения)

Подведем итоги. Что знаете? Что умеете? Чему надо научиться?

Сформулируйте тему урока и запишите тему в тетрадь.

Умение решать линейные уравнения пригодиться в дальнейшем при решении задач и изучении линейной функции.

Личностные: осознавать цели и результаты саморазвития. Регулятивные: определять цель, проблему урока; самостоятельно планировать учебную деятельность; выстраивать алгоритм действий

Отвечают на вопросы, вспоминают изученный ранее материал, формулируют с помощью учителя тему и цель урока, записывают в тетрадь

Организует работу по актуализации опорных знаний, создает проблемную ситуацию, акцентирует внимание учеников на значимость данной темы

3. Первичное закрепление

10 мин

Повторим, как используются свойства при решении уравнений.(на доске заранее написать уравнения)

Решить уравнения: (по очереди на доске с комментированием, остальные в тетрадях)

а) 14 – у = 19 — 11у (у=0,5)

б) 3х-8=х+6 (х=7)

в) -0,8х +16 = 20 — 0,7х (х=-40)

(Решают на доске и в тетради)

Какие свойства применили? Какие ошибки можно допустить?

Познавательные: уметь находить достоверную информацию, преобразовывать ее из одной формы в другую. Регулятивные:

уметь составлять план решения, выбирать

пути и средства достижения цели, работать по плану, вносить коррективы в свои действия.

Выполняют задания на ранее изученный материал

Организует работу по коррекции знаний учащихся

4. Физкультминутка

1 мин

Учащиеся выполняют упражнения для снятия усталости

Коммуникативные: умение работать в группе в

Меняют вид деятельности, выполняют упражнения

Обеспечивает эмоциональную разгрузку учащихся

5. Закрепление в измененной ситуации

15 мин

(Слайд 5) Решите задания в учебнике. При необходимости используйте объяснительный текст п.7 на стр.28-30.

№130 (в), 129 (з),131(г),

Дополнительно № 137 (б), 138(а)

Решение:

№130 (в,)- уравнение содержит обыкновенные дроби (Ответ: 5,25)

№129 (Ответ:-3)

131(г) 20х=19-(3+12х)

20х=19-3-12х

20х +12х=16

32х=16

Х=16/32

Х=0,5

137(б) 5(2у-4)=2(5у-10)

10у-20=10у-20

10у-10у=20-20

0у=0

у-любое число

№138(а) корней нет

Сделайте выводы.

Познавательные: уметь анализировать, обобщать, делать выводы; строить логически обоснованные рассуждения. Регулятивные: уметь проговаривать последовательность действий на уроке, высказывать свое предположение, выдвигать версии

Коммуникативные: вести диалог, работать в группе

Обсуждают в группах варианты решения уравнений

(коллективное обсуждение с записями на доске)

Побуждает учащихся к теоретическому объяснению фактов, стимулирует активное участие всех детей в поисковой деятельности

6. Творческое задание

7 мин

Решить устно линейные уравнения, ответ записать в виде координаты точки. Точки необходимо нанести последовательно на координатную плоскость и соединить. Должен получиться рисунок.

(домик) (слайд 7)

5х=10

у-2=-0

Х=2

У=2

2

1/3х=0

-у=-4

х=0

у=4

3

5х-3х=-4

0,5 у=1

х=-2

у=2

4

7х =-14

у+4=2

х=-2

у=-2

5

-6+Х=-4

-У+42=44

Х=2

У=-2

6

9Х-18=0

1/2Х=1

Х=2

У=2

7

3х-х+40=36

2(У-1)=У

Х=-2

У=2

Коммуникативные: продуктивно общаться и взаимодействовать с коллегами по совместной деятельности. Регулятивные: осознавать правило контроля и успешно использовать его в решении учебной задачи. Познавательные: выбирать наиболее эффективные способы решения задач; структурировать знания.

Учащиеся выполняют проблемно-поисковую задачу, работая в группе самостоятельно

организует проблемно-поисковую работу в группах

7. Домашнее задание

1 мин

Комментарий:1) домашнее задание обязательное п.7, №№130(д), 131(в), 133(в), дополнительно №135(в), 137 (а) на стр.30-31 (слайд 8)

Записывают в дневники домашнее задание

Дает комментарий к домашнему заданию, обеспечивает понимание способов выполнения

8. Подведение итогов. Рефлексия

2 мин

Синквейн составить по теме.

1 строка — одно слово (тема представлена существительным).

2 строка — 2 прилагательных (или причастия).

3 строка — 3 слова (посредством использования глаголов или деепричастий, описываются действия).

4 строка – это фраза, при помощи которых составляющий высказывает свое мнение.

5 строка – одно слово (синоним к теме)

Оценивание работы на уроке с помощьюсмайликов.

Осуществляют самопроверку, высказывают оценочные суждения

Подводит итоги урока, предлагает оценить меру личного продвижения к цели и успехи каждого ученика

infourok.ru

7 класс. Алгебра. Решение линейных уравнений с одной переменной. — Решение линейных уравнений с одной переменной.

Курсотека

• Каталог
  • Школьникам
  • Алгебра 140
  • Английский язык 481
  • Астрономия 2
  • Биология 426
  • Всеобщая история 285
  • География 230
  • Геометрия 172
  • ИЗО 24
  • Информатика 66
  • История России 338
  • Еще 17 категорий
  • Студентам
  • Адвокатура 7
  • Административное право 2
  • Английский язык 63
  • Архитектура и строительство 10
  • АФХД 11
  • Банковское дело 20
  • БЖД 38
  • Биология и химия 46
  • Бухгалтерский учет и аудит 41
  • Еще 57 категорий
  • Самообразование
  • Без категории 9
  • Бизнес 10
  • Бухгалтерия и 1C 11
  • Вождение автомобиля 7
  • Дизайн 5

www.kursoteka.ru

Линейные уравнения с параметрами в 7-м классе (методические рекомендации)

Известно, что в программе по математике для неспециализированных школ задачам с параметрами отводится незначительное место.
К задачам с параметрами, рассматриваемым в школьном курсе, относятся, например, задачи, в которых отыскивается решение линейных и квадратных уравнений в общем виде, исследуется количество их корней в зависимости от значений параметров.
Естественно, что такой небольшой класс задач не позволяет учащимся овладеть методами решения задач с параметрами. В результате, у учащихся возникает психологический барьер уже при «первом» знакомстве с параметрами — это неизвестное и известное, переменная и постоянная. Выход из сложившейся ситуации — включать задачи с параметрами в каждую тему.

• Для решения задач с параметрами требуется:

а) свободное владение навыками решения уравнений;
б) знание специфических преобразований, которые используются в уравнениях;
в) умение построить логическую цепочку рассуждений.

• Что дают задачи с параметрами:

а) отработку навыков решения уравнений;
б) повышают интеллектуальный уровень ученика и его логическое мышление;
в) формируют навыки исследовательской деятельности;
г) повышают интерес к математике.

        Прежде чем ввести понятие «параметр», учащимся необходимо напомнить роль букв в алгебре. Обратить внимание ребят на то, что за буквой скрывается число.
Предложите учащимся задания, в которых надо выразить одну переменную через другую. К этим задачам надо возвращаться постоянно, особенно в 7-м классе, поскольку умение выражать одну переменную через другую очень пригодится при решении задач по физике, где требуется вначале составить буквенное выражение и только затем подставить числовые значения.

Пример №1.
1) Из формулы S=Vt выразить: а) V, через S и t; б)  t, через  S и V.
2) Из формулы P=2(a+b) выразить :а)  a, через  P иb; б)  b, через  P и a.
3) Из формулы S=ab выразить: а)  a, через S и b; б)  b, через S и  a.
4) Из формулы V=abc выразить: а) a, через  V, b и c; б) b, через  V, a и c; в) c, через  V, a и b.
При каких значениях переменных имеют смысл эти выражения (формулы)?

 Пример №2.
Выразить  х : а)  ах = а-1; б) (а+2) х = а-1; в) а х = а -1.
Укажите, при каких значениях а имеет смысл полученное выражение.
Найдите значение х при а=2; а=3; а= -10.
Повторите на простых примерах, что такое уравнение, что значит решить уравнение. При решении уравнений типа 2х-2=-1;14х=-4; 3-3х=1 обратите внимание учащихся на то, что мы выразили неизвестное, которое надо найти, через числа.
Покажите, что в уравнение, помимо неизвестного, могут быть введены и другие буквы, и буквенные выражения. Например, ах=а-1, (а+2)х=а-1, (а+2)х=(а+2)-1, а х=а -1.
При этом, как всегда в алгебре, мы полагаем, что буквы могут принимать любые числовые значения. Например, задавая произвольно значения а для уравнения ах=а-1 получаем
при а=2  имеем 2х=2-1; при а=3  имеем 3х=3-1; при а=0 имеем 0х=0-1; при а=-4 имеем -4х=-4-1.

Пример №3.
Дано уравнение ах=5а-9.
Напишите уравнение, которое получится, если  а=10; а=-2;  а=0.

 Пример №4.
Решить уравнение относительно х:
х+2=а+7.
Решение: х=а+5.
Переменную, которую надо найти, будем называть неизвестной, а переменную, через которую будем выражать искомую неизвестную, назовем параметром.

• Параметр —это переменная величина, которая в процессе решения уравнения (задачи) считают фиксированной и относительно которой  проводится анализ полученного решения.
• Решить уравнение с параметром — это  значит для каждого значения параметра найти значение неизвестной переменной, удовлетворяющее этому уравнению.

Заметим, что в нашем примере параметр а может принимать любые значения.
Ответ запишем так: при любом значении параметра а

                                  х=а+5 .
Основное, что нужно усвоить при первом «знакомстве» с параметром, это необходимость осторожного обращения с фиксированным, но неизвестным числом.  Необходимость аккуратного обращения с параметром хорошо видна в примерах, где замена параметра числом делает задачу банальной. К таким задачам, например,  относятся задачи, в которых требуется сравнить два числа.

Пример №5.
Сравнить числа: а) а и 3а; 
б) -а и 3а.
Решение:
а) естественно рассмотреть три случая:
если  а < 0, то а > 3а;  если  а = 0, то а = 3а; если  а > 0, то а < 3а;
б) естественно рассмотреть три случая:
если а < 0, то -а > 3а; если а = 0, то -а = 3а; если а > 0, то -а < 3а.

Пример №6.  При каком значении параметра а  х=2,5 является корнем уравнения х+2=а+7?
 Решение.
Т.к.  х= 2,5 – корень уравнения  х+2=а+7, то при подстановке  х= 2,5 в уравнение
получим верное равенство  2,5+2=а+7, откуда находим  а =-2,5.
Ответ: при а=-2,5.

Пример №7. Имеет ли уравнение  3х+5 = 3х+а  решение при а=1. Подберите значение а, при котором уравнение будет иметь корни.

Пример №8. Найдите множество корней уравнения  ах = 4х+5
а)  при а=4; б)  при а≠4.
На простых примерах надо показать, что приемы, используемые для решения уравнений с параметрами, такие же, как и при решении уравнений, содержащих помимо неизвестной только числа.

Пример №9.  Решить уравнение ах=1.
Решение. На первый взгляд представляется возможным сразу дать ответ:  Однако, при а=0 данное уравнение решений не имеет и верный ответ записывается так:
если а=0, то нет решений; если а≠0, то

Пример №10. Найти все натуральные значения а, при которых корень уравнения (а-1)х=12 является

a) натуральным числом; б) неправильной дробью.

Решение:
а≠1, то так как иначе уравнение не имеет решений;
а) если а≠1, то
Перебором находим:
при а=13,  х=1;при а=7,    х=2;при а=5,    х=3;при а=4,    х=4;при а=3,    х=6;при а=2,    х=12.
Ответ: а є {13, 7, 5, 4, 3, 2}.
б) если а≠1, то
Перебором находим, что а є {2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13}.

Пример №11. Решить уравнение |х|=|а|.

Пример №12. Решить уравнение ах+8=а.
Решение. Запишем уравнение в стандартном виде  ах=а-8.
Основа правильного решения задач с параметрами состоит в грамотном разбиении области изменения параметра, к этому надо приучать путем подробного описания хода решения.
Итак, коэффициент при х равен а. Возникают два возможных случая:

1. коэффициент при х равен нулю и уравнение примет вид 0х=-8, полученное уравнение не имеет корней;
2. коэффициент при х не равен нулю, и мы имеем право разделить обе части уравнения на этот коэффициент:    а≠0,

   ах=а-8, 
Ответ:   при а=0, нет  корней;
при а≠0,
Важно зафиксировать внимание учащихся на случае, когда коэффициент при х равен нулю, и рассматривать этот случай всегда первым, чтобы помочь учащимся избежать наиболее распространенной ошибки, когда этот случай теряют. Полезно обратить внимание учащихся на конструкцию записи ответа. В различных пособиях по математике встречаются две конструкции:

1. при а …, х …;
2. если а …, то х … .

Предложите учащимся решить самостоятельно (с последующей проверкой на доске) уравнение (а+2)х+2=а, где а – параметр.
Ответ:   при а=-2, нет  корней; при а≠-2, 
Таким образом любое линейное уравнение с параметрами элементарными преобразованиями может быть приведено к виду Ах=В, где А и В – некоторые выражения, хотя бы одно из которых содержит параметр и  исследуется по схеме:

Пример № 13.  При каких значениях а уравнение (а2-1)х=а+1
а) не имеет решений; б) имеет бесконечное множество решений; в) имеет единственный корень.
Решение:
а) данное уравнение не имеет решений в том случае, если коэффициент при х равен нулю, а выражение, стоящее в правой части уравнения не обращается в нуль, то есть
Т.о., при а=1 уравнение не имеет решений.
б) данное уравнение имеет бесконечное множество решений в том случае, если коэффициент при х равен нулю и выражение, стоящее в правой части уравнения, обращается в нуль, то есть 
Т.о., при а=-1 уравнение имеет бесконечное множество решений.
в) уравнение имеет единственное решение, при а2-1≠0, то есть (а-1)(а+1)≠0, т.е. а≠±1.
Ответ:

1. Уравнение не имеет решений, при а=1.
2. Уравнение имеет бесконечное множество решений, при а=-1.
3. Уравнение имеет единственный корень, при а≠±1.

Пример №15.  Предложить учащимся решить самостоятельно уравнение (а- параметр)
                          (а-1)х+2=а+1.
Решение. Запишем уравнение в стандартном виде
(а-1)х=а-1.

1. Если а-1=0, т.е. а=1, то уравнение примет вид 0х=0, т.е. х – любое число.
2. Если а-1≠0, т.е. а≠1, то х=1.

Ответ:
при а=1, х – любое число; при а≠1, х=1.

Пример №19. Сколько корней в зависимости от параметра а имеет уравнение
2 -1-х=а?
Решение. Преобразуем уравнение к виду 2|x| -1=х+а.
Рассмотрим функции f(х)=2|x| -1 и g(х,а)= х+а.
Графиком первой из них является ломаная (рис.1), графиком второй — семейство прямых, параллельных прямой у=х.

Эти прямые пересекаются с осью ординат в точках с координатами (0;а). Очевидно, что если а будет возрастать от — , то впервые графики пересекутся тогда, когда прямая пройдет через вершину ломаной, т.е. через точку (0;-1), т.е. при а=-1. В этом случае уравнение имеет единственное решение. Если дальше увеличивать параметр а, то точек пересечения будет ровно две – с каждой из ветвей ломаной. В результате этого анализа получаем ответ.
Ответ: при а<-1 уравнение не имеет корней; при а=-1 уравнение имеет единственный корень;
при а>-1 уравнение имеет два корня.

Как было сказано ранее, к уравнениям с параметрами надо возвращаться постоянно. Поэтому, на конец учебного года можно вынести уравнения:
1) (а-3)х=а2-9;
2) (3-2а)х=4а2-12а+9;
3) (а2-4)х=а2-5а+6;
4) (а2-1)х=а3+1
      Решение.1) (а2-1)=0, а=±1.
                         При а=1 уравнение имеет вид 0х=2. Следовательно, решений нет.
                         При а=-1 уравнение имеет вид 0х=0. Следовательно, х- любое число.

Задачи для самостоятельного решения.

Для всех значений параметров а и в решите уравнения:

1. (5а+1)х+25а2+10а+1=0;
2. ах-а=х-1;
3. (а2-4)х=а2+а-2;
4. (а2-1)х-а2+2а-1=0;
5. (а-2в)х+а+в=3;
7. каких значениях параметра а уравнение а2(х-2)=х+а-3 имеет бесконечное множество решений?
8. каком значении параметра а корень уравнения х+3=2х-а будет отрицательным числом?
9. каждого значения параметра а определить число корней уравнения |x-1| =а.
10. каждого значения параметра а определить число корней уравнения|5x-3| =а.

Используемая литература.

1. Газета «Математика». Учебно-методическое приложение к газете «Первое сентября»:  Е.Пронина, « Линейные уравнения с параметрами» №12, 2000 г.;  C.Неделяева, «Особенности решения задач с параметрами» №34, 1999 г.
2. Азаров А.И., Барвенов С.А., Федосенко В.С. Методы решения задач с параметрами. Математика для старшеклассников. Минск: «Аверсэв», 2003.
3. Мочалов В.В., Сильвестров В.В. Уравнения и неравенства с параметрами. Чебоксары: Изд-во Чувашского университета,  2004.
4. Соколовская С.И., Духон М.Ю. Линейные уравнения и неравенства с параметром. Пособие для учащихся старших классов. М., 2005.

urok.1sept.ru

Тест по алгебре (7 класс) по теме: Тренажер по решению линейных уравнений.

Тренажер по теме «Решение линейных уравнений»

Чтобы найти неизвестный множитель, нужно произведение разделить на известный множитель

Образец: 2х=10 х=10:2 х=5

Решите уравнение по образцу:

1. 5х=10
2. 10х=90
3. 13у=78
4. 25m=375
5. 2х=-12
6. -3к=15
7. -12у=-36
8. 31в=-93
9. -4х=1,2
10. 6у=-0,36
11. -12к=-1,44
12. -0,2х=-1,2
13. 1.7у=-0,34
14. -7,4m=-1,48
15. 3х=1
16. 7r =-4
17. 13у=-10
18. -10v=-7
19. х=4
20. у=6
21. к=-.
22. х=-1
23. а=-1

Корни уравнения не изменяются, если какое-нибудь слагаемое перенести из одной части уравнения в другую, изменив при этом знак на противоположный.

Образец: х+5=10 х=10-5 х=5

Образец: х-4=10 х=10+4 х=6

Решите уравнения:

1. Х+6=10.
2. У+14=19,
3. а+41=60,
4. 2х+3=13,
5. 3у+14=77,
6. 5х+13=73,
7. Х-4,5=10,
8. 5-у=4,
9. 10-х=6,
10. х -7,8=1,2,
11. 2х-3=16,
12. 100-5х=17,
13. 0,2х+3=-1,5,
14. -1,2у-4,7=-3,5,
15. 4х+х=-15,
16. 3у-5у=7,
17. -4х-3у=-49,
18. Х+4=3х,
19. -3у+7=2у.
20. 5а-1,5=2а.
21. -0,2х+7=-1,6х,
22. t+5=t-7,
23. 2у=7у,
24. -3к+8=-3к+9,
25. 6,9-9n=-5n-33,1,

---

Образец: 3х+6=4х-1 3х-4х=-1-6 -х=-7 х=7

Решить уравнения:

1. 2х+8=6х-2,
2. 10у+3=2у-1,
3. -4+3к=8к+5.
4. 9+4а=8а-9,
5. 3в+9=8в+2,
6. 6-2с=3с-10,
7. 5-2у=8у+9,
8. -4х+3=4х-5,
9. 4а+4=-6а-5.
10. 3у+3=-2-7у.
11. -10х+3=-1-8х,
12. 9-4х=-4-9х,
13. -8а+9=3-4а,
14. с+3=с+5,
15. t-t+2=t-3,
16. x+x+5=x,
17. 0,2f+2,3=0,7f-3,2,
18. -0,4x-14=0,3x,
19. -40·(-7x+5)=-1600,
20. (-20t-50)·2=100,
21. 2,1·(4-6e)=-42,
22. -3·(2-15k)=-6,
23. -20·(x-13)=-220,
24. (30-7r)·8=352,
25. (2,8-0,1h)·3,7=7,4,
26. (3x-1,2)·7=10,5,
27. x-=.

---

Образец: 2·(х-7)=3, 2х-14=3, 2х=3+14, 2х=17, х=17:2, х=8,5.

Решить уравнение.

1. 5·(у-9)=-2.
2. 3=4·(к+2),
3. 5·(с+5)=-7,
4. 7·(а-1)=3а.
5. 7·(-3+2х)=-6х-1,
6. 2·(7+9к)=-6к+2,
7. 6·(5-3с)=-8с-7,
8. 4·(2-3х)=-7х+10,
9. -4·(-к+7)=к+17,
10. -5·(0,8t-1,2)=-t+7,2,
11. -5·(3а+1)-11=-16,
12. -3,2n+4,8=-2·(1,2n+2,4),
13. -5·(0,8f-1,4)=-f+7,
14. 5·(r-7)=3·(r-4)-27,
15. 8-7·(c-2)=2·(2c-3)+3c,
16. 4·(x-3)-16=5·(x-5),
17. 5·(y-3)+27=4y+3·(2y-5),
18. -4·(3-5z)=18z-7,
19. 1,2-2·(1,3y+1)=5,6y-27,04,
20. 8·(2f-6)=2·(4f+3),
21. -3·(2,1m-1)+4,8=-6,7m+9,4,
22. 6·(2c-3)+2·(4-3c)=5,
23. h+- =2-h+2h,
24. 1-1x+3x=1x-2x+2,5,
25. 2·(z+1)+3=4-·(z-1).

---

Образец: =,   9х=5·4 9х=20 х=, х=2,

Решить уравнения.

1. =,
2.  = ,
3. =,
4.  = ,
5.  = ,
6.  = ,
7.  = ,
8.  =4,
9.  =7,
10.  = ,
11.  =  ,
12.  = ,
13.  =  ,
14.  =  ,

---

Решите уравнения:

nsportal.ru