1.1.4 Степень с целым показателем
Видеоурок: Степень с целым показателем
Лекция: Степень с целым показателем
 Степень
СтепеньПод степенью некоторого числа «а» с некоторым показателем «n» понимают произведение числа «а» само на себя «n» раз.
Когда говорят о степени с целым показателем, это означает, что число «n» должно быть величиной не дробной. Если данный показатель имеет отрицательное значение, то для начала необходимо избавиться от минуса перед показателем степени, а затем производить действия над степенью.

а — основание степени, которое показывает, какое число следует умножать само на себя, n — показатель степени — он говорит, сколько раз основание нужно умножить само на себя.

Например:
84 = 8 * 8 * 8 * 8 = 4096.
В данном случае под основанием степени понимают число «8», показателем степени считается число «4», под значением степени понимается число «4096».
Самой большой и распространенной ошибкой при подсчете степени является умножение показателя на основание — ЭТО НЕ ВЕРНО!
Когда речь идет о степени с натуральным показателем, имеется в виду, что только показатель степени (n) должен быть натуральным числом. В качестве основания можно брать любые числа с числовой прямой.
Например,
(-0,1)3 = (-0,1) * (-0,1) * (-0,1) = (-0,001).
 Свойства степени
Свойства степени
Для удобства решений примеров со степенями необходимо знать основные их свойства:
1. Любое число, которое возводится в показатель степени, равный единице, равно первоначальному числу.
а1 = а.
Например,
51 = 5.
2. При возведении любого числа в степень с показателем ноль, результатом данного вычисления всегда будет единица.
а0 = 1.
Например,
70 = 1.
3. Если Вам необходимо умножить две степени, которые имеют одинаковые основания, то в таком случае основание необходимо оставить без изменения, а показатели сложить.
an * am = an+m.
Например:
52 * 54 = 56.
4. Если необходимо разделить две степени, которые имеют одинаковые основания, то в таком случае основание необходимо оставить без изменения, а показатели вычесть. Обратите внимани, для действий со степенями с натуральным показателем показатель степени делимого должен быть больше показателя степени делителя. В противном случае, частным данного действия будет число с отрицательным показателем степени.
an / am = an-m .
Например,
54 : 52 = 52.
5. Если необходимо возвести одну степень в другую, основанием результата останется то же число, а показатели степени перемножаются.
(an )m = an*m
Например,
(54 )2 = 58.
6. Если в некоторую степень необходимо возвести произведение произвольных чисел, то можно воспользоваться неким распределительным законом, при котором получим произведение различных оснований в одной и той же степени.
(a * b)m = am * bm.
Например,
(5 * 8 )2 = 52 * 82.
7. Аналогичное свойство можно применять для деления степеней, иначе говоря, для возведения обыкновенной двоби в степень.
(a / b)m = am / bm
8. Если некоторая дробь имеет отрицательный показатель степени, то для избавления от знака минуса, её следует перевернуть.
Например,

Очень важно помнить, что знак степени не влияет на знак выражения при возведении в степень.
9. Если Вы возводите отрицательное число в четную степень, то в результате Вы всегда получите положительное число. Если же необходимо возвести отрицательное число в нечетную степень, то результатом данного математического действия будет отрицательное число.
Например,
(-11)2 = 121,
(-3)3 = (-27).
Степень с целым показателем и ее свойства [wiki.eduVdom.com]
Выражение $0^n\text{ , при }n\in \mathbb{Z}\,,\, n \leq 0$ не имеет смысла.
Например:
Свойства степени с целым показателем:
Для всех а≠0 и любых $m, n\in\mathbb{Z}$ верны равенства:
$a^m\cdot a^n = a^{m+n}$
$a^m : a^n = a^{m-n}$
$(a^m)^n = a^{mn}$
Для всех а≠0, b≠0 и любого $n\in \mathbb{R}$ верны равенства
Стандартный вид числа b — это его запись в виде $a\cdot 10^n\text{, где }1\leq a < 10\,, n\in\mathbb{Z}$ . Число n называется порядком числа b.
Пример 1. Вычислите $(5\cdot 10^{-2} + 6^{-1}\cdot 36 — 20^{-1})^2$.
Решение:
$(5\cdot 10^{-2} + 6^{-1}\cdot 36 — 20^{-1})^2 = (5\cdot \frac{1}{10^2} + \frac{1}{6}\cdot 36 — \frac{1}{20})^2 = (\frac{1}{20} + 6 — \frac{1}{20})^2 = 6^2 = 36$
Ответ: 36.
Пример 2. Упростите выражение $(a^{-2} — b^{-2}):\frac{a-b}{ab}$
Решение:
$(a^{-2} — b^{-2}):\frac{a-b}{ab} = (\frac{1}{a^2} — \frac{1}{b^2})\cdot \frac{ab}{(a-b)} = \frac{b^2-a^2}{a^2b^2}\cdot\frac{ab}{a-b} = -\frac{(a-b)(a+b)}{(ab)^2}\cdot\frac{ab}{a-b} = -\frac{a+b}{ab}$
Ответ: $-\frac{a+b}{ab}$
Пример 3. Представьте число 36782 в стандартном виде и назовите его порядок.
Решение: 36782 = 3678,2 • 10 = 367,82 • 102 = 36,782 • 103 = 3,6782 • 104. Порядок числа равен 4.
Ответ: 3,6782 • 104; порядок 4.
Пример 4. Найдите значение выражения: $5\cdot\left(\frac{1}{5}\right)^2 — 16\cdot\frac{1}{16}=?$
Видео-решение.
Пример 5. Сократите дробь: $$ \frac{18^{n+3}}{ 3^{2n+5} \cdot 2^{n-2} } $$
Видео-решение.
Урок 6: Степень с целым показателем
План урока:
Определение степени с целым числом
Свойства степени с целым показателем
Преобразование выражений с целыми степенями
Стандартный вид числа
Действия с числами в стандартном виде
Определение степени с целым показателем
В 7 классе мы уже изучили степень с натуральным показателем. Напомним, что запись anозначает произведение, состоящее из n множителей, каждый из которых равен a:

Число а именуется основанием степени, а n – это показатель степени. Отдельно напомним, что число в первой степени равно самому себе:
а1 = а
Любое число, кроме нуля, возведенное в нулевую степень, дает единицу:
а0 = 1
Сам же ноль в нулевую степень возводить нельзя (так же, как и нельзя делить на ноль).
Математики стремятся по возможности расширить используемые ими понятия. Можно ли сделать показатель степени отрицательным числом? Для этого надо дать новое определение степени. При этом важно, чтобы все уже известные нам правила действий со степенями (их умножение и деление) оставались справедливыми.
При делении степеней их показатели вычитаются, например:
815:813 = 815 – 13 = 82 = 64
Теперь попробуем произвести деление в том случае, когда показатель делимого меньше показателя делителя:
815:817 = 815 – 17 = 8– 2
Получили отрицательную степень, смысл которой нам пока не понятен. Выполним это же деление с помощью дробей, при этом учтем, что 817 = 815•82:

Итак, мы получили, что

То есть 8– 2 – это число, обратное 82. Подобные рассуждения помогают сформулировать определение степени с отрицательным показателем:

Напомним, что обратными называются числа, которые при умножении друг на друга дают единицу. Примерами обратных чисел являются:
- 5 и 1/5
- 2 и 1/2
- (– 15) и – 1/15
Вообще для каждой дроби обратной является «перевернутая дробь», поэтому следующие пары чисел являются обратными:

Теперь покажем, как вычислять отрицательную степень числа, пользуясь определением:

Вообще находить отрицательную степень дроби удобней с помощью формулы

Докажем ее справедливость:

Покажем применение этой формулы:

Заметим, что возвести ноль в отрицательную степень не получится. Действительно, если мы попробуем, например, вычислить 0– 2, то получим деление на ноль:

Вообще, при возведении нуля в любую отрицательную степень получается деление на ноль, а потому выражение 0n, где n–отрицательное число, не имеет смысла.

Отрицательные степени очень удобны при работе с некоторыми выражениями. В частности, любую дробь с их помощью можно записать в виде произведения:

Пример: Запишите в виде произведения дробь

Решение.

Ответ: а2b– 4
Отдельно заметим, формулу, определяющую отрицательную степень

можно и «перевернуть». В ней число 1 выступает в роли делимого, выражение аn – это делитель, а a– n – это частное. Известно, что делитель можно получить, поделив делимое на частное, то есть верна запись

Это значит, чтосправедливо не только равенство

но и

Свойства степени с целым показателем
Правила действий со степенями, имеющими целый показатель, не отличаются от тех, которые мы изучали ранее. Напомним их.

Убедимся в этом на нескольких примерах:

Однако эти примеры ещё не являются полноценными доказательствами этого свойства степеней. Приведем общее доказательство для того случая, когда число в натуральной степени умножается на число в отрицательной степени:

Также докажем справедливость этого правила и в том случае, когда перемножаются два числа в отрицательной степени:


Проиллюстрируем это:

Для строгого доказательства заменим операцию деления на умножение. Так как

Здесь мы сначала заменяем степень an на дробь 1/а– n (по определению отрицательной степени), а потом пользуемся тем, что деление на дробь равносильно умножению на «перевернутую дробь».

Продемонстрируем применение этого правила:

Следующие правила позволяют работать со степенями, у которых различаются основания, но совпадают показатели:

Покажем, как это работает:

Для общего случая доказательство будет выглядеть так:


Это правило можно проиллюстрировать так:

Приведем доказательство этого свойства для отрицательных степеней с целым показателем:

Как видим, свойства степеней с целыми показателями (в частности, с отрицательными), не отличаются от уже изученных нами свойств степеней с натуральными показателями. Единственное исключение – добавляется дополнительное ограничение, согласно которому основанием степени с отрицательным целым показателем не может быть ноль. То есть запись 0– 3 не имеет смысла, хотя выражение 03 имеет смысл:
03 = 0•0•0 = 0
Рассмотрим несколько заданий, в которых необходимо использовать правила работы со степенями
Пример. Представьте в виде степени выражение
у– 8•у10
Решение. При перемножении степеней их показатели следует сложить:
у– 8•у10 = у– 8 + 10 = у2
Ответ: у2
Пример. Вычислите значение выражения
(10– 1)– 6 : (0,1)– 3
Решение.
(10– 1)– 6 : (0,1)– 3 = 10(– 1)•(– 6): (10– 1)– 3 = 106: 103 = 106 – 3 = 103 = 1000
Ответ: 1000
Пример. Представьте число 3– 36 в виде степени с основанием 9.
Решение.
3– 36 = 32•(– 18) = 9– 18
Ответ: 9– 18
Пример. Представьте произведение 64v– 3 как степень.
Решение.
64v– 3 = 43v– 3 = (1/4)– 3v– 3 = (v/4)– 3
Ответ: (v/4)– 3
Преобразование выражений с целыми степенями
Ранее мы рассматривали понятие рационального выражения. Так называлось выражение, в котором используются 4 основные арифметические операции (в том числе деление), а также возведение в степень. Однако использование отрицательной степени помогает избавиться от операции деления как ненужной. Например, возможны такие преобразования:

Во всех случаях мы заменили деление на возведениев отрицательную степень.
Рассмотрим несколько примеров по преобразованию выражений со степенями.
Пример. Упростите выражение

Решение. Возведение в степень (– 1) означает, по сути, переворачивание дроби:

Ответ: ab
Пример. Упростите дробь

Решение. Вынесем в числителе множитель а– 3 за скобки

Пример. Представьте в виде дроби выражение

Решение.

В данном случае мы воспользовались формулой суммы кубов:
a3 + b3 = (a + b)(a2 – ab + b2)
Пример. Упростите выражение
(h2 + ht + t2)(h– 2 + h– 1t– 1 + t– 2)– 1
Решение.
Вынесем из первой скобки множитель h2t2. При вынесении множителя каждое слагаемое делится на этот самый множитель:

C учетом этого получаем:
(h2 + ht + t2) = h2t2(t– 2 + h– 1t– 1 + h– 2) = h2t2(h– 2 + h– 1t– 1 + t– 2)
Зная это, можно записать
(h2 + ht + t2)(h– 2 + h– 1t– 1 + t– 2)– 1 = h2t2(h– 2 + h– 1t– 1 + t– 2)(h– 2 + h– 1t– 1 + t– 2)– 1
В двух скобках стоят одинаковые выражения, но одно из них в степени (– 1). Такие выражения можно сократить, ведь они являются обратными числами:
а•a– 1 = 1
Поэтому
h2t2(h– 2 + h– 1t– 1 + t– 2)(h– 2 + h– 1t– 1 + t– 2)– 1 = h2t2
Ответ: h2t2
Пример. Докажите тождество

Решение. Преобразуем левую часть:

Стандартный вид числа
В физике и других естественных науках изучаются объекты, чьи характеристики (масса, длина, скорость и т.д.) могут измеряться очень большими или очень малыми величинами. Например, масса атома железа равна 0,0000000000000000000000000927 килограмм, а масса Солнца оценивается в 1988500000000000000000000000000 килограмм. Работать с такими числами достаточно неудобно. Сложно даже сравнивать их между собой, ведь для этого надо подсчитывать количество нулей в каждом числе. Поэтому в науке часто используется особая форма чисел, которую называют стандартным видом числа. Он основан на том, что любое число можно записать как произведение числа a, находящегося в пределах от 1 до 10, и какой-нибудь целой (в том числе отрицательной) степени десятки.

Приведем примеры представления чисел в стандартном виде
90 = 9•10 = 9•101
91 = 9,1•10 = 9,1•101
900 = 9•100 = 9•102
912 = 9,12•100 = 9,12•102
Покажем случаи, когда порядок равен нулю или меньше него
7 = 7•1 = 7•100
7,63 = 7,63•1 = 7,63•100
0,8 = 8•0,1 = 8•10– 1
0,0875 = 8,75•100 = 8,75•10– 2
Посмотрите, насколько короче выглядит запись физических величин с использованием стандартного вида:
- масса Солнца: 1988500000000000000000000000000 кг = 1,9885•1030 кг;
- масса Земли: 5970000000000000000000000 кг = 5,97•1024 кг;
- масса атома железа: 0,0000000000000000000000000927 = 9,27•10-26 кг.
Пример. Укажите стандартный вид числа 76000000.
Решение. Первой ненулевой цифрой в записи является семерка, поэтому стандартный вид будет выглядеть так:
7,6•10n
гдеn– какое-то целое число, которое нам надо найти. Поставим в исходном числе запятую после семерки:
7,6000000
Видно, что мы отделили запятой 7 разрядов, то есть перенесли запятую на 7 разрядов вправо. Поэтому nравно 7:
76000000 = 7,6•107
Действительно, умножение дробного числа на 10 приводит к смещению запятой на одну позицию влево, поэтому при умножении 7,6 на 107 получим 76000000. Наши действия можно проиллюстрировать рисунком:

В случае с числами, меньшими единицы, также надо смотреть на количество разрядов между запятой и первой ненулевой цифрой. Пусть надо представить в стандартном виде десятичную дробь 0,000005605. Значащей частью числа будет 5,605. Для того чтобы получить ее, надо в исходной дроби перенести запятую на 6 разрядов вправо. Поэтому порядок будет равен (– 6):

Теперь попробуем выполнить обратное преобразование – по стандартному виду числа записать его в привычной нам десятичной форме. Пусть есть запись 2,56•105. Для начала искусственно припишем несколько ноликов к значащей части:
2,56 = 2,5600000
Теоретически мы можем дописать любое количество нулей, величина дроби от этого не изменится. Порядок числа равен 5, а потому запятую надо перенести на 5 знаков вправо:
2,5600000•105 = 256000,00
Теперь лишние нули после запятой и саму запятую можно и убрать:
256000,00 = 256000
Обратите внимание, что порядок числа был равен 5, а в итоге мы получили шестизначное число. Можно сформулировать правило: у числа, имеющего в стандартной виде порядок n, в десятичной представлении перед запятой будет стоять (n + 1)знак. Например:
1,23456789•106 = 1234567,89
Здесь порядок числа равен 6, а потому перед запятой стоит 7 знаков.
Напомним, что если число целое и, соответственно, в его записи нет запятой, то ее можно искусственно добавить:
568 = 568,0
Теперь рассмотрим похожий пример с отрицательным порядком числа. Пусть надо записать в десятичном виде число 9,8765•10– 4. Для этого сначала можно условно «подрисовать» нолики перед значащей частью:
0000009,8765
Порядок равен (– 4), а потому надо передвинуть запятую на 4 знака влево
0000009,8765 =000,00098765
Получается, что мы подрисовали слишком много ноликов. Уберем два из нихи получим число в обычной форме:
0,00098765
Вообще, если у числа отрицательный порядок (– n), то первая ненулевая цифра должна оказаться на n-ой позиции после запятой:

Действия с числами в стандартном виде
Стандартный вид чисел удобен тогда, когда есть необходимость сравнивать физические величины, а также перемножать их и делить. Рассмотрим правила сравнения умножения и деления чисел в стандартном виде.
Из двух чисел больше то, у которого больше порядок стандартного вида числа. Так, масса Солнца больше масса Земли, так как у нее порядок равен 30, а у нашей планеты – только 24. Если же порядки одинаковы, то больше то число, у которого больше значащая часть.
Пример. Радиус ядра Солнца оценивается в 1,73•108 м, а радиус Юпитера составляет 6,99•107 м. Какая из этих величин больше?
Решение. Порядок у радиуса ядра Солнца равен 8, а у Юпитера только 7, поэтому радиус ядра Солнца больше радиуса Юпитера.
Пример. Масса протона составляет 1,673•10– 27 кг, а масса нейтрона равна 1,675•10– 27 кг. Какая из этих двух частиц тяжелее?
Решение. У обоих величин одинаковый порядок, равный (– 27). Однако значащая часть у массы нейтрона больше:
1,675 > 1,673
Следовательно, нейтрон тяжелее.
Ответ: Нейтрон тяжелее.
Посмотрим, как перемножать числа, находящиеся в стандартном виде. Переставляя множители местами, можно получить:
(a•10n)•(b•10m) = a•b•10n•10m = (ab)•10n+m
В итоге можно сформулировать правило:

Пример. Земля двигается по своей орбите со средней скоростью 3•104 м/с. Какое расстояние она проходит в течение одного невисокосного календарного года (в каждом таком году 31536000 секунд)?
Решение. Переведем количество секунд в году в стандартный вид
31536000 = 3,1536 •107
Расстояние (обозначим его как S) равно произведению средней скорости на время:
S = 3•104 м/с • 3,1536•107c = 3•3,1536•104 + 7 = 9,4608•1011м.
Ответ: 9,4608•1011м.
Пример. Представьте в стандартном виде произведение чисел 9,5•108 и 1,38•10– 2.
Решение.
(9,5•108)•(1,38•10– 2) = (9,5•1,38)•108 + (– 2) = 13,11•106
Получили число НЕ в стандартном виде, так как 13,11 > 10. Поэтому следует произвести замену 13,11 = 1,311•10:
13,11•106 = 1,311•10•106 = 1,311•107
Ответ:1,311•107
Теперь попытаемся поделить два числа, находящихся в стандартном виде:

Видно, что справедливо следующее правило:

Пример. Во сколько раз масса Солнца больше массы Земли?
Решение. Выше мы приводили данные, что масса Солнца оценивается в 1,9885•1030 кг, а масса нашей планеты составляет 5,97•1024 кг. Поделим массу звезды на массу планеты:
(1,9885•1030):(5,97•1024) = (1,9885:5,97)•1030 – 24≈0,333•106 = 333000
Получили, что Солнце примерно в 333 тысячи раз тяжелее Земли.
Ответ: В 333000 раз.
Степень с целым показателем (8 класс)
. N-ой степенью числа \(a\) – называют выражение вида \(a^n\), значение которого равно произведению \(n\) множителей, каждый из которых равен \(a\).
Примеры:
\(3^5=3\cdot 3\cdot 3 \cdot3 \cdot 3 =243\)
\((-5)^3=(-5)\cdot (-5)\cdot (-5)=-125\)
\(7^1=7\)
\(0^n=0 \cdot 0 \cdot 0 \cdot … \cdot 0=0\)
Анатомия степени:
|
\(a\) — основание степени |
|
Свойства степеней:
|
1. \(a^1=a\)
2. \(1^n=1\)
3. \(0^n=0\) \((n≠0)\)
4. \(a^0=1\) \((a≠0)\)
5. \(a^n·a^m=a^{n+m}\)
6. \(\frac{a^n}{a^m}\)\( =a^{n-m}\) \((a≠0)\) 7. \(a^n·b^n=(a·b)^n\)
8. \(\frac{a^n}{b^n}\) \(=\) \((\frac{a}{b})^n\) \((b≠0)\)
9. \((a^n)^m\)=\(a^{n·m}\)
10. \(a^{-n}=\)\(\frac{1}{a^n}\) \((a≠0)\) 11. \((\frac{a}{b})^{-n}\) \(=\) \((\frac{b}{a})^{n}\) \((a≠0,b≠0)\) |
Наиболее важные свойства степени с примерами вы можете найти здесь.
Знание свойств степени позволяет упрощать выражения или вычислять их значения быстрее и легче. Продемонстрируем на примерах.
Пример. Вычислите \(\frac{x^{22}·x^{-5}}{x^{15}}\) при \(x=3\).
Решение:
|
\(=\)\(\frac{x^{22}·x^{-5}}{x^{15}}\)\(=\)\(\frac{x^{22+(-5)}}{x^{15}}\)\(=\)\(\frac{x^{17}}{x^{15}}\)\(=\)\(x^{17-15}\)\(=\)\(x^2=3^2=9\) |
\(\frac{3^{22}·3^{-5}}{3^{15}}\)\(=\)\(\frac{31381059609\cdot \frac{1}{243}}{14348907}\)\(=\)\(\frac{129140163}{14348907}\)\(=\)\(9\) |
Чувствуете разницу? В первом случае задача решается практически в уме, во втором – нам требуется инженерный калькулятор.
Пример. Вычислите \(\frac{7^{9}·2^{6}}{(\frac{1}{14})^{-8}}\).
Решение:
|
\(\frac{7^{9}·2^{6}}{(\frac{1}{14})^{-8}}\)\(=\) |
В знаменателе у нас дробь в отрицательной степени. Используем свойство \((\frac{a}{b})^{-n}\) \(=\) \((\frac{b}{a})^{n}\) |
|
|
\(=\)\(\frac{7^{9}·2^{6}}{(\frac{14}{1})^{8}}\)\(=\)\(\frac{7^{9}·2^{6}}{14^{8}}\)\(=\) |
Здесь мы не можем применить никакие свойства, потому что нам нужно, чтоб были одинаковы либо показатели, либо основания. Подумаем, как можно преобразовать выражение, чтоб это получить. Заметим, что \(14 = 7·2\). Значит, можно заменить. |
|
|
\(=\)\(\frac{7^{9}·2^{6}}{(7 \cdot 2)^{8}}\)\(=\) |
Теперь используем свойство \(a^n\cdot b^n=(a \cdot b)^n\), но только в обратную сторону, вот так: \((a \cdot b)^n=a^n \cdot b^n\) |
|
|
\(=\)\(\frac{7^{9}·2^{6}}{7^8 \cdot 2^8}\)\(=\) |
Вспоминая свойства дробей (а конкретно — их перемножение) разобьем нашу дробь на две отдельные. |
|
|
\(=\)\(\frac{7^9}{7^8}\)\(\cdot\)\(\frac{2^6}{2^8}\)\(=\) |
|
Теперь воспользуемся свойством \(\frac{a^n}{a^m}\) \(=\) \(a^{n-m}\) |
|
\(= 7^{9-8}· 2^{6-8}= 7^1·2^ {-2}=\) |
|
Любое число в первой степени равно самому себе: \(a^1=a\). |
|
\(=7 \cdot\)\(\frac{1}{2^2}\) \(= 7 \cdot\) \(\frac{1}{4}\)\(=\)\(\frac{7}{4}\)\(=1,75\) |
|
Готов ответ. |
Пример. Вычислите \((\frac{(-2,42)^{75} \cdot 0,01^{-58}}{(\frac{1}{3})^{84}})^0\)
Решение: Прежде чем падать в обморок от ужаса, обратите внимание, что вся эта страшная дробь стоит в степени \(0\). А любое число в \(0\) степени равно \(1\). Поэтому ответ: \(1\).
Ответ: \(1\)
Пример. Найдите значение выражения \(2^{1-3x} \cdot 8^x\)
Решение:
|
\(2^{1-3x} \cdot 8^x =\) |
У нас опять разные основания и разные показатели. Но мы можем сделать основания одинаковыми, так как \(8=2·2·2=2^3\). |
|
|
\( =2^{1-3x} \cdot (2^3 )^x = \) |
При возведении степени в степень – показатели перемножаются \((a^n)^m=a^{n·m}\) |
|
|
\(=2^{1-3x}·2^{3x} = \) |
Теперь основания одинаковы, можем использовать свойство \(a^n\cdot a^m=a^{n+m}\) |
|
|
\(=2^{1-3x+3x} = 2^1=2\) |
Готов ответ. |
Свойства степени с целым показателем
Из курса алгебры 7 класса вы уже знакомы с пятью свойствами степеней с натуральными показателями. Давайте проверим, можно ли пользоваться этими свойствами для преобразования степеней с целыми показателями. Проверять будем на конкретных примерах. Сразу договоримся основания степеней считать отличными от нуля.


Как видите, известные вам свойства степени с натуральным показателем справедливы и для степени с любым целым показателем. Нужно только предполагать, что основание степени не равно нулю.

Запишем свойства степени с любым целым показателем.
Для каждого  и
целых
и
целых  и
и
 выполняются
равенства:
выполняются
равенства:

Для каждых  и
любого целого
и
любого целого  выполняются
следующие равенства:
выполняются
следующие равенства:

Из свойств степени вытекает, что действия над степенями с целыми показателями выполняются по тем же правилам, что и действия над степенями с натуральными показателями.
Задание: упростите выражения.
Решение:

Задание: вычислите значение выражения.
Решение:

Итоги:
Действия над степенями с целыми показателями выполняются по тем же правилам, что и действия над степенями с натуральными показателями.
Для каждого  и
целых
и
целых  и
и
 выполняются
равенства:
выполняются
равенства:

Для каждых  и
любого целого
и
любого целого  выполняются
следующие равенства:
выполняются
следующие равенства:

Урок алгебры в 8 классе «Степень с целым показателем и её свойства»
Урок в 8 классе по теме «Степень с целым показателем и её свойства»
Цели урока:
Обобщить и систематизировать знания учащихся. Выработать умение применять свойства степени с целым показателем в вычислениях и преобразованиях; подготовить содержательную базу для сдачи ГИА.
Развивать умения применять теоретические знания на практике. Развивать познавательную активность, мышление, внимание и память, умение слушать товарища, умение наблюдать, сравнивать, делать выводы, развивать математическую речь.
Воспитывать стремление достигать поставленную цель, умение работать в коллективе, работать в группах и парах, развивая взаимовыручку, умение выслушивать мнения товарищей, отстаивать свою точку зрения. Умение управлять своим поведением.
Планируемый результат:
Знать определение степени с целым (отрицательным) показателем и её свойства,
применять свойства степени с целым показателем для преобразования выражений.
Личностные УУД:
Способность к самооценке на основе критерия успешности учебной деятельности.
Познавательные УУД:
Умение ориентироваться в своей системе знаний и умений: отличать новое от уже известного с помощью учителя; находить ответы на вопросы, используя информацию, полученную на уроке.
Обобщение и систематизация учебного материала, воспроизведение по памяти информации, необходимой для решения учебной задачи.
Предметные УУД:
Применять свойства степени к преобразованию выражений, содержащих степени с целым отрицательным показателем.
Регулятивные УУД:
Умение определять и формулировать цель на уроке с помощью учителя; оценивать свою работу на уроке. Осуществлять взаимоконтроль и самоконтроль при выполнении заданий.
КоммуникативныеУУД:
Уметь оформлять свои мысли в устной и письменной форме, слушать и понимать речь других.
Основные понятия: степень, основание, показатель, стандартный вид числа, порядок.
Методы обучения и воспитания: проблемный метод, деятельностный метод.
Оборудование: презентация «Степень с целым показателем»; раздаточный материал, мультимедийный проектор, экран.
Ход урока.
Организационный этап.Здравствуйте, ребята!
Тем, кто учит математике,
Тем, кто учит математику,
Тем, кто знает и любит математику,
И тем, кто ещё не знает, что он любит математику,
Работать сегодня на уроке всем.
У вас на столах лежит лист достижений (приложение 1). Отметьте пожалуйста, с каким настроением вы пришли сегодня на урок.
Учащиеся приветствую учителя.
Учащиеся отмечают в листах достижений своё настроение.
Мотивация к учебной деятельности.
Постановка учебной задачи
(проблемный метод)
Прочитайте (на доске) понятия
К какой теме относятся эти понятия? Правильно.
Откройте тетради и запишите число и тему урока «Свойства степени с натуральным показателем» (Слайд 1)
Сегодня у нас последний урок по этой теме. А как вы думаете, чем мы будем заниматься на уроке, какие цели поставим перед собой?
«степень, основание, показатель»
К теме «Степень».
Повторить. Уточнить. Обобщить. Применить знания по данной теме.
Умение ставить цель.
Актуализация
знаний
(проблемный метод)
Мы расширили понятие степени. В 7-м классе мы изучили степень с целым неотрицательным показателем (т.е. каким показателем?)
— “Дайте определение степени с натуральным показателем большим 1”.
— “Как определяется степень при n=1, n=0”?
На сегодня мы рассмотрели степени с целым отрицательным показателем.
— Дайте определение степени с целым отрицательным показателем.
Итак, теперь нам известно, что такое степень с целым показателем.
Мы доказали, что действия над степенями с целыми показателями выполняются по тем же правилам, что и действия над степенями с натуральными показателями. Какие действия можно выполнять со степенями?
— Как умножить две степени c одинаковыми основаниями?
— Как разделить две степени c одинаковыми основаниями?
— Как возвести степень в степень?
— Чему равна степень произведения?
— Как возвести в степень дробь? ( слайд 1,2)
— Как называются а и n в записи степени?
—У вас на парте листы с заданиями (приложение 2)
Слева указаны начала определений справа окончания определений. Соедините линиями верные высказывания (слайд 4)
Теперь, поменяйтесь листочками с соседом по парте, оцените его работу и поставьте ему оценку. Эту оценку выставите в свой оценочный лист.
Повторим свойства степеней.(слайд 5)
Вам нужно выполнить задания, т.е. записать ответ в виде степени с основанием с, и вы узнаете фамилию и имя великого французского математика, который ввёл общепринятое в настоящее время обозначение степеней.(Слайд 6)
52.
С8 : С6
7.
(С4)3 • С
3.
(С4)3
8.
С4 • С5 • С0
4.
С5 • С3 : С6
9.
С16 : С8
5.
С14 • С8
10.
(С3)5
Ответ: Рене Декарт (слайд 7)
— Прочитайте выражение «а — n»
-как перейти к положительному показателю
— Повторим формулы: (слайд 8)
а—n=1/а
(а/в)-1= в/а
а-1=1\а
(1/а)-1= а
Устный счёт:
1. Замените степень с целым отрицательным показателем дробью: (слайд 9)
2. Замените дробь степенью с целым отрицательным показателем: (слайд 10)
3. Верно-неверно? (+ или – ) (слайд 11)
+
—
+
—
—
+
+
+
Устно (слайд 14-26)
Поставьте оценку за устный счёт в лист достижений
4) Преобразуйте выражение так, чтобы оно не содержало степеней с отрицательными и нулевыми показателями: (Слайд 12)
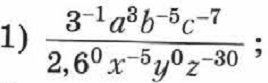
2) 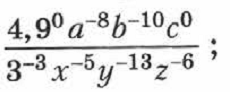
Устно (фронтально)
Учащиеся выполняют задание 2 (приложение2)
Устно (фронтально)
У доски ученик выполняет задание.
Умение с точностью выражать свои мысли, слушать и вступать в диалог, умение проверять результаты вычислений, исправлять найденные ошибки, оценивание себя.
Выявление знаний, умений и навыков, проверка уровня сформированности у учащихся общеучебных умений.
Самостоятельная практическая работа.
Выполните задание №1 и №2 (приложение 3) и оцените работу в листах достижений.
Учащиеся выполняют задание №1 и №2 самостоятельно (приложение 3) и выставление оценок в лист достижений.
Планирование путей для решения данного задания, оценивание собственных успехов, аргументация своего мнения.
Коррекция выявленных пробелов, обеспечение закрепления в памяти учащихся знаний и способов действий
Самостоятельная работа
1вариант 2 вариант












Учащиеся выполняют решения, затем обмениваются листами и проверяют решение.
Контроль и оценка процесса и результатов деятельности
Актуализация
знаний
(проблемный метод)
Где ещё применяются степени?
В науке и технике встречаются очень большие, и очень малые положительные числа. Например, большим числом выражается объём Земли, а малым – диаметр молекулы воды. В обычном виде большие и малые числа неудобно читать и записывать, неудобно выполнять над ними какие-либо действия. Как удобнее записывать эти числа?
Дайте определение стандартного вида числа
МОЗГОВОЙ ШТУРМ:
Устный счёт (слайд 29 – 34)
Число записано в виде а∙10n, где 1<а<10. N- порядок числа
Умение с точностью выражать свои мысли, слушать и вступать в диалог, умение проверять результаты вычислений, исправлять найденные ошибки, оценивание себя.
Применение знаний и умений в новой ситуации
Самостоятельная работа
Запишите число в стандартном виде (слайд 35).
Запишите ответы в листы достижений (приложение 3), обменяйтесь с соседом, поставить оценку за работу и в оценочные листы.
1) 52 000 000 = 5,2 * 10 7;
2) 2 180 000 = 2,18 * 10 6;
3) 675 000 000 = 6,75 * 10 8;
4) 40,44 = 4,044 * 10;
5) 0,00281 = 2,81 * 10 – 3;
6) 0,0000035 = 3,5 * 10— 6.
7) 45 *10 3= 4,5 * 10 4;
8) 117 * 10 5 = 1,17 * 10 7;
9) 0,74 * 10 6= 7,4 * 10 5;
10) 0,06 * 10 5 = 6 * 10 3.
Выполните задание №4 самостоятельно (приложение3)
Учащиеся выполняют работу, а затем сверяют ответы (слайд 36) и ставят оценку в лист достижений.
Умение самостоятельно контролировать время, выполнения задания, умение осознанно применять алгоритм.
Выполнение самостоятельной работы. Осуществление самоконтроля (сравнение с эталоном).
Обобщение и систематизация знаний
Работа у доски
№5,№6
Учащиеся решают у доски, остальные в тетрадях
Контроль и оценка процесса и результатов деятельности
Рефлексия учебной деятельности.
Подведение итога урока
А где же мы с вами будем применять знания , полученные по теме «Степень».
1.После каждой теме у нас и контрольная работа.
2.Конец года. Что ждёт нас впереди? Итоговая работа за курс 8 класса, пробный ОГЭ.
3.И если посмотреть дальше в перспективу.. Что нас ждёт ? Итоговая аттестация за основную школу. Данные упражнения входят в обязательный перечень знаний при проведении ГИА
Фалес Милетский великий учёный сказал:
Что больше всего на свете— пространство. (ибо оно вмещает все).
Что быстрее всего — мысль. ( ибо она бежит без остановки. )
Что мудрее всего — время. (ибо оно обнаруживается во всем)
Что приятнее всего – достичь желаемого (сдать зачёт, хорошо написать контрольную работу, итоговую, а в дальнейшем сдать ГИА надо много работать (слайд)
Подсчёт баллов и выставление оценок в листе достижений.
Ребята, заполните, пожалуйста, небольшую анкету по данному уроку:
активно/пассивно2. Своей работой на уроке я
доволен/не доволен
3. Урок мне показался
Коротким / длинным
4. За урок я
не устал / устал
5. Моё настроение
стало лучше / хуже
6. Материал урока мне
Понятен / не понятен
7.Достиг ли я цели
Да/нет
8.Изменилось ли ваше настроение (посмотрите в начало урока, изобразите рисунок)
Домашнее задание: стр 85 «Проверь себя»
Спасибо за урок!
Оценивают свои знания и умения
(приложение 1)
Каждый учащийся выставляет себе оценку за работу на уроке
Адекватное понимание успешности и неуспешности, умение выражать свои мысли и аргументировать свое мнение.
Приложение 1
Лист достижений_______________Моё настроение похоже на:
солнышко;
солнышко с тучкой;
тучку;
тучку с дождиком;
тучку с молнией.
И нарисуйте соответствующий вашему настроению рисунок.
активно/пассивно2. Своей работой на уроке я
доволен/не доволен
3. Урок мне показался
Коротким / длинным
4. За урок я
не устал / устал
5. Моё настроение
стало лучше / хуже
6. Материал урока мне
Понятен / не понятен
7.Достиг ли я цели
Да/нет
8.Изменилось ли ваше настроение (посмотрите в начало урока, изобразите рисунок)
Лист достижений_______________
Моё настроение похоже на:
солнышко;
солнышко с тучкой;
тучку;
тучку с дождиком;
тучку с молнией.
и нарисуйте соответствующий вашему настроению рисунок.
активно/пассивно2. Своей работой на уроке я
доволен/не доволен
3. Урок мне показался
Коротким / длинным
4. За урок я
не устал / устал
5. Моё настроение
стало лучше / хуже
6. Материал урока мне
Понятен / не понятен
7. Достиг ли я цели
Да/нет
8.Изменилось ли ваше настроение (посмотрите в начало урока, изобразите рисунок)
Приложение 2
Слева указаны начала определений справа окончания определений. Соедините линиями верные высказывания
2. Записать ответ в виде степени с основанием с, и вы узнаете фамилию и имя великого французского математика, который ввёл общепринятое в настоящее время обозначение степеней.
52.
С8 : С6
7.
(С4)3 • С
3.
(С4)3
8.
С4 • С5 • С0
4.
С5 • С3 : С6
9.
С16 : С8
5.
С14 • С8
10.
(С3)5
Приложение 3
32=30=
34=
33=
2-1=
2-2=
2-3=
3-1=
3-2=
=
=
=
=
(0,2) — 2=
Задание 2. Упростите
=
=
=
=
=
=
=
=
=
=
=
Задание 3
1вариант 2 вариант











Задание 4. Вычислите
Задание 5. Упростите
Задание 6.Найдите значение выражения
Определение степени с целым отрицательным показателем
В курсе математики 7 класса вы научились вычислять значение степени с любым натуральным показателем.
Напомним, что степенью числа а с
натуральным показателем  (
( ),
называется выражение
),
называется выражение  ,
которое равно произведению
,
которое равно произведению  множителей,
каждый из которых равен
множителей,
каждый из которых равен  .
.

Степенью числа а с показателем единица является само число а. А вот при возведении в степень нуля всегда получаем нуль.

Также вам уже известны свойства степеней с натуральными показателями.
При умножении степеней с одинаковыми
основаниями основание остаётся прежним, а показатели степеней складываются.
Т.е. для любого числа  и
натуральных чисел
и
натуральных чисел  и
и
 верно
равенство:
верно
равенство:

При делении степеней с одинаковыми основаниями
основание остаётся прежним, а из показателя степени делимого вычитается
показатель степени делителя. Т.е. для любого числа  и
натуральных чисел
и
натуральных чисел  и
и
 ,
таких, что
,
таких, что  ,
справедливо равенство:
,
справедливо равенство:

Чтобы возвести в степень произведение, нужно
каждый множитель возвести в эту степень и результаты перемножить. Аналогично и
для частного. Т.е. для любых чисел  и
и
 и
натурального числа
и
натурального числа  верно
равенство:
верно
равенство:

При возведении степени в степень основание
оставляют прежним, а показатели степеней перемножают. Т.е. для любого числа  и
произвольных натуральных чисел
и
произвольных натуральных чисел  и
и верно
равенство:
верно
равенство:

Заметим, что

Рассмотрим случай, когда показатель степени делимого меньше показателя степени делителя.

Такое соглашение принимается для степеней с любыми основаниями, отличными от нуля.
Определение:
Если  и
и
 –
целое отрицательное число, то верно равенство:
–
целое отрицательное число, то верно равенство:

Задание: заменить степень с целым отрицательным показателем дробью.
Решение:

Замечание: поскольку деление на
нуль невозможно, такие выражения, как  ,
не имеют смысла.
,
не имеют смысла.
Напомним, что при натуральном  выражение
выражение  .
.
Задание: представьте числа в виде степени с основанием 3.
Решение:

Задание: найдите значения выражений.
Решение:

Итоги:
