Конспект урока на тему «Решение тригонометрических неравентсв»

Решение тригонометрических неравенств.

Урок-лекция

Тема “Тригонометрические неравенства” является объективно сложной для
восприятия и осмысления учащимися 10-го класса. Поэтому очень важно последовательно, от простого к сложному формировать понимание алгоритма и
вырабатывать устойчивый навык решения тригонометрических неравенств.

Успех освоения данной темы зависит от знания основных определений и свойств
тригонометрических и обратных тригонометрических функций, знания
тригонометрических формул, умения решать целые и дробно-рациональные неравенства, основные виды тригонометрических уравнений. Особый упор нужно делать на методике обучения решения простейших тригонометрических неравенств, т.к. любое тригонометрическое неравенство сводится к решению простейших неравенств

Первичное представление о решении простейших тригонометрических неравенств предпочтительно вводить, используя графики синуса, косинуса, тангенса и котангенса. И только после учить решать тригонометрические

неравенства на окружности.

Остановлюсь на основных этапах рассуждения при решении простейших
тригонометрических неравенств.

1. Находим на окружности точки, синус (косинус) которых равен данному числу.

2. В случае строгого неравенства отмечаем на окружности эти точки, как выколотые, в случае нестрогого – как заштрихованные.

3. Точку, лежащую на главном промежутке монотонности функции синус (косинус), называем Р_t1, другую точку – Р_t2.

4. Отмечаем по оси синусов (косинусов) промежуток удовлетворяющий данному неравенству.

5. Выделяем на окружности дугу, соответствующую данному промежутку.

6. Определяем направление движения по дуге (от точки Р_t1 к точке Р_t2по дуге),
   изображаем стрелку по направлению движения, над которой пишем знак “+” или “-” в зависимости от направления движения. (Этот этап важен для
   

   контроля найденных углов. Ученикам можно проиллюстрировать распространенную ошибку нахождения границ интервала на примере решения
   неравенства по графику синуса или косинуса и по окружности).

7. Находим координаты точек Р_t1 (как арксинус или арккосинус данного числа)и Р_t2т.е. границы интервала, контролируем правильность нахождения углов, сравнивая t₁и t_2.

8. Записываем ответ в виде двойного неравенства (или промежутка) от меньшего угла до большего.

Конспект урока по теме: “Решение
тригонометрических неравенств”.

Задача урока

– изучить тему решение тригонометрических неравенств,содержащих функции синус и косинус, перейти от простейших неравенств к более сложным.

Цели урока:

 закрепление знаний тригонометрических формул, табличных значений тригонометрических функций, формул корней тригонометрических уравнений;

 формирование навыка решения простейших тригонометрических неравенств;

 освоение приёмов решения более сложных тригонометрических неравенств;

 развитие логического мышления, смысловой памяти, навыков самостоятельной работы,
самопроверки;

 воспитание аккуратности и чёткости в оформлении решения, интереса к предмету,
уважения к одноклассникам.

 формирование учебно-познавательных,информационных, коммуникативных компетенций.

Оборудование:

Проектор, компьютер,раздаточные карточки с готовыми чертежами тригонометрических кругов, переносная доска, карточки с домашним заданием.

Форма организации обучения – урок — лекция. 

Методы обучения, используемые на уроке – словесные, наглядные, репродуктивные, проблемнопоисковые,индивидуального и фронтального опроса, устного иписьменного самоконтроля, самостоятельной работы.

Учебная дисциплина:Математика.

Тема: «Решение простейших тригонометрических неравенств»

Тип урока:урок усвоения нового материала с элементами первичного закрепления.

Цели урока:

1) образовательные:

• показать алгоритм решения тригонометрических неравенств с использованием единичной окружности.

• учить решать простейшие тригонометрические неравенства.

2) развивающие:

• развитие внимания;

• развитие у учащихся грамотной устной и письменной математической речи.

3) воспитательные:

• учить высказывать свои идеи и мнения;

• формировать умения помогать товарищам и поддерживать их;

• формировать умения определять, чем взгляды товарищей отличаются от собственных.

Методическая цель: показать технологию овладения знаниями на уроке изучения новых знаний.

Методы обучения:

Дидактическая цель урока: Создание условий:

• для соединения новой информации с уже изученным материалом;

• для развития умения осуществлять анализ и отбор необходимой информации;

• для развития умений делиться своими идеями и мнениями.

• для развития логики, навыков рефлексии.

Форма организации учебной деятельности: коллективная, индивидуальная.

Оборудование:

• учебник Никольского «Алгебра и начала анализа», 10-11 класс;

• проектор, доска;

• презентация MS PowerPoint.

План урока

1. Оргмомент 1 мин

2. Проверка д\з 3 мин

3. Объяснение нового материала 35 мин

4. Д\з 3 мин

5. Подведение итогов 3 мин

Ход урока

1.Оргмомент

2. Проверка д\з у доски №11.29-11.31(в,г)

3.Объяснение нового материала

На этом занятии мы будем решать графическим способом тригонометрические неравенства одного какого-то вида. Сегодня мы решим тригонометрических неравенства вида sint. Вот они: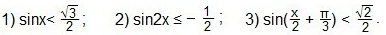

Составим алгоритм решения.

1. Если аргумент — сложный (отличен от х), то заменяем его на t.

2. Строим в одной координатной плоскости tOy графики функций y=sint  и y=a.

3. Находим такие две соседние точки пересечения графиков (поближе к оси Оу), между которыми синусоида располагается ниже прямой у=а. Находим абсциссы этих точек.

4. Записываем двойное неравенство для аргумента t, учитывая период синуса (t будет между найденными абсциссами).

5. Делаем обратную замену (возвращаемся к первоначальному аргументу) и выражаем значение х из двойного неравенства, записываем ответ в виде числового промежутка.

Решение тригонометрических неравенств с помощью графиков надежно страхует нас от ошибок только в том случае, если мы грамотно построим синусоиду.

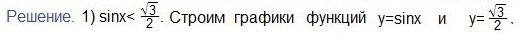
Для построения графика функции y=sinx выберем единичный отрезок, равный двум клеткам. Тогда по горизонтальной оси Ох значение π (≈3,14) составит шесть клеток. Рассчитываем остальные значения аргументов (в клетках).

Вот как будет выглядеть координатная плоскость.

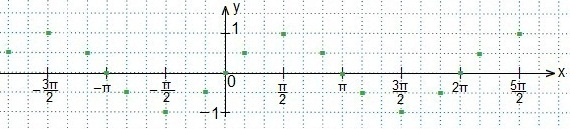
Эти точки мы взяли из таблицы значений синуса.  Также используем свойство нечетности функции y=sinx (sin (-x)=-sinx), периодичность синуса (наименьший период Т=2π) и известное равенство: sin (π-x)=sinx. Проводим синусоиду

. Проводим прямую.

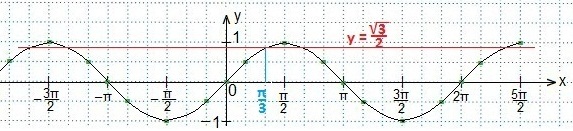
Теперь нам предстоит определить такие две точки пересечения синусоиды и прямой, между которыми синусоида располагается ниже, чем прямая. Крайняя точка справа определена, абсцисса ближайшей искомой отстоит от начала отсчета влево на 8 клеток. Построим ее и определим.

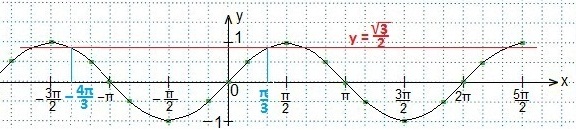
Между этими (выделенными) значениями аргумента и находится та часть синусоиды, которая лежит ниже данной прямой, а значит, промежуток между этими выделенными точками удовлетворяет данному неравенству. Учтем период синуса, запишем результат в виде двойного неравенства, а ответ в виде числового промежутка.

Решим второе неравенство.

Синусоиду строим так же, а прямая будет параллельна оси Оt и отстоять от нее на 1клетку вниз.

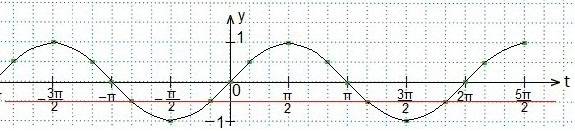
Определяем промежуток, внутри которого точки синусоиды лежат ниже прямой.

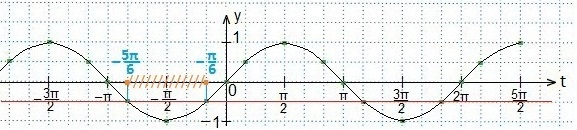
Записываем промежуток значений введенной переменной t. Возвращаемся к первоначальному значению аргумента (2х). Все части двойного неравенства делим на 2 и определяем промежуток значений х. Записываем ответ в виде числового промежутка.

Аналогично решаем и третье неравенство.

В выделенном промежутке синусоида располагается ниже прямой, поэтому, учитывая периодичность функции синуса, запишем в виде двойного неравенства значения t. Затем вместоt подставим первоначальный аргумент синуса и будем выражать х из полученного двойного неравенства.

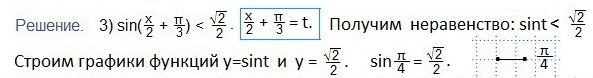
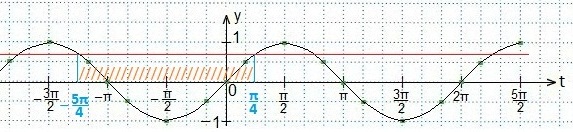
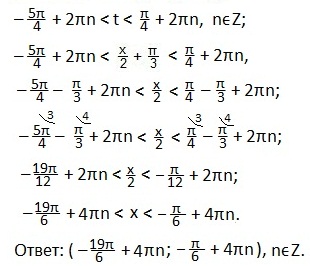
Ответ запишем в виде числового промежутка.

 И, напоследок: знаете ли вы, что математика — это определения, правила и ФОРМУЛЫ?!

Конечно, знаете! И самые любознательные, изучив эту статью и просмотрев видео, воскликнули: «Как долго и сложно! А нет ли формулы, позволяющей решать такие неравенства безо всяких графиков и окружностей?» Да, разумеется, есть!

ДЛЯ РЕШЕНИЯ НЕРАВЕНСТВ ВИДА: sint (-1≤а≤1) справедлива формула:

— π — arcsin a + 2πn < t < arcsin a + 2πn,  nєZ.

Примените ее к рассмотренным примерам и вы получите ответ гораздо быстрее!

Мы решили три неравенства вида sint. На этом уроке мы рассмотрим три неравенства вида sint>a, где -1≤а≤1.

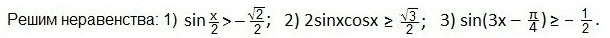
Составим алгоритм решения.

1. Если аргумент — сложный (отличен от х), то заменяем его на t.

2. Строим в одной координатной плоскости tOy графики функций y=sint  и y=a.

3. Находим такие две соседние точки пересечения графиков (поближе к оси Оу), между которыми синусоида располагается выше прямой у=а. Находим абсциссы этих точек.

4. Записываем двойное неравенство для аргумента t, учитывая период синуса (t будет между найденными абсциссами).

5. Делаем обратную замену (возвращаемся к первоначальному аргументу) и выражаем значение х из двойного неравенства, записываем ответ в виде числового промежутка.

Решаем первое неравенство:

.

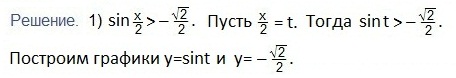
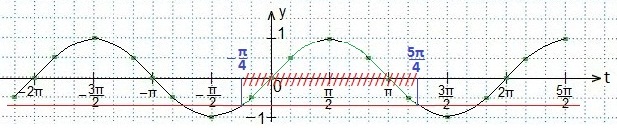
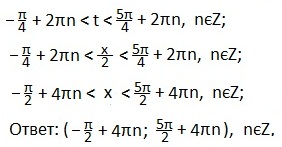
Учитывая периодичность функции синуса, запишем двойное неравенство для значений аргумента t, удовлетворяющий последнему неравенству. Вернемся к первоначальной переменной. Преобразуем полученное двойное неравенство и выразим переменную х.Ответ запишем в виде промежутка.

Решаем второе неравенство:

При решении второго неравенства нам пришлось преобразовать левую часть данного неравенства по формуле синуса двойного аргумента, чтобы получить неравенство вида:sint≥a. Далее  мы следовали алгоритму.

Решаем третье неравенство:

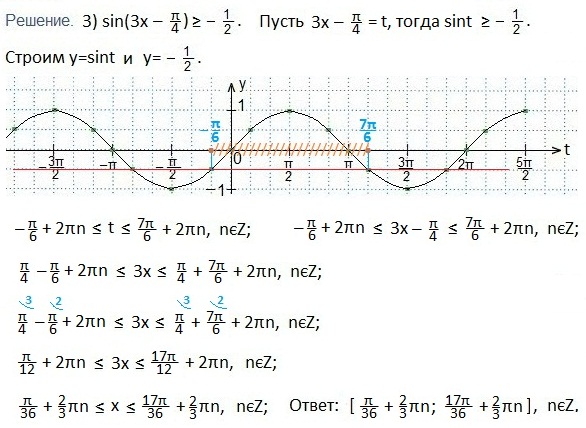
Имейте ввиду, что такие способы решения тригонометрических неравенств, как приведенный выше графический способ и, наверняка, вам известный, способ решения с помощью единичной тригонометрической окружности (тригонометрического круга)  применимы лишь на первых этапах изучения раздела тригонометрии «Решение тригонометрических уравнений и неравенств». Думаю, вы припомните, что и простейшие тригонометрические уравнения вы вначале решали с помощью графиков или круга. Однако, сейчас вам не придет в голову решать таким образом тригонометрические уравнения. А как вы их решаете? Правильно, по формулам. Вот и тригонометрические неравенства следует решать по формулам, тем более, на тестировании, когда дорога каждая минута. Итак, решите три неравенства этого урока по соответствующей формуле.

Если sint>a, где  -1≤a≤1, то  arcsin a + 2πn < t < π — arcsin a + 2πn, nєZ.

Рассмотрим неравенства вида cost:

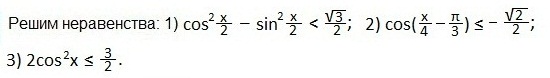
Составим алгоритм решения.

1. Если аргумент — сложный (отличен от х), то заменяем его на t.

2. Строим в одной координатной плоскости tOy графики функций y=cost  и y=a.

3. Находим такие две соседние точки пересечения графиков,  между которыми синусоида располагается ниже прямой у=а. Находим абсциссы этих точек.

4. Записываем двойное неравенство для аргумента t, учитывая период косинуса Т=2π (tбудет между найденными абсциссами).

5. Делаем обратную замену (возвращаемся к первоначальному аргументу) и выражаем значение х из двойного неравенства, записываем ответ в виде числового промежутка.

Решение тригонометрических неравенств с помощью графиков надежно страхует нас от ошибок только в том случае, если мы грамотно построим синусоиду. (График функцииy=cosx также называют синусоидой!)

Первое неравенство.

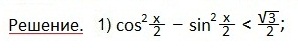
Преобразуем левую часть неравенства по формуле косинуса двойного аргумента:

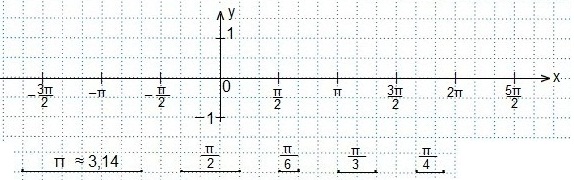
Координатную плоскость готовим так же, как готовили для построения графика функцииy=sinx., т.е. единичный отрезок берем равным двум клеткам, тогда значение π изображаем равным шести клеткам и т.д. Вот так должна выглядеть координатная плоскость для построения синусоид:

Воспользуемся таблицей значений косинусов некоторых углов:

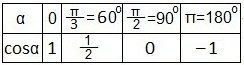 а также свойствами: графиков четных функций, непрерывностью и периодичностью функции косинуса. Отмечаем точки:

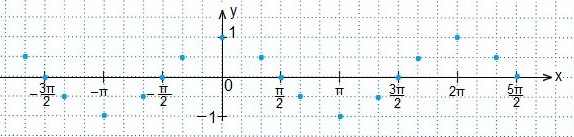
Проводим через эти точки кривую — график функции y=cosx.

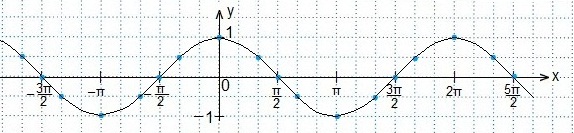
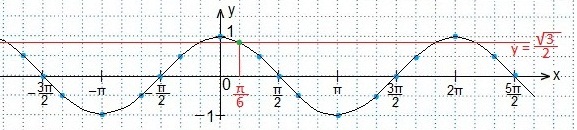
Определяем промежуток значений х, при которых точки синусоиды лежат ниже точек прямой.

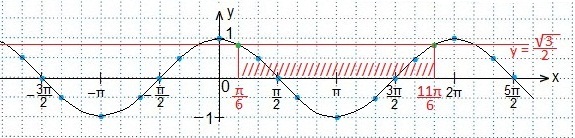
Учтем периодичность функции косинуса и запишем в виде двойного неравенства решение данного неравенства:

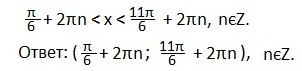
Второе неравенство.

Находим абсциссы точек пересечения графиков, между которыми график косинуса лежит ниже прямой.

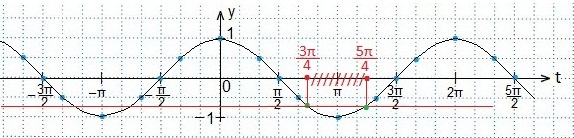
Концы этого промежутка тоже являются решениями неравенства, так как неравенство нестрогое.

Запишем решение в виде двойного неравенства  для переменной t.

Подставим вместо t первоначальное значение аргумента.

Выразим х.

Ответ запишем в виде промежутка.

Третье неравенство.

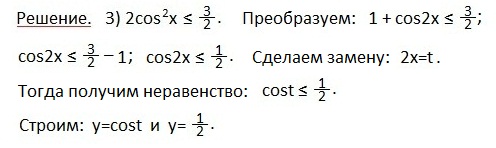
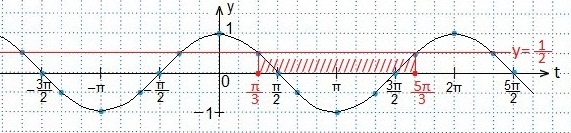
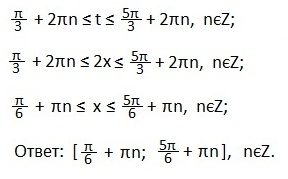
А теперь формула, которой вам следует воспользоваться на экзамен ЕГЭ при решении тригонометрического неравенства вида cost

Если  cost, (-1≤а≤1), то arccos a + 2πn < t < 2π — arccos a + 2πn, nєZ.

Примените эту формулу для решения рассмотренных неравенств, и вы получите ответ гораздо быстрее и безо всяких графиков!    

Рассмотрим тригонометрические неравенства вида: cost>a.

Используем алгоритм решения, как в предыдущем случае:

1. Если аргумент — сложный (отличен от х), то заменяем его на t.

2. Строим в одной координатной плоскости tOy графики функций y=cost  и y=a.

3. Находим такие две соседние точки пересечения графиков,  между которыми синусоида располагается выше прямой у=а. Находим абсциссы этих точек.

4. Записываем двойное неравенство для аргумента t, учитывая период косинуса (t будет между найденными абсциссами).

5. Делаем обратную замену (возвращаемся к первоначальному аргументу) и выражаем значение х из двойного неравенства, записываем ответ в виде числового промежутка.

Пример 1.

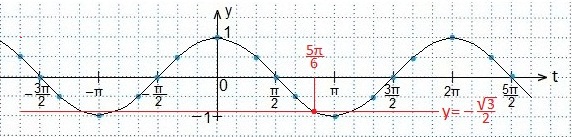
Далее, по алгоритму, определяем те значения аргумента t, при которых синусоида располагается выше прямой. Выпишем эти значения в виде двойного неравенства, учитывая периодичность функции косинуса, а затем вернемся к первоначальному аргументу х.

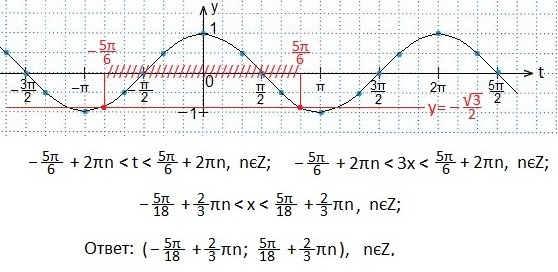
Пример 2.

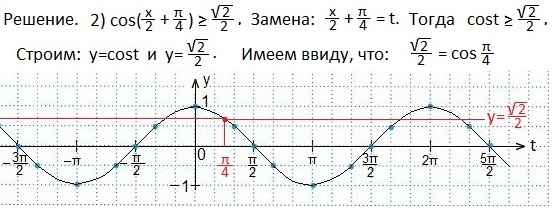
Выделяем промежуток значений t, при которых синусоида находится выше прямой.

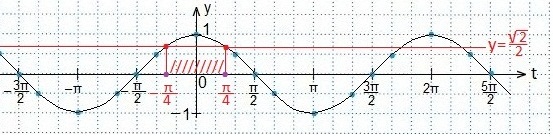
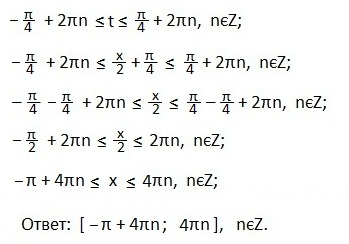
Записываем в виде двойного неравенства значения t,удовлетворяющих условию. Не забываем, что наименьший период функции y=cost равен2π. Возвращаемся к переменной х, постепенно упрощая все части двойного неравенства.

Ответ записываем в виде закрытого числового промежутка, так как неравенство было нестрогое.

Пример 3.

Нас будет интересовать промежуток значений t, при которых точки синусоиды будут лежать выше прямой.

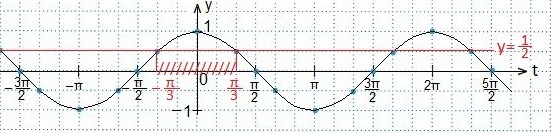
Значения t запишем в виде двойного неравенства, перезапишем эти же значения для 2хи выразим х. Ответ запишем в виде числового промежутка.

И снова формула, которой вам следует воспользоваться на ЕГЭ при решении тригонометрического неравенства вида cost>a.

Если  cost>a, (-1≤а≤1), то — arccos a + 2πn < t < arccos a + 2πn, nєZ.

Применяйте  формулы для решения тригонометрических неравенств, и вы  сэкономите время на экзаменационном тестировании.

4.Домашнее задание №11.33-11.37 (а-Б)

5.Подведение итогов

Решение однородных тригономерических неравенств

Решим систему тригонометрических неравенств:

Начнем со второго неравенства.

Это квадратное неравенство относительно .

Ветви параболы направлены вверх, следовательно, решением неравенства будет промежуток:

[]

Изобразим его на тригонометрическом круге:

Теперь решим второе неравенство:

Я приведу два решения: сначала распространенное решение, которое содержит ошибку, а потом правильное.

Итак, сначала решение с ошибкой.

Левая часть этого тригонометрического неравенства наводит на мысль решать его так же, как однородное тригонометрическое уравнение: разделить обе части на . При левая часть не равна нулю, к тому же — величина неотрицательная, поэтому, вроде как ничего страшного произойти не должно.

Делим:

Получаем:

Вводим замену и решаем квадратное неравенство относительно

Ветви параболы направлены вверх, следовательно неравенство верно при

Возвращаемся к исходной переменной, получаем

На тригонометрической окружности решение выглядит так (заметим, что  при не определен, поэтому эти точки мы выкалываем):

Мы видим, что что точки, соответствующие значениям выколоты, и решением неравенства будут промежутки:

[)(]

Совместим это решение с решением первого неравенства:

и получим ответ: (][)(]

Теперь найдем решение второго неравенства другим способом.

Будем искать решение неравенства с помощью метода интервалов. Сначала найдем при каких значениях неизвестного левая часть равна нулю, то есть решим уравнение  . Так же как в предыдущем решении разделим на и решим квадратное уравнение относительно .

Получим . То есть в точках и левая честь неравенства равна нулю.

Изобразим эти точки на тригонометрической окружности. Они разбивают ее на четыре промежутка. В этих точках происходит смена знака выражения, стоящего в левой части неравенства.

Выясним знаки этих выражений. Возьмем пробную точку . При , следовательно, знаки распределяются таким образом:

и решением неравенства

будут следующие промежутки:

[]

Мы видим, что в этом случае точки принадлежат множеству решений неравенства. И, совместив решение второго неравенства с решением первого,

получаем правильный ответ:

[][]

Что же произошло? При делении исходного неравенства на мы сузили ОДЗ. Мы исключили из решения те значения , при которых , при том, что исходное неравенство имеет смысл при этих значениях . То есть мы потеряли решения.

Какой же урок нам надо извлечь?

При решении однородных тригонометрических неравенств поступаем следующим образом:

1. Решаем соответствующее  однородное уравнение и находим точки, в которых левая часть неравенства меняет знак.

2. Исследуем знаки.

3. Записываем ответ.

И.В. Фельдман, репетитор по математике.

Конспект урока на тему:»Тригонометрические неравенства»

Урок алгебры в 10 классе

Решение тригонометрических неравенств.

Учитель математики Бабаченко Л.П.

                              Я услышал и забыл.
                             Я увидел и запомнил.
                       Я сделал и понял.

Цели и задачи урока:

Образовательная:

Изучить способы решения тригонометрических неравенств.

Организовать работу учащихся на уровне, соответствующем уровню сформированных знаний и умений.

Развивающая:

Развивать у учащихся умение стоить математические модели, в данном случае графическую модель решения неравенства.

Воспитательная:

Способствовать развитию познавательного интереса учащихся к предмету, воздействуя на интерес старшеклассников к самопознанию.

 

Тип урока: комбинированный урок.

 

Методы урока: словесный, практический, контроль и обобщение знаний.

 

Формы организации деятельности учащихся на уроке: фронтальная, работа в группах, контролирующая самостоятельная работа.

 

Метод приобретения знаний: эвристический, исследовательский.

Ход урока

 

1. Самоопределение к деятельности(3 мин)

Психологический настрой учащихся. Объявление темы урока, комментарий целей урока.

2. Проверка домашнего задания(5 мин)

Комментарий по домашнему заданию, при необходимости у доски показывают решение справившиеся учащиеся

Тихий опрос

Используя результаты домашнего задания ответить письменно  на вопросы:

 

1. В какой координатной четверти расположен угол диаметрально противоположный углу ?
2. Как на числовой окружности будут расположены точки соответствующие углам
3. Указать угол симметричный  относительно оу.
4. Будет ли угол  являться решением неравенства у<?
5. Найти сумму граничных точек интервала являющегося решением неравенства х≥.

 

 

3. Актуализация теоретических знаний учащихся (12 мин)

Фронтальный опрос учащихся:

• Область значений тригонометрических функций
• Область определения тригонометрических функций
• Значения тригонометрических функций углов 00, 300, 450,600, 900, 1200, 1350, 1500, 1800.
• Перечислить виды простейших тригонометрических уравнений.
• Способы решения  тригонометрических уравнений.

·         Решите уравнение:  а)   б)  в)   г)   д)  е)

• Способы решения систем  тригонометрических уравнений.
• Работа с тригонометрическим кругом. По значениям тригонометрических функций определить угол, найти значения обратных тригонометрических функций.

 

 

 

 

 

4. Объяснение  нового материала (20 мин).

Способы решения  тригонометрических неравенств:

1.      Приведение  к  простейшему виду.  Пример 1

       (рис.1)

            

 

 

                                      рис. 1

 π/3    

 

2.      Искусственным  путем.  Пример 2.

    Умножим данное неравенство на 0,5

Ответ:   

 

 

Рассмотрим примеры  решения (на флипчарте):

 

 

Учащиеся самостоятельно комментируют предложенное решение

 

Алгоритм решения простейших тригонометрических неравенств

1.            С помощью простейших алгебраических преобразований и тригонометрических преобразований свети заданное тригонометрическое неравенство к простейшему.

2.            Обозначить на оси, соответствующей тригонометрической функции, находящейся в левой части неравенства, значение из правой части неравенства.

3.            Провести прямую через эту точку перпендикулярно этой оси.

4.            Обозначить точки пересечения прямой с тригонометрической окружностью (выколоть их в случае строго неравенства и закрасить в ином случае).

5.            Выделить соответствующую дугу в границами в этих точках согласно знаку неравенства.

6.            Указываем направление отсчёта (против часовой стрелки).

7.            Находим начало дуги и угол, ему соответствующий.

8.            Находим угол, соответствующий концу дуги.

9.            Записываем ответ в виде промежутка с учетом периодичности функции.

 

5. Практическая часть. Закрепление изученного материала(30 мин)

 №136(а,в), №137(а,в), №138(а,в),№140(а,в), №142(а,в), №144(а,в), №142, №145 (учебник Алгебра и начала анализа 10, А.Е.Абылкасымова)

Учащиеся решают у доски по двое (либо разные примеры, если уровень класса выше среднего, и один и тот же пример в ином случае – с целью создания соревновательного эффекта).

 

6. Самостоятельная работа(12 мин)

     

    Вариант -1                                                 Вариант -2

1) sin x< /2                                              1) sin x < 1/2 

2) cos x< -1/2                                              2) cos x≥ — /2

3) tg2x ³ -1                                                  3) tg 3x ≤ 1

4) sin (2x – π/6) ³ — /2                             4) cos (3x – π/4 ) ≤ — /2

5) 2cos (4x – π/6) > 1                                5)2sin (x/2 + π/4) ≥ -1

 

Самостоятельная работа проверяет умение учащихся сводить неравенство к простейшему и решать простейшие тригонометрические неравенства. Предусмотрены ситуации: строгое – нестрогое неравенство; выделенная на окружности дуга выше – ниже, правее – левее заданного числа. 

 

 

7. Задание на дом(2 мин)

§11 (стр.80) – изучить способ решения тригонометрических неравенств с помощью графиков тригонометрических функций

Выполнить любым способом №137(б,г), №138(б,г), (учебник Алгебра и начала анализа 10, А.Е.Абылкасымова)

(Раздаю карточки с записью домашнего задания.Комментирую решение каждого неравенства).

1.      cosx > sin2x;

2.      4sin2xcos2x < -;

3.      cos2  sin2 – 0,5;

4.      sinx +  cosx > 1.

8. Итог урока(3 мин)

Кратко охарактеризовать работу класса на уроке. Обратить внимание учащихся на способы решения  тригонометрических неравенств, рассмотренных на уроке. Дать комментарий к оценкам.

– Назовите приемы решения тригонометрических неравенств.

– Каким образом знание алгоритма решения простейших тригонометрических неравенств используется при решении более сложных неравенств?

– Какие неравенства вызвали наибольшее затруднение?

(Оцениваю работу учащихся на уроке).

9. Рефлексия(3 мин)

Заполнить таблицу:

1

Доступность объяснения

 

2

Уровень понимания темы

 

3

На какую оценку ты сегодня работал(а)?

 

4

Кто, по твоему мнению, активно работал на уроке (указать оценки)

 

5

Какой тип неравенства вызывает затруднение?

 

6

Интересна ли тебе  изученная тема?

 

7

Устраивает ли тебя темп урока ? Есть необходимость его снизить или повысить?

 

 

 

Тригонометрические неравенства и их графики.

11 класс. (алгебра).

Урок №3.

Дата: 7.09

Тема урока: Тригонометрические неравенства и их графики. 

Цель: повторить способы решения тригонометрических неравенств и построение их графиков.

Развивать знания, умения , навыки по предмету.

Воспитывать аккуратность, трудолюбие.

Ход урока

I. Сообщение темы и цели урока

II. Повторение и закрепление пройденного материала

Вариант 1

Решите уравнение:

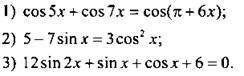
Вариант 2

Решите уравнение:

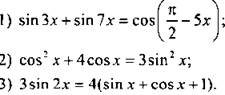
III. Повторение материала за курс 10 класса по данной теме.

Решение тригонометрических неравенств (как и уравнений), как правило, сводится к решению простейших тригонометрических неравенств. Поэтому прежде всего остановимся на решении таких неравенств. Их удобно решать, используя единичную окружность.

Пример 1Решим неравенство sin x > 1/2.

 

 

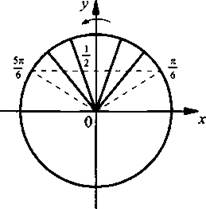
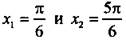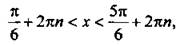На единичной окружности по оси ординат отложим значение sin х = 1/2 и построим соответствующие углы   (углы откладываются против часовой стрелки и являются положительными). На рисунке видно, что неравенству sin х > 1/2 удовлетворяют значения  Учтем, что период функции синуса составляет 2π, и получим решение данного неравенства  или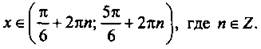

 

 

Пример 2

Решим неравенство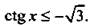

 

 

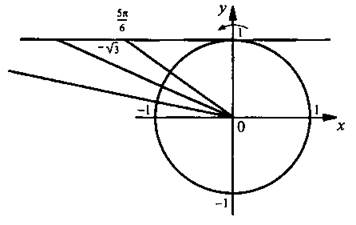
На оси котангенсов для единичной окружности отложим значение 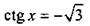 и построим соответствующий угол  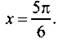Видно, что неравенству  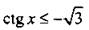удовлетворяют значения 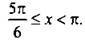Учитывая период функции котангенса (равный π), получим решение данного неравенства:  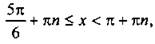или  где n ∈ Z.

В случае сложного аргумента тригонометрической функции рекомендуется обозначить его новой переменной, решить для него неравенство, а затем вернуться к старой неизвестной.

 

Пример 3

Решим неравенство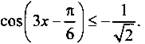

 

 

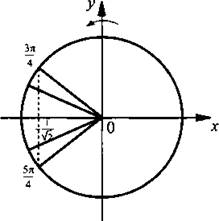
Обозначим аргумент косинуса  и получим простейшее тригонометрическое неравенство  Решим это неравенство. На единичной окружности по оси абсцисс отложим значение 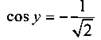и построим соответствующие углы  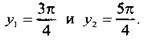Тогда неравенству  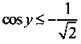удовлетворяют значения  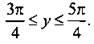Учтем периодичность функции cos y и получим решения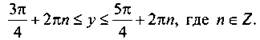

Теперь вернемся к старой неизвестной х и получим двойное линейное неравенство 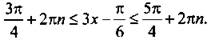 Ко всем частям неравенства прибавим число π/6. Отсюда  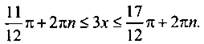Все части неравенства разделим на положительное число 3. При этом знак неравенства сохраняется. Получим:  или 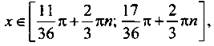 где n ∈ Z.

Если неравенство не является простейшим, то используя преобразования, аналогичные тем, которые применялись для уравнений, сводим неравенство к простейшему.

 

Пример 4

Решим неравенство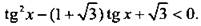

 

 

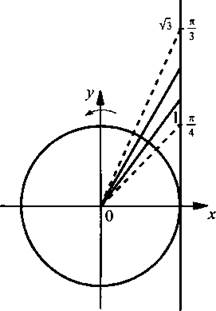
Введем новую переменную у = tg x и получим квадратное неравенство 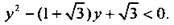 Это неравенство имеет решение  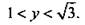Вернемся к старой неизвестной x и получим двойное неравенство  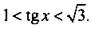На единичной окружности по оси тангенсов отложим значения 1 и  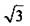и построим соответствующие углы  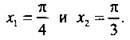Тригонометрическому неравенству удовлетворяют значения  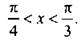Учтем периодичность функции тангенса и получим решение данного неравенства:  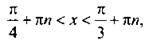или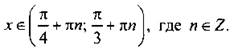

Также при решении тригонометрических неравенств можно использовать метод интервалов (который является универсальным для всех неравенств).

 

Пример 5

Решим неравенство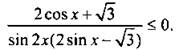

 

 

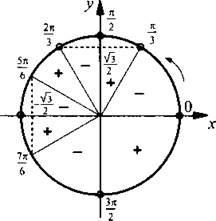
На единичной окружности отметим значения х, при которых обращается в нуль числитель 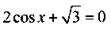  (откуда ) и знаменатель sin 2х = 0 (тогда 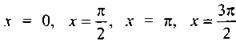)  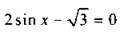 (откуда 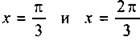) дроби. Определим знак этой дроби, например, при х = π/6 и получим:

 

Учтем, что при переходе через отмеченные значения х знак неравенства меняется на противоположный. Построим диаграмму знаков данной дроби. Также учтем значения х, при которых знаменатель дроби обращается в нуль (они отмечены кружками). Теперь легко выписать решения неравенства: 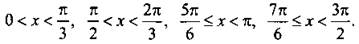 Учитывая, что через 2пn (где n ∈ Z) ситуация повторяется, выпишем решения данного неравенства: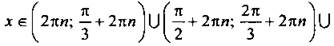

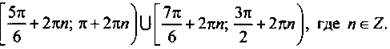
При наличии в неравенстве функций тангенса и котангенса удобно перейти к функциям синуса и косинуса и использовать рассмотренный метод интервалов.

 

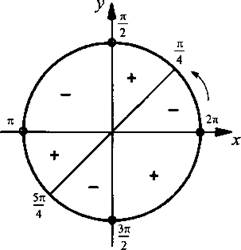
Пример 6

Решим неравенство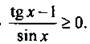

 

Учтем, что 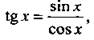 и запишем неравенство в виде  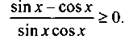Отметим на единичной окружности значения х, при которых обращается в нуль числитель sin x – cos x = 0 (откуда  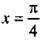и 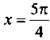) и знаменатель sin x cos x = 0 (тогда  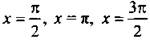и x = 2π) дроби. Определим знак данной дроби, например, при х = π/3 и получим:

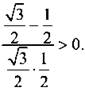
Учтем, что при переходе через отмеченные значения x знак неравенства меняется на противоположный. Построим диаграмму знаков данной дроби. Учтем также значения х, при которых знаменатель дроби обращается в нуль (они отмечены кружками). С учетом периодичности функций синуса и косинуса, входящих в неравенство, запишем окончательное решение данного неравенства  где n ∈ Z.

При использовании метода интервалов необходимо помнить, что тригонометрическое выражение может иметь кратные корни. При переходе через корень нечетной кратности знак выражения меняется на противоположный, при проходе через корень четной кратности знак сохраняется.

IV. Задание на уроке и на дом

Решите неравенство:

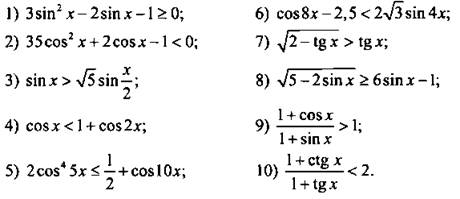
Ответы: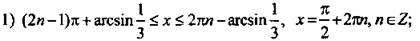

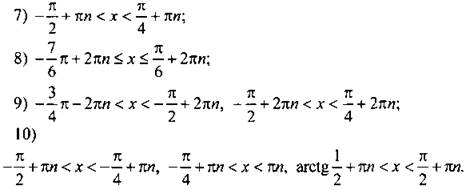
 V. Подведение итогов урока



«Тригонометрические неравенства. Решение простейших тригонометрических неравенств»

Отзыв на урок математики.

По теме: «Тригонометрические неравенства. Решение простейших тригонометрических неравенств»

Цели и задачи урока: Изучение и первичное закрепление новых знаний

Образовательная (познавательная):

а) показать алгоритм решения тригонометрических неравенств с использованием тригонометрической окружности;

б) учить решать простейшие тригонометрические неравенства;

Развивающая (практическая):

а) развитие логического мышления, внимания, памяти;

б) развивать умение анализировать изучаемое;

в) развитие умения обобщать полученные знания;

г) развитие у студентов грамотной устной математической речи;

Воспитательная:

а) учить высказывать свои идеи и мнение;

б) формировать умение помогать однокурсникам и поддерживать их;

Дата проведения: 20.04. 2016 г.

Группа: 1Г (Гостиничный сервис; социально-экономический профиль)

Предмет: ОУДп.10 Математика: алгебра и начала математического анализа; геометрия;

Тип урока: Изучение нового материала и закрепление полученных теоретических знаний;

Форма организация: Урок усвоения нового материала с элементами первичного закрепления продолжительностью 45 минут

Преподаватель: Шмакова Наталья Николаевна.

Цель посещения: Знакомство с опытом работы учителя.

Урок направлен на формирование ключевых компетентностей учащихся. В течение всего урока поддерживается активность и внимание учащихся. Сценарий урока продуман и хорошо спланирован. Каждая этап урока реализован как по времени, так и по объему.

Триединая дидактическая цель (ТДЦ) урока предусматривает взаимосвязь воспитательного, обучающего и развивающего компонентов. Цели урока были сформулированы в совместной деятельности учителя и учащихся. Чётко поставлены образовательные и развивающие цели, которые были направлены на действия всех учащихся. Поставленные цели были взаимообусловлены и поэтому приняты всеми учащимися. Образовательные цели были операциональны, так как точно определили, что учащиеся должны усвоить понятие тригонометрических неравенств и должны научиться применять их в соответствии с заданием. Эти цели были определены и находились в зоне ближайшего развития каждого студента, так как на уроке задания давались и на базовом, и на творческом уровне с учётом индивидуальных особенностей учащихся.

Реальные результаты – на уроке активно участвовали все учащиеся (на репродуктивном, конструктивном уровнях) (запись лекции, обсуждение, работа в группах, рефлексия). Ответы учащихся на уроке в основном были положительные.

Тип урока – изучение нового материала и закрепление полученных теоретических знаний. Его логика соответствует структуре урока данного типа. Включает следующие этапы урока: организационный момент, подготовка к основному этапу, усвоение новых знаний и способов действий, первичная проверка понимания, подведение итогов урока, рефлексия, информация о домашнем задании и инструктаж по его выполнению.

На этапе подготовки к основному этапу урока была обеспечена мотивация и принятие учащимися цели учебно-познавательной деятельности, актуализация опорных знаний и умений. Задача выполнена полностью. Методы, отобранные учителем, оптимально подобраны под содержание дидактической задачи. Основной способ проведения урока – урок сочетания различных форм занятий, включает в себя также практическое занятие с работой в парах.

Решение дидактической задачи обеспечило переход к главному этапу. На этапе было обеспечено восприятие, осмысление знаний и способов действий репродуктивного и конструктивного уровня, частично были использованы задания творческого уровня. Все аспекты ТДЦ урока нашли отражение в организации деятельности учащихся и в её содержании. Учитывая возможности класса и особенности изучаемого материала, учитель оптимально выбрал методы: словесные, наглядные, практические, логические, опора на личностный опыт, побуждение к поиску альтернативных решений. Темп урока посилен для учащихся. При демонстрации наглядности учащиеся привлекаются к  разговору. Учителем используется достаточное материальное и организационное обеспечение урока: проектор подключен к компьютеру, графики криволинейных трапеций, учебники, классная доска.

Первичный контроль, проверка понимания показали, что материал усвоен. Чередование словесных, практических методов, форм организации познавательной деятельности способствовали предупреждению перегрузки студентов в процессе урока.

Рефлексия показала, что своим продвижением довольны все учащиеся, отметили сотрудничество.

Формы организации познавательной деятельности соответствовали содержанию учебного материала и возрастным особенностям учащихся. Преподаватель продумал, таким образом организацию урока, чтобы учащиеся получили информацию в доступной форме и в то же время задания были высокого математического уровня.

Методы обучения, используемые преподавателем, были разнообразны (беседа, объяснение, работа с макетом, работа с графиками, решение задач, фронтальный опрос, проверочная работа, взаимоконтроль, сочетание словесных и наглядных методов) и способствовали лучшему усвоению учебного материала.

Для домашнего задания было предложено на выбор два задания, одно из которых требовало творческого подхода. Также было дано индивидуальное задание. Всё это способствовало изучению и освоению материала в зоне ближайшего развития.

Урок достиг целей, представляет целостную систему с полным набором элементов. Связи между дидактическими задачами, содержанием учебного материала, методами и формами обучения прочные и обеспечили оптимальное функционирование всей системы урока. ТДЦ урока реализована полностью.

Вывод:

1. План урока был выполнен, цель урока достигнута. К такому выводу пришли сами студенты.

Деятельность учащихся оценивается следующим образом: на уроке чётко проявился интерес к предмету, эмоциональное состояние учащихся было приподнятым в начале и к концу урока. На уроке присутствовали самоконтроль и самокоррекция со стороны студентов. Была высока степень самостоятельности в учебной деятельности.

2. Урок удался, так как созданы условия для максимального влияния образовательного процесса на развитие индивидуальности студентов.

3. Учащиеся получат оценки за самостоятельную работу и выставлены 4 оценки за устные ответы, на уроке присутствовали -17 учащихся.

Заместитель директора по учебной работе

ГБПОУ КК ТСПК: Холодова Г.И.

20.04.2016

Как решать тригонометрические неравенства

Изложенный нами способ нахождения решения линейного неопределенного уравнения с целыми коэффициентами называется алгоритмом Евклида.

Задача 25.5. Для каких целых k существует такое целое n, что

7k − 19 = 5n?

Задача 25.6. Решите уравнения в целых числах:

а) 17x + 19y = 1; б) 26x − 78y = 143; в*) 7×2 − 4y = 5.

Задача 25.7. При решении в целых числах уравнения 166n−44k = = 6 нам пришлось ввести помимо n и k четыре дополнительные переменные (t, s, v и u). Приведите пример неопределенного уравнения вида ax + by = c, в котором a и b — двузначные числа, для решения которого по изложенному методу надо ввести восемь дополнительных переменных. Попробуйте также доказать, что большего количества дополнительных переменных при двузначных a и b никогда не потребуется.

Повторить: § 6. Определение тригонометрических функций. § 11. Графики синуса и косинуса.

Мы начнем с простейших неравенств, к которым любое тригонометрическое неравенство в конечном счете сводится.

Пример 26.1. sin x > 1/2.
Решение. Для начала выясним, какие
точки на тригонометрической окружно-
сти соответствуют решениям неравен-
ства. Это — точки, ордината которых
больше 1/2, и на окружности они запол-
няют дугу P Q, отмеченную на рис. 26.1.

Теперь можно записать множество чисел, соответствующихРис. 26.1. точкам на дуге P Q. Ясно, что это множество содержит интервал

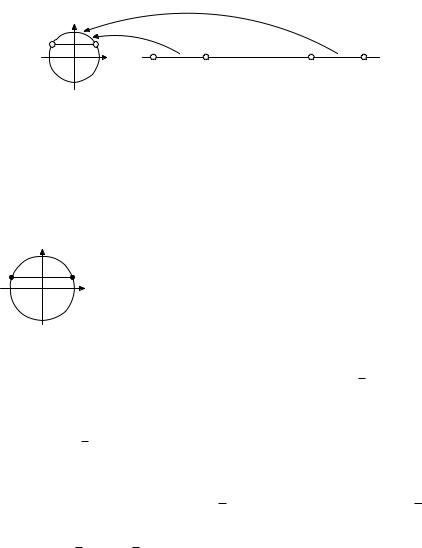
(π/6; 5π/6) (π/6 соответствует точке P , 5π/6 — точке Q), а вообще наше множество состоит из всех интервалов (π/6 + 2πk; 5π/6 + 2πk), где k — целое: ведь если точке на тригонометрической окружности соответствует число x, то ей же соответствуют и все числа вида x + 2πk (k Z) (рис. 26.2).

Рис. 26.2.

Ответ к неравенству можно записать так:

	(π/6 + 2πk; 5π/6 + 2πk)	(k Z)
или еще проще: π/6 + 2πk < x < 5π/6 + 2πk.
Пример 26.2. sin x 6 1/3.
	Решение. На тригонометрической окружности
	множество решений неравенства изобразится ду-
	гой P Q, отмеченной на рис. 26.3. Нам нужно

выбрать на числовой оси какой-нибудь отрезок, соответствующий этой дуге, и тогда останется

Рис. 26.3.

только прибавить к его границам 2πn. Выберем

какое-нибудь число, соответствующее одному из концов дуги. Очевидно, точке P соответствует arcsin 13 . Раз это число выбрано, выбор числа, соответствующего другому концу, уже предопределен. Чтобы найти это число, надо сдвинуться из точки arcsin 13 на числовой оси в отрицательном направлении на расстояние, равное длине дуги P Q. Точке O на окружности соответствует ноль, точке B — число −π, а точке Q — число, расположенное еще на arcsin 13 левее, то есть −π − arcsin 13 . Стало быть, один из отрезков, соответствующих дуге P Q, будет h−π−arcsin 13 ; arcsin 13 i, а ответом к неравенству sin x 6 1/3 будет

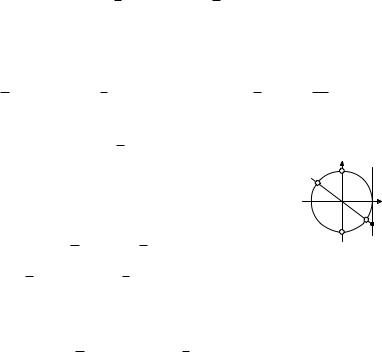
объединение отрезков

h−π − arcsin

1

1

(k Z).

3 + 2πk; arcsin 3 + 2πki

Разумеется, тот же ответ можно представить и по-иному, напри-

мер

π

1

+ 2πki;

hπ − arcsin

1

3π

h− 2

+ 2πk; arcsin 3

3 + 2πk;

2 + 2πki.

3

Пример 26.3. tg x > −4 .

Решение. Используя ось тангенсов, легко убедить-

ся, что на тригонометрической окружности ре-

шения неравенства изображаются двумя дугами,

отмеченными на рис. 26.4. Дуге P Q соответству-

ет

интервал

π ; arctg

3

, а дуге MN — ин-

π

− 2

3−

4

Рис. 26.4.

тервал

2 ; π + arctg −4

. Второй из этих ин-

тервалов получается из первого сдвигом на π, так что ясно, что

ответ к неравенству — это объединение интервалов

π

3

(n Z).

− 2 + πn; arctg −4 + πn

При решении простейших тригонометрических неравенств можно также пользоваться не тригонометрическим кругом, а графиками. Например, чтобы решить то же неравенство sin x 6 1/3, достаточно отметить на числовой оси такие точки, что лежащие над ними точки графика y = sin x имеют ординату не более 1/3 (рис. 26.5). По этому рисунку легко записать ответ.

При оформлении решений простейших тригонометрических неравенств не надо записывать рассуждений наподобие тех, что мы проводили в этих примерах: достаточно рисунка наподобие рис. 26.3 и ответа. Можно также нарисовать рисунок наподобие рис. 26.5 и опять же записать ответ.

Задача 26.1. Решите неравенства:

Рис. 26.5.

а) cos x > 0;

б) sin x < 0;

в) cos 100x > 0;

г) cos

x

6 0;

100

д) tg 2x < 0.

Задача 26.2. Решите неравенства:

√

1

а) sin 2x >

2

б) sin x < −

;

;

2

2

√

3

в) | sin x| 6

;

г) tg x > 1;

2

√

д) | tg x| >

3

.

3

Задача 26.3. Решите неравенства:

1

2

√

в) | sin x| 6

10

а) sin x <

;

б) cos 3x > −

;

;

4

9

10

г) tg x > √

.

5

Задача 26.4. Решите неравенства:

а) sin x > sin 1;

б) sin x 6 sin 7;

в) cos x > cos 10;

г) cos x 6 sin 2;

д) tg x < ctg 10.

Задача 26.5. Решите неравенства:

а) 2 sin2 x − 3 cos x − 1 > 0; б) 9 cos 4x + 6 cos 2x + 5 < 0; в) cos 2x − 2 sin x + 5 > 0.

Задача 26.6. Решите неравенства:

158

	π
а) arccos x >			;						б) arccos x < 2;
		3
в) arcsin x 6 −			1						г) arccos x <	π
					;						.
				4						6
Приведем пример решения более сложного неравенства.
	2 sin x + 1
Пример 26.4.									> 0.
					x
	2 cos							− 1
						2

Решение. Мы применим «метод интервалов», который должен быть вам знаком по решению рациональных неравенств. Рецепт таков: надо на числовой оси отметить те точки, в которых обращаются в нуль числитель и знаменатель; на каждом из интервалов, на которые делится этими точками числовая ось, знак левой части будет постоянен, и останется только записать ответ как объединение интервалов с нужным знаком. В случае тригонометрических неравенств точек и интервалов будет, как правило, бесконечно много, однако они будут периодически повторяться, поэтому достаточно все проделать на отрезке длиной в период.

Внашем случае наименьшим периодом числителя будет 2π,

азнаменателя 4π. Будем поэтому рассматривать знак левой части на отрезке [0; 4π]: его длина равна 4π, а это число служит периодом как числителя, так и знаменателя.

Легко видеть, что на отрезке [0; 4π] числитель обращается в

					7π		11π		19π		23π
нуль в точках						,		,		и		, а знаменатель — в точках
					6		6		6		6
	2π	и	10π	. Знаки числителя, знаменателя и левой части удобно
	3		3

записать в таблице (точки, в которых знаменатель обращается в нуль, мы в интервалы не включили).

h0;

2π

2π 7π

i

h

7π 11π

i

h

11π 19π

i

Интервал

;

;

;

3

3

6

6

6

6

6

2 sin x + 1

+

+

−

+

x

2 cos

− 1

+

−

−

−

2

Левая часть

+

−

+

−