Урок 47. методы решения тригонометрических уравнений — Алгебра и начала математического анализа — 10 класс
Алгебра и начала математического анализа, 10 класс
Урок №47. Методы решения тригонометрических уравнений.
Перечень вопросов, рассматриваемых в теме:
- Формирование системы знаний и умений решать тригонометрические уравнения различными методами;
- Применение метода разложения на множители при решении тригонометрических уравнений;
- Применение метода оценки при решении тригонометрических уравнений;
- Прием домножения левой и правой частей уравнения на тригонометрическую функцию при решении тригонометрических уравнений.
Глоссарий по теме
Теорема — основа метода разложения на множители
Уравнение равносильно на своей области определения совокупности .
Теорема — основа метода замены переменной
Уравнение равносильно на ОДЗ совокупности уравнений
.
Основная литература:
Колягин Ю.М., Ткачёва М.В., Фёдорова Н.Е., Шабунин М.И. под ред. Жижченко А.Б. Алгебра и начала математического анализа. 10 класс: учеб. для общеобразоват. учреждений: базовый и профил. Уровни – 2-е изд. – М.: Просвещение, 2011. – 368 с.: ил. – ISBN 978-5-09-025401-4, сс.327-332
Дополнительная литература:
Шахмейстер А.Х. Тригонометрия. М.: Издательство МЦНМО : СПб.: «Петроглиф» : «Виктория плюс», 2013. – 752 с.: илл. ISBN 978-5-4439-0050-6, сс.219-221, 245-262
Открытые электронные ресурсы:
Решу ЕГЭ образовательный портал для подготовки к экзаменам https://ege.sdamgia.ru/
Теоретический материал для самостоятельного изучения
На этом уроке мы продолжаем заниматься решением тригонометрических уравнений. И здесь мы рассмотрим такие методы как разложение на множители, метод оценки, а также продолжим решать тригонометрические уравнения методом замены переменной. Кроме того, мы узнаем, как использовать домножение правой и левой частей уравнений для получения более простого уравнения, как использовать тригонометрические формулы для решения уравнений.
Сейчас выполните несколько заданий.
Задание 1.
Представьте в виде произведения:
Решение:
Используем формулы приведения, затем формулу преобразования суммы косинусов в произведение:
.
(На последнем шаге мы фактически использовали формулу двойного аргумента:
.
Ответ: .
Задание 2.
Вычислите:
Решение:
Воспользуемся формулой понижения степени и формулой преобразования произведения косинусов в сумму косинусов. Появившийся при этом общий множитель вынесем за скобки:
Воспользуемся тем, что косинус – функция четная и известным значением косинуса. В результате получим:
Ответ: 0,25
Задание 3.
Проверьте равенство:
Решение:
При выполнении этого задания будем использовать прием домножения о деления левой части на одно и то же тригонометрическое выражение.
Но сначала заметим, что .
Теперь запишем левую часть: .
теперь домножим и разделим это выражение на : .
Теперь воспользуемся формулой синуса двойного аргумента и получим:
. Теперь еще раз воспользуемся формулой двойного аргумента, предварительно домножив числитель и знаменатель на 2:
Учитывая, что , получаем: .
То есть исходное равенство верно.
Объяснение новой темы
1. Рассмотрим метод разложения на множители
Теоретической основой метода разложения на множители является теорема:
Теорема
Уравнение равносильно на своей области определения совокупности .
Для того чтобы применить эту теоремы, нужно исходное уравнение привести к виду , используя разные приемы.
Пример 1.
Решить уравнение:
Решение:
Перенесем правую часть уравнения в левую и преобразуем:
, .
Ответ: .
В этом случае мы использовали метод группировки для разложения на множители тригонометрического выражения.
Часто для преобразования выражения в произведение нужно использовать тригонометрические формулы. Рассмотрим такой пример:
Рассмотрим такой пример:
Пример 2.
Решить уравнение:
Решение:
Преобразуем разность синусов в произведение:
Теперь вынесем за скобку общий множитель:
И решим каждое из двух уравнений: .
. Заметим, что вторая серия решений включается в первую. Поэтому мы можем оставить в ответе только первую серию.
Ответ: .
2. Замена переменной
Еще один метод решения тригонометрических уравнений — это метод разложения на множители. Мы уже знакомились с ним, когда решали уравнения, сводимые к квадратному или другому алгебраическому уравнению, когда решали однородные уравнения, а также знакомились с универсальной тригонометрической подстановкой. На этом уроке мы познакомимся еще с одной заменой, которая позволяет решать тригонометрические уравнения.
Рассмотрим уравнение вида:
или .
Для его решения введем новую переменную .
Тогда .
Выразим отсюда (или ).
Пример3.
Решите уравнение
Решение:
Сделаем замену . Тогда .
Тогда .
Вспомогательное уравнение имеет вид:
.
.
Вернемся к исходной переменной:
.
Решим каждое из этих уравнений с помощью формулы введения вспомогательного угла:
, .
Так как , то оба уравнения имеют решения:
, .
Ответ: .
3. Теперь рассмотрим метод оценки
Часто этот метод применяют в том случае, когда уравнение включает в себя функции разного типа, например, тригонометрические и показательные, и обычные преобразования на приводят к результату. Но мы рассмотрим метод оценки при решении тригонометрических уравнений. Он основан на свойстве ограниченности тригонометрических выражений.
Рассмотрим пример.
Пример 4.
Решить уравнение: .
Мы знаем, что . С другой стороны, для того чтобы произведение двух различных чисел было равно 1, то они должны быть взаимно обратными, то есть если одно из них меньше 1,то другое больше 1. Но так как косинус больше 1 быть не может, то равенство может выполняться только в двух случаях:
или .
или .
или .
Вторая система ни при каких значениях k и n не имеет решений.
Первая система имеет решения при n=3m, k=2m, поэтому ее решения, а значит, и решение уравнения:
Ответ:
Рассмотрим еще один пример, в котором метод оценки применяется для решения уравнения, правая и левая части которого являются функциями разного типа.
Пример 5.
Решите уравнение:
Решение:
Рассмотрим левую часть уравнения и преобразуем его:
.
Поэтому
Теперь рассмотрим правую часть: .
Поэтому данное уравнение решений не имеет.
Ответ: решений нет
Рассмотрим несколько задач.
Решите уравнение:
Решение:
Домножим уравнение на 2 и воспользуемся формулой понижения степени:
Теперь воспользуемся формулой преобразования суммы косинусов с произведение:
.
Теперь перенесем правую часть в левую и вынесем за скобку общий множитель:
Теперь используем формулу преобразования разности косинусов в произведение:
Теперь решим три простейших тригонометрических уравнения:
, .
В этом случае достаточно оставить первые две серии решений, так как числа вида при нечетных значениях m попадают в первую серию решений, а при четных — во вторую.
Таким образом, получаем ответ:
Ответ:
Решите уравнение:
Используя метод вспомогательного угла, оценим выражение, стоящее в левой части уравнения.
То есть будем рассматривать левую часть уравнения как выражение вида:
, где .
Получим, что
Мы знаем, что , поэтому
Поэтому уравнение решений не имеет.
Ответ: решений нет.
Рассмотрим решение более сложного уравнения методом оценки.
Решите уравнение
Запишем уравнение в виде
Преобразуем левую часть:
Так как , то
и .
Так как и , то
Равенство возможно только при одновременном выполнении условий:
.
,
.
.
, .
Решая эту систему, получим, что, .
Ответ: , .
Рассмотрим еще один прием, который применяется при решении тригонометрических уравнений.
Домножение левой и правой части на тригонометрическую функцию
Рассмотрим решение уравнения:
Решение:
Домножим обе части уравнения на :
.
Заметим, что домножая обе части уравнения на выражение с переменной, мы можем получить новые корни. Проверим те значения переменной, при которой :
не являются решением исходного уравнения, поэтому мы должны будем удалить эти числа из полученного решения.
Теперь с помощью формулы синуса двойного аргумента преобразуем полученное уравнение:
Теперь перенесем правую часть в левую и преобразуем по формуле преобразования разности синусов в произведение:
, .
Учитывая, что , получим: .
Ответ: .
Примеры и разборы решений заданий тренировочного модуля
Пример 1.
A=1
подсказка
B=2
замена
C=6
Период
Ответ:
Пример 2.
Решите уравнение. Найдите коэффициенты a, b, c
Ответ:
Представим левую и правую части уравнения в виде произведения. Затем перенесём всё в левую часть и разложим на множители
Затем перенесём всё в левую часть и разложим на множители
a=1 ВАРИАНТ
b=7 МНОЖИТЕЛЬ
c=7 СЛАГАЕМОЕ
Ответ:
Mathematica & Wolfram Language for Math Students—Fast Intro
Для базовых тригонометрических функций используются стандартные обозначения (первые буквы в именах функций — заглавные):
| In[1]:= | ⨯Sin[x]/Cos[x] == Tan[x] |
| Out[1]= |
Добавим ключевое слово “Arc” для получения обратных функций:
| In[2]:= | ⨯
|
| Out[2]= |
Для работы с радианами зачастую необходимо использовать константу Pi:
(Наберите ESCpiESC для ввода символаπ.)| In[1]:= | ⨯Sin[\[Pi]/2] |
| Out[1]= |
Или наберите ESCdegESC для использования встроенного символа Degree:
| In[2]:= | ⨯Sin[90 \[Degree]] |
| Out[2]= |
Разложим (или упростим) тригонометрические выражения, используя известные тождества:
| In[1]:= | ⨯TrigExpand[Sin[2 x]] |
| Out[1]= |
Выполним факторизацию тригонометрического полинома:
| In[2]:= | ⨯TrigFactor[Cos[x]^2 - Sin[x]^2] |
| Out[2]= |
Такие функции, как Solve, также позволяют решать подобные уравнения:
| In[1]:= | ⨯Solve[Cos[x]^2 + Sin[x]^2 == x] |
| Out[1]= |
Уточним интересующую область решений:
| In[2]:= | ⨯Solve[{Tan[x] == 1, 0 < x < 2 Pi}] |
| Out[2]= |
Справочная информация: Тригонометрические функции »
Hands–on Start to
Wolfram Mathematica »
Полная документация »
Demonstrations Project »
Решение тригонометрических уравнений.
 Как решить тригонометрическое уравнение.
Как решить тригонометрическое уравнение.Решение тригонометрических уравнений требует знания основных формул тригонометрии — сумму квадратов синуса и косинуса, выражение тангенса через синус и косинус и другие. Для тех, кто их забыл или не знает рекомендуем прочитать статью «Основные тригонометрические формулы».
Итак, основные тригонометрические формулы мы знаем, пришло время использовать их на практике. Решение тригонометрических уравнений при правильном подходе – довольно увлекательное занятие, как, например, собрать кубик Рубика.
Исходя из самого названия видно, что тригонометрическое уравнение – это уравнение, в котором неизвестное находится под знаком тригонометрической функции.
Существуют так называемые простейшие тригонометрические уравнения. Вот как они выглядят: sinх = а, cos x = a, tg x = a. Рассмотрим, как решить такие тригонометрические уравнения, для наглядности будем использовать уже знакомый тригонометрический круг.
sinх = а
cos x = a
tg x = a
cot x = a
Любое тригонометрическое уравнение решается в два этапа: приводим уравнение к простейшему виду и далее решаем его, как простейшее тригонометрическое уравнение.
Существует 7 основных методов, с помощью которых решаются тригонометрические уравнения.
Метод замены переменной и подстановки
- cos(x + /6) = 1
x + /6 = 2 k
x1 = — /6 + 2 k
- cos(x + /6) = ?
x + /6 = ±arccos 1/2 + 2 k
x2 = ± /3 — /6+ 2 k
Решение тригонометрических уравнений через разложение на множители
- 2sin(x/2) = 0
Это простейшее тригонометрическое уравнение, решение которого
х/2 = k
x1 = 2 k
- cos(x/2) — sin(x/2) = 0
Это уравнение является однородным и решается третьим методом, который мы рассмотрим ниже.
Делим уравнение на cos(x/2) и получаем опять же простейшее тригонометрическое уравнение:
1 — tg(x/2) = 0
tg(x/2) = 1
x/2 = arctg 1 + k
x/2 = /4+ k
x2 = /2+ 2 k
Приведение к однородному уравнению
Решение уравнений, через переход к половинному углу
Введение вспомогательного угла
Преобразование произведения в сумму
Универсальная подстановка
- x (2k + 1) ,
тогда, воспользовавшись тригонометрическими формулами, получим:3[(2tg(x/2))/(1 + tg2 (x/2)] — 4[(1 – tg2 (x/2))/(1 + tg2 (x/2)] = 3
6tg(x/2) – 4 + 4tg2 (x/2) = 3 + 3tg2 (x/2)
tg2 (x/2) + 6tg(x/2) – 7 = 0
Делаем замену tg(x/2) на y и получаем квадратное уравнение:
y2 + 6y -7 = 0
корни которого y1 = -7, y2 = 1
Идем обратно и получаем два простейших уравнения:
1) tg(x/2) = -7
х1 = -2arctg 7 + 2 k
2) tg(x/2) = 1
x2 = /2 + 2k
- x = (2k + 1) ,
тогда 3sin[(2k +1) ] – 4cos[(2k + 1) ] = 4 3
Получаем – решение имеет только первое условие.

Пример.
Решить уравнение 2cos2 (x + /6) – 3sin( /3 – x) +1 = 0
Используя формулы приведения получим:
2cos2 (x + /6) – 3cos(x + /6) +1 = 0
Заменим cos(x + /6) на y для упрощения и получаем обычное квадратное уравнение:
2y2 – 3y + 1 + 0
Корни которого y1 = 1, y2 = 1/2
Теперь идем в обратном порядке
cos(x + /6) = y
Подставляем найденные значения y и получаем два варианта ответа:
Пример.
Как решить уравнение sin x + cos x = 1 ?
Перенесем все влево, чтобы справа остался 0:
sin x + cos x – 1 = 0
Воспользуемся вышерассмотренными тождествами для упрощения уравнения:
sin x — 2 sin2 (x/2) = 0
Делаем разложение на множители:
2sin(x/2) * cos(x/2) — 2 sin2 (x/2) = 0
2sin(x/2) * [cos(x/2) — sin(x/2)] = 0
Получаем два уравнения
Уравнение является однородным относительно синуса и косинуса, если все его члены относительно синуса и косинуса одной и той же степени одного и того же угла. Для решения однородного уравнения, поступают следующим образом:
Для решения однородного уравнения, поступают следующим образом:
а) переносят все его члены в левую часть;
б) выносят все общие множители за скобки;
в) приравнивают все множители и скобки к 0;
г) в скобках получено однородное уравнение меньшей степени, его в свою очередь делят на синус или косинус в старшей степени;
д) решают полученное уравнение относительно tg.
Пример.
Решить уравнение 3sin2x + 4 sin x • cos x + 5 cos2x = 2
Воспользуемся формулой sin2 x + cos2 x = 1 и избавимся от открытой двойки справа:
3sin2x + 4 sin x • cos x + 5 cos x = 2sin2x + 2cos2x
sin2x + 4 sin x • cos x + 3 cos2x = 0
Делим на cos x:
tg2x + 4 tg x + 3 = 0
Заменяем tg x на y и получаем квадратное уравнение:
y2 + 4y +3 = 0, корни которого y1=1, y2 = 3
Отсюда находим два решения исходного уравнения:
1) tg x = –1
x1 = /4+ k
2) tg x = –3
x2 = arctg 3 + k
Пример.
Решить уравнение 3sin x – 5cos x = 7
Переходим к x/2:
6sin(x/2) * cos(x/2) – 5cos2 (x/2) + 5sin2 (x/2) = 7sin2 (x/2) + 7cos2 (x/2)
Пререносим все влево:
2sin2 (x/2) – 6sin(x/2) * cos(x/2) + 12cos2 (x/2) = 0
Делим на cos(x/2):
tg2 (x/2) – 3tg(x/2) + 6 = 0
Ну а дальше уже по отработанной схеме …
Для рассмотрения возьмем уравнение вида: a sin x + b cos x = c ,
где a, b, c – некоторые произвольные коэффициенты, а x – неизвестное.
Обе части уравнения разделим на :
Теперь коэффициенты уравнения согласно тригонометрическим формулам обладают свойствами sin и cos, а именно: их модуль не более 1 и сумма квадратов = 1. Обозначим их соответственно как cos и sin , где – это и есть так называемый вспомогательный угол. Тогда уравнение примет вид:
cos * sin x + sin * cos x = С
или sin(x + ) = C
Решением этого простейшего тригонометрического уравнения будет
х = (-1) k * arcsin С — + k, где
Следует отметить, что обозначения cos и sin взаимозаменяемые.
Пример.
Решить уравнение sin 3x – cos 3x = 1
В этом уравнении коэффициенты:
а = , b = -1, поэтому делим обе части на = 2
(/2) * sin 3x – (1/2)cos 3x = 1/2
cos( /6) * sin 3x – sin( /6) * cos 3x =1/2
sin(3x – /6) = 1/2
Получаем ответ
x = (-1) k * /18 + /18 + k/3
Здесь мы будем просто использовать тригонометрические формулы
Пример.
Решить уравнение 2 sin x * sin 3x = cos 4x
Левую часть преобразуем в сумму:
cos 4x – cos 8x = cos 4x
Получаем простейшее уравнение:
cos 8x = 0
8x = /2 + k
x = /16 + k/8
Пример.
Решить тригонометрическое уравнение 3sin x – 4cos x = 3
Здесь возможны 2 случая:
Основные методы решения тригонометрических уравнений, мы рассмотрели. Если у вас остались какие либо вопросы о том, как решать тригонометрические уравнения, задавайте их в комментариях ниже.
Будем рады любым ваших вопросам.
Заметка: собираетесь выступать http://prezentacii.com портал готовых презентаций.
Если материал был полезен, вы можете отправить донат или поделиться данным материалом в социальных сетях:
ЕГЭ. Задание 13. Тригонометрические (и не только) уравнения
Подготовка к профильному уровню единого государственного экзамена по математике. Полезные материалы по тригонометрии, большие теоретические видеолекции, видеоразборы задач и подборка заданий прошлых лет.
Полезные материалы
Подборки видео и онлайн-курсы
Тригонометрические формулы
{2 \sin 2x}$.
б) Найдите все корни этого уравнения, принадлежащие промежутку $\left[\dfrac{3\pi}{2}; 3\pi \right]$.
а) Решите уравнение $\sin x + \left(\cos \dfrac{x}{2} — \sin \dfrac{x}{2}\right)\left(\cos \dfrac{x}{2} + \sin \dfrac{x}{2}\right) = 0$.
б) Найдите все корни этого уравнения, принадлежащие промежутку $\left[\pi; \dfrac{5\pi}{2}\right]$.
а) Решите уравнение $\log_4 (\sin x + \sin 2x + 16) = 2$.
б) Найдите все корни этого уравнения, принадлежащие промежутку $\left[ -4\pi; -\dfrac{5\pi}{2} \right]$.
Подборка заданий прошлых лет
- а) Решите уравнение $\dfrac{\sin x}{\sin^2\dfrac{x}{2}} = 4\cos^2\dfrac{x}{2}$.
 2 x + \sin x = \sqrt2 \sin\left( x + \dfrac{\pi}{4} \right)$.
2 x + \sin x = \sqrt2 \sin\left( x + \dfrac{\pi}{4} \right)$.
б) Найдите все корни этого уравнения, принадлежащие отрезку $\left[ -4\pi; -\dfrac{5\pi}{2} \right]$. (ЕГЭ-2018. Основная волна) - а) Решите уравнение $2 \sin\left( 2x + \dfrac{\pi}{3} \right) — \sqrt{3} \sin x = \sin 2x + \sqrt3$.
б) Найдите все корни этого уравнения, принадлежащие отрезку $\left[ 2\pi; \dfrac{7\pi}{2} \right]$. (ЕГЭ-2018. Основная волна) - а) Решите уравнение $2\sqrt3 \sin\left( x + \dfrac{\pi}{3} \right) — \cos 2x = 3\cos x — 1$.
б) Найдите все корни этого уравнения, принадлежащие отрезку $\left[ 2\pi; \dfrac{7\pi}{2} \right]$. (ЕГЭ-2018. Основная волна) - а) Решите уравнение $2\sin\left( 2x + \dfrac{\pi}{6} \right) — \cos x = \sqrt3\sin 2x — 1$.
б) Найдите все корни этого уравнения, принадлежащие отрезку $\left[ \dfrac{5\pi}{2}; 4\pi \right]$. (ЕГЭ-2018. Основная волна) - а) Решите уравнение $\sqrt2\sin\left( \dfrac{\pi}{4} + x \right) + \cos 2x = \sin x — 1$.
 2 x + 5\sin\left( \dfrac{\pi}{2} — x\right) — 2 = 0$.
2 x + 5\sin\left( \dfrac{\pi}{2} — x\right) — 2 = 0$.
б) Укажите корни этого уравнения, принадлежащие отрезку $\left[ -5\pi; \ — \dfrac{7\pi}{2}\right]$. (ЕГЭ-2012, вторая волна)
Решение простейших тригонометрических уравнений
Решение простейших тригонометрических уравнений.
Решение тригонометрических уравнений любого уровня сложности в конечном итоге сводится к решению простейших тригонометрических уравнений. И в этом наилучшим помощником снова оказывается тригонометрический круг.
Вспомним определения косинуса и синуса.
Косинусом угла называется абсцисса (то есть координата по оси ) точки на единичной окружности, соответствующей повороту на данный угол .
Синусом угла называется ордината (то есть координата по оси ) точки на единичной окружности, соответствующей повороту на данный угол .
Положительным направлением движения по тригонометрическому кругу считается движение против часовой стрелки. Повороту на 0 градусов ( или 0 радиан) соответствует точка с координатами (1;0)
Повороту на 0 градусов ( или 0 радиан) соответствует точка с координатами (1;0)
Используем эти определения для решения простейших тригонометрических уравнений.
1. Решим уравнение
Этому уравнению удовлетворяют все такие значения угла поворота , которые соответствуют точкам окружности, ордината которых равна .
Отметим на оси ординат точку с ординатой :
Проведем горизонтальную линию параллельно оси абсцисс до пересечения с окружностью. Мы получим две точки, лежащие на окружности и имеющие ординату. Эти точки соответствуют углам поворота на и радиан:
Если мы, выйдя из точки, соответствующей углу поворота на радиан, обойдем полный круг, то мы придем в точку, соответствующую углу поворота на радиан и имеющую ту же ординату. То есть этот угол поворота также удовлетворяет нашему уравнению. Мы можем делать сколько угодно «холостых» оборотов, возвращаясь в ту же точку, и все эти значения углов будут удовлетворять нашему уравнению. Число «холостых» оборотов обозначим буквой (или ). Так как мы можем совершать эти обороты как в положительном, так и в отрицательном направлении, (или ) могут принимать любые целые значения.
Число «холостых» оборотов обозначим буквой (или ). Так как мы можем совершать эти обороты как в положительном, так и в отрицательном направлении, (или ) могут принимать любые целые значения.
То есть первая серия решений исходного уравнения имеет вид:
, , — множество целых чисел (1)
Аналогично, вторая серия решений имеет вид:
, где , . (2)
Как вы догадались, в основе этой серии решений лежит точка окружности, соответствующая углу поворота на .
Эти две серии решений можно объединить в одну запись:
Если мы в этой записи возьмем ( то есть четное ), то мы получим первую серию решений.
Если мы в этой записи возьмем ( то есть нечетное ), то мы получим вторую серию решений.
2. Теперь давайте решим уравнение
Так как — это абсцисса точки единичной окружности, полученной поворотом на угол , отметим на оси точку с абсциссой :
Проведем вертикальную линию параллельно оси до пересечения с окружностью. Мы получим две точки, лежащие на окружности и имеющие абсциссу . Эти точки соответствуют углам поворота на и радиан. Вспомним, что при движении по часовой стрелки мы получаем отрицательный угол поворота:
Мы получим две точки, лежащие на окружности и имеющие абсциссу . Эти точки соответствуют углам поворота на и радиан. Вспомним, что при движении по часовой стрелки мы получаем отрицательный угол поворота:
Запишем две серии решений:
,
,
(Мы попадаем в нужную точку, пройдя из основной полный круг, то есть .
Объедим эти две серии в одну запись:
3. Решим уравнение
Линия тангенсов проходит через точку с координатами (1,0) единичной окружности параллельно оси OY
Отметим на ней точку, с ординатой равной 1 (мы ищем, тангенс каких углов равен 1):
Соединим эту точку с началом координат прямой линией и отметим точки пересечения прямой с единичной окружностью. Точки пересечения прямой и окружности соответствуют углам поворота на и :
Так как точки, соответствующие углам поворота, которые удовлетворяют нашему уравнению, лежат на расстоянии радиан друг от друга, то мы можем записать решение таким образом:
,
4. Решим уравнение
Решим уравнение
Линия котангенсов проходит через точку с координатами единичной окружности параллельно оси .
Отметим на линии котангенсов точку с абсциссой -1:
Соединим эту точку с началом координат прямой и продолжим ее до пересечения с окружностью. Эта прямая пересечет окружность в точках, соответствующих углам поворота на и радиан:
Поскольку эти точки отстоят друг от друга на расстояние, равное , то общее решение этого уравнения мы можем записать так:
В приведенных примерах, иллюстрирующих решение простейших тригонометрических уравнений были использованы табличные значения тригонометрических функций.
Однако, если в правой части уравнения стоит не табличное значение, то мы в общее решение уравнения подставляем значение обратной тригонометрической функции:
ОСОБЫЕ РЕШЕНИЯ:
1
Отметим на окружности точки, ордината которых равна 0:
2.
Отметим на окружности единственную точку, ордината которой равна 1:
3.
Отметим на окружности единственную точку, ордината которой равна -1:
Так как принято указывать значения, наиболее близкие у нулю, решение запишем так:
4.
Отметим на окружности точки, абсцисса которых равна 0:
5.
Отметим на окружности единственную точку, абсцисса которой равна 1:
6.
Отметим на окружности единственную точку, абсцисса которой равна -1:
И чуть более сложные примеры:
1.
Синус равен единице, если аргумент равен
Аргумент у нашего синуса равен , поэтому получим:
. Разделим обе части равенства на 3:
Ответ:
2.
Косинус равен нулю, если аргумент косинуса равен
Аргумент у нашего косинуса равен , поэтому получим:
Выразим , для этого сначала перенесем вправо с противоположным знаком:
Упростим правую часть:
Разделим обе части на -2:
Заметим, что перед слагаемым знак не меняется, поскольку k может принимать любые целые значения.
Ответ:
И в заключение посмотрите видеоурок «Отбор корней в тригонометрическом уравнении с помощью тригонометрической окружности»
На этом разговор о решении простейших тригонометрических уравнений мы закончим. Следующий раз мы с вами поговорим о том, как решать простейшие тригонометрические неравенства.
И.В. Фельдман, репетитор по математике.
Купить видеокурс «ВСЯ ТРИГОНОМЕТРИЯ. Часть В и Задание 13»
Как начать понимать тригонометрию, если ты абсолютно ничего не понимаешь?
К полному непониманию обычно приводит бездумная зубрежка на ранних этапах. Надо вернуться к самому началу темы и изучить ее заново, добиваясь понимания на каждом этапе.
Количество формул в тригонометрии ошеломляет, к тому же среди них очень много похожих. Разве можно их все упомнить? Гораздо проще их все понять. Только на это потребуется время. Быстро выучить всю тригонометрию невозможно.
Быстро выучить всю тригонометрию невозможно.
- Чтобы понимать, не запоминайте формулы, а больше смотрите своими глазами и работайте своими руками. Когда-то мы с друзьями сделали простенькую модель:
Помогает даже незрячим школьникам, особенно для формул приведения. 2. Не подглядывайте в готовую тригонометрическую окружность, а для каждого занятия дома рисуйте себе новую и размечайте ее.
Все нужные числа на тригонометрической окружности связаны между собой. Все вместе запомнить гораздо проще, чем каждое по отдельности. На первых порах можно отмечать не все углы.
Научившись решать простейшие тригонометрические уравнения типа sin x=a, сразу же научитесь решать простейшие тригонометрические неравенства (sin x>а или sin x<а). Решение таких неравенств здорово способствует пониманию.
Не заучивайте формулы, а каждый раз быстренько их выводите. Если Вы не можете вывести тригонометрическую формулу, значит, что-то упущено на предыдущих этапах.
 Если вы выводите с трудом и долго, считайте, что вам повезло — вы нашли то самое место, куда надо прикладывать усилия для получения результата. Скоро научитесь делать это быстро. (Однако если Вам предстоит экзамен, перед экзаменом подзубрите формулы.)
Если вы выводите с трудом и долго, считайте, что вам повезло — вы нашли то самое место, куда надо прикладывать усилия для получения результата. Скоро научитесь делать это быстро. (Однако если Вам предстоит экзамен, перед экзаменом подзубрите формулы.)Чтобы хорошо освоиться с формулами, надо встречать их в разных контекстах. Ведь мало знать формулу, надо еще опознавать те места, где ее полезно применить. А потому решайте больше задач.
Дайте себе время. Музыкант, когда разучивает пьесу, не стремится сыграть ее сразу безупречно. Он останавливается на трудных местах, проигрывает их медленнее и внимательнее, над некоторыми работает особенно долго. Так и в математике. Если надо — затормозите и проработайте трудное место.
Найдите себе единомышленника и занимайтесь вместе. Это помогает не отчаиваться и не складывать крылья раньше времени.
Отличная книга — И. М. Гельфанд, С.М. Львовский, А. Л. Тоом
«ТРИГОНОМЕТРИЯ». http://ilib.mccme.ru/pdf/tr.pdf . Горячо рекомендую.
http://ilib.mccme.ru/pdf/tr.pdf . Горячо рекомендую.
- Если будут трудности с решением задач, приходите в сообщество «Незадача Кью». Поможем и ответим на вопросы, хотя решать задачи за вас не будем — это вредно. https://yandex.ru/q/loves/noproblem/
Методика формирования умений решать тригонометрические уравнения и неравенства в курсе алгебры и начал анализа (Дипломная работа)
Федеральное агентство по образованию
Государственное образовательное учреждение высшего
профессионального образования
«Поморский государственный университет имени М.В.Ломоносова»
Кафедра методики преподавания математики
Работа допущена к защите
Заведующая кафедрой
_________
«__»_____________2008 г.
Выпускная квалификационная работа
Методика формирования умений решать тригонометрические уравнения и неравенства в курсе алгебры и начал анализа
Архангельск
2008
Содержание
Введение
Глава 1 Тригонометрические
уравнения и неравенства в школьном
курсе математики.
1.1 Этапы развития тригонометрии как науки
1.2 Содержание и анализ материала по тригонометрии в различных школьных учебниках
1.3 Роль и место тригонометрических уравнений и неравенств в школьном курсе математики
1.4 Виды тригонометрических уравнений и методы их решения
1.5 Тригонометрические неравенства и методы их решения
Глава 2 Формирование умений и навыков решения тригонометрических уравнений и неравенств.
2.1 Основы формирования умений, необходимые при решении тригонометрических уравнений и неравенств
2.2 Методика формирования у учащихся умений решать тригонометрические уравнения
2.3 Методика формирования у учащихся умений решать тригонометрические неравенства
2.4 Эксперимент, его проведение и обработка результатов
Заключение
Литература
Введение
В настоящее время основной
задачей перестройки школьного образования
является переориентация на приоритет
развивающей функции обучения. Это
означает, что на первый план выходит
задача интеллектуального развития
личности, т.е. развитие учебно-познавательной
деятельности. Пожалуй, ни один школьный
предмет не может конкурировать с
возможностями математики в воспитании
мыслящей личности.
Это
означает, что на первый план выходит
задача интеллектуального развития
личности, т.е. развитие учебно-познавательной
деятельности. Пожалуй, ни один школьный
предмет не может конкурировать с
возможностями математики в воспитании
мыслящей личности.
Уже несколько десятилетий тригонометрия, как отдельная дисциплина школьного курса математики не существует, она плавно растеклась не только в геометрию и алгебру основной школы, но и в алгебру и начала анализа.
Исторически сложилось, что тригонометрическим уравнениям и неравенствам уделялось особое место в школьном курсе. Еще греки на заре человечества, считали тригонометрия важнейшей из наук. Поэтому и мы не оспаривая древних греков, будем считать тригонометрию одним из важнейших разделов школьного курса, да и всей математической науки в целом.
Тригонометрические уравнения
и неравенства занимают одно из центральных
мест в курсе математики средней школы,
как по содержанию учебного материала,
так и по способам учебно-познавательной
деятельности, которые могут и должны
быть сформированы при их изучении и
применены к решению большого числа
задач теоретического и прикладного
характера.
В школьном математическом образовании с изучением тригонометрических уравнений и неравенств связаны несколько направлений:
Решение уравнений и неравенств;
Решение систем уравнений и неравенств;
Доказательство неравенств.
Анализ учебной, научно-методической литературы показывает, что
большое внимание уделяется первому и второму направлениям.
Требованием нашего времени является необходимость усиления прикладных направлений в обучении математике. Как показал анализ содержания школьного математического образования, возможности решения тригонометрических уравнений, а особенно тригонометрических неравенств в этом плане достаточно широки.
Так же следует заметить, что
решение тригонометрических уравнений
и неравенств создаёт предпосылки для
систематизации знаний учащихся, связанных
со всем учебным материалом по тригонометрии
(например, свойства тригонометрических
функций, приёмы преобразования
тригонометрических выражений и т. д.) и
даёт возможность установить действенные
связи с изученным материалом по алгебре
(уравнения, равносильность уравнений,
неравенства, тождественные преобразования
алгебраических выражений и т.д.).[1]
д.) и
даёт возможность установить действенные
связи с изученным материалом по алгебре
(уравнения, равносильность уравнений,
неравенства, тождественные преобразования
алгебраических выражений и т.д.).[1]
Иначе говоря, рассмотрение приёмов решения тригонометрических уравнений и неравенств предполагает своего рода перенос этих умений на новое содержание.
Актуальность исследования: анализ материала, посвященного решению тригонометрических уравнений и неравенств в учебных пособиях «Алгебра и начала анализа» для 10 – 11 классов разных авторов, учет целей изучения тригонометрических уравнений и неравенств, а так же обязательных результатов обучения, связанных с рассматриваемой темой, свидетельствует о том, что перед учителем стоит задача – формировать у учащихся умения решать уравнения и неравенства каждого вида, развивая тем самым общие тригонометрические представления.
Цель исследования: Разработать
методику, направленную на формирование
у учащихся умений решать тригонометрические
уравнения и неравенства.
Объект исследования: процесс обучения математике.
Предмет исследования: методика формирования у учащихся умений решать тригонометрические уравнения и неравенства.
Гипотеза исследования: Если выделить основные умения, необходимые при решении тригонометрических уравнений и неравенств и разработать методику их формирования, то это будет способствовать качественному научению решать тригонометрические уравнения и неравенства.
Под осознанным и качественным изучением тригонометрии мы понимаем процесс обучения, осуществляемый с учетом идей личностно ориентированного обучения, при реализации которого не допускается формальной передачи знаний и схоластической отработки умений, т.е. изучение тригонометрии должно опираться как на логическую, так и на образную составляющие мышление, при этом учащимся должны быть предоставлены возможности для дифференциации и индивидуализации.
В процессе исследования и проверке достоверности гипотезы необходимо было решить следующие задачи:
1. Провести анализ
психолого-педагогической, учебной и
методической литературы по проблеме
исследования.
Провести анализ
психолого-педагогической, учебной и
методической литературы по проблеме
исследования.
2. Выявить роль тригонометрических уравнений и неравенств в обучении математики.
3. Выделить основы формирования умений необходимых для решения тригонометрических уравнений и неравенств.
4. Классифицировать методы решения тригонометрических уравнений и неравенств.
5. Разработать методику формирования умений и навыков решать тригонометрические уравнения и неравенства.
6. Провести экспериментальное исследование разработанной методики.
Для решения поставленных задач были использованы следующие методы исследования:
1. Анализ психолого-педагогической и методической литературы.
2. Анализ учебно-методических пособий, учебников, дидактических материалов.
3. Наблюдения, беседы с учителями.
4. Педагогический эксперимент.
Структура работы. Работа состоит из двух глав, введения и заключения. Во введении подчеркнута актуальность изучения проблемы. Первая глава посвящена рассмотрению значимости тригонометрического материала в школьном курсе математики, классификации тригонометрических уравнений и неравенств, а так же методов их решений. Во второй главе описаны основные умения, необходимые при решении тригонометрических уравнений и неравенств и методика формирования умений решать тригонометрические уравнения и неравенства. Список литературы включает 32 источника.
Тригонометрия
Тригонометрия (от греческого trigonon «треугольник» + метрон «мера»)
Хотите изучить тригонометрию? Вот краткий обзор.
Перейдите по ссылкам, чтобы узнать больше, или перейдите к Указатель тригонометрии
Тригонометрия … это все о треугольниках. |
Тригонометрия помогает нам находить углы и расстояния и широко используется в науке, технике, видеоиграх и многом другом!
Прямоугольный треугольник
Наиболее интересным треугольником является прямоугольный треугольник.Прямой угол показан квадратиком в углу:
Другой угол часто обозначается θ, и тогда называются три стороны:
- Смежный : смежный (рядом) угол θ
- Напротив : напротив угла θ
- и самая длинная сторона Гипотенуза
Почему треугольник прямоугольный?
Почему этот треугольник так важен?
Представьте, что мы можем измерять вдоль и поперек, но хотим знать прямое расстояние и угол:
Тригонометрия может найти недостающий угол и расстояние.
Или, может быть, у нас есть расстояние и угол, и нам нужно «начертить точку» вдоль и вверх:
Подобные вопросы часто встречаются в инженерии, компьютерной анимации и т. д.
д.
И тригонометрия дает ответы!
Синус, косинус и тангенс
Основными функциями в тригонометрии являются синус, косинус и тангенс
Это просто одна сторона прямоугольного треугольника, разделенная другой.
Для любого угла « θ «:
(Синус, косинус и тангенс часто обозначаются как sin, cos и tan.)
Пример: чему равен синус 35°?
Используя этот треугольник (длина только до одного десятичного знака):
sin(35°) = Противоположный Гипотенуза = 2,8 4,9 = 0,57…
Треугольник может быть больше, меньше или повернут, но этот угол всегда будет иметь отношение .
Калькуляторы имеют sin, cos и tan, чтобы помочь нам, поэтому давайте посмотрим, как их использовать:
Пример: какой высоты дерево?
Мы не можем добраться до вершины дерева, поэтому отходим и измеряем угол (с помощью транспортира) и расстояние (с помощью лазера):
- Мы знаем Гипотенузу
- И мы хотим знать Противоположный
Синус есть отношение Противоположность/гипотенуза :
грех(45°) = Напротив Гипотенуза
Получите калькулятор, введите «45», затем клавишу «sin»:
sin(45°) = 0.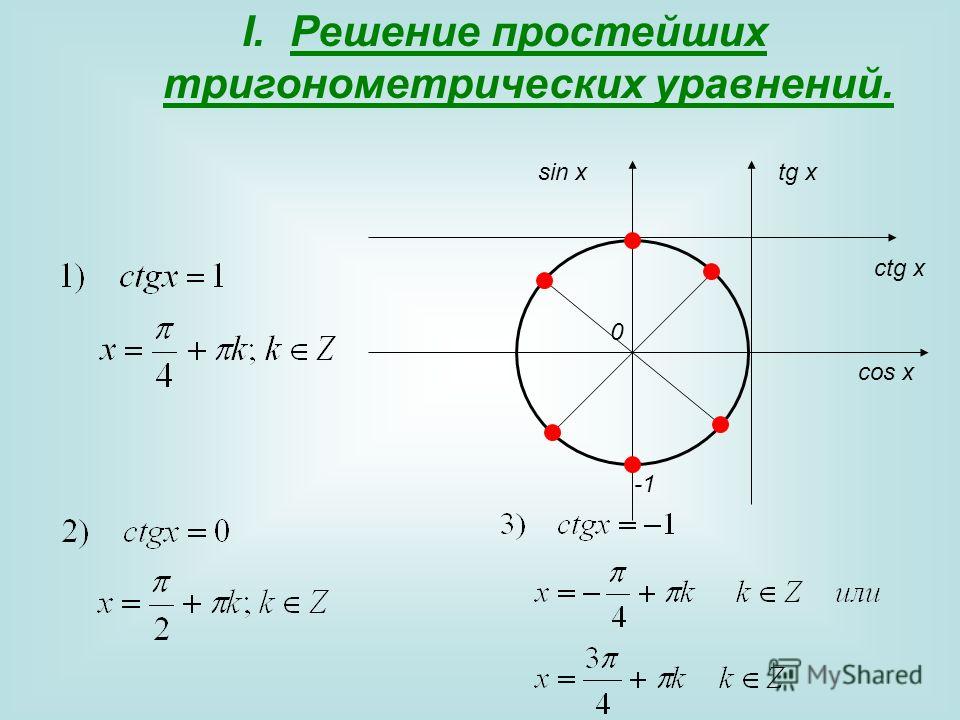 7071…
7071…
Что означает 0,7071… ? Это отношение длин сторон, поэтому противоположная сторона в раз длиннее гипотенузы примерно в 0,7071 раз.
Теперь мы можем поставить 0,7071… вместо sin(45°):
0,7071… = Напротив Гипотенуза
И мы также знаем, что гипотенуза равна 20 :
0.7071… = Напротив 20
Чтобы решить, сначала умножьте обе части на 20:
20 × 0,7071… = напротив
Наконец:
Напротив = 14,14 м (до 2 знаков после запятой)
Когда вы наберете больше опыта, вы можете сделать это быстро следующим образом:Пример: какой высоты дерево?
Начать с:sin(45°) = Напротив Гипотенуза
Мы знаем:0. 7071… = Напротив 20
7071… = Напротив 20
Поменять стороны местами: Напротив 20 = 0,7071…
Умножить обе стороны на 20 : Противоположное = 0,7071… × 20
Вычислить: наоборот = 14,14
(до 2 знаков после запятой)
Дерево высотой 14,14 м
Попробуйте Sin Cos и Tan
Поиграйте с этим некоторое время (переместите мышь) и познакомьтесь со значениями синуса, косинуса и тангенса для различных углов, таких как 0°, 30°, 45°, 60° и 90°.
../алгебра/изображения/круг-треугольник.js
Также попробуйте 120°, 135°, 180°, 240°, 270° и т. д. и обратите внимание, что положения могут быть положительными или отрицательными по правилам декартовых координат, поэтому синус, косинус и тангенс также меняются между положительными и отрицательными .
Итак, тригонометрия тоже касается кругов !
Единичный круг
То, с чем вы только что играли, это Единичный круг.
Это круг радиусом 1 с центром в 0.
Поскольку радиус равен 1, мы можем напрямую измерить синус, косинус и тангенс.
Здесь мы видим синусоидальную функцию единичного круга:
Примечание: вы можете увидеть красивые графики, сделанные с помощью синуса, косинуса и тангенса.
градусов и радианов
Углы могут быть в градусах или радианах. Вот несколько примеров:
| Уголок | Градусов | Радиан |
|---|---|---|
| Прямоугольный | 90° | №/2 |
| __ Прямоугольный | 180° | № |
| Полный оборот | 360° | 2π |
Повторяющийся шаблон
Поскольку угол равен вращению по окружности , функции синуса, косинуса и тангенса повторяются один раз за каждый полный оборот (см.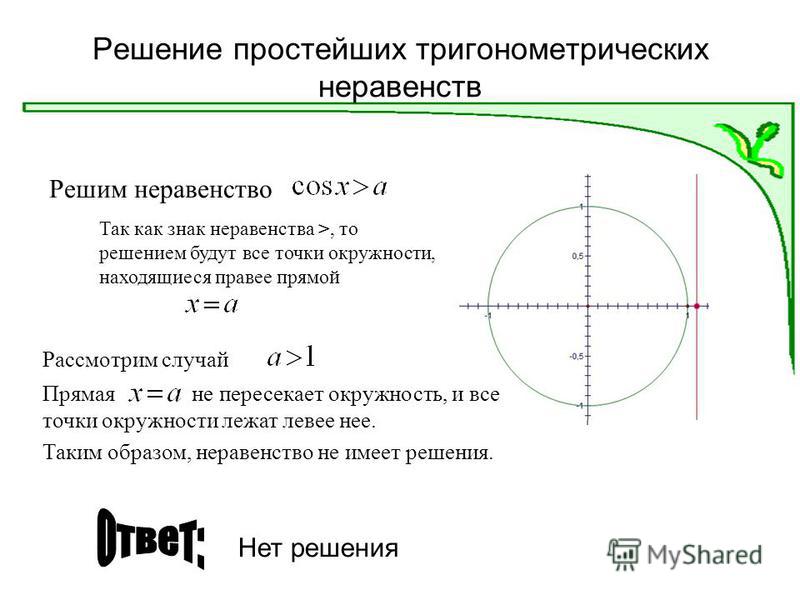 Амплитуда, период, фазовый сдвиг и частота).
Амплитуда, период, фазовый сдвиг и частота).
Когда мы хотим вычислить функцию для угла, превышающего полный оборот в 360° (2π радиан), мы вычитаем столько полных оборотов, сколько необходимо, чтобы вернуть угол ниже 360° (2π радиан):
Пример: чему равен косинус 370°?
370° больше 360°, поэтому давайте вычтем 360°
370° − 360° = 10°
cos(370°) = cos(10°) = 0,985 (до 3 знаков после запятой)
А когда угол меньше нуля, просто добавить полные обороты.
Пример: чему равен синус −3 радиан?
−3 меньше 0, поэтому добавим 2π радиан
.−3 + 2π = −3 + 6,283… = 3,283… радиан
sin(−3) = sin(3,283…) = −0,141 (до 3 знаков после запятой)
Решение треугольников
Тригонометрия также полезна для общих треугольников, а не только прямоугольных.
Помогает нам в решении треугольников. «Решение» означает нахождение недостающих сторон и углов.
«Решение» означает нахождение недостающих сторон и углов.
Мы также можем найти недостающие длины сторон. Общее правило:
Когда мы знаем любые 3 стороны или угла, мы можем найти остальные 3
(кроме случая с тремя углами)
Подробнее см. раздел «Решение треугольников».
Другие функции (котангенс, секанс, косеканс)
Подобно синусу, косинусу и тангенсу, существуют три другие тригонометрические функции , которые получаются путем деления одной стороны на другую:
Функция косеканса: | csc( θ ) = гипотенуза / напротив |
Секущая Функция: | сек( θ ) = Гипотенуза / Смежный |
Котангенс Функция: | детская кроватка( θ ) = Смежный/Напротив |
Тригонометрические и треугольные тождества
И по мере того, как вы будете лучше разбираться в тригонометрии, вы сможете выучить следующее:
Станьте экспертом по треугольникам (и кругам)!
Использование коэффициентов триггера для решения треугольников: стороны
Отношения триггера можно использовать для поиска большого количества информации, и одно из их основных назначений — помогать решать треугольники. Решить треугольник означает найти длину всех сторон и величину всех углов.
Решить треугольник означает найти длину всех сторон и величину всех углов.Этот урок расскажет, как использовать коэффициенты триггера для нахождения длин сторон треугольника.
Есть три шага:
1. Выберите коэффициент срабатывания для использования.
— Выберите sin, cos или tan, определив, какую сторону вы знаете и какую сторону ищете.
2. Замените
— Подставьте свою информацию в коэффициент срабатывания.
3.Solve
— Решите полученное уравнение, чтобы найти длину стороны.
Пример:
1. Найдите b.
Шаг 1: Выберите коэффициент срабатывания для использования.
Во-первых, мы знаем, что должны смотреть на угол B, потому что это угол, для которого мы знаем меру
. ошибка.)
Итак, глядя на угол B, мы хотим определить, какие стороны задействованы.Мы знаем, что одна сторона
равна 8 м, а эта сторона равна , смежной с углом B. Сторона, которую мы ищем, равна , противоположной углу B. Таким образом, нам нужно выбрать тригонометрический коэффициент, который имеет
Таким образом, нам нужно выбрать тригонометрический коэффициент, который имеет
напротив и смежно. Это, конечно, тангенс .
Шаг 2: Замените
Далее мы записываем коэффициент срабатывания:
Затем подставляем угол
и известную нам сторону:
Шаг 3: Решаем
Теперь переместим 8 на другую сторону
, умножив обе стороны на 8:
И воспользуемся калькулятором, чтобы найти ответ .
Колодец округлить до десятых: 3,7 м.
2. Найти c.
Теперь, когда мы знаем две стороны, вы можете использовать теорему Пифагора
, чтобы найти третью. Но это менее надежно, потому что
если вы допустили ошибку на стороне b, то и сторона c тоже будет неправильной.
Итак, мы собираемся повторить тот же процесс для стороны c.
Шаг 1: Выберите коэффициент срабатывания для использования.
Мы по-прежнему используем угол B. 8m — это , смежное с , а c — это гипотенуза.
Тригонометрическое отношение, использующее примыкающую и гипотенузу, представляет собой косинус .
Шаг 2: Подставляем
Запишем коэффициент триггера:
Затем подставляем угол
и сторону, которую мы знаем:
Шаг 3: Решаем
Поскольку наша переменная включена мы можем начать с перекрестного умножения
:
Затем мы разделим
с обеих сторон на cos 25°:
И используйте калькулятор, чтобы
найти ответ.Хорошо округляем
до десятых:
8,8 м.
Примечание: Если вам кажется, что ваш калькулятор не дает правильного ответа, прочтите руководство или попросите кого-нибудь о помощи. Все калькуляторы разные, и вы должны ввести информацию в правильном порядке, чтобы получить правильный ответ. Кроме того, убедитесь, что ваш калькулятор находится в режиме градусов (не в радианах)
Практика:
Найдите следующее. Округлите свои ответы до десятых.
1) а 2) в 3) х 4) у
Ответы: 1) 7. 4 дюйма 2) 9,5 дюйма 3) 7,0 футов 4) 5,7 футов
4 дюйма 2) 9,5 дюйма 3) 7,0 футов 4) 5,7 футов
прямоугольных треугольников
прямоугольных треугольниковДавайте снова согласимся со стандартным правилом обозначения частей прямоугольного треугольника. Пусть прямой угол обозначен как C , а гипотенуза c. Пусть A и B обозначают два других угла, а a и b стороны, противоположные им соответственно.
Решение прямоугольных треугольников
Мы можем использовать теорему Пифагора и свойства синусов, косинусов и тангенсов для решения треугольника, то есть для нахождения неизвестных частей через известные части.- Теорема Пифагора: a 2 + b 2 = c 2 .
- Синусы: sin A = a/c, sin B = b/c.
- Косинусы: cos A = b/c, cos B = a/c.
- Касательные: tan A = a/b, tan B = b/a.

Теперь предположим, что мы знаем гипотенузу и одну сторону, но должны найти другую. Например, если B = 119 и C = 169, затем A 2 = C 2 — B 2 = 169 2 — 119 2 = 28561 — 14 161 = 14 400, а квадратный корень из 14 400 равен 120, поэтому 90 003 – 90 006 = 120.
Мы можем знать только одну сторону, но мы также знаем угол. Например, если сторона a = 15 и угол A = 41°, мы можем использовать синус и тангенс, чтобы найти гипотенузу и другую сторону.Поскольку sin A = a/c, мы знаем, что c = a /sin A = 15/sin 41. С помощью калькулятора получается 15/0,6561 = 22,864. Кроме того, tan A = a/b, , поэтому b = a /tan A = 15/tan 41 = 15/0,8693 = 17,256. Используете ли вы синус, косинус или тангенс, зависит от того, какую сторону и угол вы знаете.
Например, если сторона a = 15 и угол A = 41°, мы можем использовать синус и тангенс, чтобы найти гипотенузу и другую сторону.Поскольку sin A = a/c, мы знаем, что c = a /sin A = 15/sin 41. С помощью калькулятора получается 15/0,6561 = 22,864. Кроме того, tan A = a/b, , поэтому b = a /tan A = 15/tan 41 = 15/0,8693 = 17,256. Используете ли вы синус, косинус или тангенс, зависит от того, какую сторону и угол вы знаете.
Обратные триггерные функции: арксинус, арккосинус и арктангенс
Теперь давайте рассмотрим задачу нахождения углов, если известны стороны.Опять же, вы используете триггерные функции, но наоборот. Вот пример. Предположим, что a = 12,3 и b = 50,1. Тогда тангенс A = a/b = 12,3/50,1 = 0,2455. Раньше, когда люди использовали таблицы триггерных функций, они просто смотрели в таблицу тангенсов, чтобы увидеть, какой угол имеет тангенс 0,2455. На калькуляторе мы используем обратные триггерные функции, называемые арктангенс, арксинус и арккосинус. Обычно на калькуляторе есть кнопка с надписью «inv» или «arc», которую вы нажимаете перед нажатием соответствующей кнопки триггера.Арктангенс 0,2455 равен 13,79, поэтому угол A равен 13,79°. (Если хотите, вы можете преобразовать 0,79 градуса в минуты и секунды.)
На калькуляторе мы используем обратные триггерные функции, называемые арктангенс, арксинус и арккосинус. Обычно на калькуляторе есть кнопка с надписью «inv» или «arc», которую вы нажимаете перед нажатием соответствующей кнопки триггера.Арктангенс 0,2455 равен 13,79, поэтому угол A равен 13,79°. (Если хотите, вы можете преобразовать 0,79 градуса в минуты и секунды.)Вот и все.
Остальные три тригонометрические функции: котангенс, секанс и косеканс
Для большинства целей достаточно трех триггерных функций: синуса, косинуса и тангенса. Однако бывают случаи, когда нужны какие-то другие. В исчислении часто используется секанс. Вы можете спросить: «Почему шесть триггерных функций?» Это своего рода симметрия.Есть шесть способов сделать отношения двух сторон прямоугольного треугольника, и это дает шесть функций:- sin A = a/c (opp/hyp)
- cos A = b/c (adj/hyp)
- tan A = a/b (opp/adj)
- детская кроватка A = b/a (adj/opp)
- сек A = c/b (hyp/adj)
- csc A = c/a (hyp/opp)
 Они в значительной степени избыточны, но стоит знать, что они собой представляют на случай, если вы столкнетесь с ними. Обратите внимание, что котангенсы являются тангенсами дополнительных углов, а это означает, что cot A = tan B, , а косекансы являются секущими дополнительных углов, а это означает, что csc A = sec B.
Они в значительной степени избыточны, но стоит знать, что они собой представляют на случай, если вы столкнетесь с ними. Обратите внимание, что котангенсы являются тангенсами дополнительных углов, а это означает, что cot A = tan B, , а косекансы являются секущими дополнительных углов, а это означает, что csc A = sec B. Эти три другие функции также можно интерпретировать с помощью единичной круговой диаграммы.
Мы рассматриваем угол AOB. Напомним, что его касательной является прямая AC. По симметрии тангенсом угла FOB является прямая FG, , но FOB является дополнительным углом AOB, , следовательно, котангенс угла AOB равен FG.
Далее, интерпретировать секущие геометрически. Угол AOB появляется в треугольнике COA как угол AOC, so sec AOB = sec AOC = hyp/adj = OC/OA = Итак, секанс — это линия, проведенная из центра круга к касательной AC. Причина, по которой его называют секущим, заключается в том, что он пересекает круг, а слово «секанс» происходит от латинского слова, означающего «разрезание».
Причина, по которой его называют секущим, заключается в том, что он пересекает круг, а слово «секанс» происходит от латинского слова, означающего «разрезание».
Аналогично, косекансом угла АОВ является прямая ОГ , проведенная из центра окружности к прямой котангенс ФГ.
Упражнения
Примечание: как обычно, во всех упражнениях на прямоугольные треугольники c обозначают гипотенузу, a и b перпендикулярные стороны, A и B углы, противоположные a и б соответственно. 26. В каждом из следующих прямоугольных треугольников, две стороны которых заданы, вычислите sin, cos и тангенс углов A и B. Выразите результаты в виде обыкновенных дробей.
(и). c = 41, a = 9.
(ii). c = 37, a = 35.
(iii). a = 24, b = 7.
31. В прямоугольном треугольнике c = 6 футов 3 дюйма и загар B = 1. 2. Найдите a и b.
2. Найдите a и b.
34. a = 1,2, b = 2,3. Найти A и c.
42. a = 10,11, b = 5,14. Найти B и c.
В следующих нескольких задачах треугольники не являются прямоугольными, но вы можете решить их, используя свои знания о прямоугольных треугольниках.
61. В косоугольном треугольнике ABC, A = 30°, B = 45°, а перпендикуляр из C на AB имеет длину 12 дюймов. Найдите длину АВ.
67. Если сторона равностороннего треугольника равна а, найти высоту и радиусы описанной и вписанной окружностей.
202. От вершины здания высотой 50 футов углы возвышения и углубления вершины и низа другого здания составляют 19° 41′ и 26° 34′ соответственно.Каковы высота и расстояние до второго здания.
207. С вершины маяка высотой 175 футов углы наклона вершины и низа флагштока составляют 23° 17′ и 42° 38′ соответственно. Какой высоты столб?
Какой высоты столб?
214. В двух точках на расстоянии 65 футов друг от друга на одной стороне дерева и на одной линии с ним углы возвышения вершины дерева составляют 21° 19′ и 16° 20′. Найдите высоту дерева.
215. Когда воздушный шар проходит между двумя точками A и B, находящимися на расстоянии 2 миль друг от друга, углы места воздушного шара в этих точках составляют 27° 19′ и 41° 45′ соответственно. Найдите высоту воздушного шара. Возьмите A и B одного уровня.
233. Верхняя часть маяка находится на высоте 230 футов над уровнем моря. Как далеко находится объект, который находится «на горизонте»? [Предположим, что Земля — это сфера радиусом 3956 миль.]
234. На какой высоте должен находиться наблюдатель, чтобы он мог видеть объект на земле в тридцати милях от него? Предположим, что Земля представляет собой гладкий шар.
В каждой из фигур, названных в следующих нескольких задачах, объект должен выразить свою площадь (i) через радиус R, , то есть радиус описанной окружности, (ii) через апофема r, , то есть радиус вписанной окружности, и (iii) по стороне a.
251. Равносторонний треугольник. [См. задачу 67 выше.]
252. Квадрат.
253. Правильный пятиугольник.
254. Правильный шестигранник.
255. Правильный восьмиугольник.
Советы
26. Вам нужны только sin, cos и тангенс углов A и B ; вам не нужны сами углы.Таким образом, вам нужна только третья сторона, которую вы можете вычислить с помощью теоремы Пифагора, а затем взять отношения двух сторон.
31. Вы знаете c и tan B. К сожалению, tan B — это отношение двух неизвестных вам сторон, а именно b/a. Существует несколько способов решения этой проблемы. Вот два.
Метод 1. Возьмем уравнение 1.2 = tan B = b/a, , чтобы получить соотношение между a и b, , а именно b = 1.2 а. Теорема Пифагора дает 6,25 2 = a 2 + 1,44 a 2 , из которых можно определить a, и затем найти 9
Способ 2.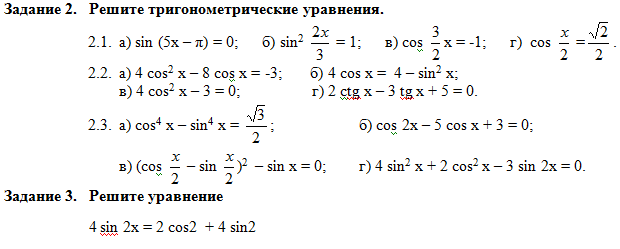 Из тангенса B, можно определить угол B (используйте арктангенс). Отсюда вы можете найти cos B, и затем a, и вы можете найти sin B, и затем b.
Из тангенса B, можно определить угол B (используйте арктангенс). Отсюда вы можете найти cos B, и затем a, и вы можете найти sin B, и затем b.
34. Поскольку у вас есть a и b, , вы можете использовать тангенсы, чтобы найти A , и теорему Пифагора, чтобы найти c.
42. Найдите B по касательной и c по теореме Пифагора.
61. Начните с рисования фигуры. Хотя треугольник ABC не является прямоугольным, он распадается на два прямоугольных треугольника. Вы можете использовать касательные, чтобы найти две части стороны AB и сложить их вместе.
67. Равносторонний треугольник ABC имеет три угла при вершине по 60°. Отбросьте перпендикуляр из одной вершины, скажем, вершины C, , и вы получите два конгруэнтных прямоугольных треугольника ACF и BCF, , и вы можете найти длину этого перпендикуляра, а это высота равностороннего треугольника. Описанная окружность — это та, которая проходит через три вершины, а вписанная окружность — это та, которая касается внутри трех сторон.Отбрасывая перпендикуляры из другой вершины равностороннего треугольника и применяя тригонометрию к полученным маленьким треугольникам, можно найти радиусы этих двух окружностей.
Описанная окружность — это та, которая проходит через три вершины, а вписанная окружность — это та, которая касается внутри трех сторон.Отбрасывая перпендикуляры из другой вершины равностороннего треугольника и применяя тригонометрию к полученным маленьким треугольникам, можно найти радиусы этих двух окружностей.
202. Зная высоту вашего здания и угол наклона к основанию другого здания, вы можете определить, насколько далеко оно находится. Тогда угол подъема на вершину другого здания скажет вам, насколько оно выше вашего.
207. Подсказка похожа на 202. Смотрите, триггер может быть полезен, если вы одинокий смотритель маяка и не знаете, что делать!
214. Это полезная задача. Вы можете использовать его, чтобы найти высоты недоступных вещей. Нарисуйте фигуру. Есть два неизвестных: высота х дерева и расстояние х ближайшей к дереву точки. Дальнейшая точка будет x + 65 футов от дерева. Используя тангенсы известных углов, вы можете составить два уравнения, которые можно решить для определения y и x.
215. Это похоже на 214, но в этой задаче шарик лежит между двумя точками. Нарисуйте фигуру. Определите свои переменные. Составьте уравнения и решите их.
233. Очень интересная задача. Различные его обратные значения использовались на протяжении веков для вычисления радиуса Земли. В этой задаче мы предполагаем, что знаем о Земле. Все, что вам нужно здесь, это теорема Пифагора. Одна сторона прямоугольного треугольника равна r, радиус Земли, а гипотенуза равна r + h , где h — высота маяка.Теорема Пифагора третья сторона треугольника.
234. Постановка этой задачи аналогична 233, но известны другие переменные.
251–255. Вы можете сделать все это сразу, оставив вычисления напоследок. Пусть n — количество сторон правильного многоугольника. Проведите линии от центра фигуры к вершинам и к серединам сторон. У вас получится 2 n маленьких треугольников. Каждый из них представляет собой прямоугольный треугольник с гипотенузой R, , один катет r, , а другой катет a /2. Угол в центре равен 360°/(2 n ) = 180°/ n. Используя тригонометрию, вы можете легко написать уравнения, связывающие площадь правильного многоугольника по мере необходимости.
Угол в центре равен 360°/(2 n ) = 180°/ n. Используя тригонометрию, вы можете легко написать уравнения, связывающие площадь правильного многоугольника по мере необходимости.
Ответы
26. (и). b = 40. Итак, SIN A = COS B = 9/41, COS A = SIN B = 40/41, Tan A = 9/40, Tan B = 40 /9.(ii). B = 12. Итак, SIN A = COS B = 35/37, COS A = SIN B = 12/37, TAN A = 35/12, Tan B = 12 /37.
(iii). C = 25. Так что SIN A = COS B = 24/25, COS A = SIN B = 7/25, Tan A = 24/7, Tan B = 7 /24.
31. a = 4 фута, b = 4,8 фута, около 4 футов 10 дюймов.
34. A = 27,55°, около 28°. c = 2,6.
42. B = 26,95° или 26°57′. c = 11.3.
61. AB = 12/тангенс A + 12/тангенс B = 12(√3 + 1) дюймов, примерно 33 дюйма.
67. ( a √3)/2, ( a √3)/3 и ( a √3)/6 соответственно.
202. Расстояние = 50/тангенс 26°34′ = 100 футов. Высота = 50 + 100 tan 19°41′ = 85,8′ = 85’9″.
207. Расстояние = 175/тангенс 42°38′ = 190 футов. Рост = 175–190°, тангенс 23°17’ = 93°.23 фута = 9 футов 3 дюйма.
214. Два уравнения
- 0,293052 = тангенс 16°20′ = ч /(65 + x ), и
0,3
= тангенс 21°19′ = ч/х .
Расстояние х = 196 футов. Высота ч = 76,5 футов.
215. Если ч — это высота шара, а х — это расстояние по земле от А до точки непосредственно под шаром, то два эквариона равны
- тангенс 27°19′ = ч/х и
тангенс 41°45′ = ч / (2 — x )

Высота = 0,654 мили = 3455 футов.
233. Мелочь больше 18.5 миль.
234. 600 футов.
251–255. Площадь правильного n -угольника равна A = nra /2. Чтобы найти A через R, r, или a, , используйте соотношения
- cos 180°/ n = r/R, и
тангенс 180°/ n = a /(2 r ).
- (i) в пересчете на R, площадь A = nR 2 cos 180°/ n sin 180°/ n ,
- Ответить
Фактор как \[\left(2\sin (t)+1\right)\left(\sin (t)+1\right)=0\nonnumber\]
\[2\sin (t)+1= 0\text{ at }t=\dfrac{7\pi }{6} ,\dfrac{11\pi }{6}\nonumber\]
\[\sin (t)+1=0\text{ at } t=\dfrac{3\pi }{2}\nonumber\]
\[t=\dfrac{7\pi }{6},\dfrac{3\pi }{2},\dfrac{11\pi} {6}\номер\]- Обзор идентификаторов триггеров
- Решение триггерных уравнений
- Факторинг
- Использование квадратичной формулы
- Использование идентификаторов триггеров для упрощения
(ii) в пересчете на r, площадь A = nr 2 tan 180°/ n , и
(iii) в пересчете на а, площадь A = na 2 /(4tan 180°/ n ).
| Проблема | Форма | (I) R | (II) R | (III) A |
|---|---|---|---|---|
| 251 | Треугольник | (3 R 2 √3)/4 | 3 р 2 √3 | ( a 2 √3)/4 |
| 252 | квадратный | 2 Р 2 | 4 р 2 | a 2 |
| 253 | пятиугольник | (5 R 2 sin 108°)/2 | 5 r 2 tan 36° | (5 a 2 tan 54°)/4 |
| 254 | шестигранник | (3 Р 2 √3)/2 | 2 р 2 √3 | (3 a 2 √3)/2 |
| 255 | восьмиугольник | 2 Р 2 √2 | 8 r 2 tan 22°30′ | 2 a 2 tan 67°30′ |
Отступление от троек Пифагора
Это не имеет ничего общего с тригонометрией, но это интересно. Вы, наверное, заметили, как Кроули часто выбирал две стороны прямоугольного треугольника целыми числами, а третья тоже оказывалась целым числом. Как в задаче 26, где стороны всех трех прямоугольных треугольников были целыми числами, а именно 9:40:41, 12:35:37 и 7:24:25. Кроме того, в начале этой страницы был треугольник 5:12:13 (на самом деле 10:24:26, но он похож на треугольник 5:12:13). И, без сомнения, вы уже знаете о прямоугольном треугольнике 3:4:5.
Вы, наверное, заметили, как Кроули часто выбирал две стороны прямоугольного треугольника целыми числами, а третья тоже оказывалась целым числом. Как в задаче 26, где стороны всех трех прямоугольных треугольников были целыми числами, а именно 9:40:41, 12:35:37 и 7:24:25. Кроме того, в начале этой страницы был треугольник 5:12:13 (на самом деле 10:24:26, но он похож на треугольник 5:12:13). И, без сомнения, вы уже знаете о прямоугольном треугольнике 3:4:5.Итак, существуют ли другие специальные прямоугольные треугольники, все стороны которых являются целыми числами? Да и изучались они давно.Три цифры A, B, и C такие, что A 2 + B 2 = C 2 Он жил около 550 г. до н. э. и, вероятно, знаю немало из них. Но древние вавилоняне около 1800 г. до н. э. знали их все, и многие были известны в других древних цивилизациях, таких как Китай и Индия.
Прежде чем читать абзац, посмотрите, сможете ли вы найти еще несколько пифагорейских троек. Не считайте за новые те, у которых есть общий множитель, например 6:8:10, так как они будут похожи на меньшие.
Не считайте за новые те, у которых есть общий множитель, например 6:8:10, так как они будут похожи на меньшие.
В « элементах » Евклида есть описание всех возможных пифагорейских троек. Вот современный парафраз Евклида. Возьмем любые два нечетных числа m и n, с m n и взаимно простые (то есть без общих множителей). Пусть a = мн, = млн., . 2 )/2.Тогда a : b : c — пифагорейская тройка. Например, если взять м = 1, а n = 3, то получится наименьшая пифагорейская тройка 3:4:5.
Нахождение тригонометрических корней — Тригонометрия
Если вы считаете, что контент, доступный с помощью Веб-сайта (как это определено в наших Условиях обслуживания), нарушает одно
или более ваших авторских прав, пожалуйста, сообщите нам, предоставив письменное уведомление («Уведомление о нарушении»), содержащее
в
информацию, описанную ниже, назначенному агенту, указанному ниже. Если университетские наставники примут меры в ответ на
ан
Уведомление о нарушении, он предпримет добросовестную попытку связаться со стороной, предоставившей такой контент
средства самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.
Если университетские наставники примут меры в ответ на
ан
Уведомление о нарушении, он предпримет добросовестную попытку связаться со стороной, предоставившей такой контент
средства самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.
Ваше Уведомление о нарушении может быть направлено стороне, предоставившей контент, или третьим лицам, таким как в виде ChillingEffects.org.
Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатов), если вы существенно искажать информацию о том, что продукт или деятельность нарушают ваши авторские права.Таким образом, если вы не уверены, что содержимое находится на Веб-сайте или на который ссылается Веб-сайт, нарушает ваши авторские права, вам следует сначала обратиться к адвокату.
Чтобы подать уведомление, выполните следующие действия:
Вы должны включить следующее:
Физическая или электронная подпись владельца авторских прав или лица, уполномоченного действовать от его имени;
Идентификация авторских прав, которые, как утверждается, были нарушены;
Описание характера и точного местонахождения контента, который, как вы утверждаете, нарушает ваши авторские права, в \
достаточно подробно, чтобы преподаватели университета могли найти и точно идентифицировать этот контент; например, мы требуем
а
ссылку на конкретный вопрос (а не только название вопроса), который содержит содержание и описание
к какой конкретной части вопроса — изображению, ссылке, тексту и т. д. — относится ваша жалоба;
Ваше имя, адрес, номер телефона и адрес электронной почты; и
Заявление от вас: (а) что вы добросовестно полагаете, что использование контента, который, как вы утверждаете, нарушает
ваши авторские права не разрешены законом или владельцем авторских прав или его агентом; б) что все
информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство вы
либо владельцем авторских прав, либо лицом, уполномоченным действовать от их имени.
д. — относится ваша жалоба;
Ваше имя, адрес, номер телефона и адрес электронной почты; и
Заявление от вас: (а) что вы добросовестно полагаете, что использование контента, который, как вы утверждаете, нарушает
ваши авторские права не разрешены законом или владельцем авторских прав или его агентом; б) что все
информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство вы
либо владельцем авторских прав, либо лицом, уполномоченным действовать от их имени.
Отправьте жалобу нашему назначенному агенту по адресу:
Чарльз Кон
Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105
Или заполните форму ниже:
Решение тригонометрических уравнений — Математические видео от Brightstorm
Концепция (1)
Когда решая тригонометрические уравнения , мы находим все углы, которые делают уравнение верным. Если интервал не указан, используйте периодичность, чтобы показать бесконечное число решений. Два способа визуализации решений: (1) график в координатной плоскости и (2) единичный круг. Единичный круг является более полезным из двух для получения ответа.
Если интервал не указан, используйте периодичность, чтобы показать бесконечное число решений. Два способа визуализации решений: (1) график в координатной плоскости и (2) единичный круг. Единичный круг является более полезным из двух для получения ответа.
Примеры проблем (3)
Нужна помощь с задачами «Решение тригонометрических уравнений»? Наблюдайте за тем, как опытные преподаватели решают аналогичные задачи, чтобы развивать свои навыки.
Проблема 1
Как решить простое косинусное уравнение: cos x = — квадратный корень(2)/2.
Задача 2
Как решить простое уравнение касательной: tan(x/4)=1.
Задача 3
Как решить простое тригонометрическое уравнение с секущей. {2} (t)+\sin (t)=0\) для всех решений с \(0\le t<2\pi\).
{2} (t)+\sin (t)=0\) для всех решений с \(0\le t<2\pi\).
Раствор
Это уравнение похоже на квадратное уравнение, но с sin( t ) вместо алгебраической переменной (мы часто называем такое уравнение «квадратным по синусу»). Как и со всеми квадратными уравнениями, мы можем использовать методы факторинга или квадратную формулу. Это выражение прекрасно факторизуется, поэтому мы продолжаем выносить на множитель sin(\(t\)):
\[\sin (t)\left(2\sin (t)+1\right)=0\nonnumber\]
Используя теорему о нулевом произведении, мы знаем, что произведение слева будет равно нулю, если любой из множителей равен нулю, что позволяет нам разбить это уравнение на два случая:
\[\sin (t)=0\text{ или}2\sin (t)+1=0\nonnumber\]
Мы можем решить каждое из этих уравнений независимо, используя наши знания о специальных углах.
\[\sin (t)=0\нечисло\]
\[2\sin (t)+1=0\нечисло\]
\[t = 0\текст{ или }t = \pi\нечисло\]
\[\sin (t)=-\dfrac{1}{2}\nonumber\]
\[t=\dfrac{7\pi }{6}\text{ или }t=\dfrac{11\pi {6}\номер\]
Вместе это дает нам четыре решения уравнения относительно \(0\le t<2\pi\):
\[t=0,\pi ,\dfrac{7\pi }{6} ,\dfrac{11\pi }{6}\номер\]
Мы могли бы проверить правильность этих ответов, построив график функции и сравнив нули. {2} -5u-2=(3u+1)(u-2)\номер\]
{2} -5u-2=(3u+1)(u-2)\номер\]
Отмена замены,
\[(3\сек (т)+1)(\сек (т)-2)=0\номер\]
Поскольку произведение равно нулю, разобьем его на два случая и решим каждый отдельно.
\[3\sec (t)+1=0\nonnumber\]Изолировать секанс
\[\sec (t)=-\dfrac{1}{3}\nonnumber\]Переписать как косинус
\[\ dfrac{1}{\cos (t)} =-\dfrac{1}{3}\nonumber\]Инвертировать обе стороны
\[\cos (t)=-3\nonumber\]
Поскольку косинус имеет диапазон [-1, 1], косинус никогда не примет выходное значение -3.В этом случае нет решений.
Продолжаем второй случай,
\[\sec (t)-2=0\nonnumber\]Изолировать секанс
\[\sec (t)=2\nonumber\]Переписать как косинус
\[\dfrac{1}{\cos (t )} =2\nonumber\]Обратить обе стороны
\[\cos (t)=\dfrac{1}{2}\nonumber\]Это дает два решения
\[t=\dfrac{\pi }{3} \text{ или}t=\dfrac{5\pi }{3}\nonumber\]
Это единственные два решения на интервале.
Используя технологию построения графика \(f(t)=3\sec ^{2} (t)-5\sec (t)-2\), взгляд на график подтверждает, что для этой функции есть только два нуля на интервал [0, 2 \(\pi\)), что гарантирует нам, что мы ничего не пропустили. {2} (t)+3\sin (t)+1=0\) для всех решений с \(0\le t<2\pi\).
{2} (t)+3\sin (t)+1=0\) для всех решений с \(0\le t<2\pi\).
При решении некоторых тригонометрических уравнений возникает необходимость сначала переписать уравнение с использованием тригонометрических тождеств.{2} (t)+\cos (t)-1=0\nonumber\]Коэффициент
\[\left(2\cos (t)-1\right)\left(\cos (t)+1\right )=0\номер\]
Этот продукт будет равен нулю, если любой из множителей равен нулю, поэтому мы можем разбить это на два отдельных случая и решить каждый независимо.
\[2\cos (t)-1=0\text{ или }\cos (t)+1=0\не число\]
\[\cos (t)=\dfrac{1}{2}\text { или }\cos (t)=-1\nonumber\]
\[t=\dfrac{\pi }{3}\text{ или }t=\dfrac{5\pi }{3}\text{ или }t=\pi\номер\]
Упражнение \(\PageIndex{3}\)
Решите \(2\sin ^{2} (t)=3\cos (t)\) для всех решений с \(0\le t<2\pi\). {2} (t)+3\cos (t)-2=0\не число\]
{2} (t)+3\cos (t)-2=0\не число\]
\[\left(2\cos (t)-1\right)\left(\cos (t)+2\right )=0\nonumber\]
\(\cos (t)+2=0\) не имеет решений \(2\cos (t)-1=0\) в точке \(t=\dfrac{\pi }{ 3} ,\dfrac{5\pi }{3}\)
В дополнение к тождеству Пифагора часто бывает необходимо переписать тангенс, секанс, косеканс и котангенс как часть решения уравнения.
Пример \(\PageIndex{4}\)
Решите \(\tan (x)=3\sin (x)\) для всех решений с \(0\le x<2\pi\).
Раствор
Используя комбинацию тангенса и синуса, мы могли бы попробовать переписать тангенс
\[\tan (x)=3\sin (x)\nonumber\]
\[\dfrac{\sin (x)}{\cos (x)} =3\sin (x)\nonumber\]Умножение обе стороны по косинусу
\[\sin (x)=3\sin (x)\cos (x) \nonnumber\]
В этот момент у вас может возникнуть соблазн разделить обе части уравнения на sin(\(x\)).
Сопротивляйтесь желанию . Когда мы делим обе части уравнения на количество, мы предполагаем, что количество никогда не равно нулю. В этом случае, когда sin(\(x\)) = 0, уравнение выполняется, поэтому мы потеряем эти решения, если будем делить на синус.
В этом случае, когда sin(\(x\)) = 0, уравнение выполняется, поэтому мы потеряем эти решения, если будем делить на синус.
Чтобы избежать этой проблемы, мы можем изменить уравнение так, чтобы одна сторона была равна нулю (технически можно разделить на на sin( x ), если вы отдельно рассматриваете случай, когда sin( x ) = 0. Поскольку этот шаг легко забыть, рекомендуется метод факторинга, использованный в примере).
\[\sin (x)-3\sin (x)\cos (x)=0\nonumber\]Разложение sin(\(x\)) из обеих частей
\[\sin (x)\left( 1-3\cos (x)\right)=0 \nonnumber\]
Отсюда видно, что мы получаем решения, когда \(\sin (x)=0\) или \(1-3\cos (x)=0\).{-1} \left(\dfrac{1}{3} \right)\приблизительно 1,231\nonumber\]Использование симметрии для поиска второго решения
\[x=2\pi -1,231=5,052 \nonumber\]
У нас есть четыре решения на \(0 \le x<2\pi\):
\[x = 0, 1,231, \quad\pi , 5,052\не число\]
Пример \(\PageIndex{3}\)
Решите \(\sec (\theta )=2\cos (\theta )\), чтобы найти первые четыре положительных решения.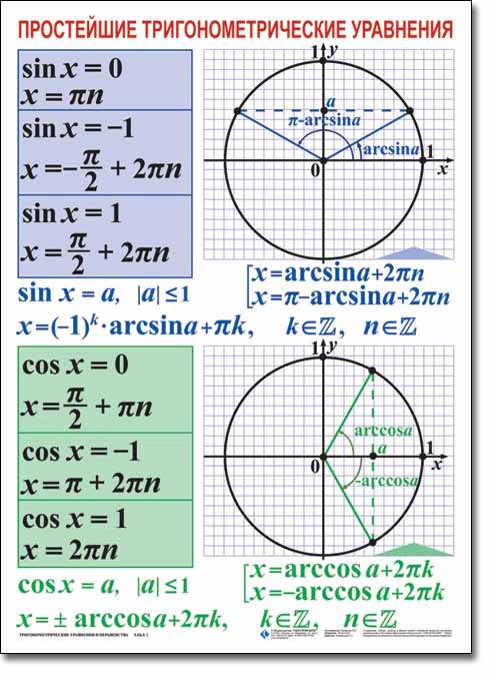 {2} (\theta )} +3\cos \left(\theta \right)=2\cot \left(\theta \right)\tan \left( \theta \right)\) для всех решений с \(0\le \theta <2\pi\).{-1} \left(0,425\right)=1,131\nonumber\] По симметрии можно найти второе решение
{2} (\theta )} +3\cos \left(\theta \right)=2\cot \left(\theta \right)\tan \left( \theta \right)\) для всех решений с \(0\le \theta <2\pi\).{-1} \left(0,425\right)=1,131\nonumber\] По симметрии можно найти второе решение
\[\theta =2\pi -1,131=5,152\nonumber\]
Важные темы этого раздела
Решение тригонометрических уравнений с бесконечными решениями — видео и расшифровка урока
Бесконечные решения
У тригонометрических уравнений есть одна интересная особенность.И это то, что они имеют бесконечное количество решений. Вы можете подумать, что это звучит странно, тем более что ваш калькулятор выдает только один ответ. Давайте посмотрим на график функции синуса и вы увидите кое-что интересное:
Видишь волны? Да, наша синусоидальная функция отображается в виде волн. Вы видите, что эти волны продолжают пересекать нашу ось x ? Итак, каждый раз, когда наш график пересекает ось x , когда y = 0, это дает нам другое решение.Этот график будет продолжаться вечно. Когда вы вычисляете обратные триггерные функции в своем калькуляторе, вы получаете ответ, ближайший к началу координат. Итак, если бы я хотел решить sin x = 0 , я бы взял арксинус 0. Я получаю ответ 0 на своем калькуляторе, но на самом деле sin x = 0 имеет бесконечное количество решений. Как вы можете видеть на графике, я получаю 0 для sin x через каждые 2pi пробела. Итак, мои ответы на самом деле таковы: x = 0 + 2*pi*n , где n означает количество дополнительных решений, которые у нас есть. N каждый раз увеличивается на 1. Мы получаем x = 0 + 2*pi*0 = 0 для нашего первого решения. Следующее решение: x = 0 + 2*pi*1 = 2pi . Следующий x = 0 + 2*pi*2 = 4pi . И так далее.
Вы видите, что эти волны продолжают пересекать нашу ось x ? Итак, каждый раз, когда наш график пересекает ось x , когда y = 0, это дает нам другое решение.Этот график будет продолжаться вечно. Когда вы вычисляете обратные триггерные функции в своем калькуляторе, вы получаете ответ, ближайший к началу координат. Итак, если бы я хотел решить sin x = 0 , я бы взял арксинус 0. Я получаю ответ 0 на своем калькуляторе, но на самом деле sin x = 0 имеет бесконечное количество решений. Как вы можете видеть на графике, я получаю 0 для sin x через каждые 2pi пробела. Итак, мои ответы на самом деле таковы: x = 0 + 2*pi*n , где n означает количество дополнительных решений, которые у нас есть. N каждый раз увеличивается на 1. Мы получаем x = 0 + 2*pi*0 = 0 для нашего первого решения. Следующее решение: x = 0 + 2*pi*1 = 2pi . Следующий x = 0 + 2*pi*2 = 4pi . И так далее.
Период
Этот интервал представляет собой период . Это зависит от используемой нами триггерной функции. Функции синуса и косинуса имеют период 2pi. Это означает, что ваши ответы находятся на расстоянии 2pi друг от друга. Касательная функция, с другой стороны, имеет период пи.Это означает, что эти ответы находятся на расстоянии пи друг от друга. Это стандартные периоды наших триггерных функций. Эти периоды можно изменить, если наше тригонометрическое уравнение будет более сложным. Но мы не будем обсуждать это в этом видеоуроке.
Это зависит от используемой нами триггерной функции. Функции синуса и косинуса имеют период 2pi. Это означает, что ваши ответы находятся на расстоянии 2pi друг от друга. Касательная функция, с другой стороны, имеет период пи.Это означает, что эти ответы находятся на расстоянии пи друг от друга. Это стандартные периоды наших триггерных функций. Эти периоды можно изменить, если наше тригонометрическое уравнение будет более сложным. Но мы не будем обсуждать это в этом видеоуроке.
Итак, в этом видеоуроке сосредоточьтесь на изучении стандартного периода функций синуса, косинуса и тангенса. Просто помните, что синус и косинус имеют общий период 2pi , а тангенс (который не похож на два других) имеет период всего pi .
Пример
Давайте теперь посмотрим, как мы используем эту информацию.
Решите 2 cos x — 1 = 0.
Чтобы решить эту проблему, мы используем наши навыки алгебры, чтобы сначала выделить cos x. Сначала мы добавляем 1 к обеим частям, а затем делим на 2. Получаем , потому что x = 1/2 . Теперь мы можем использовать наш калькулятор, чтобы выполнить функцию арккосинуса, чтобы изолировать x , или мы можем перейти к нашей единичной окружности, чтобы увидеть, какие углы дадут ответ 1/2 для нашей функции косинуса.-1 (1/2) = 1,047 или пи/3 . Однако, глядя на наш единичный круг, мы видим, что на самом деле есть два угла, которые дадут нам ответ 1/2 для нашей функции косинуса. У нас есть пи/3 и 5пи/3 . Почему это? Что ж, перейдем к графу:
Получаем , потому что x = 1/2 . Теперь мы можем использовать наш калькулятор, чтобы выполнить функцию арккосинуса, чтобы изолировать x , или мы можем перейти к нашей единичной окружности, чтобы увидеть, какие углы дадут ответ 1/2 для нашей функции косинуса.-1 (1/2) = 1,047 или пи/3 . Однако, глядя на наш единичный круг, мы видим, что на самом деле есть два угла, которые дадут нам ответ 1/2 для нашей функции косинуса. У нас есть пи/3 и 5пи/3 . Почему это? Что ж, перейдем к графу:
Посмотрите на часть графика, которая пересекает ось y , часть графика, которая изгибается вверх от y = 0, а затем снова возвращается к y = 0, и вы обратите внимание, что есть два места, где мы получаем y = 1/2.Это означает, что у нас есть два основных решения. Итак, нахождение ответов из единичного круга дает нам общее количество решений.
Помните, нам нужно учитывать период нашей функции косинуса. Наши решения повторяются каждые 2pi пробела. Итак, наш полный ответ: x = pi/3 + 2*pi*n и x = 5pi/3 + 2*pi*n .
Если наш период равен просто пи, то вместо a + 2*pi*n у нас будет a + pi*n .
Итоги урока
Давайте повторим, что мы узнали. Тригонометрические уравнения — это уравнения, включающие тригонометрические функции. Наши триггерные функции — это функции синуса, косинуса, тангенса и их обратных величин, косеканс, секанс и котангенс.
Одной интересной особенностью тригонометрических уравнений является то, что они имеют бесконечное число решений. Для функций синуса и косинуса решения повторяются через каждые 2pi. Для функции тангенса она повторяет каждое число пи. Этот интервал называется периодом .При решении тригонометрических уравнений лучше использовать единичный круг, чтобы можно было найти все ответы.
Иногда есть два основных решения.

 2 x + \sin x = \sqrt2 \sin\left( x + \dfrac{\pi}{4} \right)$.
2 x + \sin x = \sqrt2 \sin\left( x + \dfrac{\pi}{4} \right)$. 2 x + 5\sin\left( \dfrac{\pi}{2} — x\right) — 2 = 0$.
2 x + 5\sin\left( \dfrac{\pi}{2} — x\right) — 2 = 0$. Если вы выводите с трудом и долго, считайте, что вам повезло — вы нашли то самое место, куда надо прикладывать усилия для получения результата. Скоро научитесь делать это быстро. (Однако если Вам предстоит экзамен, перед экзаменом подзубрите формулы.)
Если вы выводите с трудом и долго, считайте, что вам повезло — вы нашли то самое место, куда надо прикладывать усилия для получения результата. Скоро научитесь делать это быстро. (Однако если Вам предстоит экзамен, перед экзаменом подзубрите формулы.)