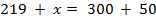Урок математики в 4 классе «Решение уравнений нового вида» — Разработки уроков — Методические разработки — Методические разработки
Корякова Людмила Николаевна, учитель начальных классов
Урок математики
в 4 классе
Тема: Решение уравнений нового вида.
Цель: Способствовать развитию умения решать сложные уравнения, где неизвестное выражено суммой или разностью чисел.
Задачи:
· формировать умения решать сложные уравнения, где неизвестное выражено суммой или разностью чисел;
· развивать логическое мышление и умение анализировать;
· применять элементы здоровьесберегающих технологий на уроке;
· воспитывать коллективизм, взаимопомощь.
Тип урока: Усвоение новых знаний.
Оборудование: Карточки уравнений; карточка с геометрическим материалом; доска; учебник.
Ход урока:
I. Организационный момент:
1. Приветствие гостей.
2. Упражнение на развитие внимания, памяти: Я покажу вам карточку и буду держать её 5 секунд. Назовите по порядку, какие вы запомнили предметы. Сколько их? (на карточке треугольник, квадрат, круг, прямоугольник, овал)
3. Я желаю получить такую оценку каждому из вас на уроке.
— А для этого надо отгадать эти анаграммы и вы узнаете, чем мы будем заниматься сегодня на уроке.
Анаграммы: ЕШАРЬТ ТОАГЫДАВЬТ МСЕТЬАК
(решать) (отгадывать) (смекать)
II. Актуализация знаний. Устный счет.
1. — Назови компоненты при сложении. Как найти неизвестное слагаемое?
— Как называются компоненты при вычитании?
— Как найти уменьшаемое? Вычитаемое?
2. Даны выражения, подумайте с чего начинается решение выражений, где больше чем одно действие (с порядка действий):
Задание: расставь действия в выражениях
a + b – (d + k) : m – n
3 4 1 2 5
500 – (280 + 120) = 100
2 1
(600 – 327) + 27 = 300
1 2
3. Реши задачи:
А) К неизвестному числу прибавить 700 и получится сумма 1800
1. Составь уравнение.
2. Чему равно неизвестное число?
Х + 700 = 1800
Х = 1100
Б) Из неизвестного числа вычли 60 и получили разность 150
1. Составь уравнение.
2. Чему равно неизвестное число?
Х – 60 = 150
III. Решение уравнений.
Мы с вами повторили решение простых уравнений, теперь переходим к решению более сложных.
У доски:
120 + Х = 200 – 75
120 + Х = 125
Х = 125 – 120
Х = 5
120 + 5 = 200 – 75
125 = 125
IV. Физминутка «Близнецы»
Дети встают между партами, кладут друг другу руки на плечи и закрывают глаза. По моему сигналу они выполняют следующие команды:
· присесть
· встать
· встать на пальчики, опуститься
· наклониться влево
· наклониться вправо
· прогнуться назад
· постоять на правой ноге, согнув левую ногу в колене
· постоять на левой ноге, согнув правую ногу в колене
· открыть глаза и тихо сесть
Задание на ошибку:
(х + 29) – 48 = 90
Диалог:
· Что случилось?
· Что вы увидели нового для себя?
· Какая возникла проблема?
· Давайте попробуем её решить?
Составление плана решения уравнения:
1. Расставим порядок действий. Если бы это был пример, с чего бы вы начали его решение?
(х + 29) – 48 = 90
1 2
2. Установим название компонентов по последнему действию. Где находится неизвестное число?
(х + 29) – 48 = 90
3. Вырази чему равен неизвестный компонент?
Х + 29 = 90 + 48 – такое уравнение мы умеем решать?
Х + 29 = 138 – получили простое уравнение.
Х = 138 – 29
Х = 109
(109 + 29) – 48 = 90
1 2
90 = 90
4. Так чем мы будем заниматься сегодня на уроке? (Решать уравнения нового вида, где неизвестное выражено суммой или разностью)
V. Еще раз назовите тему нашего урока? (Решение уравнений нового вида)
Повторим алгоритм решения уравнений:
1. Расстановка порядка действий.
2. Установление названия компонентов по последнему действию.
3. Найди уменьшаемое, вычитаемое, слагаемое.
4. Проверка (порядок действий).
VI. Цель: Да, сегодня мы научимся решать эти уравнения, где неизвестное будет выражено суммой или разностью.
VII. Закрепление нового материала (у доски)
140 – (а + 25) = 40 а + 25 = 140 – 40 а + 25 = 100 а = 100 – 25 а = 75 _________________ 140 – (75 + 25) = 4040 = 40
| 340 + (190 – х) = 400 190 – х = 400 – 340 190 – х = 60 х = 190 – 60 х = 130 _______________ 340 + (190 – 130) = 400
|
Физминутка «Клоуны»
Дети свободно стоят между партами; по моей команде:
· брови свести и развести;
· глаза прищурить, затем широко открыть;
· губы максимально открыть в импровизированной улыбке, а затем поджать;
· шею вытянуть, затем опустить;
· руками обнять себя, погладить и пожелать успехов в учебе.
VIII. Работа в парах сменного состава.
(Каждому ребенку раздать карточки с уравнением вида: 100 – (х + 25) = 52)
— Что главное при работе в паре? (Помочь своему товарищу)
IX. Объясни как решал уравнение? (Устно)
Физминутка для глаз:
· обведи глазами синий кружок по часовой стрелке;
· красный – против часовой стрелке; (Повторить 2-3 раза)
X. Самостоятельная работа (Разноуровневые задания)
1 уровень на «3»:
189 – (х – 80) = 39
х – 80 = 189 – 39
2 уровень на «4»:
350 – (45 + а) = 60
3 уровень на «5»:
Составь по задаче уравнение и реши его: Из числа 280 вычесть сумму чисел х и 40 равно 80
280 – (х + 40) = 80
х + 40 = 280 – 80
х + 40 = 200
х = 200 – 40
х = 160
________________
280 – (160 + 40) = 80
80 = 80
XI. Проверка разноуровневых заданий (по образцу):
1 уровень:
189 – (х – 80) = 39
х – 80 = 189 – 39
х – 80 = 150
х = 150 +80
х = 230
_________________
189 – (230 – 80) = 39
39 = 39
2 уровень:
350 – (45 + а) = 60
45 + а = 350 – 60
45 +а = 290
а = 290 – 45
а = 245
__________________
350 – (45 + 245) = 60
60 = 60
3 уровень:
280 – (х + 40) = 80
х + 40 = 280 – 80
х + 40 = 200
х = 200 – 40
х = 160
________________
280 – (160 + 40) = 80
80 = 80
XII. Оцениваю детей.
XIII. Рефлексия урока.
Как вы себя чувствовали сегодня на уроке?
— комфортно
— тревожно
Покажите мне карточками, чтобы я увидела всех. Почему? С чем связана твоя тревога?
XIV. Домашнее задание.
1 уровень на «3»: стр. 92 № 9
2 уровень на 4»: стр. 93 № 14
3 уровень на «5»: стр. 96 на смекалку: Подумай и попробуй исследовать и решить это уравнение самостоятельно 60 х + 180 = 420, составь план решения.
school-172.my1.ru
Решение уравнений вида х+15 = 68:2. Видеоурок. Математика 4 Класс
С помощью данного урока вы научитесь решать усложненные уравнения. Сможете без труда понять, как упростить уравнение перед непосредственным поиском корня. Также повторите и вспомните, что такое уравнения. Узнаете, что такое корень уравнения, как его искать. Научитесь решать и, главное, проверять свои вычисления. На уроке вы подробно познакомитесь с пошаговой инструкцией решения усложненных уравнений. Решите много интересных заданий и выучите важные определения.
Уравнение – это равенство с неизвестным числом. Неизвестное число обозначают латинской буквой.
Рассмотрите записи (рис. 1) и укажите, сколько на рисунке уравнений.
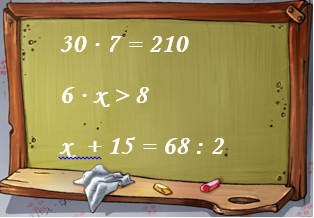
Рис. 1. Записи (Источник)
Решение: 1. Проанализируем каждую запись на доске (рис. 1). Первая строка – это равенство без неизвестных – пример. Вторая строка – неравенство. Именно в третьей строке есть уравнение, потому что только в этой записи есть равенство с неизвестным числом и данное число обозначено латинской буквой. Можно сделать вывод о том, что на рисунке 1 только одно уравнение.
Решить уравнение – это найти значение неизвестного, при котором равенство будет верным (или доказать, что таких значений не существует).
Решите уравнение (рис. 1).
Решение: 1. Сумма неизвестного числа и пятнадцати равна частному чисел шестьдесят восемь и два. Так как в этом уравнении сумма представлена числовым выражением, вначале упростим выражение и найдем значение частного. Теперь для того, чтобы найти неизвестное слагаемое, необходимо от суммы отнять известное слагаемое. После того как найдем значение неизвестного – корня уравнения, необходимо выполнить проверку – подставить значение корня в уравнение и вычислить значение, полученные результаты сравнить. Если результаты совпадают, уравнение решено верно. Если результаты не совпадают, необходимо решить уравнение сначала.
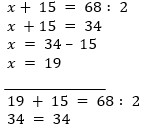
Решите уравнения (рис. 2).

Рис. 2. Уравнения (Источник)
Решение: 1. В первом уравнении вначале можно упростить его правую часть – найти разность. Потом найти неизвестное слагаемое и выполнить проверку.
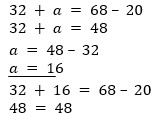
2. Для того чтобы решить второе уравнение, необходимо найти сумму в правой части. Потом определить неизвестное слагаемое и выполнить проверку.
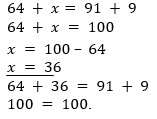
Список литературы
- Математика. 4 класс. Учеб. для общеобразоват. учреждений. В 2 ч. Ч. 1 / [М.И. Моро, М.А. Бантова, Г.В. Бельтюкова и др.] – 8-е изд. – М.: Просвещение, 2011. – 112 с. : ил. – (Школа России). Истомина Н.Б. Математика. 4 класс. – М.: Ассоциация ХХІ век.
- Петерсон Л.Г. Математика, 4 класс. – М.: Ювента.
Домашнее задание
- Математика. 4 класс. Учеб. для общеобразоват. учреждений. В 2 ч. Ч. 1 / [М.И. Моро, М.А. Бантова, Г.В. Бельтюкова и др.] – 8-е изд. – М.: Просвещение, 2011, ст. 64 № 310.
- Что такое уравнение?
- Что значит решить уравнение? Что такое корень уравнения?
- * Решите такие уравнения.
а) б)
б)  в)
в) 
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
- Интернет-портал Festival.1september.ru (Источник).
- Интернет-портал School-172.my1.ru (Источник).
- Интернет-портал Mathematics-tests.com (Источник).
interneturok.ru
Урок математики по теме «Решение уравнений» (4-й класс)
Цель: Рассмотреть практические способы решения уравнений, требующих выполнения более одного арифметического действия.
Оборудование урока: компьютерная презентация устного счета, карточки с уравнениями, карточки трех ступеней для самостоятельной работы над задачами, кубик обратной связи
Ход урока
1. Оргмомент
Проверка готовности к уроку. В тетрадях записывается число, классная работа.
2. Устный счет (компьютерная презентация, слайд №1)
Игра «Соревнование улиток»
Ваш любимый пес Алик на соревновании улиток. Две улитки должны подняться до вершины горы. Кто же из них окажется первой? Наша с вами улитка под №1 слева. Улитка делает шаг, только если мы правильно найдем значение выражения.
Вы готовы?
Сигнал к старту уже прозвучал. Повторяем порядок действий и называем правильные значения выражений.
(122 + 18) : 70 = 2
(64 : 8 + 20) : 7 = 4
20 · (26 + 14) : 100 = 8
1 · (30 + 2) – 4 · 4 = 16
5 · 4 + 12 = 32
(400 – 300) – 36 = 64
У нас получился ряд чисел.
2, 4, 8, 16, 32, 64
Какую закономерность в составлении этого ряда заметили? (каждое следующее число увеличено в два раза)
Продолжите этот ряд чисел и назовите не менее трех следующих чисел. (128, 256, 512…)
Молодцы! Мы решали все правильно, поэтому наша улитка на вершине горы.
За каждым числом зашифрована буква. Перевернем их и прочитаем тему сегодняшнего урока.
2 4 8 16 32 64 128 256 512
У Р А В Н Е Н И Е
Что называется уравнением?
Что называется корнем уравнения?
Что значит решить уравнение?
Мы уже умеем решать простые уравнения, а сегодня мы познакомимся с решением сложных уравнений, где надо выполнить несколько арифметических действий.
3. Решение простых уравнений. Подготовка к введению нового материала.
На магнитной доске в произвольном порядке карточки с уравнениями.
На какие группы можно разделить все эти уравнения? (уравнения распределяются в 3 столбика)
1) 7000 – х = 2489
7000 – х = 3489
7000 – х = 1689
Почему мы выделили эти уравнения в первую группу? (простые уравнения с одинаковым уменьшаемым) Можем мы их решить ?
Найдите среди них уравнение с наибольшим корнем и решите его (один ученик у доски)
2) 71 : х = 20 + 7
х : 3 = 16 + 11 ( это уравнения, в правой части которых выражение)
Можем ли мы решить уравнения второго столбика?
Решите любое из уравнений, но замените в правой части сумму на разность. Корень уравнения при этом должен остаться прежним. (два ученика у доски)
3) ( 490 – х ) – 250 = 70
Посмотрите на оставшееся уравнение. Легко ли нам его решить? Почему?
4. Работа над новым материалом. (фронтальная беседа с классом, в ходе которой рассматривается решение уравнения)
( 490 – х ) – 250 = 70
490 – х = 70 + 250
490 – х = 320
х = 490 – 320
х = 170
( 490 – 170 ) – 250 = 70
70 = 70
Ответ: 70
5. Закрепление.
1) Решение уравнения (один из сильных учеников у доски)
5 · а + 500 = 4500 : 5
5 · а + 500 = 900
5 · а = 900 – 500
5 · а = 400
а = 400 : 5
а = 80
5 · 80 + 500 = 900
900 = 900
Ответ: 80
2) № 399
Решите уравнения.
а + 156 = 17 ∙ 20 (1604 – у) – 108 = 800
252 : 36 ∙ х = 560 103300 : (х + 297) = 25 ∙2
Мы решили два новых сложных уравнения. Посмотрите на уравнения, которые перед вами. Все ли они сложные? Какое уравнение лишнее? Почему? Остальные – в левой части выражение в несколько действий. Найдите среди них с таким порядком действий, которое уже встречалось сегодня.
(1604 – у) – 108 = 800
1604 – у = 800 + 108
1604 – у = 908
у = 1604 – 908
у = 696
(1604 – 696) – 108 = 800
800 = 800
Ответ: 696
Уравнение решают в парах. Один ученик на развороте доски для последующей проверки.
6. Решение задачи
Самостоятельная работа по карточкам 3 ступеней. Выполнив задание первой ступени, ученик переходит к выполнению задания второй ступени, затем третьей.( различные способы дифференцированной работы)
| 1 ступень | 2 ступень | 3 ступень |
| Школьники должны были высадить 25700 саженцев деревьев. После того, как они высадили часть саженцев, им осталось посадить еще12350 деревьев. Сколько деревьев они уже высадили? Реши задачу, составив уравнение |
Измени задачу так, чтобы она решалась уравнением, в правой части которого было бы выражение. Запиши это уравнение и реши его. |
Школьники должны были высадить 25700 саженцев деревьев. После того, как они высадили несколько саженцев липы и 8580 кленов, им осталось высадить 12350саженцев. Сколько лип они уже посадили? |
Проверка фронтальная
1) 25700 – х = 12350
х = 25700 – 12350
х = 13350
25700 – 13350 = 12350
12350 = 12350
Ответ: 13350 саженцев.
2) 25700 – х = 12000 + 350
3) 25700 – (х + 8580) = 12350
х + 8580 = 25700 – 12350
х + 8580 = 13350
х = 13350 – 8580
х = 4770
25700 – (4770 + 8580) =12350
12350 = 12350
Ответ: 4770 лип.
4) А какое еще уравнение можно было составить?
(25700 – х) – 8580 = 12350
Мы решили три задачи, составив три уравнения. Какое уравнение отнесем к сложным? Почему?
7. Домашнее задание.
Рассмотреть, как решались уравнения в учебнике на стр. 106 и решить уравнение в тетради на печатной основе № 44 (а).
Решить задачу № 47. Дополнительное задание: какие еще вопросы можно поставить к этой задаче?
8. Итог урока.
Какие уравнения учились решать на уроке?
Трудно было?
Кому было легко?
urok.1sept.ru
9 х (7512 – а) = 34722 | ||
1 этап | ||
1 | Пронумеровать порядок действий | 2 1 9 х (7512 – а) = 34722 |
2 | Назвать компоненты 2 действия данного уравнения | 9 х (7512 – а) = 34722 1 множитель 2 множитель произведение |
3 | Определить компонент с неизвестным | Компонент с неизвестным – 2 множитель. |
4 | Вспомнить правило нахождения неизвестного компонента | Чтобы найти неизвестный множитель, надо произведение разделить на известный множитель. |
5 | Применить правило и найти неизвестный компонент | 7512 – а = 34722 : 9 |
6 | Сделать вычисление, записать ответ. | 7512 – а = 3858 |
2 этап | ||
7 | Назвать компоненты действия данного уравнения | 7512 – а = 3858 Уменьшаемое вычитаемое разность |
8 | Определить неизвестный компонент | Неизвестный компонент – вычитаемое. |
9 | Вспомнить правило нахождения неизвестного компонента | Чтобы найти неизвестное вычитаемое, надо из уменьшаемого вычесть разность |
10 | Применить правило и найти неизвестный компонент | а = 7512 — 3858 |
11 | Сделать вычисление Записать корень уравнения | а = 3654 |
12 | Сделать подстановку и проверку | 9 х (7512 – 3654) = 34722 34722 = 34722 |
nsportal.ru
Урок 21. решение уравнений — Математика — 4 класс
Математика, 4 класс
Урок 21. Решение уравнений
Перечень вопросов, рассматриваемых в теме:
- Что такое уравнение?
- Как решить уравнение, где в ответе не число, а числовое выражение.
- Что такое корень уравнения?
- Как найти неизвестное вычитаемое?
Глоссарий по теме:
Уравнение – это равенство с неизвестным числом. Неизвестное число обозначают латинской буквой.
Решить уравнение – это значит найти значение неизвестного, при котором равенство будет верным.
Корень уравнения – это значение неизвестного, обозначенного латинской буквой в уравнении.
Чтобы найти неизвестное вычитаемое, надо из уменьшаемого вычесть разность.
Обязательная и дополнительная литература по теме урока:
1. Моро М. И. Учебник для 4 класса четырехлетней начальной школы. М. «Просвещение» — 2017.С. 62,63
2. Волкова Е. В. математика Всероссийская проверочная работа за курс начальной школы. Издательство «Экзамен» 2018.С.27
3. Петерсон Л. Г. математика 3 класс. Часть 2. Ювента, 2015.-96с.: ил. С.77-78
Теоретический материал для самостоятельного изучения:
Рассмотрите записи:
376 + 282; (х — у) : 3
Являются ли эти записи уравнениями?
Это не уравнения, так как в уравнении должен быть знак «=». Это выражения.
Уравнение – это равенство с неизвестным числом. Неизвестное число обозначают латинской буквой.
Рассмотрите другие записи:
24 + х = 49; 24 + х = 79 — 30
Это уравнения, так как это равенства, содержащие переменную.
Попробуем их решить.
Что значит решить уравнение?
Решить уравнение – это значит найти значение неизвестного, при котором равенство будет верным.
Вспомните алгоритм решения уравнений.
Алгоритм:
- Вспомнить компоненты действия данного уравнения.
- Определить неизвестный компонент.
- Вспомнить правило нахождения неизвестного компонента.
- Применить правило и найти неизвестный компонент.
- Записать ответ.
- Сделать проверку
Используя алгоритм, решите первое уравнение
24 + х = 49
х = 49 — 24
х = 25
Значение неизвестного х = 25. Это корень уравнения.
Корень уравнения – это значение неизвестного, обозначенного латинской буквой в уравнении. В данном случае – это х.
Можно ли решить второе уравнение, используя этот же алгоритм?
Нет.
Такие уравнения не рассматривались. Какова же цель нашего урока?
Цель урока: научиться решать уравнения, в которых в ответе не число, а числовое выражение.
Такие уравнения мы будем называть составные. Поэтому тема урока: «Решение составных уравнений»
Чтобы решить это уравнение, нужно упростить правую часть.
24 + х = 79 — 30, после чего получаем уравнение известного вам вида
24 + х = 49
х = 49 — 24
х = 25
Проверка:
24 + 25 = 79 — 30
49 = 49
Ответ: корень уравнения 25
Составим алгоритм решения составных уравнений.
Алгоритм решения составных уравнений
1. Найти значение числового выражения.
2. Вспомнить компоненты действия данного уравнения.
3. Определить неизвестный компонент.
4. Вспомнить правило нахождения неизвестного компонента.
5. Применить правило и найти неизвестный компонент.
6. Записать ответ.
7. Сделать проверку.
Решим еще одно уравнение:
75 — х = 9 ∙ 7
Применяем алгоритм решения составных уравнений:
- Найти значение числового выражения: 75 — х = 9 ∙ 7
75 — х = 63
- Вспомнить компоненты действия данного уравнения: 75 — х = 63

3. Определить неизвестный компонент.
Неизвестно – вычитаемое.
4. Вспомнить правило нахождения неизвестного компонента.

5. Применить правило и найти неизвестный компонент.
х = 75 — 63
6. Записать ответ.
х = 12
7. Сделать проверку.
75 — 12 = 9 ∙ 7
63 = 63
Ответ: корень уравнения 12
Вывод: чтобы решить составное уравнение, в которых в ответе не число, а числовое выражение, необходимо упростить правую часть ( т.е решить выражение), после чего получаем уравнение известного вам вида и решаем его, используя алгоритм решения уравнений.
Решим задачу, составив уравнение:
Сумма неизвестного числа и числа 390 равна произведению чисел 70 и 6. Найди это число.
1. Сумма неизвестного числа и числа 390 – обозначим неизвестное число переменной х, тогда получим х + 390
2. Произведение чисел 70 и 6: 70 ∙ 6
3. Получаем уравнение: х + 390 = 70 ∙ 6
Применяя алгоритм решения составных уравнений, решим его:
х + 390 = 70 ∙ 6
х + 390 = 420
х = 420 — 390
х = 30
Проверка:
30 + 390 = 70 ∙ 6
420 = 420
Ответ: неизвестное число — 30
resh.edu.ru
Решение составных уравнений 3-4 классы. Карточки
Иванова Светлана Романовна
учитель МОБУ СОШ №7 г. Якутска
Республики Саха (Якутия)
Решение
составных уравнений
3-4 классы
1 карточка
Х + 65 = 165 + 2
43 + Х = 500 : 10
Х — 25 = 100 х 2
320 — Х = 45 х 2
Х х 5 = 280 — 250
35 : Х = 78 — 73
60 х Х = 36 + 84
Х : 4 = 20 х 2
2 карточка
42 + Х = 749 — 26
Х + 100 = 500 х 2
Х — 2 = 4050 — 43
624 — Х = 238 + 300
Х х 2 = 430 + 30
25 : Х = 15 : 3
Х : 10 = ( 42 + 48 ) — 83
42 х Х = 36 + 48
3 карточка
Х + 20000 = 500 х 8
65 + Х = 140 : 2
48 — Х = 140 : 2 — 65
Х — 30 = 650 + 10
Х : 5 = 36 + 14
Х х 30 = 280 + 320
400 : Х = 4 х 2
32 х Х = 25 + 7
4 карточка
Х + 43 = 4 х 2 + 50
86 + Х = 40 х 2 + 50
Х — 25 = 40 + 3 х 20
100 — Х = 42 : 7 х 5
Х х 5 = 20 : 4 + 10
600 : Х = 4 — 1 х 2
40 х Х = 50 х 2 + 20
Х : 4 = 700 — 65 х 10
5 карточка
Х + 150 = 40 х 2 + 36 х 2
41 + Х = 35 х 2 х 2
Х — 25 = 500 — 40 х 10
920 — Х = 801 — 1 х 1
Х х 7 = 5 + 150 : 5
30 х Х = 200 + 2 х 5
Х : 3 = 27 : 9 х 5
42 : Х = 90 — ( 50 + 34 )
6 карточка
39 + Х = 42 х 2 + 5
Х + 32 = ( 25 + 65 ) х 2
Х — 95 = 66 + 21 + 13
79 — Х = 33 х 2 + 4 х 1
Х : 5 = ( 62 — 22) : 5
33 х Х = ( 23 — 3 ) х 5 — 1
84 : Х = (65 — 60 ) + 37
Х : 100 = ( 45 + 5 ) х 4
7 карточка
Х + 4 = 60 х 2 : 4
92 + Х = ( 400 + 2 ) х 2
Х — 35 = ( 765 — 65 ) х 2
98 — Х = 44 х 2 + 2
Х х 3 = 43 + 8 х 4
36 х Х = 64 : 8 х 9
Х : 50 = ( 35 + 15 ) х 4
1800 : Х = 36 : 4 х 60 + 60
8 карточка
15 + Х = 7256 + 2 х 4
Х + 49 = 25 х 4 х 2 + 50
Х — 720 = 49 : 7 х 9
657 — Х = 250 : 5 х 4
Х х 23 = 150 : 3 + 19
75 х Х = 30 х 6 — 30
Х : 50 = 2 х 9 + 2
630 : Х = 36 х 2 — 2
9 карточка
Х + 64 = 36 : 9 + 21
136 + Х = 50 х 2 х 3
Х — 925 = 600 : 2 + 700
2000 — Х = ( 1000 — 2 ) х 2
Х х 8 = 820 — 45 х 4
70 х Х = 131 + 36 : 4
500 : Х = 25 : 5 х 10
Х : 25 = 42 х 2 — 68
10 карточка
Х + 29 = 990 + 60 х 2
35 + Х = ( 2 + 5 ) х 52
Х — 728 = 2 х 24 х 10
523 — Х = 21 : 3 х 10
Х х 90 = 75 х 2 + 30
60 х Х = 3 х 6 х 10
Х : 5 = 400 : 8 + 5
360 : Х = 85 х 2 + 10
11 карточка
Х + 409 = 65 х 3 + 700
260 + Х = 700 + 6 х 5
Х — 612 = 420 : 6 х 9
2694 — Х = 40 х 4 + 2
Х х 30 = ( 502 + 28 ) х 3
45 х Х = 20 х 5 — 10
Х : 200 = 680 — 40 х 2
560 : Х = ( 40 + 30 ) : 10
12 карточка
Х + 500 = 600 х 2 + 300
406 + Х = 925 — 5 х 5
Х — 39 = 1800 : 2 + 33
786 — Х = 32 х 5 : 2
Х х 100 = 59 х 3 х 1000
810 : Х=1000- ( 60 х 3+10 )
60 х Х = ( 30 х 2 ) х 10
Х : 3 = 59 х 4 : 2
13 карточка
Х + 429 = 65 х 2 х 5
728 + Х = 500 х 2 + 15
Х — 39 = 360 : 4 + 1
450 — Х = 720 : 8 + 60
Х х 7 = ( 618 + 2 ) + 10
3 х Х = 42 х 3 х 5
Х : 7 = 58 х 9 + 28
650 : Х = 81 : 9 + 1
14 карточка
62 : Х + 38 = 40
73 + (50 : Х + 2) = 100
(100 — Х : 4 ) — 30 = 54
400 — (5 х Х + 125) = 205
( 40 х Х + 140) х 5 = 2500
5 х ( 69 — 120 : Х) = 45
(150 : Х + 50) : 5 = 73 — 53
150 : (45 : Х + 35) = 27 : 9
15 карточка
(720 : Х — 2) + 40 = 128
(4 х Х + 20) + 720 = 900
(Х х 5 + 25 ) — 415 = 60
900 — (4 х Х — 60) = 360
( 42 : Х — 7 ) х 30 = 420
2 х ( 36 — 52 : Х ) = 20
( 40 х Х — 40 ) : 4 = 30
480 : (Х : 4 + 1) = 64 : 8
16 карточка
( 60 : Х + 5 ) + 25 = 50
800 + ( 420 : Х — 10 ) = 1000
( 400 : Х + 5 ) — 5 = 200
1000 — ( 4500 : Х + 80 ) = 420
(54 : Х + 30 ) х 2 = 72
8 х ( 36 + 4 х Х ) = 480
(6 х Х + 12 ) : 6 = 50
350 : (20 х Х — 15) = 70
17 карточка
420 + (4 х Х + 360) = 940
350 + (600 — 5 х Х) = 450
(4 + Х х 9) — 36 = 40
660 — (8 х Х + 20) = 480
(4 х Х + 2) х 6 = 180
9 х (4 х Х + 10) =810
(150:Х-50):5=73-53 81:(42-3хХ)=66-7х9
18 карточка
(Х : 20 + 40) — 70 = 30
64 + ( Х : 4 + 6) = 100
(64 : Х + 138) — 50 = 90
925 — (80 : Х — 15) = 900
(95 — 45 : Х) х 9 = 810
6 х (20 : Х — 15) = 30
(3 х Х — 30) : 2 = 68 — 8
720:(Хх4-46)=150х3-90
Ответы:
1. 102; 7; 225; 230; 6; 7; 2; 160.
2. 681; 900; 4009; 86; 230; 5; 700; 2.
3. 2000; 5; 43; 690; 250; 20; 50; 1.
4. 15; 44; 125; 70; 3; 300; 3; 200.
5. 2; 99; 125; 120; 5; 7; 45; 7.
6. 50; 148; 195; 9; 40; 3; 2; 20000.
7. 26; 712; 1435; 8; 25; 2; 10000; 6.
8. 7249; 201; 782; 457; 3; 2; 1000; 9.
9. 89; 164; 1925; 4; 80; 2; 10; 400.
10. 1081; 329; 1208; 453; 2; 3; 275; 2.
11. 486; 470; 1242; 2532; 53; 2; 120000; 80.
12. 1000; 494; 972; 706; 1770; 1; 10; 354.
13. 221; 287; 130; 300; 90; 210; 3850; 65.
14. 31; 2; 64; 14; 9; 2; 3; 3.
15. 8; 40; 90; 150; 2; 2; 4; 236.
16. 3; 2; 2; 9; 9; 6; 48; 1.
17. 40; 100; 8; 20; 7; 20; 1; 5.
18. 1200; 120; 32; 2; 9; 1; 50; 12.
infourok.ru
Как решать уравнения со скобками?
Не все уравнения, содержащие скобки, решаются одинаково. Конечно, чаще всего в них требуется раскрыть скобки и привести подобные слагаемые (при этом способы раскрытия скобок разняться). Но иногда скобки раскрывать не нужно. Рассмотрим все эти случаи на конкретных примерах:
- 5х — (3х — 7) = 9 + (-4х + 16).
- 2х — 3(х + 5) = -12.
- (х + 1)(7х — 21) = 0.
Решение уравнений через раскрытие скобок
Данный метод решения уравнений встречается наиболее часто, но и он при всей своей кажущейся универсальности, делится на подвиды в зависимости от способа раскрытия скобок.
1) Решение уравнения 5х — (3х — 7) = 9 + (-4х + 16).
В данном уравнении перед скобками стоят знаки минус и плюс. Чтобы раскрыть скобки в первом случае, где перед ними стоит знак минус, следует все знаки внутри скобок поменять на противоположные. Перед второй парой скобок стоит знак плюс, который на знаки в скобках никах не повлияет, значит их можно просто опустить. Получаем:
5х — 3х + 7 = 9 — 4х + 16.
Слагаемые с х перенесем в левую часть уравнения, а остальные в правую (знаки переносимых слагаемых будут меняться на противоположные):
5х — 3х + 4х = 9 + 16 — 7.
Приведем подобные слагаемые:
6х = 18.
Чтобы найти неизвестный множитель х, разделим произведение 18 на известный множитель 6:
х = 18 / 6 = 3.
2) Решение уравнения 2х — 3(х + 5) = -12.
В этом уравнении также сначала нужно раскрыть скобки, но применив распределительное свойство: чтобы -3 умножить на сумму (х + 5) следует -3 умножить на каждое слагаемое в скобках и сложить полученные произведения:
2х — 3х — 15 = -12
-х = -12 + 15
-х = 3
х = 3 / (-1) = 3.
Решение уравнений без раскрытия скобок
Третье уравнение (х + 1)(7х — 21) = 0 тоже можно решить раскрыв скобки, но гораздо проще в таких случаях воспользоваться свойством умножения: произведение равно нулю тогда, когда один из множителей равен нулю. Значит:
х + 1 = 0 или 7х — 21 = 0.
а) х + 1 = 0
х1 = -1.
б) 7х — 21 = 0
7х = 21
х = 21 / 7
х2 = 3.
vashurok.ru
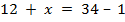 б)
б) 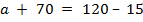 в)
в)