Урок математики в 6 классе по теме «Решение уравнений»
Муниципальное бюджетное общеобразовательное учреждение
«Коломыцевская основная общеобразовательная школа»
Прохоровского района Белгородской области
Разработка урока математики в 6 классе
по теме «Решение уравнений»
Учитель математики
Цыгулёва Татьяна Владимировна
Класс: 6 Тема урока: Решение уравнений
Тип урока: изучение нового материала и первичное закрепление новых знаний и способов действий.
Цель: создание условий для получения и осмысления новых знаний о способах решения уравнений, систематизация теоретического материала по теме, отработка навыка решения уравнений различными методами.
Задачи:
Образовательные
повторить решение уравнений на нахождение неизвестного множителя, закрепить материал о свойствах уравнений и нового способа решения уравнений; алгоритм решения уравнения, используя перенос слагаемых из одной части уравнения в другую; извлекать необходимую информацию из прослушанного материала; структурировать информацию в виде записи выводов и определений.
Развивающие (формирование регулятивных УУД): умение обрабатывать информацию и представлять информацию в виде алгоритма, выбирать способы решения уравнений в зависимости от условий; планировать собственную деятельность, определять средства для ее осуществления; способствовать развитию развития логического мышления, внимания, математической речи.
Воспитательные (формирование коммуникативных и личностных УУД): умение слушать и вступать в диалог; формировать внимательность и аккуратность в вычислениях; воспитывать чувство взаимопомощи, уважительное отношение к чужому мнению, культуру учебного труда, требовательное отношение к себе и своей работе; развивать у учащихся умение работать индивидуально и в группах.
Планируемые результаты:
Предметные: ученик научится решать уравнения; усвоит алгоритм решения уравнения, используя перенос слагаемых из одной части уравнения в другую;
Личностные: ученик научится формировать устойчивый познавательный интерес, уважение к личности и её достоинству, доброжелательное отношение к окружающим.
Метапредметные: ученик научится определять и формулировать цель на уроке с помощью учителя; проговаривать последовательность действий на уроке; работать по коллективно составленному плану; оценивать правильность выполнения действия. Ученик получит возможность планировать свое действие в соответствии с поставленной задачей; вносить необходимые коррективы в действие после его завершения на основе его оценки и учета сделанных ошибок; высказывать свое предположение.
Учебное оборудование: Учебник (УМК): Виленкин Н. Я., Жохов В. И., Чесноков А. С., Шварцбурд С. И. Математика 6 класс, проектор, компьютер, экран, раздаточный материал.
Формы работы учащихся: фронтальная, парная, индивидуальная.
Ход урока
Самоопределение к учебной деятельности (организационный момент).Цель: Создание благоприятной рабочей обстановки в классе и
условий для успешной деятельности.
Учитель приветствует учащихся, проверяет их готовность к уроку.
-Ребята! Я рада вас видеть сегодня на уроке в хорошем настроении и прошу обратить внимание на доску.
«Не мысли надобно учить, а учить мыслить» Э.Кант
Как вы понимаете это высказывание? Согласны ли вы с ним?
Абсолютно верно! Это высказывание будет девизом нашего сегодняшнего урока!Включаются во взаимодействие с одноклассниками и с учителем.
Актуализация опорных знаний Цель этапа: повторение изученного материала, необходимого для «открытия нового знания», и выявление затруднений в индивидуальной деятельности каждого учащегося
— Новые знания нам будет очень трудно осваивать без умения быстро и верно считать, поэтому, как всегда, начнем урок с устной работы:
Игра «Что лишнее?» слайд2
1) 4(x-3)=20; a- 6+b; x+7=-15; 4b-(2b -3)=13; 9x=2x+21
2) прямая, число, подобные
3) слагаемое, вычитаемое, сумма. множитель,
4)уравнение, корень, переменная, отрезок
— Ребята, вы помните правила нахождения неизвестных при решении уравнений? Слайд 3
1.Как найти неизвестное слагаемое?
2.Как найти неизвестное уменьшаемое?
3.Как найти неизвестное вычитаемое?
4.Как найти неизвестный множитель?
5.Как найти неизвестное делимое?
6.Как найти неизвестный делитель?
Слайд 4
3. Упростить выражение из правой таблицы
и поставить ему в соответствие
выражение из левой таблицы
Решить устно уравнения: х-13=21; 2х+5=-15; 3х+1,2-2х=20,4; 6х-3=4х+17 Слайд 5
Учащиеся внимательно смотрят на записи, отвечая на вопросы:
выражение
прямая
сумма
отрезок
Отвечают на вопросы
Ребята выполняют устно задания на приведение подобных слагаемых.
Ребята решают устно уравнения. Последнее задание вызвало трудности.
Постановка проблемы.
Цель этапа: сформулировать проблему, тему и цели урока.
-Почему мы не смогли решить уравнение?Сегодня на уроке у вас будет возможность учиться преодолевать эти трудности.
Как вы думаете, какая тема урока сегодня будет?
-Запишите число и тему урока. Слайд 6
-Какие цели поставим на сегодняшний урок? Чему вы хотели бы сегодня научиться?
Где можно узнать информацию по данной теме?
Переменная находится в обеих частях уравнения.
Тема данного урока: “Решение уравнений”. Записывают число, тему урока в тетради
Сегодня мы познакомимся со свойствами уравнений, которые помогут решать различные виды уравнений.
1. Узнать, какие виды записей уравнений бывают
3. Изучить свойства решения уравнений.
4. Учиться применять свойства к решению уравнений.
5. Выяснить, какие знания, полученные ранее, нужны будут для изучения этой темы.
Называют источники информации: учебник, учитель
Открытие учениками нового знания.
Цель этапа: организовать решение проблемной ситуации.
На уроках математики вы учитесь решать задачи, в том числе и при помощи составления уравнения. Уравнения у вас могут получиться самые разные, поэтому так важно умение решать любые уравнения.
– А что значит «решить уравнение»?
Загадка:
Он есть у дерева, цветка,
Он есть у уравнений
И знак особый – радикал –
С ним связан, без сомнений.
Заданий многих он итог.
И с этим мы не спорим
Надеемся что каждый смог
Ответить: это…. (корень)
слайд 7
-Ребята, я вам предлагаю сегодня поработать в группах. Перед вами уравнение 4(x-3) = 20 слайд 8
1группа решит уравнение, применив распределительное свойство умножения
2 группа по правилу отыскания неизвестных компонентов
— Как из первого уравнения можно получить второе?
Мы с вами убедились, что корнем этих двух уравнений является одно и то же число. Поэтому:
Корни уравнения не изменяются, если обе части уравнения умножить или разделить на одно и тоже число, не равное нулю. Слайд 9
Возвращение к уравнению и решение его 6х-3=4х+17
(слайд 10,11) Посмотрите на картинку и сформулируйте второе свойство уравнений.
Найдите это правило в учебнике.
. Отвечают на вопрос:
Найти все значения неизвестных, при которых оно обращается в верное равенство или установить, что таких значений нет.
Вспоминают распределительное свойство и правило умножения и решают уравнение в тетрадях
Записывают в тетрадях вывод
— Обе части уравнения можно поменять местами.
Решают уравнение.
Находят правило в учебнике, один из ребят читает его вслух
Физкультминутка
Быстро встали, улыбнулись,
Выше-выше подтянулись.
Ну-ка плечи распрямите,
Поднимите, опустите.
Вправо, влево повернитесь,
Рук коленями коснитесь.
Сели, встали, сели, встали,
И на месте побежали.
Выполняют упражнение
Первичное осмысление и закрепление знаний.
Обеспечить условия для совместной работы детей, чтобы каждый ребенок учился принимать решения, делать выводы,
осознал ценность и смысл умений работать в паре.
Самостоятельная работа
Принято при решении уравнений переносить слагаемые так, чтобы в левой части уравнения были неизвестные числа, а в правой — известные числа.
Выполнения интерактивного теста на закрепление материала
(тренажер перенос слагаемых в уравнении)
Работа в парах.
Этап закрепление изученного материала
Цель этапа:
организовать решение и объяснение задания.А сейчас мы будем закреплять данное правило.
Решить №1314 с комментированием у доски.
Наблюдение за ходом работы. Координирующая роль учителя.
— Решают в тетрадях, один из учеников комментирует
Решают по одному уравнению у доски.
Этап контроля и оценки. Итог урока
Рефлексия учебной деятельности
Цель этапа: осознание уч-ся своей учебной деятельности, самооценка результатов деятельности своей и всего класса
Подведем итоги сегодняшнего урока.
— Полностью ли реализован составленный нами план?
– Соответствовала ли наша работа целям урока?
Закончите предложения (слайд12)
— Принцип «Микрофон». (Ученики по очереди дают аргументированный ответ на один из вопросов).
На уроке я работал активно / пассивно
Своей работой на уроке я доволен / не доволен
Урок для меня показался коротким / длинным
За урок я не устал / устал
Мое настроение стало лучше / стало хуже
Материал урока мне был полезен / бесполезен
интересен / скучен
интересно / не интересно
Проводят самоанализ, отвечают на вопросы; вспоминают правила; определение уравнения, корня уравнения.
Домашнее задание
Создать условия, позволяющие каждому школьнику испытать успех при выполнении задания.
Запишите в дневник домашнее задание. (дифференцировано)
Комментирует его
Записывают домашнее задание, слушают комментарии учителя к нему.
Урок по математике на тему «Уравнения» (6 класс)
Урок математики в 6 классе по теме «Уравнения»
Пояснительная записка
Данный урок проведен, по учебнику 6 класса для общеобразовательных учреждений / Н. Я. Виленкин, В. И. Жохов, А. С. Чесноков, С, И. Шварцбурд. — М.: Мнемозина, 2009.
Устная работа направлена на закрепление вычислительных навыков и подготовку к изучению новой темы.
Этот урок является первым из восьми отведенных на изучение данной темы. Главной целью является ознакомить учащихся новым способом решения уравнений с использованием свойств: умножение или деление обеих частей уравнения на одно и то же число и переносом из одной части уравнения в другую.
Данный урок построен в соответствии с принципами здоровьесбережения. Чередование видов деятельности (устный счет, фронтальная, групповая и индивидуальная работа) позволяют сохранить работоспособность детей на хорошем уровне в течение всего урока.
Класс: 6
Предмет: Математика.
Тема: Решение уравнений.
№ урока по данной теме: Первый.
Оборудование: Документ камера
Цель: Цели урока.
Образовательные:
построить алгоритм решения уравнения методом группировки известных и неизвестных слагаемых;
формирование умения пользоваться алгоритмом при решении уравнений.
Развивающие:
формирование умения выделять главное, сравнивать, анализировать и делать выводы;
формирование умения формулировать познавательные задачи, планировать познавательную деятельность;
развивать качества личности – трудолюбие, аккуратность, настойчивость в достижении цели.
Воспитательные:
выработка объективной оценки своих достижений;
формирование честности, как составляющей законопослушания;
формирование ответственности Формирование умений и навыков решения простейших линейных уравнений при создании условий здоровьесбережения на уроке.
Воспитание взаимоподдержки в ходе совместной деятельности, настойчивости для достижения конечных результатов.
Ход урока
Начать урок словами Жен Жака Руссо «Вы — талантливые дети! Когда – нибудь вы сами приятно поразитесь, какие вы умные, как много и хорошо умеете, если будете постоянно работать над собой, ставить новые цели и стремится к их достижению»
В тетради записать дату, классная работа.
На слайде Записи: 24х – 56х 5(4а — 7) – (12 + 24а) 16 х = 32 2у + 7у = 8,1 2,7n – (3,8 n – 14,8) 8x = 2x+18.
Разделите записи на две группы. По какому признаку вы это сделали?
2 ученика записывают на доске 2 столбика: (Вахрушева А, Лабутин Н)
1.Буквенные (Алгебраические) выражения
2 Уравнения.
А) Какие действия мы умеем выполнять с буквенными выражениями?
(раскрывать скобки, приводить подобные слагаемые) Упрощаем выражения на доске ( Бурдина, Маргунов, Мига)
Б) Уравнения – решаем самостоятельно. Проверка по готовому решению ученика( через документ камеру)
— Какие правила применяли для решения?
— Какое уравнение вызвало затруднения?
— Почему?
— Чем это уравнение отличается от тех, которые мы умеем решать?
(содержит неизвестное в обеих частях уравнения).
— Значит тема сегодняшнего урока: Уравнения, содержащие неизвестное в обеих частях
— Какова цель? — Научится решать уравнения
— Что для этого нужно нам сделать? — Вывести правило, которое не изменит корни уравнения, и позволит сделать так, чтобы неизвестные оказались в одной части.
— Запишем 1) сформулировать правило
2) применять правило.
— Какие правила, не меняющие корни уравнения мы знаем?
3. Пословица: Одна голова хорошо, а две лучше.
Как она относится к нашему уроку?
Работа в группах. (3 группы)
(Детям дается задание на карточках. Решают одну и туже задачу, но разными способами).
Один представитель от группы, выходит к доске и объясняет решение.
— Какую закономерность мы увидели во всех решенных уравнениях?
— неизвестное из правой части перешло в левую, только поменяло знак на противоположный.
— Изменились ли корни? Сформулировать правило. Проработать опорный конспект. ( работа в парах)
4. Вернемся к уравнению 8x = 2x+18. Чтобы его решить, что нужно сделать? (На доске решает Лабутин)
5. Закрепим правило при решении уравнения б) 1 – 5х = — 6х + 8.
Анализирум это уравнение, чем оно отличается от предыдущего, чем дополняем правило
__ Переносим не только неизвестные, но и известные, так, чтобы в левой части собрать – неизвестные, а в правой – известные.
Решаем на доске _ (Муленко)
6. Самостоятельно: 10х + 9 = 7х
у+ 2у + 20 = — 3у — 16 Проверка через документ камеру.
Оценочный лист
Фамилия,имя_____________________________________________________Поставьте знак « + », если вы не допустили ошибки при выполнении действия, и знак « — », если действие выполнено с ошибкой.
Критерии оценки
Уравнение № 1
Уравнение № 2
Получен правильный ответ
Правильно выполнен перенос слагаемых из одной части уравнения в другую
Правильно выполнено приведение подобных слагаемых
Отсутствуют вычислительные ошибки
Самооценка работы по критериям. Кто поставил себе 8 « + «, 7, 6 ,5 Молодцы. Обратите внимание на «-« и проработайте соответствующие правила.
7. Вернемся к цели урока. Достигли ли ее?
8. Необходимо еще раз закрепить полученные знания . Домашнее задание: п. 42, правило , 1342 (а, в, д, ж)
Уравнение из ГИА – 9 №1
Электронный дневник, группа «Готовимся к экзаменам»
9 Резерв. 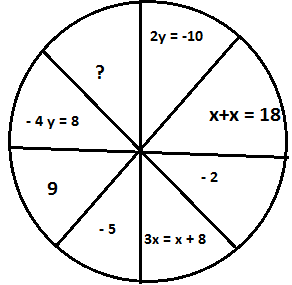
Логическая задача. Как найти неизвестное число?
— Нужно соотнести уравнение и его корни. Решить уравнение 3х = х
+ 8 и найденный корень и будет тем неизвестным, которое нужно найти х = 4.
10 Вернемся к эпиграфу урока. Кто выскажет свои мысли.
Приложения
Опорный конспект по теме «Решение уравнений».
● Если к обеим частям верного равенства прибавить или отнять одно и тоже число, не равное нулю, то получится верное равенство.
● Если обе части верного равенства умножить или разделить на одно и тоже число, не равное нулю, то получится верное равенство.
● Члены уравнения можно переносить из одной части в другую,
изменив их знак на противоположный.

Опорный конспект по теме «Решение уравнений».
● Если к обеим частям верного равенства прибавить или отнять одно и тоже число, не равное нулю, то получится верное равенство.
● Если обе части верного равенства умножить или разделить на одно и тоже число, не равное нулю, то получится верное равенство.
● Члены уравнения можно переносить из одной части в другую,
изменив их знак на противоположный.

Урок по математике для 6 класса «Решение уравнений»
ГБОУ СОШ № 448 Учитель: Баранова И.М.
Тема урока: Решение уравнений (6 класс, учебник Н.Я. Виленкина)
Тип урока: урок обобщения знаний и умений по решению уравнений
Цели урока:
Образовательные:
Продолжить формировать умение решать уравнения
Систематизировать знания учащихся по теме
Обеспечить дифференцированный подход к учащимся на уроке
Воспитательные:
Развитие внимательности, аккуратности, критичности мышления
Развитие умения осуществлять взаимоконтроль и самоконтроль
Развитие умения слушать других
Развитие логического мышления
Развитие умения организовывать свою работу
Развивающие:
Способствовать формированию умения применять знания в нестандартных ситуациях
Способствовать развитию математической речи учащихся
Развитие познавательного интереса учащихся
Оборудование: Справочные таблицы по решению уравнений, плакат с афоризмом к уроку, исторический материал, задания с кодированными ответами, задания для устной работы, опорные таблицы по решению и составлению уравнений на каждого учащегося.
Методы обучения: систематизирующий, познавательный
Формы работы: работа в парах, индивидуальная работа, фронтальная работа
Структура урока:
Организационный момент
Проверка домашнего задания в устной работе на оценку
Сообщение темы и цели урока, афоризм к уроку
Актуализация опорных знаний и умений учащихся – устная работа, задание с кодированным ответом в парах, проблемная ситуация – математический софизм
Обобщение знаний и умений по пройденному материалу (правила, алгоритм, решение уравнений разными способами, обратное задание)
Резерв: развивающие задания
Постановка домашнего задания
Подведение итогов урока
Ход урока
Организационный момент
Проверить готовность класса к уроку.
Проверка домашнего задания
Проверка домашнего задания в ходе устной работы на оценку.
Ознакомление с темой урока, постановка его целей
Сообщить учащимся тему урока. Сообщить, что мы будем сегодня продолжать учиться решать уравнения по изученному алгоритму на основании математических правил и законов, попробуем обобщить накопленные знания и постараемся искать для уравнений различные способы решения. К нашему уроку сегодня замечательно подходит следующий афоризм: «Человеку, изучающему алгебру, часто полезнее решить одну и ту же задачу тремя различными способами, чем решить три-четыре различные задачи. Решая одну задачу различными методами, можно путем сравнений выяснить, какой из них короче и эффективнее. Так вырабатывается опыт» Сойер У. – автор ряда популярных книг по математике.
Актуализация опорных знаний и умений учащихся во время устной работы
1. Устная работа на оценку (проверка выполнения домашнего задания) – см. приложение 1.
2. Задание в парах с кодированным ответом. См. приложение 2. Составить слово, значение которого, возможно, вам пока не известно. Ответ: софизм. Спросить, слышал ли кто-нибудь из учеников это слово. Зачитать объяснение этого понятия.
Математический софизм – удивительное утверждение, в доказательстве которого кроются незаметные, а подчас и довольно тонкие ошибки. История математики полна неожиданных и интересных софизмов, разрешение которых порой служило толчком к новым открытиям. Математические софизмы приучают внимательно и настороженно продвигаться вперед, тщательно следить за точностью формулировок, правильностью решения. Очень часто понимание ошибок в софизме ведет к пониманию математики в целом, помогает развивать логику и навыки правильного мышления. Если нашел ошибку в софизме, значит, ты ее осознал, а осознание ошибки предупреждает от ее повторения в дальнейших математических рассуждениях. Софизмы не приносят пользы, если их не понимать.
На доске доказать, что дважды два пять (известный софизм).
4:4=5:5
4 (1:1)=5 (1:1)
4=5, значит 2 2 = 5. Где ошибка? (Ошибка в применении несуществующего распределительного закона умножения относительно деления, посмотреть в папках, что распределительный закон есть для сложения и вычитания).
Вот и мы сейчас будем не просто решать уравнения, будем обосновывать каждый шаг, чтобы не допустить подобного промаха, искать разные способы решения.
Обобщение знаний и умений по пройденному материалу
Обобщение знаний в ходе заполнения таблицы с решением уравнений и пошаговым объяснением (разными способами). Таблицы заготовлены на каждого ученика. Иногда в алгоритм решения уравнений стоит внести изменения для удобства решения. Ученики должны предложить несколько способов решения, опираясь на подсказки и объяснить каждый шаг решения – написать рядом, что делали.
Организация работы: Учащиеся заполняют таблицу, решая уравнения разными способами. Затем по мере решения выходят к доске и записывают разные способы – объясняя по шагам свое решение. Остальные в это время проверяют себя. Доску разбить на 3 части.
Таблица 1. Решение уравнений
-14х+7=-21х-35
1 способ
2 способ
3 способ
Перенос неизвестных влево
Перенос неизвестных вправо
Деление левой и правой частей на одно и то же число
Ответ: х=-6
⅟5 х – 1 ⅟2 = ⅟2 х – 7 ⅟5
1 способ
2 способ
3 способ
Перенос слагаемых
Умножение левой и правой частей на одно и то же число
Представить обыкновенные дроби в виде десятичных и умножить обе части на одно и то же число
Ответ: х=19
2х+4 = 2 — х
-10 -5
1 способ
2 способ
3 способ
Основное свойство пропорции и раскрытие скобок
Основное свойство пропорции и деление на одно и то же число
Основное свойство пропорции и вынесение за скобки общего множителя
Ответ: х=0
6.Резерв:
Развивающие задания. Решить уравнения самостоятельно, затем разбор на доске.
– 3(х+4) –4(х-1)= -7(х+1)
Ответ: корней нет
2. – 3(х+4) –4(х-1)= -7(х+1) -1
Ответ: х-любое число
7.Постановка домашнего задания
Записать на доске: № 1358, № 1414 (На 3: решить любым 1 способом, на 4-5: предложить разные способы решения).
8. Подведение итогов.
Приложение 1
Домашнее задание для подготовки к устной работе
Что такое уравнение? Приведите примеры уравнения и не уравнения?
Что такое корень уравнения? Приведите пример того, что число является (не является) корнем уравнения.
Что означает «решить уравнение»? Приведите пример, когда нельзя считать, что уравнение решено.
Сколько корней может иметь уравнение? Приведите различные примеры.
Как выполнить проверку правильности решения уравнения? Приведите пример.
Могут ли разные уравнения иметь одинаковые корни? Приведите примеры.
Вопросы к устной работе:
Какое уравнение имеет ровно 2 корня?
Под каким номером расположено не уравнение?
Является ли число –2 корнем уравнения №3?
Найдите корень уравнения №3.
Сколько корней имеет уравнение № 10?
Какие уравнения не имеют корней?
Решите уравнение №2.
Корнем каких уравнений является число 2?
Сколько корней имеет уравнение №3?
Решите уравнение №7.
Задания для устной работы
1 вариант
2 вариант
3 (х-2)= -6
1. (х-7)(5-х)=0
2,5х+4=1,5х-3
2. 3,5х-3 = 2,5х+4
7х-14=0
3. -7х+14=0
IxI =5
4. 2(х-3)=-6
3х = 3х+7
5. 3х-5+2х-1
6. 2х – 7 – х +3
6. IxI = -7
7. m+m+m=4-10
7. a+a+a+a = 2-10
8. IxI =-6
8. IxI = 6
9. (х-7)(5-х)=0
9. 2х= 2х+5
10. 2х -3 = -2(1,5-х)
10. 3х — 4 = 2(1,5х-2)
Ответы:
1 вариант
2 вариант
4; 9
1; 8
6
5
нет
нет
2
2
Бесконечно много
Бесконечно много
8; 5
6 ; 9
-7
7
3; 10
3; 10
1 корень
1 корень
m =-2
a=-2
Приложение 2
Кодированное задание для работы в парах
Отгадайте слово
х +0,2 = 0,5 – 0,2х
-12х-15 = 3х – 28
-25 – 3х = -8х – 9
-2(3-х)= -(х+5)
15х-27 = -3х +18
2х+5 = х+8
7 4
А) -6 –х = -х +5
О) -15 +28 =3х+12х
Ф) 25+3х = 8х+9
К) 7(2х+5)=4(х+8)
М) 7(х+8) = 4(2х+5)
У) 5х-27 = -х +18
Т) х+2 = 5 – 2х
С) 10х+2 = 5-2х
И) -6+2х = -х-5
З) 5х-9 = -х+6
П) -12х – 3х = -15 — 28
Ответ:
1
2
3
4
5
6
с
о
ф
и
з
м
Урок математики «Уравнения», 6 класс
Огрызко Ирина Владимировна,
учитель математики, МБОУ СОШ №2 г. Донецка
Предмет: математика
Класс: 6
Тема урока: Уравнения
Базовый учебник: И.И. Зубарева, А.Г. Мордкович, Математика: 6 класс: учебник для учащихся общеобразовательных учреждений / М: Мнемозина, 2014 – 264 с.
Тип урока: урок «открытия» нового знания (45 минут)
Целевые установки на достижение планируемых результатов:
— личностные: умение слушать и вступать в диалог, участвовать в обсуждении проблем, содействовать формированию и развитию нравственных, трудовых, эстетических качеств личности учащихся (дисциплинированность, ответственность, аккуратность, радость и сопереживание их успехам), формировать коммуникативную компетенцию учащихся;
— метапредметные: способствовать развитию устной и письменной речи, изложению своих мыслей с применением математической терминологии, обогащению ее словарного запаса, самостоятельного мышления, навыка самооценки, самопроверки и ведения записей в собственной тетради;
— предметные: создать условия для понимания алгоритма решения уравнений и использования свойств уравнений.
Оборудование:
компьютер, экран, проектор, раздаточный материал, презентация.
ХОД УРОКА
Приветствие учеников. Проверка готовности к уроку.
1) Продолжите предложения:
— коэффициентом называется….
— подобные слагаемые – это слагаемые, у которых …
— привести подобные слагаемые – это выполнить действия с коэффициентами ….
— чтобы число умножить на сумму (разность), нужно …
— если перед скобкой стоит знак минус, то ….
— если перед скобкой стоит знак плюс, то …
2) Установите соответствие между выражениями и заполните таблицу:
На доске в два столбика размещены выражения, ребята устанавливают соответствия между ними
А) | 1) | 2х – 6 | ||||
Б) | 2) | –2х + 6 | ||||
В) | 3) | 2х + 6 | ||||
Г) | 4) | –2 – 6 | ||||
А | Б | В | Г | |||
Математический диктант (мультимедийное приложение к учебнику математики под редакцией И.И Зубаревой, п.18) с взаимопроверкой. По окончании ребята обмениваются тетрадями для проверки.
На слайде представлена таблица. На столе у обучающихся карточки с примерами и ответы.
Я предлагаю вам разгадать тему урока. Выполните вычисления в тетради, и в таблице напишите букву, соответствующую правильному ответу. Получившиеся слово – это тема урока. Я думаю, что вы справитесь с этим заданием за 4 минуты.
5 | – 14 | – 8 | – 3,2 | – | 6 | – | – 5,8 | 6 |
Раздаточный материал
– 7,3 – 0,7 | –8 (А) |
5 (У) | |
(Н) | |
–2,6 : (– 0,4) | 6 (Е) |
0,1· (– 32) | – 3,2 (В) |
72 (У) | |
– 19 + 5 | –14 (Р) |
11,2 – 17 | –5,8 (И) |
Ребята по завершении времени называют буквы, соответствующие числам в таблице ( слайды 3 – 11).
Верно, мы получили слово «уравнение». Запишите в тетрадях тему урока: «Уравнения» (слайд 12).
5. Актуализация знаний.
1) С уравнениями вы знакомы с начальной школы. Давайте вспомним: (1 мин)
— что такое уравнение;
— что значит решить уравнение;
— что такое корень уравнения?
Звучат ответы обучающихся.
2) Историческая справка: (слайд 13) (2 мин)
Учитель знакомит учащихся с историей возникновения уравнений:
Первым руководством по решению задач с неизвестным, получившим широкую известность, стал труд багдадского ученого IX в. Мухаммеда Бен Мусы аль-Хорезми. Слово «аль-джебр» из арабского названия этого трактата — «Китаб аль-джебр Валь-мукабала» (» Книга о восстановлении и противопоставлении») — со временем превратилось знакомое всем слово «алгебра». А само сочинение аль-Хорезми послужило отправной точкой в становлении науки о решении уравнений.
В сочинении аль-Хорезми неизвестные величины, так же как и все сопутствующие выкладки и преобразования уравнений, выражались словесно.
Такой стиль изложения, характерный для раннего этапа развития алгебры, историки науки называют риторическим (красноречивым).
Новый великий прорыв в алгебре связан с именем французского ученого XVI в. Франсуа Виета. Он первым из математиков ввел буквенные обозначения для коэффициентов уравнения и неизвестных величин. А традицией обозначать неизвестные величины последними буквами латинского алфавита (х, y или z) мы обязаны соотечественнику Виета — Рене Декарту.
3) Внимание на слайд! (слайд 14) (2 мин)
Перед вами уравнения. Выпишите в тетрадь те уравнения, которые вы не знаете, как решить. Что, именно, в выписанных уравнениях, вызывает у вас затруднение? Как решить остальные уравнения?
Обучающиеся выписывают уравнения №№2, 3, 5
1) | 2х + 3х = 15 |
2) | – 3(2 – х) = 18 |
3) | 5х + 24 = – 4х – 12 |
4) | 3,2х = 0,64 |
5) | 2(2 – 3х) + 4 = 18 – (3 + х) |
6) | х : = – 9 |
4) Работа с алгоритмом.
Предлагаю вам познакомиться с алгоритмом решения таких уравнений. У вас на столе лежат карточки-консультанты, в которых представлен алгоритм решения уравнений и решенные примеры. Я предлагаю вам прочитать алгоритм и рассмотреть решенные примеры. На эту работу я отвожу вам 2 минуты. А теперь попробуем вместе решить уравнение.
Учитель у доски, ребята в тетрадях. С места, фронтально, пошагово читается алгоритм и проговаривается решение (ученики), а учитель записывает на доске. (3 мин)
ПРИМЕР НА ДОСКЕ | АЛГОРИТМ (ученики читают пошагово из карточек) |
–2х + 1 –3(х –4) = 3(3 – х) + 6, –2х + 1 –3х + 12 = 9 – 3х + 6, –5х + 13 = – 3х + 15, –5х + 3х = 15 – 13, –2х = 2, х = 2 : (– 2), х = –1. | 1) Раскрыть скобки (если они есть). 2) Привести подобные слагаемые в левой и правой частях уравнения (если они есть). 3) Перенести слагаемые с переменными в левую часть уравнения, а числа в правую часть уравнения, изменяя знаки тех слагаемых, которые переносим. 4) Привести подобные слагаемые в левой и правой частях уравнения. Получаем уравнение вида: ɑ·x = b. 5) Разделить число из правой части на коэффициент перед переменной. |
Ребята, вы обратили внимание, что новое для вас правило (свойство уравнения) содержится в п.3 алгоритма. Чтобы вам было легче его запомнить предлагаю вам мнемонический прием:
— При переносе слагаемых из одной части уравнения в другую, нужно поменять знаки тех слагаемых, которые мы переносим – когда мы идем в гости – мы переодеваемся.
— Сначала записываем слагаемые, которые были в этой части уравнения (это – хозяин) – гости могут прийти, если хозяин дома (переодеваются только гости).
5. Первичное закрепление. (слайд 15) (15 мин)
Фронтально. Ученики по желанию у доски решают уравнения с использованием алгоритма.
а) 3 – 4х = 4х – 5;
б) 9(х + 7) = – х;
в) 10 – 3(1 – 7х) = –4х – 8.
г)
6. Рефлексия. (слайд 16) (5 мин)
Синквейн:
1-я строка – одно ключевое слово, определяющее содержание синквейна; (УРАВНЕНИЕ)
2-я строка – два прилагательных, характеризующих данное понятие; (ЛИНЕЙНОЕ, АЛГЕБРАИЧЕСКОЕ)
3-я строка – три глагола, обозначающих действие в рамках заданной темы; (РЕШАТЬ, УПРОЩАТЬ, ПЕРЕНОСИТЬ)
4-я строка – короткое предложение, раскрывающее суть темы или отношение к ней; (РЕШАТЬ УРАВНЕНИЕ ПО АЛГОРИТМУ)
5-я строка – синоним ключевого слова (существительное). (РАВЕНСТВО)
7. Итоги урока. Домашнее задание. (слайд 17) (3 мин)
§19, №580 (в, г), №582 (а, в), №585 (в, г)
Творческое задание: найти информацию и подготовить сообщение о способе решений уравнений, предложенном Мухаммеда Бен Мусы аль-Хорезми.
Используемые источники:
И.И. Зубарева, А.Г. Мордкович, Математика: 6 класс: учебник для учащихся общеобразовательных учреждений / М: Мнемозина, 2014 – 264 с.
И.И. Зубарева, Математика: 6 класс: мультимедийное приложение, п.18.
Шаблон презентации: http://ppt.znanio.ru/buy-now/
История возникновения уравнений http://mydocx.ru/3-94807.html
http://knowledge.allbest.ru/mathematics/3c0a65635a3bd78a5c53a89421216d37_0.html
раздаточный материал
PDF / 300.2 Кб
карточка-консультант «Алгоритм решения уравнений»
PDF / 252.23 Кб
математический диктант
PPT / 64.5 Кб
презентация к уроку «Уравнения»
PPTX / 1.7 Мб
урок «Уравнения», 6 класс
PDF / 571.74 Кб