Метод интервалов — материалы для подготовки к ЕГЭ по Математике
Метод интервалов – простой способ решения дробно-рациональных неравенств. Так называются неравенства, содержащие рациональные (или дробно-рациональные) выражения, зависящие от переменной.
1. Рассмотрим, например, такое неравенство
Метод интервалов позволяет решить его за пару минут.
В левой части этого неравенства – дробно-рациональная функция. Рациональная, потому что не содержит ни корней, ни синусов, ни логарифмов – только рациональные выражения. В правой – нуль.
Метод интервалов основан на следующем свойстве дробно-рациональной функции.
Дробно-рациональная функция может менять знак только в тех точках, в которых она равна нулю или не существует.
Найдем нули функции в левой части нашего неравенства. Для этого разложим числитель на множители. (Если вы не помните, что такое нули функции и знак функции на промежутке – смотрите статью «Исследование графика функции»).
Напомним, как раскладывается на множители квадратный трехчлен, то есть выражение вида .
, где и — корни квадратного уравнения .
Получим:
Рисуем ось и расставляем точки, в которых числитель и знаменатель обращаются в нуль.

Нули знаменателя и — выколотые точки, так как в этих точках функция в левой части неравенства не определена (на нуль делить нельзя). Нули числителя и — закрашены, так как неравенство нестрогое. При и наше неравенство выполняется, так как обе его части равны нулю.
Эти точки разбивают ось на промежутков.
Определим знак дробно-рациональной функции в левой части нашего неравенства на каждом из этих промежутков. Мы помним, что дробно-рациональная функция может менять знак только в тех точках, в которых она равна нулю или не существует. Это значит, что на каждом из промежутков между точками, где числитель или знаменатель обращаются в нуль, знак выражения в левой части неравенства будет постоянным — либо «плюс», либо «минус».
И поэтому для определения знака функции на каждом таком промежутке мы берем любую точку, принадлежащую этому промежутку. Ту, которая нам удобна.
. Возьмем, например, и проверим знак выражения в левой части неравенства. Каждая из «скобок» отрицательная. Левая часть имеет знак .

Следующий промежуток: . Проверим знак при . Получаем, что левая часть поменяла знак на .

. Возьмем . При выражение положительно — следовательно, оно положительно на всем промежутке от до .

При левая часть неравенства отрицательна.

И, наконец, . Подставим и проверим знак выражения в левой части неравенства. Каждая «скобочка» положительна. Следовательно, левая часть имеет знак .

Мы нашли, на каких промежутках выражение положительно. Осталось записать ответ:
Ответ: .
Обратите внимание: знаки на промежутках чередуются. Это произошло потому, что при переходе через каждую точку ровно один из линейных множителей поменял знак, а остальные сохранили его неизменным
.Мы видим, что метод интервалов очень прост. Чтобы решить дробно-рациональное неравенство методом интервалов, приводим его к виду:
, или , или , или .
(в левой части — дробно-рациональная функция, в правой — нуль).
Затем — отмечаем на числовой прямой точки, в которых числитель или знаменатель обращаются в нуль.
Эти точки разбивают всю числовую прямую на промежутки, на каждом из которых дробно-рациональная функция сохраняет свой знак.
Остается только выяснить ее знак на каждом промежутке.
Мы делаем это, проверяя знак выражения в любой точке, принадлежащей данному промежутку. После этого — записываем ответ. Вот и всё.
Но возникает вопрос: всегда ли знаки чередуются? Нет, не всегда! Надо быть внимательным и не расставлять знаки механически и бездумно.
Ты нашел то, что искал? Поделись с друзьями!
2. Рассмотрим еще одно неравенство.
Снова расставляем точки на оси . Точки и — выколотые, поскольку это нули знаменателя. Точка — тоже выколота, поскольку неравенство строгое.

При числитель положителен, оба множителя в знаменателе отрицательны. Это легко проверить, взяв любое число с данного промежутка, например, . Левая часть имеет знак :

При числитель положителен; первый множитель в знаменателе положителен, второй множитель отрицателен. Левая часть имеет знак :

При ситуация та же! Числитель положителен, первый множитель в знаменателе положителен, второй отрицателен. Левая часть имеет знак :

Наконец, при все множители положительны, и левая часть имеет знак :
Ответ: .
Почему нарушилось чередование знаков? Потому что при переходе через точку «ответственный» за неё множитель не изменил знак. Следовательно, не изменила знак и вся левая часть нашего неравенства.
Вывод: если линейный множитель стоит в чётной степени (например, в квадрате), то при переходе через точку знак выражения в левой части не меняется. В случае нечётной степени знак, разумеется, меняется.
3. Рассмотрим более сложный случай. От предыдущего отличается тем, что неравенство нестрогое:
Левая часть та же, что и в предыдущей задаче. Та же будет и картина знаков:

Может, и ответ будет тем же? Нет! Добавляется решение Это происходит потому, что при и левая, и правая части неравенства равны нулю — следовательно, эта точка является решением.
Ответ: .
В задаче на ЕГЭ по математике такая ситуация встречается часто. Здесь абитуриенты попадают в ловушку и теряют баллы. Будьте внимательны!
4. Что делать, если числитель или знаменатель не удается разложить на линейные множители? Рассмотрим такое неравенство:
Квадратный трехчлен на множители разложить нельзя: дискриминант отрицателен, корней нет. Но ведь это и хорошо! Это значит, что знак выражения при всех одинаков, а конкретно — положителен. Подробнее об этом можно прочитать в статье о свойствах квадратичной функции.
И теперь мы можем поделить обе части нашего неравенства на величину , положительную при всех . Придём к равносильному неравенству:
— которое легко решается методом интервалов.
Обратите внимание — мы поделили обе части неравенства на величину, о которой точно знали, что она положительна. Конечно, в общем случае не стоит умножать или делить неравенство на переменную величину, знак которой неизвестен.
5. Рассмотрим еще одно неравенство, на вид совсем простое:
Так и хочется умножить его на . Но мы уже умные, и не будем этого делать. Ведь может быть как положительным, так и отрицательным. А мы знаем, что если обе части неравенства умножить на отрицательную величину — знак неравенства меняется.
Мы поступим по другому — соберём всё в одной части и приведём к общему знаменателю. В правой части останется нуль:
И после этого — применим метод интервалов.
Метод интервалов
Метод интервалов — это специальный алгоритм, предназначенный для решения сложных неравенств вида f(x) > 0. Алгоритм состоит из 5 шагов:
- Решить уравнение f(x) = 0. Таким образом, вместо неравенства получаем уравнение, которое решается намного проще;
- Отметить все полученные корни на координатной прямой. Таким образом, прямая разделится на несколько интервалов;
- Найти кратность корней. Если корни четной кратности, то над корнем рисуем петлю. (Корень считается кратным, если существует четное количество одинаковых решений)
- Выяснить знак (плюс или минус) функции f(x) на самом правом интервале. Для этого достаточно подставить в f(x) любое число, которое будет правее всех отмеченных корней;
- Отметить знаки на остальных интервалах, чередуя их.
После этого останется лишь выписать интервалы, которые нас интересуют. Они отмечены знаком «+», если неравенство имело вид f(x) > 0, или знаком «−», если неравенство имеет вид f(x) < 0.
В случае с нестрогими неравенствами( ≤ , ≥) необходимо включить в интервалы точки, которые являются решением уравнения f(x) = 0;
Пример 1:
Решить неравенство:
(x — 2)(x + 7) < 0
Работаем по методу интервалов.
Шаг 1: заменяем неравенство уравнением и решаем его:
(x — 2)(x + 7) = 0
Произведение равно нулю тогда и только тогда, когда хотя бы один из множителей равен нулю:
x — 2 = 0 => x = 2
x + 7 = 0 => x = -7
Получили два корня.
Шаг 2: отмечаем эти корни на координатной прямой. Имеем:
Шаг 3: находим знак функции на самом правом интервале (правее отмеченной точки x = 2). Для этого надо взять любое число, которое больше числа x = 2. Например, возьмем x = 3 (но никто не запрещает взять x = 4, x = 10 и даже x = 10 000).
Получим:
f(x) = (x — 2)(x + 7)
x = 3
f(3)=(3 — 2)(3 + 7) = 1*10 = 10
Получаем, что f(3) = 10 > 0 (10 – это положительное число), поэтому в самом правом интервале ставим знак плюс.
Шаг 4: нужно отметить знаки на остальных интервалах. Помним, что при переходе через каждый корень знак должен меняться. Например, справа от корня x = 2 стоит плюс (мы убедились в этом на предыдущем шаге), поэтому слева обязан стоять минус. Этот минус распространяется на весь интервал (−7; 2), поэтому справа от корня x = −7 стоит минус. Следовательно, слева от корня x = −7 стоит плюс. Осталось отметить эти знаки на координатной оси.
Вернемся к исходному неравенству, которое имело вид:
(x — 2)(x + 7) < 0
Итак, функция должна быть меньше нуля. Значит, нас интересует знак минус, который возникает лишь на одном интервале: (−7; 2). Это и будет ответ.
Пример 2:
Решить неравенство:
(9x2 — 6x + 1)(x — 2) ≥ 0
Решение:
Для начала необходимо найти корни уравнения
(9x2 — 6x + 1)(x — 2) = 0
Свернем первую скобку, получим:
(3x — 1)2(x — 2) = 0
Отсюда:
x — 2 = 0; (3x — 1)2 = 0
Решив эти уравнения получим:
x1 = 2; x2 = ; x3= ;
Нанесем точки на числовую прямую:
Т.к. x2 и x3 – кратные корни, то на прямой будет одна точка и над ней “петля”.
Возьмем любое число меньшее самой левой точки и подставим в исходное неравенство. Возьмем число -1.
(9*(-1)2 — 6*(-1) + 1)(-1 — 2) = -12
Т.к. решение уравнения при x = -1 отрицательное (-12), то на графике в крайнем левом интервале пишем -, и далее чередуя знак записываем его в следующие интервалы:
Далее выбираем отрицательные интервалы, т.к. знак нашего неравенства ≤.
Не забываем включать решение уравнения (найденные X), т.к. наше неравенство нестрогое.
Ответ: {} U [2;+∞)
Пример 3:
Решить неравенство:
(9x2 — 6x + 1)(x — 2) > 0
Все, чем данное неравенство отличается от предыдущего – вместо нестрогого неравенства (≥) стоит строгое (>). Как ни странно, решение данного неравенства будет иным.
Найдем корни уравнения (9x2 — 6x + 1)(x — 2) ≠ 0 (знак ≠ означает, что найденные корни не могут быть решениями нашего неравенства, т.к. оно строгое). Проделав все этапы, что и в предыдущем примере получим:
x1= 2; x2,3 =;
Вынесем наши решения на числовую прямую (обратите внимания, что данные точки не включены, т.к. неравенство строгое, т.е. левая часть неравенства не равна нулю)
Обратите внимание, что корни x2 и x3 совпадают, корень “” является кратным. Соответственно, в данной точке на числовой прямой рисуем петлю.
Возьмем число -1.
(9*(-1)2 — 6*(-1) + 1)(-1 — 2) = -12
Т.к. решение уравнения при x = -1 отрицательное (-12), то на графике в крайнем левом интервале пишем -, и далее чередуя знак записываем его в следующие интервалы:
Далее выбираем отрицательные интервалы, т.к. знак нашего неравенства <.
Найденные корни не включаем в ответ.
Ответ: (2;+∞).
Метод интервалов. Видеоурок. Алгебра 11 Класс
Тема: Уравнения и неравенства. Системы уравнений и неравенств
Урок: Метод интервалов
Изложим метод интервалов на примере решения конкретного неравенства:
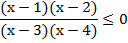
Решить данное неравенство означает найти все х, при которых неравенство выполняется.
Данный метод заключается в ом, что мы вводим функцию, стоящую в левой части, когда справа ноль.

Следует изучить данную функцию, ее свойства и интервалы знакопостоянства, после этого вернуться к решению неравенства.
Введенная функция у непрерывна в своей ОДЗ, укажем ОДЗ:
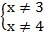
Найдем корни:
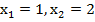
Выделим интервалы знакопостоянства. Мы нашли корни функции и точки разрыва области определения – корни знаменателя. Функция может изменить свой знак только при переходе через корень числителя или корень знаменателя. Важно отметить, что внутри каждого интервала функция сохраняет знак.

Рис. 1. Интервалы знакопостоянства функции
Чтобы определить знак функции на каждом интервале, необходимо взять любую точку, принадлежащую интервалу, подставить ее в функцию и определить ее знак. Например:
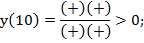
На интервале 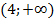 функция имеет знак плюс.
функция имеет знак плюс.
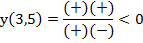
На интервале 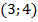
В этом преимущество метода интервалов: мы определяем знак в единственной пробной точке и заключаем, что функция будет иметь такой же знак на всем выбранном интервале.
Обратим внимание на то, что функция не всегда меняет знак при переходе на соседний интервал.
Теперь мы можем вернуться к неравенству и получить ответ. Нас интересуют значения функции, меньшие либо равные нулю. Отсюда ответ:
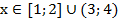
При решении неравенств методом интервалов несложно получить решение такой задачи, как построение эскиза графика функции.
Пример 1 – построить эскиз графика функции:

1. Выделим интервалы знакопостоянства и определим на каждом знак функции (рисунок 1)
2. Построим график в окрестности каждого корня. Напомним, что корни данной функции 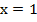 и
и 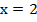 :
:
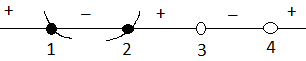
Рис. 2. График в окрестностях корней
Поскольку в точке 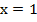 знак функции меняется с плюса на минус, то кривая сначала находится над осью, потом проходит через ноль и далее расположена под осью х. В точке
знак функции меняется с плюса на минус, то кривая сначала находится над осью, потом проходит через ноль и далее расположена под осью х. В точке 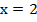 наоборот.
наоборот.
3. Построим график в окрестности каждого разрыва ОДЗ. Напомним, что корни знаменателя данной функции 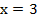 и
и 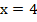 :
:
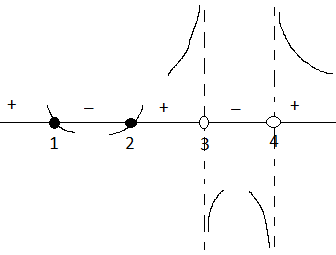
Рис. 3. График функции в окрестностях точек разрыва ОДЗ
Когда 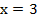 или
или 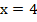 , знаменатель дроби практически равен нулю, значит, когда значение аргумента стремится к этим числам, значение дроби стремится к бесконечности. В данном случае, когда аргумент подходит к тройке слева, функция положительна и стремится к плюс бесконечности, справа функция отрицательна и выходит из минус бесконечности. Около четверки, наоборот, слева функция стремится к минус бесконечности, а справа выходит из плюс бесконечности.
, знаменатель дроби практически равен нулю, значит, когда значение аргумента стремится к этим числам, значение дроби стремится к бесконечности. В данном случае, когда аргумент подходит к тройке слева, функция положительна и стремится к плюс бесконечности, справа функция отрицательна и выходит из минус бесконечности. Около четверки, наоборот, слева функция стремится к минус бесконечности, а справа выходит из плюс бесконечности.
Согласно построенному эскизу, мы можем в некоторых промежутках угадать характер поведения функции (рис. 4).
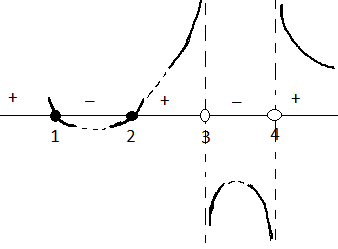
Рис. 4. Эскиз графика к примеру 1
Рассмотрим следующую важную задачу – построить эскиз графика функции в окрестностях бесконечно удаленных точек, т. е. когда аргумент стремится к плюс или минус бесконечности (рис. 5). Постоянными слагаемыми при этом можно пренебречь. Имеем:
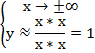
Иногда можно встретить такую запись данного факта:
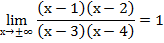
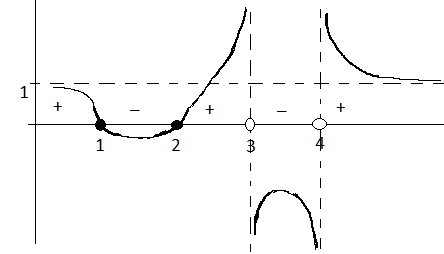
Рис. 5. Эскиз графика функции в окрестностях бесконечно удаленных точек
Мы получили приблизительный характер поведения функции на всей ее области определения, далее нужно уточнять построения с применением производной.
Следующий пример предостережет нас от типовых ошибок, в частности, от потери изолированного решения.
Пример 2 – решить неравенство:
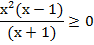
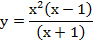
ОДЗ: 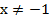
Корни: 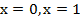
Выделяем интервалы знакопостоянства и определяем знаки функции на выбранных интервалах:
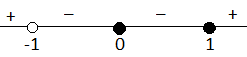
Рис. 6. Интервалы знакопостоянства к примеру 2
Отметим, что в данном случае один из корней имеет четную степень, а именно 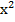 , поэтому, проходя через ноль, функция не меняет знак.
, поэтому, проходя через ноль, функция не меняет знак.
Ответ: 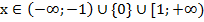
Теперь построим эскиз графика функции по общей методике. Интервалы знакопостоянства уже определены (рисунок 8). теперь построим график в окрестностях корней и точек разрыва ОДЗ:

Рис. 7. График функции в окрестностях корней и точек разрыва
Рассмотрим поведение функции в окрестностях бесконечно удаленных точек.
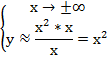
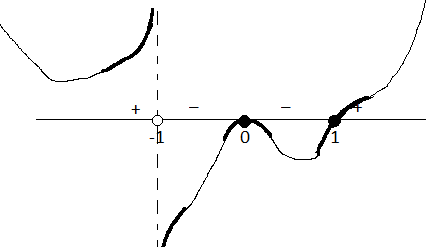
Рис. 8. Эскиз к примеру 2
Метод интервалов применим для решения самых разнообразных неравенств, в том числе иррациональных.
Пример 3 – решить неравенство:
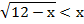
Переносим х в левую часть и рассматриваем ее как функцию:
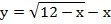
ОДЗ: 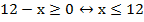
Корни: 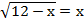
В данном случае корень можно легко угадать. Слева стоит убывающая функция, справа – возрастающая, значит, если уравнение имеет корень, то он единственный, таким образом, имеем корень 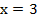
Покажем интервалы знакопостоянства и определим знаки функции на каждом интервале:
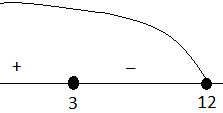
Рис. 10. Интервалы знакопостоянства к примеру 3
Для определения знаков берем пробные точки:
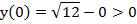
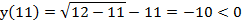
Здесь важно проверить значения в граничных точках. Левая граница интервала 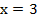 – это корень уравнения, в данной точке функция равна нулю, значит, ее не нужно включать в ответ.
– это корень уравнения, в данной точке функция равна нулю, значит, ее не нужно включать в ответ.
Проверим правую границу:
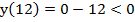
Таким образом, получили ответ: 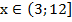
Итак, мы рассмотрели решение различных неравенств методом интервалов, решили некоторые типовые задачи и показали типовые ошибки. Далее перейдем к системам и совокупностям неравенств.
Список литературы
1. Мордкович А.Г. Алгебра и начала математического анализа. – М.: Мнемозина.
2. Муравин Г.К., Муравина О.В. Алгебра и начала математического анализа. – М.: Дрофа.
3. Колмогоров А.Н., Абрамов А.М., Дудницын Ю.П. и др. Алгебра и начала математического анализа. – М.: Просвещение.
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
1. ЕГЭ по математике (Источник).
2. Terver.ru (Источник).
3. Павел Бердов (Источник)
Домашнее задание
1. Решить неравенство:
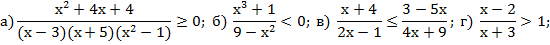
2. Построить эскиз графика функции:
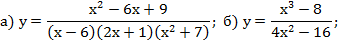

3. Решить неравенство:
а) 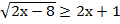 ;
;
б) 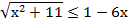 ;
;
в) 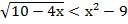 ;
;
г) 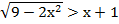
Подготовка к ЕГЭ «Метод интервалов»
Метод интервалов
1. Рассмотрим, например, неравенство:
В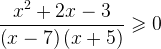 левой части этого неравенства – дробно-рациональная функция. Рациональная, потому что не содержит ни корней, ни синусов, ни логарифмов – только рациональные выражения. В правой – нуль.
левой части этого неравенства – дробно-рациональная функция. Рациональная, потому что не содержит ни корней, ни синусов, ни логарифмов – только рациональные выражения. В правой – нуль.
Известно, что дробно-рациональная функция может менять знак только в тех точках, в которых она равна нулю или не существует.
Найдем нули функции в левой части нашего неравенства. Для этого разложим числитель на множители.
Напомним, что если где 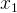 и
и 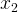 — корни квадратного уравнения
— корни квадратного уравнения 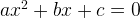 , тогда
, тогда 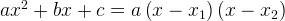 ,.
,.
Расставляем на оси Ох точки, в которых числитель и знаменатель обращаются в нуль.
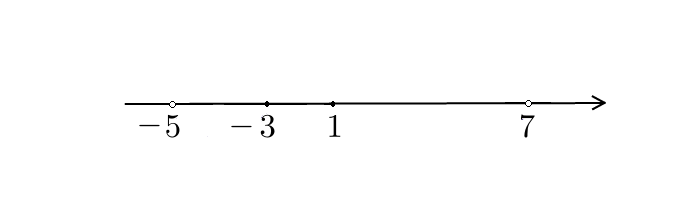
Нули знаменателя 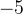 и
и 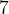 — выколотые точки, так как в этих точках функция в левой части неравенства не определена (на нуль делить нельзя). Нули числителя
— выколотые точки, так как в этих точках функция в левой части неравенства не определена (на нуль делить нельзя). Нули числителя 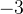 и
и  — закрашены, так как неравенство нестрогое. При
— закрашены, так как неравенство нестрогое. При  и
и 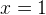 наше неравенство выполняется, так как обе его части равны нулю.
наше неравенство выполняется, так как обе его части равны нулю.
Эти точки разбивают ось 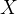 на
на 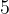 промежутков.
промежутков.
Определим знак дробно-рациональной функции в левой части нашего неравенства на каждом из этих промежутков. На каждом из промежутков между точками, где числитель или знаменатель обращаются в нуль, знак выражения в левой части неравенства будет постоянным — либо «плюс», либо «минус».
И поэтому для определения знака функции на каждом таком промежутке берем любую «пробную» точку, принадлежащую этому промежутку, обычно ту, которая удобна для вычисления.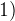
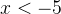 . Возьмем, например,
. Возьмем, например, 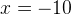 и проверим знак выражения в левой части неравенства. Левая часть имеет знак
и проверим знак выражения в левой части неравенства. Левая часть имеет знак  .
.
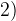 Следующий промежуток:
Следующий промежуток: 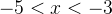 . Проверим знак при
. Проверим знак при 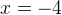 . Получаем, что левая часть поменяла знак на
. Получаем, что левая часть поменяла знак на 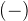 .
.
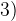
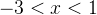 . Возьмем
. Возьмем 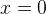 , выражение левой части неравенства положительно — следовательно, оно положительно на всем промежутке от
, выражение левой части неравенства положительно — следовательно, оно положительно на всем промежутке от 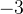 до
до  .
.
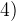 При
При 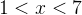 левая часть неравенства отрицательна.
левая часть неравенства отрицательна.
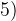 И, наконец,
И, наконец, 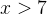 . Подставим
. Подставим 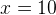 и проверим знак выражения в левой части неравенства. Левая часть имеет знак
и проверим знак выражения в левой части неравенства. Левая часть имеет знак  .
.
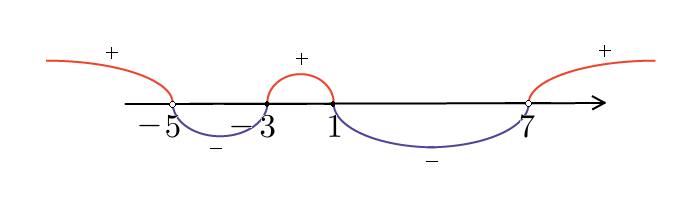
Мы нашли, на каких промежутках выражение положительно. Осталось записать ответ:
Ответ: 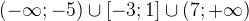 .
.
Мы видим, что метод интервалов очень прост. Чтобы решить дробно-рациональное неравенство методом интервалов, приводим его к виду:
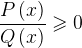 , или
, или 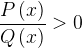 , или
, или 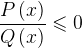 , или
, или 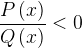 .
.
(в левой части — дробно-рациональная функция, в правой — нуль).
Затем — отмечаем на числовой прямой точки, в которых числитель или знаменатель обращаются в нуль. Эти точки разбивают всю числовую прямую на промежутки, на каждом из которых дробно-рациональная функция сохраняет свой знак. Остается только выяснить ее знак на каждом промежутке.
Мы делаем это, проверяя знак выражения  в любой точке, принадлежащей данному промежутку. После этого — записываем ответ.
в любой точке, принадлежащей данному промежутку. После этого — записываем ответ.
В рассмотренном примере знаки выражения чередовались, возникает вопрос: всегда ли знаки чередуются? Нет, не всегда!
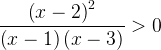
2. Рассмотрим еще одно неравенство.
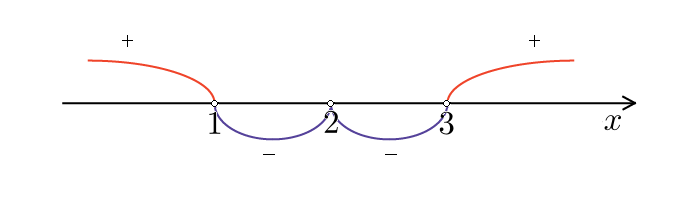
Снова расставляем точки на оси 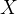 . Точки
. Точки  и
и 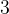 — выколотые, поскольку это нули знаменателя. Точка
— выколотые, поскольку это нули знаменателя. Точка 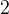 — тоже выколота, поскольку неравенство строгое.
— тоже выколота, поскольку неравенство строгое.
При 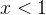 числитель положителен, оба множителя в знаменателе отрицательны. Это легко проверить, взяв любое число с данного промежутка, например,
числитель положителен, оба множителя в знаменателе отрицательны. Это легко проверить, взяв любое число с данного промежутка, например, 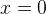 . Левая часть имеет знак
. Левая часть имеет знак  :
:
При 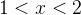 числитель положителен; первый множитель в знаменателе положителен, второй множитель отрицателен. Левая часть имеет знак
числитель положителен; первый множитель в знаменателе положителен, второй множитель отрицателен. Левая часть имеет знак 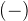 :
:
При 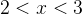 ситуация та же! Числитель положителен, первый множитель в знаменателе положителен, второй отрицателен. Левая часть имеет знак
ситуация та же! Числитель положителен, первый множитель в знаменателе положителен, второй отрицателен. Левая часть имеет знак 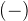 :
:
Наконец, при 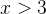 все множители положительны, и левая часть имеет знак
все множители положительны, и левая часть имеет знак  :
:
Ответ: 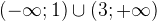 .
.
Почему нарушилось чередование знаков? Потому что при переходе через точку 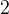 «ответственный» за неё множитель
«ответственный» за неё множитель  не изменил знак. Следовательно, не изменила знак и вся левая часть нашего неравенства.
не изменил знак. Следовательно, не изменила знак и вся левая часть нашего неравенства.
Вывод: если линейный множитель  стоит в чётной степени (например, в квадрате), то при переходе через точку
стоит в чётной степени (например, в квадрате), то при переходе через точку 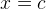 знак выражения в левой части не меняется. В случае нечётной степени знак, разумеется, меняется.
знак выражения в левой части не меняется. В случае нечётной степени знак, разумеется, меняется.
3. Рассмотрим более сложный случай. От предыдущего отличается тем, что неравенство нестрогое:
Левая часть та же, что и в предыдущей задаче. Та же будет и картина знаков:
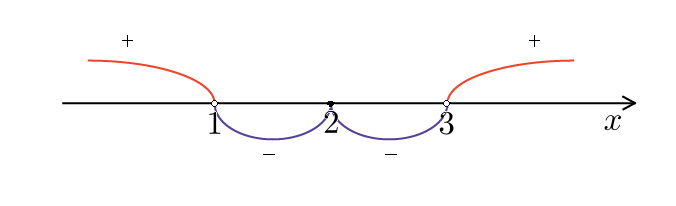
Ответ будет тем же? Нет! Добавляется решение 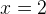 Это происходит потому, что при
Это происходит потому, что при 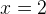 и левая, и правая части неравенства равны нулю — следовательно, эта точка является решением.
и левая, и правая части неравенства равны нулю — следовательно, эта точка является решением.
Ответ: 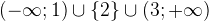 .
.
В задачах на ЕГЭ по математике такая ситуация встречается часто. Здесь абитуриенты попадают в ловушку и теряют баллы. Будьте внимательны!
4. Что делать, если числитель или знаменатель не удается разложить на линейные множители? Рассмотрим такое неравенство:
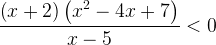
Квадратный трехчлен  на множители разложить нельзя: дискриминант отрицателен, корней нет. Это значит, что знак выражения
на множители разложить нельзя: дискриминант отрицателен, корней нет. Это значит, что знак выражения  при всех
при всех 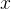 одинаков, а конкретно — положителен.
одинаков, а конкретно — положителен.
И теперь мы можем поделить обе части нашего неравенства на величину  , положительную при всех
, положительную при всех 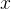 . Придём к неравенству:
. Придём к неравенству:
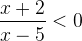 , которое легко решается методом интервалов.
, которое легко решается методом интервалов.
Обратите внимание — мы поделили обе части неравенства на величину, о которой точно знали, что она положительна. Конечно, в общем случае не стоит умножать или делить неравенство на переменную величину, знак которой неизвестен.
5. Рассмотрим еще одно неравенство:  .
.
Хочется умножить его на 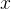 . Но мы не будем этого делать. Ведь
. Но мы не будем этого делать. Ведь 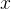 может быть как положительным, так и отрицательным. Но, если обе части неравенства умножить на отрицательную величину — знак неравенства меняется.
может быть как положительным, так и отрицательным. Но, если обе части неравенства умножить на отрицательную величину — знак неравенства меняется.
Мы поступим по другому — соберём всё в одной части и приведём к общему знаменателю. В правой части останется нуль:
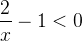
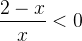
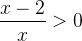
И только после этого можно применять метод интервалов…
Задания:
Задание 1Реши неравенство (t−8)(t+2)≤0
Задание 2
Реши неравенство (z−12)(4z+3)≤0
Задание 3
Реши неравенство (x+4)(x+7)≤0.
Задание 4
Реши неравенство x(2x + 8)(x − 3) > 0
Задание 5
Реши неравенство 
Задание 6
Реши неравенство 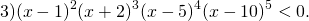
Задание 7
Реши неравенство 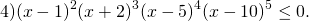
Задание 8
Реши неравенство 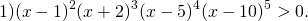
Задание 9
Реши неравенство 
Задание 10
Реши неравенство 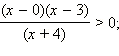
Задание 11
Реши неравенство 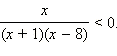
Задание 12
Реши неравенство 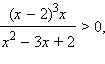
Задание 13
Реши неравенство 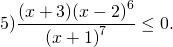
Задание 14
Реши неравенство 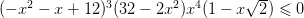
Задание 15
Реши неравенство 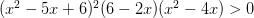
Задание 16
Реши неравенство 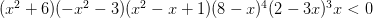
Задание 17
Реши неравенство 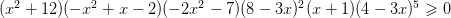
Задание 18
Реши неравенство 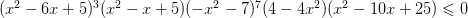
Задание 19
Реши неравенство 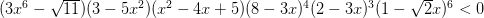
Задание 20
Реши неравенство 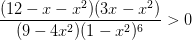
Решение неравенств методом интервалов
Описание презентации по отдельным слайдам:
1 слайд Описание слайда:
Описание слайда:Решение неравенств методом интервалов
2 слайд Описание слайда:
Описание слайда:Цели урока: Познакомить учащихся с решением неравенств методом интервалов. Отработка навыка решения неравенств методом интервалов. Повторить решение неравенств второй степени с одной переменной с помощью графика. Для подготовки к ГИА повторить нахождение «нулей функции», решение квадратных уравнений по формуле, решение неполных квадратных уравнений. Воспитание внимания, ответственного отношения к учебе; тренировать память.
3 слайд Описание слайда:
Описание слайда:а) x2 16, б)x2 121, в) 3x 48, г) x2 5x + 6, 1.Разложить на множители: (х 4)(х + 4) (х 11)(х + 11) 3(х 16) (х 2)(х 3)
4 слайд Описание слайда:
Описание слайда:2. Найти область определения функции. х -любое х ≠ ±2 х ≠ 0 и х ≠ 3 х ≠ 0 и х ≠ 2 y=(x+2)(x-3)
5 слайд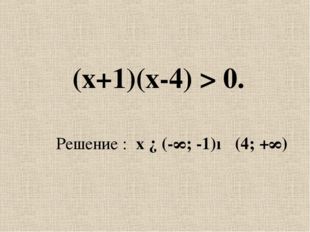 Описание слайда:
Описание слайда:(х+1)(х-4) > 0. Решение : x ∈(-∞; -1)∪ (4; +∞)
6 слайд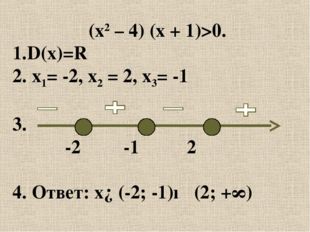 Описание слайда:
Описание слайда:(х2 – 4) (х + 1)>0. 1.D(x)=R 2. х1= -2, х2 = 2, х3= -1 3. -2 -1 2 4. Ответ: x∈(-2; -1)∪ (2; +∞)
7 слайд Описание слайда:
Описание слайда:№305 А) D =49 Х1 =1; Х2 = -2,5 1 -2,5 Ответ: Б) D=900 Х1 = -2; Х2 = 3 -2 3 Ответ: Правило
8 слайд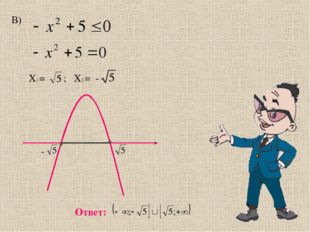 Описание слайда:
Описание слайда:В) Х1 = ; Х2 = — — Ответ:
9 слайд Описание слайда:
Описание слайда:№304(д-з) Д) Ответ: Е) Ответ: Ж) Ответ: З) Ответ: Решений нет 1,5 -0,6 0 0,9 0 3,5
10 слайд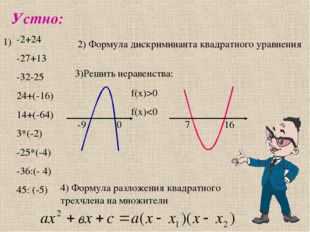 Описание слайда:
Описание слайда:Устно: -2+24 -27+13 -32-25 24+(-16) 14+(-64) 3*(-2) -25*(-4) -36:(- 4) 45: (-5) 1) 2) Формула дискриминанта квадратного уравнения 3)Решить неравенства: f(x)>0 f(x)<0 -9 0 7 16 4) Формула разложения квадратного трехчлена на множители
11 слайд Описание слайда:
Описание слайда:Гимнастика для глаз
12 слайд Описание слайда:
Описание слайда:решение с помощью графика квадратичной функции; методом интервалов. 1 2 Назад на титульный лист Рассмотрим решение неравенств второй степени с одной переменной.
13 слайд Описание слайда:
Описание слайда:1) Рассмотрим квадратичную функцию f(x) = x2 – 5 x — 50 и найдем такие значения x, для которых f(x) < 0. 2) Графиком рассматриваемой функции является парабола, ветви которой направлены вверх, так как a = 1, 1 > 0. 3) Найдем нули функции (то есть абсциссы точек пересечения параболы с осью Ox), для этого решим квадратное уравнение x2 – 5 x – 50 = 0. x2 – 5 x – 50 = 0, a = 1, b = -5, c = -50. D = b2 – 4ac; D = (-5)2 –4*1*(-50) = 25 + 200 = 225 = 152, 225 > 0, значит уравнение имеет два действительных корня. x1 = (-(-5) – 15) : 2 = -5; x2 = (-(-5) + 15) : 2 = 10. Нули функции: x = -5 и x = 10. далее » Метод рассмотрения квадратичной функции « назад
14 слайд Описание слайда:
Описание слайда:4) Изобразим схематично параболу f(x) = x2 – 5x –50 в координатной плоскости Oxy. 5) Из рисунка видим, что f(x) < 0, при –5 < x < 10 (то есть берем в рассмотрение ту часть параболы, которая лежит ниже оси Ox). Замечание: ответ записываем в виде числового промежутка. Ответ: (-5; 10). « назад
15 слайд Описание слайда:
Описание слайда:далее » Метод интервалов « назад Рассмотрим функцию f(x) = (х+2)(х-3)(х-5) . Область определения D(f) = R (то есть множество всех действительных чисел). 2) Найдем нули функции, т.е.решим уравнений f(x)=0. (х+2)(х-3)(х-5)=0 х+2=0 или х-3=0 или х-5=0 х = -2 х = 3 х=5 или или Числа -2, 3, 5 – нули функции, они разбивают область определения функции на промежутки -2 3 5
16 слайд Описание слайда:
Описание слайда:« назад далее» -2 3 5 Выясним, каковы знаки этой функции в каждом из указанных промежутков Выражение (х+2)(х-3)(х-5) представляет собой произведение 3 множителей. Знак каждого из этих множителей в рассматриваемых промежутках указан в таблице Мы видим, что в каждом из промежутков функция сохраняет знак, а при переходе через точки -2, 3, 5 ее знак изменяется. Правило: стр 89
17 слайд Описание слайда:
Описание слайда:далее » Это свойство используется для решения неравенств вида (х-х1)(х-х2)(х-х3)…(х-хn)>0 или (х-х1)(х-х2)(х-х3)…(х-хn)<0, где х1, х2, …хn – не равные нулю числа. №1. Решить неравенство (х+6)(х+1)(х-4)<0 Находим нули функции (х+6)(х+1)(х-4)=0 х+6=0 или х+1=0 или х-4=0 х = -6 или х = -1 или х = 4 Отмечаем эти числа -6, -1, 4 (нули функции) пустыми кружками (т.к неравенство строго больше 0) на числовой прямой. Числа разбивают числовую прямую на промежутки, в каждом из которых функция сохраняет знак. -6 -1 4
18 слайд Описание слайда:
Описание слайда:-6 -1 4 Определим знак функции f(x)= (х+6)(х+1)(х-4) на каждом из промежутков -7 -3 0 6 Если х = -7, то f(-7) = (-7+6)(-7+1)(-7-4) < 0 — — — Если х = -3, то f(-3) = (-3+6)(-3+1)(-3-4) > 0 + — — + + Если х = 0, то f(0) = (()+6)(0+1)(()-4) < 0 Если х = 6, то f(6) = (6+6)(6+1)(6-4) + + + + + + + Мы решаем неравенство (х+6)(х+1)(х-4)<0. Нас интересует, на каких промежутках функция принимает значения меньшие нуля. Ответ:
19 слайд Описание слайда:
Описание слайда:Данный метод решения неравенств называется методом интервалов Попробуйте решить неравенства данным методом: №325 (х+8)(х-5) > 0 (х+8)(х-5)=0 х+8=0 или х-5=0 х = — 8 или х = 5 -8 5 -10 0 7 f(x) = (x+8)(x-5) х = — 10, f(-10)=(-10+8)(-10-5) > 0 х = 0, f(0)=(0+8)(0-5) < 0 х = 7, f(7)=(7+8)(7-5)>0 + + Ответ:
20 слайд Описание слайда:
Описание слайда:Алгоритм решения неравенств методом интервалов: 1. Выделить функцию вида f(x)=(x-x1)…(x-xn) 2.Найти ОДЗ функции y = f(x). 3. Найти нули функции y = f(x) (f(x)=0) 4. Нанести нули на ОДЗ. Определить знаки функции f(x) в каждом интервале, на которые разбивается ОДЗ нулями функции. 5. Записать ответ.
21 слайд Описание слайда:
Описание слайда:Проверяем Б) Ответы В) Г) № 327. Ответы № 327 А) Б) В) Самостоятельная работа № 326
22 слайд Описание слайда:
Описание слайда:Домашнее задание: Правило на стр 89 № 326 — решить методом интервалов, № 306 – решить с помощью параболы (графически) Итог урока: Что узнали нового? Как называется новый метод решения неравенств второй степени с одной переменной? Какой способ решения неравенств вам больше понравился? Есть ли вопросы по д/з? Сможете ли вы его решить? Оценки
23 слайд Описание слайда:
Описание слайда:С каким настроением вы пришли сегодня на урок?

Курс профессиональной переподготовки
Учитель математики

Курс повышения квалификации
Курс повышения квалификации
Найдите материал к любому уроку,
указав свой предмет (категорию), класс, учебник и тему:
Выберите категорию: Все категорииАлгебраАнглийский языкАстрономияБиологияВсеобщая историяГеографияГеометрияДиректору, завучуДоп. образованиеДошкольное образованиеЕстествознаниеИЗО, МХКИностранные языкиИнформатикаИстория РоссииКлассному руководителюКоррекционное обучениеЛитератураЛитературное чтениеЛогопедия, ДефектологияМатематикаМузыкаНачальные классыНемецкий языкОБЖОбществознаниеОкружающий мирПриродоведениеРелигиоведениеРодная литератураРодной языкРусский языкСоциальному педагогуТехнологияУкраинский языкФизикаФизическая культураФилософияФранцузский языкХимияЧерчениеШкольному психологуЭкологияДругое
Выберите класс: Все классыДошкольники1 класс2 класс3 класс4 класс5 класс6 класс7 класс8 класс9 класс10 класс11 класс
Выберите учебник: Все учебники
Выберите тему: Все темы
также Вы можете выбрать тип материала:

Общая информация
Номер материала: ДБ-1219644
Похожие материалы
Вам будут интересны эти курсы:
Оставьте свой комментарий