Решение матричных уравнений
I. ВВЕДЕНИЕ В ЛИНЕЙНУЮ АЛГЕБРУ. КРАТКИЙ ОБЗОР
Матрицы. Начальные сведения
Рассматриваем
новый математический объект – матрицу.
Это абстрактная таблица, состоящая из  строк и
строк и  столбцов вида:
столбцов вида:
 , (1)
, (1)
где 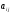 – элементы матрицы, стоящие на пересечении
– элементы матрицы, стоящие на пересечении  -ой
строки и
-ой
строки и 
 могут быть любой природы (числа,
многочлены, функции и др.) При этом
говорят, что матрица
могут быть любой природы (числа,
многочлены, функции и др.) При этом
говорят, что матрица  имеет размерность
имеет размерность  ,
и кратко записывают
,
и кратко записывают 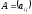 ,
где
,
где 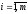 ,
,  .
. Если число строк
равно числу столбцов, то матрица
называется квадратной. Например, 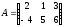
 – квадратная матрица.
– квадратная матрица. Элементы 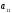 ,
, ,
,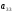 ,…,
,…, образуют главную диагональ в матрице
образуют главную диагональ в матрице 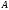 .
Если ниже главной диагонали стоят
нулевые элементы, то матрица называется
треугольной, например
.
Если ниже главной диагонали стоят
нулевые элементы, то матрица называется
треугольной, например

Матрица вида 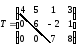
Если вне главной диагонали стоят нулевые элементы, то матрица называется диагональной, например

Матрица вида 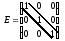 является
единичной.
является
единичной.
Матрица, состоящая только из нулевых элементов, называется нулевой матрицей:

Если элементы
матрицы, стоящие на симметричных местах
относительно главной диагонали совпадают: 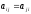 ,
то такая матрица называется симметрической.
,
то такая матрица называется симметрической.
Например

Матрица вида  называется матрицей-строкой, а матрица
вида называется
называется матрицей-строкой, а матрица
вида называется  – матрицей-столбцом.
– матрицей-столбцом.
Операции над матрицами
Сложение матриц и умножение матрицы на число называются линейными операциями. Они выполняются по следующим правилам:
 ,
где
,
где  .
. , где
, где 
Пример 1
 .
.
Умножение матриц выполняется по следующей схеме:
, где 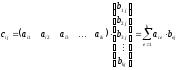 .
.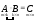
Заметим, что в левой матрице число столбцов совпадает с числом строк в правой матрице. Только в этом случае операция умножения возможна.
Пример 2

Пример 3
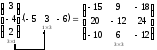
Замечание. В общем
случае умножение матриц неперестановочно,
т.е. 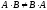 .
Однако, можно подобрать две квадратные
матрицы, чтобы
.
Однако, можно подобрать две квадратные
матрицы, чтобы  ,
в этом случае говорят, что матрицы
коммутируют.
,
в этом случае говорят, что матрицы
коммутируют.
Пример 4
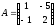 ,
,  ,
,
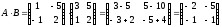 ;
;
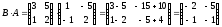 .
.
Матрицы можно возводить в степень, причем только квадратные, т.е. число столбцов должно соответствовать числу строк.
Рассмотрим еще одну операцию над матрицами – транспонирование. При транспонировании матрицы
 ее строки и столбцы меняются местами
с сохранением порядка. Обозначается
ее строки и столбцы меняются местами
с сохранением порядка. Обозначается  или
или  .
Транспонировать можно матрицы любой
размерности.
.
Транспонировать можно матрицы любой
размерности.
Пример 5
 .
.
Определители квадратных матриц
Прежде чем ввести
операцию обращения матриц 
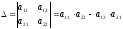 (2)
(2)
Таким образом,  ,
где
,
где 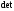 – первые три буквы от латинского
determinantis
(определитель). Так легко получается
детерминант 2-го порядка.
– первые три буквы от латинского
determinantis
(определитель). Так легко получается
детерминант 2-го порядка.
Пример 6
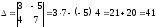 .
.
Однако для матрицы размера 3×3 определитель строится сложнее:

 (3)
(3)Для простоты запоминания пользуются следующими схемами:
первые три суммы последние три суммы
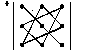
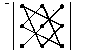
Схема называется правилом треугольников.
Модифицируем его, т.е. распрямим треугольники.
 –
схема Саррюса.(4)
–
схема Саррюса.(4)
Если квадратная матрица имеет размер 4×4 и выше, то для вычисления ее определителя применяется правило Лапласа:
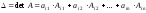
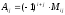 ,(5)
,(5) т.е. детерминант
матрицы 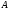 равен сумме произведений элементов
равен сумме произведений элементов 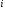 -ой
строки (или
-ой
строки (или 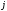 -го
столбца) на соответствующие алгебраические
дополнения.
-го
столбца) на соответствующие алгебраические
дополнения.
При этом  – минор (определитель
– минор (определитель  -го
порядка), получающийся из матрицы
-го
порядка), получающийся из матрицы  вычеркиванием
вычеркиванием 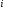
 -го
столбца,
-го
столбца,  – алгебраическое
дополнение к элементу
– алгебраическое
дополнение к элементу  .
. Заметим, что правило
Лапласа позволяет определители  -го
порядка вычислять через определители
-го
порядка вычислять через определители  -го
порядка.
-го
порядка.
Пример 7

Замечание. Если определитель матрицы приведен к треугольному виду
 ,
,
то его значение
равно произведению элементов, стоящих
по главной диагонали, т.е.  .
Это автоматически следует из правила
Лапласа.
.
Это автоматически следует из правила
Лапласа.
Отметим элементарные преобразования (Э.П.) над строками определителя, которые не меняют его значения:
вынесение общего множителя строки за знак определителя;
прибавление к одной строке элементов другой строки;
прибавление к одной строке элементов другой, умноженных на некоторое число.
Пример 8





 + =
+ =

 +
+ 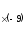

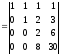





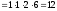
Замечание 1. Такие же Э.П. можно выполнять и над столбцами определителя.
Замечание 2. Определитель
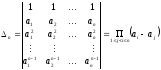
и называется определителем Вандермонда.
Студентам предлагается доказать это самостоятельно.
Нахождение обратной матрицы
Теперь можно
перейти к обращению квадратных матриц.
В этом случае  должен быть отличным от нуля, и матрица
должен быть отличным от нуля, и матрица  является невырожденной. Для такой
матрицы существует обратная матрица
является невырожденной. Для такой
матрицы существует обратная матрица  ,
причем
,
причем 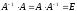 дает единичную матрицу. Легко показать,
что обратная матрица имеет вид:
дает единичную матрицу. Легко показать,
что обратная матрица имеет вид:
 ,(6)
,(6)
где  – алгебраические дополнения элементов
– алгебраические дополнения элементов 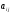 исходной матрицы:
исходной матрицы:

Поскольку

Предлагаем студентам самостоятельно это проверить.
Замечание. Обратную матрицу можно построить с помощью элементарных преобразований по следующей схеме:
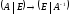 . (7)
. (7)
Пример 9
С помощью элементарных преобразований провести обращение матрицы
 .
.
Решение

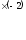 + –
+ – 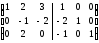
 +
+ 

 +
+ 
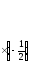


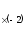 +
+ 
 +
+ 


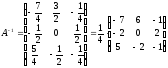 .
.
Действительно,
 .
.
Пусть задано уравнение
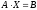 , (8)
, (8)
где матрица 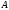 квадратная с
квадратная с  .
Тогда умножим слева заданное равенство
на
.
Тогда умножим слева заданное равенство
на 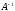 и получим
и получим
 или
или
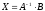 (9)
(9)
Заметим, что если
размерность матрицы  есть
есть 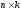 ,
то искомая матрица
,
то искомая матрица 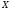 имеет такую же размерность, что и
имеет такую же размерность, что и 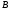 ,
поскольку
,
поскольку
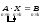

Аналогично решается уравнение
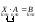

при этом
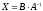 . (10)
. (10)
Пример 10
Решить матричное уравнение
 .
.
Решение
Имеем уравнение  ,
где
,
где 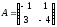 ,
,  .
Находим
.
Находим  ,
тогда
,
тогда  .
.
Вычислим
алгебраические дополнения матрицы 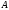 :
:
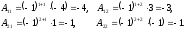
Таким образом, 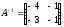 .
.
Сделаем проверку:  .
.
Искомое решение:  .
.
Проверить, что 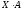 дает матрицу
дает матрицу 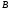 .
.
Решение квадратных систем линейных алгебраических уравнений (слау) матричным методом и по правилу Крамера
Пусть задана система вида:
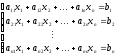 (11)
(11)
Запишем квадратную
матрицу системы размерности 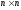 :
:
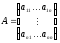 ,
матрицу-столбец из неизвестных
,
матрицу-столбец из неизвестных 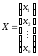 ,
и матрицу-столбец из свободных
коэффициентов
,
и матрицу-столбец из свободных
коэффициентов  .
.
В этих обозначениях система (11) примет вид:
 . (12)
. (12)
Если  ,
то решение матричного уравнения (12)
следующее:
,
то решение матричного уравнения (12)
следующее:
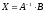 . (13)
. (13)
Заметим, что 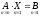 ,
т.е.
,
т.е.  –
матрица такой же размерности, что и
–
матрица такой же размерности, что и 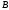 .
Формула для обратной матрицы
.
Формула для обратной матрицы
 .
.
Решение:
 .
.
Тем самым мы получили формулы Крамера:
 . (14)
. (14)
для СЛАУ (11), где
главный определитель системы 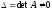 ,
а
,
а  – вспомогательные определители
(получающиеся из главного заменой
– вспомогательные определители
(получающиеся из главного заменой 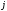 -го
столбца на столбец из свободных
коэффициентов). Например
-го
столбца на столбец из свободных
коэффициентов). Например
 можно обозначить
можно обозначить  .
.
Теорема 1 (Крамера).
СЛАУ (11) можно привести к виду:
 . (15)
. (15)
Тогда возможны три случая:
Если главный определитель
 ,
то система (11) имеет единственное
решение:
,
то система (11) имеет единственное
решение:
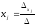 ,
где
,
где 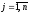 .
.
Если
 ,
а хотя бы один
,
а хотя бы один  ,
то система не
совместна (решений не имеет), поскольку
имеется противоречивое уравнение
,
то система не
совместна (решений не имеет), поскольку
имеется противоречивое уравнение  .
.Если
 и все
,
то система
имеет бесконечное число решений.
и все
,
то система
имеет бесконечное число решений.
Метод Гаусса
Для систем произвольного вида
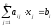 ,
где
,
где  (16)
(16)
(прямоугольных), где число уравнений не совпадает с числом неизвестных, применяется общий метод последовательного исключения (МПИ) неизвестных, основанный на элементарных преобразованиях типа:
умножение некоторого уравнения системы на отличное от нуля число;
прибавление к одному уравнению системы другого ее уравнения, умноженного на произвольное число, отличное от нуля;
перестановка местами двух уравнений системы.
Такие преобразования системы не изменяют множество ее решений и называются преобразованиями типа Гаусса. Заметим, что, выполняя преобразования 1–3 над уравнениями системы, соответствующие элементарные преобразования производятся над строками расширенной матрицы системы:
 .
.
Поэтому на практике экономичней проводить МПИ в матричной форме. После конечного числа шагов элементарных преобразований приходим к матрицам вида:
а)  или
или
б) 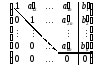
В случае а) система
примет треугольную форму и будет иметь
единственное решение, а в случае б)
система примет трапециевидную форму 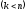 и будет иметь множество решений.
и будет иметь множество решений.
Заметим, что если
на некотором шаге появится строка  ,
, 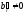 ,
то система будет несовместной, т.е. не
будет иметь решений.
,
то система будет несовместной, т.е. не
будет иметь решений.
Нахождение
неизвестных 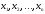 из преобразованной (треугольной или
трапецевидной) системы идет снизу вверх
и называется обратным ходом в методе
Гаусса.
из преобразованной (треугольной или
трапецевидной) системы идет снизу вверх
и называется обратным ходом в методе
Гаусса.
studfile.net
РЕШЕНИЕ МАТРИЧНЫХ УРАВНЕНИЙ — ПриМат
Матричные уравнения бывают трех типов.
Пример 1. Чтобы решить уравнение первого типа нужно обе части уравнения умножить на обратную к матрице слева.
,
, полученную матрицу транспонируем и умножим на . Обратная матрица к равна .
, . Сделаем проверку . Уравнение решили правильно.
Пример 2. Чтобы решить уравнение второго типа нужно обе части уравнения умножить на обратную к матрице справа.
Матрица обратная к равна .
Пример 3. Чтобы решить уравнение третьего типа нужно обе части уравнения умножить на обратную к матрице справа и на обратную матрице слева.
. Обратная матрица к равна обратная матрица к равна . .
Проверка .
Пример 4. Случай когда обратная матрица не существует.
.
Матрицу запишем как , .
\begin{cases}
3 \cdot x_{1}+4 \cdot x_{2} = 2\\
6 \cdot x_{1}+8 \cdot x_{2} = 4\\
3 \cdot x_{3}+4 \cdot x_{4} = 9\\
6 \cdot x_{3}+8 \cdot x_{4}=18
\end{cases}
Эта система эквивалентна
\begin{cases}
3 \cdot x_{1}+4 \cdot x_{2} = 2\\
3 \cdot x_{3}+4 \cdot x_{4} = 9
\end{cases}
Решив данную систему получим общей вид решения
Литература
Решение матричных уравнений
Лимит времени: 0
Навигация (только номера заданий)
0 из 2 заданий окончено
Вопросы:
- 1
- 2
Информация
Обращение матриц. Решение матричных уравнений
Вы уже проходили тест ранее. Вы не можете запустить его снова.
Тест загружается…
Вы должны войти или зарегистрироваться для того, чтобы начать тест.
Вы должны закончить следующие тесты, чтобы начать этот:
Результаты
Правильных ответов: 0 из 2
Ваше время:
Время вышло
Вы набрали 0 из 0 баллов (0)
| Средний результат |
|
| Ваш результат |
|
Рубрики
- Нет рубрики 0%
Загрузка
Имя: E-Mail: Капча:- 1
- 2
- С ответом
- С отметкой о просмотре
Задание 1 из 2
1.
Количество баллов: 1Решите матричное уравнение
$$X \cdot \begin{pmatrix} 5 & 3 & 1 \\ 1 & -3 & -2 \\ -5 & 2 & 1 \end{pmatrix}=\begin{pmatrix} 1 & -3 & 0 \\ 10 & 2 & 7 \\ 10 & 7 & 8 \end{pmatrix}$$- $$ \begin{pmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \\ 7 & 8 & 9 \end{pmatrix}$$
- $$ \begin{pmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \\ 7 & 8 & -9 \end{pmatrix}$$
- $$ \begin{pmatrix} 1 & 2 & -3 \\ 4 & 5 & 6 \\ 7 & 8 & 9 \end{pmatrix}$$
Правильно
Неправильно
Задание 2 из 2
2.
Количество баллов: 1Решите матричное уравнение
$$\begin{pmatrix} 2 & -3 & 1 \\ 14 & -5 & 2 \\ 5 & -7 & 3 \end{pmatrix} \cdot X \cdot \begin{pmatrix} 9 & 7 & 6 \\ 1 & 1 & 2 \\ 1 & 1 & 1 \end{pmatrix}=\begin{pmatrix} 2 & 0 & -2 \\ 18 & 12 & 9 \\ 23 & 15 & 11 \end{pmatrix}$$- $$ \begin{pmatrix} 1 & 1 & 1 \\ 1 & 2 & 3 \\ 2 & 3 & 1 \end{pmatrix}$$
- $$ \begin{pmatrix} 1 & 1 & 1 \\ 1 & 2 & 3 \\ 2 & -3 & 1 \end{pmatrix}$$
- $$ \begin{pmatrix} 1 & 1 & -1 \\ 1 & 2 & 3 \\ 2 & 3 & 1 \end{pmatrix}$$
Правильно
Неправильно
Таблица лучших: Решение матричных уравнений
| Место | Имя | Записано | Баллы | Результат |
|---|---|---|---|---|
| Таблица загружается | ||||
| Нет данных | ||||
Поделиться ссылкой:
- Нажмите здесь, чтобы поделиться контентом на Facebook. (Открывается в новом окне)
- Нажмите, чтобы поделиться на LinkedIn (Открывается в новом окне)
- Нажмите, чтобы поделиться на Twitter (Открывается в новом окне)
- Нажмите, чтобы поделиться на Reddit (Открывается в новом окне)
- Нажмите для печати (Открывается в новом окне)
Похожее
ib.mazurok.com
Простейшие матричные уравнения
⇐ ПредыдущаяСтр 3 из 4Следующая ⇒
Рассмотрим матрицы
 ;
; 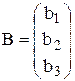 ;
; 
Причем элементы матриц А и В заданы, а Х1, Х2, Х3 – неизвестные.
Тогда уравнение А × Х = В называется простейшим матричным уравнением.
Чтобы его решить, т.е. найти элементы матрицы неизвестных Х, поступим следующим образом:
1. Умножим обе части уравнения на матрицу А-1, обратную для матрицы А, слева:
А-1 (А × Х) = А-1 × В
2. Используя свойство умножения матриц, запишем
(А-1 × А) Х = А-1 × В
3. Из определения обратной матрицы
(А-1 × А = Е) имеем Е × Х = А-1 × В.
4. Используя свойство единичной матрицы (Е × Х = Х), окончательно получим Х = А-1 × В
Замечание. Если матричное уравнение имеет вид Х × С = Д, то для нахождения неизвестной матрицы Х уравнение необходимо умножать на С-1справа.
Пример. Решить матричное уравнение

Решение. Введем обозначения
А = 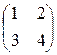 ; В =
; В = 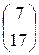 ,
,
Их определения умножения матриц с учетом размерностей А и В матрица неизвестных Х будет иметь вид
Х = 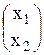
С учетом введенных обозначений имеем
А × Х = В откуда Х = А-1 × В
Найдем А-1 по алгоритму построения обратной матрицы
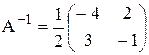
Вычислим произведение

Тогда для Х получим
Х = 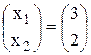 откуда х1 = 3, х2 = 2
откуда х1 = 3, х2 = 2
Ранг матрицы
Рассмотрим матрицу А размера (m x n)
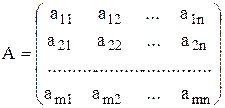
Минором к-ого порядка матрицы А будем называть определитель порядка к, элементами которого являются элементы матрицы А, стоящие на пересечении любых К строк и любых К столбцов. Очевидно, к £ min (m, n).
Определение. Рангом r(A) матрицы А называется наибольший порядок минора этой матрицы, отличного от нуля.
Определение. Всякий отличный от нуля минор матрицы, порядок которого равен ее рангу, называется базисным минором.
Определение. Матрицы, имеющие одинаковые ранги, называются эквивалентными.
Вычисление ранга матрицы
Определение. Матрица называется ступенчатой, если под первым ненулевым элементом каждой ее строки стоят нули в нижележащих строках.
Теорема. Ранг ступенчатой матрицы равен числу ее ненулевых строк.
Таким образом, преобразуя матрицу к ступенчатому виду, несложно определить ее ранг. Эта операция осуществляется с помощью элементарных преобразований матрицы, которые не изменяют ее ранга:
— умножение всех элементов ряда матрицы на число l ¹ 0;
— замена строк столбцами и наоборот;
— перестановка местами параллельных рядов;
— вычеркивание нулевого ряда;
— прибавление к элементам некоторого ряда соответствующих элементов параллельного ряда, умноженных на любое действительное число.
Пример. Вычислить ранг матрицы
А = 
Решение. Преобразуем матрицу к ступенчатому виду. Для этого к третьей строке прибавим вторую, умноженную на (-3).
А ~ 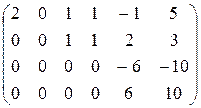
К четвертой строке прибавим третью.





 А ~
А ~ 
Число ненулевых строк в полученной эквивалентной матрице равно трем, следовательно r(А) = 3.
Системы n линейных уравнений с n неизвестными.
Методы их решения
Рассмотрим систему n линейных уравнений с n неизвестными.
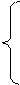 а11х1 + а12х2 + … + а1nxn = b1
а11х1 + а12х2 + … + а1nxn = b1
а21х1 + а22х2 + … + а2nxn = b2 (1)
……………………………….
аn1х1 + аn2х2 + … + аnnxn = bn
Определение: Решением системы (1) называется совокупность чисел (х1, х2, …, хn), которая обращает каждое уравнение системы в верное равенство.
Матрица А, составленная из коэффициентов при неизвестных, называется основной матрицей системы (1).
A = 
Матрица В, состоящая из элементов матрицы А и столбца свободных членов системы (1), называется расширенной матрицей.
В = 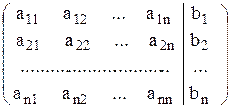
Матричный метод
Рассмотрим матрицы
Х =  — матрица неизвестных;
— матрица неизвестных;
С = 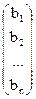 — матрица свободных членов системы (1).
— матрица свободных членов системы (1).
Тогда по правилу умножения матриц систему (1) можно представить в виде матричного уравнения
А × Х = С (2)
Решение уравнения (2) изложено выше, то есть Х = А-1 × С, где А-1 – обратная матрица для основной матрицы системы (1).
Метод Крамера
Система n линейных уравнений с n неизвестными, главный определитель которой отличен от нуля, всегда имеет решение и притом единственное, которое находится по формулам:

где D = det А – определитель основной матрицы А системы (1), который называется главным, Dхi получаются из определителя D заменой i-ого столбца столбцом из свободных членов, т.е.
D =  ;
;
Dх1 = 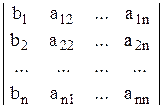 ;
;
Dх2 = 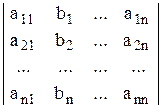 ; … ;
; … ;
Dхn =  ;
;
Пример. Решить систему уравнений методом Крамера
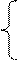 2х1 + 3х2 + 4х3 = 15
2х1 + 3х2 + 4х3 = 15
х1 + х2 + 5х3 = 16
3х1 — 2х2 + х3 = 1
Решение.
Вычислим определитель основной матрицы системы
D = det A = 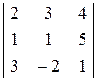 = 44 ¹ 0
= 44 ¹ 0
Вычислим вспомогательные определители
Dх1 =  = 0;
= 0;
Dх2 = 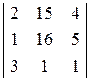 = 44;
= 44;
Dх3 =  = 132.
= 132.
По формулам Крамера найдем неизвестные
 ;
; 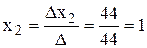 ;
; 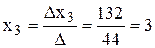 .
.
Таким образом, х1 = 0; х2 = 1; х3 = 3.
Метод Гаусса
Суть метода Гаусса заключается в последовательном исключении неизвестных из уравнений системы, т.е. в приведении основной матрицы системы к треугольному виду, когда под ее главной диагональю стоят нули. Это достигается с помощью элементарных преобразований матрицы над строчками. В результате таких преобразований не нарушается равносильность системы и она приобретает также треугольный вид, т.е. последнее уравнение содержит одну неизвестную, предпоследнее две и т.д. Выражая из последнего уравнения n-ую неизвестную и с помощью обратного хода, используя ряд последовательных подстановок, получают значения всех неизвестных.
Пример. Решить систему уравнений методом Гаусса
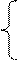 3х1 + 2х2 + х3 = 17
3х1 + 2х2 + х3 = 17
2х1 — х2 + 2х3 = 8
х1 + 4х2 — 3х3 = 9
Решение. Выпишем расширенную матрицу системы и приведем, содержащуюся в ней матрицу А к треугольному виду.
В = 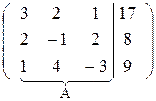
Поменяем местами первую и третью строки матрицы, что равносильно перестановке первого и третьего уравнений системы. Это позволит нам избежать появления дробных выражений при последующих вычислениях
В ~ 
Первую строку полученной матрицы умножим последовательно на (-2) и (-3) и сложим соответственно со второй и третьей строками, при этом В будет иметь вид:
В ~ 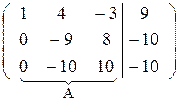
После умножения второй строки на 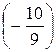 и сложения ее с третьей строкой матрица А примет треугольный вид. Однако чтобы упростить вычисления можно поступить следующим образом: умножим третью строку на (-1) и сложим со второй. Тогда получим:
и сложения ее с третьей строкой матрица А примет треугольный вид. Однако чтобы упростить вычисления можно поступить следующим образом: умножим третью строку на (-1) и сложим со второй. Тогда получим:
В ~ 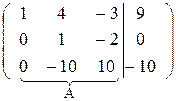
Далее, умножая вторую строку матрицы на 10 и складывая с третьей, окончательно получим:
В ~ 
Восстановим из полученной матрицы В систему уравнений, равносильную данной
 х1 + 4х2 — 3х3 = 9
х1 + 4х2 — 3х3 = 9
х2 — 2х3 = 0
— 10х3 = -10
Из последнего уравнения находим 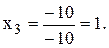 Найденное значение х3 = 1 подставим во второе уравнение системы, из которого х2 = 2х3 = 2 × 1 = 2.
Найденное значение х3 = 1 подставим во второе уравнение системы, из которого х2 = 2х3 = 2 × 1 = 2.
После подстановки х3 = 1 и х2 = 2 в первое уравнение для х1 получим х1 = 9 — 4х2 + 3х3 = 9 — 4 × 2 + 3 × 1 = 4.
Итак, х1 = 4, х2 = 2, х3 = 1.
Замечание. Для проверки правильности решения системы уравнений необходимо подставить найденные значения неизвестных в каждое из уравнений данной системы. При этом, если все уравнения обратятся в тождества, то система решена верно.
Проверка:
 3 × 4 + 2 × 2 + 1 = 17 верно
3 × 4 + 2 × 2 + 1 = 17 верно
2 × 4 — 2 + 2 × 1 = 8 верно
4 + 4 × 2 — 3 × 1 = 9 верно
Итак, система решена верно.
Рекомендуемые страницы:
lektsia.com
 ,
где
,
где 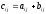 .
. , где
, где 
 ее строки и столбцы меняются местами
с сохранением порядка. Обозначается
ее строки и столбцы меняются местами
с сохранением порядка. Обозначается 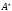 или
или 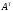 .
Транспонировать можно матрицы любой
размерности.
.
Транспонировать можно матрицы любой
размерности.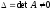 ,
то система (11) имеет единственное
решение:
,
то система (11) имеет единственное
решение: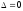 ,
а хотя бы один
,
а хотя бы один 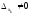 ,
то система не
совместна (решений не имеет), поскольку
имеется противоречивое уравнение
,
то система не
совместна (решений не имеет), поскольку
имеется противоречивое уравнение 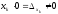 .
. и все
,
то система
имеет бесконечное число решений.
и все
,
то система
имеет бесконечное число решений.