Формула решения уравнения 4 степени / Хабр
Существует несколько методов нахождения корней полиномиального уравнения 4-ой степени.
Однако они не очень удобны при решении уравнений с коэффициентами, которые представляют собой выражения с параметрами.
Инстаграм
1. Формула решения уравнения 4 степени
Рассмотрим уравнение 4-ой степени, сумма корней которого равна нулю. Коэффициенты могут быть вещественными или комплексными.
Произведение следующих двух квадратов тождественно рассматриваемому уравнению 4-ой степени.
Значение R является решением следующего кубического уравнения.
Почти такое же уравнение появляется при решении уравнения 4-ой степени путем разложения на разность полных квадратов. Будем называть данное кубическое уравнение вспомогательным.
Вычислим произведение двух квадратов new.
То же самое, но в форме коэффициентов при степенях x (в порядке убывания степеней).
Упростим выражения для коэффициентов при второй и первой степени x.
Получается выражение
В общем описанные в п.2 преобразования не являются тождественными. Но если считать интересными только значения x, которые являются корнями исходного уравнения, то данные преобразования можно считать квазитождественными. И тогда y представляется выражением, соответствующим корням исходного уравнения.
3. Для кубического уравнения операция в п.2 производится еще один раз. В итоге получается система из 3 уравнений по x, которая имеет три ненулевых решения, соответствующих корням исходного уравнения. Из коэффициентов x формируем матрицу
4. Находим определитель матрицы, который представляется кубическим выражением по y.
Вычисляем значения, обеспечивающие равенство определителя нулю.
5. В уравнении по y имеются два параметра P и Q. Вычислим их так, чтобы нулю равнялись коэффициенты при второй и первой степени y.
Любое P
, где
6. В итоге имеем уравнение c тремя кратными корнями для y
7. Остается решить квадратное уравнение с известными y, P, Q
Остается решить квадратное уравнение с известными y, P, Q
Одно из решений будет решением исходного уравнения.
3. Параметры решения вспомогательного кубического уравнения
Для конкретных значений коэффициентов все выглядит не таким страшным образом.
Отметим, что для формулы решения уравнения 4-ой степени требуется только один корень R вспомогательного кубического уравнения.
Для конкретных коэффициентов вспомогательного уравнения имеем
При использовании формулы решения уравнения 4-ой степени необходимо ссылаться — «Метод ftvmetrics».
Интересные задачи присылайте в Direct Инстаграмм.
Решение уравнения четвертой степени одной переменной
Решение уравнения четвертой степени одной переменной
0 Предисловие
В процессе обучения необходимо решить квадратное уравнение одной переменной.
Поскольку он имеет неизвестные параметры, я хотел использовать MATLAB для решения своего аналитического решения и записать его в C ++ для расчета.
Если вы поместите его непосредственно в C ++, то даже на решение в реальном времени с помощью аналитического решения потребуется больше времени, чем на решение унарного квартичного уравнения. Так что найдите другой способ выяснить, как решить унарное уравнение квартики.
1. Способ первый
Метод Ferrari, который также является самым простым способом попасть в Google.
Я перестал смотреть на принцип ограничения времени и пошел прямо, чтобы узнать. По совпадению, есть код на энциклопедии.Link.
Ferrari.cpp
#include <math.h> #include <float.h> #include <complex> #include <iostream> std::complex<double> sqrtn(const std::complex<double>&x,double n) { double r = hypot(x.real(),x.imag()); if(r > 0.0) { double a = atan2(x.imag(),x.real()); n = 1.0 / n; r = pow(r,n); a *= n; return std::complex<double>(r * cos(a),r * sin(a)); } return std::complex<double>(); } std::complex<double> Ferrari(std::complex<double> x[4] ,std::complex<double> a ,std::complex<double> b ,std::complex<double> c ,std::complex<double> d ,std::complex<double> e) { a = 1.0 / a; b *= a; c *= a; d *= a; e *= a; std::complex<double> P = (c * c + 12.0 * e - 3.0 * b * d) / 9.0; std::complex<double> Q = (27.0 * d * d + 2.0 * c * c * c + 27.0 * b * b * e - 72.0 * c * e - 9.0 * b * c * d) / 54.0; std::complex<double> D = sqrtn(Q * Q - P * P * P,2.0); std::complex<double> u = Q + D; std::complex<double> v = Q - D; if(v.real() * v.real() + v.imag() * v.imag() > u.real() * u.real() + u.imag() * u.imag()) { u = sqrtn(v,3.0); } else { u = sqrtn(u,3.0); } std::complex<double> y; if(u.real() * u.real() + u.imag() * u.imag() > 0.0) { v = P / u; std::complex<double> o1(-0.5,+0.86602540378443864676372317075294); std::complex<double> o2(-0.5,-0.86602540378443864676372317075294); std::complex<double>&yMax = x[0]; double m2 = 0.0; double m2Max = 0.0; int iMax = -1; for(int i = 0;i < 3;++i) { y = u + v + c / 3.
0; u *= o1; v *= o2; a = b * b + 4.0 * (y - c); m2 = a.real() * a.real() + a.imag() * a.imag(); if(0 == i || m2Max < m2) { m2Max = m2; yMax = y; iMax = i; } } y = yMax; } else { y = c / 3.0; } std::complex<double> m = sqrtn(b * b + 4.0 * (y - c),2.0); if(m.real() * m.real() + m.imag() * m.imag() >= DBL_MIN) { std::complex<double> n = (b * y - 2.0 * d) / m; a = sqrtn((b + m) * (b + m) - 8.0 * (y + n),2.0); x[0] = (-(b + m) + a) / 4.0; x[1] = (-(b + m) - a) / 4.0; a = sqrtn((b - m) * (b - m) - 8.0 * (y - n),2.0); x[2] = (-(b - m) + a) / 4.0; x[3] = (-(b - m) - a) / 4.0; } else { a = sqrtn(b * b - 8.0 * y,2.0); x[0] = x[1] = (-b + a) / 4.0; x[2] = x[3] = (-b - a) / 4.0; } return x[4]; } int main() { std::complex<double> x[4]; x[4] = Ferrari(x,1,2,3,4,5); std::cout<<"root1: "<<x[0]<<std::endl<<"root2: "<<x[1]<<std::endl<<"root3: "<<x[2]<<std::endl<<"root4: "<<x[3]<<std::endl; return true; }
Коэффициент испытаний: 1, 2, 3, 4, 5
Убедитесь, что результат правильный, используйте matlab для проверки:
p = [1 2 3 4 5];
x = roots(p)
Результаты соответствуют, хорошо. {n-2}+\cdots+c_1x+c_0
P(x)=xn+cn−1xn−1+cn−2xn−2+⋯+c1x+c0
{n-2}+\cdots+c_1x+c_0
P(x)=xn+cn−1xn−1+cn−2xn−2+⋯+c1x+c0
Сопутствующая матрица:
M x = [ 0 0 . . . 0 − c 0 1 0 . . . 0 − c 1 0 1 . . . 0 − c 2 . . . . . . . . . . . . . . . 0 0 . . . 1 − c n − 1 ] M_x = \left[\begin{array}{ccccc} 0 & {0} & {…} & {0} & {-c_0} \\ 1 &0 & {…} & {0} & {-c_1} \\ {0} & {1} & {…} & {0} & {-c_2} \\ { …} & {…} & {…} & {…} & {…} \\ {0} & {0} & {…} & {1} & {-c_{n-1}} \end{array}\right]
Mx=⎣⎢⎢⎢⎢⎡010…0001…0……………000…1−c0−c1−c2…−cn−1⎦⎥⎥⎥⎥⎤
Так что используйте Eigen для решения полинома:
#include <iostream>
#include <Eigen/Core>
#include <Eigen/Dense>
using namespace std;
int main( int argc, char** argv )
{
Eigen::Matrix<double, 4, 4> matrix_44;
Eigen::Matrix<complex<double>, Eigen::Dynamic, Eigen::Dynamic> matrix_eigenvalues;
matrix_44 << 0, 0, 0, -5,
1, 0, 0, -4,
0, 1, 0, -3,
0, 0, 1, -2;
std::cout<<"matrix_44: "<<std::endl<<matrix_44<<std::endl<<std::endl;
matrix_eigenvalues = matrix_44. eigenvalues();
std::cout<<"matrix_eigenvalues: "<<std::endl<<matrix_eigenvalues<<std::endl;
return 0;
}
eigenvalues();
std::cout<<"matrix_eigenvalues: "<<std::endl<<matrix_eigenvalues<<std::endl;
return 0;
}
Результат такой же, как указано выше:
3. Вывод
Уравнения четвертой степени — Уравнения — Математика — Каталог статей
Уравнения четвертой степени
Метод решения уравнений четвертой степени нашел в XVI в. Лудовико Феррари, ученик Джероламо Кардано. Он так и называется – метод Феррари.
Как и при решении кубического и квадратного уравнений, в уравнении четвертой степени
x4+px³ +qx²+ix+s = 0
можно избавиться от члена px³ подстановкой x = y-p/4 . Поэтому будем считать, что коэффициент при кубе неизвестного равен нулю:
. x4ax²+bx+c = 0
Идея Феррари состояла
в том, чтобы представить уравнение в виде A² = B² ,
где левая часть – квадрат выражения A = x² + s, а
правая часть – квадрат линейного уравнения B от X, коэффициенты которого
зависят от S .
. (15)
Правая часть этого уравнения – квадратный трехчлен от x. Полным квадратом он будет тогда, когда его дискриминант равен нулю, т.е.
, или
b² = 2t(4t² + a² -4c)
Это уравнение называется резольвентным (т.е. «разрешающим»). Относительно t оно кубическое, и формула Кардано позволяет найти какой-нибудь его корень t0. При t = t0 правая часть уравнения (15) принимает вид
,
а само уравнение сводится к двум квадратным:
.
Их корни и дают все решения исходного уравнения.
Решим для примера уравнение
.x4
Здесь удобнее будет
воспользоваться не готовыми формулами, а самой идеей решения. Перепишем
уравнение в виде
Перепишем
уравнение в виде
x4-10x²+8x-5
и добавим к обеим частям выражение 2sx²+s², чтобы в левой части образовался полный квадрат:
.(x²+s)² = (10+2s)·x²+8x+s²-5
Теперь приравняем к нулю дискриминант правой части уравнения: 16-(10-2s)·(s²-5) =0
или, после упрощения,
.s³+5s²-5s-33=0
Один из корней полученного уравнения можно угадать, перебрав делители свободного члена: s0 = -3. После подстановки этого значения получим уравнение
(x²-3)² = 4x²+8x+4 = 4·(x+1)²,
откуда x²-3 = ±2·(x+1). Корни образовавшихся квадратных уравнений — и . Разумеется, в общем случае могут получиться и комплексные корни.
Решение уравнений 3 и 4 степени
1. Исследовательская работа по теме: «Решение уравнений 3-ей и 4-ой степени»
Выполнил:ученик 9 класса
Кравченко Виталий
Руководитель:
учитель математики
Нечаева
Елена Николаевна
© Фокина Лидия Петровна
2.
 Основные методы решения уравнений высших порядков 1. Метод разложения на множители
Основные методы решения уравнений высших порядков 1. Метод разложения на множителилевой части уравнения.
2.Метод введения новой переменной.
3.Функционально-графический метод
© Фокина Лидия Петровна
3. Уравнения вида ax3 + bx2 + cx + d = 0, где a ≠ 0, называются уравнениями 3-ей степени
Уравнение видаx 3 + px + q = 0
называется приведённым
кубическим уравнением
Известные формулы Кардано для решения уравнений этого типа
очень сложны и почти не применяются на практике.
© Фокина Лидия Петровна
4. Решу уравнение х3 -7х+6=0 разными способами
1. Разложение на множителих3 -7х + 6 =0
х3 — х2 + х2 – х — 6х + 6=0
х2 (х-1)+ х(х-1)-6(х-1)=0
(х-1)(х2 + х — 6) = 0
х-1=0 или х2 + х – 6 = 0
х1 =1
х2 =-3 х3 = 2
Ответ: 1; 2; -3
© Фокина Лидия Петровна
5. 2.Метод деления на многочлен
х3 -7х+6 = 0 делители 6: ±1; ±2; ±3; ±61³-7+6=0
3-7х+6 =(х-1)(х2 +х-6)=0
х
x³-0х2-7x+6 x-1
2 +х-6=0
х-1=0
или
х
x³-x²
x²+x-6
х1 =1
х2 =-3 х3 = 2
x²-7x
x²-x
-6x+6
-6x+6
0
© Фокина Лидия Петровна
Ответ: 1; 2; -3
6.
 3.Функционально-графический метод х3 -7х+6 = 0 у = х3 и у = 7х-6
3.Функционально-графический метод х3 -7х+6 = 0 у = х3 и у = 7х-6Ответ:1;2;-3
© Фокина Лидия Петровна
7. Уравнение четвертой степени общего вида ax4 + bx3 + cx2 + dx + e = 0 где а ≠ 0
Уравнение четвертой степени общего видаax4 + bx3 + cx2 + dx + e = 0 где а ≠ 0
1.Разложение на множители
x4 + 2×3 + 5×2 + 4x – 12 = 0
x4 + 2×3 + 5×2 + 10x – 6x – 12 = 0
(x4 + 2×3) + (5×2 + 10x) – (6x + 12 ) = 0
x3 (x+2) +5х (х+2) – 6 (х+2) =0
(x + 2) (x3 + 5x – 6) = 0
(x + 2)(x – 1)(x2 + x + 6) = 0
x1 = -2, x2 = 1.
Ответ: -2 ; 1
© Фокина Лидия Петровна
8. 2.Деление на многочлен Х4 — Х3-13 Х -15=0 -1 делитель числа -15 (1+1+13-15=0) Х4 — Х3-13 Х -15 = (Х+1)(Х-3)(Х2 +Х +5) = 0 Х+1
=0 или Х-3=0 или Х2 +Х +5 =0 (ДХ1=-1 Х 2=3
Ответ: -1; 3
© Фокина Лидия Петровна
9. Биквадратное уравнение вида ax4 + bx2 + с = 0. 3.Метод: введение новой переменной
Биквадратное уравнение вида ax4 + bx2 + с = 0.
3.Метод: введение новой переменной
x4 + 5×2 – 36 = 0.
Замена y = x2.
У2+ 5У-36=0
У1*У2 =-36= -9*4
У1=-9
У1 + У1 =-5= -9+4
У2 =4
X2 =-9
x2 =4
Корней нет
х1 =2 х2 =-2
Ответ: 2; -2
© Фокина Лидия Петровна
10. Задание:Решите уравнение Х3+2Х2- 5Х — 6 = 0
Делители -6: ±1; ±2; ±3; ±6-1 корень уравнения (-1+2+5-6=0)
Х3+2Х2- 5Х — 6 = (Х+1)(Х2+Х -6) = 0
Х+1= 0 или Х2+Х -6=0
Х1 =-1
Х2 =-3 Х3 = 2
Ответ: -1; -3; 2
© Фокина Лидия Петровна
Уравнение четвертой степени — Энциклопедия по машиностроению XXL
Ответ Система устойчива, если все корни уравнения четвертой степени [c.436]Из таблицы видно, что непрерывные функции / р) и / р) при изменении аргумента р от -— оо до со четыре раза меняют знак. Вспоминая, что (23) и (24) являются уравнениями четвертой степени, можно утверждать, что каждое из уравнений (23) и (24) имеет по два отрицательных и два положительных корня, т. е. корни обоих уравнений вещественны. Отметим, что рассматриваемые корни обладают интересным свойством отрицательные корни одного уравнения равны по абсолютной величине положительным корням другого, и наоборот.
[c.630]
е. корни обоих уравнений вещественны. Отметим, что рассматриваемые корни обладают интересным свойством отрицательные корни одного уравнения равны по абсолютной величине положительным корням другого, и наоборот.
[c.630]
Получено характеристическое уравнение для A, являющееся уравнением четвертой степени. В развернутом виде характеристическое уравнение имеет форму [c.441]
А. Уравнение четвертой степени [c.385]
Итак, решение уравнения четвертой степени сведено к решению уравнений третьей и второй степени. [c.84]
Для вычисления температуры поверхности необходимо отыскать корень следующего уравнения четвертой степени [c.85]
Уравнение А = 0 называется характеристическим и служит для определения постоянной р. В общем виде оно записывается как уравнение четвертой степени относительно р
[c. 40]
40]
Рассмотрение произвольной анизотропии не представляет каких бы то ни было принципиальных трудностей, вся техническая трудность состоит в необходимости решения алгебраического уравнения четвертой степени, корни которого, вообще говоря, комплексны. Для приложений нам будет достаточно ограничиться плоской задачей для ортотропного материала. Будем записывать уравнения закона Гука по отношению к осям упругой симметрии материала следующим образом [c.343]
Для уравнения четвертой степени вида [c.120]
Таким образом, критерий Гурвица для уравнения четвертой степени вида (25.7) следующий [c.121]
Рассмотрим характеристическое уравнение четвертой степени вида [c.239]
Представим рассматриваемое уравнение четвертой степени в следующем виде [c.239]
Таким образом, для устойчивости движения системы, имеющей характеристическое уравнение четвертой степени, необходимо, чтобы все коэффициенты Л были положительными и выполнялось неравенство
[c. 240]
240]
Эти условия также совпадают с установленными условиями устойчивости движения системы, имеющей характеристическое уравнение четвертой степени. [c.242]
Решение. Так как все коэффициенты характеристического уравнения положительны, то для устойчивости извилистого движения паровоза, имеющего характеристическое уравнение четвертой степени, должно выполняться следующее условие [c.244]
Из двух уравнений (4.63) получим уравнение четвертой степени общего вида для определения параметра h [c.101]
Применение этого метода встречает, однако, затруднение. Алгебраическое решение системы уравнений (19), (20) приводит к уравнению четвертой степени, и предшествующие вычисления вводят корни этого уравнения. Мы не будем останавливаться на этом осложнении вычислительного характера. [c.263]
Таким образом, мы придем к уравнению четвертой степени относительно г [c.54]
Пример 4 (Уравнение четвертой степени).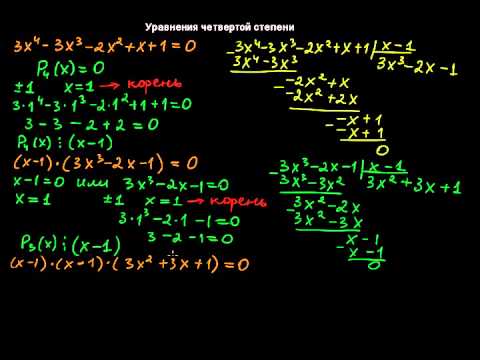 [c.535]
[c.535]
Х3, Х4 суть корни уравнения четвертой степени [c.198]
После подстановки (3. 9) в уравнения колебаний оболочек [48, 51] получим уравнение четвертой степени относительно с действительными коэффициентами [c.123]
В результате преобразований решение настоящей задачи становится возможным при помощи обыкновенных дифференциальных уравнений четвертой степени [c.100]
Подставляя эти выражения в уравнение (25), представляющее уравнение четвертой степени относительно и ,3, получим уравнение второй степени относительно Я и [c.144]
Соответственно для уравнения четвертой степени X ДзЯ + Д Я + Д Я -f До = о [c.155]
Отсюда следует характеристическое уравнение четвертой степени для Я [c.176]
Раскрывая выражения левой и правой частей уравнения (16-64) и проводя соответствующие преобразования, находим, что равновесная температура шарика определяется из решения уравнения четвертой степени следующего вида (полагая отражательную способность эллиптического зеркала равной единице)
[c. 444]
444]
Если раскрыть определитель (11), то получим уравнение четвертой степени относительно с четырьмя вещественными корнями V … /,4. Два положительных корня V ,- и > 4—собственные частоты прямой и два отрицательных / , и —обратной прецессии. [c.216]
В развернутом виде выражение представляет собой алгебраическое уравнение четвертой степени относительно В зависимости от параметров системы уравнение может иметь до четырех положительных корней (критических скоростей). [c.374]
Полученное уравнение представляет собой уравнение четвертой степени относительно корни его являются частотами свободных поперечных колебаний системы. В действительности судовые валопроводы имеют естественно не четыре, а бесчисленное множество частот свободных поперечных колебаний, так как сами податливости, играющие роль коэффициентов в полученном уравнении, определяются с учетом инерционных характеристик вала и зависят от частоты. Однако в решаемой задаче нас будут интересовать лишь низшие корни частотного уравнения и прежде всего вторая частота по следующим соображениям. [c.241]
[c.241]
Решение уравнения четвертой степени по методу Эйлера сводится к решению его кубической резольвенты [c.505]
О корнях уравнения четвертой степени можно судить по характеру корней кубической резольвенты. Так, например, при [c.505]
При исследовании устойчивости систем, процессы которых описываются линейными дифференциальными уравнениями восьмого и девятого порядка, уравнения (754) и (755) становятся уравнениями четвертой степени относительно Корни таких уравнений можно также определить при помощи диаграммы (см. фиг. 293), так как [c.534]
Получили алгебраическое уравнение четвертой степени, значит, прямой клин есть поверхность четвертого порядка. Эта поверхность плоскостями (Z = onst) пересекается по эллипсам, в чем нетрудно убедиться, подставив в формулу (2.47) вместо Z какое-либо число. [c.71]
С этой целью преобразуем его в уравнение четвертой степени путем двукратного возведения в квадргт
[c. 336]
336]
При исследовании системы с д)зумя степенями свободы приходится иметь дело с двумя дифференциальными уравнениями второго порядка и в соответствии с этим получается характеристическое уравнение четвертой степени. Существует точный способ решения таких уравнений, но из-за громозкости его рекомендовать нельзя. Ознакомимся с приближенным способом решения, позволяющим получать результаты с любой наперед заданной степенью точности. [c.285]
Пример. Для более детального ознакомления о предлагаемым спфсобом решения уравнения четвертой степени рассмотрим пример [c.286]
В некоторых случаях динамического исследования механизмов характеристическое уравнение четвертой степени имеет один корень, равный нулю, и задача сводится к решению уравнения третьей степени. Приближенный способ решения уравнения третьей степени быстрее ведет к цели, чем точный способ Кардано и поэтому ознакомимся со способом приближенного решения.
[c. 287]
287]
При этом некоторые коэффициенты й/ могут быть равными нулю. Так, на-прР1мер, для характеристического уравнения четвертой степени [c.383]
Система (67)—(68) может быть приведена к одному уравнению четвертой степени относительно одного из коэффициентов уравне ния (66). Такое уравнение может быть решено в радикалах по способу Феррари. Решение системы уравнений может быть най дено также путем последовательных приближений. [c.41]
С этими уравнениями можно обращаться как с алгебраическими. Обращение в нуль предадителя, составленного из коэффициентов при неизвестных х (s) и г (s) в системы (111.35), — условие существования решений, отличных от нуля. Развернув этот определитель, получим характеристическое уравнение четвертой степени [c.92]
Как избежать решения уравнения четвертой степени? | Соловьева Светлана Александровна
Математика онлайн. Доступно о сложном. Серия «Нестандартные задачи»
Здравствуйте, уважаемые любители математики!
Дано уравнение четвертой степениДано уравнение четвертой степени
Ищем способ решения уравнения
Перед нами уравнение четвертой степени, следовательно, оно имеет не более четырех действительных корней.
Если внимательно посмотреть на уравнение, то можно заметить, что в левой части стоят четыре последовательных числа. Так как 15 невозможно представить в виде произведения четырех последовательных целых чисел, то корни уравнения (если они есть) не будут целыми. Следовательно, подбором их найти не получится.
Далее, если перемножить все выражения в левой части, то получим уравнение четвертой степени. Его решение выходит за рамки школьной программы.
Как же тогда его решать?
Заметим, что если перемножить первый и четвертый множители, а также второй и третий, то произведения будут отличаться только свободным членом.
Следовательно, можно ввести новую переменную.
Замена переменной
Замена переменнойЗамена переменной
Теперь уравнение превратилось в квадратное, которое легко решить при помощи теоремы, обратной к теореме Виета.
Решение получившегося квадратного уравненияРешение получившегося квадратного уравнения
Возвращаемся к первоначальной переменной. Решение исходного уравнения сводится к решению совокупности двух квадратных уравнений.
Решение исходного уравнения сводится к решению совокупности двух квадратных уравнений.
Решаем еще два квадратных уравнения
Первое уравнение не имеет действительных корней.
Решаем второе:
Исходное уравнение имеет два иррациональных корняИсходное уравнение имеет два иррациональных корня
Ответ готов.
______________
Информация для подписчиков и постоянных читателей
У меня появился паблик ВКонтакте.
Заходите, читайте (материалы там другие).
Если будет интересно, подписывайтесь.
______________
Все статьи серии «Нестандартные задачи»
Рубрикатор канала
Двучленные уравнения четвертой степени решение примеров онлайн
Двучленными уравнениями четвертой степени называются уравнения вида:
или
где — любые действительные числа, но , x – неизвестная искомая переменная.
Корнем двучленного уравнения четвертой степени называется такое значение переменной , при подстановке которого двучлен или обращается в ноль.
Решить уравнение – это значит найти все его корни или установить, что корней нет.
При решении двучленного уравнения вида необходимо придерживаться следующей схемы:
1) Вынести за скобки общий множитель , преобразовав тем самым заданное уравнение к виду
2) Решить полученное уравнение, приравняв каждый множитель к нулю:
Пример 1: Решить уравнение
Данное уравнение является двучленным уравнением четвертой степени.
Вынесем за скобки общий множитель :
Поэтому либо , либо
Ответ:
Пример 2: Решить уравнение
Данное уравнение является двучленным уравнением четвертой степени.
Вынесем за скобки общий множитель :
Поэтому либо , либо а данное уравнение решений не имеет (См. «Решение квадратных уравнений»)
Таким образом, заданное уравнение имеет одно решение
Ответ:
При решении двучленного уравнения вида необходимо придерживаться следующей схемы:
1) Привести уравнение к виду
2) Решить полученное уравнение:
Пример 3: Решить уравнение
Данное уравнение является двучленным уравнением четвертой степени.
Решим данное уравнение по вышеприведенной формуле:
Таким образом, заданное уравнение имеет одно решение
Ответ:
Пример 4: Решить уравнение
Данное уравнение является двучленным уравнением четвертой степени.
Решим данное уравнение по вышеприведенной формуле:
Таким образом, заданное уравнение не имеет решений, так как значение переменной в четной степени не может быть отрицательным.
Ответ: Решений нет.
Примечание: Уравнения примеров 2 и 4 не имеют решений только для курса школьной математики. (См. «Решение двучленных уравнений четвертой степени. Курс высшей школы»).
(PDF) Классический новый метод решения уравнений четвертой степени
Прикладная и вычислительная математика, 2013, 2 (2): 24-27 27
ii
N
5622.06624.0,5622.06624.0
67.1398688.0 , 32.408688.0
3
+ −− → ∠ − ∠ =
Выбираются корни, удовлетворяющие уравнению (18):
3247,1
1
= N
iN 5619.06224.0
2
−− =
5622.06624.0
3
+ — = N
iN 8749. 03210.0,8749.03210.0
03210.0,8749.03210.0
41
+ −− =
iiN 8749.03210.0,8749.03210.0
42
−− + =
15095.1,15095.1
43
N
которые удовлетворяют уравнению (16), выбраны:
7929.1
1
— = x
ix
ix
x
75.11510.1
75.11510.1
5089.0
4 2
— = + =
Используя второй метод, мы проверяем следующий пример
.
5. Выводы
Самым важным моментом во всех методах
решения уравнения четвертой степени является сложность этих
решений.
Чтобы доказать эффективность и простоту предложенного метода
, в четвертом разделе статьи
приведен пример квартики, который решается с помощью предложенного инициированного метода.
Ссылки
[1] «Простой метод решения уравнений четвертой степени» Амир Фатхи,
Пуйя Мобадерсани, Рахим Фатхи, Австралийский журнал
Основные и прикладные науки, 6 (6): 331-336, 2012, ISSN
1991-8178.
[2] Кардано, Джироламо, (перевод Т. Ричарда Уитмера), Ars
Magna или правила алгебры, Довер, Нью-Йорк, штат Нью-Йорк, 1993.
[3] Фосетт, ВМ «Геометрическая интерпретация Решение
общего многочлена четвертой степени ». Амер. Математика. Ежемесячно
103, 51-57, 1996.
[4] Gellert, W .; Gottwald, S .; Hellwich, M .; Kästner, H .; и
Künstner, H. (Eds.). ВНР Краткая энциклопедия
Математика, 2-е изд.Нью-Йорк: Ван Ностранд Рейнхольд,
1989.
[5] Хазевинкель М. (Управляющий ред.). Энциклопедия
Математика: обновленный и аннотированный перевод советской «Математической энциклопедии
». Дордрехт,
Нидерланды: Рейдел, 1988.
[6] MathPages. «Преобразование квартиков в кубики».
http://www.mathpages.com/home/kmath396.htm.
[7] Смит Д. Э. Справочник по математике. Нью-Йорк:
Дувр, 1994.
[8] ван дер Варден, Б. Л. §64 по алгебре, Vol. 1. Нью-Йорк:
Springer-Verlag, 1993.
[9] Бейер, У. Х. Стандартные математические таблицы CRC, 28-е изд.
Бока-Ратон, Флорида: CRC Press, стр. 12, 1987а.
[10] Бейер, У. Х. Справочник по математическим наукам, 6-е изд.
Бока-Ратон, Флорида: CRC Press, 1987b.
[11] Биркгоф, Г., Мак Лейн, С. Обзор современной алгебры,
5-е изд. Нью-Йорк: Macmillan, стр.107-108, 1996.
[12] Borwein, P. and Erdélyi, T. «Quartic Equations». §1.1.E.1e
в полиномах и полиномиальных неравенствах. Нью-Йорк:
Springer-Verlag, p. 4, 1995.
[13] Бойер, К. Б., Мерцбах, У. С. История математики,
2-е изд. New York: Wiley, pp. 286-287, 1991.
[14] И. Стюарт, «Теория Галуа», изд: Chapman & Hall / CRC
Mathematics, 2004.
[15] JJ O’Connor and Э.Ф. Робертсон, «Лодовико Феррари», в
Архив истории математики MacTutor, изд. Школа
математики и статистики, Сент-Эндрюсский университет
Шотландия.
[16] ЛЕГКИЙ ВЗГЛЯД НА КУБИЧЕСКУЮ ФОРМУЛУ. Томас Дж.
Томас Дж.
Ослер. Математический факультет, Университет Роуэна,
Глассборо, штат Нью-Джерси, 08028.
почему мы не можем решать полиномиальные уравнения выше четвертой степени? : managelikeimfive
Вот версия, которая безопасна (умная) 5-летней давности.Ведь они знают о многочленах.
Учитывая многочлен, мы, конечно, хотели бы его решить. Для степени 1,2,3,4 у нас есть формул в терминах радикалов , то есть они могут использовать +, -, x, /, как обычно, и брать корни n-й степени (радикалы), и все.
Теперь у многих многочленов есть решения, которые не находятся внутри обычных чисел (те, которые могут быть записаны в виде дробей, рациональные числа ). Попробуйте X 2 + 1 = 0. Нет решения!
Итак, мы могли бы представить, что делаем нашу систему счисления больше, чтобы включать этих чисел.Это возможно! И самая маленькая такая система счисления называется полем расщепления полинома . Он «разбивает» многочлен на множители. (потому что вы, умный 5-летний ребенок, знаете о соответствии между факторами и решениями.)
(потому что вы, умный 5-летний ребенок, знаете о соответствии между факторами и решениями.)
Теперь эта система счисления (или просто поле для краткости) является наименьшей, которая имеет решения для нашего многочлена, но содержит ли она другие системы счисления ? Насколько большим нужно было сделать поле? Француз Эварист Галуа сумел доказать, что существует структура, называемая группой , в которой есть элементы, и эти элементы в ней соединяются один в один с полями, содержащимися в нашем поле расщепления.
Я не уверен, кто это заметил, но какой-то чувак, у которого, должно быть, был гигантский мозг, кое-что заметил. Эти группы обладали особым свойством, когда решения в поле расщепления можно было записать в терминах радикалов. Это особое свойство известно как растворимость , но это hella Technical , поэтому я больше не буду о нем говорить. Еще одна вещь, группа, которую люди называют A_5, — , а не .
Итак, вот где мы находимся прямо сейчас: нам может быть дан многочлен, и мы можем построить новую систему счисления (его поле расщепления), в которой он имеет решения. С этим полем связана группа, которая описывает, какие другие поля оно содержит, и если эта группа разрешима, то решения можно записывать в радикалах. Итак, вы должны знать, что теперь происходит: если мы не можем записать решения некоторого полинома 5-й степени в радикалах, у него должно быть поле расщепления, группа которого не разрешима .
С этим полем связана группа, которая описывает, какие другие поля оно содержит, и если эта группа разрешима, то решения можно записывать в радикалах. Итак, вы должны знать, что теперь происходит: если мы не можем записать решения некоторого полинома 5-й степени в радикалах, у него должно быть поле расщепления, группа которого не разрешима .
Именно это и происходит. Некоторые полиномы 5-й степени имеют группу A_5, которая неразрешима! Итак, некоторые многочлены 5-й степени не могут хорошо записать свои решения.
Конечно, если некоторые из них не могут быть написаны таким образом, это мешает нам использовать уравнение. Какую бы формулу вы ни записали, есть некоторые квинтики, которые она не решит, потому что ее решениями являются числа, которые просто не могут быть записаны таким образом !
Edit Итак, чтобы объяснить 5-летнему ребенку, мы скрываем, что в основном является всей плотью, в которой разрешимые группы соответствуют полям разбиения, в которых решения могут быть записаны в радикалах. Что там происходит? Что ж, группа описывает для нас подполя в поле разделения, и это фактически кодирует, как числа в больших полях строятся в терминах чисел в меньших полях.Разрешаемые группы означают, что мы «красиво» строим числа, так что корни можно записать в терминах радикалов.
Что там происходит? Что ж, группа описывает для нас подполя в поле разделения, и это фактически кодирует, как числа в больших полях строятся в терминах чисел в меньших полях.Разрешаемые группы означают, что мы «красиво» строим числа, так что корни можно записать в терминах радикалов.
РЕШЕНИЕ: а. Открытые Напишите и решите полиномиальное уравнение четвертой степени, которое включает разность квадратов. б. Критическое мышление. Все ли корни — реальные числа? Обосновать ответ.
Стенограмма видео
и говорит, в частности, что Райан видел многочлен 1/4 степени, который включает в себя разность квадратов. Так что я знаю, просто делая несколько других, что мы можем добавить четвертый минус один.Гм, потому что это разница квадратов, даже между собой и ее четвертой степенью с этими 4-мя 4 степенями s. Это даст нам X в квадрате минус R плюс один, умноженный на X в квадрате, минус один. Хорошо, разбив его еще дальше, мы снова получим X в квадрате плюс один. Дайте нам мнимые корни и эксперты один раз на Х минус один. То есть мы на самом деле имеем разницу квадратов вдвое. Есть окончательный ответ, потому что он сказал, что для решения этой проблемы X будет равно Это минус один и плюс или минус. Я пришел.Итак, теперь вторая часть только что сказала, говорит, есть ли они действительно корни? Ну, плюс минус, я как бы показываю, что они не обязательно должны быть настоящими корнями, поэтому я понимаю, что из этого выходит. Но, ммм, я думаю, что вы могли бы сделать, так это показать, что если у вас есть воображаемый маршрут, вам придется это сделать. Таким образом, он мог получить до четырех из-за разницы в квадратах. Однако, если вы для полинома 1/4 степени. Однако, если вы используете разницу квадратов, так или иначе связанную с этим, тогда два ответа должны быть действительно так, чтобы быть.И у вас могут быть все четыре b riel, Um, и один пример, где все четыре будут riel, — это если вы разложите X в квадрате минус девять, потому что есть ваша разница квадратов, а затем doh X плюс один.
Дайте нам мнимые корни и эксперты один раз на Х минус один. То есть мы на самом деле имеем разницу квадратов вдвое. Есть окончательный ответ, потому что он сказал, что для решения этой проблемы X будет равно Это минус один и плюс или минус. Я пришел.Итак, теперь вторая часть только что сказала, говорит, есть ли они действительно корни? Ну, плюс минус, я как бы показываю, что они не обязательно должны быть настоящими корнями, поэтому я понимаю, что из этого выходит. Но, ммм, я думаю, что вы могли бы сделать, так это показать, что если у вас есть воображаемый маршрут, вам придется это сделать. Таким образом, он мог получить до четырех из-за разницы в квадратах. Однако, если вы для полинома 1/4 степени. Однако, если вы используете разницу квадратов, так или иначе связанную с этим, тогда два ответа должны быть действительно так, чтобы быть.И у вас могут быть все четыре b riel, Um, и один пример, где все четыре будут riel, — это если вы разложите X в квадрате минус девять, потому что есть ваша разница квадратов, а затем doh X плюс один. И это плюс три Linden, которые включают разницу квадратов, имеют два других реальных корня. Вы также можете сделать разность квадратов дважды. Так что эта область просто означает, что вот еще одна. Но как если бы вы поставили X в квадрате минус девять и, возможно, X в квадрате минус два, а затем, как факт, да? Распределил это, чтобы получить исходный многочлен четвертой степени.Так что два из них должны быть настоящими, если вы имеете дело с разницей квадратов. Но могут быть все четыре бриеля. Хорошо, но у вас не может быть трех B или одного B. Правда? Хорошо. Спасибо.
И это плюс три Linden, которые включают разницу квадратов, имеют два других реальных корня. Вы также можете сделать разность квадратов дважды. Так что эта область просто означает, что вот еще одна. Но как если бы вы поставили X в квадрате минус девять и, возможно, X в квадрате минус два, а затем, как факт, да? Распределил это, чтобы получить исходный многочлен четвертой степени.Так что два из них должны быть настоящими, если вы имеете дело с разницей квадратов. Но могут быть все четыре бриеля. Хорошо, но у вас не может быть трех B или одного B. Правда? Хорошо. Спасибо.
3. Как разложить многочлены на множители
На этой странице мы узнаем, как разложить многочлены на множители с 3 членами (степень 2), 4 членами (степень 3) и 5 членами (степень 4).
Мы будем использовать теоремы об остатке и множителях , чтобы разложить многочлены на их множители.
Что мы ищем?
Пример 1
Пример полинома (с углом градусов 3):
p ( x ) = 4 x 3 — 3 x 2 -25 x — 6
множителей этого многочлена:
( x — 3), (4 x + 1) и ( x + 2)
Обратите внимание, что существует 3 множителя для полинома 3 степени . Когда мы умножаем эти 3 члена в скобках, мы получим многочлен p ( x ).
Когда мы умножаем эти 3 члена в скобках, мы получим многочлен p ( x ).
Мы увидим, как найти эти множители ниже, в разделе Как разложить многочлены на множители с 4 членами?
Краткое описание процесса
В общем, мы:
- Найдите один множитель , используя теорему об остатке
- Разделим многочлен на коэффициент , который мы нашли, что даст нам более простой многочлен для работы с
- Найдите один множитель более простого полинома и разделите еще раз
- Продолжайте, пока не дойдете до трехчлена , который мы обычно легко можем разложить на множители.
Как разложить многочлены на 3 члена?
Пример 2
Вот пример полинома с 3 членами:
q ( x ) = x 2 — x + 6
Мы узнали, что это квадратичный многочлен (также называемый трехчленом из-за трех членов), и мы видели, как разложить их на множители ранее в разделах «Факторизация трехчленов» и «Решение квадратичных уравнений путем разложения на множители».
Нам нужно найти числа a и b такие, что
q ( x ) = x 2 -5 x + 6 = ( x — a ) ( x — b )
Это обычно включает в себя некоторые угадывания и проверки, чтобы получить правильную комбинацию чисел. Число 6 (константа полинома ) имеет множители 1, 2, 3 и 6 (и отрицательные значения каждого из них также возможны), поэтому очень вероятно, что наши a и b будут выбраны из этих числа.
После непродолжительных испытаний получаем:
x 2 — 5 x + 6 = ( x — 2) ( x — 3)
Мы говорим, что коэффициенты из x 2 -5 x + 6 равны ( x -2) и ( x -3).
Обратите внимание, что наш трехчленный многочлен имеет степени 2 , а количество множителей также равно 2.
Как разложить многочлены на множители с 4 членами?
Пример 3
Выше мы обсудили кубический многочлен p ( x ) = 4 x 3 — 3 x 2 — 25 x — 6, который имеет степень 3 (поскольку наибольшая степень из x получается 3).
Найдем множители p ( x ).
Обратите внимание, что коэффициент x 3 равен 4, и нам нужно будет учесть это в нашем решении.
Мы ищем решение в следующих строках (в скобках 3 выражения, потому что наибольшая степень нашего многочлена равна 3):
4 x 3 — 3 x 2 — 25 x — 6 = ( ax — b ) ( cx — d ) ( fx — — — г )
Множители 4 равны 1, 2 и 4 (и, возможно, их отрицания), поэтому из этих чисел будут выбраны a , c и f . Это должно быть так, чтобы мы получили 4 x 3 в нашем полиноме.
Это должно быть так, чтобы мы получили 4 x 3 в нашем полиноме.
Мы наблюдаем −6 как постоянный член нашего многочлена, поэтому числа b , d и g , скорее всего, будут выбраны из множителей −6, которые равны ± 1, ± 2, ± 3 или ± 6.
Однако нам потребовалось бы слишком много времени, чтобы перепробовать все рассмотренные комбинации. Нам нужно будет их все перемножить, чтобы увидеть, какая комбинация на самом деле дала p ( x ).
Итак, мы пойдем по другому пути.
Находим один фактор: Мы пробуем некоторые из возможных более простых факторов и проверяем, «сработают» ли они. Если мы разделим полином на выражение и не найдем остатка , то мы найдем коэффициент .
Более простой способ — использовать теорему об остатке , с которой мы встречались в предыдущем разделе, Теоремы о множителях и остатках. Там написано:
Если полином f ( x ) разделить на ( x — r ) и получить остаток R , то f ( r ) = R .
Мы ищем выражение (называемое линейным членом ) , которое даст нам остаток от 0, если мы разделим на него многочлен.
Испытание 1: Мы пробуем ( x — 1) и находим остаток, подставляя 1 (обратите внимание, что он положительный 1) на p ( x ).
p (1) = 4 (1) 3 — 3 (1) 2 — 25 (1) — 6 = 4 — 3 — 25 — 6 = −30 ≠ 0
Испытание 2: Мы пробуем ( x + 1) и находим остаток, подставляя -1 (обратите внимание, что он отрицательный 1) на p ( x ).
p (−1) = 4 (−1) 3 -3 (−1) 2 -25 (−1) — 6 = −4-3 + 25-6 = 12 ≠ 0
Испытание 3: Мы пробуем ( x -2) и находим остаток, подставляя 2 (обратите внимание, что он положительный) на p ( x ).
p (2) = 4 (2) 3 — 3 (2) 2 — 25 (2) — 6 = 32 — 12 — 50 — 6 = −36 ≠ 0
Испытание 4: Мы пробуем ( x + 2) и находим остаток, подставляя −2 (обратите внимание, что он отрицательный) на p ( x ).
p (−2) = 4 (−2) 3 -3 (−2) 2 -25 (−2) — 6 = −32-12 + 50-6 = 0
Поскольку остаток равен 0, мы можем заключить, что ( x + 2) является множителем .
Итак, мы можем написать p ( x ) = ( x + 2) × (что-то)
Чтобы узнать, что входит во вторую скобку, нам нужно разделить p ( x ) на ( x + 2). Мы видели, как делить многочлены в предыдущем разделе, теоремы о множителях и остатках.2-22x`.
Итак, теперь мы можем написать p ( x ) = ( x + 2) (4 x 2 -11 x — 3).
Итак, эта вторая скобка представляет собой всего лишь трехчлен (трехчленный квадратичный многочлен), и мы можем довольно легко разложить его на множители, используя процесс разложения триномов на множители.
(4 x 2 -11 x -3) = (4 x +1) ( x -3)
Итак, сложив все вместе, можно записать многочлен p ( x ):
p ( x ) = 4 x 3 — 3 x 2 — 25 x — 6 = ( x — 3) (4 x + 1) ( x + 2)
То есть коэффициенты из p ( x ) равны:
( x — 3), (4 x + 1) и ( x + 2)
Как разложить многочлены на 5 членов?
Пример 4
Разложите на множители полином r ( x ) = 3 x 4 + 2 x 3 -13 x 2 -8 x + 4.
Решение
Поскольку степень этого многочлена равна 4, мы ожидаем, что наше решение будет иметь вид
3 x 4 + 2 x 3 -13 x 2 -8 x + 4 = (3 x — a 1 ) ( x — a 2 ) ( x — a 3 ) ( x — a 4 )
В первой скобке стоит 3 (поскольку множители 3 равны 1 и 3, и она должна быть в одной из скобок.) Остальные неизвестные должны быть выбраны из 4 множителей, которые равны 1, 2 или 4.
Еще раз воспользуемся теоремой об остатке , чтобы найти один множитель. Мы разделим r ( x ) на этот множитель, и это даст нам кубический многочлен (степени 3). Мы найдем множитель , этого куба, а затем разделим кубический на этот множитель. Тогда у нас остается трехчлен, который обычно относительно просто множить.
Тогда у нас остается трехчлен, который обычно относительно просто множить.
Trial 1: Мы пытаемся подставить x = 1 и обнаруживаем, что это не удалось (это не дает нам ноль).
r (1) = 3 (1) 4 + 2 (1) 3 — 13 (1) 2 — 8 (1) + 4 = −12
Испытание 2: Мы пытаемся заменить x = -1, и на этот раз мы нашли множитель.
r (1) = 3 (-1) 4 + 2 (-1) 3 -13 (-1) 2 -8 (-1) + 4 = 0
Мы заключаем, что ( x + 1) — это фактор из r ( x ).Таким образом, наши коэффициенты будут выглядеть примерно так:
3 x 4 + 2 x 3 -13 x 2 -8 x + 4 = (3 x — a 1 ) ( x + 1) ( x — a 3 ) ( x — a 4 )
Теперь нам нужно разделить ( x + 1) на r ( x ). 2-12x + 4`.2 + 5x-2 = (3x-1) (x + 2) `
2-12x + 4`.2 + 5x-2 = (3x-1) (x + 2) `
Итак, сложив все вместе, получаем:
r ( x ) = 3 x 4 + 2 x 3 -13 x 2 -8 x + 4 = (3 x — 1 ) ( x + 1) ( x — 2) ( x + 2)
Использование системы компьютерной алгебры для разложения многочленов на множители
Что, если нам нужно разложить такие многочлены на множители?
Пример 5: x 2 — 5.2 x + 6.751
У этого трехчлена нет «хороших» чисел, и потребуется немного повозиться, чтобы разложить его на множители путем осмотра. Мы могли бы использовать квадратичную формулу, чтобы найти факторы.
Пример 6: 2,9 x 3 — π x 2 — 4,97 x + 43883
Вышеупомянутый кубический многочлен также имеет довольно неприятные числа. Найти первый множитель и затем разделить полином на него было бы довольно сложно.
Найти первый множитель и затем разделить полином на него было бы довольно сложно.
Пример 7: 3175 x 4 + 256 x 3 — 139 x 2 — 8 7x + 480
Этот многочлен четвертой степени (степень 4) имеет «хорошие» числа, но комбинация чисел, которую нам нужно было бы попробовать, огромна. Коэффициенты 480 равны
.{1, 2, 3, 4, 5, 6, 8, 10, 12, 15, 16, 20, 24, 30, 32, 40, 48, 60, 80, 96, 120, 160, 240, 480}
Мы также должны рассмотреть недостатки каждого из них.
Когда многочлен имеет достаточно высокую степень, даже с «хорошими» числами, рабочая нагрузка по нахождению множителей будет довольно высокой. Например:
Пример 8: x 5 -4 x 4 — 7 x 3 + 14 x 2 -44 x + 120
Коэффициенты 120 следующие, и нам нужно будет продолжать, пока один из них не «сработает».
{1, 2, 3, 4, 5, 6, 8, 10, 12, 15, 20, 24, 30, 40, 60, 120}
Фактически в этом случае первый множитель (после попытки `+ -1` и` -2`) на самом деле является `(x-2)`.
В таких случаях лучше реализовать:
- Мы в основном занимаемся конечными факторами, поэтому мы можем решать полиномиальные уравнения (где многочлен установлен равным нулю, и нам нужно найти «корни» уравнения)
- Вышеупомянутые методы — математические методы, которые «приятно знать», но они действительно полезны только в том случае, если числа в полиноме «хороши», а множители легко вычисляются без особых проб и ошибок
Рассмотрим решение получше.
Решение с использованием систем компьютерной алгебры
В примерах 5 и 6 на самом деле нет хороших факторов, даже когда мы получаем компьютер, чтобы найти их для нас.
В примере 7 есть факторы (данные Wolfram | Alpha)
`3175,` (x — 0,637867), `(x + 0,645296),` (x + (0,0366003 — 0,604938 i)), `(x + (0,0366003 + 0,604938 i))`
Я не тороплюсь делать это на бумаге!
Рассмотрим пример 8, который был:
x 5 -4 x 4 — 7 x 3 + 14 x 2 -44 x + 120
Используя Wolfram | Alpha, получаем
( x — 2) ( x — 5) ( x + 3) ( x 2 + 4) = 0
Обратите внимание, что в этом примере 5 элементов в скобках не указаны.
Следующий выглядит устрашающе:
Пример 9: x 4 + 0,4 x 3 — 6,49 x 2 + 7,244 x — 2,112 = 0
Позволяя Wolfram | Alpha делать за нас работу, мы получаем:
`0,002 (2 x — 1) (5 x — 6) (5 x + 16) (10 x — 11)`
Итак, хотя процесс поиска этих факторов интересно узнать, лучше использовать доступные инструменты.
В ближайшее время
В следующем разделе мы узнаем, как решать полиномиальные уравнения.
формул для решения полиномиальных уравнений.
Формулы для решения полиномиальных уравнений.| Формулы для решения полинома Уравнения. |
Общая форма уравнения энной степени : a 0 x n + a 1 x n-1 + a 2 x n-2 +. .. + а н-1 х
+ A n = 0
.. + а н-1 х
+ A n = 0
Уравнения n-й степени всегда имеют n корни. В конкретных случаях некоторые или все из этих n корней могут быть равны друг другу.
Если коэффициенты a i равны реальные числа , тогда корни могут быть реальный или сложный номеров. (Любая комбинация, со следующим ограничением: если одна корней комплекс , затем его конъюгат также является корнем.Это означает, что происходит сложных корней. в парах и в уравнениях нечетной степени есть хотя бы один реальный рут.)
| Уравнения первой степени: | |
| ax + b = 0 Один корень : | |
| Уравнения второй степени (или квадраты): | |
ax 2 + bx + c = 0 | |
| Уравнения третьей степени (или кубики): | |
| ось 3 + bx 2 + cx + д = 0 Три корня : | |
| Уравнения четвертой степени (или квартики): | |
| ось 4 + bx 3 + cx 2 + dx + e = 0 Четыре корня : | |
| Уравнения степени выше четырех: | |
| Корни уравнений степени больше четырех не может , как правило, может быть выражено с использованием только операции сложение, вычитание, умножение, деление и извлечение n-го числа корни [Руффини, Абель, Галуа].Однако эти корни можно найти с численные алгоритмы. | |
| |
— CodeProject
Введение
Недавно я столкнулся с ситуацией, когда мне нужно было решить полиномиальное уравнение 4-й степени в. NET, и, к своему удивлению, я не смог найти ни одного кода, написанного на C # или VB .NET, который содержал либо явные алгебраические формулы, либо численный алгоритм Jenkins-Traub. (Однако я нашел несколько переводов алгоритма Дженкинса-Трауба, написанного Дженкинсом Хаймельфом на FORTRAN (все еще можно загрузить здесь Netlib). Однако мне удалось перепутать реализации, сделанные на C ++, которые я перевел на C # и VB.NET В свою защиту я перевел и тот, что написал Лоран Бартольди, но он не был включен в статью.Я использовал один алгоритм C ++, переведенный Дэвидом Биннером только для реальных коэффициентов. Примите мои искренние извинения за эту ошибку. C ++, на который я полагался для сложных коэффициентов, был написан Хенриком Вестермарком. Оба этих приложения преобразованы мной из C ++ и C в код C # и VB.
NET, и, к своему удивлению, я не смог найти ни одного кода, написанного на C # или VB .NET, который содержал либо явные алгебраические формулы, либо численный алгоритм Jenkins-Traub. (Однако я нашел несколько переводов алгоритма Дженкинса-Трауба, написанного Дженкинсом Хаймельфом на FORTRAN (все еще можно загрузить здесь Netlib). Однако мне удалось перепутать реализации, сделанные на C ++, которые я перевел на C # и VB.NET В свою защиту я перевел и тот, что написал Лоран Бартольди, но он не был включен в статью.Я использовал один алгоритм C ++, переведенный Дэвидом Биннером только для реальных коэффициентов. Примите мои искренние извинения за эту ошибку. C ++, на который я полагался для сложных коэффициентов, был написан Хенриком Вестермарком. Оба этих приложения преобразованы мной из C ++ и C в код C # и VB.
 Для повторного поиска и личного использования нет проблем.
Для повторного поиска и личного использования нет проблем.Явные алгебраические формулы, которые также реализованы, отвратительны и определенно засорят ваш день, если вам когда-нибудь понадобится такая, поэтому я решил поделиться ею с вами. Я внес некоторые исправления в формулу благодаря приведенному ниже комментарию Бенуа Андриё.
У меня также есть довольно длинный рассказ, чтобы следить за ним, так как я прочитал «Уравнение, которое не могло быть решено» Марио Ливио. Название книги отсылает к истории неразрешимости полиномиального уравнения 5-й степени, но оно также проходит через историческое развитие решений полиномиальных уравнений более низкой степени.
Я не буду давать никаких объяснений того, как были получены эти формулы, поскольку формулы становятся довольно длинными, настолько длинными, что даже у Тартальи (одного из людей, принимавших участие в решении кубического уравнения) были проблемы с запоминанием всего. правила, которые он открыл.
Что касается числового алгоритма Jenkins-Traub, он был полностью переведен мной из версий C ++ и C в VB.NET и C #, и, насколько я его тестировал, похоже, он работает нормально. Следует отметить, что алгоритм Дженкинса-Трауба обычно использует явные формулы для 1-й и 2-й степени, а численное приближение — для 3-й степени и выше.
Полиномиальное уравнение 1-й степени
Это довольно легко решить математически, поэтому, если у вас возникли проблемы, вам, вероятно, не следует загружать код. Я, конечно, говорю об уравнениях в форме 2x + 3 = 7, а простое уравнение называется линейными уравнениями, так как они могут быть представлены линиями при построении графика (или рисовании).
Однако история, лежащая в основе уравнений, довольно интересна, поэтому я собираюсь вернуться в 2000 г. до н.э. — 600 г. до н.э., к вавилонской цивилизации в Месопотамии.Слово уравнение следует использовать в этом контексте с осторожностью, поскольку вавилоняне на самом деле не использовали алгебру для решения этих уравнений, а вместо этого отважились на длительные дискуссии и логику для решения проблем. Это может быть способом сделать математику еще более сложной и непонятной, чем когда-либо, особенно когда мы имеем дело с полиномиальными уравнениями более высокого порядка.
Это может быть способом сделать математику еще более сложной и непонятной, чем когда-либо, особенно когда мы имеем дело с полиномиальными уравнениями более высокого порядка.
Результат такого решения математических задач без использования алгебры означал, что вавилоняне не могли найти никаких общих закономерностей или формул, лежащих в основе различных математических задач.Несмотря на громоздкие формулировки математических задач, им все же удалось решить пары (т.е. уравнения с неизвестными x и y) линейных уравнений.
Вавилоняне, похоже, не были так заинтересованы в создании большого количества текстов с уравнением 1-й степени, как, например, египтяне, поскольку кажется, что вавилоняне считали это слишком элементарным для любого подробного обсуждения. Однако в Египте существуют большие рукописи на эту тему, в которых представлены математические «рецепты» с решением некоторых проблем, как своего рода поваренная книга.
Следует отметить, что в китайском сборнике «Девять глав по математическому искусству» (Jiu zhang suan shu) можно найти решения не менее чем трех линейных уравнений с тремя неизвестными, что является настоящим подвигом, учитывая, насколько громоздкой была процедура. 2 + x = 4, и они также могли только найти положительное решение.
2 + x = 4, и они также могли только найти положительное решение.
Греческой цивилизации вскоре удалось решить некоторые проблемы с помощью блестящего математика Диафаноуса. Он эффективно продвинул способ представления решений, сделав промежуточный пункт между вавилонскими формулировками уравнений и современным способом использования алгебры. Его книга «Арифметика» показывает решения трех различных типов квадратных уравнений, а также знаменитых уравнений Диафаноуса, примером которых является Великая теорема Ферма. Фактически Ферма читал «Аритметику», и именно в этой книге Диафануса он написал свою знаменитую последнюю теорему на полях.Что касается самого Диафануса, то на самом деле мы знаем о нем очень мало, невозможно даже представить себе занавес, когда он на самом деле жил, за исключением того, что это, вероятно, было в Александрии в период между 200 и 214-284 или 298 годами нашей эры.
С падением греческой цивилизации математический прогресс на западе остановился и впал в спячку почти на тысячелетие. Прогресс математики теперь повернулся на восток, и один из великих математиков его возраста, Брахмагупта из Индии, сумел решить некоторые из уравнений Диафаноуса, а также первым дал решения полиномиальных уравнений 2-й степени, которые также включали отрицательные числа.Он понял, что отрицательные числа можно рассматривать как «долги», а положительные числа — как «состояние», как это сделал бы сегодня бухгалтер, и таким образом совершил огромный прорыв в математике.
Прогресс математики теперь повернулся на восток, и один из великих математиков его возраста, Брахмагупта из Индии, сумел решить некоторые из уравнений Диафаноуса, а также первым дал решения полиномиальных уравнений 2-й степени, которые также включали отрицательные числа.Он понял, что отрицательные числа можно рассматривать как «долги», а положительные числа — как «состояние», как это сделал бы сегодня бухгалтер, и таким образом совершил огромный прорыв в математике.
Следующим крупным шагом в решении уравнений стало развитие алгебры, получившее свое название от арабского математика Мухаммада ибн Мусы аль-Хорезми, а точнее его книги «Китаб аль-Джабр ва аль-Мукабала», относящейся к слово аль-джабр как основа современной алгебры слов. Аль-Джабр означает «восстановление» или «завершение», что вполне соответствует важности математического развития, которое это повлечет за собой.Его книги не были новаторскими в плане нового материала; вместо этого именно систематическое рассмотрение решений квадратного уравнения было настоящим гением в этом вопросе. Однако полный набор решений квадратного уравнения появился в Европе только в XII веке в Испании.
Однако полный набор решений квадратного уравнения появился в Европе только в XII веке в Испании.
Однако реализация формулы квадратного уравнения на компьютере не так проста, как может показаться на первый взгляд. Принимаем уравнение в виде:
Решение — это хорошо известная формула, и я, конечно, думаю об этом:
Однако у вас могут возникнуть проблемы, если вы действительно реализовали формулу на компьютере таким образом.Причина в том, что если коэффициенты a или c очень близки к нулю, вы можете получить большие ошибки усечения. Правильная реализация для поиска корней на компьютере:
Даже если коэффициенты сложны, компьютерная формула все еще верна, хотя нужно учитывать, как брать знак квадратного корня:
В приведенной выше формуле Re означает действительную часть решения, а звездочка — комплексное сопряжение комплексного числа.
Полиномиальное уравнение 3-й и 4-й степени
Это часто называют кубическим или четвертым уравнением или функцией, и неудивительно, что оно появляется, когда мы хотим найти объем чего-либо. Фактическое общее уравнение не было решено до шестнадцатого века, хотя несколько частных случаев были решены вавилонянами, а еще несколько были даны персидским поэтом Омаром Хайямом в двенадцатом веке. Однако реальной ощутимой необходимости в решении кубического уравнения не было.Никто не ждал, когда это откроется, это был скорее умственный вызов, своего рода Олимпийские игры по математике, которые определят величайший интеллект его времени.
Фактическое общее уравнение не было решено до шестнадцатого века, хотя несколько частных случаев были решены вавилонянами, а еще несколько были даны персидским поэтом Омаром Хайямом в двенадцатом веке. Однако реальной ощутимой необходимости в решении кубического уравнения не было.Никто не ждал, когда это откроется, это был скорее умственный вызов, своего рода Олимпийские игры по математике, которые определят величайший интеллект его времени.
Первое частное решение кубического уравнения могло быть получено в старейшем в настоящее время открытом университете, Болонском университете, который был открыт с момента его основания в 1088 году. После того, как в 1501 году перед ним была поставлена задача, связанная с полиномиальными уравнениями третьей степени, Сципионе дель Ферро решил поработать над проблемой.И примерно в 1515 году ему удалось найти метод решения кубических уравнений, который имел вид x3 + mx = n. Дель Ферро не опубликовал свой результат, который, к сожалению, был вполне нормальным в те дни, и только рассказал своему ученику Антонио Фиоре и его зятю о своем открытии на собственном смертном одре. Тогда Фиоре, похоже, подумал, что формула была его, чтобы использовать с этого момента, как ему заблагорассудится, но не опубликовал ее сразу, а вместо этого дождался подходящего момента, чтобы появиться.
Тогда Фиоре, похоже, подумал, что формула была его, чтобы использовать с этого момента, как ему заблагорассудится, но не опубликовал ее сразу, а вместо этого дождался подходящего момента, чтобы появиться.
Итак, когда Никколо Тарталья в 1530 году объявил, что он может решить некоторые задачи, касающиеся кубических уравнений, Фиоре решил, что его момент настал, и вызвал Тарталью на математический спор.Каждый участник давал другому 30 задач для решения, а проигравший платил победителю денежную цену. У каждого из них будет сорок или пятьдесят дней на решение проблем.
К тому времени, когда задачи были переданы Тарталье, он сумел решить их все за два часа! И Фиоре не мог решить ни одну из поставленных ему задач, и он не знал уравнений в форме x3 + mx2 = n, поэтому Тарталья выиграл соревнование.
В 1539 году, после масштабной кампании по сохранению, персонаж по имени Джероламо Кардано (на самом деле он получал свое пособие, играя в азартные игры, когда был студентом и был известен тем, что был грубой и грубостью по отношению к окружающим), сумел убедить Тарталья раскрыть формулу при условии, что Кардано ее не раскроет. Однако Кардано узнал о решениях дель Ферро от зятя дель Ферро и решил, что он не связан соглашением с Тартальей, поскольку он представит решение дель Ферро, а не Тарталья, поэтому он опубликовал результат в своей книге. Ars Magna. Многие современные математики считают эту книгу началом современной алгебры, и в ней используются решения с комплексными числами, хотя Кардано не понимал этого в деталях, поскольку некоторая часть этого была взята из Тартальи. .(Рафаэля Бомбелли часто считают первооткрывателем комплексных чисел, поскольку он провел гораздо больше исследований по этому предмету.) После того, как книга была опубликована, Тарталья немедленно бросил вызов Кардано, который был довольно плохим математиком по стандартам Тартальи: и он сразу же отказался. Однако ученик Кардано, Лодовико Феррари, бросил Тарталье многочисленные публичные вызовы, которые Тарталья отрицал. В конце концов Тарталье предложили работу в университете, учитывая, что он победит Феррари в споре.Феррари открыл общий способ решения кубического уравнения, который не был известен Тарталье, он также нашел решение уравнения четвертой степени еще в 1540 году, но для этого требовалось решение кубического уравнения, поэтому оно не было опубликовано, пока Кардано не нашел о решениях дель Ферро.
Однако Кардано узнал о решениях дель Ферро от зятя дель Ферро и решил, что он не связан соглашением с Тартальей, поскольку он представит решение дель Ферро, а не Тарталья, поэтому он опубликовал результат в своей книге. Ars Magna. Многие современные математики считают эту книгу началом современной алгебры, и в ней используются решения с комплексными числами, хотя Кардано не понимал этого в деталях, поскольку некоторая часть этого была взята из Тартальи. .(Рафаэля Бомбелли часто считают первооткрывателем комплексных чисел, поскольку он провел гораздо больше исследований по этому предмету.) После того, как книга была опубликована, Тарталья немедленно бросил вызов Кардано, который был довольно плохим математиком по стандартам Тартальи: и он сразу же отказался. Однако ученик Кардано, Лодовико Феррари, бросил Тарталье многочисленные публичные вызовы, которые Тарталья отрицал. В конце концов Тарталье предложили работу в университете, учитывая, что он победит Феррари в споре.Феррари открыл общий способ решения кубического уравнения, который не был известен Тарталье, он также нашел решение уравнения четвертой степени еще в 1540 году, но для этого требовалось решение кубического уравнения, поэтому оно не было опубликовано, пока Кардано не нашел о решениях дель Ферро.
Феррари выиграла спор с Тартальей, который ушел незадолго до того, как закончился первый день спора. (Феррари был настоящим персонажем, так как он потерял все пальцы на правой руке в возрасте семнадцати лет в драке).С этого момента его карьера резко пошла вверх, хотя, как утверждается, позже он был отравлен своей сестрой и умер.
Настоящий первооткрыватель формулы третьей степени, как вы понимаете, довольно сложен, хотя решение уравнения 4-й степени, похоже, является делом только Феррари.
Формулы обычно не реализуются на компьютере, так как решения, найденные численным методом, почти всегда лучше с ними. Если вы все же хотите использовать явные формулы, вам следует реализовать формулу Вите, которая использует тригонометрические функции вместо решений Феррари.
Полиномиальные уравнения высшей степени
После того, как квадратное уравнение было решено с помощью алгебры, многие пытались решить полиномиальное уравнение пятой степени или 5-й степени, и все они потерпели неудачу. Это не было доказано до тех пор, пока в 1823 году Авель не нашел общего доказательства, в котором говорилось, что на самом деле это невозможно. Теорема известна сегодня как теорема Абеля – Руффини или теорема невозможности Абеля. Причина двойного названия в том, что Руффини дал неполное доказательство теоремы в 1799 году, о котором Абель не знал до 1826 года.Прочитав и изучив ее, он сказал, что работа Руффини была настолько сложной для понимания, что он не был уверен, правильна ли она.
Это не было доказано до тех пор, пока в 1823 году Авель не нашел общего доказательства, в котором говорилось, что на самом деле это невозможно. Теорема известна сегодня как теорема Абеля – Руффини или теорема невозможности Абеля. Причина двойного названия в том, что Руффини дал неполное доказательство теоремы в 1799 году, о котором Абель не знал до 1826 года.Прочитав и изучив ее, он сказал, что работа Руффини была настолько сложной для понимания, что он не был уверен, правильна ли она.
Однако важно знать, что на самом деле означает доказательство, и, что особенно важно, что оно не означает. Доказательство Абеля просто утверждает, что нельзя найти общее решение всех корней в квинтике или любом полиномиальном уравнении более высокого порядка с помощью алгебры. Абель использовал обобщение интегралов Эйлера, чтобы доказать это, и немецкий математик Якоби был вне себя от того, что это открытие осталось незамеченным математическим сообществом.
Однако можно найти решение уравнений 5-й степени с помощью численных методов (Ньютона-Рэпсона) или с помощью эллиптических интегралов. Если использовать теорию Эвариста Галуа, можно также выяснить, какие решения можно было бы найти. Эварист Галуа также доказал, что полиномиальное уравнение 5-й степени не может быть решено независимо от работ Абеля и Руффини, и его доказательство было опубликовано посмертно в 1846 году
Если использовать теорию Эвариста Галуа, можно также выяснить, какие решения можно было бы найти. Эварист Галуа также доказал, что полиномиальное уравнение 5-й степени не может быть решено независимо от работ Абеля и Руффини, и его доказательство было опубликовано посмертно в 1846 году
Задача с явными формулами
Существуют проблемы с явными формулами, которые связаны с ограниченным пространством памяти на компьютере, которое в некоторых случаях может давать такую высокую ошибку, что может привести к тому, что вычисленные решения будут далеки от истинных значений.На практике решения для 3-го и выше почти всегда лучше с алгоритмом Дженкинса-Трауба или другими подобными методами, чем решения, рассчитанные с помощью явных формул.
Однако существуют проблемы с численной оценкой полинома, поскольку любой человек с достаточным пониманием лежащих в основе алгоритмов легко может построить пример, который не сойдется. Возьмите уравнение (1) ниже:
Учитывая, что это полиномиальные решения 5-й степени, можно найти только с помощью численного алгоритма, но мы знаем из Фундаментальной теоремы алгебры, что уравнение будет иметь ровно 5 действительных или комплексных решений, как доказали Гаусс и другие. Точные решения уравнения 1: Проблема с этим примером заключается в том, что реализованный Jenkins-Traub в C # и VB не будет сходиться (скорее всего, с двойной точностью, которая выбрана для хранения данных, а также эпсилон , минимальные и максимальные значения, которые были «экспортированы» из библиотеки с плавающей запятой в VC ++). На самом деле, для такого алгоритма всегда может быть проблематично сойтись, учитывая количество множественных корней. Причина в том, что алгоритм извлекает найденные корни из исходного уравнения, и при слишком большой числовой ошибке это может привести к тому, что другие решения не будут найдены.Так что обратите внимание на тот факт, что любой метод, использующий итерации типа Ньютона, может иметь проблемы с несколькими корнями. Это также применимо к обстоятельствам, когда корни расположены близко (или очень далеко) друг от друга.
Точные решения уравнения 1: Проблема с этим примером заключается в том, что реализованный Jenkins-Traub в C # и VB не будет сходиться (скорее всего, с двойной точностью, которая выбрана для хранения данных, а также эпсилон , минимальные и максимальные значения, которые были «экспортированы» из библиотеки с плавающей запятой в VC ++). На самом деле, для такого алгоритма всегда может быть проблематично сойтись, учитывая количество множественных корней. Причина в том, что алгоритм извлекает найденные корни из исходного уравнения, и при слишком большой числовой ошибке это может привести к тому, что другие решения не будут найдены.Так что обратите внимание на тот факт, что любой метод, использующий итерации типа Ньютона, может иметь проблемы с несколькими корнями. Это также применимо к обстоятельствам, когда корни расположены близко (или очень далеко) друг от друга.
Jenkins-Traub действительно использует метод типа Ньютона для поиска корней, и это также может иметь другие проблемы. Если многочлен без линейного члена равен нулю в нуле, итерационный метод не сможет сойтись, учитывая, что и функция, и ее производная равны нулю в нуле.
Если многочлен без линейного члена равен нулю в нуле, итерационный метод не сможет сойтись, учитывая, что и функция, и ее производная равны нулю в нуле.
Есть еще одна довольно удивительная особенность многочленов, имеющих кратные корни. это то, что производный многочлен будет иметь на один корень меньше. Возьмем пример формы уравнения 1, если мы выведем уравнение, мы получим:
И когда мы пытаемся решить это уравнение, используя тот же алгоритм Дженкинса-Трауба, что и раньше, мы обнаруживаем, что действительно те же корни все еще существуют, с дополнительным, который не был. Решения можно легко проверить, подставив значения в исходное уравнение (1):
Фактический код стал настолько сложным, что объяснить все это трудно, а то и невозможно.Вместо этого я собираюсь отослать вас к процедуре Дженкинса-Трауба, описанной в Википедии.
Однако важно знать, что алгоритм Дженкинса-Трауба де-факто считается способом численного вычисления корней многочлена. Он тщательно протестирован, а также внедрен во многие продукты, которые используются в коммерческих целях (например, Matematica и другие).
Он тщательно протестирован, а также внедрен во многие продукты, которые используются в коммерческих целях (например, Matematica и другие).
Что касается явных формул, их следует использовать с осторожностью, и нельзя предполагать, что они дают правильные результаты для любых реальных коэффициентов, которые вы вводите, хотя описание, данное в программе, должно указывать, является ли это распознанным типом, и если описание вывода соответствует вычисленным корням.Для нахождения корней используются несколько различных методов, среди которых уравнение Феррари, двуквадратное уравнение с депрессией и многие другие.
Список литературы
Сайт Wolfram, на котором представлены некоторые используемые формулы и другие ссылки на используемый числовой алгоритм:
Исходный код C ++:
Книг:
Другие ссылки:
.
 0 / a;
b *= a;
c *= a;
d *= a;
e *= a;
std::complex<double> P = (c * c + 12.0 * e - 3.0 * b * d) / 9.0;
std::complex<double> Q = (27.0 * d * d + 2.0 * c * c * c + 27.0 * b * b * e - 72.0 * c * e - 9.0 * b * c * d) / 54.0;
std::complex<double> D = sqrtn(Q * Q - P * P * P,2.0);
std::complex<double> u = Q + D;
std::complex<double> v = Q - D;
if(v.real() * v.real() + v.imag() * v.imag() > u.real() * u.real() + u.imag() * u.imag())
{
u = sqrtn(v,3.0);
}
else
{
u = sqrtn(u,3.0);
}
std::complex<double> y;
if(u.real() * u.real() + u.imag() * u.imag() > 0.0)
{
v = P / u;
std::complex<double> o1(-0.5,+0.86602540378443864676372317075294);
std::complex<double> o2(-0.5,-0.86602540378443864676372317075294);
std::complex<double>&yMax = x[0];
double m2 = 0.0;
double m2Max = 0.0;
int iMax = -1;
for(int i = 0;i < 3;++i)
{
y = u + v + c / 3.
0 / a;
b *= a;
c *= a;
d *= a;
e *= a;
std::complex<double> P = (c * c + 12.0 * e - 3.0 * b * d) / 9.0;
std::complex<double> Q = (27.0 * d * d + 2.0 * c * c * c + 27.0 * b * b * e - 72.0 * c * e - 9.0 * b * c * d) / 54.0;
std::complex<double> D = sqrtn(Q * Q - P * P * P,2.0);
std::complex<double> u = Q + D;
std::complex<double> v = Q - D;
if(v.real() * v.real() + v.imag() * v.imag() > u.real() * u.real() + u.imag() * u.imag())
{
u = sqrtn(v,3.0);
}
else
{
u = sqrtn(u,3.0);
}
std::complex<double> y;
if(u.real() * u.real() + u.imag() * u.imag() > 0.0)
{
v = P / u;
std::complex<double> o1(-0.5,+0.86602540378443864676372317075294);
std::complex<double> o2(-0.5,-0.86602540378443864676372317075294);
std::complex<double>&yMax = x[0];
double m2 = 0.0;
double m2Max = 0.0;
int iMax = -1;
for(int i = 0;i < 3;++i)
{
y = u + v + c / 3.
 eigenvalues();
std::cout<<"matrix_eigenvalues: "<<std::endl<<matrix_eigenvalues<<std::endl;
return 0;
}
eigenvalues();
std::cout<<"matrix_eigenvalues: "<<std::endl<<matrix_eigenvalues<<std::endl;
return 0;
}

