Подкоренные выражения: как решать
Понятие корня
Тема о подкоренных выражениях относится к курсу алгебры. Будем считать, что понятие степени читателю уже известно. Понятие корня актуально, когда речь идёт примерах с иррациональными числами. Такие примеры встречаются и в курсе геометрии и даже могут описывать длины. Но перейдём к определениям.
Решение подкоренных выражений строится на знании и применении свойств корня. Для начала, приведём определение корня.
Определение 1
Корень $n$-ой степени из числа $a$, то есть $\sqrt[n]a$ — это число, которое будучи возведено в степень $n$, даёт $a$.
Из данного определения следует свойство $(\sqrt[n]a)^n=a$.
Свойства корня с примерами
Основное свойство корня: величина корня не изменится, если показатель корня и показатель подкоренного выражения умножить или разделить на одно и то же число. Отсюда следует, что корни разных степеней можно привести к одинаковым показателям.
Приведём простой пример.
Пример 2
Рисунок 1. Пример. Автор24 — интернет-биржа студенческих работ
Также имеются следующее свойства:
Рисунок 2. Свойства. Автор24 — интернет-биржа студенческих работ
Рисунок 3. Свойства. Автор24 — интернет-биржа студенческих работ
Рисунок 4. Свойства. Автор24 — интернет-биржа студенческих работ
Решим простые примеры.
Пример 3
Рисунок 5. Пример. Автор24 — интернет-биржа студенческих работ
Пример 4
Рисунок 6. Пример. Автор24 — интернет-биржа студенческих работ
Преобразования корней
При решении корней кроме вышеуказанных свойств применяют простейшие преобразования, такие как
- вынесение множителей за знак корня
Рисунок 7. Вынесение множителей за знак корня. Автор24 — интернет-биржа студенческих работ
- подведение множителей под знак корня
Рисунок 8. Подведение множителей под знак корня. Автор24 — интернет-биржа студенческих работ
- освобождение подкоренного выражения от знаменателей.
Для последнего случая приведём пример с числами:
Рисунок 9. Освобождение подкоренного выражения от знаменателей. Автор24 — интернет-биржа студенческих работ
Рассмотрим пример, в котором показывается как происходит освобождение знаменателя дроби от корней.
Пример 5
Имеем:
Рисунок 10. Пример. Автор24 — интернет-биржа студенческих работ
Произведём умножение членов дробей на $\sqrt5$:
Рисунок 11. Пример. Автор24 — интернет-биржа студенческих работ
Пример решения
На практике необходимо помнить все перечисленные свойства и преобразования корней, а также свойства степеней, которые, как мы условились, читателю уже известны. Решим типичный пример, который встречается, например, в ЕГЭ.
Пример 6
Нужно вычислить выражение: $9+\sqrt[6]{2\sqrt5-3\sqrt3}\cdot\sqrt[6]{47+12\sqrt{15}}\cdot\sqrt[3]{49}$.
$9+\sqrt[6]{(2\sqrt5-3\sqrt3)^2\cdot(47+12\sqrt{15})}\cdot\sqrt[3]{7^2}=9+\sqrt[6]{(20-12\sqrt{15}+27)\cdot(47+12\sqrt{15})\cdot7^4}=9+\sqrt[6]{(2209-2160)}\cdot\sqrt[3]{7^2}=9+\sqrt[6]{7^2}\cdot\sqrt[3]{7^2}=9+\sqrt[3]{7\cdot7^2}=9+7=16.$
spravochnick.ru
Преобразование выражений, содержащих квадратные корни
Ранее с вами научились преобразовывать рациональные выражения. Тождественные преобразования, которые умеем выполнять: это приведение подобных слагаемых; раскрытие скобок; разложение на множители; приведение рациональных дробей к общему знаменателю. Также для преобразования рациональных выражений используют формулы сокращённого умножения.

Теперь же мы ввели новую операцию – операцию извлечения квадратного корня. Вы уже знаете, что арифметическим квадратным корнем из числа а называют неотрицательное число, квадрат которого равен а.

Используя эти формулы, можно выполнять различные преобразования выражений, содержащих операцию извлечения квадратного корня. Давайте рассмотрим примеры преобразований выражений, которые содержат квадратные корни.
Задание: упростите выражение.

Задание: преобразуйте выражения.

Задание: сократите дробь.

Очень важное место в преобразовании выражений, содержащих квадратные корни, занимает избавление от иррациональности в знаменателе или числителе дроби. Можно рассмотреть это на простом примере.
Например: преобразуем дробь так, чтобы знаменатель не содержал квадратного корня.
Как сделать так, чтобы знаменатель дроби не содержал квадратный корень? Следует вспомнить основное свойство дроби: если числитель и знаменатель дроби умножить или разделить на одно и то же число, не равное нулю, то значение дроби не изменится

Обратите внимание, дробь 
 .
Причем, в знаменателе второй дроби нет знака корня. В таких случаях говорят,
что мы освободились от иррациональности в знаменателе дроби.
.
Причем, в знаменателе второй дроби нет знака корня. В таких случаях говорят,
что мы освободились от иррациональности в знаменателе дроби.Задание: освободиться от иррациональности в знаменателе дроби.

videouroki.net
Как упростить сложный радикал

Методы упрощения сложных радикалов
Упростить сложный радикал — значит избавиться от внешнего корня. Правильнее всего начать изучение этой темы с упрощения двойных радикалов. Ведь если мы научимся упрощать двойные радикалы, то и более сложные тоже сумеем.
| Пример 1. Упростить сложный радикал: |
Как нам избавиться от внешнего корня? Понятно, что для этого нужно преобразовать подкоренное выражение, представив его в виде полного квадрата. Для этого воспользуемся известной формулой «Квадрат разности»:
![Rendered by QuickLaTeX.com \[ (a-b)^2=a^2-2ab+b^2. \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-e2e0d78e3bfb092646ed3cc65c485681_l3.png)
Здесь, как видите, справа у отрицательного члена есть множитель 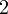 . Поэтому и под корнем давайте получим этот множитель. Для этого
. Поэтому и под корнем давайте получим этот множитель. Для этого 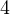 представим в виде произведения
представим в виде произведения 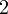 на
на 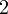 :
:
![Rendered by QuickLaTeX.com \[ \sqrt{9-4\sqrt{5}} = \sqrt{9-2\cdot 2\cdot\sqrt{5}} . \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-d8e25d40dfcbae163558ff7c038d64c8_l3.png)
Тогда 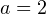 и
и 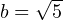 . Осталось только обратить внимание на то, что
. Осталось только обратить внимание на то, что 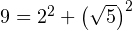 . Теперь видно, что под корнем у нас получился квадрат разности:
. Теперь видно, что под корнем у нас получился квадрат разности:
![Rendered by QuickLaTeX.com \[ \sqrt{9-4\sqrt{5}} = \sqrt{2-2\cdot 2\cdot\sqrt{5}+\left(\sqrt{5}\right)^2} = \sqrt{(2-\sqrt{5})^2}. \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-3d5d023f45335d05b7a05d39daa11e25_l3.png)
Теперь вспоминаем, что 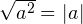 . Именно модулю. Здесь это очень важно, потому что квадратный корень – положительное число. Тогда получаем:
. Именно модулю. Здесь это очень важно, потому что квадратный корень – положительное число. Тогда получаем:

Ну а поскольку 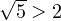 , модуль раскрывается со знаком минус. В результате в ответе получаем:
, модуль раскрывается со знаком минус. В результате в ответе получаем:
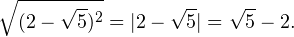
Вот так просто нам удалось упростить этот радикал. Но есть и более сложные случаи, когда не сразу удаётся догадаться, как представить подкоренное выражение в виде полного квадрата. Например, в следующем примере.
| Пример 2. Упростите сложный радикал: |
Чтобы долго не ломать голову, можно воспользоваться следующим способом.
Напоминаю, что наша цель состоит в том, чтобы представить выражение под корнем в виде полного квадрата. Конкретно в этом примере в виде квадрата суммы:
![Rendered by QuickLaTeX.com \[ \sqrt{75+12\sqrt{21}} =\sqrt{(a+b)^2}. \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-2255e2b170f4a9266e9c9f2bb3944a9f_l3.png)
Ну а квадрат суммы раскрывается по известной формуле, которую мы сегодня уже писали:
![Rendered by QuickLaTeX.com \[ \sqrt{75+12\sqrt{21}} =\sqrt{(a+b)^2} = \sqrt{a^2+2ab+b^2} . \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-752b72f0b8efc161742a7961200758af_l3.png)
Так вот, идея, собственно, состоит в том, чтобы за 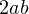 взять иррациональную часть подкоренного выражения, а за
взять иррациональную часть подкоренного выражения, а за 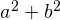 – рациональную. Тогда получается следующая система уравнений:
– рациональную. Тогда получается следующая система уравнений:
![Rendered by QuickLaTeX.com \[ \begin{cases} a^2+b^2 = 75 \\ 2ab = 12\sqrt{21}. \end{cases} \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-78742489fbc06e3c377ece782e7a8c71_l3.png)
Понятно, что 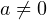 и
и 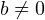 . Иначе не выполняется второе уравнение системы. Тогда выражаем коэффициент
. Иначе не выполняется второе уравнение системы. Тогда выражаем коэффициент  из второго уравнения:
из второго уравнения:
![Rendered by QuickLaTeX.com \[ b=\frac{6\sqrt{21}}{a}. \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-563cd34a307ba84850f6d29ea945696b_l3.png)
Далее подставляем получившееся выражение в первое уравнение. В результате приходим к следующему уравнению:
![Rendered by QuickLaTeX.com \[ a^2+\frac{756}{a^2} = 75\Leftrightarrow \frac{a^4-75a^2+756}{a^2} = 0. \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-8b57de502ac6391e1f6600b974f15724_l3.png)
Знаменатель этой дроби не равен нулю, значит нулю равен её числитель. Получаем биквадратное уравнение, которое решается стандартным способом (подробнее смотрите в приложенном видео). Решая его, мы получаем аж 4 корня. Можно взять любой. Мне больше нравится 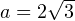 . Тогда
. Тогда 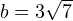 . Итак, получаем окончательно:
. Итак, получаем окончательно:
![Rendered by QuickLaTeX.com \[ \sqrt{75+12\sqrt{21}} = \sqrt{\left(2\sqrt{3}+3\sqrt{7}\right)^2} = \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-e0e84ccde64935110e26fdd2957d0748_l3.png)
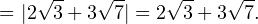
Вот такой способ, как упростить сложный радикал. Есть ещё один. Для любителей запоминать сложные формулы, коим я не являюсь. Но для полноты описания расскажу и о нём тоже.
Формула сложных радикалов
Вот так выглядит эта формула:
![Rendered by QuickLaTeX.com \[ \sqrt{a\pm\sqrt{b}} = \sqrt{\frac{a+\sqrt{a^2-b}}{2}}\pm\sqrt{\frac{a-\sqrt{a^2-b}}{2}}. \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-72682915964147ced636e38a52efc066_l3.png)
Довольно страшная, не правда ли? Но не бойтесь, её действительно можно успешно применять в некоторых случаях. Разберём на примере:
| Пример 3. Упростить выражение, используя формулу сложных радикалов: |
Подставляем в формулу соответствующие значения:
![Rendered by QuickLaTeX.com \[ \sqrt{57-24\sqrt{3}} = \sqrt{57-\sqrt{1728}} = \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-74370d34f009a175f2ca8610a2519931_l3.png)
![Rendered by QuickLaTeX.com \[ \sqrt{\frac{57+\sqrt{57^2-1728}}{2}}-\sqrt{\frac{57-\sqrt{57^2-1728}}{2}} = \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-143b920f1b6a0b552478acfa935741c9_l3.png)
![Rendered by QuickLaTeX.com \[ =\sqrt{\frac{57+39}{2}}-\sqrt{\frac{57-39}{2}} = \sqrt{48}-\sqrt{9} = 4\sqrt{3}-3. \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-40407dc304c5bd0c7e8371178ce3ebe4_l3.png)
Вот такой получается ответ.
Итак, сегодня на занятии я рассказал о том, как упростить сложный радикал. Если вы не знали ранее методы, о которых сегодня шла речь, то скорее всего вам еще нужно очень многому научиться, чтобы чувствовать себя уверенным на ЕГЭ или на вступительном экзамене по математике. Но не переживайте, я могу вас всему этому научить. Вся необходимая информация о моих занятиях находится на этой странице. Удачи вам!
Материал подготовил репетитор по математике и физике, Сергей Валерьевич
yourtutor.info
![Rendered by QuickLaTeX.com \[ \sqrt{9-4\sqrt{5}}. \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-325620950a0a769905738ad91167e265_l3.png)
![Rendered by QuickLaTeX.com \[ \sqrt{75+12\sqrt{21}}. \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-32596aded9cd72f9ab9e1da8badbc067_l3.png)
![Rendered by QuickLaTeX.com \[ \sqrt{57-24\sqrt{3}}. \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-8ce98a50fd187da51bf3c0eba3f1b461_l3.png)