6/2(2+1)= Как решается этот проклятый пример: denis_demakhin — LiveJournal

Уже давно я увлечен этим примером:

Делал по нему опросы

И сейчас попробую обосновать мою новую точку зрения, которая теперь выглядит так:

Дело в том, что между алгеброй и арифметикой есть разница в порядке действий:

Теперь понятно, почему инженерный калькулятор показывает ответ: 1.

Он не сломался. Он алгебраический.

Алгебраический калькулятор считает по правилам алгебры.

Осталось понять, алгебраический это пример или арифметический. От этого будет зависеть ответ.

Букв в примере нет, однако, в нем есть пропущенный знак умножения перед скобкой:

Случаи возможного пропуска знака умножения:

1. Между буквенными множителями;


2. Между числовым и буквенным множителем;


3. Между множителем и скобкой;


4. Между выражениями в скобках.

Тут подходит только правило №3. И тогда пропущенный знак умножения равносилен скобкам, то есть 2(2+1) = (2*(2+1)), следуя правилам из скана выше.

И получается, что если выражение (2+1) заменить на икс, то написание 6/2Х читается как «шесть, разделить на два икса».

Тогда ответ: 1.

Но почему тогда самая умная штука на Земле — Гугл-поисковик считает, что ответ 9?

Потому что и Гугл и смартфон считают по арифметическим правилам.

Но вот тут есть тонкий момент. Арифметические правила должны, по-правильному то, действовать при указании знака умножения. Так, как я написал здесь:

Тут уже нет оснований применять правила алгебры, в которых пропущенный знак умножения считается неразрывным. И ответ получается: 9.

Вывод:

Всё зависит от того, алгебра это или арифметика.

Еще интересные штуки:

Задачи, ломающие мозг (с ответами, спрятанными под спойлер)

Тренировка ума развивальщика предприятий

Подписывайся, мыслитель!

Решение уравнений с дробями — как решать дробные уравнения

Понятие дроби

Прежде чем отвечать на вопрос, как найти десятичную дробь, разберемся в основных определениях, видах дробей и разницей между ними.

Дробь — это запись числа в математике, в которой a и b — числа или выражения. По сути, это всего лишь одна из форм, в которое можно представить число. Есть два формата записи:

    
• обыкновенный вид — ½ или a/b,
    
• десятичный вид — 0,5.

Над чертой принято писать делимое (число, которое делим) — числитель. А под чертой всегда находится делитель (на сколько делим), его называют знаменателем. Черта между числителем и знаменателем означает деление.

Дроби бывают двух видов:

    
1. Числовые — состоят из чисел. Например, 2/7 или (1,8 — 0,3)/5.
    
2. Алгебраические — состоят из переменных. Например, (x + y)/(x — y). Значение дроби зависит от данных значений букв.

Дробь называют правильной, когда ее числитель меньше знаменателя. Например, 4/9 и 23/57.

Неправильная дробь — та, у которой числитель больше знаменателя или равен ему. Например, 13/5. Такое число называют смешанным — читается так: «две целых три пятых», а записывается — 2 3\5.

                                                                       

Основные свойства дробей
Дробь не имеет значения, при условии, если делитель равен нулю.                  Дробь равна нулю, если числитель равен нулю, а знаменатель — нет.                  Две дроби a/b и c/d называются равными, если a * d = b * c.                  Если числитель и знаменатель умножить или разделить на одно и то же натуральное число, то получится равная ей дробь

Действия с дробями можно выполнять те же, что и с обычными числами: складывать, вычитать, умножать и делить. Также, дроби можно сравнивать между собой и возводить в степень.

Понятие уравнения

Уравнение — это математическое равенство, в котором неизвестна одна или несколько величин. Наша задача — найти неизвестные числа так, чтобы при их подстановке в пример получилось верное числовое равенство. Давайте на примере:

    
• Возьмем выражение 4 + 5 = 9. Это верное равенство, потому что 4+5 действительно 9. Если бы вместо 9 стояло любое другое число — мы бы сказали, что числовое равенство неверное.
    
• Уравнением можно назвать выражение 4 + x = 9, с неизвестной переменной x, значение которой нужно найти. Результат должен быть таким, чтобы знак равенства был оправдан, и левая часть равнялась правой.

Корень уравнения —

то самое число, которое уравнивает выражения справа и слева, когда мы подставляем его на место неизвестной. В таком случае афоризм «зри в корень» — очень кстати при усердном решении уравнений.

Равносильные уравнения — это те, в которых совпадают множества решений. Другими словами, у них одни и те же корни.

Решить уравнение значит найти все его корни или убедиться, что корней нет.

Алгебраические уравнения могут быть разными, самые часто встречающиеся — линейные и квадратные. Расскажем и про них.

                                                                                                 

Линейное уравнение выглядит так	ах + b = 0, где a и b — действительные числа.              Что поможет в решении:                               если а не равно нулю, то у уравнения единственный корень: х = -b : а;                  если а равно нулю — у уравнения нет корней;                  если а и b равны нулю, то корень уравнения — любое число.
Квадратное уравнение выглядит так:	ax2 + bx + c = 0, где коэффициенты a, b и c — произвольные числа, a ≠ 0.

Приходите решать увлекательные задачки по математике в детскую школу Skysmart. Поможем разобраться в сложной теме, подтянем оценки и покажем, что математика может быть захватывающим приключением.

Запишите ребенка на бесплатный вводный урок: познакомим с форматом, выявим пробелы и наметим индивидуальную программу обучения.

Ты можешь записаться на онлайн-уроки по математике для учеников 1-11 классов!

Понятие дробного уравнения

Дробное уравнение — это уравнение с дробями. Да, вот так просто. Но это еще не все. Чаще всего неизвестная стоит в знаменателе. Например, вот так:

Такие уравнения еще называют дробно-рациональными. В них всегда есть хотя бы одна дробь с переменной в знаменателе.

Если вы видите в знаменателях числа, то это уравнения либо линейные, либо квадратные. Решать все равно нужно, поэтому идем дальше. Примеры:

На алгебре в 8 классе можно встретить такое понятие, как область допустимых значений — это множество значений переменной, при которых это уравнение имеет смысл. Его используют, чтобы проверить корни и убедиться, что решение правильное.

Мы уже знаем все важные термины, их определения и наконец подошли к самому главному — сейчас узнаем как решить дробное уравнение.

 

Как решать уравнения с дробями

                                                                       

Универсальный алгоритм решения

Определить область допустимых значений.                  Найти общий знаменатель.                  Умножить каждый член уравнения на общий знаменатель и сократить полученные дроби. Знаменатели при этом пропадут.                  Раскрыть скобки, если нужно и привести подобные слагаемые.                  Решить полученное уравнение.                  Сравнить полученные корни с областью допустимых значений.                  Записать ответ, который прошел проверку.

А теперь еще несколько способов, которые пригодятся ребенку на уроках математики.

1. Метод пропорции

Чтобы решить уравнение методом пропорции, нужно привести дроби к общему знаменателю. А само правило звучит так: произведение крайних членов пропорции равно произведению средних. Проверим, как это работает.

Итак, у нас есть линейное уравнение с дробями:

В левой части стоит одна дробь — оставим без преобразований.

В правой части видим сумму, которую нужно упростить так, чтобы осталась одна дробь.

Как решаем:

После того, как в левой и правой части осталась одна дробь, можно применить метод пропорции и перемножить крест-накрест числители и знаменатели.

2. Метод избавления от дробей

Возьмем то же самое уравнение, но попробуем решить его по-другому.

В уравнении есть две дроби, от которых мы очень хотим избавиться. Вот, как это сделать:

    
• подобрать число, которое можно разделить на каждый из знаменателей без остатка;
    
• умножить на это число каждый член уравнения.

Ищем самое маленькое число, которое делится на 5 и 9 и без остатка — 45 как раз подходит. Умножаем каждый член уравнения на 45 и избавляемся от знаменателей. Вуаля!

Вот так просто мы получили тот же ответ, что и в прошлый раз.

                                                                       

Что еще важно учитывать при решении
если значение переменной обращает знаменатель в 0, значит это неверное значение;                  делить и умножать уравнение на 0 нельзя.

А вот и полезные видео для закрепления материала:

Примеры решения дробных уравнений

Чтобы стать успешным в любом деле, нужно чаще практиковаться. Мы уже знаем, как решаются дробные уравнения — давайте перейдем к решению задачек.

Пример 1. Решить дробное уравнение: 1/x + 2 = 5.

Как решаем:

    
1. Вспомним правило х ≠ 0. Это значит, что область допустимых значений: х — любое число, кроме нуля.
    
2. Отсчитываем справа налево в числителе дробной части три знака и ставим запятую.
    
3. Избавимся от знаменателя. Умножим каждый член уравнения на х.     

   1 + 2x = 5х

       
    
4. Решим обычное уравнение.     

   5x — 2х = 1

       

   3x = 1

       

   х = 1/3

       

Ответ: х = 1/3.

Пример 2. Найти корень уравнения

Как решаем:

    
1. Область допустимых значений: х ≠ −2.
    
2. Умножим обе части уравнения на выражение, которое сократит оба знаменателя: 2(х+2)
    
3. Избавимся от знаменателя. Умножим каждый член уравнения на х.     
       
    
4. Переведем новый множитель в числитель..     
       
    
5. Сократим левую часть на (х+2), а правую на 2.     

   4 = х + 2

       

   х = 4 — 2 = 2

       

Ответ: х = 2.

Пример 3. Решить дробное уравнение:

Как решаем:

    
1. Найти общий знаменатель:     

   3(x-3)(x+3)

       
    
2. Умножим обе части уравнения на общий знаменатель. Сократим. Получилось:     
   3(x+3)(x+3)+3(x-3)(x-3)=10(x-3)(x+3)+3*36
       
    
3. Выполним возможные преобразования. Получилось квадратное уравнение:     

   x²-9=0

       
    
4. Решим полученное квадратное уравнение:     

   x²=9

       
    
5. Получили два возможных корня:     

   x₁=−3, x₂=3

       

   х = 4 — 2 = 2

       
    
6. Если x = −3, то знаменатель равен нулю:     

   3(x-3)(x+3)=0

       

   Если x = 3 — знаменатель тоже равен нулю.

       
    
7. Вывод: числа −3 и 3 не являются корнями уравнения, значит у данного уравнения нет решения.

Ответ: нет решения.

Если нужно решить уравнение с дробями быстро — поможет онлайн-калькулятор дробей. Пользуйтесь им, если уже разобрались с темой и щелкаете задачки легко и без помощников:

Порядок действий

В уроке выражения мы узнали, что они бывают числовые и буквенные. Мы рассмотрели несколько числовых и буквенных выражений. Это были самые простейшие выражения.

Настало время сдвинуться с мёртвой точки и рассмотреть более сложные выражения. В данном уроке мы познакомимся с порядком выполнения действий.

Выражения могут состоять из нескольких чисел. Таковыми к примеру являются следующие выражения:

10 − 1 + 2 + 3
(3 + 5) + 2 × 3
5 × 2 + (5 − 3) : 2 + 1

Такие выражения нельзя вычислить сразу, то есть поставить знак равенства и записать значение выражения. Да и выглядят они не так просто, как 2 + 2 или 9 − 3.

Для подобных выражений принято соблюдать так называемый порядок действий. Суть в том, что выражение вычисляется кусочками по определённому порядку.

Когда нам требуется решить подобные примеры, мы сразу должны мысленно прочитать следующее правило:

Сначала вычислить то, что находится в скобках!

Посмотрим на выражение 10 − 1 + 2 + 3. Видим, что в нём нет никаких скобок. Тогда переходим к следующему правилу, которое выглядит так:

Читаем выражение слева направо. Если встретится умножение или деление, то сразу же выполняем эту операцию!

Читаем наше выражение 10 − 1 + 2 + 3 слева направо. Видим, что в нём нет никакого умножения или деления. Тогда переходим к следующему правилу:

Читаем выражение слева направо. Если встретится сложение или вычитание, то сразу же выполняем эту операцию!

Читаем наше выражение 10 − 1 + 2 + 3 слева направо. Встречаем вычитание 10 − 1. Сразу выполняем эту операцию: 10 − 1 = 9. Полученную девятку запишем в главном выражении вместо 10 − 1

Затем снова читаем те, правила, которые мы прочитали выше. Читать их нужно в следующем порядке:

1. Сначала вычислить то, что находится в скобках!

2. Читаем выражение слева направо. Если встретится умножение или деление, то сразу же применяем эту операцию!

3. Читаем выражение слева направо. Если встретится сложение или вычитание, то сразу же применяем эту операцию!

Сейчас у нас имеется выражение 9 + 2 + 3 Читаем его слева направо и встречаем сложение 9 + 2. Выполняем эту операцию: 9 + 2 = 11. Запишем число 11 в главном выражении вместо 9 + 2:

Осталось простейшее выражение 11 + 3, которое вычисляется легко:

11 + 3 = 14

Таким образом, значение выражения 10 − 1 + 2 + 3 равно 14

10 − 1 + 2 + 3 = 14

Иногда удобно расставить порядок действий над самим выражением. Для этого над операцией, которую необходимо выполнить, указывают её очередь. К примеру, в выражении 10 − 1 + 2 + 3 все действия выполняются последовательно слева направо, поэтому для него можно определить следующий порядок:

И далее можно выполнить действия по отдельности, что очень удобно:

1)  10 − 1 = 9

2)   9 + 2 = 11

3)  11 + 3 = 14

Также, можно поставить знак равенства и сразу начать вычислять выражение в порядке приоритета действий. Например, решение для выражения 10 − 1 + 2 + 3 можно записать следующим образом:

Но если человек не научился быстро считать в уме, то не рекомендуется использовать такой способ.

---

Пример 2. Найти значение выражения (3 + 5) + 2 × 3

Применим правила порядка действий. Прочитаем правила в порядке их приоритета.

Сначала вычислить то, что находится в скобках!

Посмотрим на выражение (3 + 5) + 2 × 3. Видим, что в нём есть выражение в скобках (3 + 5). Вычислим то, что в этих скобках: 3 + 5 = 8. Запишем полученную восьмёрку в главном выражении вместо выражения в скобках:

8 + 2 × 3

Снова читаем первое правило:

Сначала вычислить то, что находится в скобках!

Видим, что в выражении 8 + 2 × 3 нет никаких скобок. Тогда читаем следующее правило:

Читаем выражение слева направо. Если встретится умножение или деление, то сразу же выполняем эту операцию!

Посмотрим на наше выражение 8 + 2 × 3. Видим, что в нём есть умножение 2 × 3. Выполним эту операцию: 2 × 3 = 6. Запишем полученную шестёрку в главном выражении вместо 2 × 3

8 + 6

Осталось простейшее выражение 8 + 6, которое вычисляется легко:

8 + 6 = 14

Таким образом, значение выражения (3 + 5) + 2 × 3 равно 14

(3 + 5) + 2 × 3 = 14

Также, этот пример можно решить, расставив порядок действий над самим выражением. Действие в скобках будет первым действием, умножение — вторым действием, а сумма — третьим:

И далее можно выполнить действия по отдельности, что очень удобно:

1)  3 + 5 = 8

2)   2 × 3 = 6

3)  8 + 6 = 14

Также, можно поставить знак равенства и сразу начать вычислять выражение в порядке приоритета действий:

Но опять же, используя такой способ, нужно быть очень внимательным.

---

Пример 3. Найти значение выражения 5 × 2 + (5 − 3) : 2 + 1

Расставим порядок действий над выражением. Действие в скобках будет первым действием, умножение — вторым действием, деление — третьим действием,  четвёртое и пятое действие являются суммами и они будут выполнены в порядке их следования:

1)  5 − 3 = 2

2)  5 × 2 = 10

3)  2 : 2 = 1

4)  10 + 1 = 11

5)  11 + 1 = 12

Также, можно поставить знак равенства и сразу начать вычислять выражение в порядке приоритета действий:

Четвёртое и пятое действие заключалось в том, чтобы вычислить оставшееся простейшее выражение 10 + 1 + 1. Мы не стали тратить время на выполнение каждого из этих действий, а поставили знак равенства и записали ответ 12.

---

Пример 4. Найти значение выражения (3250 − 2905) : 5

Расставим порядок действий над выражением. Действие в скобках будет первым действием, а деление — вторым

1)  3250 − 2905 = 345

2)  345 : 5 = 69

В скобках могут выполняться два и более действия. Бывает даже так, что в скобках встречаются другие скобки. В таких случаях нужно применять те же правила, которые мы изучили ранее.

Пример 5. Найти значение выражения (6 411 × 8 − 40799) × 6

Расставим порядок действий над выражением. Действие в скобках будет первым действием. При этом в скобках выполняется умножение и вычитание. Согласно порядку действий, умножение выполняется раньше вычитания.

В данном случае сначала нужно 6 411 умножить на 8, и из полученного результата вычесть 40 799. Полученный результат будет значением выражения, содержащегося в скобках. Этот результат будет умножен на 6.

В результате будем иметь следующий порядок:

1)  6 411 × 8 = 51 288

2)  51 288 − 40 799 = 10 489

3)  10 489 × 6 = 62 934

---

Пример 6. Найти значение выражения: 1 657 974 : 822 × 106 − (50 377 + 20 338)

Расставим порядок действий над выражением. Действие в скобках будет первым действием, деление будет вторым действием, умножение — третьим, вычитание — четвёртым.

1) 50 377 + 20 338 = 70 715

2) 1 657 974 : 822 = 2 017

3) 2 017 × 106 = 213 802

4) 213 802−70 715 = 143 087

---

Пример 7. Найти значение выражения: 14 026 − (96 : 4 + 3680)

Расставим порядок действий над выражением. Действие в скобках будет первым действием. При этом в скобках выполняется деление и сложение. Согласно порядку действий деление выполняется раньше сложения.

В данном случае сначала нужно 96 разделить на 4, и полученный результат сложить с 3 680. Полученный результат будет значением выражения, содержащегося в скобках. Этот результат нужно вычесть из 14 026. В результате будем иметь следующий порядок:

1) 96 : 4 = 24

2) 24 + 3 680 = 3 704

3) 14026 − 3 704 = 10 322

---

Задания для самостоятельного решения

Задание 1. Найдите значение выражения:

5 + 2 − 2 − 1

Решение

Задание 2. Найдите значение выражения:

14 + (6 + 2 × 3) − 6

Решение

Задание 3. Найдите значение выражения:

486 : 9 − 288 : 9

Решение

Задание 4. Найдите значение выражения:

756 : 3 : 4 × 28

Решение

Задание 5. Найдите значение выражения:

807 : 3 − (500 − 58 × 4)

Решение

---

Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках

Возникло желание поддержать проект?
Используй кнопку ниже

Навигация по записям

Как решить проблему установки пакета обновления 1 для Windows 7

Это — статья с пошаговым руководством.

Аннотация

Иногда при установке Windows 7 могут возникнуть ошибки, прерывающие установку. В этой статье объясняются возможные решения этих ошибок и осуществление правильной установки системы.

Решение

Решение 1. Исправить Центр обновления Windows
Решение 2. Удалить языки
Решение 3. Восстановить систему
Решение 4. Ошибка 0x80073701
Решение 5. Ошибка 0x800F0A12
Решение 6. Ошибка C0000034
solución 7: Error C0000034
Решение 7. Ошибка 0x800f0a136 или ошибка 0x800f0826

Решение 1. Исправить Центр обновления Windows

Возможно, проблема прямо не относится к установщику пакета обновления 1, и ошибка случается из-за того, что Центр обновления Windows работает неправильно. Для его исправления выполните следующие действия.

1. Нажмите кнопку Пуск и выберите Панель управления

   
   

2. В верхней правой части окна в окне поиска введите устранение неполадок.

   
   

3. Щелкните Устранение неполадок.

   
   

4. Щелкните Устранение неполадок с помощью Центра обновления Windows.

   
   

5. В окне Центр обновления Windows нажмите Далее.

   
   

6. Подождите, пока Windows определит и решит проблемы.

   
   

7. Щелкните Устранение неполадок.

   В начало

Решение 2.

Удалить языки

1. Нажмите кнопку Пуск и выберите Панель управления.

   
   

2. Выберите пункт Часы, язык и регион в Панели управления.

   
   

3. В разделе Язык и региональные стандарты выберите Установка или удаление языков отображения.

   
   

4. В окне Установка или удаление языков интерфейса выберите Удалить языки интерфейса.

   
   

5. Выберите установленные языки, которые не соответствуют языку, используемому на вашем ПК, и нажмите Далее.

   Теперь SP1 установится правильно

   Примечание. Если появится запрос на ввод пароля администратора или подтверждение, введите пароль или подтвердите его при необходимости.

   В начало

Решение 3. Восстановление системы

Восстановление системы может помочь определить проблему, поскольку оно создает точки восстановления операционной системы на момент, когда проблемы не существовало, но имейте в виду, что при этом установленные программы и обновления будут удалены.

Чтобы восстановить предыдущее состояние системы, выполните следующие действия:

1. Нажмите кнопку Пуск, введите Восстановление системы и выберите Восстановление системы в списке программ.

   
   

2. В окне Восстановление системы нажмите Далее.

   
   

3. В окне Восстановление системы включите параметр Показать другие точки восстановления, выберите точку, созданную до возникновения проблемы, и нажмите Далее.

   
   

4. Нажмите Готово.

   Теперь компьютер перезагрузится, после чего файлы и параметры системы вернутся к тому состоянию, которое имело место на момент создания точки восстановления.

   Примечание. Если запрашивается пароль администратора или подтверждение, введите пароль или подтвердите его и нажмите Продолжить.

   В начало

Решение 4. Ошибка 0x80073701

Ресурсы операционной системы, такие как файлы данных, данные регистрации и другие данные, во время срока службы операционной системы могут создавать несоответствия даже в памяти. Эти несоответствия могут быть причиной различных ошибок оборудования или проблем, связанных с программным обеспечением. Иногда эти несоответствия могут влиять на работу Windows и отключать обновления программного обеспечения. Средство проверки готовности системы к обновлению служит для разрешения этих несоответствий.

1. Загрузите с сайта Майкрософт средство проверки готовности системы к обновлению (Microsoft):
   http://www.microsoft.com/downloads/KB947821/details.aspx?FamilyID=44e15787-66b0-4e9c-9c3b-1fc9ea40f69f. Для этого нажмите кнопку Скачать.

   
   

2. В панели загрузки нажмите Открыть.

   
   

3. Откроется панель установки, нажмите Да.

   
   

4. Подождите, пока обновления установятся надлежащим образом.

   
   

5. Как только установка завершится, нажмите Закрыть.

   
   

6. Нажмите кнопку Пуск, введите cmd и нажмите ВВОД, чтобы открыть окно командной строки..

   
   

7. В командной строке введите sfc/scannow, нажмите ВВОД и дождитесь завершения процесса.

   
   

8. Запустите средство проверки готовности системы к обновлению и убедитесь, что ошибок больше не возникают.

   Теперь SP1 установится правильно.

   В начало

Решение 5. Ошибка 0x800F0A12

Ошибка 0×800f0a12 возникает, если программа установки SP1 проводит постоянную проверку для подтверждения того, что Windows 7 может запуститься самостоятельно с активного раздела:

1. Нажмите кнопку Пуск и выберите Панель управления.

   
   

2. В Панели управления выберите пункт Система и безопасность.

   
   

3. Далее выберите Администрирование.

   
   

4. Выберите Управление компьютером.

   
   

5. В разделе области навигации Запоминающие устройства выберите Управление дисками.

   
   

6. Наконец, правой кнопкой мыши щелкните тот раздел диска, где установлена Windows 7, и выберите пункт Сделать раздел активным.

   Теперь SP1 установится правильно.

   Volver al Inicio

Если системный раздел не устанавливается при запуске, можно для автоматического подключения всех томов использовать команду mountvol в окне командной строки.

Примечание. Перед тем как продолжить, свяжитесь с администратором, чтобы узнать, почему не был предоставлен доступ к системному разделу.

1. Нажмите кнопку Пуск и введите cmd в окне поиска. Далее щелкните правой кнопкой мыши  значок командной строки и выберите Запуск от имени администратора.

   Примечание. Если вас попросят ввести пароль администратора или подтверждение, введите пароль или подтвердите его.

2. Введите mountvol/E и нажмите ВВОД.

   
   

3. Перезагрузите компьютер.

   Теперь SP1 установится правильно.

   В начало

Решение 7. Ошибка C0000034

Восстановление системы может помочь определить проблему, поскольку оно создает точки восстановления операционной системы на момент, когда проблемы не существовало, но имейте в виду, что при этом установленные программы и обновления будут удалены. Дополнительные сведения об использовании средства восстановления системы см. в разделе «Ошибка C000009A: Решение 2. Восстановление системы.

Volver al Inicio

Решение 8. Ошибка 0x800f0a136 или ошибка 0x800f0826

Ресурсы операционной системы, такие как файлы данных, данные регистрации и другие данные, во время срока службы операционной системы могут создавать несоответствия даже в памяти. Эти несоответствия могут быть причиной различных ошибок оборудования или проблем, связанных с программным обеспечением. Иногда эти несоответствия могут влиять на работу Windows и отключать обновления программного обеспечения. Средство проверки готовности системы к обновлению служит для разрешения этих несоответствий.

Дополнительные сведения см. в разделе Ошибка 0x80073701.

В начало

Нас интересует ваше мнение! Мы ждем ваших отзывов по данным статьям; их можно ввести в поле для комментариев в нижней части страницы. Ваши отзывы помогают нам повышать качество контента. Заранее спасибо!

Вся часть 1 за 45 минут!

Интенсив состоится с 18 по 22 февраля, ждем вас в нашем уютном офисе.

Что будет на интенсиве?

— Мы научим вас решать 12 заданий ЕГЭ-2018 за 45 минут. Быстро, легко и правильно.

— Напомним, как записывать ответы. Научим быстро считать без калькулятора и без ошибок.

— Дадим ТЕХНОЛОГИИ решения необычных задач первой части.

— Поработаем с вами индивидуально. Покажем, что необходимо исправить и улучшить.

— Мы расскажем вам секреты, о которых знает не каждый репетитор.

Зачем?

— Получить 65 баллов;

— Потратить на это 45 минут;

— Сделать это легко, не тратить лишние силы и нервы;

— Уделить сложным задачам оставшиеся 3 часа;

— Получить нужные для выбранного вуза баллы.

Эти навыки вы получите на интенсиве «ЕГЭ по математике. Вся часть 1 за 45 минут».

Звоните сейчас: 8 (495) 984-09-27

ЕГЭ по математике в 2018 году состоит из двух частей.

Первая часть — 12 заданий по всем темам школьного курса математики. В них проверяется только ответ. Если вы получили в такой задаче правильный ответ, но не записали его в бланк или записали не так, как надо, задача, увы, не засчитывается. Правильное решение с арифметической ошибкой тоже не засчитывается.

Вот и выходит, что даже школьные отличники редко решают первую часть ЕГЭ (12 задач) без ошибок.

И это не всё. Чтобы решить эти 12 задач, нужно время! Необходимо отлично подготовиться, чтобы решить их быстро и правильно. Потому что впереди — вторая часть ЕГЭ, 7 сложных задач, где надо думать, доказывать, математически грамотно записывать каждый шаг решения.

Как часто бывает, что выпускник тратит 2 часа на решение задач части 1, и на сложные задачи у него уже не остается ни сил, ни времени!

Мы проводим такие интенсивы с 2008 года. Те, кто с трудом решали 3 задачи (которых не хватает даже для получения аттестата), в результате выходят на уровень 65-70 баллов ЕГЭ. Отличники оттачивают свои навыки решения задач на скорость, тренировки внимания, приемов быстрого счета.

А секреты, большие и маленькие, которые являются ключами к задачам первой части, интересны всем ученикам.

И это не всё!

На нашем интенсиве:

— Веселая, легкая и доброжелательная атмосфера, в которой знания воспринимаются эффективно и приятно.

— Домашние пироги, пицца и другие вкусности.

Ведущая курса — Анна Георгиевна Малкова.

• Автор и ведущая Курса подготовки к ЕГЭ по математике.
• Автор видеокурса по математике.
• Продюсер образовательных программ. Автор сайта, на котором вы находитесь.
• Образование: Московский физико-технический институт.
• Репетиторский стаж — с 1990 года.
• Автор книг «Моя профессия — репетитор», «Математика. Авторский курс подготовки к ЕГЭ» и других.

 
С нами вы получите подготовку на самом высоком уровне!

Звоните и записывайтесь в группу интенсивной подготовки по математике!

Мест мало. Спешите.

Урок 50. решение задач в 2 действия — Математика — 1 класс

Математика

1 класс

Урок №50

Решение задач в 2 действия

Перечень вопросов, рассматриваемых в теме:

Глоссарий по теме:

Задача – это математический рассказ, в котором есть условие и вопрос. Чтобы ответить на вопрос задачи, ее нужно решить.

Части задачи – условие, вопрос, решение, ответ.

Список литературы:

1. Моро М. И., Бантова М. А., Бельтюкова Г. В. и др.Математика. 1 класс. Учебник для общеобразовательных организаций. В 2 ч. Ч.1/ –6-е изд. – М.: Просвещение, 2015. – с.62, 63

2. Волкова С. И. Математика. Проверочные работы. 1 кл: учебное пособие для общеобразовательных организаций. М.: Просвещение, 2014.- с.50, №2, с.51, №2

3. Волкова С. И. Математика. Рабочая тетрадь. 1 кл. 2 часть: учебное пособие для общеобразовательных организаций. М.: Просвещение, 2016.-с.33

Теоретический материал для самостоятельного изучения

Решим задачу.

В одной коробке 6 карандашей, во второй на 2 карандаша меньше. Сколько карандашей в двух коробках?

О чём говорится в задаче? Правильно, о коробках и карандашах.

Что нам известно в задаче? Что в одной коробке было 6 карандашей.

Что сказано о количестве карандашей во второй коробке? Их на 2 меньше, чем в первой коробке.

Что нужно узнать в задаче? Сколько карандашей в двух коробках? Сразу можно ответить на вопрос задачи? Сразу ответить на вопрос задачи нельзя, потому что не сказано, сколько карандашей во второй коробке. Как это можно узнать? От шести отнять два. Теперь можно узнать, сколько всего карандашей в двух коробках? Да.

Составим план решения задачи:

1) Сначала надо узнать, сколько карандашей во второй коробке.

2) Потом можно узнать, сколько всего карандашей в двух коробках.

Решение:

1) 6 – 2 = 4 (к.)

2) 6 + 4 = 10 (к.)

Ответ: всего 10 карандашей.

Рассуждая так же, решим следующую задачу.

На верхней полке 6 книг, а на нижней – на 4 книги больше. Сколько книг на двух полках?

О чём говорится в задаче? О полках и книгах.

Сколько книг на верхней полке? Шесть.

Сколько книг на второй полке? Неизвестно, но сказано, что на 4 книги больше. Т.е. их столько же, сколько на верхней полке, и ещё четыре.

Что нужно узнать в задаче? Сколько книг на двух полках.

Можно ли сразу узнать, сколько книг на двух полках? Нет.

Почему? Мы не знаем, сколько книг на второй полке.

Как найти, сколько книг на второй полке?

Нужно к шести прибавить четыре,получится десять книг.

Теперь можем узнать, сколько книг на двух полках? Да.

Составим план решения задачи:

1) Сначала надо узнать, сколько книг на нижней полке.

2) Потом можно узнать, сколько книг на двух полках.

Решение:

1) 6 + 4 = 10 (кн.)

2) 6 + 10 = 16 (кн.)

Ответ: 16 книг на двух полках.

Тренировочные задания.

1. Выберите задачу, которая решается два действия

Варианты ответов:

1. На одной полке стоят 4 книги, на другой — на 3 книги больше. Сколько книг на второй полке?

2. На одной клумбе распустилось 6 тюльпанов, а на другой — на 3 тюльпана меньше. Сколько тюльпанов распустилось на двух клумбах?

3. На первой проволоке 5 шариков, на второй — на 4 шарика больше. Сколько шариков на второй проволоке?

Правильный ответ:

2. На одной клумбе распустилось 6 тюльпанов, а на другой — на 3 тюльпана меньше. Сколько тюльпанов распустилось на двух клумбах?

2. Решите задачу и выделите цветом правильное решение.

В одной вазе лежало 6 яблок, в другой на 3 яблока меньше. Сколько яблок в двух вазах?

Варианты ответов:

Первый вариант: 6 – 3 = 3 (яб.)

Второй вариант: 6 + 3 = 9 (яб.)

Третий вариант:

1) 6-3=3 (яб.)

2) 6+3=9 (яб.)

Вспомним, что эта задача решается в 2 действия, следовательно, верным будет третий вариант.

Правильный ответ:

1) 6-3=3 (яб.)

2) 6+3=9 (яб.)

ЕГЭ по математике, подготовка к ЕГЭ по математике 2021 в Москве, шкала перевода баллов — Учёба.ру

Что требуется

Решить планиметрическую задачу.

Особенности

Под этим номером может быть два варианта задания. Первый вариант: в задаче два пункта — а и b. В пункте a требуется что-то доказать, в пункте b — что-то найти. Могу сказать, что чаще всего надо начинать решать эту задачу именно с пункта b, а уже решение этого пункта поможет доказать пункт а. Как правило, абитуриентам проще что-то найти, чем доказать.

Второй вариант: задача без подпунктов. Здесь чаще всего скрыт подводный камень: задача требует рассмотрения двух случаев и приводит к двум разным ответам. Например, в условии задачи сказано, что окружности касаются в точке A, но не сказано каким образом, внешним или внутренним. Часто бывает так, что выпускник рисует один рисунок и возможно даже находит правильный ответ. А второй случай он не рассматривает, в результате чего получает ровно половину баллов за это задание.

Советы

Необходимое условие для решения этой задачи — хорошее владение теоретическим материалом, например, из классического учебника по геометрии для 7-9 классов (Л.С. Атанасян). Необходимо знать формулировки аксиом и определений, уметь формулировать и доказывать теоремы, признаки, свойства и формулы. Изучите дополнительные методы: метод дополнительного построения, метод подобия, метод замены, метод введения вспомогательного неизвестного, метод удвоения медианы, метод вспомогательной окружности, метод площадей.

Также здесь важен рисунок. 80% успеха геометрической задачи — это правильно нарисованный рисунок. Сделайте большой, хороший, наглядный рисунок, не экономьте на нем место.

И последнее, лайфхак для абитуриента — для решения задач по планиметрии выучите пять формул площади треугольника: через высоту и основание, через две стороны и угол между ними, через радиус вписанной окружности, через радиус описанной окружности и формулу Герона.

Решайте неравенства с помощью программы «Пошаговое решение математических задач»

В этой главе мы разработаем определенные методы, которые помогут решить проблемы, сформулированные на словах. Эти методы включают переписывание задач в виде символов. Например, заявленная проблема

«Найдите число, которое при добавлении к 3 дает 7»

можно записать как:

3+? = 7, 3 + n = 7, 3 + x = 1

и так далее, где символы?, N и x представляют число, которое мы хотим найти.Мы называем такие сокращенные версии поставленных задач уравнениями или символическими предложениями. Такие уравнения, как x + 3 = 7, являются уравнениями первой степени, поскольку переменная имеет показатель степени 1. Члены слева от знака равенства составляют левую часть уравнения; те, что справа, составляют правую часть. Таким образом, в уравнении x + 3 = 7 левый член равен x + 3, а правый член равен 7.

РЕШЕНИЕ УРАВНЕНИЙ

Уравнения могут быть истинными или ложными, так же как словесные предложения могут быть истинными или ложными.Уравнение:

3 + х = 7

будет ложным, если вместо переменной подставлено любое число, кроме 4. Значение переменной, для которой верно уравнение (4 в этом примере), называется решением уравнения. Мы можем определить, является ли данное число решением данного уравнения, подставив число вместо переменной и определив истинность или ложность результата.

Пример 1 Определите, является ли значение 3 решением уравнения

4x — 2 = 3x + 1

Решение Мы подставляем значение 3 вместо x в уравнение и смотрим, равен ли левый член правому.

4 (3) — 2 = 3 (3) + 1

12 — 2 = 9 + 1

10 = 10

Отв. 3 — это решение.

Уравнения первой степени, которые мы рассматриваем в этой главе, имеют не более одного решения. Решения многих таких уравнений можно определить путем осмотра.

Пример 2 Найдите решение каждого уравнения путем осмотра.

а. х + 5 = 12
б. 4 · х = -20

Решения а. 7 — решение, так как 7 + 5 = 12.
b. -5 — это решение, поскольку 4 (-5) = -20.

РЕШЕНИЕ УРАВНЕНИЙ С ИСПОЛЬЗОВАНИЕМ СВОЙСТВ СЛОЖЕНИЯ И ВЫЧИТАНИЯ

В разделе 3.1 мы решили несколько простых уравнений первой степени путем проверки. Однако решения большинства уравнений не сразу видны при осмотре. Следовательно, нам нужны некоторые математические «инструменты» для решения уравнений.

ЭКВИВАЛЕНТНЫЕ УРАВНЕНИЯ

Эквивалентные уравнения — это уравнения, которые имеют идентичные решения. Таким образом,

3x + 3 = x + 13, 3x = x + 10, 2x = 10 и x = 5

— эквивалентные уравнения, потому что 5 — единственное решение каждого из них. Обратите внимание, что в уравнении 3x + 3 = x + 13 решение 5 не очевидно при осмотре, но в уравнении x = 5 решение 5 очевидно при осмотре. Решая любое уравнение, мы преобразуем данное уравнение, решение которого может быть неочевидным, в эквивалентное уравнение, решение которого легко заметить.

Следующее свойство, иногда называемое свойством сложения-вычитания , является одним из способов создания эквивалентных уравнений.

Если одно и то же количество добавляется или вычитается из обоих элементов уравнения, полученное уравнение эквивалентно исходному уравнение.

в символах,

a — b, a + c = b + c и a — c = b — c

— эквивалентные уравнения.

Пример 1 Напишите уравнение, эквивалентное

х + 3 = 7

путем вычитания 3 из каждого члена.

Решение Если вычесть 3 из каждого члена, получится

х + 3 — 3 = 7 — 3

или

х = 4

Обратите внимание, что x + 3 = 7 и x = 4 — эквивалентные уравнения, поскольку решение одинаково для обоих, а именно 4. В следующем примере показано, как мы можем генерировать эквивалентные уравнения, сначала упростив один или оба члена уравнения.

Пример 2 Напишите уравнение, эквивалентное

4x- 2-3x = 4 + 6

, объединив одинаковые термины, а затем добавив по 2 к каждому члену.

Объединение одинаковых терминов дает

х — 2 = 10

Добавление 2 к каждому члену дает

х-2 + 2 = 10 + 2

х = 12

Чтобы решить уравнение, мы используем свойство сложения-вычитания, чтобы преобразовать данное уравнение в эквивалентное уравнение вида x = a, из которого мы можем найти решение путем проверки.

Пример 3 Решить 2x + 1 = x — 2.

Мы хотим получить эквивалентное уравнение, в котором все члены, содержащие x, находятся в одном члене, а все члены, не содержащие x, — в другом. Если мы сначала прибавим -1 к каждому члену (или вычтем 1 из него), мы получим

.

2x + 1-1 = x — 2-1

2x = х — 3

Если мы теперь прибавим -x к каждому члену (или вычтем x из него), мы получим

2х-х = х — 3 — х

х = -3

, где решение -3 очевидно.

Решением исходного уравнения является число -3; однако ответ часто отображается в виде уравнения x = -3.

Поскольку каждое уравнение, полученное в процессе, эквивалентно исходному уравнению, -3 также является решением 2x + 1 = x — 2. В приведенном выше примере мы можем проверить решение, подставив — 3 вместо x в исходном уравнении.

2 (-3) + 1 = (-3) — 2

-5 = -5

Симметричное свойство равенства также помогает при решении уравнений. В этом объекте указано

Если a = b, то b = a

Это позволяет нам менять местами члены уравнения в любое время, не беспокоясь о каких-либо изменениях знака.Таким образом,

Если 4 = x + 2, то x + 2 = 4

Если x + 3 = 2x — 5, то 2x — 5 = x + 3

Если d = rt, то rt = d

Может быть несколько разных способов применить свойство сложения, указанное выше. Иногда один метод лучше другого, а в некоторых случаях также полезно симметричное свойство равенства.

Пример 4 Решите 2x = 3x — 9. (1)

Решение Если мы сначала добавим -3x к каждому члену, мы получим

2x — 3x = 3x — 9 — 3x

-x = -9

, где переменная имеет отрицательный коэффициент.Хотя при осмотре мы можем видеть, что решение равно 9, поскольку — (9) = -9, мы можем избежать отрицательного коэффициента, добавив -2x и +9 к каждому члену уравнения (1). В этом случае получаем

2x-2x + 9 = 3x- 9-2x + 9

9 = х

, из которого решение 9 очевидно. При желании последнее уравнение можно записать как x = 9 по симметричному свойству равенства.

РЕШЕНИЕ УРАВНЕНИЙ С ИСПОЛЬЗОВАНИЕМ СВОЙСТВА DIVISION

Рассмотрим уравнение

3x = 12

Решение этого уравнения — 4.Также обратите внимание, что если мы разделим каждый член уравнения на 3, мы получим уравнения

, решение которого также равно 4. В общем, мы имеем следующее свойство, которое иногда называют свойством деления.

Если оба члена уравнения делятся на одно и то же (ненулевое) количество, полученное уравнение эквивалентно исходному уравнению.

в символах,

— эквивалентные уравнения.

Пример 1 Напишите уравнение, эквивалентное

-4x = 12

, разделив каждый член на -4.

Решение Разделив оба элемента на -4, получим

При решении уравнений мы используем указанное выше свойство для создания эквивалентных уравнений, в которых переменная имеет коэффициент 1.

Пример 2 Решите 3y + 2y = 20.

Сначала мы объединяем одинаковые термины, чтобы получить

5лет = 20

Тогда, разделив каждый член на 5, получим

В следующем примере мы используем свойство сложения-вычитания и свойство деления для решения уравнения.

Пример 3 Решить 4x + 7 = x — 2.

Решение

Сначала мы добавляем -x и -7 к каждому члену, чтобы получить

4x + 7 — x — 7 = x — 2 — x — 1

Далее, объединяя одинаковые термины, получаем

3x = -9

Наконец, мы разделим каждый член на 3, чтобы получить

РЕШЕНИЕ УРАВНЕНИЙ С СВОЙСТВОМ УМНОЖЕНИЯ

Рассмотрим уравнение

Решение этого уравнения — 12. Также обратите внимание, что если мы умножим каждый член уравнения на 4, мы получим уравнения

, решение которого также равно 12.В общем, мы имеем следующее свойство, которое иногда называют свойством умножения.

Если оба члена уравнения умножаются на одну и ту же ненулевую величину, полученное уравнение эквивалентно исходному уравнению.

в символах,

a = b и a · c = b · c (c ≠ 0)

— эквивалентные уравнения.

Пример 1 Напишите уравнение, эквивалентное

путем умножения каждого члена на 6.

Решение Умножение каждого члена на 6 дает

При решении уравнений мы используем указанное выше свойство для создания эквивалентных уравнений, не содержащих дробей.

Пример 2 Решить

Решение Во-первых, умножьте каждый член на 5, чтобы получить

Теперь разделите каждого члена на 3,

Пример 3 Решить.

Решение Во-первых, упростите над дробной чертой, чтобы получить

Затем умножьте каждый член на 3, чтобы получить

Наконец, разделив каждого члена на 5, получим

ДАЛЬНЕЙШИЕ РЕШЕНИЯ УРАВНЕНИЙ

Теперь мы знаем все методы, необходимые для решения большинства уравнений первой степени. Не существует определенного порядка, в котором следует применять свойства. Может оказаться подходящим любой один или несколько из следующих шагов, перечисленных на странице 102.

Шаги по решению уравнений первой степени:

1. Объедините одинаковые члены в каждом члене уравнения.
2. Используя свойство сложения или вычитания, запишите уравнение со всеми членами, содержащими неизвестное в одном члене, и всеми членами, не содержащими неизвестное в другом.
3. Объедините одинаковые термины в каждом элементе.
4. Используйте свойство умножения для удаления дробей.
5. Используйте свойство деления, чтобы получить коэффициент 1 для переменной.

Пример 1 Решите 5x — 7 = 2x — 4x + 14.

Решение Во-первых, мы объединяем одинаковые члены, 2x — 4x, чтобы получить

5x — 7 = -2x + 14

Затем мы добавляем + 2x и +7 к каждому члену и объединяем одинаковые термины, чтобы получить

5x — 7 + 2x + 7 = -2x + 14 + 2x + 1

7x = 21

Наконец, мы разделим каждый член на 7, чтобы получить

В следующем примере мы упрощаем над дробной чертой перед применением свойств, которые мы изучали.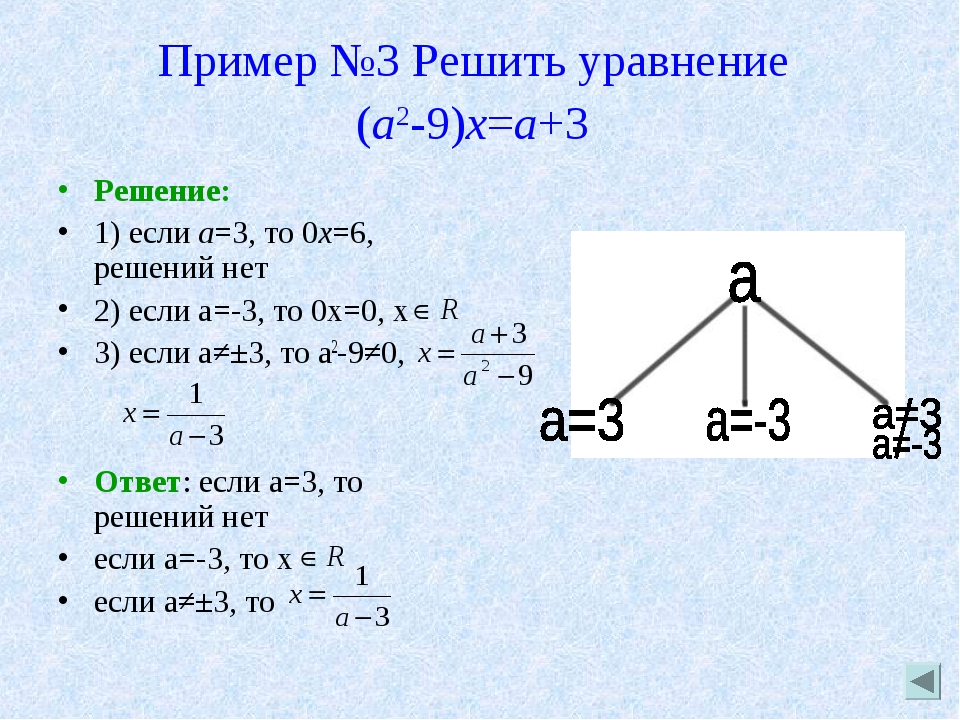

Пример 2 Решить

Решение Сначала мы объединяем одинаковые термины, 4x — 2x, чтобы получить

Затем мы добавляем -3 к каждому члену и упрощаем

Затем мы умножаем каждый член на 3, чтобы получить

Наконец, мы разделим каждый член на 2, чтобы получить

РЕШЕНИЕ ФОРМУЛ

Уравнения, в которых используются переменные для измерения двух или более физических величин, называются формулами. Мы можем найти любую из переменных в формуле, если известны значения других переменных.Мы подставляем известные значения в формулу и решаем неизвестную переменную методами, которые мы использовали в предыдущих разделах.

Пример 1 В формуле d = rt найти t, если d = 24 и r = 3.

Решение Мы можем найти t, заменив 24 на d и 3 на r. То есть

d = rt

(24) = (3) т

8 = т

Часто бывает необходимо решить формулы или уравнения, в которых есть более одной переменной для одной из переменных в терминах других. Мы используем те же методы, что и в предыдущих разделах.

Пример 2 В формуле d = rt найдите t через r и d.

Решение Мы можем решить для t в терминах r и d, разделив оба члена на r, чтобы получить

из которых по закону симметрии

В приведенном выше примере мы решили для t, применив свойство деления для создания эквивалентного уравнения. Иногда необходимо применить более одного такого свойства.

Пример 3 В уравнении ax + b = c найдите x через a, b и c.

Решение Мы можем решить для x, сначала добавив -b к каждому члену, чтобы получить

, затем разделив каждый член на a, мы получим

Основы решения уравнений за один или несколько шагов (Алгебра 1, Как решать линейные уравнения) — Mathplanet

Формулы очень распространены в физике и химии, например, скорость равна расстоянию, разделенному на время.Таким образом, мы используем общие символы для скорости ( v ), расстояния ( d ) и времени (t) и выражаем это так:

$$ v = \ frac {d} {t} $$

Мы можем просто описать формулу как переменную и выражение, разделенные знаком равенства между ними. Другими словами, формула — это то же самое, что и уравнение.

---

Пример

Книжный клуб требует членского взноса в размере 10 долларов в дополнение к 2 долларам, взимаемым за каждую заказанную книгу. Если бы мы перечислили стоимость заказа нескольких книг, это выглядело бы так:

Кол-во книг	Стоимость
1	10 + 2 ∙ 1 = 12
2	10 + 2 ∙ 2 = 14
3	10 + 2 ∙ 3 ​​= 16
4	10 + 2 ∙ 4 = 18
5	10 + 2 ∙ 5 = 20
x	10 + 2x

Если мы обозначим общую стоимость книжного клуба как C, мы можем вывести следующую формулу для выражения:

$$ C = 10 + 2x $$

Если мы затем захотим узнать, сколько книг мы можем получить в книжном клубе за 30 долларов, мы можем продолжить заполнение таблицы выше или использовать свойства уравнений, которые мы рассмотрели в предыдущем разделе.

Мы можем купить 10 книг за 30 долларов.

Когда мы хотим решить уравнение, включающее одну неизвестную переменную, например x в приведенном выше примере, мы всегда стремимся изолировать неизвестную переменную. Можно сказать, что все остальное мы ставим по ту сторону знака равенства. Всегда рекомендуется сначала изолировать термины, включающие переменную, от констант, чтобы начать с них, как мы делали выше, путем вычитания или сложения перед делением или умножением коэффициента перед переменной.Пока вы делаете одно и то же по обе стороны от знака равенства, вы можете делать все, что хотите, и в каком порядке.

Выше мы начали с вычитания константы с обеих сторон. Вместо этого мы могли бы начать с деления на 2. Это выглядело бы как

$$ \ frac {30} {{\ color {blue} 2}} = \ frac {10 + 2x} {{\ color {blue} 2}} $$

$$ \ frac {30} {{\ color {blue} 2}} = \ frac {10} {{\ color {blue} 2}} + \ frac {2x} {{\ color {blue} 2}}

$

$$ 15 = 5 + x $$

$$ 15 \, {\ color {blue} {- \, 5}} = 5 + x \, {\ color {blue} {- \, 5}} $$

$$ 10 = x $$

Опять тот же ответ, просто подтверждающий точку зрения.

Если ваше уравнение содержит одинаковые члены, желательно начать с объединения одинаковых членов, прежде чем продолжить решение уравнения.

---

Пример

$$ 5x + 14 + 2x + 2 = 30 $$

Начните с объединения одинаковых терминов (все термины, включая одну и ту же переменную x и все константы)

$$ \ влево (5x + 2x \ вправо) + \ влево (14 + 2 \ вправо) = 30 $$

$$ 7x + 16 = 30 $$

Теперь пора изолировать переменную от постоянной части. Это делается путем вычитания 16 с обеих сторон

$$ 7x + 16 \, {\ color {green} {- \, 16}} = 30 \, {\ color {green} {- \, 16}} $$

$$ 7x = 14 $$

Разделите обе стороны на 7, чтобы изолировать переменную

$$ \ frac {7x} {{\ color {green} 7}} = \ frac {14} {{\ color {green} 7}} $$

$$ x = 2 $$

Если у вас есть уравнение, в котором у вас есть переменные с обеих сторон, вы делаете в основном то же самое, что и раньше.Собираешь все подобные термины. Раньше вы работали, сначала собирая все постоянные члены с одной стороны и сохраняя переменные члены с другой. То же самое и здесь. Вы собираете все постоянные члены с одной стороны и переменные члены — с другой. Обычно рекомендуется собирать все переменные на той стороне, которая имеет переменную с наивысшим коэффициентом, т.е. в приведенном ниже примере больше x: es на левой стороне (4x) по сравнению с правой стороной (2x), и, следовательно, мы собираем все x: es слева.

---

Пример

$$ 4x + 3 = 2x + 11 $$

вычесть 2x с обеих сторон

$$ 4x + 3 \, {\ color {blue} {- \, 2x}} = 2x + 11 \, {\ color {blue} {- \, 2x}} $$

Теперь оно похоже на любое другое уравнение

$$ 2x + 3 = 11 $$

вычесть 3 с обеих сторон

$$ 2x + 3 \, {\ color {blue} {- \, 3}} = 11 \, {\ color {blue} {- \, 3}} $$

$$ 2x = 8 $$

Разделить на 2 с обеих сторон

$$ \ frac {2x} {{\ color {blue} 2}} = \ frac {8} {{\ color {blue} 2}} $$

$$ x = 4 $$

В начале этого раздела мы показали формулу для расчета скорости, где скорость (v) равна расстоянию (d), деленному на время (t), или

$$ v = \ frac {d} {t} $$

Если мы случайно захотим узнать, сколько грузовик проезжает за 3 часа со скоростью 60 миль в час, мы можем использовать приведенную выше формулу и переписать ее, чтобы вычислить расстояние, d.

$$ \ frac {d} {t} \, {\ color {green} {\ cdot \, t}} = v \, {\ color {green} {\ cdot \, t}} $$

$$ d = v \ cdot t $$

Когда это будет сделано, мы можем просто подставить наши числа в формулу и вычислить ответ

$$ d = 60 \ cdot 3 = 180 $$

Грузовик преодолевает 180 миль за 3 часа.

Это верно для всех формул и уравнений.

---

Видеоурок

Решите уравнение

$$ 3 \ влево (x + 2 \ вправо) — 3 + x + 17 = 40 $$

Решение одношаговых уравнений — ChiliMath

Решение одношаговых уравнений — действительно ваш «первый шаг» в мире решения линейных уравнений.Если вы можете решать одношаговые уравнения, вы готовы справиться с проблемой более сложных уравнений, таких как двухшаговые и многоступенчатые уравнения. Поверьте, это не сложно. Овладев этим конкретным навыком, вы откроете для себя множество возможностей.

В этом уроке мы рассмотрим пять (5) типов или случаев одношаговых уравнений в зависимости от того, как они решаются. Однако пятый тип на самом деле представляет собой смесь или комбинацию умножения и деления, выполняемую как одну операцию.Это действительно важный случай, потому что другие могут рассматривать его как двухэтапную задачу уравнения, хотя на самом деле ее можно решить за один шаг.

---

Пять (5) случаев решения одношаговых уравнений

• Случай 1 : Уравнения, которые можно решить, добавив одно и то же число к обеим сторонам уравнения.

• Случай 2 : Уравнения, которые можно решить, вычитая одно и то же число из обеих частей уравнения.

• Случай 3 : Уравнения, которые можно решить, умножив одно и то же число на обе части уравнения.

• Случай 4 : Уравнения, которые можно решить, разделив одно и то же число на обе части уравнения.

• Случай 5 : Уравнения, которые решаются путем умножения обратной величины коэффициента члена на переменную для обеих сторон уравнения.

---

Что значит решить уравнение?

Вот простой ответ. Если вы можете изолировать или сохранить переменную отдельно на одной стороне уравнения (левая или правая сторона), так что переменная или буква имеет коэффициент +1, а константа или число находятся на противоположной стороне, тогда у вас есть просто решил рассматриваемое уравнение.

---

Примеры решения одношаговых уравнений

Пример 1: Решите одношаговое уравнение.

Обратите внимание, что левая часть уравнения содержит переменную x, которая вычитается на 3, а правая часть содержит положительное число девять, +9. Поскольку переменная уже находится слева, оставим ее там.

Однако, чтобы изолировать переменную x, мы должны избавиться от -3. Мы можем исключить -3, добавив его противоположность — +3.Чтобы уравнение оставалось сбалансированным, мы также должны добавить +3 в правую часть уравнения.

Повторюсь, это Случай 1 решения одношаговых уравнений, потому что мы, , добавили одно и то же число к обеим сторонам уравнения.

---

Пример 2: Решите одношаговое уравнение.

Это одношаговое линейное уравнение немного отличается от первого примера. Обратите внимание, что переменная расположена в правой части уравнения. Не беспокойтесь об этом, потому что это не имеет большого значения.🙂

Помните, что при решении уравнения вы можете оставить переменную по обе стороны от уравнения. Пока в конечном итоге решаемая вами переменная изолирована с одной стороны с коэффициентом +1. Поэтому для этого уравнения удобно оставить переменную в правой части.

Легко видеть, что вычитание обеих частей уравнения на 7 даст «трюк», потому что это избавит от +7, тем самым изолировав переменную y в правой части.

Это Случай 2 , поскольку мы, , вычли из уравнения с обеих сторон на то же самое число , чтобы решить его.

---

Пример 3: Решите одношаговое уравнение.

В этой задаче наша переменная «k» делится на 4. Помните, что наша цель — всегда изолировать переменную на одной стороне уравнения. Следовательно, мы должны найти операцию, которая может отменить деление.

Операция, отменяющая деление, — это умножение. Это означает, что мы умножим обе части уравнения на 4.

---

Пример 4: Решите одношаговое уравнение.

В примере № 3 переменная делится на число.На этот раз у нас есть переменная, умноженная на число. Чтобы избавиться от числа 6, которое умножает переменную m, мы собираемся разделить обе части на 6. Мы используем деление, чтобы отменить или отменить эффект умножения.

---

Пример 5: Решите одношаговое уравнение.

Многие студенты не согласны с этим типом одношагового уравнения из-за наличия дроби в качестве коэффициента. То есть в данном случае \ Large {5 \ over 7}.

Так как же нам исключить дробь \ Large {5 \ over 7}? Когда мы говорим, что хотим исключить дробь, это не значит, что мы должны сделать ее нулевой.Вместо этого мы хотим преобразовать его в \ large \ color {red} 1.

Единственный способ сделать это — умножить дробь на обратную.

Следовательно, чтобы решить это уравнение, мы умножим обе части на \ Large {7 \ over 5}, который является обратной величиной коэффициента.

---

Практика с рабочими листами

Решение одностадийных линейных уравнений: сложение и вычитание

Purplemath

«Линейные» уравнения — это уравнения с простой старой переменной, такой как « x », а не с чем-то более сложным, например, x ² или ^x / _y , или квадратными корнями, или другими более сложные выражения.Линейные уравнения — это самые простые уравнения, с которыми вам придется иметь дело.

Вы, наверное, уже решили линейные уравнения; ты просто не знал этого. Еще в ранние годы, когда вы учились сложению, ваш учитель, вероятно, дал вам рабочие листы для выполнения, в которых были упражнения, подобные следующим:

Заполните поле: & квадрат; + 3 = 5

Заполните поле: & квадрат; + 3 = 5

Как только вы достаточно хорошо усвоили факты сложения, вы знали, что вам нужно поставить цифру «2» внутри квадрата.

MathHelp.com

Решение уравнений работает примерно так же, но теперь мы должны выяснить, что входит в x , а не то, что входит в коробку.Однако, поскольку сейчас мы старше, чем когда заполняли поля, уравнения также могут быть намного сложнее, и поэтому методы, которые мы будем использовать для решения уравнений, будут немного более продвинутыми.

В общем, чтобы решить уравнение для данной переменной, нам нужно «отменить» все, что было сделано с переменной. Мы делаем это для того, чтобы получить переменную сама по себе; технически мы «изолируем» переменную. Это приводит к тому, что уравнение изменяется так, чтобы сказать: «(переменная) равно (некоторому числу)», где (некоторое число) — это ответ, который они ищут.Например:

Переменная — это буква x . Чтобы решить это уравнение, мне нужно получить x отдельно; то есть мне нужно получить x с одной стороны от знака «равно» и какое-то число с другой стороны.

Поскольку я хочу только x с одной стороны, это означает, что мне не нравится «плюс шесть», который в настоящее время находится на той же стороне, что и x . Поскольку 6 — это , добавленное к x , мне нужно вычесть из этого 6, чтобы избавиться от него.То есть мне нужно будет вычесть 6 из x , чтобы «отменить» их добавление к нему 6.

Это вызывает наиболее важное соображение с уравнениями:

Неважно, с каким уравнением мы имеем дело — линейным или каким-либо другим — что бы мы ни делали с одной стороной уравнения, мы должны сделать то же самое, что и , с другой стороной уравнения. В этом отношении уравнения похожи на малышей:

Мы должны быть полностью, полностью справедливыми по отношению к обеим сторонам, иначе последует несчастье!

Что бы вы ни делали с уравнением, проделайте ТОЧНО ТАК ЖЕ с ОБЕИМИ сторонами этого уравнения!

Вероятно, лучший способ отследить это вычитание 6 с обеих сторон — это отформатировать свою работу следующим образом:

Изображение выше анимировано на «живой» странице.

Здесь вы видите, что я вычел 6 с обеих сторон, нарисовал горизонтальную полосу «равно» под всем уравнением, а затем сложил. В левой части (LHS) уравнения это дает мне:

x плюс ничего равно x , а 6 минус 6 равно нулю

В правой части (RHS) уравнения у меня:

Решение — последнее направление моей работы; а именно:

---

Та же процедура «отмены» работает для уравнений, в которых переменная была объединена в пару с вычитанием.

Переменная находится в левой части (LHS) уравнения в паре с оператором «вычесть три». Поскольку я хочу получить x отдельно, мне не нравится «3», которое в настоящее время вычитается из него. Противоположность вычитанию — это сложение, поэтому я отменю «вычитание 3», добавив 3 к обеим частям уравнения, а затем добавлю вниз, чтобы упростить, чтобы получить свой ответ:

Тогда мой ответ:

---

Вас могут попросить «проверить свои решения», по крайней мере, на ранних этапах обучения решению уравнений.Чтобы выполнить эту «проверку», вам нужно всего лишь подставить свой ответ в исходное уравнение и убедиться, что вы получили верное утверждение. (В конце концов, это определение решения уравнения; а именно, решение — это любое значение или набор значений [для более сложных уравнений, позже], что делает исходное уравнение истинным.)

Итак, чтобы проверить мое решение вышеприведенного уравнения, вы должны подставить «–2» вместо x в левую часть (LHS) исходного уравнения и проверить, что это упрощает, чтобы получить исходное значение. для правой части (RHS) уравнения:

Проверок:

LHS: (–2) — 3 = –5

RHS: –5

Поскольку каждая сторона исходного уравнения теперь дает одно и то же значение, это подтверждает, что решение действительно правильное.

---

• Решите 4 =

  x — 3 и проверьте свое решение.

На этот раз переменная находится в правой части (RHS) уравнения. Это нормально; не имеет значения, где находится переменная, пока я могу изолировать ее (то есть, пока я могу получить ее отдельно от знака «равно»).

В этом уравнении у меня вычитается тройка из переменной.Чтобы отменить вычитание, я добавлю по три с каждой стороны уравнения.

4 = х — 3
+3 + 3
———-
7 = х

(Я мог бы записать правую часть после добавления как « x + 0», но «плюс ноль» обычно игнорируется. Поэтому я перенес только x с правой стороны .)

Теперь, в рамках моей ручной работы, мне нужно показать, что я проверил это решение, вставив его обратно в правую часть исходного уравнения и подтвердив, что в итоге я получил левую часть исходного уравнения; то есть я получаю 4:

«Проверка» — это то, что я сделал выше.Я постарался четко обозначить вещи, чтобы оценщик смог найти мой «чек» (так что я получу полную оценку за упражнение). Мой окончательный ответ:

---

Когда я решил последнее упражнение выше, переменная оказалась справа от знака «равно». Но в своем решении я написал ответ, указав переменную слева от знака «равно». Это довольно стандартно. Когда вы решаете, переменная окажется там, где она окажется.Когда вы записываете решение, переменная идет слева. Почему? Так как.

---

Это уравнение почти решено. Но не совсем так. У меня нет старого доброго x справа; вместо этого у меня — x . Что делать?

Я могу представить — x как 0- x . Итак, что произойдет, если я добавлю x к каждой стороне уравнения?

2 = –x
+ х + х
——-
х + 2 = 0

Хорошо; это помогло.Взяв переменную и «добавив ее на другую сторону», я получил переменную в том формате, который мне нравится. И это также преобразовало исходное уравнение в простое одношаговое уравнение. Я избавлюсь от двойки в левой части, «вычтя ее» в правой части:

х + 2 = 0
-2 = -2
———-
х = -2

Этот ответ имеет смысл.Если отрицательное значение переменной равняется положительным двум, то положительное значение переменной должно равняться отрицательным двум. Итак, мой ответ:

---

Технически последний пример представлял собой двухэтапное уравнение, потому что для его решения требовалось прибавить одно к обеим сторонам уравнения, а затем вычесть другое к обеим сторонам. Важно отметить, что вы можете добавлять и вычитать переменные к другой стороне уравнения, точно так же, как вы можете складывать и вычитать числа с другой стороны.Точно такие же методы работают как с переменными, так и с числами.

---

Вы можете использовать виджет Mathway ниже, чтобы попрактиковаться в решении линейного уравнения путем сложения или вычитания. Попробуйте выполнить указанное упражнение или введите свое собственное. Затем нажмите кнопку, чтобы сравнить свой ответ с ответом Mathway. (Или пропустите виджет и продолжите урок.)

(Нажмите «Нажмите, чтобы просмотреть шаги», чтобы перейти непосредственно на сайт Mathway для платного обновления.)

---

---

URL: https://www.purplemath.com/modules/solvelin.htm

Как решать одношаговые уравнения

Если вы считаете, что контент, доступный через Веб-сайт (как определено в наших Условиях обслуживания), нарушает или другие ваши авторские права, сообщите нам, отправив письменное уведомление («Уведомление о нарушении»), содержащее в информацию, описанную ниже, назначенному ниже агенту.Если репетиторы университета предпримут действия в ответ на ан Уведомление о нарушении, оно предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.

Ваше Уведомление о нарушении прав может быть отправлено стороне, предоставившей доступ к контенту, или третьим лицам, таким как в виде ChillingEffects.org.

Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатам), если вы существенно искажать информацию о том, что продукт или действие нарушает ваши авторские права.Таким образом, если вы не уверены, что контент находится на Веб-сайте или по ссылке с него нарушает ваши авторские права, вам следует сначала обратиться к юристу.

Чтобы отправить уведомление, выполните следующие действия:

Вы должны включить следующее:

Физическая или электронная подпись правообладателя или лица, уполномоченного действовать от их имени; Идентификация авторских прав, которые, как утверждается, были нарушены; Описание характера и точного местонахождения контента, который, по вашему мнению, нарушает ваши авторские права, в \ достаточно подробностей, чтобы позволить репетиторам университетских школ найти и точно идентифицировать этот контент; например нам требуется а ссылка на конкретный вопрос (а не только на название вопроса), который содержит содержание и описание к какой конкретной части вопроса — изображению, ссылке, тексту и т. д. — относится ваша жалоба; Ваше имя, адрес, номер телефона и адрес электронной почты; а также Ваше заявление: (а) вы добросовестно считаете, что использование контента, который, по вашему мнению, нарушает ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство, что вы либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.

Отправьте жалобу нашему уполномоченному агенту по адресу:

Чарльз Кон Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Или заполните форму ниже:

Решение одношаговых неравенств — методы и примеры

Прежде чем мы сможем узнать, как решить одноэтапное неравенство, давайте вспомним несколько основных сведений о неравенствах.

Слово неравенство означает математическое выражение, в котором стороны не равны друг другу. По сути, для представления уравнений неравенства используются пять символов неравенства.

Это:
меньше ( <),
больше (> ),
меньше или равно ( ≤ ),
больше или равно ( ≥ )
и не равно символ ( ≠ ).

Неравенства используются для сравнения чисел и определения диапазона или диапазонов значений, которые удовлетворяют условиям данной переменной.

Как решить пошаговые неравенства?

Решение одношагового неравенства — это простой процесс, как может показаться. Для полного решения уравнений требуется всего один шаг.

Основная цель решения одношагового неравенства — выделить переменную на одной стороне символа неравенства и сделать коэффициент переменной равным единице.

Стратегия выделения переменной предполагает использование противоположной операции s.Например, чтобы переместить число, вычитаемое из другой стороны неравенства, вы должны сложить.

Самый важный шаг , который следует запомнить при решении любых линейных уравнений или уравнений неравенства, чтобы выполнить одну и ту же операцию как с правой, так и с левой частью уравнения.

Другими словами, если вы вычитаете или добавляете с одной стороны неравенства, вы также должны вычесть или сложить с тем же значением с противоположной стороны. Точно так же, если вы умножаете или делите на одной стороне уравнения, вы также должны умножать или делить на то же значение на другой стороне уравнения.

Единственное исключение при делении и умножении на отрицательное число в уравнении неравенства состоит в том, что символ неравенства переворачивается.

Мы можем резюмировать правила решения одношаговых неравенств, как показано ниже:

• Вычитание или сложение одного и того же числа с обеих сторон неравенства приводит к тому, что символ неравенства остается неизменным.
• В результате деления или умножения обеих сторон на положительное число символ неравенства не изменяется.
• Умножение или деление обеих сторон на отрицательное число изменяет неравенство. Это означает, что <меняется на>, и наоборот.

В этой статье мы рассмотрим пять различных случаев решения одношаговых неравенств. Эти случаи одношаговых неравенств основаны на том, как манипулируют уравнениями.

Пять случаев включают:

• Решение одноступенчатых неравенств добавлением
• Решение пошаговых неравенств вычитанием
• Одношаговые неравенства решаются умножением обеих частей уравнения на число.
• Одношаговые неравенства решаются путем деления одного и того же числа на обе части уравнения.
• Одношаговые неравенства решаются путем умножения обратного коэффициента члена на переменную в обеих частях уравнения.

Решение одношаговых неравенств добавлением

Чтобы понять это, выполните действия, описанные в примерах ниже.

Пример 1

Решите одношаговое уравнение x — 4> 10

Решение

Обратите внимание, что в левой части символа неравенства есть переменная x, вычитаемая на 4, а в левой части — положительное число 10.В этом случае мы оставим нашу переменную слева.

Чтобы изолировать переменную x, мы складываем обе части уравнения на 4, что дает;

х — 4 + 4> 10 +4

х> 14

Пример 2

Решить x — 6> 14

Решение

х — 6> 14

Сложите обе части уравнения как 6
x — 6 + 6> 14 + 6
x> 20

Пример 3

Решите неравенство –7 — x <9

Решение

–7 — x <9

Добавьте 7 к обеим частям уравнения.
7 — x + 7 <9 + 7
— x <16 Умножить обе стороны на –1 и поменять знак x> –16

Пример 4

Решить 4> x -3

Решение

В этом примере переменная расположена справа в уравнении. Мы можем изолировать переменную в уравнении независимо от того, где она находится. Поэтому оставим правую часть и для этого прибавим 3 к обеим частям уравнения.

4+ 3> x — 3 + 3

7> x

И готово!

Решение пошаговых неравенств вычитанием

Чтобы понять это, выполните действия, описанные в примерах ниже.

Пример 5

Решить x + 10 <16

Решение

х + 10 <16

Вычтем 7 из обеих частей уравнения.
x + 10-10 <16-10
x <6

Пример 6

Решите неравенство 15> 26 — y

Решение

15> 26 — лет

Вычтем 26 из обеих частей уравнения
15-26> 26-26 -y
-11> -y

Умножьте обе части на –1 и переверните знак

11

Пример 7

Решить x + 6> –3

Решение

Вычтем обе стороны на 6.

x + 6 — 6> –3 — 6

x > — 9

Пример 8

Решите одношаговое уравнение 13

Решение

В этом случае переменная y также находится в правой части уравнения. Это нормально! Мы будем придерживаться левой стороны, вычтя обе части на 8.

13–8

5

Пример 9

Решите относительно t в следующем уравнении:

т + 18 <21

Решение

Чтобы выделить t в левой части уравнения, мы вычтем обе части уравнения на 18.

т + 18-18 <21-18

т <3

Решение одношаговых неравенств путем умножения обеих частей уравнения на число

Чтобы понять это, выполните действия, описанные в примерах ниже.

Пример 10

Решите относительно x в следующем одношаговом уравнении:

х / 4> 8

Решение

Чтобы исключить дробь, умножьте обе части уравнения на знаменатель дроби.

4 (х / 4)> 8 х 4

х> 32

Вот и все!

Пример 11

Решите одношаговое уравнение -x / 5> 9

Решение

В этом неравенстве переменная x делится на 5. Поскольку наша цель — отменить деление переменной, мы умножаем обе части неравенства на

.

5 (-x / 5)> 9 x 5

-x> 45

Теперь умножьте обе стороны на -1 и поменяйте знак местами.

х <- 45

Пример 11

Решить 2> –x

Решение

Вы можете заметить, что это уравнение почти решено. Но не совсем так. Итак, нам нужно убрать отрицательный знак из переменной. Мы можем сделать это, умножив обе части уравнения на -1 и поменяв знак местами.

2 * -1> –x * -1

-2 <х

Решение одношаговых неравенств путем деления одного и того же числа на обе части уравнения

Чтобы понять это, выполните действия, описанные в примерах ниже.

Пример 12

Решить относительно x, 2x — 4 <0

Решение

Складываем 4 с обеих сторон

2x — 4 + 4 <0 + 4

2x <4

Делим каждую сторону на 2, получаем

2x / 2 <4/2

х <4/2

Итак, x <2 - это ответ!

Пример 13

Решите одношаговое уравнение. 5x <100.

Решение

В этом примере переменная x умножается на число.Чтобы отменить умножение, мы разделим обе части уравнения на коэффициент переменной. Деление обычно используется для отмены эффекта умножения.

5x / 5 <100/5

х <20

Пример 14

21 <-3x

Решение

В этом случае переменная находится справа от уравнения, поэтому не беспокойтесь о замене уравнения. Поскольку коэффициент переменной не равен 1, это означает, что нам нужно выполнить противоположную операцию, чтобы удалить 3 из -x.Итак, мы разделим обе части на -3.

21/3 <-3 / 3x

7 <-x Поскольку это неравенство не упрощается, нам нужно удалить отрицательный знак переменной. Поэтому умножаем обе части уравнения на -1 и меняем знак. -7> х

Пример 15

Решить −2x <4

Решение

Чтобы решить это одношаговое уравнение, нам нужно разделить обе части на −2.

Поскольку мы делим обе части уравнения на отрицательное число, мы изменим знак неравенства местами.

х> -2

Пример 16
Решите одношаговое неравенство −2x> −8

Решение

Разделите обе части уравнения на 2.

−2x / 2> −8/2

−x> — 4

Умножьте обе части на -1 и переверните знак неравенства.

х <4

Решение одношагового неравенства путем умножения обратной величины коэффициента переменной на обе части уравнения.

Чтобы понять это, выполните действия, описанные в примерах ниже.

Пример 17

Решите одношаговое уравнение (4x / 11) <4

Решение

Многие люди сбиты с толку, когда им представляются одношаговые неравенства, содержащие дроби.

Итак, как мы решаем такие проблемы?

Мы можем решить одношаговые неравенства с дробями, умножив обе части уравнения на величину, обратную дроби.В этом случае наша обратная величина — 11/4.

(4x / 11) 11/4 <4 * 11/4

х <11

Практические вопросы

Решите следующие одношаговые неравенства для неизвестных.

1. 26 <8 + v
2. −15 + n> −9
3. 14b <−56
4. −6> б / 18
5. −15x <0
6. −17> х — 15
7. -16 + х <-15
8. п — 8> −10
9. м / 4> −13
10. −5 <а / 18

Предыдущий урок | Главная страница | Следующий урок

Как решать одношаговые уравнения с дробями

Шаги для решения

Когда дело доходит до решения одношаговых уравнений, количество шагов, которые мы делаем, — это именно то число, которое следует из названия — один! Одноэтапные уравнения — это уравнения, которые включают сложение, вычитание, умножение или деление обеих сторон уравнения на одно и то же число, переменную или член, чтобы выделить и решить для переменной.

Мы видим, что для решения одношаговых уравнений мы просто складываем, вычитаем, умножаем или делим одно и то же число с обеих сторон, чтобы найти неизвестную переменную. Поэтому, чтобы решить одношаговое уравнение с дробями, нам просто нужно знать, как складывать, вычитать, умножать и делить дроби, поэтому давайте быстро освежим правила этих операций с дробями.

Чтобы сложить или вычесть дроби, мы находим общий знаменатель, складываем или вычитаем числители, а затем упрощаем результат.Мы можем использовать следующее правило для сложения или вычитания дробей.

Удивительно, но умножение и деление дробей проще, чем сложение и вычитание дробей, особенно умножение дробей. Чтобы умножить дроби, мы просто умножаем числители, умножаем знаменатели, а затем упрощаем результат.

Довольно просто, не правда ли? Наконец, чтобы разделить дроби, мы просто превращаем это в задачу умножения, умножая числитель на обратную величину знаменателя, где , обратное дроби, получается заменой числителя и знаменателя.