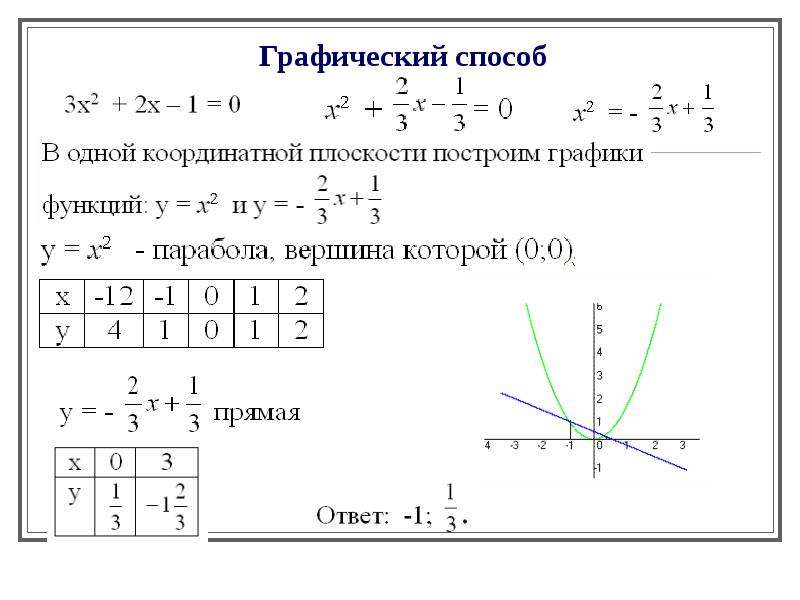
Графическое решение квадратных уравнений
На уроке учащиеся продемонстрировали знания и умения программы:
– распознавать виды функции, строить их графики;
– отрабатывали навыки построения квадратичной функции;
– отрабатывали графические способы решения квадратных уравнений, используя метод выделения полного квадрата.
Мне захотелось уделить особое внимание решению задач с параметром, так как ЕГЭ по математике предлагает очень много заданий такого типа.
Возможность применить на уроке такой вид работы дали мне сами ученики, так как они имеют достаточную базу знаний, которые можно углубить и расширить.
Заранее подготовленные учащимися шаблоны позволили экономить время урока. В ходе урока мне удалось реализовать поставленные задачи в начале урока и получить ожидаемый результат.
Использование физкультминутки помогло
избежать переутомления учащихся, сохранить
продуктивную мотивацию получения знаний.
В целом результатом урока я довольна, но думаю, что есть еще резервные возможности: современные инновационные технологические средства, которыми мы, к сожалению, не имеем возможности пользоваться.
Тип урока: закрепление изученного материала.
Цели урока:
- Общеобразовательные и дидактические:
- развивать разнообразные способы мыслительной деятельности учащихся;
- формировать способности самостоятельного решения задач;
- воспитывать математическую культуру учащихся;
- развивать интуицию учащихся и умение пользоваться полученными знаниями.
- Учебные цели:
- обобщить ранее изученные сведения по теме «Графическое решение квадратных уравнений»;
- повторить построение графиков квадратичной функции;
- сформировать навыки использования алгоритмов
решения квадратичных уравнений графическим
методом.

- Воспитательные:
- привитие интереса к учебной деятельности, к предмету математики;
- формирование толерантности (терпимости), умения работать в коллективе.
ХОД УРОКА
I. Организационный момент
– Сегодня на уроке мы обобщим и закрепим
графическое решение квадратных уравнений
различными способами.
В дальнейшем эти навыки нам будут нужны в старших
классах на уроках математики при решении
тригонометрических и логарифмических
уравнений, нахождения площади криволинейной
трапеции, а также на уроках физики.
II. Проверка домашней работы
Разберем на доске № 23.5(г).
Решить это уравнение с помощью параболы и прямой.
Решение:
х2 + х – 6 = 0
Преобразуем уравнение: х2 = 6 – х
Введем функции:
у = х2; квадратичная
функция
у
= 6 – х линейная,
графиком явл. парабола,
графиком явл. прямая,
парабола,
графиком явл. прямая,
Строем в одной системе координат графики функций (по шаблону)
Получили две точки пересечения.
Решением квадратного уравнения являются абсциссы этих точек х1 = – 3, х 2 = 2.
Ответ: – 3; 2.
III. Фронтальный опрос
- Что является графиком квадратичной функции?
- Скажите алгоритм построения графика квадратичной функции?
- Что называется квадратичным уравнением?
- Приведите примеры квадратичных уравнений?
- Запишите на доске свой пример квадратичного уравнения, Назовите, чему равны коэффициенты?
- Что значит решить уравнение?
- Сколько способов вы знаете графического решения квадратных уравнений?
- В чем заключается графические способы решение квадратных уравнений:
IV. Закрепление материала
Закрепление материала
№ 23.6 (а)
На доске решают учащиеся первым, вторым, третьим способами.
Класс решает четвертым
– х2 + 6х – 5 = 0
Преобразую квадратное уравнение, выделяя полный квадрат двучлена:
– х2 + 6х – 5 = – (х2 – 6х + 5) = – (х2 – 6х + 32 – 9 + 5) = – ((х – 3)2 – 4) = – (х – 3)2 + 4
Получили квадратное уравнение:
– (х – 3)2 + 4 = 0
Введем функцию:
у = – (х2 – 3)2 + 4
Квадратичная функция вида у = а (х + L)2 + m
Графиком явл. парабола, ветви направлены вниз, сдвиг основной параболы по оси Ох в право на 3 ед., по оси Оу вверх на 4 ед., вершина (3; 4).
Строим по шаблону.
Нашли точки пересечения параболы с осью Ох. Абсциссы этих точек явл. решением данного уравнения. х = 1, х = 5.
Давайте посмотрим другие графические решение у
доски. Прокомментируйте свой способ решения
квадратных уравнений.
Прокомментируйте свой способ решения
квадратных уравнений.
1 ученик
Решение:
– х2 + 6х – 5 = 0
Введем функцию у = – х + 6х – 5, квадратичная функция, графиком является парабола, ветви направлены вниз, вершина
х0 = – в/2а
х0 = – 6/– 2 = 3
у0 = – 32 + 18 = 9; точка (3; 9)
ось симметрии х = 3
Строим по шаблону
Получили точки пересечения с осью Ох, абсциссы этих точек являются решением квадратного уравнения. Два корня х1 = 1, х2 = 5
2 ученик
Решение:
– х2 + 6х – 5 = 0
Преобразуем: – х2 + 6х = 5
Введем
функции: у1 = – х2 + 6х, у2 = 5, линейная
функция, квадратичная функция, графиком
графиком явл. прямая у || Ох явл. парабола, ветви
направлены вниз, вершина х0 = –
в/2а
х0 = – 6/– 2 = 3
(3; 9).

ось симметрии х = 3
Строим по шаблону
Получили точки пересечения
параболы и прямой, их абсциссы являются решением квадратного уравнения. Два корня х1 = 1, х2 = 5
Итак, одно и тоже уравнение можно решать различными способами, а ответ получаться должен один и тот же.
V. Физкультминутка
VI. Решение задачи с параметром
№ 23.19
При каких значениях р уравнение х2
+ 6х + 8 = р:
– Не имеет корней?
– Имеет один корень?
– Имеет два корня?
Чем отличается это уравнение от предыдущего?
Правильно, буквой!
Эту букву в дальнейшем мы будем называть параметром,
Р.
Пока она вам ни о чем не говорит. Но мы будем в
дальнейшем решать различные задачи с параметром.
Ученик помогает учителю решать у доски.
С чего начнем решать?
Зададим функции:
у1 = х2 + 6х +
8
у2 = р линейная функция,
квадратичная
функция,
графиком является прямая
графиком явл. парабола,
ветви направлены вниз, вершина
х0 = – в/2а,
х0 = – 6/2 = – 3
у0 = (– 3)2 + 6(– 3) + 8 = – 1
(– 3; – 1)
Ось симметрии х = 3, таблицу строить не буду, а
возьму шаблон у = х
Парабола построена! Теперь надо провести прямую у
= р.
– Где надо начертить прямую р, чтобы
получить два корня?
– Где надо начертить прямую р, чтобы
получить один корень?
– Где надо начертить прямую р, чтобы не
было корней?
– Итак, сколько наше уравнение может иметь
корней?
– Понравилась задача? Спасибо за помощь! Оценка 5.
VII. Самостоятельная работа по вариантам (5 мин.)
I В. II В.
у = х2 – 5х + 6 у = – х2 + х – 6
Решить квадратное уравнение графическим способом, выбирая для вас удобный способ. Если кто-то справится с заданием раньше, проверьте свое решение другим способом. За это будет выставляться дополнительная оценка.
VIII. Итог урока
– Чему научились вы на сегодняшнем уроке?
– Сегодня на уроке мы с вами квадратные
уравнения решали графическим методом, используя
различные способы решения, и рассмотрели
графический способ решения квадратного
уравнения с параметром!
– Переходим к домашнему заданию.
IХ. Домашнее задание
1. Домашняя контрольная работа на стр. 147, из
задачника Мордковича по вариантам I и II.
2. На кружке, в среду, будем решать V-м способом,
(гипербола и прямая).
Х. Литература:
1. А.Г. Мордкович. Алгебра-8. Часть 1.
Учебник для учащихся образовательных
учреждений. М.: Мнемозина, 2008 г.
3. А.Г. Мордкович. Алгебра 7-9. Методическое пособие для учителя.М.: Мнемозина, 2004 г.
4. Л.А. Александрова. Алгебра-8. Самостоятельные работы для учащихся образовательных учреждений./Под ред. А.Г. Мордковича. М.: Мнемозина, 2009 г.
Графическое решений квадратных уравнений — презентация онлайн
Алгебра 8 класс2. Немного истории
Еще в древнем Вавилоне моглирешить некоторые виды
квадратных уравнений.
Диофант Александрийский,
Аль- Хорезми
Решали уравнения
геометрическими и
.

графическими способами
Евклид
Омар Хайям
Квадратное уравнение имеет вид
ax2 + bx + c = 0
Для графического решения квадратного уравнения
представьте его в одном из видов:
ax2 + bx +c = 0
2
ax = -bx – c
2
ax + c = — bx
a(x + b/2a)2 = ( 4ac — b2 )/4a
4. Алгоритм графического решения квадратных уравнений
Ввести функцию f(x), равную левой части иg(x) , равную правой части
Построить графики функций y=f(x) и y=g(x)
на одной координатной плоскости
Отметить точки пересечения графиков
Найти абсциссы точек пересечения,
сформировать ответ
Способы графического решения
квадратного уравнения
ах² + bх + с = 0
I
Способ
поcтроения
параболы
y=ах²
+bx+c
III
II
(a)
Способ
поcтроения
прямой
у= bx+c и
параболы
у = ах²
(b)
Способ
поcтроения
прямой
у= bx и
параболы
у = ах²+с
(в)
Способ
поcтроения
прямой
у= с и
параболы
у = ах²+ bx
Способ
выделения
полного
квадрата
«Человеку, изучающему алгебру,
часто полезнее решить одну и ту же
задачу различными способами, чем
решать три-четыре различные
задачи.
 Решая одну задачу
Решая одну задачуразличными способами, можно путем
сравнения выяснить, какой из них
короче и эффективнее. Так
вырабатывается опыт». У. У. Сойер.
7. Графическое решение квадратного уравнения
Иллюстрация на одном примере8. Алгоритм решения квадратного уравнения графическим способом
Способ 1• Построить график функции
y=ax2+bx+c
• Найти точки пересечения графика с
осью абсцисс
Решить уравнение
у х2 2х 3
1 способ
Построим график функции у =
1.
2.
х 2х 3 0
2
у
х2 2х 3
График-парабола, а=1>0,ветви вверх.
Вершина ( х0 ; у0)
в
х0 =- 2а
3
Хο=1
у0 12 2 3 4
о
(1; -4)-вершина
3. Ось параболы
х0 1
-1
1
3
4. Дополнительные точки:
х -1 0 1 2 3
у
0
-3 -4
-3
0
Корнями уравнения являются
абсциссы точек пересечения графика с осью х, т.е. где у=0.
Значит, корни уравнения -1 и 3.
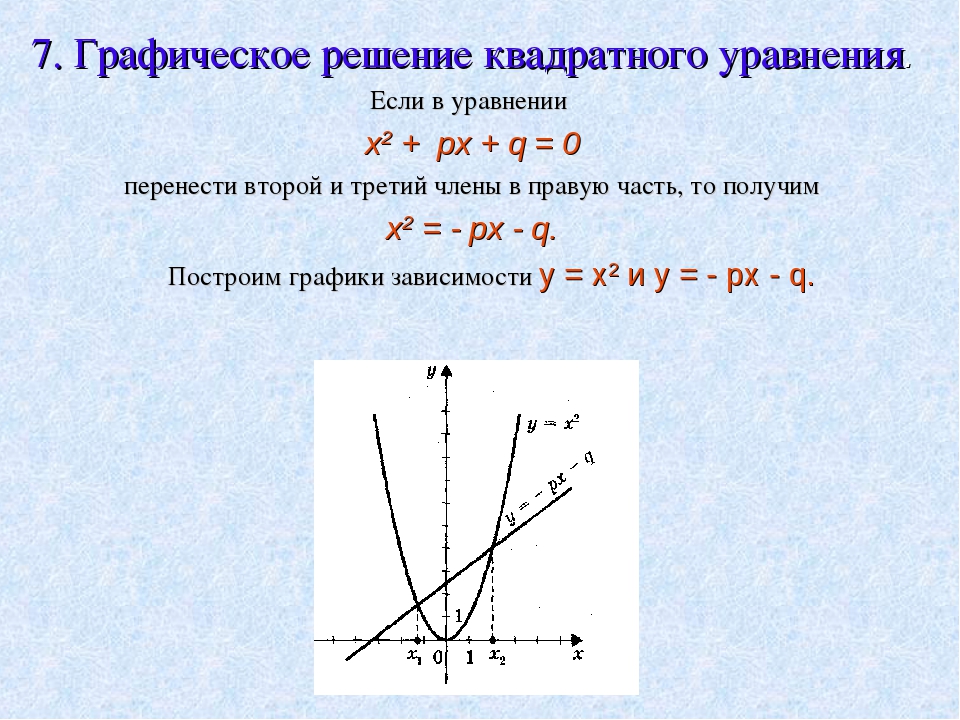 Проверка устно. Ответ: -1; 3.
Проверка устно. Ответ: -1; 3.х
10. Алгоритм построения параболы
найти координаты вершины;провести ось параболы;
отметить на оси абсцисс две точки,
симметричные относительно оси
параболы; найти значения функции в
этих точках;
провести параболу через полученные
точки.
11. Примеры графического решения квадратных уравнений
Решение уравнения•Пусть f(x)= x2 – 2x -3 и g(x) =0
x2-2x –3=0
у=x2 – 2x -3
а = 1>0, ветви вверх
•Координаты вершины x۪ ۪
ο
=-b/2a; x۪ ۪
ο
=1 .
y ο = 1² — 2 – 3 = -4; y ο = -4; ( 1; -4)
Найти точки абсциссы которых
симметричны относительно х=1
-1
2 -2x -3
•Построить
по
таблице
график
y=x
x 0 2 -1 3
y
-3 -3 0
0
3
Корни уравнения равны абсциссам точек
пересечения параболы с осью ОХ
12. Графический способ решения квадратных уравнений
Парабола и прямая неПарабола и
прямая
касаются
Квадратное
уравнение
имеет два равных
корня
Парабола и прямая
пересекаются
Квадратное
уравнение
имеет два
различных корня
пересекаются и не
касаются
Квадратное
уравнение не имеет
корней
13.
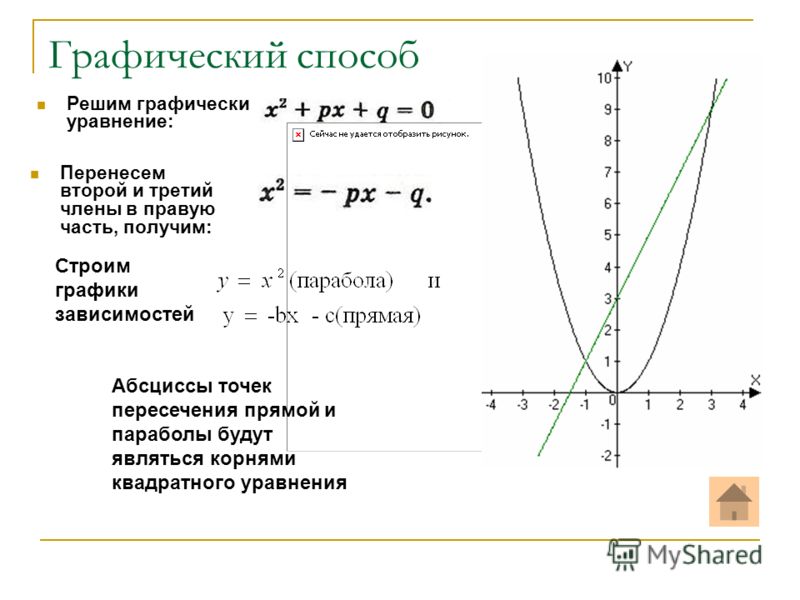 Алгоритм решения квадратного уравнения графическим способом Способ 2(а)
Алгоритм решения квадратного уравнения графическим способом Способ 2(а)• Построить графики функции y=ax2 и
у = bx+ с
• Найти абсциссы точек пересечения
графиков.
14. x2 – 2x – 3 =0 Представим в виде x2 = 2x +3
Пусть f(x)=x2 и g(x)=2x +3Построим на одной
координатной плоскости
графики функций
y=x2 иy= 2x + 3
Корни уравнения
абсциссы точек
пересечения
параболы с прямой
-1
3
2 способ
Преобразуем уравнение
х2 2х 3 0
к виду
х2 2х 3
у х2 ; у 2х 3
Построим в одной системе координат графики функций
у х2
у 2х 3
-это
парабола
у
-это прямая
у 2х 3
у х2
х
0
1
у
3
5
Корнями уравнения являются
абсциссы точек пересечения: -1 и 3
3
х
-1
3
4 x2 – 4x + 1 =0
Представим в виде
4×2 = 4x -1
1). Построим графики функций:
у = 4 x2 , у = 4x — 1
2). Строим параболу у = 4 x2
а = 4, ветви вверх
хο = — в ; хο= 0; ; уο= 0.

2а
По шаблону строим параболу
у
3
1
0,5
0
-1
3). Строим прямую у = 4x — 1
x
0
1
y
-1 3
Корнем уравнения является
абсцисса точки пересечения: 0,5
1
х
17. Алгоритм решения квадратного уравнения графическим способом
Способ 2 (b)• Преобразовать уравнение к виду
ax2+с = bx
• Построить:
параболу y = ax2+с и прямую y = bx
• Найти абсциссы точек пересечения
графиков функции.
18. x2 – 2x – 3 =0 Представим в виде x2 –3 = 2x
y=x2 –3Пусть f(x)=x2 –3 и g(x)=2x
Построим на одной
координатной плоскости
графики функций
y=x2 –3 и y =2x
-1
Корни уравнения
абсциссы точек
пересечения параболы с
прямой
y =2x
3
19. x2 – 4x + 5 =0 Представим в виде x2 +5 = 4x
yПусть f(x)=x2 +5 и g(x)=4x
Построим на одной
координатной плоскости
графики функций
y=x2 +5 и y =4x
y=x2 +5
y =4x
Точек пересечения
параболы с прямой нет
Ответ: корней нет
о
x
20.
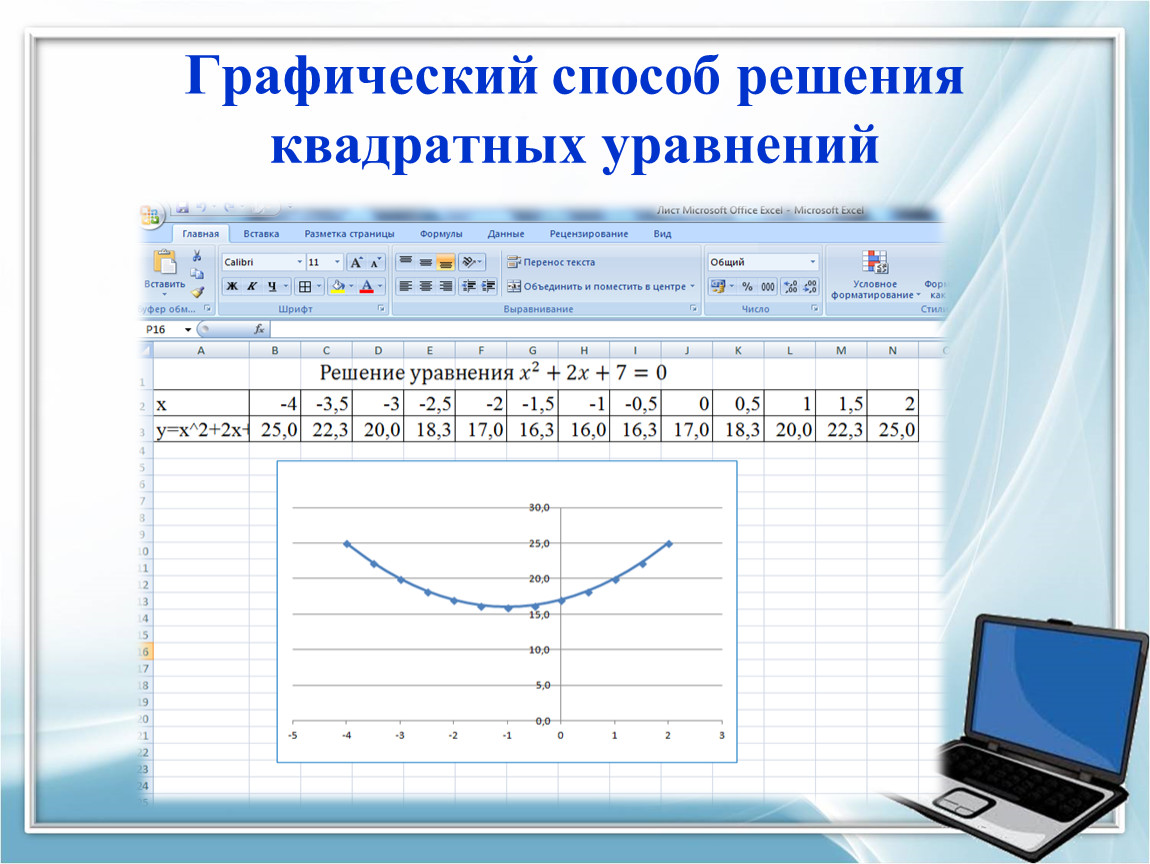 Алгоритм решения квадратного уравнения графическим способом Способ 2(в)
Алгоритм решения квадратного уравнения графическим способом Способ 2(в)• Построить графики функции
• y=ax2 + bx и
у=с
• Найти абсциссы точек пересечения
графиков.
21. x2 – 2x – 3 =0 Представим в виде x2 – 2x = 3
yПусть f(x)= х² — 2х и g(x)=3
Построим на одной
координатной плоскости
графики функций
y= х² — 2х и y=3
-1
y= х² — 2х
y=3
о
Корни уравнения
абсциссы точек
пересечения параболы
с прямой
-1
2
х
3
3
22. Алгоритм решения квадратного уравнения графическим способом
Способ 3(выделение полного квадрата)
• Преобразовать уравнение к виду
a(x+l)2 = m
• Построить:
параболу y = a(x+l)2 и прямую y = m
• Найти абсциссы точек пересечения
графиков функций.
Выделение квадрата двучлена.
x2 – 2x = 3
x2 – 2x + 1 = 3 + 1
( x –1)2=4.
( x –1)2 — 4 = 0
( x –1)2 — 2² = 0
( x –1 – 2) ( x –1 + 2 ) = 0
( x –3 ) ( x + 1 ) = 0
x –3 = 0
x+1=0
x =3
x =-1
24.
 x2 – 2x – 3 =0 Представим в виде (x –1)2=4 y= (x –1)2
x2 – 2x – 3 =0 Представим в виде (x –1)2=4 y= (x –1)2Пусть f(x)= (x – 1)2 и g(x)=4
Построим на одной
координатной плоскости
графики функций
y= (x –1)2 и y=4
y=4
-1
Корни уравнения
абсциссы точек
пересечения параболы
с прямой
3
25. Решите графически уравнение
Группа АГруппа В
Бычев Андрей
Баличев Илья
Ерофеева Ксения
Помигуев Павел
Каминская Света
Фролов Саша
Лобов Егор
Лукьяненко Вероника
Осипов Павел
Циорба Влад
х² + 2х – 8= 0
4х² — 8х + 3= 0
Группа С
Григорьева Катя
Соловьев Илья
3х² + 2х – 1= 0
Сколько нам открытий
чудных готовит
просвещения дух?
27. Решить графически уравнение
x 2x 8 02
28. Как решить уравнение?
x 2x 8 02
Построить график квадратичной функции и
абсциссы точек пересечения параболы с осью x
будут являться корнями уравнения.
Выполнить преобразование уравнения, рассмотреть
функции, построить графики этих функций,
установить точки пересечения графиков функций,
абсциссы которых и будут являться корнями
уравнения.

29. Решить графически уравнение
x 2 x 82
30. Построить график функции
y x2
31. Построить график функции
y 2 x 832. Корни уравнения: абсциссы точек пересечения графиков функций
x1 4x2 2
33. Построить график функции
y x 2x 82
Корни уравнения:
точки пересечения
параболы с осью ОХ
x1 4
x2 2
34. Решить графически уравнение
x 8 2 x2
Корни уравнения:
точки пересечения
параболы и прямой
x1 4
x2 2
35. Решить графически уравнение
( x 1) 92
Корни уравнения:
точки пересечения
параболы и прямой
x1 4
x2 2
36. Итог
Познакомились:• с графическим методом решения
квадратных уравнений;
• с различными способами графического
решения квадратных уравнений.
• закрепили знания по построению
графиков различных функций.
37. Заключительное слово учителя:
«Чем больше и глубже вамудастся усвоить азы
математики и научиться
пользоваться ее методами, тем
дальше и быстрее вы сумеете
продвинуться в использовании
математических средств в той
области деятельности, которой
займетесь после школы»
«Графическое решение квадратных уравнений».

Графическое
решение
квадратных
уравнений
Алгебра 8 класс
Квадратное уравнение имеет вид ax 2 + bx + c = 0
Для графического решения квадратного уравнения представьте его в одном из видов:
- ax 2 + bx +c = 0 ax 2 = -bx – c ax 2 + c = — bx a(x + b/2a) 2 = (b 2 – 4ac)/2a
- ax 2 + bx +c = 0
- ax 2 = -bx – c
- ax 2 + c = — bx
- a(x + b/2a) 2 = (b 2 – 4ac)/2a
Алгоритм графического решения квадратных уравнений
- Ввести функцию f(x), равную левой части и g(x) , равную правой части.

- Построить графики функций y=f(x) и y=g(x) на одной координатной плоскости.
- Отметить точки пересечения графиков.
- Найти абсциссы точек пересечения, сформировать ответ.
Примеры графического решения квадратных уравнений
Решение уравнения x 2 -2x –3=0
- Пусть f(x)= x 2 – 2x -3 и g(x) = 0
- Координаты вершины x b =-b/2a=1 y b = -4
- Найти точки абсциссы которых симметричны относительно х=1
- Построить по таблице график
y=x 2 -2x -3
x
y
0
-3
2
-1
-3
0
3
0
3
-1
Корни уравнения равны абсциссам точек пересечения параболы с осью ОХ
x 2 – 2x – 3 =0 Представим в виде x 2 = 2x +3
Пусть f(x)=x 2 и g(x)=2x +3
Построим на одной координатной плоскости графики функций
y=x 2 и y= 2x + 3
Корни уравнения абсциссы точек пересечения параболы с прямой
-1
3
x 2 – 2x – 3 =0 Представим в виде x 2 –3 = 2x
Пусть f(x)=x 2 –3 и g(x)=2x
Построим на одной координатной плоскости графики функций
y=x 2 –3 и y =2x
-1
Корни уравнения абсциссы точек пересечения параболы с прямой
3
x 2 – 2x – 3 =0 Представим в виде (x –1) 2 =4
Пусть f(x)= (x – 1) 2 и g(x)=4
Построим на одной координатной плоскости графики функций
y= (x –1) 2 и y=4
-1
Корни уравнения абсциссы точек пересечения параболы с прямой
3
Немного истории
Еще в древнем Вавилоне могли решить некоторые виды квадратных уравнений.
Диофант Александрийский и Евклид , Аль-Хорезми и Омар Хайям решали уравнения геометрическими и графическими способами.
В 1591 году Франсуа Виет ввел формулы для решения квадратных уравнений
На следующем уроке мы послушаем доклады о жизни
этих великих математиков, которые подготовят ваши
одноклассники.
Приступим к практике!
Алгебра 8 класс Немного истории Еще в
Алгебра 8 класс
Немного истории Еще в древнем Вавилоне могли решить некоторые виды квадратных уравнений. Диофант Александрийский, Аль- Хорезми Решали уравнения геометрическими и. графическими способами Евклид Омар Хайям
Квадратное уравнение имеет вид ax 2 + bx + c = 0 Для графического решения квадратного уравнения представьте его в одном из видов: q ax 2 + bx +c = 0 2 q ax = -bx – c 2 q ax + c = — bx q a(x + b/2 a)2 = ( 4 ac — b 2 )/4 a
Алгоритм графического решения квадратных уравнений q Ввести функцию f(x), равную левой части и g(x) , равную правой части q Построить графики функций y=f(x) и y=g(x) на одной координатной плоскости q Отметить точки пересечения графиков q Найти абсциссы точек пересечения, сформировать ответ
Способы графического решения квадратного уравнения ах² + bх + с = 0 I Способ поcтроения параболы y=ах² +bx+c III II (a) Способ поcтроения прямой у= bx+c и параболы у = ах² (b) Способ поcтроения прямой у= bx и параболы у = ах²+с (в) Способ поcтроения прямой у= с и параболы у = ах²+ bx Способ выделения полного квадрата
«Человеку, изучающему алгебру, часто полезнее решить одну и ту же задачу различными способами, чем решать три-четыре различные задачи. Решая одну задачу различными способами, можно путем сравнения выяснить, какой из них короче и эффективнее. Так вырабатывается опыт» . У. У. Сойер.
Решая одну задачу различными способами, можно путем сравнения выяснить, какой из них короче и эффективнее. Так вырабатывается опыт» . У. У. Сойер.
Графическое решение квадратного уравнения Иллюстрация на одном примере
Алгоритм решения квадратного уравнения графическим способом Способ 1 Построить график функции y=ax 2+bx+c Найти точки пересечения графика с осью абсцисс
Решить уравнение 1 способ у Построим график функции у = 1. 2. График-парабола, а=1>0, ветви вверх. Вершина ( ) =- Хο=1 3 -1 о (1; -4)-вершина -1 3. Ось параболы 1 3 4. Дополнительные точки: х -1 0 1 2 3 у 0 -3 -4 -3 0 Корнями уравнения являются абсциссы точек пересечения графика с осью х, т. е. где у=0. Значит, корни уравнения -1 и 3. Проверка устно. Ответ: -1; 3. х
Алгоритм построения параболы найти координаты вершины; провести ось параболы; отметить на оси абсцисс две точки, симметричные относительно оси параболы; найти значения функции в этих точках; провести параболу через полученные точки.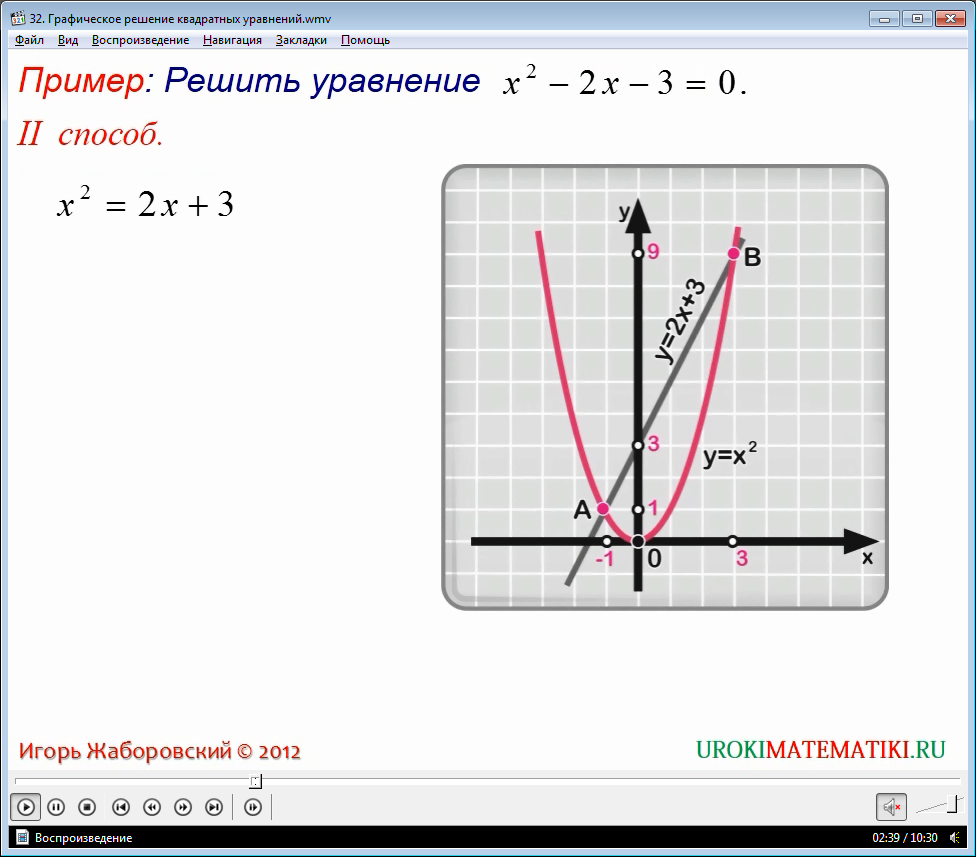
Примеры графического решения квадратных уравнений Решение уравнения • Пусть f(x)= x 2 – 2 x -3 и g(x) =0 x 2 -2 x – 3=0 у=x 2 – 2 x -3 а = 1>0, ветви вверх • Координаты вершины x ο =-b/2 a; x ο =1. y ο = 1² — 2 – 3 = -4; y ο = -4; ( 1; -4) Найти точки абсциссы которых симметричны относительно х=1 • Построить по таблице график x y 0 2 -1 3 -3 -3 0 0 y=x 2 -1 -2 x -3 3 Корни уравнения равны абсциссам точек пересечения параболы с осью ОХ
Графический способ решения квадратных уравнений Парабола и прямая не Парабола и прямая касаются уравнение имеет два равных корня Квадратное Парабола и прямая пересекаются уравнение имеет два различных корня Квадратное пересекаются и не касаются Квадратное уравнение не имеет корней
Алгоритм решения квадратного уравнения графическим способом Способ 2(а) Построить графики функции y=ax 2 и у = bx+ с Найти абсциссы точек пересечения графиков.
x 2 – 2 x – 3 =0 Представим в виде x 2 = 2 x +3 Пусть f(x)=x 2 и g(x)=2 x +3 Построим на одной координатной плоскости графики функций y=x 2 иy= 2 x + 3 Корни уравнения абсциссы точек пересечения параболы с прямой -1 3
2 способ к виду Преобразуем уравнение Построим в одной системе координат графики функций -это парабола -это прямая х 0 1 у 3 5 Корнями уравнения являются абсциссы точек пересечения: -1 и 3 3 -1 3
4 x 2 – 4 x + 1 =0 Представим в виде 4 x 2 = 4 x -1 1). Построим графики функций: у = 4 x 2 , у = 4 x — 1 2). Строим параболу у = 4 x 2 а = 4, ветви вверх хο = — ; хο= 0; ; уο= 0. По шаблону строим параболу у 3 1 0, 0 5 -1 3). Строим прямую у = 4 x — 1 x y 0 1 -1 3 Корнем уравнения является абсцисса точки пересечения: 0, 5 1 х
Построим графики функций: у = 4 x 2 , у = 4 x — 1 2). Строим параболу у = 4 x 2 а = 4, ветви вверх хο = — ; хο= 0; ; уο= 0. По шаблону строим параболу у 3 1 0, 0 5 -1 3). Строим прямую у = 4 x — 1 x y 0 1 -1 3 Корнем уравнения является абсцисса точки пересечения: 0, 5 1 х
Алгоритм решения квадратного уравнения графическим способом Способ 2 (b) Преобразовать уравнение к виду ax 2+с = bx Построить: параболу y = ax 2+с и прямую y = bx Найти абсциссы точек пересечения графиков функции.
x 2 – 2 x – 3 =0 Представим в виде x 2 – 3 = 2 x y=x 2 – 3 Пусть f(x)=x 2 – 3 и g(x)=2 x Построим на одной координатной плоскости графики функций y=x 2 – 3 и y =2 x -1 Корни уравнения абсциссы точек пересечения параболы с прямой y =2 x 3
x 2 – 4 x + 5 =0 Представим в виде x 2 +5 = 4 x y Пусть f(x)=x 2 +5 и g(x)=4 x Построим на одной координатной плоскости графики функций y=x 2 +5 и y =4 x y=x 2 +5 y =4 x Точек пересечения параболы с прямой нет Ответ: корней нет о x
Алгоритм решения квадратного уравнения графическим способом Способ 2(в) Построить графики функции y=ax 2 + bx и у=с Найти абсциссы точек пересечения графиков.
x 2 – 2 x – 3 =0 Представим в виде x 2 – 2 x = 3 y Пусть f(x)= х² — 2 х и g(x)=3 Построим на одной координатной плоскости графики функций y= х² — 2 х и y=3 -1 y= х² — 2 х y=3 о Корни уравнения абсциссы точек пересечения параболы с прямой -1 2 3 х 3
Алгоритм решения квадратного уравнения графическим способом Способ 3 (выделение полного квадрата) Преобразовать уравнение к виду a(x+l)2 = m Построить: параболу y = a(x+l)2 и прямую y = m Найти абсциссы точек пересечения графиков функций.
Выделение квадрата двучлена. x 2 – 2 x = 3 x 2 – 2 x + 1 = 3 + 1 ( x – 1)2=4. ( x – 1)2 — 4 = 0 ( x – 1)2 — 2² = 0 ( x – 1 – 2) ( x – 1 + 2 ) = 0 ( x – 3 ) ( x + 1 ) = 0 x – 3 = 0 x+1=0 x =3 x =-1
x 2 – 2 x – 3 =0 Представим в виде (x – 1)2=4 y= (x – 1)2 Пусть f(x)= (x – 1)2 и g(x)=4 Построим на одной координатной плоскости графики функций y= (x – 1)2 и y=4 -1 Корни уравнения абсциссы точек пересечения параболы с прямой 3
Решите графически уравнение Группа А Группа В Бычев Андрей Баличев Илья Ерофеева Ксения Помигуев Павел Каминская Света Фролов Саша Лобов Егор Лукьяненко Вероника Осипов Павел Циорба Влад х² + 2 х – 8= 0 4 х² — 8 х + 3= 0 Группа С Григорьева Катя Соловьев Илья 3 х² + 2 х – 1= 0
Сколько нам открытий чудных готовит просвещения дух?
Решить графически уравнение
Как решить уравнение? Построить график квадратичной функции и абсциссы точек пересечения параболы с осью x будут являться корнями уравнения. Выполнить преобразование уравнения, рассмотреть функции, построить графики этих функций, установить точки пересечения графиков функций, абсциссы которых и будут являться корнями уравнения.
Выполнить преобразование уравнения, рассмотреть функции, построить графики этих функций, установить точки пересечения графиков функций, абсциссы которых и будут являться корнями уравнения.
Решить графически уравнение
Построить график функции
Построить график функции
Корни уравнения: абсциссы точек пересечения графиков функций
Построить график функции Корни уравнения: точки пересечения параболы с осью ОХ
Решить графически уравнение Корни уравнения: точки пересечения параболы и прямой
Решить графически уравнение Корни уравнения: точки пересечения параболы и прямой
Итог Познакомились: с графическим методом решения квадратных уравнений; с различными способами графического решения квадратных уравнений. закрепили знания по построению графиков различных функций.
Заключительное слово учителя: «Чем больше и глубже вам удастся усвоить азы математики и научиться пользоваться ее методами, тем дальше и быстрее вы сумеете продвинуться в использовании математических средств в той области деятельности, которой займетесь после школы»
Как решить квадратное уравнение с помощью графика
Решение квадратных уравнений с помощью графика
Решение квадратных уравнений с помощью графика Все вращается вокруг того факта, что точки пересечения двух графиков являются точками, которые удовлетворяют обоим графическим уравнениям. Следовательно, если мы возьмем квадратное уравнение и пусть y 1 равны левой части уравнения, а y 2 равны правой части уравнения, то, когда мы можем изобразить оба этих уравнения, x -значения их точек пересечения дадут нам решения исходного уравнения.
Давайте немного уточним, разбив этот метод решения на шаги. Учитывая квадратичное уравнение AX 2 + BX + C = D , мы принимаем следующие шаги, чтобы решить графиком:
Учитывая квадратичное уравнение AX 2 + BX + C = D , мы принимаем следующие шаги, чтобы решить графиком:
- Let Y 1 = AX 2 + BX + c и y 2 = d .
- График y 1 и y 2 на одном графике.
- Найдите точки пересечения двух графиков.Значения x точек пересечения являются решениями вашего уравнения.
- Сверьте свой ответ с исходным уравнением.
Выглядит не так уж плохо. Давайте рассмотрим уравнение Брайана через эти шаги!
уравнение Брайана -16 x 2 + 100 x = 0, поэтому мы выпустим
y 1 = -16 x 2 + 100 x 2 + 100
y 2 = 0
Это достаточно легко! Следующим шагом мы хотим изобразить оба уравнения на одном графике.Это можно сделать вручную или воспользоваться графическим калькулятором. Использование графического калькулятора значительно упростит третий шаг, как мы увидим через минуту.
Все еще не так уж плохо! Теперь самое сложное! Нам нужно найти точки пересечения двух графиков.
Если из графика видно, то можно сделать это на глаз. Тем не менее, это оставляет много места для человеческой ошибки.Мы могли бы также сделать это алгебраически, но для этого мы приравняли бы два уравнения друг к другу, получив -16 x 2 + 100 x = 0, и найдем x . Но ждать! Вот с чего мы начали, и этот урок связан с решением с помощью графика. Наш последний и лучший вариант — использовать графический калькулятор. Графические калькуляторы могут построить ваши уравнения для вас и найти их точки пересечения — определенно самый простой путь! Конечно, у каждого графического калькулятора есть разные способы нахождения точек пересечения, но в инструкции к вашему калькулятору должно быть объяснено, как именно это сделать!
Отлично! Мы видим, что точками пересечения являются (0,0) и (6. 25,0). Вау, этот калькулятор когда-нибудь упрощает жизнь! У нас есть ответ! В соответствии с этим мяч для гольфа находится на высоте 0 в 0 секунд, когда он впервые ударяет по мячу, и в 6,25 секунды, когда мяч падает на землю, поэтому ответ на вопрос Брайана состоит в том, что мяч находится в воздухе 6,25 секунды. секунды. Просто чтобы убедиться, мы можем проверить наши решения, x = 0 и x = 6,25, подставив их в исходное уравнение и убедившись, что они дают верное утверждение.
25,0). Вау, этот калькулятор когда-нибудь упрощает жизнь! У нас есть ответ! В соответствии с этим мяч для гольфа находится на высоте 0 в 0 секунд, когда он впервые ударяет по мячу, и в 6,25 секунды, когда мяч падает на землю, поэтому ответ на вопрос Брайана состоит в том, что мяч находится в воздухе 6,25 секунды. секунды. Просто чтобы убедиться, мы можем проверить наши решения, x = 0 и x = 6,25, подставив их в исходное уравнение и убедившись, что они дают верное утверждение.
Ура! Мы все сделали правильно!
Другой пример
Рассмотрим еще один пример.Предположим, площадь прямоугольного сада, который вы создаете на заднем дворе, может быть смоделирована по формуле x 2 + 2 x , где x — это ширина сада в футах. Вы хотите, чтобы площадь была 35 квадратных футов, поэтому вы хотите решить уравнение x 2 + 2 x = 35.
Это квадратное уравнение! Решим по графику.
Шаг 1:
y 1 = x 2 + 2 x
y 2 = 35
Оба уравнения на одном графике.
Шаг 3: Найдите точки пересечения.
Похоже, наши решения x = 5 и x = -7. Мы можем отбросить отрицательный ответ, так как мы имеем дело с шириной. Это говорит нам о том, что если сад имеет ширину 5 футов, то площадь будет 35 квадратных футов, как вы и хотели. Очень просто!
Краткий обзор урока
Квадратное уравнение представляет собой полиномиальное уравнение со старшим показателем степени два, которое можно представить в виде x 2 + bx + c = 0, где а,
, , и c являются константами.Мы можем решить квадратичное уравнение AX 2 + BX + C = D с помощью графики с использованием следующих шагов:
- Пусть y 1 = AX 2 + BX + C и y 2 = d .

- График y 1 и y 2 на одном графике.
- Найдите точки пересечения двух графиков. Значения x точек пересечения являются решениями вашего уравнения.
- Сверьте свой ответ с исходным уравнением.
Графический калькулятор, наряду с пошаговым выполнением этого процесса, действительно упрощает задачу — несомненный плюс при решении математических задач!
«Решение» квадратных уравнений с помощью графика
Пурпурная математика
Честно говоря, решение «по графику» — несколько фиктивная тема.Основная идея решения с помощью графика заключается в том, что, поскольку (действительные) решения любого уравнения (включая квадратные уравнения) являются точками пересечения x этого уравнения, мы можем посмотреть на точки пересечения x на графике. найти решения соответствующего уравнения. Однако при таком «решении» возникают трудности.
Однако при таком «решении» возникают трудности.
Когда мы рисуем прямую линию, такую как « y = 2 x + 3″, мы можем найти точку пересечения x (с определенной степенью точности), нарисовав действительно аккуратную систему осей, построив пару точек, хватаем нашу линейку, рисуем красивую прямую линию и считываем (приблизительный) ответ с графика с достаточной степенью уверенности.
MathHelp.com
Однако единственный способ узнать, что у нас есть точная точка пересечения x и, следовательно, решение, — это использовать алгебру, приравняв уравнение прямой к нулю, и решив:
0 = 2 х + 3
–3 = 2 х
–1.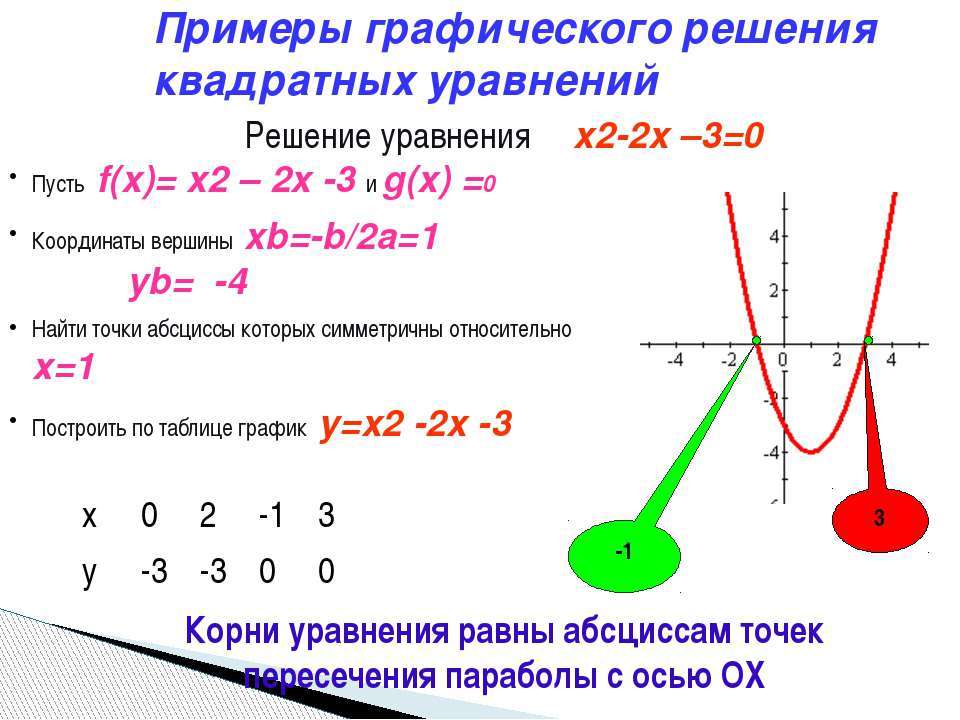 5 = х
5 = х
Если бы линейное уравнение выглядело примерно так: y = 47 x – 103, очевидно, что нам будет очень трудно угадать решение по графику. Мы можем предположить, что x 90 248 -intercept составляет около 90 247 x 90 248 = 2, но это будет не совсем правильно. Алгебра была бы единственным надежным методом решения.
Квадратичная функция более беспорядочна, чем прямая; он изображается волнистой параболой.Если мы нанесем несколько точек пересечения, отличных от x , а затем проведем через них кривую линию, как мы узнаем, получили ли мы пересечения x хотя бы близко к правильным? Мы не знаем. Единственный способ, которым мы можем быть уверены в наших x -перехватах, состоит в том, чтобы установить квадратное число равным нулю и решить.
Но весь смысл «решения с помощью графика» в том, что они не хотят, чтобы мы занимались (точной) алгеброй; они хотят, чтобы мы угадывали по красивым картинкам.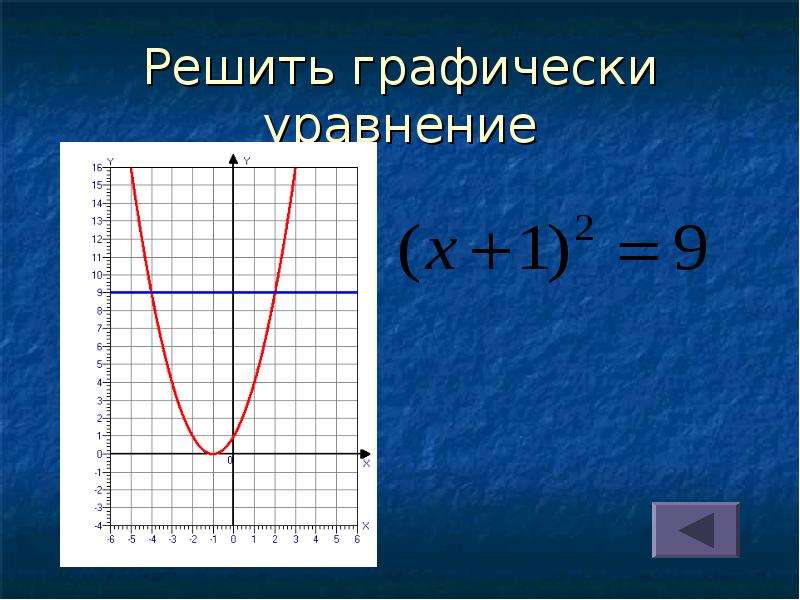
Таким образом, «решение с помощью графика» обычно не является ни «решением», ни «графическим построением». В типичном упражнении вы на самом деле ничего не рисуете и ничего не решаете. Вместо этого вам предлагается угадывать числа по распечатанному графику. Или же, если вы «используете технологию», вам говорят нажать несколько кнопок на вашем графическом калькуляторе и посмотреть на красивую картинку; а затем вам говорят нажать еще несколько кнопок, чтобы программа могла вычислить перехваты.
Я предполагаю, что воспитатели пытаются помочь вам увидеть связь между x -пересечениями графиков и решениями уравнений.Но концепция имеет тенденцию теряться во всех нажатиях кнопок.
Ладно, хватит разглагольствовать.
Чтобы решить с помощью графика, книга может дать нам очень четкий график, вероятно, по крайней мере с несколькими отмеченными точками. Книга попросит нас указать точки на графике, которые представляют решения. В противном случае это даст нам квадратное число, и мы будем использовать наш графический калькулятор, чтобы найти ответ. Поскольку разные модели калькуляторов имеют разные последовательности клавиш, я не могу дать инструкции о том, как «использовать технологию» для поиска ответов; вам нужно будет обратиться к руководству пользователя для любого калькулятора, который вы используете (или к файлу «Справка» для любой электронной таблицы или другого программного обеспечения, которое вы используете).Я приведу лишь пару примеров решения по картинке, которая вам дана.
В противном случае это даст нам квадратное число, и мы будем использовать наш графический калькулятор, чтобы найти ответ. Поскольку разные модели калькуляторов имеют разные последовательности клавиш, я не могу дать инструкции о том, как «использовать технологию» для поиска ответов; вам нужно будет обратиться к руководству пользователя для любого калькулятора, который вы используете (или к файлу «Справка» для любой электронной таблицы или другого программного обеспечения, которое вы используете).Я приведу лишь пару примеров решения по картинке, которая вам дана.
Решите
x 2 – 8 x + 15 = 0, используя следующий график.
Уравнение, которое мне дали решить:
На картинке, которую мне дали, показан график соответствующей квадратичной функции:
x -отрезков графика функции соответствуют где y = 0.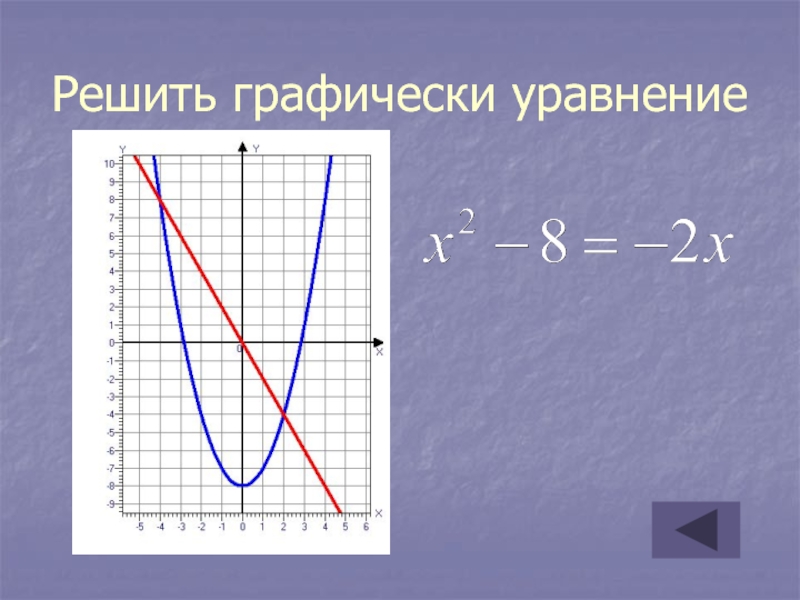 Дело в том, что мне нужно посмотреть на картинку (надеясь, что точки действительно пересекаются при целых числах, как кажется) и прочитать x -пересечения графика (и, следовательно, решения уравнения) из изображение.
Дело в том, что мне нужно посмотреть на картинку (надеясь, что точки действительно пересекаются при целых числах, как кажется) и прочитать x -пересечения графика (и, следовательно, решения уравнения) из изображение.
График пересекает ось x в точках x = 3 и x = 5. Я должен предположить, что график точен, и то, что выглядит как целочисленное значение, на самом деле является единицей. Так что мой ответ:
Так как они представили квадратное уравнение в приведенном выше упражнении, я могу проверить свое решение с помощью алгебры.Даны квадратичные множители, что дает мне:
( х – 3)( х – 5) = 0
х – 3 = 0, х – 5 = 0
х = 3, 5
Теперь я знаю, что решения представляют собой целые числа. График может подсказывать решения, но только алгебра верна и точна.
График может подсказывать решения, но только алгебра верна и точна.
Решите 0.3
x 2 – 0,5 x – 5/3 = 0 из следующего графика.
A
= (–5/3, 0), B = (0, –5/3), C = (5/6, –15/8), D = (10/3, 0)Для этой картинки они пометили кучу точек. Отчасти это должно было помочь, потому что перехваты x беспорядочны, поэтому я не смог бы угадать их значения без меток. Но в основном это было сделано в надежде запутать меня, на случай, если я забыл, что только x -перехваты, а не вершины или y -перехваты соответствуют «решениям».
Точка B является точкой пересечения y (поскольку x = 0 для этой точки), поэтому я могу игнорировать эту точку. Точка C кажется вершиной, поэтому я также могу игнорировать эту точку.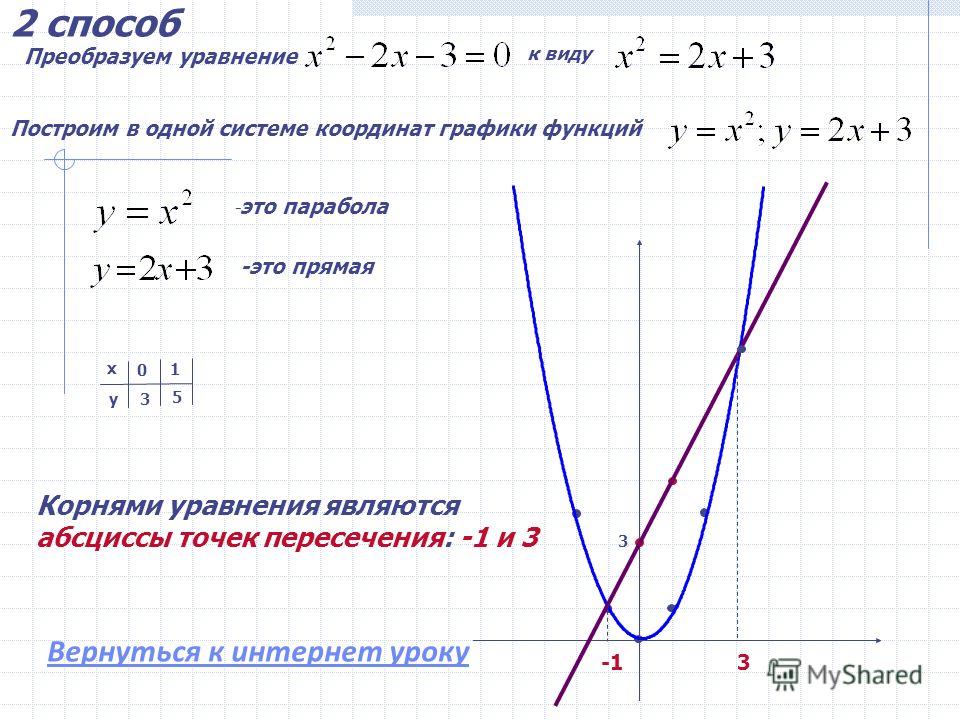 Точки A и D находятся на оси x (поскольку y = 0 для этих точек). Поэтому я могу предположить, что значения x этих точек на графике дают мне значения решения для соответствующего квадратного уравнения.
Точки A и D находятся на оси x (поскольку y = 0 для этих точек). Поэтому я могу предположить, что значения x этих точек на графике дают мне значения решения для соответствующего квадратного уравнения.
Поскольку они предоставили уравнение в дополнение к графику связанной функции, можно проверить ответ с помощью алгебры.Но целью здесь было подтвердить, что учащийся знает, какие точки являются точками пересечения x , и знает, что эти точки пересечения на графике являются решениями связанного уравнения.
Найдите решения квадратного уравнения по следующему графику:
A = (–2,1429, 0), B = (2,8, 0), C = (0,3286, -3,0540), D = (0, –3)
Мне не дали решить квадратное уравнение, поэтому я не могу проверить свою работу алгебраически. Они только дали мне изображение параболы, созданной связанной с ней квадратичной функцией, из которой я должен аппроксимировать x отрезков, что на самом деле является другим вопросом. Но я знаю, что они означают.
Они только дали мне изображение параболы, созданной связанной с ней квадратичной функцией, из которой я должен аппроксимировать x отрезков, что на самом деле является другим вопросом. Но я знаю, что они означают.
Я могу игнорировать точку, которая, вероятно, является вершиной (точка C). Я могу игнорировать точку пересечения и (точка D).Поэтому я обращу внимание только на x -перехваты, т.е. на те точки, где y равно нулю. Так что мой ответ:
Решение квадратичных уравнений с помощью графика глупо с точки зрения «реальной жизни» и требует, чтобы решения были простыми решениями факторного типа, такими как « x = 3», а не что-то вроде « x = –4 + кврт(7)». Другими словами, они либо должны «дать» вам ответы (б обозначая график), либо просить вас о решениях, которые вы могли бы легко найти с помощью факторинга.
Единственное, что вы можете извлечь из этой темы, — это укрепить свое понимание связи между решениями уравнений и x — пересечениями графиков функций; то есть тот факт, что решения «(некоторый многочлен) равен (нулю)» соответствуют x -пересечениям графика « y равно (тот же самый многочлен)».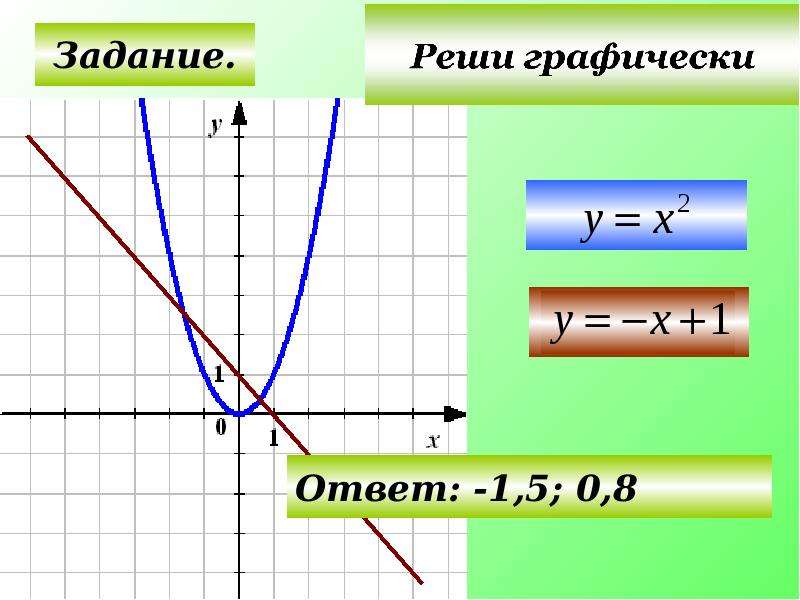 Если вы уйдете с пониманием этой концепции, то вы будете знать, когда лучше всего использовать свой графический калькулятор или другое программное обеспечение для построения графиков, чтобы помочь вам решить общие полиномы; а именно, когда они не факторизуемы.И вы поймете, как делать первоначальные предположения и приближения к решениям, глядя на график, знания, которые могут быть очень полезны на более поздних занятиях, когда вы будете работать с программным обеспечением, чтобы найти приблизительные «числовые» решения.
Если вы уйдете с пониманием этой концепции, то вы будете знать, когда лучше всего использовать свой графический калькулятор или другое программное обеспечение для построения графиков, чтобы помочь вам решить общие полиномы; а именно, когда они не факторизуемы.И вы поймете, как делать первоначальные предположения и приближения к решениям, глядя на график, знания, которые могут быть очень полезны на более поздних занятиях, когда вы будете работать с программным обеспечением, чтобы найти приблизительные «числовые» решения.
Но на практике, если вам нужно решить квадратное уравнение на уроке алгебры, вам не следует начинать с рисования графика. В связи с этим возникает вопрос: какой метод для любого заданного квадратичного числа следует использовать для его решения?
URL-адрес: https://www.Purplemath.com/modules/solvquad5.htm
График квадратичных функций моделирует функцию x 2 в двумерном пространстве. Эти функции обычно образуют параболу.
Эти функции обычно образуют параболу.
Параболическую форму часто сравнивают со смайликом или хмурым лицом. Математически такие функции называются вогнутыми и выпуклыми или «вогнутыми вверх» и «вогнутыми вниз».”
Графики квадратичных вычислений требуют глубокого понимания координатной геометрии и построения графиков. Обязательно ознакомьтесь с этими концепциями, прежде чем двигаться дальше.
Эта тема будет покрывать:
- Как график определить квадратичную функцию
- 0 Как решить квадратичные уравнения
Как диаграмма квадратичная функция
Напомним, что квадратичные функции имеют форму AX 2 +bx+c, где a, b и c — действительные числа.Если значение a равно 0, то у нас просто есть линейная функция, и мы можем изобразить ее, как любую другую линейную функцию.
Однако, когда a не равно 0, нам нужно использовать значения a, b и c, чтобы рассказать нам о графике.
 В частности, нас интересуют вершина, точка пересечения по оси y, точка пересечения с осью x и общая форма графа.
В частности, нас интересуют вершина, точка пересечения по оси y, точка пересечения с осью x и общая форма графа.Форма
Каждая парабола повернется вверх, как смайлик, или повернется вниз, как хмурый взгляд. Мы называем параболы, изгибающиеся вверх, «вогнутыми», а параболы, изгибающиеся вниз, выпуклыми.Решения первого будут простираться до положительной бесконечности, когда x стремится к положительной или отрицательной бесконечности. С другой стороны, значения y последнего будут простираться до отрицательной бесконечности, когда x приближается к положительной или отрицательной бесконечности.
Обратите внимание, что вогнутые параболы могут также называться вогнутыми вверх, а выпуклые параболы также могут называться вогнутыми вниз.
Мы знаем, повернется ли парабола нашей квадратичной функции вверх или вниз в зависимости от значения a. Если а положительно, парабола направлена вверх.Если a отрицательно, парабола направлена вниз. Это имеет смысл, потому что мы отражаем функции по оси X, умножая их на минус.

Ось симметрии
Функция x 2 является четной функцией. Это означает, что функция имеет одно и то же значение для x и -x. Это имеет смысл, потому что (-x) 2 =x 2 .
Четные функции имеют линию симметрии, равную x=0, ось y. Это означает, что график функции с одной стороны является зеркальным отражением графика функции с другой стороны.
Не каждая квадратичная функция является четной, потому что у некоторых есть член x, но у каждой квадратичной функции есть линия симметрии. Эта линия проходит прямо через вершину функции. Следовательно, поскольку вершина имеет координаты ( -b / 2a , f( -b / 2a )). Таким образом, линия симметрии x= -b / 2a.
Точка пересечения с осью Y
Точка пересечения с осью Y параболы или любой функции — это точка, где x=0. Это означает, что мы можем найти точку пересечения по оси y квадратичной функции, вычислив функцию, когда x=0.

Для квадратичной функции вида ax 2 +bx+c мы получаем a(0) 2 +b(0)+c=0+0+c.
Следовательно, точка пересечения с осью y равна (0, c).
Вершина
Вершина параболы является нижней точкой параболы, направленной вверх, и высшей точкой параболы, направленной вниз.
Вершиной параболы является точка ( -b / 2a , f( -b / 2a )). Обратите внимание, что когда у нас есть только функция x 2 , вершина является началом координат (0, 0).
Эта формула для нахождения вершины может показаться сложной, но на самом деле она связана с определенными точками на параболе. Однако, чтобы найти их, мы должны знать, как решать квадратные уравнения.
Как решать квадратные уравнения
«Решением» квадратного уравнения является значение x, для которого f(x)=0. То есть, если мы подставим значение x в уравнение для квадратного уравнения, оно упростится до 0. Это, в свою очередь, будут значения x точек пересечения x парабол, моделирующих f(x).

Обратите внимание, что не каждая параболическая функция имеет точку пересечения по оси x. Например, если вершина функции находится над осью абсцисс и функция направлена вверх, или если вершина находится ниже оси абсцисс и функция направлена вниз, парабола не будет пересекать ось абсцисс. Точно так же, если вершина функции лежит на оси x, функция будет иметь только одну точку пересечения с x. В противном случае функция будет иметь два x-перехвата.
Есть несколько способов найти эти значения x. Самый простой метод — разложение на множители, но мы также можем использовать квадратичную формулу для отрезков x, которые не являются целыми числами.
Факторинг
Некоторые квадратичные формулы вида f(x)=ax 2 +bx+c приводятся к форме (x+d)(x+f), где d и f — целые числа. Если квадратное уравнение может быть сокращено таким образом, график f (x) будет пересекать ось x в точках (-d, 0) и (-f, 0).
Это имеет смысл, потому что если два числа, a и b, таковы, что ab=0, либо a=0, либо b=0, либо оба.

Аналогично, если (x+d)(x+f)=0, то x+d=0 (и x=-d) или x+f=0 (и x=-f).
Чтобы найти d и f, нам нужно проанализировать исходное уравнение.2+(d+f)x+df. Поэтому мы ищем два числа, d и f, такие, что d+f=b и df=c.
Мы можем найти эти два числа, перечислив множители c и найдя два, которые в сумме дают b. Если это не очевидно после нескольких испытаний или двух таких целых чисел не существует, мы можем вместо этого использовать квадратичную формулу.
Квадратная формула
Квадратная формула дает нам решение задачи f(x)=0 при f(x)=ax 2 +bx+c. Это особенно полезно, когда а не равно 1, с имеет много множителей или числа d и f, удовлетворяющие вышеуказанным требованиям, не очевидны сразу.
В некоторых случаях фактически невозможно разложить функцию на множители. Например, рассмотрим квадратичную функцию x 2 +10x+1. 1 имеет только два делителя: 1, 1 и -1, -1. Ясно, что ни один из них не дает в сумме 10.
Здесь может пригодиться квадратичная формула.
 Квадратичная формула: x = (-b±√(b²-4ac)) / 2a . Да, это немного длинно, но запоминание этого может сэкономить много времени и нервов!
Квадратичная формула: x = (-b±√(b²-4ac)) / 2a . Да, это немного длинно, но запоминание этого может сэкономить много времени и нервов!У этой формулы есть два ответа: один для x= (-b+√(b²-4ac)) / 2a a и один для x= (-b-√(b²-4ac)) / 2а .Таким образом, две точки пересечения x уравнения равны ( (-b+√(b²-4ac)) / 2a , 0) и ( (-b-√(b²-4ac)) / 2a , 0).
Обратите внимание, что по-прежнему бывают ситуации, когда квадратичная формула не дает ни одной точки пересечения с х. Например, если x 2 -4(3)(2) отрицательно, мы должны взять квадратный корень из отрицательного числа, чтобы найти точку пересечения с x. Таким образом, единственные решения в подобных ситуациях находятся в комплексной системе счисления, а не в реальной системе счисления.
Линия симметрии
Мы можем использовать эти две точки пересечения, чтобы найти линию симметрии параболы.
 Это воображаемая вертикальная линия, которая делит параболу пополам. Это означает, что он пройдет через вершину параболы, поэтому он будет включать точку пересечения x с вершиной. Затем мы можем определить точку пересечения по оси y, найдя f(x).
Это воображаемая вертикальная линия, которая делит параболу пополам. Это означает, что он пройдет через вершину параболы, поэтому он будет включать точку пересечения x с вершиной. Затем мы можем определить точку пересечения по оси y, найдя f(x).Линия симметрии будет точно между двумя точками пересечения с х. Следовательно, линия симметрии также будет включать в себя среднюю точку двух точек пересечения с х.
Напоминаем, что середина двух точек будет ( (х 1 + х 2 ) / 2 0). Таким образом, мы можем вывести линию симметрии следующим образом:
( (-b+√(b²-4ac)) / 2a + (-b+√(b²-4ac)) / 2a )/2
Это упрощается до – (2b/2a) / 2 = -b/a / 2 = -b / 2a .
Таким образом, заключаем, что линия симметрии x= -b / 2a , а вершина равна ( -b / 2a , f( -b / 2a )).

Использование преобразований графика для построения квадратичного графика
Мы также можем подумать о построении графика квадратичной функции, рассматривая ее родительскую функцию и то, как преобразования графика влияют на эту родительскую функцию.
Простейшей формой квадратного уравнения является функция f(x)=x 2 , которая выглядит как график ниже.
Умножение этой функции на отрицательное значение отражает функцию по оси x, переворачивая параболу вверх ногами.
Сдвиг вершины
Мы можем добавить числа к квадрату функции, чтобы сместить вершину влево и вправо. Положительные числа сместят его влево, а отрицательные — вправо. Например, функция (x-1) 2 имеет вершину на единицу справа от родительской функции в точке (0, 1).
Точно так же мы можем перемещать вершину вверх и вниз, добавляя или вычитая числа после возведенной в квадрат части. В этом случае положительные числа сместят вершину вверх, а отрицательные — вниз.
 Например, x 2 +1 имеет вершину в точке (0, 1).
Например, x 2 +1 имеет вершину в точке (0, 1).Сжатие и расширение
Мы также можем изменить ширину или толщину графика. Чтобы растянуть функцию и сделать ее шире, мы умножаем значение x на число больше 1. Чтобы сжать функцию, мы умножаем ее на число от 0 до 1.
Примеры
В этом разделе мы перейдем к на типичных примерах вопросов, связанных с графиками квадратичных функций и их пошаговыми решениями.
Пример 1
Каковы точки пересечения по оси x графика квадратного уравнения f(x)=x 2 -12x+27?
Пример 1 Решение
Точка пересечения функции с осью x.Это точки (x1, 0) и (x2, 0). Помните, что не каждая квадратичная функция имеет две точки пересечения по оси x. У некоторых есть один, когда вершина лежит на оси X. Другие функции не имеют реальных x-перехватов. Например, если функция указывает вверх, а ее вершина лежит выше оси x, эта функция не будет иметь точки пересечения с x.
Самый простой способ найти эти точки — найти две точки d и f такие, что f(x)=(x+d)(x+f).
 В этом случае нам нужны два числа, такие что d+f=-12 и df=27.
В этом случае нам нужны два числа, такие что d+f=-12 и df=27.К счастью, множителей числа 27 очень мало:
1×27
-1×-27
3×9
-3×-9.
Поскольку значение b отрицательно, нам нужно учитывать только те факторы, которые оба отрицательны.
Из этих двух -1×-27 и -3×-9, -3+-9=-12=b. Следовательно, d=-3 и f=-9.
Теперь мы знаем, что можем разложить эту функцию на два члена (x-3) и (x-9).
Следовательно, когда любой из этих терминов равен 0, вся функция будет равна 0.Первый член равен 0, когда x=-3, а второй равен 0, когда x=9.
Таким образом, решения (то есть, когда f(x)=0) равны 3 и 9, поэтому точки пересечения x равны (3, 0) и (9, 0). Это точки пересечения параболы, моделирующей эту функцию.
Пример 2
Найдите вершину, точку пересечения по оси y и по оси x функции f(x)=x 2 +9x+8. Затем постройте график функции.
Пример 2 Решение
Сначала мы можем найти точку пересечения функции по оси y, найдя f(0)=c.
 В этом случае c=8, поэтому точка пересечения с осью y является точкой (0, 8).
В этом случае c=8, поэтому точка пересечения с осью y является точкой (0, 8).Теперь мы можем найти точки пересечения, если они существуют. Во-первых, давайте посмотрим, можем ли мы легко разложить выражение x 2 +9x+8 на (x+d)(x+f), где d+f=b и f=c. Самый простой способ сделать это требует, чтобы мы нашли делители 8.
-1, -8
1, 8
-2, -4
2, 4.
Нахождение суммы каждой из этих пар говорит нам, что 1+8=9, поэтому эти два числа удовлетворяют условиям для d и f.Таким образом, пересечения по оси x равны -d=-1 и -f=-8. Это означает, что точки пересечения x — это точки (-1, 0) и (-8, 0).
Наконец, нам нужно найти вершину этой параболы. Напоминаем, что x-координата вершины равна -b / 2a . Подстановка этих значений дает нам:
-9 / 2 .
Соответствующий y-отрезок равен
f( -9 / 2 )=( 81 / 4 )- 81 / 2 + 90.

Это упрощается до -49 / 4 .
Следовательно, вершина находится в точке ( -9 / 2 , -49 / 4 )=(-4,5, -12,25).
Поскольку значение a положительно, парабола будет направлена вверх.
Итак, мы знаем, что эта парабола имеет вершину (-4,5, -12,25) и проходит через точки (-1, 0), (-8, 0) и (0, 8). Таким образом, у нас достаточно информации для построения графика функции, и график показан ниже.
Пример 3
Определите точки пересечения по оси Y, точки по оси X и вершину функции, показанной ниже.
Пример 3 Решение
Как и прежде, мы должны начать с определения точки пересечения с осью y (0, c). В этом случае график пересекает ось Y в точке на три единицы выше начала координат. Следовательно, точка пересечения по оси y находится в точке (0, 3).
Далее мы должны определить x-перехваты этой функции. Видно, что график пересекает ось абсцисс в точках -3 и +1.
 Следовательно, точки пересечения по оси x равны (-3, 0) и (1, 0). Это означает, что если мы подставим -3 или 1 вместо x в алгебраическом выражении функции, оно упростится до 0.
Следовательно, точки пересечения по оси x равны (-3, 0) и (1, 0). Это означает, что если мы подставим -3 или 1 вместо x в алгебраическом выражении функции, оно упростится до 0.Наконец, нам нужно определить вершину этой функции. Проще всего это сделать, найдя среднюю точку между двумя пересечениями по оси x. Это будет точка, проходящая через ось симметрии, вертикальная линия, разрезающая параболу пополам и также пересекающая вершину. Здесь средняя точка между (-3, 0) и (1, 0) равна (-1, 0).
Следовательно, ось симметрии x=-1, а координата x вершины равна -1.
Теперь мы можем видеть, какая самая нижняя точка на графике равна -4.Таким образом, эта точка является вершиной (-1, -4).
Мы называем эти точки (вершину, точку пересечения по оси x, если они существуют, и точку пересечения по оси y) как ключевые точки графа.
В следующих примерах мы будем использовать ту же стратегию для получения алгебраического выражения для параболической функции.
Пример 4
Нарисуйте график функции с вершиной (0, 1) и точками пересечения x 1 и -1 и найдите соответствующее алгебраическое выражение.

Пример 4 Решение
Во-первых, давайте определим точку пересечения этой функции по оси Y.Функция пересекает ось x в точке (0, 1).
Интересно, что это тоже вершина этой функции. Это означает, что ось симметрии также является осью y, а точки пересечения x будут противоположны друг другу.
Глядя на ось x, видно, что функция пересекает ось в точках x=1 и x=-1.
Также стоит отметить, что парабола направлена вниз. Это означает, что значение a отрицательно.
Теперь нам нужно использовать эту информацию, чтобы найти алгебраическое представление этого графа.
Мы знаем, что вершина функции есть ( -b / 2a , f( -b / 2a )). Здесь мы знаем, что -b / 2a =0. Следовательно, b=0.
Точно так же мы знаем, что f(0)=1. Это означает с=1.
Мы можем использовать x-отрезки, чтобы найти значение a. Обратите внимание, однако, что если бы эта функция не имела точек пересечения по оси x, нам пришлось бы найти другие точки на графике, чтобы сделать это.

Имеем f(1)=0. Мы знаем, что функция имеет вид ax+1.Следовательно, а(1)+1=0. Решение для a говорит нам, что a=-1.
Таким образом, алгебраическая форма этой функции имеет вид -x 2 +1.
Пример 5
Нарисуйте график функции -x 2 -9x+6 и линии симметрии.
Пример 5 Решение
Опять же, нам нужно найти точку пересечения по оси Y, точку пересечения по оси X, если они существуют, и вершину.
Начнем с того, что отметим, что a отрицательно. Следовательно, нам нужно будет построить параболу, направленную вниз.
Далее находим точку пересечения по оси y, которая имеет вид (0, c).В этом случае c=6, а точка пересечения с осью y равна (0, 6).
Чтобы найти точки пересечения, мы начнем с выяснения, может ли функция быть разложена на два бинома. В этом случае множители 6 равны
1, 6
-1, -6
2, 3
-2, -3.
Ни один из них не добавляет к -9. Следовательно, нам придется использовать квадратичную формулу, чтобы найти точку пересечения с х.

Квадратная формула говорит нам, что
x= (-b±√(b²-4ac)) / 2a .
Подстановка значений дает нам:
(9±√(81+24)) / -2
(9±√(105)) / -2 , таким образом, наши два точки пересечения:
(-4,5+√(105)) / 2 и (-4,5-√(105)) / 2 .
Эти числа приблизительно равны -9,62 и 0,62. Линия симметрии проходит через точку на полпути между -9,62 и 0,62. То есть он проходит через x= (-9,62+0,62) / 2 = -9 / 2 = 4.5.
Таким образом, график и линия симметрии такие, как показано.
Пример 6
График функции 3x 2 -6x+2.
Пример 6 Решение
Опять же, мы начинаем с поиска ключевых точек, включая точку пересечения по оси Y, точку пересечения по оси X, если они существуют, и вершину. Заметим также, что поскольку а положительно, парабола будет направлена вверх.

В этой функции c=2. Следовательно, точка пересечения с осью y находится в точке (0, 2).
Теперь нам нужно найти точки пересечения.Поскольку значение а в этой функции больше 1, вероятно, проще всего их найти с помощью квадратичной формулы.
В этом случае имеем:
x= (6±√(36-4(3)(2)) / 6
x= (-1±√(12)) / 6.
Разделив два, получим:
x=1+ 1 / (3√3) или x=1- 1 / (3√3) .
Десятичные приближения этих двух чисел равны 1,58 и 0,42.
Наконец, вершина этой функции будет в точке x=- b / 2a В этом случае вершина будет иметь координату x 6 / ((2)(3) ) =1.Значение y будет равно f(1)=3-6+2=-1.
Таким образом, вершина равна (1, -1).
Таким образом, график функции выглядит следующим образом.
Предыдущий урок | Главная страница | Следующий урокКак вы решаете квадратные уравнения графическим методом?
Как вы решаете квадратные уравнения графическим методом?
Как графически решать квадратные уравнения с использованием точек пересечения x
- Используйте график y = x2 + x — 6, чтобы решить x2 + x — 6 = 0.

- Используйте график y = -x2 + 4, чтобы решить -x2 + 4 = 0.
- Используйте график y = x2 -2x + 1, чтобы решить x2 -2x + 1.
- Используйте график y = x2 + 1 для решения x2 + 1.
Что значит решить квадратное уравнение графически?
Основная идея решения с помощью графика заключается в том, что, поскольку (действительных чисел) решений любого уравнения (включая квадратные уравнения) являются точками пересечения по оси x этого уравнения, мы можем посмотреть точки пересечения по оси x на графике, чтобы найти решения соответствующего уравнения.
Как вы решаете квадратные уравнения с B?
9:3312:28Как решать квадратные уравнения с помощью факторинга — быстро и просто …YouTubeНачало предложенного клипаКонец предложенного клипа Итак, B равно 2, что означает, что B в квадрате будет положительным 4 минус 4, умноженное на aa, равно 8 C отрицательноеMoreSo B равно 2, что означает, что B в квадрате будет положительным 4 минус 4, умноженное на aa, равно 8 C равно отрицательному числу 15, разделенному на 2a, или 2, умноженное на 8, что равно 16.
 Итак, это отрицательное 2 плюс или минус квадратный корень.
Итак, это отрицательное 2 плюс или минус квадратный корень.Какое уравнение является исходным для квадратного уравнения?
Родительская функция квадратичного семейства f(x) = x2 . Преобразование графика родительской функции представлено функцией g(x) = a(x − h)2 + k, где a ≠ 0,
Что такое корни квадратного уравнения?
Корни также называются x-перехватами или нулями . Квадратичная функция графически изображается параболой с вершиной, расположенной в начале координат, ниже оси x или выше оси x…. Корни функции — это x-перехваты. По определению координата y точек, лежащих на оси x, равна нулю.
Как решить квадратное уравнение?
Решение квадратных уравнений
- Поместите все члены с одной стороны от знака равенства, оставив ноль с другой стороны.
- Фактор.
- Установить каждый коэффициент равным нулю.
- Решите каждое из этих уравнений.

- Проверьте, вставив свой ответ в исходное уравнение.
Как легко решать квадратные уравнения?
0:005:22Как решать простые квадратные уравнения — YouTubeYouTube
Можно ли решить квадратное уравнение графическим методом?
Мы можем решить квадратное уравнение, разлагая на множители, дополняя квадрат, используя квадратную формулу или используя графический метод. По сравнению с другими методами графический метод дает только оценку решения (решений).2 + bx + c \), решениями уравнения являются значения x-координат точек пересечения графика с осью x.
Какое решение квадратной формулы x = 3?
Обратите внимание, что график не пересекает ось x, а касается оси x в точке x = 3. Это означает, что уравнение 6x – 9 – x 2 = 0 имеет одно решение (или одинаковые корни) x = 3. Напомним, что в квадратной формуле в таком случае, когда корни равны, дискриминант b 2 – 4ac = 0.Решить уравнение x 2 + 4x + 8 = 0 графическим методом.

Что нужно знать о графическом решении уравнений?
Знание построения линейных и квадратичных графиков необходимо для графического решения уравнений. Чтобы найти решения по графикам, ищите точку пересечения двух графиков. Это точка решения. Например, решением для графиков (y = x + 1) и (x + y = 3) является координатная точка (1, 2).
⇐ Почему Питер Гэбриэл покинул Бытие? Как рассчитывается индекс Пааше? ⇒Похожие сообщения:
Квадратные уравнения | Сыграйте в обучающую игру
Сегодняшний кахут дня — это «Квадратные уравнения» от sksnokahoots. Вы можете предварительно просмотреть его, воспроизвести или даже адаптировать для своих учеников! Чтобы помочь вам научиться делать отличные математические кахуты, подобные этому, мы добавили несколько заметок ниже о том, что нам в нем понравилось.
 Happy Kahoot! 🙂
Happy Kahoot! 🙂1. Одной из самых распространенных ошибок при решении квадратных уравнений является забывание обнуления уравнения. Этот проницательный Kahoot!’er решает проблему, добавляя напоминание прямо на экран запуска!
2. Студенты, изучающие алгебру, вполне могут запомнить квадратное уравнение, не зная, что оно на самом деле означает, и не визуализируя график. Нам очень нравится, как создатель начал с быстрого обновления того, чем НЕ является квадратичный график, прежде чем погрузиться в квадратичные графики и уравнения.
ПОЛЕЗНЫЙ СОВЕТ. Этот вопрос — отличная возможность выявить пробелы в знаниях. Кто-нибудь неправильно понял этот вопрос? Нажмите «Показать изображение», чтобы снова открыть график, и уделите некоторое время объяснению различий между линейными, полиномиальными, экспоненциальными и квадратичными графиками.
3. В каждом вопросе есть тонкое маленькое напоминание о том, что «квадрат» — это то, что придает квадратному уравнению его… э-э… квадратичность.
 (квадрат = квадрат… понял?) В повторении заключена великая сила, поэтому повторение основных математических фактов вроде этого — понемногу, но часто — отличный способ закрепить знания.
(квадрат = квадрат… понял?) В повторении заключена великая сила, поэтому повторение основных математических фактов вроде этого — понемногу, но часто — отличный способ закрепить знания.4. Проверьте настройки таймера! Для сложных вопросов, таких как на самом деле решение квадратных уравнений, этот Kahoot!’er позаботился о том, чтобы у учеников было время взять карандаш и бумагу и обработать свои ответы, а не просто угадывать.
5. Использование правильных тегов — такая маленькая деталь, которую часто упускают из виду. Этот Kahoot!’er позволяет людям, изучающим или преподающим алгебру, легко найти именно то, что они ищут.
Советы по игре или адаптации этого Math kahoot
- Убедитесь, что у каждого есть под рукой карандаш и бумага – квадратные уравнения, как известно, сложно решить в уме!
- При запуске на большом экране или интерактивной доске замените изображения четкими изображениями с высоким разрешением.




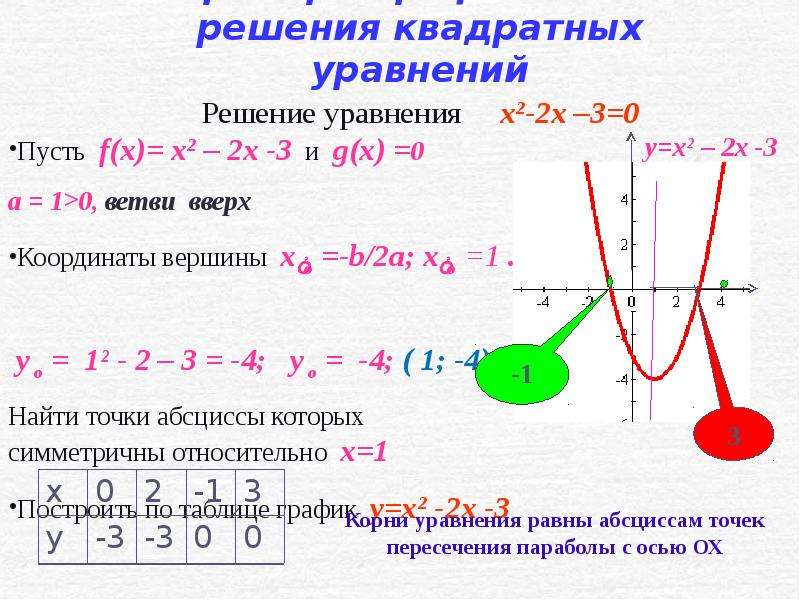 В частности, нас интересуют вершина, точка пересечения по оси y, точка пересечения с осью x и общая форма графа.
В частности, нас интересуют вершина, точка пересечения по оси y, точка пересечения с осью x и общая форма графа.



 Квадратичная формула: x = (-b±√(b²-4ac)) / 2a . Да, это немного длинно, но запоминание этого может сэкономить много времени и нервов!
Квадратичная формула: x = (-b±√(b²-4ac)) / 2a . Да, это немного длинно, но запоминание этого может сэкономить много времени и нервов! Это воображаемая вертикальная линия, которая делит параболу пополам. Это означает, что он пройдет через вершину параболы, поэтому он будет включать точку пересечения x с вершиной. Затем мы можем определить точку пересечения по оси y, найдя f(x).
Это воображаемая вертикальная линия, которая делит параболу пополам. Это означает, что он пройдет через вершину параболы, поэтому он будет включать точку пересечения x с вершиной. Затем мы можем определить точку пересечения по оси y, найдя f(x).
 Например, x 2 +1 имеет вершину в точке (0, 1).
Например, x 2 +1 имеет вершину в точке (0, 1). В этом случае нам нужны два числа, такие что d+f=-12 и df=27.
В этом случае нам нужны два числа, такие что d+f=-12 и df=27.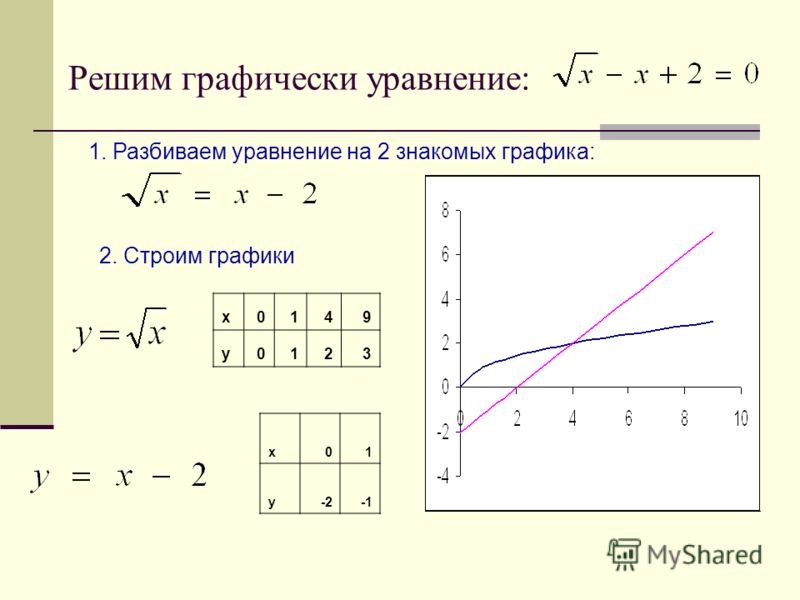 В этом случае c=8, поэтому точка пересечения с осью y является точкой (0, 8).
В этом случае c=8, поэтому точка пересечения с осью y является точкой (0, 8).
 Следовательно, точки пересечения по оси x равны (-3, 0) и (1, 0). Это означает, что если мы подставим -3 или 1 вместо x в алгебраическом выражении функции, оно упростится до 0.
Следовательно, точки пересечения по оси x равны (-3, 0) и (1, 0). Это означает, что если мы подставим -3 или 1 вместо x в алгебраическом выражении функции, оно упростится до 0.




 Итак, это отрицательное 2 плюс или минус квадратный корень.
Итак, это отрицательное 2 плюс или минус квадратный корень.

 Happy Kahoot! 🙂
Happy Kahoot! 🙂 (квадрат = квадрат… понял?) В повторении заключена великая сила, поэтому повторение основных математических фактов вроде этого — понемногу, но часто — отличный способ закрепить знания.
(квадрат = квадрат… понял?) В повторении заключена великая сила, поэтому повторение основных математических фактов вроде этого — понемногу, но часто — отличный способ закрепить знания.