Решение квадратных уравнений графическим способом
Урок по алгебре в 8 классе
«Решение квадратных уравнений графическим способом»
Учитель математики
Дрозд Екатерина Георгиевна
Алгебра
8 класс
Тема: «Решение квадратных уравнений графическим способом»
Цели урока:
1. Образовательные: познакомить учащихся с графическим способом решения квадратных уравнений, повторить ранее изученные методы решения квадратных уравнений, виды графиков и свойства функций у = 
2. Развивающие: развивать навыки творческой, познавательной, мыслительной деятельности, логическое мышление, вырабатывать умение анализировать и сравнивать.
3. Воспитательные: воспитывать сознательное отношение к учебному труду, развивать интерес к математике, самостоятельность, прививать аккуратность и трудолюбие.
Оборудование: мультимедийный проектор, компьютеры, карточки с дифференцированными заданиями, сигнальные карточки.
Тип урока: урок формирования знаний.
Вид урока: урок – практикум.
Методы урока: словесные, наглядные, практические.
Организационные формы общения: индивидуальная, парная, коллективная.
Структура урока:
1. Мотивационная беседа с последующей постановкой цели.
2. Актуализация опорных знаний – устная работа, с помощью которой ведётся повторение основных фактов, свойств на основе систематизации знаний.
3. Изучение нового материала – рассматривается ещё один способ решения квадратных уравнений – графический.
4. Закрепление изученного материала.
5. Практическая работа с использованием компьютеров.
6. Обогащение знаний – знакомство с траекториями движения космических аппаратов
7. Подведение итогов урока.
8. Творческое домашнее задание.
9. Рефлексия.
Ход урока.
I. Мотивационная беседа.
Учитель: Как вы думаете, зачем надо изучать математику?
Ответ на этот вопрос вы найдёте, если узнаете, что означает в переводе с греческого слово «математика». «Математика» — знание, наука. Именно поэтому, если человек был умен в математике, то это всегда означало высшую ступень учености. А умение правильно видеть и слышать – первый шаг к мудрости. Вот поэтому мне сегодня очень хочется, чтобы вы стали немного мудрее и расширили свои знания по математике.
Итак, запишите в тетрадь число и тему урока. Сегодня необычный день, 25 января – Татьянин день. Это день всех студентов, день молодости.
Цель урока — познакомить вас еще с одним способом решения квадратных уравнений – графическим, закрепить этот способ решения практической работой с использованием компьютеров.
У вас находятся одинаковые трафареты, состоящие из 10 комбинаций, которые обозначены римскими цифрами.
I II III IV V
VI VII VIII
IX X
В каждую клетку нужно вписать букву или знак препинания. Тогда сложится фраза. Но на трафарете нет места для самого первого слова зашифрованной фразы. Это слово мы получим, решив графические уравнения. У нас получится крылатое изречение из романа А. С. Пушкина «Евгений Онегин». Следует вам ответить на соответствующие тестовые задания I –X и вписать в трафарет знак или букву, которой обозначен верный ответ.
Тестовые задания.
II. Актуализация опорных знаний.
1. Линию, являющуюся графиком функции у = х2, называют…
?) синусоидой; 🙂 гиперболой; …) параболой.
I
…
2. Составьте слово, назвав подряд буквы, соответствующие правильному ответу. Является ли функция у = х
е) а = — 3; в = 3;
к) а = 1; в = 4;
д) а = — 2; в = — 1;
а) а = 0; в = 0,5;
к) а = 9; в = 10;
б) а = — 9; в = 10;
II
к
а
к
3. Назовите буквы, соответствующие точкам, принадлежащим графику функции у = х2 :
М(3; 9), Ж(5; 5), С(-100; -100), Н(-2; 4), О1 (-1; 1),
Г(0; 0), В(-7; 7), А(2; 8), О2(2; 4).
III
м
н
о
г
о
4. Графиком функции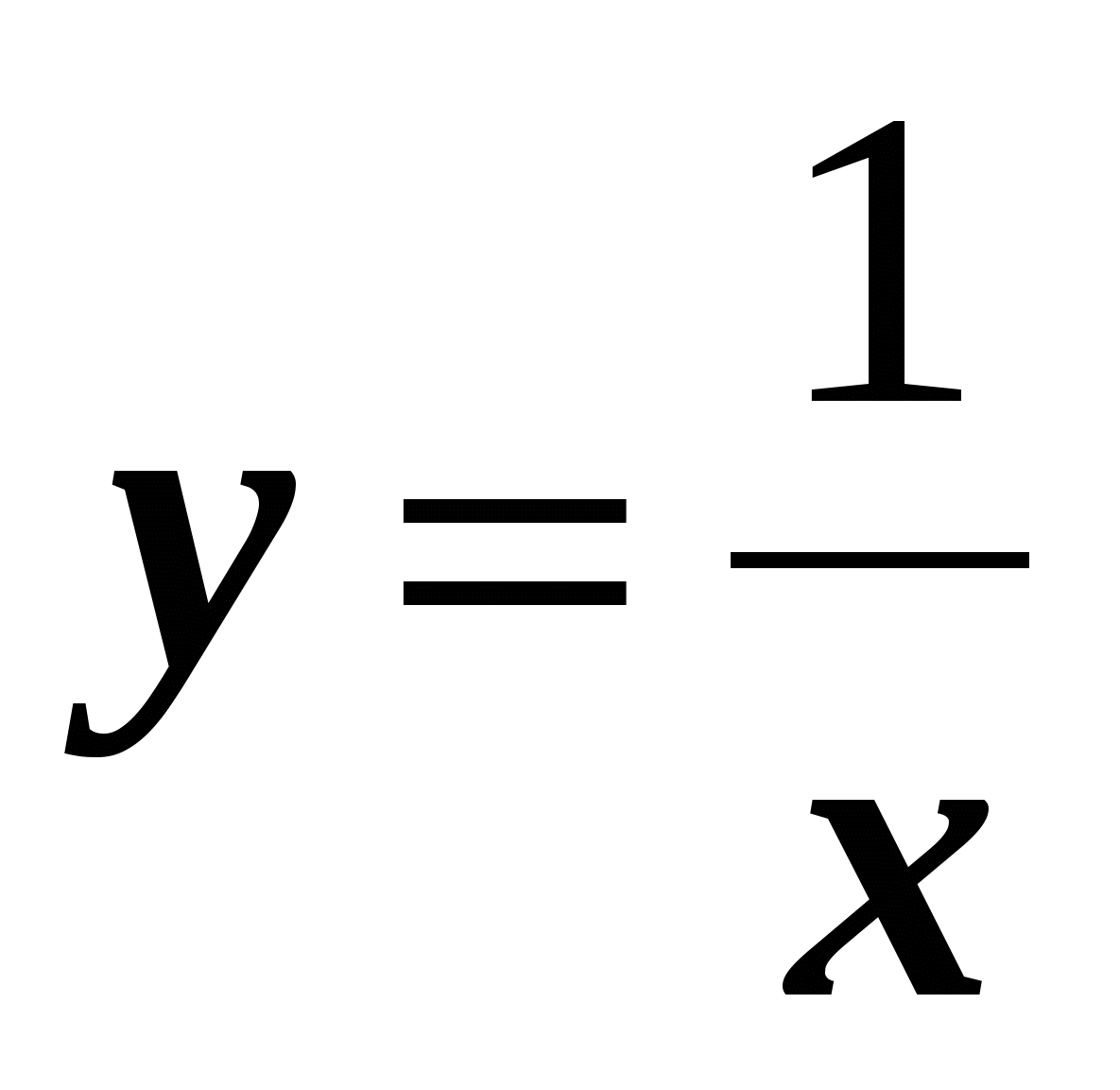 
является …
а) прямая; б) отрезок; в) гипербола; г) ветвь параболы.
IV
в
5. Назовите буквы, которые соответствуют правильному ответу.
а) Какие из данных уравнений являются квадратными?
в) 5х + 1 = 0. к) х3 – 2х2 + 1 = 0. н) 5 – 8х = 0.
э) 2х2 – 9х + 5 = 0. з) 2х ─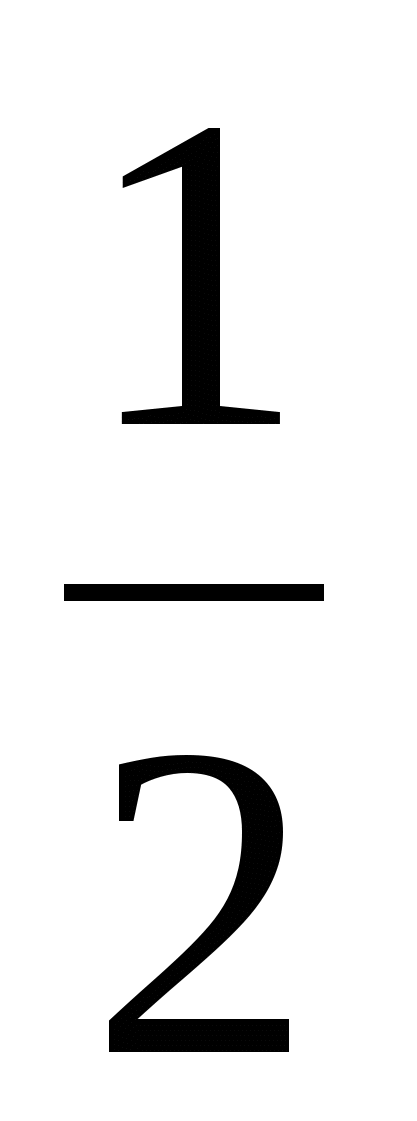 
= 0. м) х2 + 3х + 2 = 0.
т) 3х2 – 5х – 8 = 0. о) х2 + 5х – 6 = 0.
V
э
т
о
м
б) Какие из данных квадратных уравнений являются приведенными?
к) 2х2 – 9х + 5 = 0. в) х2 – 4х2 + 3 = 0. о) 3х2 + 5х + 2 = 0.
л) 3х2 – 4х – 7 = 0. ф) 3х2 – 2х – 5 = 0. к) х2
з) х2 – 14х + 49 = 0. у) х2 – 10х + 25 = 0. е) х2 + 11х – 12 = 0.
VI
з
в
у
к
е
III. Изучение нового материала.
Решим уравнение: х2 + 2х – 3 = 0.
Какое это уравнение?
Как это уравнение можно решить?
Ответ: С помощью формул, с помощью теоремы Виета.
Можно его решить устно?
Ответ: Можно, по теореме Виета.
Какие же корни?
Ответ: -3 и 1.
Я сегодня покажу ещё один способ решения – графический. Представим данное уравнение в следующем виде:
х2 = ─ 2х + 3.
Чтобы решить данное уравнение, нужно найти такое значение х, при котором левая часть уравнения была бы равна правой. Введем две функции f(x), равной левой части уравнения и g(x), равной правой части уравнения. Теперь нужно найти такое значение х, при котором f(x)=g(x), т. е. общую точку, принадлежащую графику функции f(x) и графику функции g(x). Эта точка будет являться точкой пересечения графиков функций f(x)=х 2 и g(x)=-2х+3. Абсцисса точки пересечения будет являться решением исходного уравнения.
В координатной плоскости построим графики функций f(x) = х2 и
g(x) = ─2х + 3.
Для этого составим таблицы их значений.
f(x) = х2─ парабола
х
0
+1
+2
+3
у
0
1
4
9
[-3; 3]
g(x) = ─2х + 3 ─ прямая
х
-3
у
9
1
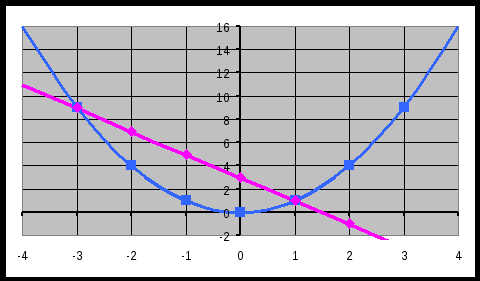
А
В
х = -3, х = 1.А(-3;9) и В(1;1)-точки пересечения. Абсциссы этих точек равны -3 и 1.
Значит х = -3 и х = 1 – решение уравнения х2 + 2х – 3 =0
Ответ: так) х = ─ 1 и х = 3
для) х = ─ 3 и х = 1
вот) х = ─ 5 и х = 0
VII
д
л
я
Рассмотрим алгоритм решения.
Алгоритм решения:
1. дано уравнение х2 + 2х – 3 = 0.
2. представим уравнение в следующем виде х2 = ─ 2х + 3.
3. в одной системе координат строятся графики функций
у1 = х2 и у2 = ─ 2х + 3.
4. абсциссы точек пересечения являются решением данного уравнения
IV. Закрепление изученного материала.
1). Решить уравнение х2 – х – 2 = 0. x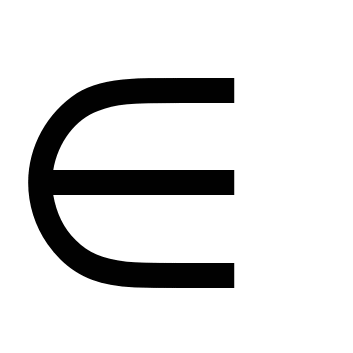 
[-5; 5] с шагом 0,5
у1 = х2 у2 = х + 2
Ответ: души) х = — 2 и х = 1
школы) х = 3 и х = 1
сердца) х = 2 и х = — 1.
VIII
с
е
р
д
ц
а
2). Решить самостоятельно.
а) один ученик решает графически;
б) другой ученик решает аналитически с помощью теоремы Виета.
Ответ : широкого) х = 5 и х = 1;
русского) х = 4 и х = — 2;
красного) х = 3 и х = — 1.
IX
р
у
с
с
к
о
г
о
а) один ученик решает графически;
б) другой ученик решает аналитически с помощью квадратных корней
Ответ: слилось) х = 1 и х = -1,5;
расцвело) х = 3 и х = — 2;
приснилось) х = -1 и х = 2.
X
с
л
и
л
о
с
ь
Физминутка.
Отвели свой взгляд направо,
Отвели свой взгляд налево,
Оглядели потолок,
Посмотрели все вперёд.
Раз – согнуться – разогнуться,
Два ─ согнуться – потянутся,
Три – в ладоши три хлопка,
Головою три кивка.
Пять и шесть тихо сесть.
V. Практическая работа.
Раздаются учащимся дифференцированные задания на карточках.
С помощью графиков нескольких функций, построенных на заданных промежутках, получаются буквы: М; О; С; К; В; А. и фигуры: КИТ; ЗОНТИК; ОЧКИ. (см. приложение к уроку).
Учитель: Какие буквы у вас получились?
Ответы учащихся: М О С К В А
Учитель: Получилась фраза А.С. Пушкина из романа «Евгений Онегин» «Москва… как много в этом звуке для сердца русского слилось».
(Как часто в горестной разлуке,
В моей блуждающей судьбе,
Москва, я думал о тебе!
Москва … как много в этом звуке
Для сердца русского слилось!
Как много в нём отозвалось.)
VI. Обогащение знаний.
Высвечивается слайд, на котором находится парабола и гипербола.
а) мы сегодня на уроке применяли эти два графика: параболу и гиперболу.
Я хочу вам сказать ребята, что окружающий нас мир тесно связан с математикой. Валерий Чкалов говорил: «Полёт–это математика». Оказывается, траектории движения космических аппаратов описываются параболой, гиперболой, эллипсом. При первой космической скорости (7,91 км/с) космический аппарат движется по эллипсу относительно Земли. (на рис. орбита 3) При второй космической скорости (11,2 км/с) аппарат движется по параболе (на рис. орбита4) и движется в пределах Солнечной системы. При третьей космической скорости (16,6 км/с) космические аппараты движутся по гиперболе (на рис. орбита5) и навсегда покидают пределы Солнечной системы. В 70-х годах ХХ века были запущены такие космические аппараты «Пионер-10», «Пионер-11»,которые навсегда покинули Солнечную систему в поисках разумных цивилизаций во Вселенной. Они несут в себе платиновые пластинки, на которых нанесены силуэты мужчины и женщины на фоне космического корабля, Солнечная система и траектория «Пионера», схема атома водорода и положение Солнца по отношению к наиболее ярким галактическим пульсарам.
б) графики помогают нам наглядно увидеть изменения различных величин: изменение роста, веса, температуры, скорости и т.д.
Вот посмотрите на эти графики, характеризующие ваш класс:
1. График успеваемости (Знание – сила. Кто много читает, тот много знает – пословица.
2. График роста, график веса учащихся 8-го класса.
Чтобы достичь нормального веса и роста подростку 15-ти лет нужно заниматься спортом, вести здоровый образ жизни, не увлекаться пагубными привычками: алкоголем, табакокурением, наркотиками. Никогда не забывать пословицу «В здоровом теле здоровый дух»
VII. Подведение итогов урока.
Вы замечательно поработали на уроке. Проверив ваши работы и учитывая ваши ответы за устную работу, я поставила вам оценки в индивидуальную таблицу.
Каждый ученик класса принимал участие в уроке. Во время урока заполняется индивидуальная таблица, в которой виден результат его работы на уроке.
Ф.И
Устная работа
Практическая
работа
Общая
оценка
Надеюсь, этот материал вы не забудете. Помните слова французского инженера-физика Лауэ: «Образование есть то, что остается, когда все выученное уже забыто». Думаю, что образование, которое вы получите, будет соответствовать времени, в котором мы живем. А чтобы это случилось на самом деле, предлагаю вам выполнить следующую творческую домашнюю работу.
VIII. Домашнее задание.
Творческое задание: составить рекламу параболе или гиперболе;
сочинить сказку или рассказ на тему «Замечательные
кривые».
IX. Рефлексия.
В конце урока проводится беседа, в которой выясняется:
— Что нового узнали на уроке?
— Понравился ли урок? (с помощью сигнальных карточек)
— Что понравилось на уроке?
— Что не понравилось?
— Что необходимо изменить, чтобы было еще интереснее?
Решение квадратных уравнений графическим способом
Урок алгебры по теме «Графическое решение квадратных уравнений». 8 класс
Филиппова Жанна Михайловна, учитель математики
Цели урока:
Образовательные:
Закрепить умение строить графики различных функций.
Формировать умение решать квадратные уравнения графическим способом
Развивающие:
Развить творческие способности у учащихся в ходе выполнения самостоятельных творческих работ.
Развить умение обосновывать своё решение.
Развивать умение находить свои ошибки
Воспитательные:
Развивать умение вести индивидуальную, групповую дискуссию, самостоятельного поиска решения, конструирования обобщённого способа решения новой задачи.
Формировать ответственность каждого за конечные результаты работы в группе, этичного поведения при обсуждении, ораторского мастерства, самооценки качества своего труда.
Формирование графической культуры
Оборудование: плакаты с изображением координатной плоскости, карточки с заданиями, проектор.
Структура урока:
Организационный момент (3 мин).
Постановка цели урока (3 мин).
Подготовка к изучению нового материала через повторение и актуализацию опорных знаний (5 мин).
Ознакомление с новым материалом (15 мин).
Осмысление и закрепление связей и отношений в объектах изучения. Работа в группах (15 мин).
Постановка задания на дом (2 мин).
Подведение итогов (2 мин).
Ход урока
1. Организационный момент.
Разделить учащихся на группы, используя жетоны. (Создать группы).
2. Постановка цели урока.
Учитель: Тема сегодняшнего урока «Графическое решение квадратных уравнений». (Слайд №1)
(Ученики записывают тему в тетрадь.)
Учитель: Сформулируйте цели урока. (Слайд №2)
Ученики отвечают: Познакомиться с графическим решением квадратных уравнений, научиться решать этим способом, повторить построение графиков различных функций.
3. Актуализация опорных знаний.
Учитель: Подскажите, пожалуйста, о чём мы говорили, что делали на прошлых занятиях.
(Ученики отвечают.)
Учитель: Посмотрите на слайд. Что общего у всех этих графиков? В чём отличия? А что общего у этих графиков? (Слайд №3) В чём отличия? Молодцы. Вспомним алгоритм построения параболы. (Слайд №4)
Учитель: Рассмотрим следующую математическую модель. (Слайд №5) Что из себя представляет этот математический объект?
Ученики отвечают: Уравнение. Левая часть – график квадратичной функции. Правая часть – график обратной пропорциональности.
Учитель: Поработаем с этой моделью:
Введём функции.
Построим в одной системе координат графики этих функций.
Установим по графику точки пересечения.
Выполняем проверку.
Записываем ответ.
(По окончании решения проверка на слайде №5.)
4. Ознакомление с новым материалом.
Учитель: А сейчас, каждая группа решит ещё уравнение.
(Учитель раздаёт карточки с уравнением и заданием построить график функции. (Приложение 2) По окончании решения, учащийся от каждой группы, комментируя, выполняет чертёж графиков функций на плакате. Записывает корни данного уравнения. Проверка (Слайды №6-№10). Учитель, вывешивает условия всех групп.)
Учитель: Что объединяет все эти уравнения и функцию?
Ученики отвечают: Возможно они получены из одного общего уравнения – квадратного
x2 + 2x – 8 = 0.
Учитель: Так как же можно решить данное квадратное уравнение? (Слайд №11) Попытайтесь выполнить преобразование другого уравнения. (Слайд №12) Последующая проверка (Слайде №13).
Учитель: Сделаем вывод: для того чтобы решить графически квадратное уравнение можно воспользоваться одним из пяти способов. (Слайды №14-№18)
(Учащиеся каждой группы комментируют графики каких функций они строили. На столах у учащихся опорные конспекты (Приложение 3) на которых все пять способов.)
Учитель: Какой из этих способов менее трудоёмкий по вашему мнению? Сколько имеет решений данное уравнение?
5. Закрепление полученных знаний.
Учитель: А сейчас, используя один из способов, определите, сколько корней имеет уравнение?
(Учитель раздаёт карточки с уравнением каждой группе. (Приложение 3) По окончанию решения проверка. (Слайды №19-№24)
Учитель: Какие трудности возникли у вас при выполнении этого задания?
Ученики отвечают: По графику не видны точные значения, размеры листа не позволяют отмечать большие координаты.
Учитель: Отметьте в опорном конспекте какой способ для вас удобен и выполните номера из задачника: №23.4 (а,б), №23.7(а, б).
(Учитель помогает, если есть необходимость учащимся. По окончании работы идёт взаимопроверка – учащиеся обмениваются тетрадями между группами. Выставляют отметки карандашом и заносят в зачётный лист).
По окончании всей работы учитель просит не забыть группы выставить отметки за работу на уроке в зачётные листы.
6. Домашнее задание: №23.5 (в, г), №23.6(а, б), Решите уравнение 3х2+5х+2=0 пятью способами.
7. Итог. (Слайд №25)
В конце урока учитель спрашивает ребят, о том как они поняли объяснение новой темы.
Приложение №1
1. 2.
3. 4.
5. 6.
7. 8.
9. 10.
11. 12.
13. 14.
15. 16.
17. 18.
19. 20.
21. 22.
23. 24.
Приложение №3
1. Сколько корней имеет уравнение y=x2-4x+6?
2. Сколько корней имеет уравнение y= x2-6x+9?
3. Сколько корней имеет уравнение y= x2-15x-80?
4. Сколько корней имеет уравнение y= x2+4x+3?
Сколько корней имеет уравнение y= x2—x-4?
8 класс. Решение квадратных уравнений графическим способом
Мамедова Азельма Билаловна
МАОУ «Видновская гимназия»
Алгебра
8 класс
Тема: «Решение квадратных уравнений графическим способом»
Цели урока:
1. Образовательные: познакомить учащихся с графическим способом решения квадратных уравнений, повторить ранее изученные методы решения квадратных уравнений, виды графиков и свойства функций у =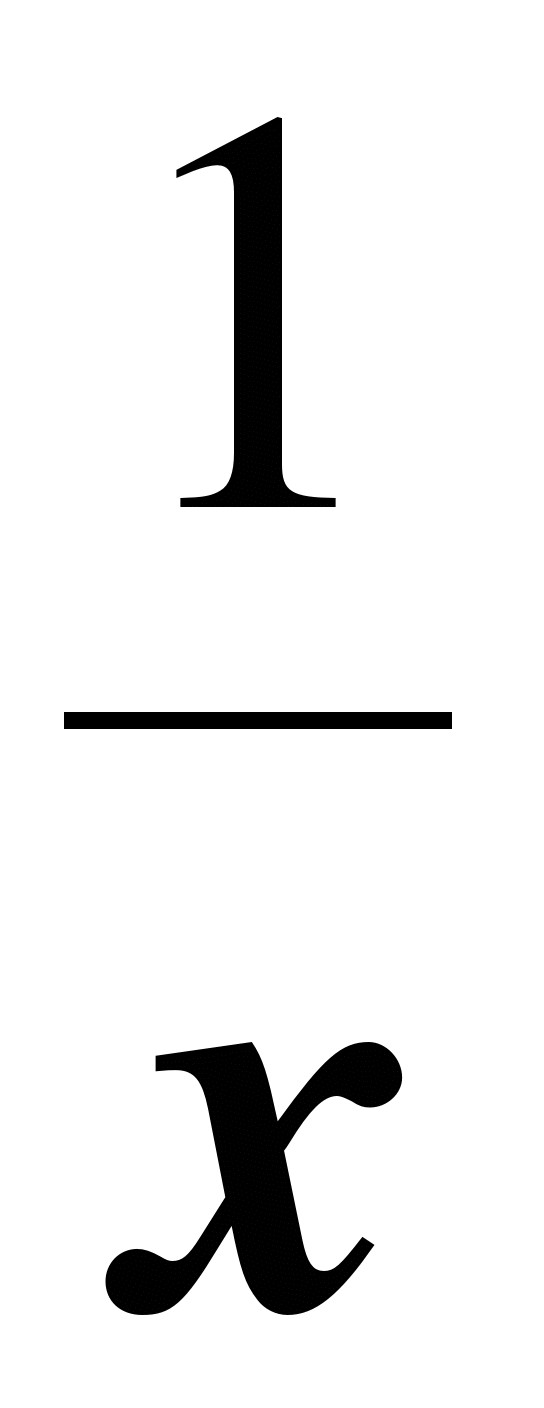 
, у = х2, закрепить навыки построения графиков функций.
2. Развивающие: развивать навыки творческой, познавательной, мыслительной деятельности, логическое мышление, вырабатывать умение анализировать и сравнивать.
3. Воспитательные: воспитывать сознательное отношение к учебному труду, развивать интерес к математике, самостоятельность, прививать аккуратность и трудолюбие.
Ход урока
1. Актуализация опорных знаний.
1. Линию, являющуюся графиком функции у = х2, называют…
?) прямой; 🙂 гиперболой; …) параболой.
2. Назовите буквы, соответствующие точкам, принадлежащим графику функции у = х2 :
М(3; 9), Ж(5; 5), С(-100; -100), Н(-2; 4), О1 (-1; 1),
Г(0; 0), В(-7; 7), А(2; 8), О2(2; 4).
4. Графиком функции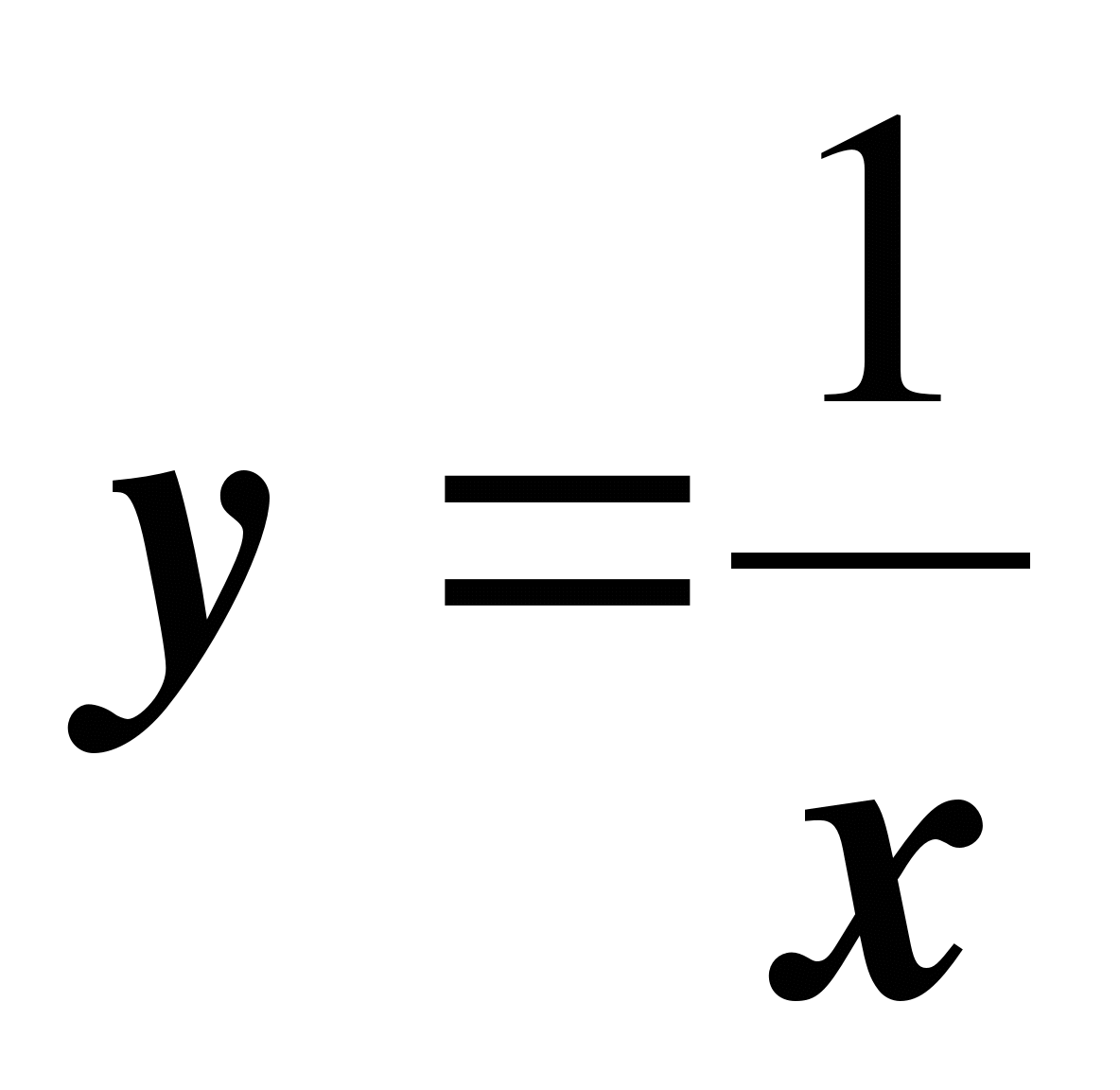 
является …
а) прямая; б) отрезок; в) гипербола; г) ветвь параболы.
2. Изучение нового материала.
Решим уравнение: х2 + 2х – 3 = 0.
Какое это уравнение?
Как это уравнение можно решить?
Ответ: С помощью формул, с помощью теоремы Виета.
Можно его решить устно?
Ответ: Можно, по теореме Виета.
Какие же корни?
Ответ: -3 и 1.
Я сегодня покажу ещё один способ решения – графический. Представим данное уравнение в следующем виде:
х2 = ─ 2х + 3.
В координатной плоскости построим графики функций f(x) = х2 и
g(x) = ─2х + 3.
Для этого составим таблицы их значений.
g(x) = ─2х + 3 ─ прямая
А
В
х = -3, х = 1.
А(-3;9) и В(1;1)-точки пересечения. Абсциссы этих точек равны -3 и 1.
Значит х = -3 и х = 1 – решение уравнения х2 + 2х – 3 =0
Рассмотрим алгоритм решения.
Алгоритм решения:
1. дано уравнение х2 + 2х – 3 = 0.
2. представим уравнение в следующем виде х2 = ─ 2х + 3.
3. в одной системе координат строятся графики функций
у1 = х2 и у2 = ─ 2х + 3.
4. абсциссы точек пересечения являются решением данного уравнения
3. Закрепление изученного материала.
1). Решить уравнение х2 – х – 2 = 0. x 
[-5; 5] с шагом 0,5
у1 = х2 у2 = х + 2
2). Решить самостоятельно.
а) один ученик решает графически;
б) другой ученик решает аналитически с помощью теоремы Виета.
4. Подведение итогов урока.
5. Домашнее задание: составить рекламу параболе и гиперболе.
Презентация к уроку по алгебре (8 класс) по теме: Графические способы решение квадратных уравнений.
Разработка урока «Графическое решение квадратных уравнений»
- Тихомирова Любовь Алексеевна
- учитель математики
Я. А. Коменский : «Учиться нелегко, но интересно».
(чешский педагог-гуманист, писатель, общественный деятель, епископ Чешско братской церкви, основоположник научной педагогики, систематизатор и популяризатор классно-урочной системы.)
Цели урока:
- Формировать умения и навыки в решении квадратных уравнений графически;
- Расширение кругозора учащихся; развитие мышления, умения работать в парах;
- Воспитание общей культуры, взаимовыручки.
Ход урока
I. Организационный момент
Приветствие учащихся.
Тема нашего урока: » Графическое решение квадратных уравнений «. Мы рассмотрим несколько графических способов решения квадратных уравнений. А значит, нам нужно вспомнить графики каких функций мы уже умеем строить в координатной плоскости. Остановимся на построении графика квадратичной функции.
Математический диктант. (интерактивная доска)
1 вариант
1. Какая из следующих функций является квадратичной: а) ; б)
2. Назовите коэффициенты а, в, с квадратичной функции:
3. Назовите коэффициенты а, в, с квадратичной функции:
4. Составьте квадратный трехчлен , у которого а = 9,в = -3, с = -1
5. Не выполняя построения, ответьте на вопрос, куда (вверх или вниз) направлены ветви параболы у =
6. Запишите уравнение прямой, которая является осью симметрии параболы
7. Найдите координаты вершины параболы
2 вариант
1. Какая из следующих функций является квадратичной: а) ; б)
2. Назовите коэффициенты а, в, с квадратичной функции:
3. Назовите коэффициенты а, в, с квадратичной функции:
4. Составьте квадратный трехчлен , у которого а = 2, в = -1, с = 4
5. Не выполняя построения, ответьте на вопрос, куда (вверх или вниз) направлены ветви параболы у =
6. Запишите уравнение прямой, которая является осью симметрии параболы
7. Найдите координаты вершины параболы
Взаимопроверка. (учащиеся в парах обмениваются тетрадями)
II. Актуализация знаний (интерактивная доска)
Для решения квадратных уравнений графическим способом существует несколько вариантов.
- Способ.
Решить уравнение: х2-2х-3=0
А) Построим график функции у=х2-2х-3 – функция квадратичная, графиком является парабола, ветви которой направлены вверх.
Б)Найдём координаты вершины параболы А(х0;у0): а=1; в=-2
Х0=, У0=12-2∙1-3=-4
Осью симметрии является прямая х=1
в) Возьмём на оси х две точки, симметричные относительно оси параболы, например х= -1 и х=3. Имеем f(-1)=0; f(3)=0. Построим на координатной плоскости точки (-1;0), (3;0).
г)Через точки(-1;0),(1;-4), (3;0) проводим параболу.
Корнями уравнения являются абсциссы точек пересечения параболы с осью х; значит, корни уравнения таковы: х=-1, х=3.
Ответ: -1;3.
- Способ
А) Преобразуем уравнение к виду х2=2х+3.
Б) Построим в одной системе координат графики функций у= х2 и у = 2х+3.
Для построения этих графиков я предлагая вам использовать специальные заготовки, которые лежат у вас на стола. Поработаем в парах. Один из вас строит график у= х2 на миллиметровой бумаге, а другой, график функции у = 2х+3 — на кальке.
1 УЧЕНИК |
2 УЧЕНИК |
После построения графиков, накладываем один на другой, мы можем заметить, что они пересекаются в двух точках, это точки : А (-1; -2) и В (3;6). Координаты х этих точек и будут являться решениями этого уравнения.
Физминутка.
- Способ. (Овсянникова У.)
Преобразуем уравнение к виду х2-3 = 2х.
1. Рассмотрим функции у = х2-3 и у = 2х.
2. Построим график функции у = х2-3
а) Данная функция получена из функции у = х2
б) Построим график функции у = х2:
в) Переместим начало системы координат на 3 единичных отрезка вниз вдоль оси у.
3. Построим график функции у = 2х – функция прямая пропорциональность, графиком является прямая, проходящая через начало координат.
4. Найдём координаты точек пересечения:
(-1;-2) и (3;6). Решением уравнения являются их абсциссы.
Ответ: -1; 3.
С другими способами решения квадратных уравнений графическим способом мы познакомимся на следующем уроке. А сейчас давайте проанализируем суть этих способов:
- 1 способ: Строят график функции у=ах2+вх+с и находят точки его пересечения с осью х .
- 2 способ: Преобразуют уравнение к виду ах2=-вх-с, строят параболу у=ах2 и прямую у=-вх-с, находят точки их пересечения(корнями уравнения служат абсциссы точек пересечения, если, разумеется, таковые имеются)
- 3 способ: Преобразуем уравнение к виду ах2+с=-вх, строят параболу у=ах2+с и прямую у=-вх; находят точки их пересечения
V. Подведение итогов.
Итак, графические способы решения квадратного уравнения красивы и приятны, но не дают стопроцентной гарантии решения любого квадратного уравнения. Стопроцентную гарантию дает алгоритм решения квадратных уравнений, выработанный математиками, о котором мы поговорим позже. VI. Домашнее задание. п. 23 № 23. 3
№ П/П | Ответ: |
1 способ | |
2 способ | |
3 способ |