Методическая разработка по алгебре (8 класс) по теме: Решение дробных рациональных уравнений. 8 класс
Урок по теме «Решение дробных рациональных уравнений». 8-й класс
Цели урока:
Обучающая:
- закрепление понятия дробного рационального уравнения;
- рассмотреть различные способы решения дробных рациональных уравнений;
- рассмотреть алгоритм решения дробных рациональных уравнений, включающий условие равенства дроби нулю;
- обучить решению дробных рациональных уравнений по алгоритму.
Развивающая:
- развитие умения правильно оперировать полученными знаниями, логически мыслить;
- развитие интеллектуальных умений и мыслительных операций — анализ, синтез, сравнение и обобщение;
- развитие инициативы, умения принимать решения, не останавливаться на достигнутом;
- развитие критического мышления;
- развитие навыков исследовательской работы.
Воспитывающая:
- воспитание познавательного интереса к предмету;
- воспитание самостоятельности при решении учебных задач;
- воспитание воли и упорства для достижения конечных результатов.
Тип урока: урок – закрепление и систематизация знаний, умений и навыков.
Ход урока
1. Организационный момент.
Здравствуйте, ребята! Сегодня на уроке мы рассмотрим с вами различные способы решения дробных рациональных уравнений. На доске написаны уравнения, посмотрите на них внимательно. Все ли из этих уравнений вы сможете решить?
1. 7х – 14 = 0
2.
3.
4.
5.
6.
7.
Уравнения, в которых левая и правя часть, являются дробно-рациональными выражениями, называются дробные рациональные уравнения. Как вы думаете, что мы будем изучать сегодня на уроке? Сформулируйте тему урока. Итак, открываем тетради и записываем тему урока «Решение дробных рациональных уравнений».
2. Актуализация знаний. Фронтальный опрос, устная работа с классом, решение уравнений
Ответьте, пожалуйста, на следующие вопросы:
- Как называется уравнение №1? (Линейное.) Способ решения линейных уравнений. (Все с неизвестным перенести в левую часть уравнения, все числа — в правую. Привести подобные слагаемые. Найти неизвестный множитель).
Решим уравнение №1
- Как называется уравнение №3? (Квадратное.) Способы решения квадратных уравнений. (Выделение полного квадрата, по формулам, используя теорему Виета и ее следствия.)
Решим уравнение №3
- Что представляет собой уравнение №2? (Пропорцию). Что такое пропорция? (Равенство двух отношений.) Основное свойство пропорции. (Если пропорция верна, то произведение ее крайних членов равно произведению средних членов.)
Решим уравнение №2
Решение:
9х = 18 ∙ 5
9х = 90
х = 90 : 9
х = 10
Ответ: 10
Какое дробно-рациональное уравнение можно попробовать решить, используя основное свойство пропорции? (№5). Но так как данное уравнение имеет знаменатель, содержащий неизвестное, то необходимо написать …? ОДЗ.
Решение:
ОДЗ: х ≠ − 2, х ≠ 4
(х – 2)(х – 4) = (х + 2)(х + 3)
х2 – 4х – 2х + 8 = х2 + 3х + 2х + 6
х2 – 6х – х2 – 5х = 6 – 8
-11х = -2
х = -2 : (-11)
Ответ:
- Решим уравнение №4. Какие свойство используются при решении этого уравнения? (Если обе части уравнения умножить на одно и то же отличное от нуля число, то получится уравнение, равносильное данному.)
Решение:
| ∙ 6
3х – 3 + 4х = 5х
7х – 5х = 3
2х = 3
х = 3 : 2
х = 1,5
Ответ: 1,5
Какое дробно-рациональное уравнение можно решить, умножая обе части уравнения на знаменатель? (№6).
Решение:
| ∙ (7 – х)
12 = х(7 – х)
12 = 7х – х2
х2 – 7х + 12 = 0
D = 1 > 0, х1 = 3, х2 = 4.
Ответ: 3; 4.
- Теперь решим уравнение №7 двумя способами.
Решение:
1 способ:
ОДЗ: х ≠ 0, х ≠ 5
Когда дробь равна нулю? (Дробь равна нулю, когда числитель равен нулю, а знаменатель не равен нулю.)
х² − 3 х + х – 5 – х – 5 = 0
х² − 3 х – 10 = 0
D = 49 > 0, х1 = 5, х2 = − 2
х = 5 не удовлетворяет ОДЗ. Говорят, 5 – посторонний корень.
Ответ: − 2
Решение:
2 способ:
| ∙ х(х – 5) ОДЗ: х ≠ 0, х ≠ 5
х(х – 3) + х – 5 = х + 5
х² − 3 х + х – 5 – х – 5 = 0
х² − 3 х – 10 = 0
D = 49 > 0, х1 = 5, х2 = − 2
х = 5 не удовлетворяет ОДЗ. 5 – посторонний корень.
Ответ: − 2
Давайте попробуем сформулировать алгоритм решения дробных рациональных уравнений данным способом. Дети сами формулируют алгоритм.
Алгоритм решения дробных рациональных уравнений:
- Перенести все в левую часть.
- Привести дроби к общему знаменателю.
- Решить уравнение, используя правило: дробь равна нулю, когда числитель равен нулю, а знаменатель не равен нулю.
- Исключить из его корней те, которые обращают знаменатель в нуль (с помощью ОДЗ или проверкой)
- Записать ответ.
Другой способ решения.
Алгоритм решения дробных рациональных уравнений:
1. Найти общий знаменатель дробей, входящих в уравнение;
2. Умножить обе части уравнения на общий знаменатель; не забыв написать ОДЗ
3. Решить получившееся целое уравнение;
4. Исключить из его корней те, которые обращают в нуль общий знаменатель (используя ОДЗ или проверкой)
5. Записать ответ.
Также можно решить уравнение, используя основное свойство пропорции, не забыв исключить из его корней те, которые обращают знаменатель в нуль (с помощью ОДЗ или проверкой)
8. Подведение итогов урока.
Итак, сегодня на уроке мы с вами познакомились с дробными рациональными уравнениями, научились решать эти уравнения различными способами. На следующем уроке, дома у вас будет возможность закрепить полученные знания.
Какой метод решения дробных рациональных уравнений, по вашему мнению, является более легким, доступным, рациональным? Не зависимо от метода решения дробных рациональных уравнений, о чем необходимо не забывать? В чем «коварство» дробных рациональных уравнений?
Всем спасибо, урок окончен.
Методическая разработка урока «Решение дробных рациональных уравнений» (алгебра, 8 класс)
Алгебра 8 класс
Урок № ______
Тема урока. Решение дробных рациональных уравнений
Цели и задачи урока:
образовательные:
– повторить и закрепить понятие дробных рациональных уравнений;
– повторить, закрепить и отработать способ решения дробных рациональных уравнений;
– отрабатывать умения и навыки приводить дроби к общему знаменателю, решать квадратные уравнения;
– отрабатывать вычислительные умения и навыки;
развивающие:
– развивать память, внимание, наблюдательность;
– развивать аналитические способности;
– расширять предметный кругозор;
воспитательные:
– воспитывать уважение к учителю;
– прививать интерес к предмету и к учебе в целом.
Тип урока: урок обобщения и закрепления знаний и умений.
Форма проведения: фронтальная, индивидуальная.
Методы: объяснительно-иллюстративный, репродуктивный, проблемный.
Ход урока.
Организационный момент.
Приветствие.
Проверка готовности класса к уроку.
Актуализация опорных знаний (15 мин.)
Задание 1. Составь уравнение (задание выполняется на доске)
На доске расположены карточки с фрагментами уравнений, составить из них дробно-рациональные уравнения.
Задание 2. Найди пару (задание выполняется в презентации + самопроверка)На слайдах изображены числа и корни, собрать соответствующие пары, установив между ними соответствие. Задание проверяется программой автоматически.
Задание 3. «Разбить по группам» (задание выполняется в тетрадях и на доске).
На доске на карточках приведены части формул сокращенного умножения и таблица с названиями формул. Надо поместить карточку в нужный столбец и дописать формулу.
Задание 4. Найди дискриминант (задание выполняется в тетрадях, условие и проверка – в презентации).
На слайде презентации дано квадратное уравнение, учащиеся должны назвать его коэффициенты и самостоятельно его решить, выполнить проверку с решением, приведенном в презентации.
Повторение теоретического материала (решение дробных рациональных уравнений).
Задание 5. Решить уравнение
На доске цепочкой выполняется решение уравнения
(каждый учащийся делает в решении на доске один шаг).
Закрепление теоретического материала.
Задание 6. Решить уравнение
(обсуждение уравнения – на доске, решение уравнения – самостоятельно в тетрадях, самопроверка – в презентации).
Домашнее задание.
Повторить п. 25, выполнить № 605 (а-в)
Подведение итогов урока.
Рефлексия.
Выставление оценок.
Разработка урока «Решение дробных рациональных уравнений» (8 класс)
Государственное общеобразовательное учреждение«Стахановская специализированная школа № 9
имени Алексея Стаханова»
Разработка урока
«Решение дробных
рациональных уравнений»
(8 класс)
Учитель математики
ССШ № 9
им. А. Стаханова
Стоженко С.В.
2019
Цели урока:
закрепление понятия дробного рационального уравнения;
развитие навыков исследовательской работы;
воспитание воли и упорства для достижения конечных результатов.
Тип урока: урок закрепления и систематизации знаний, умений и навыков
Ход урока
2. Актуализация знаний. Фронтальный опрос, устная работа с классом, решение уравнений
1. 7х – 14 = 0
2. 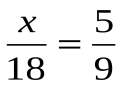
3. 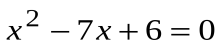
4. 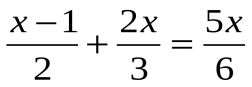
5. 
6. 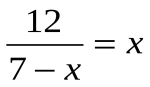
7. 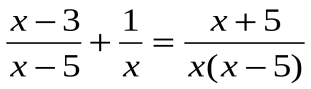
Как называется уравнение №1? (Линейное.) Способ решения линейных уравнений. (Все с неизвестным перенести в левую часть уравнения, все числа — в правую. Привести подобные слагаемые. Найти неизвестный множитель).
Решим уравнение №1
Как называется уравнение №3? (Квадратное.) Способы решения квадратных уравнений. (Выделение полного квадрата, по формулам, используя теорему Виета и ее следствия.)
Решим уравнение №3
Что представляет собой уравнение №2? (Пропорцию). Что такое пропорция? (Равенство двух отношений.) Основное свойство пропорции. (Если пропорция верна, то произведение ее крайних членов равно произведению средних членов.)
Решим уравнение №2
Решение:
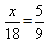
9х = 18 ∙ 5
9х = 90
х = 90 : 9
х = 10
Ответ: 10
Какое дробно-рациональное уравнение можно попробовать решить, используя основное свойство пропорции? (№5). Но так как данное уравнение имеет знаменатель, содержащий неизвестное, то необходимо написать …? ОДЗ.
Решение:
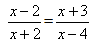 ОДЗ: х ≠ − 2, х ≠ 4
ОДЗ: х ≠ − 2, х ≠ 4
(х – 2)(х – 4) = (х + 2)(х + 3)
х2 – 4х – 2х + 8 = х2 + 3х + 2х + 6
х2 – 6х – х2 – 5х = 6 – 8
-11х = -2х = -2 : (-11)
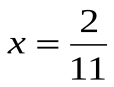
Ответ: 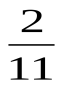
Решим уравнение №4. Какие свойство используются при решении этого уравнения? (Если обе части уравнения умножить на одно и то же отличное от нуля число, то получится уравнение, равносильное данному.)
Решение:
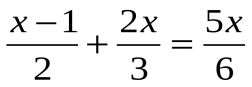 | ∙ 6
| ∙ 6
3х – 3 + 4х = 5х
7х – 5х = 3
2х = 3
х = 3 : 2
х = 1,5
Ответ: 1,5
Какое дробно-рациональное уравнение можно решить, умножая обе части уравнения на знаменатель? (№6).
Решение:
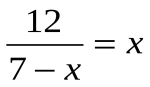 | ∙ (7 – х)
| ∙ (7 – х)
12 = х(7 – х)
12 = 7х – х2
х2 – 7х + 12 = 0
D = 1 0, х1 = 3, х2 = 4.
Ответ: 3; 4.
Теперь решим уравнение №7 двумя способами.
Решение:
1 способ:
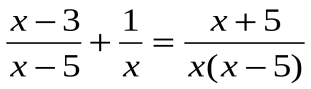 ОДЗ: х ≠ 0, х ≠ 5
ОДЗ: х ≠ 0, х ≠ 5
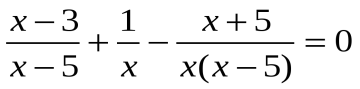
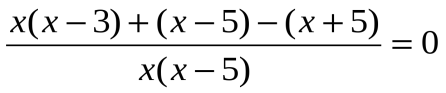
Когда дробь равна нулю? (Дробь равна нулю, когда числитель равен нулю, а знаменатель не равен нулю.)
х² − 3 х + х – 5 – х – 5 = 0
х² − 3 х – 10 = 0
D = 49 0, х1 = 5, х2 = − 2
х = 5 не удовлетворяет ОДЗ. Говорят, 5 – посторонний корень.
Ответ: − 2
Решение:
2 способ:
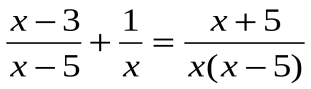 | ∙ х(х – 5) ОДЗ: х ≠ 0, х ≠ 5
| ∙ х(х – 5) ОДЗ: х ≠ 0, х ≠ 5
х(х – 3) + х – 5 = х + 5
х² − 3 х + х – 5 – х – 5 = 0
D = 49 0, х1 = 5, х2 = − 2
х = 5 не удовлетворяет ОДЗ. 5 – посторонний корень.
Ответ: − 2
Давайте попробуем сформулировать алгоритм решения дробных рациональных уравнений данным способом. Дети сами формулируют алгоритм.
Алгоритм решения дробных рациональных уравнений:
Перенести все в левую часть.
Привести дроби к общему знаменателю.
Решить уравнение, используя правило: дробь равна нулю, когда числитель равен нулю, а знаменатель не равен нулю.
Исключить из его корней те, которые обращают знаменатель в нуль (с помощью ОДЗ или проверкой)
Записать ответ.
Другой способ решения.
Алгоритм решения дробных рациональных уравнений:
1. Найти общий знаменатель дробей, входящих в уравнение;
2. Умножить обе части уравнения на общий знаменатель; не забыв написать ОДЗ
3. Решить получившееся целое уравнение;
4. Исключить из его корней те, которые обращают в нуль общий знаменатель (используя ОДЗ или проверкой)
5. Записать ответ.
Также можно решить уравнение, используя основное свойство пропорции, не забыв исключить из его корней те, которые обращают знаменатель в нуль (с помощью ОДЗ или проверкой)
3. Подведение итогов урока, выставление оценок
Какой метод решения дробных рациональных уравнений, по вашему мнению, является более легким, доступным, рациональным? Не зависимо от метода решения дробных рациональных уравнений, о чем необходимо не забывать? В чем «коварство» дробных рациональных уравнений?
4. Домашнее задание
Урок алгебры в 8 классе «Решение задач с помощью дробно-рациональных уравнений»
Открытый урок по алгебре
Тема: «Решение задач с помощью рациональных уравнений»
Класс: 8
Предмет: Алгебра
Цели урока:
Обучающая:
-закрепление понятия дробно-рационального уравнения;
-составление математической модели задачи, перевод условия задачи с обычного языка на математический;
-проверка уровня усвоения темы путем проведения проверочной работы.
Развивающая:
-развитие умения правильно оперировать полученными знаниями, логически мыслить;
-развитие интеллектуальных умений;
-развитие умения принимать решения.
Воспитательная:
-воспитание познавательного интереса к предмету;
-воспитание самостоятельности при решении учебных задач;
-воспитание воли и упорства для достижения конечных результатов.
Задачи:
1) актуализировать знание решения дробных рациональных уравнений, умение решать задачи при помощи рациональных уравнений; добиться усвоения алгоритма решения задач;
2) Познавательные: овладение основами логического и алгоритмического мышления;
Регулятивные: развитие умения читать и записывать информацию в виде различных математических моделей, планировать действия в соответствии с поставленной задачей;
Коммуникативные: строить высказывания, аргументировано доказывать свою точку зрения;
Личностные: развитие навыков сотрудничества со сверстниками,
3) — воспитывать чувство товарищества.
Оборудование: презентация, конспект урока, компьютер, проектор.
Ход урока:
1. Организационный момент.
Здравствуйте, ребята.
Прозвенел звонок — начинается новый урок, на котором будем учиться математике, а значит жизни.
Ведь жизнь перед нами ставит постоянно много вопросов, задач, на которые надо найти ответ непременно и именно только нам. И от правильности найденного решения зависит порою очень многое в жизни. Бывает так, что жизнь ошибок не прощает…
Математика считается царицей всех наук, потому что……?… «ум, который решает все наши жизненные вопросы, в порядок приводит», ……. через умения мыслить, анализировать, сопоставлять, делать выводы, считать. Все эти мыслительные процессы и помогают нам найти правильное решение жизненных проблем.
На доске ребусы, которые необходимо разгадать и тем самым определить
ключевое слово урока.


Правильно, это слово «задача». Ведь именно при решении различного рода задач развиваются эти мыслительные процессы.
Задачам отводится много места, как в школьном курсе математики, так и на экзамене по математике в 9 классе и на ЕГЭ в 11классе.
Ещё начиная с начальной школы, вы учились решать разные, теперь уже не сложные для вас, задачи. С каждым годом вы узнавали всё новые и новые методы и способы их решения. А сегодня мы будем ……(ответы обучающихся на определение темы урока):
-решать задачи, решение которых сводится к дробно-рациональным уравнениям, а также составлять задачи.
Итак, тема урока «Решение задач с помощью рациональных уравнений»
-Какой урок мы уже решаем задачи? (третий).
Предлагаю самостоятельно сформулировать цели урока.
Пожелания обучающимся:
1. Увеличить объем своих знаний на уроке.
2. Смело высказывать свое мнение, приводить свои способы решения задач, сомневаться, и даже ошибаться в чем-то.
3. Сделать себе установку: « Я все могу, все решу».
Эпиграфами к нашему уроку я взяла такие слова:
высказывание великого английского ученого Альберта Энштейна, открывшего «теорию относительности»: «Мне приходится делить время между политикой и уравнением. Однако уравнение, по – моему, гораздо важнее. Политика существует только для данного момента, а уравнения будут существовать вечно»;
«Если хотите научиться плавать, смело входите в воду, а если хотите научиться решать задачи, то решайте их». Джордж Пойя
Проверим ваше внимание
На руках 10 пальцев. Сколько пальцев на 10 руках?
Двое играли в шашки четыре часа. Сколько часов играл каждый из них?
Экипаж, запряженный тройкой лошадей, проехал за один час 15 км. С какой скоростью бежала каждая лошадь?
Актуализация знаний
Любая работа будет результативной, если она будет спланирована. Есть план и нашей работы на уроке. Перед вами маршрутные листы (приложение 1) , в которых определены этапы нашего урока. Я попрошу вас объективно оценить себя на каждом этапе.
Фронтальный опрос, устная работа с классом.
-Исходя из темы урока, чтобы решать сами задачи первоначально надо уметь решать рациональные уравнения, которые включают в себя…..целые уравнения и дробно-рациональные, и квадратные уравнения.
-Скажите, что вы видите на этом слайде? ( Уравнения)
— Правильно. Какие это уравнения? ( Дробно-рациональные)
— а могу я сказать, что это рациональные уравнения? ( Да. Т.к. рациональные включают в себя и дробно-рациональные вместе с целыми)
— Какие уравнения называют рациональными?
-Назовите алгоритм решения дробно-рациональных уравнений?
Решите устно данные уравнения.

Какие еще уравнения надо уметь решать? – Квадратные.
Повторение теории квадратных уравнений.
Проверка домашнего задания
Какие виды задач мы научились решать?
На какую тему были задачи из домашнего задания?
№628
В предложенную таблицу вставить ключевые слова.
№628. Моторная лодка, скорость которой в стоячей воде 15 км/ч, прошла по течению реки 35 км, а против течения 25 км. По течению она шла столько же времени, сколько против течения. Какова скорость течения реки?
Учащимся
Ответ: 2,5 км/ч (Слайд 9).
2. Решение задач.
-Прежде чем приступать к решению задачи необходимо несколько раз внимательно прочитать условие задачи, и ответить для себя на ряд вопросов. Каких?
( Тип задачи — объекты, участвующие в ней, — величины, характеризующие эти объекты — связи между этими величинами – какую величину обозначим за х.)
Получив ответы на эти вопросы, далее или составляем краткую запись в том виде, как нам удобно, а затем математическую модель, или, логически рассуждая, составляем математическую модель задачи, предварительно все величины выразив через введенную переменную х.
Постановка проблемы
Всегда говорят, сколько людей, столько и мнений. У каждого из вас после прочтения задачи есть право выбора как ее решить. Я предлагаю вам решить задачу № 620.( Работа в группах)
I гр. – за X принимает скорость I автомобиля
II гр. – за X принимает скорость II автомобиля
III гр. – за X принимает время движения I автомобиля
IV гр. – за X принимает время движения II автомобиля
Таблицы ко всем четырем задачам приготовлены на доске.
Выясняют, что было удобнее всего обозначить через X после представления каждой группой решения своего уравнения.
Вывод
Зарядка
Следующий наш этап – это составление задачи по готовому уравнению. Предлагается придумать задачу, ответом которой является решение предложенного уравнения (работа в парах).
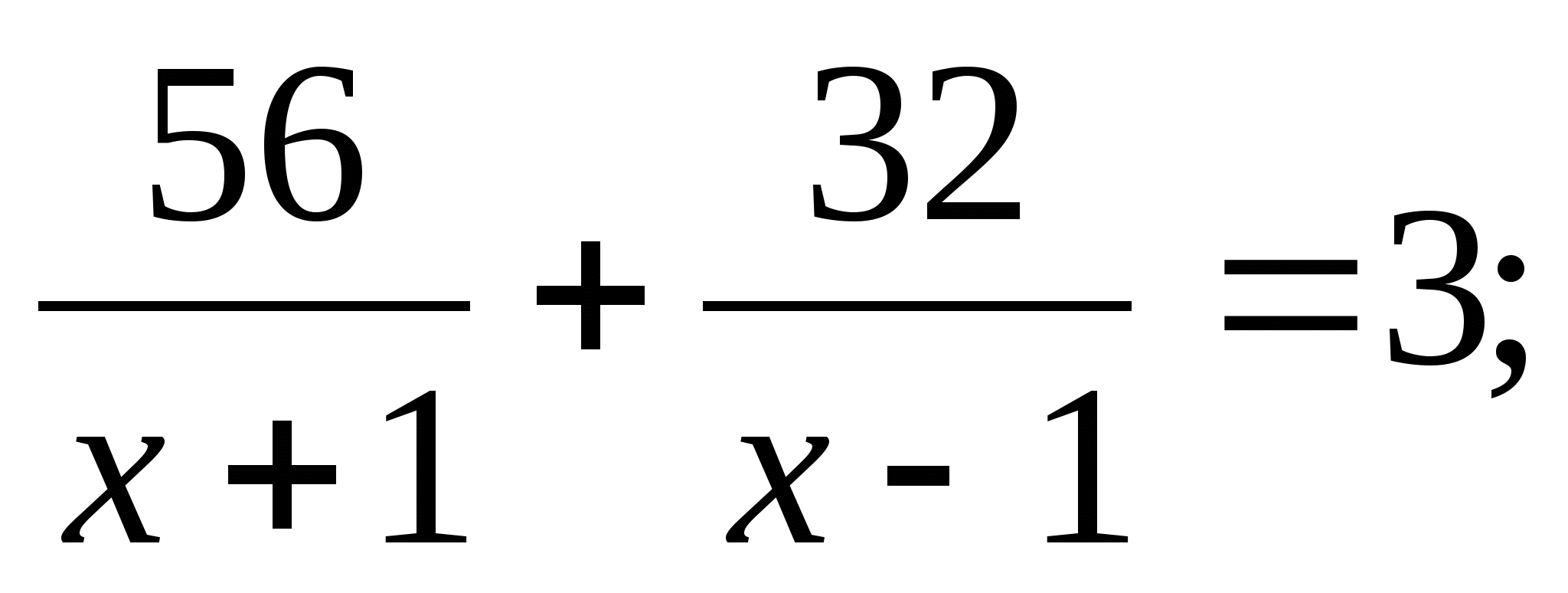
4. Выполнение контролирующего задания
Индивидуальная работа выполняется на листочках.
Работа оценивается
На «3» за правильно выполненное 1 задание;
На «4» — за 1-2;
На «5»- за 1-3( в 3-ем задании достаточно только составить уравнение).
Самопроверка
Д.З. повторить теорию по квадратным уравнениям;
Уровень А) №703
Уровень Б) №705
Подведение итогов урока. Рефлексия.
Рефлексия (Притча).
Шел мудрец, а навстречу ему три человека везли под горячим солнцем тележки с камнями для строительства храма. Мудрец остановил их и задал каждому один и тот же вопрос «Что ты делал целый день?» Первый ответил, что целый день возил эти проклятые камни. Второй ответил: «Добросовестно выполнял свою работу», а третий: «Строил храм».
Ребята, вот и я задаю каждому из вас тот же вопрос: «Что ты делал целый урок?» Кто из вас считает, что он таскал тяжелые камни – поднимите желтые треугольники, добросовестно работал – зеленые, строил храм знаний – красные.
— Какую тему рассмотрели на уроке?
— Оценить свой уровень умения решать задач с помощью дробных рациональных уравнений.
— Что вызывает затруднения?
(Заполнить последнюю строчку листов. Заслушать высказывания обучающихся по желанию).

Приложение 1
Маршрутный лист
учени___ 8 класса _______________________________________
Составление задачи по готовому уравнению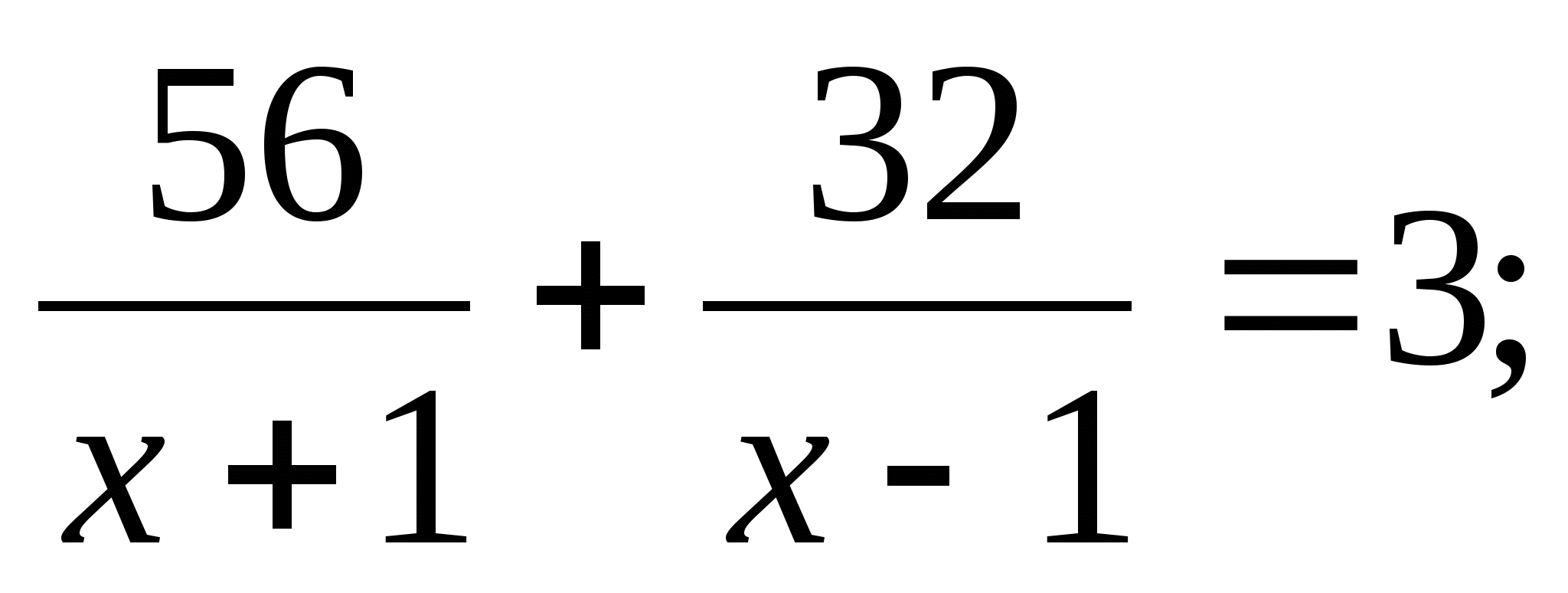
Тест.
1. Решите уравнение. Выберите верный вариант ответа:
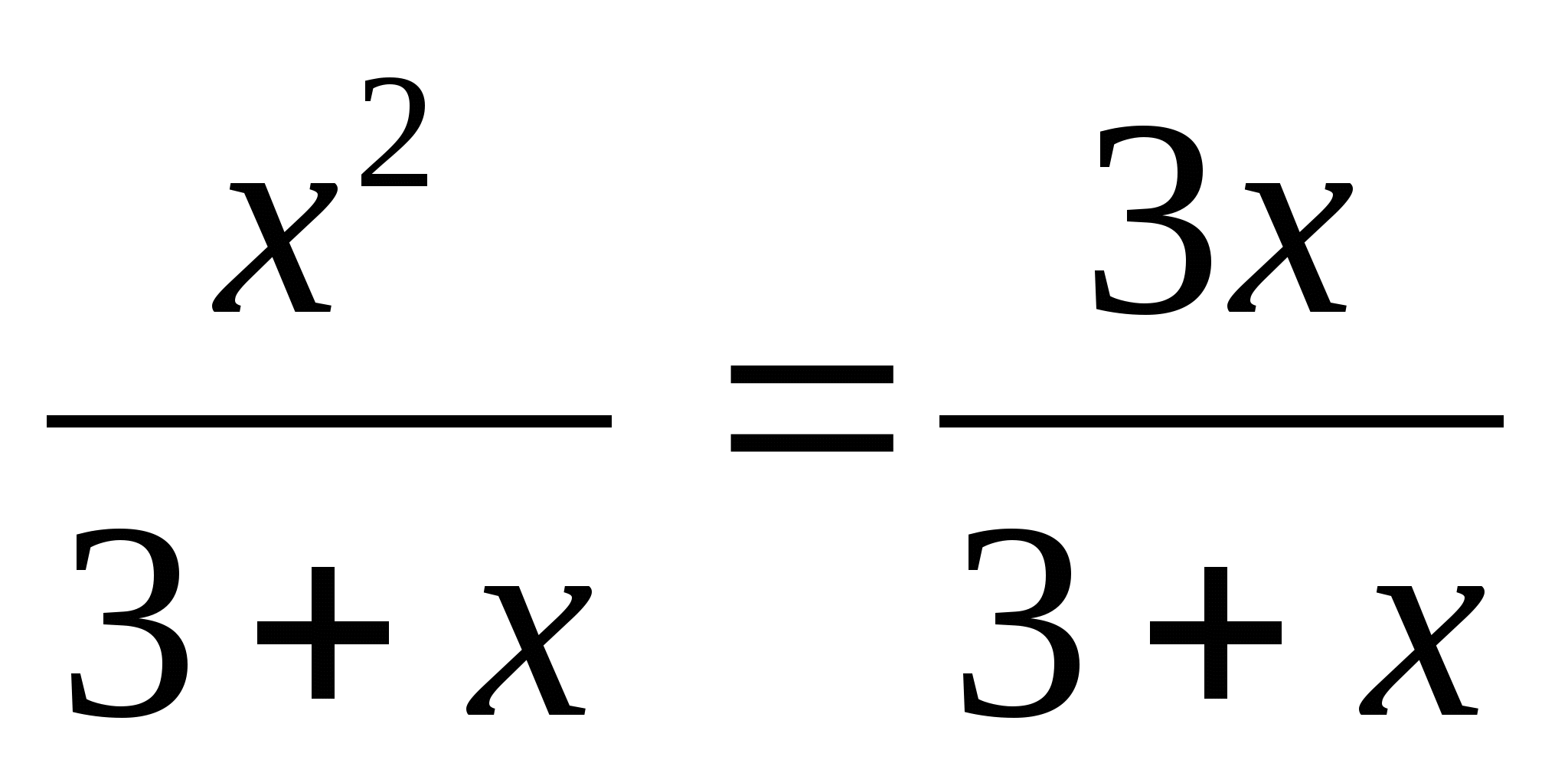 1) 0; 2) 0; 3; 3) 3; -3.
1) 0; 2) 0; 3; 3) 3; -3.
2.Прочитав условие задачи, составьте уравнение, которое ему соответствует:
Теплоход прошёл 108 км по течению реки и 84 км против течения, затратив на весь путь 8ч. Найдите собственную скорость теплохода, обозначив её х км/, если скорость течения реки 3 км/ч
1) 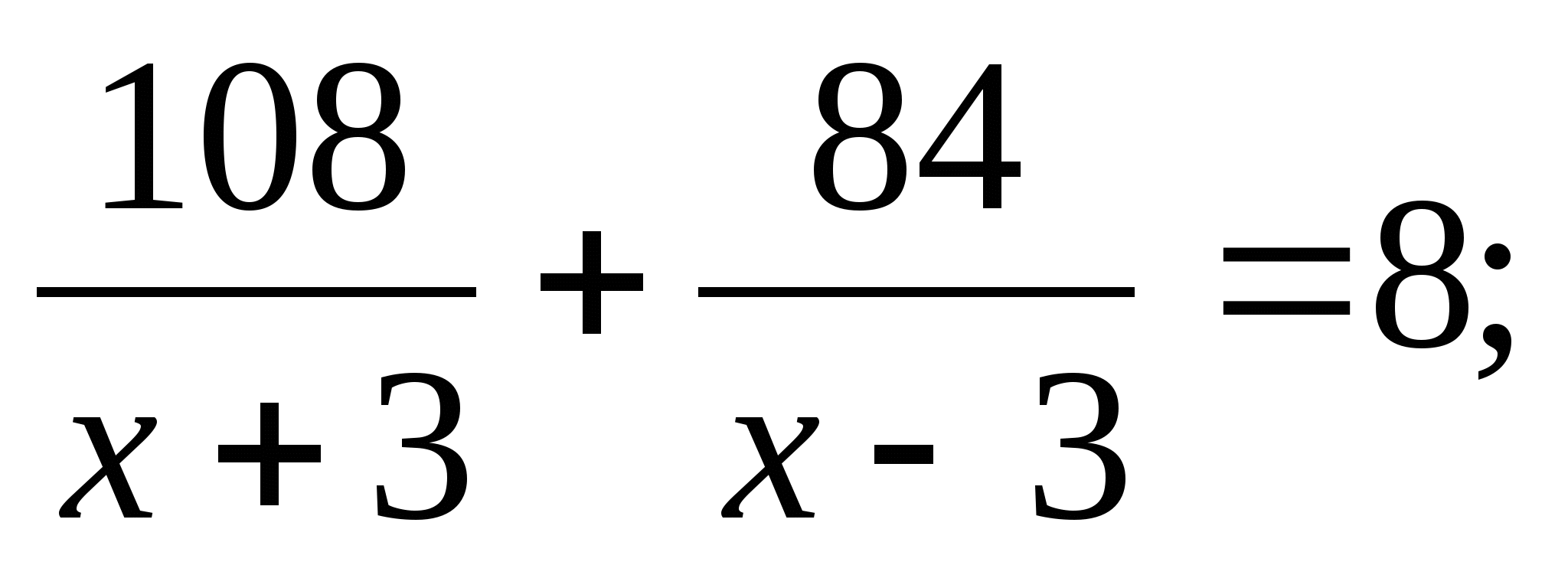 2)
2) 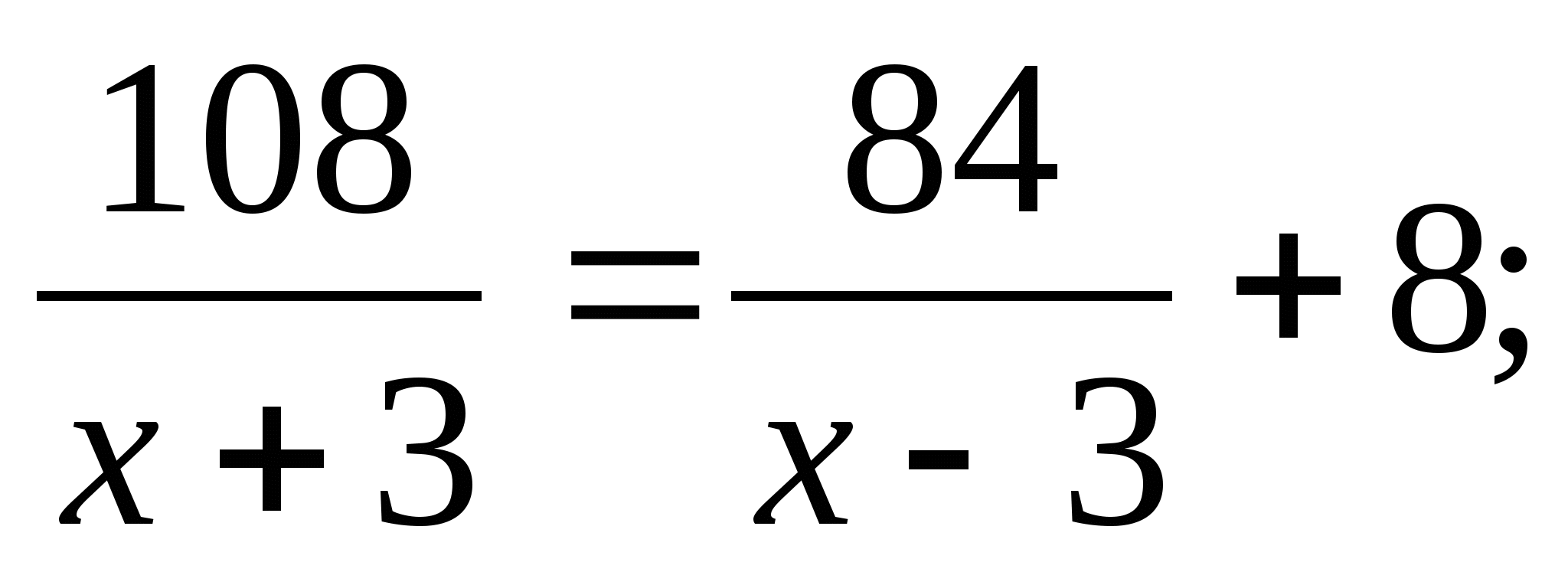
3) 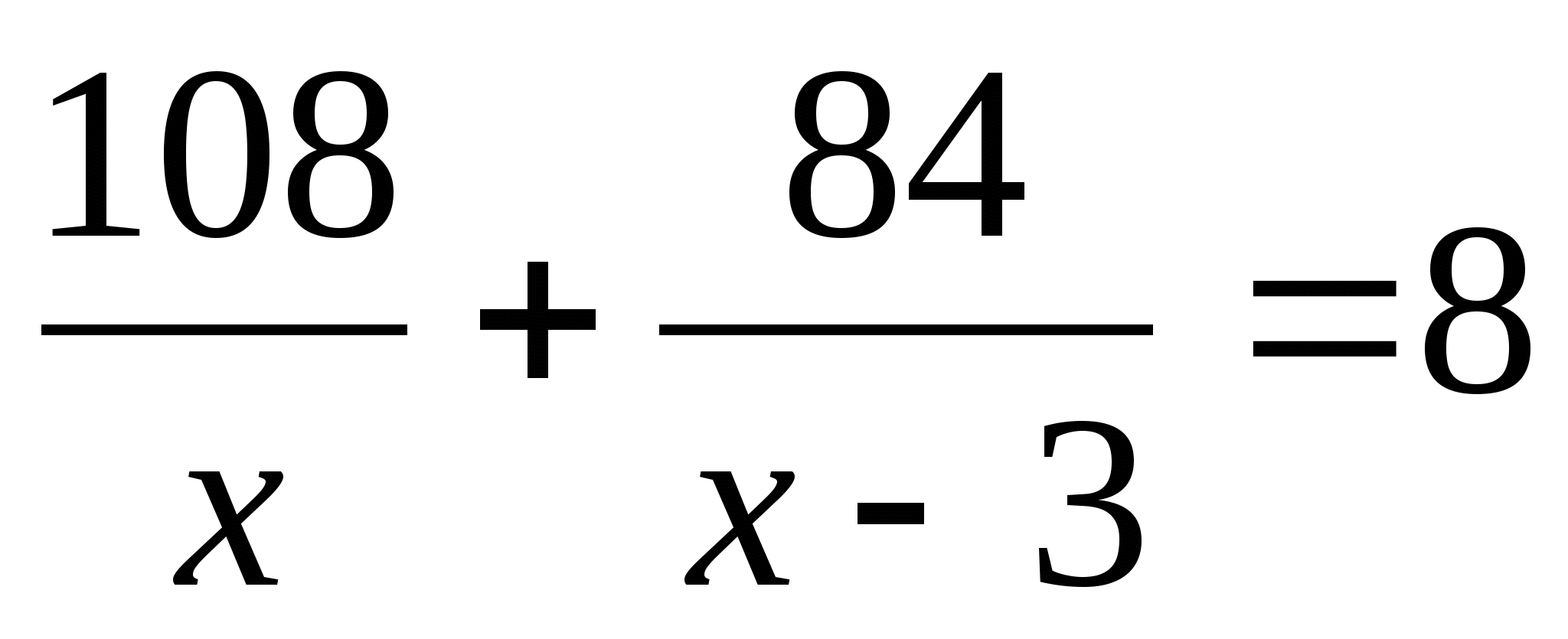 ; 4)
; 4) 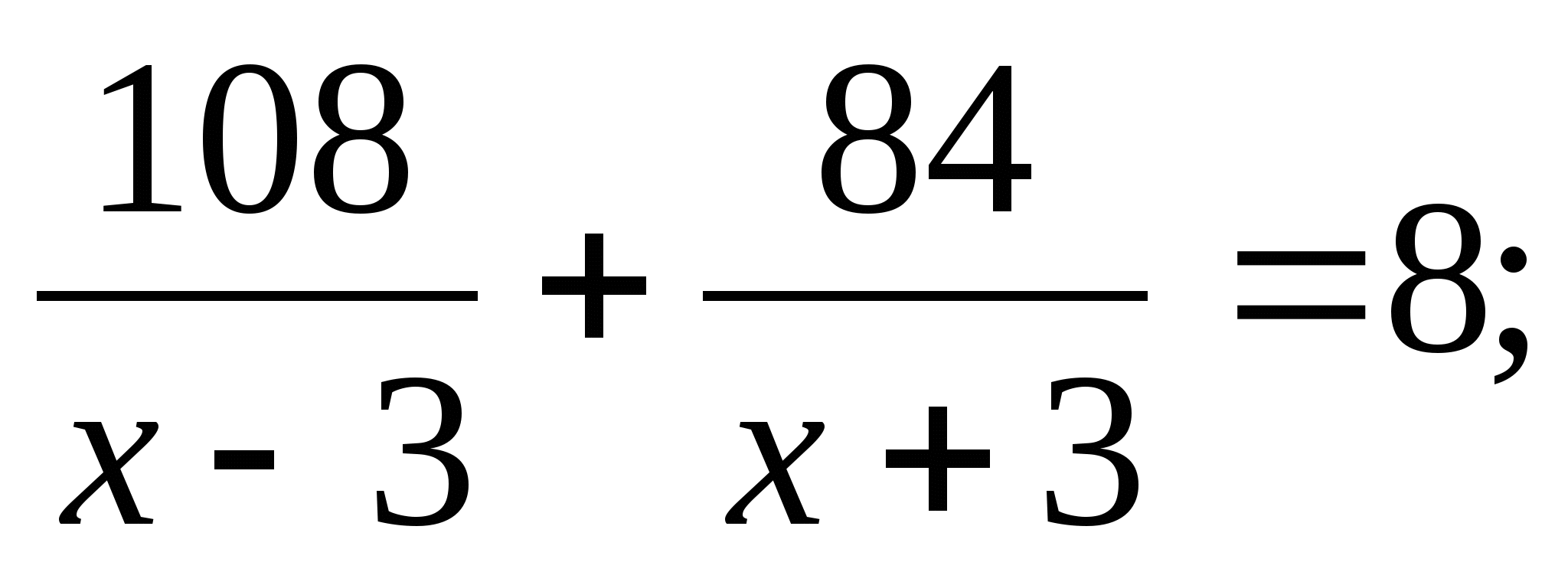
3. Заказ на 110 деталей первый рабочий выполняет на 1 час быстрее, чем второй. Сколько деталей в час делает второй рабочий, если известно, что первый за час делает на 1 деталь больше?
Ответ.
V. Рефлексия:

Маршрутный лист
учени___ 8 класса _______________________________________
Составление задачи по готовому уравнению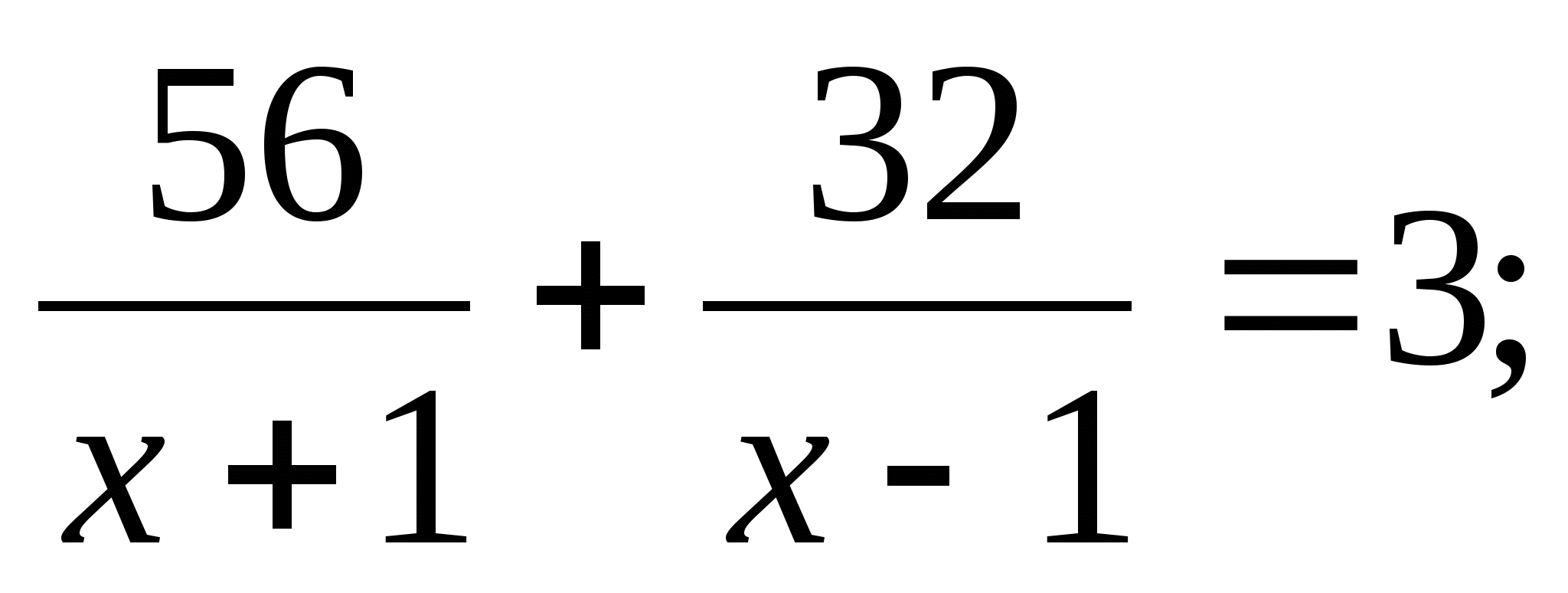
Тест.
1. Решите уравнение. Выберите верный вариант ответа:
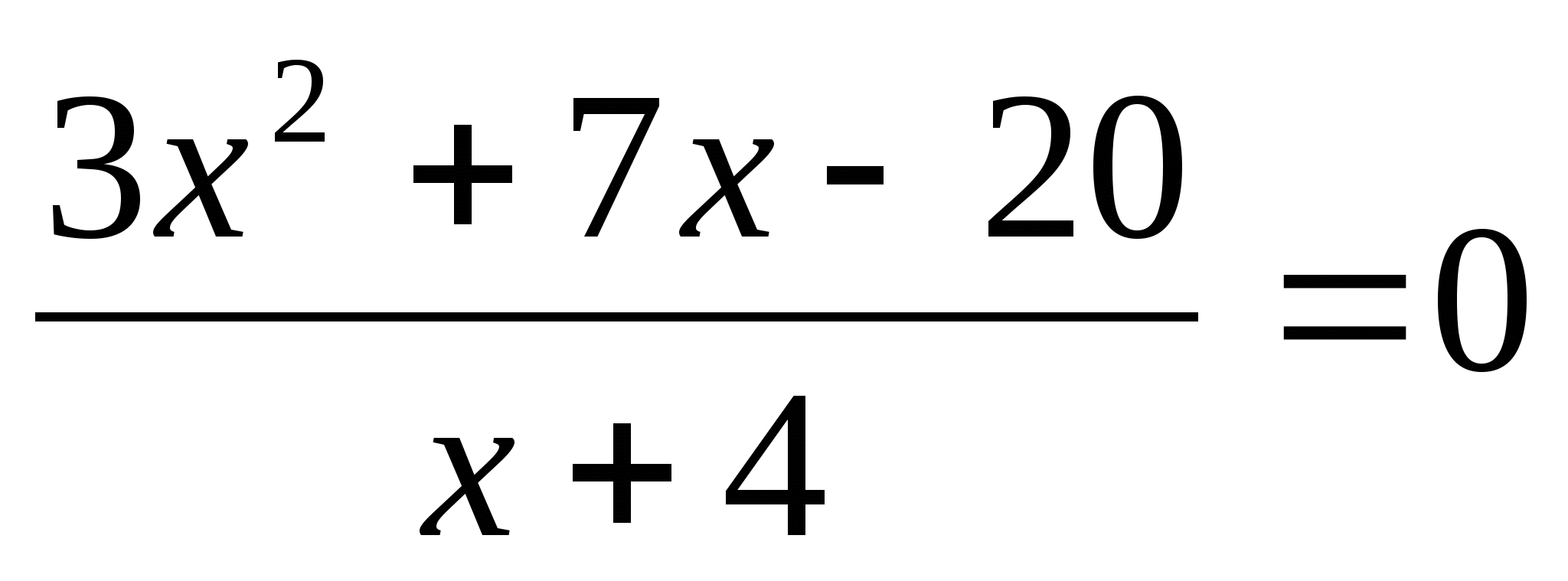
- 2.Прочитав условие задачи, составьте уравнение, которое ему соответствует:
Моторная лодка прошла 56 км против течения реки и 32 км по течению, затратив на весь путь 3ч. Найдите собственную скорость лодки, обозначив её через х км/ч, при условии, что скорость течения реки равна 1км/ч.
- 1)
 ; 2)
; 2)  ;
;3)
 ; 4)
; 4) 
3. Заказ на 156 деталей первый рабочий выполняет на 1 час быстрее, чем второй. Сколько деталей в час делает первый рабочий, если известно, что он за час делает на 1 деталь больше?/ч.
Ответ.
- 1)
V. Рефлексия:

Презентация к уроку по алгебре (8 класс) на тему: Презентация к уроку «Решение дробных рациональных уравнений»
Слайд 1
Решение дробных рациональных уравнений Алгебра 8 классСлайд 2
Устная работа
Слайд 3
2. Найдите наименьший общий знаменатель
Слайд 4
3. Вспомним несколько определений а ) Какие выражения называются целыми? ( а уравнения?) б)Какие выражения называются дробными ? ( а уравнения?) в)Какие выражения называются рациональными? ( а уравнения?) Целые выражения – это выражения из чисел и переменных, которые составлены с помощью действий сложения, вычитания и умножения, а также деления на число, отличное от нуля . Дробные выражения – это частное двух чисел или выражений, в котором знак деления обозначен чертой . Рациональные выражения — это все целые и дробные выражения. 4
Слайд 5
Сформулируем понятие дробно рационального уравнения Дробным рациональным уравнением называется уравнение, о бе части которого являются рациональными выражениями, причем хотя бы одно из них- дробным выражением . 5
Слайд 6
Левая и правая части каждого равенства являются рациональными выражениями. Такие уравнения называются рациональными уравнениями . Целое рациональное уравнение Дробные рациональные уравнения
Слайд 7
Решим целое уравнение Ответ: 1,5 ∙ 6 Наименьший общий знаменатель
Слайд 8
Решим целое уравнение ∙ 6 Решим дробное рациональное уравнение 0 0 Если x = 5, то Если x = — 2 , то Ответ: — 2 Ответ: 1,5
Слайд 9
Решим дробное рациональное уравнение 0 0 Если x = 5, то Если x = — 2 , то Ответ: — 2 Алгоритм решения дробно-рационального уравнения: 1) найти общий знаменатель дробей, входящих в уравнение; 2) умножить обе части уравнения на общий знаменатель; 3) решить получившееся целое уравнение; 4) исключить из его корней те, которые обращают в нуль общий знаменатель.
Слайд 10
Алгоритм решения дробно-рационального уравнения: 1 ) найти общий знаменатель дробей, входящих в уравнение; 2 ) умножить обе части уравнения на общий знаменатель; 3 ) решить получившееся целое уравнение; 4 ) исключить из его корней те, которые обращают в нуль общий знаменатель. Пример. Ответ: 3
Слайд 11
Решите в тетради № 600 (а, в, д, з) № 601 (а, в, з) Алгоритм решения дробно-рационального уравнения: 1 ) найти общий знаменатель дробей, входящих в уравнение; 2 ) умножить обе части уравнения на общий знаменатель; 3 ) решить получившееся целое уравнение; 4 ) исключить из его корней те, которые обращают в нуль общий знаменатель.
Слайд 12
Домашнее задание П. 25 № 600 (б, г, е), 601 (б, ж)
Слайд 13
Источники Ю.Н. Макарычев и др. Алгебра 8, учебник. М.: «Просвещение», 2009
Открытый урок по алгебре «Решение дробных рациональных уравнений» (8-й класс)
Цель:
- сформировать умение решать дробные рациональные уравнения;
- уметь решать дробно- рациональные уравнения;
- воспитание внимательности. (Слайд № 1)
Тип урока: объяснение нового материала.
Ход урока
I. Организационный момент.
II. Устная работа.
1. При каких значениях х имеет смысл выражения (слайд № 2):
2. Назовите простейший из общих знаменателей для каждой из следующих пар (слайд № 3).
3. Решить уравнения (слайд № 4):
х(х – 5) = 0;
х2 – 4х = 0;
х2 – 4 = 0;
х2 + 4 = 0.
III. Объяснение нового материала:
1. Вспомним как решают данное уравнение (слайд № 5):
Повторили алгоритм решения уравнения.
Решим уравнение:
I способ (слайд № 6).
х2 – 3х + х – 5 – х – 5 = 0
х2 – 3х –10 = 0
Д = 9 + 40 = 49
х1 = 5 х2 = –2
Проверим являются ли –2 и 5 корнями уравнения (слайд № 8).
При х = –2 х(х – 5) = –2(–2 – 5) 0;
При х = 5 х(х – 5) = 5(5 – 5) = 0.
Т.к. решение х = 5 обращает общий знаменатель в
нуль, корнем оно не является.
х = –2 – корень уравнения.
Ответ: –2.
II способ (слайд № 9).
Допустимые значения дробей, входящих в уравнение: х 0, х 5.
2. Решаем уравнение.
3. Выбираем корни, принадлежащие области определения.
Алгоритм решения дробных рациональных
уравнений.
II способ (слайд № 10).
Найти допустимые значения дробей, входящих в уравнение.
Найти общий знаменатель дробей, входящих в уравнение.
Умножить обе части уравнения на общий знаменатель.
Решить получившееся уравнение.
Исключить корни, не входящие в допустимые значения дробей уравнения.
IV. Закрепление (слайд № 11).
№ 590 (г, д).
V. Домашнее задание (слайд № 12).
П. 24, № 592 (а, б, в, г), 602, в № 593 указать простейшие из общих знаменателей.
VI. Итог урока.
– Повторить алгоритм.
Приложение
План-конспект урока по алгебре (8 класс) по теме: урок» Решение дробных рациональных уравнений»-8 класс
Разработка урока алгебры в 8 классе.
Тема урока : « Решение дробных рациональных уравнений»
Учащиеся овладевают способами решения дробных рациональных уравнений, которые состоят в том, что решение таких уравнений сводится к решению квадратных уравнений разными способами.
Один из принципов развивающего обучения — принцип активности и сознательности. Ребенок может быть активен, если осознает цель учения, его необходимость, если каждое его действие является осознанным и понятным. С целью создания развивающей среды на уроке является этап рефлексии.
Основная дидактическая цель урока – обобщить и систематизировать знания учащихся по определению методов решения дробных рациональных уравнений.
Задачи урока:
образовательные
- актуализировать и расширить полученные ранее знания учащихся по данной теме,
- ликвидировать пробелы в знаниях учащихся,
- совершенствовать умения и навыки учащихся по выбору метода решения пробных рационального уравнения,
- установить внутри предметные связи изученной темы с другими темами алгебры.
развивающие
- развивать познавательные процессы, память, воображение, мышление, внимание, наблюдательность, сообразительность;
- расширение кругозора учащихся,
воспитывающие
- воспитание трудолюбия, взаимопомощи, математической культуры,
- воспитание чувства ответственности перед товарищами, умение контролировать свои действия.
Тип урока – урок обобщения и систематизации знаний.
Средства обучения: раздаточный материал, мультимедийный проектор, экран.
Технологии: ИКТ-технологии, технология проблемного обучения.
Формы работы: индивидуальная, групповая.
Ход урока.
- Организационный момент.
Цель: подготовка учащихся к работе, активизация внимания для быстрого включения в деятельность.
Проведение рефлексии настроения и эмоционального состояния в начале урока с целью установления эмоционального контакта с учениками. Применяются карточки с изображением лиц.
Вывешивается эпиграф урока: «Если вы хотите научиться плавать, то смело входите в воду, а если хотите научиться решать задачи, то решайте их» (Д.Пойа)- выяснение смысла.
- Проверка домашнего задания
Цель: выявить пробелы в знаниях.
Рефлексия деятельности: осмысления способов и приемов работы с учебным материалом, поиска наиболее рациональных.
Ученики зачитывают получившиеся ответы. Выясняем используемые методы. К какому виду уравнения пришли после преобразований: к приведенным, к полным квадратным, к неполным квадратным. Кто применил далее теорему Виета. Ученики сверяют решения с решениями на экране.
Повторяем правило: 1. Если в квадратном уравнении a+b+c=0, то один из корней равен 1, а второй по теореме Виета равен
2. Если в квадратном уравнении a+c=b, то один из корней равен -1, а второй по теореме Виета равен
Вывод: при решении квадратного уравнения стандартного вида полезно сначала проверить являются ли числа 1 и -1 корнями уравнения.
Работа с карточками( весь класс )-(2мин)
№ | Вопросы | Ответы |
1 | Какой формулой задаётся квадратное уравнение ? | А. ax2+bx+c=0 Б. X+2х=0 В. ax+c=0 |
2 | Если Д=0, то сколько корней имеет квадратное уравнение? | А. не имеет Б. один В. два |
3 | Какого вида квадратное уравнение называется приведённым? | А. ax2+bx+c=0 Б. ax2+c=0 В. x2+px+q=0 |
4 | Как записывается теорема Виета для приведённого квадратного уравнения? | А. x1+x2= -p x1*x2= q Б. x1-x2= p x1*x2= q В. x1+x2= p x1*x2= -q |
5 | Решить уравнение x2 – 9=0 | А. 9 Б. -3; 3 В. 0 |
Учитель собирает карточки.
- Актуализация знаний.
Цель: повторение ранее изученного материала и применение его на практике.
Пока идет работа с классом 2 сильных ученика работают с карточками №1 и №2.
№1. Решить графически. Х2= Х+2 ( применение метода при решении квадратного уравнения).
В ходе проверки решения делаем вывод: Для решения уравнения f(x) = g(x) необходимо построить графики функций y = f(x), y = g(x) и найти точки их пересечения; абсциссы точек пересечения и будут корнями уравнения. Применяя графический метод в данном случае мы нашли точное значение корней, но так бывает не всегда. Однако, графический метод часто применяют не для нахождения корней уравнения, а для определения их количества.
№2. Метод разложения на множители. 3х2+2х-1=0
Привести квадратное уравнение общего вида к виду А(х)·В(х)=0, где А(х) и В(х) – многочлены относительно х.
В ходе проверки выяснить каким способом пользовалась и какие еще способы знаем. (Вынесение общего множителя за скобки; использование формул сокращенного умножения; способ группировки.)
Работа с классом: с примением экрана.
Рефлексия: в случае неправильного ответа вывешивается картинка «лупы».
- При каких значениях Х имеет смысл выражения:
А) В) Г) Д) Е)
2. Найти общий знаменатель дробей:
А) = В) Г) = 0
— Какие это уравнения?
— Каков алгоритм решения таких уравнений?
— К какому виду часто приводятся дробно рациональные уравнения?
-Какие уравнения называются квадратными? ( ах2 +вх +с = 0)
— Как можно определить сколько корней имеет квадратное уравнение?
-Какие виды квадратных уравнений бывают? ( с=0; в=0; с=0 и в=0)
— Какие уравнения называются приведенными? ( а=0)
— Какие методы решения приведенных уравнений знаем?
— Как быстро определить корни уравнений? ( а+в+с=0) Х1=1; Х 2 =
Х2 + Х — 2=0 Х2 +2Х-3=0 Х2 -3Х+2=0 5Х2 -8Х+3=0
- Физкультурная минутка для глаз.
Цель: улучшение мозгового кровообращения и снятие утомляемости.
- Быстро поморгать, закрыть глаза и посидеть спокойно, медленно считая до 5. Повторить 4-5 раз.
- Крепко зажмурить глаза (считая до 3), открыть, посмотреть вдаль (считая до 5). Повторить 4-5 раз.
- Исходное положение -сидя на стуле, 1-2-плавно наклонить голову назад, 3-4 голову наклонить вперед, плечи не поднимать. Повторить 4-6 раз. Темп медленный.
- Решение дробных рациональных уравнений.
Цель: отработка навыка приведения к общему знаменателю; отработка навыка решения.
- Привести дробно рациональное уравнение к общему знаменателю – (3 уравнения)
- Решить уравнения -3 ученика у доски, остальные самостоятельно:
А) = В) +1= Г) =
- Самостоятельная работа.
Решить дробные рациональные уравнения.
№ 690 ( д,з) – взаимопроверка с использованием экране.
- Подведение итогов.
Цель: каждый оценивает свой вклад в достижение поставленных в начале урока целей, свою активность, эффективность работы класса, увлекательность и полезность выбранных форм работы. Ребята по кругу высказываются одним предложением, выбирая начало фразы из рефлексивного окна на экране:
- сегодня я узнал…
- было интересно…
- было трудно…
- я выполнял задания…
- я понял, что…
- теперь я могу…
- я почувствовал, что…
- я приобрел…
- я научился…
- у меня получилось …
- я смог…
- Задание на дом. № 690( в,е,ж) , решить 5-ю способами уравнение 3х2 +5х+2=0
Список литературы:
- Алгебра. 8 класс: учеб.для общеобразовательных учреждений/ А45/ Ю.Н.Макарычев, Н.Г.Миндюк, : под ред С.А.Теляковского.- М6Просвещение, 2010г.
- Уроки алгебры в 8 классе: В.И.Жохов .М6Просвещение. 2009г.
- Дидактические материалы по алгебре.8 кл. В.И.Жохов, Ю.Н.Макарычев. М: Просвещение, 2011г.
- Контрольно измерительные материалы по алгебре. 8 кл. М: «Вако», 2011г.
Районный конкурс
« Звездный урок учителя»
НОМИНАЦИЯ
Физико-математические науки
( математика)
Автор:
Болгова Светлана Ивановна,
учитель математики
МБОУ « Весенненская СОШ»
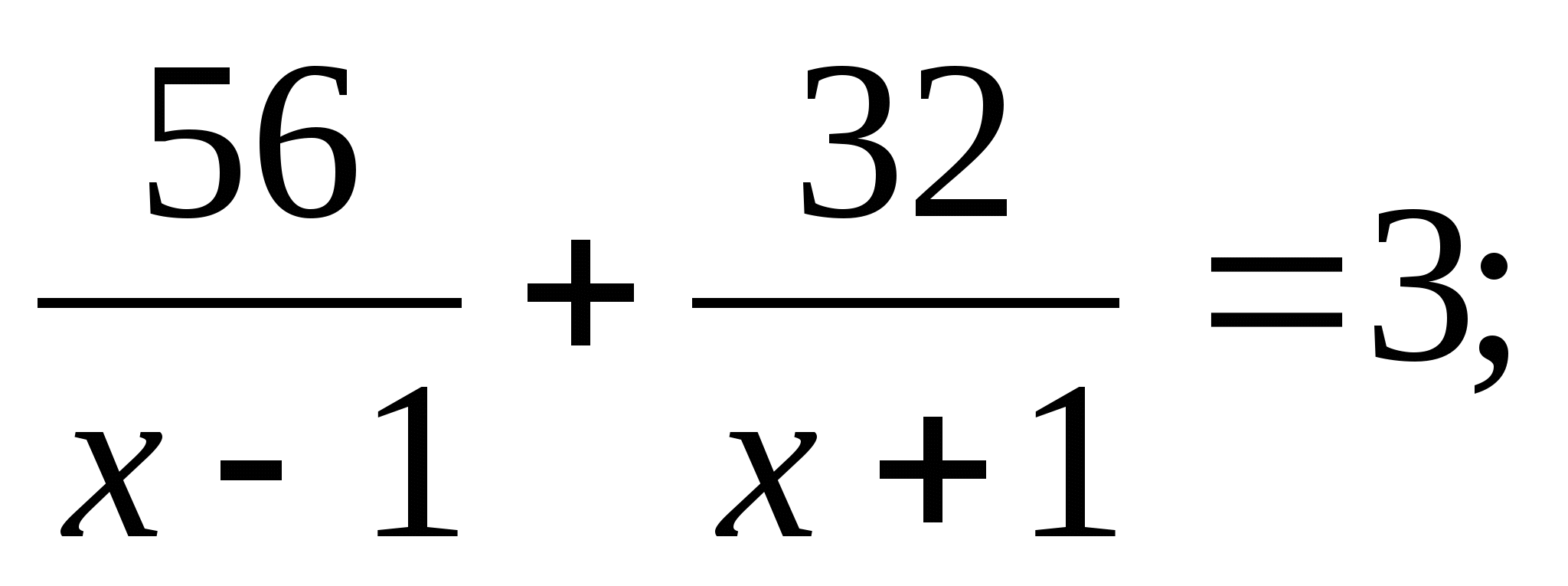 ;
;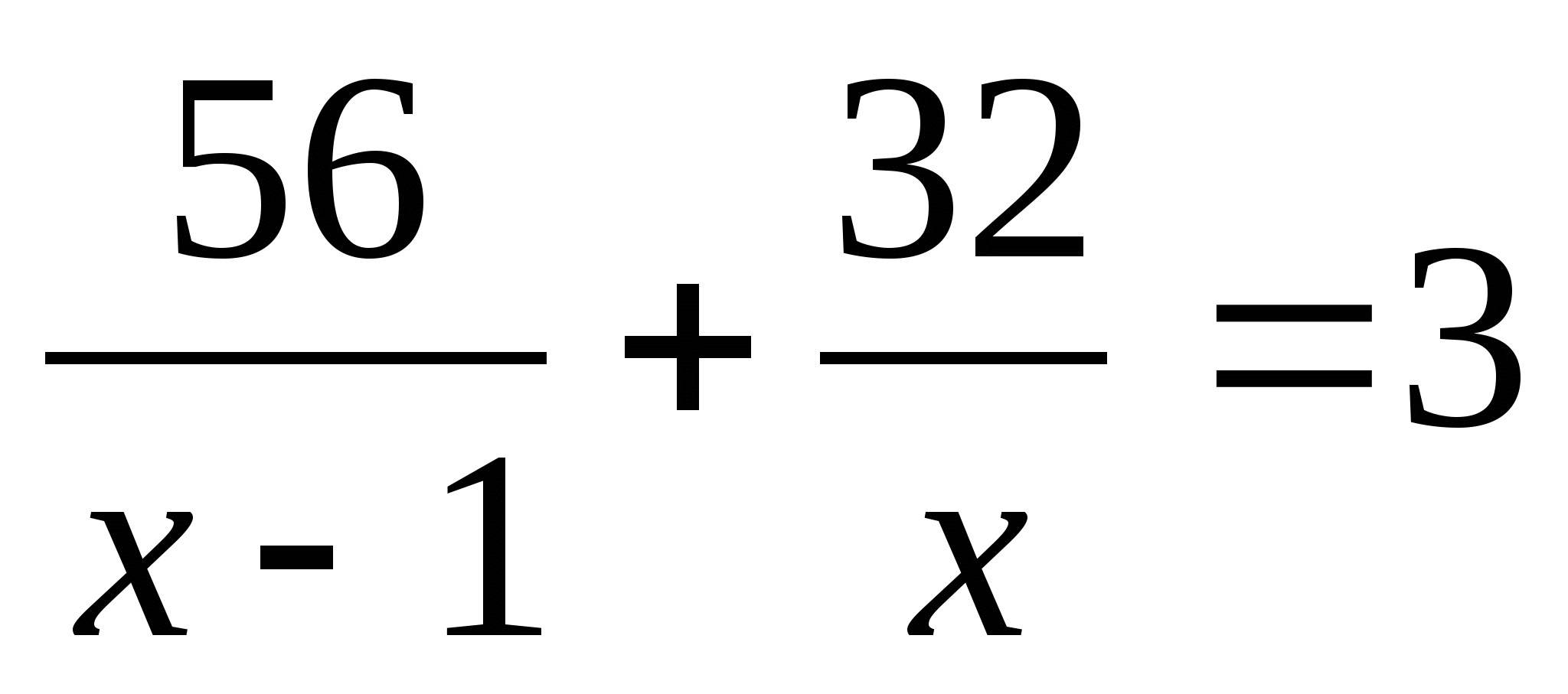 ; 4)
; 4)