Конспект «Сравнение арифметических корней» — УчительPRO

Сравнение арифметических корней

Алгоритм решения задач по алгебре на тему «Сравнение арифметических корней»

---

Свойства корней:

АЛГОРИТМ
«Сравнение арифметических корней»

1. Запишите каждую часть равенства или неравенства в виде корней a = √a², а > 0.
2. Сравните числа, стоящие под знаком корня:
   если а > b > 0, то √a > √b;
   если 0 < а < b, то √a < √b.

3. Сделайте вывод относительно заданных чисел.

---

 

ПРИМЕР 1. Сравните числа: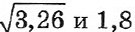 

Решение.

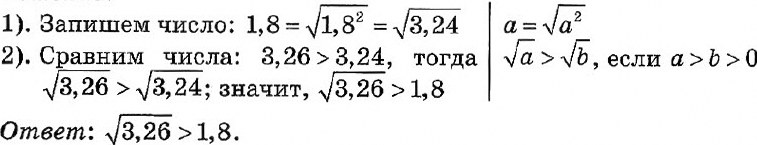
ПРИМЕР 2. (Сравнение суммы корней) Какое из чисел больше — (√5 + √6) или (2 + √7)?

Решение.

Ответ: первое число больше.

ПРИМЕР 3. (Сравнение разности корней) Сравните числа: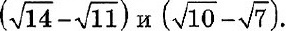 

Ответ: первое число меньше.

ПРИМЕР 4. При каких значениях а равенство 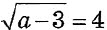 будет верным?

Решение.

Ответ: равенство будет верным при а = 19.

---

Вы смотрели алгоритм решения задач по алгебре на тему «Сравнение корней».

Вернуться в раздел «АЛГЕБРА»

Как сравнить корни разной степени. Формулы корней

Корнем n-ой степени из действительного числа a называется такое число b, для которого выполняется равенство b^n = a. Корни нечетной степени существуют для отрицательных и положительных чисел, а корни четной степени — только для положительных. Значением корня часто является бесконечная десятичная дробь, что затрудняет его точное вычисление, поэтому важно уметь сравнивать корни.

Инструкция

Пусть требуется сравнить два иррациональных числа. Первое, на что следует обратить внимание — это показатели степени корней у сравниваемых чисел. Если показатели одинаковы, то сравнивают подкоренные выражения. Очевидно, что чем больше подкоренное число, тем больше значение корня при равных показателях. Например, пусть надо сравнить из двух и кубический корень из восьми. Показатели одинаковы и равны 3, подкоренные выражения 2 и 8, причем 2

В другом случае показатели степени могут быть разными, а подкоренные выражения одинаковыми. Тоже вполне понятно, что при извлечении корня большей степени получится меньшее число.Возьмите для примера кубический корень из восьми и корень шестой степени из восьми. Если обозначить значение первого корня как a, а второго — как b, то a^3 = 8 и b^6 = 8. Легко видеть, что a должно быть больше b, таким образом кубический корень из восьми больше корня шестой степени из восьми.

Более сложной представляется ситуация с разными показателями степени корня и разными подкоренными выражениями. В таком случае надо найти наименьшее общее кратное для показателей корней и возвести оба выражения в степень, равную наименьшему общему кратному.Пример: надо сравнить 3^1/3 и 2^1/2 (математическая запись корней есть на рисунке). Наименьшее общее кратное для 2 и 3 равно 6. Возведите оба корня в шестую степень. Тут же получится, что 3^2 = 9 и 2^3 = 8, 9 > 8. Следовательно, и 3^1/3 > 2^1/2.

Соблюдение Вашей конфиденциальности важно для нас. По этой причине, мы разработали Политику Конфиденциальности, которая описывает, как мы используем и храним Вашу информацию. Пожалуйста, ознакомьтесь с нашими правилами соблюдения конфиденциальности и сообщите нам, если у вас возникнут какие-либо вопросы.

Сбор и использование персональной информации

Под персональной информацией понимаются данные, которые могут быть использованы для идентификации определенного лица либо связи с ним.

От вас может быть запрошено предоставление вашей персональной информации в любой момент, когда вы связываетесь с нами.

Ниже приведены некоторые примеры типов персональной информации, которую мы можем собирать, и как мы можем использовать такую информацию.

Какую персональную информацию мы собираем:

• Когда вы оставляете заявку на сайте, мы можем собирать различную информацию, включая ваши имя, номер телефона, адрес электронной почты и т.д.

Как мы используем вашу персональную информацию:

• Собираемая нами персональная информация позволяет нам связываться с вами и сообщать об уникальных предложениях, акциях и других мероприятиях и ближайших событиях.
• Время от времени, мы можем использовать вашу персональную информацию для отправки важных уведомлений и сообщений.
• Мы также можем использовать персональную информацию для внутренних целей, таких как проведения аудита, анализа данных и различных исследований в целях улучшения услуг предоставляемых нами и предоставления Вам рекомендаций относительно наших услуг.
• Если вы принимаете участие в розыгрыше призов, конкурсе или сходном стимулирующем мероприятии, мы можем использовать предоставляемую вами информацию для управления такими программами.

Раскрытие информации третьим лицам

Мы не раскрываем полученную от Вас информацию третьим лицам.

Исключения:

• В случае если необходимо — в соответствии с законом, судебным порядком, в судебном разбирательстве, и/или на основании публичных запросов или запросов от государственных органов на территории РФ — раскрыть вашу персональную информацию. Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях.
• В случае реорганизации, слияния или продажи мы можем передать собираемую нами персональную информацию соответствующему третьему лицу – правопреемнику.

Защита персональной информации

Мы предпринимаем меры предосторожности — включая административные, технические и физические — для защиты вашей персональной информации от утраты, кражи, и недобросовестного использования, а также от несанкционированного доступа, раскрытия, изме

Как сравнить числа с разными степенями корня. Сравнение чисел. Исчерпывающий гид (2019)

Факт 1.
\(\bullet\) Возьмем некоторое неотрицательное число \(a\) (то есть \(a\geqslant 0\) ). Тогда (арифметическим) квадратным корнем из числа \(a\) называется такое неотрицательное число \(b\) , при возведении которого в квадрат мы получим число \(a\) : \[\sqrt a=b\quad \text{то же самое, что }\quad a=b^2\] Из определения следует, что \(a\geqslant 0, b\geqslant 0\) . Эти ограничения являются важным условием существования квадратного корня и их следует запомнить!
Вспомним, что любое число при возведении в квадрат дает неотрицательный результат. То есть \(100^2=10000\geqslant 0\) и \((-100)^2=10000\geqslant 0\) .
\(\bullet\) Чему равен \(\sqrt{25}\) ? Мы знаем, что \(5^2=25\) и \((-5)^2=25\) . Так как по определению мы должны найти неотрицательное число, то \(-5\) не подходит, следовательно, \(\sqrt{25}=5\) (так как \(25=5^2\) ).
Нахождение значения \(\sqrt a\) называется извлечением квадратного корня из числа \(a\) , а число \(a\) называется подкоренным выражением.
\(\bullet\) Исходя из определения, выражения \(\sqrt{-25}\) , \(\sqrt{-4}\) и т.п. не имеют смысла.

Факт 2.
Для быстрых вычислений полезно будет выучить таблицу квадратов натуральных чисел от \(1\) до \(20\) : \[\begin{array}{|ll|} \hline 1^2=1 & \quad11^2=121 \\ 2^2=4 & \quad12^2=144\\ 3^2=9 & \quad13^2=169\\ 4^2=16 & \quad14^2=196\\ 5^2=25 & \quad15^2=225\\ 6^2=36 & \quad16^2=256\\ 7^2=49 & \quad17^2=289\\ 8^2=64 & \quad18^2=324\\ 9^2=81 & \quad19^2=361\\ 10^2=100& \quad20^2=400\\ \hline \end{array}\]

Факт 3.
Какие действия можно выполнять с квадратными корнями?
\(\bullet\) Сумма или разность квадратных корней НЕ РАВНА квадратному корню из суммы или разности, то есть \[\sqrt a\pm\sqrt b\ne \sqrt{a\pm b}\] Таким образом, если вам нужно вычислить, например, \(\sqrt{25}+\sqrt{49}\) , то первоначально вы должны найти значения \(\sqrt{25}\) и \(\sqrt{49}\) , а затем их сложить. Следовательно, \[\sqrt{25}+\sqrt{49}=5+7=12\] Если значения \(\sqrt a\) или \(\sqrt b\) при сложении \(\sqrt a+\sqrt b\) найти не удается, то такое выражение дальше не преобразуется и остается таким, как есть. Например, в сумме \(\sqrt 2+ \sqrt {49}\) мы можем найти \(\sqrt{49}\) – это \(7\) , а вот \(\sqrt 2\) никак преобразовать нельзя, поэтому \(\sqrt 2+\sqrt{49}=\sqrt 2+7\) . Дальше это выражение, к сожалению, упростить никак нельзя \(\bullet\) Произведение/частное квадратных корней равно квадратному корню из произведения/частного, то есть \[\sqrt a\cdot \sqrt b=\sqrt{ab}\quad \text{и}\quad \sqrt a:\sqrt b=\sqrt{a:b}\] (при условии, что обе части равенств имеют смысл )
Пример: \(\sqrt{32}\cdot \sqrt 2=\sqrt{32\cdot 2}=\sqrt{64}=8\) ; \(\sqrt{768}:\sqrt3=\sqrt{768:3}=\sqrt{256}=16\) ; \(\sqrt{(-25)\cdot (-64)}=\sqrt{25\cdot 64}=\sqrt{25}\cdot \sqrt{64}= 5\cdot 8=40\) . \(\bullet\) Пользуясь этими свойствами, удобно находить квадратные корни из больших чисел путем разложения их на множители.
Рассмотрим пример. Найдем \(\sqrt{44100}\) . Так как \(44100:100=441\) , то \(44100=100\cdot 441\) . По признаку делимости число \(441\) делится на \(9\) (так как сумма его цифр равна 9 и делится на 9), следовательно, \(441:9=49\) , то есть \(441=9\cdot 49\) .
Таким образом, мы получили: \[\sqrt{44100}=\sqrt{9\cdot 49\cdot 100}= \sqrt9\cdot \sqrt{49}\cdot \sqrt{100}=3\cdot 7\cdot 10=210\] Рассмотрим еще один пример: \[\sqrt{\dfrac{32\cdot 294}{27}}= \sqrt{\dfrac{16\cdot 2\cdot 3\cdot 49\cdot 2}{9\cdot 3}}= \sqrt{ \dfrac{16\cdot4\cdot49}{9}}=\dfrac{\sqrt{16}\cdot \sqrt4 \cdot \sqrt{49}}{\sqrt9}=\dfrac{4\cdot 2\cdot 7}3=\dfrac{56}3\]
\(\bullet\) Покажем, как вносить числа под знак квадратного корня на примере выражения \(5\sqrt2\) (сокращенная запись от выражения \(5\cdot \sqrt2\) ). Так как \(5=\sqrt{25}\) , то \ Заметим также, что, например,
1) \(\sqrt2+3\sqrt2=4\sqrt2\) ,
2) \(5\sqrt3-\sqrt3=4\sqrt3\)
3) \(\sqrt a+\sqrt a=2\sqrt a\) .

Почему так? Объясним на примере 1). Как вы уже поняли, как-то преобразовать число \(\sqrt2\) мы не можем. Представим, что \(\sqrt2\) – это некоторое число \(a\) . Соответственно, выражение \(\sqrt2+3\sqrt2\) есть не что иное, как \(a+3a\) (одно число \(a\) плюс еще три таких же числа \(a\) ). А мы знаем, что это равно четырем таким числам \(a\) , то есть \(4\sqrt2\) .

Факт 4.
\(\bullet\) Часто говорят “нельзя извлечь корень”, когда не удается избавиться от знака \(\sqrt {} \ \) корня (радикала) при нахождении значения какого-то числа. Например, извлечь корень из числа \(16\) можно, потому что \(16=4^2\) , поэтому \(\sqrt{16}=4\) . А вот извлечь корень из числа \(3\) , то есть найти \(\sqrt3\) , нельзя, потому что нет такого числа, которое в квадрате даст \(3\) .
Такие числа (или выражения с такими числами) являются иррациональными. Например, числа \(\sqrt3, \ 1+\sqrt2, \ \sqrt{15}\) и т.п. являются иррациональными.
Также иррациональными являются числа \(\pi\) (число “пи”, приблизительно равное \(3,14\) ), \(e\) (это число называют числом Эйлера, приблизительно оно равно \(2,7\) ) и т.д.
\(\bullet\) Обращаем ваше внимание на то, что любое число будет либо рациональным, либо иррациональным. А вместе все рациональные и все иррациональные числа образуют множество, называющееся множеством действительных (вещественных) чисел. Обозначается это множество буквой \(\mathbb{R}\) .
Значит, все числа, которые на данный момент мы знаем, называются вещественными числами.

Факт 5.
\(\bullet\) Модуль вещественного числа \(a\) – это неотрицательное число \(|a|\) , равное расстоянию от точки \(a\) до \(0\) на вещественной прямой. Например, \(|3|\) и \(|-3|\) равны 3, так как расстояния от точек \(3\) и \(-3\) до \(0\) одинаковы и равны \(3\) .
\(\bullet\) Если \(a\) – неотрицательное число, то \(|a|=a\) .
Пример: \(|5|=5\) ; \(\qquad |\sqrt2|=\sqrt2\) . \(\bullet\) Если \(a\) – отрицательное число, то \(|a|=-a\) .
Пример: \(|-5|=-(-5)=5\) ; \(\qquad |-\sqrt3|=-(-\sqrt3)=\sqrt3\) .
Говорят, что у отрицательных чисел модуль “съедает” минус, а положительные числа, а также число \(0\) , модуль оставляет без изменений.
НО такое правило годится только для чисел. Если у вас под знаком модуля находится неизвестная \(x\) (или какая-то другая неизвестная), например, \(|x|\) , про которую мы не знаем, положительная она, равна нулю или отрицательная, то избавиться от модуля мы не можем. В этом случае это выражение таким и остается: \(|x|\) . \(\bullet\) Имею

Подскажите как сравнивать корни? — MatFaq.ru

Как сравнивать корни?

1. Самая простая ситуация, когда один  корень оказался числом отрицательным, а другой — положительным. Такое возможно, когда один из корней нечётной степени, и под корнем стоит отрицательное число, а другой корень любой степени, но под ним стоит неотрицательное число.

Примеры

Сравнить  

и .

Отрицательное число всегда меньше положительного 

Пример извлекаемых корней

2. Для остальных случаев правило простое. Нужно возвести оба корня в такую одинаковую степень, чтобы избавиться от обоих корней. Необходимо только обязательно помнить о том, что корень чётной степени всегда неотрицательный, а корень нечётной степени может иметь любой знак в зависимости от знака выражения под корнем.

Примеры:

Сравнить 

 и  

————————

Сравнить  

  и   

————————

Сравнить 

 и  

Наименьшее общее кратное чисел 3 и 7 равно 21, поэтому возводить корни следует в степень 21

128 > 8    ⇒     

————————

Сравнить

 и  

-128 < -8    ⇒     

————————-

Сравнить    

 и   

Наименьшее общее кратное чисел 15 и 20 равно 60, поэтому возводить оба корня следует в 60 степень

16 < 27   ⇒    

—————————

Сравнить  

 и   

Наименьшее общее кратное чисел 2 и 3 равно 6, поэтому корни нужно возводить в степень 6.

  ⇒   

————————-

Сравнить  

 и   

-0,00001 < -0,000001   ⇒   

Помогите решить / разобраться (М)

SpiderHulk
Методы избавления от квадратных корней это возведение в квадрат и умножение суммы на разность. Или разности на сумму.
Можно применять последовательно.

Если у нас есть неравенство например 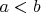и число , то во-первых 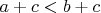а если положительно, то
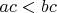
Если

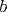и оба положительные, то .
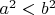Так что операции прибавления числа к обоим частям неравенства, умножения обоих частей неравенства на положительное число, а также возведение обоих частей неравенства (если они положительные) в квадрат — не меняет знак неравенства.

Если в обоих частях неравенства есть квадратные корни, то сперва надо избавиться от них в одной части неравенства, а затем в другой.

Если в одной части неравенства есть только произведение, часть множителей которого — квадратные корни, то избавиться от корней можно возведением в квадрат, предварительно убедившись что обе части неравенства больше нуля.
После этого корни останутся только в одной части неравенства (допустим это оказалась правая сторона). Тогда мы слагаемые без квадратных корней переносим вправо, где корней уже нет, и получаем неравенство с целыми числами справа и корнями слева. Опять убедившись в том что обе части неравенства все еще больше нуля, возводим их обе в квадрат и получаем неравенство без корней.

Другой способ — домножить разность на сумму или сумму на разность. То есть воспользоваться формулой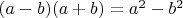
Если у нас в одной части неравенства есть сумма например 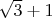то домножаем её (и другую сторону неравенства естественно) на разность 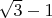, получаем 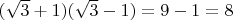и корень пропал. Здесь надо следить за тем, что домножаем обе части неравенства на положительное число.