Как найти функцию по графику

Хочешь подготовиться к ОГЭ или ЕГЭ по математике на отлично?

Понятие «функция» пронизывает все сферы математики и не только. Мы все знаем, что функция записывается как , но можешь ли ты ответить, что обозначает эта формула? Если да, то ты большой молодец! А если нет – не страшно! Сейчас быстренько во всем разберемся!

Так вот, функция отражает зависимость величин друг от друга: то есть при изменении одного числа , по некоторому закону изменяется . Зависимость, или взаимосвязь — вот ключевые слова при определении понятия функции.

Попробуй самостоятельно придумать несколько примеров из жизни, где четко проявляется зависимость одного от другого.

И. Не можешь придумать ни один пример? Как так! Смотри:

Допустим автомобиль движется со средней скоростью км/ч, как тогда выразить зависимость пути от времени ? Правильно:

То есть чем больше времени автомобилист проведет за рулем, тем больше расстояние он преодолеет на своем автомобиле.

Чем не зависимость?

Что в этом случае будет , что , и как будет выражено в итоге ? Проведем параллели между физической формулой и привычной нам записью функции :

• , то есть путь, который проедет автомобилист;
• , время, которое он проведет в пути;
• — зависимость пути от времени, учитывая, что скорость на всем пути постоянна.

Разобрался что к чему? Теперь перейдем на математический язык. Итак. Еще раз смотрим на нашу формулу:

Слева стоит — это и есть функция. За этой буквой может быть все что угодно: температура, скорость, сила, путь – неважно! — зависимая величина. Она может зависеть от множества критериев. Например, как в нашем случае, зависимость пути от времени, проведенном в дороге при движении с постоянной скоростью.

Справа у нас стоит . Эта величина переменная, или, как говорят математики, «аргумент». Логично, что чем больше времени проведет автомобилист в дороге, тем большее расстояние он проедет (конечно, если скорость будет постоянна, и он не встрянет намертво в московских пробках).

Справа у нас также есть , за этим скрываются все действия, совершаемые над . В нашем случае мы говорим, что , а так как км/ч, то под скрывается умножение на , вот мы и получаем — .

Теперь думаю тебе все понятно? Подведем краткий итог:

1. — это формула, обозначающая функцию, то есть зависимость одной переменной от другой;
2. — переменная величина, или, аргумент;
3. — зависимая величина – изменяется при изменении аргумента, то есть согласно какой-либо определенной формуле , отражающей зависимость одной величины от другой.

Теперь, когда ты понял суть понятия «функция», знаешь что такое переменная величина, а что постоянная, посмотрим на определение функции, каким его дают математики:

Вроде и есть… и есть, и даже правило есть, но что это за множества такие? «О них мы ни слова не говорили!» — воскликнешь ты. Не паникуй!:) Множества – это очень просто, сейчас все-все проясним!

Вернемся к нашему примеру – автомобилист едет с постоянной скоростью и проезжает расстояние, которое зависит от того, сколько времени он провел в пути. Все верно? Разбираемся дальше. Мы говорили, что , это как раз и есть время, проведенное в пути. Каким оно может быть?

Ты сейчас крайней удивлен, но все же, каким может быть это время? Правильно, чисто теоретически от до . Вот ты сам и определил для нашего конкретного случая множество , а иначе говоря, допустимые значения аргумента или область определения функции . Запомнить очень легко: что определяет нашу функцию? От чего зависит игрек, и что мы меняем? Функцию определяет икс! Соответственно, область определения – это возможные значения .

Теперь давай рассматривать, что такое множество . Думаю, ты сам ответишь, что путь не может быть отрицательным, так что в нашей с тобой придуманной функции так же может принимать значения в промежутке от до . Это называется областью значений функции , то есть множество , которые существуют для данной функции.

1. Допустимые значения аргумента, или область определения функции — это то, что связано с возможными , при которых функция имеет смысл.
2. Область значений функции — это то, какие значения принимает , при допустимых значениях .

Легко? То-то же. Давай потренируемся находить области определения функции и ее допустимые значения.

Для начала попробуй найти область определения функции:

Все верно? Молодец! Теперь попробуем найти область значения функции:

Сошлось? Молодец! Еще раз поработаем с графиками, только теперь чуть-чуть посложнее – найти и область определения функции, и область значения функции:

С графиками, я думаю, ты разобрался. Теперь попробуем в соответствии с формулами найти область определения функции (если ты не знаешь как это сделать, прочитай раздел про ОДЗ):

1. , так как подкоренное выражение должно быть больше или равно нулю.
2. , так как на ноль делить нельзя и подкоренное выражение не может быть отрицательным.
3. , так как , соответственно при всех .
4. , так как на ноль делить нельзя.

Однако, у нас остался еще один не разобранный момент… Еще раз повторю определение и сделаю на нем акцент:

Заметил? Слово «единственный» — это очень-очень важный элемент нашего определения. Постараюсь объяснить тебе на пальцах.

Допустим, у нас есть функция, заданная прямой. . При , мы подставляем данное значение в наше «правило» и получаем, что . Одному значению соответствует одно значение . Мы даже можем составить таблицу различных значений и построить график данной функции, чтобы убедится в этом.

Как ты убедился – графиком является прямая, в которой одному значению соответствует одно значение (данный факт показан красными линиями).

Соответственно, данная зависимость подходит под определение функции.

А что ты скажешь о такой зависимости: , то есть параболы? Является ли она функцией? Давай составим также табличку значений:

«Смотри! — скажешь ты, -« » встречается два раза!» Так быть может парабола не является функцией? Нет, является! То, что « » встречается два раза далеко не повод обвинять параболу в неоднозначности! Дело в том, что, при расчёте для , мы получили один игрек.

И при расчёте с мы получили один игрек. Так что все верно, парабола является функцией. Посмотри на график:

Разобрался? Если нет, вот тебе жизненный пример сооовсем далекий от математики!

Допустим, у нас есть группа абитуриентов, познакомившихся при подаче документов, каждый из которых в разговоре рассказал, где он живет:

Согласись, вполне реально, что несколько ребят живут в одном городе, но невозможно, чтобы один человек жил в нескольких городах одновременно. Это как бы логичное представление нашей «параболы» — нескольким разным икс соответствует один и тот же игрек.

Теперь придумаем пример, когда зависимость не будет функцией. Допустим, эти же ребята рассказывали, на какие специальности они подали документы:

Здесь у нас совершенно другая ситуация: один человек может спокойно подать документы как на одно, так и на несколько направлений. То есть одному элементу множества ставится в соответствие

несколько элементов множества . Соответственно, это не функция.

Проверим твои знания на практике. Определи по рисункам, что является функцией, а что нет:

На всех рисунках кроме В) и Е) на один приходится несколько !

Уверена, теперь, ты с легкостью отличишь функцию от не функции, скажешь, что такое аргумент и что такое зависимая переменная, а так же определишь область допустимых значений аргумента и область определения функции. Приступаем к следующему разделу – как задать функцию?

Как ты думаешь, что означают слова «задать функцию»? Правильно, это значит объяснить всем желающим, о какой функции в данном случае идет речь. Причем объяснить так, чтобы каждый понял тебя правильно и нарисованные людьми по твоему объяснению графики функций были одинаковы.

Как это можно сделать? Как задать функцию?

Самый простой способ, который уже не раз применялся в этой статье – с помощью формулы. Мы пишем формулу, и, подставляя в нее значение , высчитываем значение . А как ты помнишь, формула – это закон, правило, по которому нам и другому человеку становится ясно, как икс превращается в игрек.

Обычно, именно так и делают – в заданиях мы видим уже готовые функции, заданные формулами, однако, существуют и другие способы задать функцию, про которые все забывают, в связи с чем вопрос «как еще можно задать функцию?» ставит в тупик. Разберемся во всем по порядку, а начнем с аналитического способа.

Аналитический способ это и есть задание функции с помощью формулы. Это самый универсальный и исчерпывающий и однозначный способ. Если у тебя есть формула, то ты знаешь о функции абсолютно все – ты можешь составить по ней табличку значений, можешь построить график, определить, где функция возрастает, а где убывает, в общем, исследовать ее по полной программе.

Напомню, что в записи выражение в скобках называется аргументом. И этот аргумент может быть любым выражением, не обязательно просто . Соответственно, каким бы ни был аргумент (выражение в скобках), мы его запишем вместо в выражении .

Рассмотрим еще задание, связанное с аналитическим способом задания функции, которое будет у тебя на экзамене. Задание звучит следующим образом:

Уверена, что сначала, ты испугался, увидев такое выражение, но в нем нет абсолютно ничего страшного!

Все как и в прошлом примере: каким бы ни был аргумент (выражение в скобках), мы его запишем вместо в выражении . Например, для функции .

Что же нужно сделать в нашем примере? Вместо надо написать , а вместо – :

А дальше, используя свойства степени (можешь лишний раз одним глазком заглянуть в соответствующую тему – не помешает), а именно:

Теперь попробуй самостоятельно найти значение следующих выражений:

Мы привыкли, что функция имеет вид , даже в наших примерах мы задаем функцию именно таким образом, однако аналитически можно задать функцию в неявном виде, например . Попробуй построить эту функцию самостоятельно.

Какое уравнение мы в итоге вывели? Правильно! Линейное, а это значит, что графиком будет прямая линия. Сделаем табличку, чтобы определить, какие точки принадлежат нашей прямой:

Вот так из неявной формулы получилась линейная функция. А теперь посмотри следующую формулу: . Является ли она функцией? Согласись, вызывает затруднение… Попробуй подставить различные значения и посмотреть, какой им соответствует.

Вот как раз то, о чем мы говорили… Одному соответствует несколько . Попробуем нарисовать то, что получилось:

Является ли то, что у нас получилось функцией? Правильно, нет! Почему? Попробуй ответить на этот вопрос с помощью рисунка. Что у тебя вышло?

«Потому что одному значению соответствует несколько значений !»

Какой вывод мы можем из этого сделать? Правильно, функция не всегда может быть выражена явно, и не всегда то, что «замаскировано» под функцию является функцией!

Как следует из названия, этот способ представляет собой простую табличку. Да, да. Наподобие той, которой мы с тобой уже составляли. Например:

Как ты уже знаешь, в первой строчке мы ставим значение аргумента, а во второй строчке — соответствующие ему значение функции. Таким образом, в таблице каждому иксу соответствует одно значение игрека.

Заметь, в последней приведенной табличке невозможно четко определить правило, по которому игрек зависит от икс. Так тоже бывает и в этом нет ничего страшного, просто мы не можем вот так сразу взять и определить правило.

Если тебя это смущает, приведу в пример другую таблицу:

Здесь ты сразу подметил закономерность – игрек в три раза больше чем икс. А теперь задание на «очень хорошо подумать»: как ты считаешь, равносильная ли функция, заданная в виде таблицы, функции ?

Видишь разницу? Дело совсем не в отмеченных точках! Присмотрись внимательнее:

Теперь увидел? Когда мы задаем функцию табличным способом, мы на графике отражаем только те точки, которые есть у нас в таблице и линия (как в нашем случае) проходит только через них. Когда мы задаем функцию аналитическим способом, мы можем взять любые точки, и наша функция ими не ограничивается. Вот такая вот особенность. Запоминай!

Графический способ построения функции не менее удобен. Мы рисуем нашу функцию, а другой заинтересованный человек может найти чему равен игрек при определенном икс и так далее. Графический и аналитический способы одни из самых распространенных. Однако, здесь нужно помнить о чем мы с тобой говорили в самом начале – не каждая «загогулина» нарисованная в системе координат является функцией! Вспомнил? На всякий случай скопирую тебе сюда определение, что функцией является:

Как правило, люди обычно называют именно те три способа задания функции, которые мы разобрали – аналитический (с помощью формулы), табличный и графический, напрочь забывая о том, что функцию можно словесно описать. Как это? Да очень просто!

Как же описать функцию словесно? Возьмем наш недавний пример — . Данную функцию можно описать «каждому действительному значению икс соответствует его утроенное значение». Вот и все. Ничего сложного. Ты, конечно, возразишь — «есть настолько сложные функции, которые словесно задать просто невозможно!» Да, есть и такие, но есть функции, которые описать словесно легче, чем задать формулой. Например: «каждому натуральному значению икс соответствует разница между цифрами, из которых он состоит, при этом за уменьшаемое берется наибольшее цифра, содержащиеся в записи числа». Теперь рассмотрим, как наше словесное описание функции реализуется на практике:

Наибольшая цифра в данном числе – , соответственно, – уменьшаемое, тогда:

Теперь перейдем к самому интересному — рассмотрим, основные виды функций, с которыми ты работал/работаешь и будешь работать в курсе школьной и институтской математики, то есть познакомимся с ними, так сказать и дадим им краткую характеристику. Более подробно про каждую функцию читай в соответствующем разделе.

Графиком данной функции служит прямая, поэтому построение линейной функции сводится к нахождению координат двух точек.

Положение прямой на координатной плоскости зависит от углового коэффициента .

Графиком функции является парабола, при ветви параболы направлены вниз, при — вверх.

Многие свойства квадратичной функции зависят от значения дискриминанта. Дискриминант вычисляется по формуле

Положение параболы на координатной плоскости относительно значения и коэффициента показаны на рисунке:

Область определения зависит от экстремума данной функции (точки вершины параболы) и коэффициента (направления ветвей параболы)

Функция, представляющая собой обратную пропорциональность.

Число называется коэффициентом обратной пропорциональности. В зависимости от того, какое значение , ветви гиперболы находятся в разных квадратах:

Хочешь проверить свои силы и узнать результат насколько ты готов к ЕГЭ или ОГЭ?

Тому кто написал данную статью большое спасибо.Побольше бы таких людей.Вы мне очень помогли. СПАСИБО.

Влад, всегда рады помочь. Спасибо большое за теплые слова. Мы правда тронуты. Следи за нашей рассылкой. Будут еще такие же полезные посты. Надеюсь ты на нее подписан.

Учебник написан «с нуля». Поэтому ошибки могут быть. Но мы их постоянно исправляем. Будем признательны, если подскажете где ошибка.

Ошибка в слове «тоже» у Rai ))) Большое спасибо за материал!

Добрый вечер!Подскажите, а то запутался. Я что-то упустил или всё таки в первом задании-где нужно ответить на области определения функции и найти её значение в варианте Б) D(y)=(2;2)u (2;6) необходимо D(y)=(-2;2)(2;6)-пропущен ,,-. Также и в следующем задании вариант Б) E(y) = (-&;1) u (1;+&), а нужно E(y) = (-&;-1) (и здесь знак не объединения, а другой скорей всего) (1;+&).

Добрый вечер!Подскажите, а то запутался. Я что-то упустил или всё таки в первом задании-где нужно ответить на области определения функции и найти её значение в варианте Б) D(y)=(2;2)u (2;6) необходимо D(y)=(-2;2)(2;6)-пропущен ,,-. Также и в следующем задании вариант Б) E(y) = (-&;1) u (1;+&), а нужно E(y) = (-&;-1) (и здесь знак не объединения, а другой скорей всего) (1;+&).

Арсений, спасибо за замечание! Нужен именно знак объединения, который показывает, что подходят значения из обеих областей.

Здравствуйте, только начал изучать функции и столкнулся с проблемой. Не могли бы вы прояснить: Почему в начале Б: D(y)=(2;2)∪(2;6), а не D(y)=(-2;2)∪(6;2) ? Почему во вторых рисунках Б) E(y)=(−∞;1]∪[1;+∞), а не E(y)=(−∞;-1]∪[-1;+∞) и точно ли так функция записывается?

Распространение материалов без согласования допустимо при наличии dofollow-ссылки на страницу-источник.

Соблюдение Вашей конфиденциальности важно для нас. По этой причине, мы разработали Политику Конфиденциальности, которая описывает, как мы используем и храним Вашу информацию. Пожалуйста, ознакомьтесь с нашими правилами соблюдения конфиденциальности и сообщите нам, если у вас возникнут какие-либо вопросы.

Под персональной информацией понимаются данные, которые могут быть использованы для идентификации определенного лица либо связи с ним.

От вас может быть запрошено предоставление вашей персональной информации в любой момент, когда вы связываетесь с нами.

Ниже приведены некоторые примеры типов персональной информации, которую мы можем собирать, и как мы можем использовать такую информацию.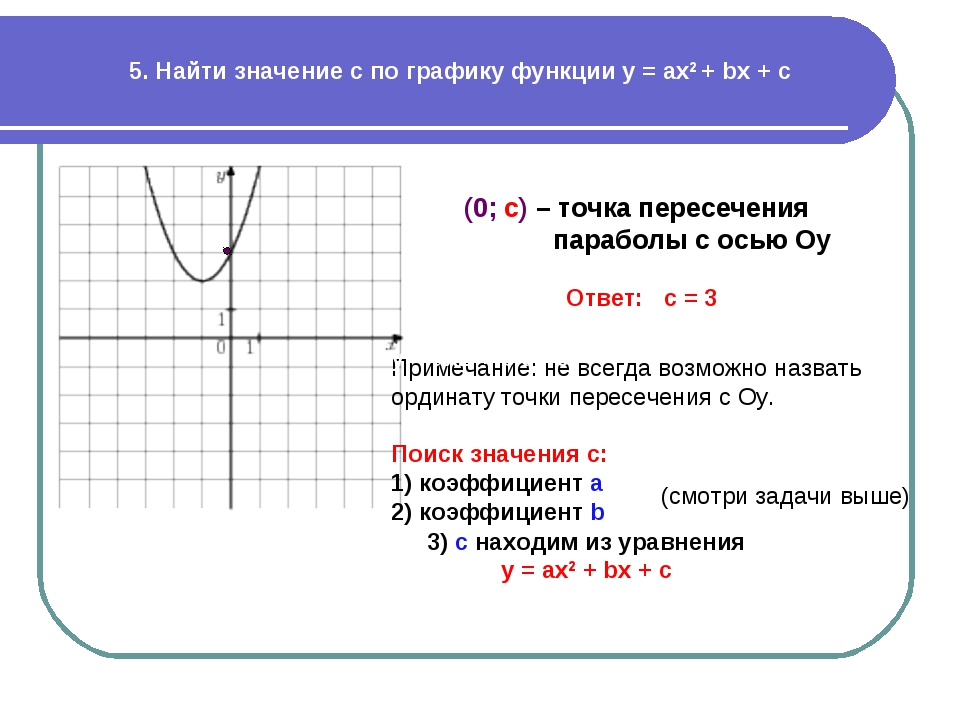

• Когда вы оставляете заявку на сайте, мы можем собирать различную информацию, включая ваши имя, номер телефона, адрес электронной почты и т.д.

• Собираемая нами персональная информация позволяет нам связываться с вами и сообщать об уникальных предложениях, акциях и других мероприятиях и ближайших событиях.
• Время от времени, мы можем использовать вашу персональную информацию для отправки важных уведомлений и сообщений.
• Мы также можем использовать персональную информацию для внутренних целей, таких как проведения аудита, анализа данных и различных исследований в целях улучшения услуг предоставляемых нами и предоставления Вам рекомендаций относительно наших услуг.
• Если вы принимаете участие в розыгрыше призов, конкурсе или сходном стимулирующем мероприятии, мы можем использовать предоставляемую вами информацию для управления такими программами.

Мы не раскрываем полученную от Вас информацию третьим лицам.

• В случае если необходимо — в соответствии с законом, судебным порядком, в судебном разбирательстве, и/или на основании публичных запросов или запросов от государственных органов на территории РФ — раскрыть вашу персональную информацию. Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях.
• В случае реорганизации, слияния или продажи мы можем передать собираемую нами персональную информацию соответствующему третьему лицу – правопреемнику.

Мы предпринимаем меры предосторожности — включая административные, технические и физические — для защиты вашей персональной информации от утраты, кражи, и недобросовестного использования, а также от несанкционированного доступа, раскрытия, изменения и уничтожения.

Для того чтобы убедиться, что ваша персональная информация находится в безопасности, мы доводим нормы соблюдения конфиденциальности и безопасности до наших сотрудников, и строго следим за исполнением мер соблюдения конфиденциальности.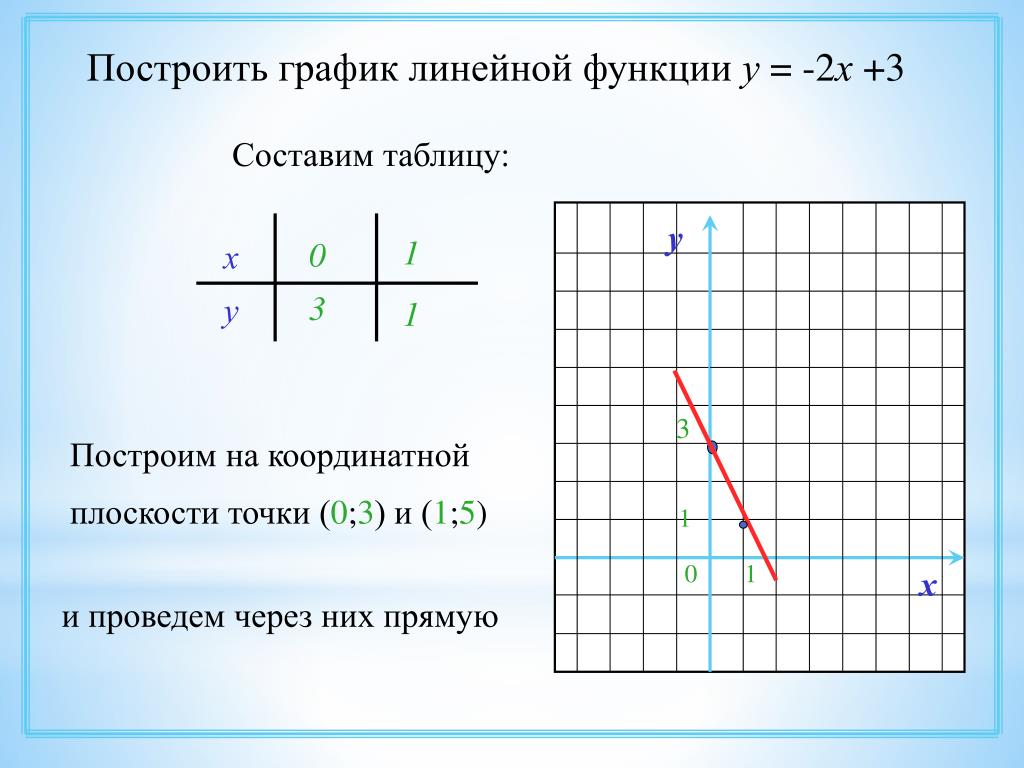

Ваш комментарий принят, после модерации он будет опубликован на данной странице.

Хотите узнать что скрыто под катом и получать эксклюзивные материалы по подготовке к ОГЭ и ЕГЭ? Оставьте e-mail

Хотите открыть все скрытые тексты в учебнике? Приобретите подписку и тексты будут открыты до даты экзамена. Стоимость подписки 499 руб

Вопросы по статистике к экзамену

Как по графику определить формулу функции

Графики функций являются одним из важнейших знаний, необходимых в учебе, наравне с таблицей умножения. Они являются фундаментом, на них все основано, из них все строится и к ним все сводится.

Таблица графиков функций.

Название функции	Формула функции	График функции	Название графика

Линейная (прямопропорциональная) функция.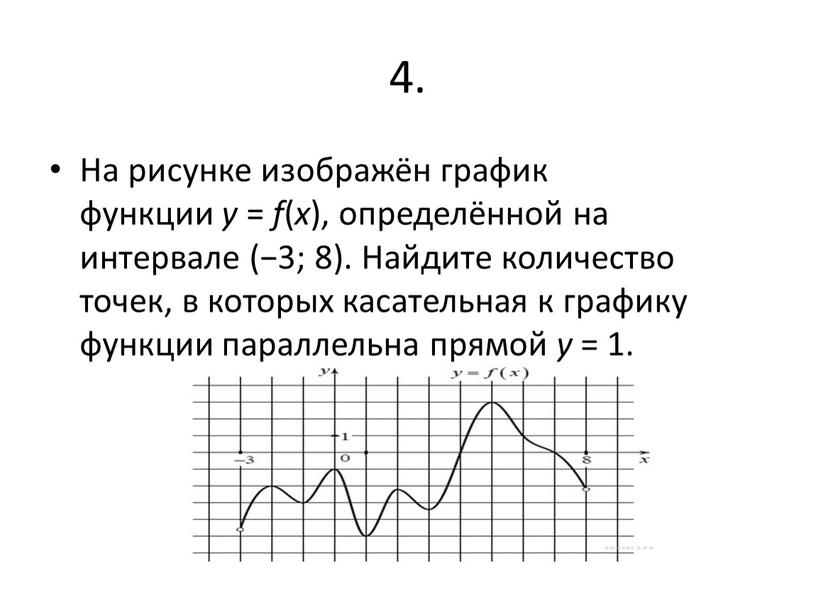

Основное свойство линейных функций: приращение функции пропорционально приращению аргумента. Т.е. функция оказывается обобщением прямой пропорциональности.

Степенная функция – обратнопропорциональная – это функциональная зависимость, когда увеличение аргумента вызывает соответствующее уменьшение функции.

Функция Бесселя первого рода.

График функции Бесселя похож на синусоиду, колебания которой затухают пропорционально , хотя на самом деле нули функции расположены не периодично.

Квадратичная функция – парабола.

Большинство свойств квадратичной функции связаны с значением дискриминанта.

Квадратичная функция.

Общий случай квадратичной зависимости: коэффициент a – произвольное действительное число не равное нулю (a принадлежит R, a ≠ 0), b, c – любые действительные числа.

Степенная функция – это функция y = x a , где a — некоторое вещественное число. К степенным часто относят и функцию вида y = kx a , где k — некоторый (ненулевой) коэффициент.

Степенная функция – корень квадратный.

Самый простой случай для дробной степени (x 1/2 = √x).

Степенная – обратная пропорциональность.

Самый простой случай для целой отрицательной степени (1/x = x -1 ) – обратно-пропорциональная зависимость. Здесь k = 1.

Показательная функция – математическая функция f (x) = a x , где a называется основанием степени, а x — показателем степени.

Показательная функция.

Показательная функция определена для a > 0 и a ≠ 1. Графики функции существенно зависят от значения параметра a. Здесь пример для y = 2 x (a = 2 > 1).

1″ longdesc=»График показательной функции а>1″ src=»https://www. calc.ru/imgs/articles3/16/87/964599587e5e40d85067.63997678.jpg» />

График показательной функции а>1

Показательная функция.

Показательная функция определена для a > 0 и a ≠ 1. Графики функции существенно зависят от значения параметра a. Здесь пример для y = 0,5 x (a = 1/2 x

График показательной функции 0

Логарифмическая функция.

График любой логарифмической функции проходит через точку (1;0).

Логарифмическая функция.

Логарифмы определены для a > 0 и a ≠ 1. Графики функции сильно связаны со значением параметра a. Здесь пример для y = log₂x (a = 2 > 1).

1″ src=»https://www.calc.ru/imgs/articles3/10/83/105346587e608e0e0759.16931934.jpg» />

График логарифмической функции – логарифм по основанию а>1

Синус.

Синусоида – периодическая функция с периодом Т = 2π

Косинус.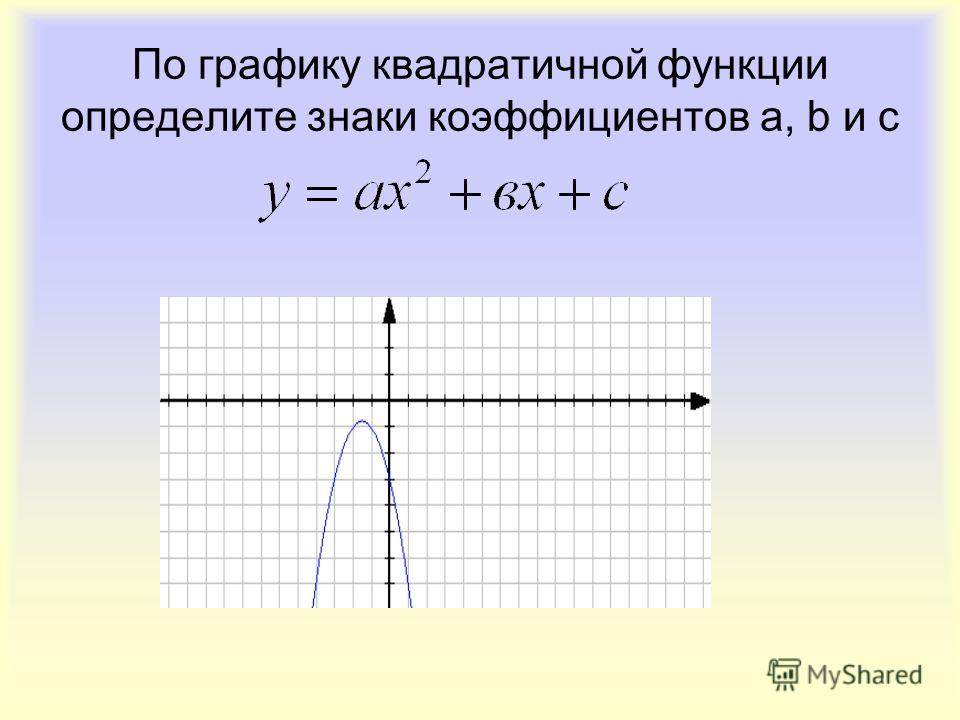

Тригонометрическая функция косинус. Графики у = sinx и у = cosx сдвинуты по оси х на .

Тангенс.

Тригонометрическая функция тангенс. Точки разрыва при х = (2k -1), где k = 0, ±1, ±2. Вертикальные асимптоты в этих точках.

Гиперболический синус – это элементарная функция, выражающаяся через экспоненту и тесно связанная с ее тригонометрическими функциями.

Гиперболический косинус – это элементарная функция, выражающаяся через экспоненту и тесно связанная с ее тригонометрическими функциями.

Гиперболический тангенс – это элементарная функция, выражающаяся через экспоненту и тесно связанная с ее тригонометрическими функциями.

Гиперболический котангенс – это элементарная функция, выражающаяся через экспоненту и тесно связанная с ее тригонометрическими функциями.

Гиперболический секанс – это элементарная функция, выражающаяся через экспоненту и тесно связанная с ее тригонометрическими функциями.

Гиперболический косеканс – это элементарная функция, выражающаяся через экспоненту и тесно связанная с ее тригонометрическими функциями.

Изучение свойств функций и их графиков занимает значительное место как в школьной математике, так и в последующих курсах. Причем не только в курсах математического и функционального анализа, и даже не только в других разделах высшей математики, но и в большинстве узко профессиональных предметов. Например, в экономике – функции полезности, издержек, функции спроса, предложения и потребления. в радиотехнике – функции управления и функции отклика, в статистике – функции распределения. Чтобы облегчить дальнейшее изучение специальных функций, нужно научиться свободно оперировать графиками элементарных функций. Для этого после изучения следующей таблицы рекомендую пройти по ссылке «Преобразования графиков функций».

«К движению» графиков) ограничен. За месяц перед экзаменом кнопка открывается для общего пользования без регистрации. Просьба ко всем, кто в связи с этим столкнулся с какими-либо «глюками» или «багами», сообщать мне подробности. О возможности получения полного доступа см. комментарии к активностям.

Кнопка уже без пароля! Готовимся к экзамену рационально – сдаём успешно.

Друзья, абсолютное большинство разделов этого сайта были и остаются бесплатными для пользователей, которыми преимущественно являются дети. Однако любой сайт требует финансовых вложений: хостинг, доменное имя, разработка . В связи с этим я обычно закрываю свободный доступ к интерактивным упражнениям (по кнопке «К движению» графиков) и открываю его непосредственно перед экзаменом. В этом году я намерена оставить открытым доступ к этим упражнениям в течение всего года, если найдутся взрослые (учителя или родители), которые внесут очень символические суммы на погашение обязательных платежей. Выберите один из трёх способов перевода и затем напишите мне своё мнение о сайте и предложения по его развитию.
С уважением, mathematichka.

В школьном курсе математики изучаются следующие
элементарные функции.Название функцииФормула функцииГрафик функцииНазвание графикаКомментарийЛинейнаяy = kxПрямаяCамый простой частный случай линейной зависимости – прямая пропорциональность у = kx, где k ≠ 0 – коэффициент пропорциональности. На рисунке пример для k = 1, т.е. фактически приведенный график иллюстрирует функциональную зависимость, которая задаёт равенство значения функции значению аргумента.Линейнаяy = kx + bПрямаяОбщий случай линейной зависимости: коэффициенты k и b – любые действительные числа. Здесь k = 0. 5, b = -1.Квадратичнаяy = x 2ПараболаПростейший случай квадратичной зависимости – симметричная парабола с вершиной в начале координат.Квадратичнаяy = ax 2 + bx + cПараболаОбщий случай квадратичной зависимости: коэффициент a – произвольное действительное число не равное нулю (a принадлежит R, a ≠ 0), b, c – любые действительные числа.Степеннаяy = x 3Кубическая параболаСамый простой случай для целой нечетной степени. Случаи с коэффициентами изучаются в разделе «Движение графиков функций».Степеннаяy = x 1/2График функции
y = √xСамый простой случай для дробной степени (x 1/2 = √x). Случаи с коэффициентами изучаются в разделе «Движение графиков функций».Степеннаяy = k/xГиперболаСамый простой случай для целой отрицательной степени (1/x = x -1 ) – обратно-пропорциональная зависимость. Здесь k = 1.Показательнаяy = e xЭкспонентаЭкспоненциальной зависимостью называют показательную функцию для основания e – иррационального числа примерно равного 2,7182818284590.Показательнаяy = a xГрафик показательной функцииПоказательная функция определена для a > 0 и a ≠ 1. Графики функции существенно зависят от значения параметра a. Здесь пример для y = 2 x (a = 2 > 1).Показательнаяy = a xГрафик показательной функцииПоказательная функция определена для a > 0 и a ≠ 1. Графики функции существенно зависят от значения параметра a. Здесь пример для y = 0,5 x (a = 1/2 0 и a ≠ 1. Графики функции существенно зависят от значения параметра a. Здесь пример для y = log₂x (a = 2 > 1).Логарифмическаяy = log_axГрафик логарифмической функцииЛогарифмы определены для a > 0 и a ≠ 1. Графики функции существенно зависят от значения параметра a. Здесь пример для y = log_0,5x (a = 1/2Название функцииФормула функцииГрафик функцииНазвание графикаКомментарийАрксинусy = arcsinxГрафик арксинусаТригонометрическая функция обратная к y = sinx. Определена на отрезке [−1; 1].
Принимает значения от −π/2 до π/2.Арккосинусy = arccosxГрафик арккосинусаТригонометрическая функция обратная к y = cosx. Определена на отрезке [−1; 1].
Принимает значения от 0 до π.Арктангенсy = arctgxГрафик арктангенсаТригонометрическая функция обратная к y = tgx. Определена на множестве действительных чисел.
Принимает значения на интервале (−π/2; π/2) .
Имеет асимптоты.Арккотангенс.y = arcctgxГрафик арккотангенсаТригонометрическая функция обратная к y = ctgx. Определена на множестве действительных чисел.
Принимает значения на интервале (0 π) .
Имеет асимптоты.

На занятиях школьники часто спрашивают: «Зачем это нужно знать?» Особенно волнует их этот вопрос при построении и преобразовании графиков тригонометрических функций. Что ж, давайте попробуем посмотреть на одном из сайтов в сети (например, RADIOLINK: Аксессуары) технические характеристики любимых всеми современных приборов связи – мобильников, роутеров. О чем Вам говорят термины «используемый диапазон частот», «прогрессивный метод модуляции» .
А теперь прочитайте в учебнике математики параграф «График гармонических колебаний», а в учебнике физики параграф «Электромагнитные волны». Стало понятнее?

”

Перейти на главную страницу.

Есть вопросы? пожелания? замечания?
Обращайтесь –
[email protected]

Внимание, ©mathematichka. Прямое копирование материалов на других сайтах запрещено. Ставьте гиперссылку.

Ответ

Если точка принадлежит графику квадратичной функции, подстановка её координат в уравнение функции y =”” ax² + bx + c должно давать справедливое равенство.

Координаты трёх точек позволяет составить систему из трёх уравнений с тремя неизвестными. Её решением будут коэффициенты уравнения квадратичной функции.

>

Как определить нули функции по графику

Что такое нули функции? Как определить нули функции аналитически и по графику?

Нули функции — это значения аргумента, при которых функция равна нулю.

Чтобы найти нули функции, заданной формулой y=f(x), надо решить уравнение f(x)=0.

Если уравнение не имеет корней, нулей у функции нет.

1) Найти нули линейной функции y=3x+15.

Чтобы найти нули функции, решим уравнение 3x+15 =0.

Таким образом, нуль функции y=3x+15 — x= -5 .

2) Найти нули квадратичной функции f(x)=x²-7x+12.

Для нахождения нулей функции решим квадратное уравнение

Его корни x1=3 и x2=4 являются нулями данной функции.

3)Найти нули функции

Дробь имеет смысл, если знаменатель отличен от нуля. Следовательно, x²-1≠0, x² ≠ 1,x ≠±1. То есть область определения данной функции (ОДЗ)

Из корней уравнения x²+5x+4=0 x1=-1 x2=-4 в область определения входит только x=-4.

Чтобы найти нули функции, заданной графически, надо найти точки пересечения графика функции с осью абсцисс.

Если график не пересекает ось Ox, функция не имеет нулей.

функция, график которой изображен на рисунке,имеет четыре нуля —

В алгебре задача нахождения нулей функции встречается как в виде самостоятельного задания, так и при решения других задач, например, при исследовании функции, решении неравенств и т.д.

Это можно сделать и графически. Просто построить функцию по точкам и начертить, точки пересечения графика с осью Х и будут нулями функции.

Посмотрите еще здесь:

2.Ну просто f(x)=0
Приравниваем функцию к нулю и считаем «нули» 🙂

Ответ или решение 1

Решение: Точки пересечения графика с осью абсцисс, на которой откладываются аргументы х, называются нулями функции. Поиск возможных нулей – одна из задач по исследованию заданной функции. Другими словами, нуль функции – что такое значение аргумента х, при котором значение функции равно нулю. Однако нулями могут быть лишь те аргументы, которые входят в область определения исследуемой функции. То есть в такое множество значений, для которых функция f(x) имеет смысл.

С осью абсцисс она пересекается один раз в точке (92;0).

С осью ординат она пересекается при x = 0 , y = 46, (0;46).

Представление данных в виде точечной диаграммы или графика

Основное различие между точечная и графиками заключается в способе их отстройки на горизонтальной оси. Например, если использовать следующие данные листа для построения точечной диаграммы и графика, они будут представлены по-разному:

На точечной диаграмме значения суточного количества осадков из столбца A отображаются в виде значений X на горизонтальной оси (X), а показатели содержания твердых частиц из столбца B — в виде значений на вертикальной оси (Y). На точечной диаграмме категории никогда не отображаются на горизонтальной оси.

На точечной диаграмме всегда есть две оси значений, то есть один набор числовых данных представлен вдоль горизонтальной оси, а другой — вдоль вертикальной. На пересечении координат X и Y отображается точка данных, объединяющая эти два числовых значения. Такие точки данных могут быть распределены по горизонтальной оси равномерно или неравномерно, в зависимости от конкретных данных.

Первая точка данных на точечной диаграмме представляет значение Y (содержание частиц), равное 137, и значение X (суточная норма осадков), равное 1,9. Эти числа представляют значения в ячейках A9 и B9 на листе.

На графике те же значения суточного количества осадков и содержания частиц будут показаны как две разные точки данных, которые равномерно распределяются вдоль горизонтальной оси. Дело в том, что на графике есть только одна ось значений (вертикальная ось). Горизонтальная ось графика предназначена для отображения группировок (категорий) данных с равномерными интервалами. Так как категории не были заданы, они генерируются автоматически, например 1, 2, 3 и т. д.

Это наглядный пример ситуации, когда график использовать не следует.

На графиках данные категории равномерно распределяются вдоль горизонтальной оси (оси категорий), а все числовые значения откладываются по вертикальной оси (оси значений).

Значение Y (содержание частиц), равное 137 (ячейка B9), и значение X (суточное количество осадков), равное 1,9 (ячейка A9), показаны на графике двумя разными точками данных. Ни одна из этих точек данных не является первой точкой данных, отображаемой на диаграмме. Вместо этого первая точка данных для каждого значения ряд данных ссылается на значения в первой строке данных на этом сайте (ячейки A2 и B2).

Различия между типами и шкалами осей

Так как горизонтальная ось точечной диаграммы всегда является осью значений, на ней можно показывать числа и даты (в том числе дни и часы), представляемые в виде числовых значений. Чтобы отображать числовые значения вдоль горизонтальной оси с большей гибкостью, можно изменить параметры ее шкалы аналогично тому, как изменяется настройка шкалы вертикальной оси.

Поскольку горизонтальная ось графика — это ось категорий, она может быть только осью текста или осью дат. На оси текста отображается только текст (нечисловые данные или числовые категории, не являющиеся значениями) с равномерными интервалами. На оси дат отображаются даты в хронологическом порядке через заданные интервалы (базовые единицы измерения), такие как число дней, месяцев или лет, даже если даты на листе расположены в ином порядке или выражены в других единицах.

Набор параметров шкалы оси категорий ограничен по сравнению с параметрами шкалы оси значений. Доступные параметры шкалы также зависят от типа используемой оси.

Исследование функций и построение графиков

Опорными точками при исследовании функций и построения их графиков служат характерные точки – точки разрыва, экстремума, перегиба, пересечения с осями координат. С помощью дифференциального исчисления можно установить характерные особенности изменения функций: возрастание и убывание, максимумы и минимумы, направление выпуклости и вогнутости графика, наличие асимптот.

Эскиз графика функции можно (и нужно) набрасывать уже после нахождения асимптот и точек экстремума, а сводную таблицу исследования функции удобно заполнять по ходу исследования.

Обычно используют следующую схему исследования функции.

1. Находят область определения, интервалы непрерывности и точки разрыва функции.

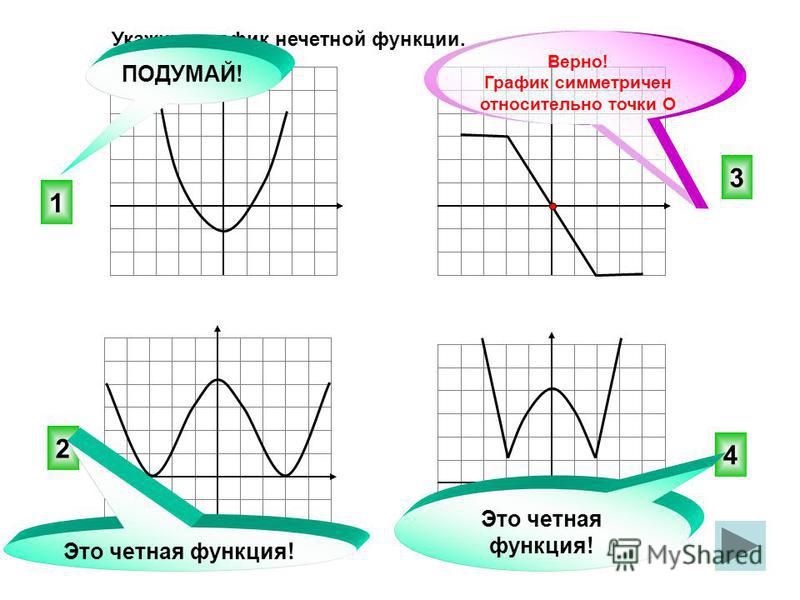
2. Исследуют функцию на чётность или нечётность (осевая или центральная симметрия графика.

3. Находят асимптоты (вертикальные, горизонтальные или наклонные).

4. Находят и исследуют промежутки возрастания и убывания функции, точки её экстремума.

5. Находят интервалы выпуклости и вогнутости кривой, точки её перегиба.

6. Находят точки пересечения кривой с осями координат, если они существуют.

7. Составляют сводную таблицу исследования.

8. Строят график, учитывая исследование функции, проведённое по вышеописанным пунктам.

---

 Пример. Исследовать функцию

и построить её график.

Решение.

1. Область определения функции – вся числовая прямая. Множеством значений данной функции, как и всякой показательной функции, служит интервал ]0, +∞[. Поэтому график функции расположен выше оси Ox,

2. Напомним: из школьного курса известно, что функция y = f(x) называется чётной, если

для всех x, принадлежащих области определения функции.

.

График чётной функции симметричен относительно оси Oy, так как, по определению, вместе с любой своей точкой (x; y) он содержит и точку (-x; y).

Функция y = f(x) называется нечётной, если

для всех x, принадлежащих области определения функции.

График нечётной функции симметричен относительно начала координат, так как, по определению, вместе с любой своей точкой (x; y) он содержит и точку (-x; -y).

Наша исследуемая функция чётная, так как

её график симметричен относительно оси Oy. Поэтому исследование можно выполнять только для ]0, +∞[.

3. Вертикальных асимптот у графика нет, поскольку функция непрерывна на всей числовой прямой. Горизонтальной асимптотой является ось Ox, так как

Поскольку кривая имеет двустороннюю горизонтальную асимптоту y = 0, у неё не может быть наклонных асиптот.

4. Находим . Из уравнения имеем .

Так как при переходе через значение x = 0 меняет знак с плюса на минус, то функция в точке x = 0 переходит от возрастания к убыванию, а (0; 1) – точка максимума. Касательная к кривой в этой точке горизонтальна, поскольку .

5. Находим Из уравнения получаем т.е. .

Учитывая чётность функции, исследуем знаки в окрестности только точки .

Следовательно, при x = 1 кривая меняет выпуклость на вогнутость. Так как то — точка перегиба кривой. Угловой коэффициент касательной к кривой в этой точке . Поэтому в точке перегиба касательная образует с осью Ox тупой угол.

6. График не пересекает оси Ox, поскольку он расположен выше неё. Найдём точки пересечения кривой с осью Oy: полагая x=0, имеем

Тем самым получим точку (0; 1) графика, которая совпадает с точкой максимума.

7. Составим сводную таблицу исследования функции, куда внесём все характерные точки и интервалы между ними. Учитывая чётность функции, получаем следующую таблицу:

				Особенности графика
[-1, 0[	+	—	Возрастает	Выпуклый
0	0	—	1	(0; 1) – точка максимума
]0, 1[	—	—	Убывает	Выпуклый
1	—	0		— точка перегиба, образует с осью Ox тупой угол
]1, +∞[	—	+	Убывает	Вогнутый
+∞	—	+		y = 0 – горизонтальная асимптота

 

8. Используя результаты исследования, строим график функции (см. рисунок).

Весь блок «Производная»

2 Пользовательские графики [Zabbix Documentation 5.2]

2 Пользовательские графики

Обзор

Пользовательские графики, как следует из названия, предлагают возможность индивидуальной настройки.

В то время как простые графики хороши для просмотра данных по одному элементу данных, они не дают возможности индивидуальной настройки.

Таким образом, если вы захотите изменить стиль графика или способ отрисовки линий, или сравнить несколько элементов данных, например, входящий и исходящий трафик на одном графике, то вам необходим пользовательский график.

Пользовательские графики настраиваются вручную.

Они могут быть созданы для одного узла сети, для нескольких узлов или в пределах одного шаблона.

Настройка пользовательских графиков

Для создания пользовательского графика, сделайте следующее:

• Перейдите в Настройка → Узлы сети (или Шаблоны)

• Нажмите на Графики в строке с желаемым узлом сети или шаблоном

• На странице графиков нажмите на Создать график

• Измените атрибуты графика

Все обязательные поля ввода отмечены красной звёздочкой.

Атрибуты графика:

Параметр	Описание
Имя	Уникальное имя графика. Начиная с Zabbix 2.2 в имени можно обращаться к значениям элементов данных, используя простые макросы со стандартным синтаксисом {узел сети:ключ.функция(параметр)}. Поддерживаются только функции avg,last,max и min с секундами в качестве параметров в этом макросе. Макросы {HOST.HOST<1-9>} поддерживаются для использования в ранее упомянутом макросе, как ссылки на первый, второй, третий и т.д. узел сети узла сети в графике, например, {{HOST.HOST1}:ключ.функция(параметр)}.
Ширина	Ширина графика в пикселах (только при предпросмотре и для кругового/расширенного кругового графиков).
Высота	Высота графика в пикселах.
Тип графика	Тип графика: Нормальный — нормальный график, значения отображаются линиями Стекируемый — стекируемый график, отображаются заполненные области Круговой — круговой график Расширенный круговой — расширенный круговой график, части отображаются как “вырезанные” из круга
Показывать легенду	При выборе этой опции будет отображена легенда графика.
Отображать рабочее время	Если выбрано, на графике будут отображаться нерабочие часы серым цветом фона. Недоступно для кругового и расширенного кругового графиков.
Отображать триггеры	Если выбрано, на графике будут отображаться простые триггеры красными линиями. Недоступно для кругового и расширенного кругового графиков.
Процентная линия (слева)	Отображение процентной линии для левой оси Y. Если, например, задана 95% процентная линия, то на графике будет отображена линия на уровне отношения 95 процентов значений. Отображается светло зеленой линией. Доступно только для нормальных графиков.
Процентная линия (справа)	Отображение процентной линии для правой оси Y. Если, например, задана 95% процентная линия, то на графике будет отображена линия на уровне отношения 95 процентов значений. Отображается светло красной линией. Доступно только для нормальных графиков.
МИН значение оси Y	Минимальное значение оси Y: Вычисляемое — минимальное значение оси Y будет автоматически вычисляться Фиксированное — фиксированное минимальное значение оси Y. Недоступно для кругового и кругового расширенного графиков. Элемент данных — последнее значение выбранного элемента данных будет являться минимальным значением
МАКС значение оси Y	Максимальное значение оси Y: Вычисляемое — максимальное значение оси Y будет автоматически вычисляться Фиксированное — фиксированное максимальное значение оси Y. Недоступно для кругового и кругового расширенного графиков. Элемент данных — последнее значение выбранного элемента данных будет являться максимальным значением
3D вид	Включение 3D стиля. Только для круговых и расширенных круговых графиков.
Элементы данных	Элементы данных, данные которых будут отображены на этом графике.

Настройка элементов графика

Для добавления элементов данных, данные которых будут отображаться на графике, кликните на Добавить в блоке Элементы данных, выберите элементы данных и задайте атрибуты для способа отображения данных из элементов данных.

Атрибуты отображения элементов данных:

Параметр	Описание
Порядок сортировки (0→100)	Порядок отрисовки. 0 будет обрабатываться в первую очередь. Можно использовать для отрисовки линий или областей позади (или спереди) другой. Вы можете перетаскивать элементы данных за стрелку в начале строки, тем самым изменять порядок сортировки или задать какие элементы данных должны отображаться поверх остальных.
Имя	Название элемента данных, данные которого будут отображаться.
Тип	Тип (доступен только для кругового и расширенного кругового графиков): Простой — значение элемента данные отображается пропорционально кругу Суммарный график — значение элемента данных представляет целый круг. Обратите внимание, что цвет элемента данных с типом “суммарный график” виден только у не занятого пространства “порционными” элементами данных.
Функция	Какие значения будут отображаться, когда существует более одного значения у элемента данных: все — все (минимальное, среднее и максимальное) мин — только минимальное сред — только среднее макс — только максимальное
Стиль отрисовки	Стиль отрисовки (доступен только для нормальных графиков; для стекируемых графиков всегда используется стиль заполнения области): Линия — отрисовывать линии Заполнение — отрисовывать заполнение области Жирная линия — отрисовывать толстые линии Точечная линия — отрисовывать точками Пунктирная линия — отрисовывать пунктирной линией
Расположение оси Y	С какой стороны отображать ось Y для элемента.
Цвет	Цвет RGB в HEX представлении.

Предпросмотр графика

На вкладке Предпросмотр отображается предпросмотр графика, так что вы сразу сможете увидеть что создаете.

Обратите внимание, что предварительный просмотр не будет отображать какие-либо данные у элементов данных из шаблона.

В этом примере, обратите внимание на жирную пунктирную линию отображающую уровень триггера и информацию о триггере, которая отображается в легенде.

3 триггера жестко заданы в исходном коде и являются максимальным количеством отображаемых триггеров в легенде.

Если высота графика меньше 120 пикселей, то триггеры в легенде к графику отображаться не будут.

График уравнения

Пример графика функции

Как нарисовать функциональный график

Во-первых, начните с такого пустого графика. Он имеет значения x, идущие слева направо, и значения y, идущие снизу вверх:

Ось x и ось y пересекают
, где x и y равны нулю.

Точки графика

Простой (но не идеальный) подход — вычислить функцию в некоторых точках и затем построить их.

График функции — это набор точек значений, принимаемых функцией.

Пример: y = x

² — 5

Вычислим некоторых точек :

x	y = x 2 −5
-2	-1
0	−5
1	−4
3	4

И начертите их так:

Пока не очень полезно.Добавим еще точек :

Выглядит лучше!

Теперь мы можем предположить, что при нанесении все точки будут выглядеть так:

Хорошая парабола.

Мы должны попытаться нанести достаточно точек, чтобы быть уверенными в том, что происходит!

Пример: y = x

³ — 5x

С этими расчетными точками:

x	y = x 3 −5x
-2	2
0	0
2	-2

Можно подумать, что это график:

Но это реальный график:

Так что «нанесение точек» полезно, но может привести к ошибкам .

Полный график

Чтобы график был «законченным», нам нужно показать все важные особенности:

• Пункты пропуска
• Пики
• Долины
• Плоские участки
• Асимптоты
• Любые другие специальные функции

Это часто означает, что нужно тщательно продумать функцию.

Пример: (x − 1) / (x

² −9)

На странице Rational Expressions мы проделали некоторую работу, чтобы обнаружить, что функция:

• пересекает ось x в точке 1,
• пересекает ось Y на 1/9,
• имеет вертикальные асимптоты (где он направлен к минус / плюс бесконечности) в −3 и +3

В результате мы можем сделать этот набросок:

Набросок (x − 1) / (x ² −9) из Rational Expressions.2 = 9 дюймов (что означает x ² + y ² = 9 ).

Но помните, что они всего лишь помощники! Это всего лишь компьютерные программы, и легко мог пропустить что-то важное на графике или не нанести что-то правильно.

Примечание. Вы можете услышать фразу «удовлетворить уравнению», что означает, что уравнение является истинным .

Описание графика функции

Иногда вам нужно описать график функции несимвольным образом.Например, вас могут спросить

1. увеличивается или уменьшается функция;


2. имеет ли он одно минимальное значение или максимальное значение, или несколько таких значений


3. линейно это или нет


4. будь то скорость изменения постоянно, увеличивается или уменьшается


5. имеет ли он верхнюю или нижнюю границу.

Пример 1:

Опишите две функции ж ( Икс ) а также грамм ( Икс ) , используя термины «возрастание», «убывание», «максимум» и «минимум».

График ж ( Икс ) периодический. Он уменьшается для — 3 < Икс < - 1 , то увеличивается при - 1 < Икс < 1 , затем снова уменьшается при 1 < Икс < 3 , так далее.

Имеет максимальное значение 1 и минимальное значение — 1 , и он многократно достигает этих максимумов и минимумов.Верхняя граница функции равна 1 и нижняя граница — 1 .

График грамм ( Икс ) увеличивается для — ∞ < Икс < - 1 и уменьшается для - 1 < Икс < ∞ . График принимает максимальное значение 3 в Икс знак равно - 1 .У него нет минимума.

Пример 2:

Какой график имеет более высокую скорость изменения?

Оба графика начинаются вместе в ( 0 , 0 ) . Сначала линейная функция, грамм ( Икс ) , имеет более высокую скорость изменения.

Но ж ( Икс ) скоро догоняет и превосходит грамм ( Икс ) в ( 8 , 16 ) , и продолжает увеличиваться более быстрыми темпами.

Напишите уравнение полиномиальной функции на основе ее графика

Если вы считаете, что контент, доступный через Веб-сайт (как определено в наших Условиях обслуживания), нарушает или другие ваши авторские права, сообщите нам, отправив письменное уведомление («Уведомление о нарушении»), содержащее в информацию, описанную ниже, назначенному ниже агенту.Если репетиторы университета предпримут действия в ответ на ан Уведомление о нарушении, оно предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.

Ваше Уведомление о нарушении прав может быть отправлено стороне, предоставившей доступ к контенту, или третьим лицам, таким как в виде ChillingEffects.org.

Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатам), если вы существенно искажать информацию о том, что продукт или действие нарушает ваши авторские права.Таким образом, если вы не уверены, что контент находится на Веб-сайте или по ссылке с него нарушает ваши авторские права, вам следует сначала обратиться к юристу.

Чтобы отправить уведомление, выполните следующие действия:

Вы должны включить следующее:

Физическая или электронная подпись правообладателя или лица, уполномоченного действовать от их имени; Идентификация авторских прав, которые, как утверждается, были нарушены; Описание характера и точного местонахождения контента, который, по вашему мнению, нарушает ваши авторские права, в \ достаточно подробностей, чтобы позволить репетиторам университетских школ найти и точно идентифицировать этот контент; например, мы требуем а ссылка на конкретный вопрос (а не только на название вопроса), который содержит содержание и описание к какой конкретной части вопроса — изображению, ссылке, тексту и т. д. — относится ваша жалоба; Ваше имя, адрес, номер телефона и адрес электронной почты; а также Ваше заявление: (а) вы добросовестно полагаете, что использование контента, который, по вашему мнению, нарушает ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство, что вы либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.

Отправьте жалобу нашему уполномоченному агенту по адресу:

Чарльз Кон Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Или заполните форму ниже:

способов узнать, является ли что-то функцией

Обновлено 2 ноября 2020 г.

Даниэль Пинзоу

Функции — это отношения, которые выводят один выход для каждого входа или одно значение y для любого значения x, вставленного в уравнение.3 — 1

— это функции, потому что каждое значение x дает другое значение y . В графических терминах функция — это отношение, в котором первые числа в упорядоченной паре имеют одно и только одно значение в качестве второго числа, другой части упорядоченной пары.

Проверка упорядоченных пар

Упорядоченная пара — это точка на координатном графике x — y со значениями x и y. Например, (2, −2) — это упорядоченная пара с 2 в качестве значения x и −2 в качестве значения y .При наличии набора упорядоченных пар убедитесь, что ни одно значение x не имеет более одного парного значения y . Когда задан набор упорядоченных пар [(2, −2), (4, −5), (6, −8), (2, 0)], вы знаете, что это не функция, потому что x -Значение — в данном случае — 2, имеет более одного значения y . Однако этот набор упорядоченных пар [(−2, 4), (−1, 1), (0, 0), (1, 1), (2, 4)] является функцией, потому что y -value может иметь более одного соответствующего x -значения.

Решение для Y

Относительно легко определить, является ли уравнение функцией, решив для y . Когда вам дается уравнение и конкретное значение для x , должно быть только одно соответствующее значение y для этого значения x . Например,

y = x + 1

— это функция, потому что y всегда будет на единицу больше x . Уравнения с показателями также могут быть функциями.2 = 9

имеет два возможных ответа (3 и −3).

Тест вертикальной линии

Определить, является ли отношение функцией на графике, относительно легко с помощью теста вертикальной линии. Если вертикальная линия пересекает отношение на графике только один раз во всех местах, отношение является функцией. Однако, если вертикальная линия пересекает отношение более одного раза, отношение не является функцией. При использовании теста вертикальной линии все линии, кроме вертикальных, являются функциями.Круги, квадраты и другие замкнутые формы не являются функциями, но параболические и экспоненциальные кривые — это функции.

Использование диаграммы ввода-вывода

На диаграмме ввода-вывода отображается вывод или результат для каждого ввода или исходного значения. Любая диаграмма ввода-вывода, где у входа есть два или более разных выхода, не является функцией. Например, если вы видите число 6 в двух разных входных пространствах, а на выходе получается 3 в одном случае и 9 в другом, отношение не является функцией.Однако, если два разных входа имеют одинаковый выход, все еще возможно, что отношение является функцией, особенно если задействованы квадратные числа.

Определение разумных доменов и диапазонов (вербальный / график)

Вы также можете изучить вербальные отношения и узнать, как определить домен и / или диапазон в конкретной ситуации.

Пример 1

Периметр правильного пятиугольника не более 30 сантиметров. Определите набор, чтобы описать ℓ, длину каждой стороны пятиугольника.

Поскольку у пятиугольника пять сторон, мы знаем, что его периметр будет 5 раз или P = 5ℓ.

Ранее в этом ресурсе мы узнали, что домен связан с входом , а диапазон связан с выходом . В этом примере входными данными является длина, а выходными данными — периметр.

Чтобы найти домен, нам нужно знать все возможные значения для ℓ, которые дадут нам периметр, меньший или равный 30 сантиметрам.

Мы уже знаем, что расстояние всегда больше 0.Так что ℓ> 0. Мы также знаем, что периметр равен 30 сантиметрам или меньше. Итак, 5ℓ ≤ 30.

Решая неравенство 5ℓ ≤ 30, мы находим, что наибольшая возможная длина равна 6, потому что 5 умноженное на 6 равно 30. Итак, ℓ ≤ 6.

Наш окончательный ответ должен быть записан в обозначениях множества, потому что нас попросили идентифицировать множество для описания ℓ. Итак, наш ответ будет {0

Пример 2

Количество теннисных мячей в n банках может быть выражено функцией s = 3 n .Каков домен и диапазон этой функции?

Согласно функции количество имеющихся у нас банок будет определять количество теннисных мячей. Таким образом, входная / независимая переменная — n , а выходная / зависимая переменная — s .

Давайте построим график, чтобы увидеть, что происходит.

В этом примере у нас нет таких вещей, как 1,5 банки теннисных мячей. Это 1 банка, 2 банки, 3 банки и так далее. Поскольку мы не можем использовать значения от 1 до 2, мы говорим, что это дискретная функция.

В виде графика это соотношение будет выглядеть так:

Каков домен и диапазон для этой функции? Нажмите ниже, чтобы проверить свой ответ.

College Algebra Урок 35: Графики полиномиальных функций Цели обучения После изучения этого руководства вы сможете: Определите полиномиальную функцию. Используйте тест опережающего коэффициента, чтобы определить конечное поведение графика заданной полиномиальной функции. Найдите нули полиномиальной функции. Найдите кратность нуля и узнайте, пересекает ли график ось абсцисс в нуле или касается оси x и поворачивается вокруг нуля. Знать максимальное количество точек поворота на графике многочлена функция мог бы иметь. Изобразите полиномиальную функцию. Введение В этом уроке мы рассмотрим графики полиномиальные функции. Если вам нужен обзор функций, смело переходите к Tutorial 30: Введение в функции . Если вам нужен обзор многочлены в общем, смело переходите к Tutorial 6: Многочлены. В принципе, график многочлена функция — гладкая непрерывная кривая. Есть несколько основных аспектов это тип графика, который можно использовать для построения кривой. я мы расскажем, как использовать главный член вашего многочлена функция чтобы определить конечное поведение его графика. Мы также будем Ищу при нахождении нулей, также называемых перехватами x , а также пересечение графика y . Если вам нужен обзор перехватов, смело переходите к Tutorial 26: Уравнения линий .Еще одна важная концепция — знать максимально возможное количество поворотных точек. Это будет помощь будьте более точными на графике, который вы рисуете. Это примерно покрывает это. Думаю, вы готовы к этому. Учебник Полиномиальная функция Полиномиальная функция — это функция что можно написать по форме , г. где вещественные числа и n — целое неотрицательное число. Ведущий срок Когда полиномиальная функция написано в стандарте форма, , ведущий член. Другими словами, ведущий член — это термин, который переменная имеет его наивысший показатель. Главный член функции было бы . Ведущий коэффициент Когда полиномиальная функция написано в стандарте форма, , старший коэффициент. В основном старший коэффициент — это коэффициент на ведущей срок. Старший коэффициент функции будет — 4. Степень члена многочлена Функция Степень члена полиномиальной функции — это экспонента на Переменная. Степень полиномиальной функции Когда полиномиальная функция написано в стандарте форма, , степень полиномиальной функции это n . Степень полинома — это наибольшая степень все его условия. Степень функции будет 7. Тест ведущего коэффициента Этот тест проходит в четырех случаях: Дана полиномиальная функция в стандартной форме: Корпус 1: Если n нечетное И старший коэффициент , положительный , график падает влево и поднимается до в правый : Корпус 2: Если n нечетное И старший коэффициент , отрицательно, график поднимается влево и падает до в верно. Корпус 3: Если n равно И старший коэффициент , положительный, график поднимается влево и вверх верно. Корпус 4: Если n равно И старший коэффициент , отрицательно, график падает влево, и — влево. верно. Первый вопрос: что такое ведущий термин? Если вы сказали, ты прав!! Второй вопрос: какая степень ведущего термина? Если вы сказали 3, вы правы !! 3 — это показатель на ведущей термин, который также означает, что это степень многочлена. Третий вопрос: каков коэффициент ведущий термин? Если вы сказали 5, похлопайте себя по спине !! Собираем эту информацию вместе с Ведущим Коэффициент Тест мы можем определить конечное поведение графика нашего данного многочлена: Поскольку степень многочлена 3 нечетна и ведущий коэффициент, 5, положительна, то график данного многочлена попадает в влево и поднимается вправо. Первый вопрос: что такое ведущий термин? Если вы сказали, ты прав!! Второй вопрос: какая степень ведущего термина? Если вы сказали 4, вы правы !! 4 — это показатель на ведущей термин, который также означает, что это степень многочлена. Третий вопрос: каков коэффициент ведущий термин? Если вы сказали -1, похлопайте себя по спине !! Собираем эту информацию вместе с Ведущим Коэффициент Тест мы можем определить конечное поведение графика нашего данного многочлена: Поскольку степень многочлена 4 четная и ведущий коэффициент, -1, отрицателен, тогда график данного многочлен падает влево и падает вправо. Первый вопрос: что такое ведущий термин? Если вы сказали, ты прав!! Второй вопрос: какая степень ведущего термина? Если вы сказали 5, вы правы !! 5 — это показатель на ведущей термин, который также означает, что это степень многочлена. Третий вопрос: каков коэффициент ведущий термин? Если вы сказали -7, похлопайте себя по спине !! Собираем эту информацию вместе с Ведущим Коэффициент Тест мы можем определить конечное поведение графика нашего данного многочлена: Поскольку степень многочлена 5 нечетна и ведущий коэффициент, -7, отрицательный, тогда график данного многочлен поднимается влево и опускается вправо. Первый вопрос: что такое ведущий термин? Если вы сказали, ты прав!! Второй вопрос: какая степень ведущего термина? Если вы сказали 6, вы правы !! 6 — это показатель на ведущей термин, который также означает, что это степень многочлена. Третий вопрос: каков коэффициент ведущий термин? Если вы сказали 1, похлопайте себя по спине !! Собираем эту информацию вместе с Ведущим Коэффициент Тест мы можем определить конечное поведение графика нашего данного многочлена: Поскольку степень многочлена 6 четная и ведущий коэффициент, 1, положительный, тогда график данного многочлена поднимается влево и поднимается вправо. нулей (или корней) многочлена Функции Нуль или корень полиномиальной функции — это значение x , так что f ( x ) = 0. Другими словами, это перехват x , где функциональное значение или y равно 0. Нуль кратности k Если есть фактор полиномиальной функции f и это не множитель f , тогда r называется нулем кратность k из f . Другими словами, когда полиномиальная функция установлена ​​равной к нулю и был полностью учтен, и каждый отдельный фактор записан с наивысший подходящий показатель, в зависимости от того, сколько раз фактор встречается в продукте, показатель степени на множителе, который равен нулю является решением для, дает кратность этого нуля. Показатель степени показывает, сколько раз этот множитель будет быть выписанным в продукте это дает нам множественность. Кратность нулей и интервал x Этой концепции соответствуют два случая: Корпус 1: Если r — ноль четной кратности: Это означает, что график касается оси x . при r и разворачивается. Это происходит потому, что знак f ( x ) не меняется с одной стороны на другую r . Корпус 2: Если r — ноль нечетной кратности: Это означает, что график пересекает ось x . при р . Это происходит потому, что знак f ( x ) меняется с одной стороны на другую r . Точки поворота Если f — полиномиальная функция степени n , затем есть не более n — 1 поворотные моменты на график ф . Точка поворота — это точка, в которой график меняет направление. Имейте в виду, что у вас может быть меньше n — 1 поворотных точек, но оно никогда не превысит n — 1 поворотных точек. Пример 5 : Найдите нули полиномиальной функции и укажите кратность каждого нуля.Укажите, есть ли график пересекает ось x или касается оси x и поворачивается на каждом нуле. Первый фактор: Первый множитель — 3, это постоянная величина. Следовательно, есть нет нулей, которые идут с этим множителем. * Установка 2-го коэффициента = 0 * Решить относительно x * x = -1/2 — это ноль Какой была бы кратность нуля x = -1/2? Если вы сказали , кратность для x = -1/2 это 4 , вы правы !!!! Поскольку показатель на этом фактор равно 4, то его кратность равна 4. Пересекает ли график ось x ? или прикоснуться ось x и развернуться в нулевой точке x = -1/2? Если вы сказали , он касается оси x а также разворачивается в нуле x = -1/2 , погладить себя на спине !!! Это происходит потому, что кратность 4, что является четным. * Установка 3-го фактора = 0 * Решить относительно x * x = 4 — ноль Какой будет кратность нуля x = 4? Если вы сказали , кратность для x = 4 это 3 , вы правы !!!! Поскольку показатель этого множителя равно 3, то его кратность равна 3. Пересекает ли график ось x ? или прикоснуться ось x и развернуться в нулевой точке x = 4? Если вы сказали , он пересекает ось x в ноль x = 4 , похлопайте себя по назад!!! Это происходит потому, что кратность равна 3, что нечетно. Пример 6 : Найдите нули полиномиальной функции и укажите кратность каждого нуля. Укажите, есть ли график пересекает ось x или касается оси x и поворачивается на каждом нуле. Давайте сначала разложим на множители: * Установка 1-го коэффициента = 0 * Решить относительно x * x = 0 — это ноль Какой будет кратность нуля x = 0? Если вы сказали , кратность для x = 0 это 2 , вы правы !!!! Поскольку показатель этого множителя равно 2, то его кратность равна 2. Пересекает ли график ось x ? или прикоснуться ось x и развернуться в нулевой точке x = 0? Если вы сказали , он касается оси x а также разворачивается в нуле х = 0 , пат сам сзади!!! Это происходит потому, что кратность равна 2, что даже. * Установка 2-го множителя = 0 * Решить относительно x * x = -3 — это ноль Какой была бы кратность нуля x = -3? Если вы сказали , кратность для x = -3 это 1 , вы правы !!!! Поскольку показатель на этом фактор равно 1, то его кратность равна 1. Пересекает ли график ось x ? или прикоснуться ось x и развернуться в нулевой точке x = -3? Если вы сказали , он пересекает ось x в ноль x = -3 , похлопайте себя по спина!!! Это происходит потому, что кратность равна 1, что нечетно. * Установка 3-го фактора = 0 * Решить относительно x * x = 3 — ноль Какой будет кратность нуля x = 3? Если вы сказали , кратность для x = 3 — это 1 , вы правы !!!! Поскольку показатель этого множителя равно 1, то его кратность равна 1. Пересекает ли график ось x ? или прикоснуться ось x и развернуться в нулевой точке x = 3? Если вы сказали , он пересекает ось x в ноль x = 3 , похлопайте себя по назад!!! Это происходит потому, что кратность равна 1, что нечетно. Построение полиномиальной функции Шаг 1: Определите конечное поведение графика. Шаг 2: Найдите точки пересечения x- или нули функции. Напомним, что вы нашли точку перехвата x или же ноль, установив вашу функцию равной 0, f ( x ) = 0, полностью факторизуя многочлен и устанавливая каждый множитель равным до 0. Если нужен обзор на x -перехваты, Чувствовать бесплатно перейти к Урок 26: Уравнения линий. Имейте в виду, что когда является множителем вашего многочлена и а) если k четное, график касается оси x при r и разворачивается. b) если k нечетное, то график пересекает ось x при р . Шаг 3. Найдите точку пересечения y функции. Напомним, что вы можете найти свой y -intercept положив x = 0, и найдите свой функциональная ценность при x = 0, f (0). Если нужен обзор на y -перехватчики, Чувствовать бесплатно перейти к Урок 26: Уравнения линий. Шаг 4: Определите, если есть какая-то симметрия. y — симметрия оси: Напомним, что ваша функция симметрична относительно оси y если это четная функция.Другими словами, если f (- x ) = f ( x ), тогда твой функция симметрична относительно оси y . Симметрия начала координат: Напомним, что ваша функция симметрична относительно начала координат, если это нечетная функция. Другими словами, если f (- x ) = — f ( x ), тогда ваша функция симметрична относительно начала координат. Если вам нужен обзор четных и нечетных функций, пощупайте бесплатно перейти к Tutorial 32: Графики функций, часть II. Шаг 5: Найдите номер максимальных точек поворота. Как обсуждалось выше, если f является полиномом функция степени n , то есть при большинство n — 1 поворотная точка на графике f . Шаг 6: Найдите дополнительные баллы, если нужно. Иногда может потребоваться найти точки, которые находятся в между теми вы нашли в шагах 2 и 3, чтобы помочь вам быть более точным на своем графике. Постройте точки, найденные на шагах 2, 3 и 6, и используйте Информация собраны на шагах 1, 2, 4 и 5, чтобы нарисовать график. График полиномиальных функций всегда гладкий непрерывная кривая. Пример 7 : Учитывая полиномиальную функцию а) используйте тест опережающего коэффициента, чтобы определить конец графика поведение, б) найти x -перехваты (или нули) и государственный пересекает ли график ось x или касается ось x и поворачивается на каждом пересечении x , в) найти точку пересечения и , г) определить симметрия графика, e) указывают максимально возможные точки поворота, и f) график. Считаете ли вы, что график поднимается или опускается до слева и в верно? Поскольку степень многочлена 4 четная и ведущий коэффициент 1 положителен, то график данного многочлена поднимается вверх влево и поднимается вправо. * Установка 1-го коэффициента = 0 * Решить относительно x * x = 0 — это ноль Поскольку показатель этого множителя равен 2, то кратность для ноль x = 0 равен 2. Поскольку кратность равна 2, то граф касается ось x и поворачивается в нуле x = 0. * Установка 2-го множителя = 0 * Решить относительно x * x = 3 — ноль Поскольку показатель этого множителя равен 1, то кратность для ноль x = 3 равен 1. Поскольку кратность равна 1, что нечетно, тогда граф пересекает ось x в нуле x = 3. * Установка 3-го фактора = 0 * Решить относительно x * x = -1 — это ноль Поскольку показатель степени этого множителя равен 1, то множественность для ноль x = -1 равно 1. Поскольку кратность равна 1, что нечетно, то график пересекает ось x в нуле х = -1. * Разъем 0 для x Перехват y (0, 0). Шаг 4: Определите, если есть какая-то симметрия. * Вставка — x для x Он не симметричен относительно оси y . * Вставка — x для x * Возьмем противоположность f ( x ) Не симметрично относительно начала координат. Поскольку степень функции равна 4, то на большинство 4 — 1 = 3 точки поворота. Чтобы получить более точную кривую, давайте найдем несколько точек которые находятся между точки, которые мы нашли на шагах 2 и 3: x ( x , y ) -.5 (-.5, -.437) 1 (1, -4) 2 (2, -12) Пример 8 : Учитывая полиномиальную функцию а) используйте тест опережающего коэффициента, чтобы определить конец графика поведение, б) найти x -перехваты (или нули) и государственный пересекает ли график ось x или касается ось x и поворачивается на каждом пересечении x , в) найти точку пересечения и , г) определить симметрия графика, e) указывают максимально возможные точки поворота, и f) график. Считаете ли вы, что график поднимается или опускается до слева и в верно? Поскольку степень многочлена 3 нечетна и ведущий коэффициент, -2, отрицателен, то график данного многочлена поднимается вверх влево и падает вправо. * Установка 1-го коэффициента = 0 * Решить относительно x * x = 0 — это ноль Поскольку показатель этого множителя равен 1, то кратность для ноль x = 0 равен 1. Поскольку кратность равна 1, что нечетно, тогда график пересекает ось x в нуле x = 0. * Установка 2-го множителя = 0 * Решить относительно x * x = -1 — это ноль Поскольку показатель этого множителя равен 1, то кратность для ноль x = -1 равен 1. Поскольку кратность равна 1, что нечетно, тогда граф пересекает ось x в нуле x = -1. * Установка 3-го фактора = 0 * Решить относительно x * x = 1 — ноль Поскольку показатель степени этого множителя равен 1, то множественность для ноль x = 1 равно 1. Поскольку кратность равна 1, что нечетно, то график пересекает ось x в нуле x = 1. * Разъем 0 для x Перехват y (0, 0). Шаг 4: Определите, если есть какая-то симметрия. * Вставка — x для x Он не симметричен относительно оси y . * Вставка — x для x * Возьмем противоположность f ( x ) Он симметричен относительно начала координат. Поскольку степень функции равна 3, то в большинство 3 — 1 = 2 поворотные точки. Чтобы получить более точную кривую, давайте найдем несколько точек которые находятся между точки, которые мы нашли на шагах 2 и 3: x ( x , y ) -1/2 (-1/2, -3/4) 1/2 (1/2, 3/4) Практические задачи Это практические задачи, которые помогут вам перейти на следующий уровень. Это позволит вам проверить и понять, понимаете ли вы эти типы проблем. Math работает как и все в противном случае, если вы хотите добиться успеха в этом, вам нужно практиковать это. Даже лучшие спортсмены и музыканты получали помощь и много практиковаться, практиковаться, практиковаться, чтобы хорошо освоить свой вид спорта или инструмент На самом деле не бывает слишком много практики. Чтобы получить максимальную отдачу от них, вы должны решить проблему на свой, а затем проверьте свой ответ, щелкнув ссылку для ответа / обсуждения для этой проблемы .По ссылке вы найдете ответ а также любые шаги, которые позволили найти этот ответ. Практика Задачи 1a — 1b: Учитывая полиномиальную функцию а) используйте ведущую Тест коэффициента для определения конечного поведения графика, б) найти точки пересечения x (или нулей) и укажите, пересекает ли график ось x или касается ось x и поворачивается на каждом пересечении x , c) найти пересечение y , d) определение симметрии графика, e) указывать максимально возможные точки поворота; е) график. Нужна дополнительная помощь по этим темам? Последний раз редактировал Ким Сьюард 14 марта 2012 г. Авторские права на все содержание (C) 2002 — 2012, WTAMU и Kim Seward. Все права защищены.

Как построить график функции в Excel | Small Business

Математическая функция — это формула, которая принимает входные данные x, применяет к ним набор вычислений и производит выходные данные с именем y.Вычисляя функцию с большим количеством заданных интервалов, можно создать диаграмму рассеяния функции. В бизнесе это имеет множество применений. Например, вы можете построить график прибыли за вычетом затрат на различных уровнях продаж, или общие затраты можно оценить, нанеся на график постоянные затраты с разными приращениями переменных затрат.

Создайте заголовки для таблицы данных. Введите входную переменную в ячейку A1 и выходную переменную в ячейку B1. Если хотите, вы можете использовать математические стандарты «x» и «y» или использовать что-то более наглядное, например «продажи» и «прибыль».«

Введите первый и второй интервалы входной переменной (например,« x »или« продажи »), которые вы будете использовать для построения графика функции. Например, если ваши интервалы представляют собой целые числа, вы можете начать с введите «1» в ячейку A2 и «2» в ячейку A3. Выберите обе эти ячейки, а затем щелкните и перетащите маленький черный квадрат в правом нижнем углу области выбора вниз, пока не получите столько значений, сколько хотите. plot

Введите знак равенства «=» в ячейку B2, а затем введите формулу сразу после него, не оставляя пробелов.Например, чтобы определить количество продаж определенного продукта для покрытия расходов, вы можете использовать:

= (A2 * 50) -3500

Замените «50» продажной ценой, а «3500» — на ваши расходы.

Выберите ячейку B2, а затем перетащите, чтобы скопировать формулу вниз по столбцу тем же методом, который вы использовали на шаге 2.