Преобразование выражений с корнями (внесение множителя под знак корня)

Тема: Функция 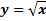. Свойства квадратного корня

Урок: Преобразование выражений с корнями (внесение множителя под знак корня)

Начнем урок с повторения теории.

Определение. Квадратным корнем из неотрицательного числа 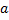 называется такое неотрицательное число 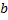, квадрат которого равен .

.

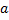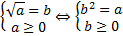
Из определения следует тождество 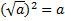 при .

При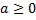мер 1. Вычислите 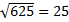, т. к. .

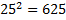Пример 2. Решите уравнение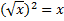

Решение. Уравнение может показаться очевидным и выполненным всегда при всех значениях переменной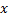

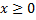. Действительно, мы уже знакомы с тождеством, которое представляет собой это уравнение, однако, важно помнить, что оно выполнено при , что и будет являться решением уравнения. Это тот случай, в котором решением уравнения может являться не одно или несколько чисел, как мы привыкли, а целая числовая полуось.

Ответ..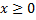

Основные свойства квадратного корня:

а)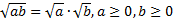

б)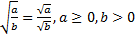

в)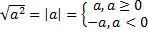

Рассмотрим две важнейшие типовые задачи урока, на методе решения которых будет базироваться подход к другим подобным задачам.

Пример 3. Внесите множитель под знак корня: а) 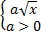, б) .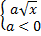

Решение. Задачи отличаются только знаком выражения, которое является множителем перед корнем, но это принципиальный аспект дальнейшего решения.

а) Внесение положительного множителя под знак корня. Если 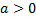, то

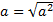
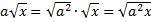, тогда .

б) Внесение отрицательного множителя под знак корня. Если 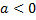, то 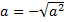 (т. к. 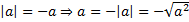), тогда .

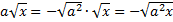Ответ.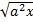

; .

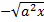Как видно из приведенного примера, знак вносимого под корень выражения важен, и если он отрицательный, то перед корнем после внесения множителя должен остаться минус, в случае внесения положительного множителя, значение выражения остается положительным.

Когда нам известны два принципиальных подхода к решению задач, можем перейти к различным примерам.

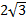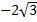Пример 4. Внесите множитель под знак корня: а) , б) , в) .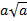

Решение. а) Т. к. множитель перед корнем положительный, то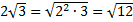

.

б) Т. к. множитель перед корнем отрицательный, то .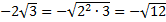

в) В этой задаче может показаться, что решение имеет различные варианты, т. к. знак выражения перед корнем не известен, но следует заметить, что такое же выражение находится и под знаком корня, т. е. оно неотрицательно по определению квадратного корня (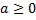). Имеем вариант для внесения неотрицательного числа .

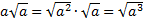Ответ.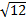

; ; .

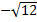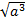Пример 5. Внесите множитель под знак корня и упростите: а) 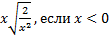, б) .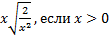

Решение. Задачи похожи, однако, отличаются знаками вносимых под корень множителей, подход к решению нам уже известен, применим его.

а) 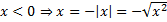, тогда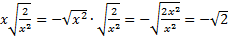

.

б) 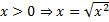, тогда .

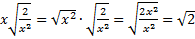Ответ..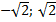

Пример 6. Внесите множитель под знак корня и упростите: а) 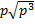, б) .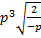

Решение. а) По определению квадратного корня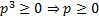

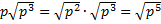, т. к. если произведение трех одинаковых чисел неотрицательно, то и эти числа неотрицательны, тогда вносим под корень неотрицательное число: .

б) По определению квадратного корня 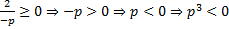, тогда вносим под корень отрицательное число: .

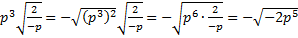Ответ.; .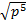

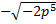На следующем уроке рассмотрим более сложные задачи на преобразования выражений с корнями, в которых нам понадобятся знания обо всех основных свойствах квадратного корня.

 

Список литературы

1. Башмаков М.И. Алгебра 8 класс. – М.: Просвещение, 2004.

2. Дорофеев Г.В., Суворова С.Б., Бунимович Е.А. и др. Алгебра 8. – 5-е изд. – М.: Просвещение, 2010.

3. Никольский С.М., Потапов М.А., Решетников Н.Н., Шевкин А.В. Алгебра 8 класс. Учебник для общеобразовательных учреждений. – М.: Просвещение, 2006.

 

Дополнительные рекомендованные ссылки на ресурсы сети Интернет

1. Старая школа (Источник).

2. Фестиваль педагогических идей «Открытый урок» (Источник).

3. Обучающие курсы (Источник).

 

Домашнее задание

1. №318, 319, 332, 339, 340, 343. Дорофеев Г.В., Суворова С.Б., Бунимович Е.А. и др. Алгебра 8. – 5-е изд. – М.: Просвещение, 2010.

2. Внесите множитель под знак корня: а)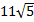

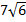, б) , в) .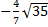

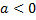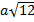3. Внесите множитель под знак корня, если известно, что : а) , б) .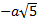

4. Расположите в порядке возрастания числа: а) 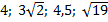, б) .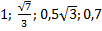

interneturok.ru

Извлечение корней: определение, методы извлечения, примеры

Из этой статьи вы узнаете:

• что такое «извлечение корня»;
• в каких случаях он извлекается;
• принципы нахождения значения корня;
• основные способы извлечения корня из натуральных и дробных чисел.

Что такое «извлечение корня»

Для начала введем определение «извлечение корня».

Определение 1

Извлечение корня — процесс нахождения значения корня.

При извлечении корня n-ной степени из числа a, мы находим число b, n-ная степень которого равняется a. Если мы нашли такое число b, можно утверждать, что корень извлечен.

Замечание 1

Выражения «извлечение корня» и «нахождение значения корня» равнозначны.

В каких случаях извлекается корень?

Определение 2

Корень n-ной степени можно извлечь из числа a точно в случае, если a можно представить в виде n-ной степени некоторого числа b. 

Пример 1

4=2×2, следовательно, из числа 4 можно точно извлечь квадратный корень, который равен 2

Определение 3

Когда корень n-ной степени из числа a невозможно представить в виде n-ной степени числа b, то такой корень не извлекается либо извлекается только приближенное значение корня с точностью до любого десятичного разряда. 

Пример 2

Принципы нахождения значения корня и способы их извлечения

• Использование таблицы квадратов, таблицы кубов и т.д.
• Разложение подкоренного выражения (числа) на простые множители
• Извлечение корней из дробных чисел
• Извлечение корня из отрицательного числа
• Поразрядное нахождение значения корня

Необходимо понять, по каким принципам находится значение корней, и каким образом они извлекаются.

Определение 4

Главный принцип нахождения значения корней — основываться на свойствах корней, в том числе на равенстве: bnn=b, которое является справедливым для любого неотрицательного числа b.

Начать следует с наиболее простого и очевидного способа: таблицы квадратов, кубов и т.д.

Когда таблицы под руками нет, вам поможет способ разложения подкоренного числа на простые множители (способ незатейливый).

Стоит уделить внимание извлечению корня из отрицательного числа, что является возможным для корней с нечетными показателями.

Изучим, как извлекать корни из дробных чисел, в том числе из смешанных чисел, обыкновенных и десятичных дробей.

И потихоньку рассмотрим способ поразрядного нахождения значения корня — наиболее сложного и многоступенчатого.

Использование таблицы квадратов, кубов и т.д.

Таблица квадратов включает в себя все числа от 0 до 99 и состоит из 2 зон: в первой зоне можно составить любое число до 99 с помощью вертикального столбца с десятками и горизонтальной стр

zaochnik.com

Внесение множителя под знак корня: правила, примеры, решения

В этой статье мы продолжим говорить о том, как преобразовывать иррациональные выражения, а конкретно о том, как внести множитель под знак корня. Сначала поясним, в чем состоит смысл такого преобразования, приведем теоретические обоснования и сформулируем основные правила, после чего проиллюстрируем их на примерах решений задач.

Понятие внесения множителя под знак корня

Начнем с определения этого преобразования.

Определение 1

Внесение множителя под знак корня представляет собой преобразование произведения B·Cn, где B и C являются числами или выражениями, а n – натуральным числом, в тождественно равное выражение Bn·Cn или -Bn·Cn.

Первое знакомство с этим видом преобразования, как правило, происходит сразу после изучения понятия квадратного корня и его свойств в рамках школьного курса алгебры. При этом определение берется только для n, равного 2, то есть для выражений с квадратным корнем. Позже, когда начинают изучаться корни n-ной степени, разбираются и случаи с более сложными выражениями.

Учитывая все сказанное выше, легко понять, почему данное преобразование называется именно так: в его результате множитель B перемещается под знак корня. Также очевидно, что изменить таким образом можно не любые выражения, а только конкретные произведения некоторых чисел (выражений) и корней, под знаками которых также расположено некоторое число или выражение. В качестве примера можно привести 5·3, -0,7·x+2·y3, x-2·1-x4 и  т.д.

В результате мы должны прийти к выражению вполне определенного вида. Так, указанные выше примеры после преобразования будут выглядеть так: 52·3, -0,73·x+2·y3, -x-24·1-x4. Возможно и дальнейшее упрощение этих выражений, если такая необходимость есть.

После того, как мы определились, что из себя представляет внесение множителя под знак корня, можно перейти к теоретическим обоснованиям преобразования. В следующем пункте мы объясним, когда -Bn·Cn следует заменять на Bn·Cn, а когда Bn·Cn на -Bn·Cn.

Теоретические основы внесения множителя под корень

Ранее, когда мы объясняли, как можно изменить иррациональные выражения, применяя основные свойства корня, у нас получился ряд важных результатов. Здесь нам потребуются два из них:

Опре

zaochnik.com

Как написать корень на клавиатуре?

Есть множество символов, которые зачастую требуется вставить в текст, но на клавиатуре мы их не видим. Пользователи нередко считают, что раз символа на клавиатуре нет, значит, и поставить его невозможно. Однако это не так. К примеру, вы легко можете поставить знак квадратного корня, пусть даже его нельзя увидеть на клавиатуре. А вот как это сделать, вы узнаете прямо сейчас.

Сначала нужно включить цифровую клавиатуру, которая находится в правой части — именно ею мы и будем пользоваться. Нажмите на клавишу Num Lock.

Как правило, чуть выше находится светодиод-сигнализатор. Когда цифровая клавиатура включена, загорается светодиод.

Теперь вам необходимо зажать клавишу ALT и, удерживая ее, набрать цифру 251 на цифровой клавиатуре.

Если все сделано верно, то у вас получится знак корня. При необходимости его можно скопировать и перенести в другой текст.

Что делать, если у вас ноутбук без цифровой клавиатуры справа? Если вы внимательно посмотрите на клавиатуру ноутбука, то сможете обнаружить дополнительные цифры. Взгляните на пример ниже:

Единица находится на клавише J, двойка — на K и т.д. Вопрос только в том, как включить эту клавиатуру. Как правило, включается она нажатием на клавиши Fn+F1-F12 в зависимости от версии ноутбука (на клавише обычно указан замочек с цифрой). В примере ниже нужно нажать на клавиши Fn+F5.

После этого будет включена цифровая клавиатура и тогда вы проделываете то же самое: зажимаете клавишу ALT и вводите 251 на цифровой клавиатуре. Все должно получиться.

Таблица символов

Если по какой-то причине вы не можете использовать цифровую клавиатуру, вы можете воспользоваться таблицей символов.

На примере Windows 7: нажимаете клавишу «Пуск», выбираете «Все программы» — «Стандартные» — «Служебные» — «Таблица символов».

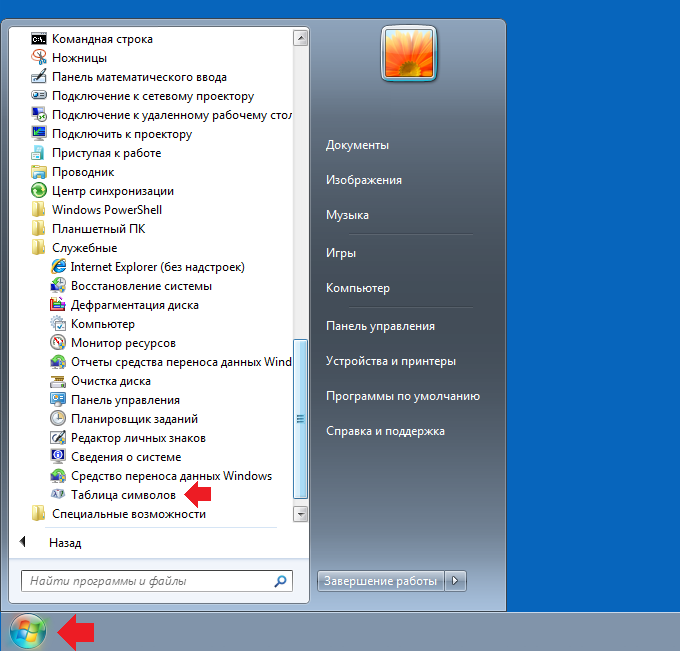
Можно вызвать таблицу символов иначе: нажмите Win+R на клавиатуре, чтобы появилось окно «Выполнить», укажите команду charmap.exe и нажмите ОК.

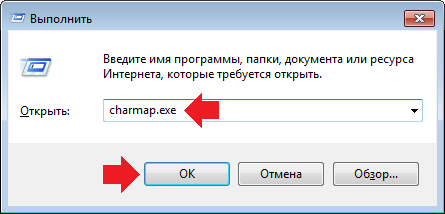
Здесь выбираете шрифт Times New Roman (на самом деле знак корня можно найти и в других шрифтах, а Times New Roman мы приводим в качестве примера), находите знак корня.

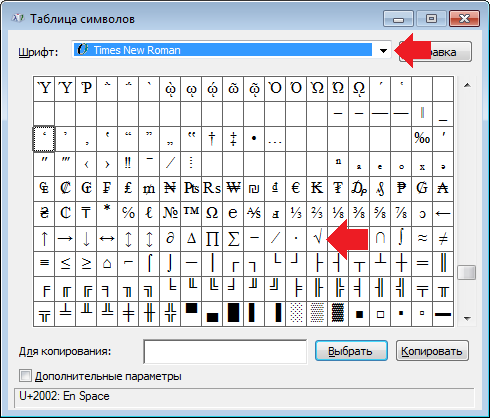
Далее нажимаете на знак корня, следом — кнопку «Выбрать», чтобы символ появился в поле «Для копирования», а уже затем — «Копировать».

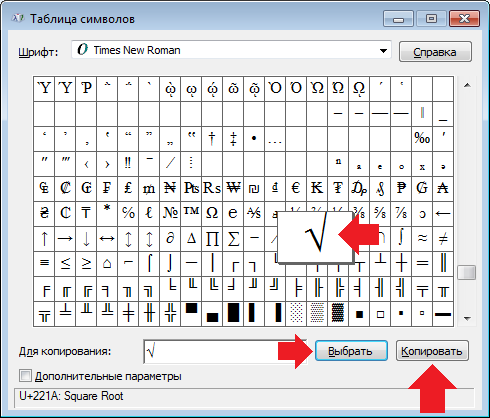
Знак корня скопирован, можете вставлять его в текст. Только помните, что не все редакторы поддерживают подобные символы, хотя и большинство.

siteprokompy.ru

Как поставить корень в Ворде

Иногда работа с документами Microsoft Word выходит за пределы обычного набора текста, благо, возможности программы это позволяют. Мы уже писали о создании таблиц, графиков, диаграмм, добавлении графических объектов и тому подобном. Также, мы рассказывали о вставке символов и математических формул. В этой статье мы рассмотрим смежную тему, а именно, как в Ворде поставить корень квадратный, то есть, обычный знак корня.

Урок: Как в Word поставить квадратные и кубические метры

Вставка знака корня происходит по той же схеме, что и вставка любой математической формулы или уравнения. Однако, пара нюансов все же присутствует, поэтому данная тема заслуживает детального рассмотрения.

Урок: Как в Ворде написать формулу

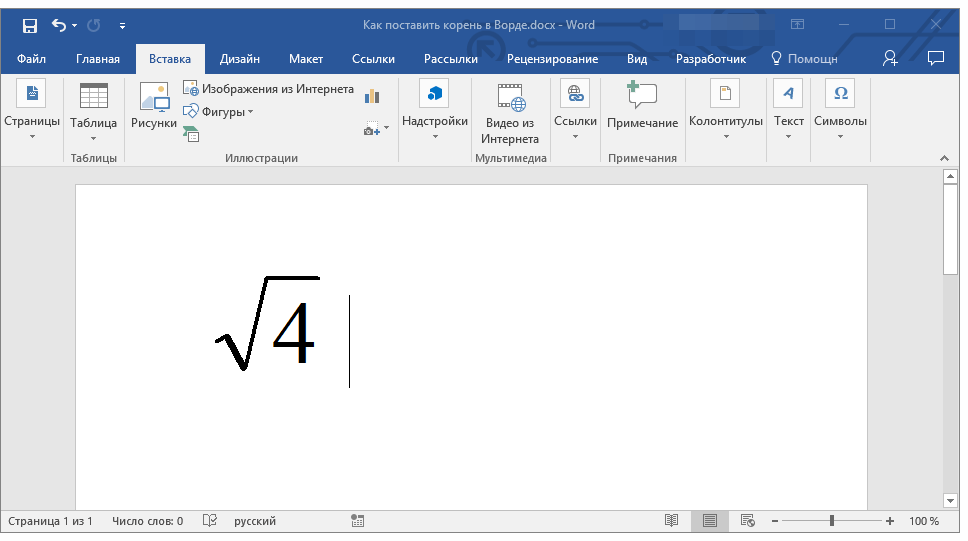
1. В документе, в котором нужно поставить корень, перейдите во вкладку “Вставка” и кликните в том месте, где должен находиться этот знак.

2. Кликните по кнопке “Объект”, расположенной в группе “Текст”.

3. В окне, которое появится перед вами, выберите пункт “Microsoft Equation 3.0”.

4. В окне программы будет открыт редактор математических формул, внешний вид программы полностью изменится.

5. В окне “Формула” нажмите на кнопку “Шаблоны дробей и радикалов”.

6. В выпадающем меню выберите знак корня, который нужно добавить. Первый — квадратный корень, второй — любой другой выше по степени (вместо значка “x” можно будет вписать степень).

7. Добавив знак корня, введите под него необходимо числовое значение.

8. Закройте окно “Формула” и кликните по пустому месту документа, чтобы перейти в обычный режим работы.

Знак корня с цифрой или числом под ним будет находиться в поле, похожем на текстовое поле или поле объекта “WordArt”, которое можно перемещать по документу и изменять в размерах. Для этого достаточно потянуть за один из маркеров, обрамляющих это поле.

Урок: Как повернуть текст в Word

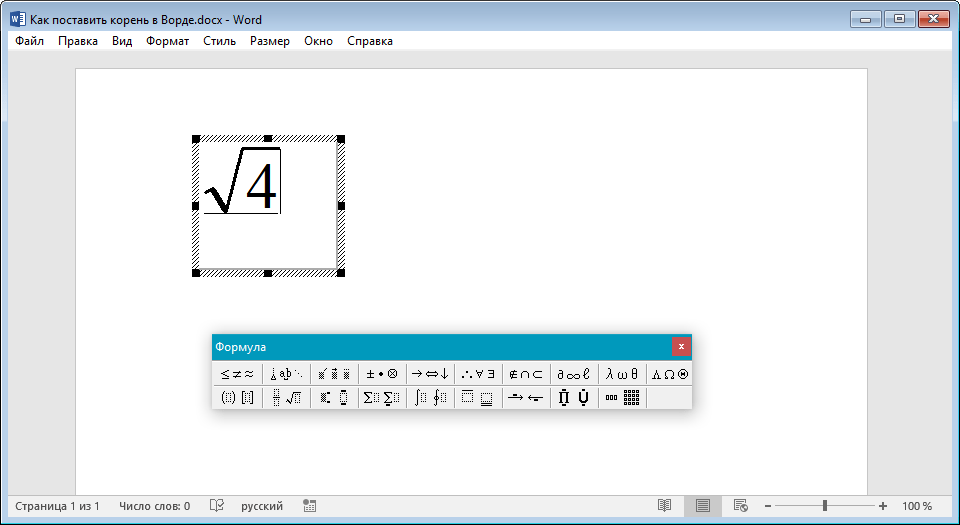
Чтобы выйти из режима работы с объектами, просто кликните в пустом месте документа.

Совет: Чтобы вернутся в режим работы с объектом и повторно открыть окно “Формула”, дважды кликните левой кнопкой мышки в поле, в котором находится добавленный вами объект

Урок: Как в Ворд вставить знак умножения

На этом все, теперь вы знаете, как в Word поставить знак корня. Осваивайте новые возможности этой программы, а наши уроки вам в этом помогут.

Мы рады, что смогли помочь Вам в решении проблемы.
Опишите, что у вас не получилось. Наши специалисты постараются ответить максимально быстро.

Помогла ли вам эта статья?

ДА НЕТ

lumpics.ru

Калькулятор корней с решением онлайн

Корень в математике

Операция извлечения корня из числа, является обратной операцией к операции возведения в степень.

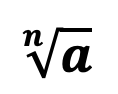
Обозначение: корень обозначается при помощи символа, который называется знаком корня. Число a, которое находится под корнем называется подкоренным выражением, а число n, расположенное слева от символа корня, называется – степенью корня.

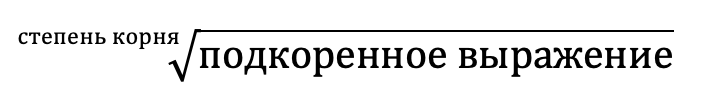
Степень корня – должна быть выражена натуральным числом (1, 2, 3, 4, 5…), т.е. не может быть отрицательной, нулем или дробным числом.

По сути, как уже было сказано выше извлечь корень из числа а означает возведение числа a  в дробную степень, числителем которой выступает степень числа a, а знаменателем – степень корня.

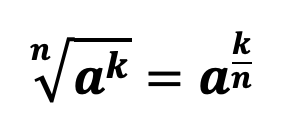
Следует заметить, что если степень корня равна 2, то число два как правило не пишут, а такой корень называется – квадратным.

Приведем примеры:

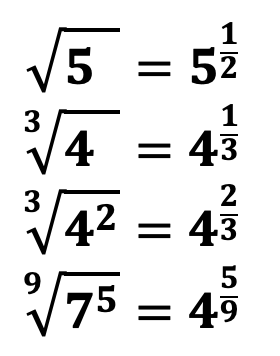
Приведем примеры извлечения корня:

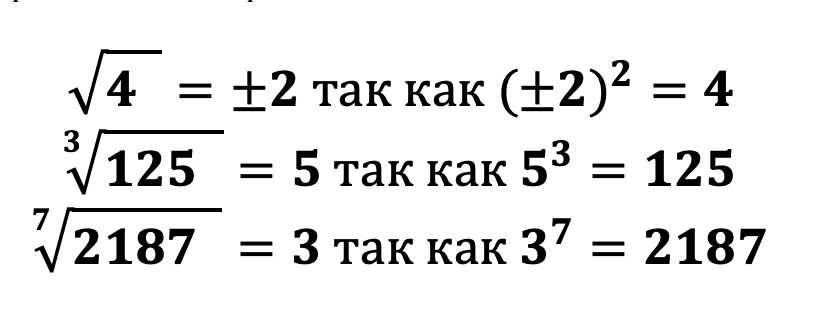
Исходя из вышенаписанных примеров можно сделать вывод, что когда мы хотим извлечь корень, к примеру 2-й степени, то нам необходимо найти такое число, что при возведении во 2-ю степень мы получим подкоренное выражение. То есть под корнем всегда находится число, уже возведенное в степень равную степени корня!

 

Четная и нечетная степень корня

 

Корень нечетной степени

При извлечении корня нечетной степени из положительного числа будем всегда получать положительное число, например:

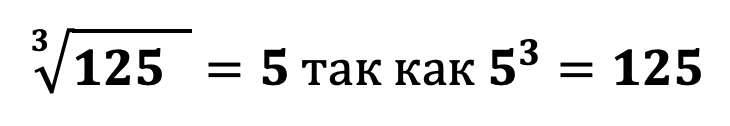
При извлечении корня нечетной степени из отрицательного числа будем всегда получать отрицательное число, например

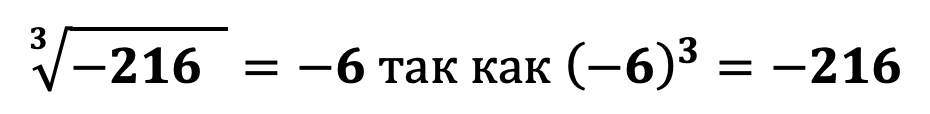
В данном примере можно легко увидеть почему при извлечении корня нечетной степени из отрицательного числа всегда будет получаться отрицательно число. Как известно чтобы возвести число в степень необходимо его умножить само на себя в количестве показателя степени : если (-6) умножить на (-6) получится положительное число 36 (мы знаем, что при умножении двух отрицательных чисел будет получаться положительное число), затем если умножить число 36 на (-6) получим -216, так как при умножении отрицательного числа на положительное всегда будет получаться отрицательное число.

Корень четной степени

 

При извлечении корня четной степени из положительного числа всегда будет получать два значения с противоположенными знаками. Это связанно с тем, что если представить, к примеру функцию квадратного корня y= √x  и посмотреть на ее график, то мы увидим, что каждому значению xсоответствует два значения корня, одно положительное, а другое отрицательное.

Для понимания данного факта, нет необходимости строить график, рассмотрим на примере извлечение квадратного корня из числа 4:

Квадратный корень из 4 равен 2 так как  = 4 и . Проверим 2 ⋅ 2 = 4 и -2 ⋅(-2) = 4.

Приведем еще пример с четной степенью корня для положительного числа.

Корень степени 4 за числа 81 равен 3 так как  = 81 и . Проверим 3 ⋅ 3  ⋅ 3 ⋅ 3 = 81 и  -3 ⋅ (-3)  ⋅ (-3) ⋅ (-3)   = 81

 

Теперь рассмотрим ситуацию, когда под корнем четной степени стоит отрицательное число.

Допустим, мы ходим извлечь квадратный корень из отрицательного числа, например, √-4 теперь подумаем есть ли вообще такое число, которое при возведении в квадрат давало бы -4? Ответ – нет! Любое число при возведении в четную степень всегда будет положительным. Поэтому корня чётной степени из любого отрицательного числа не существует в области вещественных чисел, поскольку при возведении любого вещественного числа в степень с чётным показателем результатом будет неотрицательное число.

Тем не менее извлечь корень четной степени всё-таки можно, но результатом будет всегда комплексное число, например:

 

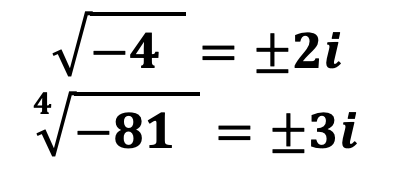
Арифметический и алгебраический корни

Для упрощения записи корня четной степени из положительного числа, в калькуляторах, школьных учебниках и т.д. было введено понятие арифметического корня, значение которого, представляется всегда положительным числом. Алгебраический корень в свою очередь для корня четной степени из положительного числа является полным ответом и содержит как положительные, так и отрицательные значения.

Арифметический корень – упрощенная запись корня четной степени из положительного числа, всегда положительный. Например:

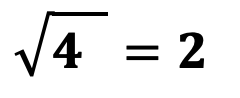
Алгебраический корень – полная запись корня четной степени из положительного числа. Например:

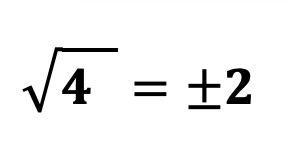
Как упростить корень

Для того, чтобы упростить любой корень, необходимо разложить подкоренное выражение на простые множители (для разложения числа на простые множители можно воспользоваться калькулятором разложения числа на простые множители) и вынести за знак корня тот множитель, который повторяется равное степени корня число раз. Например:

 

 

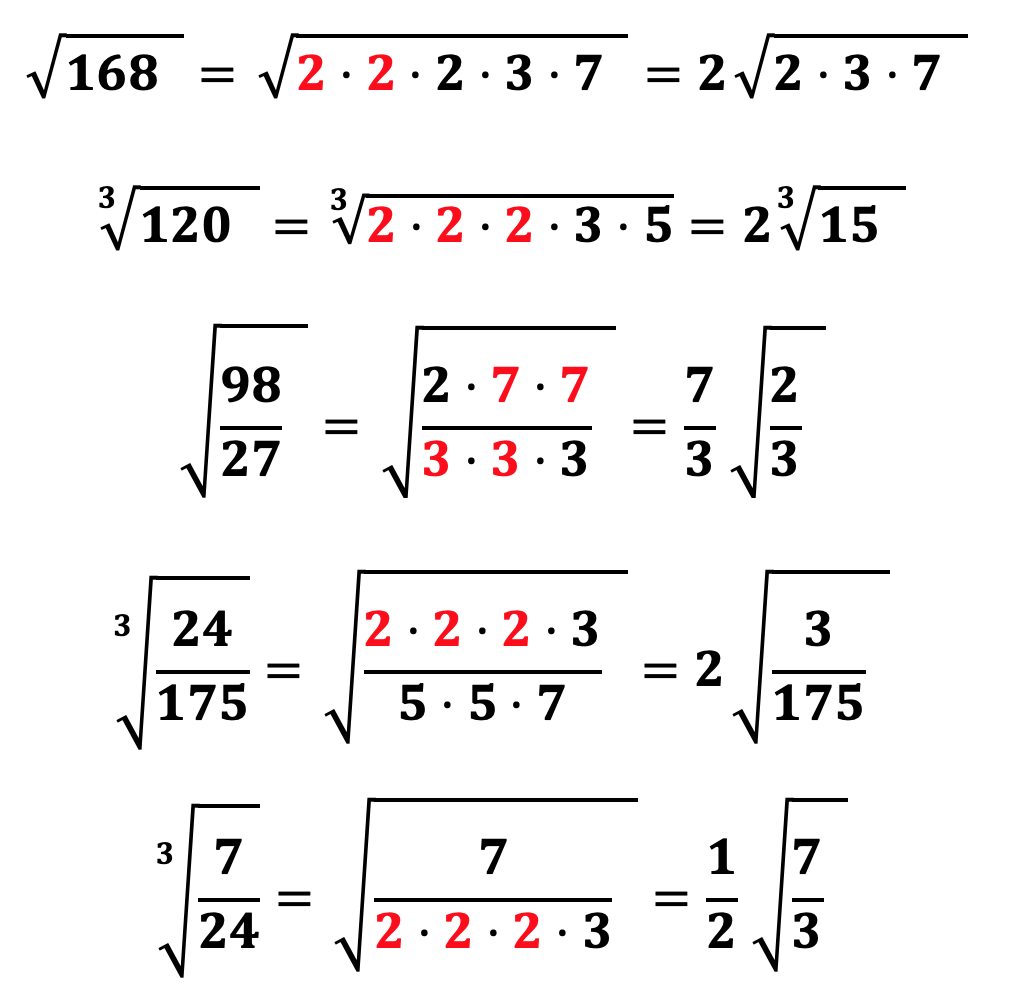
Как мы уже разобрали извлечь корень из числа а означает возведение числа a  в дробную степень, числителем которой выступает степень числа a, а знаменателем – степень корня, поэтому следуя данному правилу мы легко выносим множители из под корня. Распишем предыдущие два примера еще раз:

 

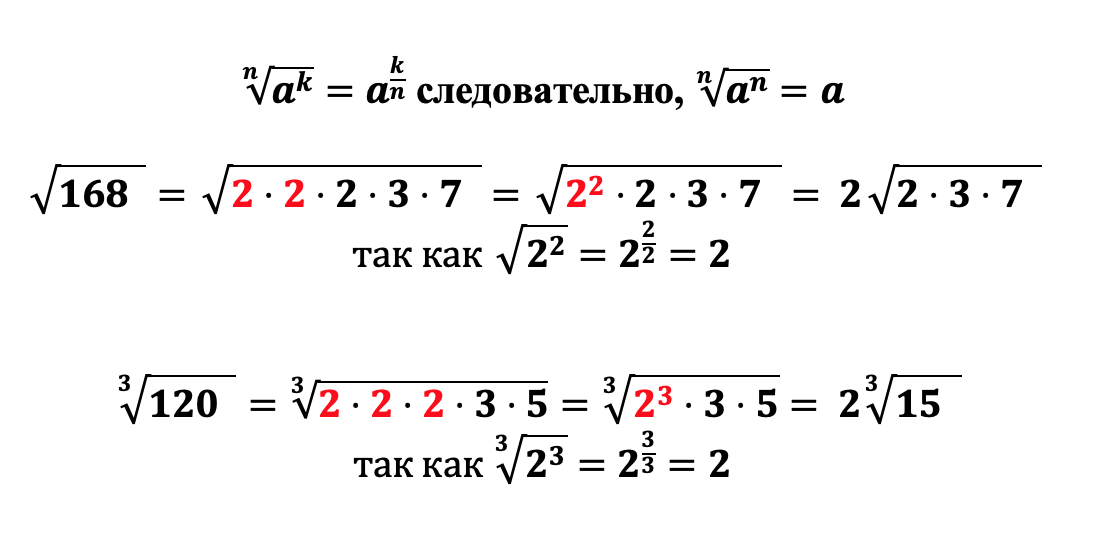
matematika-club.ru

Как написать корень на клавиатуре

У ряда пользователей, активно работающих с математикой, статистикой и прочими точными науками может возникнуть потребность набрать на клавиатуре символ корня √. При этом ни на одной из кнопок клавиатуры нет изображения подобного символа, и пользователь задаётся вопросом: как же осуществить подобное? В этом материале я помогу таким пользователям расскажу, как написать корень на клавиатуре, поясню, какие методы для этого существуют, и как обозначить корень 3,4,5 степени на клавиатуре.

Пишем корень на компьютере

Как поставить знак квадратный корень на клавиатуре

Многие пользователи в решении вопроса о том, как же написать корень на клавиатуре ПК, используют суррогатный символ «^», расположенный на клавише 6 в верхней части клавиатуры (активируется переходом на английскую раскладку, нажатием клавиши Shift и кнопки «6» сверху).

Некоторые пользователи также пользуются буквосочетанием sqrt (квадратный корень), cbrt (кубический корень) и так далее.

При этом это хоть и быстрые, но недостаточные приёмы. Для нормального набора знака корня выполните следующее:

Если вы не знаете, как ввести собаку с клавиатуры, тогда вам обязательно нужно ознакомить с подробной инструкцией по её вводу, так как при наборе E-mail почты без знака собачки не обойтись.

Как написать корень на клавиатуре используя таблицу символов

Альтернативой этому варианту является использование специальной таблицы символов, имеющейся в ОС Виндовс.

1. Нажмите на «Пуск», затем выберите «Все программы»;
2. Потом «Стандартные», затем «Служебные», где выберите «Таблица символов».
3. Там найдите знак корня √, кликните на него, нажмите на кнопку «Выбрать», затем «Копировать» и скопируйте его в нужный вам текст с помощью клавиш Ctrl+V.

Таблица символов

В текстовом редакторе Word (а также в Excel) также имеется соответствующая таблица символов, которую можно использовать для наших задач. Вы можете найти её, перейдя во вкладку «Вставка», и нажав на «Символ» справа, а затем и кликнув на надпись «Другие символы» чуть снизу, это поможет вам в решении вопроса написании корня в Ворде.

Можно, также, использовать опцию «Формула» во вкладке «Вставка» по описанному в данном ролике алгоритму.

Как обозначить корень 3,4,5 степени на клавиатуре

При этом также может возникнуть вопрос о том, как написать обозначить квадратный корень на клавиатуре и другие, подобные им.

Например, корень 3,4,5 степени на клавиатуре можно записать так:

X^1/3

X^1/4

X^1/5

Или так:

3√X  (вместо числа 3 можете использовать соответствующее обозначение из таблицы символов (³)

4√X

5√X

При этом, несмотря на то, что в системе имеется изображение кубического корня ∛ и четвёртого корня ∜, набрать их через Alt и цифровые клавиши не получится. Это возможно лишь с помощью кодов десятичной системы HTML-код (&#8731 и &#8732)  и шестнадцатеричной Юникод (&#x221B и &#x221C). По мне, так лучше использовать формы обозначения, описанные мной чуть выше.

Заключение

В данном материале мной были описаны разные варианты того, как писать корень на клавиатуре вашего компьютера. Самые нетерпеливые могут воспользоваться знаком ^, но точнее и правильнее будет, всё же, воспользоваться комбинацией клавиш Alt+251, и поставить знак корня таким, каким он обозначается в соответствии с общепризнанным стандартом символов.

rusadmin.biz