Энтальпия — Википедия

Энтальпи́я (от др.-греч. ενθαλπω — «нагреваю», также теплова́я фу́нкция^[1][2], теплова́я фу́нкция Гиббса^[3], теплосодержа́ние^[1][3] и изобарно-изоэнтропийный потенциал^[4]) — функция состояния H{\displaystyle H} термодинамической системы, определяемая как сумма внутренней энергии U{\displaystyle U} и произведения давления P{\displaystyle P} на объём V{\displaystyle V}^{[1][5][6][K 1]}:

H≡U+PV.{\displaystyle H\equiv U+PV.\qquad \qquad \qquad \qquad }(Определение энтальпии)

Из уравнения для дифференциала внутренней энергии^[9][10]:

dU=TdS−PdV,{\displaystyle \mathrm {d} U=T\mathrm {d} S-P\mathrm {d} V,\qquad }(Дифференциал внутренней энергии)

где T{\displaystyle T} — термодинамическая температура, а S{\displaystyle S} — энтропия, следует выражение для дифференциала энтальпии

[3]^{[11][K 2]}:

dH=TdS+VdP,{\displaystyle \mathrm {d} H=T\mathrm {d} S+V\mathrm {d} P,\qquad \qquad \qquad }(Дифференциал энтальпии)

которое является полным дифференциалом функции H(S,P){\displaystyle H(S,P)}^{[K 3]}. Она представляет собой термодинамический потенциал^[⇨] относительно естественных независимых переменных — энтропии, давления и, возможно, числа частиц^[⇨] и других переменных состояния ^[⇨].

Понятие энтальпии существенно дополняет математический аппарат термодинамики^[⇨] и гидродинамики^[⇨]. Важно, что в изобарном процессе при постоянном P{\displaystyle P} изменение энтальпии

h3−h2=U2−U1+P(V2−V1)=Q,{\displaystyle H_{2}-H_{1}=U_{2}-U_{1}+P\left(V_{2}-V_{1}\right)=Q,}

равное сумме изменения внутренней энергии U2−U1{\displaystyle U_{2}-U_{1}} и совершённой системой работы P(V2−V1){\displaystyle P\left(V_{2}-V_{1}\right)}, в силу первого начала термодинамики равно количеству теплоты Q{\displaystyle Q}, сообщенной системе. Это свойство энтальпии позволяет использовать её для вычисления тепловыделения при различных изобарных процессах, например, химических

[⇨].

Отношение малого количества теплоты, TdS=dH,{\displaystyle T\mathrm {d} S=\mathrm {d} H,} переданного системе в изобарном процессе, к изменению температуры dT{\displaystyle \mathrm {d} T} является теплоёмкостью при постоянном давлении^{[K 4][20]}:

CP≡T(∂S∂T)P=(∂H∂T)P.{\displaystyle C_{P}\equiv T\left({\frac {\partial S}{\partial T}}\right)_{P}=\left({\frac {\partial H}{\partial T}}\right)_{P}.}

Это экспериментально измеримая величина, и из её измерений находят температурную зависимость энтальпии^[⇨].

Энтальпия — экстенсивная величина: для составной системы она равна сумме энтальпий её независимых частей. Как и внутренняя энергия, энтальпия определяется с точностью до произвольного постоянного слагаемого.

Первое упоминание об использовании термина «энтальпия» в его современном значении^[21]

Понятие энтальпии было введено и развито Дж. В. Гиббсом^[22][23][24] в 1875 году в классической работе «О равновесии гетерогенных веществ». Для обозначения этого понятия Гиббс использовал термин «тепловая функция при постоянном давлении»^[25][26].

Автором термина «энтальпия» в его современном значении считают Х. Камерлинг-Оннеса. Впервые о его авторстве упоминает работа 1909 года^[27][28] в связи с обсуждением сохранения энтальпии в эффекте Джоуля — Томсона^[⇨], хотя в печатных публикациях самого Камерлинг-Оннеса это слово не встречается^[29]. Что же касается буквенного обозначения H{\displaystyle H}, до 1920-х годов оно использовалось для количества теплоты вообще. Определение физической величины H{\displaystyle H} строго как энтальпии или «теплосодержания при постоянном давлении» было официально предложено Альфредом У. Портером в 1922 году

[23].

Энтальпия как термодинамический потенциал[править | править код]

Поскольку внутренняя энергия является термодинамическим потенциалом относительно энтропии и объёма^[30], определение энтальпии можно рассматривать как преобразование Лежандра для перехода от потенциала относительно переменных S, V{\displaystyle S,\ V} к таковому относительно переменных S, P.{\displaystyle S,\ P.} Как и для любого термодинамического потенциала, естественные независимые переменные S, P{\displaystyle S,\ P} совокупно с производными энтальпии по этим переменным позволяют выразить любой термодинамический параметр системы, поэтому задание термодинамического потенциала является самым общим способом задания уравнения состояния^[31].

Из выражения для дифференциала энтальпии получаются ещё два уравнения состояния, непосредственно выражающие температуру и объём через энтропию и давление

[32]:

T(S,P)=(∂H∂S)P,V(S,P)=(∂H∂P)S.{\displaystyle T(S,P)=\left({\frac {\partial H}{\partial S}}\right)_{P},\qquad V(S,P)=\left({\frac {\partial H}{\partial P}}\right)_{S}.}

Если известна энтальпия, другие термодинамические потенциалы — внутренняя энергия U{\displaystyle U}, свободная энергия Гельмгольца F{\displaystyle F} и энергия Гиббса G{\displaystyle G} — могут быть получены с помощью преобразования Лежандра:

G=H−TS=H−S(∂H∂S)P,U=H−PV=H−P(∂H∂P)S,{\displaystyle G=H-TS=H-S\left({\frac {\partial H}{\partial S}}\right)_{P},\qquad U=H-PV=H-P\left({\frac {\partial H}{\partial P}}\right)_{S},}

F=H−TS−PV=H−S(∂H∂S)P−P(∂H∂P)S.{\displaystyle F=H-TS-PV=H-S\left({\frac {\partial H}{\partial S}}\right)_{P}-P\left({\frac {\partial H}{\partial P}}\right)_{S}.}

Из равных друг другу смешанных производных энтальпии выводятся две термодинамические производные, связанные третьим соотношением Максвелла^[33]:

(∂T∂P)S=∂∂P(∂H∂S)P=∂∂S(∂H∂P)S=(∂V∂S)P.{\displaystyle \left({\frac {\partial T}{\partial P}}\right)_{S}={\frac {\partial }{\partial P}}\left({\frac {\partial H}{\partial S}}\right)_{P}={\frac {\partial }{\partial S}}\left({\frac {\partial H}{\partial P}}\right)_{S}=\left({\frac {\partial V}{\partial S}}\right)_{P}.}

Через вторые производные энтальпии выражаются ещё две термодинамические производные:

(∂2H∂S2)P=(∂T∂S)P,(∂2H∂P2)S=(∂V∂P)S.{\displaystyle \left({\frac {\partial ^{2}H}{\partial S^{2}}}\right)_{P}=\left({\frac {\partial T}{\partial S}}\right)_{P},\qquad \left({\frac {\partial ^{2}H}{\partial P^{2}}}\right)_{S}=\left({\frac {\partial V}{\partial P}}\right)_{S}.}

Первая из этих производных характеризует теплоёмкость при постоянном давлении (∂T∂S)P=TCP,{\displaystyle \left({\frac {\partial T}{\partial S}}\right)_{P}={\frac {T}{C_{P}}},} вторая — адиабатическую сжимаемость. Метод якобианов позволяет получить тождества, аналогичные соотношениям Бриджмена, для выражения любых термодинамических производных через приведённые производные энтальпии.

Зависимость энтальпии от числа частиц[править | править код]

Для состоящей из одинаковых частиц открытой системы число частиц N{\displaystyle N} может быть переменным^{[K 5]}. В этом случае выражения для дифференциалов внутренней энергии и энтальпии обобщаются следующим образом^[35][36]:

dU=TdS−PdV+μNdN,dH=TdS+VdP+μNdN,{\displaystyle \mathrm {d} U=T\mathrm {d} S-P\mathrm {d} V+\mu _{N}\mathrm {d} N,\qquad \mathrm {d} H=T\mathrm {d} S+V\mathrm {d} P+\mu _{N}\mathrm {d} N,}

где μN=(∂U∂N)S,V=(∂H∂N)S,P{\displaystyle \mu _{N}=\left({\frac {\partial U}{\partial N}}\right)_{S,V}=\left({\frac {\partial H}{\partial N}}\right)_{S,P}} — химический потенциал, который равен энергии Гиббса G=H−TS{\displaystyle G=H-TS}^[37], приходящейся на одну частицу^[38]: μN=(H−TS)/N{\displaystyle \mu _{N}=(H-TS)/N}. Если частицы не рождаются и не уничтожаются в рассматриваемом процессе, можно характеризовать их количество, например, (переменной) массой тела m{\displaystyle m} и химический потенциал также относить к единице массы. В этом случае вклад от изменения массы вещества в дифференциалы энергии и энтальпии описывается членом μdm{\displaystyle {\mu }\mathrm {d} m}, где модифицированный химический потенциал равен удельной (отнесенной к единице массы) энергии Гиббса: μ=H−TSm{\displaystyle {\mu }={\frac {H-TS}{m}}}.

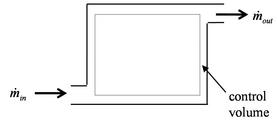Схема контрольного объёма. За малый интервал времени dt{\displaystyle \mathrm {d} t} изменение массы равно dm=(m˙in−m˙out)dt.{\displaystyle \mathrm {d} m=\left({\dot {m}}_{\rm {in}}-{\dot {m}}_{\rm {out}}\right)dt.}

В англоязычной литературе, особенно технической, понятие открытой системы обычно отождествляют с понятием «контрольного объёма» (англ. control volume)^[39], который ограничен воображаемой неподвижной контрольной^[40] поверхностью, проницаемой для вещества, но оставляющей неизменной заключённый в ней объём. В то же время закрытую систему называют «контрольной массой» (англ. control mass). Последнее название подчеркивает постоянство массы (dm≡0{\displaystyle \mathrm {d} m\equiv 0}), вследствие которого справедливо приведённое выше соотношение для дифференциала внутренней энергии и термодинамическое состояние системы характеризуется только двумя параметрами, например, S{\displaystyle S} и V{\displaystyle V}. С другой стороны, при постоянстве контрольного объёма (dV≡0{\displaystyle \mathrm {d} V\equiv 0}) заключённая в нём внутренняя энергия тоже характеризуется только двумя параметрами, например, энтропией S{\displaystyle S} и переменной массой m{\displaystyle m}, причём в практически важное выражение для дифференциала внутренней энергии контрольного объёма входит (удельная) энтальпия^[41]:

dU=TdS+μdm=TdS+H−TSmdm=mTd(Sm)+Hmdm.({\displaystyle \mathrm {d} U=T\mathrm {d} S+{\mu }\mathrm {d} m=T\mathrm {d} S+{\frac {H-TS}{m}}\mathrm {d} m=mT\mathrm {d} \left({\frac {S}{m}}\right)+{\frac {H}{m}}\mathrm {d} m.\qquad (}Энергия контрольного объёма)

Если в системе присутствуют несколько различных веществ характеризующихся массами mj{\displaystyle m_{j}} и химическими потенциалами μj{\displaystyle \mu _{j}}, выражение для дифференциала энтальпии обобщается следующим образом^[42][43]:

dH=TdS+VdP+∑jμjdmj.{\displaystyle \mathrm {d} H=T\mathrm {d} S+V\mathrm {d} P+\sum _{j}\mu _{j}\mathrm {d} m_{j}.}

Молярная (мольная) энтальпия
Hm= Hn=hMrMu{\displaystyle \ H_{m}=\ {\frac {H}{n}}=hM_{r}M_{u}}
Размерность	L2MT−2{\displaystyle L^{2}MT^{-2}}
СИ	Дж/моль (Mu=10−3{\displaystyle M_{u}=10^{-3}\,}кг/моль)
СГС	эрг/моль (Mu={\displaystyle M_{u}=\,}1 г/моль)
Внесистемная единица: кал/моль

Вместо экстенсивной величины энтальпии часто используют её отношение h=Hm{\displaystyle h={\frac {H}{m}}} её величины к массе тела m{\displaystyle m}, называемое удельной энтальпией. Продолжая обозначать экстенсивные величины заглавными буквами, соответствующие им удельные величины будем обозначать строчными, за исключением удельного объёма, вместо которого введём обратную к этой величине плотность:

s=Sm,1ρ=Vm,u=Um,h=Hm=u+Pρ.{\displaystyle s={\frac {S}{m}},\qquad {\frac {1}{\rho }}={\frac {V}{m}},\qquad u={\frac {U}{m}},\qquad h={\frac {H}{m}}=u+{\frac {P}{\rho }}.}

Соотношение для полного дифференциала удельной энтальпии можно получить, разделив уравнение для дифференциала энтальпии на m{\displaystyle m}:

dh=Tds+1ρdP.{\displaystyle \mathrm {d} h=T\mathrm {d} s+{\frac {1}{\rho }}\mathrm {d} P.\qquad }(Дифференциал удельной энтальпии)

Удельную энтальпию можно представлять графически в виде h,s{\displaystyle h,s}-диаграммы Молье. На диаграмме кривые (изобары) для различных значений давления задают функцию h(s,P){\displaystyle h(s,P)}^[44]. Большой практический интерес представляет диаграмма Молье для воды/водяного пара^[45], схематически изображённая на рисунке: синие линии — изобары, зелёные — изотермы. Область ниже красной кривой соответствует двухфазной среде пара и воды. В этой области красные линии соответствуют различным значениям величины x{\displaystyle x} — массовой доли водяного пара — и пересекаются в критической точке K, а изобары совпадают с изотермами и являются прямыми линиями.

Вводят также молярную (мольную) энтальпию Hm=Hn{\displaystyle H_{m}={\frac {H}{n}}}, отнесённую не к массе, а к количеству вещества в теле в молях n, что удобно для приложений к химии. Молярные величины обозначают нижним индексом m. Альтернативное определение через удельную энтальпию: Hm=hMrMu{\displaystyle H_{m}=hM_{r}M_{u}}, где Mr{\displaystyle M_{r}} — относительная молекулярная масса, а

Лекция1

1

Лекция 1

Основы термодинамики.

В ходе протекания химических реакций происходит разрыв одних химических связей (поглощение энергии) и образование других (выделение энергии). Поэтому для предсказания направления протекания химического процесса, общего баланса выделившейся энергии необходимо знать законы обмена энергией между различными телами и окружающей средой. Изучением этих законов занимается термодинамика. Термин термодинамика ввел В.Томсон в 1854 г. и в переводе с греческого означает «теплота-работа».

Перед тем как перейти к рассмотрению основных законов термодинамики, рассмотрим некоторые важнейшие понятия, которыми мы будем пользоваться в дальнейшем.

Система — тело или группа тел, которые могут взаимодействовать между собой и мысленно или реально отделенных от окружающей среды границей раздела. Под взаимодействием подразумевается обмен энергией и веществом. Например, наша лекционная аудитория. Если обмен энергией и веществом возможен не только внутри системы, но и между системой и окружающей средой, то такая система называется открытой. Пример, чашка чая на столе. Если обмен веществом с окружающей средой не возможен, система называется закрытой. Пример, консервная банка. Если, наконец, невозможен обмен ни веществом, ни энергией система называется изолированной. Близкое к такому состоянию можно считать, например, горячий чай в термосе.

Энергия — общая количественная мера движения и взаимодействия всех видов материи. В соответствии с различными формами движения материи энергию разделяют на механическую, электрическую, ядерную, тепловую и т.д.

Теплота (Q) — форма беспорядочного (теплового) движения образующих тело частиц (атомы, молекулы, электроны, ионы и т.д.). Количественная мера теплоты — количество теплоты, т.е. энергии получаемой или отдаваемой системой при теплообмене.

[Единицы измерения кал, Дж, 1 кал = 4,184 Дж.]

Работа (А) — произведение обобщенной силы на обобщенную координату. Механическая работа А = Рh, электрическая работа А = q(U₂ -U₁), А = рΔv.

Параметры состояния — это величины позволяющие определить состояние системы, непосредственно измерив эти величины. Пример, кусок железа, чтобы его охарактеризовать, необходимы следующие параметры m, Т, v. В химии используют в основном р,v,Т,с. Параметры состояния бывают экстенсивные, зависящие от размера объекта (масса, объем, внутренняя энергия) и интенсивные, не зависящие от размера объекта (давление, температура, вязкость).

Состояние, свойства системы описывается различными функциями, которые называются функциями состояния. Главное свойство функции состояния это независимость ее от пути

2

перехода системы из начального в конечное состояние, т.е. функция состояния зависит только от состояния системы в начальной и конечной точках. Изменение функции состояния равно разности ее значений в конечном (В) и исходном (А) состояниях.

В

Fа — Fв А ΔF = I F_А — F_в I

Внутренняя энергия (U) — энергия системы, зависящая только от количества вещества, его состава и состояния т.е. внутренняя энергия включает в себя энергию хаотического (теплового) движения всех микрочастиц системы, энергию колебательных, вращательных движений молекул, энергию взаимодействия этих частиц т.е. характеризует весь запас энергии системы. Рассчитать абсолютное значение внутренней энергии невозможно, можно лишь с достаточной точностью измерить изменение внутренней энергии при переходе из одного энергетического состояния в другое ΔU = U₁ — U₂ . Внутренняя энергия это функция состояния системы.

Рассмотрев основные понятия термодинамики, можно перейти и к основным законам термодинамики.

Нулевой закон термодинамики.

Две системы, находящиеся в термическом равновесии с третьей системой, состоят в термическом равновесии друг с другом.

Первый закон термодинамики.

Суть первого закона термодинамики заключается в том, что тела могут обмениваться между собой энергией в виде тепла и работы, при этом энергия не исчезает и не возникает ниоткуда. Первый закон термодинамики имеет несколько формулировок, но все они выражают одну идею: неуничтожимость и эквивалентность различных видов энергии при их взаимных переходах. Отсюда следует, что в изолированных системах сумма всех видов энергии есть величина постоянная. Из постоянства запаса энергии в изолированной системе вытекает другая формулировка первого закона: тепло сообщенное системе (Q) расходуется на увеличение внутренней энергии системы (ΔU) и работу (А) совершаемую системой.

Q = ΔU +А (1)

Если система совершает работу расширения, то А = pΔv и выражение (1) примет вид

О = ΔU + pΔv (2)

3

Выражение (1) есть математическая запись первого закона термодинамики. В этом выражении только изменение внутренней энергии не зависит от пути процесса, Q и А зависят от пути и не являются функциями состояния.

Химические реакции могут протекать или при постоянном объеме (изохорный процесс) или при постоянном давлении (изобарный процесс). Рассмотрим изменению каких функций состояния будет соответствовать тепловой эффект химических реакций при этих условиях. Если реакция протекает при постоянном объеме Δv = 0, то А = 0 и тепловой эффект реакции будет равен изменению внутренней энергии

Qv = ΔU (3)

Если реакция протекает при постоянном давлении то выражение (2) можно записать в виде, учитывая, что ΔU = U₂ — U₁, а Δv =v₂ – v1

Qp = (U₂ — U₁)+ p(v₂ – v1) = (U₂ + p v₂) — (U₁+ p v1) (4)

Работа расширения зависит только от начального и конечного состояний, следовательно выражение стоящее в скобках является функцией состояния, которую назвали

энтальпия.

U + рv=Н (5)

Таким образом тепловой эффект химической реакции при постоянном давлении можно представить в виде

Qp = Н₂-Н₁=ΔН (6),

где Н₁ — энтальпия исходных веществ, а Н₂ — энтальпия продуктов реакции. Таким образом тепловой эффект химической реакции (Qp) или изменение энтальпии (ΔН) при протекании химической реакции при постоянном давлении равен разности энтальпии продуктов реакции и энтальпии исходных веществ.

По знаку теплового эффекта реакции делятся на

Эндотермические — реакции протекают с поглощением тепла, + ΔН = — Qp и

Экзотермические — реакции протекают с выделением тепла, — ΔН = + Qp.

Поскольку для нахождения изменения функций состояния U, Н и сравнения их между собой необходим единый уровень отсчета, ввели понятие стандартного состояния. Стандартное состояние это давление 1 атм = 1,01.10

5 Па и концентрация 1 моль/л. Значения термохимических величин в стандартном состоянии называют стандартными величинами и обозначают с «нулем» Н°, U°.

Запись термохимических уравнений отличается от записи уравнений химических реакций. При термохимических уравнений необходимо указывать дополнительную информацию. Для всех участников реакций указывают их агрегатное состояние: к — кристаллическое, ж — жидкое, г — газообразное, р — в виде раствора, в правой части указывают тепловой эффект реакции, например: 2 Na (к) + Н₂O (ж) = 2 NaОН (р) + Н₂ (г) + 368 кДж

4

При термодинамической записи все остается то же самое, только вместо теплового эффекта Qp, Qv указывают изменение энтальтии или внутренней энергии

2 Na (к) + Н₂O (ж) = 2 NaOH (р) + Н₂ (г) ΔН°_Т = — 368 кДж

Как, правило, в термохимических таблицах обычно приводятся тепловые эффекты реакций при постоянном давлении, то есть энтальпии, которые обозначаются следующим образом Δ_ГН°_Т, где нижний индекс Т соответствует температуре к которой относится данное значение энтальпии, обычно это или 298 К или 0 К, верхний индекс «°» означает, что все участники реакции находятся в стандартном состоянии. Экспериментальным определением тепловых эффектов различных реакций занимается раздел химии, называемый термохимией. К настоящему времени определены энтальпии громадного количества химических реакций, величины которых составляют фундаментальные справочники термодинамических характеристик. С помощью справочных величин можно рассчитать энтальпии химических реакций, даже тех, экспериментальное определение которых невозможно. Ключевыми величинами справочных изданий являются стандартные энтальпии образования химических соединений.

Стандартной энтальпией образования химического соединения называют стандартное изменение энтальпии реакции образования одного моля этого вещества из простых веществ, взятых в том агрегатном состоянии, в котором они находятся при стандартных условиях и данной температуре. Например, для КNO₃ стандартная энтальпия образования это изменение энтальпии следующей реакции К (к) + 0,5 N₂ (г) + 1,5 O₂ (г) = КNO₃ (к),

для глюкозы С₆Н₁₂O₆ 6 С(к) + 6 Н₂ (г) + 3 O₂ = С₆Н₁₂O₆ (к),

для воды Н₂O Н₂(г) + 0,5 O₂ (г) = Н₂O (ж).

Энтальпия образования измеряется в величинах кДж/моль, ккал/моль. Стандартные энтальпии образования простых веществ O₂, Н₂, К, Fе, Сl и т.д. принимаются равными нулю. Для стандартных энтальпий образования принята следующая запись ΔfН°т(КNO₃ к)

Второй ключевой справочной термохимической величиной является стандартная энтальпия сгорания. Стандартной энтальпией сгорания называется энтальпия реакции сгорания вещества в кислороде с образованием оксидов элементов в высших степенях окисления или простых веществ, если они более устойчивы в данных условиях, чем оксиды. Например, для метана энтальпия сгорания это энтальпия следующей реакции

СН₄ (г) + 2 O₂ (г) = СO₂(г) + 2 Н₂O (ж), для аммиака Nh4 (г) + 1,5 O₂(г) = 0,5 N₂ + 1,5 Н₂O (ж).

В основе всех термохимических расчетов лежит закон Гесса, который формулируется следующим образом — тепловой эффект (энтальпия) химической реакции зависит только от начального и конечного состояния системы и не зависит от пути перехода. Рассмотрим простой

5

пример — окисление углерода кислородом. Начальное состояние (1) это {С(к) + O₂(г)}, конечное состояние (2) {СO₂(г)}. Из (1) в (2) можно перейти сразу по реакции

1 → 2 С(к) + O₂(г) = СO₂(г) ΔН°₂₉₈ = -394 кДж/моль

или через промежуточное состояние (3) {СО(г) + O₂(г)}

1 → 3 С(к) + 0,5О₂(г) = СО(г) ΔН°₂₉₈ = -110,5 кДж/моль

3 →2 СО(г) +0,5 O₂(г) = СO₂(г) ΔН°₂₉₈ = -283,5 кДж/моль

Видно, что суммарный тепловой эффект по пути 1→ 3→2 (-110,5 — 283,5 = 394 ) равен тепловому эффекту по прямому пути1 → 2.

Из закона Гесса следует два важных практических следствия:

I. Стандартная энтальпия химической реакции равна сумме стандартных энтальпий образования продуктов реакции минус сумма стандартных энтальпий образования исходных веществ с учетом стехиометрических коэффициентов.

Рассмотрим реакцию в общем виде

аА + bВ + сС + …. = kК + lL + mM +…. Энтальпия этой реакции будет равна

Δ r Н°₂₉₈ = (k Δ f Н°₂₉₈(К) + l Δ f Н°₂₉₈(L) + m Δ f Н°₂₉₈(М) + …) — (а Δ f Н°₂₉₈(А) + b Δ f Н°₂₉₈(В) + с Δ f Н°₂₉₈(С) + ….), Энтальпия реакции

Аl₂O₃(к) + 3 SOз (г)= Аl₂(SO₄)₃(к) будет равна Δ r Н°₂₉₈ = { Δ f Н°₂₉₈(Аl₂(SO₄)3)} — {( Δ f Н°₂₉₈(Аl₂O3 )+ 3 Δ f Н°₂₉₈(SO₃)}

II. Стандартная энтальпия химической реакции равна сумме стандартных энтальпий сгорания исходных веществ минус сумма стандартных энтальпий сгорания продуктов реакции с учетом стехиометрических коэффициентов.

Пример: 3 С₂Н₂ (г) = С₆Н₆ (ж) реакция Зинина

Стандартная энтальпия этой реакции равна

Δ r Н°₂₉₈ = 3 Δ_сгорН°г98(С₂Н₂) — Δ_сгорН°₂₉₈ (С₆Н₆)

С помощью закона Гесса можно определить стандартные энтальпии образования веществ, которые невозможно измерить непосредственно, например, глюкозы

6 С(к) + 6 Н₂ (г) + 3 O₂(г) = С₆Н₁₂O₆ (к) Δ f Н°т(С₆Н₁₂O₆ к) -?

Но если измерить экспериментально ее стандартную энтальпию сгорания

С₆Н₁₂O₆ (к) + 6 O₂(г) = 6 СO₂(г) + 6 Н₂O (ж), Δ_сгорН°₂₉₈(С₆Н₁₂O₆)

и воспользоваться первым следствием закона Гесса, легко рассчитать искомую величину Δ r Н°₂₉₈ =6 Δ f Н°₂₉₈(СO₂) + 6 Δ f Н°₂₉₈(Н₂O) – Δ f Н°_т(С₆Н₁₂O₆ к ) отсюда

Δ f Н°т(С₆Н₁₂O₆ к ) = 6 Δ f Н°₂₉₈(СO₂) + 6 Δ f Н°₂₉₈(Н₂O) – Δ r Н°₂₉₈

Значения первых двух слагаемых находятся в справочниках, а третье слагаемое, стандартная энтальпия сгорания, определено экспериментально.

8.4. Определение энтальпии образования соли

Энтальпию образования соли MgSO₄ можно вычислить, используя следующие термохимические уравнения:

Mg_(к) + Н₂SO_{4(ратвор)} → MgSO_{4(раствор)}+ Н_2(г); ΔН₁

Н_2(г) + S_(к) + 2O_2(г) +aq → Н₂SO_{4(ратвор)}; ΔН₂

MgSO_{4(раствор)} → MgSO_4(к)+ aq; ΔН₃

Складывая эти уравнения, получают

Mg_(к) + S_(к) + 2O_2(г) → MgSO_4(к);

= ΔН₁ + ΔН₂ + ΔН₃.

Энтальпию растворения магния в серной кислоте ΔН₁, и его безводного сульфата в воде –ΔН₃ определяют экспериментально, а энтальпия образования 0,5 н раствора H₂SO₄ ΔН₂, по справочным данным, равна –894 кДж/моль.

Выполнение работы

1. Поместить во внутренний стакан калориметра 200 мл 0,5 н. раствора серной кислоты и отметить начальную температуру при работающей мешалке.

2. Опустить через воронку туда же точно взвешенное количество магния (около 0,2 г). Зафиксировать изменение температуры по методике, описанной в общих указаниях (гл. 7).

3. Вычислить ΔН₁, используя формулы (11) и (12), где

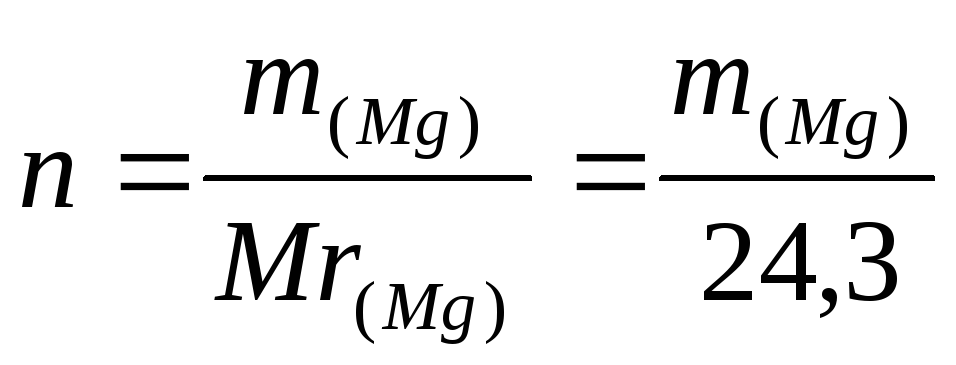, а m_(Mg) – навеска магния, г.

4. Таким же способом определить (–ΔН₃), растворяя точную навеску MgSO₄ (около 2 г) в 200 мл воды.

5. Вычислить ΔН₃, используя формулы (6) и (7),

где ,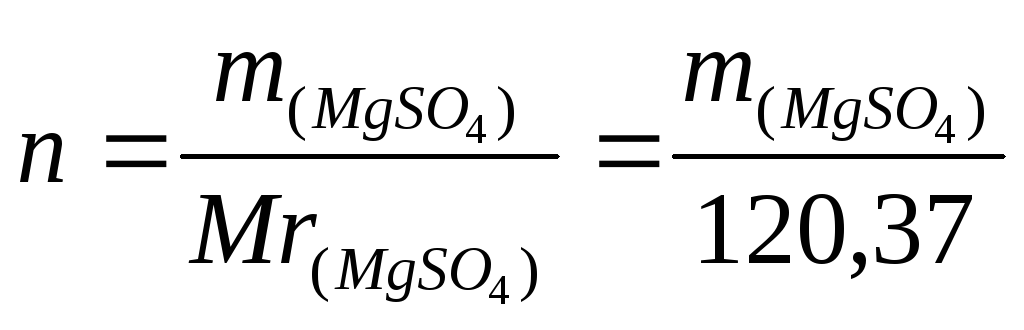

m – навеска MgSO₄, г.

6. Вычислить и сравнить ее с табличным значением, равным –1280 кДж/моль.

Определить относительную ошибку вычисленной величины:

.

9. Вычисления энергии связи по тепловому эффекту

И НАОБОРОТ

Значениями энергии связи часто пользуются для вычисления тепловых эффектов реакций, если неизвестны ΔН_обр соединений, участвующих в реакциях. С другой стороны, значения теплот образования, возгонки, диссоциации и других энергетических эффектов используются для определения прочности межатомных и межмолекулярных связей. Расчеты эти не очень точны, т.к. на величину энергии химической связи между двумя атомами оказывают влияние другие, входящие в молекулу атомы. Поэтому энергия химической связи между какими-либо конкретными атомами, входящими в состав различных молекул, не совсем одинакова.

Энергия связи или энтальпия связи – это энтальпия процессаобразования ковалентной связи между двумя атомами, взятыми в газообразном состоянии. Например:

Н_(г) + CI_(г) → HCI_(г); ΔН_(H–CI) = –431,4 кДж

Не путать энтальпию связи с энтальпией образования:

½ Н_2(г) + ½ CI_2(г) → HCI_(г); ΔН_обр.(HCI) = –92,3 кДж.

Значения энтальпий различных связей приведены в табл. 3 приложения.

Рассмотрим следующие, примеры вычислений.

Пример 1

Считая связь N–N в молекуле гидразина одинарной, а среднюю энергию связи N–Н в аммиаке и гидразине одинаковой и пользуясь табличными значениями энергий связи Н–Н, вычислить изменение энтальпии реакции

2NH_3(г) → N₂H_4(г) + Н_2(г)

Решение. Представим уравнение реакции в следующем виде:

На разрыв связей в исходных веществах энергия затрачивается, а при образовании связей в продуктах реакции она выделяется, поэтому, подсчитывая число определенных связей в продуктах реакции и исходном веществе, можно записать:

ΔН_{реакции} = – (ΔН_N–N + 4ΔН_N–H + ΔН_H–H) + 6ΔН_N–H =2ΔН_N–H – ΔН_N–N – ΔН_H–H =

= 2·390,6 – 113,4 – 436 = 231,8 кДж

Процесс является эндотермическим, так как на разрыв связей в исходном веществе затрачивается больше энергии, чем ее выделяется при образовании связей в продуктах реакции.

Пример 2

Рассчитать энтальпии связей С–H и С–С, используя следующие данные:

C_{(графит)} + 2H_2(г) → СH_4(г); ΔН₁ = –74,85 кДж

2C_{(графит)} + 3H_2(г) → С₂H_6(г); ΔН₂ = –84,67 кДж

C_{(графит)} → С_(г); ΔН₃ = 724 кДж

H_2(г) → 2Н_(г); ΔН₄ = 435,9 кДж

Решение:

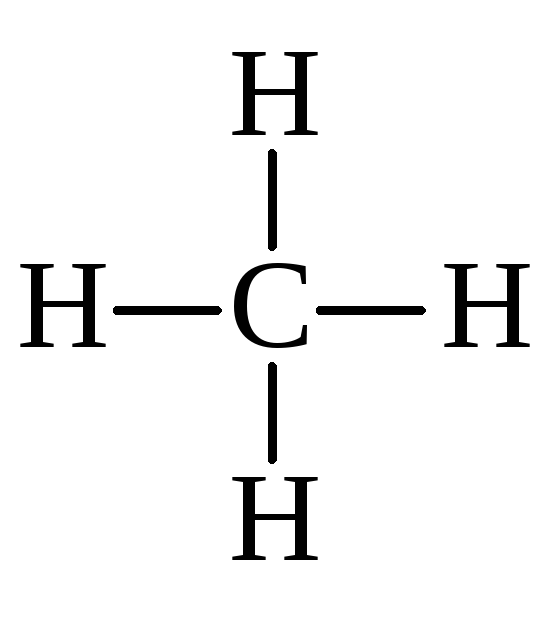
→ C_(г) + 4H_(г); ΔH₅ = –4 ΔH_C–H

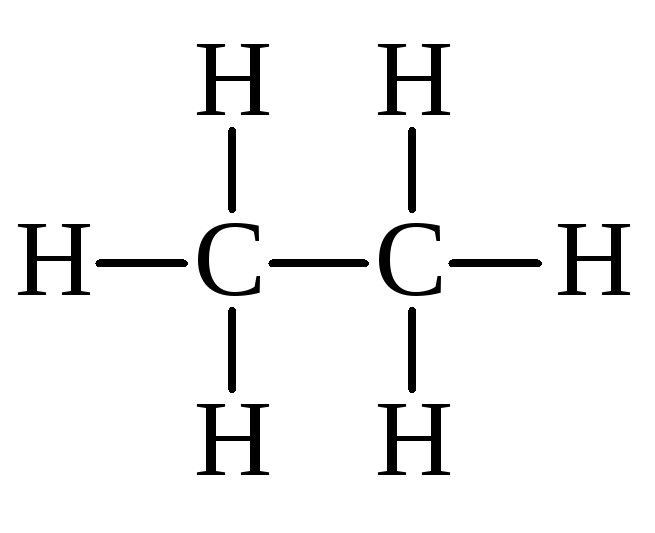
→ 2C_(г) + 6H_(г); ΔH₆ = –(ΔH_C–C + 6 ΔH_С–H)

Такие термохимические уравнения можно получить из исходных. Умножим четвертое уравнение на 2 и вычтем из первого уравнения, а результат вычтем еще из третьего уравнения, получим следующее термохимическое уравнение:

СН_4(г) → С_(г) + 4Н_(г);

ΔН₅ = ΔН₃ – (ΔН₁ – 2ΔН₄) = 1670,65 кДж.

Из второго уравнения вычтем удвоенное третье уравнение и из полученной разности вычтем утроенное четвертое уравнение:

С₂Н_6(г) → 2С_(г) + 6Н_(г);

ΔН₆ = – (ΔН₂ – 2ΔН₃ –3ΔН₄) = 2843,7 кДж

ΔН₅ = – 4ΔН_С–Н = 1670,65 кДж;

ΔН₆ = – (ΔН_С–С + 6ΔН_С–Н) = 2671 кДж

Решая систему уравнений, находим ΔН_С–Н = –419 кДж/моль,

ΔН_С–С = –330 кДж/моль.

Урок 19. Изменение энтальпии – HIMI4KA

В уроке 19 «Изменение энтальпии» из курса «Химия для чайников» рассмотрим понятие теплоты реакции и ее единицу измерения; выясним, что происходит при экзотермических и эндотермических реакциях, а также познакомимся с законом Гесса. Данный урок потребует от вас знания химических основ из прошлых уроков. Обязательно прочитайте о составлении химических реакций и формулировку законов сохранения массы и энергии, чтобы не возникало лишних вопросов.

Хоть данная глава и называется «Законы сохранения массы и энергии«, однако пока мы ничего не говорили о законе сохранения энергии. Для тех, кто забыл: закон сохранения энергии гласит, что теплОты реакций аддитивны и энергия процесса не зависит от того, проводится ли он в одну или несколько стадий.

Единица измерения теплоты

Так как это курс химии, а не физики, то совсем мельком напомню, что теплота и работа являются хоть и различными, но формами энергии, поэтому измеряются в одинаковых единицах (в Дж). Если вы совершаете работу над каким-либо телом или совокупностью тел, можно повысить энергию этой системы или нагреть ее в зависимости от того, каким образом совершается работа. К примеру, когда мы поднимает какой-либо предмет, работа превращается в потенциальную энергию, а если потереть этот предмет, то работа (трение) переходит в теплоту. И наоборот, при падении тяжелого предмета энергия превращается в теплоту, а при работе двигателя внутреннего сгорания выделяемая в нем теплота переходит в работу. Химиков, в отличии от физиков, занимает не работа, а теплота, которая может поглощаться и выделяться при протекании химической реакции.

Единицей измерения теплоты служит — Джоуль (Дж). 1 Джоуль можно определить как количество теплоты, необходимое для повышения температуры 1 г чистой воды на 1/4 градуса. В повседневной жизни 1 джоуль энергии требуется для поднятия небольшого яблока (102 г) строго вертикально на высоту один метр.

Теплота реакции

Представление о законе сохранения энергии можно получить на примере разложения пероксида водорода, H₂O₂. Когда водный раствор H₂O₂ реагирует с образованием газообразного кислорода и жидкой воды, происходит заметное выделение тепла: разложение 1 моля H₂O₂ при 25°С (комнатная температура) сопровождается выделением 94,7 кДж (94700 Дж) тепла.

Теплоту химической реакции, проводимой при постоянном давлении, принято называть изменением энтальпии реагирующей системы, ΔH (читается «дельта-аш»). Если в процессе реакции выделяется теплота, то энтальпия реагирующей системы убывает и ΔH отрицательно, а сами реакции называются экзотермическими. Напротив, эндотермические реакции протекают с поглощением теплоты и сопровождаются возрастанием энтальпии реакционной смеси. Для реакции разложения пероксида водорода можно записать:

• H₂O₂(водн.) → H₂O(ж.) + ½O₂(г.)  ΔH = -94,7 кДж (1)

Это количество теплоты, которое выделяется при разложении 1 моля пероксида водорода на 1 моль воды и 1/2 моля газообразного кислорода, т.е. в расчете на 1 моль реагента. Если удвоить все коэффициенты в уравнении реакции, то придется удвоить и теплоту реакции, поскольку она будет относиться теперь к вдвое большему количеству реагента:

• 2H₂O₂(водн.) → 2H₂O(ж.) + O₂(г.)  ΔH = -189,4 кДж (2)

Физическое состояние реагентов и продуктов также оказывает влияние на теплоту реакции (изменение энтальпии). Если H₂O₂ заставить разлагаться на газообразный кислород и водяной пар, а не жидкую воду, часть молярной теплоты разложения H₂O₂ (94,7 кДж) затратится на испарение H₂O, которое описывается уравнением:

• H₂O(водн.) → H₂O(г.)  ΔH = +44,0 кДж (3)

и поэтому при таком разложении пероксида водорода будет выделяться меньше теплоты:

• H₂O₂(водн.) → H₂O(г.) + ½O₂(г.)  ΔH = -50,7 кДж (4)

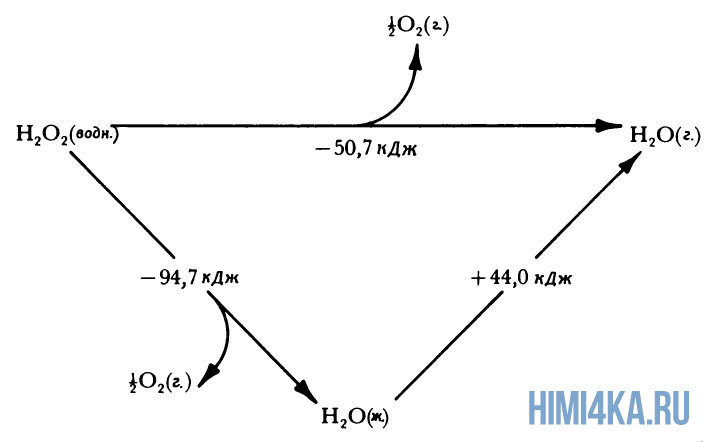
Здесь мы молчаливо воспользовались очень важным предположением, что теплоты реакций аддитивны. Уравнение (1) в сумме с уравнением (3) дает уравнение (4), и поэтому мы предположили, что теплота третьей из этих реакций должна быть равна сумме первых двух:

• ΔH = -94,7 кДж + 44,0 кДж = -50,7 кДж (5)

Закон Гесса

Аддитивность теплот реакций вытекает непосредственно из первого закона термодинамики: изменение энергии или энтальпии между двумя состояниями системы зависит только от самих этих состояний, а не от того, каким образом осуществляется переход между ними. Следовательно, разность между энтальпиями реагентов и продуктов, т.е теплота реакции, должна зависеть только от исходного и конечного состояний, а не от того конкретного пути, по которому следует реакция. Это утверждение носит название закон аддитивности теплот реакций (закон Гесса).

Благодаря закону Гесса совсем не обязательно измерять изменение энтальпии каждой возможной химической реакции. Например, если известны теплота испарения жидкой воды (3), то совсем не обязательно измерять теплоту разложения пероксида водорода с образованием водяного пара; эту величину гораздо проще получить путем вычислений. Если какую-либо реакцию трудно провести в лабораторных условиях, можно попытаться подобрать последовательность легче осуществляемых реакций, сумма которых дает необходимую реакцию. После измерения изменений энтальпии для всех индивидуальных реакций в такой последовательности можно просуммировать соответствующие изменения энтальпии подобно самим химическим уравнениям и найти теплоту трудно проводимой реакции.

Урок 19 «Изменение энтальпии» бесспорно был сложным, но чрезвычайно важным. Скорее всего у вас сейчас каша в голове, но не пугайтесь, ведь в следующем уроке все встанет на свои места. Если у вас возникли вопросы по данному уроку, то пишите их в комментарии.

Помогите, пожалуйста!) Как рассчитать энтальпию и энтропию химической реакции??? Подскажите формулы!

В любом веществе содержится некоторое количество тепла. Это тепло называют энтальпией. Энтальпия есть величина, характеризующая энергию системы. В физике и химии она показывает теплоту реакции. Она является альтернативой внутренней энергии, и эту величину чаще всего указывают при постоянном давлении, когда система имеет некоторый запас энергии. Как рассчитать энтальпию Инструкция 1 В физико-химических процессах происходит передача тепла от одного тела к другому. Это возможно, как правило, при постоянном давлении и температуре. В роли постоянного давления обычно выступает атмосферное. Энтальпия, как и внутренняя энергия, является функцией состояния. Внутренняя энергия представляет собой сумму кинетической и потенциальной энергий всей системы. Она является основой для уравнения энтальпии. Энтальпия представляет собой сумму внутренней энергии и давления, умноженного на объем системы, и равна: H=U+pV, где p — давление в системе, V — объем системы. Вышеуказанная формула применяется для расчета энтальпии в том случае, когда даны все три величины: давление, объем и внутренняя энергия. Однако, далеко не всегда энтальпия рассчитывается таким образом. Помимо него, существует еще несколько способов вычисления энтальпии. 2 Зная свободную энергию и энтропию, можно вычислить энтальпию. Свободная энергия, или энергия Гиббса, представляет собой часть энтальпии системы, затраченную на превращение в работу, и равна разности энтальпии и температуры, умноженной на энтропию: ΔG=ΔH-TΔS (ΔH, ΔG, ΔS — приращения величин) Энтропия в данной формуле является мерой неупорядоченности частиц системы. Она возрастает при увеличении температуры T и давления. При ΔG<0 процесс идет самопроизвольно, при ΔG>0 — не идет. 3 Кроме того, энтальпия также рассчитывается исходя из уравнения химической реакции. Если дано уравнение химической реакции вида A+B=C, то энтальпию можно определить по формуле: dH=dU+ΔnRT, где Δn=nk-nн (nk и nн — число молей продуктов реакции и исходных веществ) При изобарном процессе энтропия равна изменению теплоты в системе: dq=dH.При постоянном давлении энтальпия равна: H=∫СpdTВ случае, если энтальпийный и энтропийный факторы уравновешивают друг друга, приращение энтальпии равно произведению температуры на приращение энтропии: ΔH=TΔS