Линейная функция
•Линейной функцией называется функция вида y=kx+b, где x-независимая переменная, k и b-любые числа.
•Графиком линейной функции является прямая.
1.Чтобы постороить график функции, нам нужны координаты двух точек, принадлежащих графику функции. Чтобы их найти, нужно взять два значения х, подставить их в уравнение функции, и по ним вычислить соответствующие значения y.
Например, чтобы построить график функции y= ⅓ x+2, удобно взять x=0 и x=3, тогда ординаты эти точек будут равны y=2 и y=3.
Получим точки А(0;2) и В(3;3). Соединим их и получим график функции y= ⅓ x+2:
2. В формуле y=kx+b число k называется коэффицентом пропорциональности:
• если k>0, то функция y=kx+b возрастает
• если k
Коэффициент b показывает смещение графика функции вдоль оси OY:
• если b>0, то график функции y=kx+b получается из графика функцииy=kx сдвигом на b единиц вверх вдоль оси OY
На рисунке ниже изображены графики функций y=2x+3; y= ½ x+3; y=x+3
Заметим, что во всех этих функциях коэффициент k больше нуля, и функции являются возрастающими. Причем, чем больше значение k, тем больше угол наклона прямой к положительному направлению оси OX.
Во всех функциях b=3 – и мы видим, что все графики пересекают ось OY в точке (0;3)
Теперь рассмотрим графики функций y=-2x+3; y=- ½ x+3; y=-x+3
На этот раз во всех функциях коэффициент k меньше нуля, и функции убывают. Коэффициент b=3, и графики также как в предыдущем случае пересекают ось OY в точке (0;3)
Рассмотрим графики функций y=2x+3; y=2x; y=2x-3
Теперь во всех уравнениях функций коэффициенты k равны 2. И мы получили три параллельные прямые.
Но коэффициенты b различны, и эти графики пересекают ось OY в различных точках:
• График функции y=2x+3 (b=3) пересекает ось OY в точке (0;3)
• График функции y=2x (b=0) пересекает ось OY в точке (0;0) — начале координат.
• График функции y=2x-3 (b=-3) пересекает ось OY в точке (0;-3)
Итак, если мы знаем знаки коэффициентов k и b, то можем сразу представить, как выглядит график функции y=kx+b.
Если k0, то график функции y=kx+b имеет вид:
Если k>0 и b>0, то график функции y=kx+b имеет вид:
Если k>0 и b, то график функции y=kx+b имеет вид:
Если k, то график функции y=kx+b имеет вид:
Если k=0, то функция y=kx+b превращается в функцию y=b и ее график имеет вид:
Ординаты всех точек графика функции y=b равны b Если b=0, то график функции y=kx (прямая пропорциональность) проходит через начало координат:
3.Отдельно отметим график уравнения x=a. График этого уравнения представляет собой прямую линию, параллельую оси OY все точки которой имеют абсциссу x=a.
Например, график уравнения x=3 выглядит так:
Внимание! Уравнение x=a не является функцией, так одному значению аргумента соотвутствуют разные значения функции, что не соответствует определению функции.
4.Условие параллельности двух прямых:
График функции y=k1x+b1 параллелен графику функции y=k2x+b2, если k1=k2
5.Условие перепендикулярности двух прямых:
График функции y=k1x+b1 перепендикулярен графику функции y=k2x+b2, если k1*k2=-1 или k1=-1/k2
6.Точки пересечения графика функции y=kx+b с осями координат.
С осью ОY. Абсцисса любой точки, принадлежащей оси ОY равна нулю. Поэтому, чтобы найти точку пересечения с осью ОY нужно в уравнение функции вместо х подставить ноль. Получим y=b. То есть точка пересечения с осью OY имеет координаты (0;b).
С осью ОХ: Ордината любой точки, принадлежащей оси ОХ равна нулю. Поэтому, чтобы найти точку пересечения с осью ОХ нужно в уравнение функции вместо y подставить ноль. Получим 0=kx+b. Отсюда x=-b/k. То есть точка пересечения с осью OX имеет координаты (-b/k;0):
tofmal.ru
Линейная функция. Часть 2. График линейной функции и его свойства
Чтобы охарактеризовать поведение функции, обычно строят ее график.
Пример 1. Построить график функции 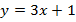 .
.
Решение:
Найдем несколько значений  при различных значениях
при различных значениях  .
.
Теперь возьмем пары 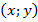 и отметим их в декартовой системе координат (Рис. 8).
и отметим их в декартовой системе координат (Рис. 8).

Рис. 8. Построение графика линейной функции
Соединим отмеченные точки линией (Рис. 9).

Рис. 9. Построение графика линейной функции
Похоже, что все точки лежат на одной прямой. И на самом деле графиком любой линейной функции является прямая.
Полученная прямая и есть график линейной функции 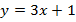 .
.
На уроках геометрии мы уже обсуждали, что через две точки можно провести только одну прямую. Поэтому, если мы найдем две точки, которые принадлежат графику линейной функции (т.е. прямой), мы сможем его построить. Вывод: для построения графика линейной функции достаточно найти координаты двух точек, которые ей принадлежат (найти значения
прямую. Поэтому, если мы найдем две точки, которые принадлежат графику линейной функции (т.е. прямой), мы сможем его построить. Вывод: для построения графика линейной функции достаточно найти координаты двух точек, которые ей принадлежат (найти значения 
 ).
).
Интерполяция и аппроксимация
При проведении различных исследований возникает такая задача: по некоторым известным значениям функции попытаться восстановить саму функцию (график или формулу) (Рис. 1). Если мы знаем, что функция линейная, то достаточно двух значений (прямая однозначно задаётся двумя точками).
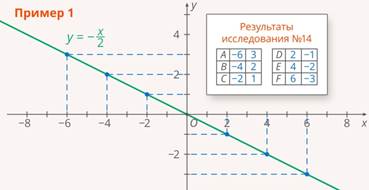
Рис. 1. Восстановление функции по некоторым известным значениям функции
Например, сила растяжения пружины зависит от растяжения пружины по закону Гука (Рис. 2).
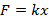
Достаточно измерить силу для двух различных значений растяжения пружины, чтобы найти жёсткость пружины (коэффициент 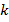 ) и восстановить функцию (Рис. 3).
) и восстановить функцию (Рис. 3).
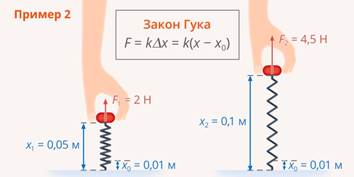
Рис. 2. Закон Гука
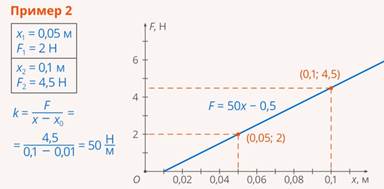
Рис. 3. Нахождение жёсткости пружины при помощи закона Гука
Но можно ли попытаться восстановить функцию, не зная, какой вид она имеет? (Рис. 4).
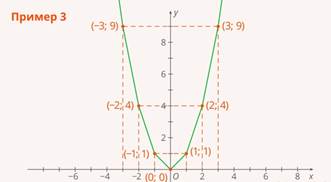
Рис. 4. Восстановление функции, вид которой заранее неизвестен
Такая задача называется аппроксимацией – на основании экспериментального набора значений функции в нескольких точках построить функцию, на которую с высокой точностью попадут получаемые в ходе эксперимента значения (как те, что у нас уже есть, так и остальные, которые можно получить).
Если мы хотим, чтобы построенной функции точно принадлежали все имеющиеся значения функции, то этот частный случай аппроксимации называется интерполяцией.
Существует также близкая к интерполяции задача, которая заключается в аппроксимации (т.е. приближении) какой-либо сложной функции другой, более простой функцией. (Рис. 5).
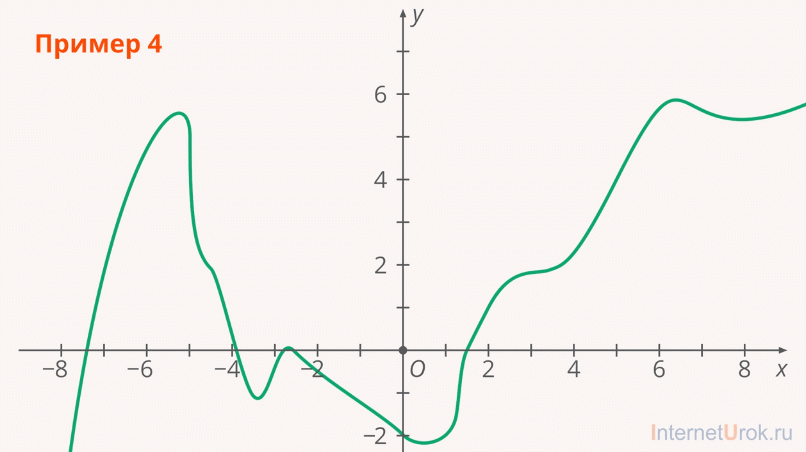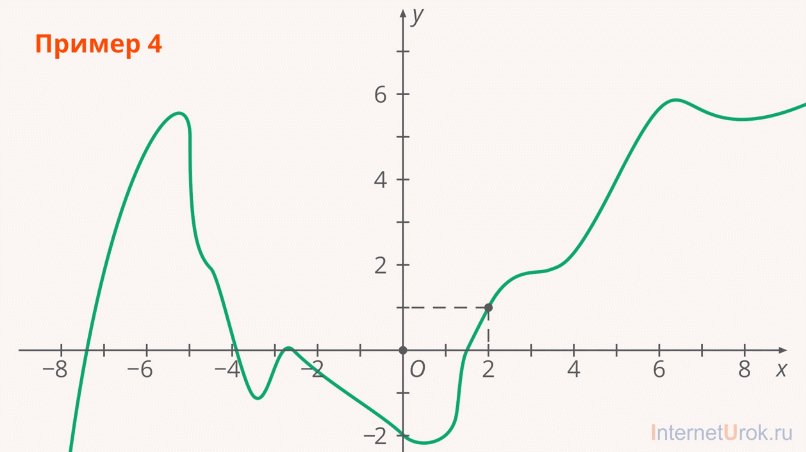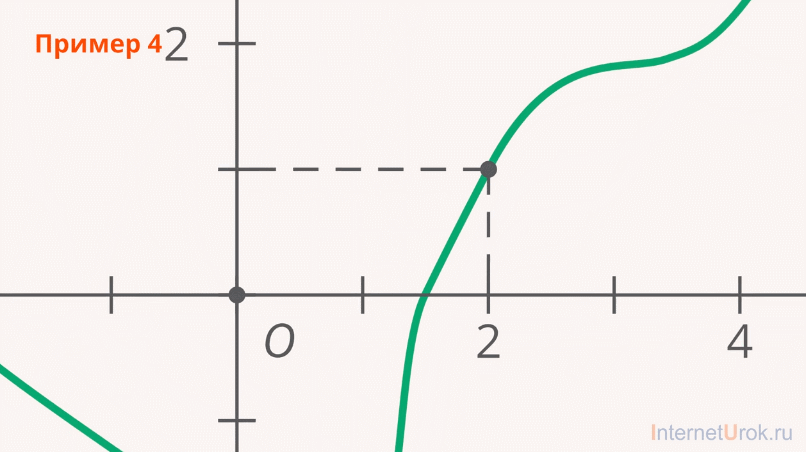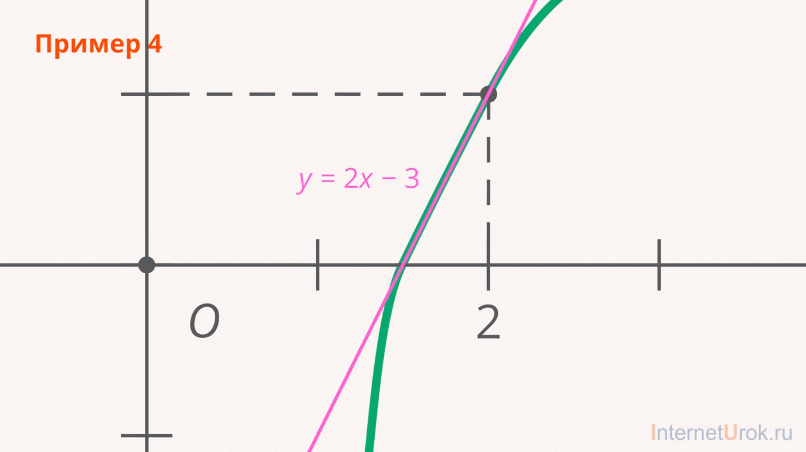
Рис. 5. Приближение сложной функции к более простой
Разумеется, использование упрощенной функции не позволяет получить такие же точные результаты, какие давала бы первоначальная функция. Но для некоторых задач достигнутый выигрыш в простоте и скорости вычислений может перевесить получаемую погрешность в результатах.
Подробнее почитать об интерполяции и аппроксимации можно в Интернете.
Пример 2. Построить график функции  .
.
Решение:
Возьмем два произвольных значения переменной  , например, 0 и 4.
, например, 0 и 4.
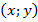 , отметим их в декартовой системе координат и соединим их линией (Рис. 10).
, отметим их в декартовой системе координат и соединим их линией (Рис. 10).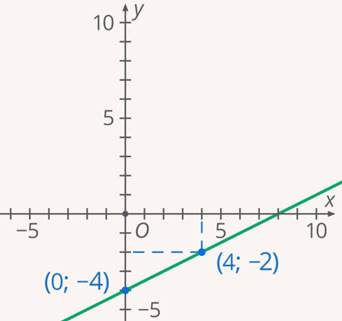
Рис. 10. Иллюстрация к примеру 2
Отдельно рассматривают два частных случая линейной функции  :
:
 ,
, .
.
Если  , то функцию
, то функцию  называют прямой пропорциональностью. Ее график всегда проходит через начало координат. Например,
называют прямой пропорциональностью. Ее график всегда проходит через начало координат. Например, 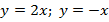 (Рис. 11).
(Рис. 11).

Рис. 11. Графики прямой пропорциональности
О втором типе линейных функций мы поговорим чуть позже.
Название углового коэффициента 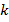 неслучайно: в зависимости от его значений будет изменяться угол наклона прямой по отношению к положительному направлению оси абсцисс.
неслучайно: в зависимости от его значений будет изменяться угол наклона прямой по отношению к положительному направлению оси абсцисс.
1. 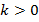 – угол наклона острый.
– угол наклона острый.
Рассмотрим на примере функции
interneturok.ru
Что такое функция? Часть 2. Линейные и нелинейные функции
Анализировать функцию иногда легче, если построен её график. По нему часто легко определить, на каких промежутках функция убывает или возрастает, где у неё максимум и минимум и т.д. Таким образом, у графического способа задания функции (задание функции с помощью графика) и аналитического разные цели. Если сказать грубо, то аналитический способ более точный, он позволяет вычислить значение функции в любой точке и выполнять с функцией различные преобразования. Графический способ более наглядный – по графику можно сделать вывод о тех или иных свойствах функции.
Рассмотрим графический способ подробнее. График функции представляет собой совокупность точек 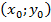 , где
, где 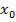 и
и  – соответствующие значения из областей определения и значений (Рис. 4).
– соответствующие значения из областей определения и значений (Рис. 4).

Рис. 4. График функции
График задает соответствие между множествами 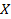 и
и 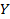 или – что то же самое – задает функцию. При этом для изображения необходимо задать соответствующую систему координат. Чаще всего мы будем использовать декартову систему координат.
или – что то же самое – задает функцию. При этом для изображения необходимо задать соответствующую систему координат. Чаще всего мы будем использовать декартову систему координат.
Область определения и область значений функции при графическом задании функции
Рассмотрим функцию, заданную следующим графическим образом (Рис.1).

Рис. 1. График функции
Область определения функции – это все значения, при которых определена функция. Для рассматриваемой функции область определения функции – это все числа от 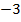 до
до  включительно (Рис. 2).
включительно (Рис. 2).

Рис. 2. Область определения рассматриваемой функции
Область значений функции – это все значения 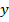 , которые принимает функция.
, которые принимает функция.
Для рассматриваемой функции область значений функции – это все числа от  до
до  включительно (см. рис. 3):
включительно (см. рис. 3):
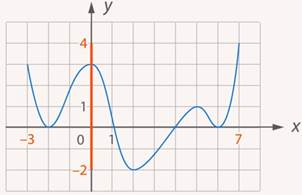
Рис. 3. Область значений рассматриваемой функции
Если строго, то область определения функции – это проекция графика на ось абсцисс, а область значений функции – проекция графика на ось ординат. Проекция – понятие, которое нам знакомо из геометрии. Слово неслучайно созвучно со словом прожектор (оба от латинского projectio – «бросание вперёд») Если мы посветим на график функции прожектором следующим образом, то тень, которую мы увидим на экране, 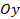 – это проекция графика на ось
– это проекция графика на ось 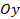 , т.е. область значений функции (Рис. 4).
, т.е. область значений функции (Рис. 4).
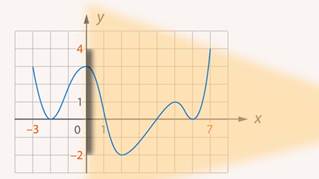
Рис. 4. Проекция графика на ось 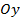
Аналогично тень на 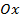 будет проекцией графика на ось
будет проекцией графика на ось 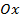 (Рис. 5), т.е. область определения функции.
(Рис. 5), т.е. область определения функции.
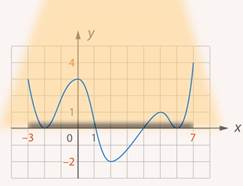
Рис. 5. Проекция графика на ось 
Словесный и табличный способы задания
Любую функцию можно задать различными способами. Рассмотрим на примере конкретной функции.
Словесный способ: функция, которая ставит в соответствие каждому числу его квадрат.
Табличный способ: при задании табличным способом указываются пары соответствующих значений.
При таком задании функции область определения функции и область задания функции – это множество значений переменных, которые указаны в таблице:
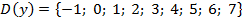

Аналитический способ: с помощью формулы: 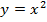 .
.
Графический способ задания функции (Рис. 1).
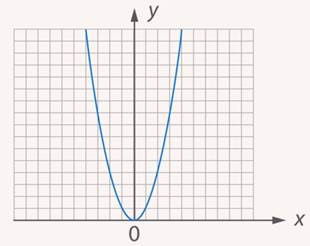
Рис. 1. Графический способ задания функции
Для задания числовых функций мы чаще всего будем использовать аналитический и графический методы, т.к. при использовании этих методов легче изучать свойства функций. Различные свойства функции мы будем изучать на протяжении всего курса алгебры, а сейчас рассмотрим несколько частных случаев функций. Вернемся к функции пройденного пути при равномерном движении, т.е. 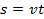 , где
, где 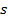 – путь,
– путь, 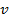 – скорость,
– скорость,  – время. Например, при скорости
– время. Например, при скорости  получим функцию
получим функцию  . Если
. Если  , то
, то  , если
, если 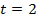 , то
, то  , если
, если 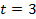 , то
, то  . Мы видим, что при одинаковом изменении аргумента
. Мы видим, что при одинаковом изменении аргумента  , у нас одинаковое изменение значения функции – пройденного пути
, у нас одинаковое изменение значения функции – пройденного пути 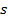 . Функции, обладающие таким свойством,называются линейными, в общем виде их можно записать так:
. Функции, обладающие таким свойством,называются линейными, в общем виде их можно записать так:  . Графиком таких функций будет прямая. Пример линейной функции: пусть
. Графиком таких функций будет прямая. Пример линейной функции: пусть  . Построим график этой функции. Нарисуем таблицу и заполним ее, т.е. при двух разных значениях
. Построим график этой функции. Нарисуем таблицу и заполним ее, т.е. при двух разных значениях  найдем, чему равен
найдем, чему равен 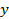 . И по полученным значениям построим прямую на координатной плоскости.
. И по полученным значениям построим прямую на координатной плоскости.
Итак, точки  принадлежат графику функции. Отметим эти точки на плоскости и проведем через них прямую (Рис. 5).
принадлежат графику функции. Отметим эти точки на плоскости и проведем через них прямую (Рис. 5).

Рис. 5. График линейной функции 
Эта прямая и является графиком функции  . Обратим внимание, что для построения графика линейной функции нам достаточно двух точек. Это связано с тем, что мы знаем: графиком будет прямая, а любая прямая на плоскости однозначно задаётся по двум точкам.
. Обратим внимание, что для построения графика линейной функции нам достаточно двух точек. Это связано с тем, что мы знаем: графиком будет прямая, а любая прямая на плоскости однозначно задаётся по двум точкам.
Естественно, не все функции линейные. Например, мы знаем, что площадь квадрата зависит от его стороны следующим образом:  . Попробуем приблизительно построить ее график по точкам. Поскольку сторона квадрата больше 0, то
. Попробуем приблизительно построить ее график по точкам. Поскольку сторона квадрата больше 0, то 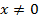 . Значит, точка
. Значит, точка 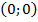 не принадлежит графику функции (точку
не принадлежит графику функции (точку 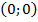 «выкалывают», на графике обводят в кружок).
«выкалывают», на графике обводят в кружок).
Снова нарисуем таблицу, возьмем некоторые значения  и найдем значения
и найдем значения 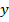 при этих фиксированных значениях
при этих фиксированных значениях  .
.
Нарисуем эти точки на плоскости и посмотрим, какая линия через них проходит (Рис. 6).
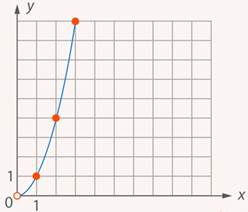
Рис. 6. График нелинейной функции 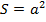
Данная функция уже не является линейной, так как при увеличении  на 1,
на 1, 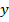 увеличивался на разные величины, в зависимости от начального значения переменной
увеличивался на разные величины, в зависимости от начального значения переменной  . Такие функции называются нелинейными. Рассмотренная функция является примером квадратичной функции.
. Такие функции называются нелинейными. Рассмотренная функция является примером квадратичной функции.
Сторона квадрата не может быть отрицательной или равной 0, поэтому обобщим и построим график функции 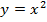 для любых значений аргумента. Построим график данной функции по точкам. Снова нарисуем таблицу, заполним ее разными значениями
для любых значений аргумента. Построим график данной функции по точкам. Снова нарисуем таблицу, заполним ее разными значениями  и посчитаем, чему равен
и посчитаем, чему равен 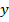 при каждом из этих значений
при каждом из этих значений  .
.
Отметим эти точки на плоскости и проведем кривую, которая проходит через них (Рис. 7). Полученный график называют параболой.

Рис. 7. График квадратичной функции 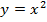
В общем виде квадратичная функция записывается так:  , где
, где 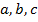
interneturok.ru
3.3.1 Линейная функция, её график
Видеоурок: График линейной функцииЛекция: Линейная функция, её график
Мы уже умеем характеризовать функции, а также касались некоторых основных из них. Сейчас бы хотелось поговорить о каждой из них более детально. И начнем мы с линейной функции и её графика.
Любая функция, которая имеет вид: y = kx + b, называется линейной.
Коэффициент, находящийся перед переменной, называется коэффициентом угла наклона и определяет крутизну графика функции относительно оси ОХ. Свободный коэффициент показывает смещение графика относительно начала координат по оси ОУ.
Если Вам необходимо построить график данной функции, то Вы должны знать, что это будет прямая.
Как строить график?
Для построения данного графика необходимо выбрать две точки данного графика. Почему нам не достаточно одной точки, но достаточно двух? Потому что из геометрии мы знаем, что через любые две точки можно провести только одну прямую.
А теперь давайте разберемся, как это сделать. Допустим, возьмем функцию вида:
у = х/3 +2.
Итак, для начала нам необходимо взять произвольные два значения «х», подставить их в уравнение и найти значение «у». Далее по двум полученным точкам строим прямую.
Возьмем в качестве координаты «х» для первой точки значение 3. Тогда у = 3. В качестве второй точки возьмем х = 0, тогда у = 2.
Получим:
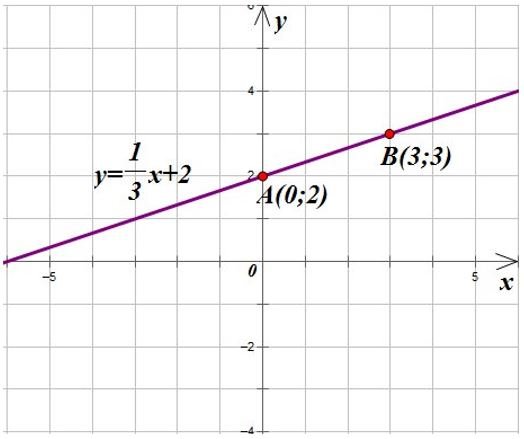
Теперь давайте разберемся, на что влияет коэффициент при переменной. Как уже говорилось ранее, по нему определяется наклон графика относительно ОХ. Если коэффициент больше нуля k > 0, то угол между осью ОХ и графиком прямой получается острый.

Если же коэффициент меньше нуля k < 0, то угол между осью ОХ и построенной прямой будет тупым.

Если коэффициент при переменной равен нулю, то график приобретает вид прямой, параллельной оси ОХ. Если свободный коэффициент больше нуля b > 0, то прямая будет находиться выше оси ОХ, если коэффициент меньше нуля, то прямая ниже оси ОХ.
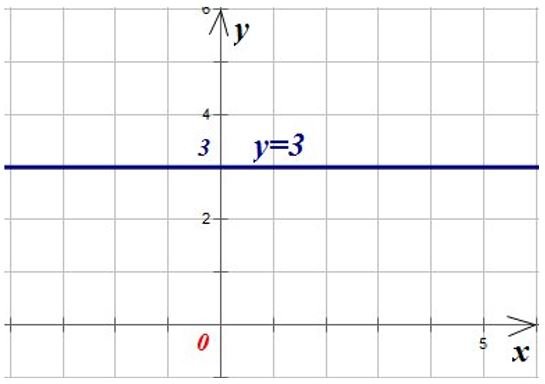
Свободный коэффициент отвечает за параллельный перенос графика. График заданной функции пересекает ось ОУ в точке (0;b).
То есть, если значение свободного коэффициента больше нуля b > 0, то график смещается относительно начала координат вверх по оси ОУ, а если свободный коэффициент меньше нуля b < 0, то смещение происходит по оси ОУ вниз от начала координат.

cknow.ru
Линейная функция
Функция называется линейной, если ее можно записать в виде \(y=kx+b\), где \(k\) и \(b\) -некоторые числа.
Примеры:
|
\(y=\frac{1}{3}x-5\) |
\(k=\frac{1}{3}\), \(b=-5\) |
|
|
\(y=2x\) |
\(k=2\), \(b=0\) |
|
|
\(y=8\) |
\(k=0\), \(b=8\) |
Функция не всегда сразу задана в виде \(y=kx+b\), иногда такой вид получится только после преобразований. Например, \(y=6(x-1)+10x\) — это линейная функция, потому что если раскрыть скобки и привести подобные слагаемые мы получим \(y=16x-6\).
График линейной функции всегда представляет собой прямую линию – отсюда и название: «линейная функция».
Чтобы в этом убедиться построим графики функций \(y=2x\), \(y=\frac{1}{3}x-5\), \(y=8\).
Если вы вдруг забыли, как строить графики, можете прочитать об этом здесь.
Как меняется график при разных \(k\)?
Чтобы определить, как влияет на график коэффициент \(k\), построим несколько функций разными \(k\): \(\frac{1}{3}\),\(-\frac{1}{3}\),\(2\),\(-2\) и \(0\). При этом во всех функциях сделаем \(b\) одинаковым (равным нулю), чтобы убрать его влияние.
То есть, построим графики для функций: \(y=\frac{1}{3}x\), \(y=-\frac{1}{3}x\), \(y=2x\), \(y=-2x\), \(y=0\).
Заметьте, что при \(k=2\) и \(\frac{1}{3}\) — функция возрастает, а при \(k=-2\) и \(-\frac{1}{3}\) — убывает. На самом деле:
При любом \(k>0\) функция возрастает и при любом \(k<0\) — убывает. Когда же \(k=0\) — она не возрастает и не убывает, а идет параллельна оси \(x\) (или совпадает с ней).
Так же можно заметить, чем больше модуль \(k\), тем «круче» график.
Как по графику определить коэффициент k?
- Сначала определим, возрастает или убывает функция. Если возрастает – знак коэффициента \(k\) плюс, если убывает – минус.
- Дальше надо построить на прямой прямоугольный треугольник, так чтобы гипотенуза лежала на графике функции, а вершины треугольника совпадали с вершинами клеточек. Примерно вот так:
Чтобы определить значение \(k\) по модулю (то есть, без учета знака), надо вертикальную сторону треугольника поделить на горизонтальную. Можно использовать правило для запоминания: «стоячий бьет лежачего». В данных случаях \(|k|=\frac{AC}{BC}\). То есть на первом графике \(k=2\),а на втором \(k=-\frac{1}{4}\).
Как меняется график при разных значениях \(b\)?
Чтобы определить, как \(b\) влияет на график, построим несколько функций с разными \(b\): \(6\), \(2\), \(0\), \(-3\) и \(-8\). При этом \(k\) пусть во всех функциях будет равен \(2\).
Не сложно заметить, что прямая либо поднимается на \(b\) (если \(b>0\)) либо опускается на \(|b|\) если
(\(b<0\)).
Как по графику функции определить значение \(b\)?
Очень просто — прямая пересекает ось \(y\) всегда в точке \(b\). Вы можете это увидеть на предыдущем графике.
Пример (ОГЭ): На рисунке изображены графики функций вида \(y=kx+b\). Установите соответствие между графиками функций и знаками коэффициентов \(k\) и \(b\).
A. B.C.
Коэффициенты
| 1) \(k>0\),\(b>0\) | 2) \(k<0\), \(b>0\) | 3) \(k<0\), \(b<0\) | 4) \(k>0\), \(b<0\) |
Решение:
А. – функция убывает, поэтому \(k<0\). Точка пересечения оси \(y\) и прямой находится выше нуля, значит \(b>0\). Подходит вариант под цифрой 2).
B. — функция возрастает — \(k>0\). Точка пересечения оси \(y\) и прямой находится выше нуля, значит \(b>0\). Подходит вариант под цифрой 1).
C. – функция убывает — \(k<0\). Точка пересечения оси \(y\) и прямой находится ниже нуля, значит \(b<0\). Подходит вариант под цифрой 3).
Ответ: 213.
«Читерский» способ строить график линейной функции
Можно конечно строить график линейной функции по точкам, как описано здесь, но можно и быстрее, буквально в три шага:-
Отмечаем точку \(b\) на оси игреков.
-
От неё идем вправо на количество клеточек равное знаменателю \(k\), и вверх на количество клеточек равное числителю \(k\) (если \(k>0\)) или вниз на тоже количество (если \(k<0\)).
-
Проводим через эти две точки прямую.
Пример: Построить график функции \(y=3x+1\).
|
Шаг 1. \(b=1\), поэтому отмечаем точку с этим значением на оси \(y\)
|
Шаг 2. \(k=3\), а тройка это тоже самое, что \(\frac{3}{1}\). При этом \(k>0\). Поэтому идем вправо на единицу и вверх на \(3\). Ставим точку. |
Шаг 3. Проводим через эти две точки прямую. |
Пример: Построить график функции \(y=-\frac{1}{4} x-3\).
|
Шаг 1. \(b=-3\) отмечаем точку с этим значением на оси \(y\).
|
Шаг 2. \(k=-\frac{1}{4}\), \(k<0\), числитель \(1\), знаменатель \(4\). Значит, идем вправо на \(4\) и вниз на единицу. |
Шаг 3. Проводим через эти две точки прямую. |
Немного потренируйтесь и вы сами поймете, какой это классный способ строить линейную функцию.
Скачать статьюcos-cos.ru
Линейная функция — это… Что такое Линейная функция?
Примеры линейных функций.Линейная функция — функция вида
- (для функций одной переменной).
Основное свойство линейных функций: приращение функции пропорционально приращению аргумента. То есть функция является обобщением прямой пропорциональности.
График линейной функции является прямой линией, с чем и связано ее название. Это касается вещественной функции одной вещественной переменной.
- Частный случай линейной функции называется однородными линейными функциями (это в сущности синоним прямой пропорциональности), в отличие от — неоднородных линейных функций.
Свойства
Линейная функция нескольких переменных
Линейная функция переменных — функция вида
где — некоторые фиксированные числа. Областью определения линейной функции является всё -мерное пространство переменных вещественных или комплексных. При линейная функция называется однородной, или линейной формой.
Если все переменные и коэффициенты — вещественные числа, то графиком линейной функции в -мерном пространстве переменных является -мерная гиперплоскость
в частности при — прямая линия на плоскости.
Абстрактная алгебра
Термин «линейная функция», или, точнее, «линейная однородная функция», часто применяется для линейного отображения векторного пространства над некоторым полем в это поле, то есть для такого отображения , что для любых элементов и любых справедливо равенство
причём в этом случае вместо термина «линейная функция» используются также термины линейный функционал и линейная форма — также означающие линейную однородную функцию определённого класса.
Алгебра логики
Булева функция называется линейной, если существуют такие , где , что для любых имеет место равенство:
- .
Нелинейные функции
Для функций, не являющихся линейными (то есть достаточно произвольных), когда хотят подчеркнуть некие свойства, употребляют термин нелинейные функции. Обычно это происходит, когда функциональную зависимость вначале приближают линейной, а потом переходят к изучению более общего случая, часто начиная с младших степеней, например рассматривая квадратичные поправки.
То же относится и к употреблению слова нелинейные в отношении других объектов, не обладающих свойством линейности, например — нелинейные дифференциальные уравнения.
В ряде случаев этот термин может применяться и к зависимостям , где , то есть к неоднородным линейным функциям, поскольку они не обладают свойством линейности, а именно в этом случае и . Например, нелинейной зависимостью считают для материала с упрочнением (см. теория пластичности).
См. также
Ссылки
- Справочник по математике для инженеров и учащихся втузов. Бронштейн И. Н., Семендяев К. А.- М.: Наука, 1981.- 720с., ил.
dic.academic.ru
Линейная функция — Википедия
Примеры линейных функций.Линейная функция — функция вида
- y=kx+b{\displaystyle y=kx+b} (для функций одной переменной).
Основное свойство линейных функций: приращение функции пропорционально приращению аргумента. То есть функция является обобщением прямой пропорциональности.
Графиком линейной функции является прямая, с чем и связано её название. Это касается вещественной функции одной вещественной переменной.
- Частный случай b=0{\displaystyle b=0} линейной функции называется однородными линейными функциями (это в сущности синоним прямой пропорциональности), в отличие от b≠0{\displaystyle b\neq 0} — неоднородных линейных функций.
Свойства
Угол между двумя прямыми, задаваемыми уравнениями y=k1x+b1,{\displaystyle y=k_{1}x+b_{1},} и y=k2x+b2,{\displaystyle y=k_{2}x+b_{2},} определяется равенством: tgα=|k1−k21+k1k2|,{\displaystyle \mathrm {tg} \,\alpha =\left|{\frac {k_{1}-k_{2}}{1+k_{1}k_{2}}}\right|,} где k1k2≠−1,{\displaystyle k_{1}k_{2}\neq -1,} то есть прямые не являются взаимно перпендикулярными; при k1=k2, α=0{\displaystyle k_{1}=k_{2},~\alpha =0} и прямые параллельны.
- b{\displaystyle b} является показателем ординаты точки пересечения прямой с осью ординат.
- При b=0{\displaystyle b=0}, прямая проходит через начало координат.
Линейная функция нескольких переменных
Линейная функция n{\displaystyle n} переменных x=(x1,x2,…,xn){\displaystyle x=(x_{1},x_{2},\dots ,x_{n})} — функция вида
- f(x)=a0+a1x1+a2x2+⋯+anxn{\displaystyle f(x)=a_{0}+a_{1}x_{1}+a_{2}x_{2}+\dots +a_{n}x_{n}}
где a0,a1,a2,…,an{\displaystyle a_{0},a_{1},a_{2},\dots ,a_{n}} — некоторые фиксированные числа. Областью определения линейной функции является всё n{\displaystyle n}-мерное пространство переменных x1,x2,…,xn{\displaystyle x_{1},x_{2},\dots ,x_{n}} вещественных или комплексных. При a0=0{\displaystyle a_{0}=0} линейная функция называется однородной, или линейной формой.
Если все переменные x1,x2,…,xn{\displaystyle x_{1},x_{2},\dots ,x_{n}} и коэффициенты a0,a1,a2,…,an{\displaystyle a_{0},a_{1},a_{2},\dots ,a_{n}} — вещественные числа, то графиком линейной функции в (n+1){\displaystyle (n+1)}-мерном пространстве переменных x1,x2,…,xn,y{\displaystyle x_{1},x_{2},\dots ,x_{n},y} является n{\displaystyle n}-мерная гиперплоскость
- y=a0+a1x1+a2x2+⋯+anxn{\displaystyle y=a_{0}+a_{1}x_{1}+a_{2}x_{2}+\dots +a_{n}x_{n}}
в частности при n=1{\displaystyle n=1} — прямая линия на плоскости.
Абстрактная алгебра
Термин «линейная функция», или, точнее, «линейная однородная функция», часто применяется для линейного отображения векторного пространства X{\displaystyle X} над некоторым полем k{\displaystyle k} в это поле, то есть для такого отображения f:X→k{\displaystyle f:X\to k}, что для любых элементов x,y∈X{\displaystyle x,y\in X} и любых α,β∈k{\displaystyle \alpha ,\beta \in k} справедливо равенство
- f(αx+βy)=αf(x)+βf(y){\displaystyle f(\alpha x+\beta y)=\alpha f(x)+\beta f(y)}
причём в этом случае вместо термина «линейная функция» используются также термины линейный функционал и линейная форма — также означающие линейную однородную функцию определённого класса.
Алгебра логики
Булева функция f(x1,x2,…,xn){\displaystyle f(x_{1},x_{2},\dots ,x_{n})} называется линейной, если существуют такие a0,a1,a2,…,an{\displaystyle a_{0},a_{1},a_{2},\dots ,a_{n}}, где ai∈{0,1},∀i=1,n¯{\displaystyle a_{i}\in \{0,1\},\forall i={\overline {1,n}}}, что для любых x1,x2,…,xn{\displaystyle x_{1},x_{2},\dots ,x_{n}} имеет место равенство:
- f(x1,x2,…,xn)=a0⊕a1⋅x1⊕a2⋅x2⊕⋯⊕an⋅xn{\displaystyle f(x_{1},x_{2},\dots ,x_{n})=a_{0}\oplus a_{1}\cdot x_{1}\oplus a_{2}\cdot x_{2}\oplus \dots \oplus a_{n}\cdot x_{n}}.
Нелинейные функции
Для функций, не являющихся линейными, употребляют термин нелинейные функции. То же относится и к употреблению слова нелинейные в отношении других объектов, не обладающих свойством линейности, например — нелинейные дифференциальные уравнения. Обычно термин используется, когда функциональную зависимость вначале приближают линейной, а потом переходят к изучению более общего случая, часто начиная с младших степеней, например рассматривая квадратичные поправки.
Нелинейные уравнения достаточно произвольны. К примеру, нелинейной является функция y=x2{\displaystyle y=x^{2}}.
В ряде случаев этот термин может применяться и к зависимостям f=kx+b{\displaystyle f=kx+b}, где b≠0{\displaystyle b\neq 0}, то есть к неоднородным линейным функциям, поскольку они не обладают свойством линейности, а именно в этом случае f(x1+x2)≠f(x1)+f(x2){\displaystyle f(x_{1}+x_{2})\neq f(x_{1})+f(x_{2})} и f(cx)≠cf(x){\displaystyle f(cx)\neq cf(x)}. Например, нелинейной зависимостью считают σ(τ){\displaystyle \sigma (\tau )} для материала с упрочнением (см. теория пластичности).
См. также
Ссылки
- Справочник по математике для инженеров и учащихся втузов. Бронштейн И. Н., Семендяев К. А.- М.: Наука, 1981.- 720с., ил.
wikipedia.green
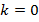 ,
,