Правильная пирамида

Правильная пирамида — частный случай пирамиды.

Определение 1. Пирамида называется правильной, если её  основанием является правильный многоугольник, при этом вершина такой пирамиды проецируется в центр ее основания. 

Определение 2. Пирамида называется правильной, если ее основание – правильный многоугольник, а высота проходит через центр основания.

Элементы правильной пирамиды

• Высота боковой грани, проведенная из ее вершины называется апофема. На рисунке обозначена как отрезок ON
• Точка, соединяющая боковые рёбра и не лежащая в плоскости основания, называется вершиной пирамиды (О)
• Треугольники, имеющие общую сторону с основанием и одну из вершин, совпадающую с вершиной, называются боковыми гранями (AOD, DOC, COB, AOB)  
• Отрезок перпендикуляра, проведённого через вершину пирамиды к плоскости её основания называется высотой пирамиды (ОК)
• Диагональное сечение пирамиды — это сечение, проходящее через вершину и диагональ основания (AOC, BOD)
• Многоугольник, которому не принадлежит вершина пирамиды, называется основанием пирамиды (ABCD)

Если в основании правильной пирамиды лежит треугольник, четырехугольник и т.д. то она называется правильной треугольной, четырехугольной и т.д.

Треугольная пирамида есть четырехгранник — тетраэдр.

Свойства правильной пирамиды

Для решения задач необходимо знать свойства отдельных элементов, которые в условии обычно опускаются, так как считается, что ученик должен это знать изначально.

• боковые ребра равны между собой
• апофемы равны
• боковые грани равны между собой (при этом, соответственно, равны их площади, боковые стороны и основания), то есть они являются равными треугольниками
• все боковые грани являются равными равнобедренными треугольниками
• в любую правильную пирамиду можно как вписать, так и описать около неё сферу
• если центры вписанной и описанной сферы совпадают, то сумма плоских углов при вершине пирамиды равна π, а каждый из них соответственно π/n, где n — количество сторон многоугольника основания
• площадь боковой поверхности правильной пирамиды равна половине произведения периметра основания на апофему
• около основания правильной пирамиды можно описать окружность (см. также радиус описанной окружности треугольника)
• все боковые грани образуют с плоскостью основания правильной пирамиды равные углы
• все высоты боковых граней равны между собой

Указания к решению задач. Свойства, перечисленные выше, должны помочь в практическом решении. Если требуется найти углы наклона граней, их поверхность и т. д., то общая методика сводится к разбиению всей объемной фигуры на отдельные плоские фигуры и применение их свойств для нахождения отдельных элементов пирамиды, поскольку многие элементы являются общими для нескольких фигур.

Необходимо разбить всю объемную фигуру на отдельные элементы — треугольники, квадраты, отрезки. Далее, к отдельным элементам применить знания из курса планиметрии, что существенно упрощает нахождение ответа.

Формулы для правильной пирамиды

Формулы для нахождения объема и площади боковой поверхности:

Обозначения:
V — объем пирамиды
S — площадь основания
h — высота пирамиды
Sb — площадь боковой поверхности 

a — апофема (не путать с α)
P — периметр основания
n — число сторон основания
b — длина бокового ребра
α — плоский угол при вершине пирамиды

Данная формула нахождения объема может применяться только для правильной пирамиды:

, где

V — объем правильной пирамиды
h — высота правильной пирамиды
n — число сторон правильного многоугольника, который является основанием для правильной пирамиды
a — длина стороны правильного многоугольника

Правильная усеченная пирамида

Если провести сечение, параллельное основанию пирамиды, то тело, заключённое между этими плоскостями и боковой поверхностью, называется усеченной пирамидой. Это сечение для усеченной пирамиды является одним из её оснований. 

Высота боковой грани (которая является равнобокой трапецией), называется — апофема правильной усеченной пирамиды.

Усечённая пирамида называется правильной, если пирамида, из которой она была получена – правильная.

•  Расстояние между основаниями усеченной пирамиды называется высотой усеченной пирамиды
• Все грани правильной усеченной пирамиды являются равнобокими (равнобедренными) трапециями 

Примечания

См. также: частные случаи (формулы) для правильной пирамиды:

Как воспользоваться приведенными здесь теоретическими материалами для решения своей задачи:

1. Ознакомьтесь со справочными материалами
2. Выясните, по условию задачи, о какой именно правильной пирамиде идет речь
3. После этого в дереве знаний справа, найдите подходящий урок с данной фигурой (см. решение задач про правильную пирамиду с треугольником в основании, с четырехугольником в основании). Если нужного решения не нашлось, попробуйте ознакомиться с содержанием соседних уроков, возможно, решение подобной задачи есть именно там
4. Если Вы просмотрели весь раздел, но аналогичной задачи не нашлось, напишите о своей проблеме на форуме «раздел для школьников» в соответствующей теме. Обязательно ознакомьтесь предварительно с правилами форума.

Содержание главы:
 Пирамида и вписанный конус | Описание курса | Апофема правильной пирамиды 

   

profmeter.com.ua

Правильная пирамида — урок. Геометрия, 10 класс.

Пирамида, основанием которой является правильный многоугольник, а вершина которой проецируется в центр основания, называется правильной пирамидой.

Боковые грани правильной пирамиды — равные равнобедренные треугольники.

Высота боковой грани правильной пирамиды называется апофемой.

 

Правильная треугольная пирамида, у которой все рёбра равны, называется тетраэдром.

Все грани тетраэдра — равные равносторонние треугольники.

 

В средней школе нужно уметь решать задачи, где дана:

— правильная треугольная пирамида;

— правильная четырёхугольная пирамида;

— правильная шестиугольная пирамида.

 

Правильная треугольная пирамида

  

Основание правильной треугольной пирамиды — равносторонний треугольник.

Вершина пирамиды проецируется в точку пересечения медиан.

Запомни:

\(BN:NK = 2:1\),

\(KD\) — апофема,

∢ \(NKD\) и ∢ \(NLD\) — двугранные углы при основании пирамиды,

∢ \(DCN\) и ∢ \(DBN\) — углы между боковым ребром и плоскостью основания пирамиды.

 

Правильная четырёхугольная пирамида

  

Основание правильной четырёхугольной пирамиды — квадрат.

Вершина пирамиды проецируется в точку пересечения диагоналей основания (квадрата).

\(ML\) — апофема,

∢ \(MLO\) — двугранный угол при основании пирамиды,

∢ \(MCO\) — угол между боковым ребром и плоскостью основания пирамиды.

 

Правильная шестиугольная пирамида

  

Основание правильной шестиугольной пирамиды — правильный шестиугольник.

Вершина пирамиды проецируется в точку пересечения диагоналей основания (шестиугольника).

\(SE = h\) — апофема,

∢ \(OES\) — двугранный угол при основании пирамиды.

Для вычисления площади боковой поверхности правильной пирамиды существуют две формулы:

Sб=12Pоснования⋅hиSб=Sоснованияcosϕ, где \(P\) — периметр основания, \(h\) — апофема, ϕ — двугранный угол при основании.

 

Объём пирамиды \(V =\) 13Sосн⋅H, где \(H\) — высота пирамиды.

Обрати внимание!

Не путай \(h\) — апофему с \(H\) — высотой пирамиды!

www.yaklass.ru

Пирамида. Виды пирамид | Подготовка к ЕГЭ по математике

Пирамида – многогранник,  основание которого — многоугольник , а остальные грани — треугольники, имеющие общую вершину.

По числу углов основания различают пирамиды треугольные, четырёхугольные и т. д.

Вершина пирамиды — точка, соединяющая боковые рёбра и не лежащая в плоскости основания.

Основание — многоугольник, которому не принадлежит вершина пирамиды.

Апофема — высота боковой грани правильной пирамиды, проведенная из ее вершины.

Высота — отрезок перпендикуляра, проведённого через вершину пирамиды к плоскости её основания (концами этого отрезка являются вершина пирамиды и основание перпендикуляра).

Диагональное сечение пирамиды — сечение пирамиды, проходящее через вершину и диагональ основания.

Некоторые свойства пирамиды 

 

1) Если все боковые ребра равны, то 

– около основания пирамиды можно описать окружность, причём вершина пирамиды проецируется в её центр

– боковые ребра образуют с плоскостью основания равные углы

Верно и обратное.

Если боковые ребра образуют с плоскостью основания равные углы, то все боковые ребра пирамиды равны.

Если около основания пирамиды можно описать окружность, причём вершина пирамиды проецируется в её центр, то все боковые ребра пирамиды равны.

 

2) Если все грани пирамиды наклонены к плоскости основания под одним углом, то в основание пирамиды можно вписать окружность, причём вершина пирамиды проецируется в её центр

Верно и обратное.

Виды пирамид

 

Пирамида называется правильной, если основанием её является правильный многоугольник, а вершина проецируется в центр основания.

Для правильной пирамиды справедливо:

– боковые ребра правильной пирамиды равны;

– в правильной пирамиде все боковые грани — равные  равнобедренные треугольники;

– в любую правильную пирамиду можно  вписать сферу;

– около любой правильной пирамиды можно описать сферу;

– площадь боковой поверхности правильной пирамиды равна половине произведения периметра основания на апофему.

Видео

Пирамида называется прямоугольной, если одно из боковых рёбер пирамиды перпендикулярно основанию. Тогда  это ребро и есть высота пирамиды.

Усечённой пирамидой называется многогранник, заключённый между основанием пирамиды и секущей плоскостью, параллельной её основанию.

Тетраэдр – треугольная пирамида. В тетраэдре любая из граней может быть принята за основание пирамиды.

 

Смотрите также таблицу «Объемы пирамиды и призмы. Площадь поверхности пирамиды и призмы».

egemaximum.ru

Пирамида. Правильная и усечённая пирамиды. Видеоурок. Геометрия 10 Класс

Данный урок поможет получить представление о теме «Пирамида. Правильная и усеченная пирамида». На этом занятии мы познакомимся с понятием правильной пирамиды, дадим ей определение. Затем докажем теорему о боковой поверхности правильной пирамиды и теорему о боковой поверхности правильной усеченной пирамиды.

Тема: Пирамида

Урок: Правильная и усечённая пирамиды

Определение: правильной n-угольной пирамидой называется такая пирамида, у которой в основании лежит правильный n-угольник, и высота проецируется в центр этого n-угольника (рис. 1).

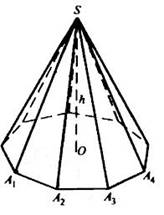
Рис. 1

Правильная треугольная пирамида

Для начала рассмотрим ∆ABC (рис. 2), в котором AB=BC=CA (то есть в основании пирамиды лежит правильный треугольник). У правильного треугольника центр вписанной и описанной окружности совпадают и являются центром самого треугольника. В данном случае центр находится следующим образом: находим середину АВ – С₁, проводим отрезок СС₁, который является медианой, биссектрисой и высотой; аналогично находим середину AC – B₁ и проводим отрезок BB₁. Пересечением BB₁ и СС₁ будет точка О, которая является центром ∆АВС.

Если соединить центр треугольника O с вершиной пирамиды S, то получим высоту пирамиды SO ⊥ ABC, SO = h.

Соединив точку S с точками А, В и С получим боковые ребра пирамиды.

Мы получили правильную треугольную пирамиду SABC (рис. 2).

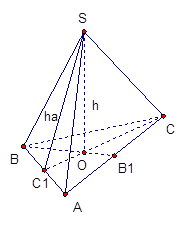
Рис. 2

Известны стороны основания – а и высота пирамиды – h. Необходимо найти:

1. S_осн

2. S_бок  ,h_a

3. ∠(AB)

4. ∠(SC)

Решение:

1. Найти S_осн

Если есть ∆АВС (рис. 3), сторона которого равна а, то

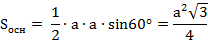
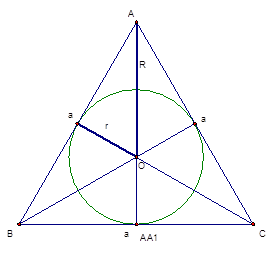
Рис. 3

2. Найти S_бок ,h_а

Отрезок SC₁ называется апофемой h_a(рис. 2). Апофему найдем из прямоугольного треугольника SC₁O. Известен катет SO=h, второй катет С₁О найдем из ∆АВС (рис. 3).

Для начала найдем высоту АА₁ из прямоугольного треугольника АА₁С:

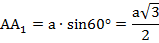
Высота АА₁ состоит из радиуса вписанной окружности r=С₁О и из радиуса описанной окружности R (причем R=2r).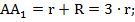

Следовательно

 

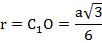
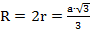
Зная катеты ∆SC₁O, мы можем найти гипотенузу

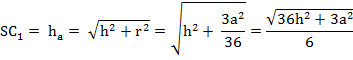
Найдя апофему h_aможно без труда найти

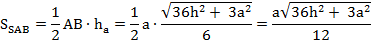
interneturok.ru

Пирамида. Формулы и свойства

Определение.

Пирамида — это многогранная объемная фигура, ограниченная плоским многоугольником (основой) и треугольниками, имеющих общую вершину, не лежащую в плоскости основания.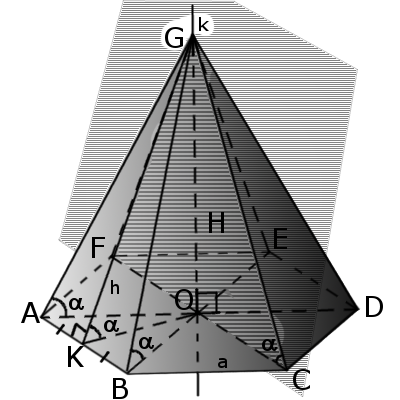

Рис.1

Определение. Боковая грань — это треугольник, у которого один угол лежит в вершине пирамиды, а противоположная ему сторона совпадает со стороной основания (многоугольника).

Определение. Боковые ребра — это общие стороны боковых граней. У пирамиды столько ребер сколько углов у многоугольника.

Определение. Высота пирамиды — это перпендикуляр, опущенный из вершины на основание пирамиды.

Определение. Апофема — это перпендикуляр боковой грани пирамиды, опущенный из вершины пирамиды к стороне основания.

Определение. Диагональное сечение — это сечение пирамиды плоскостью, проходящей через вершину пирамиды и диагональ основания.

Определение. Правильная пирамида — это пирамида, в которой основой является правильный многоугольник, а высота опускается в центр основания.

Объём и площадь поверхности пирамиды

Формула. Объём пирамиды через площадь основы и высоту:

Определение. Боковая поверхность пирамиды — это совокупная площадь всех боковых граней пирамиды.

Определение. Полная поверхность пирамиды — это совокупность площадей боковой поверхности и площади основания пирамиды.

Формула. Площадь боковой поверхности правильной пирамиды через периметр основания и апофему:

Свойства пирамиды

Если все боковые ребра равны, то вокруг основания пирамиды можно описать окружность, а центр основания совпадает с центром окружности. Также перпендикуляр, опущенный из вершины, проходит через центр основания (круга).

Если все боковые ребра равны, то они наклонены к плоскости основания под одинаковыми углами.

Боковые ребра равны тогда, когда они образуют с плоскостью основания равные углы или если вокруг основания пирамиды можно описать окружность.

Если боковые грани наклонены к плоскости основания под одним углом, то в основание пирамиды можно вписать окружность, а вершина пирамиды проектируется в ее центр.

Если боковые грани наклонены к плоскости основания под одним углом, то апофемы боковых граней равны.

Свойства правильной пирамиды

1. Вершина пирамиды равноудалена от всех углов основания.

2. Все боковые ребра равны.

3. Все боковые ребра наклонены под одинаковыми углами к основанию.

4. Апофемы всех боковых граней равны.

5. Площади всех боковых граней равны.

6. Все грани имеют одинаковые двугранные (плоские) углы.

7. Вокруг пирамиды можно описать сферу. Центром описанной сферы будет точка пересечения перпендикуляров, которые проходят через середину ребер.

8. В пирамиду можно вписать сферу. Центром вписанной сферы будет точка пересечения биссектрис, исходящие из угла между ребром и основанием.

9. Если центр вписанной сферы совпадает с центром описанной сферы, то сумма плоских углов при вершине равна π или наоборот, один угол равен π/n, где n — это количество углов в основании пирамиды.

Связь пирамиды со сферой

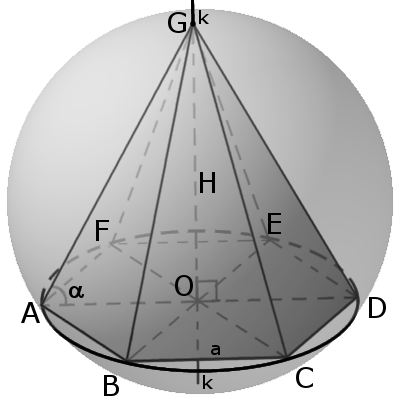Вокруг пирамиды можно описать сферу тогда, когда в основании пирамиды лежит многогранник вокруг которого можно описать окружность (необходимое и достаточное условие). Центром сферы будет точка пересечения плоскостей, проходящих перпендикулярно через середины боковых ребер пирамиды.

Вокруг любой треугольной или правильной пирамиды всегда можно описать сферу.

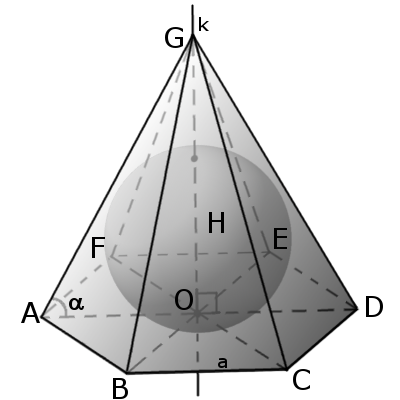В пирамиду можно вписать сферу, если биссекторные плоскости внутренних двугранных углов пирамиды пересекаются в одной точке (необходимое и достаточное условие). Эта точка будет центром сферы.

Связь пирамиды с конусом

Конус называется вписанным в пирамиду, если их вершины совпадают, а основание конуса вписано в основание пирамиды.

Конус можно вписать в пирамиду, если апофемы пирамиды равны между собой.

Конус называется описанным вокруг пирамиды, если их вершины совпадают, а основание конуса описана вокруг основания пирамиды.

Конус можно описать вокруг пирамиды если, все боковые ребра пирамиды равны между собой.

Связь пирамиды с цилиндром

Пирамида называется вписанной в цилиндр, если вершина пирамиды лежит на одной основе цилиндра, а основание пирамиды вписано в другую основу цилиндра.

Цилиндр можно описать вокруг пирамиды если вокруг основания пирамиды можно описать окружность.

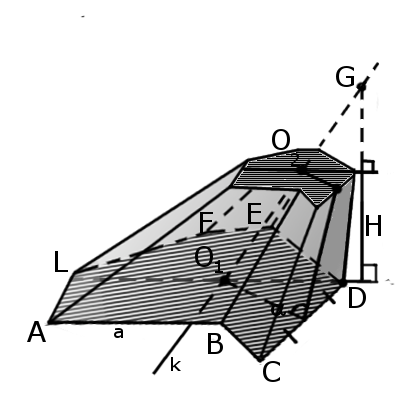Определение. Усеченная пирамида (пирамидальная призма) — это многогранник, который находится между основанием пирамиды и плоскостью сечения, параллельной основанию. Таким образом пирамида имеет большую основу и меньшую основу, которая подобна большей. Боковые грани представляют собой трапеции. 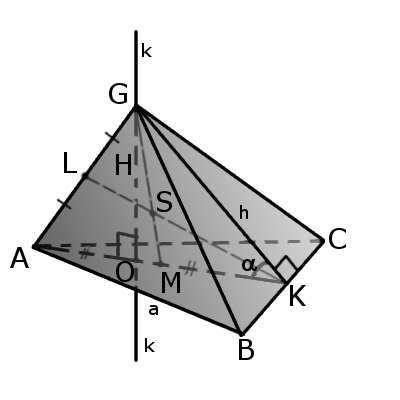Определение. Треугольная пирамида (четырехгранник) — это пирамида в которой три грани и основание являются произвольными треугольниками.

В четырехгранник четыре грани и четыре вершины и шесть ребер, где любые два ребра не имеют общих вершин но не соприкасаются.

Каждая вершина состоит из трех граней и ребер, которые образуют трехгранный угол.

Отрезок, соединяющий вершину четырехгранника с центром противоположной грани называется медианой четырехгранника (GM).

Бимедианой называется отрезок, соединяющий середины противоположных ребер, которые не соприкасаются (KL).

Все бимедианы и медианы четырехгранника пересекаются в одной точке (S). При этом бимедианы делятся пополам, а медианы в отношении 3:1 начиная с вершины.

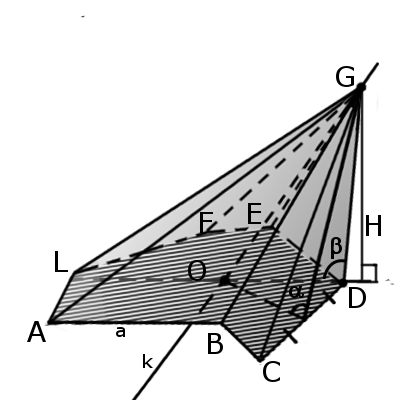Определение. Наклонная пирамида — это пирамида в которой одно из ребер образует тупой угол (β) с основанием. 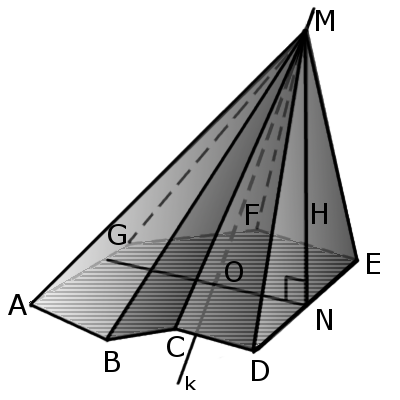Определение. Прямоугольная пирамида — это пирамида в которой одна из боковых граней перпендикулярна к основанию.

Определение. Остроугольная пирамида — это пирамида в которой апофема больше половины длины стороны основания.

Определение. Тупоугольная пирамида — это пирамида в которой апофема меньше половины длины стороны основания.

Определение. Правильный тетраэдр — четырехгранник у которого все четыре грани — равносторонние треугольники. Он является одним из пяти правильных многоугольников. В правильного тетраэдра все двугранные углы (между гранями) и трехгранные углы (при вершине) равны.

Определение. Прямоугольный тетраэдр называется четырехгранник у которого прямой угол между тремя ребрами при вершине (ребра перпендикулярны). Три грани образуют прямоугольный трехгранный угол и грани являются прямоугольными треугольниками, а основа произвольным треугольником. Апофема любой грани равна половине стороны основы, на которую падает апофема.

Определение. Равногранный тетраэдр называется четырехгранник у которого боковые грани равны между собой, а основание — правильный треугольник. У такого тетраэдра грани это равнобедренные треугольники.

Определение. Ортоцентричный тетраэдр называется четырехгранник у которого все высоты (перпендикуляры), что опущены с вершины до противоположной грани, пересекаются в одной точке.

Определение. Звездная пирамида называется многогранник у которого основой является звезда.

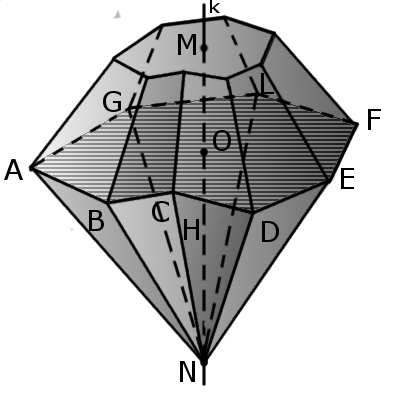Определение. Бипирамида — многогранник, состоящий из двух различных пирамид (также могут быть срезаны пирамиды), имеющих общую основу, а вершины лежат по разные стороны от плоскости основания.

ru.onlinemschool.com

Усеченная пирамида. Видеоурок. Геометрия 10 Класс

На данном уроке мы рассмотрим усеченную пирамиду, познакомимся с правильной усеченной пирамидой, изучим их свойства.

Вспомним понятие n-угольной пирамиды на примере треугольной пирамиды. Задан треугольник АВС. Вне плоскости треугольника взята точка Р, соединенная с вершинами треугольника. Полученная многогранная поверхность и называется пирамидой (рис. 1).

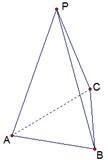
Рис. 1. Треугольная пирамида

Рассечем пирамиду плоскостью 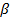, параллельной плоскости основания пирамиды 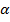. Полученная между этими плоскостями фигура  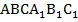и называется усеченной пирамидой (рис. 2).

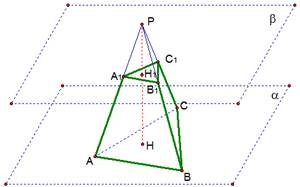
Рис. 2. Усеченная пирамида

Основные элементы:

-верхнее основание ;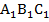

-нижнее основание АВС;

-боковая грань ;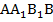

-если РН – высота исходной пирамиды, то 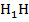 – высота усеченной пирамиды.

Свойства усеченной пирамиды вытекают из способа ее построения, а именно из параллельности плоскостей оснований:

-все боковые грани усеченной пирамиды являются трапециями. Рассмотрим, например, грань 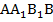. У нее  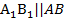по свойству параллельных плоскостей (поскольку плоскости параллельны, то боковую грань исходной пирамиды АВР они рассекают по параллельным прямым), в то же время  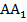и 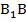 не параллельны. Очевидно, что четырехугольник  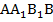является трапецией, как и все боковые грани усеченной пирамиды.

-отношение оснований одинаково для всех трапеций:

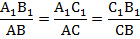
Имеем несколько пар подобных треугольников с одинаковым коэффициентом подобия. Например, треугольники 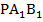 и РАВ подобны в силу параллельности плоскосте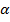й  и 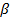, коэффициент подобия:

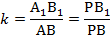
В то же время подобны треугольники 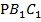 и РВС с коэффициентом подобия:

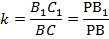
Очевидно, что коэффициенты подобия для всех трех пар подобных треугольников равны, поэтому отношение оснований одинаково для всех трапеций.

interneturok.ru

Свойства пирамиды, с примерами

В зависимости от того, какой многоугольник лежит в основании, пирамиды бывают треугольные, четырехугольные и т.д.

Свойства пирамиды

1. Около основания пирамиды можно описать окружность, если боковые ребра имеют одинаковую длину, при этом вершина пирамиды будет проецироваться в центр этой окружности. Боковые ребра образуют с плоскостью основания одинаковые углы.
2. Если боковые грани одинаково наклонены к плоскости основания, то около основания пирамиды можно описать окружность, при этом вершина пирамиды будет проецироваться в центр этой окружности, а также высоты боковых граней имеют равную длину.
3. Площадь боковой поверхности равняется половине произведения периметра основания на высоту боковой грани

      

4. Объем пирамиды равен одной третьей произведения площади основания на высоту пирамиды

      

Свойства правильной пирамиды

1. Боковые ребра правильной пирамиды равны между собой.
2. Боковые грани правильной пирамиды равны между собой и являются равнобедренными треугольниками.
3. Апофемы правильной пирамиды равны.
4. В любую правильную пирамиду можно как вписать, так и описать около неё сферу.
5. Все боковые грани образуют с плоскостью основания правильной пирамиды равные углы.

Примеры решения задач

Понравился сайт? Расскажи друзьям!

ru.solverbook.com