Треугольники

Задача

На стороне ромба построен равносторонний треугольник. Отрезок, соединяющий точку пересечения диагоналей ромба с серединой стороны треугольника, составляет с ней угол 70 градусов. Найти острый угол ромба.

Решение:

Читать далее

Ромб

Теорема (Птолемея)

Произведение диагоналей вписанного четырёхугольника равно сумме произведений двух пар его противолежащих сторон.

Дано:

4-угольник ABCD вписан в окр. (O; R)

Доказать:

AC·BD=AB·CD+AD·BC

Доказательство:

Читать далее

Окружность, Четырехугольники

Утверждение

Если диагонали вписанного четырехугольника перпендикулярны, то сумма квадратов его противоположных сторон равна квадрату диаметра описанной окружности.

Дано:

окружность (O;d),

ABCD — вписанный четырёхугольник,

AC⊥BD

Доказать: AD² +BC² = d²

Доказательство:

Читать далее

Окружность, Четырехугольники

Утверждение 1

Если диагонали выпуклого четырехугольника взаимно перпендикулярны, то суммы квадратов его противолежащих сторон равны.

Дано: ABCD — выпуклый четырёхугольник,

AC⊥BD

Доказать:

AB²+CD²=AD²+BC²

Доказательство:

Читать далее

Четырехугольники

Утверждение

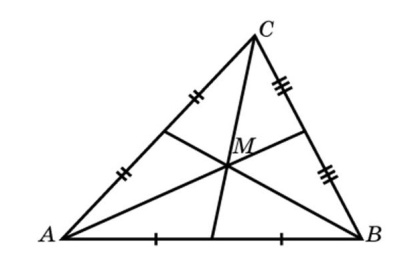
Если две медианы треугольника равны, то этот треугольник — равнобедренный.

Дано: ΔABC,

AF, BK — медианы,

AF=BK

Доказать: ΔABC — равнобедренный

Читать далее

Равнобедренный треугольник

Теорема (Штейнера-Лемуса)

Если в треугольнике две биссектрисы равны, то этот треугольник — равнобедренный.

Дано:

ΔABC,

AF, BK — биссектрисы ΔABC,

AF=BK

Доказать: ΔABC — равнобедренный

Доказательство:

Читать далее

Равнобедренный треугольник

Длина биссектрисы треугольника может быть найдена разными способами, в зависимости от исходных данных.

I. Через длины двух сторон и отрезки, на которые биссектриса делит третью сторону.

Утверждение 1

Квадрат биссектрисы треугольника равен разности между произведением двух его сторон и произведением отрезков, на которые эта биссектриса делит третью сторону.

Соответственно, длина биссектрисы равна квадратному корню из разности между произведением двух его сторон и произведением отрезков, на которые эта биссектриса делит третью сторону.

Читать далее

Элементы треугольника

www.treugolniki.ru

Треугольник. Свойства и признаки треугольника.

Треугольник произвольный

 

Треугольник – это многоугольник с тремя сторонами (тремя углами).

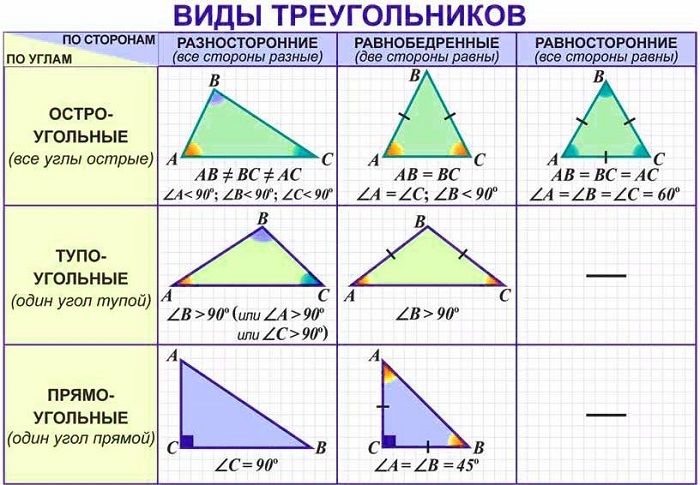
Виды треугольников:+ показать

Остроугольный треугольник  – треугольник, у которого все углы острые (то есть меньше 90˚).

Тупоугольный треугольник – треугольник, у которого один из углов  тупой (больше 90˚).

Прямоугольный треугольник – треугольник, у которого один из углов прямой (равен 90˚).

Равнобедренным называется треугольник, у которого две стороны равны. Эти стороны называются боковыми

, третья сторона называется основанием.

Равносторонний (правильный) треугольник –  треугольник, у которого все три стороны равны.

 Свойства 

+ показать

1. Против большей стороны лежит больший угол, и наоборот.

2. Против равных сторон лежат равные углы, и наоборот.

3. Сумма углов треугольника равна 180 º .

4. Внешний угол треугольника  равен сумме внутренних углов,
не смежных с ним:

(Внешний угол образуется в результате продолжения одной из сторон треугольника).

5. Любая сторона треугольника меньше суммы двух других сторон.

Признаки равенства треугольников

+ показать

1. Треугольники равны, если у них соответственно равны две стороны и угол между ними.

 2. Треугольники равны, если у них соответственно равны два угла и прилегающая к ним сторона.

 

3. Треугольники равны, если у них соответственно равны три стороны.

Биссектриса, высота, медиана

 

Здесь подробно о биссектрисе, высоте, медиане треугольника.

Средняя линия треугольника

Средняя линия треугольника – отрезок, соединяющий середины двух сторон треугольника.

Средняя линия треугольника параллельна третьей  стороне и равна ее половине.

 

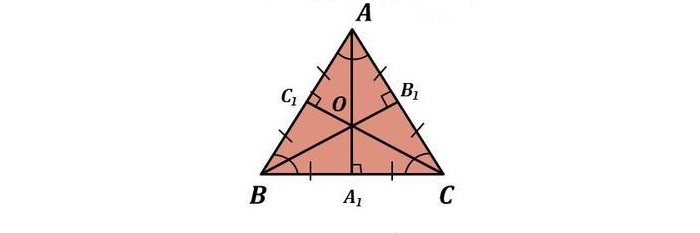
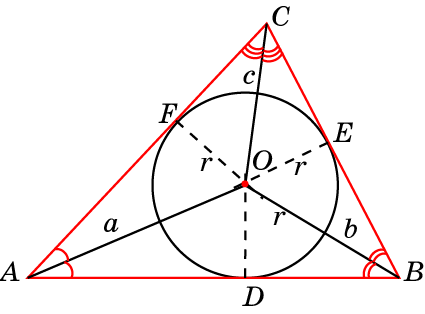
Вписанная окружность

Центр вписанной окружности – точка пересечения биссектрис треугольника.

Описанная окружность

Центр описанной окружности – точка пересечения серединных перпендикуляров.

Соотношение сторон в произвольном треугольнике

 

Теорема косинусов:

Теорема синусов:

Площадь треугольника

 

Через сторону и высоту

Через две стороны и угол между ними

Через радиус описанной окружности

Через радиус вписанной окружности

, где – полупериметр

Формула Герона

, где  – полупериметр

 

Смотрите также площадь треугольника здесь.

И, думаю, будет полезна  таблица формул для треугольника.

 

egemaximum.ru

Какими могут быть стороны треугольника

Какими могут быть стороны треугольника? Могут ли стороны треугольника быть равными данным числам? Существует ли треугольник со сторонами той или иной длины? . Рассмотрим конкретные задачи.

1) Существует ли треугольник со сторонами

а)  1 см, 2 см, 3 см;

б)  7 см, 10 см, 12 см?

Решение:

Согласно неравенству треугольника, длина любой стороны треугольника меньше суммы длин двух других сторон. Проверяем, выполнено ли это условие для каждого отрезка. Для задачи а):

   

   

   

Третье неравенство неверно, следовательно, треугольника со сторонами 1 см, 2 см и 3 см не существует.

б)

   

   

   

Все три условия выполнены, значит, треугольник со сторонами 7 см, 10 см и 12 см существует.

2) Можно ли построить треугольник со сторонами 3 см, 4 см, 8 см?

Решение:

Проверяем, выполняется ли неравенство треугольника для каждого из отрезков:

   

   

   

Последнее неравенство не выполнено, поэтому треугольник со сторонами 3 см, 4 см и 8 см построить нельзя.

3) Какими могут быть стороны треугольника:

а)  5 м, 7 м, 10 м;

б)  11 дм, 15 дм, 30 дм?

Решение:

Проверяем выполнение неравенства треугольника для каждой тройки отрезков:

   

Все три неравенства верны, следовательно, стороны треугольника могут быть равными 5 м, 7 м и10 м.

   

Третье неравенство не является верным, значит, стороны треугольника не могут быть равными 11 дм, 15 дм и 30 дм.

 

www.treugolniki.ru

Как называются стороны треугольника | Треугольники

Всегда ли возможно ответить на вопрос: «Как называются стороны треугольника?» Ответ зависит от того, что конкретно требуется — назвать стороны треугольника как отрезки, соединяющие вершины треугольника или речь идет об общем названии сторон треугольника определенного вида.

Как называются стороны прямоугольного треугольника

 

Сторона прямоугольного треугольника, которая лежит напротив прямого угла, называется гипотенузой.

Две другие стороны прямоугольного треугольника называются катетами.

 

Как называются стороны равнобедренного треугольника

 Две равные стороны равнобедренного треугольника называются боковыми.

Третья сторона называется основанием.

Как называются стороны произвольного треугольника

Специальных названий стороны произвольного треугольника не имеют.

Иногда в задачах одну из сторон произвольного треугольника называют основанием. Как правило, это делают для того, чтобы облегчить построение чертежа (такую сторону располагают горизонтально).

 

Как можно назвать стороны любого треугольника

Стороны треугольника — это отрезки, соединяющие вершины треугольника. Поэтому название сторон треугольника любого вида — это название соответствующих отрезков.

 

Например, для треугольника АВС название сторон — АВ, ВС и АС.

www.treugolniki.ru

Остроугольный треугольник 📐 определение, свойства и признаки, виды и классификация, правила и теоремы о треугольниках

Одна из центральных тем на уроках геометрии – остроугольный треугольник, составная часть своих более сложных аналогов и иных тригонометрических форм. 

Азы изучения точной науки начинаются с рассмотрения уникальной комбинации из трех сторон и острых углов.

Виды, признаки и свойства остроугольных треугольников

Трехсторонние фигуры разделяются на множество подвидов и категорий. 

Общая классификация по наибольшему углу делит их на 3 группы:

 

Они располагают как общими для формы с тремя сторонами характеристиками, так и специфическими признаками.

Общие признаки:

• 3 угла, сумма которых равна 180°, (величина каждого меньше 90°) и 3 стороны;

• сумма длин любых двух сторон больше оставшейся третьей.

Свойства остроугольной фигуры определяются вспомогательными геометрическими линиями, всегда находящимися внутри него:

1. Биссектрисы, делящие углы пополам, являются центром, вокруг которого можно нарисовать вписанную окружность.

2. Высоты пересекаются в одной точке, образуя ортоцентр.
3. Медианы в точке пересечения пролегают в пропорции 2:1 (2 трети до центра и 1 треть после).

Уникальные особенности зависят от разновидностей фигуры.

Равносторонний треугольник

«Идеальный» правильный треугольник, облегчающий решение задач. Определение, форма и свойства данной геометрической формы исходят из названия — все углы равны 60°, а стороны равны друг другу.

Полное равенство придает и другую особенность: медианы, биссектрисы и высоты полностью совпадают.

 

 

Разносторонний треугольник

 

Наиболее часто встречаемый на чертежах в геометрии вариант, один из самых трудноразрешимых видов. Разносторонними бывают и прямоугольные, и тупоугольные фигуры.

Уникальных отличий не имеет, только общие:

Равнобедренный остроугольный треугольник

Здесь при основании (стороне, не равной остальным) находятся равные друг другу 2 стороны и 2 угла. Выглядит как вытянутый в одну сторону равносторонний треугольник.

Особенности:

• проведенная к основанию линия – и биссектриса, и высота, и медиана;

• вспомогательные линии из крайних точек при основании совпадают.

Равнобедренный тупоугольный треугольник

Пусть он и называется равнобедренным, но из-за наличия угла более 90° не является остроугольным и является представителем другой группы.

Начертить его сложнее (рисунок следует начинать с основания и 2 острых углов и уже после создавать тупой), но процесс решения и изучения прост.

Отличие у него одно – точка пересечения двух высот, проведенных от углов при основании, выходит за периметр треугольника. Чтобы ее обозначить, необходимо нарисовать «продолжения» равнобедренных линий. Все остальные свойства совпадают.

В ключевых и фундаментальных разделах математики именно треугольник является основой для доказательства многих теорем и помощью в решении множества задач. Твердое знание его свойств откроет путь к успехам в расчетах, вычислениях, оформлении чертежей и фото в проектных работах.

nauka.club

Как называются углы треугольника | Треугольники

Как называются углы треугольника? Ответ может зависеть от того, сколько углов имеется при вершине треугольника.

Если при вершине треугольника есть только один угол, то его можно назвать одной буквой, по названию вершины.

Например, в треугольнике MKF (рисунок 1) при каждой вершине есть только один угол. Следовательно, каждый из углов   можно назвать одной буквой, по названию вершины, из которой исходят образующие этот угол лучи:

рисунок 1

Угол M, угол K и угол F.

  Для обозначения угла существует специальный знак: ∠

Запись ∠M читают как «угол M».

Каждый из углов треугольника MKF можно назвать также тремя буквами. При этом вершина в названии угла должна стоять посередине.

Угол M также можно назвать углом KMF или углом FMK,

∠K — ∠MKF или ∠FKM,

∠F — ∠MFK или ∠KFM.

рисунок 2

 

В треугольниках, изображенных на рисунке 2, одной буквой могут быть названы только углы при вершинах A и D: ∠A и ∠D.

При вершине B есть три угла, поэтому каждый из этих углов нужно назвать тремя буквами: ∠ABC, ∠CBD и ∠ABD.

Аналогично, углы при вершине C могут быть названы только тремя буквами: ∠ACB, ∠BCD и ∠ACD. Назвать какой-либо из этих углов ∠C нельзя.

рисунок 3

Каждый из углов треугольников, изображенных на рисунке 3, может быть назван только тремя буквами.

Углы треугольника ABO: ∠ABO, ∠BAO, ∠AOB.

Углы треугольника BOC: ∠BOC,  ∠OBC,  ∠BCO.

Углы треугольника OCD: ∠OCD, ∠COD,  ∠CDO.

Углы треугольника AOD: ∠AOD, ∠ADO,∠OAD.

Углы треугольника ABC: ∠ABC, ∠BAC, ∠BCA.

Углы треугольника BCD: ∠BCD, ∠CBD, ∠BDC.

Углы треугольника ACD: ∠ACD, ∠CAD, ∠ADC.

Углы треугольника ABD: ∠ABD, ∠BAD, ∠ADB.

 

www.treugolniki.ru

Треугольник и его виды

Сценарий урока математики учителя МОУ «Чернавская школа»

Грачевой Ирины Вячеславовны

Тема урока: «Треугольник и его виды»

Тип урока: изучение и первичное закрепление новых знаний.

1.Мотивация к учебной деятельности, постановка темы урока

Цели:

-актуализировать требования к ученику с позиции учебной деятельности;

-создать условия для формирования у учеников внутренней потребности во включении в учебную деятельность;

-установить тематические рамки

Устанавливает тематические рамки. Проверяет уровень знаний

(работа с презентацией)

-Здравствуйте, дети! Проверьте свою готовность к уроку! Садитесь!

-Начнем урок с творческой работы! Посмотрите, какая сегодня чудесная погода! За окном ярко светит солнышко! На парте у вас так же есть рисунок с изображением солнца. Из каких геометрических фигур оно состоит?

-Что можете о них сказать?

-Предположите, о чем мы будем говорить сегодня на уроке.

-Верно! Открываем тетради и записываем тему урока «Треугольник и его виды»

-Сегодня я пришла к вам на урок не с пустыми руками: я принесла 3 колышка и веревку, на которой завязано 12 узелков на равном расстоянии друг от друга. Как вы думаете, для чего я их принесла? И как это связано с темой урока?

-выполняют просьбу учителя

-Из треугольников

-они все не равны

-О треугольниках и о том, чем они отличаются

-Делают предположения о назначении принесенных предметов

2. Актуализация и фиксирование индивидуального затруднения в пробном действии

Цели:

-создать условия для выполнения учащимися пробного учебного действия;

-организовать фиксирование учащимися индивидуального затруднения;

-выявить место затруднения;

-зафиксировать во внешней речи причину затруднения.

Организует фиксирование индивидуального затруднения, выявление места затруднения во внешней речи, обобщение актуализированных знаний

-Давайте вспомним, из каких элементов состоит треугольник?

-Как называются эти точки? Отрезки?

— Какой еще элемент есть в треугольнике?

-А теперь подумайте, по каким признакам мы можем классифицировать треугольники?

-Молодцы! А если быть точнее, то по равным сторонам. А как можно классифицировать треугольники по углам?

Какие вообще углы бывают?

Сколько, например тупых углов может быть в треугольнике? Попробуйте построить треугольник, в котором, например, два тупых угла

-Из трех точек и отрезков, их соединяющих.

-точки называются вершинами, отрезки- сторонами треугольника

-Угол

-по сторонам, по углам

Острые, прямые, тупые, развернутые.

Дети выдвигают свои предположения.

Возникает затруднение, возможно несогласие обучающихся с мнением друг друга

3.Этап выявления места и причины затруднения

Выявляет причины затруднения

-Пока вы не пришли к единому мнению. А причина этому- отсутствие необходимых знаний

4. Этап целеполагания по теме урока

Фиксирует цели и задачи, названные учащимися

-Какие цели и задачи мы поставим для себя сегодня на уроке? (фиксируются на доске)

Цели: научиться классифицировать треугольники по различным признакам

Задачи: узнать, какие виды треугольников бывают;

научиться строить треугольники разных видов

5.Построение проекта выхода из затруднения.

Цель: организовать уточнение следующего шага учебной деятельности, составление плана действий

Организует уточнение следующего шага учебной деятельности, составление совместного плана действий.

Сегодня на уроке мы разделимся на группы. Каждая группа попробует построить треугольники по заданным параметрам. Заслушав каждую группу, мы составим интеллект-карту по теме урока.

6. Реализация построенного проекта и первичное закрепление с проговариванием во внешней речи.

Цели:

-реализовать построенный проект в соответствии с планом;

-зафиксировать новое знание;

-организовать устранение и фиксирование преодоления затруднений.

Организует реализацию построенного проекта в соответствии с планом, фиксирует новое знание в речи

На своих партах вы видите карточку, на которой изображен угол. Прошу в первую команду ребят, у которых угол изображен острый, во вторую- у кого прямой, в третью-тупой.

-Именно с классификации по виду углов мы и начнем.1 команда попробует построить такой треугольник, в котором будут только острые углы, вторая- в котором будет один или несколько прямых углов ( попробовать различные случаи), третья- треугольник, содержащий одни или несколько тупых углов.

-Справились с заданием?

-1 команда, расскажите нам о своих успехах

-2 команда

-3 команда

Дети расходятся по командам

Выполняют задание, пробное действия

-Да

-У нас получился треугольник, в котором все три угла- острые.

-у нас один треугольник содержит только один прямой угол, а два других-острые. Треугольник, в котором будет хотя бы два прямых угла, нам построить не удалось

-Мы построили треугольник с одним тупым углом, другого случая быть не может.

7. Этап самостоятельной работы с самопроверкой по эталону

Цели:

-организовать самопроверку

Организует работу с учебником

Организует работу групп

-Молодцы! Подумайте, как могут называться такие треугольники?

Давайте обратимся к учебнику и найдем определение для остроугольного, прямоугольного и тупоугольного треугольников.

Теперь 1 группа построит такой треугольник, у которого все стороны будут различны; 2 группа- треугольник с двумя равными сторонами, а 3 группа-треугольник, у которого все три стороны равны.

1-остроугольный

2-прямоугольный

3-тупоугольный

Работают с учебником

8. Этап включения в систему знаний и повторения

Цели:

-зафиксировать новое содержание урока

Проводит физкультминутку

Знакомит учащихся с вариантами применения нового знания в жизни

-Итак, давайте подведем итог первого этапа нашей работы. У каждой группы получилось начертить треугольник по заданным условиям?

-Какой вывод можем сделать?

-На следующем слайде даны 3 определения: для равностороннего, равнобедренного и разностороннего треугольника. Пожалуйста, команды, подумайте, у кого какой треугольник получился?

—Физкультминутка

Выполним небольшую гимнастику для глаз.

Закроем глаза и чуть-чуть придавим их пальцами. Сосчитаем про себя до пяти. Откроем глаза .

Взяли в руку карандаш и, глядя на него, медленно приближаем его к глазам. При этом карандаш должен находиться на уровне глаз. Затем медленно отодвигаем его от глаз на вытянутую руку (считаем до 5).выполняем это упражнение еще один раз. Спасибо.

-Как вы думаете, есть применение в жизни тем знаниям, которые мы с вами открыли для себя сегодня?

-Еще в древнем Египте люди научились строить прямоугольные треугольники. Это было необходимо при построении всем известных Египетских пирамид. Есть предположения, как они это делали? Ведь тогда еще не было измерителя углов- транспортира?

-На самом деле, египтяне придумали хитрый способ. Они брали веревку, завязывали на ней 12 узлов на равном расстоянии друг от друга и строили треугольник по следующей схеме (обращаю внимание на слайд). Таким образом, получается известный египетский треугольник со сторонами 3,4,5. Теперь понятно, для чего я сегодня принесла колышки и веревку? Попробуем и мы построить прямоугольный треугольник без транспортира?

-Мы можем сделать вывод, что в треугольнике могут быть все три стороны различны, могут быть две равны, а третья отлична от них, а могут и все три стороны быть равны

1-разносторонний, 2-равнобедренный, 3 равносторонний

Выполняют физкультминутку

-Наверное, есть.

Делают предположения

Комментируют египетский треугольник, пробуют нарисовать схему

Строят по схеме египетский треугольник

9. Рефлексия учебной деятельности на уроке.

Цели:

-зафиксировать новое содержание урока;

-организовать рефлексию и самооценку учениками собственной учебной деятельности

Организует фиксирование нового содержания, работу с интеллект-картами, демонстрацию интеллект-карт с помощью документ-камеры, рефлексию, самооценку учебной деятельности

Организует рефлексию настроения

Благодарит за урок, сообщает домашнее задание

—Итогом нашей групповой работы станет создание интеллект-карты по данному уроку! Поработайте в группах, предложите свои варианты.

-Давайте вернемся к тем целям и задачам, которые мы поставили в начале урока. Мы смогли классифицировать треугольники?

-Вы смогли начертить треугольники данных видов?

-Мы достигли поставленных целей и задач? Узнали новое?

-У всех легко получилось справиться с задачами урока? Или у кого-то возникли затруднения? В чем?

-Давайте вернемся к нашему солнышку! Из каких треугольников оно состоит?

-Я предлагаю вам раскрасить тупоугольные треугольники в желтый цвет, если сегодня на уроке у вас все получилось, в красный цвет остроугольные треугольники- если получилось, но не все, в голубой цвет равносторонние треугольники, если сегодня у вас все скорее не получилось и вам есть над чем поработать дома.

Домашнее задание: параграф 14, вопросы 1-6, №340,342,345.

Спасибо за активную творческую работу на уроке!

Предлагают свой вариант интеллект-карты с пояснением

(интеллект-карты демонстрируются с помощью документ-камеры)

-Да. Оказывается, треугольники бывают равносторонние, равнобедренные, разносторонние- если классифицировать их по количеству равных сторон. А еще они бывают прямоугольными, тупоугольными и остроугольными

-Да

-Да, мы достигли поставленные цели и задачи.

Дети, у которых в процессе урока возникали затруднения, рассказывают о них, делают выводы о необходимости поработать дополнительно с учебником

-Из равнобедренных, равносторонних, остроугольных

Обучающиеся раскрашивают солнышко, демонстрируют результат учителю.

Записывают домашнее задание

infourok.ru