Какие бывают треугольники / Бери и делай
Треугольник — это геометрическая фигура. Она образована 3 отрезками, которые соединяют 3 точки, не лежащие на одной прямой. Эти точки называются вершинами треугольника, а отрезки — его сторонами. Стороны, в свою очередь, образуют углы. Последние два параметра и лежат в основе классификации треугольников.
«Бери и Делай» рассказывает, какие бывают треугольники. А в бонусе мы повторим некоторые термины из школьного курса геометрии.
Виды треугольников по величине углов
- Прямоугольный — треугольник, один из углов которого равен 90°.
- Остроугольный — треугольник, у которого все 3 угла меньше 90°.
- Тупоугольный — треугольник, один из углов которого превышает 90°.
Виды треугольников по числу равных сторон
- Равносторонний — треугольник, все 3 стороны которого равны между собой. Еще такой треугольник называют правильным.
 Поскольку все 3 стороны фигуры имеют одинаковую длину, все 3 угла у нее также равны. Каждый внутренний угол равностороннего треугольника равен 60°.
Поскольку все 3 стороны фигуры имеют одинаковую длину, все 3 угла у нее также равны. Каждый внутренний угол равностороннего треугольника равен 60°. - Равнобедренный — треугольник, у которого 2 стороны из 3 имеют одинаковую длину.
- Разносторонний — треугольник, все 3 стороны которого имеют разную длину.
Бонус: термины для описания элементов треугольника
- Катет — одна из сторон прямоугольного треугольника, образующая его прямой угол (90°).
- Гипотенуза — самая длинная сторона прямоугольного треугольника, противоположная его прямому углу.
- Медиана — прямой отрезок, соединяющий одну из вершин треугольника с серединой противоположной стороны.
- Высота — линия от вершины треугольника к его противоположной стороне, расположенная перпендикулярно.
- Биссектриса угла — отрезок, который исходит из вершины угла треугольника и делит его пополам на 2 равных угла.

Конспект урока математики «Виды треугольников»; 3 класс — Математика — Начальные классы
Тема: Виды треугольников.
Цель: Формирование представления учащихся о разных видах треугольников.
Задачи:
Научить классифицировать треугольники по видам углов;
Выявить названия треугольников;
Развивать логическое мышление, внимание,
Планируемые результаты: к концу урока дети должны узнать виды треугольников, знать их названия, умнеть их классифицировать по видам углов
Материально- техническое обеспечение : Моро М.И, Бантова М.А-М.: Просвещение, 2015.-112с. ПК, мультимедийный проектор, экран.
Ход урока
I. Организационный момент.
Я пришел сюда учиться,
Не лениться, а трудиться!
Только тот, кто много знает
В жизни что-то достигает.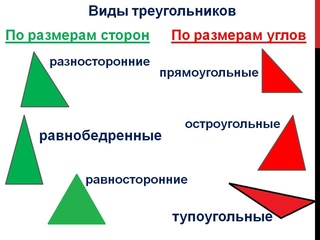
— Вы с ним согласны?
— А вы готовы не лениться, а трудиться? (Готовы!)
— Оформим к уроку тетрадь.
II. Сообщение темы урока и цели.
м/у: на слайде
— Напомню, наши несколько урок будут посвящены геометрии.
— Что такое геометрия? (раздел математики, который изучает фигуры, их свойства и т.д.)
— А о каких фигурах пойдет сегодня речь на уроке, вы узнаете, если правильно выполните задания.
О Т У Г Л К | 40 ∙ 80 : 100 3 ∙ 26 – 18 250 + 700 4 + 96 : 2 560 : 7 ∙ 4 902 – 348 |
| Е Н Р И Ь | 200 ∙ 7 – 300 649 – 40 – 19 880 : 44 ∙ 9 482 – 60 300 ∙ 9 – 200
|
60 | 180 | 110 | 950 | 52 | 32 | 320 | 2500 | 590 | 422 | 554 |
|
|
|
|
|
|
|
|
|
|
— Какое слово получилось?.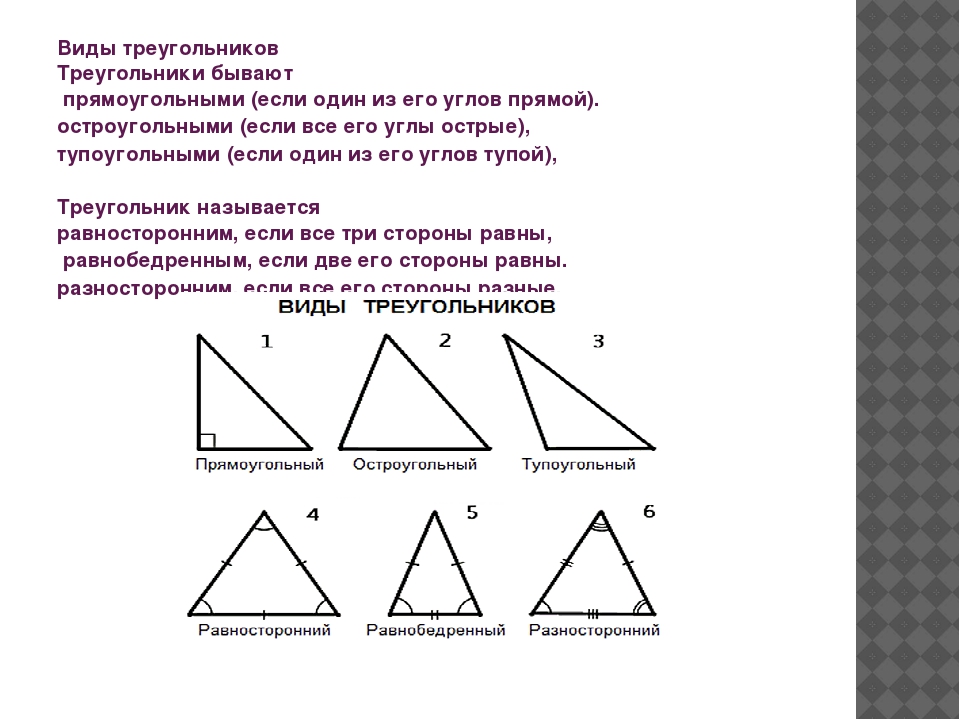
— Ребята, а что вы знаете про треугольники?
— И тема нашего урока: треугольники, а точнее их виды.
— А зачем нам надо знать виды треугольников?
Где нам в жизни могут треугольники понадобиться?
— Определите цель нашего урока. (узнать какие виды треугольников бывают)
III. Актуализация ранее изученного материала.
— А поможет нам в реализации нашей цели другая геометрическая фигура.
— Что за фигура изображена на экране?
— Из чего она состоит?
— А какие углы вы знаете?
— А что вы можете рассказать о прямом угле?
— Какой угол называется острым?
— Какой – тупым углом?
IV. Изучение нового материала.
— Мы не просто вспомнили об углах, эти знания вам пригодятся на сегодняшнем уроке и при выполнении следующего задания.
м/у: работа в паре
— У вас на столах лежат конверты с фигурами.
— Что общего у всех этих фигур?
— Задание: подумайте, на сколько групп можно разделить эти треугольники и разделите.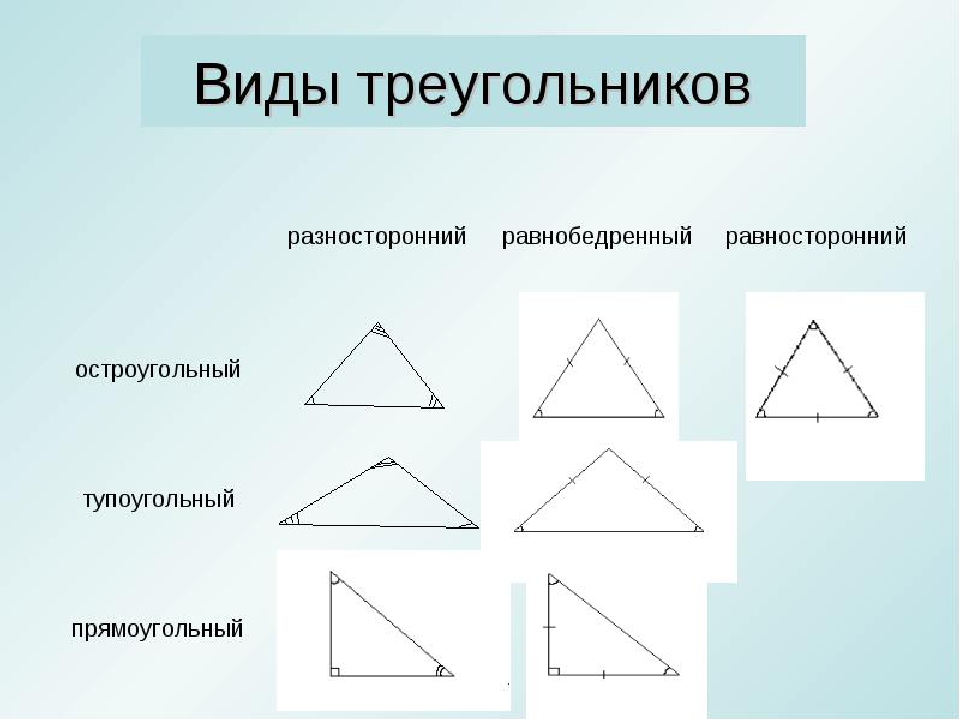
— Проверяем. На сколько групп разделила первая пара?
— А по какому признаку вы их разделили? (по типу углов)
— Объясните.
— Треугольник № 1 с какими треугольниками объединили?
— Что общего между треугольниками 1, 4, 7? (есть прямой угол)
— Треугольник № 2 с какими треугольниками объединили?
— Что общего между треугольниками 2, 5, 8? (есть острый угол)
— Треугольник № 3 с какими треугольниками объединили?
— И что общего между треугольниками 3, 6, 9? (есть тупой угол)
— Давайте попытаемся дать этим группам имена.
— Если у треугольника есть прямой угол, то он какой? Как его можно назвать?
— Если тупой угол есть?
— А если все углы острые?
— Итак, подведем итог.
— На сколько видов делятся треугольники?
— Как называются треугольники в каждой группе?
— Что значит прямоугольный треугольник?
— Какой треугольник называют остроугольным?
— Какой тупоугольным?
Физминутка для глаз.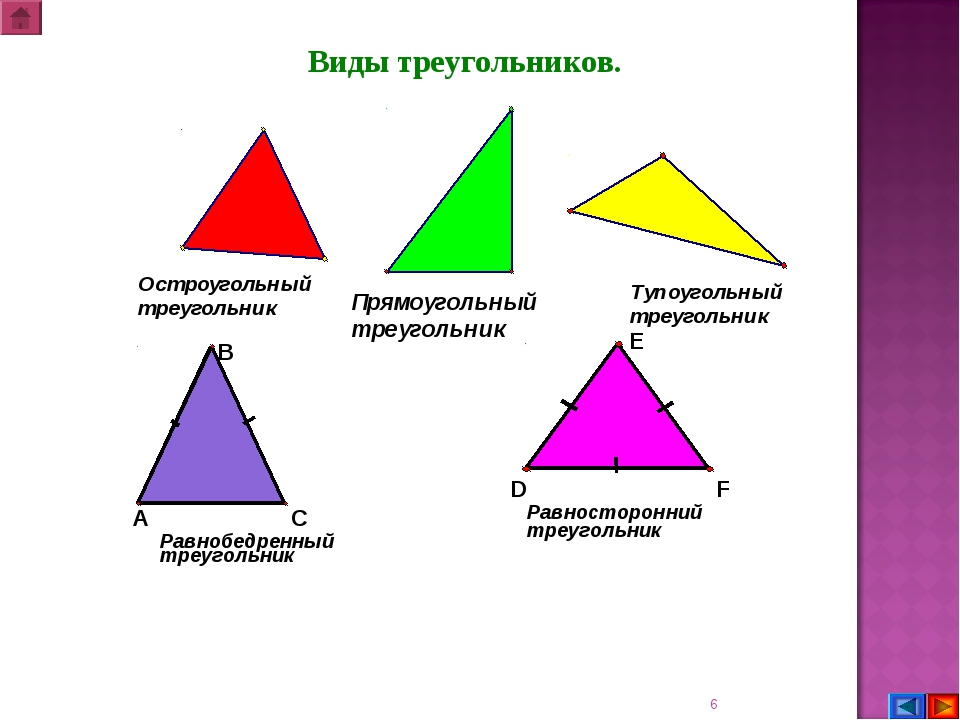
— Сейчас немного отдохнем. Сядьте равно. Руки положите на стол.
— Представьте себе треугольник. Переведите взгляд на самый верхний его угол, из верхнего угла — в левый нижний – в верхний, в правый нижний.
— Продолжаем работать.
— Мы узнали, какие виды треугольников бывают, теперь попробуем проверить, как вы усвоили этот материал, для этого выполним следующее задание.
«Найди лишнее»
-м/у: на слайде даны треугольники, найдите лишний.
( У детей возникает затруднение, разногласия, так как на глаз не всегда можно определить вид треугольника)
— Почему у вас возник спор? Что не понятно?
— Как все-таки узнать, какой это треугольник?
— С помощью чего? (треугольника или простой линейки)
— Если мы сомневаемся в том, какой это треугольник, надо приложить одну сторону линейки к линии и посмотреть, как соединяться другие. (слайд 9)
— Если обе стороны линейки и треугольника совпали , значит он прямоугольный.
— Итак, какая фигура лишняя? (голубой, он прямоугольный)
— Пришла пора применить полученные знания при выполнении геометрических задач:
— “Постройте прямоугольный треугольник”.
— Перед выполнением внимательно посмотрите на экран. Чтобы у вас все получилось, внимательно следите за каждым этапом на экране (слайд 10).
Дети чертят в своих тетрадях три разных небольших треугольника.
— Сколько треугольников вы начертили? (3)
— Почему три? (так как три вида)
— Как называются виды треугольников?
— Найдите у себя прямоугольный треугольник. Сколько в нем прямых углов? (1)
— Найдите тупоугольный треугольник. Сколько в нем тупых углов? (1)
— Найдите остроугольный треугольник. Сколько в нем острых углов? (3 ,т.е. все)
— Попробуйте сделать вывод, какой треугольник называют прямоугольным, тупоугольным, а какой остроугольным.
м/у: Если дети не смогут сами сделать вывод, то показать готовое правило и спросить: «Что общего в правилах и в чем отличие?»
Физминутка
— Сейчас все встанем и поиграем.
— На экране буду будут показываться треугольники, а вы в зависимости от его вида, будете выполнять команду.
Если треугольник тупоугольный — присесть,
если остроугольный — хлопнуть,
если прямоугольный – прыгнуть.
V. Закрепление нового материала
— Итак мы узнали какие виды треугольников бываю, сейчас мы будем закреплять новый материал.
м/у: стр 4 № 8
Выпиши номера остроугольных, прямоугольных и тупоугольных треугольников.
Ответы: остроугольные-
Прямоугольные
Тупоугольные
м/у: стр 4 № 9
Начерти прямоугольный, остроугольный и тупоугольный прямоугольники. Обозначь их буквами
м/у: стр 4 № 13
— Сейчас каждая группа оформит памятку по видам треугольников. В памятке должны отразиться название видов треугольников, по какому признаку они отличаются.
VI. Итог урока.
— Сейчас каждая группа оформит памятку по видам треугольников. В памятке должны отразиться название видов треугольников, по какому признаку они отличаются.
— Вспомните цель нашего урока.
— На сколько видов делятся треугольники?
— Какие виды треугольников бывают?
— Что значит прямоугольный треугольник?
— Какой треугольник называют остроугольным?
— Какой тупоугольным?
— Найдите вокруг себя предметы с прямым углом?
VII. Рефлексия.
— Передайте сове настроение с помощью изображенного треугольника.
(Дан треугольник с глазками, нужно дорисовать ротик)
VIII. Домашнее задание.
С. 4, №15,12 ( 2 примера)
«Виды треугольников».
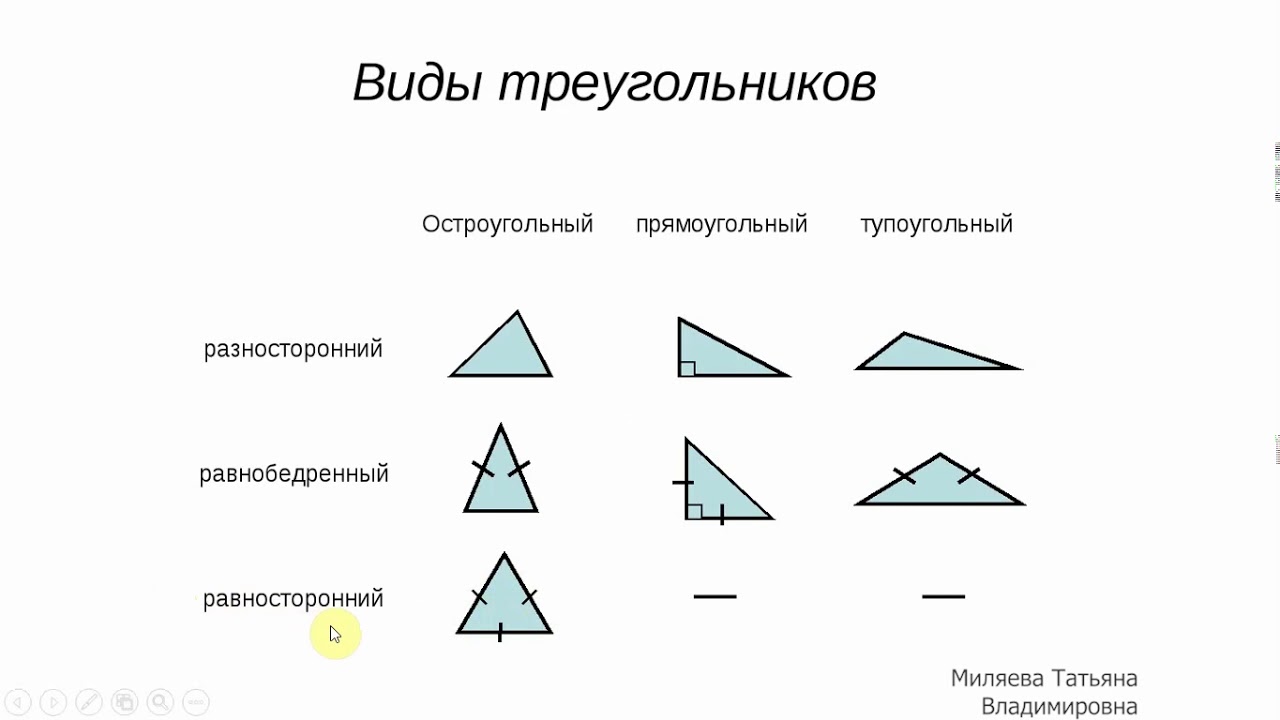 (прямоугольные, тупоугольные, остроугольные) – Документ 2 – УчМет
(прямоугольные, тупоугольные, остроугольные) – Документ 2 – УчМетУчитель: Пастуховой Светланы Анатольевны
МКОУ «СОШ№ 1» г. Николаевска
Предмет: математика
Класс: 4
УМК: Школа России
Тема: «Виды треугольников». (прямоугольные, тупоугольные, остроугольные)
Тип урока: получение новых знаний ( частично поисково — исследовательский)
Цель: сформировать представление обучающихся о разных видах треугольников;
Задачи:
образовательные: добиться осмысленности понятий: прямой, тупой, острый, развернутый угол; прямоугольный, тупоугольный, остроугольный треугольник: добиться умения выделять углы треугольника в заданных фигурах; выделять треугольники в заданных фигурах.
развивающие: способствовать развитию у обучающихся
интуиции и воображения; внимания,
наблюдательности и вооружать логическим
методом, — основным методом, с помощью
которого обосновывается истинность
или ложность утверждений; помочь обучающимся осознать социальную,
практическую и личностную значимость
данного учебного материала, обеспечить развитие умения ставить цель и
формулировать задачи, планировать свою
деятельность.
— реализовать право каждого ученика на полноценное личностное развитие, на основе качественного и индивидуализированного обучения.
воспитательные: способствовать развитию математического языка (его основным диалектам, алгебраическому и геометрическому) на котором говорит современная наука, интереса к предмету математика, создавать положительный образ математики у обучающихся.
Планируемые предметные результаты:
— умение различать треугольники: остроугольный, прямоугольный, тупоугольный: умение, выделять треугольники в заданных фигурах; развивать навыки выделения соответственных элементов в треугольниках, нахождение треугольников всех видов.
Планируемые метапредметные результаты:
личностные: положительное отношение к учению, понимание необходимости сотрудничества с учителем, готовности к взаимодействию с ним и дружескому взаимопониманию, понимание необходимости товарищеского сотрудничества с одноклассниками, готовности к взаимодействию и взаимопониманию;
регулятивные: умение определять и формулировать цель на уроке с помощью учителя, проговаривать последовательность действий, планировать свои действия, оценивать правильность выполнения действий на уровне адекватной ретроспективной оценки;
познавательные: умение ориентироваться в своей системе знаний, отличать полученное новое, от уже известного с помощью учителя, добывать новые знания, находить ответы на вопросы учителя, используя учебник, свой жизненный опыт и информацию, полученную на уроке;
коммуникативные: умение с достаточной полнотой и
точностью выражать свои мысли, слушать
и понимать речь других, учиться работать
в паре, формулировать собственное
мнение.
Ход урока.
I. Организационный момент.
-Итак, друзья, внимание –
Садитесь правильно, начинаем наш урок.
Есть у математики молва,
Что она в порядок ум приводит,
Потому хорошие слова
Часто говорят о ней в народе.
Ты нам, математика, даёшь
Для победы важную закалку.
Учится с тобою молодёжь
Развивать и волю, и смекалку.
— соберитесь и ответьте мне, какие качества нам необходимо включить в работу, чтобы для всех этот урок стал полезным?
— Внимание.
— Старание.
— Хорошее настроение.
— Покажите смайликами ваше настроение?
Зеленый
— отличное, синий – не
очень, красный — плохое.
Древнегреческий поэт Нивей утверждал, что математику нельзя изучать, наблюдая, как это делает сосед.
— Почему он так говорил?
(ответы детей)
— Поэтому, каждый из вас должен работать на уроке в полную силу, слушать друг – друга внимательно, дополнять, выполнять все задания, а не смотреть, как работает сосед.
Оценивать себя вы будите по «Рабочей карте урока». Она есть у каждого из вас на парте. Сюда вы будете вносить свою отметку за каждый этап урока.
В конце урока подведете итог своей работы и выставите себе средний балл за урок, то есть за усвоение темы.
Кто знает, как работать с «Рабочей картой урока», покажите смайликом?
Да – зеленый, не уверен — синий, нет – красный.
Рабочая карта урока
(с/о – самооценка, о/т – оценка товарища)
Работа с классом с/о | Работа по рисунку в учебнике с/о | Работа
в паре. «Собери пару» о/т | Самостоятельная работа (дифференцированная) с/о | диктант. (графический) с/о | Итог. с/о |
II. Актуализация опорных знаний.
— ребята, повторим, то, что уже знаем?
— откройте тетради и начнем работать со мной.
— в тетрадях, отметим три точки, не лежащие на одной прямой, точку А, точку В и точку С и соединим их отрезками.
В
А С
—
вы изобразили фигуру у себя, а я заранее
на доске.
— посмотрите, какая фигура у меня получилась и проверьте себя.
— какую фигуру мы получили? (треугольник)
— почему эта фигура так называется?
(три угла, три вершины, три стороны)
— Приведите примеры, где встречаются треугольники в нашей повседневной жизни?
(примеры детей)
1. Треуго́льник — ударный музыкальный инструмент в виде металлического прута, изогнутого в форме треугольника. Один из углов оставлен открытым (концы прута почти касаются).
2. Начиная игру в бильярд, необходимо расположить шары в виде треугольника. Для этого используют специальную треугольную рамку.
3. Бермудский треугольник — район в Атлантическом океане, в котором происходят якобы таинственные исчезновения морских и воздушных судов. Район ограничен линиями от Флориды к Бермудским островам, далее к Пуэрто-Рико и назад к Флориде через Багамы
4.
Треугольники в конструкции мостов.
5. Высоковольтные линии электропередачи.
6. Треугольники делают конструкции надежными.
7. Настенные часы в виде треугольника
8. Детская игрушка пирамидка.
9. Детские спасательные круги в идее треугольника.
10. Женские украшения.
— посмотрите на наш треугольник.
— прочитайте, как называется построенный треугольник?
( ВСА, СВА ) и т. д.
— назовите углы этого треугольника?
— угол ( ВСА, СВА, АСВ).
— можно его назвать просто, угол А, угол В, угол С.
— вспомните, какие углы вы знаете?
(острый, тупой, прямой,)
— посмотрите на слайд и скажите.
— какие вы видите углы?
— покажите прямой угол.
— как можно это проверить? (с помощью треугольника, угольника)
— выйди к доске и проверь.
—
покажите тупой угол.
— как можно это проверить?
— выйди к доске и проверь.
— покажите острый угол.
— как можно это проверить?
— выйди к доске и проверь.
— а как называется вот этот угол, кто знает?
(развернутый)
— на что он похож?
(на веер)
— правильно.
— встаньте и покажите мне развернутый угол, с помощь рук.
— Что мы сейчас с вами повторили?
(острые, тупые, прямые, развернутые углы)
— оцените свою работу в рабочей карте.
III. Формирование новых знаний.
— подошло время узнать тему нашего урока.
— перед вами ребус, прочитав ребус, вы узнаете тему нашего урока.
Замените букву и на е, в первой цифре.
Виды.
— как называется тема нашего урока?
Тема урока «Виды треугольник».
— ребята, давайте поставим цель урок,
— продолжите фразу.
— что мы должны узнать в ходе урока?
— чему научимся?
— что попробуем выполнить?
Мы узнаем – какие виды треугольников бывают?
Мы научимся — различать разные виды треугольников?
Мы
попробуем применить на практике
наши знания в самостоятельной работе.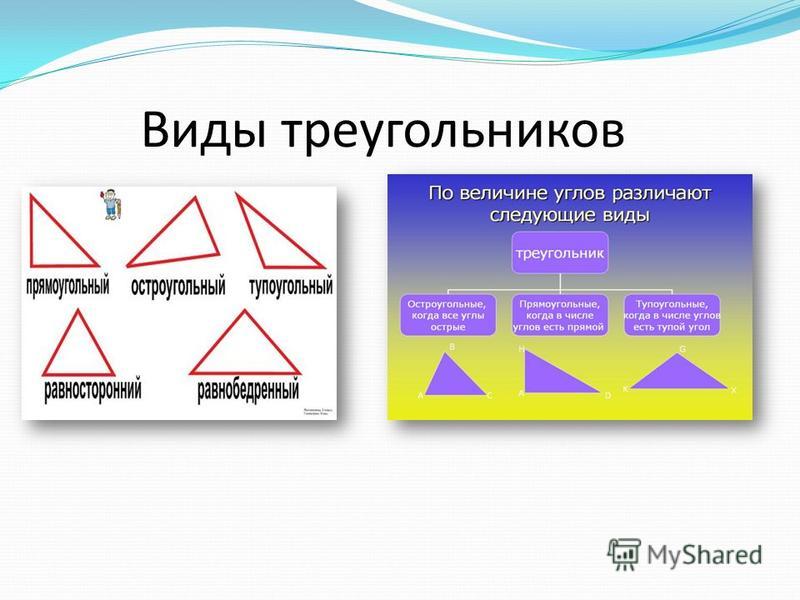
— давайте с вами узнаем, какие виды треугольников бывают?
— как вы думаете, кто нам может помочь в этом?
(учитель, учебник)
— правильно, с помощью учебника мы узнаем на уроке, какие виды треугольников бывают?
Учитель:
Если бы треугольники создали себе бога, он был бы с тремя сторонами. Сказал известный французский философ
Шарль Монтескьё
2. Работа по учебнику.
Откройте стр 4 учебника математика часть № 2
— Какие треугольники вы видите на рисунке, назовите их?
треугольник АВС, треугольник ДЕК, треугольник МТО.
— есть ли среди них треугольник с прямым углом? (да)
— назовите его? ДЕК
— назовите угол, который у него прямой? Е
— как вы определили, что угол Е, у него прямой?
— давайте проверим?
—
и так в треугольнике Е, прямой.
— как можно назвать этот треугольник? (прямоугольный)
(да – это прямоугольный треугольник)
— посмотрите и скажите, два других угла в этом треугольнике, какие? (острые)
— почему вы так решили?
— давайте проверим?
— посмотрите и скажите, есть ли среди этих треугольников треугольник с тупым углом? (да)
— назовите его? ТОМ
— какой угол у него тупой? (О)
— давайте проверим?
— какие два других угла в треугольнике ТОМ? (острые)
— давайте проверим.
— как мы можем назвать этот треугольник? (тупоугольный)
(да – это тупоугольный треугольник)
— а остался ли у нас еще треугольник?
— назовите его? АВС
— посмотрите и скажите, какие у него углы? (все острые)
— давайте проверим.
— как же мы, можем его назвать? (остроугольный)
— сделайте вывод, какие бывают треугольники в зависимости от их углов?
(тупоугольные, остроугольные, прямоугольные)
—
давайте узнаем, совпадает ли наш вывод
с выводом в учебнике.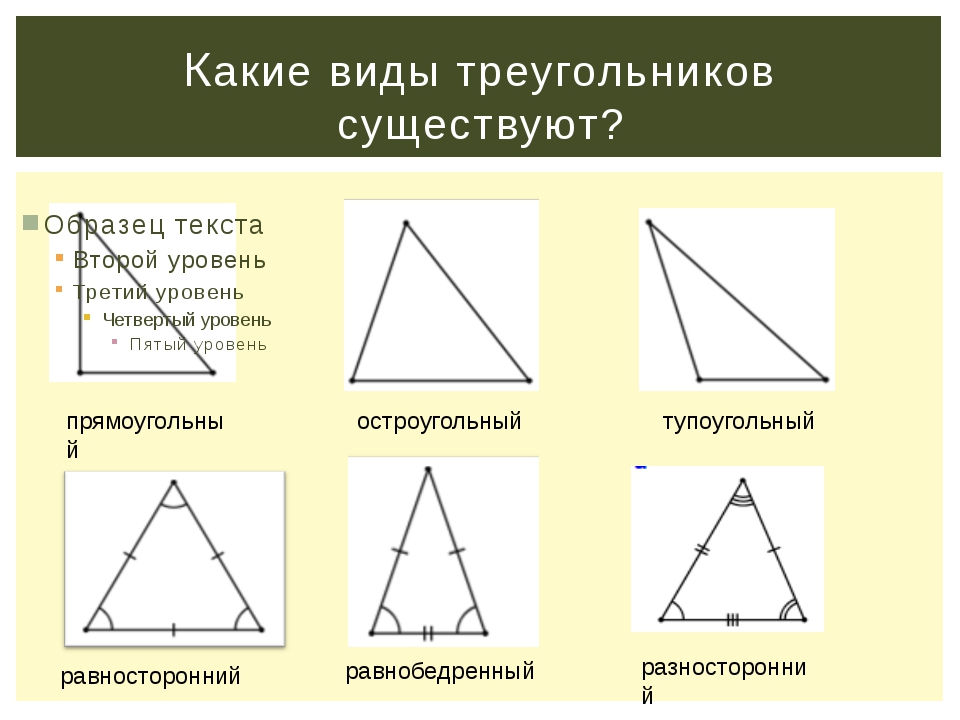
— прочитайте вывод в учебнике.
(читают вывод в учебнике стр 4)
— совпадает ли наш вывод с выводом учебника? (да)
— какие треугольники называются прямоугольными – есть прямой угол, остроугольными – есть острый угол, тупоугольными – есть тупой угол.
— покажите смайликами, как вы поняли этот материал?
— значит, первую цель мы с вами достигли.
— мы узнали, какие виды треугольников бывают?
— а теперь, мы с вами должны закрепить изученный материал, научится различать треугольники на практике по видам.
— посмотрите на странице 4 № 8.
— прочитайте задание.
— что нужно сделать в этом задании?
— выпишите сначала остроугольные, затем прямоугольные, а потом тупоугольные треугольники.
(самостоятельно выполняют работу)
Проверьте себя по слайду и поставьте отметку в карту.
Остроугольный – 6, 1
Прямоугольный
– 7, 4.
Тупоугольный – 2. 3, 5.
— отодвиньте учебник.
— Скажите, чему мы учились, работая с упражнением № 8 ?
— мы учились – различать виды треугольников
3. Первичное закрепление. (фронтальная работа)
Физкультминутка.
Полет – это математика. Писал советский летчик
Валерий Чкалов
Давайте попробуем, умеет ли ваша мысль летать, и проверим ваше внимание?
— встаньте ребята, когда я вам показываю тупоугольный треугольник – поднимите руки так, как будь-то, вы тянитесь к солнышку, когда я вам показываю остроугольный треугольник – поставьте ноги на ширину плеч, когда я вам покажу прямоугольный треугольник – вы вытяните руки вперед.
(показываю не путая детей, так как новый материал)
— мы с вами отдохнули и повторили, что, продолжите фразу?
— Повторили — виды треугольников
Оцените
свой ответ в таблице самостоятельно.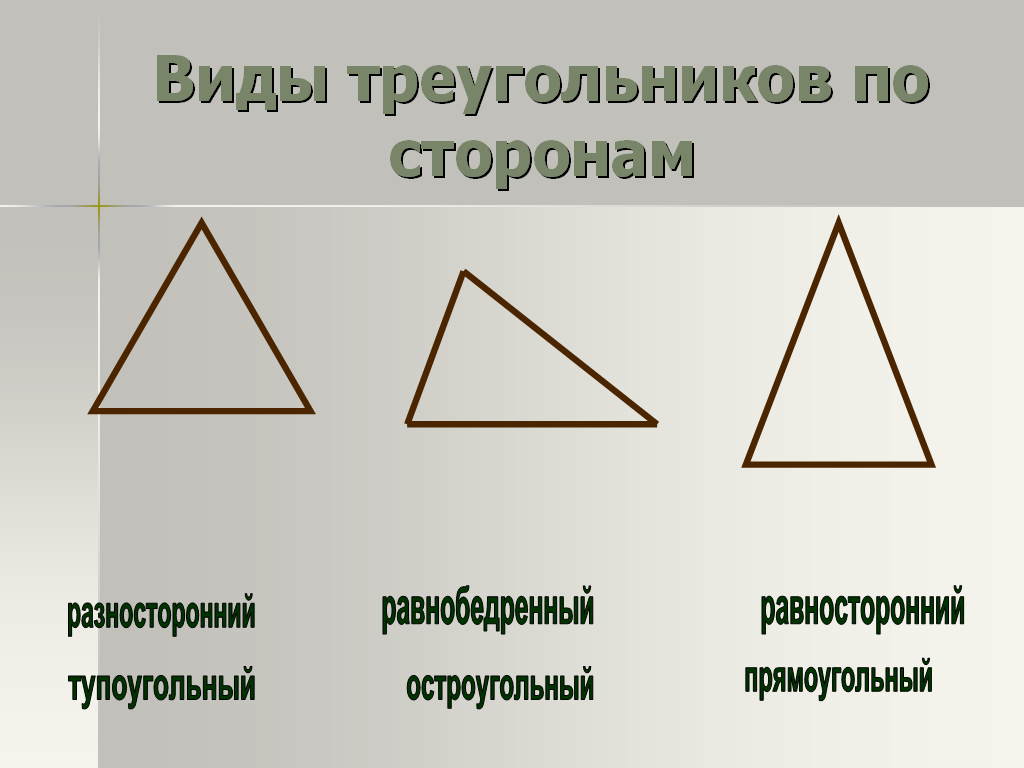
4. Работа в парах. (вторичное закрепление)
Величие человека — в его способности мыслить.
Писал великий французский ученый, математик
Блез Паскаль.
Давайте же с вами помыслим, работая в парах.
— Возьмите карточку с видами треугольников.
(соедините треугольник и объясните своему товарищу, почему именно этот треугольник называется тупоугольным, прямоугольным, остроугольным, работайте в парах по очереди, вспомните принципы работы в парах).
ВИДЫ ТРЕУГОЛЬНИКОВ
треугольник | Вид треугольника |
Остроугольный | |
Тупоугольный | |
Прямоугольный | |
—
проверьте полученный результат по
слайду.
— проверьте свою работу, поменяйтесь картами со своим товарищем и поставьте ему отметку.
— оцените работу в паре, было ли вам комфортно, понимал ли вас, товарищ?
Смайликом: отлично, не очень, плохо.
III. Закрепление изученного материала.
(самостоятельная работа)
Математика уступает свои крепости лишь сильным и смелым.
Писал о людях известный математик Андрей Григорьевич Конфорович.
Поднимите руку, кто считает себя сильным?
Перед вами Самостоятельная работа. Выберите себе уровень по силам. Если вы взяли сильный уровень, а почувствовали, что не справляетесь, можете поменять уровень в процессе работы, на тот который вам доступен.
(у каждого варианта 3 уровня, А, Б, С.)
А – уровень слабый на «3»,
Б – уровень средний на «4»,
В – уровень
сильный на «5».
У первого варианта свои уровни, у второго варианта свои уровни.
Ответы записывайте внизу. У вас при выполнении задания правильно получится имя мальчика или девочки.
.
Дифференцированная самостоятельная работа.
Самостоятельная работа
Вариант № 1
Уровень А (слабый) | Уровень Б (средний) | Уровень В (сильный) | |||||||||
1. Определи, какой это вид треугольника? А) остроугольный И) прямоугольный М) тупоугольный | 1. А) прямоугольный Ю) тупоугольный Н) остроугольный | 1. Дострой по данным вершинам треугольник, определи вид получившегося треугольника? . . . О) прямоугольный В) остроугольный Е) тупоугольный | |||||||||
2. определи сколько треугольников на рисунке? Р) 3 , Б) 2, К) 6 . | 2. Определи сколько треугольников на рисунке? М) 4 Л) 6 Н) 5 | 2. треугольников на рисунке? К) 3, Д) 4, Л) 5. | |||||||||
3. Может ли в треугольнике быть два тупых угла? К) да, Л) не знаю, А) нет. | 3. Может ли быть в треугольнике два тупых угла. Г) да, Я) нет, В) не знаю. | 3. Может ли в треугольнике быть один угол прямой, другой угол тупой, а третий острый? М) да, Я) нет, Ф) не знаю. | |||||||||
ОТВЕТ: | и | р | а | ОТВЕТ: | ю | л | я | ОТВЕТ: | о | л | я |
Самостоятельная работа
Вариант № 2
Уровень А (слабый) | Уровень Б (средний) | Уровень В (сильный) | |||||||||
1. А) тупоугольный Ю) остроугольный В) прямоугольный | 1. Дострой треугольник до логического завершения, определи, какой вид треугольника у тебя получился? К ) тупоугольный М) тупоугольный Я) прямоугольный | 1. Дострой по данным вершинам треугольник до логического завершения, определи, какой вид треугольника получился? . . . З) остроугольный Р) тупоугольный М) прямоугольный | |||||||||
2. Определи, сколько треугольников на рисунке? И)
4 , Д) 1, Р) 3. | 2. Определи, сколько треугольников на рисунке? Н) 5, Г) 4, Д) 3. | 2. Определи, сколько треугольников на рисунке? А) 7 Б) 8 В) 10 | |||||||||
3. Может ли в треугольнике быть три острых угла? А) да Г) не знаю Е) нет. | 3. Может ли в треугольнике быть два прямых угла? У) да, С) не знаю, А) нет. | 3. Может ли быть в треугольнике один угол тупой, другой угол прямой, а третий угол острый? Я) нет, М) да, Т) не знаю. | |||||||||
ОТВЕТ: | Ю | Р | А | ОТВЕТ: | Я | Н | А | ОТВЕТ: | Р | А | Я |
—
посмотрите на слайд.
— проверьте свои ответы.
Поставьте себе в таблицу отметку, за эту работу.
IV. Подведение итога урока.
— вспомните, какие цели мы ставили на уроке?
— продолжите фразу.
Мы узнали — какие виды треугольников бывают?
Мы научились — различать разные виды треугольников?
Мы применили — на практике знания в самостоятельной работе.
— какие качества вам помогли сегодня на уроке?
— Внимание.
— Старание.
— Хорошее настроение.
— давайте поставим отметку себе за урок.
— Покажите смайликами ваше настроение в конце урока?
Зеленый — отличное, синий – не очень, красный — плохое.
V. Домашнее задание. (деференцированное с учетом способностей детей)
— учитель комментирует данное задание, перед тем как его дать, каждое упражнение.
—
запишите домашнее задание.
Д/З стр 4, № 12 или если вам тяжело выполнить задание, то сочините сказку о треугольниках, стр 5 № 15 (1 строка)
| Признаки равенства прямоугольных треугольников |
| Рисунок | Тип треугольника | Определение |
| Остроугольный треугольник | Треугольник, у которого все углы острые , называют остроугольным | |
| Прямоугольный треугольник | Треугольник, у которого один из углов прямой , называют прямоугольным | |
| Тупоугольный треугольник | Треугольник, у которого один из углов тупой , называют тупоугольным |
| Остроугольный треугольник |
Определение: Треугольник, у которого все углы острые , называют остроугольным |
| Прямоугольный треугольник |
Определение: Треугольник, у которого один из углов прямой , называют прямоугольным |
| Тупоугольный треугольник |
Определение: Треугольник, у которого один из углов тупой , называют тупоугольным |
В зависимости от длин сторон выделяют два важных типа треугольников.
Таблица 2 – Равнобедренный и равносторонний треугольники
| Рисунок | Тип треугольника | Определение |
| Равнобедренный треугольник | боковыми сторонами , а третью сторону называют основанием равнобедренного треугольника | |
| Равносторонний (правильный) треугольник | Треугольник, у которого все три стороны равны, называют равносторонним или правильным треугольником |
| Равнобедренный треугольник |
Определение: Треугольник, у которого две стороны равны, называют равнобедренным треугольником. В этом случае две равные стороны называют боковыми сторонами , а третью сторону называют основанием равнобедренного треугольника |
| Равносторонний (правильный) треугольник |
Определение: Треугольник, у которого все три стороны равны, называют равносторонним или правильным треугольником |
Признаки равенства треугольников
Треугольники называют равными
, если их можно совместить наложением .
В таблице 3 приведены признаки равенства треугольников .
Таблица 3 – Признаки равенства треугольников
| Рисунок | Название признака | Формулировка признака |
| по двум сторонам и углу между ними | ||
| Признак равенства треугольников по стороне и двум прилежащим к ней углам | ||
| Признак равенства треугольников по трём сторонам |
| Признак равенства треугольников по двум сторонам и углу между ними |
| Формулировка признака . Если две стороны одного треугольника и угол между ними соответственно равны двум сторонам другого треугольника и углу между ними, то такие треугольники равны |
| Признак равенства треугольников по стороне и двум прилежащим к ней углам |
Формулировка признака . Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны |
| Признак равенства треугольников по трём сторонам |
| Формулировка признака . Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны |
Признаки равенства прямоугольных треугольников
Для сторон прямоугольных треугольников принято использовать следующие названия.
Гипотенузой называют сторону прямоугольного треугольника, лежащую против прямого угла (рис. 2), две другие стороны называют катетами .
Таблица 4 – Признаки равенства прямоугольных треугольников
| Признак равенства прямоугольных треугольников по двум катетам |
Формулировка признака .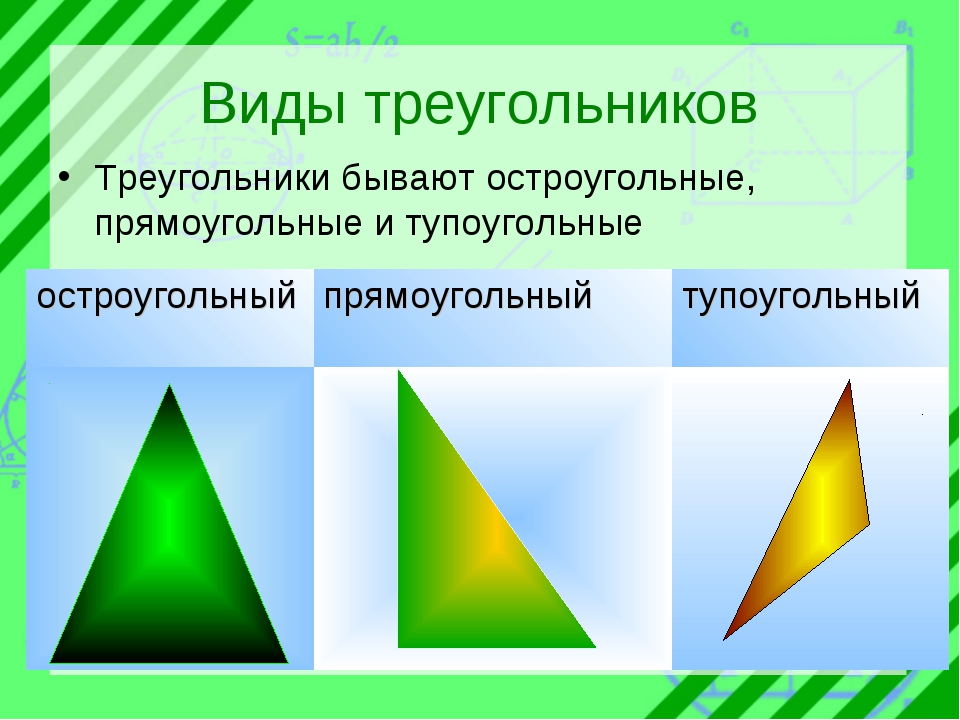 Если два катета одного прямоугольного треугольника соответственно равны двум катетам другого прямоугольного треугольника, то такие прямоугольные треугольники равны |
| Признак равенства прямоугольных треугольников по катету и прилежащему острому углу |
| Формулировка признака . Если катет и прилежащий к нему острый угол одного прямоугольного треугольника соответственно равны катету и прилежащему к нему острому углу другого прямоугольного треугольника, то такие прямоугольные треугольники равны |
| Признак равенства прямоугольных треугольников по катету и противолежащему острому углу |
Самый простой многоугольник, который изучается в школе — это треугольник. Он более понятен для учащихся и встречает меньше трудностей. Несмотря на то что существуют различные виды треугольников, у которых имеются особенные свойства.
Какая фигура называется треугольником?
Образованная тремя точками и отрезками. Первые называются вершинами, вторые — сторонами. Причем все три отрезка должны быть соединены, чтобы между ними образовывались углы. Отсюда и название фигуры «треугольник».
Первые называются вершинами, вторые — сторонами. Причем все три отрезка должны быть соединены, чтобы между ними образовывались углы. Отсюда и название фигуры «треугольник».
Различия в названиях по углам
Поскольку они могут быть острыми, тупыми и прямыми, то и виды треугольников определяются по этим названиям. Соответственно, групп таких фигур три.
- Первая. Если все углы треугольника острые, то он будет иметь название остроугольного. Все логично.
- Вторая. Один из углов тупой, значит треугольник тупоугольный. Проще некуда.
- Третья. Имеется угол, равный 90 градусам, который называется прямым. Треугольник становится прямоугольным.
Различия в названиях по сторонам
В зависимости от особенностей сторон выделяют такие виды треугольников:
общий случай — разносторонний, в котором все стороны имеют произвольную длину;
равнобедренный, у двух сторон которого имеются одинаковые числовые значения;
равносторонний, длины всех его сторон одинаковые.
Если в задаче не указан конкретный вид треугольника, то нужно чертить произвольный. У которого все углы острые, а стороны имеют разную длину.
Свойства, общие для всех треугольников
- Если сложить все углы треугольника, то получится число, равное 180º. И неважно, какого он вида. Это правило действует всегда.
- Числовое значение любой стороны треугольника меньше, чем сложенные вместе две другие. При этом она же больше, чем их разность.
- Каждый внешний угол имеет значение, которое получается при сложении двух внутренних, не смежных с ним. Причем он всегда больше, чем смежный с ним внутренний.
- Напротив меньшей стороны треугольника всегда лежит самый маленький угол. И наоборот, если сторона большая, то и угол будет самым большим.
Эти свойства справедливы всегда, какие бы виды треугольников ни рассматривались в задачах. Все остальные вытекают из конкретных особенностей.
Свойства равнобедренного треугольника
- Углы, которые прилегают к основанию, равны.

- Высота, которая проведена к основанию, является также медианой и биссектрисой.
- Высоты, медианы и биссектрисы, которые построены к боковым сторонам треугольника, соответственно равны друг другу.
Свойства равностороннего треугольника
Если имеется такая фигура, то будут верны все свойства, описанные немного выше. Потому что равносторонний всегда будет равнобедренным. Но не наоборот, равнобедренный треугольник не обязательно будет равносторонним.
- Все его углы равны друг другу и имеют значение 60º.
- Любая медиана равностороннего треугольника является его высотой и биссектрисой. Причем они все равны друг другу. Для определения их значений существует формула, которая состоит из произведения стороны на квадратный корень из 3, деленного на 2.
Свойства прямоугольного треугольника
- Два острых угла дают в сумме значение в 90º.
- Длина гипотенузы всегда больше, чем у любого из катетов.
- Числовое значение медианы, проведенной к гипотенузе, равно ее половине.

- Этому же значению равен катет, если он лежит напротив угла в 30º.
- Высота, которая проведена из вершины со значением 90º, имеет определенную математическую зависимость от катетов: 1/н 2 = 1/а 2 + 1/в 2 . Здесь: а, в — катеты, н — высота.
Задачи с разными видами треугольников
№1. Дан равнобедренный треугольник. Его периметр известен и равен 90 см. Требуется узнать его стороны. В качестве дополнительного условия: боковая сторона меньше основания в 1,2 раза.
Значение периметра напрямую зависит от тех величин, которые нужно найти. Сумма всех трех сторон и даст 90 см. Теперь нужно вспомнить признак треугольника, по которому он является равнобедренным. То есть две стороны равны. Можно составить уравнение с двумя неизвестными: 2а + в = 90. Здесь а — боковая сторона, в — основание.
Настала очередь дополнительного условия. Следуя ему, получается второе уравнение: в = 1,2а. Можно выполнить подстановку этого выражения в первое. Получится: 2а + 1,2а = 90.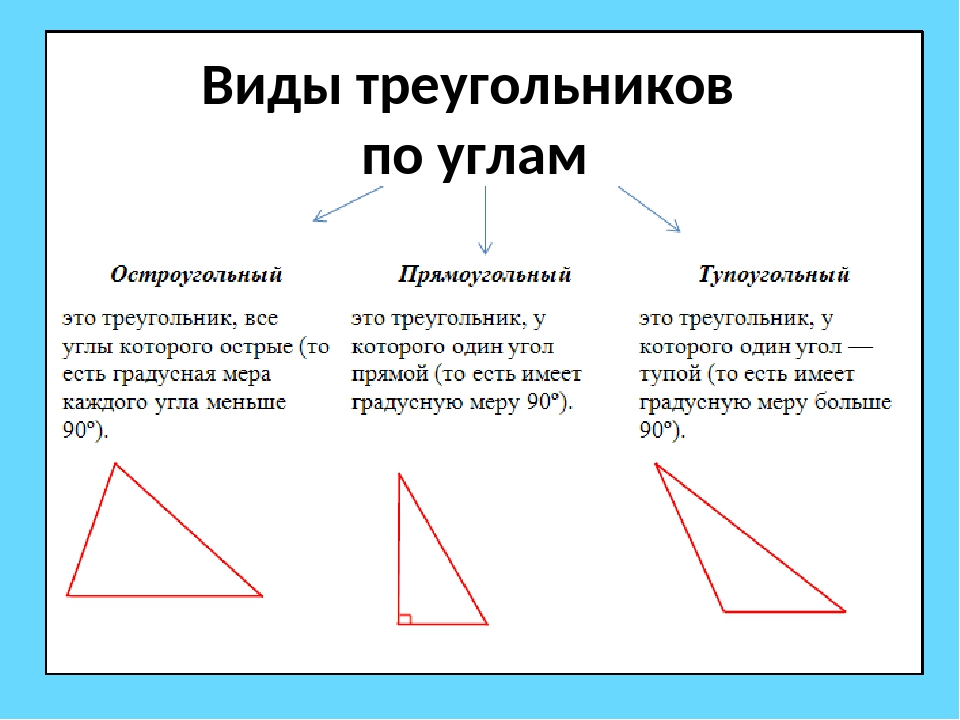 После преобразований: 3,2а = 90. Отсюда а = 28,125 (см). Теперь несложно узнать основание. Лучше всего это сделать из второго условия: в = 1,2 * 28,125 = 33,75 (см).
После преобразований: 3,2а = 90. Отсюда а = 28,125 (см). Теперь несложно узнать основание. Лучше всего это сделать из второго условия: в = 1,2 * 28,125 = 33,75 (см).
Для проверки можно сложить три значения: 28,125 * 2 + 33,75 = 90 (см). Все верно.
Ответ: стороны треугольника равны 28,125 см, 28,125 см, 33,75 см.
№2. Сторона равностороннего треугольника равна 12 см. Нужно вычислить его высоту.
Решение. Для поиска ответа достаточно вернуться к тому моменту, где были описаны свойства треугольника. Так указана формула для нахождения высоты, медианы и биссектрисы равностороннего треугольника.
н = а * √3 / 2, где н — высота, а — сторона.
Подстановка и вычисление дают такой результат: н = 6 √3 (см).
Эту формулу необязательно запоминать. Достаточно вспомнить, что высота делит треугольник на два прямоугольных. Причем она оказывается катетом, а гипотенуза в нем — это сторона исходного, второй катет — половина известной стороны. Теперь нужно записать теорему Пифагора и вывести формулу для высоты.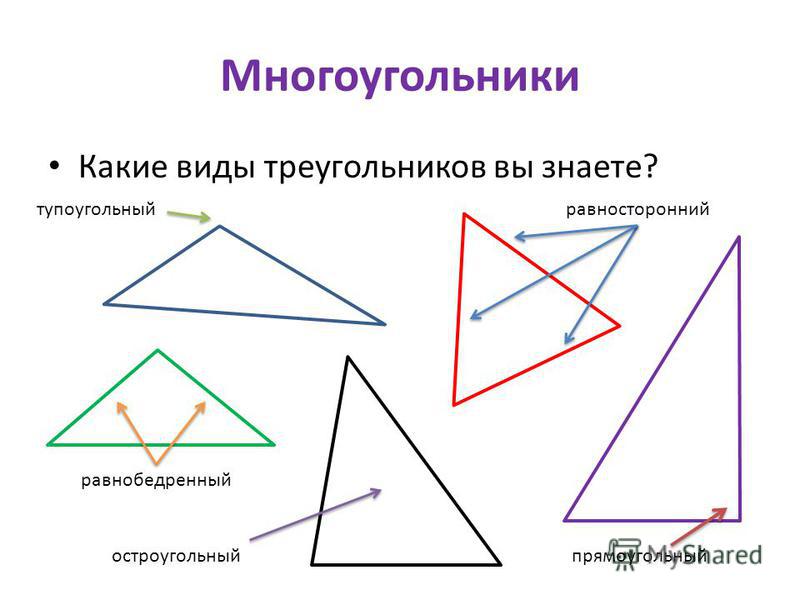
Ответ: высота равна 6 √3 см.
№3. Дан МКР — треугольник, 90 градусов в котором составляет угол К. Известны стороны МР и КР, они равны соответственно 30 и 15 см. Нужно узнать значение угла Р.
Решение. Если сделать чертеж, то становится ясно, что МР — гипотенуза. Причем она в два раза больше катета КР. Снова нужно обратиться к свойствам. Одно из них как раз связано с углами. Из него понятно, что угол КМР равен 30º. Значит искомый угол Р будет равен 60º. Это следует из другого свойства, которое утверждает, что сумма двух острых углов должна равняться 90º.
Ответ: угол Р равен 60º.
№4. Нужно найти все углы равнобедренного треугольника. Про него известно, что внешний угол от угла при основании равен 110º.
Решение. Поскольку дан только внешний угол, то этим и нужно воспользоваться. Он образует с внутренним углом развернутый. Значит в сумме они дадут 180º. То есть угол при основании треугольника будет равен 70º. Так как он равнобедренный, то второй угол имеет такое же значение.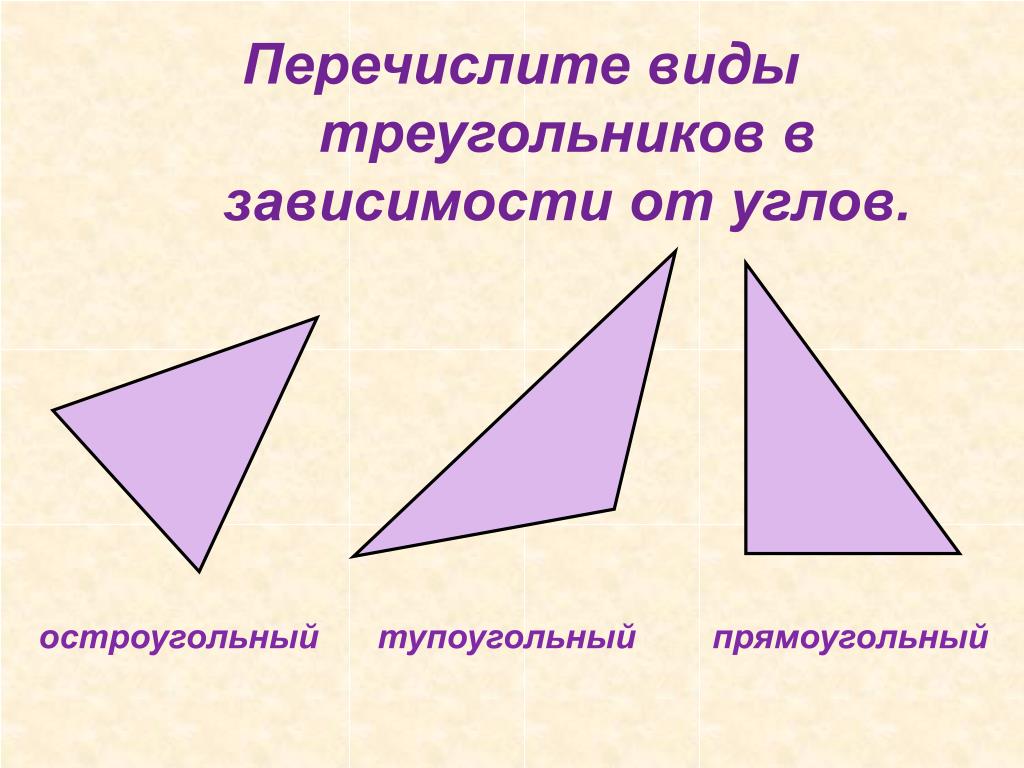 Осталось вычислить третий угол. По свойству, общему для всех треугольников, сумма углов равна 180º. Значит, третий определится как 180º — 70º — 70º = 40º.
Осталось вычислить третий угол. По свойству, общему для всех треугольников, сумма углов равна 180º. Значит, третий определится как 180º — 70º — 70º = 40º.
Ответ: углы равны 70º, 70º, 40º.
№5. Известно, что в равнобедренном треугольнике угол, лежащий напротив основания, равен 90º. На основании отмечена точка. Отрезок, соединяющий ее с прямым углом, делит его в отношении 1 к 4. Нужно узнать все углы меньшего треугольника.
Решение. Один из углов можно определить сразу. Поскольку треугольник прямоугольный и равнобедренный, то те, что лежат у его основания, будут по 45º, то есть по 90º/2.
Второй из них поможет найти известное в условии отношение. Поскольку оно равно 1 к 4, то частей, на которые он делится получается всего 5. Значит, чтобы узнать меньший угол треугольника нужно 90º/5 = 18º. Осталось узнать третий. Для этого из 180º (суммы всех углов треугольника) нужно вычесть 45º и 18º. Вычисления несложные, и получится: 117º.
Еще дети дошкольного возраста знают, как выглядит треугольник. А вот с тем, какие они бывают, ребята уже начинают разбираться в школе. Одним из видов является тупоугольный треугольник. Понять, что это такое, проще всего, если увидеть картинку с его изображением. А в теории это так называют «простейший многоугольник» с тремя сторонами и вершинами, одна из которых является
А вот с тем, какие они бывают, ребята уже начинают разбираться в школе. Одним из видов является тупоугольный треугольник. Понять, что это такое, проще всего, если увидеть картинку с его изображением. А в теории это так называют «простейший многоугольник» с тремя сторонами и вершинами, одна из которых является
Разбираемся с понятиями
В геометрии различают такие виды фигур с тремя сторонами: остроугольный, прямоугольный и тупоугольный треугольники. При этом свойства этих простейших многоугольников одинаковы для всех. Так, для всех перечисленных видов будет соблюдаться такое неравенство. Сумма длин любых двух сторон обязательно будет больше протяженности третьей стороны.
Но для того чтобы быть уверенным, что речь идет именно о законченной фигуре, а не о наборе отдельных вершин, необходимо проверить, чтобы соблюдалось основное условие: сумма углов тупоугольного треугольника равняется 180 о. Это же верно и для других видов фигур с тремя сторонами. Правда, в тупоугольном треугольнике один из углов будет еще больше 90 о, а два оставшихся обязательно будут острыми. При этом именно наибольший угол будет находиться напротив самой длинной стороны. Правда, это далеко не все свойства тупоугольного треугольника. Но и зная лишь эти особенности, школьники могут решать многие задачи по геометрии.
При этом именно наибольший угол будет находиться напротив самой длинной стороны. Правда, это далеко не все свойства тупоугольного треугольника. Но и зная лишь эти особенности, школьники могут решать многие задачи по геометрии.
Для каждого многоугольника с тремя вершинами верно и то, что, продолжая любую из сторон, мы получим угол, размер которого будет равен сумме двух несмежных с ним внутренних вершин. Периметр тупоугольного треугольника рассчитывается так же, как и для других фигур. Он равняется сумме длин всех его сторон. Для определения математиками были выведены различные формулы, в зависимости от того, какие изначально присутствуют данные.
Правильное начертание
Одним из важнейших условий решения задач по геометрии является верный рисунок. Часто учителя математики говорят о том, что он поможет не только наглядно представить, что дано и что от вас требуется, но на 80% приблизиться к правильному ответу. Именно поэтому важно знать, как построить тупоугольный треугольник. Если вам нужна просто гипотетическая фигура, то вы можете нарисовать любой многоугольник с тремя сторонами так, чтобы один из углов был больше 90 о.
Если вам нужна просто гипотетическая фигура, то вы можете нарисовать любой многоугольник с тремя сторонами так, чтобы один из углов был больше 90 о.
Если даны определенные значения длин сторон или градусы углов, то чертить тупоугольный треугольник необходимо в соответствии с ними. При этом необходимо стараться максимально точно изобразить углы, высчитывая их при помощи транспортира, и пропорционально данным в задании условиям отобразить стороны.
Основные линии
Зачастую школьникам мало знать только то, как должны выглядеть те или иные фигуры. Они не могут ограничиться лишь информацией о том, какой треугольник тупоугольный, а какой прямоугольный. Курсом математики предусмотрено, что их знания об основных особенностях фигур должны быть более полными.
Так, каждому школьнику должно быть понятно определение биссектрисы, медианы, серединного перпендикуляра и высоты. Кроме того, он должен знать и их основные свойства.
Так, биссектрисы делят угол пополам, а противоположную сторону — на отрезки, которые пропорциональны прилегающим сторонам.
Медиана делит любой треугольник на два равных по площади. В точке, в которой они пересекаются, каждая из них разбивается на 2 отрезка в пропорции 2: 1, если смотреть от вершины, из которой она вышла. При этом большая медиана всегда проведена к его наименьшей стороне.
Не меньше внимания уделяется и высоте. Это перпендикуляр к противоположной от угла стороне. Высота тупоугольного треугольника имеет свои особенности. Если она проведена из острой вершины, то она попадает не на сторону этого простейшего многоугольника, а на ее продолжение.
Серединный перпендикуляр — это отрезок, который выходит из центра грани треугольника. При этом он расположен к ней под прямым углом.
Работа с окружностями
В начале изучения геометрии детям достаточно понять, как начертить тупоугольный треугольник, научиться отличать его от остальных видов и запомнить его основные свойства. А вот старшеклассникам этих знаний уже мало. Например, на ЕГЭ часто встречаются вопросы про описанные и вписанные окружности. Первая из них касается всех трех вершин треугольника, а вторая имеет по одной общей точке со всеми сторонами.
Первая из них касается всех трех вершин треугольника, а вторая имеет по одной общей точке со всеми сторонами.
Построить вписанный или описанный тупоугольный треугольник уже намного сложнее, ведь для этого необходимо для начала выяснить, где должен находиться центр окружности и ее радиус. Кстати, необходимым инструментом станет в этом случае не только карандаш с линейкой, но и циркуль.
Те же сложности возникают при построении вписанных многоугольников с тремя сторонами. Математиками были выведены различные формулы, которые позволяют определить их месторасположение максимально точно.
Вписанные треугольники
Как уже было сказано ранее, если круг проходит через все три вершины, то это называется описанной окружностью. Главным ее свойством является то, что она единственная. Чтобы выяснить, как должна располагаться описанная окружность тупоугольного треугольника, необходимо помнить, что ее центр находится на пересечении трех серединных перпендикуляров, которые идут к сторонам фигуры. Если в остроугольном многоугольнике с тремя вершинами эта точка будет находиться внутри него, то в тупоугольном — за его пределами.
Если в остроугольном многоугольнике с тремя вершинами эта точка будет находиться внутри него, то в тупоугольном — за его пределами.
Зная, например, что одна из сторон тупоугольного треугольника равна его радиусу, можно найти угол, который лежит напротив известной грани. Его синус будет равен результату от деления длины известной стороны на 2R (где R — это радиус окружности). То есть sin угла будет равен ½. Значит, угол будет равен 150 о.
Если вам необходимо найти радиус описанной окружности тупоугольного треугольника, то вам пригодятся сведения о длине его сторон (c, v, b) и его площади S. Ведь радиус высчитывается так: (c х v х b) : 4 х S. Кстати, неважно, какого именно у вас вида фигура: разносторонний тупоугольный треугольник, равнобедренный, прямо- или остроугольный. В любой ситуации, благодаря приведенной формуле, вы можете узнать площадь заданного многоугольника с тремя сторонами.
Описанные треугольники
Также довольно часто приходится работать со вписанными окружностями. По одной из формул, радиус такой фигуры, умноженный на ½ периметра, будет равняться площади треугольника. Правда, для ее выяснения вам необходимо знать стороны тупоугольного треугольника. Ведь для того чтобы определить ½ периметра, необходимо сложить их длины и разделить на 2.
По одной из формул, радиус такой фигуры, умноженный на ½ периметра, будет равняться площади треугольника. Правда, для ее выяснения вам необходимо знать стороны тупоугольного треугольника. Ведь для того чтобы определить ½ периметра, необходимо сложить их длины и разделить на 2.
Чтобы понять, где должен находиться центр круга, вписанного в тупоугольный треугольник, необходимо провести три биссектрисы. Это линии, которые делят углы пополам. Именно на их пересечении и будет находиться центр окружности. При этом он будет равноудален от каждой из сторон.
Радиус такой окружности, вписанной в тупоугольный треугольник, равняется из частного (p-c) х (p-v) х (p-b) : p. При этом p — это полупериметр треугольника, c, v, b — его стороны.
Пожалуй, самой основной, простой и интересной фигурой в геометрии является треугольник. В курсе средней школы изучаются его основные свойства, однако иногда знания по этой теме формируются неполными. Виды треугольников изначально определяют их свойства. Но подобное представление остается смешанным. Поэтому сейчас разберем немного подробнее эту тему.
Но подобное представление остается смешанным. Поэтому сейчас разберем немного подробнее эту тему.
Виды треугольников зависят от градусной меры углов. Эти фигуры бывают остро-, прямо- и тупоугольными. Если все углы не превышают значения в 90 градусов, то фигуру смело можно назвать остроугольной. Если хотя бы один угол треугольника равен 90 градусам, то вы имеете дело с прямоугольным подвидом. Соответственно, во всех остальных случаях рассматриваемую называют тупоугольной.
Существует множество задач для остроугольных подвидов. Отличительной чертой является внутреннее местонахождение точек пересечения биссектрис, медиан и высот. В других случаях это условие может не выполняться. Определить тип фигуры “треугольник” нетрудно. Достаточно знать, например, косинус каждого угла. Если какие-нибудь значения меньше нуля, значит, треугольник в любом случае является тупоугольным. В случае нулевого показателя фигура обладает прямым углом. Все положительные значения гарантированно подскажут вам о том, что перед вами остроугольный вид.
Нельзя не сказать о правильном треугольнике. Это самый идеальный вид, где совпадают все точки пересечения медиан, биссектрис и высот. Центр вписанной и описанной окружности лежит также в одном месте. Для решения задач необходимо знать только одну сторону, так как вам углы изначально заданы, а две другие стороны известной. То есть фигура задается только одним параметром. Существуют Их главная особенность — равенство двух сторон и углов при основании.
Иногда встречается вопрос о том, существует ли треугольник с заданными сторонами. На самом деле вас спрашивают, подходит ли данное описание под основные виды. Например, если сумма двух сторон меньше третьей, то в реальности такой фигуры не существует вообще. Если в задании просят найти косинусы углов треугольника со сторонами 3,5,9, то здесь очевидный можно объяснить без сложных математических приемов. Предположим, вы хотите из пункта A попасть в пункт B. Расстояние по прямой равно 9 километрам. Однако вы вспомнили, что необходимо зайти в пункт C в магазин. Расстояние от А до С равно 3 километрам, а от С до В — 5. Таким образом получается, что, двигаясь через магазин, вы пройдете на один километр меньше. Но так как пункт C не расположен на прямой AB, то вам придется пройти лишнее расстояние. Здесь возникает противоречие. Это, конечно, условное объяснение. Математика знает не один способ доказательства того, что все виды треугольников подчиняются основному тождеству. Оно гласит о том, что сумма двух сторон больше длины третьей.
Расстояние от А до С равно 3 километрам, а от С до В — 5. Таким образом получается, что, двигаясь через магазин, вы пройдете на один километр меньше. Но так как пункт C не расположен на прямой AB, то вам придется пройти лишнее расстояние. Здесь возникает противоречие. Это, конечно, условное объяснение. Математика знает не один способ доказательства того, что все виды треугольников подчиняются основному тождеству. Оно гласит о том, что сумма двух сторон больше длины третьей.
Любой вид обладает следующими свойствами:
1) Сумма всех углов равняется 180 градусам.
2) Всегда существует ортоцентр — точка пересечения всех трех высот.
3) Все три медианы, проведенные из вершин внутренних углов, пересекаются в одном месте.
4) Вокруг любого треугольника можно описать окружность. Также можно вписать круг так, чтобы он имел только три точки соприкосновения и не выходил за внешние стороны.
Теперь вы познакомились с основными свойствами, которыми обладают различные виды треугольников. В будущем важно понимать, с чем вы имеете дело при решении задачи.
В будущем важно понимать, с чем вы имеете дело при решении задачи.
Треугольник — определение и общие понятия
Треугольник – это такой простой многоугольник, состоящий из трех сторон и имеющий столько же углов. Его плоскости ограничиваются 3 точками и 3 отрезками, попарно соединяющими даные точки.
Все вершины любого треугольника, независимо от его разновидности, обозначаются заглавными латинскими буквами, а его стороны изображаются соответствующими обозначениями противоположных вершин, только не большими буквами, а малыми. Так, например, треугольник с вершинами обозначенными буквами А, В и С имеет стороны a, b, c.
Если рассматривать треугольник в евклидовом пространстве, то это такая геометрическая фигура, которая образовалась с помощью трех отрезков, соединяющих три точки, которые не лежат на одной прямой.
Посмотрите внимательно на рисунок, который изображен вверху. На нем точки А, В и С являются вершинами этого треугольника, а его отрезки носят названия сторон треугольника. Каждая вершина этого многоугольника образует внутри его углы.
Каждая вершина этого многоугольника образует внутри его углы.
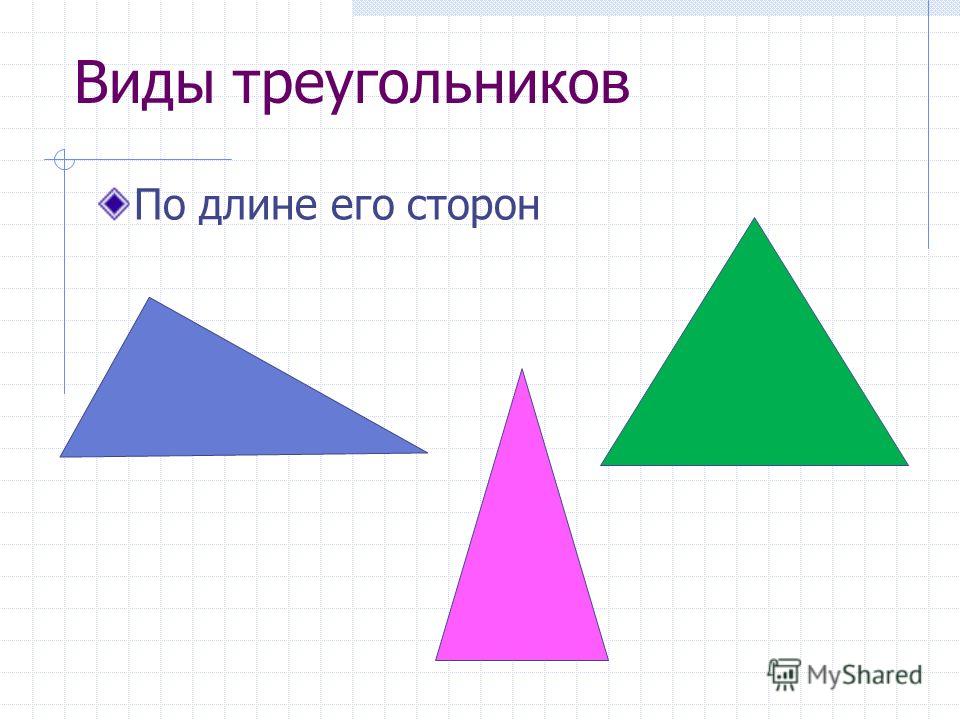
Виды треугольников
Согласно величины, углов треугольников, они делятся на такие разновидности, как:
Прямоугольные;
Остроугольные;
Тупоугольные.
К прямоугольным принадлежат такие треугольники, у которых в наличии есть один прямой угол, а остальные два имеют острые углы.
Остроугольные треугольники – это те, у которых все его углы острые.
А если у треугольника имеется один тупой угол, а два остальных угла острые, то такой треугольник относится к тупоугольным.
Каждый из вас прекрасно понимает, что не все треугольники имеют равные стороны. И соответственно тому, какую длину имеют его стороны, треугольники можно поделить на:
Равнобедренные;
Равносторонние;
Разносторонние.
Задание: Нарисуйте разные виды треугольников. Дайте им определение. Какое между ними отличие вы видите?
Основные свойства треугольников
Хотя эти простые многоугольники могут отличаться друг от друга величиной углов или сторон, но в каждом треугольнике есть основные свойства, характерны для этой фигуры.
В любом треугольнике:
Общая сумма всех его углов равняется 180º.
Если он принадлежит к равносторонним, то каждый его угол равен 60º.
Равносторонний треугольник имеет одинаковые и ровные между собой углы.
Чем меньше сторона многоугольника, тем меньший угол расположен напротив него и наоборот напротив большей стороны находиться больший угол.
Если стороны равные, то напротив них расположены равные углы, и наоборот.
Если взять треугольник и продлить его сторону, то в итоге мы образуется внешний угол. Он равен сумме внутренних углов.
В любом треугольнике его сторона, независимо от того, какую бы вы не выбрали, все равно будет меньше, чем сумма 2-х других сторон, но больше чем их разность:
1. a b – c;
2. b a – c;
3. c a – b.
Задание
В таблице приведены уже известные два угла треугольника. Зная общую сумму всех углов найдите, чему равен третий угол треугольника и занесите в таблицу:
1. Сколько градусов имеет третий угол?
2. К какому виду треугольников он относится?
К какому виду треугольников он относится?
Признаки равности треугольников
I признак
II признак
III признак
Высота, биссектриса и медиана треугольника
Высота треугольника — перпендикуляр, проведенный из вершины фигуры к его противоположной стороне, называется высотой треугольника. Все высоты треугольника пересекаются в одной точке. Точка пересечения всех 3-х высот треугольника является его ортоцентром.
Отрезок, проведенный из данной вершины и соединяющий ее на средине противоположной стороны, является медианой. Медианы, также как и высоты треугольника, имеют одну общую точку пересечения, так называемый центр тяжести треугольника или центроид.
Биссектриса треугольника — отрезок, соединяющий вершину угла и точку противоположной стороны, а также делящий этот угол пополам. Все биссектрисы треугольника пересекаются в одной точке, которую называют центром окружности, вписанной в треугольник.
Отрезок, который соединяет середины 2-х сторон треугольника, называется средней линией.
Историческая справка
Такая фигура, как треугольник, была известна еще в Древние времена. Об этой фигуре и ее свойствах упоминалось на египетских папирусах четырех тысячелетней давности. Немного позже, благодаря теореме Пифагора и формуле Герона, изучение свойства треугольника, перешло на более высокий уровень, но все же, это происходило более двух тысяч лет назад.
В XV – XVI веках стали проводить много исследований о свойствах треугольника и в итоге возникла такая наука, как планиметрия, которая получила название «Новая геометрия треугольника».
Ученый из России Н. И.Лобачевский внес огромный вклад в познание свойств треугольников. Его труды в дальнейшем нашли применение как в математике, так и физике и кибернетике.
Благодаря знаниям свойств треугольников возникла и такая наука, как тригонометрия. Она оказалась необходимой для человека в его практических потребностях, так как ее применение просто необходимо при составлении карт, измерении участков, да и при конструировании различных механизмов.
А какой самый известный треугольник вы знаете? Это конечно же Бермудский треугольник! Он получил такое название в 50-х годах из-за географического расположения точек (вершин треугольника), внутри которых, согласно существующей теории, возникали связанные с ним аномалии. Вершинами Бермудского треугольника выступают Бермудские острова, Флорида и Пуэрто-Рико.
Задание: А какие теории о Бермудском треугольнике слышали вы?
А известно ли вам, что в теории Лобачевского при сложении углов треугольника их сумма всегда имеет результат меньший, чем 180º. В геометрии Римана, сумма всех углов треугольника больше 180º, а в трудах Эвклида она равна 180 градусам.
Домашнее задание
Решите кроссворд на заданную тему
Вопросы к кроссворду:
1. Как называется перпендикуляр, который провели из вершины треугольника к прямой, расположенной на противоположной стороне?
2. Как, одним словом можно назвать сумму длин сторон треугольника?
3. Назовите треугольник, у которого две стороны равны?
Назовите треугольник, у которого две стороны равны?
4. Назовите треугольник, у которого есть угол, равный 90°?
5. Какое название носит большая, из сторон треугольника?
6. Название стороны равнобедренного треугольника?
7. Их всегда три в любом треугольнике.
8. Какое название носит треугольник, у которого один из углов превышает 90°?
9. Название отрезка, соединяющего вершину нашей фигуры со срединой противоположной стороны?
10. В простом многоугольнике АВС, заглавная буква А является …?
11. Какое название носит отрезок, делящий угол треугольника пополам.
Вопросы к теме треугольников:
1. Дайте определение.
2. Сколько высот он имеет?
3. Сколько биссектрис у треугольника?
4. Чему равна его сумма углов?
5. Какие виды этого простого многоугольника вам известны?
6. Назовите точки треугольников, которые носят название замечательных.
7. Каким прибором можно измерить величину угла?
8. Если стрелки часов показывают 21 час. Какой угол образуют часовые стрелки?
Какой угол образуют часовые стрелки?
9. На какой угол поворачивается человек, если ему дана команда «налево», «кругом»?
10. Какие еще определения вам известны, которые связанные с фигурой, имеющей три угла и три стороны?
Какими бывают виды треугольников, углы и стороны
Пожалуй, самой основной, простой и интересной фигурой в геометрии является треугольник. В курсе средней школы изучаются его основные свойства, однако иногда знания по этой теме формируются неполными. Виды треугольников изначально определяют их свойства. Но подобное представление остается смешанным. Поэтому сейчас разберем немного подробнее эту тему.
Виды треугольников зависят от градусной меры углов. Эти фигуры бывают остро-, прямо- и тупоугольными. Если все углы не превышают значения в 90 градусов, то фигуру смело можно назвать остроугольной. Если хотя бы один угол треугольника равен 90 градусам, то вы имеете дело с прямоугольным подвидом. Соответственно, во всех остальных случаях рассматриваемую геометрическую фигуру называют тупоугольной.
Соответственно, во всех остальных случаях рассматриваемую геометрическую фигуру называют тупоугольной.
Существует множество задач для остроугольных подвидов. Отличительной чертой является внутреннее местонахождение точек пересечения биссектрис, медиан и высот. В других случаях это условие может не выполняться. Определить тип фигуры “треугольник” нетрудно. Достаточно знать, например, косинус каждого угла. Если какие-нибудь значения меньше нуля, значит, треугольник в любом случае является тупоугольным. В случае нулевого показателя фигура обладает прямым углом. Все положительные значения гарантированно подскажут вам о том, что перед вами остроугольный вид.
Нельзя не сказать о правильном треугольнике. Это самый идеальный вид, где совпадают все точки пересечения медиан, биссектрис и высот. Центр вписанной и описанной окружности лежит также в одном месте. Для решения задач необходимо знать только одну сторону, так как вам углы изначально заданы, а две другие стороны известной. То есть фигура задается только одним параметром. Существуют равнобедренные треугольники. Их главная особенность – равенство двух сторон и углов при основании.
То есть фигура задается только одним параметром. Существуют равнобедренные треугольники. Их главная особенность – равенство двух сторон и углов при основании.
Иногда встречается вопрос о том, существует ли треугольник с заданными сторонами. На самом деле вас спрашивают, подходит ли данное описание под основные виды. Например, если сумма двух сторон меньше третьей, то в реальности такой фигуры не существует вообще. Если в задании просят найти косинусы углов треугольника со сторонами 3,5,9, то здесь очевидный подвох. Это можно объяснить без сложных математических приемов. Предположим, вы хотите из пункта A попасть в пункт B. Расстояние по прямой равно 9 километрам. Однако вы вспомнили, что необходимо зайти в пункт C в магазин. Расстояние от А до С равно 3 километрам, а от С до В — 5. Таким образом получается, что, двигаясь через магазин, вы пройдете на один километр меньше. Но так как пункт C не расположен на прямой AB, то вам придется пройти лишнее расстояние. Здесь возникает противоречие. Это, конечно, условное объяснение. Математика знает не один способ доказательства того, что все виды треугольников подчиняются основному тождеству. Оно гласит о том, что сумма двух сторон больше длины третьей.
Это, конечно, условное объяснение. Математика знает не один способ доказательства того, что все виды треугольников подчиняются основному тождеству. Оно гласит о том, что сумма двух сторон больше длины третьей.
Любой вид обладает следующими свойствами:
1) Сумма всех углов равняется 180 градусам.
2) Всегда существует ортоцентр – точка пересечения всех трех высот.
3) Все три медианы, проведенные из вершин внутренних углов, пересекаются в одном месте.
4) Вокруг любого треугольника можно описать окружность. Также можно вписать круг так, чтобы он имел только три точки соприкосновения и не выходил за внешние стороны.
Теперь вы познакомились с основными свойствами, которыми обладают различные виды треугольников. В будущем важно понимать, с чем вы имеете дело при решении задачи.
Виды треугольников, углы и стороны. Виды треугольников: прямоугольный, остроугольный, тупоугольный
Сегодня мы отправляемся в страну Геометрия, где познакомимся с различными видами треугольников.
Рассмотрите геометрические фигуры и найдите среди них «лишнюю» (рис. 1).
Рис. 1. Иллюстрация к примеру
Мы видим, что фигуры № 1, 2, 3, 5 — четырехугольники. Каждая из них имеет свое название (рис. 2).
Рис. 2. Четырехугольники
Значит, «лишней» фигурой является треугольник (рис. 3).
Рис. 3. Иллюстрация к примеру
Треугольником называется фигура, которая состоит из трех точек, не лежащих на одной прямой, и трех отрезков, попарно соединяющих эти точки.
Точки называются вершинами треугольника , отрезки — его сторонами . Стороны треугольника образуют в вершинах треугольника три угла.
Основными признаками треугольника являются три стороны и три угла. По величине угла треугольники бывают остроугольные, прямоугольные и тупоугольные.
Треугольник называется остроугольным, если все три угла его острые, то есть меньше 90° (рис. 4).
Рис. 4. Остроугольный треугольник
4. Остроугольный треугольник
Треугольник называется прямоугольным, если один из его углов равен 90° (рис. 5).
Рис. 5. Прямоугольный треугольник
Треугольник называется тупоугольным, если один из его углов тупой, то есть больше 90° (рис. 6).
Рис. 6. Тупоугольный треугольник
По числу равных сторон треугольники бывают равносторонние, равнобедренные, разносторонние.
Равнобедренным называется треугольник, у которого две стороны равны (рис. 7).
Рис. 7. Равнобедренный треугольник
Эти стороны называются боковыми , третья сторона — основанием . В равнобедренном треугольнике углы при основании равны.
Равнобедренные треугольники бывают остроугольными и тупоугольными (рис. 8).
Рис. 8. Остроугольный и тупоугольный равнобедренные треугольники
Равносторонним называется треугольник, у которого все три стороны равны (рис.
9).
Рис. 9. Равносторонний треугольник
В равностороннем треугольнике все углы равны . Равносторонние треугольники всегда остроугольные.
Разносторонним называется треугольник, у которого все три стороны имеют разную длину (рис. 10).
Рис. 10. Разносторонний треугольник
Выполните задание. Распределите данные треугольники на три группы (рис. 11).
Рис. 11. Иллюстрация к заданию
Сначала распределим по величине углов.
Остроугольные треугольники: № 1, № 3.
Прямоугольные треугольники: № 2, № 6.
Тупоугольные треугольники: № 4, № 5.
Эти же треугольники распределим на группы по числу равных сторон.
Разносторонние треугольники: № 4, № 6.
Равнобедренные треугольники: № 2, № 3, № 5.
Равносторонний треугольник: № 1.
Рассмотрите рисунки.
Подумайте, из какого куска проволоки сделали каждый треугольник (рис. 12).
12).
Рис. 12. Иллюстрация к заданию
Можно рассуждать так.
Первый кусок проволоки разделен на три равные части, поэтому из него можно сделать равносторонний треугольник. На рисунке он изображен третьим.
Второй кусок проволоки разделен на три разные части, поэтому из него можно сделать разносторонний треугольник. На рисунке он изображен первым.
Третий кусок проволоки разделен на три части, где две части имеют одинаковую длину, значит, из него можно сделать равнобедренный треугольник. На рисунке он изображен вторым.
Сегодня на уроке мы познакомились с различными видами треугольников.
Список литературы
- М.И. Моро, М.А. Бантова и др. Математика: Учебник. 3 класс: в 2-х частях, часть 1. — М.: «Просвещение», 2012.
- М.И. Моро, М.А. Бантова и др. Математика: Учебник. 3 класс: в 2-х частях, часть 2. — М.: «Просвещение», 2012.
- М.И. Моро. Уроки математики: Методические рекомендации для учителя. 3 класс. — М.
 : Просвещение, 2012.
: Просвещение, 2012. - Нормативно-правовой документ. Контроль и оценка результатов обучения. — М.: «Просвещение», 2011.
- «Школа России»: Программы для начальной школы. — М.: «Просвещение», 2011.
- С.И. Волкова. Математика: Проверочные работы. 3 класс. — М.: Просвещение, 2012.
- В.Н. Рудницкая. Тесты. — М.: «Экзамен», 2012.
- Nsportal.ru ().
- Prosv.ru ().
- Do.gendocs.ru ().
Домашнее задание
1. Закончите фразы.
а) Треугольником называется фигура, которая состоит из …, не лежащих на одной прямой, и …, попарно соединяющих эти точки.
б) Точки называются … , отрезки — его … . Стороны треугольника образуют в вершинах треугольника ….
в) По величине угла треугольники бывают … , … , … .
г) По числу равных сторон треугольники бывают … , … , … .
2. Начертите
а) прямоугольный треугольник;
б) остроугольный треугольник;
в) тупоугольный треугольник;
г) равносторонний треугольник;
д) разносторонний треугольник;
е) равнобедренный треугольник.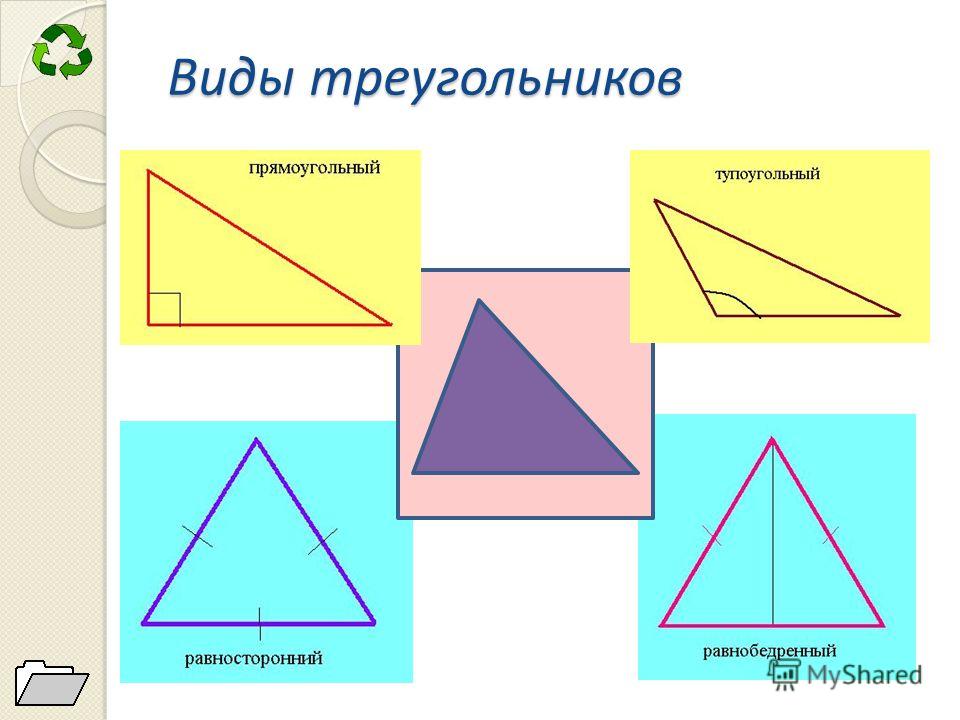
3. Составьте задание по теме урока для своих товарищей.
Задачи:
1. Познакомить учащихся с разными видами треугольников в зависимости от вида углов (прямоугольный, остроугольный, тупоугольный). Учиться находить на чертежах треугольники и их виды. Закреплять основные геометрические понятия и их свойства: прямая линия, отрезок, луч, угол.
2. Развитие мышления, воображения, математической речи.
3. Воспитание внимания, активности.
Ход урока
I. Организационный момент.
Много ль надо нам, ребята,
Для умелых наших рук?
Нарисуем два квадрата,
А на них огромный круг.
А потом ещё кружочки,
Треугольник колпачок.
Вот и вышел очень — очень
Развесёлый Чудачок.
II. Объявление темы урока.
Сегодня на уроке мы с вами совершим путешествие
по городу Геометрии и побываем в микрорайоне
Треугольники (т.е. познакомимся с разными видами
треугольников в зависимости от их углов, будем
учиться находить эти треугольники на чертежах. )
Проведём урок в форме “игры-соревнования” по
командам.
)
Проведём урок в форме “игры-соревнования” по
командам.
1 команда — “Отрезок”.
2 команда — “Луч”.
3 команда — “Угол”.
А гости будут представлять жюри.
Жюри нас по пути направит
И без вниманья не оставит. (Оценивать по баллам 5,4,3,…).
А на чём же мы будем путешествовать по городу Геометрии? Вспомните, какие виды пассажирского транспорта есть в городе? Нас очень много, какой же мы выберем? (Автобус).
Автобус. Чётко, кратко. Начинается посадка.
Усаживаемся поудобнее и начнём наше путешествие. Капитаны команд получите билеты.
Но билеты эти непростые, а билеты — “задания”.
III. Повторение пройденного материала.
Первая остановка “ Повторяй-ка”.
Вопрос всем командам.
Найти на чертеже прямую линию и назвать её свойства.
Без конца и края линия прямая!
Хоть сто лет по ней иди,
Не найдёшь конца пути!
- Прямая не имеет ни начала, ни конца — она
бесконечна, поэтому её измерить нельзя.

Начинаем наше соревнование.
Защита названий своих команд.
(Все команды читают первые вопросы и обсуждают. По очереди капитаны команд зачитывают вопросы, 1 команда читает 1 вопрос).
1. Показать на чертеже отрезок. Что называется отрезком. Назвать его свойства.
- Часть прямой, ограниченная двумя точками, называется отрезком. У отрезка есть начало и конец, потому его можно измерить при помощи линейки.
(2 команда читает 1 вопрос).
1. Показать на чертеже луч. Что называется лучом. Назвать его свойства.
- Если отметить точку и из неё провести часть прямой, то получится изображение луча. Точка, из которой проведена часть прямой, называется началом луча.
Конца у луча нет, поэтому его измерить нельзя.
(3 команда читает 1 вопрос).
1 .Показать на чертеже угол. Что называется углом. Назвать его свойства.
- Проведя из одной точки два луча, получается
геометрическая фигура, которая называется углом.
 У угла есть вершина, а сами лучи называются
сторонами угла. Углы измеряются в градусах с
помощью транспортира.
У угла есть вершина, а сами лучи называются
сторонами угла. Углы измеряются в градусах с
помощью транспортира.
Физкультминутка (под музыку).
IV. Подготовка к изучению нового материала.
Вторая остановка “Сказочная”.
На прогулке Карандаш встретил разные углы. Хотел с ними поздороваться, да забыл, как зовут каждого из них. Придётся Карандашу помочь.
(Углы уч-ся проверяют с помощью модели прямого угла).
Задание командам. Прочитайте вопросы №2, обсудите.
1 команда читает 2 вопрос.
2. Найти прямой угол, дать определение.
- Угол величиной 90°называется прямым углом.
2 команда читает 2 вопрос.
2. Найти острый угол, дать определение.
- Угол меньше прямого, называется острым.
3 команда читает 2 вопрос.
2. Найти тупой угол, дать определение.
Угол больше прямого, называется тупым.
В микрорайоне, где любил гулять Карандаш, все
углы отличались от других жителей тем, что гуляли
всегда втроём, пили чай втроём, ходили в кино
втроём. И Карандаш никак не мог понять, что за
геометрическую фигуру вместе составляют три
угла?
И Карандаш никак не мог понять, что за
геометрическую фигуру вместе составляют три
угла?
А подсказкой вам будет стихотворение.
Ты на меня, ты на него,
На всех нас посмотри.
У нас всего, у нас всего,
У нас всего по три!
О свойствах какой фигуры говорится?
- О треугольнике.
Какая же фигура называется треугольником?
- Треугольник — это геометрическая фигура, у которой три вершины, три угла, три стороны.
(Уч-ся показывают на чертеже треугольник, называют вершины, углы и стороны).
Вершины: А, В, С (точки)
Углы: ВАС, АВС, ВСА.
Стороны: АВ, ВС, СА (отрезки).
V. Физкультминутка:
8 раз ногою топнем,
9 раз руками хлопнем,
мы присядем 10 раз,
и наклонимся 6 раз,
мы подпрыгнем ровно
столько (показ треугольника)
Ай, да, счёт! Игра и только!
VI. Изучение нового материала.
Скоро углы подружились и стали неразлучны.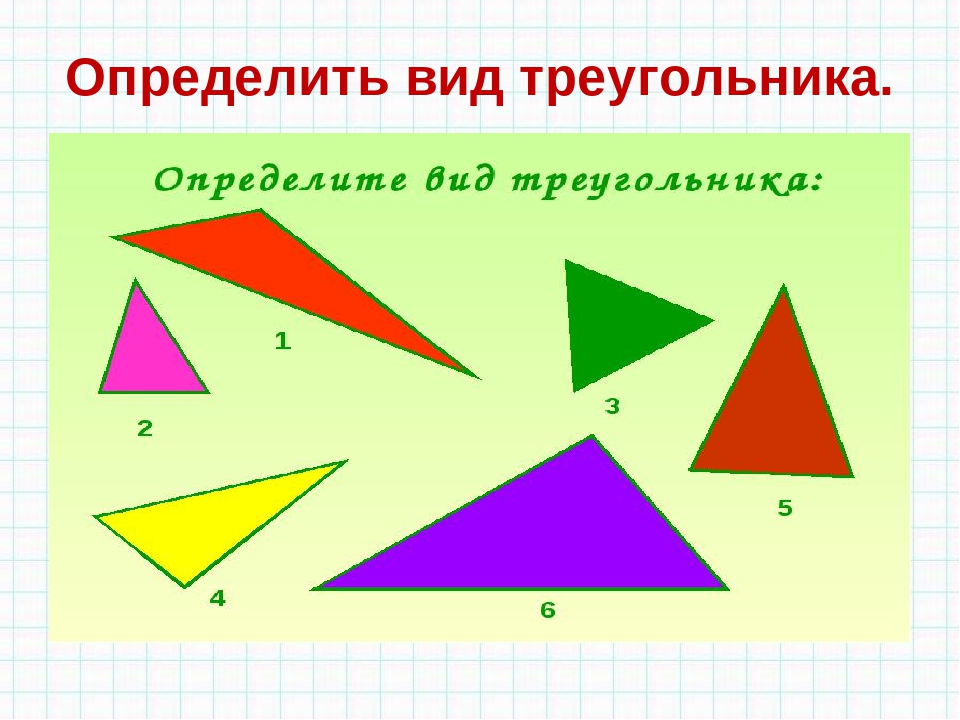
И теперь микрорайон мы будем так и называть: микрорайон Треугольники.
Третья остановка “Знайка”.
А как зовут эти треугольники?
Давайте дадим им имена. И попробуем сами сформулировать определение.
2. Найди треугольники разных видов
1 команда найдет и покажет тупоугольные треугольники.
2 команда найдёт и покажет прямоугольные треугольники.
3 команда найдёт и покажет остроугольные треугольники.
VIII. Следующая остановка “Соображай-ка”.
Задание всем командам.
Переложив 6 палочек, составьте из фонаря 4 равных треугольника.
Какие по виду углов получились треугольники? (Остроугольные).
IX. Итог урока.
В каком же микрорайоне мы с вами побывали?
С какими видами треугольников познакомились?
Треугольник — определение и общие понятия
Треугольник – это такой простой многоугольник, состоящий из трех сторон и имеющий столько же углов. Его плоскости ограничиваются 3 точками и 3 отрезками, попарно соединяющими даные точки.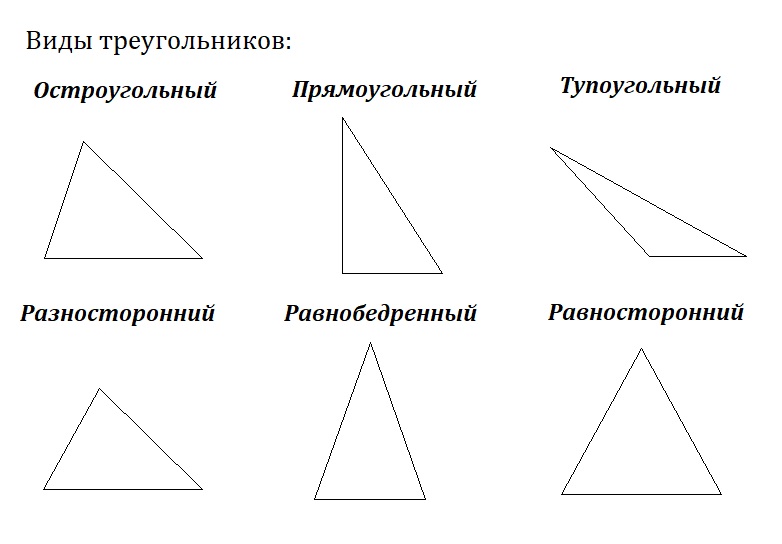
Все вершины любого треугольника, независимо от его разновидности, обозначаются заглавными латинскими буквами, а его стороны изображаются соответствующими обозначениями противоположных вершин, только не большими буквами, а малыми. Так, например, треугольник с вершинами обозначенными буквами А, В и С имеет стороны a, b, c.
Если рассматривать треугольник в евклидовом пространстве, то это такая геометрическая фигура, которая образовалась с помощью трех отрезков, соединяющих три точки, которые не лежат на одной прямой.
Посмотрите внимательно на рисунок, который изображен вверху. На нем точки А, В и С являются вершинами этого треугольника, а его отрезки носят названия сторон треугольника. Каждая вершина этого многоугольника образует внутри его углы.
Виды треугольников
Согласно величины, углов треугольников, они делятся на такие разновидности, как:
Прямоугольные;
Остроугольные;
Тупоугольные.
К прямоугольным принадлежат такие треугольники, у которых в наличии есть один прямой угол, а остальные два имеют острые углы.
Остроугольные треугольники – это те, у которых все его углы острые.
А если у треугольника имеется один тупой угол, а два остальных угла острые, то такой треугольник относится к тупоугольным.
Каждый из вас прекрасно понимает, что не все треугольники имеют равные стороны. И соответственно тому, какую длину имеют его стороны, треугольники можно поделить на:
Равнобедренные;
Равносторонние;
Разносторонние.
Задание: Нарисуйте разные виды треугольников. Дайте им определение. Какое между ними отличие вы видите?
Основные свойства треугольников
Хотя эти простые многоугольники могут отличаться друг от друга величиной углов или сторон, но в каждом треугольнике есть основные свойства, характерны для этой фигуры.
В любом треугольнике:
Общая сумма всех его углов равняется 180º.
Если он принадлежит к равносторонним, то каждый его угол равен 60º.
Равносторонний треугольник имеет одинаковые и ровные между собой углы.
Чем меньше сторона многоугольника, тем меньший угол расположен напротив него и наоборот напротив большей стороны находиться больший угол.
Если стороны равные, то напротив них расположены равные углы, и наоборот.
Если взять треугольник и продлить его сторону, то в итоге мы образуется внешний угол. Он равен сумме внутренних углов.
В любом треугольнике его сторона, независимо от того, какую бы вы не выбрали, все равно будет меньше, чем сумма 2-х других сторон, но больше чем их разность:
1. a b – c;
2. b a – c;
3. c a – b.
Задание
В таблице приведены уже известные два угла треугольника. Зная общую сумму всех углов найдите, чему равен третий угол треугольника и занесите в таблицу:
1. Сколько градусов имеет третий угол?
2. К какому виду треугольников он относится?
Признаки равности треугольников
I признак
II признак
III признак
Высота, биссектриса и медиана треугольника
Высота треугольника — перпендикуляр, проведенный из вершины фигуры к его противоположной стороне, называется высотой треугольника. Все высоты треугольника пересекаются в одной точке. Точка пересечения всех 3-х высот треугольника является его ортоцентром.
Все высоты треугольника пересекаются в одной точке. Точка пересечения всех 3-х высот треугольника является его ортоцентром.
Отрезок, проведенный из данной вершины и соединяющий ее на средине противоположной стороны, является медианой. Медианы, также как и высоты треугольника, имеют одну общую точку пересечения, так называемый центр тяжести треугольника или центроид.
Биссектриса треугольника — отрезок, соединяющий вершину угла и точку противоположной стороны, а также делящий этот угол пополам. Все биссектрисы треугольника пересекаются в одной точке, которую называют центром окружности, вписанной в треугольник.
Отрезок, который соединяет середины 2-х сторон треугольника, называется средней линией.
Историческая справка
Такая фигура, как треугольник, была известна еще в Древние времена. Об этой фигуре и ее свойствах упоминалось на египетских папирусах четырех тысячелетней давности.
Немного позже, благодаря теореме Пифагора и формуле Герона, изучение свойства треугольника, перешло на более высокий уровень, но все же, это происходило более двух тысяч лет назад.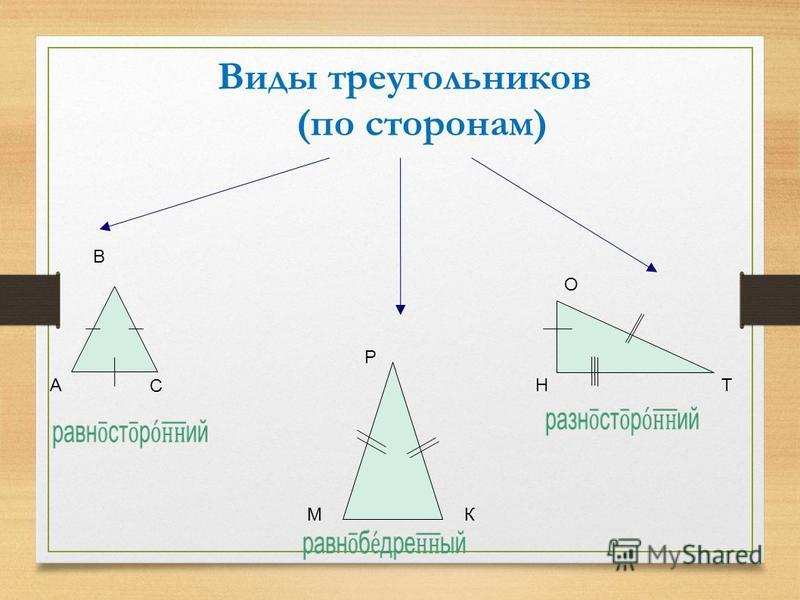
В XV – XVI веках стали проводить много исследований о свойствах треугольника и в итоге возникла такая наука, как планиметрия, которая получила название «Новая геометрия треугольника».
Ученый из России Н. И.Лобачевский внес огромный вклад в познание свойств треугольников. Его труды в дальнейшем нашли применение как в математике, так и физике и кибернетике.
Благодаря знаниям свойств треугольников возникла и такая наука, как тригонометрия. Она оказалась необходимой для человека в его практических потребностях, так как ее применение просто необходимо при составлении карт, измерении участков, да и при конструировании различных механизмов.
А какой самый известный треугольник вы знаете? Это конечно же Бермудский треугольник! Он получил такое название в 50-х годах из-за географического расположения точек (вершин треугольника), внутри которых, согласно существующей теории, возникали связанные с ним аномалии. Вершинами Бермудского треугольника выступают Бермудские острова, Флорида и Пуэрто-Рико.
Задание: А какие теории о Бермудском треугольнике слышали вы?
А известно ли вам, что в теории Лобачевского при сложении углов треугольника их сумма всегда имеет результат меньший, чем 180º. В геометрии Римана, сумма всех углов треугольника больше 180º, а в трудах Эвклида она равна 180 градусам.
Домашнее задание
Решите кроссворд на заданную тему
Вопросы к кроссворду:
1. Как называется перпендикуляр, который провели из вершины треугольника к прямой, расположенной на противоположной стороне?
2. Как, одним словом можно назвать сумму длин сторон треугольника?
3. Назовите треугольник, у которого две стороны равны?
4. Назовите треугольник, у которого есть угол, равный 90°?
5. Какое название носит большая, из сторон треугольника?
6. Название стороны равнобедренного треугольника?
7. Их всегда три в любом треугольнике.
8. Какое название носит треугольник, у которого один из углов превышает 90°?
9. Название отрезка, соединяющего вершину нашей фигуры со срединой противоположной стороны?
Название отрезка, соединяющего вершину нашей фигуры со срединой противоположной стороны?
10. В простом многоугольнике АВС, заглавная буква А является …?
11. Какое название носит отрезок, делящий угол треугольника пополам.
Вопросы к теме треугольников:
1. Дайте определение.
2. Сколько высот он имеет?
3. Сколько биссектрис у треугольника?
4. Чему равна его сумма углов?
5. Какие виды этого простого многоугольника вам известны?
6. Назовите точки треугольников, которые носят название замечательных.
7. Каким прибором можно измерить величину угла?
8. Если стрелки часов показывают 21 час. Какой угол образуют часовые стрелки?
9. На какой угол поворачивается человек, если ему дана команда «налево», «кругом»?
10. Какие еще определения вам известны, которые связанные с фигурой, имеющей три угла и три стороны?
О том, что такое треугольник, квадрат, куб, нам рассказывает наука геометрия. В современном мире ее изучают в школах все без исключения. Также наукой, которая изучает непосредственно то, что такое треугольник и какие у него свойства, является тригонометрия. Она исследует подробно все явления, связанные с данными О том, что такое треугольник, мы и поговорим сегодня в нашей статье. Ниже будут описаны их виды, а также некоторые теоремы, связанные с ними.
В современном мире ее изучают в школах все без исключения. Также наукой, которая изучает непосредственно то, что такое треугольник и какие у него свойства, является тригонометрия. Она исследует подробно все явления, связанные с данными О том, что такое треугольник, мы и поговорим сегодня в нашей статье. Ниже будут описаны их виды, а также некоторые теоремы, связанные с ними.
Что такое треугольник? Определение
Это плоский многоугольник. Углов он имеет три, что понятно из его названия. Также он имеет три стороны и три вершины, первые из них — это отрезки, вторые — точки. Зная, чему равны два угла, можно найти третий, отняв сумму первых двух от числа 180.
Какими бывают треугольники?
Их можно классифицировать по различным критериям.
В первую очередь они делятся на остроугольные, тупоугольные и прямоугольные. Первые обладают острыми углами, то есть такими, которые равны менее чем 90 градусам. У тупоугольных один из углов — тупой, то есть такой, который равен более 90 градусам, остальные два — острые.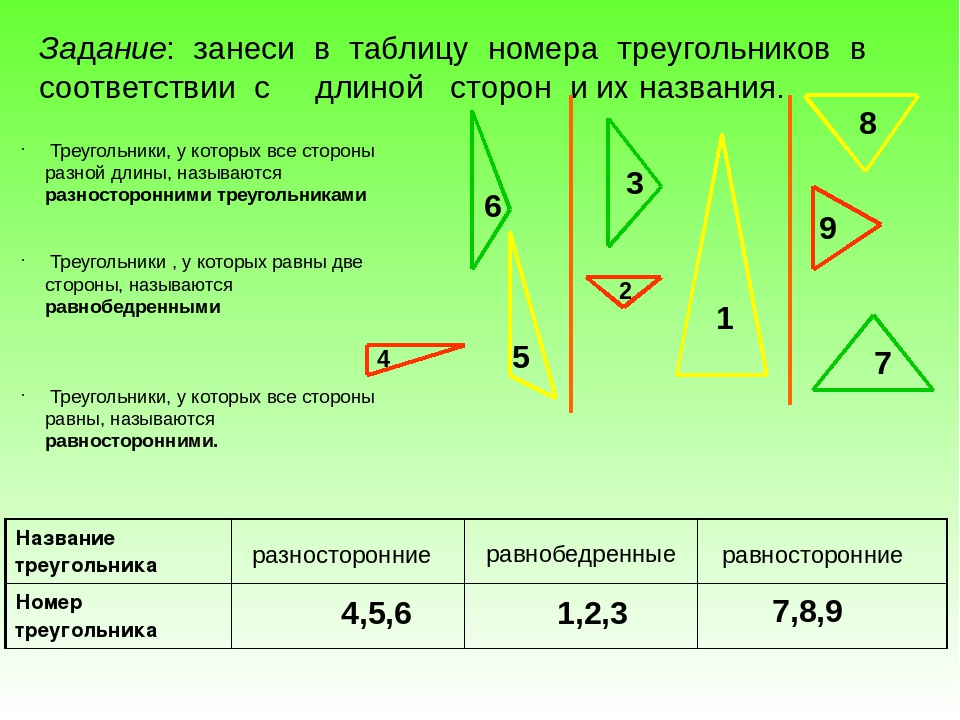 К остроугольным треугольникам относятся также и равносторонние. У таких треугольников все стороны и углы равны. Все они равны 60 градусам, это можно легко вычислить, разделив сумму всех углов (180) на три.
К остроугольным треугольникам относятся также и равносторонние. У таких треугольников все стороны и углы равны. Все они равны 60 градусам, это можно легко вычислить, разделив сумму всех углов (180) на три.
Прямоугольный треугольник
Невозможно не поговорить о том, что такое прямоугольный треугольник.
У такой фигуры один угол равен 90 градусам (прямой), то есть две из его сторон расположены перпендикулярно. Остальные два угла являются острыми. Они могут быть равными, тогда он будет равнобедренным. С прямоугольным треугольником связана теорема Пифагора. При помощи ее можно найти третью сторону, зная две первые. Согласно данной теореме, если прибавить квадрат одного катета к квадрату другого, можно получить квадрат гипотенузы. Квадрат же катета можно подсчитать, отняв от квадрата гипотенузы квадрат известного катета. Говоря о том, что такое треугольник, можно вспомнить и о равнобедренном. Это такой, у которого две из сторон равны, также равны и два угла.
Что такое катет и гипотенуза?
Катет — это одна из сторон треугольника, которые образуют угол в 90 градусов. Гипотенуза — это оставшаяся сторона, которая расположена напротив прямого угла. Из него на катет можно опустить перпендикуляр. Отношение прилежащего катета к гипотенузе называется не иначе как косинус, а противоположного — синус.
Гипотенуза — это оставшаяся сторона, которая расположена напротив прямого угла. Из него на катет можно опустить перпендикуляр. Отношение прилежащего катета к гипотенузе называется не иначе как косинус, а противоположного — синус.
— в чем его особенности?
Он прямоугольный. Его катеты равны трем и четырем, а гипотенуза — пяти. Если вы увидели, что катеты данного треугольника равны трем и четырем, можете не сомневаться, что гипотенуза будет равна пяти. Также по такому принципу можно легко определить, что катет будет равен трем, если второй равен четырем, а гипотенуза — пяти. Чтобы доказать данное утверждение, можно применить теорему Пифагора. Если два катета равны 3 и 4, то 9 + 16 = 25, корень из 25 — это 5, то есть гипотенуза равна 5. Также египетским треугольником называется прямоугольный, стороны которого равны 6, 8 и 10; 9, 12 и 15 и другим числам с соотношением 3:4:5.
Каким еще может быть треугольник?
Также треугольники могут быть вписанными и описанными.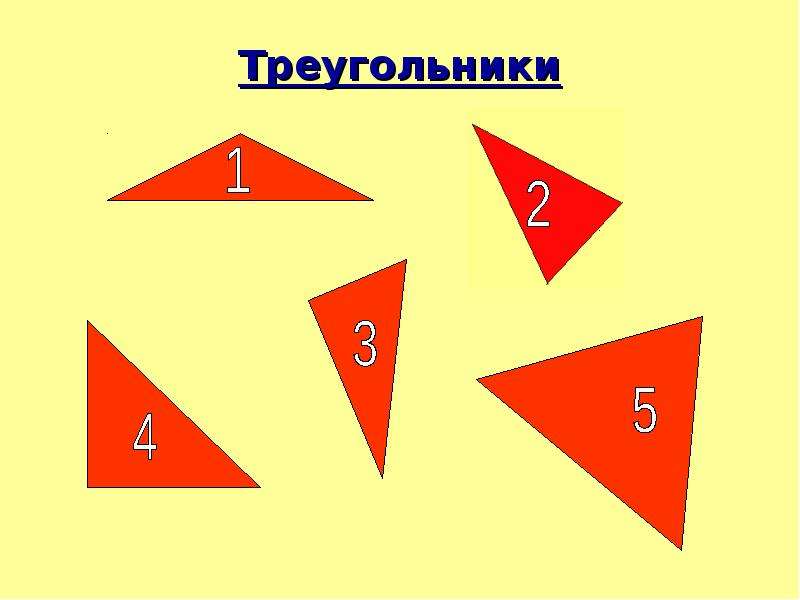 Фигура, вокруг которой описана окружность, называется вписанной, все ее вершины являются точками, лежащими на окружности. Описанный треугольник — тот, в который вписана окружность. Все его стороны соприкасаются с ней в определенных точках.
Фигура, вокруг которой описана окружность, называется вписанной, все ее вершины являются точками, лежащими на окружности. Описанный треугольник — тот, в который вписана окружность. Все его стороны соприкасаются с ней в определенных точках.
Как находится
Площадь любой фигуры измеряется в квадратных единицах (кв. метрах, кв. миллиметрах, кв. сантиметрах, кв. дециметрах и т. д.) Данную величину можно рассчитать разнообразными способами, в зависимости от вида треугольника. Площадь какой угодно фигуры с углами можно найти, если умножить ее сторону на перпендикуляр, опущенный на нее из противоположного угла, и разделив данную цифру на два. Также можно найти эту величину, если умножить две стороны. Потом умножить это число на синус угла, расположенного между данными сторонами, и разделить это получившееся на два. Зная все стороны треугольника, но не зная его углов, можно найти площадь еще и другим способом. Для этого нужно найти половину периметра. Затем поочередно отнять от данного числа разные стороны и перемножить полученные четыре значения.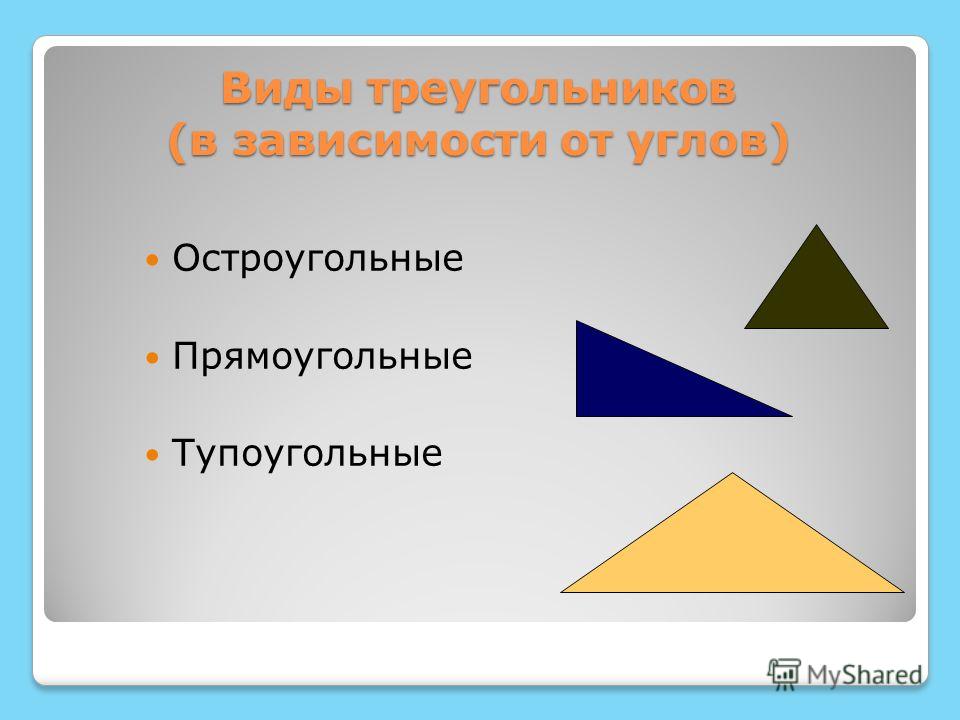 Далее найти из числа, которое вышло. Площадь вписанного треугольника можно отыскать, перемножив все стороны и разделив полученное число на которая описана вокруг него, умноженный на четыре.
Далее найти из числа, которое вышло. Площадь вписанного треугольника можно отыскать, перемножив все стороны и разделив полученное число на которая описана вокруг него, умноженный на четыре.
Площадь описанного треугольника находится таким образом: половину периметра умножаем на радиус окружности, которая в него вписана. Если то его площадь можно найти следующим образом: сторону возводим в квадрат, умножаем полученную цифру на корень из трех, далее делим это число на четыре. Похожим образом можно вычислить высоту треугольника, у которого все стороны равны, для этого одну из них нужно умножить на корень из трех, а потом разделить данное число на два.
Теоремы, связанные с треугольником
Основными теоремами, которые связаны с данной фигурой, являются теорема Пифагора, описанная выше, и косинусов. Вторая (синусов) заключается в том, что, если разделить любую сторону на синус противоположного ей угла, то можно получить радиус окружности, которая описана вокруг него, умноженный на два.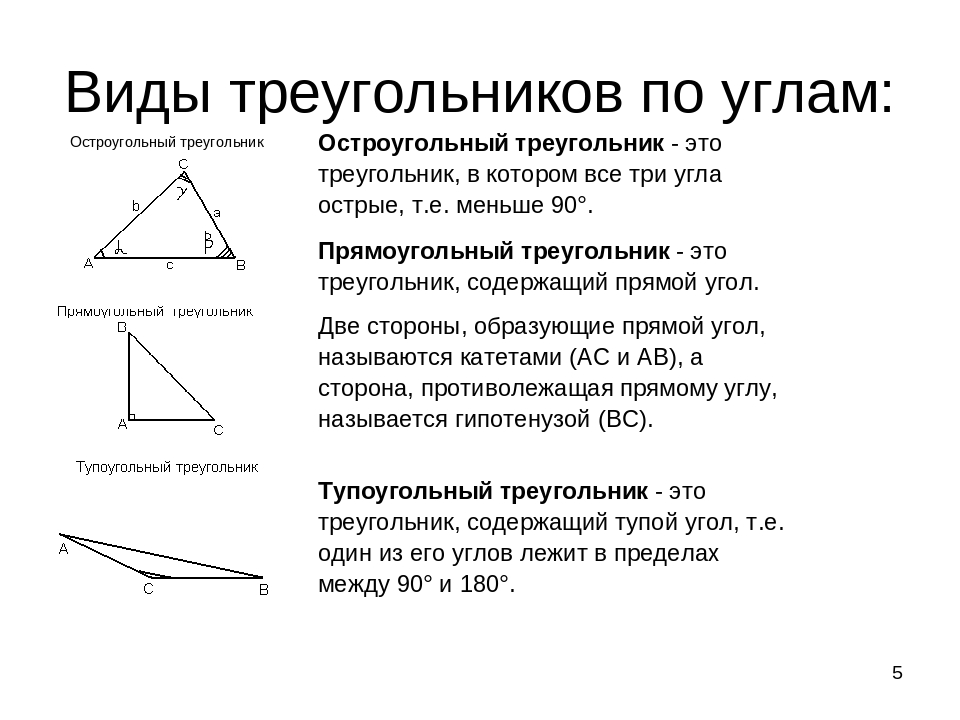 Третья (косинусов) заключается в том, что, если от суммы квадратов двух сторон отнять их же произведение, умноженное на два и на косинус угла, расположенного между ними, то получится квадрат третьей стороны.
Третья (косинусов) заключается в том, что, если от суммы квадратов двух сторон отнять их же произведение, умноженное на два и на косинус угла, расположенного между ними, то получится квадрат третьей стороны.
Треугольник Дали — что это?
Многие, столкнувшись с этим понятием, сначала думают, что это какое-то определение в геометрии, но это совсем не так. Треугольник Дали — это общее название трех мест, которые тесно связаны с жизнью знаменитого художника. «Вершинами» его являются дом, в котором Сальвадор Дали жил, замок, который он подарил своей жене, а также музей сюрреалистических картин. Во время экскурсии по этим местам можно узнать много интереснейших фактов об этом своеобразном креативном художнике, известном во всем мире.
Предмет: математика
Класс: 3 класс
Учебник: «Математика» 2 часть.
Тема: Виды треугольников
Тип урока: открытие новых знаний
Цель: Научить определять виды треугольников по измерениям длин их сторон.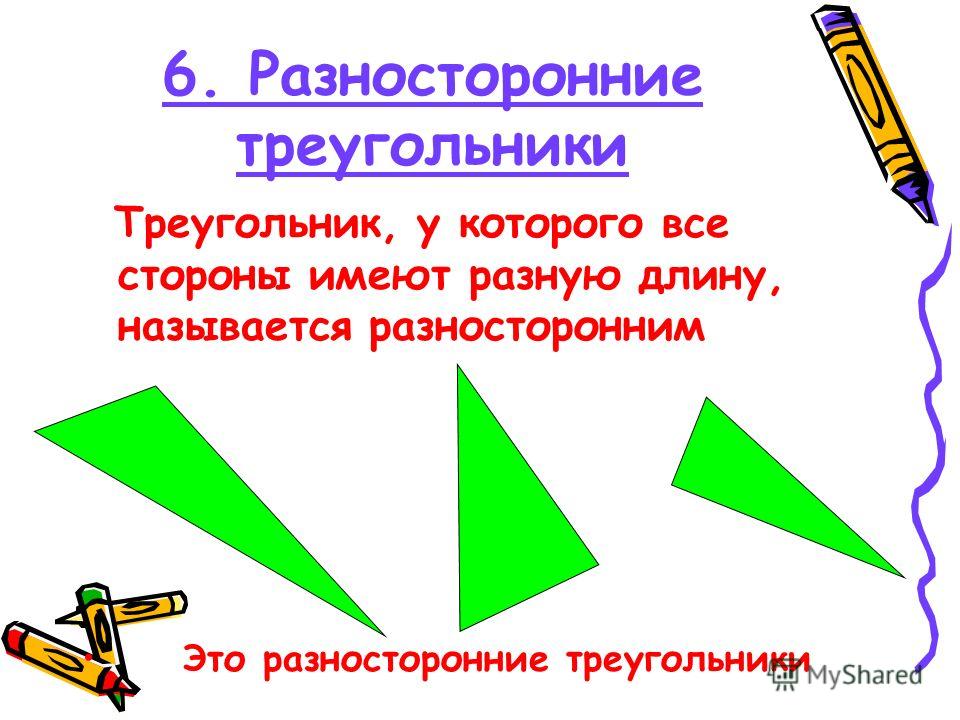
Задачи :
1)Актуализировать знания о геометрических фигурах — прямоугольник, квадрат, треугольник.
2)Актуализировать сложение и вычитание трёхзначных чисел, деление двузначного числа на однозначное, двузначное и круглое; умножение двузначного на однозначное число.
3)Ввести термины: равнобедренный, равносторонний, разносторонний треугольник.
Ход урока
1.Мотивация к учебной деятельности
Посмотрите, скажите, что это такое?
(пирамида)
Скажите, из чего она состоит? (из частей, уровней …)
Можно ли эту пирамиду сравнить с нашим знанием? (да)
Каждый день вы строите всё новые и новые пирамиды, каждый уровень пирамиды- это новое знание, которое вы получаете на уроке. А что будет с пирамидой, если мы уберём синий уровень? (Она разрушиться, станет меньше.)
А как из-за чего может разрушиться наша пирамида знаний? (Из-за не выполненного д/з, пропусков уроков, не внимательно слушать учителя. )
)
Что нужно делать, чтобы наша пирамида становилась прочнее, росла? (Учить уроки, хорошо работать на уроке, выполнять д/з, не прогуливать школу.)
Ребята, вы сказали всё верно. А теперь давайте представим, что наша пирамида отбросила тень. Скажите, на какую геометрическую фигуру тень похожа?
(На треугольник.)
Сегодня мы продолжим работать с такой геометрической фигурой, как треугольник.
2.Актуальзация знаний и фиксация затруднений в проблемной ситуации
С какими геометрическими фигурами вы знакомы? (квадрат, прямоугольник, треугольник).
На доске таблица, заполните её, опираясь на свои знания (у каждого обучающегося карточка с такой таблицей):
Как называются первые две геометрические фигуры? (прямоугольник и квадрат, одним словом это четырёхугольники.)
Скажите, какие виды четырёхугольников вы знаете? Ответить на этот вопрос вам поможет изображение их на слайде.
Названия четырёхугольников появляются после ответов детей.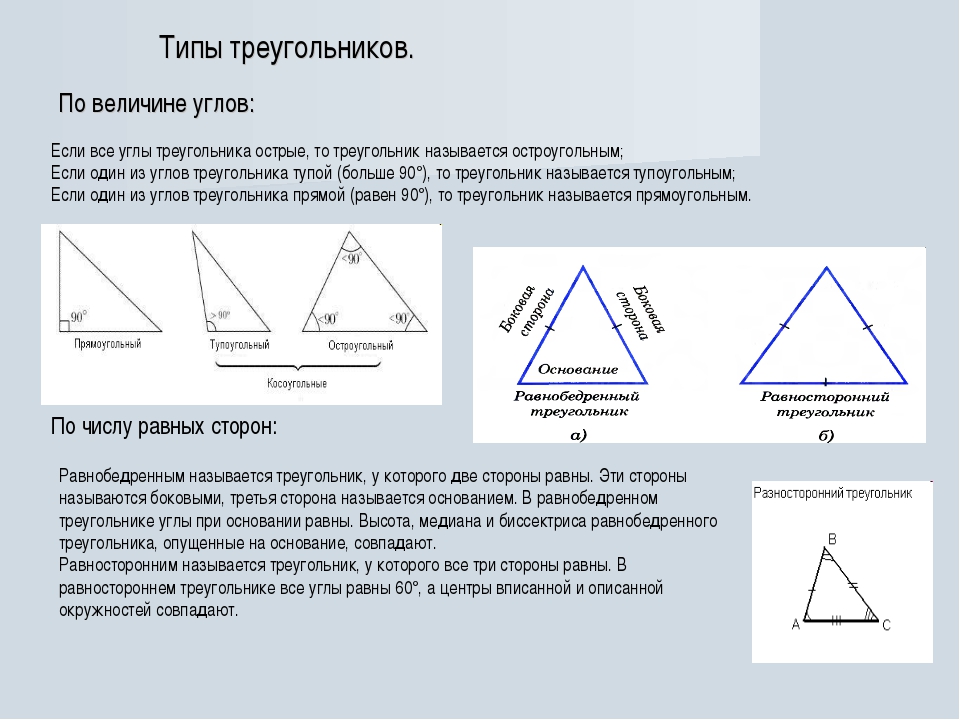
(ромб, квадрат, прямоугольник, трапеция, параллелограмм — называют их по изображениям на слайде или доске.)
Можете ли вы сказать, что такое прямоугольник, а что такое квадрат?
(Прямоугольник — четырёхугольник, у которого все углы прямые.
Квадрат — это прямоугольник, у которого все стороны равны)
Найдите лишнюю геометрическую фигуру, опираясь на результаты таблицы. (Треугольник).
Хорошо, четырёхугольники все очень разные, а что вы знаете о треугольнике? (Треугольники бывают: остроугольные, тупоугольные, прямоугольные.)
Что вы ещё знаете о треугольнике? (Определение)
Треугольник — это геометрическая фигура, у которой 3 угла, 3 вершины, 3 стороны.
Заполните следующую таблицу, опираясь на свои знания:
(Учитель заполняет таблицу в соответствии ответам детей. В колонках «название» возникают разные мнения, а некоторые дети оставляют их пустыми.)
3.Выявление места и причины затруднения.
Какое задание вы выполняли? (Заполни таблицу. )
)
Где возникло затруднение? (При записи названий треугольников)
Почему возникло затруднение? (Не знаем как они называются)
Какую цель урока нужно поставить? (Узнать, какие ещё есть виды треугольников кроме изученных (тупоугольный, остроугольный, прямоугольный) , научиться определять эти виды у треугольников.)
Какая тема нашего урока? (Виды треугольников)
4.Открытие нового знания.
Давайте вернёмся к таблице.
Впишем размеры сторон треугольников. (Вписывают.)
Хорошо, а сейчас посмотрите и скажите, что вы заметили? (У первого треугольника все стороны равны, у второго 2 стороны равны, а у третьего все стороны разные.)
Верно, а можете ли вы придумать названия этим треугольникам, основываясь на том объяснении, которое вы сейчас дали? (Да)
Как вы назовёте треугольник, у которого все стороны равные? Придумай прилагательное, состоящее из 2х слов: равные стороны. (Равносторонний)
Как назвать треугольник, у которого все стороны различные? (Разносторонний)
Как называется треугольник, у которого 2 стороны равные? (Дети сомневаются, чтобы ответить на этот вопрос они пользуются учебником с.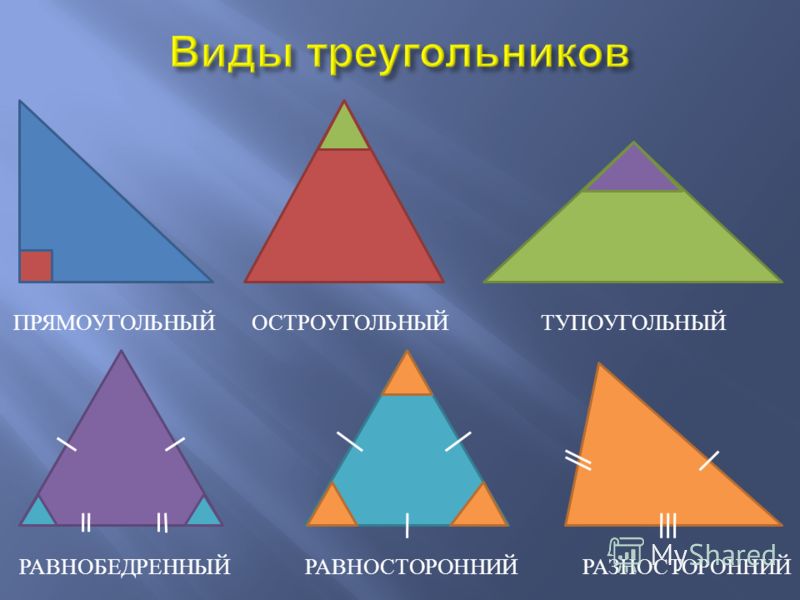 73) (Равнобедренный) А какой ещё треугольник можем назвать равнобедренным? (Равносторонний)
73) (Равнобедренный) А какой ещё треугольник можем назвать равнобедренным? (Равносторонний)
Заполните таблицу самостоятельно, опираясь на новые знания.
А можем ли сейчас дать определение видам треугольников? (Да)
Равносторонний — треугольник, у которого все три стороны равны.
Равнобедренный — треугольник, у которого равны хотя бы две стороны. Равнобедренным треугольником является и равносторонний треугольник.
Разносторонний — треугольник, у которого все стороны разные.
Проверьте свои определения с.73 -учебник. (Проверяют.)
Верно ли вы составили определения? (Да.)
5.Первичное закрепление с проговариванием во внешней речи
Выполните задание из учебника с.74 (под?)
1)Разносторонние: 2,3,5
2)Равнобедренные: 1, 4 , 6, 7
(Учащиеся записывают в тетради. По очереди говорят ответы, аргументируя. Образец фиксируется на доске).
6.Самостоятельная работа с самопроверкой по эталону.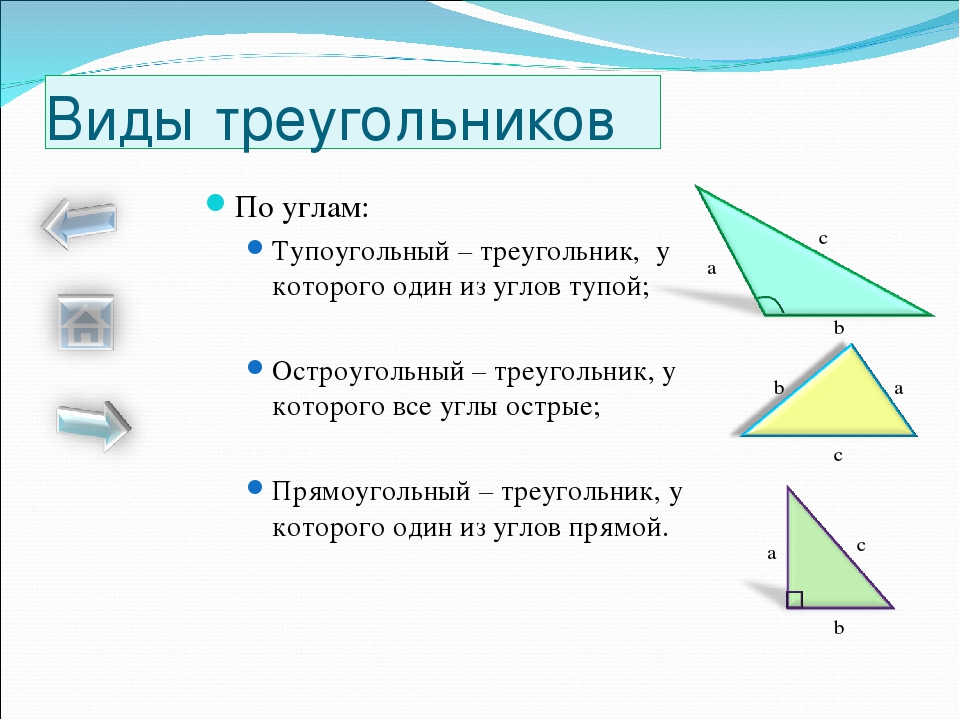
Выполнение задания самостоятельно. По окончанию работы — самопроверка по образцу (на доске или на индивидуальных карточках).
№1.Заполни таблицу , схематично изобрази треугольники.
№2.Выпиши номера:
1)Разносторонних треугольников.
2)Равнобедренных, из выписанных номеров подчеркни номера равносторонних треугольников.
Эталон:
Задание №1:
Задание №2:
1)Разносторонние треугольники: 2,3,4
2)Равнобедренные треугольники (подчеркнут номер равностороннего треугольника): 1, 5
7.Включение в систему знаний и повторение
На песке мальчик нарисовал треугольники и зашифровал слова, найди значения выражений, записанные в треугольниках. Сначала решай те, которые записаны в разносторонних треугольниках, а потом в равнобедренных треугольниках. И отгадаешь зашифрованные слова.
Подсказка: Запиши числа в порядке возрастания и слова у тебя получатся.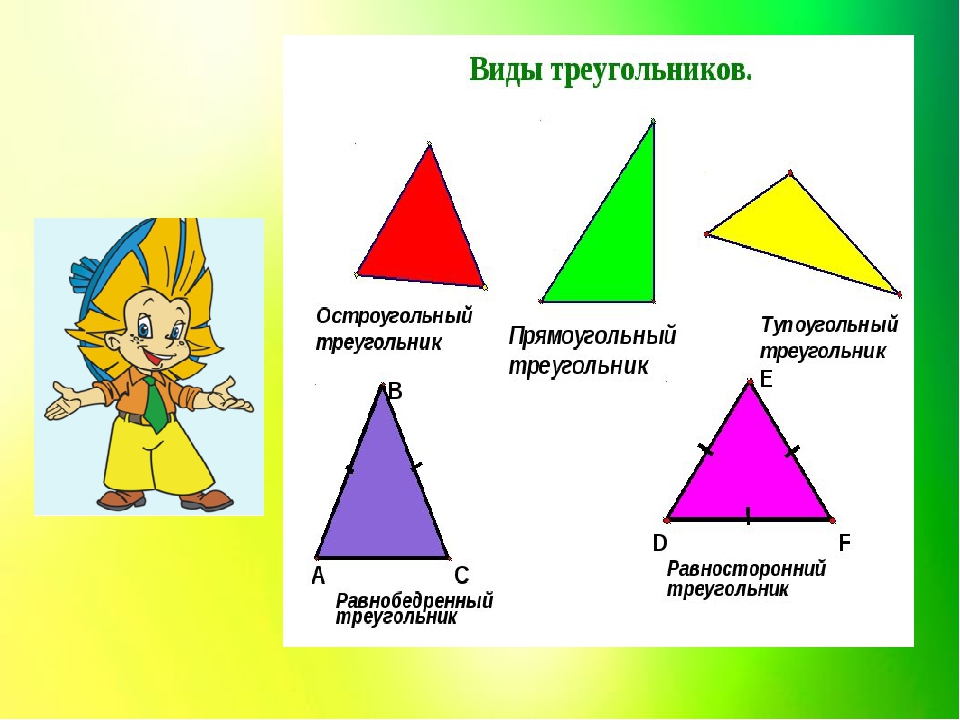
Карточка:
Решение:
Ответ: Виды треугольников
8.Рефлексия учебной деятельности.
Нарисуй соответственно пирамиду знаний, состоящую из 7 уровней. Каждый уровень — это ответ на вопрос.
Ответьте на вопросы:
1)Ребята, что такое вы записали «виды треугольников»? (Тему нашего урока)
2)Какова была наша цель? (Узнать, как называются все 3 вида треугольников, научиться определять эти виды по измерениям длин сторон.)
3)Какие виды треугольников вы узнали? (разносторонний, равнобедренный, равносторонний)
4) А почему они так называются?
( Равносторонний — треугольник, у которого все стороны равны.
Равнобедренный — треугольник, у которого хотя бы две стороны равны, в том числе и равносторонний треугольник, потому что у него есть две равные стороны.)
Разносторонний — треугольник, у которого все стороны разные.)
5) Научились схематично изображать все виды треугольников? (Да, на самостоятельной работе. )
)
6) Какие открытия вы сегодня сделали? (Новые виды треугольников, их названия.)
7) Ребята, а вы сможете определить вид треугольника по его измерениям? (Да) Я вам сейчас буду говорить измерения, а вы поднимать вверх карточку с названием вида треугольника (карточки выданы дополнительно- по 3 карточки.)
1. 2см, 3см,5 см.- разносторонний
2. 4см, 4см, 2 см — равнобедренный
3.6см, 6см,6см — равносторонний, равнобедренный
Поднимите руки, кто сегодня достиг вершины этого знания? (Поднимают)
А поднимите руки, кому не хватило 1, 2 уровней. (Поднимают.)
(Учитель анализирует «пирамиды знаний у детей, делает выводы — какой уровень западает и на следующем уроке начинает актуализацию знаний с этого.)
Треугольник и его виды
Давайте представим себе такую историю.
– Да как же их тут может оказаться 12? – удивился Саша.
– Саша, что ты там бормочешь? – спросил у
друга Паша.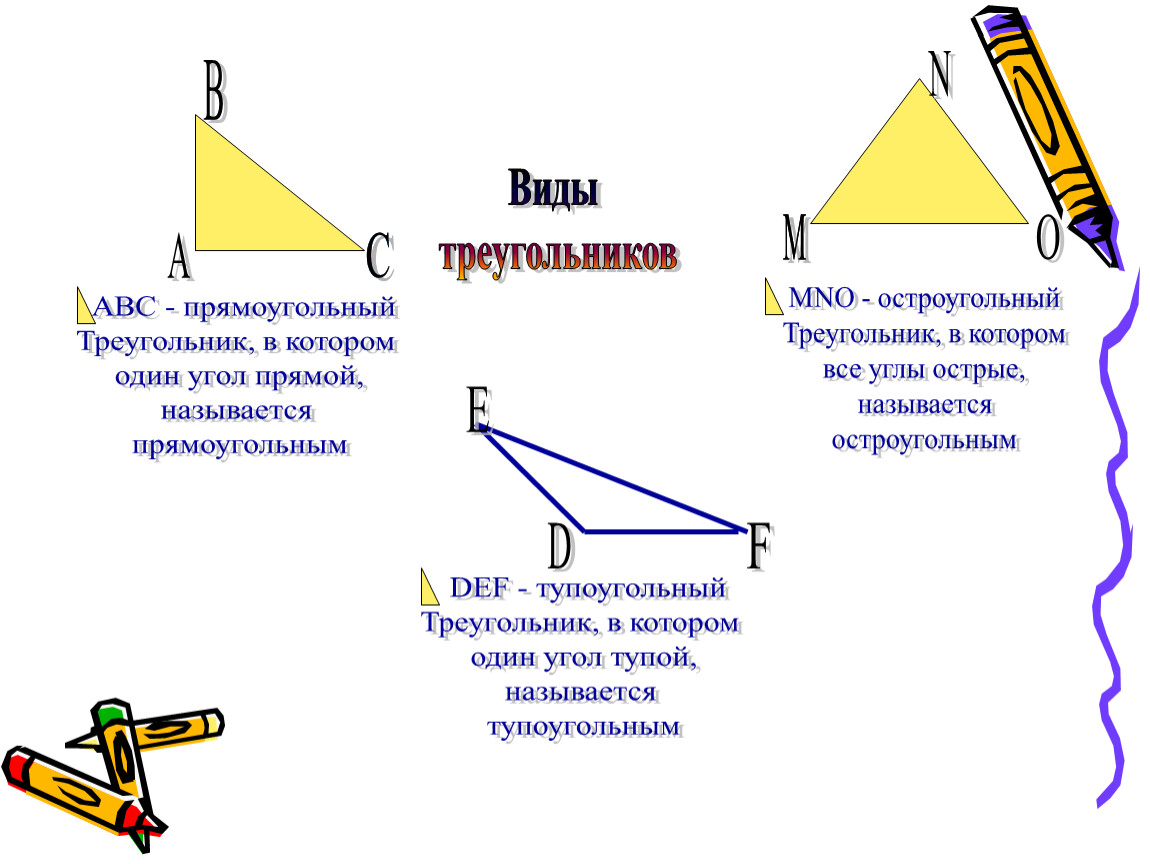
– Да я тут нашёл интересную задачку. Посмотри: нужно посчитать сколько треугольников изображено на рисунке.
– И что тут сложного? – сказал Паша. – Посчитай и всё!
– Так я и посчитал! – пробормотал Саша. – У меня их получилось 6, а в ответе к задаче почему-то написано, что на рисунке изображено 12 треугольников.
– Саша, чтобы увидеть все треугольники на этом рисунке, нужно прежде всего знать, какие бывают виды треугольников.
– Треугольник, он же и в Африке – треугольник! – возмутился Саша. – Какие ещё могут быть виды треугольников?
– А давай спросим у Электроши, он точно знает, какие виды треугольников бывают.
– Ребята, прежде чем я вам расскажу о треугольниках и их видах, давайте немного разомнёмся и выполним устные задания, – предложил Электроша.
– Давайте сверимся! Посмотрите, что у вас должно было получиться!
– А теперь поговорим о треугольниках, –
предложил Электроша. – И сразу начнём с вопроса: как
вы понимаете, что такое треугольник?
– И сразу начнём с вопроса: как
вы понимаете, что такое треугольник?
– Треугольник – это геометрическая фигура, – начал Саша.
– Треугольник – это многоугольник, который состоит из 3 углов, 3 вершин и 3 сторон, – продолжил Паша.
– Молодцы! – похвалил ребят Электроша. – Но хотелось бы уточнить ваши представления о треугольнике. Запомните! Треугольник – это геометрическая фигура, образованная тремя точками, не лежащими на одной прямой, и тремя отрезками, попарно соединяющими эти точки.
Традиционно вершины треугольника обозначают заглавными буквами латинского алфавита: А, B, C. Но, конечно, можно использовать и другие буквы. В тексте треугольник обозначают вот таким символом и тремя прописными буквами, стоящими при вершинах.
– А теперь давайте рассмотрим треугольник ABC. Вы уже знакомы с элементами
многоугольников. Назовите, из каких элементов состоит наш треугольник.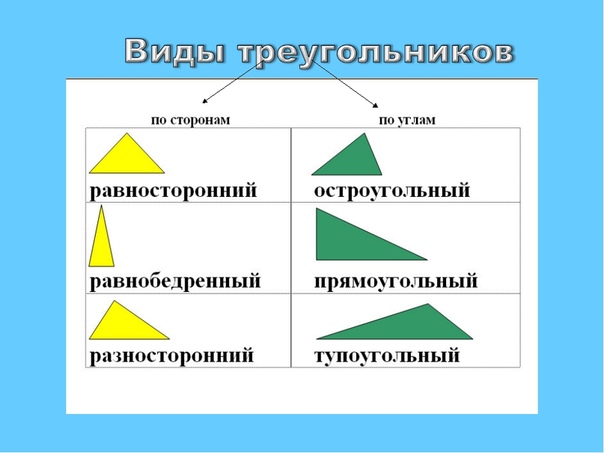
– Треугольник ABC состоит из 3 вершин: А, B, C, 3 углов: А, B, C и 3 сторон: AB, BC, CA, – перечислили мальчишки.
– Всё верно! – подтвердил Электроша.
Основными признаками треугольника являются 3 угла и 3 стороны. Вот как раз по этим элементам можно выделить 6 видов треугольников.
– Ого! Как много! – удивились ребята.
– Итак, треугольники можно различать по виду их углов. Вы знаете, что углы могут быть острыми, прямыми и тупыми.
В зависимости от величин углов различают следующие виды треугольников: остроугольные, прямоугольные и тупоугольные.
Запомните! Если все углы треугольника острые, то есть меньше 90 градусов, то его называют остроугольным треугольником.
Если один из углов треугольника прямой, то
есть равен 90 градусам, то его называют прямоугольным
треугольником.
Если же один из углов треугольника тупой, то есть больше 90 градусов, то его называют тупоугольным треугольником.
– Треугольники также можно классифицировать ещё и по количеству равных сторон, – продолжил Электроша. – Выделяют следующие типы: равнобедренный треугольник, равносторонний треугольник и разносторонний треугольник.
Запомните! Если две стороны треугольника равны, то его называют равнобедренным треугольником. Посмотрите: на листе изображён треугольник ABC, у которого стороны AB и BC равны. Такой треугольник называют равнобедренным. На рисунке равные стороны принято отмечать равным количеством чёрточек. Равные стороны AB и BC называют боковыми сторонами, а сторону AC – основанием равнобедренного треугольника ABC. В равнобедренном треугольнике углы при основании равны.
Если три стороны треугольника равны, то его
называют равносторонним треугольником. Посмотрите: на рисунке
изображён треугольник MNP. Его стороны MN, NP и PM равны. Такой треугольник называют равносторонним.
В равностороннем треугольнике все углы равны. Если сторона равностороннего
треугольника равна а, то его периметр вычисляют по
формуле: P = 3a.
Посмотрите: на рисунке
изображён треугольник MNP. Его стороны MN, NP и PM равны. Такой треугольник называют равносторонним.
В равностороннем треугольнике все углы равны. Если сторона равностороннего
треугольника равна а, то его периметр вычисляют по
формуле: P = 3a.
Если три стороны треугольника имеют различную длину, то его называют разносторонним треугольником.
– Электроша, а в разностороннем треугольнике стороны могут быть совершенно любыми? – спросил Саша.
– Нет, – ответил Электроша, – для того чтобы треугольник существовал, должно выполняться особое условие. Запомните! В треугольнике длина каждой стороны меньше суммы длин двух других сторон.
– Электроша, теперь я понял, о каких видах треугольников мне говорил Паша, – обрадовался Саша. – Сейчас я точно смогу посчитать треугольники на рисунке.
На рисунке можно увидеть 6 маленьких
равнобедренных треугольников,
4 прямоугольных треугольника и 2 больших равнобедренных
треугольника.
Посчитаем… Точно! На рисунке 12 треугольников, – обрадовался Саша.
– Электроша, а существует ли какой-нибудь особый инструмент для построения треугольников? – спросил Паша.
– Любой треугольник можно построить при помощи линейки и транспортира. Сейчас я покажу вам, как это сделать.
Давайте построим треугольник ABC, у которого угол А равен 30 градусам, сторона AB имеет длину 4 см, а сторона AC – 5 см.
Итак, с помощью транспортира построим угол А, градусная мера которого равна 30 градусам. Затем на одной стороне угла от его вершины с помощью линейки отложим отрезок AB равный 4 см, а на второй стороне – отрезок AC равный 5 см. Осталось соединить отрезком точки B и C. Так мы построили искомый треугольник ABC.
– А теперь, ребята, давайте посмотрим, как вы всё поняли, и выполним несколько заданий.
Задание первое: определите вид каждого треугольника.
Решение: так как в первом треугольнике
одинаковыми чёрточками отмечены 3 стороны, значит, он равносторонний. Также мы знаем, что равносторонний треугольник является и остроугольным.
Во втором треугольнике 2 стороны отмечены одинаковыми чёрточками. Это говорит
нам о том, что данный треугольник является равнобедренным. Судя по
углам, можем сказать, что он ещё и остроугольный. В следующем
треугольнике все три стороны отмечены разными чёрточками. Значит, он имеет 3 стороны
разной длины. Следовательно, этот треугольник разносторонний. Также
видно, что он остроугольный. В четвёртом треугольнике снова 3 стороны
отмечены разными чёрточками. Значит, он разносторонний. Видим, что один
угол этого треугольника прямой. Следовательно, треугольник прямоугольный.
И последний треугольник. Три стороны отмечены разными чёрточками, значит, треугольник
разносторонний. Видим, что один из углов этого треугольника больше 90 градусов.
Следовательно, треугольник тупоугольный.
Также мы знаем, что равносторонний треугольник является и остроугольным.
Во втором треугольнике 2 стороны отмечены одинаковыми чёрточками. Это говорит
нам о том, что данный треугольник является равнобедренным. Судя по
углам, можем сказать, что он ещё и остроугольный. В следующем
треугольнике все три стороны отмечены разными чёрточками. Значит, он имеет 3 стороны
разной длины. Следовательно, этот треугольник разносторонний. Также
видно, что он остроугольный. В четвёртом треугольнике снова 3 стороны
отмечены разными чёрточками. Значит, он разносторонний. Видим, что один
угол этого треугольника прямой. Следовательно, треугольник прямоугольный.
И последний треугольник. Три стороны отмечены разными чёрточками, значит, треугольник
разносторонний. Видим, что один из углов этого треугольника больше 90 градусов.
Следовательно, треугольник тупоугольный.
Следующее задание: определите по сторонам
существование треугольника.
Решение: чтобы треугольник существовал, должно выполняться следующее условие: в треугольнике длина каждой стороны должна быть меньше суммы длин двух других сторон. В первом случае стороны треугольника равны 10 см, 1 см и 2 см. Проверим, выполняется ли условие. И сразу видим, что 10 больше суммы 1 и 2. То есть условие не выполняется. Значит, такой треугольник не существует. Во втором случае стороны треугольника равны 18 см, 30 см и 36 см. Проверим, выполняется ли условие. Видим, что любая сторона данного треугольника меньше суммы длин двух других сторон. Значит, такой треугольник существует.
И последнее задание: равнобедренный треугольник имеет периметр 37 см, а его основание имеет длину 9 см. Определите длину боковой стороны треугольника.
Решение: равнобедренный треугольник имеет 2 равные
стороны. Сумма равных сторон будет равна 37 – 9 = 28 см. Значит, каждая из них
будет равна 14 см. Ответ: боковая сторона треугольника имеет длину 14 см.
различных типов треугольников [Видео и практика]
Привет, и добро пожаловать в этот обзор различных типов треугольников! Прежде чем мы начнем, рассмотрим основы.
Треугольник имеет три соединяющиеся прямые стороны. Длина сторон может быть разной, но длина самой большой стороны не может быть равна или больше суммы двух других сторон. Кроме того, треугольник имеет три внутренних угла, и сумма этих трех углов всегда равна 180 градусам. Это верно для всех треугольников, включая шесть типов, которые мы рассматриваем сегодня.
Различные типы треугольников
Мы собираемся разбить наши шесть типов треугольников на две группы по три.
Начнем с трех типов треугольников, которые классифицируются по величине наибольшего угла. Это острый, правый и тупой треугольники.
Но как узнать, что есть что? Взгляните на самый большой угол каждого треугольника и отметьте, больше ли он, меньше или равен 90 градусам.
Острый треугольник
Мы видим, что наибольший угол в треугольнике слева составляет 70 градусов.70 меньше 90, значит, это острый треугольник. Только помните, что острые углы меньше 90 градусов. Это легко запомнить, так как «милые» вещи часто бывают маленькими, например, щенками и котятами.
Прямой треугольник
Мы видим, что в среднем треугольнике наибольший угол составляет ровно 90 градусов. Возможно, вы помните, что угол в 90 градусов — это прямой угол, поэтому этот треугольник является прямоугольным.
Тупой треугольник
Наконец, в треугольнике справа наибольший угол равен 117 градусам.Поскольку это более 90 градусов, это тупой угол, поэтому мы называем этот треугольник тупым треугольником.
Вот и все, что касается этих трех типов! Мы просто находим наибольший угол, и название треугольника будет соответствовать названию этого угла.
Наш второй набор треугольников классифицируется по тому, сколько сторон имеют одинаковую длину. Вот три треугольника с длинами сторон:
Вот три треугольника с длинами сторон:
Равносторонний треугольник
В треугольнике слева мы видим, что все три стороны имеют одинаковую длину и имеют размер 9 сантиметров.Такой треугольник, как этот, у которого все стороны равны, называется равносторонним треугольником. Это имя не так уж сложно запомнить, так как начало равностороннего слова звучит как слово «равный», а слово «боковой» означает «сторона».
Равнобедренный треугольник
В среднем треугольнике мы видим, что две стороны имеют одинаковую длину и составляют 8 см, а третья — 9 см. Когда две стороны треугольника совпадают, он называется равнобедренным треугольником. Его сложно написать по буквам, но легко распознать!
Масштабный треугольник
В нашем последнем треугольнике ни одна из сторон не имеет одинаковой длины, поэтому это называется неравномерным треугольником.
Хотя вы часто видите эти три типа треугольников, идентифицируемых по длине их сторон, их также можно разделить на категории по их углам.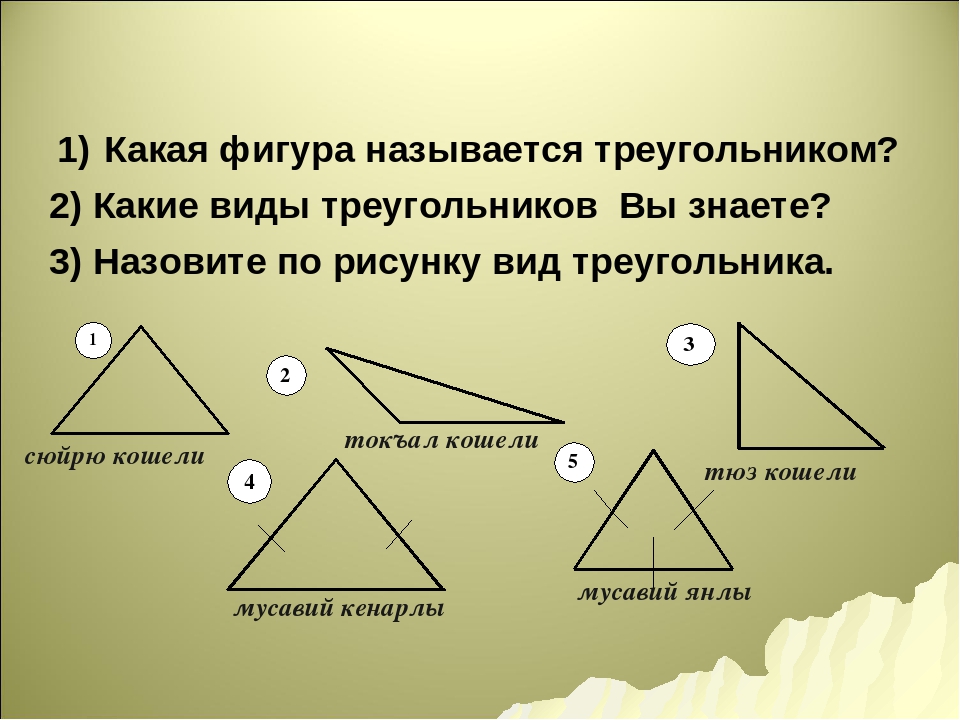 Это работает точно так же:
Это работает точно так же:
Когда все углы равны 60 градусам, получается равносторонний треугольник . Технически это называется равносторонним треугольником, но это одно и то же, потому что все равносторонние треугольники также являются равноугольными треугольниками. Когда два угла совпадают, получается равнобедренный треугольник. А когда ни один из углов не совпадает, получается разносторонний треугольник.
На данный момент мы рассмотрели шесть типов треугольников, которые технически являются всеми типами, но мы еще не закончили. Если мы хотим быть действительно конкретными при именовании треугольников, мы можем комбинировать имена из каждой группы; один из первой группы и один из второй группы.
Например, треугольник выше — это остроугольный треугольник . Его наибольший угол меньше 90 градусов, поэтому он острый, и ни один из его углов не совпадает, поэтому он разносторонний.
Прежде чем мы продолжим, как насчет того, чтобы вы попробовали. Определите эти два треугольника, выбрав острый, правый или тупой, а затем выбрав равносторонний, равнобедренный или разносторонний.
Определите эти два треугольника, выбрав острый, правый или тупой, а затем выбрав равносторонний, равнобедренный или разносторонний.
Думаете, вы поняли? Треугольник слева — это тупоугольный разносторонний треугольник , а правый — прямоугольный равнобедренный треугольник .
Надеюсь, этот обзор был полезен! Спасибо за просмотр и удачной учебы!
Типы треугольников — определения, свойства, примеры
различных типов треугольников классифицируются по длине их сторон и по величине углов.Треугольник — одна из самых распространенных форм, которая используется в строительстве из-за своей жесткости и стабильной формы. Понимание этих свойств позволяет нам применять идеи во многих реальных проблемах.
Какие бывают типы треугольников?
В математике есть разные типы треугольников, которые можно различить по их сторонам и углам.Классифицирующие треугольники
Характеристики сторон и углов треугольника используются для их классификации. Различные типы треугольников следующие:
Различные типы треугольников следующие:
| Типы треугольников по сторонам | Типы треугольников на основе углов |
|---|---|
| Равносторонний треугольник | Острый треугольник (Acute Triangle) |
| Равнобедренный треугольник | Прямоугольный треугольник (Right Triangle) |
| Масштабный треугольник | Тупоугольный треугольник (Тупоугольный треугольник) |
Типы треугольников по сторонам
По длине сторон треугольники подразделяются на следующие типы:
- Равносторонний треугольник: Треугольник считается равносторонним, если все три стороны имеют одинаковую длину.
- Равнобедренный треугольник: Если две стороны треугольника равны или совпадают, он называется равнобедренным треугольником.
- Масштабный треугольник: Если ни одна из сторон треугольника не равна, он называется неравномерным треугольником.

Типы треугольников по углам
По углам треугольники подразделяются на следующие типы:
- Острый треугольник : Когда все углы треугольника острые, то есть меньше 90 °, он называется остроугольным или острым треугольником.
- Прямоугольник : Когда один из углов треугольника равен 90 °, он называется прямоугольным или прямоугольным.
- Тупоугольный треугольник : Когда один из углов треугольника является тупым углом, то есть его размер превышает 90 °, он называется треугольником с тупым углом или тупым треугольником.
Типы треугольников по сторонам и углам
Различные типы треугольников также классифицируются в зависимости от их сторон и углов следующим образом:
- Равносторонний или равносторонний треугольник : Когда все стороны и углы треугольника равны, он называется равносторонним или равноугольным треугольником.

- Равнобедренный прямоугольный треугольник : Треугольник, в котором 2 стороны равны и один угол равен 90 °, называется равнобедренным прямоугольным треугольником. Итак, в равнобедренном прямоугольном треугольнике две стороны и два острых угла совпадают.
- Тупой равнобедренный треугольник : Треугольник, в котором 2 стороны равны, а один угол является тупым, называется тупым равнобедренным треугольником.
- Острый равнобедренный треугольник : Треугольник, в котором все 3 угла являются острыми углами, а две стороны имеют одинаковое значение, называется острым равнобедренным треугольником.
- Прямоугольный разносторонний треугольник : Треугольник, в котором любой из углов является прямым, а все три стороны не равны, называется прямоугольным разносторонним треугольником.
- Тупой разносторонний треугольник : Треугольник с тупым углом и сторонами разных размеров называется тупо-разносторонним треугольником.

- Острый разносторонний треугольник : Треугольник с 3 неравными сторонами и 3 острыми углами называется острым разносторонним треугольником.
☛Важные примечания:
Вот список из нескольких моментов, которые следует помнить при изучении типов треугольников:
- В равностороннем треугольнике каждый из трех внутренних углов равен 60 °.
- Сумма трех внутренних углов в треугольнике всегда составляет 180 °.
- У всех треугольников по два острых угла.
- Когда все стороны и углы треугольника равны, он называется равносторонним или равноугольным треугольником.
☛ Связанные темы:
Часто задаваемые вопросы о типах треугольников
Какие типы треугольников в геометрии?
В геометрии существует шесть типов треугольников. Их можно разделить на 2 группы. По сторонам эти 3 треугольника классифицируются как равносторонние треугольники, равнобедренные треугольники и равносторонние треугольники. В зависимости от их углов, три типа треугольников перечислены как острый треугольник, тупой треугольник и прямоугольный треугольник.Таким образом, в геометрии существует шесть типов треугольников.
В зависимости от их углов, три типа треугольников перечислены как острый треугольник, тупой треугольник и прямоугольный треугольник.Таким образом, в геометрии существует шесть типов треугольников.
Какие 3 типа треугольников в зависимости от их углов?
На основании углов треугольники подразделяются на острый треугольник, прямоугольный треугольник и тупой треугольник.
- Острый треугольник: В остром треугольнике все углы меньше 90 °.
- Прямой треугольник: когда один угол треугольника равен 90 °, он называется прямоугольным треугольником.
- Тупоугольный треугольник: Когда один из углов треугольника является тупым углом, он называется тупоугольным треугольником.
Какие типы треугольников основаны на сторонах?
По сторонам треугольники подразделяются на 3 типа.
- Равносторонний треугольник: когда все три стороны имеют одинаковую длину, треугольник считается равносторонним.
- Равнобедренный треугольник: Если две стороны треугольника равны, он называется равнобедренным треугольником.

- Масштабный треугольник: Если все стороны треугольника имеют разную длину, он называется разносторонним треугольником.
Какие типы треугольников имеют три линии симметрии?
Все равносторонние треугольники имеют 3 линии симметрии, поскольку три линии симметрии могут проходить через вершину этого треугольника.
Какие типы треугольников имеют симметрию отражения?
Все равносторонние и равнобедренные треугольники обладают симметрией отражения.
Какие 6 типов треугольников?
Можно перечислить 6 типов треугольников: острый треугольник, тупой треугольник, прямоугольный треугольник, равносторонний треугольник, равнобедренный треугольник и разносторонний треугольник.
типов треугольников и их свойства — стенограмма видео и урока
Основание, высота, высота и площадь
Основание треугольника относится к нижней стороне треугольника. Любая сторона может быть основой, если она считается нижней стороной треугольника. Высота треугольника — это линия, перпендикулярная основанию треугольника и проходящая через угол напротив основания. Длина высоты от основания до противоположного угла равна высотой треугольника.Наконец, область — это количество места внутри треугольника.
Высота треугольника — это линия, перпендикулярная основанию треугольника и проходящая через угол напротив основания. Длина высоты от основания до противоположного угла равна высотой треугольника.Наконец, область — это количество места внутри треугольника.
Эти четыре части треугольника объединяются в формулу для площади треугольника:
A = (1/2) b h
где b = длина основания и h = высота (или высота над уровнем моря)
Например, если треугольник имеет длину основания 4 сантиметра и высоту 10 сантиметров, то мы можем найти площадь треугольника, вставив b = 4 и ч = 10 в формулу и упрощение.
A = (1/2) (4) (10) = 20
Мы видим, что площадь описанного треугольника составляет 20 квадратных сантиметров.
Когда дело доходит до высоты треугольника, есть один тип треугольника, в котором высота может быть одной из сторон, и это прямоугольный треугольник.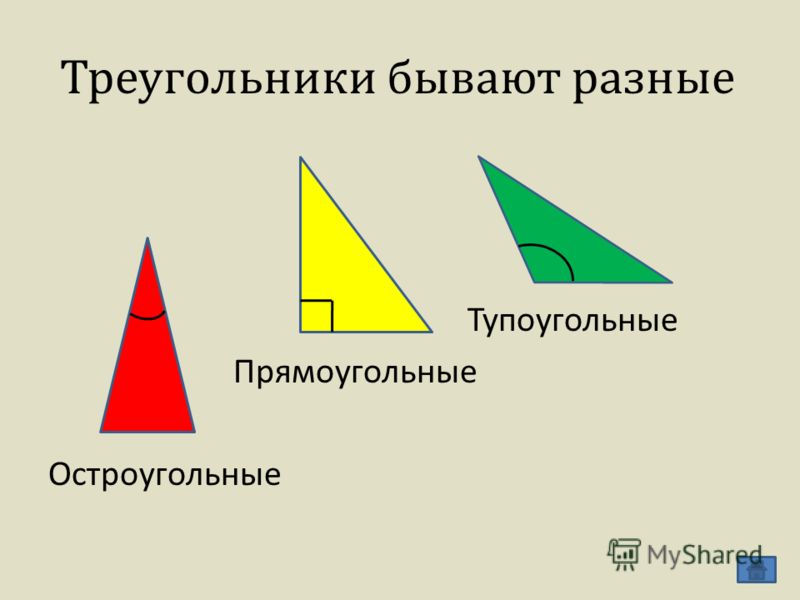 Прямоугольный треугольник имеет угол 90 градусов, поэтому две его стороны перпендикулярны. Если мы рассматриваем одну из перпендикулярных сторон как основание, тогда другая перпендикулярная сторона перпендикулярна основанию и проходит через угол напротив основания, делая его высотой.
Прямоугольный треугольник имеет угол 90 градусов, поэтому две его стороны перпендикулярны. Если мы рассматриваем одну из перпендикулярных сторон как основание, тогда другая перпендикулярная сторона перпендикулярна основанию и проходит через угол напротив основания, делая его высотой.
Другой треугольник с особой высотой — это равносторонний треугольник. Высота равностороннего треугольника делит основание ровно пополам и разделяет треугольник на два равных прямоугольных треугольника
Есть также очень важное свойство прямоугольных треугольников, которое связывает длины сторон треугольника вместе. Это называется теорема Пифагора. Давайте обсудим!
Теорема Пифагора
В прямоугольном треугольнике мы называем самую длинную сторону треугольника гипотенузой , а две короткие стороны — катетами .Теорема Пифагора показывает взаимосвязь между этими длинами сторон и утверждает, что если катеты прямоугольного треугольника имеют длины a и b , а длина гипотенузы c , то
a 2 + b 2 = c 2
Например, предположим, что есть болото, заполненное аллигаторами, через которое вы хотите построить мост. Вы, конечно, не собираетесь идти в болото, чтобы измерить длину моста, поэтому вы рассматриваете равносторонний треугольник, высота которого равна длине моста.Одна сторона треугольника полностью находится на суше, так что вы можете измерить ее как 100 футов в длину.
Вы, конечно, не собираетесь идти в болото, чтобы измерить длину моста, поэтому вы рассматриваете равносторонний треугольник, высота которого равна длине моста.Одна сторона треугольника полностью находится на суше, так что вы можете измерить ее как 100 футов в длину.
Поскольку это равносторонний треугольник, основание должно иметь ту же длину, что и измеренная сторона (или 100 футов), а высота создает два прямых угла внутри треугольника. Кроме того, мы знаем, что высота разрезает основание прямо пополам, поэтому мы знаем, что гипотенуза прямоугольного треугольника составляет 100 футов, а длина одного из катетов — 50 футов. Мы просто подставляем a = 50 и c = 100 в формулу, а затем решаем для a , и у нас есть длина моста.
Теорема Пифагора говорит нам, что мост будет примерно 86,6 футов в длину.
Резюме урока
Напомним, что треугольник — это трехсторонний трехугольный многоугольник.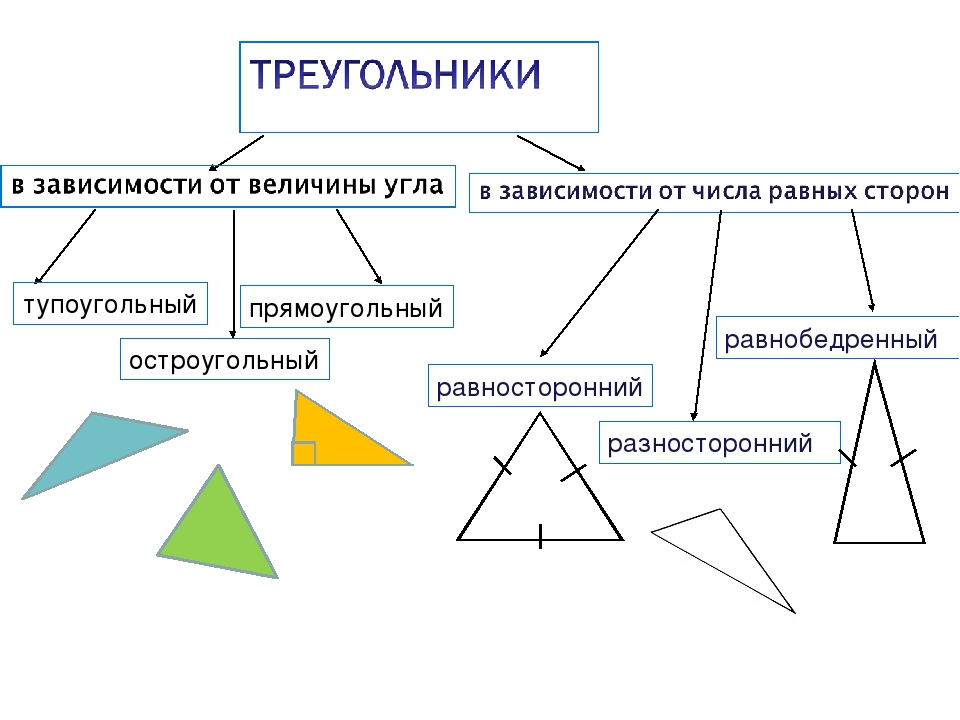 Существует ряд различных типов треугольников, таких как равносторонних треугольников , прямоугольных треугольников , разносторонних треугольников , тупых треугольников , острых треугольников и равнобедренных треугольников .Все эти треугольники имеют четыре общие черты: основания, высоты, высоты и площади, и они связаны в формуле для площади треугольника.
Существует ряд различных типов треугольников, таких как равносторонних треугольников , прямоугольных треугольников , разносторонних треугольников , тупых треугольников , острых треугольников и равнобедренных треугольников .Все эти треугольники имеют четыре общие черты: основания, высоты, высоты и площади, и они связаны в формуле для площади треугольника.
Еще одно важное свойство треугольников связано именно с прямоугольными треугольниками, и это теорема Пифагора , которая утверждает, что если прямоугольный треугольник имеет катеты с длинами , a, и , b , а гипотенуза длиной c , затем
a 2 + b 2 = c 2
Знание типов и свойств треугольников оказывается очень полезным как в абстрактных, так и в реальных приложениях треугольников, поэтому рекомендуется поместить их на память и продолжать практиковаться с этими свойствами.
Сколько существует типов треугольников?
Вы знаете свои формы? Конечно, если вы видите круг, вы, вероятно, сможете его идентифицировать, верно? Но как насчет этих форм с множеством сторон и множеством углов? Это может быть немного сложнее.
Как вы определяете формы? Многие дети начинают с подсчета количества сторон. Например, если вы видите фигуру с четырьмя сторонами, что бы это было? В зависимости от длины сторон получается квадрат или прямоугольник.
Если вы наткнетесь на фигуру с трех сторон, как вы ее назовете? Если вы сказали треугольник, вы поняли! Но что это за треугольник? Знаете ли вы, что существует более одного типа треугольников? Это так! Простой трехсторонний треугольник можно определить несколькими способами.
Помимо трех сторон, у каждого треугольника есть еще три угла. Эти три угла всегда составляют 180 °. Математики дали треугольникам специальные имена в зависимости от того, сколько из этих углов равно.
Например, у равностороннего треугольника три равных угла (и три равные стороны). Каждый угол в равностороннем треугольнике равен 60 °, так как три угла по 60 ° в сумме дают 180 °.
Равнобедренный треугольник имеет два равных угла (и две равные стороны). Углы могут быть разными, если они равны.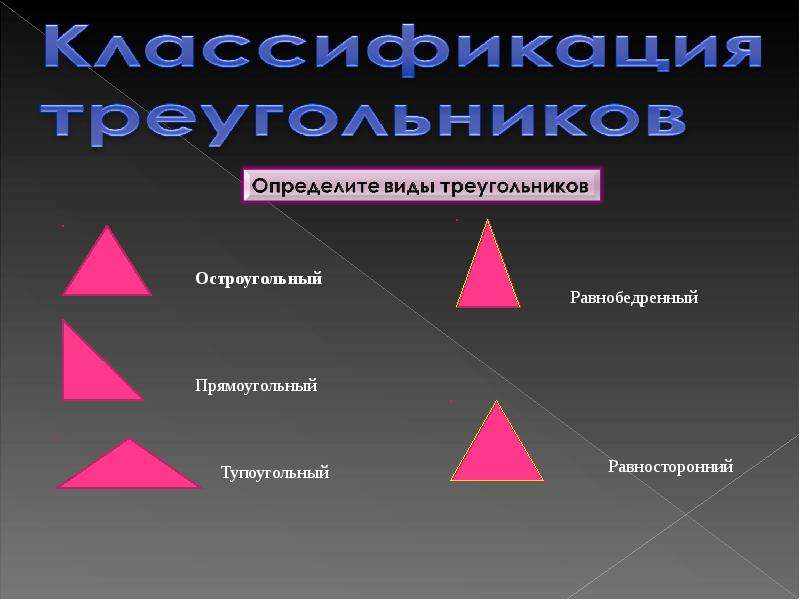 Например, треугольник с двумя углами 70º и одним углом 40º будет равнобедренным треугольником.
Например, треугольник с двумя углами 70º и одним углом 40º будет равнобедренным треугольником.
Если вы внимательно подсчитали, то знаете, что есть еще один вариант. Если у треугольника нет двух или трех равных углов, у него может быть ноль равных углов.Эти треугольники, у которых также нет равных сторон, называются разносторонними треугольниками.
Можете ли вы поверить, что существует три разных типа треугольников? Но подождите … это еще не все! Специалистов по геометрии не удовлетворили всего три типа треугольников. Они также решили классифицировать треугольники по типу углов внутри треугольника.
Например, у некоторых треугольников прямой угол. Это угол, равный 90º. Они известны как прямоугольные треугольники. Однако у некоторых треугольников три угла меньше 90 °.Такой треугольник называется острым треугольником. Треугольник также может иметь угол более 90º. Эти треугольники называются тупыми треугольниками.
Конечно, разновидностей треугольников еще больше.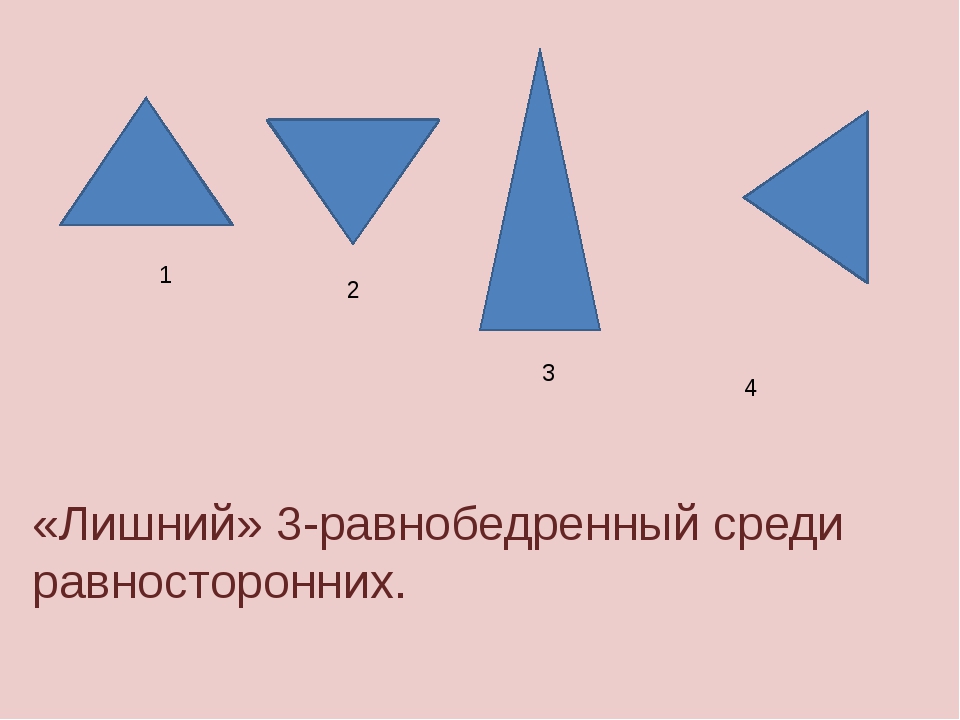 Вы можете комбинировать имена в зависимости от их особенностей. Например, треугольник с углами 45º, 45º и 90º является правильным равнобедренным треугольником. Это прямоугольный треугольник, потому что у него угол 90 градусов. Это равнобедренный треугольник, потому что у него два равных угла по 45º.
Вы можете комбинировать имена в зависимости от их особенностей. Например, треугольник с углами 45º, 45º и 90º является правильным равнобедренным треугольником. Это прямоугольный треугольник, потому что у него угол 90 градусов. Это равнобедренный треугольник, потому что у него два равных угла по 45º.
Так что в следующий раз, когда вы увидите фигуру с тремя сторонами, не кричите просто «треугольник!» Вместо этого попытайтесь выяснить, что это за треугольник.
Стандарты: CCSS.MATH.CONTENT.1.GA.1, CCSS.MATH.CONTENT.2.GA.1, CCSS.MATH.CONTENT.4.GA.2, CCRA.L.3, CCRA.L.6, CCRA .R.1, CCRA.R.2, CCRA.R.10, CCRA.SL.1
типов треугольников — объяснения и примеры
В геометрии треугольник является наиболее важной формой , определяемой как замкнутая двумерная диаграмма, содержащая 3 стороны, 3 угла и 3 вершины. Проще говоря, треугольник — это многоугольник с 3 сторонами. Слово «треугольник» происходит от латинского слова «triangulus», что означает треугольник.
Проще говоря, треугольник — это многоугольник с 3 сторонами. Слово «треугольник» происходит от латинского слова «triangulus», что означает треугольник.
В древние времена астрономы создали метод, называемый триангуляцией, для определения расстояний до далеких звезд. Они измеряют расстояние от двух разных мест, а затем измеряют угол, образованный сдвигом или параллаксом, образованным движением наблюдателя между двумя точками. Затем они применили закон синусов для вычисления необходимого расстояния.
Египтяне создали пирамиды около 2900 г. до н. Э. По форме он напоминает трехмерную пирамиду с треугольными гранями. Это идеально спроектированная модель, длина и углы которой одинаковы со всех сторон. Милет (624 г. до н.э. — 547 г. до н.э.), греческий математик, перенял геометрию Египта и был доставлен в Грецию.
Аристарх (310 г. до н.э. — 250 г. до н.э.), греческий математик, использовал вышеуказанный метод, чтобы найти расстояние между Землей и Луной. Эратосфен (276 г. до н.э. — 195 г. до н.э.) снова использовал тот же метод для определения расстояния вокруг поверхности Земли (называемого окружностью).
до н.э. — 195 г. до н.э.) снова использовал тот же метод для определения расстояния вокруг поверхности Земли (называемого окружностью).
В этой статье будет обсуждаться значение треугольника , различных типов треугольников и их свойства, а также их практическое применение.
Что такое треугольник?
Треугольник — это двумерная замкнутая фигура с 3 сторонами. Это многоугольник с тремя углами, тремя вершинами и тремя углами, соединенными вместе, которые образуют замкнутую диаграмму. Мы используем символ ∆ для обозначения треугольника.
Рисунки A и B представляют собой треугольники.
Различные типы треугольников
Типы треугольников классифицируются на основе:
- Длины их сторон
- Внутренние углы
Классификация треугольников по величине внутренних углов
Согласно Что касается внутренних углов, мы можем разделить треугольники на три категории:
- Острый угол
- Тупоугольный
- Прямоугольный
Острый треугольник
Треугольник с острым углом — это треугольник, в котором все три внутренние углы менее 90 градусов.
Каждый из углов a, b и c меньше 90 градусов.
Тупой треугольник
Тупой треугольник — это треугольник, в котором один из внутренних углов больше 90 градусов.
Угол a более тупой, а углы b и c острые.
Прямой треугольник
Прямоугольный треугольник — это треугольник, в котором один из углов равен точно 90 градусам. Гипотенуза — это сторона прямоугольного треугольника с наибольшей длиной.
На рисунке выше угол a = 90 градусов, а углы b и c являются острыми углами.
Классификация треугольников по длине их сторон
Мы можем классифицировать треугольники на 3 типа в зависимости от длины их сторон:
- Скален
- Равнобедренный
- Равносторонний
Равнобедренный треугольник
Равнобедренный треугольник треугольник, в котором две стороны и два угла равны. Треугольники одинаковой длины показаны по дуге с каждой стороны.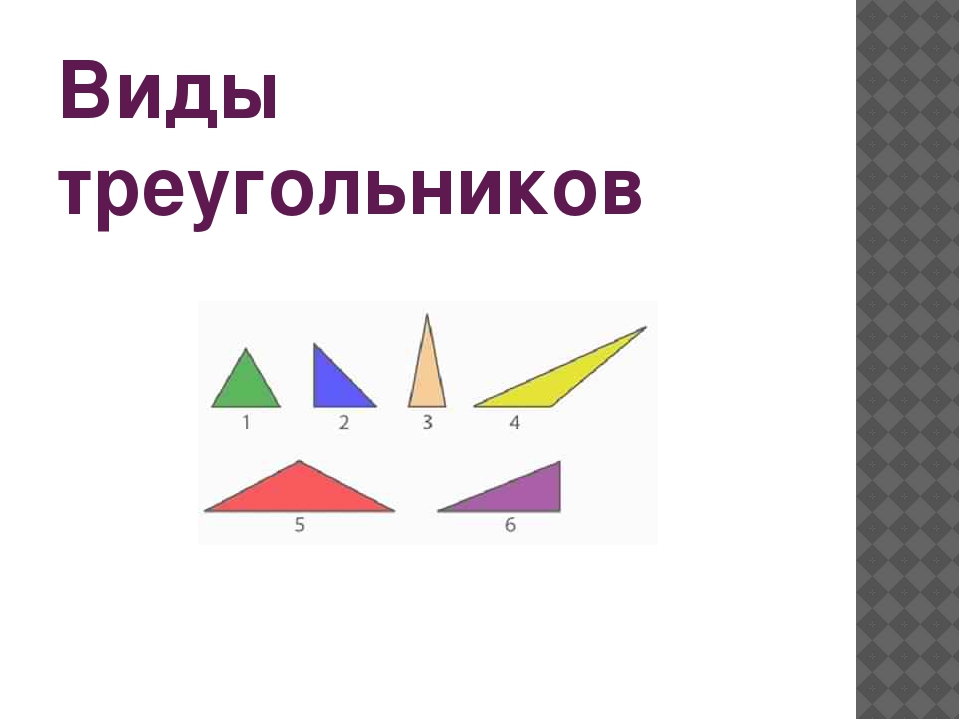
На диаграмме выше , длина стороны AB = AC и ∠ ABC = ∠ ACB.
Равносторонний треугольник
У равностороннего треугольника все три стороны равны, и все три внутренних угла также равны. В этом случае каждый внутренний угол равностороннего треугольника составляет 60 градусов. Равносторонний треугольник иногда называют равносторонним треугольником, потому что все три угла равны.
В равностороннем треугольнике стороны AB = BC = AC и ∠ ABC = ∠ ACB = ∠ BAC
Обратите внимание, что углы равностороннего треугольника не зависят по длинам сторон.
Масштабный треугольник
Разносторонний треугольник — это треугольник, в котором все стороны имеют разные размеры, и все внутренние углы также разные.
Свойства треугольника
Свойства треугольников широко используются. Многие математики использовали его при решении своих задач. Евклидова геометрия и тригонометрия широко используют свойства треугольников.
Евклидова геометрия и тригонометрия широко используют свойства треугольников.
Вот несколько основных свойств треугольника:
- Треугольник — это двумерный многоугольник
- Треугольник имеет 3 стороны, 3 угла и 3 вершины.
- Сумма длин любых двух сторон треугольника больше длины оставшейся стороны.
- Сумма длин трех сторон дает периметр треугольников.
- Площадь треугольника равна произведению основания на высоту.
Рабочие примеры на различных типах треугольников
Пример 1
Найдите значение угла x в треугольнике ниже.
Решение
Это равнобедренный треугольник, в котором две стороны равны, а также два угла равны.Следовательно,
x = (180 ° — 70 °) / 2
x = 110 ° / 2
= 55 °
Пример 2
Найдите угол y в прямоугольном треугольнике, показанном ниже.
Решение
Один угол прямоугольного треугольника равен 90 °.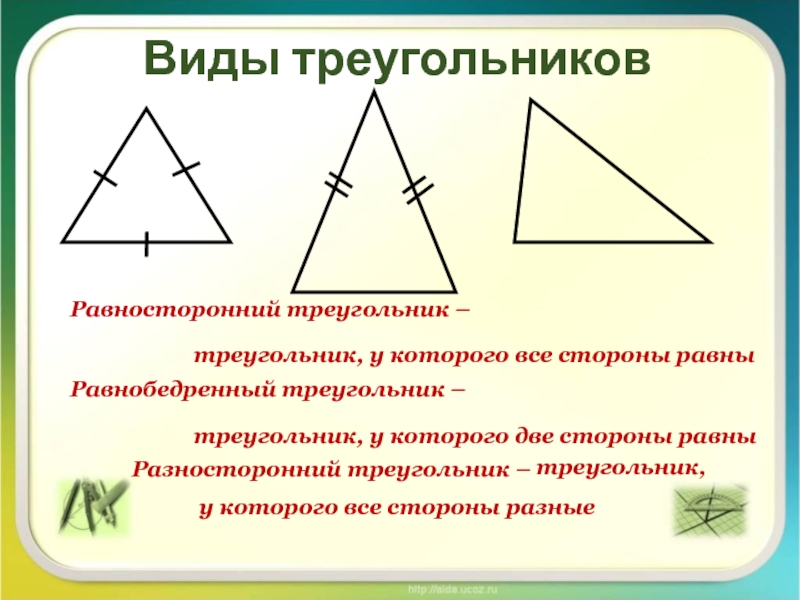 Итак, мы;
Итак, мы;
y + 50 + 90 = 180
y = (180 — 140) °
y = 40 °
Пример 3
Классифицируйте следующий треугольник.
Решение
Это разносторонний треугольник, потому что все стороны и углы имеют разные размеры.Точно так же треугольник также можно классифицировать как тупой треугольник, потому что один угол тупой.
Пример 4
Классифицируйте треугольник, показанный ниже.
Решение
Это равнобедренный треугольник. Две стороны равны, и два угла равны по размеру.
Применение треугольников
Давайте рассмотрим некоторые из реальных приложений треугольников:
- Дорожные знаки. Большинство дорожных знаков отображаются на треугольных структурах.
- Пирамиды Египта: пирамиды — древние памятники, построенные египтянами. Пирамиды имеют треугольную форму.
- Ферма: Фермы крыш или мостов изготавливаются треугольной формы, потому что треугольник считается самой прочной формой.

- Бермудский треугольник: Бермудский треугольник — это треугольная область в Атлантическом океане, где считается, что любое судно или самолет, проходящие через точку, проглатываются. Считается, что 50 кораблей и 20 самолетов загадочным образом исчезли в Бермудском треугольнике.
- Глобальная система позиционирования (GPS) работает с алгоритмами триангуляции для определения долготы и широты объекта.
- Лестница, прислоненная к стене, имеет форму треугольника.
- Эйфелева башня имеет треугольную форму.
- Концепция треугольников вычисляет высоту или высоту высоких объектов, таких как флагштоки, горы, здания и т. Д.
- Сэндвичи и кусочки пиццы имеют треугольную форму.
Классификация треугольников по сторонам или углам
Классификация треугольников по сторонам или углам
Треугольники можно классифицировать по их сторонам или по углам.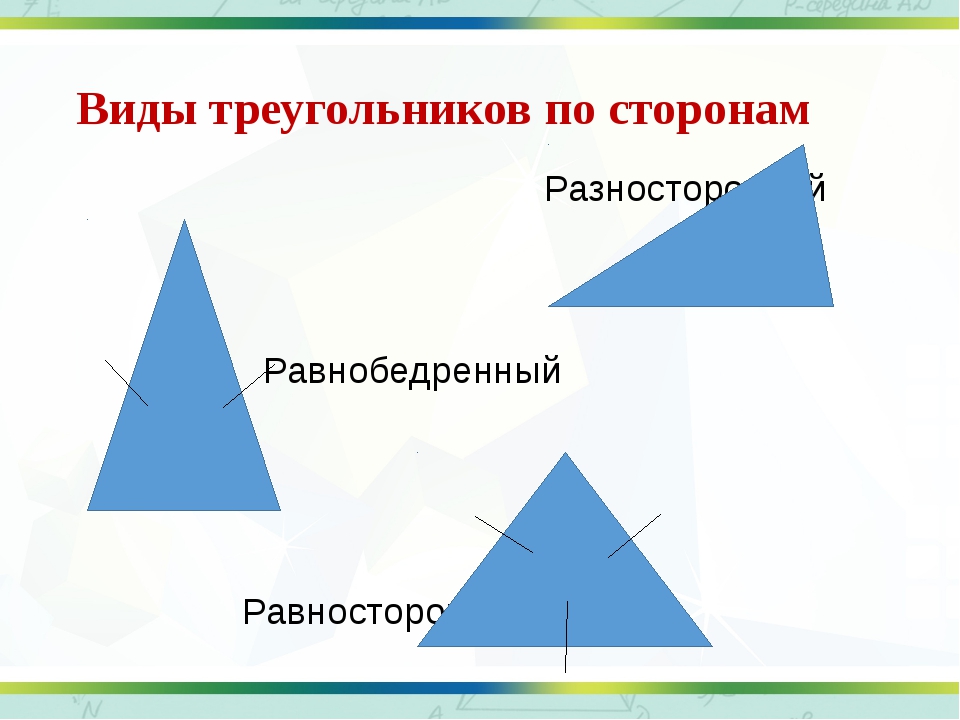 Все они могут быть разных или одинаковых размеров; любые две стороны или углы могут быть одного размера; может быть один отличительный угол.
Все они могут быть разных или одинаковых размеров; любые две стороны или углы могут быть одного размера; может быть один отличительный угол.
Типы треугольников, классифицируемые по их сторонам , следующие:
- Равносторонний треугольник: Треугольник, все три стороны которого равны по размеру. На рис. 1 косая черта обозначает одинаковую меру.
Рисунок 1 Равносторонний треугольник
- Равнобедренный треугольник: Треугольник, в котором по крайней мере две стороны имеют одинаковую меру (рисунок 2).
Рисунок 2 Равнобедренные треугольники
- Масштабный треугольник: Треугольник, все три стороны которого имеют разные размеры (рис. 3).
Рисунок 3 Чешуйчатый треугольник
Типы треугольников, классифицируемые по их углам , включают следующие:
- Прямой треугольник: Треугольник с прямым углом внутри (Рис.
 4).
4).
Рисунок 4 Прямой треугольник
- Тупой треугольник: Треугольник с тупым углом (больше 90 °, но меньше 180 °) внутри. На рисунке 5 показан тупой треугольник.
Рисунок 5 Тупой треугольник
- Острый треугольник: Треугольник, имеющий все острые углы (менее 90 °) внутри (рисунок 6).
Рисунок 6 Острый треугольник.
- Равносторонний треугольник: Треугольник, все углы которого равны (рис. 7).
Рисунок 7 Равноугольный треугольник
Поскольку сумма всех углов треугольника равна 180 °, легко показать следующую теорему.
Теорема 27: Каждый угол равностороннего треугольника имеет меру 60 °.
Какие бывают типы треугольников
Классификация треугольников Треугольник — это многоугольник с тремя сторонами. У него три стороны и три вершины. Есть семь типов треугольников. Сумма углов треугольника равна 180 °.
У него три стороны и три вершины. Есть семь типов треугольников. Сумма углов треугольника равна 180 °.
Треугольники можно классифицировать двумя способами:
- По их сторонам
- По их углам
каковы шесть типов треугольников?
Шесть различных типов треугольников: равнобедренный, равносторонний, тупой, острый и чешуйчатый.
Классификация треугольников по сторонам Скалистый треугольник:
Треугольник, у которого нет равных по длине сторон, называется разносторонним треугольником.
На рисунке PQ ≠ QR ≠ PR, поэтому ΔPQR представляет собой разносторонний треугольник.
Равнобедренный треугольник:
Треугольник с двумя сторонами равной длины называется равнобедренным треугольником.
На рисунке AB = AC, поэтому ΔABC — равнобедренный треугольник.
Равносторонний треугольник:
Треугольник, у которого все три стороны равны по длине, называется равносторонним треугольником.
На рисунке PQ = QR = PR, поэтому ΔPQR — равносторонний треугольник.
Классификация треугольников по углам
Остроугольный треугольник:
Треугольник, все углы которого острые (менее 90 °), называется остроугольным треугольником или просто острым треугольником.
На рисунке все ∠A, ∠B и ∠C меньше 90 °, следовательно, ΔABC — это остроугольный треугольник.
Прямоугольный треугольник:
Треугольник, один из углов которого является прямым, т.е.е., 90 °, называется прямоугольным треугольником или просто прямоугольным треугольником.
На рисунке ∠B = 90 °, следовательно, ΔABC — прямоугольный треугольник.
Треугольник с тупым углом:
Треугольник, один угол которого тупой, называется треугольником с тупым углом или просто тупым треугольником.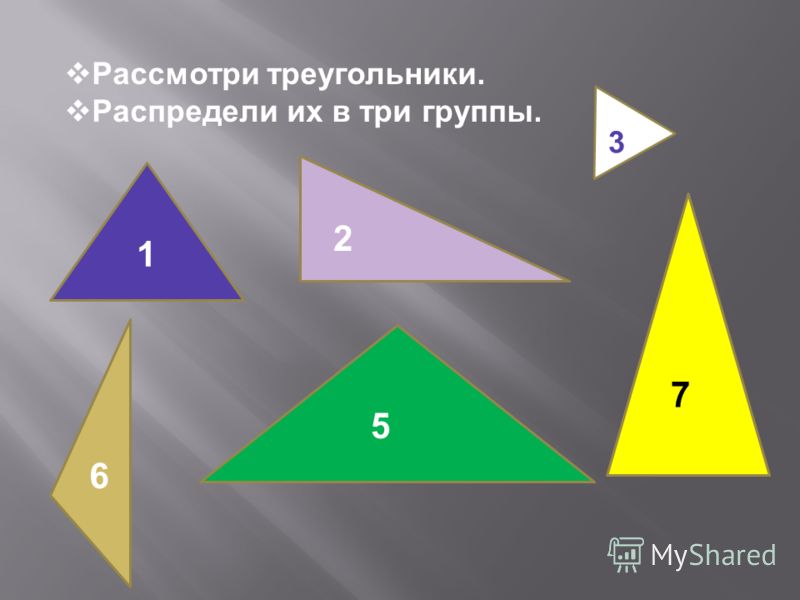
На рисунке ∠Y тупой, следовательно, ΔXYZ — это тупоугольный треугольник или просто тупой треугольник.
Равноугольный треугольник:
Когда все три угла треугольника равны, он называется равноугольным треугольником.
Равносторонний треугольник также известен как равносторонний треугольник, потому что все три стороны равны.
На рисунке ∠A = ∠B = ∠C = 60 ° и AB = BC = AC, следовательно, ΔABC — равноугольный треугольник.
Пример 1: Один из равных углов равнобедренного треугольника равен 50 °. Найдите его третий угол.
Решение: Пусть третий угол = x
∴ x + 50 ° + 50 ° = 180 °
(свойство суммы углов треугольника)
или, x + 100 ° = 180 °
или, x = 180 ° — 100 °
= 80 °
∴ Третий угол = 80 °
Пример 2: Каждый из двух равных углов треугольника в четыре раза больше третьего угла.Найдите все углы треугольника.
Решение: Пусть меньший угол = x
∴ другие два угла = 4x и 4x
Таким образом, x + 4x + 4x = 180 °
(свойство суммы углов треугольника) или 9x = 180 °
∴ 4x = 4 x 20 °
= 80 °
Таким образом, углы треугольника равны 20 °, 80 ° и 80 °.
 Поскольку все 3 стороны фигуры имеют одинаковую длину, все 3 угла у нее также равны. Каждый внутренний угол равностороннего треугольника равен 60°.
Поскольку все 3 стороны фигуры имеют одинаковую длину, все 3 угла у нее также равны. Каждый внутренний угол равностороннего треугольника равен 60°.

 Дострой треугольник до логического
завершения, определи, какой вид
треугольника у тебя получился?
Дострой треугольник до логического
завершения, определи, какой вид
треугольника у тебя получился?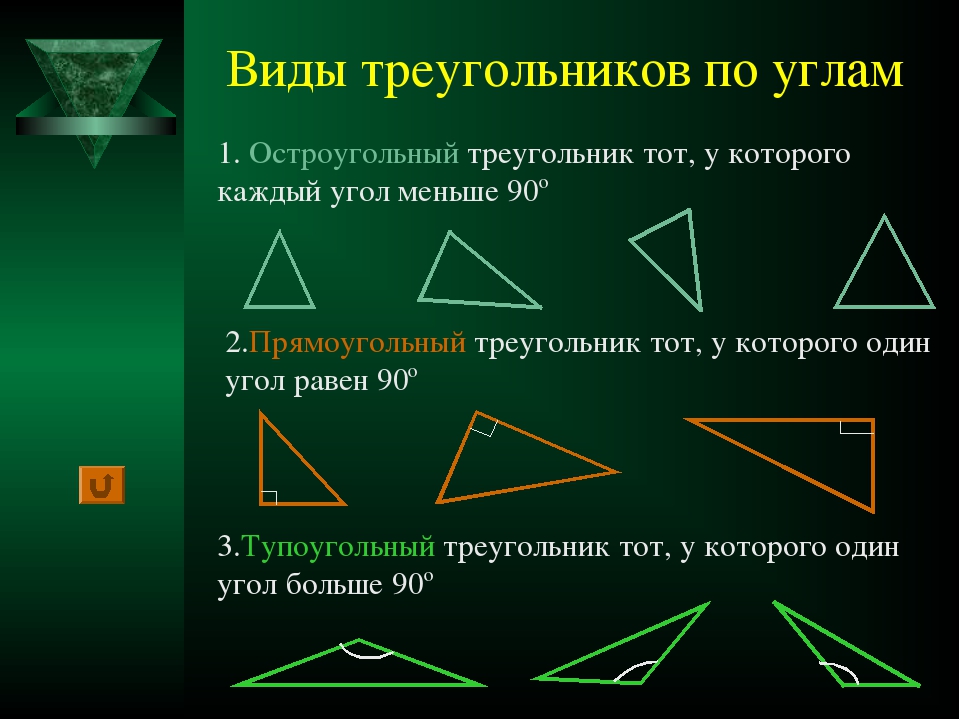 Определи сколько
Определи сколько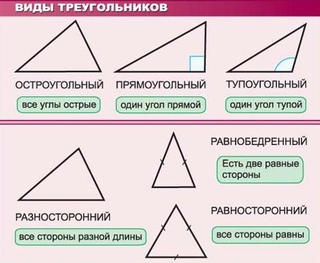 Определи, какой это вид треугольника?
Определи, какой это вид треугольника?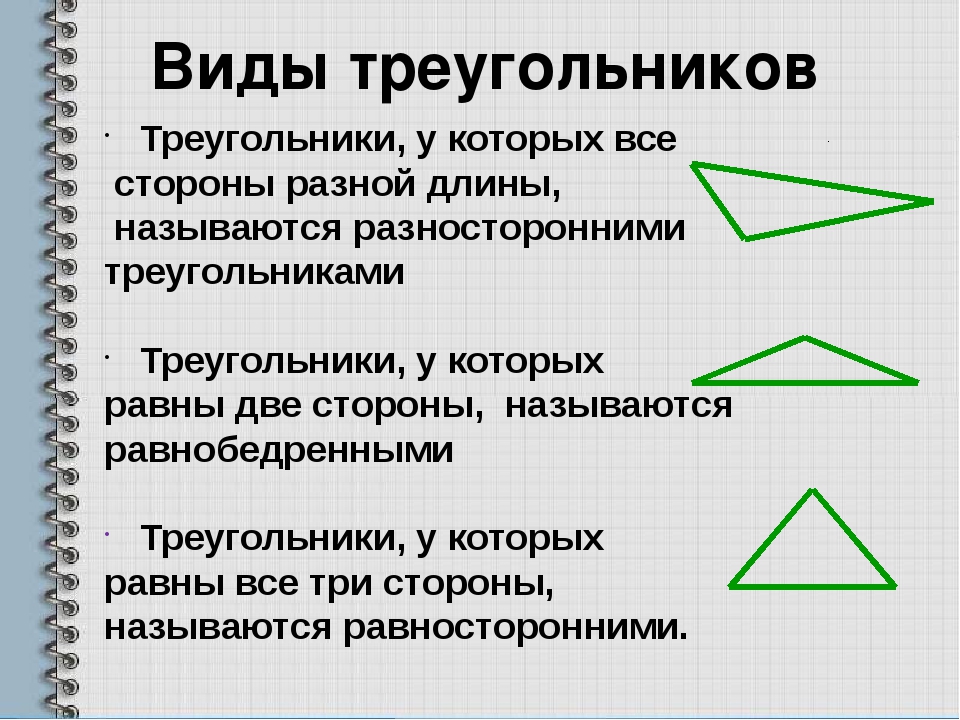

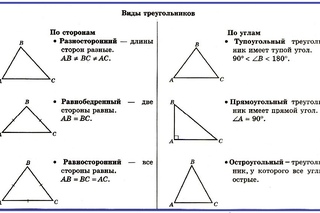
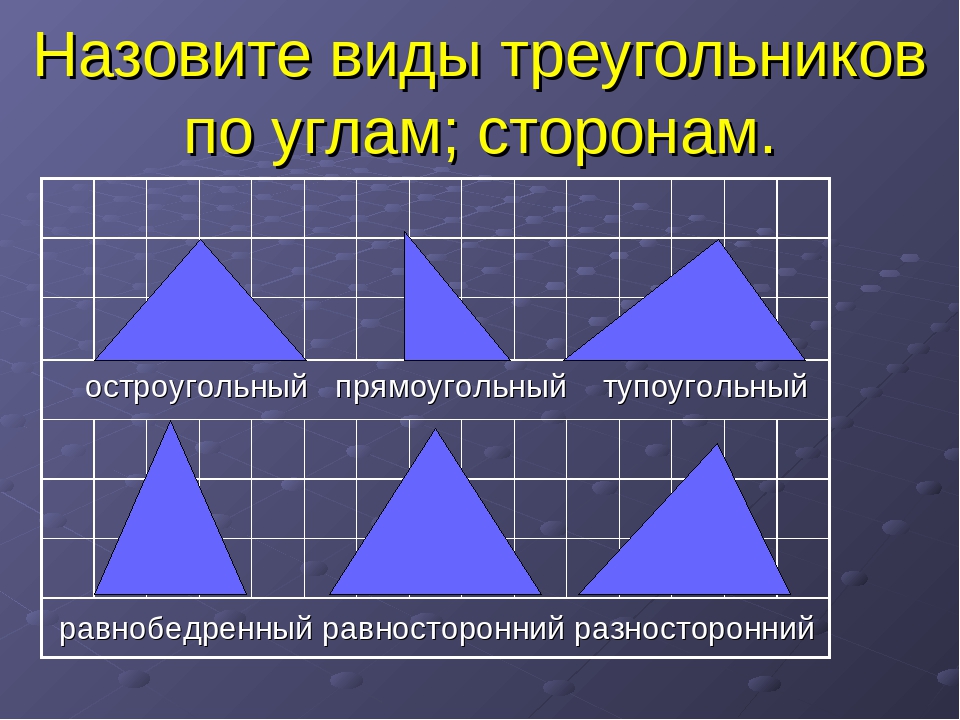 9).
9). : Просвещение, 2012.
: Просвещение, 2012.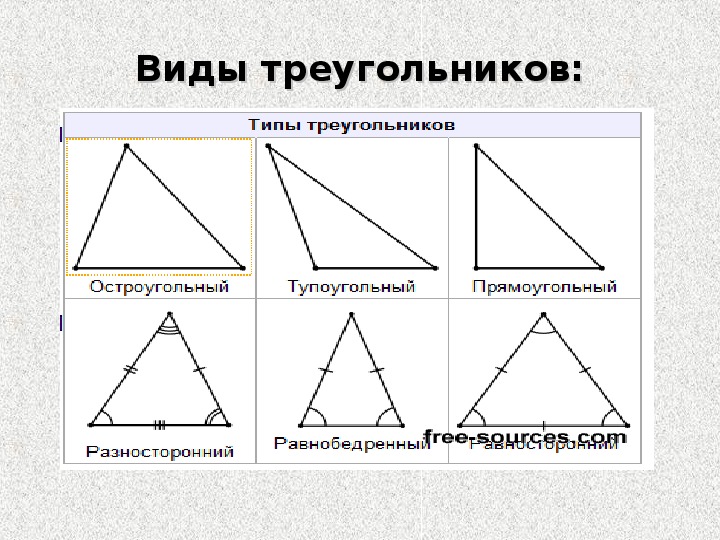
 У угла есть вершина, а сами лучи называются
сторонами угла. Углы измеряются в градусах с
помощью транспортира.
У угла есть вершина, а сами лучи называются
сторонами угла. Углы измеряются в градусах с
помощью транспортира.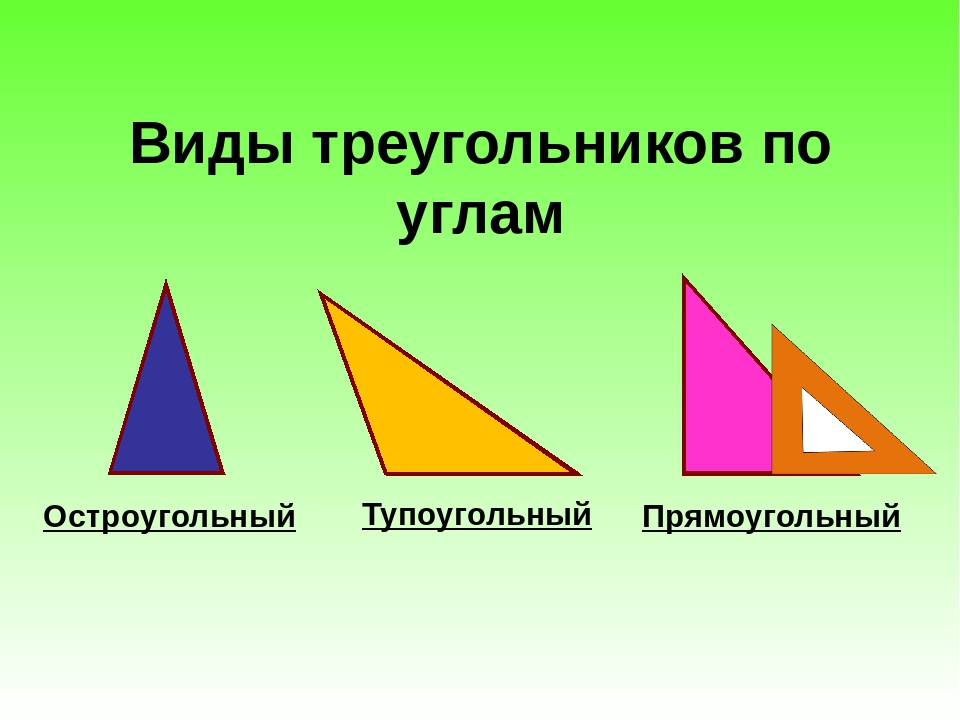

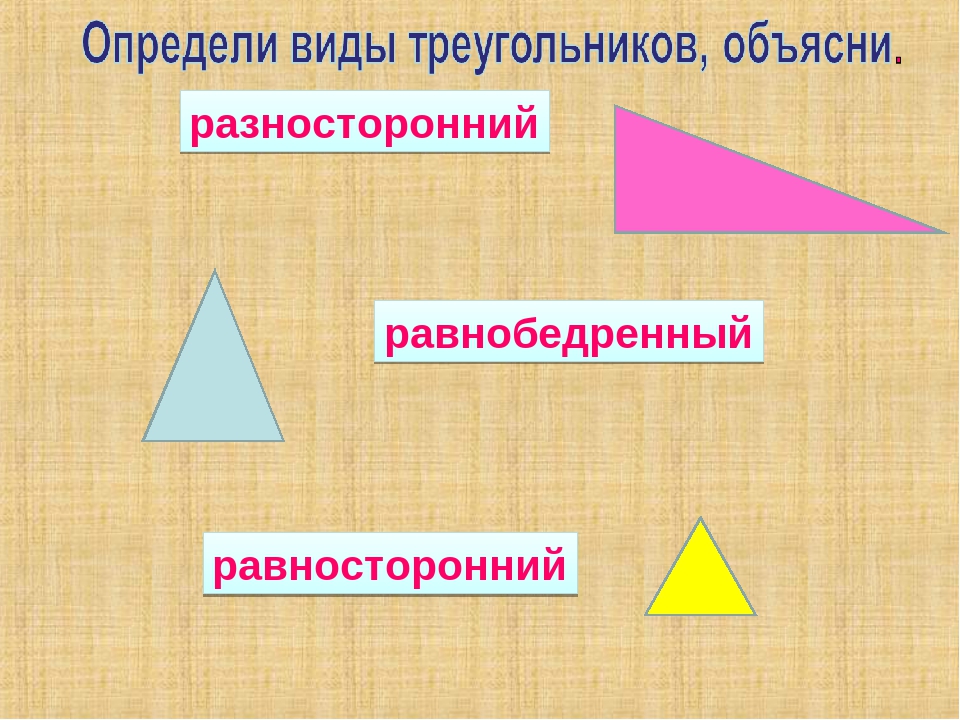
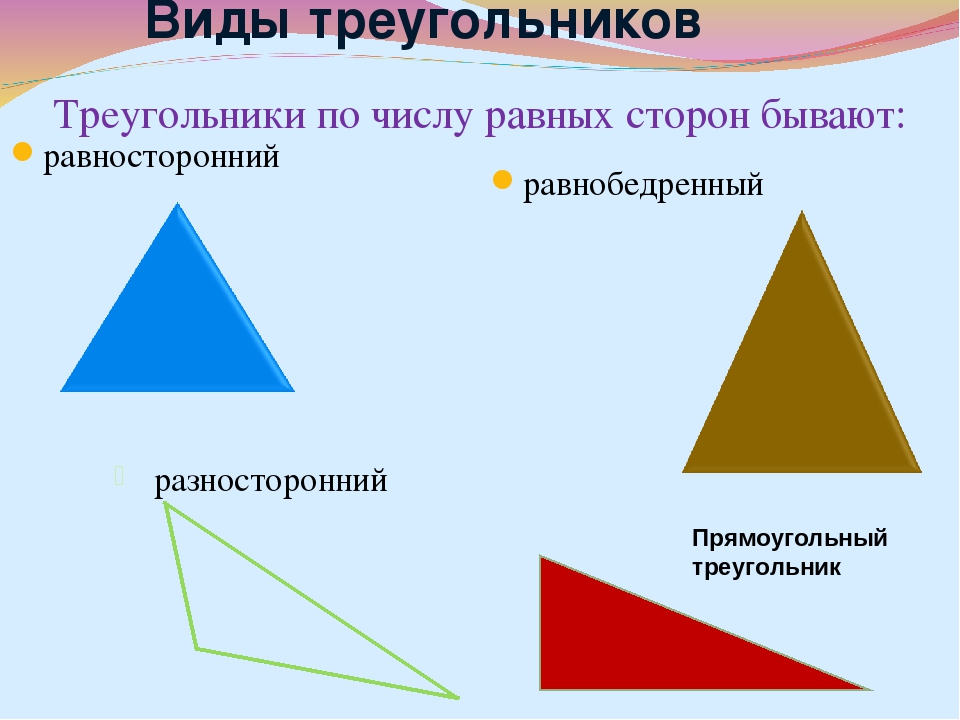

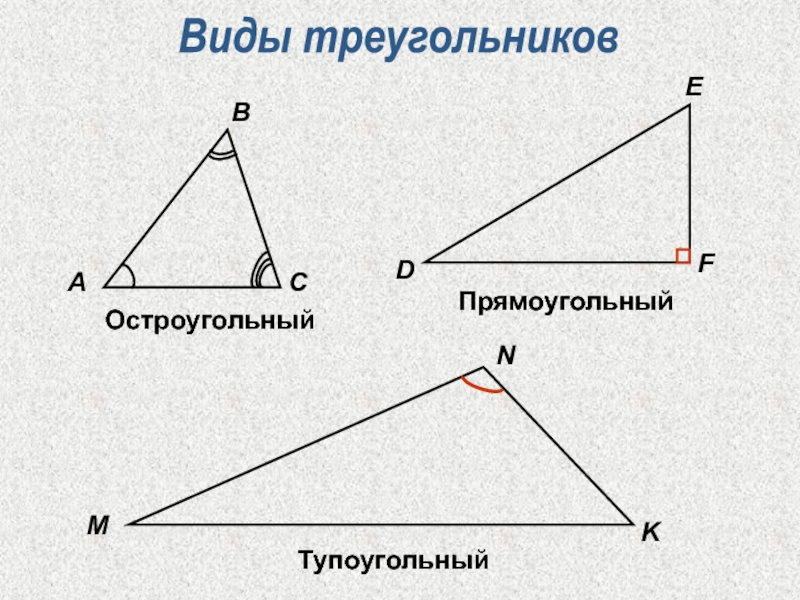 4).
4).