2 +b*x+c. Его еще называют квадратным трехчленом.

Нужна помощь в учебе?

Предыдущая тема: Преобразование выражений с квадратными корнями: свойства и примеры
Следующая тема:&nbsp&nbsp&nbspРешение квадратных уравнений выделением квадрата двучлена

Квадратные уравнения: приведённые уравнения, формулы корней

Квадратное уравнение или уравнение второй степени с одним неизвестным — это уравнение, которое после преобразований может быть приведено к следующему виду:

ax² + bx + c = 0  — квадратное уравнение,

где  x  — это неизвестное, а  a,  b  и  c  — коэффициенты уравнения. В квадратных уравнениях  a  называется первым коэффициентом  (a ≠ 0),  b  называется вторым коэффициентом, а  c  называется известным или свободным членом.

Уравнение:

ax² + bx + c = 0

называется полным квадратным уравнением.

Если один из коэффициентов  b  или  c  равен нулю, или нулю равны оба эти коэффициента, то уравнение представляют в виде неполного квадратного уравнения.

Приведённое квадратное уравнение

Полное квадратное уравнение можно привести к более удобному виду, разделив все его члены на  a,  то есть на первый коэффициент:

Затем можно избавиться от дробных коэффициентов, обозначив их буквами  p  и  q:

если	b	= p,  а	c	= q,
	a		a

то получится   x² + px + q = 0.

Уравнение  x² + px + q = 0  называется приведённым квадратным уравнением. Следовательно, любое квадратное уравнение, в котором первый коэффициент равен 1, можно назвать приведённым.

Например, уравнение:

x² + 10x — 5 = 0

является приведённым, а уравнение:

-3x² + 9x — 12 = 0

можно заменить приведённым уравнением, разделив все его члены на  -3:

x² — 3x + 4 = 0.

Решение квадратных уравнений

Чтобы решить квадратное уравнение, надо привести его к одному из следующих видов:

ax² + bx + c = 0;

ax² + 2kx + c = 0;

x² + px + q = 0.

Для каждого вида уравнения есть своя формула нахождения корней:

Вид уравнения	Формула корней
ax2 + bx + c = 0
ax2 + 2kx + c = 0
x2 + px + q = 0	или если коэффициент  p  нечётный

Обратите внимание на уравнение:

ax² + 2kx + c = 0

это преобразованное уравнение  ax² + bx + c = 0,  в котором коэффициент  b  — четный, что позволяет его заменить на вид  2k.   Поэтому формулу нахождения корней для этого уравнения можно упростить, подставив в неё  2k  вместо  b:

Пример 1. Решить уравнение:

3x² + 7x + 2 = 0.

Так как в уравнении второй коэффициент не является чётным числом, а первый коэффициент не равен единице, то искать корни будем по самой первой формуле, называемой общей формулой нахождения корней квадратного уравнения. Сначала определим, чему равны коэффициенты:

a = 3,  b = 7,  c = 2.

Теперь, для нахождения корней уравнения, просто подставим значения коэффициентов в формулу:

x1 =	-2	= —	1	,   x2 =	-12	= -2
	6		3		6

Пример 2:

x² — 4x — 60 = 0.

Определим, чему равны коэффициенты:

a = 1,  b = -4,  c = -60.

Так как в уравнении второй коэффициент — чётное число, то будем использовать формулу для квадратных уравнений с чётным вторым коэффициентом:

x₁ = 2 + 8 = 10,   x₂ = 2 — 8 = -6

Ответ:  10,  -6.

Пример 3.

y² + 11y = y — 25.

Приведём уравнение к общему виду:

y² + 11y = y — 25;

y² + 11y — y + 25 = 0;

y² + 10y + 25 = 0.

Определим, чему равны коэффициенты:

a = 1,  p = 10,  q = 25.

Так как первый коэффициент равен  1,  то будем искать корни по формуле для приведённых уравнений с чётным вторым коэффициентом:

Ответ:  -5. 2
И другие

6 месяцев назад

20х15 = 300 м2 = 3000000см2 — площадь пола

20х20= 400см2 — площадь плитки (1шт)

 

3000000/400= 7500 плиток

 

x — в первую палатку

y — во 2 палатку 

z — в 3 палатку

получаем: x+y=400 y+z=300 x+z=440

 

вычтем из 2ого третье уравнение: y-x = -140  x = y+140 

 

подставим в 1ое уравнение:  y+140+y=400

                                             2y=260

                                             y=130

 во вторую палатку привезли 130кг

5 месяцев назад

Перевод: Числитель дроби на 2 меньше знаменателя .

Если эту дробь сложить с обратной ей дробью , то получится 130/63 . Найдите исходную дробь.

Пусть числитель дроби равен х, тогда её знаменатель — (x+2). Обратная ей дробь — (x+2)/x. Составим уравнение согласно условию:

ОДЗ:

Домножим левую и правую части уравнения на 63x(x+2), получим:

По теореме Виета:

Корни удовлетворяет области допустимых значений.

Исходная дробь: или

4 месяца назад

Наименьшее значение достигается в вершине, так как графиком данной функции является парабола, ветви которой направлены вверх; поэтому же не достигается и наибольшее значение.

Найдем вершину В(х; у)
х(В) = -b/2a  в формуле ax²+bx+c
х(В) = 5/8
у(В) = 4* (5/8)² — 5 *5/8 +3 = (4*25)/64 — 25/8 + 3 = 25/16-25/8 + 3 = -25/8+3 =3 — 3_1/8 =

-1/8 — наименьшее значение 
у = +∞ — наибольшее значение

«Решение квадратных уравнений».

1)Какое уравнение называется квадратным? 2)Как называются числа а,в,с? 3)Что значит решить уравнение? 4)От чего зависит количество корней квадратного уравнения? 5)Как найти дискриминант? 6)Каким образом количество корней зависит от дискриминанта? 7) Если в квадратном уравнении в=0или с=0, как называется такое уравнение? 8)Какие вы знаете виды неполных квадратных уравнений?

а)2х 2 -3х-5=0 б)х 2 +2х-15=0 в)4х 2 +5х=0 г)8х 2 =0 д)3х 2 -10х+8=0 е)3х 2 -12х=0

Впервые квадратное уравнение сумели решить математики Древнего Египта. Неполные квадратные уравнения умели решать вавилоняне (около2 тысяч лет до н.э.). Некоторые виды квадратных уравнений, сводя их решения к геометрическим построениям, могли решать древнегреческие математики. Примеры решения уравнений без обращения к геометрии дает Диофант Александрийский ( III в). Правило решения квадратного уравнения дал индийский ученый Брахмагупта ( VII в).

Общее правило решения квадратных уравнений было сформулировано немецким математиком М.Штифелем. Выводом формулы решения квадратного уравнения общего вида занимался Франсуа Виет.

Задание:  Решите уравнения

1 уровень

2 уровень

x 2 +5х+6=0

7x 2 +8х+1=0

3 уровень

х+32=2х+6

(х -2)(х+2) =5х — 10

(х- 3)(х+ 3) = 5х -13

2x 2 +х5=4х-23

Ответы

1 уровень

x 2 +5х+6=0

2 уровень

3 уровень

Х=-3,х=-2

х 2 +32=2х+6

7x 2 +8х+1=0

Корней нет

(х -2)(х+2) =5х – 10

Х=-1/7,х=-1

(х- 3)(х+ 3) = 5х -13

Х=2,х=3

Х=1,х=8

2x 2 +5х=4х-23

Корней нет

Составьте квадратное уравнение.

Неполные квадратные уравнения

Учитель математики и физики: Балакина Е.Н.

ЦЕЛИ УРОКА:

• Познакомиться с понятием квадратного уравнения;

• Научиться определять является ли уравнение квадратным; Научиться определять коэффициенты квадратного уравнения; Составлять по заданным коэффициентам квадратное уравнение; Научиться определять вид квадратного уравнения: полное или неполное; Научиться выбирать алгоритм решения неполного квадратного уравнения.
• Научиться определять является ли уравнение квадратным;
• Научиться определять коэффициенты квадратного уравнения;
• Составлять по заданным коэффициентам квадратное уравнение;
• Научиться определять вид квадратного уравнения: полное или неполное;
• Научиться выбирать алгоритм решения неполного квадратного уравнения.

ВОПРОСЫ:

• Что такое уравнение?
• Что значит решить уравнение?
• Что называется корнем уравнения?
• Какие уравнения мы знаем?

Выберите квадратные уравнения:

5х + 26 = 8х – 3,

— 13х = 0,

9х + 2 — 17 = 0,

34 + 5 — 22х = 11

9х + 7 — 13 = 0,

— 42х – 29 = 0,

-3 — 35х + 14 = 0,

+22 – 5х = 0,

-7 — 46х + 17 = 0,

8х – 6 = 0,

25 — 4х – 9 = 0.

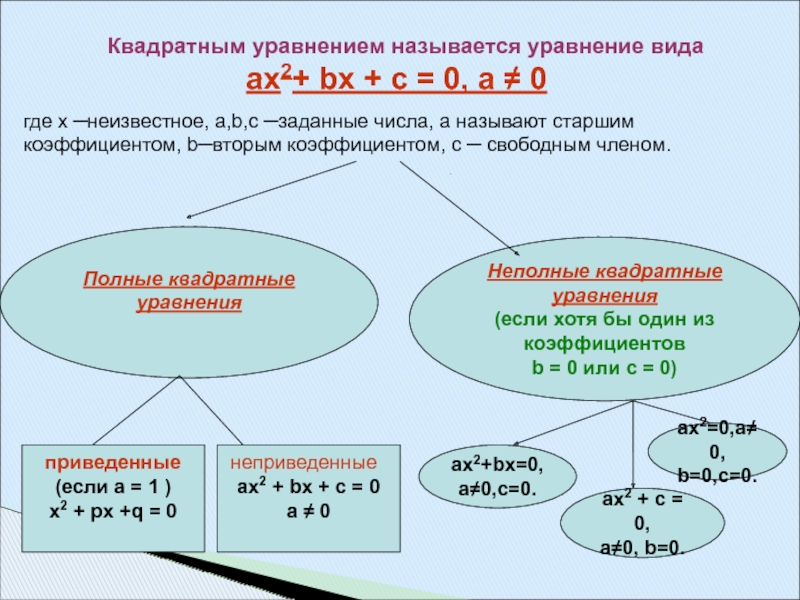
КВАДРАТНЫМ УРАВНЕНИЕМ НАЗЫВАЕТСЯ

УРАВНЕНИЕ ВИДА

a + bx+c=0,

где х — переменная,

a,b,c — некоторые числа,

причем a = 0.

а – первый коэффициент,

b – второй коэффициент,

c – свободный член.

Составьте квадратное уравнение

-9 + 23x – 11 = 0

-4 + x + 5 = 0

4 + 9x = 0

+ 7x + 1 = 0

-3 + 15 = 0

-3 — x + 7 = 0

4 + 3 = 0

a = 3, b = -7, c = 12

a = -9, b = 23, c = -11

a = 8, b = 0, c = 0

a = 5, b = -22, c = -3

a = -4, b = 1, c = 5

a = 4, b = 9, c = 0

a = 1, b = 7, c = 1

a = -3, b = 0, c =15

a = -3, b = -1, c =7

a = 4, b = 0, c = 3

Если в квадратном уравнении a + bx+c=0 хотя бы один из коэффициентов b или с равен нулю, то такое уравнение называют неполным квадратным уравнением.

Неполные квадратные уравнения бывают трех видов:

• a = 0
• a + b x = 0
• a + c = 0

1 вариант

— ; У 0;3 И 0;-2 П н.р. В -3;3 Р 0;2 Е 0 Н 0;4 А -2,5;2,5 О — ; Д

2 вариант

• + 2х = 0
• 2 — 18 = 0
• 4 — 11= — 11+ 9х
• 9 + 1 = 0
• 2 = 4х
• 7 — 14 = 0
• 9 – 2 + 16х = 6 + 9
• — 4 = 0
• 9 + 1 = 1
• 4 — 25 = 0

• -2 + 4х = 0
• — 3х = 0
• 7 = 0
• 12х = 6
• 2 = 7 + 2
• 6 + 24 = 0
• 3 + 7 = 12х + 7
• + 2х – 3 = 2х + 6
• 9 — 4 = 0
• 7х = 2 + 3х

На доске выписаны числа 1 2 3 4 5 6 7 8 9 10 10 9 8 7 6 5 4 3 2 1

Ученики выписывают буквы соответствующие корням данных уравнений; варианты работают навстречу друг другу.

ПРИВЕДЕННЫМ КВАДРАТНЫМ УРАВНЕНИЕМ

Называют квадратное

уравнение, в котором коэффициент

при равен 1:

+ bx+c=0

ДОМАШНЕЕ ЗАДАНИЕ

№ 24.11 (УСТНО),

№ 24.16 (б, в, г),

№ 24.18 (б, в, г).

Историческая справка

Квадратные уравнения решали в Вавилоне около 2000 лет до нашей эры.

В Европе в 2002 году праздновали 800-летие квадратных уравнений, т.к. именно в 1202 году итальянский ученый Леонард Фибоначчи изложил формулы квадратного уравнения.

Только в 17 веке, благодаря Ньютону, Декарту и другим ученым эти формулы приняли современный вид.

В Древней Индии уже в 499 году были распространены публичные соревнования по решению задач на составление квадратных уравнений. Одной из таких задач является задача знаменитого индийского математика Бхаскары :

Обезьянок резвых стая Всласть поевши, развлекаясь, Их в квадрате часть восьмая На поляне забавлялась. А двенадцать по лианам Стали прыгать, повисая. Сколько было обезьянок Ты скажи мне в этой стае?

Слайд 2

«Мне приходится делить своё время между политикой и уравнениями. Однако уравнения по-моему, гораздо важнее, потому что политика существует только для данного момента, а уравнения будут существовать вечно». А. Эйнштейн.

Слайд 3

Здравствуйте, ребята!

Повторим: Я — ваш помощник, я проведу вас по всей большой теме » Квадратные уравнения». В 7 и 8 классе вы уже рассматривали и даже решали квадратные уравнения.

Слайд 4

Сегодня вы узнаете: 1. Какие уравнения называют квадратными? 2. Что в определении квадратного уравнения основное, что следует запомнить и учитывать? 3. Какие частные случаи квадратных уравнений бывают? 4. Каковы способы решения квадратных уравнений в каждом частном случае? А теперь давайте вместе искать ответы на эти вопросы. Желаю удачи!

Слайд 5

Что общего у этих уравнений?

Слайд 6

Квадратным уравнением называют уравнение вида … ax² + bx + c = 0, где а ≠ 0, х — переменная, а, в, с — некоторые числа. а–старший (первый) коэффициент, b-второй коэффициент, с-свободный член. а–старший (первый) коэффициент, b-второй коэффициент, с-свободный член. а – старший (первый) коэффициент, в — второй коэффициент, с — свободный член.

Слайд 7

Если a = 1, то квадратное уравнение x² + bx + c= 0 называют приведенным. Решим № 513 (устно).

Слайд 8

Попробуем решить:

5 5 -3 3 2 -4 1 4 3 -2 1 -1 4 -4 1

Слайд 9

Интересно, а что будет, если коэффициенты квадратного уравнения по очереди или все сразу (кроме а) превратятся в нули. Давайте проведём исследование.

Слайд 10

Неполные квадратные уравнения

10.01.2017 10 Если с=0, ax2+ bх= 0 ax2 ax2 Если b,с=0, ax2= 0 Если b =0, ax2+ c = 0

Слайд 11

Рассмотрим все возможные случаи

Слайд 12

Слайд 13

Неполные квадратные уравнения вида: нет корней.

Слайд 14

Неполные квадратные уравнения вида:

Слайд 15

Ответ: х=0. нет корней. Выпишите неполные квадратные уравнения:

Слайд 16

Запишите квадратные уравнения с указанными коэффициентами: а=1, b=0, c=16; a=-1, b=5, c=0; b=0, a=-3, c=0; c=-8, a=1, b=0; a=1,5, c=0,b=-3; b= , a= , c Установите соответствие между уравнениями и следующими а) уравнение имеет два корня, б) уравнение имеет один корень, в) уравнение не имеет корней. (в) (а) (б) (а) (а) (а) Установите соответствие между уравнениями и следующими утверждениями:

Слайд 17

17 Проверьте решение № 515 (а, в, г). а).4х2-9=0 в). -0,1х2+10=0 г). 6v2+24=0 4х2 =9 -0,1х2 =-10 6v2 =-24 х2 =9/4х2 =-10/(-0,1)v2 =-24/6 х1=-3/2=-1,5; х2=100 v2 =-4 х2 =3/2=1,5; х1=-10 Ответ: нет решения. Ответ:-1,5;1,5;Ответ:-10;10;

Слайд 18

10.01.2017 18 Рассмотрим решение неполных квадратных уравнений №517 (б, г, д) б). -5х2+ 6х=0 г). 4а2 — 3а=0д). 6z2– z =0 х(-5х+6)=0 а(4а-3)=0 z(6z –1) =0 х=0 или -5х+6=0 а=0 или 4а-3=0 z=0 или 6z –1 =0 -5х= -6 4а=36z=1 х = -6/(-5) =1,2 а=3/4=0,75 z=1/6 Ответ: 0; 1,2. Ответ: 0; 0,75. Ответ: 0; 1/6.. .

Презентация урока алгебры в 8 классе по теме «Квадратные уравнения. Решение неполных квадратных уравнений». Введение понятия полного и неполного квадратных уравнений. Первичное закрепление способов решения неполных квадратных уравнений.

Скачать:

Предварительный просмотр:

Чтобы пользоваться предварительным просмотром презентаций создайте себе аккаунт (учетную запись) Google и войдите в него: https://accounts.google.com

Подписи к слайдам:

Презентация урока алгебры в 8 классе « Квадратные уравнения. Решение непо л н ых квадратн ых у равнений »

Загадочное, но нам знакомое, В нем есть что-то неизвестное Его корень – вот искомое Найти его – интересно всем Каждый скажет без сомнения Перед вами (уравнение)

Решите уравнения а) у – 7 = 0; б) х + 0,5 = 0; в) а х = 0; г) 2 х – 1/3 = 0; д) а (а – 1) = 0; е) х 2 + 4 = 0.

Задача В кинозале количество зрительскихх мест в каждом ряду на 8 больше количества рядов. Всего на сеанс пришло 884 зрителя и все места были заняты. Сколько рядов в кинозале?

x – рядов; x +8 – мест в каждом ряду C оставим уравнение: x (х+8)=884; x 2 +8х-884=0.

« Квадратные уравнения. Решение непо л н ых квадратн ых у равнений » Тема урок а: эпиграф: уравнение – это ключ, которым можн о открыть т ы сячу дверей в не известное.

цель: ввести понятие квадратного уравнения; Научиться решать непо лные квадратн ые у равнения.

О пр е деление квадратного у равнения Квадратн ы м у равнением наз ы ва е тся у равнение вид а ax²+bx+c=0 , де х – переменная, а, b , с – параметры, а≠0. Число а называ е тся пер вым ко э ф фи ц ие нтом, число b – вторым ко эф ф ицие нтом и с – свободным членом. Квадратное у равнение наз ы вают также у равнением второй степен и, так как е го л е вая част ь является многочлен ом второй степен и.

При меры квадратн ы х у равнений: a b c -2x²+x-1,4=0 -2 1 -1,4 5x²-4x=0 5 -4 0 3X²+10,3=0 3 0 10,3

За дание 1 Являются ли данные уравнения квадратными? 4x²-5x+2=0 -5,6x²-2x- 0,5 =0 13-7x²=0 16x²-x³-5=0 1-16x=0 -x²=0

За дание 2 Наз овите ко э ффиц ие нт ы в квадратном у равнении. 3x²-6x+2=0 -x²+5x+10=0 x²-8x+1,5=0 -4x²+5=0 -36x²-3x=0 12x²=0

Непо лные квадратн ые у равнения Если в квадратном уравнении ax²+bx+c=0 хотя бы один и з ко э ф фи ц ие нт о в b или c р а вен нулю, то так ое уравнение наз ы вают непо л н ы м квадратн ы м у равнением. a b c -3x²+5=0 -3 0 5 2x²-10x=0 2 -10 0 16x²=0 16 0 0

Классификация квадратных уравнений полные неполные Аль-Хорезми, где a ≠ 0 b=0 b=0, c=0 c=0 или или или

Ре ши м уравнение если b=0. -4x²+25=0 — 4x² =- 25 4x² = 25 или I

Решим уравнение если b=0 ,c=0. III

Решим уравнение если C=0 . (35 + у) y = 0 35 + у = 0 или II y = 0 y=-35

Тестирование

1 . 2. 3. 4. 5 0; -5 -5; 5 0 За дание №1. Укажите корни уравнения помощь

За дание №2. Укажите корни уравнения 1. 2. 3. 4. -4 ; 4 — 4 ; 0 16 0 ; 4

За дание №3. Укажите корни уравнения 1 . 2. 3. 4. 3 -3 ; 0 -3 0 ; 3

За дание №4. Укажите корни уравнения 1. 2. 3. 4. 0; 4 16 -4; 4 -4; 0

05/01/17 За дание №5. Укажите корни уравнения 1. 2. 3. 4. -2; 2 4 2 2; 0

Итоги урока: Сегодня на уроке я узнал… понял… научился… мои успехи – это… трудности я почувствовал… я не умел, а теперь умею… на следующем уроке я хочу…

Чтобы пользоваться предварительным просмотром презентаций создайте себе аккаунт (учетную запись) Google и войдите в него: https://accounts.google.com

Подписи к слайдам:

Урок по теме «Неполные квадратные уравнения». Подготовили учителя математики МОУ «Успенская ООШ МО «Ахтубинский район» Зенина Н.Г., Крамаренко Т.Н.

«Мне приходится делить своё время между политикой и уравнениями. Однако уравнения по-моему, гораздо важнее, потому что политика существует только для данного момента, а уравнения будут существовать вечно». А. Эйнштейн.

Здравствуйте, ребята! Повторим: Я — ваш помощник, я проведу вас по всей большой теме » Квадратные уравнения». В 7 и 8 классе вы уже рассматривали и даже решали квадратные уравнения.

Сегодня вы узнаете: 1. Какие уравнения называют квадратными? 2. Что в определении квадратного уравнения основное, что следует запомнить и учитывать? 3. Какие частные случаи квадратных уравнений бывают? 4. Каковы способы решения квадратных уравнений в каждом частном случае? А теперь давайте вместе искать ответы на эти вопросы. Желаю удачи!

Что общего у этих уравнений?

Квадратным уравнением называют уравнение вида … ax ² + bx + c = 0, где а ≠ 0, х — переменная, а, в, с — некоторые числа. а–старший (первый) коэффициент, b -второй коэффициент, с-свободный член. а–старший (первый) коэффициент, b -второй коэффициент, с-свободный член. а – старший (первый) коэффициент, в — второй коэффициент, с — свободный член.

Если a = 1 , то квадратное уравнение x ² + bx + c = 0 называют приведенным. Решим № 513 (устно) .

а в с 5x² + 5х – 3 = 0 3 x² + 2 х – 4 = 0 х² + 4х + 3 = 0 -2 x² + х – 1 = 0 4 х ²- 4 х + 1 = 0 5 5 -3 3 2 -4 1 4 3 -2 1 — 1 4 — 4 1 Попробуем решить:

Интересно, а что будет, если коэффициенты квадратного уравнения по очереди или все сразу (кроме а) превратятся в нули. Давайте проведём исследование.

Неполные квадратные уравнения 28.04.17 Если с = 0 , ax 2 + b х = 0 ax 2 ax 2 Если b, с = 0 , ax 2 = 0 Если b = 0 , ax 2 + c = 0

Рассмотрим все возможные случаи

Неполные квадратные уравнения вида: нет корней.

Неполные квадратные уравнения вида:

Ответ: х= 0. нет корней. Выпишите неполные квадратные уравнения:

Запишите квадратные уравнения с указанными коэффициентами: а=1, b=0, c=16; a=-1, b=5, c=0; b=0, a=-3, c=0; c=-8, a=1, b=0; a=1,5, c=0,b=-3; b= , a= , c Установите соответствие между уравнениями и следующими а) уравнение имеет два корня, б) уравнение имеет один корень, в) уравнение не имеет корней. (в) (а) (б) (а) (а) (а) Установите соответствие между уравнениями и следующими утверждениями:

Проверьте решение № 515 (а, в, г). а).4х 2 -9=0 в). -0,1х 2 +10=0 г). 6 v 2 +24=0 4х 2 = 9 -0,1х 2 =- 10 6 v 2 =-24 х 2 = 9 /4 х 2 =- 10 /(-0,1) v 2 =-24/6 х 1 = -3/2=-1,5; х 2 =100 v 2 =-4 х 2 =3/2=1,5; х 1 = -10 Ответ: нет решения. Ответ:-1,5;1,5; Ответ:-10;10 ;

28.04.17 Рассмотрим решение неполных квадратных уравнений № 517 (б, г, д) б). -5х 2 + 6х=0 г). 4а 2 — 3а=0 д). 6 z 2 – z =0 х(-5х+6)=0 а(4а-3)= 0 z (6 z –1) =0 х=0 или -5х+6=0 а=0 или 4а-3=0 z =0 или 6 z –1 =0 -5х= -6 4а=3 6 z =1 х = -6/(-5) =1,2 а=3/4=0,75 z =1/6 Ответ: 0; 1 ,2. Ответ: 0; 0,75. Ответ: 0; 1/6.. .

1) При каких значениях а уравнение является квадратным уравнением? Нет решений 2) При каких значениях a уравнение является неполным квадратным уравнением?

3) Решите уравнение при полученных значениях а. Ответ: а = − 2, х= − 15, х= 0; а = 0,

Подведем итоги Какое же уравнение называется квадратным? Почему а≠ 0 ? Как называются числа а, в и с? Сколько видов неполных квадратных уравнений мы узнали? Как решают уравнения I вида? II вида? III вида?

Вот и завершается наш урок. Ребята! Вы получили ответы на интересующие вас вопросы? Поняли, что нас впереди ждут интересные, а самое главное – важные темы? Я только хочу вам напомнить, что при решении задач, примеров надо искать рациональные подходы и применять разнообразные способы.

Домашнее задание: П. 21 учебника; №№ 318, 321 а,в, 323 а. Дополнительно: 520, 532. П. 21 (определения), №518, 520 (а,в) 511 Дополнительно (для учащихся с повышенным интересом) №520, №531.

Виды неполных квадратных уравнений

☰

Квадратное уравнение имеет вид ax² + bx + c = 0.

Неполными квадратными уравнениями являются уравнения трех видов:

• ax² + bx = 0, когда коэффициент c = 0.
• ax² + c = 0, когда коэффициент b = 0.
• ax² = 0, когда и b и с равны 0.

Коэффициент же a по определению квадратного уравнения не может быть равен нулю.

Неполные квадратные уравнения решаются проще, чем полные квадратные. Способы решения различаются в зависимости от вида неполного квадратного уравнения.

Проще всего решаются уравнения вида ax² = 0. Если a по определению квадратного уравнения не может быть равно нулю, то очевидно, что нулю может быть равен только x², а значит, и сам x. У уравнений такого вида всегда есть один корень, он равен 0. Например:

–3x² = 0
x² = 0/–3
x² = 0
x = √0
x = 0

Уравнения вида ax² + c = 0 преобразуются к виду ax² = –c и решаются аналогично предыдущему. Однако корней здесь либо два, либо не одного.

ax² + c = 0
ax² = –c
x² = –c/a
x = √(–c/a)

Здесь если подкоренное выражение отрицательно, то корней у уравнения нет. Если положительно, то корней будет два: √(–c/a) и –√(–c/a). Пример решения подобного уравнения:

4x² – 16 = 0
4x² = 16
x² = 16 / 4
x² = 4
x = √4
x₁ = 2; x₂ = –2

Неполные квадратные уравнения вида ax² + bx = 0 решается вынесением общего множителя за скобку. В данном случае им является x. Получается уравнение x(ax + b) = 0. Это уравнение имеет два корня: либо x = 0, либо ax + b = 0. Решая второе уравнение получаем x = –b/a. Таким образом, уравнения вида ax² + bx = 0 имеют два корня: x₁ = 0, x₂ = –b/a. Пример решения такого уравнения:

3x² – 10x = 0
x(3x – 10) = 0
x₁ = 0; x₂ = 10/3 = 3,(33)

{2} + bx + c = d \).

НАЗВАНИЕ СТРАННОЕ!

Префикс quad означает «четыре», а квадратные выражения — это выражения, которые включают степени \ (x \) до второй степени, а не четвертой степени. Так почему же квадратные уравнения связаны с числом четыре? Разве у нас не должно быть названия, связанного с номером два: Diatics? Дуо-атикс? Би-атики? Может быть, два-датика?

Small Aside : Вы заметили, что многие слова в английском языке, связанные с числом два, начинаются с «tw»? В качестве примеров: двойник, шпагат (две нити переплетены), твикс, сумерки и сама цифра два!

ТАК… ПОЧЕМУ НАИМЕНОВАНИЕ QUADRATIC?

Квадратные уравнения тесно связаны с задачами о квадратах и ​​четырехугольниках (другое название прямоугольников). 2 + bx + c [/ latex].2 + bx + c [/ latex], где a — ненулевая константа, b и c — константы любого значения, а x — независимая переменная.

Решения квадратного уравнения известны как его нули или корни.

Ключевые термины

• зависимая переменная : зависит от изменения ввода, т.е. изменяется в зависимости от значения ввода.
• независимая переменная : вход функции, который можно произвольно изменять.
• вершина : точка минимума или максимума квадратичной функции.2 + bx + c = 0 [/ латекс]

  Когда все константы известны, можно решить квадратное уравнение, чтобы найти решение [latex] x [/ latex]. Такие решения называются нулями. Есть несколько способов найти [latex] x [/ latex], но об этих методах мы поговорим позже.

  Различия между квадратичными и линейными функциями

  Квадратные уравнения отличаются от линейных функций несколькими ключевыми способами.

  • Линейные функции либо всегда уменьшаются (если они имеют отрицательный наклон), либо всегда увеличиваются (если они имеют положительный наклон). Все квадратичные функции как увеличиваются, так и уменьшаются.
  • При линейной функции каждый вход имеет индивидуальный уникальный выход (при условии, что выход не является константой). В случае квадратичной функции пары уникальных независимых переменных будут давать одну и ту же зависимую переменную, за одним исключением (вершина) для данной квадратичной функции.
  • Наклон квадратичной функции, в отличие от наклона линейной функции, постоянно меняется.

  Формы квадратичных функций

  Квадратичные функции могут быть выражены во многих различных формах.2 + к [/ латекс]

  где [latex] h [/ latex] и [latex] k [/ latex] соответственно координаты вершины, точки, в которой функция достигает своего максимума (если [latex] a [/ latex] отрицательное) или минимум (если [latex] a [/ latex] положительный).

  Квадратичная формула

  Нули квадратного уравнения можно найти, решив квадратную формулу.

  Цели обучения

  Найдите корни квадратичной функции, используя формулу корней квадратного уравнения

  Ключевые выводы

  Ключевые моменты

  • Квадратичная формула: [latex] x = \ frac {-b \ pm \ sqrt {b ^ 2-4ac}} {2a} [/ latex], где [latex] a [/ latex] и [latex] b [/ latex] — коэффициенты при членах [latex] x ^ 2 [/ latex] и [latex] x [/ latex], соответственно, в квадратном уравнении, а [latex] c [/ latex] — значение постоянной уравнения. 2-4 (2) (3)}} {2 (2)} [/ латекс]

    [латекс] x = \ dfrac {-5 \ pm \ sqrt {25-24}} {4} [/ латекс]

    [латекс] x = \ dfrac {-5 \ pm \ sqrt {1}} {4} [/ латекс]

    [латекс] \ displaystyle x = \ frac {-5} {4} + \ frac {1} {4} [/ latex], [латекс] \ displaystyle \ frac {-5} {4} — \ frac {1 } {4} [/ латекс]

    [латекс] x = \ dfrac {-3} {4} [/ latex], [латекс] \ dfrac {-6} {4} [/ latex]

    [латекс] x = \ dfrac {-3} {4} [/ latex], [латекс] \ dfrac {-3} {2} [/ latex]

    Дискриминант

    Дискриминант многочлена — это функция его коэффициентов, которая раскрывает информацию о корнях многочлена.2-4ac [/ latex] — это формула дискриминанта квадратичной функции.

  • Если Δ больше нуля, многочлен имеет два действительных различных корня.
  • Если Δ равно нулю, многочлен имеет только один действительный корень.
  • Если Δ меньше нуля, многочлен не имеет действительных корней, только два различных комплексных корня.
  • Ноль — это значение x, когда функция пересекает ось x. То есть это координата x, при которой значение функции равно нулю.

  Ключевые термины

  • квадратичный : второй степени; может применяться к многочленам.
  • ноль : также известен как корень; значение x, при котором функция x равна нулю.
  • дискриминант : выражение, которое дает информацию о корнях многочлена.

  Дискриминант квадратичной функции — это функция ее коэффициентов, которая раскрывает информацию о ее корнях. Корень — это значение координаты [latex] x [/ latex], где функция пересекает ось [latex] x [/ latex]. То есть это координата [latex] x [/ latex], в которой значение функции равно нулю.2-4ac [/ latex] — это часть формулы квадратного корня.

  Положительный дискриминант

  Если [latex] {\ Delta} [/ latex] положительно, квадратный корень в формуле корней квадратного уравнения положителен, и решения не включают мнимые числа.

  [латекс] x = {\ dfrac {-b \ pm \ sqrt {\ text {положительное число}}} {2a}} [/ латекс]

  Поскольку сложение и вычитание положительного числа приведет к разным значениям, положительный дискриминант дает два различных решения и два различных корня квадратичной функции.

  Нулевой дискриминант

  Если [latex] {\ Delta} [/ latex] равно нулю, квадратный корень в формуле корней квадратного уравнения равен нулю:

  [латекс] x = {\ dfrac {-b \ pm \ sqrt {0}} {2a}} [/ латекс]

  Поскольку добавление нуля и вычитание нуля в квадратном уравнении приводят к тому же результату, существует только один отличный корень квадратичной функции.

  Отрицательный дискриминант

  Если [latex] {\ Delta} [/ latex] меньше нуля, значение квадратного корня в формуле корней квадратного уравнения отрицательное:

  [латекс] x = \ dfrac {-b \ pm \ sqrt {\ text {отрицательное число}}} {2a} [/ latex]

  Это означает, что квадратный корень сам по себе является мнимым числом, поэтому корни квадратичной функции различны и не являются действительными.2 — х — 2 [/ латекс]. Поскольку значение больше 0, функция имеет два различных действительных нуля. График показывает, что он явно имеет два корня: функция пересекает ось [latex] x [/ latex] в [latex] x = -1 [/ latex] и [latex] x = 2 [/ latex]. 2 + c [/ latex].2 [/ латекс]).

• Значения [latex] p [/ latex] можно найти, построив график, разложив на множители, завершив квадрат или используя формулу корней квадратного уравнения. Их квадратные корни (положительные и отрицательные) — это значения [latex] x [/ latex], которые удовлетворяют исходному уравнению.
• Уравнения высшего порядка могут быть решены аналогичным процессом, который включает уменьшение их показателей. Требование состоит в том, чтобы было два члена [латекс] x [/ латекс], так что отношение высшего показателя [латекса] x [/ латекса] к нижнему было [латекс] 2: 1 [/ латекс].

Ключевые термины

• ноль : также известен как корень; значение [latex] x [/ latex], при котором функция [latex] x [/ latex] равна нулю.
• биквадратный : Когда многочлен включает только вторую и четвертую степени переменной.
• функция четвертого порядка : Любая полиномиальная функция, наибольший показатель которой имеет степень четыре.

Полиномиальные уравнения более высокой степени могут быть очень трудными для решения. Однако в некоторых особых ситуациях их можно сделать более управляемыми, уменьшив их показатели с помощью замены.2 + bp + c [/ латекс]

С помощью подстановки мы смогли свести многочлен более высокого порядка к квадратному уравнению. Теперь ее можно решить с помощью любого из ряда методов (с помощью построения графиков, факторизации, завершения квадрата или использования формулы квадратичного уравнения).

После того, как значения [latex] p [/ latex] найдены, каждое положительное значение временной переменной [latex] p [/ latex] может использоваться для нахождения двух значений [latex] x [/ latex], таких как:

[латекс] x = \ sqrt p [/ латекс]

Как и любой квадратный корень, корень из [латекс] p [/ latex] будет иметь два значения: одно положительное и одно отрицательное.2 [/ latex], мы можем использовать каждое значение [latex] p [/ latex] для решения двух значений [latex] x [/ latex]:

[латекс] x = \ pm \ sqrt 2 [/ latex] и [латекс] x = \ pm \ sqrt 10 [/ latex]

Аналогичную процедуру можно использовать для решения уравнений высшего порядка. Требование состоит в том, чтобы было два члена [латекс] x [/ латекс], так что отношение высшего показателя [латекса] x [/ латекса] к нижнему было [латекс] 2: 1 [/ латекс].

Квадратичная формула | Уравнение, как использовать и примеры

Определение квадратичной формулы

Квадратичная формула — это алгебраическая формула, используемая для решения квадратных уравнений.

Квадратичная формула — это веха на пути к полному пониманию алгебры. Чтобы понять его, ценить его и правильно применять, вам нужно немного знать его предысторию, а затем ценить каждый термин в нем.

Содержание

1. Определение квадратичной формулы

Что такое квадратичная формула?

Как использовать квадратичную формулу

Найдите X-Intercepts

Примеры квадратичных формул

Когда использовать квадратичную формулу

Многочлены (выражения с множеством членов) могут иметь линейные, квадратные и кубические значения. Путаница возникает, когда мы смотрим на слово «квадратичный», потому что оно подразумевает четыре из чего-то, например, четырехугольник. Но происхождение слова означает «сделать квадрат», поскольку длина умножена на ширину. В математике значение квадрата — это показатель степени второй степени. Эти показатели являются степенью 2:

.

Итак, квадратичный многочлен имеет в качестве наивысшего значения что-то второй степени; что-то в квадрате.

Квадратное уравнение в стандартной форме

Квадратичная формула используется для решения квадратных уравнений.Рассмотрим квадратное уравнение в стандартной форме:

Вы также можете увидеть стандартную форму, называемую общим квадратным уравнением, или общую форму.

Пока 0, вы сможете разложить квадратное уравнение на множители. Иногда, однако, это сбивает с толку или беспорядочно, или вы не можете это учитывать.

Что такое квадратная формула?

Вы всегда можете найти решение любого квадратного уравнения, используя формулу корней квадратного уравнения. Квадратичная формула:

х = -b ± b2 — 4ac2a

Эту формулу можно использовать для решения квадратных уравнений.Или, если ваше уравнение факторизовано, вы можете использовать квадратную формулу, чтобы проверить правильность ваших решений квадратного уравнения.

Выражение b2 — 4ac, которое находится под (sqrt) внутри формулы корней квадратного уравнения, называется дискриминантом. Дискриминант используется, чтобы определить, сколько решений имеет квадратное уравнение.

• , если b2 — 4ac = 0 → 1 раствор
• , если b2 — 4ac> 0 → 2 решения
• , если b2 — 4ac <0 → нет реального решения

Как использовать квадратичную формулу

Начнем с простого квадратного уравнения:

х2 + 5х + 6 = 0

Для применения квадратичной формулы уравнение, которое вы распутываете, должно иметь форму, в которой все переменные помещаются с одной стороны от знака равенства, а с другой — 0:

(квадратичный) = 0

Шаги решения квадратных уравнений

Наше квадратное уравнение будет множителем, так что это отличное место для начала. Сначала мы разложим уравнение на множители. Мы ищем два числа, которые умножаются на 6 и прибавляются к 5:

х2 + 5х + 6 = 0

(х + 2) (х + 3) = 0

Мы видим, что любое выражение равно 0 (так как умножение его на другое выражение дает 0). Мы можем установить каждое выражение равным 0, а затем решить относительно x:

(х + 2) = 0

х = -2

(х + 3) = 0

х = -3

Наши два значения x — -2 и -3.

Сравнивая наш пример, x2 + 5x + 6 = 0, со стандартной формой квадратного уравнения (которое также можно назвать просто «квадратичным»), мы получаем следующие значения:

Теперь мы можем использовать их в квадратичной формуле и проверить, так как мы уже знаем, что наши ответы — -2 и -3:

Всегда надежная Квадратичная формула подтверждает значения x как -2 и -3.

Найдите X-Intercepts

В уравнении типа ax2 + bx + c = y установите y = 0 и определите уравнение. Возможные значения x будут отрезками x; где линия пересекает ось абсцисс.

Подумайте, сколько мы знаем о нашем графическом решении еще до того, как мы выполним какие-либо алгебраические вычисления:

• Поскольку уравнение дает два решения для x, у нас есть два пересечения с x
• У нас будет парабола
• Мы можем начать построение параболы с двух упорядоченных пар, (x1, 0) и (x2, 0)
• Вершина параболы будет между двумя точками пересечения по оси x

Решая алгебраическое уравнение, вы начинаете рисовать его в виде графика.

Графические калькуляторы, вероятно, будут равны , а не , с точностью квадратичной формулы. Используйте калькулятор, чтобы проверить округленные результаты, но ожидайте, что они будут немного отличаться.

Например, предположим, что у вас есть ответ из квадратичной формулы. Для большей точности оставьте как есть, а не записывайте его как десятичный эквивалент (3,16227766).

Примеры квадратичных формул

При решении квадратичных уравнений вы помогаете себе, зная несколько способов решения любого уравнения. Начните решать квадратичную функцию с того, чтобы посмотреть, будет ли она множителем (какие два множителя умножаются, чтобы получить c, которое также суммируется, чтобы получить b?).

Вы также можете попробовать заполнить квадрат. Вы все еще боретесь? Затем примените квадратичную формулу.

Используйте любой из этих методов и построение графиков, чтобы проверить ответ, полученный с помощью любого другого метода. Используйте квадратичную формулу, например, для проверки факторинга.

Давайте попробуем другой пример, используя следующее уравнение:

2×2 — 5x — 7 = 0

Сначала мы можем разложить на множители:

(2x — 7) (x + 1) = 0

2x — 7 = 0

х = 72 = 3.5

х + 1 = 0

х = -1

Затем мы можем проверить это с помощью квадратичной формулы, используя эти значения:

• а = 2
• b = -5
• с = -7

Если вы затем построите эту квадратичную функцию на графическом калькуляторе, ваша парабола будет иметь вершину (1,25, -10,125) с пересечением по оси x равным -1 и 3,5.

Вот квадратичный коэффициент , а не : x2 — 7x — 3 = 0

Никакие множители -3 не добавляют к -7, поэтому вы не можете использовать факторинг.Что делать? Если бы все, что вы знали, было факторингом, вы бы застряли. Но вы знаете, что нужно попробовать квадратичную формулу со следующими значениями:

• а = 1
• b = -7
• с = -3

Когда использовать квадратичную формулу

Квадратные уравнения фактически используются каждый день. Их можно использовать для расчета площадей, определения скорости движения объекта и даже для определения прибыли от продукта. Важно, чтобы вы знали, как находить решения квадратных уравнений, используя квадратную формулу.

При использовании квадратичной формулы вы должны быть внимательны к мельчайшим деталям. Например, размещение числителя всего над 2a будет , а не необязательно. Все, от -b до квадратного корня, больше 2а.

Als, обратите внимание на знак ± перед квадратным корнем, который напоминает вам найти два значения для x.

Это надоедливое b в самом начале тоже сложно, поскольку квадратичная формула заставляет вас использовать -b.Старайтесь думать о -b не как о «отрицательном b», а как о напротив любого значения «b». Предположим, ваш b положительный; противоположное отрицательно. Что делать, если ваш исходный b уже отрицательный? Подумайте: негатив негативного есть позитив; так -b положительно!

Под скобкой квадратного корня вы также должны работать осторожно. Иногда перед b2 стоит отрицательный знак, что означает, что вы возводите в квадрат все b, даже если оно отрицательное. Квадрат отрицательного значения является положительным, поэтому значение b2 всегда будет положительным.

Суть: работать очень аккуратно. Следите за своими знаками, работайте методично и ничего не пропускайте. Затем используйте другой метод, чтобы проверить свою работу. Независимо от того, какой метод вы используете, квадратичная формула доступна вам каждый раз. Это всегда будет работать.

Следующий урок:

Доказательство четырехугольника как параллелограмма

Квадратные уравнения — Полный курс алгебры

37

Стандартная форма квадратного уравнения

корень квадратичной

Решение с факторингом

Раздел 2 :

Завершение квадрата

Квадратичная формула

Дискриминант

Доказательство квадратичной формулы

Раздел 3 :

График y = квадратичный: парабола

КВАДРАТИКА — это многочлен, старший показатель которого равен 2.

ax ² + bx + c .

Коэффициент x ² называется ведущим коэффициентом.

Вопрос 1. Какая стандартная форма квадратного уравнения ?

ax ² + bx + c = 0.

Квадратичный находится слева. 0 справа.

Вопрос 2.Что мы подразумеваем под корнем квадратичного?

Решение квадратного уравнения.

Например, корни этой квадратичной —

x ² + 2 x — 8

— решения для

x ² + 2 x — 8 = 0.

Чтобы найти корни, мы можем разложить этот квадратичный коэффициент на

.

( x + 4) ( x — 2).

Теперь, если x = −4, то первый множитель будет 0. (Урок 2.) А если x = 2, второй множитель будет 0. Но если какой-либо множитель равен 0, тогда все произведение будет целиком. будет 0. Следовательно, если x = −4 или 2, то

x ² + 2 x — 8 = 0.

−4 или 2 являются решениями квадратного уравнения. Они корни этой квадратичной.

И наоборот, если корни равны a или b , то квадратичный коэффициент можно разложить на множители как

( x — a ) ( x — b ).

Корень квадратичного также называется нулем. Потому что, как мы увидим, для каждого корня значение графика равно 0. (См. Тему 7 Precalculus, вопрос 2.)

Вопрос 3. Сколько корней имеет квадратичный?

Всегда двое. Поскольку квадратичный (с ведущим коэффициентом не менее 1) всегда можно разложить на множители как ( x — a ) ( x — b ), и a , b — два корня.

Другими словами, когда старший коэффициент равен 1, корень имеет знак, противоположный знаку числа в множителе.
Если ( x + q ) — множитель, то x = — q — корень.

— q + q = 0.

Проблема 1. Если квадратичный коэффициент можно разложить на множители как ( x + 3) ( x — 1), то каковы два корня?

Чтобы увидеть ответ, наведите указатель мыши на цветную область.
Чтобы закрыть ответ еще раз, нажмите «Обновить» («Reload»).
Сначала решите проблему сами!

−3 или 1.

Мы говорим «или», потому что x может принимать только одно значение за раз.

Вопрос 4. Что мы подразумеваем под двойным корнем?

Два корня равны. Коэффициенты будут ( x — a ) ( x — a ), так что два корня будут a , a .

Например, этот квадратичный

x ² — 12 x + 36

можно разложить на

( x — 6) ( x — 6).

Если x = 6, то каждый коэффициент будет равен 0, и, следовательно, квадратичный будет 0. 6 называется двойным корнем.

Когда у квадратичной будет двойной корень? Когда квадратичный — это полный квадрат трехчлена.

Пример 1. Решите для x : 2 x ² + 9 x — 5.

Решение . Эта квадратичная величина факторизуется следующим образом:

2 x ² + 9 x — 5 = (2 x — 1) ( x + 5).

Урок 17.

.

Теперь легко увидеть, что второй множитель будет равен 0, когда x = −5.

Что касается значения x , то получится

2 x — 1	=	0,
мы должны решить это маленькое уравнение.(Урок 9.)
У нас:
2 x	=	1
x	=	1 2

Решения:

Проблема 2. Как возможно, что произведение двух множителей ab = 0?

Решение с факторингом

Проблема 3.Найдите корни каждого квадратичного уравнения путем факторизации.

а)	x ² — 3 x + 2		б)	x ² + 7 x + 12
	( x — 1) ( x — 2)			( x + 3) ( x + 4)
	x = 1 или 2.			x = −3 или −4.

Мы снова используем союз «или», потому что x принимает только одно значение за раз.

в)	x ² + 3 x — 10		г)	x ² — x — 30
	( x + 5) ( x — 2)			( x + 5) ( x — 6)
	x = −5 или 2.			x = −5 или 6.

e)	2 x ² + 7 x + 3				е)	3 x ² + x — 2
	(2 x + 1) ( x + 3)					(3 x -2) ( x + 1)
	x = —	1 2	или −3.			х =	2 3	или -1.

г)	x ² + 12 x + 36		ч)	x ² — 2 x + 1
	( x + 6) ²			( x — 1) ²
	х = −6, −6.			x = 1, 1.
	Двойной корень.			Двойной корень.

Пример 2. c = 0. Решите это квадратное уравнение:

ax ² + bx = 0

Решение . Поскольку нет постоянного члена: c = 0, x является общим множителем:

		x ( a x + b)	=	0.
	Это означает:
x			=	0
		или
x			=	–	b a	.

Это два корня.

Задача 4. Найдите корни каждой квадратичной.

а)	x ² — 5 x		б)	x ² + x
	x ( x — 5)			x ( x + 1)
	x = 0 или 5.			x = 0 или -1.

в)	3 x ² + 4 x			г)	2 x ² — x
	x (3 x + 4)				x (2 x — 1)
	x = 0 или —	4 3			x = 0 или ½

Пример 3. b = 0. Решите это квадратное уравнение:

ax ² — c = 0.

Решение . В случае отсутствия среднего срока можно написать:

	ось ²	=	с .
	Это означает:
	x ²	=	c a
	x	=	, согласно Уроку 26.

Однако, если форма разница двух квадратов —

x ² — 16

— тогда мы можем разложить на множители:

( x + 4) ( x −4).

Корни равны ± 4.

Фактически, если квадратичный равен

x ² — c ,

, то мы можем разложить его на множители:

( x +) ( x -),

так, чтобы корни были ±.

Задача 5. Найдите корни каждой квадратичной.

а)	x ² — 3		б)	x ² — 25		в)	x ² — 10
	x ² = 3			( x + 5) ( x -5)			( x +) ( x -)
	x = ±.			x = ± 5.			x = ±.

Пример 4. Решите это квадратное уравнение:

x ²	=	x + 20.
Решение . Сначала перепишите уравнение в стандартной форме, переставив все члены влево:
x ² — x — 20	=	0
( x + 4) ( x -5)	=	0
x	=	−4 или 5.

Итак, уравнение решается, когда x изолированы слева.

x = ± не является решением.

Задача 6. Решите каждое уравнение относительно x .

а)	x ² = 5 x — 6		б)	x ² + 12 = 8 x
	x ² — 5 x + 6 = 0			x ² — 8 x + 12 = 0
	( x — 2) ( x — 3) = 0			( x — 2) ( x — 6) = 0
	x = 2 или 3.			x = 2 или 6.
в)	3 x ² + x = 10		г)	2 x ² = x
	3 x ² + x — 10 = 0			2 x ² — x = 0
	(3 x -5) ( x + 2) = 0			x (2 x — 1) = 0
	x = 5/3 или — 2.			x = 0 или 1/2.

Пример 5. Решите это уравнение

3–

5 2

x — 3 x ²

=

0

Решение . Мы можем придать этому уравнению стандартную форму, поменяв все знаки с обеих сторон.0 не изменится. Имеем стандартную форму:

3 x ² +

5 2

x — 3

=

0

Затем мы можем избавиться от дроби, умножив обе части на 2. Опять же, 0 не изменится.

6 x ² + 5 x — 6	=	0
(3 x — 2) (2 x + 3)	=	0.

Корни

2 3

или —

3 2

.

Задача 7. Решите для x .

а)

3–

11 2

x — 5 x ²

= 0

б)

4 +

11 3

x — 5 x ²

= 0

5 x ² +	11 2	x — 3	= 0		5 x ² —	11 3	x — 4	= 0
10 x ² + 11 x — 6			= 0		15 x ² — 11 x — 12			= 0
(5 x — 2) (2 x + 3)			= 0		(3 x -4) (5 x + 3)			= 0

Корни

2 5

или —

3 2

.

Корни

4 3

или —

3 5

.

в)	— x ² — x + 20	= 0		г)	— x ² + 3 x + 18	= 0
	x ² + x — 20	= 0			x ² — 3 x — 18	= 0
	( x + 5) ( x -4)	= 0.			( x — 6) ( x + 3)	= 0.
	x = −5 или 4.				x = 6 или −3.

Участок 2: Завершение квадрата

Содержание | Дом

---

Сделайте пожертвование, чтобы TheMathPage оставалась в сети. 2} + bx + c, где a, b и c — действительные числа, но a \ ne 0.

• Шаг 2: Переместите константу \ color {red} c в правую часть уравнения, вычтя обе части на \ color {red} c.

• Шаг 3: Разделите все уравнение на коэффициент при квадрате члена, который равен \ large {a}.

• Шаг 4: Теперь определите коэффициент линейного члена \ large {x}.

• Шаг 5: Разделите полученное значение на 2 и возведите в 2-ю степень. Затем упростите его еще больше.

• Шаг 6: Добавьте результат шага 5 к обеим сторонам уравнения.

• Шаг 7: Упростите правую часть уравнения. Будьте осторожны, складывая дроби с разными знаменателями. Убедитесь, что вы нашли правильный наименьший общий знаменатель (ЖКД) при выполнении сложения.

• Шаг 8: Выразите трехчлен в левой части уравнения как квадрат бинома.

• Шаг 9: Извлеките квадратный корень из обеих частей уравнения, чтобы исключить показатель степени 2 бинома.

• Шаг 10: Упростить. Убедитесь, что вы добавили \ color {red} \ pm с правой стороны уравнения. Левая часть больше не содержит мощности 2.

• Шаг 11: Сохраните переменную x слева, вычтя обе части на \ Large {b \ over {2a}}.

• Шаг 12: Упростите, и готово!

Я надеюсь, что вы найдете пошаговое решение полезным в выяснении того, как квадратная формула выводится с использованием метода завершения квадрата.

---

Возможно, вас заинтересует:

Квадратичная формула

решений или корней квадратных уравнений

решений или корней квадратных уравнений

Рассмотрим квадратное уравнение

Действительное число x будет называться решением или корнем, если оно удовлетворяет уравнению, то есть. Легко видеть, что корни являются точками пересечения квадратичной функции по оси x, то есть пересечения графика квадратичной функции с осью x.

a <0	a> 0

Пример 1: Найдите корни уравнения

Решение. Это уравнение эквивалентно

Поскольку 1 имеет два квадратных корня, решениями этого уравнения являются

Пример 2: Найдите корни уравнения

Решение. Этот пример несколько сложнее предыдущего, но мы увидим, как с ним работать в общем случае. Сначала обратите внимание, что у нас есть

Следовательно, уравнение эквивалентно

который совпадает с

Поскольку 3 имеет два квадратных корня, получаем

которые дают решения уравнения

Тогда мы можем задаться вопросом, можно ли свести какое-либо квадратное уравнение к самые простые, описанные в предыдущих примерах. Ответ несколько сложнее, но он был известен очень давно (вавилонянам около 2000 г. до н. Э.). Их идея была основана в основном на завершении квадрата , что мы и сделали при решении второго примера.

[Алгебра] [Комплексные переменные] [Геометрия] [Тригонометрия] [Исчисление] [Дифференциальные уравнения] [Матричная алгебра] Домашняя страница S.O.S MATHematics

Вам нужна дополнительная помощь? Пожалуйста, разместите свой вопрос на нашем S.O.S. Математика CyberBoard.

Автор: Мохамед Амин Хамси

Авторские права 1999-2021 MathMedics, LLC.Все права защищены.
Свяжитесь с нами
Math Medics, LLC. — П.О. Box 12395 — El Paso TX 79913 — США
пользователей онлайн за последний час

Различий между квадратными и линейными уравнениями

Обновлено 16 ноября 2020 г.

Крис Дезиел

Линейное уравнение с двумя переменными не требует степени выше единицы для любой из переменных. Он имеет общий вид:

Ax + By + C = 0

, где A, B и C — константы. 2 + bx + c

Помимо дополнительной сложности решения квадратного уравнения по сравнению с линейным, эти два уравнения создают разные типы графиков.

TL; DR (слишком долго; не читал)

Линейные функции взаимно однозначны, а квадратичные — нет. Линейная функция дает прямую линию, а квадратичная функция дает параболу. Построение графика линейной функции несложно, в то время как построение графика квадратичной функции — более сложный многоэтапный процесс.

Характеристики линейных и квадратных уравнений

При построении графика линейное уравнение дает прямую линию. Каждое значение x дает одно и только одно значение y , поэтому связь между ними считается однозначной. Когда вы строите квадратное уравнение, вы создаете параболу, которая начинается в одной точке, называемой вершиной, и простирается вверх или вниз в направлении y . Связь между x и y не однозначна, потому что для любого заданного значения y , кроме значения y точки вершины, есть два значения для x .

Решение и построение графиков линейных уравнений

Линейные уравнения в стандартной форме ( Ax + By + C = 0) легко преобразовать в форму пересечения наклона ( y = м x + b ), и в этой форме вы можете сразу определить наклон линии, который составляет м , и точку, в которой линия пересекает y — ось. Вы можете легко изобразить уравнение, потому что все, что вам нужно, это две точки.Например, предположим, что у вас есть линейное уравнение

y = 12x + 5

. Выберите два значения для x , скажем 1 и 4, и вы сразу получите значения 17 и 53 для y . Постройте две точки (1, 17) и (4, 53), проведите через них линию, и все готово.

Решение и построение графика квадратных уравнений

Вы не можете решить и построить график квадратного уравнения так просто.