Квадратичная функция творит чудеса
Наступает первое сентября, и счастливые родители ведут свое чадо первый раз в первый класс. А дальше дорога для большинства учащихся длиною в 11 лет. Математика с ними на всем пути, но не у всех детей прирожденная склонность к ней.
Перед учителем встает ряд нелегких проблем. Выделим три из них:
1. Искать те крупицы воздействия на учащихся, которые способствовали бы стремлению приобретать знания, расширять их, а значит помогать начинать мыслить, включаться в урок.
2. Сделать урок таким, чтобы осталась пища для размышлений.
3. Предвидеть, что есть учащиеся с тягой к гуманитарным наукам, и стремиться помочь пробудить в них желание погрузиться в математический мир, но одновременно не забывать увлеченных математикой и давать пищу жаждущему ее уму.
Мы обратим внимание на материал статьи “Рисуем графиками функций” [3]. Автор, А. Я. Цукарь из Новосибирска предлагает выполнить 6 рисунков в качестве упражнений для домашних заданий, заметив, что они будут полезны школьникам с гуманитарной направленностью. Там же приведен список изображаемых объектов (зонтик, очки, кит, шахматный король, лягушка, бабочка) и перечень функций, графики которых участвуют в этом изображении. Заметим, что продолжение, в смысле новых рисунков, напечатано в газете “Математика” [2].
О том, как этот материал можно использовать с целью попытки решения тех проблем, которые выделили выше, дальше пойдет речь.
Наш век – век компьютеров, значит, они
должны работать и на уроках математики, а не
только на уроках информатики. Мы предлагаем
воспользоваться программой, по которой возможно
выполнить эти 6 рисунков.
Все графики вычерчиваются исходя из математических формул. На экране отображается координатная сетка и оси. При нажатии на изображение уравнения происходит вычерчивание графика, причем это построение можно повторить несколько раз. Размер чертежа можно увеличить или уменьшить, что позволяет уточнить координаты той или иной точки. Программу, выполняющую данные построения, можно найти в Интернете по адресу http://kgpu.real.kamchatka.ru
Приводим наши предложения о том, что можно добавить к материалу при изучении квадратичных функций и как это сделать.
Начнем с фрагмента начала урока перед
рассмотрением построения графика квадратичной
функции «y=ax
На экране телевизора или компьютера
медленно вырисовываются в разных цветах части
парабол, которые в итоге дают изображение
лягушки.
Учитель замечает, что детали для рисунка предоставила нам очень интересная функция, называемая квадратичной, построение графиков которой – цель нашего урока. После освоения материала (на него уйдет не один урок) каждый сможет сам рисовать, а проверять свои художества можно, используя компьютер. Учитель примерно так вводит учащихся в новую тему.
Какая задумка была у учителя в самом начале урока? Вызвать эмоциональные переживания через удивление. На это работает необычность приводимого факта, красота обозреваемого объекта, скорость получения результата…
В этом случае внутренние переживания ученика подключаются к таким процессам, как запоминание, внимание, осмысливание. Они будут протекать более интенсивно и способствовать достижению решаемых задач в обучении.
В конце урока в качестве итога учитель
обращает внимание на материал стенда, который до
этого был закрыт “Изучаем на уроке”.
На нем привлекает внимание лягушонок, который запомнился учащимся и держит их в ожидании нового урока. Этого нам очень хотелось бы достичь. Потому приведены все функции, принимавшие участие в выполнении рисунка. Они отличаются от тех, с которыми учащиеся имели дело на прошедшем уроке, что особо подмечал учитель.
Там же запечатлена хроника начала урока с конкретизацией ряда моментов в шутливой стихотворной форме и подчеркнута возможность ученика, усвоившего изучаемый материал, в дальнейшем так же, как компьютер, рисовать графиками функции.
Творчески работающий учитель найдет,
где и как использовать при изучении программного
материала нижеследующие задания. Они будоражат
фантазию, развивают эстетические наклонности,
приобщают к поиску, пониманию математических
истин, увлекают в загадочный мир знаний.
Задание 1.
1) Построить график функции и сделать трафарет.
3) Записать формулы парабол, прямых, которые определили Ваш рисунок.
2) С помощью трафарета дорисовать построенную параболу до того, на чем остановится Ваша фантазия. При этом трафарет можно переворачивать, перемещать влево или вправо, вверх или вниз, использовать любую его часть и оси координат.
Приводим пример выполнения задания 1. Парабола построена .
После несложных размышлений принято решение рисовать тюльпан. Из параболы получается цветок, если ее прервать, проведя вверху изящную волнистую линию. Ось игреков от точки О вниз – это стебелек, справа и слева от него можно сделать по листочку.
Наши действия: трафарет
переворачиваем (т. е. ветви направляем вниз) и
перемещаем по параболе…
е. ветви направляем вниз) и
перемещаем по параболе…
Находятся такие точки С, D, Е, которые после совмещения (трижды) с точкой О (на трафарете) дадут нужную линию.
Запишем формулы трех парабол, позволившие это сделать. Работает формула , где точка (m; n) — вершина параболы. У нас первая точка С (-4; 19) – вершина одной из парабол, а именно . Мы обводим только участок параболы при . Аналогичным будет подход в описании всех остальных случаев.
В итоге тюльпан рисовали семь квадратичных функций и одна линейная:
1.
2.
3.
4.
5.
6.
7.
8.
Задание 2.
Графиками функций [3] сделать рисунок, дать ему название.
Например. Даны функции:
1.
2.
3.
4.
5.
6.
7.
Учащиеся строят графики, получают рисунок. Если не сделано ошибок, он должен выглядеть так, как показано:
Задание 3.
После завершения работы над заданием 2, проверить правильность его выполнения на компьютере.
Задание 4.
Придумать рисунки, которые создадут
графики функций (квадратичной и линейной) и
записать эти функции аналитически.
Задание 5.
Выполнить желаемые рисунки (кошка, птица, динозаврик, верблюд, фазан, сидящая кошка, голова женщины, соболь, женщина с ведрами) графиками функций: параболами, прямыми, воспользовавшись материалами, опубликованными в [2].
Задание 6.
Перед Вами ландыш – , рыба — «, лицо клоуна – . Напишите формулы функций, которые их определили, если они выполнены с помощью только трафарета графика функции .
Замечание.
Рисунок ландыша выполнили графики
19 функций, рыбы – 16 функций; над изображением
лица клоуна трудились графики 17 функций.
Список литературы
1. Алгебра: Учеб. для 9 кл. общеобразоват. учреждений / Под ред. С.А. Теляковского. – М.: Просвещение, 2002.
2. Цукарь А.Я. Рисуем графиками функций // Математика. – 1999. – № 7, № 22, № 23, № 24, № 25.
3. Цукарь А.Я. Рисуем графиками функций // Математика в школе. – 1999. – № 4. – С. 80-81.
Добавление векторной графики в веб-документ — Изучение веб-разработки
Векторная графика очень полезна во многих случаях. Она имеет малые размеры файла и высокую масштабируемость – при увеличении масштаба пиксели не увеличиваются вместе с графикой. В данной статье мы покажем, как встраивать векторную графику на Вашу страницу.
Примечание: Данная статья не научит вас векторной графике, а даст понимание что это и как её использовать в веб-документах.
В веб-разработке вы будете сталкиваться с двумя типами изображений — растровым и векторным:
- Растровое изображение задаётся сеткой пикселей — файл растрового изображения содержит информацию о расположении и цвете каждого пикселя.
 Среди популярных форматов изображений данного типа числятся Bitmap (.bmp), PNG (.png), JPEG (.jpg) и GIF (.gif)
Среди популярных форматов изображений данного типа числятся Bitmap (.bmp), PNG (.png), JPEG (.jpg) и GIF (.gif) - Векторное изображение определяется алгоритмом — файл векторного изображения содержит фигуры и правила, по которым компьютер может вычислить как должно выглядеть изображение, когда выводится на экран.SVG формат позволяет нам создавать векторную графику для использования в веб-документах.
Для демонстрации различий между типами изображений, давайте взглянем на пример. Вы можете найти данный пример на Github как vector-versus-raster.html — в нем демонстрируются два, на первый взгляд, одинаковых изображения, расположенных рядом друг с другом. Каждое из изображений представляет собой красную звезду с тенью. Различие их в том, что левое изображение имеет формат PNG, а правое — SVG.
Различия становятся заметны, когда вы изменяете масштаб страницы — PNG изображение становится неровным (становятся видны пиксели), потому что оно содержит информацию о положении и цвете каждого пикселя. При увеличении каждый пиксель также увеличивается, охватывая несколько пикселей дисплея, поэтому становятся заметны «кирпичики». Векторное изображение продолжает выглядеть ровным и красивым, потому что фигуры, масштабируются совместно с ним.
При увеличении каждый пиксель также увеличивается, охватывая несколько пикселей дисплея, поэтому становятся заметны «кирпичики». Векторное изображение продолжает выглядеть ровным и красивым, потому что фигуры, масштабируются совместно с ним.
Примечание: Оба изображения сверху имеют формат PNG — слева показано растровое изображение, справа условно показано векторное изображение. Напоминаем, что пример с реальными растровым и векторными изображениями находится по ссылке: vector-versus-raster.html !
Более того, файлы векторных изображений намного меньше растровых, т.к. в них содержится алгоритмы построения вместо информации о каждом пикселе.
SVG это язык на базе XML для описания векторных изображений. По сути это язык разметки, как и HTML, только содержащий множество различных элементов для определения фигур вашего изображения, а также параметров их отображения. SVG предназначен для разметки графики, а не содержимого. В простейшем случае, вы можете использовать элементы для создания простых фигур, таких как <circle>(круг) и <rect>(прямоугольник). Более сложные SVG элементы включают
Более сложные SVG элементы включают <feColorMatrix> (en-US) (разложение цвета с использованием матрицы), <animate> (анимация частей вашего векторного изображения) и <mask> (en-US) (применение маски к изображению.)
В качестве простого примера, следующий код создаёт круг и прямоугольник:
<svg version="1.1"
baseProfile="full"
xmlns="http://www.w3.org/2000/svg">
<rect fill="black" />
<circle cx="150" cy="100" r="90" fill="blue" />
</svg>В результате получается следующее:
Исходя из примера выше, может показаться, что SVG легко создавать вручную. Да, простые SVG можно создавать, используя текстовый редактор, но в случае сложного изображения это становится сложным. Для создания SVG изображений используются редакторы векторной графики, такие как Inkscape или Illustrator. Данные приложения позволяют создавать различные изображения, используя множество графических инструментов, и создавать приближения фотографий (например опция Trace Bitmap feature приложения Inkscape. )
)
Дополнительные преимущества SVG:
- Текст в векторном изображении остаётся машинописным (то есть доступным для поисковика, что улучшает SEO).
- SVG легко поддаются стилизации/программированию (scripting), потому что каждый компонент изображения может быть стилизован с помощью CSS или запрограммирован с помощью JavaScript.
Так почему же тогда вообще используют растровые изображения, а не только SVG? Дело в том, что SVG имеет ряд недостатков:
- SVG может очень быстро стать сложным в том смысле, что размер файла увеличивается; сложные SVG-изображения также создают большую вычислительную нагрузку на браузер.
- SVG может быть сложнее создать, нежели растровое изображение, в зависимости от того, какое изображение необходимо создать.
- не поддерживается старыми версиями браузеров, то есть не подойдёт для сайтов, поддерживающих Internet Explorer 8 или старее.
В целом, растровая графика лучше подходит для сложных изображений, например, фотографий.
В данном разделе мы рассмотрим различные варианты, с помощью которых можно добавить SVG векторную графику на веб-страницу.
Быстрый путь:
<img>Чтобы встроить SVG используя элемент <img>, вам просто нужно сослаться на него в атрибуте src, как и следовало ожидать. Вам понадобится атрибут height или width (или оба, если ваш SVG не имеет собственного соотношения сторон). Если вы ещё этого не делали, пожалуйста, прочтите Изображения в HTML.
<img
src="equilateral.svg"
alt="triangle with all three sides equal"
/>Плюсы
- Быстрый, знакомый синтаксис изображения со встроенным текстовым эквивалентом, доступным в атрибуте
alt - Вы можете легко превратить изображение в гиперссылку, поместив
<image>в элемент<a>.
Минусы
- Вы не можете изменять изображение с помощью JavaScript.

- Если вы хотите управлять содержимым SVG с помощью CSS, вы должны использовать встроенные CSS стили в своём SVG коде. (Внешние таблицы стилей, вызываемые из файла SVG, не действуют.)
- Вы не можете изменить стиль изображения с помощью псевдоклассов CSS (например
:focus).
Устранение неполадок и кросс-браузерная поддержка
Для браузеров которые не поддерживают SVG (IE 8 и ниже, Android 2.3 и ниже), вы можете ссылаться на PNG или JPG в src атрибуте и использовать srcset атрибут (который распознают только последние браузеры) чтобы сослаться на SVG. В этом случае SVG будут загружаться только поддерживающими браузерами — старые же браузеры будут загружать PNG:
<img src="equilateral.png" alt="triangle with equal sides" srcset="equilateral.svg">Также вы можете использовать SVG в качестве фоновых изображение CSS, как показано ниже. В приведённом коде ниже старые браузеры будут придерживаться PNG, который они понимают, тогда как новые браузеры будут загружать SVG:
background: url("fallback. png") no-repeat center;
background-image: url("image.svg");
background-size: contain;
png") no-repeat center;
background-image: url("image.svg");
background-size: contain;Подобно методу <img>, описанному выше, вставка SVG с использованием фоновых изображений CSS означает, что SVG нельзя манипулировать при помощи JavaScript, и что SVG будет иметь те же ограничения, что и CSS.
Если ваши SVG не отображаются вовсе, возможно, ваш сервер не настроен должным образом. Если проблема в этом, то данная статья укажет вам верное направление.
Как включить SVG в ваш HTML код
Вы можете открыть файл SVG в текстовом редакторе, скопировать этот код и вставить его в ваш HTML документ — такой приём иногда называют встраиванием SVG (SVG inline или inlining SVG). Убедитесь, что фрагмент вашего SVG кода начинается и заканчивается с тегов <svg></svg> (не включайте ничего, кроме них). Вот очень простой пример того, что вы можете вставить в ваш документ:
<svg>
<rect fill="green" />
</svg>
Плюсы
- Вставка вашего SVG путём SVG inline позволяет сохранить HTTP запросы и, следовательно, может уменьшить время загрузки.

- Вы можете присваивать
class-ы иidэлементам SVG и стилизовать их при помощи CSS, либо в пределах SVG, либо внутри SVG, либо там, где вы размещаете правила стиля CSS для вашего HTML документа. По факту вы можете использовать любой атрибут представления SVG как свойство CSS. - SVG inline единственный метод, который позволяет вам использовать CSS-взаимодействия (как
:focus) и CSS-анимацию на вашем SVG изображении (даже в вашей обычной таблице стилей). - Вы можете разметить SVG как гиперссылку, обернув в элемент
<a>.
Минусы
- Этот метод подходит, только если вы используете SVG лишь в одном месте. Дублирование делает обслуживание ресурсоёмким.
- Дополнительный SVG код увеличивает размер вашего HTML файла.
- Браузер не может кешировать встроенный SVG, так как он кеширует обычные изображения.
- Вы можете добавить альтернативный вариант в элементе
<foreignObject>, но браузеры поддерживающие SVG будут продолжать загружать все альтернативные изображения. Вы должны взвесить действительно стоит ли поддержка устаревших браузеров дополнительных накладных расходов (ресурсов).
Вы должны взвесить действительно стоит ли поддержка устаревших браузеров дополнительных накладных расходов (ресурсов).
Как встраивать SVG при помощи
<iframe> (en-US)Вы можете открывать ваши SVG изображения в браузере просто как веб-страницы. Таким образом встраивание SVG документа с помощью <iframe> выполняется как мы изучали ранее в главе От <object> к <iframe> — другие технологии внедрения.
Вот краткий обзор:
<iframe src="triangle.svg" sandbox>
<img src="triangle.png" alt="Triangle with three unequal sides" />
</iframe>Это — определённо не самый лучший метод для выбора:
Минусы
- Как вы можете видеть, у
iframe-ов есть резервный механизм, но браузеры отображают резервный вариант только если они вообще не поддерживаютiframe-ы. - Более того, до тех пор пока SVG и ваша текущая веб-страница имеют одинаковый origin, вы не можете использовать JavaScript на вашей основной веб-странице, чтобы манипулировать SVG.

В этом разделе активного изучения мы бы хотели, чтобы вы просто попробовали поиграть с SVG. Ниже, в области Input, вы увидите, что мы уже предоставили некий пример для того, чтобы вы начали. А ещё вы можете посетить SVG Element Reference, чтобы узнать больше деталей о других игрушках, которые могут быть использованы в SVG, и тоже попробовать их. Этот раздел полностью посвящён практике ваших исследовательских навыков и вашему развлечению.
Если Вы где-то застряли и ваш код не работает, вы всегда можете начать сначала, нажав кнопку Reset.
Эта статья предоставила вам краткий обзор по тому, что такое векторная графика и SVG, почему полезно знать о них и как внедрять SVG в вашу веб-страницу. Эта статья не является полным руководством по изучению SVG, а всего лишь указатель, чтоб вы знали что такое SVG, на случай, если вы встретите его во время странствий по Сети. Так что не переживайте, если вы ещё не чувствуете себя экспертом в SVG. Ниже мы включили несколько ссылок, которые могут вам помочь, если вы хотите узнать больше о том, как это работает.
В последней статье этого модуля мы будем исследовать адаптивные изображения в деталях, рассматривая инструменты HTML, которые позволяют делать ваши изображения так, чтоб они могли лучше работать на разных устройствах.
|
«Как построить график функции F(x)+m»
Дата публикации: .
Презентация и урок на тему: «Как построить график функции f(x)+m»
Дополнительные материалы
Уважаемые пользователи, не забывайте оставлять свои комментарии, отзывы, пожелания! Все материалы проверены антивирусной программой.
Скачать: Как построить график функции f(x)+m (PPTX)
Ребята, сегодня мы научимся еще одному методу построения графиков функций!
Поступим как на прошлом уроке, построим в одной системе координат три параболы: $y=x^2$,
$y=x^2+3$, $y=x^2-3$.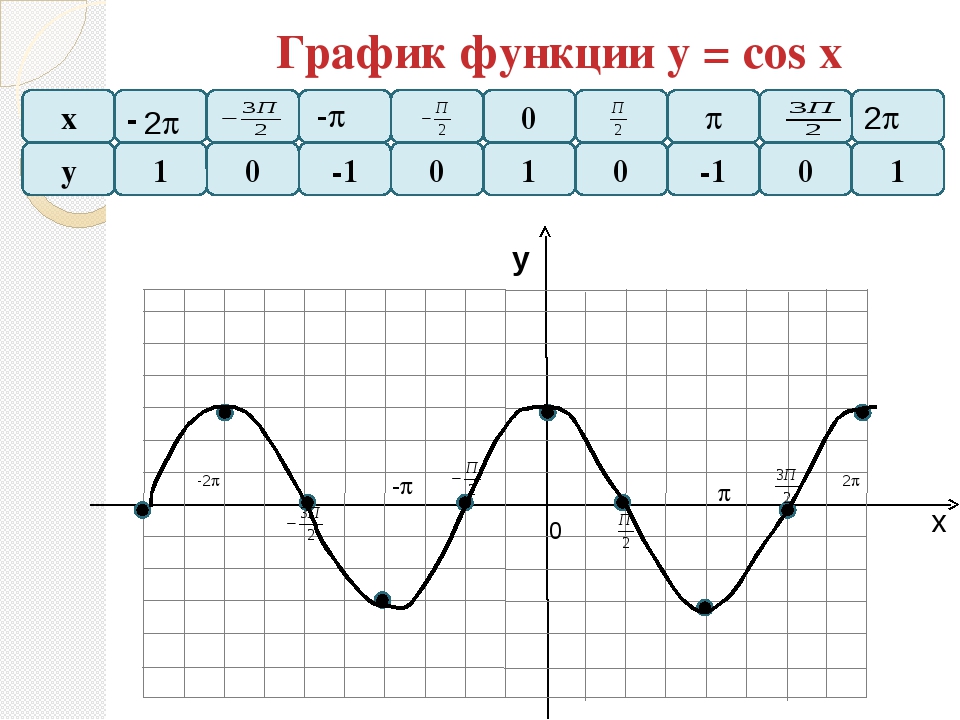 2-4, -1<x≤2. \end {cases}$
2-4, -1<x≤2. \end {cases}$
Как график любые изображения. Пересечение искусства и математики | Cat Lewis
Если у вас есть скучающая минута, я бы порекомендовал необычную форму развлечения. Он находится на академическом веб-сайте, наполненном математикой, известном как Wolfram Alpha.
Введите «банановая кривая» в строку поиска.
Для тех, кто более требователен к художественному чутью, вы можете попробовать «Изгиб в стиле Северуса Снейпа». Или всегда есть «первая» и «вторая» «кривые Альберта Эйнштейна».И если вы не склонны тратить лишние семь секунд работы, чтобы удовлетворить свое любопытство, вот изображение «симбоподобной кривой»:
(http://m.wolframalpha.com/input/?i =simba+curve&x=0&y=0)Математика уже не кажется такой нехудожественной, не так ли? Но как именно можно осуществить эти визуальные подвиги, используя только графическое программное обеспечение и человеческий мозг?
По своей сути координатный график представляет собой визуальное представление отношений между числами или переменными. Но это работает и наоборот: формулы представляют собой математическое представление изображений, которые они создают при графическом отображении.Эта перспектива внезапно предлагает целый ряд новых возможностей, поскольку теперь изображения можно создавать только с помощью чисел, символов и графического программного обеспечения.
Но это работает и наоборот: формулы представляют собой математическое представление изображений, которые они создают при графическом отображении.Эта перспектива внезапно предлагает целый ряд новых возможностей, поскольку теперь изображения можно создавать только с помощью чисел, символов и графического программного обеспечения.
Это может показаться знакомым дизайнеру или цифровому художнику. Разве программы для создания векторных иллюстраций, такие как Adobe Illustrator, не полагаются на математику? Да, и во многом это схожая идея. Пользователь вводит изображение, будь то простая линия, типографика или сложный набросок, и программа сохраняет это изображение в виде математических уравнений и геометрических фигур.¹ Эта зависимость от математики делает векторные иллюстрации бесконечно масштабируемыми.
Это подводит нас к простому примеру создания изображения с графиком: кривой Бэтмена. Это изображение было популярно в Интернете в старые добрые времена, еще в 2011 году. Но, несмотря на свою устаревшую природу мема, оно служит вечным примером того, как объединение математических функций может создать эстетически узнаваемый и даже привлекательный образ. Первоначальным создателем графика был школьный учитель Дж.Мэтью Регистр, который стремился вдохновить своих учеников на математику.
Первоначальным создателем графика был школьный учитель Дж.Мэтью Регистр, который стремился вдохновить своих учеников на математику.
При разложении уравнения каждый член в скобках представляет собой отдельный набор линий на графике Бэтмена. Например, самый первый член (кусок переменных в первых скобках) — это внешние крылья летучей мыши, основанные на общей формуле овала. В отличие от графиков, которые вы изучаете в старшей школе по алгебре и которые растягиваются до бесконечности, эти линии управляются с использованием математических понятий, таких как мнимые числа.Это уравнение Бэтмена нельзя изобразить на заурядном графическом калькуляторе. Он был разработан для более надежного графического программного обеспечения под названием Mathematica, хотя TI-89 все еще может рисовать довольно надежные изображения (см. соответствующие ссылки ниже).
Теоретически этот метод построения графиков можно использовать для создания любого существенно упрощенного изображения на координатной сетке. Тем не менее, это требует много времени и субъективно — г-н Регистр приводит пять или шесть часов времени для создания своего исходного уравнения.
Тем не менее, это требует много времени и субъективно — г-н Регистр приводит пять или шесть часов времени для создания своего исходного уравнения.
Но есть и другой способ, который делает возможными сложные кривые иллюстраций Wolfram Alpha, такие как «Simba-like» кривая выше.Он основан на так называемом преобразовании Фурье. Этот инструмент используется для записи любой функции в виде суммы функций синуса и косинуса. Первоначально меня познакомил с графиками Wolfram Alpha и основами математики, лежащими в их основе, мой профессор физики AP, еще один учитель, который, как и г-н Регистр, глубоко заботился об образовательном опыте и фундаментальном понимании своих студентов.
Преобразование Фурье является расширением ряда Фурье, концепции исчисления, которая объясняет, как любая периодическая (также известная как повторяющаяся) функция может быть записана в виде суммы синусов и косинусов.На самом деле многие функции требуют бесконечного числа синусов и косинусов. Оказывается, синусы и косинусы могут быть полезны не только для того, чтобы раздражать студентов тригонометрии; изучение рядов Фурье и способов работы с ними составляет целую область математики, известную как гармонический анализ. Преобразование Фурье было открыто Жаном Батистом Жозефом Фурье, который в 1822 году после ряда статей опубликовал книгу по математике теплоты. Он был первым, кто математически представил диффузию тепла; он также был изобретателем обозначения определенных интегралов.²
Преобразование Фурье было открыто Жаном Батистом Жозефом Фурье, который в 1822 году после ряда статей опубликовал книгу по математике теплоты. Он был первым, кто математически представил диффузию тепла; он также был изобретателем обозначения определенных интегралов.²
Ряды Фурье аппроксимируют функцию, и каждый «шаг» в этом процессе — каждая дополнительная функция синуса или косинуса — приближает аппроксимацию к любой воспроизводимой функции. Добавьте еще синус или косинус, добейтесь более реалистичного «изображения». Вот почему ряд может быть бесконечным; приближение становится все лучше и лучше, но никогда действительно не становится точным. Весь процесс выглядит примерно так:
(https://giphy.com/search/fourier) Преобразование Фурье — это математический инструмент, связанный с рядом Фурье.Преобразование разлагает функцию на набор синусоид или периодических функций. Это удобно, потому что эти периодические функции могут быть записаны в виде синусов и косинусов с использованием ряда Фурье. Да, вы правильно прочитали: любую математическую функцию можно создать, сложив варианты sin(x) и cos(x) .
Да, вы правильно прочитали: любую математическую функцию можно создать, сложив варианты sin(x) и cos(x) .
Преобразование Фурье изобилует практическими приложениями в науке и технике, особенно потому, что в реальном мире меньше проблем непрерывности и сходимости, чем в теоретической математике.И как только вы можете использовать преобразование Фурье, чтобы превратить любую функцию в синусы и косинусы, что ж, бесконечность — это предел (шутка, предел sin(x) при стремлении x к бесконечности не существует).
Чтобы еще больше развить причудливую вездесущность синусов и косинусов, скажем, что график — не единственная вещь, которую можно преобразовать в синусоиду с помощью преобразования Фурье. Математический инструмент также используется при обработке пиксельных изображений. Чтобы понять, как это возможно, нужно вернуться к основам того, что такое периодическая функция.Общая форма читается как A sin(bx)+c , где каждый коэффициент (A, b и c) описывает другую характеристику графа. В этом формате A — это амплитуда, b — период, а c — фазовый сдвиг. Используя аналогичную информацию, пиксели изображения можно «закодировать» в виде синусоидальной функции. Например, «интенсивность» пикселя соответствует амплитуде (A) синусоидальной функции, а «местоположение» пикселя — фазовому сдвигу (c).³
В этом формате A — это амплитуда, b — период, а c — фазовый сдвиг. Используя аналогичную информацию, пиксели изображения можно «закодировать» в виде синусоидальной функции. Например, «интенсивность» пикселя соответствует амплитуде (A) синусоидальной функции, а «местоположение» пикселя — фазовому сдвигу (c).³
Таким образом, преобразование Фурье создает уникальное представление весь образ.Для каждого изображения существует только одно преобразование Фурье, и наоборот, только одно изображение для каждого преобразования Фурье. По сути, каждое когда-либо созданное цифровое изображение соответствует цепочке синусоид; этот математический инструмент так же богат и разнообразен, как цифровая фотография и искусство.
Если вы посмотрите на любую кривую изображения Wolfram Alpha, вы увидите, что уравнения представляли собой головокружительно длинные линии — как вы уже догадались — синусов и косинусов. Преобразование Фурье делает возможными все эти графические изображения.И самое интересное, что, в конце концов, этот небольшой подмножество математики преследует ту же цель, что и многие другие области искусства и дизайна: поиск наилучшего представления визуального явления. Специфика сильно различается, но трюки с перспективой и веса линий являются такими же инструментами, как исчисление и косинусы.
Специфика сильно различается, но трюки с перспективой и веса линий являются такими же инструментами, как исчисление и косинусы.
Помимо новых графиков на Wolfram Alpha, было предпринято несколько попыток использовать преобразование Фурье для более художественных целей. Одним из наиболее интересных, которые я нашел, было (очевидно, устаревшее или никогда не выпущенное) приложение для рисования под названием «DrawAnything.Приложение попыталось научить своих пользователей рисовать любое загруженное изображение с помощью преобразования Фурье. Каждый «шаг» в сгенерированном приложением руководстве по рисованию будет шагом в приближении преобразования Фурье. Идея хорошая — объединить математику и рисование, переходить от простого к сложному так же, как рисуют что угодно. Однако ясно, что он был разработан кем-то, кто больше интересовался рядом Фурье, чем рисованием, потому что простейшая фаза ряда Фурье совсем не похожа на то, как обычно строится рисунок.
Синусы и косинусы вряд ли волшебным образом превратят любого художника в ботаника-математика, точно так же, как красивый график вряд ли волшебным образом превратит любого математика в художника. Но синусоиды гораздо красивее, чем можно было бы ожидать. По сути, каждая картина, фотография или сцена, которые вас вдохновили, на расстоянии одного преобразования Фурье от уравнения на экране. Они говорят, что картинка стоит тысячи слов; Я не уверен, кто такие они , хотя могу поспорить, что им платят за то, что они что-то рисуют.Но если картинка стоит тысячи слов, то, значит, и функция тоже. В конце концов, они совпадают — строка за строкой, пиксель за пикселем.
Но синусоиды гораздо красивее, чем можно было бы ожидать. По сути, каждая картина, фотография или сцена, которые вас вдохновили, на расстоянии одного преобразования Фурье от уравнения на экране. Они говорят, что картинка стоит тысячи слов; Я не уверен, кто такие они , хотя могу поспорить, что им платят за то, что они что-то рисуют.Но если картинка стоит тысячи слов, то, значит, и функция тоже. В конце концов, они совпадают — строка за строкой, пиксель за пикселем.
Все еще интересно?
Если вас увлекло простое наблюдение за этими графиками преобразования Фурье, то вы знаете, откуда они взялись. Посетите страницу Wolfram Alpha о популярных кривых здесь или посмотрите полный список именованных кривых на Wolfram Alpha здесь .
Чтобы увидеть полное и подробное объяснение процесса разработки кривой Бэтмена, см.Зарегистрируйте исходные сообщения в блоге здесь или другой пошаговый процесс здесь .
Чтобы получить уравнение Бэтмена, которое можно построить на стандартном калькуляторе TI-89, а также уравнения TI-89 для многих других изображений, введите здесь .
Для прекрасного и ясного подробного объяснения преобразования Фурье и большей части связанной с ним математики посетите http://www.thefouriertransform.ком/ .
Нахождение графиков функций в природе
Найди функции в природе и сфотографируй их!
Изучаете графики функций?
Что ж, некоторые графики функций встречаются часто, поэтому знание их формы дает вам гораздо больше возможностей для правильного построения графика и обнаружения распространенных ошибок.
Что тебе нужно?
- Либо графический калькулятор, либо распечатка графиков функций
- Парк или природная тропа с большим количеством деревьев или задний двор
- Камера
- Острый глаз на естественные (не искусственные) формы
Вот несколько примеров:
f(x) = mx + b | f(x) = 1/x |
f(x) = x 2 | f(x) = √x |
f(x) = |x| | f(x) = е х |
А вот несколько примеров фотографий, которые мы сделали, чтобы дать вам представление:
График f(x) = mx + b
График функции f(x) = mx+b представляет собой прямую линию, поэтому вы ищете в природе что-то похожее на прямую линию. Например:
Например:
СДЕЛАЙ ФОТО!
График f(x) = x 2 или -x 2
График f(x) = x 2 выглядит как U, а -x 2 как ∩, поэтому вы ищете что-то похожее на U или ∩. Например:
СДЕЛАЙ ФОТО!
График квадратного корня: f(x) = √x
График f(x) = √x выглядит примерно как строчная буква r, например:
СДЕЛАЙ ФОТО!
График абсолютного значения: f(x) = |x|
График f(x) = |x| выглядит как буква V, например:
СДЕЛАЙ ФОТО!
Посмотрите, какие еще графики вы можете найти…
Когда закончите, сравните свои фотографии природы с графиками функций и составьте презентацию.
Упражнение любезно предоставлено Hands On Math
Типы графиков и диаграмм и их использование: с примерами и изображениями
Если вам интересно, каковы различные типы графиков и диаграмм , их использование и названия, эта страница суммирует их с примерами и изображениями.
Поскольку различные виды графиков предназначены для представления данных, они используются во многих областях, таких как: статистика, наука о данных, математика, экономика, бизнес и т. д.
Каждый тип графика представляет собой визуальное представление данных на диаграммах (например, гистограмма, круговая диаграмма, линейная диаграмма), которые показывают различные типы тенденций графика и отношения между переменными.
Хотя трудно сказать все типы графиков, на этой странице представлены все распространенные типы статистических графиков и диаграмм (и их значения), широко используемые в любой науке.
1. Линейные графики
Линейная диаграмма графически отображает данные, которые непрерывно изменяются во времени.Каждый линейный график состоит из точек, которые соединяют данные, чтобы показать тенденцию (непрерывное изменение). Линейные графики имеют ось X и ось Y. В большинстве случаев время распределяется по горизонтальной оси.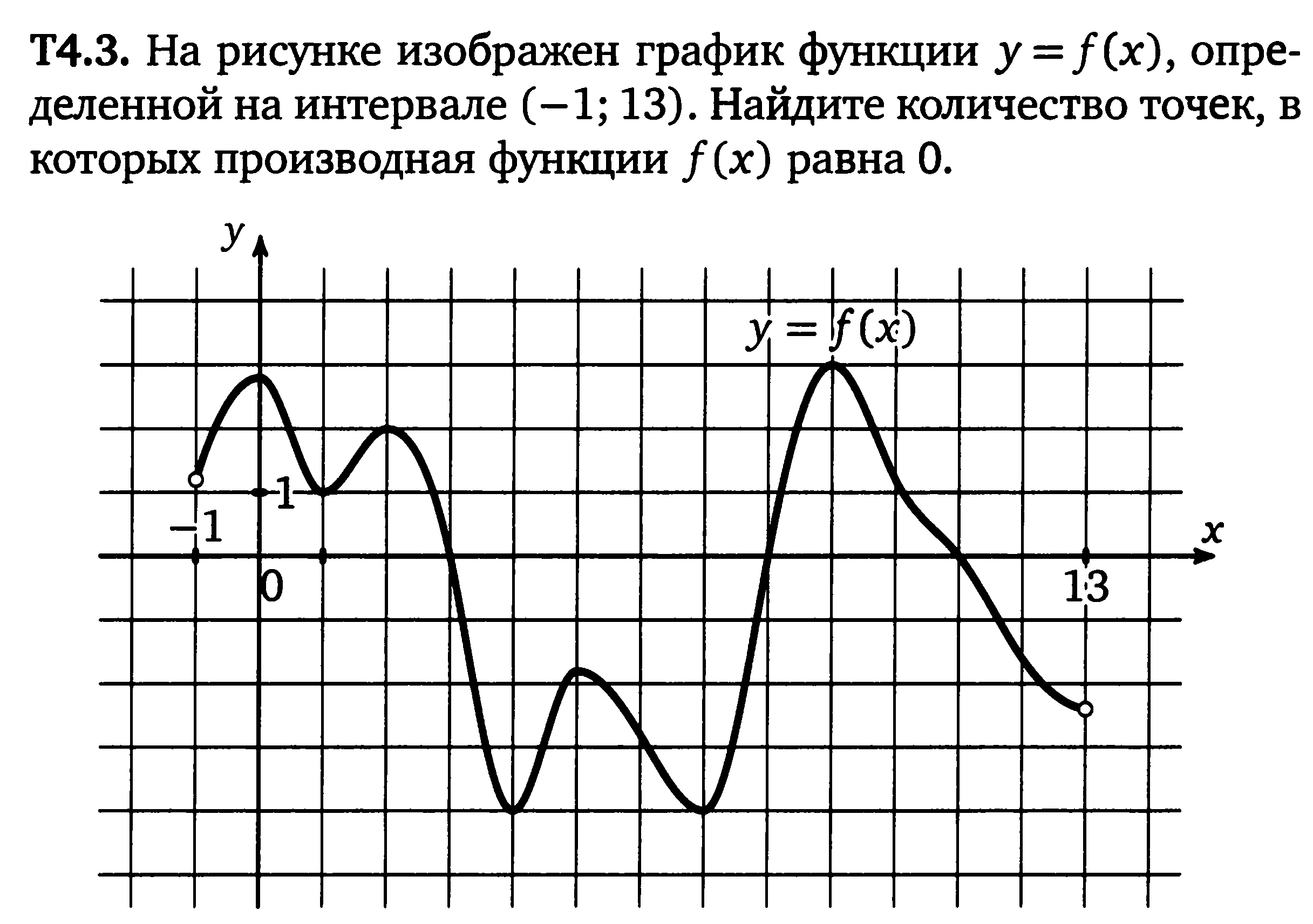
Использование линейных графиков:
- Когда вы хотите показать тренды . Например, как цены на жилье выросли с течением времени.
- Если вы хотите, чтобы делал прогнозы на основе истории данных с течением времени.
- При сравнении двух или более различных переменных, ситуаций и информации за определенный период времени.
Пример:
На следующем линейном графике показаны годовые продажи конкретной коммерческой компании за шесть лет подряд:
Примечание: приведенный выше пример состоит из 1 строки. Однако на одном линейном графике можно сравнивать несколько трендов по нескольким линиям распределения.
2. Гистограммы
Гистограммы представляют категориальные данные с прямоугольными столбцами (чтобы понять, что такое категориальные данные, см. примеры категориальных данных). Гистограммы являются одними из самых популярных типов графиков и диаграмм в экономике, статистике, маркетинге и визуализации в цифровом клиентском опыте. Они обычно используются для сравнения нескольких категорий данных.
Они обычно используются для сравнения нескольких категорий данных.
Длина и высота каждой прямоугольной полосы пропорциональны значениям, которые они представляют.
На одной оси гистограммы представлены сравниваемые категории. Другая ось показывает измеренное значение.
Столбчатые диаграммы Использование:
- Когда вы хотите отобразить данные, сгруппированные в номинальные или порядковые категории (см. номинальные и порядковые данные).
- Для сравнения данных по разным категориям.
- Гистограммы также могут отображать большие изменения данных с течением времени.
- Гистограммы идеально подходят для визуализации распределения данных при наличии более трех категорий.
Пример:
На приведенной ниже гистограмме представлена общая сумма продаж продукта А и продукта Б за три года.
Стержни бывают 2-х типов: вертикальные или горизонтальные. Неважно, какой вид вы будете использовать. Вышеупомянутый является вертикальным типом.
Неважно, какой вид вы будете использовать. Вышеупомянутый является вертикальным типом.
3. Круговые диаграммы
Когда речь идет о статистических типах графиков и диаграмм, круговая диаграмма (или круговая диаграмма) занимает важное место и значение. Он отображает данные и статистику в простом для понимания формате «срезов пирога» и иллюстрирует числовую пропорцию.
Размер каждой части круговой диаграммы зависит от размера конкретной категории в данной группе в целом. Другими словами, круговая диаграмма разбивает группу на более мелкие части. Он показывает отношения часть-целое.
Чтобы построить круговую диаграмму, вам нужен список категориальных переменных и числовых переменных.
Круговая диаграмма Использование:
- Когда вы хотите создать и представить композицию чего-либо.
- Это очень полезно для отображения номинальных или порядковых категорий данных.
- К показать процент или пропорциональные данные.

- Когда сравнения областей роста в рамках бизнеса, таких как прибыль.
- Круговые диаграммы лучше всего подходят для отображения данных от 3 до 7 категорий .
Пример:
На приведенной ниже круговой диаграмме представлена пропорция видов транспорта, используемых 1000 учащимися для поездки в школу.
Круговые диаграммы широко используются маркетологами, работающими с данными, для отображения маркетинговых данных.
4. Гистограмма
Гистограмма показывает непрерывные данные в упорядоченных прямоугольных столбцах (чтобы понять, что такое непрерывные данные, см. нашу публикацию о дискретных и непрерывных данных). Обычно между столбцами нет промежутков .
На гистограмме отображается частотное распределение (форма) набора данных. На первый взгляд гистограммы похожи на гистограммы. Однако между ними есть ключевое различие. Гистограмма представляет собой категориальные данные, а гистограмма представляет непрерывные данные.
Гистограмма Использование:
- Когда данные непрерывны .
- Когда вы хотите представить форму распределения данных .
- Если вы хотите увидеть, отличаются ли выходные данные двух или более процессов.
- Чтобы обобщить больших наборов данных графически.
- Для быстрой передачи данных о распределении другим.
Пример:
На приведенной ниже гистограмме представлен доход на душу населения для пяти возрастных групп.
Гистограммы очень широко используются в статистике, бизнесе и экономике.
5. Точечная диаграмма
Точечная диаграмма представляет собой диаграмму X-Y, которая показывает взаимосвязь между двумя переменными. Он используется для построения точек данных по вертикальной и горизонтальной осям.Цель состоит в том, чтобы показать, насколько одна переменная влияет на другую.
Обычно при наличии связи между двумя переменными первая называется независимой.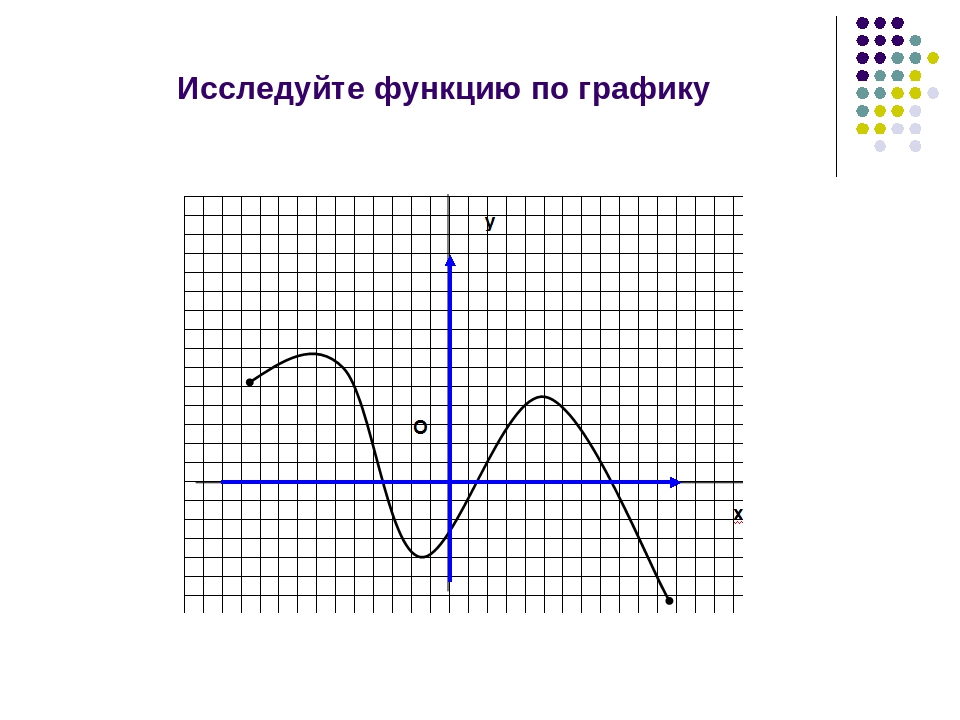 Вторая переменная называется зависимой, потому что ее значения зависят от первой переменной.
Вторая переменная называется зависимой, потому что ее значения зависят от первой переменной.
Диаграммы рассеивания также помогают прогнозировать поведение одной переменной (зависимой) на основе измерения другой переменной (независимой).
Точечная диаграмма использует:
- При попытке выяснить, существует ли связь между двумя переменными .
- Чтобы предсказать поведение зависимой переменной на основе меры независимой переменной.
- При наличии парных числовых данных.
- При работе с инструментами анализа первопричин для выявления потенциальных проблем.
- Когда вы просто хотите визуализировать корреляцию между двумя большими наборами данных без учета времени .
Пример:
На приведенном ниже точечном графике представлены данные по 7 интернет-магазинам, их ежемесячным продажам электронной коммерции и затратам на интернет-рекламу за последний год.
Оранжевая линия, которую вы видите на графике, называется «линия наилучшего соответствия» или «линия тренда». Эта линия используется, чтобы помочь нам делать прогнозы, основанные на прошлых данных.
Эта линия используется, чтобы помочь нам делать прогнозы, основанные на прошлых данных.
Точечные диаграммы широко используются в науке о данных и статистике. Они являются отличным инструментом для визуализации моделей линейной регрессии.
Дополнительные примеры и объяснения для точечных диаграмм вы можете увидеть в нашем посте, что показывает точечная диаграмма, и простые примеры линейной регрессии.
6.Диаграмма Венна
Диаграмма Венна (также называемая первичной диаграммой, диаграммой множества или логической диаграммой) использует перекрывающиеся круги для визуализации логических отношений между двумя или более группами элементов.
Диаграмма Венна — это один из типов графиков и диаграмм, используемых в научных и инженерных презентациях, в компьютерных приложениях, в математике и статистике.
Базовая структура диаграммы Венна обычно представляет собой перекрывающиеся круги. Элементы в перекрывающемся разделе имеют определенные общие характеристики. Предметы во внешних частях кругов не имеют общих черт.
Предметы во внешних частях кругов не имеют общих черт.
Диаграмма Венна Использование:
- Когда вы хотите, чтобы сравнил и противопоставил группы вещей.
- Для классификации или группировки предметов.
- Для иллюстрации логических отношений из различных наборов данных.
- Чтобы определить все возможные отношения между коллекциями наборов данных.
Пример:
В следующем научном примере диаграммы Венна сравниваются особенности птиц и летучих мышей.
7. Диаграммы с областями
Диаграммы с площадями показывают изменение одной или нескольких величин с течением времени. Они очень похожи на линейный график. Однако область между осью и линией обычно заполняется цветом.
Несмотря на то, что линейные диаграммы и диаграммы с областями поддерживают один и тот же тип анализа, их не всегда можно использовать взаимозаменяемо. Линейные диаграммы часто используются для представления нескольких наборов данных. Диаграммы с областями не могут четко отображать несколько наборов данных, поскольку диаграммы с областями показывают заштрихованную область под линией.
Диаграммы с областями не могут четко отображать несколько наборов данных, поскольку диаграммы с областями показывают заштрихованную область под линией.
Диаграмма с областями Использование:
- Когда вы хотите, чтобы отображал тренды , а не выражал конкретные значения.
- Чтобы показать простое сравнение тенденции наборов данных за период времени.
- Для отображения величины изменения.
- Для сравнения небольшого количества категорий.
Диаграмма с областями имеет 2 варианта: вариант с графиками данных, перекрывающими друг друга, и вариант с графиками данных, расположенными друг над другом (известный как диаграмма с областями с накоплением — как показано в следующем примере).
Пример:
На приведенной ниже диаграмме с областями показаны квартальные продажи продуктов категорий A и B за последний год.
На этой диаграмме с областями показано быстрое сравнение тенденции квартальных продаж продукта А и продукта В за период прошлого года.
8. Сплайн-диаграмма
Сплайн-диаграмма — один из наиболее распространенных типов графиков и диаграмм, используемых в статистике. Это форма линейной диаграммы, которая представляет плавные кривые через различные точки данных.
Сплайн-диаграммы обладают всеми характеристиками линейных диаграмм, за исключением того, что сплайн-диаграммы имеют подогнанную изогнутую линию для соединения точек данных. Для сравнения, линейные диаграммы соединяют точки данных прямыми линиями.
Сплайн-диаграмма Используется:
- Когда вы хотите отобразить данные, требующие использования аппроксимации кривой, например , диаграмму жизненного цикла продукта или диаграмму импульсной реакции.
- Сплайн-диаграммы часто используются в при разработке диаграмм Парето .
- Сплайн-диаграмма также часто используется для моделирования данных при ограниченном количестве точек данных и оценке промежуточных значений.

Пример:
В следующем примере сплайн-диаграммы показаны продажи компании за несколько месяцев года:
числовых данных через их квартили. Он отображает частотное распределение данных.
Диаграмма с ячейками и усами помогает отображать разброс и асимметрию для заданного набора данных, используя принцип сводки из пяти чисел: минимум, максимум, медиана, нижняя и верхняя квартили. Принцип «сводки по пяти числам» позволяет предоставить статистическую сводку для определенного набора чисел. Он показывает диапазон (минимальное и максимальное число), разброс (верхний и нижний квартили) и центр (медиану) для набора чисел данных.
Очень простое изображение графика с прямоугольниками и усами, которое вы можете увидеть ниже:
Диаграмма с прямоугольниками и усами Использование:
- Когда вы хотите, чтобы наблюдал верхние и нижние квартили, среднее значение, медиану, отклонения и т.
 д. .для большого набора данных.
д. .для большого набора данных. - Если вы хотите быстро просмотреть распределение набора данных .
- Когда у вас есть несколько наборов данных , которые поступают из независимых источников и каким-то образом связаны друг с другом.
- Когда вам нужно для сравнения данных из разных категорий.
Пример:
В приведенной ниже таблице и диаграммах в виде прямоугольников и усов показаны результаты тестов по математике и литературе для одного и того же класса.
| Математика | 35 | 77 | 92 | 43 | 55 | 66 | 73 | 70 |
| Литература | 35 | 43 | 40 | 43 | 50 | 60 | 70 | 92 |
Диаграммы Box and Whisker применяются во многих научных областях, а также при анализе данных, статистическом анализе, анализе результатов испытаний и таких видах анализа, как анализ данных и Т. Д.
Д.
10. Пузырьковая диаграмма
Пузырьковая диаграмма — это чрезвычайно полезный тип графиков для сравнения взаимосвязей между данными в трех измерениях числовых данных: данные по оси Y, данные по оси X и данные, отображающие размер пузыря.
Пузырьковая диаграмма очень похожа на точечную диаграмму по осям XY, но пузырьковая диаграмма обладает большей функциональностью — третье измерение данных, которое может быть чрезвычайно ценным.
Обе оси (X и Y) пузырьковой диаграммы являются числовыми.
Пузырьковая диаграмма Использование:
- Когда вам нужно отобразить три или четыре измерения данных.
- Если вы хотите сравнить и отобразить отношения между категоризированными кругами, используя пропорции.
Пример:
На приведенной ниже пузырьковой диаграмме показано соотношение между стоимостью (ось X), прибылью (ось Y) и вероятностью успеха (%) (размер кружка).
11.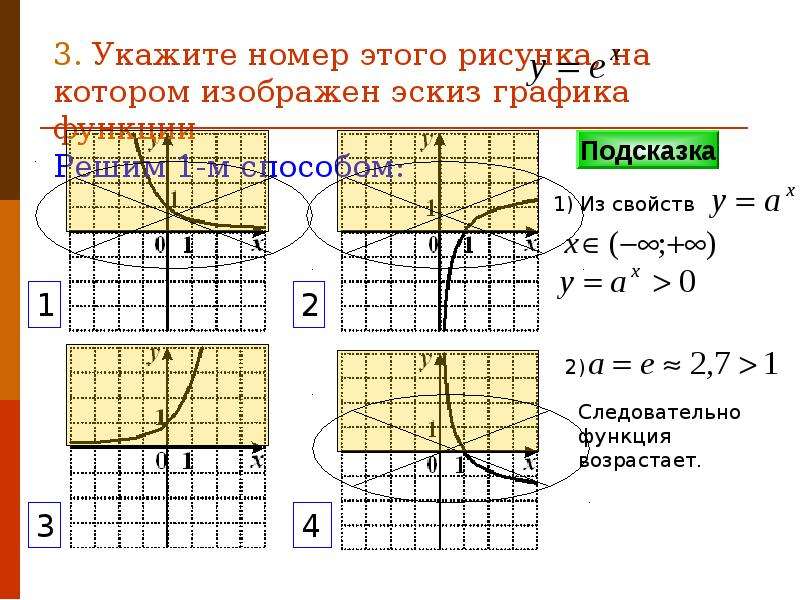 Пиктограммы
Пиктограммы
Пиктограмма или пиктограмма — это один из наиболее визуально привлекательных типов графиков и диаграмм, которые отображают числовую информацию с использованием значков или графических символов для представления наборов данных.
Очень удобный для чтения статистический способ визуализации данных. Пиктограмма показывает частоту данных в виде изображений или символов. Каждое изображение/символ может представлять одну или несколько единиц данного набора данных.
Пиктограмма Использование:
- Когда ваша аудитория предпочитает и лучше понимает дисплеи со значками и иллюстрациями. Веселье может способствовать обучению.
- Для инфографики привычно использование пиктограммы.
- Когда вы хотите, чтобы сравнил две точки эмоционально сильным способом.
Пример:
Следующая пиктограмма представляет количество компьютеров, проданных коммерческой компанией за период с января по март.
Пиктографический пример выше показывает, что в январе было продано 20 компьютеров (4×5 = 20), в феврале было продано 30 компьютеров (6×5 = 30), а в марте было продано 15 компьютеров.
12. Точечный график
Точечный график или точечный график — это лишь один из многих типов графиков и диаграмм для организации статистических данных.Он использует точки для представления данных. Точечный график используется для относительно небольших наборов данных, а значения попадают в ряд дискретных категорий.
Если значение появляется более одного раза, точки располагаются одна над другой. Таким образом, высота столбца точек показывает частоту этого значения.
Точечный график Использование:
- Для построения графика подсчета частоты, когда у вас есть небольшое количество категорий .
- Точечные диаграммы очень полезны, когда переменная является количественной или категориальной .

- Точечные графики также используются для одномерных данных (данные только с одной переменной, которую можно измерить).
Пример:
Предположим, у вас есть класс из 26 учеников. Их просят назвать свой любимый цвет. Точечный график ниже представляет их выбор:
Очевидно, что ученики этого класса предпочитают синий цвет.
13. Радарная диаграмма
Радарная диаграмма — один из самых современных типов графиков и диаграмм — идеально подходит для множественных сравнений.Радарные диаграммы используют круговой дисплей с несколькими различными количественными осями, похожими на спицы на колесе. Каждая ось показывает количество для различных категориальных значений.
Радиолокационные карты также известны как паутинные карты, веб-карты, звездные графики, неправильные многоугольники, полярные карты, паутинные карты или диаграмма Кивиата.
Радарная диаграмма в настоящее время имеет множество применений в статистике, математике, бизнесе, спортивном анализе, анализе данных и т. д. каждой переменной.
д. каждой переменной.
Пример:
Например, мы можем сравнить производительность сотрудника по шкале от 1 до 8 по таким предметам, как пунктуальность, решение проблем, соблюдение сроков, маркетинговые знания, коммуникации. Точка, расположенная ближе к центру оси, показывает более низкое значение и худшую производительность.
| Label 9025 | пунктуальность | Решение проблем | Сроки встречи | Маркетинговые знания | коммуникаций | |
| Jane | 6 | 5 | 8 | 7 | 8 | |
Samanta| Samanta | 7 | 5 | 5 | 4 | 8 | |
Это очевидно, что Джейн имеет лучшую производительность, чем Саманта.
14. Пирамидальная диаграмма
Когда дело доходит до понятных и красивых типов графиков и диаграмм, пирамидальная диаграмма занимает первое место.
Пирамидальная диаграмма представляет собой диаграмму в форме пирамиды или треугольника. Эти типы диаграмм лучше всего подходят для данных, организованных в какой-либо иерархии. Уровни показывают прогрессивный порядок.
Пирамидальная диаграмма Использование:
- Когда вы хотите указать уровень иерархии среди тем или других типов данных.
- Пирамидальный график часто используется для представления прогрессивных порядков, таких как: «от более старых к более новым», «от более важных к менее важным», «от конкретных к менее конкретным» и т. д.
- Когда у вас есть пропорциональные или взаимосвязанные отношения между данными наборы.
Пример:
Классическим примером диаграммы пирамиды является пирамида здорового питания, которая показывает, что жиры, масла и сахар (вверху) следует есть меньше, чем многие другие продукты, такие как овощи и фрукты (внизу пирамиды). ).
).
Заключение:
Вы, наверное, знаете, что выбор правильного типа диаграммы — дело непростое.
На практике выбор зависит от двух основных факторов: от типа анализа, который вы хотите выполнить, и от типа имеющихся у вас данных.
Обычно, когда мы стремимся облегчить сравнение, мы используем гистограмму или лепестковую диаграмму. Когда мы хотим показать тенденции во времени, мы используем линейную диаграмму или диаграмму с областями и т. д.
В любом случае, у вас есть широкий выбор типов графиков и диаграмм.При правильном использовании они являются мощным оружием, которое поможет вам сделать ваши отчеты и презентации профессиональными и четкими.
Какие ваши любимые типы графиков и диаграмм? Поделитесь своими мыслями в поле ниже.
Функция Преобразования: Отражения | Пурпурная математика
Пурпурная математика
Последние два простых преобразования включают в себя переворачивание функций вверх ногами (переворачивание их вокруг оси x ) и их отражение по оси y .
Первая, перевернутая вверх ногами, находится путем взятия отрицательной исходной функции; то есть правило для этого преобразования — f ( x ).
Чтобы увидеть, как это работает, взгляните на график ч ( x ) = x 2 + 2 x – 3. График исходной функции выглядит следующим образом:
Справка по математике.ком
Чтобы представить, как этот график переворачивается вверх дном, представьте, что график нарисован на листе прозрачного пластика, который был помещен поверх чертежа только с осью y , а ось x представляет собой застрявшую шпажку. через лист.Чтобы перевернуть график, поверните вертел на 180°. (Изображения здесь.) Тогда новый график, представляющий собой график – ч ( x ), выглядит так:
через лист.Чтобы перевернуть график, поверните вертел на 180°. (Изображения здесь.) Тогда новый график, представляющий собой график – ч ( x ), выглядит так:
Переворачивание функции вверх ногами всегда работает таким образом: вы ставите «минус» на все это. «Переворачивание вверх ногами» — это чуть более технически «зеркальное отражение» исходного графика по оси x . Если вы подумаете о том, чтобы взять зеркало и расположить его вертикально на оси x , вы увидите (часть) исходного графика в зеркале вверх ногами.Когда они говорят об «отражении» или «отражении» относительно оси, они имеют в виду именно эту ментальную картину.
Чтобы понять, что делает это преобразование, помните, что f ( x ) — это то же самое, что и y . Итак, ставя «минус» на все, вы меняете все положительные (над осью) значения y на отрицательные (ниже оси) значения y и наоборот. (Любые точки на оси x остаются там, где они есть.Двигаются только внеосевые точки.)
(Любые точки на оси x остаются там, где они есть.Двигаются только внеосевые точки.)
Предыдущее отражение было отражением по оси x . Это оставляет нам преобразование для отражения по оси y .
Для этого преобразования я переключусь на кубическую функцию: г ( x ) = x 3 + x 2 – 3 x – 03.901.
Вот график исходной функции:
Если я поставлю – x вместо x в оригинальной функции, то я получаю:
г (– x ) = (– x ) 3 + (– x ) 2 – 3(– x ) – 3 9000
= – х 3 + х 2 – (–3 х ) – 1
= – х 3 + х 2 + 3 х – 1
График этой новой функции выглядит следующим образом:
Это преобразование повернуло исходный график вокруг оси y . Любые точки на оси y остаются на оси y ; это точки вне оси, которые меняют стороны. Это всегда верно: г (– x ) является зеркальным отражением г ( x ); вставка «минус» аргумента дает вам график, который является оригиналом, отраженным на оси y .
Любые точки на оси y остаются на оси y ; это точки вне оси, которые меняют стороны. Это всегда верно: г (– x ) является зеркальным отражением г ( x ); вставка «минус» аргумента дает вам график, который является оригиналом, отраженным на оси y .
Чтобы понять, что делает это преобразование, помните, что вы меняете местами значения x .Что бы вы ни получили для значений x в положительной (или правой) части графика, теперь вы получаете значения x в отрицательной (или левой) части графика, и наоборот. Поскольку входы поменялись местами, то же самое и с графиком.
Учитывая приведенный ниже график функции
f ( x ), определите, какой из графиков A и B представляет f (– x ) и – f ( x ).
Мне дали График А:
.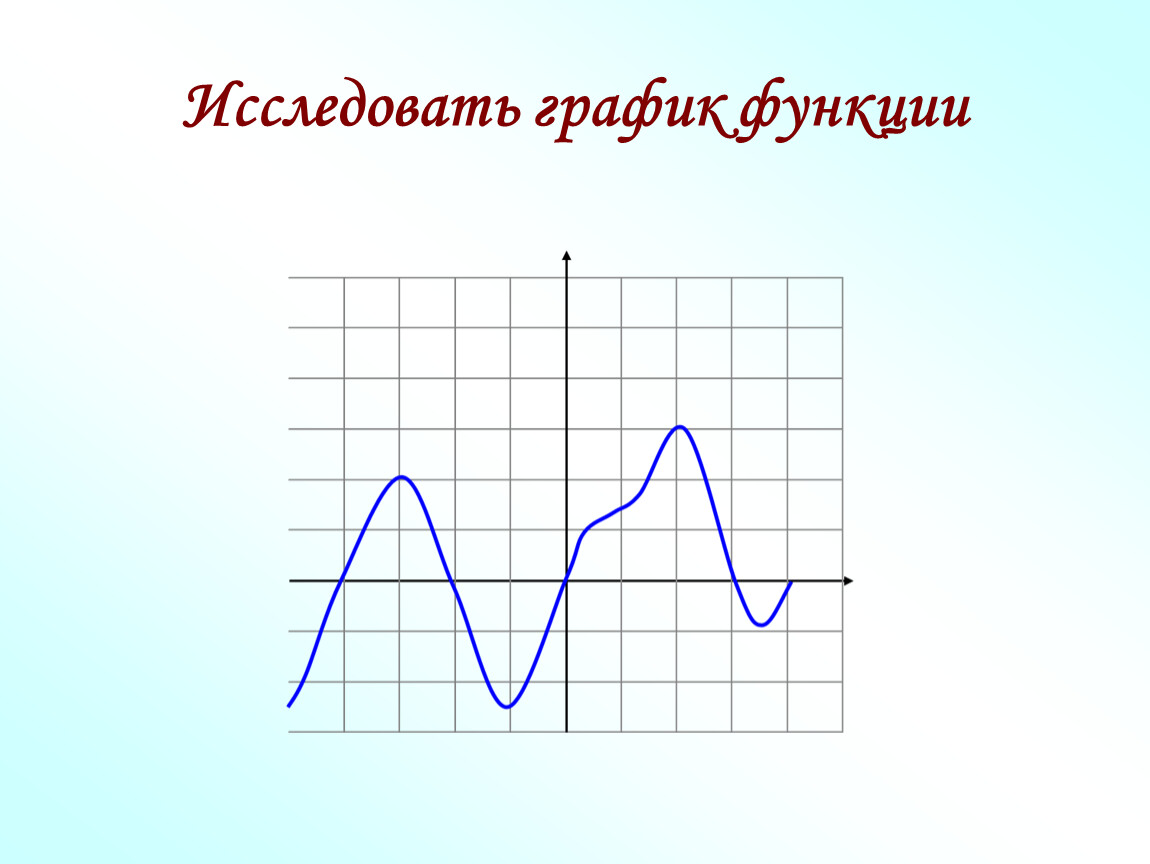 ..и график B:
..и график B:
Сравнивая графики A и B с исходным графиком, я вижу, что график A является перевернутой версией исходного графика. Это было отражено по оси x . Это означает, что это «минус» исходной функции; это график – f ( x ).
Левая и правая части графика B поменяны местами по сравнению с исходным графиком; это было отражено по оси y . Это означает, что это «минус» аргумента функции; это график f (– x ).
График А представляет – f ( x )
График B представляет f (– x )
Учитывая функцию
f ( x ) = x 2 + x – 3, найдите операторы функции в упрощенной форме для отражения функции в каждом из x — и и -оси. Подпишите отражения соответствующим образом.
Подпишите отражения соответствующим образом.
Ну, «соответствующим образом» немного расплывчато; Я просто буду уверен, что на этикетке все очень четко.
Мне нужно найти упрощенные функциональные операторы для каждого из отражений. Одно из размышлений заключается в том, чтобы поставить «минус» на функцию; другой включает в себя добавление «минуса» к аргументу функции.Так что я сделаю каждый из них.
Во-первых, я поставлю «минус» на аргумент функции:
f (– x ) = (– x ) 2 + (– x ) – 3
Теперь другое отражение:
– е ( х ) = –( х 2 + х – 3)
Присвоение аргументу знака «минус» отражает график по оси y . Помещение «минус» на всю функцию отражает график по оси x . Итак, мой (четко обозначенный) ответ:
Помещение «минус» на всю функцию отражает график по оси x . Итак, мой (четко обозначенный) ответ:
отражение в y -оси:
f (– x ) = x 2 – x – 3
отражения по оси x :
– f ( x ) = – x 2 – x + 3
Во многих учебниках дальше этого нет.Если это все правила, которые вам нужны, то запишите их и убедитесь, что вы достаточно попрактиковались, чтобы иметь возможность соблюдать их правильно на следующем тесте:
Функция перевода/преобразования правил:
f ( x ) + b сдвигает функцию на b единиц вверх.
f ( x ) – b сдвигает функцию b единиц вниз.
f ( x + b ) сдвигает функцию b единиц на влево .
f ( x — b ) сдвигает функцию b единиц на вправо .
– f ( x ) отражает функцию по оси x (то есть в перевернутом виде).
f (– x ) отражает функцию по оси y (то есть меняет местами левую и правую стороны).
URL: https://www.purplemath.com/modules/fcntrans2.htm
Что такое графическое изображение? — Определение и примеры — Видео и стенограмма урока
График активности изображений
Мы будем использовать наши знания графических изображений из урока, чтобы создать наши собственные графические изображения. Вам понадобятся следующие материалы:
Вам понадобятся следующие материалы:
Материалы
- Бумага и карандаш для сбора данных
- Чистая, нелинованная бумага или картон для плакатов
- Маркеры, цветные карандаши, мелки или цветные материалы для рисования на ваш выбор
- Линейка
Инструкции
1) Решите, какие данные вы хотите представить на графическом изображении. Некоторые возможные идеи:
- Любимое животное
- Любимый вид пиццы
- Любимый овощ
- Нелюбимый овощ
- Количество братьев и сестер
- Количество домашних животных
Вы можете использовать любую идею — это всего лишь предложения.
2) Соберите данные для графического изображения. Спросите людей о теме вашего графика. Например, если ваша графическая картинка посвящена любимым животным, спросите у многих людей, какое у них любимое животное. Убедитесь, что вы записываете каждый полученный вами ответ — чем больше людей вы спросите, тем интереснее может быть графическая картинка.
3) Изучите данные — узнайте, сколько ответов у вас было на каждый ответ. Зная числа каждого ответа, вы сможете определить масштаб графика.
4) Возьмите картон для плакатов или чистую неразлинованную бумагу и установите оси для вашего графика. Убедитесь, что вы используете линейку, чтобы ваши линии были прямыми. Как правило, вертикальная ось будет осью подсчета, а горизонтальная ось будет содержать ответы. Не забудьте также название для вашего графика. В зависимости от количества ответов вы можете захотеть, чтобы шкала вашего графика учитывалась единицами, пятерками, десятками или даже больше. В большинстве случаев единицы или пятерки будут лучшим выбором. Например, если 3 человека больше всего любят зебр, 2 больше всего любят собак и 5 больше всего любят слонов, подсчет единицами будет отображать данные хорошо, но если у вас 30 зебр, 20 собак и 50 слонов, получится пятерка. или десятки могут работать лучше (поскольку 50 слонов — это много!)
5) После того, как оси настроены и помечены шкалой и ответами, создайте график с изображением, нарисовав изображение, представляющее каждый ответ.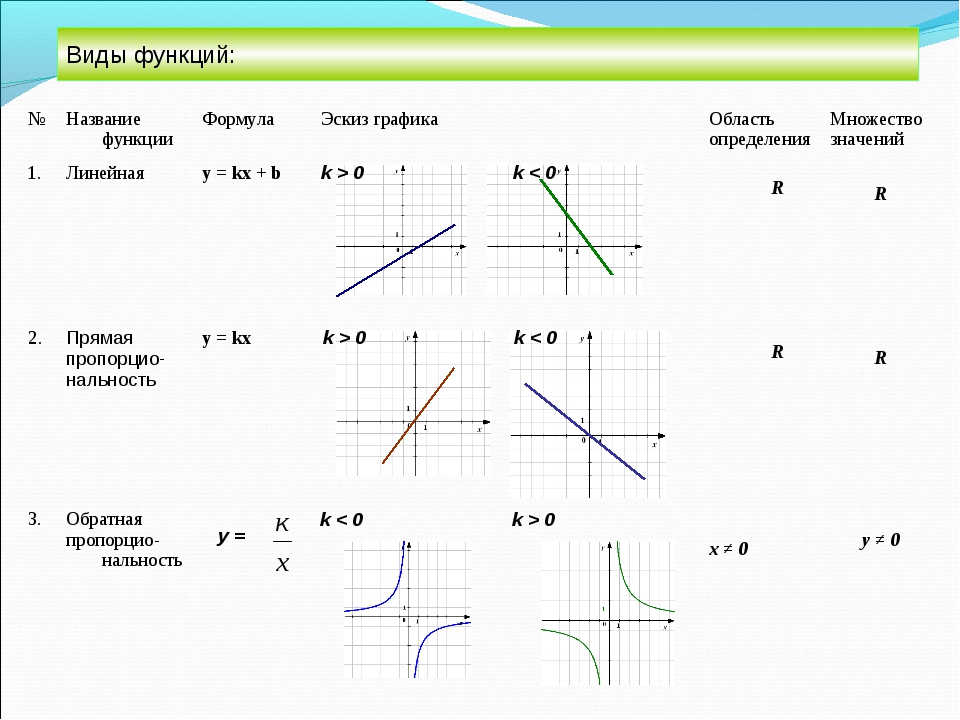 Ниже приведен пример того, как может выглядеть завершенный граф изображения.
Ниже приведен пример того, как может выглядеть завершенный граф изображения.
6) Поделитесь своим графическим изображением с людьми, у которых вы собрали данные. Объясните, как читать графическое изображение, и используйте графическое изображение для объяснения результатов вашего опроса.
задач, обучение и обучение на JSTOR
Абстрактный В обзоре вводного учебного материала функций и графиков анализируются исследования по задачам интерпретации и построения, связанные с функциями и некоторыми их представлениями: алгебраическими, табличными и графическими.В обзоре также анализируется природа обучения с точки зрения интуиции и заблуждений, а также возможные подходы к обучению с помощью последовательностей, объяснений и примеров. Эта тема важна из-за (а) более широкого признания организующей силы концепции функций из математики средней школы через более продвинутые темы в средней школе и колледже, и (б) символических связей, которые представляют потенциал для лучшего понимания между графическими и алгебраические миры. Это обзор определенной части предмета математики и того, как ее изучают и можно преподавать; эта специфика отражает вопросы, поднятые недавними теоретическими исследованиями относительно того, как конкретный контекст и содержание способствуют обучению и смыслу.
Это обзор определенной части предмета математики и того, как ее изучают и можно преподавать; эта специфика отражает вопросы, поднятые недавними теоретическими исследованиями относительно того, как конкретный контекст и содержание способствуют обучению и смыслу.
Review of Educational Research (RER) публикует критические комплексные обзоры исследовательской литературы по вопросам образования. Такие обзоры должны включать концептуализацию, интерпретацию и синтез литературы и научных работ в данной области.RER поощряет представление исследований, имеющих отношение к образованию, из любой дисциплины, таких как обзоры исследований в области психологии, социологии, истории, философии, политологии, экономики, информатики, статистики, антропологии и биологии, при условии, что обзор касается вопросов образования. .
Информация об издателе Американская ассоциация исследований в области образования (AERA) занимается улучшением
образовательный процесс, поощряя научные исследования, связанные с образованием
и путем содействия распространению и практическому применению результатов исследований. AERA — самая известная международная профессиональная организация с
основная цель продвижения образовательных исследований и их практического применения.
Его 20 000 членов являются педагогами; администраторы; директора по исследованиям, тестированию
или оценка в федеральных, государственных и местных агентствах; советники; оценщики;
аспиранты; и ученые-бихевиористы. Широкий спектр дисциплин
представленный членством включает образование, психологию, статистику, социологию,
история, экономика, философия, антропология и политология.
AERA — самая известная международная профессиональная организация с
основная цель продвижения образовательных исследований и их практического применения.
Его 20 000 членов являются педагогами; администраторы; директора по исследованиям, тестированию
или оценка в федеральных, государственных и местных агентствах; советники; оценщики;
аспиранты; и ученые-бихевиористы. Широкий спектр дисциплин
представленный членством включает образование, психологию, статистику, социологию,
история, экономика, философия, антропология и политология.
Обзор — Graph API — Документация
Публикация, обновление и удаление
Посетите наше руководство по совместному использованию Facebook, чтобы узнать, как публиковать на Facebook пользователя, или нашу документацию по Pages API для публикации в ленте Страницы на Facebook.
Некоторые узлы позволяют обновлять поля с помощью операций POST . Например, вы можете обновить поле электронной почты следующим образом:
curl -i -X ПОСТ \ "https://граф.facebook.com/[email protected]&access_token=ACCESS-TOKEN"
Чтение-после-записи
Для конечных точек создания и обновления Graph API может немедленно прочитать успешно опубликованный или обновленный объект и вернуть любые поля, поддерживаемые соответствующей конечной точкой чтения.
По умолчанию будет возвращен идентификатор созданного или обновленного объекта. Чтобы включить в ответ дополнительную информацию, включите в свой запрос параметр fields и перечислите поля, которые вы хотите вернуть.Например, чтобы опубликовать сообщение «Привет» в ленте Страницы, вы можете сделать следующий запрос:
curl -i - X POST "https://graph.facebook.com/PAGE-ID/feed?message=Hello& fields=created_time,from,id,message&access_token=ACCESS-TOKEN"
Приведенный выше пример кода отформатирован для удобочитаемости.
Это вернет указанные поля в виде ответа в формате JSON, например:
{
"created_time": "2017-04-06T22:04:21+0000",
"от": {
"name": "Моя страница в Facebook",
"id": "ИДЕНТИФИКАТОР СТРАНИЦЫ"
},
"id": "POST_ID",
"сообщение": "Привет",
} Обратитесь к справочной документации каждой конечной точки, чтобы узнать, поддерживает ли она чтение после записи и какие поля доступны.
Ошибки
Если чтение не удается по какой-либо причине (например, при запросе несуществующего поля), API Graph ответит стандартной ошибкой. Посетите наше руководство по обработке ошибок для получения дополнительной информации.
Обычно вы можете удалить узел, например узел Post или Photo, выполнив операцию DELETE над идентификатором объекта:
curl -i -X УДАЛИТЬ \ "https://graph.facebook.com/PHOTO-ID?access_token=ACCESSS-TOKEN"
Обычно вы можете удалять только созданные вами узлы, но проверьте справочное руководство каждого узла, чтобы увидеть требования к операциям удаления.
.

 Среди популярных форматов изображений данного типа числятся Bitmap (.bmp), PNG (.png), JPEG (.jpg) и GIF (.gif)
Среди популярных форматов изображений данного типа числятся Bitmap (.bmp), PNG (.png), JPEG (.jpg) и GIF (.gif)
 png") no-repeat center;
background-image: url("image.svg");
background-size: contain;
png") no-repeat center;
background-image: url("image.svg");
background-size: contain;
 Вы должны взвесить действительно стоит ли поддержка устаревших браузеров дополнительных накладных расходов (ресурсов).
Вы должны взвесить действительно стоит ли поддержка устаревших браузеров дополнительных накладных расходов (ресурсов).

 После щелчка по кнопке на форме прорисуется график функции
После щелчка по кнопке на форме прорисуется график функции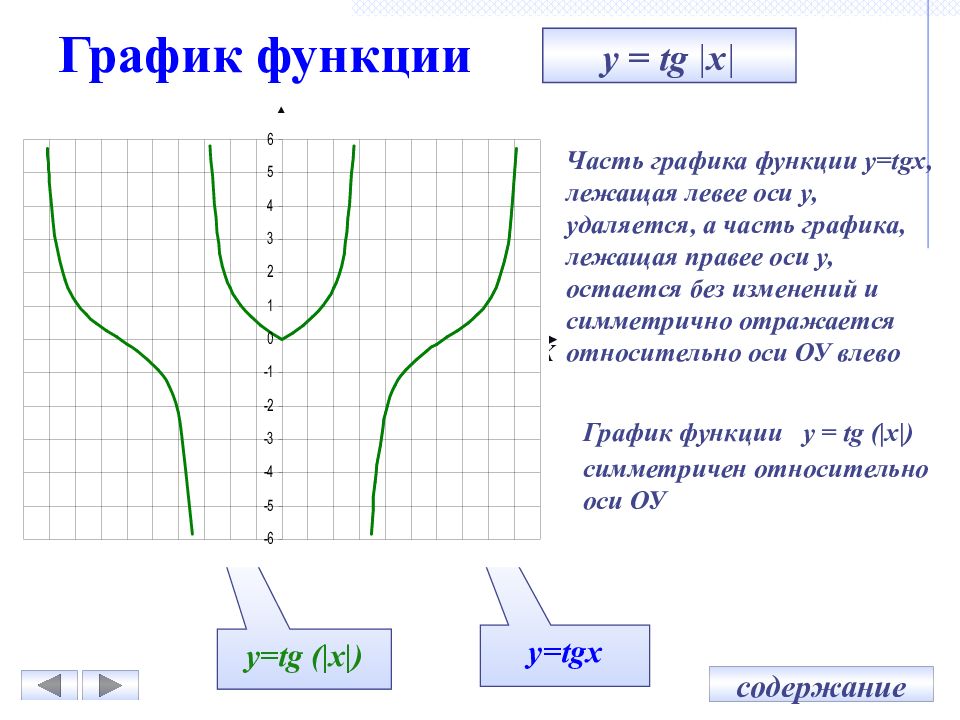

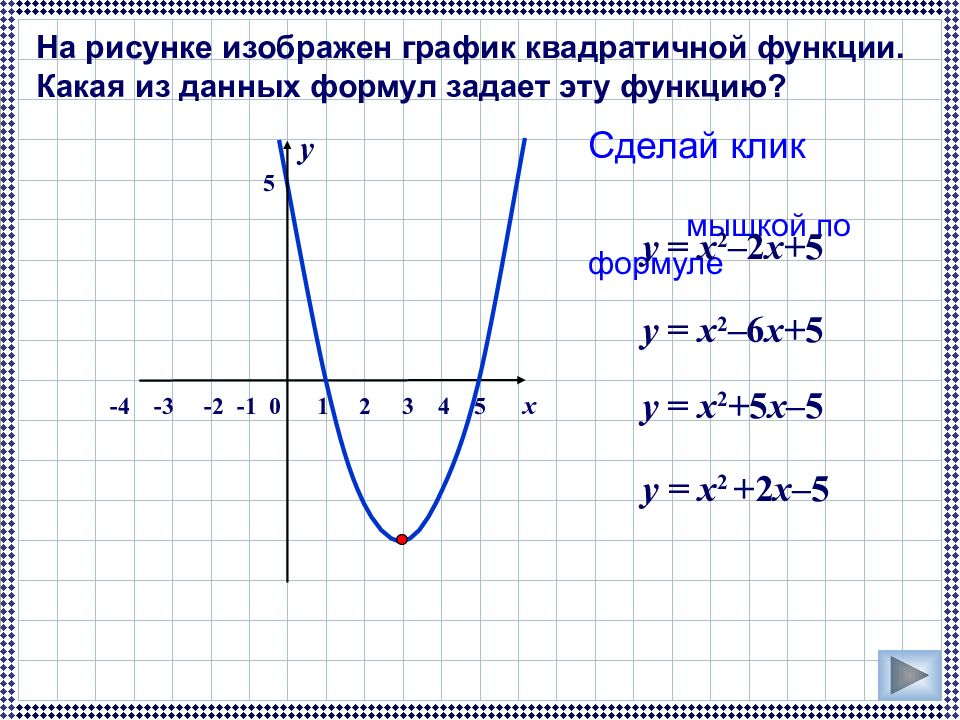 д. .для большого набора данных.
д. .для большого набора данных.
 Подпишите отражения соответствующим образом.
Подпишите отражения соответствующим образом. facebook.com/
facebook.com/