2. Кинетическая энергия точки и механической системы.

Кинетическая энергия материальной точки — скалярная положительная величина, равная половине произведения массы точки на квадрат ее скорости, т. е. .

Кинетическая энергия механической системы — арифме­тическая сумма кинетических энергий всех материальных точек этой системы

.

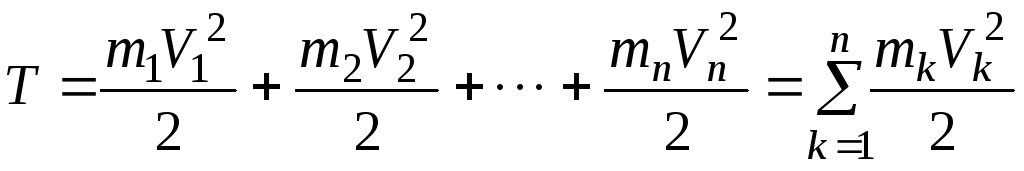Кинетическая энергия системы, состоящей из п связанных между собой тел, равна арифметической сумме кинетических энергий всех тел этой системы:

.

Теорема Кенига. Кинетическая энергия механической системы в общем случае ее движения равна сумме кинетической энергии движения системы вместе с центром масс и кинетической энергии системы при ее движении относительно центра масс:

,

где — скоростьk — й точки системы относительно центра масс.

Поступательное движение.

При поступательном движении тела

.

Вращение тела вокруг неподвижной оси .

.

,

где — момент инерции тела относительно оси вращения.

Плоскопараллельное движение.

,

где — момент инерции плоской фигуры относительно оси, проходящей через центр масс.

Задача 1. Вычислить кинетическую энергию однородного диска массы М =10 кг, катящегося без скольжения со скоростью 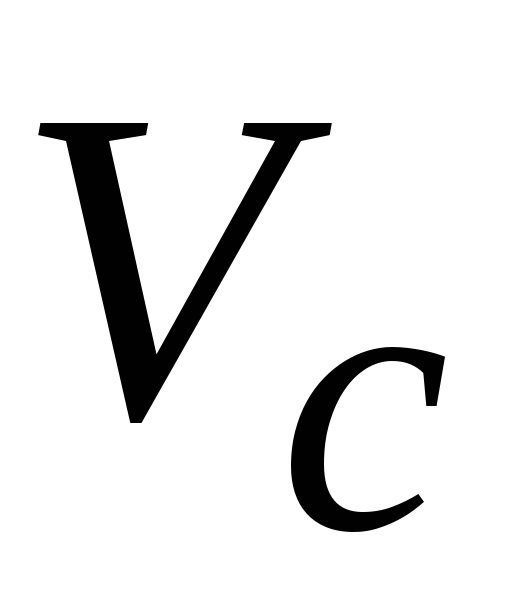= 5м/с.

Решение. Диск совершает плоскопарал­лельное движение .

.

3. Теорема об изменении кинетической энергии точки

Теорема в дифференциальной форме. Дифференциал от кинетической энергии материальной точки равен элементарной работе силы, действующей на точку.

Доказательство:

.

Подставим в выражение второго закона динамики

;

.

Теорема интегральной (конечной) форме. Изменение кинетической энергии материальной точки на некотором перемещении равно работе силы, действующей на точку, на том же перемещении.

Доказательство

Дифференциал от кинетической энергии точки равен эле­ментарной работе:

.

Проинтегрируем

.

4. Теорема об изменении кинетической энергии механической системы.

Теорема в дифференциальной форме. Дифференциал от кинетической энергии механической системы равен сумме элементарных работ внешних и внутренних сил, действующих на систему.

Доказательство: Для k — й точки системы

.

где исоответственно — элементарная работа внешней и внутренней сил, приложенных кk— й точке.

Для всей системы

.

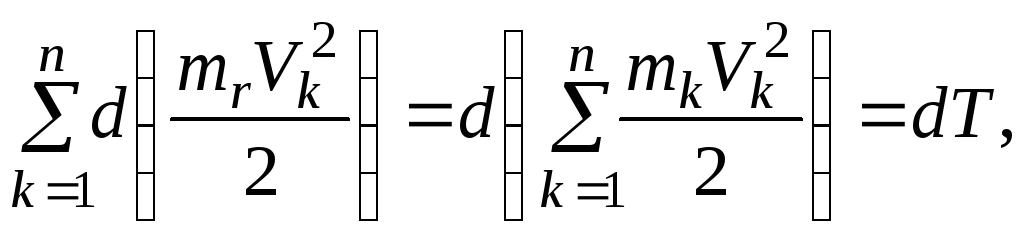
где — кинетическая энергия системы;— соответственно элементарная работа всех внешних и внутренних сил, приложенных к системе. Таким образом,

.

Для системы твердых тел

.

Тогда

.

Разделим на dt

,

где — мощность внешних сил;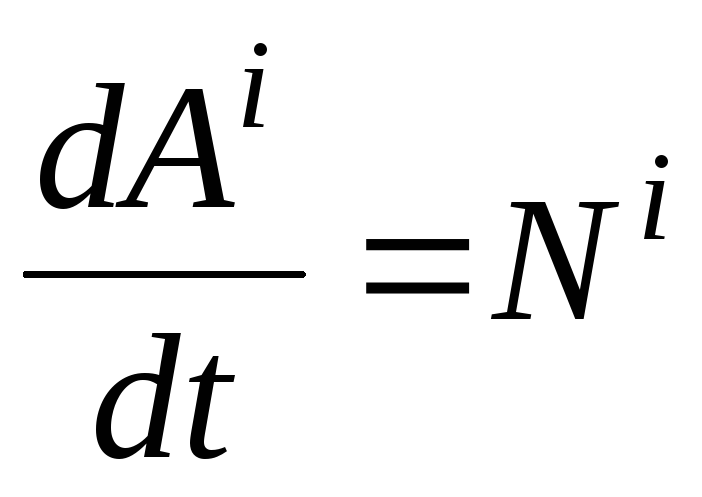— мощность внутренних. Тогда

.

.

Теорема в интегральной (конечной) форме. Изменение кинетической энергии механической системы на некотором перемещении равно сумме работ внешних и внутренних сил, приложенных к системе, на том же перемещении.

Доказательство: Запишем теорему в интегральной форме для k— й точки системы:

,

где и— соответственно работа внешней и внутренней сил, приложенных кk-й точке, на некотором перемещении.

Суммируя по всем точкам системы, получим

Для системы твердых тел (по свойству внутренних сил). Тогда

.

Задача 2. Каток А приводится в движение из состояния покоя по­средством троса, который одним концом намотан на каток, а вто­рым — на барабан В. Каток А считать однородным цилиндром массы = 50кг и радиуса = 0,4м. Масса барабана = 20кг распределена по его ободу радиуса

= 0,2м. К барабану при­ложен вращающий момент = 100Нм. Пренебрегая сколь­жением и трением качения катка по горизонтальной плоскости и весом троса, определить скорость катка, когда он переместится на расстояние s = 2 м.

Решение. Применим теорему об изменении кинетической энергии механической системы в интегральной форме:

,

где — система движется из состояния покоя

—по свойству внутренних сил. Тогда

.. КатокА совершает плоскопараллельное движение.

.

Барабан В совершает вращательное движение.

.

.

Внешними силами являются силы тяжести , нормальная реакция, сила сцепления

, вращающий мо­мент, реакци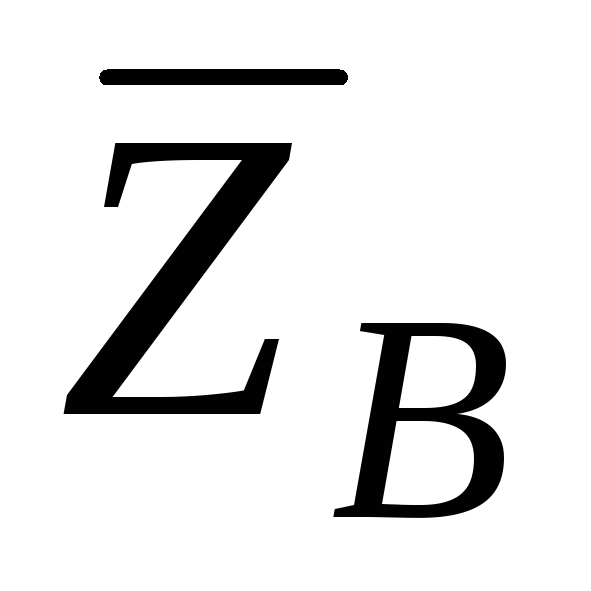ии.

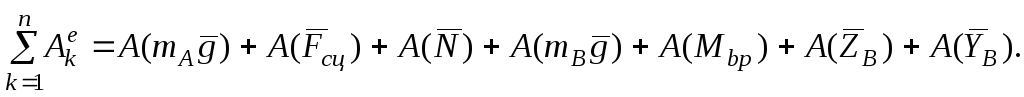
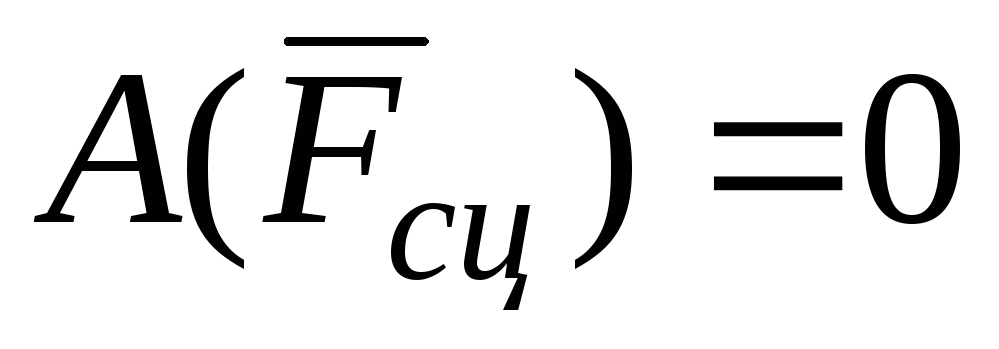так как сила ;так как силаприложена в МЦС;так как;,,— точка приложения сил не перемещается.

, где .

Тогда

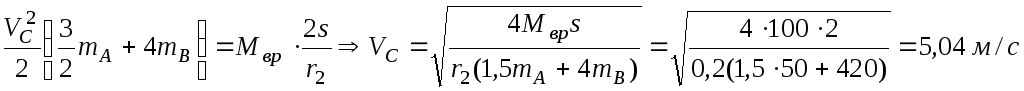
Теорема Кёнига (механика) — Википедия

Материал из Википедии — свободной энциклопедии

Теоре́ма Кёнига позволяет выразить полную кинетическую энергию механической системы через энергию движения центра масс и энергию движения относительно центра масс. Сформулирована и доказана И. С. Кёнигом в 1751 г.^[1]

Кинетическая энергия механической системы есть энергия движения центра масс плюс энергия движения относительно центра масс:

T=T0+Tr,{\displaystyle {T\;=\;T_{0}+T_{r}}\;,}

где T{\displaystyle T} — полная кинетическая энергия системы, T0{\displaystyle T_{0}} — кинетическая энергия движения центра масс, Tr{\displaystyle T_{r}} — относительная кинетическая энергия системы^[2].

Иными словами, полная кинетическая энергия тела или системы тел в сложном движении равна сумме энергии системы в поступательном движении и энергии системы в её движении относительно центра масс.

Более точная формулировка^[3]:

Кинетическая энергия системы материальных точек равна сумме кинетической энергии всей массы системы, мысленно сосредоточенной в её центре масс и движущейся вместе с ним, и кинетической энергии той же системы в её относительном движении по отношению к поступательно движущейся системе координат с началом в центре масс.

Приведём доказательство теоремы Кёнига для случая, когда массы тел, образующих механическую систему S{\displaystyle S},  распределены непрерывно^[4].

Найдём относительную кинетическую энергию Tr{\displaystyle T_{r}} системы S{\displaystyle S},  трактуя её как кинетическую энергию, вычисленную относительно подвижной системы координат. Пусть ρ→{\displaystyle {\vec {\rho }}} — радиус-вектор рассматриваемой точки системы S{\displaystyle S}  в подвижной системе координат. Тогда^[5]:

Tr=12∫dρ→dt⋅dρ→dtdm,{\displaystyle T_{r}\;=\;{\frac {1}{2}}\int {\frac {{\rm {d}}{\vec {\rho }}}{{\rm {d}}t}}\cdot {\frac {{\rm {d}}{\vec {\rho }}}{{\rm {d}}t}}\,{\rm {d}}m\;,}

где точкой обозначено скалярное произведение, а интегрирование ведётся по области пространства, занимаемой системой в текущий момент времени.

Если r→0{\displaystyle {\vec {r}}_{0}} — радиус-вектор начала координат подвижной системы, а r→{\displaystyle {\vec {r}}} — радиус-вектор рассматриваемой точки системы S{\displaystyle S}  в исходной системе координат, то верно соотношение:

r→=r→0+ρ→.{\displaystyle {\vec {r}}\;=\;{\vec {r}}_{0}+{\vec {\rho }}\;.}

Вычислим полную кинетическую энергию системы в случае, когда начало координат подвижной системы помещено в её центр масс. С учётом предыдущего соотношения имеем:

T=12∫dr→dt⋅dr→dtdm=12∫(dr→odt+dρ→dt)⋅(dr→odt+dρ→dt)dm.{\displaystyle T\;=\;{\frac {1}{2}}\int {\frac {{\rm {d}}{\vec {r}}}{{\rm {d}}t}}\cdot {\frac {{\rm {d}}{\vec {r}}}{{\rm {d}}t}}\,{\rm {d}}m\;=\;{\frac {1}{2}}\int \left({\frac {{\rm {d}}{\vec {r}}_{o}}{{\rm {d}}t}}+{\frac {{\rm {d}}{\vec {\rho }}}{{\rm {d}}t}}\right)\cdot \left({\frac {{\rm {d}}{\vec {r}}_{o}}{{\rm {d}}t}}+{\frac {{\rm {d}}{\vec {\rho }}}{{\rm {d}}t}}\right)\,{\rm {d}}m\;.}

Учитывая, что радиус-вектор r→0{\displaystyle {\vec {r}}_{0}} одинаков для всех dm{\displaystyle {\rm {d}}m}, можно, раскрыв скобки, вынести dr→0dt{\displaystyle {\frac {{\rm {d}}{\vec {r}}_{0}}{{\rm {d}}t}}} за знак интеграла:

T=12dr→0dt⋅dr→0dt∫dm+dr→0dt⋅∫dρ→dtdm+12∫dρ→dt⋅dρ→dtdm.{\displaystyle T\;=\;{\frac {1}{2}}{\frac {{\rm {d}}{\vec {r}}_{0}}{{\rm {d}}t}}\cdot {\frac {{\rm {d}}{\vec {r}}_{0}}{{\rm {d}}t}}\int \,{\rm {d}}m\,\,+\,\,{\frac {{\rm {d}}{\vec {r}}_{0}}{{\rm {d}}t}}\cdot \int {\frac {{\rm {d}}{\vec {\rho }}}{{\rm {d}}t}}\,{\rm {d}}m\,\,+\,\,{\frac {1}{2}}\int {\frac {{\rm {d}}{\vec {\rho }}}{{\rm {d}}t}}\cdot {\frac {{\rm {d}}{\vec {\rho }}}{{\rm {d}}t}}\,{\rm {d}}m\;.}

Первое слагаемое в правой части этой формулы (совпадающее с кинетической энергией материальной точки, которая помещена в начало координат подвижной системы и имеет массу, равную массе механической системы) может интерпретироваться^[2] как кинетическая энергия движения центра масс.

Второе слагаемое равно нулю, поскольку второй сомножитель в нём получается дифференцированием по времени произведения радиус-вектора центра масс на массу системы^[6], но упомянутый радиус-вектор (а с ним и всё произведение) равен нулю:

∫ρ→dm=0,{\displaystyle \int {\vec {\rho }}\,\,{\rm {d}}m=0\;,}

так как начало координат подвижной системы находится (по сделанному предположению) в центре масс.

Третье же слагаемое, как было уже показано, равно Tr{\displaystyle T_{r}}, т. е. относительной кинетической энергии системы S{\displaystyle S}.

1. ↑ Гернет, 1987, с. 258.
2. ↑ ^{1 2} Журавлёв, 2001, с. 72.
3. ↑ Сивухин Д. В. Общий курс физики. — М.: Физматлит, 2005. — Т. I. Механика. — С. 137—138. — 560 с. — ISBN 5-9221-0225-7.
4. ↑ Журавлёв, 2001, с. 71—72.
5. ↑ Журавлёв, 2001, с. 71.
6. ↑ Журавлёв, 2001, с. 66.

• Гернет М. М.  Курс теоретической механики. 5-е изд. — М.: Высшая школа, 1987. — 344 с.
• Журавлёв В. Ф.  Основы теоретической механики. 2-е изд. — М.: Физматлит, 2001. — 320 с. — ISBN 5-94052-041-3.

Кинетическая энергия — это… Что такое Кинетическая энергия?

Кинети́ческая эне́ргия — энергия механической системы, зависящая от скоростей движения её точек. Часто выделяют кинетическую энергию поступательного и вращательного движения.

Более строго, кинетическая энергия есть разность между полной энергией системы и её энергией покоя; таким образом, кинетическая энергия — часть полной энергии, обусловленная движением.

История

Впервые понятие кинетической энергии было введено в трудах Г. Лейбница, посвященных понятию «живой силы»

Физический смысл

Рассмотрим систему, состоящую из одной частицы, и запишем второй закон Ньютона:

 — есть результирующая всех сил, действующих на тело. Скалярно умножим уравнение на перемещение частицы . Учитывая, что , Получим:

Если система замкнута, то есть , то , а величина

остаётся постоянной. Эта величина называется кинетической энергией частицы. Если система изолирована, то кинетическая энергия является интегралом движения.

Для абсолютно твёрдого тела полную кинетическую энергию можно записать в виде суммы кинетической энергии поступательного и вращательного движения:

где:

 — масса тела

 — скорость центра масс тела

 — момент инерции тела

 — угловая скорость тела.

Физический смысл работы

Работа всех сил, действующих на частицу, идёт на приращение кинетической энергии частицы:

Релятивизм

При скоростях, близких к скорости света, кинетическая энергия любого объекта равна

где:

 — масса объекта;

 — скорость движения объекта в инерциальной системе отсчета;

 — скорость света в вакууме ( — энергия покоя).

Данную формулу можно переписать в следующем виде:

При малых скоростях () последнее соотношение переходит в обычную формулу .

Соотношение кинетической и внутренней энергии

Кинетическая энергия зависит от того, с каких позиций рассматривается система. Если рассматривать макроскопический объект (например, твёрдое тело видимых размеров), то тело неподвижно как единое целое, и можно говорить о такой форме энергии, как внутренняя энергия. Кинетическая энергия в этом случае появляется лишь тогда, когда тело движется как целое.

То же тело, рассматриваемое с микроскопической точки зрения, состоит из атомов и молекул, и внутренняя энергия обусловлена движением атомов и молекул и рассматривается как следствие теплового движения этих частиц, а абсолютная температура тела прямо пропорциональна средней кинетической энергии такого движения атомов и молекул. Коэффициент пропорциональности — Постоянная Больцмана.

См. также

16Кинетическая энергия

Кинети́ческая эне́ргия — скалярная функция, являющаяся мерой движения материальной точки и зависящая только от массы и модуля скоростиматериальных точек, образующих рассматриваемую физическую систему^[1], энергия механической системы, зависящая от скоростей движения её точек в выбранной системе отсчёта. Часто выделяют кинетическую энергию поступательного и вращательного движения.

Более строго, кинетическая энергия есть разность между полной энергией системы и её энергией покоя; таким образом, кинетическая энергия — частьполной энергии, обусловленная движением^[3].

Простым языком, кинетическая энергия — это энергия, которую тело имеет только при движении. Когда тело не движется, кинетическая энергия равна нулю.

Физический смысл

Рассмотрим систему, состоящую из одной частицы, и запишем второй закон Ньютона:

 — есть равнодействующая всех сил, действующих на тело. Скалярно умножим уравнение на перемещение частицы . Учитывая, что , получим:

Если система замкнута, то есть внешние по отношению к системе силы отсутствуют, или равнодействующая всех сил равна нулю, то , а величина

остаётся постоянной. Эта величина называется кинетической энергией частицы. Если система изолирована, то кинетическая энергия является интегралом движения.

Для абсолютно твёрдого тела полную кинетическую энергию можно записать в виде суммы кинетической энергии поступательного и вращательного движения:

где:

 — масса тела

 — скорость центра масс тела

 — момент инерции телакг·м²

 — угловая скорость тела. рад/с

Найдем кинетическую энергию при различных случаях движения:

1. Поступательное движение

Скорости всех точек системы равны скорости центра масс . Тогда

Кинетическая энергия системы при поступательном движении равна половине произведения массы системы на квадрат скорости центра масс.

2. Вращательное движение (рис. 77)

Скорость любой точки тела: . Тогда

или используя формулу (15.3.1):

Кинетическая энергия тела при вращении равна половине произведения момента инерции тела относительно оси вращения на квадрат его угловой скорости.

3. Плоскопараллельное движение

При данном движении кинетическая энергия складывается из энергии поступательного и вращательных движений

Общий случай движения дает формулу, для вычисления кинетической энергии, аналогичную последней.

Определение работы и мощности мы сделали в параграфе 3 главы 14. Здесь же мы рассмотрим примеры вычисления работы и мощности сил действующих на механическую систему.

Физический смысл работы

Работа всех сил, действующих на частицу при её перемещении, идёт на приращение кинетической энергии частицы^[4]:

Свойства кинетической энергии

Аддитивность. Это свойство означает, что кинетическая энергия механической системы, состоящей из материальных точек, равна сумме кинетических энергий всех материальных точек, входящих в систему.^[1]

Инвариантность по отношению к повороту системы отсчета. Кинетическая энергия не зависит от положения точки, направления её скорости и зависит лишь от модуля скорости или, что то же самое, от квадрата её скорости.^[1]

Сохранение. Кинетическая энергия не изменяется при взаимодействиях, изменяющих лишь механические характеристики системы.Это свойство инвариантно по отношению к преобразованиям Галилея^[1] Свойства сохранения кинетической энергии и второго закона Ньютона достаточно, чтобы вывести математичекую формулу кинетической энергии.^[5][6]

Релятивизм

При скоростях, близких к скорости света, кинетическая энергия любого объекта равна

где:

 — масса объекта;

 — скорость движения объекта в выбранной инерциальной системе отсчета;

 — скорость света в вакууме ( — энергия покоя).

Данную формулу можно переписать в следующем виде:

При малых скоростях () последнее соотношение переходит в обычную формулу .

Соотношение кинетической и внутренней энергии

Кинетическая энергия зависит от того, с каких позиций рассматривается система. Если рассматривать макроскопический объект (например, твёрдое тело видимых размеров) как единое целое, можно говорить о такой форме энергии, как внутренняя энергия. Кинетическая энергия в этом случае появляется лишь тогда, когда тело движется как целое.

То же тело, рассматриваемое с микроскопической точки зрения, состоит из атомов и молекул, и внутренняя энергия обусловлена движением атомов и молекул и рассматривается как следствие теплового движения этих частиц, а абсолютная температура тела прямо пропорциональна средней кинетической энергии такого движения атомов и молекул. Коэффициент пропорциональности — Постоянная Больцмана.