Кинематика (физика) — это… Что такое Кинематика (физика)?

У этого термина существуют и другие значения, см. Кинематика.

Кинема́тика (греч. κινειν — двигаться) в физике — раздел механики, изучающий математическое описание (средствами геометрии, алгебры, математического анализа…) движения идеализированных тел (материальная точка, абсолютно твердое тело, идеальная жидкость), без рассмотрения причин движения (массы, сил и т. д.). Исходные понятия кинематики — пространство и время. Например, если тело движется по окружности, то кинематика предсказывает необходимость существования центростремительного ускорения без уточнения того, какую природу имеет сила, его порождающая. Причинами возникновения механического движения занимается другой раздел механики — динамика.

Различают классическую кинематику, в которой пространственные (длины отрезков) и временные (промежутки времени) характеристики движения считаются абсолютными, то есть не зависящими от выбора системы отсчёта, и релятивистскую. В последней длины отрезков и промежутки времени между двумя событиями могут изменяться при переходе от одной системы отсчёта к другой. Относительной становится также одновременность. В релятивистской механике вместо отдельных понятий пространство и время вводится понятие пространства-времени, в котором инвариантным относительно преобразований Лоренца является величина, называемая интервалом.

История кинематики

Долгое время понятия о кинематике были основаны на работах Аристотеля, в которых утверждалось, что скорость падения пропорциональна весу тела, а движение в отсутствие сил невозможно. Только в конце XVI века этим вопросом подробно занялся Галилео Галилей. Изучая свободное падение (знаменитые опыты на Пизанской башне) и инерцию тел, он доказал неправильность идей Аристотеля. Итоги своей работы по данной теме он изложил в книге «Беседы и математические доказательства, касающиеся двух новых отраслей науки, относящихся к механике и местному движению»^[1].

Рождением современной кинематики можно считать выступление Пьера Вариньона перед Французской Академией наук 20 января 1700 года. Тогда впервые были даны понятия скорости и ускорения в дифференциальном виде.

В XVIII веке Ампер первый использовал вариационное исчисление в кинематике.

После создания СТО, показывающей, что время и пространство не абсолютны и скорость имеет принципиальное ограничение, кинематика вошла в новый этап развития в рамках релятивистской механики (см. Релятивистская кинематика).

Основные понятия кинематики

Задачи кинематики

Главной задачей кинематики является математическое (уравнениями, графиками, таблицами и т. п.) определение положения и характеристик движения точек или тел во времени. Любое движение рассматривается в определённой системе отсчёта. Также кинематика занимается изучением составных движений (движений в двух взаимно перемещающихся системах отсчёта).

Положение точки (или тела) относительно заданной системы отсчёта определяется некоторым количеством взаимно независимых функций координат:

,

где определяется количеством степеней свободы. Так как точка не может быть в нескольких местах одновременно, все функции должны быть однозначными. Также в классической механике выдвигается требование их дифференцируемости на промежутках. Производные этих функций определяют скорость тела^[2].

Скорость движения определяется как производная координат по времени:

,

где  — единичные векторы, направленные вдоль соответствующих координат.

Ускорение определяется как производная скорости по времени:

Следовательно, характер движения можно определить, зная зависимость скорости и ускорения от времени. А если кроме этого известны ещё и значения скорости/координат в определённый момент времени, то движение полностью задано.

Деление кинематики по типам объекта исследования

В зависимости от свойств изучаемого объекта, кинематика делится на кинематику точки, кинематику твёрдого тела, кинематику деформируемого тела, кинематику газа, кинематику жидкости и т. д.

Кинематика точки

Основная статья: Кинематика точки

Кинематика точки изучает движение материальных точек — тел, размерами которых можно пренебречь по сравнению с характерными размерами изучаемого явления. Поэтому в кинематике точки скорость, ускорение, координаты всех точек тела считаются равными.

Частные случаи движения в кинематике точки:

• Если ускорение равно нулю, движение прямолинейное (траектория представляет собой прямую) и равномерное (скорость постоянна).

,

где  — длина пути траектории за промежуток времени от до ,  — проекции на соответствующие оси координат.

• Если ускорение постоянно и лежит в одной прямой со скоростью, движение прямолинейное, равнопеременное (равноускоренное, если ускорение и скорость направлены в одном направлении; равнозамедленное — если в разные).

,

где  — длина пути траектории за промежуток времени от до ,  — проекции на соответствующие оси координат,  — проекции на соответствующие оси координат.

• Если ускорение постоянно и перпендикулярно скорости, движение происходит по окружности — вращательное движение.

,

где  — радиус окружности, по которой движется тело.

Если выбрать систему декартовых координат xyz так, чтобы центр координат был в центре окружности, по которой движется точка, оси y и x лежали в плоскости этой окружности, так чтобы движение осуществлялось против часовой стрелки, то значения координат можно вычислить по формулам:

Для перехода в другие системы координат используются преобразования Галилея для скоростей намного меньших скорости света, и преобразования Лоренца для скоростей, сравнимых со скоростью света.

• Если ускорение постоянно и не лежит на одной прямой с начальной скоростью, движение параболическое.

Если выбрать систему декартовых координат xyz так, чтобы ускорение и начальная скорость лежали в плоскости xy и ускорение было сонаправленно с осью y, то значения координат можно вычислить по формулам:

,

где и  — проекции на соответствующие оси.

Для перехода в другие системы координат используются преобразования Галилея для скоростей намного меньших скорости света, и преобразования Лоренца для скоростей, сравнимых со скоростью света.

• Если тело выполняет разные движения в разных направлениях, то эти движения могут рассчитываться отдельно и складываться по принципу суперпозиции. Например, если в одной плоскости тело совершает вращательное движение, а по оси, перпендикулярной этой плоскости — равномерное поступательное, то вид движения — винтовая линия с постоянным шагом.

• В общем виде скорость, ускорение и координаты вычисляются по общим формулам (см. задачи кинематики), путь вычисляется по формуле:

Кинематика твёрдого тела

Кинематика твёрдого тела изучает движение абсолютно твёрдых тел (тел, расстояние между двумя любыми точками которого не может изменяться).

Так как любое тело ненулевого объёма имеет бесконечное число точек, и соответственно бесконечное число фиксированных связей между ними, тело имеет 6 степеней свободы и его положение в пространстве определяется шестью координатами (если нет дополнительных условий).

Связь скорости двух точек твердого тела выражается через формулу Эйлера:

,

где  — вектор угловой скорости тела.

Кинематика деформируемого тела, Кинематика жидкости

Основные статьи: Кинематика деформируемого тела, Кинематика жидкости

Кинематика деформируемого тела и кинематика жидкости относятся к

кинематике непрерывной среды.

Кинематика газа

Основная статья: Кинематика газа

Кинематика газа изучает деление газа на скопления при движении и описывает движение этих скоплений. В рамках кинематики газа описываются не только основные параметры движения, но и типы движения газа.

Примечания

Литература

• Алешкевич В. А., Деденко Л. Г., Караваев В. А. Механика твердого тела. Лекции. — М.: Изд-во Физического факультета МГУ, 1997.
• Матвеев. А. Н. Механика и теория относительности. — М.: Высшая школа, 1986. (3-е изд. М.: ОНИКС 21 век: Мир и Образование, 2003. — 432с.)
• Павленко Ю. Г. Лекции по теоретической механике. — М.: ФИЗМАТЛИТ, 2002. — 392 с.
• Сивухин Д. В. Общий курс физики. В 5 т. Том I. Механика. 4-е изд. — М.: ФИЗМАТЛИТ; Изд-во МФТИ, 2005. — 560с.
• Стрелков С. П. Механика. — М.: Наука, 1975.
• Яворский Б. М., Детлаф А. А. Справочник по физике для инженеров и студентов вузов (4-е изд.). — М.: Наука, 1968.

Кинематика. Механическое движение. Система отсчета. Материальная точка. Траектория. Путь

Сегодня мы поговорим о систематическом изучении физики и первом ее разделе – механике. Физика изучает разные виды изменений или процессов, происходящих в природе, а какие процессы в первую очередь интересовали наших предков? Конечно, это процессы, связанные с движением. Им было интересно, долетит ли копье, которое они бросили, и попадет ли оно в мамонта; им было интересно, успеет ли гонец с важной вестью добежать до заката к соседней пещере. Все эти виды движения и вообще механическое движение как раз и изучает раздел, который называется механика.

Куда бы мы ни посмотрели – вокруг нас масса примеров механического движения: что-то вращается, что-то прыгает вверх-вниз, что-то движется вперед-назад, а другие тела могут находиться в состоянии покоя, которое тоже является примером механического движения, скорость которого равна нулю.

Определение

Механическим движением называется изменение положения тел в пространстве относительно других тел с течением времени (рис. 1).

Рис. 1. Механическое движение

Как физика делится на несколько разделов, так и механика имеет свои разделы. Первый из них называется кинематика. Раздел механики кинематика отвечает на вопрос, как движется тело. Прежде чем начать работать над изучением механического движения, необходимо определить и выучить основные понятия, так называемую азбуку кинематики. На уроке мы научимся:

— выбирать систему отсчета для изучения движения тела;

— упрощать задачи, мысленно заменяя тело материальной точкой;

— определять траекторию движения, находить путь;

— различать виды движений.

В определении механического движения особое значение имеет выражение относительно других тел. Нам всегда необходимо выбрать так называемое тело отсчета, то есть тело, относительно которого мы будем рассматривать движение исследуемого нами объекта. Простой пример: подвигайте рукой и скажите – движется ли она? Да, конечно, по отношению к голове, но по отношению к пуговице на вашей рубашке она будет недвижима. Поэтому выбор отсчета очень важен, ведь относительно некоторых тел движение совершается, а относительно других тел движения не происходит. Чаще всего телом отсчета выбирают тело, которое всегда есть под руками, точнее под ногами, – это наша Земля, которая является телом отсчета в большинстве случаев.

Издавна ученые спорили о том, Земля ли вращается вокруг Солнца или Солнце вращается вокруг Земли. На самом деле, с точки зрения физики, с точки зрения механического движения это всего лишь спор о теле отсчета. Если телом отсчета считать Землю, то да – Солнце вращается вокруг Земли, если телом отсчета считать Солнце – то Земля вращается вокруг Солнца. Поэтому тело отсчета – это важное понятие.

Как же описывать изменение положения тела?

Чтобы точно задать положение интересующего нас тела относительно тела отсчета, надо связать с телом отсчета систему координат (рис. 2).

Рис. 2. Декартовая система координат

При движении тела координаты меняются, а для того чтобы описать их изменение, нам необходим прибор для измерения времени. Чтобы описывать движение, нужно иметь:

— тело отсчета;

— связанную с телом отсчета систему координат;

— прибор для измерения времени (часы).

Все эти объекты составляют вместе систему отсчета. До тех пор пока мы не выбрали систему отсчета, не имеет смысла описывать механическое движение – мы не будем уверены в том, как движется тело. Простой пример: чемодан, лежащий на полке в купе поезда, который движется, для пассажира просто покоится, а для человека, стоящего на перроне, движется. Как мы видим, одно и то же тело и движется, и покоится, вся проблема в том, что системы отсчета различны (рис. 3).

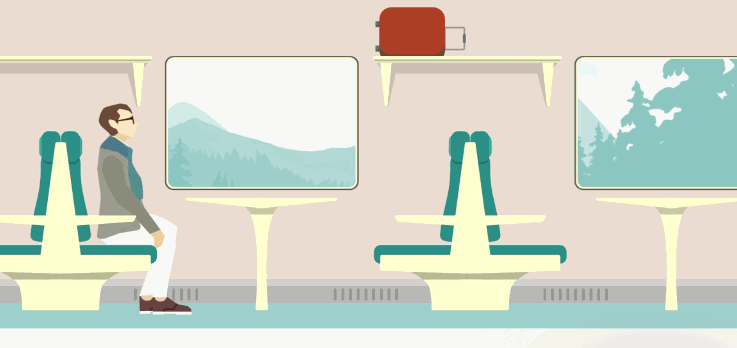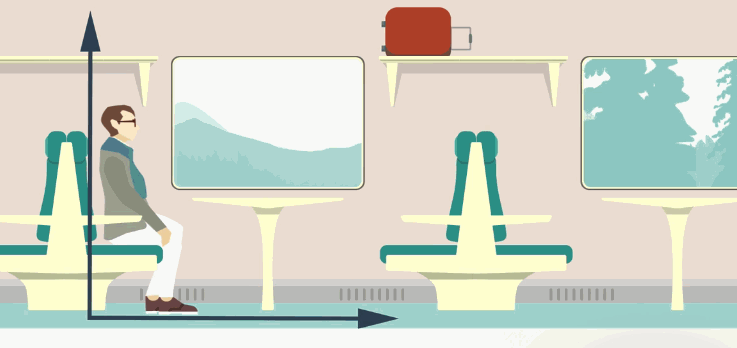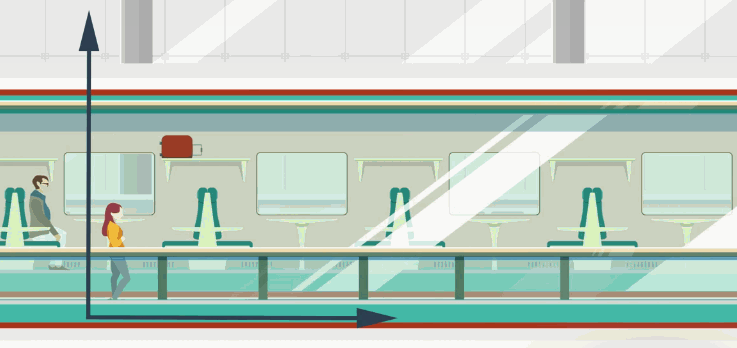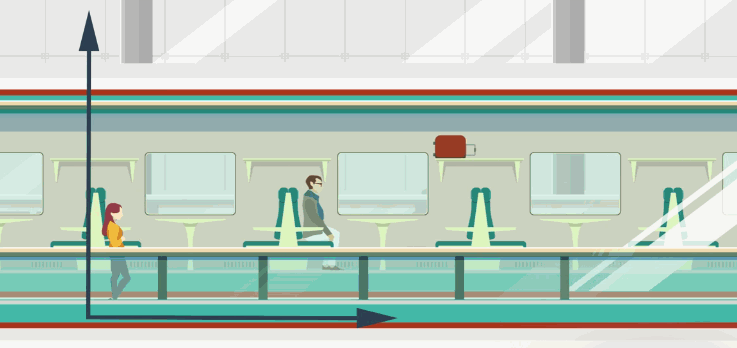
Рис. 3. Различные системы отчета

---

Зависимость траектории от выбора системы отсчета

Ответим на интересный и важный вопрос, зависит ли форма траектории и пройденный телом путь от выбора системы отсчета. Рассмотрим ситуацию, когда есть пассажир поезда, радом с которым на столе стоит стакан с водой. Какой же будет траектория стакана в системе отчета, связанной с пассажиром (телом отсчета является пассажир)?

Конечно, относительно пассажира стакан неподвижен. Это значит, что траектория является точкой, а перемещение равно  (рис. 4).

Рис. 4. Траектория стакана относительно пассажира в поезде

Какой же будет траектория стакана относительно пассажира, который ожидает поезда на перроне? Для этого пассажира будет казаться, что стакан движется по прямой линии и у него ненулевой путь (рис. 5).

Рис. 5. Траектория стакана относительно пассажира на перроне

Из вышесказанного можно сделать вывод, что траектория и путь зависят от выбора системы отсчета.

Для того чтобы описывать механическое движение, в первую очередь необходимо определиться с системой отсчета.

Движение изучается нами для того, чтобыпредсказать, где окажется тот или иной объект в необходимый момент времени. Основная задача механики – определить положение тела в любой момент времени. Что же значит описать движение тела?

Рассмотрим пример: автобус едет из Москвы в Санкт-Петербург (рис. 6). Важны ли нам размеры автобуса по сравнению с расстоянием, которое он преодолеет?

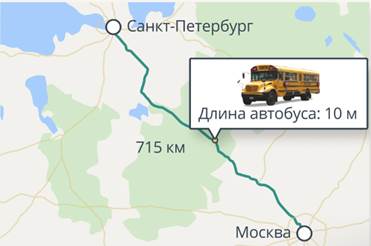
Рис. 6. Движение автобуса из Москвы в Санкт-Петербург

Конечно же, размерами автобуса в данном случае можно пренебречь. Мы можем описывать автобус как одну движущуюся точку, по-другому ее называют материальной точкой.

Определение

Тело, размерами которого в данной задаче можно пренебречь, называют материальной точкой.

Одно и то же тело, в зависимости от условий задачи, может быть или не быть материальной точкой. При перемещении автобуса из Москвы в Санкт-Петербург автобус можно считать материальной точкой, ведь его размеры несопоставимы с расстоянием между городами. Но если в салон автобуса влетела муха и мы хотим исследовать ее движение, тогда в этом случае нам важны размеры автобуса, и он уже не будет являться материальной точкой.

Чаще всего в механике мы будем изучать именно движение материальной точки. При своем перемещении материальная точка последовательно проходит положение вдоль некоторой линии.

Определение

Линия, вдоль которой движется тело (или материальная точка), называется траекторией движения тела (рис. 7).

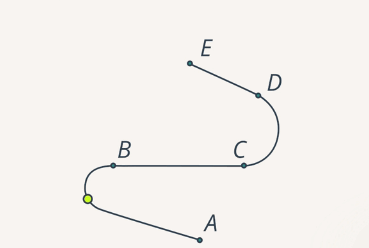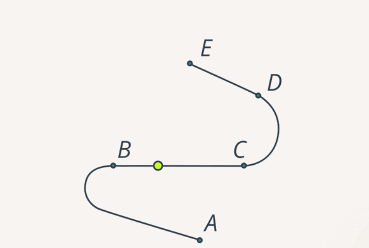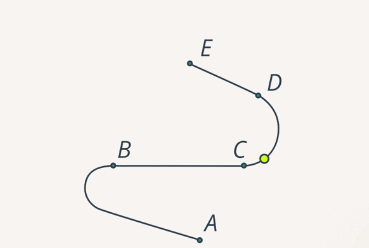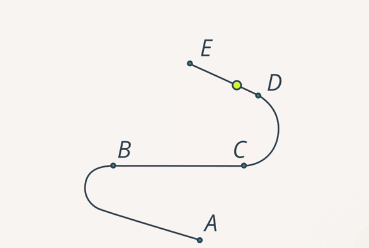
Рис. 7. Траектория точки

Иногда мы наблюдаем траекторию (например, процесс выставления оценки за урок), но чаще всего траектория – это какая-то воображаемая линия. При наличии средств измерения мы можем замерить длину траектории, вдоль которой двигалось тело, и определим величину, которая называется путь (рис. 8).

Определение

Путь, пройденный телом за некоторое время, – это длина участка траектории.

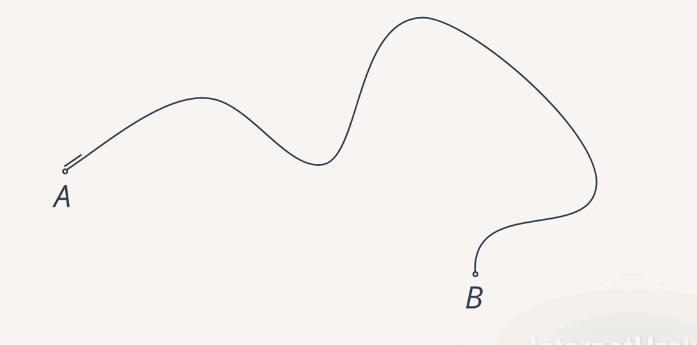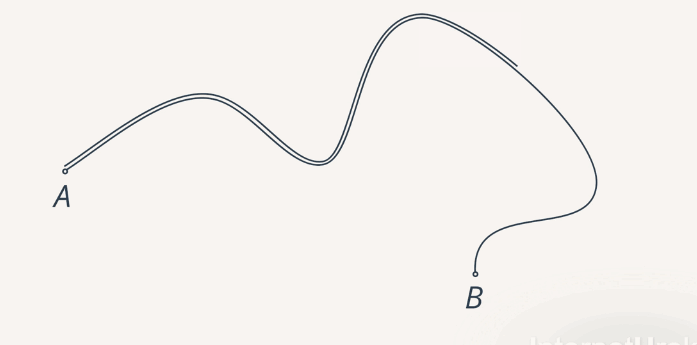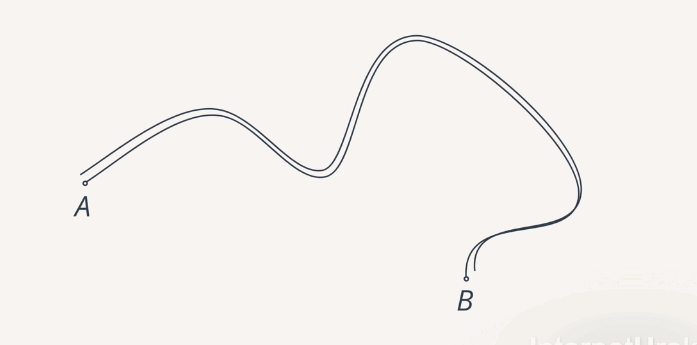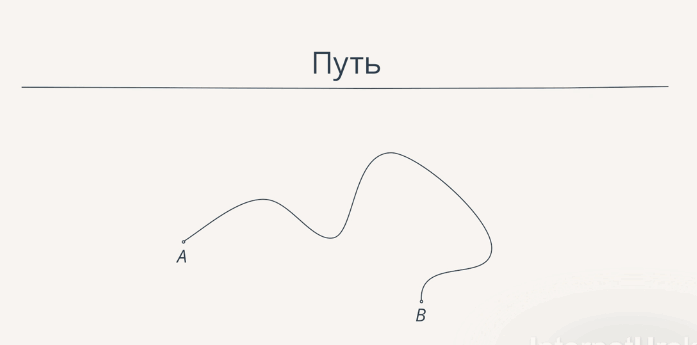
Рис. 8. Путь

Разделяют два основных вида движения – это прямолинейное и криволинейное движение.

Если траектория тела – это прямая линия, то движение называется прямолинейным. Если тело движется по параболе или по любой другой кривой – мы говорим о криволинейном движении. При рассмотрении движения не просто материальной точки, а движения реального тела различают еще два вида движения: поступательное движение и вращательное движение.

---

Поступательное и вращательное движение. Пример

Какие же движения называются поступательными, а какие – вращательными? Рассмотрим этот вопрос на примере колеса обозрения. Как движется кабина колеса обозрения? Отметим две произвольные точки кабины и соединим их прямой. Колесо вращается. Через некоторое время отметим те же точки и соединим их. Полученные прямые будут лежать на параллельных прямых (рис. 9).

Рис. 9. Поступательное движение кабины колеса обозрения

Если прямая, проведенная через любые две точки тела, при движении остается параллельной сама себе, то такое движение называют поступательным.

В противном случае мы имеем дело с вращательным движением. Если бы прямая не была параллельной сама тебе, то пассажир, скорее всего, вывалился бы из кабины колеса (рис. 10).

Рис. 10. Вращательное движение кабины колеса

Вращательным называют такое движение тела, при котором его точки описывают окружности, лежащие в параллельных плоскостях. Прямая, соединяющая центры окружностей, называется осью вращения. 

Очень часто нам приходится сталкиваться с комбинацией поступательного и вращательного движения, так называемым поступательно-вращательным движением. Самый простой пример такого движения – это движение прыгуна в воду (рис. 11). Он выполняет вращение (сальто), но при этом центр его масс поступательно движется в направлении воды.

Рис. 11. Поступательно-вращательное движение

Мы сегодня изучили азбуку кинематики, то есть основные, самые важные понятия, которые в дальнейшем позволят нам перейти к решению главной задачи механики – определению положения тела в любой момент времени.    

 

Список литературы

1. Тихомирова С.А., Яворский Б.М. Физика (базовый уровень) – М.: Мнемозина, 2012.
2. Генденштейн Л.Э., Дик Ю.И. Физика 10 класс. – М.: Мнемозина, 2014.
3. Кикоин И.К., Кикоин А.К. Физика – 9, Москва, Просвещение, 1990.

 

Дополнительные рекомендованные ссылки на ресурсы сети Интернет

1. Интернет-портал «Av-physics.narod.ru» (Источник).
2. Интернет-портал «Rushkolnik.ru» (Источник).
3. Интернет-портал «Testent.ru» (Источник).

 

Домашнее задание

Подумайте, что является телом отсчета, когда мы говорим:

• книга неподвижно лежит на столике в купе движущегося поезда;
• стюардесса после взлета проходит по пассажирскому салону самолета;
• Земля вращается вокруг своей оси.

2.1. Кинематика. Механика. Физика. Курс лекций

2.1.1. Механическое движение. Физические модели реальных тел, используемые в механике. Система отсчета. Траектория. Виды движений

2.1.2. Кинематические уравнения движения. Длина пути и вектор перемещения

2.1.3. Кинематические характеристики. Скорость

2.1.4. Кинематические характеристики. Ускорение

2.1.5. Поступательное и вращательное движение твердого тела

2.1.6. Связь между кинематическими характеристиками при различных видах движений

2.1.1. Механическое движение. Физические модели реальных тел, используемые в механике. Система отсчета. Траектория. Виды движений

1. Механическое движение — изменение положения тела или отдельных его частей в пространстве с течением времени.

Внутреннее строение движущихся тел, их химический состав не влияет на механическое движение. Для описания движения реальных тел в зависимости от условий задачи пользуются различными моделями: материальная точка, абсолютно твердое тело, абсолютно упругое тело, абсолютно неупругое тело и т.д.

Материальной точкой называется тело, размерами и формой которого можно пренебречь в условиях данной задачи. В дальнейшем вместо термина «материальная точка» будем употреблять термин «точка». Одно и то же тело можно свести к материальной точке в одной задаче, и необходимо учитывать его размеры в условиях другой задачи. Например, расчет движения самолета, летящего над Землей, можно производить, считая его материальной точкой. А при расчете обтекания воздухом крыла того же самолета надо учитывать форму и размеры крыла.

Любое протяженное тело можно рассматривать как систему материальных точек.

Абсолютно твердое тело (а.т.т.) — тело, деформацией которого можно пренебречь в условиях данной задачи. А.т.т. можно рассматривать как систему жестко связанных между собой материальных точек, т.к. расстояние между ними не изменяются при любых взаимодействиях.

Абсолютно упругое тело — тело, деформация которого подчиняется закону Гука (см. § 2.2.2.), и после прекращения силового воздействия оно полностью восстанавливает первоначальные размеры и форму.

Абсолютно неупругое тело — тело, которое после прекращения силового воздействия на него не восстанавливается, а полностью сохраняет деформированное состояние.

2. Для определения положения тела в пространстве и во времени надо ввести понятие системы отсчета. Выбор системы отсчета произволен.

Системой отсчета называется тело или группа тел, считающиеся условно неподвижными и снабженные устройством отсчета времени (часами, секундомером и т.д.), относительно которых рассматривается движение данного тела.

Неподвижное тело (или группу тел) называют телом отсчета и для удобства описания движения с ним связывают систему координат (декартову, полярную, цилиндрическую и т.д.).

Выберем в качестве системы координат декартову прямоугольную систему XYZ (подробно см.[8]). Положение точки С в пространстве можно определить координатами х, y, z (Рисунок 1).

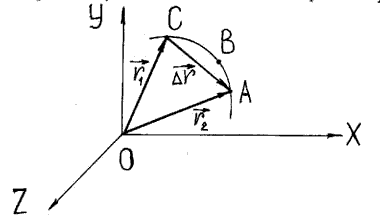
Рисунок 1 — Определение положения точки в декартовой системе координат

Однако положение той же точки в пространстве можно задать с помощью одной векторной величины r = r(x, y, z), называемой радиус-вектором точки С (Рисунок 1).

3. Линия, которую тело описывает при своем движении, называется траекторией. По виду траектории движения можно разделить на прямолинейные и криволинейные. Траектория зависит от выбора системы отсчета. Так, траектория движения точек винта самолета относительно летчика — окружность, а относительно Земли — винтовая линия. Другой пример: какова траектория движения кончика иглы проигрывателя относительно пластинки? корпуса проигрывателя? корпуса звукоснимателя? Ответы таковы: спираль, дуга окружности, состояние покоя (игла неподвижна).

2.1.2. Кинематические уравнения движения. Длина пути и вектор перемещения

1. При движении тела относительно выбранной системы координат его положение изменяется с течением времени. Движение материальной точки будет полностью определено, если заданы непрерывные и однозначные функции времени t:

x = x(t), y = y(t), z = z(t).

Эти уравнения описывают изменение координат точки от времени и называются кинематическими уравнениями движения.

2. Путь — часть траектории, пройденной телом за определенный промежуток времени. Момент времени t₀, от которого начинается его отсчет, называется начальным моментом времени, обычно t₀=0 в силу произвольного выбора начала отсчета времени.

Длиной пути называется сумма длин всех участков траектории. Длина пути не может быть величиной отрицательной, она всегда положительна. Например, материальная точка переместилась из точки траектории С сначала в точку А, а затем в точку В (Рисунок 1). Длина ее пути равна сумме длин дуги СА и дуги АВ.

2.1.3. Кинематические характеристики. Скорость

1. Для характеристики быстроты движения тел в физике вводится понятие скорости. Скорость — вектор, а значит, характеризуется величиной, направлением, точкой приложения.

Рассмотрим движение вдоль оси Х. Положение точки будет определяться изменением со временем координаты Х.

Если за время ∆ произошло перемещение точки на ∆r, то величина 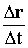является средней скоростью движения: .

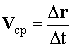Средней скоростью движущегося тела называется вектор, равный отношению вектора перемещения к величине промежутка времени, за которое это перемещение произошло.

Модуль средней скорости есть физическая величина, численно равная изменению пути за единицу времени.

2. Для определения скорости в данный момент времени, мгновенной скорости, нужно рассмотреть интервал времени ∆t→0, тогда

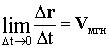
Используя понятие производной, можно записать для скорости

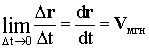
Скорость тела в данный момент времени называется мгновенной скоростью (или просто скоростью).

Вектор V мгновенной скорости направлен по касательной к траектории в сторону движения тела.

2.1.4. Кинематические характеристики. Ускорение

1. Быстрота изменения вектора скорости характеризуется величиной, называемой ускорением. Ускорение может возникнуть как за счет изменения величины скорости, так и за счет изменения направления скорости.

Пусть в момент времени t скорость тела равна v₁, а через промежуток времени ∆t в момент времени t + ∆t равна v₂, приращение вектора скорости за ∆t равно ∆v.

Средним ускорением тела в интервале времени от t до t + ∆t называется вектор а_ср, равный отношению приращения вектора скорости ∆v к промежутку времени ∆t: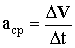

Cреднее ускорение есть физическая величина, численно равная изменению скорости за единицу времени.

2. Для определения ускорения в данный момент времени, т.е. мгновенного ускорения, нужно рассмотреть малый интервал времени ∆t→0. Тогда вектор мгновенного ускорения равен пределу вектора среднего ускорения при стремлении промежутка времени ∆t к нулю:

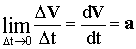
Используя понятие производной, можно дать для ускорения следующее определение: Ускорением (или мгновенным ускорением) тела называется векторная величина а, равная первой производной по времени от скорости тела v или второй производной по времени от пути.

3. При вращении точки по окружности ее скорость может изменяться по величине и по направлению (рисунок 2)

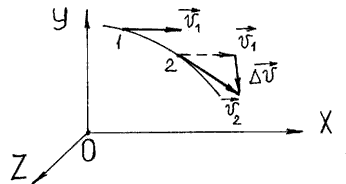
Рисунок 2 — Изменение скорости точки при вращении по окружности

На рисунке 2 в положении 1 скорость точки v_1, в положении 2 скорость точки v₂. Модуль скорости v₂ больше модуля скорости v₁ , ∆v— вектор изменения скорости ∆v = v₂ —v₁

Вращающаяся точка имеет тангенциальное ускорение, равное а_τ=dv/dt, оно изменяет скорость по величине и направлено по касательной к траектории; и нормальное ускорение, равное а_n= v²/R, оно меняет направление скорости и направлено по радиусу окружности (R) (см. Pисунок 3)

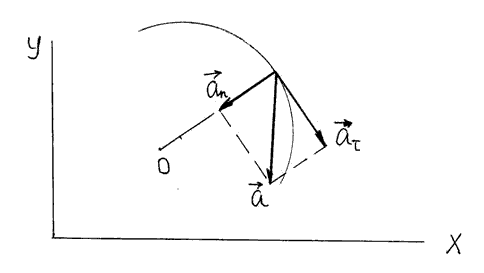
Рисунок 3 — Полное, тангенциальное и нормальное ускорения вращающейся точки

Вектор полного ускорения равен 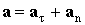, т.е. он может быть представлен как сумма векторов тангенциального a_τ и нормального a_n ускорений. Модуль полного ускорения равен:

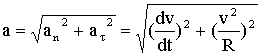
2.1.5. Поступательное и вращательное движение абсолютно твердого тела

1. До сих пор речь шла о характере движения, о траектории, о кинематических характеристиках, но не рассматривалось само движущееся тело. Пример. Движется автомобиль. Он является сложным телом. Движения его кузова и колес различны. Если тело сложное, то возникает вопрос: к движению каких частей тела относятся понятия пути, скорости, ускорения, введенные ранее?

Прежде, чем ответить на этот вопрос, надо выделить формы механического движения. Каким бы сложным не было движение тела, его можно свести к двум основным: поступательному движению и вращению вокруг неподвижной оси. Колебательное движение будет рассмотрено отдельно. В примере с автомобилем поступательно движется кузов автомобиля. Сам автомобиль является телом, которое может быть рассмотрено с помощью модели абсолютно твердого тела (а.т.т.). Для краткости мы будем называть абсолютно твердое тело просто твердое тело.

Поступательным движением твердого тела называется движение, при котором любая прямая, проведенная между его двумя точками, остается при движении параллельна самой себе.

Поступательное движение может быть и не прямолинейным движением.

Примеры. 1) В аттракционе «Колесо обозрения» кабинки — люльки, в которых сидят люди, двигаются поступательно. 2) Если стакан с водой перемещать по траектории, представленной на рисунке 5 так, чтобы поверхность воды и направляющая стакана составляли бы прямой угол, то движение стакана является не прямолинейным, но поступательным. Прямая АВ остается при движении стакана параллельна самой себе.

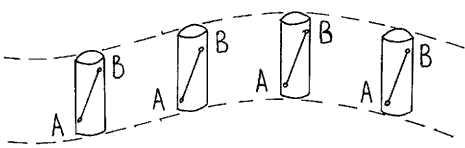
Рисунок 4 — Пример поступательного движения твердого тела.

Особенностью поступательного движения твердого тела является то, что все точки тела описывают одинаковую траекторию, проходят за определенные промежутки времени ∆t одинаковые пути и в любой момент времени имеют одинаковые скорости. Поэтому кинематическое рассмотрение поступательного движения твердого тела сводится к изучению движения любой из его точек. Поступательное движение тела может быть сведено к движению материальной точки. В динамике обычно за такую точку принимают центр масс тела. Кинематические характеристики и кинематические уравнения, вводимые для материальной точки, описывают и поступательное движение твердого тела.

2. Движение колес автомобиля отличается от движения кузова. Точки колеса, находящиеся на разных расстояниях от его оси, описывают разные траектории, проходят различные пути и имеют разные скорости. Чем дальше точка находится от оси колеса, тем больше ее скорость, тем больший путь она проходит за определенный промежуток времени. Движение, в котором участвуют колеса автомобиля, называется вращательным. Ясно, что модель материальной точки для описания вращения реального тело не подходит. Но и здесь вместо реального тела (например, колеса автомобиля с деформируемыми шинами и т.д.) используют физическую модель — абсолютно твердое тело.

Вращательным движением твердого тела называется движение, когда все точки тела описывают окружности, центры которых лежат на прямой, называемой осью вращения и перпендикулярной к плоскостям, в которых вращаются точки тела (Рисунок 5).

Так как для разных точек вращающегося тела траектории, пути, скорости различны, то встает вопрос: можно ли найти физические величины, которые имели бы одинаковые значения для всех точек вращающегося тела, Да, оказывается, есть такие величины, они называются угловыми.

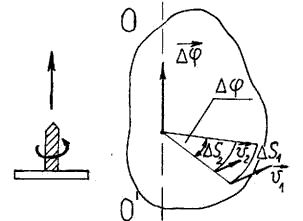
Рисунок 5 — Вращение твердого тела

Твердое тело, вращающееся вокруг неподвижной оси, имеет одну степень свободы, его положение в пространстве полностью определяется значением угла поворота ∆φ из некоторого начального положения (Рисунок 5). Все точки твердого тела повернутся за промежуток времени ∆ на угол ∆φ.

При малых промежутках времени, когда углы поворота невелики, их можно рассматривать как векторы, хотя и не совсем обычные. Вектор элементарного (бесконечно малого) угла поворота ∆φ направлен вдоль оси вращения по правилу правого буравчика, его модуль равен углу поворота (Рисунок 5). Вектор ∆φ называется угловым перемещением.

Правило правого буравчика заключается в следующем:

Если рукоятка правого буравчика вращается вместе с телом (точкой), то поступательное движение буравчика совпадает с направлением ∆φ.

Другая формулировка правила: Из конца вектора ∆φ видно, что движение точки (тела) происходит против часовой стрелки.

Положение тела в любой момент времени t определяется кинематическим уравнением вращательного движения ∆φ = ∆φ(t).

3. Для характеристики быстроты вращения служит угловая скорость.

Средней угловой скоростью называется физическая величина, равная отношению углового перемещения к промежутку времени, за которое это перемещение произошло

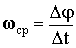
Предел, к которому стремится средняя угловая скорость при ∆→0, называется мгновенной угловой скоростью тела в данный момент времени или просто угловой скоростью вращения твердого тела (точки).

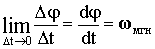
Угловая скорость равна первой производной от углового перемещения по времени. Направление мгновенной угловой скорости определяется по правилу правого буравчика и совпадает с направлением ∆φ (Рисунок 6). Кинематическое уравнение движения для угловой скорости имеет вид ω = ω (t).

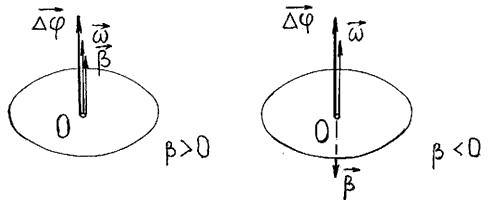
Рисунок 6 — Направление векторов угловых характеристик при вращательном движении.

4. Для характеристики быстроты изменения угловой скорости тела при неравномерном вращении вводится вектор углового ускорения β, равный первой производной от его угловой скорости ω по времени t.

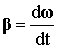
Среднее угловое ускорение есть величина отношения изменения угловой скорости ∆ω к промежутку времени ∆t, за которое это изменение произошло β _ср = ∆ω/∆t

Вектор углового ускорения направлен вдоль оси вращения и совпадает с направлением угловой скорости, если движение ускоренное, и противоположен ему, если вращение замедленное (Рисунок 6).

5. При вращательном движении твердого тела все его точки двигаются так, что вращательные характеристики (угловое перемещение, угловая скорость, угловое ускорение) для них одинаковы. А линейные характеристики движения зависят от расстояния точки до оси вращения.

Связь между этими величинами v, ω, r задается следующим соотношением:

v = [ω∙r],

т.е. линейная скорость v любой точки С твердого тела, вращающегося вокруг неподвижной оси с угловой скоростью ω, равна векторному произведению ω на радиус-вектор r точки С относительно произвольной точки О на оси вращения.

Подобное соотношение существует между линейным и угловым ускорениями вращающейся точки твердого тела:

а = [β∙r].

2.1.6. Связь между кинематическими характеристиками при различных видах движений

По зависимости скорости и ускорения от времени все механические движения делятся на равномерное, равнопеременное (равноускоренное и равнозамедленное) и неравномерное.

Рассмотрим кинематические характеристики и кинематические уравнения, введенные в предыдущих параграфах, для разных видов движений.

1. Прямолинейное движение

Прямолинейное равномерное движение.

Направление движения задается осью ОХ.

Ускорение а = 0 (а_n = 0, а_τ = 0), скорость v = const, путь s = v∙t, координата x = x₀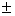 v∙t, где x₀ — начальная координата тела на оси ОХ.

Путь — величина всегда положительная. Координата может быть и положительной и отрицательной, поэтому в уравнении, задающем зависимость координаты от времени, перед величиной v∙t в уравнении стоит знак плюс, если направление оси ОХ и направление скорости совпадают, и знак минус, если они противоположно направлены.

Прямолинейное равнопеременное движение.

Ускорение а = а_τ = const, а_n = 0, скорость 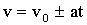, путь 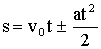, координата .

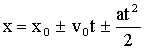Перед величиной (at) в кинематическом уравнении для скорости знак плюс соответствует равноускоренному движению, а знак минус — равнозамедленному движению. Это замечание верно и для кинематического уравнения пути, разные знаки перед величинами (at²/2) соответствуют разным видам равнопеременного движения.

В уравнении для координаты знак перед (v₀t) может быть и плюс, если направления v₀ и оси ОХ совпадают, и минус, если они направлены в разные стороны.

Разные знаки перед величинами 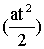соответствуют равноускоренному или равнозамедленному движениям.

Прямолинейное неравномерное движение.

Ускорение а = а_τ>≠ const, а_n = 0,

скорость 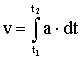, путь .

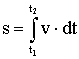2. Поступательное движение

Для описания поступательного движения можно использовать законы, приведенные в §2.1.6. (пункт 2) или §2.1.4. (пункт3). Использование тех или иных законов для описания поступательного движения зависит от его траектории. Для прямолинейной траектории используются формулы из §2.1.6. (пункт 2), для криволинейной — §2.1.4. (пункт3).

3. Вращательное движение

Отметим, что решение всех задач на вращательное движение твердого тела вокруг неподвижной оси аналогично по форме задачам на прямолинейное движение точки. Достаточно заменить линейные величины s, v_х, a_х на соответствующие угловые величины φ, ω, β, и мы получим все закономерности и соотношения для вращающегося тела.

Равномерное вращение по окружности

(R — радиус окружности).

Ускорение: полное а = а_n, нормальное 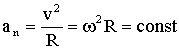, тангенциальное а_τ = 0, угловое β = 0.

Скорость: угловая ω = const, линейная v = ωR = const.

Угол поворота ∆φ = ∆ φ₀ + ωt, ∆φ₀ — начальное значение угла. Угол поворота величина положительная (аналог пути).

Периодом вращения называется промежуток времени T, в течении которого тело, равномерно вращаясь с угловой скоростью ω, совершает один оборот вокруг оси вращения. При этом тело поворачивается на угол 2π.

.

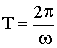Частота вращения показывает число оборотов, совершаемых телом за единицу времени при равномерном вращении с угловой скоростью ω:

.

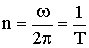Равнопеременное вращение по окружности

Ускорение: угловое β = const, тангенциальное а_τ = βR=const, нормальное а_n = ω ²R ≠ const, полное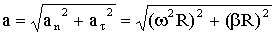

Скорость: угловая ω = ω₀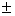 ( βt), линейная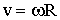

Угловое перемещение .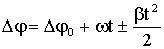

Все сказанное ранее относительно знаков в кинематических уравнениях для прямолинейного равнопеременного движения остается верным и для кинематических уравнений вращательного движения: плюс в формулах относится к равноускоренному вращению, минус — к равнозамедленному.

Неравномерное вращение

Ускорение: а_τ = а_τ (t), а_n = а _n(t), β ≠ const,

Скорость:

Угловая ω = dφ/dt, линейная .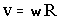

КИНЕМАТИКА • Большая российская энциклопедия

КИНЕМА́ТИКА (от греч. ϰίνημα, род. п. ϰινήματος – дви­же­ние), раз­дел ме­ха­ни­ки, в ко­то­ром опи­сы­ва­ют­ся гео­мет­рич. ха­рак­те­ри­сти­ки дви­же­ния ме­ха­ни­че­ско­го – дви­же­ния ма­те­ри­аль­ных то­чек и их сис­тем, аб­со­лют­но твёр­дых тел и т. д. Со­от­вет­ст­вен­но вы­де­ля­ют раз­де­лы К.: К. ма­те­ри­аль­ной точ­ки, К. сис­те­мы то­чек, К. твёр­до­го те­ла и т. д.

Осн. по­ня­тия К. (мгно­вен­ная ско­рость и мгно­вен­ное ус­ко­ре­ние ма­те­ри­аль­ной точ­ки) бы­ли вве­де­ны Г. Га­ли­ле­ем в фун­дам. тру­де «Бе­се­ды и ма­те­ма­тич. до­ка­за­тель­ст­ва, ка­саю­щие­ся двух но­вых от­рас­лей нау­ки, от­но­ся­щих­ся к ме­ха­ни­ке и ме­ст­но­му дви­же­нию» (1638). Га­ли­лей по­лу­чил стро­гие ма­те­ма­тич. за­ко­ны К. на ос­но­ве обоб­ще­ния экс­пе­рим. дан­ных, ус­та­но­вил прин­цип от­но­си­тель­но­сти (см. Га­ли­лея прин­цип от­но­си­тель­но­сти). Х. Гюй­генс (1672) кон­кре­ти­зи­ро­вал прин­ци­пы и по­ня­тия К., вве­дён­ные Га­ли­ле­ем. Ра­бо­ты Гюй­ген­са по­слу­жи­ли ба­зой для соз­да­ния ме­ха­ни­ки И. Нью­то­на (1687). В 1765 Л. Эй­лер за­ло­жил ос­но­вы К. твёр­до­го те­ла. В нач. 19 в. Г. Ко­рио­лис дал окон­ча­тель­ную фор­му­ли­ров­ку тео­рии от­но­си­тель­но­го дви­же­ния. С сер. 19 в. К. на­ча­ла ак­тив­но ис­поль­зо­вать­ся для опи­са­ния пре­об­ра­зо­ва­ния дви­же­ния в ме­ха­низ­мах и вы­де­ли­лась в са­мо­стоя­тель­ный раз­дел тео­ре­тич. ме­ха­ни­ки.

Кинематика материальной точки

Дви­же­ние ма­те­ри­аль­ной точ­ки опи­сы­ва­ет­ся по от­но­ше­нию к вы­бран­ной сис­те­ме ко­ор­ди­нат $Oxyz$. Ки­не­ма­тич. ха­рак­те­ри­сти­ка­ми дви­же­ния точ­ки слу­жат век­то­ры $\boldsymbol r$, $\boldsymbol v$ и $\boldsymbol w$, за­даю­щие в мо­мент вре­ме­ни $t$ со­от­вет­ст­вен­но мгно­вен­ное по­ло­же­ние, мгно­вен­ную ско­рость и мгно­вен­ное ус­ко­ре­ние точ­ки: $\boldsymbol r(t)=\{x(t),y(t),z(t)\}, \boldsymbol v(t)=d \boldsymbol r/dt=\{dx/dt, dy/dt, dz/dt \}$ и $\boldsymbol w(t)=d^2 \boldsymbol r/dt^2=\{d^2x/dt^2, d^2y/dt^2, d^2z/dt^2\}$. Кро­ме пря­мо­уголь­ных ко­ор­ди­нат ($x,y,z$) в К. для опи­са­ния дви­же­ния точ­ки ис­поль­зу­ют­ся так­же и кри­во­ли­ней­ные ко­ор­ди­на­ты (ци­лин­д­ри­че­ские, по­ляр­ные, сфе­ри­че­ские и т. п.).

Гео­мет­рич. ме­сто по­сле­до­ва­тель­ных по­ло­же­ний точ­ки в про­цес­се её дви­же­ния на­зы­ва­ет­ся тра­ек­то­ри­ей. Со­от­но­ше­ние $\boldsymbol r=\boldsymbol r(t)$ пред­став­ля­ет со­бой па­ра­мет­рич. фор­му урав­не­ния тра­ек­то­рии как не­ко­то­рой кри­вой в про­стран­ст­ве. За­кон дви­же­ния ма­те­ри­аль­ной точ­ки мо­жет быть так­же оп­ре­де­лён фор­мой тра­ек­то­рии, её по­ло­же­ни­ем в про­стран­ст­ве, по­ло­же­ни­ем на­чаль­ной точ­ки $O$ на тра­ек­то­рии и по­ло­жи­тель­ным на­прав­ле­ни­ем от­счё­та ду­го­вой ко­ор­ди­на­ты $s$ от на­чаль­ной точ­ки до её те­ку­ще­го зна­че­ния.

Урав­не­ние $s=s(t)$ оп­ре­де­ля­ет за­кон дви­же­ния точ­ки по тра­ек­то­рии. Ско­рость ма­те­ри­аль­ной точ­ки рав­на $\boldsymbol v=\boldsymbol \tau ds/dt$, где $\boldsymbol \tau$  – еди­нич­ный век­тор ка­са­тель­ной к тра­ек­то­рии в не­ко­то­рой точ­ке $M$. В диф­фе­рен­ци­аль­ной гео­мет­рии вво­дят­ся три вза­им­но ор­то­го­наль­ных еди­нич­ных век­то­ра: $\boldsymbol \tau$, $\boldsymbol n$ (век­тор глав­ной нор­ма­ли к кри­вой) и век­тор би­нор­ма­ли $\boldsymbol \beta=[\boldsymbol \tau, \boldsymbol n]$. Век­то­ры $\boldsymbol \tau$ и $\boldsymbol n$ оп­ре­де­ля­ют со­при­ка­саю­щую­ся плос­кость в точ­ке $M$ тра­ек­то­рии.

Ус­ко­ре­ние точ­ки вы­ра­жа­ет­ся фор­му­лой $\boldsymbol w(t)=d \boldsymbol v/dt=d^2 \boldsymbol r/dt^2=\boldsymbol \tau dv/dt+\boldsymbol n v^2/R$. Здесь пол­ное ус­ко­ре­ние точ­ки пред­став­ле­но в ви­де сум­мы двух вза­им­но ор­то­го­наль­ных век­то­ров – ка­са­тель­но­го ус­ко­ре­ния $\boldsymbol w_\tau$ (пер­вое сла­гае­мое) и цен­тро­ст­ре­ми­тель­но­го ус­ко­ре­ния $\boldsymbol w_n$ (вто­рое сла­гае­мое), на­прав­лен­но­го вдоль глав­ной нор­ма­ли к тра­ек­то­рии в сто­ро­ну цен­тра кри­виз­ны, от­стоя­ще­го от точ­ки $M$ на рас­стоя­ние $R$. Про­ек­ция век­то­ра ус­ко­ре­ния на би­нор­маль все­гда рав­на ну­лю.

Для тра­ек­то­рии, пред­став­ляю­щей со­бой пря­мую, в лю­бой её точ­ке рас­стоя­ние $R= \infty$; та­кое дви­же­ние ма­те­ри­аль­ной точ­ки на­зы­ва­ет­ся пря­мо­ли­ней­ным. Ес­ли ве­ли­чи­на ско­ро­сти ма­те­ри­аль­ной точ­ки ос­та­ёт­ся по­сто­ян­ной $[v(t)=\text {const} \neq0]$, то та­кое её дви­же­ние на­зы­ва­ет­ся рав­но­мер­ным. Ес­ли ка­са­тель­ное ус­ко­ре­ние точ­ки по­сто­ян­но $(dv(dt)=\text {const} \neq0)$, то та­кое дви­же­ние на­зы­ва­ет­ся рав­но­ус­ко­рен­ным.

Путь, прой­ден­ный точ­кой в её дви­же­нии вдоль тра­ек­то­рии, оп­ре­де­ля­ет­ся как ин­те­грал по вре­ме­ни от мо­ду­ля ско­ро­сти. Ве­ли­чи­на пу­ти мо­но­тон­но воз­рас­та­ет, в то вре­мя как ко­ор­ди­на­та точ­ки мо­жет то воз­рас­тать, то умень­шать­ся. Напр., при не­за­ту­хаю­щих ко­ле­ба­ни­ях ма­те­ма­тич. ма­ят­ни­ка путь ко­леб­лю­щей­ся ма­те­ри­аль­ной точ­ки не­пре­рыв­но воз­рас­та­ет, а её ду­го­вая ко­ор­ди­на­та при­ни­ма­ет зна­че­ния, ог­ра­ни­чен­ные ам­пли­ту­дой $A$ ко­ле­ба­ний (от $-A$ до $+A$).

Кинематика относительного движения

Сис­те­ма ко­ор­ди­нат $Oxyz$, от­но­си­тель­но ко­то­рой рас­смат­ри­ва­ет­ся дви­же­ние ма­те­ри­аль­ной точ­ки $M$, мо­жет быть свя­за­на с не­ко­то­рым те­лом, ко­то­рое са­мо дви­жет­ся от­но­си­тель­но не­под­виж­ной сис­те­мы $Ox_1y_1z_1$. В этом слу­чае ско­рость и ус­ко­ре­ние точ­ки $M$ от­но­си­тель­но сис­те­мы $Oxyz$ на­зы­ва­ют от­но­си­тель­ны­ми и обо­зна­ча­ют со­от­вет­ст­вен­но $\boldsymbol v_{отн}$ и $\boldsymbol w_{отн}$. Дви­же­ние той же ма­те­ри­аль­ной точ­ки от­но­си­тель­но сис­те­мы $Ox_1y_1z_1$ на­зы­ва­ют аб­со­лют­ным, его ско­рость и ус­ко­ре­ние обо­зна­ча­ют $\boldsymbol v_{абс}$ и $\boldsymbol w_{абс}$. При от­сут­ст­вии от­но­си­тель­но­го дви­же­ния $(v_{отн}=0)$ точ­ка $M$ пе­ре­но­сит­ся дви­жу­щим­ся те­лом, с ко­то­рым свя­за­на сис­те­ма $Oxyz$, и её ско­рость сов­па­да­ет со ско­ро­стью $\boldsymbol v_{пер}$ той точ­ки $N$ те­ла, в ко­то­рой в дан­ный мо­мент на­хо­дит­ся точ­ка $M$: $\boldsymbol r_N(t)=\boldsymbol r_M(t)$, но не то­ж­де­ст­вен­но (т. к. речь идёт о не­за­ви­си­мых точ­ках). Век­тор $\boldsymbol v_{пер}=d \boldsymbol r_N/dt$ на­зы­ва­ет­ся пе­ре­нос­ной ско­ро­стью или ско­ро­стью пе­ре­нос­но­го дви­же­ния. Фор­му­ла $\boldsymbol v_{абс}=\boldsymbol v_{отн}+ \boldsymbol v_{пер}$ вы­ра­жа­ет т. н. тео­ре­му сло­же­ния ско­ро­стей. Ус­ко­ре­ние точ­ки $N$ на­зы­ва­ют пе­ре­нос­ным и обо­зна­ча­ют $\boldsymbol w_{пер}$. Сло­же­ние ус­ко­ре­ний опи­сы­ва­ет­ся тео­ре­мой Ко­рио­ли­са: $\boldsymbol w_{абс}=\boldsymbol w_{отн}+ \boldsymbol w_{пер}+ \boldsymbol w_{Кор}$. Здесь до­пол­ни­тель­ное сла­гае­мое $\boldsymbol w_{Кор}$ (Ко­рио­ли­са ус­ко­ре­ние) воз­ни­ка­ет в том слу­чае, ес­ли сис­те­ма $Oxyz$ вра­щает­ся от­но­си­тель­но сис­те­мы $O_1x_1y_1z_1$: $\boldsymbol w_{Кор}=2[\boldsymbol \omega, \boldsymbol v_{отн}]$, где $\boldsymbol \omega$  – век­тор уг­ло­вой ско­ро­сти под­виж­ной сис­те­мы ко­ор­ди­нат.

Кинематика систем связанных точек и тел

Ма­ши­ны, ме­ха­низ­мы и др. объ­ек­ты тех­ни­ки час­то мо­де­ли­ру­ют сис­те­мой свя­зан­ных ма­те­ри­аль­ных то­чек и тел (см. Свя­зи ме­ха­ни­че­ские). В сис­те­ме со свя­зя­ми по­ло­же­ния и ско­ро­сти разл. то­чек сис­те­мы не мо­гут быть за­да­ны про­из­воль­но. Пер­вой за­да­чей К. та­ких сис­тем яв­ля­ет­ся фор­ма­ли­за­ция свя­зей, ко­то­рые за­пи­сы­ва­ют в ви­де урав­не­ний свя­зей – пол­но­го на­бо­ра не­за­ви­си­мых со­от­но­ше­ний ме­ж­ду ко­ор­ди­на­та­ми то­чек сис­те­мы. Вто­рая за­да­ча К. сис­тем свя­зан­ных то­чек и тел сво­дит­ся к со­кра­ще­нию чис­ла ве­ли­чин, не­об­хо­ди­мых для пол­но­го опи­са­ния дви­же­ния объ­ек­та. Для это­го из об­ще­го чис­ла ве­ли­чин ис­клю­ча­ют те, ко­то­рые вы­ра­жа­ют­ся че­рез дру­гие ве­ли­чи­ны при по­мо­щи урав­не­ний свя­зей. По­след­няя за­да­ча не­ред­ко ре­ша­ет­ся с по­мо­щью под­хо­дя­ще­го вы­бо­ра обоб­щён­ных ко­ор­ди­нат.

Обе за­да­чи К. до­пус­ка­ют не­од­но­знач­ные ре­ше­ния. Из всех ре­ше­ний вы­би­ра­ют­ся та­кие, ко­то­рые по­зво­ля­ют при­дать сис­те­ме диф­фе­рен­ци­аль­ных урав­не­ний дви­же­ния объ­ек­та наи­бо­лее удоб­ную фор­му. В тео­рии ма­шин и ме­ха­низ­мов, кро­ме то­го, не­об­хо­ди­мо свя­зать вход­ные и вы­ход­ные ха­рак­те­ри­сти­ки дви­же­ния (cм. Ки­не­ма­ти­ка ме­ха­низ­мов).

Кинематика твёрдого тела

В этом раз­де­ле К. рас­смат­ри­ва­ют­ся разл. ти­пы дви­же­ний аб­со­лют­но твёр­до­го те­ла. Под аб­со­лют­но твёр­дым те­лом по­ни­ма­ют сис­те­му ма­те­ри­аль­ных то­чек, вза­им­ное по­ло­же­ние ко­то­рых не из­ме­ня­ет­ся. Осн. за­да­ча К. твёр­до­го те­ла – оп­ре­де­ле­ние ско­ро­стей и ус­ко­ре­ний всех его то­чек. 

С гео­мет­рич. точ­ки зре­ния дви­же­ние аб­со­лют­но твёр­до­го те­ла от­но­си­тель­но не­под­виж­ной сис­те­мы ко­ор­ди­нат $O_1x_1y_1z_1$ с на­ча­лом в точ­ке $O_1$ эк­ви­ва­лент­но дви­же­нию свя­зан­ной с этим те­лом сис­те­мы $Oxyz$ с на­ча­лом в про­из­воль­но вы­бран­ной точ­ке $O$ те­ла. По­ло­же­ние те­ла од­но­знач­но оп­ре­де­ля­ет­ся по­ло­же­ни­ем трёх его то­чек, не ле­жа­щих на од­ной пря­мой. По­ло­же­ние трёх то­чек в сис­те­ме $O_1x_1y_1z_1$ за­да­ёт­ся с по­мо­щью де­вя­ти ко­ор­ди­нат, на ко­то­рые на­ло­же­ны три ус­ло­вия по­сто­ян­ст­ва вза­им­ных рас­стоя­ний ме­ж­ду точ­ка­ми. Это со­кра­ща­ет чис­ло не­за­ви­си­мых ве­ли­чин (оп­ре­де­ляю­щих макс. чис­ло сте­пе­ней сво­бо­ды те­ла) до шес­ти. До­пол­нит. ог­ра­ни­че­ния на дви­же­ние те­ла умень­ша­ют чис­ло сте­пе­ней сво­бо­ды и оп­ре­де­ля­ют тип дви­же­ния те­ла. Так, при фик­си­ро­ван­ных ко­ор­ди­на­тах ука­зан­ных то­чек те­ло на­хо­дит­ся в со­стоя­нии по­коя от­но­си­тель­но сис­те­мы $O_1x_1y_1z_1$.

По­сту­па­тель­ное дви­же­ние те­ла. Дви­же­ние твёр­до­го те­ла на­зы­ва­ют по­сту­па­тель­ным, ес­ли ка­ж­дый пря­мо­ли­ней­ный от­ре­зок, со­стоя­щий из то­чек те­ла, пе­ре­ме­ща­ет­ся па­рал­лель­но са­мо­му се­бе. В этом слу­чае оси сис­те­мы ко­ор­ди­нат, свя­зан­ной с те­лом, мож­но рас­по­ло­жить со­на­прав­лен­но осям не­под­виж­ной сис­те­мы. Ско­рость и ус­ко­ре­ние лю­бой точ­ки те­ла рав­ны со­от­вет­ст­вен­но ско­ро­сти и ус­ко­ре­нию точ­ки $O$ (на­ча­ла сис­те­мы ко­ор­ди­нат, свя­зан­ной с те­лом). Точ­ка $O$ мо­жет дви­гать­ся как по пря­мой, так и по пло­ской или про­стран­ст­вен­ной кри­вой. Напр., ва­гон по­ез­да на пря­мом уча­ст­ке пу­ти дви­жет­ся по­сту­па­тель­но и пря­мо­ли­ней­но. Ка­би­на ко­ле­са обо­зре­ния то­же дви­жет­ся по­сту­па­тель­но, но её точ­ки опи­сы­ва­ют ок­руж­но­сти.

Те­ло, дви­жу­щее­ся по­сту­па­тель­но, име­ет три сте­пе­ни сво­бо­ды (столь­ко же, сколь­ко у ма­те­ри­аль­ной точ­ки), для опи­са­ния его дви­же­ния дос­та­точ­но за­дать три не­за­ви­си­мые ко­ор­ди­на­ты.

Вра­ще­ние те­ла во­круг оси. При вра­ща­тель­ном дви­же­нии те­ла свя­зан­ная с ним сис­те­ма ко­ор­ди­нат из­ме­ня­ет свою ори­ен­та­цию от­но­си­тель­но не­под­виж­ной сис­те­мы, т. е. со­вер­ша­ет по­во­рот. Наи­бо­лее про­стой слу­чай вра­ща­тель­но­го дви­же­ния – вра­ще­ния те­ла во­круг не­по­движ­ной оси. Для опи­са­ния та­ко­го дви­же­ния три точ­ки те­ла вы­би­ра­ют сле­дую­щим об­ра­зом: две точ­ки – на оси вра­ще­ния, а тре­тью – вне этой оси. При дви­же­нии те­ла две пер­вые точ­ки не из­ме­ня­ют сво­его по­ло­же­ния от­но­си­тель­но не­под­виж­ной сис­те­мы ко­ор­ди­нат, а тре­тья точ­ка опи­сы­ва­ет ок­руж­ность с цен­тром на оси вра­ще­ния. Т. о., те­ло име­ет од­ну сте­пень сво­бо­ды, его по­ло­же­ние оп­ре­де­ля­ет­ся од­ной ко­ор­ди­на­той – уг­лом $\phi$ ме­ж­ду те­ку­щим по­ло­же­ни­ем плос­ко­сти трёх вы­бран­ных то­чек и плос­ко­стью $Ox_1z$, оп­ре­де­ляю­щей по­ло­же­ние не­под­виж­ной сис­те­мы ко­ор­ди­нат. Урав­не­ние $\phi=\phi(t)$ за­да­ёт за­кон вра­ще­ния те­ла во­круг не­под­виж­ной оси. Ки­не­ма­тич. ха­рак­те­ри­сти­ка­ми это­го дви­же­ния слу­жат уг­ло­вая ско­рость $\omega(t)=d \phi/dt$ и уг­ло­вое уско­ре­ние $\varepsilon=d\omega/dt=d^2 \phi/dt^2$.

Ско­рость $\boldsymbol v_N$ про­из­воль­ной точ­ки $N$ те­ла, не при­над­ле­жа­щей оси вра­ще­ния, на­прав­ле­на по ка­са­тель­ной к со­от­вет­ст­вую­щей ок­руж­но­сти и рав­на $v_N=\omega R_N$, где $R_N$ – рас­стоя­ние от точ­ки $N$ до оси вра­ще­ния. Век­тор ус­ко­ре­ния $\boldsymbol w_N$ точ­ки мо­жет быть пред­став­лен в ви­де сум­мы век­то­ров ка­са­тель­но­го ус­ко­ре­ния $\boldsymbol w_\tau$ и цен­тро­ст­ре­ми­тель­но­го ус­ко­ре­ния $\boldsymbol w_n$, при­чём $w_\tau=\varepsilon R_N=dv_N/dt$, $w_n=\omega^2R_N=v^2_N/R_N$.

Дан­ный раз­дел К. твёр­до­го те­ла ис­поль­зу­ют для опи­са­ния разл. ме­ха­низ­мов, со­дер­жа­щих вра­щаю­щие­ся эле­мен­ты (ро­то­ры, тур­би­ны, ко­лё­са).

При бо­лее слож­ных вра­ща­тель­ных дви­же­ни­ях учи­ты­ва­ет­ся пре­цес­сия оси вра­ще­ния. В этом слу­чае вра­ща­тель­ное дви­же­ние те­ла мо­жет быть пред­став­ле­но су­пер­по­зи­ци­ей двух про­стых вра­ще­ний: те­ло вра­ща­ет­ся во­круг сво­ей оси $Oz$, ко­то­рая в свою оче­редь вра­ща­ет­ся во­круг не­под­виж­ной оси $Oz_1$. То­гда ори­ен­та­ция те­ла в про­стран­ст­ве оп­ре­де­ля­ет­ся тре­мя ко­ор­ди­на­та­ми – т. н. Эй­ле­ра уг­ла­ми [$\psi(t)$ – угол пре­цес­сии, $\phi(t)$ – угол соб­ст­вен­но­го вра­ще­ния, $\theta$ – по­сто­ян­ный угол ну­та­ции].

Вра­ще­ние те­ла во­круг не­по­движ­ной точ­ки. При про­из­воль­ном вра­ще­нии те­ла во­круг не­под­виж­ной точ­ки $O$ все три уг­ла Эй­ле­ра за­ви­сят от вре­ме­ни, при­чём дви­же­ние те­ла нель­зя све­сти к двум про­стым вра­ще­ни­ям. Как по­ка­зал Л. Эй­лер, для опи­са­ния дан­но­го дви­же­ния мож­но най­ти та­кой век­тор $\omega$ (на­зы­вае­мый мгно­вен­ной уг­ло­вой ско­ро­стью те­ла), что ско­рость $\boldsymbol v_N$ точ­ки $N$ те­ла оп­ре­де­ля­ет­ся фор­му­лой $\boldsymbol v_N=\boldsymbol [\omega, \boldsymbol r_N]$. Те точ­ки те­ла, для ко­то­рых век­то­ры $\boldsymbol r_N$ и $\boldsymbol \omega$ кол­ли­не­ар­ны, об­ра­зу­ют мгно­вен­ную ось вра­ще­ния те­ла (мгно­вен­ная ско­рость этих то­чек рав­на ну­лю). Век­тор $\boldsymbol \omega=\{\omega_x, \omega_y, \omega_z \}$ пред­став­ля­ет со­бой гео­мет­рич. сум­му трёх век­то­ров: $\boldsymbol e_1d\psi/dt$ – уг­ло­вая ско­рость пре­цес­сии (орт $\boldsymbol e_1$ не­из­ме­нен в не­под­виж­ной сис­те­ме ко­ор­ди­нат), $\boldsymbol e_2d\phi/dt$ – уг­ло­вая ско­рость соб­ст­вен­но­го вра­ще­ния (орт $\boldsymbol e_2$ не­из­ме­нен от­но­си­тель­но те­ла), $\boldsymbol e_3d\theta/dt$ – уг­ло­вая ско­рость ну­та­ции (орт $\boldsymbol e_3$ вра­ща­ет­ся во­круг $\boldsymbol e_1$). Дви­же­ние твёр­до­го те­ла от­но­си­тель­но не­под­виж­ной точ­ки опи­сы­ва­ет­ся сле­дую­щи­ми ки­не­ма­ти­чес­ки­ми Эй­ле­ра урав­не­ния­ми: $$\omega_x=(d\theta/dt)\cos \phi — (d \psi /dt)\sin \theta \sin \phi;\\ \omega_y=(d\theta/dt)\sin \phi — (d \psi /dt)\sin \theta \cos \phi;\\ \omega_z=d\phi/dt+(d\psi/dt)\cos \theta.$$

Кро­ме уг­лов Эй­ле­ра для опи­са­ния вра­ща­тель­но­го дви­же­ния те­ла мо­гут быть ис­поль­зо­ва­ны и др. па­ра­мет­ры: уг­лы Кры­ло­ва, па­ра­мет­ры Род­ри­га – Га­миль­то­на и т. п. Ус­ко­ре­ние $\boldsymbol w_N$ точ­ки $N$ те­ла вы­чис­ля­ет­ся по фор­му­ле Ри­валь­са: $\boldsymbol w_N=[d\boldsymbol\omega/dt, \boldsymbol r_N]+[\boldsymbol\omega,[\boldsymbol\omega,\boldsymbol r_N]]$.

Про­из­воль­ное дви­же­ние те­ла. Про­из­воль­ное дви­же­ние твёр­до­го те­ла мож­но раз­ло­жить на две со­став­ляю­щие: по­сту­па­тель­ное дви­же­ние со ско­ро­стью $\boldsymbol v_O$ не­ко­то­рой точ­ки $O$ те­ла и вра­ще­ние во­круг этой точ­ки с уг­ло­вой ско­ро­стью $\boldsymbol \omega$. За­ме­на точ­ки $O$ на др. точ­ку, напр. точ­ку $N$, вно­сит из­ме­не­ние в опи­са­ние это­го же дви­же­ния. Во­об­ще го­во­ря, из­ме­ня­ет­ся на­прав­ле­ние и ве­ли­чи­на ско­ро­сти $\boldsymbol v_N$ по­сту­па­тель­но­го дви­же­ния, но не из­ме­ня­ет­ся уг­ло­вая ско­рость $\boldsymbol \omega$ вра­ще­ния, со­вер­шае­мо­го те­перь во­круг точ­ки $N$. Ес­ли $\omega \neq 0$ и $(\boldsymbol v_O, \boldsymbol \omega) \neq 0$, в те­ле су­ще­ст­ву­ет мно­же­ст­во то­чек, для ко­то­рых век­то­ры $\boldsymbol v$ и $\boldsymbol \omega$ кол­ли­не­ар­ны. Эти точ­ки об­ра­зу­ют мгно­вен­ную вин­то­вую ось дви­же­ния те­ла (см. Вин­то­вое дви­же­ние).

Плос­ко­па­рал­лель­ное дви­же­ние те­ла. Те­ло со­вер­ша­ет плос­ко­па­рал­лель­ное дви­же­ние, ес­ли ско­ро­сти всех его то­чек в лю­бой мо­мент вре­ме­ни па­рал­лель­ны не­ко­то­рой не­под­виж­ной плос­ко­сти. Спро­ек­ти­ро­вав те­ло на эту плос­кость, по­лу­чим пло­скую фи­гу­ру, дви­же­ние ко­то­рой по плос­ко­сти эк­ви­ва­лент­но дви­же­нию те­ла. Ес­ли в этом дви­же­нии $w(t) \neq0$, то век­тор $\boldsymbol \omega$ ор­то­го­на­лен ука­зан­ной плос­ко­сти, $(\boldsymbol v_O, \boldsymbol \omega) \neq 0$ и ось мгно­вен­но­го вин­та пе­ре­се­ка­ет фи­гу­ру в мгно­вен­ном цен­тре вра­ще­ния. Ес­ли $\omega=0$, но $v_O \neq 0$, то те­ло на­хо­дит­ся в со­стоя­нии мгно­вен­но по­сту­па­тель­но­го дви­же­ния.

К. сплош­ных сред (де­фор­ми­руе­мо­го те­ла, не­сжи­мае­мой и сжи­мае­мой жид­ко­сти) тре­бу­ет бо­лее слож­ных про­це­дур опи­са­ния: рас­смат­ри­ва­ет­ся об­щая тео­рия де­фор­ма­ций, оп­ре­де­ля­ют­ся т. н. урав­не­ния не­раз­рыв­но­сти и т. д. (см. Ме­ха­ни­ка сплош­ной сре­ды, Ме­ха­ни­ка жид­ко­сти и га­за).

Кинематика точки и твердого тела. Базовый уровень. Видеоурок. Физика 10 Класс

Грузовик едет со средней скоростью 70 км/час. Сколько времени он потратит на дорогу из одного города в другой, если расстояние между городами 350 км?

Вы решите эту задачу в одно действие, получится 5 часов. Но для водителя может быть важнее ответ на другой вопрос: сколько времени займёт обгон другого такого же грузовика, который движется со скоростью 60 км/ч, а длина каждого грузовика – 7 м? Попробуйте решить задачу самостоятельно, ответ получится около 5 с.

Задачи простые, но вот что интересно: в первой нам было вообще всё равно, совершал ли обгоны грузовик, важно было только общее время движения. Мы рассмотрели его как материальную точку, которая движется с постоянной скоростью. А вторую задачу мы бы не решили, не зная длин грузовиков, здесь модель материальной точки уже неприменима.

У нас есть в запасе различные модели – это инструменты. Которые мы можем с той или иной степенью точности использовать для решения различных практических задач. Если эта точность нас не устраивает, то мы используем другую модель или разрабатываем новую, например, уточняя текущую.

Так, для описания движения в кузове пустого баллона или вибрации двигателя грузовика описанные выше модели не подойдут, понадобятся новые. При этом рассмотренные модели не имеют отношения к грузовику – они могут применяться к автобусу, поезду, бильярдному шару или любому другому объекту. Задачи могут быть самыми разными, но то немногое, что для нас в них является самым важным, может быть описано одной и той же моделью.

Обратите внимание, что в рассмотренных задачах про грузовик нас интересовали только время, скорость и расстояние, которое он проехал. Нам было не важно, как работал двигатель, сколько бензина понадобилось, почему вообще грузовик двигался и тяжелый ли вёз груз.

Решением таких задач занимается кинематика — раздел физики, посвященный моделям движения, которые не учитывают причины движения, а только описывают его. О задачах кинематики и моделях, которые используются для их решения, мы сегодня и будем говорить.

Рассмотрим такую задачу: с горки известной высоты и известного наклона соскальзывает шайба и скатывается шар. На одинаковом ли расстоянии от горки они остановятся?

Рис. 1. Задача на скатывание тел с наклонной поверхности

Может оказаться, что не на одинаковом, даже при одинаковом трении с поверхностью.  Если использовать модель материальной точки и для шайбы, и для шара, то этот результат необъясним.

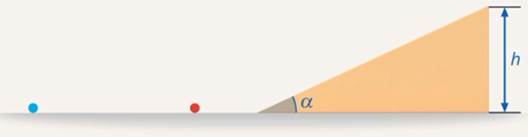
Рис. 2. В модели материальной точки тела неразличимы

Действительно, потенциальная энергия перешла в кинетическую – можем вычислить скорость тела внизу горки, а по ней рассчитать расстояние, на котором они оба остановятся. Чтобы объяснить разные расстояния, нам придётся учесть вращение шара – тогда потенциальная энергия будет расходоваться не только на увеличение кинетической энергии, но и на увеличение энергии вращения шара. В данном случае для шара мы можем применить модель твёрдого тела, в которой различаются поступательное и вращательное движения.

---

 

Поступательное и вращательное движение

Поступательное движение – это такое движение, при котором все точки тела движутся одинаково: с одинаковой скоростью, совершая одинаковое перемещение.

Рис. 3. Поступательное движение

А как еще может быть? Взмахните рукой и проследите: понятно, что ладонь и плечо двигались по-разному. Посмотрите на колесо обозрения: точки вблизи оси почти не движутся, а кабинки движутся с другой скоростью и по другим траекториям.

Рис. 4. Вращательное движение

Посмотрите на прямолинейно движущийся автомобиль: если не учитывать вращение колес и движение частей мотора, все точки автомобиля движутся одинаково, движение автомобиля считаем поступательным. Тогда нет смысла описывать движение каждой точки, можно описать движение одной. Автомобиль считаем материальной точкой. Обратите внимание, что при поступательном движении линия, соединяющая любые две точки тела при движении, остается параллельной сама себе.

Второй вид движения по этой классификации – вращательное движение. При вращательном движении все точки тела движутся по окружности вокруг какой-то одной оси. Эта ось может пересекать тело, как в случае с колесом обозрения, а может не пересекать, как в случае с автомобилем на повороте (рисунок).

Но не любое движение можно отнести к какому-то одному из двух видов. Как описать движение педалей велосипеда относительно земли – это какой-то третий тип? Наша модель удобна тем, что можно рассматривать движение как комбинацию поступательного и вращательного движений: относительно своей оси педали вращаются, а ось вместе со всем велосипедом движется поступательно относительно Земли.

---

Возьмем другой пример: фигуристка вращается на месте, и, когда она прижимает руки к груди, она начинает вращаться значительно быстрее.

Рис. 5. Вращение фигуристки

---

 

Момент инерции

Как узнать, варёное перед нами яйцо или сырое? Можно это определить по вращению. Раскрутить яйцо на столе: варёное будет долго вращаться, а сырое остановится быстрее. Как это объяснить? Для описания вращательного движения ввели понятие момента инерции. Можно провести аналогию с массой.

Масса – это мера инертности при поступательном движении: чтобы разогнать или остановить более тяжелое тело, потребуется бóльшая сила, чем для более легкого тела. Для момента инерции справедливо то же, только описывается вращательное движение и угловая скорость. Кинетическая энергия вращательного движения определяется моментом инерции и угловой скоростью.

Возвращаемся к вращению яйца. У сырого яйца во вращении участвует по сути только скорлупа, её момент инерции меньше, чем момент инерции вареного яйца – сплошного твердого тела. Поэтому и энергия вращения, а значит и время вращения меньше. Мы не учли, что жидкость внутри сырого яйца вязкая и тоже как-то движется, но мы и не делаем точных расчетов, а для сравнения такого предположения достаточно.

Рассмотрим в рамках нашей модели вращение фигуристки. Момент инерции зависит от распределения массы – чем она ближе к оси вращения, тем меньше момент инерции. Прижимая руки к груди, фигуристка меняет распределение массы, и момент инерции уменьшается. И из закона сохранения энергии понятно: если уменьшился момент инерции, увеличилась скорость.

Мы иногда и не замечаем, как используются модели: фигуристка умеет управлять моментом инерции, даже не зная о нём. Задача физики – создать модель, чтобы можно было управлять осознанно. Тогда можно посчитать, как управлять, поставить задачу компьютеру, чтобы он всё рассчитал.

---

В целом ясно, что энергия одного вида движения превращается в энергию другого, и это нельзя описать, считая фигуристку материальной точкой. Как материальная точка она вообще неподвижна.

Как это вращение описать? Удобно использовать то, что уже хорошо разобрали. Обычно, чтобы описать движение тела, достаточно описать движение нескольких его точек, а для описания движения у нас есть готовые инструменты. Например, для катящегося с горки шара можно рассматривать движение одной из точек поверхности относительно центра шара, и движение центра шара относительно горки.

Итак, несколько моделей в нашем наборе инструментов уже есть: это равномерное и равноускоренное прямолинейное движение материальной точки и равномерное движение по окружности. И некоторые задачи мы уже умеем решать.

На уроках математики мы успели овладеть новыми математическими инструментами, такими, как вектор и система координат, с помощью которых мы можем создать более удобные физические модели и решать с их помощью больше задач. Давайте упорядочим информацию о тех инструментах кинематики, которые у нас уже есть, и заодно научимся пользоваться новыми.

Рис. 6. Определение материальной точки

Здесь мы под точкой понимаем то же, что и в геометрии: дать определение точке нельзя, это базовое понятие, но мы можем сформулировать, что мы с её помощью будем описывать – объект, на размеры которого мы при решении данной задачи можем не обращать внимания, но на положение которого мы можем указать. Только в отличие от точки в геометрии, в физике мы ей приписываем еще и массу.

Обратите внимание, что само по себе выражение «материальная точка» — оксюморон (как, например, «живой труп»). Действительно, сама по себе точка не может быть материальной, у неё нет длины, ширины, мы, в принципе, не можем на неё указать. Но в этом и заключается смысл модели – не существовать в реальности, а приближать с достаточной точностью множество реальных ситуаций и помогать их описывать.

Мы говорим о движении, то есть об изменении положения точки со временем. Но изменение положения может быть только относительно других объектов. В жизни, чтобы обозначить положение чего-либо, мы говорим: возле окна, в десяти километрах от города. Можем указать адрес: улица Пушкина, и номер дома и квартиры. Можем указать место в театре: ряд 7, место 15. В зависимости от задачи, которую мы решаем, мы выбираем точку отсчёта и систему координат.

Воспользуемся уже готовым математическим инструментом – декартовой (прямоугольной) системой координат. Но система координат позволяет задать положение точки относительно какого-то объекта, то есть нужно еще задать этот объект – тело отсчета.

Добавим к системе координат и телу отсчета часы, чтобы рассматривать процессы с течением времени, и получим систему отсчета. Раздел физики, механика, занимается решением следующей задачи, которая так и называется:

Основная задача механики – точно определять положение тела в пространстве в любой момент времени.

В этой стандартной формулировке все слова следует пояснить.

1. Абсолютно точно мы в реальном мире ничего не определяем. Точность всегда конечна: иногда нас устраивает определить положение чего-то с точностью до метра, иногда – до миллиметра, а ведь можно и до десятой, и до тысячной доли миллиметра – на чём-то всё равно остановимся. И, как мы уже много раз говорили, точность определяется конкретной задачей, которую мы сейчас решаем.
2. Для тела можно использовать разные модели, мы договорились изучать модель материальной точки.
3. Нас не интересует любой момент времени, нас интересует конкретный период в рамках решаемой задачи. Если автомобиль едет с постоянной скоростью 70 км/ч, то через 5 часов он будет в 350 километрах от начала пути. В решение мы действительно можем подставить любое время и получить ответ: за 10 часов проедет 700 км, а за месяц обогнёт земной шар. Только эти результаты лишены смысла, автомобиль не будет ехать дальше пункта назначения, и уж тем более плыть во время кругосветного путешествия по океану.

На математическом языке основная задача механики звучит так: определить положение точки в п

Кинематика (физика) — это… Что такое Кинематика (физика)?

У этого термина существуют и другие значения, см. Кинематика.

Кинема́тика (греч. κινειν — двигаться) в физике — раздел механики, изучающий математическое описание (средствами геометрии, алгебры, математического анализа…) движения идеализированных тел (материальная точка, абсолютно твердое тело, идеальная жидкость), без рассмотрения причин движения (массы, сил и т. д.). Исходные понятия кинематики — пространство и время. Например, если тело движется по окружности, то кинематика предсказывает необходимость существования центростремительного ускорения без уточнения того, какую природу имеет сила, его порождающая. Причинами возникновения механического движения занимается другой раздел механики — динамика.

Различают классическую кинематику, в которой пространственные (длины отрезков) и временные (промежутки времени) характеристики движения считаются абсолютными, то есть не зависящими от выбора системы отсчёта, и релятивистскую. В последней длины отрезков и промежутки времени между двумя событиями могут изменяться при переходе от одной системы отсчёта к другой. Относительной становится также одновременность. В релятивистской механике вместо отдельных понятий пространство и время вводится понятие пространства-времени, в котором инвариантным относительно преобразований Лоренца является величина, называемая интервалом.

История кинематики

Долгое время понятия о кинематике были основаны на работах Аристотеля, в которых утверждалось, что скорость падения пропорциональна весу тела, а движение в отсутствие сил невозможно. Только в конце XVI века этим вопросом подробно занялся Галилео Галилей. Изучая свободное падение (знаменитые опыты на Пизанской башне) и инерцию тел, он доказал неправильность идей Аристотеля. Итоги своей работы по данной теме он изложил в книге «Беседы и математические доказательства, касающиеся двух новых отраслей науки, относящихся к механике и местному движению»^[1].

Рождением современной кинематики можно считать выступление Пьера Вариньона перед Французской Академией наук 20 января 1700 года. Тогда впервые были даны понятия скорости и ускорения в дифференциальном виде.

В XVIII веке Ампер первый использовал вариационное исчисление в кинематике.

После создания СТО, показывающей, что время и пространство не абсолютны и скорость имеет принципиальное ограничение, кинематика вошла в новый этап развития в рамках релятивистской механики (см. Релятивистская кинематика).

Основные понятия кинематики

Задачи кинематики

Главной задачей кинематики является математическое (уравнениями, графиками, таблицами и т. п.) определение положения и характеристик движения точек или тел во времени. Любое движение рассматривается в определённой системе отсчёта. Также кинематика занимается изучением составных движений (движений в двух взаимно перемещающихся системах отсчёта).

Положение точки (или тела) относительно заданной системы отсчёта определяется некоторым количеством взаимно независимых функций координат:

,

где определяется количеством степеней свободы. Так как точка не может быть в нескольких местах одновременно, все функции должны быть однозначными. Также в классической механике выдвигается требование их дифференцируемости на промежутках. Производные этих функций определяют скорость тела^[2].

Скорость движения определяется как производная координат по времени:

,

где  — единичные векторы, направленные вдоль соответствующих координат.

Ускорение определяется как производная скорости по времени:

Следовательно, характер движения можно определить, зная зависимость скорости и ускорения от времени. А если кроме этого известны ещё и значения скорости/координат в определённый момент времени, то движение полностью задано.

Деление кинематики по типам объекта исследования

В зависимости от свойств изучаемого объекта, кинематика делится на кинематику точки, кинематику твёрдого тела, кинематику деформируемого тела, кинематику газа, кинематику жидкости и т. д.

Кинематика точки

Основная статья: Кинематика точки

Кинематика точки изучает движение материальных точек — тел, размерами которых можно пренебречь по сравнению с характерными размерами изучаемого явления. Поэтому в кинематике точки скорость, ускорение, координаты всех точек тела считаются равными.

Частные случаи движения в кинематике точки:

• Если ускорение равно нулю, движение прямолинейное (траектория представляет собой прямую) и равномерное (скорость постоянна).

,

где  — длина пути траектории за промежуток времени от до ,  — проекции на соответствующие оси координат.

• Если ускорение постоянно и лежит в одной прямой со скоростью, движение прямолинейное, равнопеременное (равноускоренное, если ускорение и скорость направлены в одном направлении; равнозамедленное — если в разные).

,

где  — длина пути траектории за промежуток времени от до ,  — проекции на соответствующие оси координат,  — проекции на соответствующие оси координат.

• Если ускорение постоянно и перпендикулярно скорости, движение происходит по окружности — вращательное движение.

,

где  — радиус окружности, по которой движется тело.

Если выбрать систему декартовых координат xyz так, чтобы центр координат был в центре окружности, по которой движется точка, оси y и x лежали в плоскости этой окружности, так чтобы движение осуществлялось против часовой стрелки, то значения координат можно вычислить по формулам:

Для перехода в другие системы координат используются преобразования Галилея для скоростей намного меньших скорости света, и преобразования Лоренца для скоростей, сравнимых со скоростью света.

• Если ускорение постоянно и не лежит на одной прямой с начальной скоростью, движение параболическое.

Если выбрать систему декартовых координат xyz так, чтобы ускорение и начальная скорость лежали в плоскости xy и ускорение было сонаправленно с осью y, то значения координат можно вычислить по формулам:

,

где и  — проекции на соответствующие оси.

Для перехода в другие системы координат используются преобразования Галилея для скоростей намного меньших скорости света, и преобразования Лоренца для скоростей, сравнимых со скоростью света.

• Если тело выполняет разные движения в разных направлениях, то эти движения могут рассчитываться отдельно и складываться по принципу суперпозиции. Например, если в одной плоскости тело совершает вращательное движение, а по оси, перпендикулярной этой плоскости — равномерное поступательное, то вид движения — винтовая линия с постоянным шагом.

• В общем виде скорость, ускорение и координаты вычисляются по общим формулам (см. задачи кинематики), путь вычисляется по формуле:

Кинематика твёрдого тела

Кинематика твёрдого тела изучает движение абсолютно твёрдых тел (тел, расстояние между двумя любыми точками которого не может изменяться).

Так как любое тело ненулевого объёма имеет бесконечное число точек, и соответственно бесконечное число фиксированных связей между ними, тело имеет 6 степеней свободы и его положение в пространстве определяется шестью координатами (если нет дополнительных условий).

Связь скорости двух точек твердого тела выражается через формулу Эйлера:

,

где  — вектор угловой скорости тела.

Кинематика деформируемого тела, Кинематика жидкости

Основные статьи: Кинематика деформируемого тела, Кинематика жидкости

Кинематика деформируемого тела и кинематика жидкости относятся к кинематике непрерывной среды.

Кинематика газа

Основная статья: Кинематика газа

Кинематика газа изучает деление газа на скопления при движении и описывает движение этих скоплений. В рамках кинематики газа описываются не только основные параметры движения, но и типы движения газа.

Примечания

Литература

• Алешкевич В. А., Деденко Л. Г., Караваев В. А. Механика твердого тела. Лекции. — М.: Изд-во Физического факультета МГУ, 1997.
• Матвеев. А. Н. Механика и теория относительности. — М.: Высшая школа, 1986. (3-е изд. М.: ОНИКС 21 век: Мир и Образование, 2003. — 432с.)
• Павленко Ю. Г. Лекции по теоретической механике. — М.: ФИЗМАТЛИТ, 2002. — 392 с.
• Сивухин Д. В. Общий курс физики. В 5 т. Том I. Механика. 4-е изд. — М.: ФИЗМАТЛИТ; Изд-во МФТИ, 2005. — 560с.
• Стрелков С. П. Механика. — М.: Наука, 1975.
• Яворский Б. М., Детлаф А. А. Справочник по физике для инженеров и студентов вузов (4-е изд.). — М.: Наука, 1968.

Кинематика (физика) — это… Что такое Кинематика (физика)?

У этого термина существуют и другие значения, см. Кинематика.

Кинема́тика (греч. κινειν — двигаться) в физике — раздел механики, изучающий математическое описание (средствами геометрии, алгебры, математического анализа…) движения идеализированных тел (материальная точка, абсолютно твердое тело, идеальная жидкость), без рассмотрения причин движения (массы, сил и т. д.). Исходные понятия кинематики — пространство и время. Например, если тело движется по окружности, то кинематика предсказывает необходимость существования центростремительного ускорения без уточнения того, какую природу имеет сила, его порождающая. Причинами возникновения механического движения занимается другой раздел механики — динамика.

Различают классическую кинематику, в которой пространственные (длины отрезков) и временные (промежутки времени) характеристики движения считаются абсолютными, то есть не зависящими от выбора системы отсчёта, и релятивистскую. В последней длины отрезков и промежутки времени между двумя событиями могут изменяться при переходе от одной системы отсчёта к другой. Относительной становится также одновременность. В релятивистской механике вместо отдельных понятий пространство и время вводится понятие пространства-времени, в котором инвариантным относительно преобразований Лоренца является величина, называемая интервалом.

История кинематики

Долгое время понятия о кинематике были основаны на работах Аристотеля, в которых утверждалось, что скорость падения пропорциональна весу тела, а движение в отсутствие сил невозможно. Только в конце XVI века этим вопросом подробно занялся Галилео Галилей. Изучая свободное падение (знаменитые опыты на Пизанской башне) и инерцию тел, он доказал неправильность идей Аристотеля. Итоги своей работы по данной теме он изложил в книге «Беседы и математические доказательства, касающиеся двух новых отраслей науки, относящихся к механике и местному движению»^[1].

Рождением современной кинематики можно считать выступление Пьера Вариньона перед Французской Академией наук 20 января 1700 года. Тогда впервые были даны понятия скорости и ускорения в дифференциальном виде.

В XVIII веке Ампер первый использовал вариационное исчисление в кинематике.

После создания СТО, показывающей, что время и пространство не абсолютны и скорость имеет принципиальное ограничение, кинематика вошла в новый этап развития в рамках релятивистской механики (см. Релятивистская кинематика).

Основные понятия кинематики

Задачи кинематики

Главной задачей кинематики является математическое (уравнениями, графиками, таблицами и т. п.) определение положения и характеристик движения точек или тел во времени. Любое движение рассматривается в определённой системе отсчёта. Также кинематика занимается изучением составных движений (движений в двух взаимно перемещающихся системах отсчёта).

Положение точки (или тела) относительно заданной системы отсчёта определяется некоторым количеством взаимно независимых функций координат:

,

где определяется количеством степеней свободы. Так как точка не может быть в нескольких местах одновременно, все функции должны быть однозначными. Также в классической механике выдвигается требование их дифференцируемости на промежутках. Производные этих функций определяют скорость тела^[2].

Скорость движения определяется как производная координат по времени:

,

где  — единичные векторы, направленные вдоль соответствующих координат.

Ускорение определяется как производная скорости по времени:

Следовательно, характер движения можно определить, зная зависимость скорости и ускорения от времени. А если кроме этого известны ещё и значения скорости/координат в определённый момент времени, то движение полностью задано.

Деление кинематики по типам объекта исследования

В зависимости от свойств изучаемого объекта, кинематика делится на кинематику точки, кинематику твёрдого тела, кинематику деформируемого тела, кинематику газа, кинематику жидкости и т. д.

Кинематика точки

Основная статья: Кинематика точки

Кинематика точки изучает движение материальных точек — тел, размерами которых можно пренебречь по сравнению с характерными размерами изучаемого явления. Поэтому в кинематике точки скорость, ускорение, координаты всех точек тела считаются равными.

Частные случаи движения в кинематике точки:

• Если ускорение равно нулю, движение прямолинейное (траектория представляет собой прямую) и равномерное (скорость постоянна).

,

где  — длина пути траектории за промежуток времени от до ,  — проекции на соответствующие оси координат.

• Если ускорение постоянно и лежит в одной прямой со скоростью, движение прямолинейное, равнопеременное (равноускоренное, если ускорение и скорость направлены в одном направлении; равнозамедленное — если в разные).

,

где  — длина пути траектории за промежуток времени от до ,  — проекции на соответствующие оси координат,  — проекции на соответствующие оси координат.

• Если ускорение постоянно и перпендикулярно скорости, движение происходит по окружности — вращательное движение.

,

где  — радиус окружности, по которой движется тело.

Если выбрать систему декартовых координат xyz так, чтобы центр координат был в центре окружности, по которой движется точка, оси y и x лежали в плоскости этой окружности, так чтобы движение осуществлялось против часовой стрелки, то значения координат можно вычислить по формулам:

Для перехода в другие системы координат используются преобразования Галилея для скоростей намного меньших скорости света, и преобразования Лоренца для скоростей, сравнимых со скоростью света.

• Если ускорение постоянно и не лежит на одной прямой с начальной скоростью, движение параболическое.

Если выбрать систему декартовых координат xyz так, чтобы ускорение и начальная скорость лежали в плоскости xy и ускорение было сонаправленно с осью y, то значения координат можно вычислить по формулам:

,

где и  — проекции на соответствующие оси.

Для перехода в другие системы координат используются преобразования Галилея для скоростей намного меньших скорости света, и преобразования Лоренца для скоростей, сравнимых со скоростью света.

• Если тело выполняет разные движения в разных направлениях, то эти движения могут рассчитываться отдельно и складываться по принципу суперпозиции. Например, если в одной плоскости тело совершает вращательное движение, а по оси, перпендикулярной этой плоскости — равномерное поступательное, то вид движения — винтовая линия с постоянным шагом.

• В общем виде скорость, ускорение и координаты вычисляются по общим формулам (см. задачи кинематики), путь вычисляется по формуле:

Кинематика твёрдого тела

Кинематика твёрдого тела изучает движение абсолютно твёрдых тел (тел, расстояние между двумя любыми точками которого не может изменяться).

Так как любое тело ненулевого объёма имеет бесконечное число точек, и соответственно бесконечное число фиксированных связей между ними, тело имеет 6 степеней свободы и его положение в пространстве определяется шестью координатами (если нет дополнительных условий).

Связь скорости двух точек твердого тела выражается через формулу Эйлера:

,

где  — вектор угловой скорости тела.

Кинематика деформируемого тела, Кинематика жидкости

Основные статьи: Кинематика деформируемого тела, Кинематика жидкости

Кинематика деформируемого тела и кинематика жидкости относятся к кинематике непрерывной среды.

Кинематика газа

Основная статья: Кинематика газа

Кинематика газа изучает деление газа на скопления при движении и описывает движение этих скоплений. В рамках кинематики газа описываются не только основные параметры движения, но и типы движения газа.

Примечания

Литература

• Алешкевич В. А., Деденко Л. Г., Караваев В. А. Механика твердого тела. Лекции. — М.: Изд-во Физического факультета МГУ, 1997.
• Матвеев. А. Н. Механика и теория относительности. — М.: Высшая школа, 1986. (3-е изд. М.: ОНИКС 21 век: Мир и Образование, 2003. — 432с.)
• Павленко Ю. Г. Лекции по теоретической механике. — М.: ФИЗМАТЛИТ, 2002. — 392 с.
• Сивухин Д. В. Общий курс физики. В 5 т. Том I. Механика. 4-е изд. — М.: ФИЗМАТЛИТ; Изд-во МФТИ, 2005. — 560с.
• Стрелков С. П. Механика. — М.: Наука, 1975.
• Яворский Б. М., Детлаф А. А. Справочник по физике для инженеров и студентов вузов (4-е изд.). — М.: Наука, 1968.