Конспект «Кинетическая и потенциальная энергия»

«Кинетическая и потенциальная  энергия»

Код ОГЭ 1.17. Кинетическая и потенциальная  энергия. Формула для вычисления кинетической энергии. Формула для вычисления потенциальной энергии тела, поднятого над Землей.

---

---

Энергия – физическая величина, характеризующая состояние тела или системы тел. Причиной изменения состояния системы тел (изменения энергии) является работа внешних по отношению к рассматриваемой системе сил. В механике энергия тела или системы тел определяется взаимным положением тел (потенциальная энергия) и их скоростями (кинетическая энергия).

Единица измерения энергии в СИ – джоуль.

 Кинетическая энергия – часть механической энергии, энергия движущегося тела. Скалярная величина, численно равная половине произведения массы тела на квадрат скорости: 

Теорема о кинетической энергии

: Работа, совершаемая силой при изменении скорости тела, равна изменению кинетической энергии тела: A = W_k2 – W_k1 = ΔW_k.

Причём если А > 0, то W_k увеличивается, и если А < 0, то W_k уменьшается.
Эта теорема справедлива для любого движения и для сил любой природы.

Кинетическая энергия – величина относительная, зависящая от выбора СО, так как скорость тела зависит от выбора СО. Если тело разгоняется из состояния покоя, то W_k1 = 0, А = W_k2. Следовательно, физический смысл кинетической энергии: кинетическая энергия численно равна работе, которую необходимо совершить, чтобы разогнать тело из состояния покоя до данной скорости.

 Внимание! Кинетическая энергия механической системы тел равна сумме кинетических энергий всех частей системы.

 Потенциальная энергия – часть механической энергии тела (системы тел), энергия взаимодействия тел или частей тела. Потенциальная энергия определяется взаимным расположением тел или частей тела, то есть расстояниями между ними.

Потенциальная энергия относительна, зависит от выбора системы отсчёта, в частности от выбора тела отсчёта, которому соответствует нулевой уровень потенциальной энергии.

Потенциальная энергия тела в поле силы тяжести численно равна произведению массы тела на ускорение свободного падения и на высоту относительно выбранного нулевого уровня: W_п = mgh.

Связь работы силы тяжести и изменения потенциальной энергии:
A = mg (h₁ – h₂) = – (mgh₂ – mgh₂) = – (Wп2 – Wп1) = – ΔW

п

 Внимание! Работа сила тяжести равна изменению потенциальной энергии тела в поле силы тяжести, взятому с противоположным знаком.

---

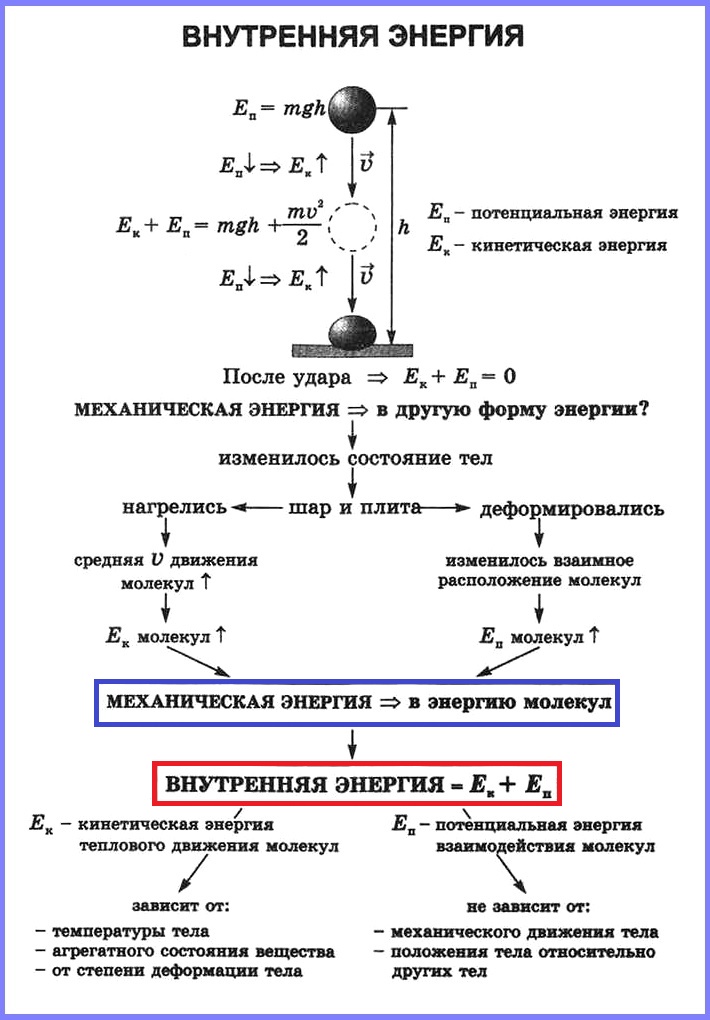
Конспект урока «Кинетическая и потенциальная  энергия».

Следующая тема: «Механическая энергия».

 

uchitel.pro

Кинетическая энергия | Все Формулы

   

Кинетическая энергия — скалярная физическая величи­на, равная половине произведения массы тела на квадрат его скорости.

   

Что бы понять, что же такое кинетическая энергия тела, рассмотрим случай, когда тело массой m под действием постоянной силы (F=const) движется прямолинейно равноускоренно (а=const). Определим работу силы, приложенной к телу, при изменении модуля скорости этого тела от v1 до v2.

Кинетическая-энергия-тела

Как мы знаем, работа постоянной силы вычисляют по формуле

   

. Так как в рассматриваемом нами случае направление силы F и перемещения s совпадают, то

   

, и тогда у нас получается, что работа силы равна

   

. По второму закону Ньютона найдем силу F=ma. Для прямолинейного равноускоренного движения справедлива формула:

   

Из это формулы мы выражаем перемещение тела:

   

Подставляем найденные значения F и S в формулу работы, и получаем:

   

Из последней формулы видно, что работа силы, приложенной к телу, при изменении скорости этого тела равна разности двух значений некоторой величины

   

. А механическая работа это и есть мера изменения энергии. Следовательно, в правой части формулы стоит разность двух значений энергии данного тела. Это значит, что величина

   

представляет собой энергию, обусловленную движением тела. Эту энергию называют кинетической. Она обозначается Wк.

   

Если взять выведенную нами формулу работы, то у нас получится

   

Работа, совершаемая силой при изменении скорости тела, равна изменению кинетической энергии этого тела

Так же есть :

Потенциальная энергия :

   

В формуле мы использовали :

   

— Кинетическая энергия

m — Масса тела

   

— Скорость движения тела

   

— Начальная скорость тела

   

— Конечная скорость тела

A — Работа тела

a — Ускорение тела

F — Сила, действующая на тело

S — Перемещение тела

xn—-ctbjzeloexg6f.xn--p1ai

Формула кинетической энергии в физике

Определение и формула кинетической энергии

Определение

Кинетическую энергию тела определяют при помощи работы, которая совершается телом при его торможении от начальной скорости, до скорости, равной нулю.

Кинетическая энергия тела – мера механического движения тела. Она зависит от относительной скорости тел.

Встречаются следующие обозначения кинетической энергии: E_k,W_k,T.

Работу, которую производят над телом (A’) можно связать с изменением его кинетической энергии:

Кинетическая энергия материальной точки и тела

Кинетическая энергия материальной точки равна:

где m – масса материальной точки, p – импульс материальной точки, v – скорость ее движения. Кинетическая энергия является скалярной физической величиной.

Если тело нельзя принять за материальную точку, то его кинетическая энергия рассчитывается как сумма кинетических энергий всех материальных точек, которые составляют исследуемое тело:

где dm – элементарный участок тела, который можно считать материальной точкой, dV – объем выделенного элементарного участка тела, v – скорость перемещения рассматриваемого элемента, — плотность участка, m–масса всего рассматриваемого тела, V – объем тела.

В том случае, если тело (отличное от материальной точки) движется поступательно, то его кинетическую энергию можно рассчитать, применяя формулу (2), в которой все параметры отнесены к телу в целом.

При вращении тело вокруг неподвижной оси его кинетическую энергию можно вычислить, применяя формулу:

где J – момент инерции тела по отношению к оси вращения, ?–модуль угловой скорости вращения тела, r – расстояние от элементарного участка тела до оси вращения, L – проекция момента импульса вращающегося тела на ось во круг которой идет вращение.

Если твердое тело совершает вращение относительно неподвижной точки (например, точки O), то его кинетическую энергию находят как:

где – момент импульса рассматриваемого тела относительно точки О.

Единицы измерения кинетической энергии

Основной единицей измерения кинетической энергии (как и любого другого вида энергии) в системе СИ служит:

[E_k]=Дж (джоуль),

в системе СГС –[E_k]= эрг.

При этом: 1 дж= 10⁷ эрг.

Теорема Кенига

Для самого общего случая при расчете кинетической энергии применяют теорему Кенига. В соответствии с которой, кинетическая энергия совокупности материальных точек есть сумма кинетической энергии поступательного перемещения системы со скоростью центра масс (v_c) и кинетической энергии (E’_k) системы при ее относительном движении к поступательному перемещению системы отсчета. При этом начало системы отсчета связывают с центром масс системы. Математически данную теорему можно записать как:

где –суммарная масса системы материальных точек.

Так, если рассматривать твердое тело, то его кинетическую энергию можно представить как:

www.webmath.ru

Потенциальная и кинетическая энергия. Закон сохранения механической энергии

1. Камень, упав с некоторой высоты на Землю, оставляет на поверхности Земли вмятину. Во время падения он совершает работу по преодолению сопротивления воздуха, а после касания земли — работу по преодолению силы сопротивления почвы, поскольку обладает энергией. Если накачивать в закрытую пробкой банку воздух, то при некотором давлении воздуха пробка вылетит из банки, при этом воздух совершит работу по преодолению трения пробки о горло банки, благодаря тому, что воздух обладает энергией. Таким образом, тело может совершить работу, если оно обладает энергией. Энергию обозначают буквой ​\( E \)​. Единица работы — ​\( [E\,] \)​ = 1 Дж.

При совершении работы изменяется состояние тела и изменяется его энергия. Изменение энергии равно совершенной работе: ​\( E=A \)​.

2. Потенциальной энергией называют энергию взаимодействия тел или частей тела, зависящую от их взаимного положения.

Поскольку тела взаимодействуют с Землёй, то они обладают потенциальной энергия взаимодействия с Землёй.

Если тело массой ​\( m \)​ падает с высоты ​\( h_1 \)​ до высоты ​\( h_2 \)​, то работа силы тяжести ​\( F_т \)​ на участке ​\( h=h_1-h_2 \)​ равна: ​\( A = F_тh = mgh = mg(h_1 — h_2) \)​ или \( A = mgh_1 — mgh_2 \) (рис. 48).

В полученной формуле ​\( mgh_1 \)​ характеризует начальное положение (состояние) тела, \( mgh_2 \) характеризует конечное положение (состояние) тела. Величина \( mgh_1=E_{п1} \) — потенциальная энергия тела в начальном состоянии; величина \( mgh_2=E_{п2} \) — потенциальная энергия тела в конечном состоянии.

Можно записать ​\( A=E_{п1}-E_{п2} \)​, или \( A=-(E_{п2}-E_{п1}) \), или \( A=-E_{п} \).

Таким образом, работа силы тяжести равна изменению потенциальной энергии тела. Знак «–» означает, что при движении тела вниз и соответственно при совершении силой тяжести положительной работы потенциальная энергия тела уменьшается. Если тело поднимается вверх, то работа силы тяжести отрицательна, а потенциальная энергия тела увеличивается.

Если тело находится на некоторой высоте ​\( h \)​ относительно поверхности Земли, то его потенциальная энергия в данном состоянии равна ​\( E_п=mgh \)​. Значение потенциальной энергии зависит от того, относительно какого уровня она отсчитывается. Уровень, на котором потенциальная энергия равна нулю, называют нулевым уровнем.

В отличие от кинетической энергии потенциальной энергией обладают покоящиеся тела. Поскольку потенциальная энергия — это энергия взаимодействия, то она относится не к одному телу, а к системе взаимодействующих тел. В данном случае эту систему составляют Земля и поднятое над ней тело.

3. Потенциальной энергией обладают упруго деформированные тела. Предположим, что левый конец пружины закреплён, а к правому её концу прикреплён груз. Если пружину сжать, сместив правый её конец на ​\( x_1 \)​, то в пружине возникнет сила упругости ​\( F_{упр1} \)​, направленная вправо (рис. 49).

Если теперь предоставить пружину самой себе, то её правый конец переместится, удлинение пружины будет равно \( x_2 \)​, а сила упругости \( F_{упр2} \).

Работа силы упругости равна

\[ A=F_{ср}(x_1-x_2)=k/2(x_1+x_2)(x_1-x_2)=kx_1^2/2-kx_2^2/2 \]

​\( kx_1^2/2=E_{п1} \)​ — потенциальная энергия пружины в начальном состоянии, \( kx_2^2/2=E_{п2} \) — потенциальная энергия пружины во конечном состоянии. Работа силы упругости равна изменению потенциальной энергии пружины.

Можно записать ​\( A=E_{п1}-E_{п2} \)​, или \( A=-(E_{п2}-E_{п1}) \), или \( A=-E_{п} \).

Знак «–» показывает, что при растяжении и сжатии пружины сила упругости совершает отрицательную работу, потенциальная энергия пружины увеличивается, а при движении пружины к положению равновесия сила упругости совершает положительную работа, а потенциальная энергия уменьшается.

Если пружина деформирована и её витки смещены относительно положения равновесия на расстояние ​\( x \)​, то потенциальная энергия пружины в данном состоянии равна ​\( E_п=kx^2/2 \)​.

4. Движущиеся тела так же могут совершить работу. Например, движущийся поршень сжимает находящийся в цилиндре газ, движущийся снаряд пробивает мишень и т.п. Следовательно, движущиеся тела обладают энергией. Энергия, которой обладает движущееся тело, называется кинетической энергией. Кинетическая энергия ​\( E_к \)​ зависит от массы тела и его скорости \( E_к=mv^2/2 \). Это следует из преобразования формулы работы.

Работа ​\( A=FS \)​. Сила ​\( F=ma \)​. Подставив это выражение в формулу работы, получим ​\( A=maS \)​. Так как ​\( 2aS=v^2_2-v^2_1 \)​, то ​\( A=m(v^2_2-v^2_1)/2 \)​ или \( A=mv^2_2/2-mv^2_1/2 \), где ​\( mv^2_1/2=E_{к1} \)​ — кинетическая энергия тела в первом состоянии, \( mv^2_2/2=E_{к2} \) — кинетическая энергия тела во втором состоянии. Таким образом, работа силы равна изменению кинетической энергии тела: ​\( A=E_{к2}-E_{к1} \)​, или ​\( A=E_к \)​. Это утверждение — теорема о кинетической энергии.

Если сила совершает положительную работу, то кинетическая энергия тела увеличивается, если работа силы отрицательная, то кинетическая энергия тела уменьшается.

5. Полная механическая энергия ​\( E \)​ тела — физическая величина, равная сумме его потенциальной ​\( E_п \)​ и кинетической \( E_п \) энергии: \( E=E_п+E_к \).

Пусть тело падает вертикально вниз и в точке А находится на высоте ​\( h_1 \)​ относительно поверхности Земли и имеет скорость ​\( v_1 \)​ (рис. 50). В точке В высота тела \( h_2 \) и скорость \( v_2 \) Соответственно в точке А тело обладает потенциальной энергией ​\( E_{п1} \)​ и кинетической энергией \( E_{к1} \), а в точке В — потенциальной энергией \( E_{п2} \) и кинетической энергией \( E_{к2} \).

При перемещении тела из точки А в точку В сила тяжести совершает работу, равную А. Как было показано, ​\( A=-(E_{п2}-E_{п1}) \)​, а также \( A=E_{к2}-E_{к1} \). Приравняв правые части этих равенств, получаем: ​\( -(E_{п2}-E_{п1})=E_{к2}-E_{к1} \)​, откуда \( E_{к1}+E_{п1}=E_{п2}+E_{к2} \) или ​\( E_1=E_2 \)​.

Это равенство выражает закон сохранения механической энергии: полная механическая энергия замкнутой системы тел, между которыми действуют консервативные силы (силы тяготения или упругости) сохраняется.

В реальных системах действуют силы трения, которые не являются консервативными, поэтому в таких системах полная механическая энергия не сохраняется, она превращается во внутреннюю энергию.

ПРИМЕРЫ ЗАДАНИЙ

Часть 1

1. Два тела находятся на одной и той же высоте над поверхностью Земли. Масса одного тела ​\( m_1 \)​ в три раза больше массы другого тела ​\( m_2 \)​. Относительно поверхности Земли потенциальная энергия

1) первого тела в 3 раза больше потенциальной энергии второго тела
2) второго тела в 3 раза больше потенциальной энергии первого тела
3) первого тела в 9 раз больше потенциальной энергии второго тела
4) второго тела в 9 раз больше потенциальной энергии первого тела

2. Сравните потенциальную энергию мяча на полюсе ​\( E_п \)​ Земли и на широте Москвы ​\( E_м \)​, если он находится на одинаковой высоте относительно поверхности Земли.

1) ​\( E_п=E_м \)​
2) \( E_п>E_м \)
3) \( E_п<E_м \)
4) \( E_п\geq E_м \)

3. Тело брошено вертикально вверх. Его потенциальная энергия

1) одинакова в любые моменты движения тела
2) максимальна в момент начала движения
3) максимальна в верхней точке траектории
4) минимальна в верхней точке траектории

4. Как изменится потенциальная энергия пружины, если её удлинение уменьшить в 4 раза?

1) увеличится в 4 раза
2) увеличится в 16 раз
3) уменьшится в 4 раза
4) уменьшится в 16 раз

5. Лежащее на столе высотой 1 м яблоко массой 150 г подняли относительно стола на 10 см. Чему стала равной потенциальная энергия яблока относительно пола?

1) 0,15 Дж
2) 0,165 Дж
3) 1,5 Дж
4) 1,65 Дж

6. Скорость движущегося тела уменьшилась в 4 раза. При этом его кинетическая энергия

1) увеличилась в 16 раз
2) уменьшилась в 16 раз
3) увеличилась в 4 раза
4) уменьшилась в 4 раза

7. Два тела движутся с одинаковыми скоростями. Масса второго тела в 3 раза больше массы первого. При этом кинетическая энергия второго тела

1) больше в 9 раз
2) меньше в 9 раз
3) больше в 3 раза
4) меньше в 3 раза

8. Тело падает на пол с поверхности демонстрационного стола учителя. (Сопротивление воздуха не учитывать.) Кинетическая энергия тела

1) минимальна в момент достижения поверхности пола
2) минимальна в момент начала движения
3) одинакова в любые моменты движения тела
4) максимальна в момент начала движения

9. Книга, упавшая со стола на пол, обладала в момент касания пола кинетической энергией 2,4 Дж. Высота стола 1,2 м. Чему равна масса книги? Сопротивлением воздуха пренебречь.

1) 0,2 кг
2) 0,288 кг
3) 2,0 кг
4) 2,28 кг

10. С какой скоростью следует бросить тело массой 200 г с поверхности Земли вертикально вверх, чтобы его потенциальная энергия в наивысшей точке движения была равна 0,9 Дж? Сопротивлением воздуха пренебречь. Потенциальную энергию тела отсчитывать от поверхности земли.

1) 0,9 м/с
2) 3,0 м/с
3) 4,5 м/с
4) 9,0 м/с

11. Установите соответствие между физической величиной (левый столбец) и формулой, по которой она вычисляется (правый столбец). В ответе запишите подряд номера выбранных ответов

ФИЗИЧЕСКАЯ ВЕЛИЧИНА
A. Потенциальная энергия взаимодействия тела с Землёй
Б. Кинетическая энергия
B. Потенциальная энергия упругой деформации

ХАРАКТЕР ИЗМЕНЕНИЯ ЭНЕРГИИ
1) ​\( E=mv^2/2 \)​
2) \( E=kx^2/2 \)​
3) \( E=mgh \)​

12. Мяч бросили вертикально вверх. Установите соответствие между энергией мяча (левый столбец) и характером её изменения (правый столбец) при растяжении пружины динамометра. В ответе запишите подряд номера выбранных ответов.

ФИЗИЧЕСКАЯ ВЕЛИЧИНА
A. Потенциальная энергия
Б. Кинетическая энергия
B. Полная механическая энергия

ХАРАКТЕР ИЗМЕНЕНИЯ ЭНЕРГИИ
1) Уменьшается
2) Увеличивается
3) Не изменяется

Часть 2

13. Пуля массой 10 г, движущаяся со скоростью 700 м/с, пробила доску толщиной 2,5 см и при выходе из доски имела скорость 300 м/с. Определить среднюю силу сопротивления, воздействующую на пулю в доске.

Ответы

Потенциальная и кинетическая энергия. Закон сохранения механической энергии

Оценка

fizi4ka.ru

Кинетическая энергия — Википедия

Кинети́ческая эне́ргия — скалярная функция, являющаяся мерой движения материальных точек, образующих рассматриваемую механическую систему, и зависящая только от масс и модулей скоростей этих точек^[1]. Для движения со скоростями значительно меньше скорости света кинетическая энергия записывается как

T=∑mivi22{\displaystyle T=\sum {{m_{i}v_{i}^{2}} \over 2}},

где индекс  i{\displaystyle \ i} нумерует материальные точки. Часто выделяют кинетическую энергию поступательного и вращательного движения^[2]. Более строго, кинетическая энергия есть разность между полной энергией системы и её энергией покоя; таким образом, кинетическая энергия — часть полной энергии, обусловленная движением^[3]. Когда тело не движется, его кинетическая энергия равна нулю. Возможные обозначения кинетической энергии: T{\displaystyle T}, Ekin{\displaystyle E_{kin}}, K{\displaystyle K} и другие. В системе СИ она измеряется в джоулях (Дж).

История понятия

Впервые понятие кинетической энергии было введено в трудах Готфрида Лейбница (1695 г.), посвящённых понятию «живой силы»^[4].

Видео по теме

Кинетическая энергия в классической механике

Случай одной материальной точки

По определению, кинетической энергией материальной точки массой m{\displaystyle m} называется величина

T=mv22{\displaystyle T={{mv^{2}} \over 2}},

при этом предполагается, что скорость точки v{\displaystyle v} всегда значительно меньше скорости света. С использованием понятия импульса (p→=mv→{\displaystyle {\vec {p}}=m{\vec {v}}}) данное выражение примет вид  T=p2/2m{\displaystyle \ T=p^{2}/2m}.

Если F→{\displaystyle {\vec {F}}} — равнодействующая всех сил, приложенных к точке, выражение второго закона Ньютона запишется как F→=ma→{\displaystyle {\vec {F}}=m{\vec {a}}}. Скалярно умножив его на перемещение материальной точки ds→=v→dt{\displaystyle {\rm {d}}{\vec {s}}={\vec {v}}{\rm {d}}t} и учитывая, что a→=dv→/dt{\displaystyle {\vec {a}}={\rm {d}}{\vec {v}}/{\rm {d}}t}, причём d(v2)/dt=d(v→⋅v→)/dt=2v→⋅dv→/dt{\displaystyle {\rm {d}}(v^{2})/{\rm {d}}t={\rm {d}}({\vec {v}}\cdot {\vec {v}})/{\rm {d}}t=2{\vec {v}}\cdot {\rm {d}}{\vec {v}}/{\rm {d}}t}, получим  F→ds→=d(mv2/2)=dT{\displaystyle \ {\vec {F}}{\rm {d}}{\vec {s}}={\rm {d}}(mv^{2}/2)={\rm {d}}T}.

Если система замкнута (внешние силы отсутствуют) или равнодействующая всех сил равна нулю, то стоящая под дифференциалом величина  T{\displaystyle \ T} остаётся постоянной, то есть кинетическая энергия является интегралом движения.

Случай абсолютно твёрдого тела

При рассмотрении движения абсолютно твёрдого тела его можно представить как совокупность материальных точек. Однако, обычно кинетическую энергию в таком случае записывают, используя формулу Кёнига, в виде суммы кинетических энергий поступательного движения объекта как целого и вращательного движения:

T=Mv22+Iω22.{\displaystyle T={\frac {Mv^{2}}{2}}+{\frac {I\omega ^{2}}{2}}.}

Здесь  M{\displaystyle \ M} — масса тела,  v{\displaystyle \ v} — скорость центра масс, ω→{\displaystyle {\vec {\omega }}} и I{\displaystyle I} — угловая скорость тела и его момент инерции относительно мгновенной оси, проходящей через центр масс^[5].

Кинетическая энергия в гидродинамике

В гидродинамике вместо массы материальной точки рассматривают массу единицы объёма, то есть плотность жидкости или газа ρ=dM/dV{\displaystyle \rho ={\rm {d}}M/{\rm {d}}V}. Тогда кинетическая энергия, приходящаяся на единицу объёма, двигающегося со скоростью v→{\displaystyle {\vec {v}}}, то есть плотность кинетической энергии wT=dT/dV{\displaystyle w_{T}={\rm {d}}T/{\rm {d}}V} (Дж/м³), запишется:

wT=ρvαvα2,{\displaystyle w_{T}=\rho {\frac {v_{\alpha }v_{\alpha }}{2}},}

где по повторяющемуся индексу α=x,y,z{\displaystyle {\alpha }=x,y,z}, означающему соответствующую проекцию скорости, предполагается суммирование.

Поскольку в турбулентном потоке жидкости или газа характеристики состояния вещества (в том числе, плотность и скорость) подвержены хаотическим пульсациям, физический интерес представляют осреднённые величины. Влияние гидродинамических флуктуаций на динамику потока учитывается методами статистической гидромеханики, в которой уравнения движения, описывающие поведение средних характеристик потока, в соответствии с методом О. Рейнольдса, получаются путём осреднения уравнений Навье-Стокса^[6]. Если, в согласии с методом Рейнольдса, представить  ρ=ρ¯+ρ′{\displaystyle \ \rho ={\overline {\rho }}+\rho ‘}, vα=vα¯+vα′{\displaystyle v_{\alpha }={\overline {v_{\alpha }}}+v’_{\alpha }}, где черта сверху — знак осреднения, а штрих — отклонения от среднего, то плотность кинетической энергии приобретёт вид:

wT¯=12ρvαvα¯=Es+Est+Et,{\displaystyle {\overline {w_{T}}}={\frac {1}{2}}{\overline {\rho v_{\alpha }v_{\alpha }}}=E_{s}+E_{st}+E_{t},}

где Es=ρ¯vα¯vα¯/2{\displaystyle E_{s}={\overline {\rho }}\,{\overline {v_{\alpha }}}\,{\overline {v_{\alpha }}}/2} — плотность кинетической энергии, связанной с упорядоченным движением жидкости или газа, Et=ρ¯vα′vα′¯/2+ρ′vα′vα′¯/2{\displaystyle E_{t}={\overline {\rho }}\,{\overline {v’_{\alpha }\,v’_{\alpha }}}/2+{\overline {\rho ‘v’_{\alpha }v’_{\alpha }}}/2} — плотность кинетической энергии, связанной с неупорядоченным движением («плотность кинетической энергии турбулентности»^[6], часто называемой просто «энергией турбулентности»), а Est=Sαvα¯{\displaystyle E_{st}=S_{\alpha }{\overline {v_{\alpha }}}} — плотность кинетической энергии, связанная с турбулентным потоком вещества (Sα=ρ′vα′¯{\displaystyle S_{\alpha }={\overline {\rho ‘v’_{\alpha }}}} — плотность флуктуационного потока массы, или «плотность турбулентного импульса»). Эти формы кинетической энергии жидкости обладают разными трансформационными свойствами при преобразовании Галилея: кинетическая энергия упорядоченного движения Es{\displaystyle E_{s}} зависит от выбора системы координат, в то время как кинетическая энергия турбулентности Et{\displaystyle E_{t}} от него не зависит. В этом смысле кинетическая энергия турбулентности дополняет понятие внутренней энергии.

Подразделение кинетической энергии на упорядоченную и неупорядоченную (флуктуационную) части зависит от выбора масштаба осреднения по объёму или по времени. Так, например, крупные атмосферные вихри циклоны и антициклоны, порождающие определённую погоду в месте наблюдения, рассматриваются в метеорологии как упорядоченное движение атмосферы, в то время как с точки зрения общей циркуляции атмосферы и теории климата это — просто большие вихри, относимые к неупорядоченному движению атмосферы.

В квантовой механике кинетическая энергия представляет собой оператор, записывающийся, по аналогии с классической записью, через импульс, который в этом случае также является оператором (p^=−jℏ∇{\displaystyle {\hat {p}}=-j\hbar \nabla },  j{\displaystyle \ j} — мнимая единица):

T^=p^22m=−ℏ22mΔ{\displaystyle {\hat {T}}={\frac {{\hat {p}}^{2}}{2m}}=-{\frac {\hbar ^{2}}{2m}}\Delta }

где ℏ{\displaystyle \hbar } — редуцированная постоянная Планка, ∇{\displaystyle \nabla } — оператор набла, Δ{\displaystyle \Delta } — оператор Лапласа. Кинетическая энергия в таком виде входит в важнейшее уравнение квантовой механики — уравнение Шрёдингера^[7].

Если в задаче допускается движение со скоростями, близкими к скорости света, кинетическая энергия материальной точки определяется как

T=mc21−v2/c2−mc2,{\displaystyle T={\frac {mc^{2}}{\sqrt {1-v^{2}/c^{2}}}}-mc^{2},}

где  m{\displaystyle \ m} — масса,  v{\displaystyle \ v} — скорость движения в выбранной инерциальной системе отсчёта,  c{\displaystyle \ c} — скорость света в вакууме (mc2{\displaystyle mc^{2}} — энергия покоя). Как и в классическом случае, имеет место соотношение  F→ds→=dT{\displaystyle \ {\vec {F}}{\rm {d}}{\vec {s}}={\rm {d}}T}, получаемое посредством умножения на ds→=v→dt{\displaystyle {\rm {d}}{\vec {s}}={\vec {v}}{\rm {d}}t} выражения второго закона Ньютона (в виде  F→=m⋅d(v→/1−v2/c2)/dt{\displaystyle \ {\vec {F}}=m\cdot {\rm {d}}({\vec {v}}/{\sqrt {1-v^{2}/c^{2}}})/{\rm {d}}t}).

Выражение для  T{\displaystyle \ T} можно переписать в форме T=mv2/(1−v2/c2+1−v2/c2).{\displaystyle T=mv^{2}/(1-v^{2}/c^{2}+{\sqrt {1-v^{2}/c^{2}}}).} При малых скоростях (v≪c{\displaystyle v\ll c}) оно переходит в классическую формулу  T=1/2⋅mv2{\displaystyle \ T=1/2\cdot mv^{2}}.

Свойства кинетической энергии

• Аддитивность. Это свойство означает, что кинетическая энергия механической системы, состоящей из материальных точек, равна сумме кинетических энергий всех материальных точек, входящих в систему^[1].
• Инвариантность по отношению к повороту системы отсчёта. Кинетическая энергия не зависит от положения точки, направления её скорости и зависит лишь от модуля скорости или, что то же самое, от квадрата её скорости^[1].
• Неинвариантность по отношению к смене системы отсчёта в общем случае. Это ясно из определения, так как скорость претерпевает изменение при переходе от одной системы отсчёта к другой.
• Сохранение. Кинетическая энергия не изменяется при взаимодействиях, изменяющих лишь механические характеристики системы. Это свойство инвариантно по отношению к преобразованиям Галилея^[1]. Свойства сохранения кинетической энергии и второго закона Ньютона достаточно, чтобы вывести математическую формулу кинетической энергии^[8][9].

Физический смысл кинетической энергии

Работа всех сил, действующих на материальную точку при её перемещении, идёт на приращение кинетической энергии^[10]:

 A12=T2−T1.{\displaystyle \ A_{12}=T_{2}-T_{1}.}

Это равенство актуально как для классической, так и для релятивистской механики (получается интегрированием выражения  F→ds→=dT{\displaystyle \ {\vec {F}}{\rm {d}}{\vec {s}}={\rm {d}}T} между состояниями 1 и 2).

Соотношение кинетической и внутренней энергии

Кинетическая энергия зависит от того, с каких позиций рассматривается система. Если рассматривать макроскопический объект (например, твёрдое тело видимых размеров) как единое целое, можно говорить о такой форме энергии, как внутренняя энергия. Кинетическая энергия в этом случае появляется лишь тогда, когда тело движется как целое.

То же тело, рассматриваемое с микроскопической точки зрения, состоит из атомов и молекул, и внутренняя энергия обусловлена движением атомов и молекул и рассматривается как следствие теплового движения этих частиц, а абсолютная температура тела прямо пропорциональна средней кинетической энергии такого движения атомов и молекул. Коэффициент пропорциональности — постоянная Больцмана.

См. также

Примечания

1. ↑ ^{1 2 3 4} Айзерман, 1980, с. 49.
2. ↑ Тарг С. М. Кинетическая энергия // Физическая энциклопедия : [в 5 т.] / Гл. ред. А. М. Прохоров. — М.: Советская энциклопедия, 1990. — Т. 2: Добротность — Магнитооптика. — С. 360. — 704 с. — 100 000 экз. — ISBN 5-85270-061-4.
3. ↑ Батыгин В. В., Топтыгин И. Н. 3.2. Кинематика релятивистских частиц // Современная электродинамика, часть 1. Микроскопическая теория. — Москва-Ижевск: Институт компьютерных исследований, 2002. — С. 238. — 736 с. — 1000 экз. — ISBN 5-93972-164-8.
4. ↑ Мах Э.  Механика. Историко-критический очерк её развития. — Ижевск: «РХД», 2000. — С. 252. — 456 с. — ISBN 5-89806-023-5.
5. ↑ Голубева О. В. Теоретическая механика. — М.: «Высшая школа», 1968. — С. 243—245.
6. ↑ ^{1 2} Монин А. С., Яглом А. М. Статистическая гидромеханика. Часть 1. — М.: Наука, 1965. — 639 с.
7. ↑ Блохинцев Д. И. Основы квантовой механики, 5-е изд. Наука, 1976. — 664 с., см. § 26.
8. ↑ Айзерман, 1980, с. 54.
9. ↑ Сорокин В. С. «Закон сохранения движения и мера движения в физике» // УФН, 59, с. 325—362, (1956)
10. ↑ Сивухин Д. В. § 22. Работа и кинетическая энергия. // Общий курс физики. — М.: Наука, 1979. — Т. I. Механика. — С. 131. — 520 с.

Литература

wiki2.red

Кинетическая энергия — энергия движения тел :: SYL.ru

Потенциальная и кинетическая энергия позволяют охарактеризовать состояние любого тела. Если первая применяется в системах взаимодействующих объектов, то вторая связана с их движением. Эти виды энергии, как правило, рассматриваются тогда, когда сила, связывающая тела, независима от траектории движения. При этом важны только начальное и конечное их положения.

Общие сведения и понятия

Кинетическая энергия системы является одной из важнейших ее характеристик. Физики выделяют два вида такой энергии в зависимости от вида движения:

• поступательная;

• вращения.

Кинетическая энергия (Е_к) представляет собой разность между полной энергией системы и энергией покоя. Исходя из этого, можно сказать, что она обусловлена движением системы. Тело имеет ее только тогда, когда оно движется. В состоянии покоя объекта она равняется нулю. Кинетическая энергия любых тел зависит исключительно от скорости движения и их масс. Полная энергия системы находится в прямой зависимости от скорости ее объектов и расстояния между ними.

Основные формулы

В том случае, когда любая сила (F) действует на тело, находящееся в покое так, что оно приходит в движение, можно говорить о совершении работы dA. При этом величина этой энергии dE будет тем выше, чем больше совершается работы. В этом случае верно такое равенство: dA = dE.

С учетом пути, пройденного телом (dR) и его скорости (dU), можно воспользоваться 2 законом Ньютона, исходя из которого: F = (dU/dE)*m.

Вышеуказанный закон используется только тогда, когда имеется инерциальная система отсчета. Существует еще один важный нюанс, учитываемый при расчетах. На значение энергии влияет выбор системы. Так, согласно системе СИ, она измеряется в джоулях (Дж). Кинетическая энергия тела характеризуется массой m, а также скоростью перемещения υ. В этом случае она составит: E_k = ((υ*υ)*m)/2.

Исходя из вышеуказанной формулы, можно сделать вывод, что кинетическую энергию определяют массой и скоростью. Иными словами, она представляет собой функцию движения тела.

Энергия в механической системе

Кинетическая энергия представляет собой энергию механической системы. Она зависит от скорости движения ее точек. Данная энергия любой материальной точки представляется такой формулой: E = 1/2mυ 2, где m – масса точки, а υ – ее скорость.

Кинетическая энергия механической системы являет собой арифметическую сумму таких же энергий всех ее точек. Ее также можно выразить следующей формулой: E_k = 1/2Mυ c2 + Ec, где υc — скорость центра масс, М – масса системы, Ec – кинетическая энергия системы при движении вокруг центра масс.

Энергия твердого тела

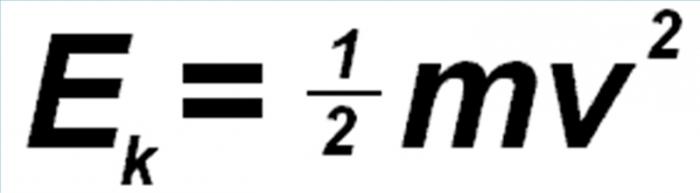Кинетическая энергия тела, которое движется поступательно, определяется как и такая же энергия точки с массой, равной массе всего тела. Для расчета показателей при перемещении применяются более сложные формулы. Изменение этой энергии системы в момент ее перемещения из одного положения в другое происходит под воздействием приложенных внутренних и внешних сил. Оно равняется сумме работ Aue и A’u данных сил при этом перемещении: E2 – E1 = ∑u Aue + ∑u A’u.

Данное равенство отражает теорему, касающуюся изменения кинетической энергии. С ее помощью решаются самые разные задачи механики. Без этой формулы невозможно решить целый ряд важнейших задач.

Кинетическая энергия при высоких скоростях

Если скорости тела близки к скорости света, кинетическую энергию материальной точки можно рассчитать по следующей формуле:

E = m0c2/√1-υ2/c2 — m0c2,

где с — скорость света в вакууме, m0 — масса точки, m0с2 — энергия точки. При маленькой скорости (υ<c), предыдущее соотношение можно выразить обычной формулой: 1/2mu2.

Энергия при вращении системы

Во время вращения тела вокруг оси каждый его элементарный объем массой (mi) описывает окружность радиусом ri. В этот момент объем имеет линейную скорость υi. Поскольку рассматривается твердое тело, угловая скорость вращения всех объемов будет одинакова: ω = υ1/r1 = υ2/r2 = … = υn/rn (1).

Кинетическая энергия вращения твердого тела представляет собой сумму всех таких же энергий его элементарных объемов: E = m1υ1 2/2 + miυi 2/2 + … + mnυn 2/2 (2).

При использовании выражения (1), получаем формулу: E = Jz ω 2/2, где Jz – это момент инерции тела вокруг оси Z.

При сравнении всех формул становится ясно, что момент инерции – это и есть мера инертности тела во время вращательного движения. Формула (2) подходит для объектов, вращающихся относительно неподвижной оси.

Плоское движение тела

Кинетическая энергия тела, движущегося вниз по плоскости, складывается из энергии вращения и поступательного движения: E = mυc2/2 + Jz ω 2/2, где m – масса движущегося тела, Jz — момент инерции тела вокруг оси, υc – скорость центра масс, ω — угловая скорость.

Изменение энергии в механической системе

Изменение значения кинетической энергии тесно связано с потенциальной. Суть этого явления можно понять благодаря закону сохранения энергии в системе. Сумма E + dP во время перемещения тела всегда будет одинаковой. Изменение значения E всегда происходит одновременно с изменением dP. Таким образом, они преобразуются, словно перетекая друг в друга. Такое явление можно встретить практически во всех механических системах.

Взаимосвязь энергий

Потенциальная и кинетическая энергии тесно связаны между собой. Их сумму можно представить как полную энергию системы. На молекулярном уровне — это внутренняя энергия тела. Она присутствует постоянно, пока существует хотя бы какое-то взаимодействие между телами и тепловое движение.

Выбор системы отсчета

Для проведения вычисления значения энергии выбирают произвольный момент (его считают начальным) и систему отсчета. Определить точную величину потенциальной энергии возможно только в зоне воздействия сил, которые не зависят от траектории движения тела при совершении работы. В физике данные силы называют консервативными. Они имеют постоянную связь с законом сохранения энергии.

Суть разницы между потенциальной и кинетической энергией

Если внешнее воздействие минимально или сводится к нулю, изучаемая система всегда будет тяготеть к состоянию, в котором ее потенциальная энергия также будет стремиться к нулю. Например, подброшенный вверх мячик достигнет предела этой энергии в верхней точке траектории движения и в тот же момент начнет падать вниз. В это время накопленная в полете энергия преобразуется в движение (выполняемую работу). Для потенциальной энергии в любом случае существует взаимодействие как минимум двух тел (в примере с мячиком гравитация планеты оказывает на него влияние). Кинетическую энергию можно рассчитать индивидуально для любого движущегося тела.

Взаимосвязь разных энергий

Потенциальная и кинетическая энергия изменяются исключительно при взаимодействии тел, когда действующая на тела сила совершает работу, значение которой отлично от нуля. В замкнутой системе работа силы тяготения или упругости равняется изменению потенциальной энергии объектов со знаком «-»: A = — (Ep2 – Ep1).

Работа силы тяготения или упругости равняется изменению энергии: A = Ek2 – Ek1.

Из сравнения обоих равенств ясно, что изменение энергии объектов в замкнутой системе равняется изменению потенциальной энергии и противоположно ему по знаку: Ek2 – Ek1 = — (Ep2 – Ep1), или иначе: Ek1 + Ep1 = Ek2 + Ep2.

Из указанного равенства видно, что сумма этих двух энергий тел в замкнутой механической системе и взаимодействующих силами упругости и тяготения, всегда остается постоянной. Исходя из вышеизложенного, можно сделать вывод о том, что в процессе изучения механической системы следует рассматривать взаимодействие потенциальной и кинетической энергий.

www.syl.ru

Кинетическая, потенциальная энергии тела. Тест

Тестирование онлайн

• Энергия. Основные понятия

• Энергия

Потенциальная энергия

Энергия — скалярная величина. Можно назвать эту величину абстрактной. Просто тот факт, что тело подняли на некоторую высоту, означает, что тело обладает потенциальной энергией, которая определяется по формуле

Это энергия взаимодействия тела с Землей.

Потенциальная энергия имеет место быть при взаимодействии частиц в микромире, заряженных тел. Следовательно, можно говорить, что взаимодействующие тела обладают энергией. Энергия, обусловленная взаимодействием тел, их взаимным расположением, называется потенциальной.

Кинетическая энергия

Если тело движется, то оно обладает кинетической энергией, которая определяется по формуле

Полная механическая энергия

Это сумма кинетической и потенциальной энергии тел

Теорема об изменении кинетической энергии

Работа равнодействующей силы равна изменению кинетической энергии тела

Главное запомнить

1) Формулы и условия существования;
2) Теорему об изменении кинетической энергии

Потенциальная энергия упруго деформированного тела — это энергия взаимодействия частиц, из которых состоит тело. Определяется по формуле

В случае, когда действует сила упругости, полная механическая энергия определяется как

В общем случае материальная точка может двигаться относительно инерциальной системы отсчета поступательно и одновременно вращаться вокруг некоторой оси. Полная кинетическая энергия тела в этом случае представляет собой сумму кинетических энергий поступательного и вращательного движений

fizmat.by