Комбинаторные задачи (5 класс)
Этапы урока
Задачи этапа
Визуальный ряд
Деятельность учителя
Деятельность учащихся
Формируемые УУД
Организационный
Собрать домашнее задание, настроить на урок
Слайд на доске:
«тяжело в учении легко в бою»
Прошу теперь сдать на проверку тетради с домашней работой. Напоминаю, что мы сегодня приступаем к изучению новой темы.
Дежурные проходят по классу собирают тетради.
Саморегуляция, прогнозирование и оценка
Актуализации теоретических знаний
Определить цель урока
На доске: дата и название темы: «Комбинаторные задачи»
Ребята, сегодня мы совершим увлекательное путешествие в мир «Комбинаторики»
Мысленно задают вопрос: «а что это такое»
Целеполагание, предметная рефлексия.
Объяснения нового материа
ла
Первичное знакомство с основными понятиями,
методами, способами
решения
комбинаторных задач
Слайд на доске: Слово «комбинаторика» произошло от латинского слова COMBINARE, что означает «соединять», «сочетать»
Учитель задаёт вопрос как вы думаете что означает слово «комбинаторика»?
Учитель делает паузу, слушает ответы потом говорит определение.
Слово «комбинаторика» произошло от латинского слова COMBINARE, что означает «соединять», «сочетать»
Дети отвечают, выдвигая гипотезы
Внимательно слушают, читают определение на раздаточных листках
Выдвижение и проверка гипотез.
Слайд на доске
Чтобы запереть чемодан с кодовым замком, состоящий из двух каких-либо цифр. Хозяин чемодана решил использовать только цифры 1, 2 и 3. Сколькими способами он может выбрать код?
Решить эту задачу можно с помощью древа возможных вариантов или перебора всех возможных вариантов
Внимательно слушают, смотрят слайд, думают, запоминают.
Смысловое чтение.
Слайд на доске:
Решение древом возможных
Вариантов
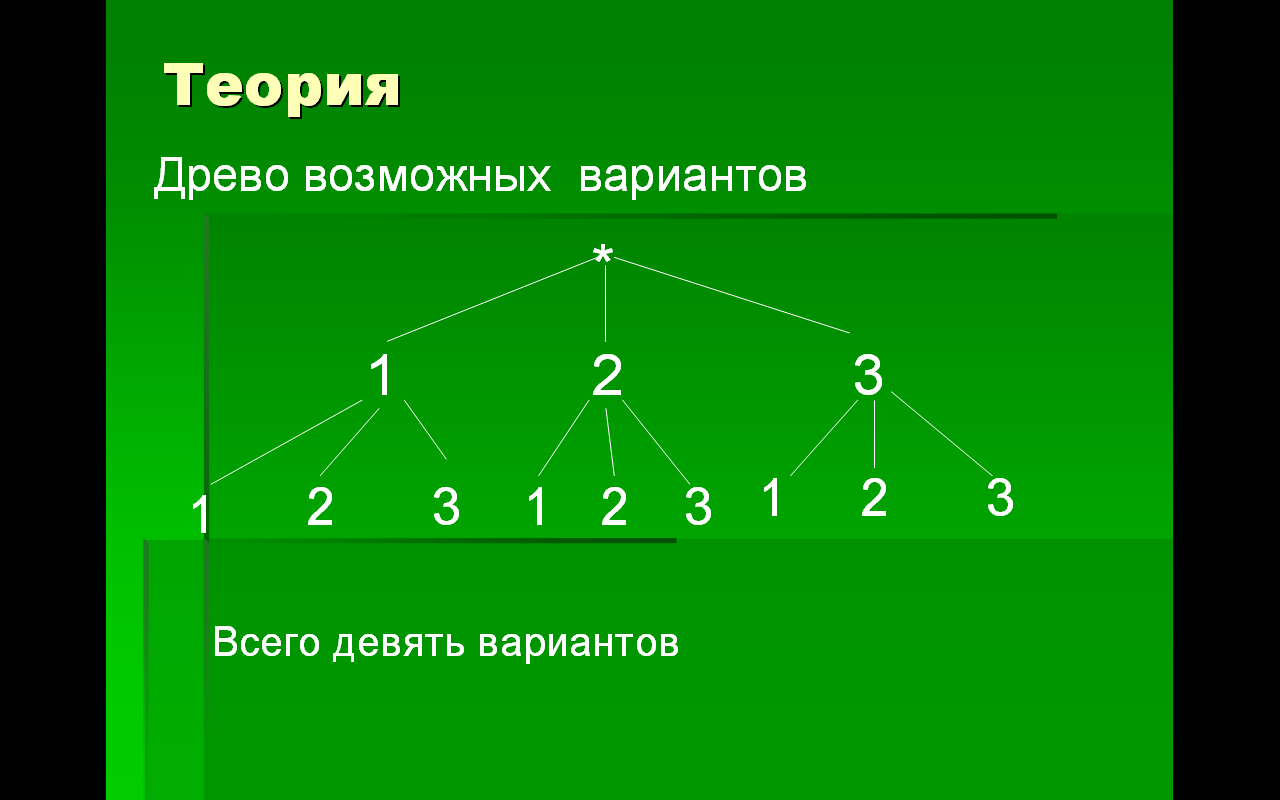
ДЕРЕВО ВОЗМОЖНЫХ ВАРИАНТОВ Часто процесс перебора удобно осуществлять путем построения специальной схемы — так называемого дерева возможных вариантов
изобразите корень дерева, для этого поставьте знак *.
Чтобы выбрать первую цифру кода, у нас есть три варианта: 1; 2; 3. Поэтому от корня дерева проведите три ветви и на их концах поставите цифры 1; 2; 3.
Для выбора второй цифры есть те же три варианта. Проводим «веточки»
Двигаясь от корня дерева по ветвям, мы получим все возможные коды
Внимательно слушают, смотрят слайды, думают, анализируют, классифицируют, запоминают.
Анализ объекта.
Выбор оснований критериев для сравнения, сериации, классификации объектов.
Создание и преобразование модели и схемы для решения задач в зависимости от конкретных условий.
Слайд на доске:
Решение перебором

Подходящие коды — это двузначные числа, которые можно составить из цифр
1, 2, 3. Будем выписывать все такие цифры в порядке возрастания. Такой способ перебора позволит нам не пропустить никакой из кодов и в то же время не повторить ни один из них.
С начало запишем в порядке возрастания все коды, начинающиеся с цифры 1: 11, 12, 13. Затем запишем в порядке возрастания коды, начинающиеся с цифры 2: 21, 22, 23.
Затем запишем в порядке возрастания коды, начинающиеся с цифры 3: 31, 32, 33
Таким образом, имеется 9 способов выбора
кода: 11, 12, 13, 21, 22, 23, 31, 32, 33.
Внимательно слушают, смотрят слайды, думают, анализируют, классифицируют, запоминают.
Анализ объекта.
Выбор оснований критериев для сравнения, сериации, классификации объектов.
Создание и преобразование модели и схемы для решения задач в зависимости от конкретных условий.
Закрепления новых знаний
Показать практическое применение теоретических знаний
через их применение в решении практических задач
Слайд на доске с условием задачи №1
В столовой на завтрак можно выбрать пиццу, плюшку, бутерброд, а запить их можно чаем, соком. Из скольких вариантов завтрака можно выбирать ?
Слайд на доске с решением
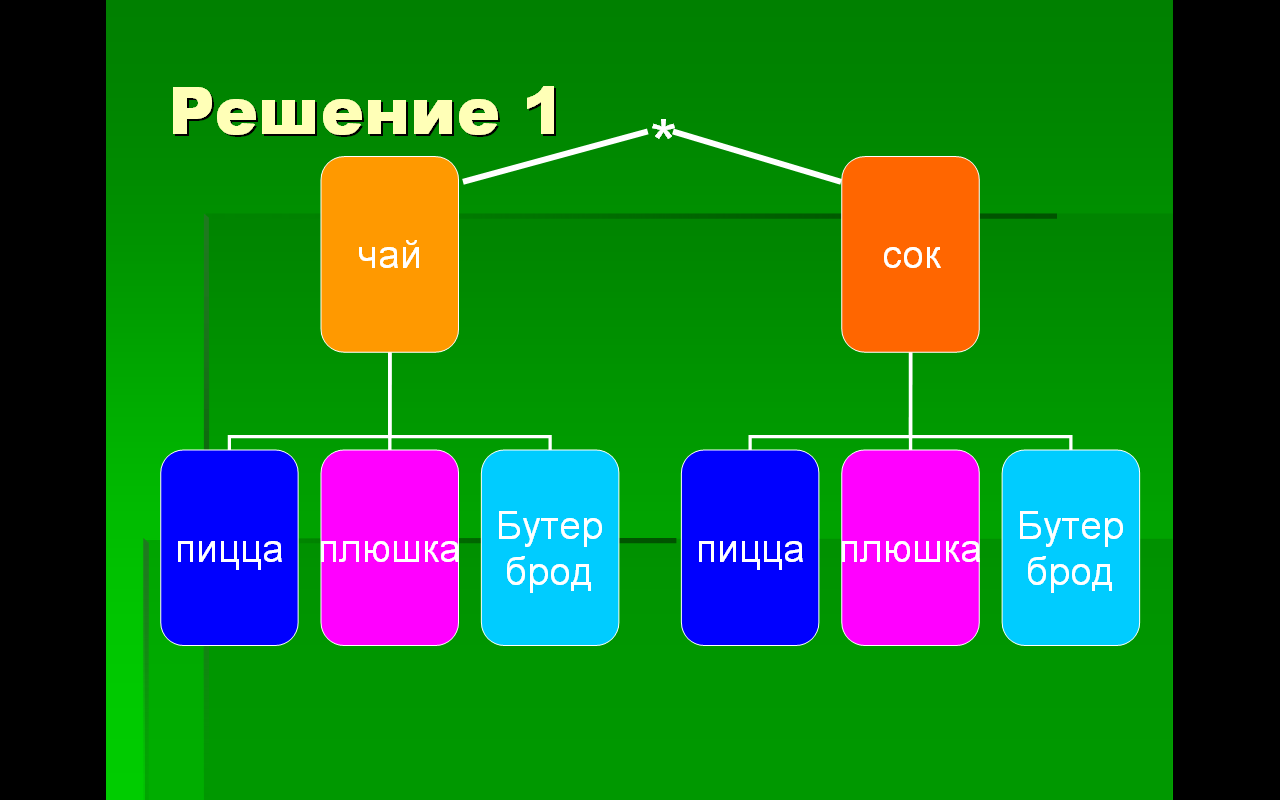
На слайде изображено дерево возможных вариантов
первый уровень «НАПИТКИ»
два варианта: ЧАЙ, СОК.
второй уровень три варианта: ПИЦЦА, ПЛЮШКА, БУТЕРБРОД.
Итого шесть ВАРИАНТОВ завтрака:
ЧАЙ+ПИЦЦА, ЧАЙ+ПЛЮШКА, ЧАЙ+БУТЕРБРОД, СОК+ПИЦЦА, СОК+ПЛЮШКА, СОК+БУТЕРБРОД.
Внимательно слушают, смотрят слайды, думают, анализируют, классифицируют, запоминают.
Знакомятся с моделями и схемами для решения задач в зависимости от конкретных условий.
Знакомство с профессиями.
Анализ объекта.
Выбор оснований критериев для сравнения, сериации, классификации объектов.
Создание и преобразование модели и схемы для решения задач в зависимости от конкретных условий.
Слайд на доске с условием задачи №2
Из страны «Математика» в страну «Литература» ведут три дороги, а из страны «Литература» в страну «Физкультура» — четыре дороги. Сколькими способами можно попасть из страны «Математика» в
Страну «Физкультура» через страну «Литература»?
Слайд на доске с решением

Рисунок поможет нам решить эту задачу.
Переберём все «ПУТИ»
Обозначим дороги идущие из страны «МАТЕМАТИКА» так: М1, М2, М3,
а из «ЛИТЕРАТУРА» Л1, Л2, Л3,Л4.
Переберём М1+Л1, М1+Л2, М1+Л3,М1+Л4, М2+Л1, М2+Л2, М2+Л3,
М2+Л4, М3+Л1, М3+Л2, М3+Л3, М3+Л4
Натолкнуть
Детей на мысль о перемножении Количества дорог
А можно взять и перемножить количество дорог 3*4 =12
Внимательно слушают, смотрят слайды, думают, анализируют, классифицируют, запоминают.
Знакомятся с моделями и схемами для решения задач в зависимости от конкретных условий.
Слайд на доске с условием задачи №3
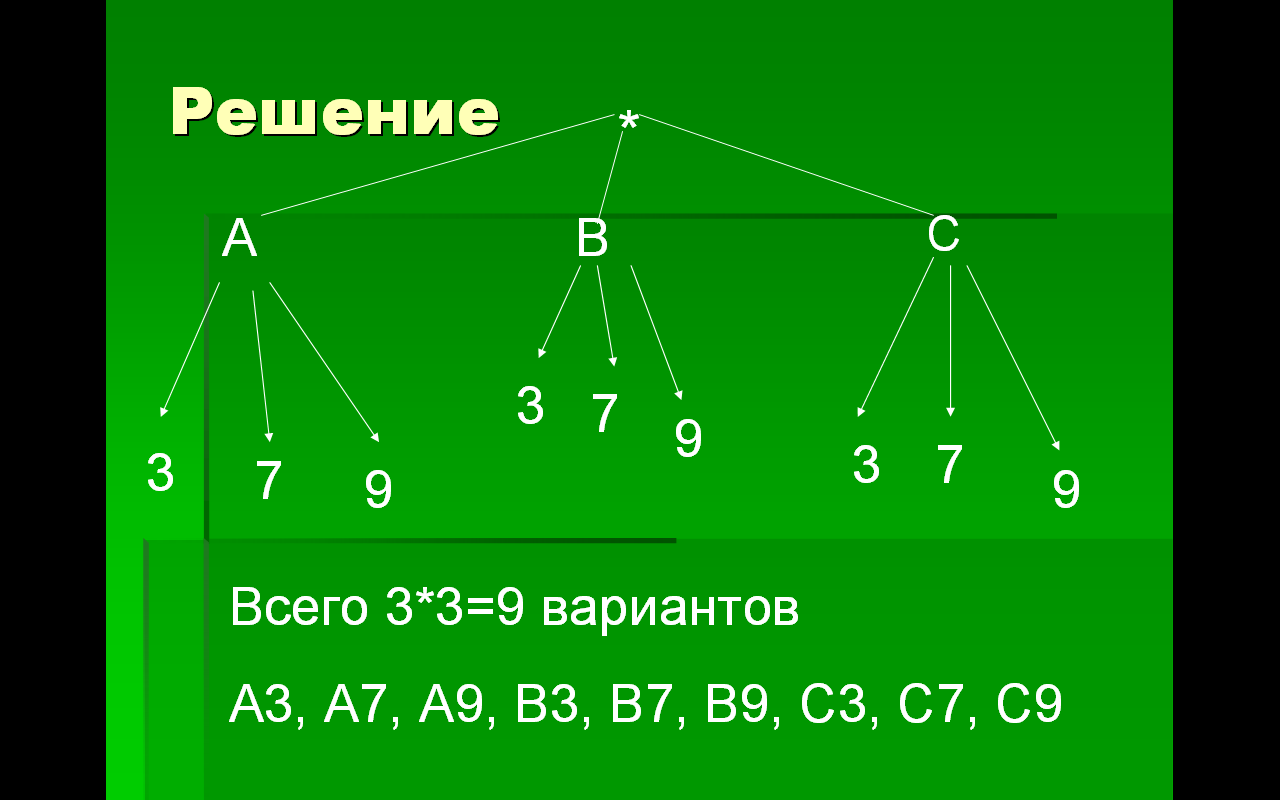
Шифр сейфа составляют из букв и цифр, причём на первом месте ставится буква (например А7). Сколько различных вариантов шифра можно составить, используя буквы А, В, С и цифры 3, 7, 9?
Слайд на доске с решением
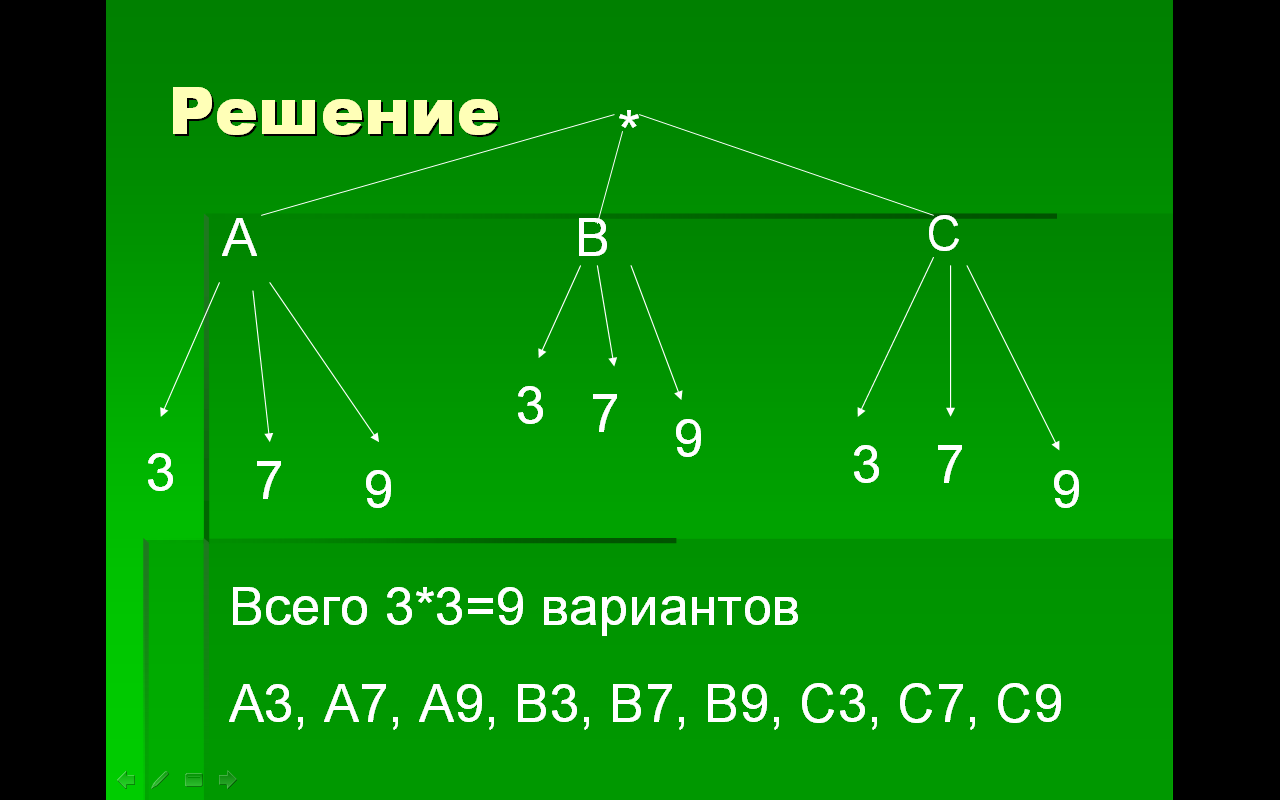
1) на слайде изображён корень дерева, в виде знака *.
2)Чтобы выбрать букву кода, у нас есть три варианта: А; B; C. Поэтому от корня дерева проведены три ветви и на их концах поставлены буквы: А; B; C .
3)Для выбора цифры есть те же три варианта. Проводим «веточки»
Двигаясь от корня дерева по ветвям, мы получим все возможные коды
А3, А7, А9, В3, В7, В9, С3, С7, С9
Или Всего 3*3=9 вариантов
Внимательно слушают, смотрят слайды, думают, анализируют, классифицируют, запоминают.
Знакомятся с моделями и схемами для решения задач в зависимости от конкретных условий.
Слайд на доске с условием задачи №4
Несколько стран в качестве символа своего государства решили использовать флаг в виде трёх горизонтальных полос одинаковых по ширине, но разных по цвету: белый, синий, красный. Сколько стран могут использовать такую символику при условии, что у каждой страны свой, отличный от других, флаг?
Слайд на доске с решением

Первый способ: обозначим цвета полосок первыми буквами названий цветов
Б – белый, К – красный, С – синий.
Решим перебором:
БСК, БКС, СБК, СКБ, КБС, КСБ
Всего шесть вариантов.
Второй способ:
Берем карандаши и рисуем флаги
Внимательно слушают, смотрят слайды, думают, анализируют, классифицируют, запоминают.
Знакомятся с моделями и схемами для решения задач в зависимости от конкретных условий.
Слайд на доске с условием задачи №5
В семье 4 человек, и за столом в кухне стоят 4 стула. В семье решили каждый вечер, ужиная, рассаживаться на эти 4 стула по новому. Сколько дней члены семьи смогут делать это без повторений?
Слайд на доске с решением
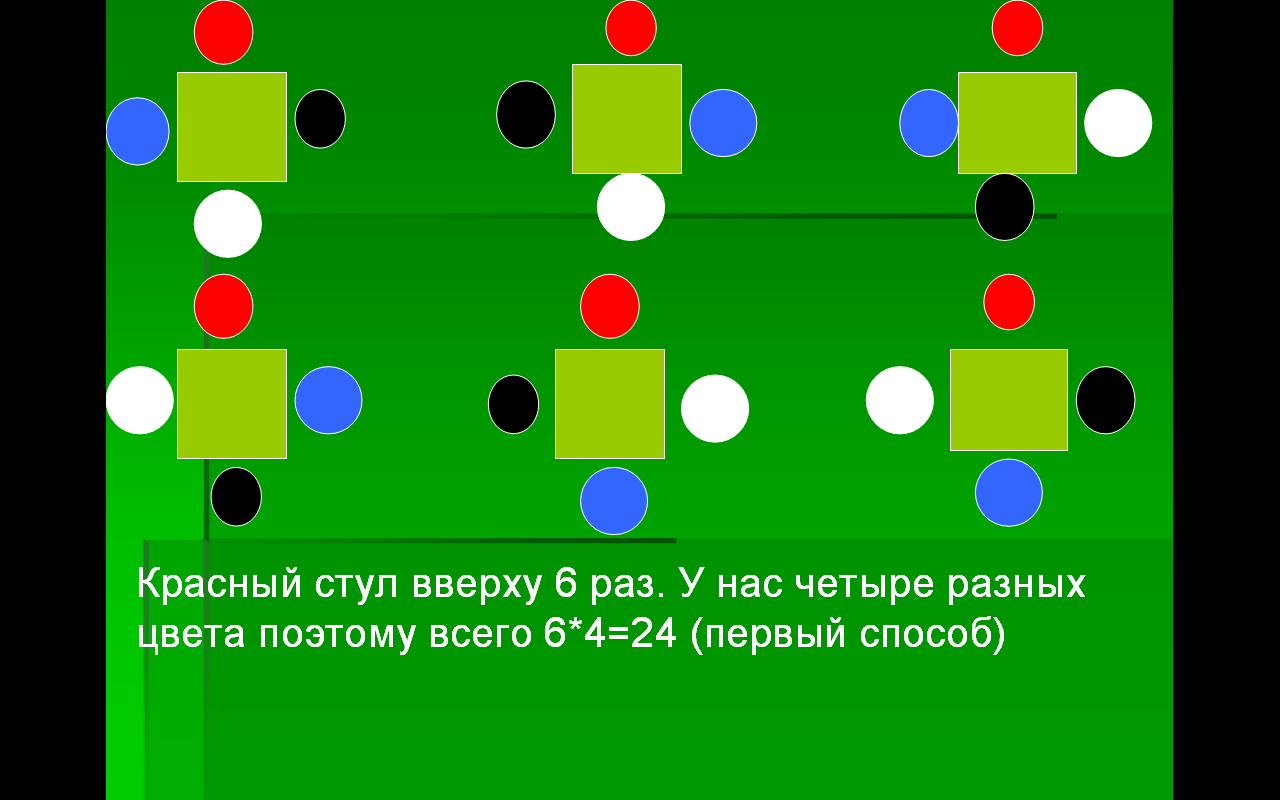
Второй способ решения

Для наглядности раскрасим стулья разными цветами.
Зафиксируем красный стул вверху и, будем переставлять остальные три, получим шесть вариантов.
Эту же операцию проделаем с остальными цветами, получим 6*4=24 различных вариантов.
Второй способ:
На первый стул может сесть любой член семьи, т. е. 4 варианта; на второй – 3 человека так, как один член семьи уже сидит; на третий – 2 человека так, как
двое сидят; на четвёртый только один так, как три члена семьи уже сидят.
Итак, перемножим все варианты
4*3*2*1= 24
Внимательно слушают, смотрят слайды, думают, анализируют, классифицируют, запоминают.
Знакомятся с моделями и схемами для решения задач в зависимости от конкретных условий.
Слайд на доске с условием задачи №6
Вася решил пойти на новогодний
карнавал в костюме мушкетёра. В ателье проката ему предложили на выбор: три вида брюк, два камзола, три шляпы. Сколько различных карнавальных костюмов можно составить из этих предметов?
Слайд на доске с решением
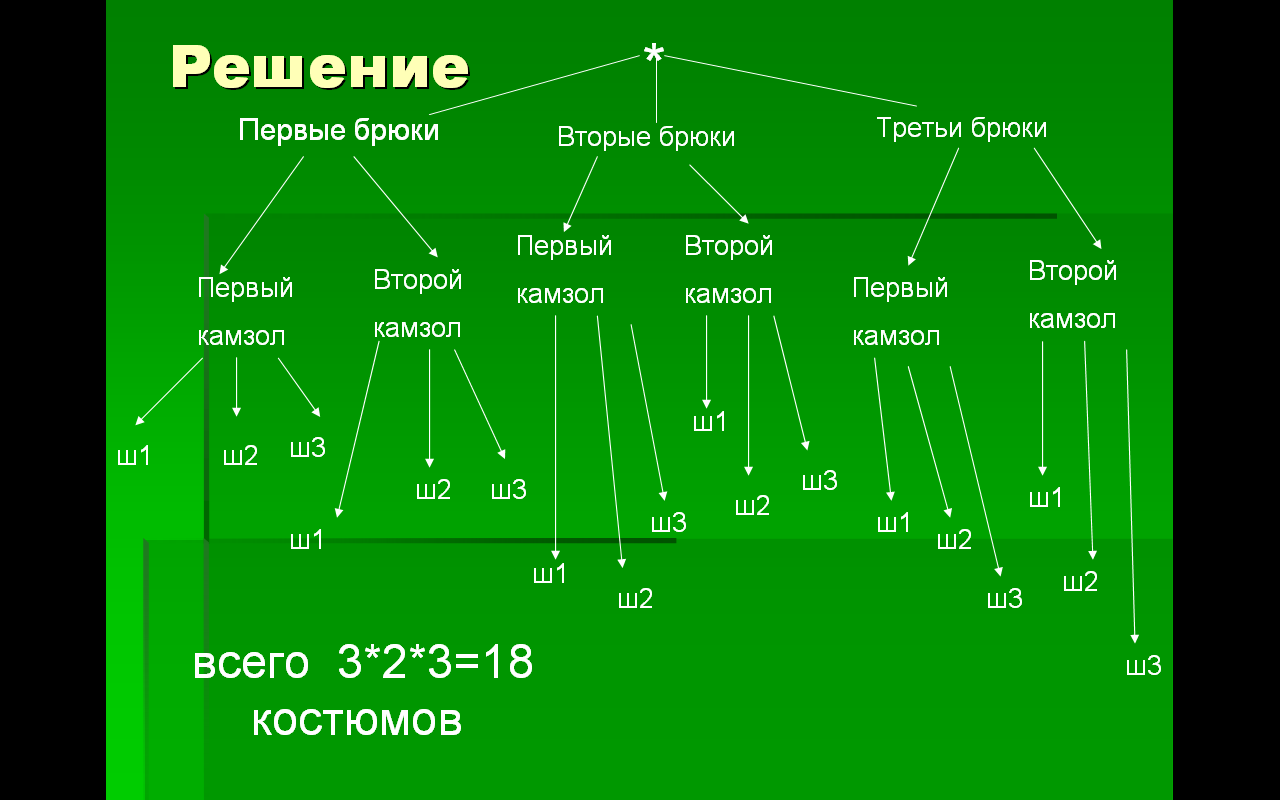
Обозначим: первую шапку Ш1, вторую – Ш2, третью – Ш3
1) на слайде изображён корень дерева, в виде знака *.
2) первый уровень трое брюк;
3) второй уровень два камзола;
4) третий уровень три шапки;
Всего 18 вариантов
Или просто перемножить «уровни»
3*2*3=18
Внимательно слушают, смотрят слайды, думают, анализируют, классифицируют, запоминают.
Знакомятся с моделями и схемами для решения задач в зависимости от конкретных условий.
Слайд на доске с условием задачи №7
При встрече 7 гномов обменялись рукопожатиями. Сколько всего было сделано рукопожатий?
Семь гномов решили обменяться фотографиями. Сколько нужно фотографий?
Слайд на доске с решением: а)
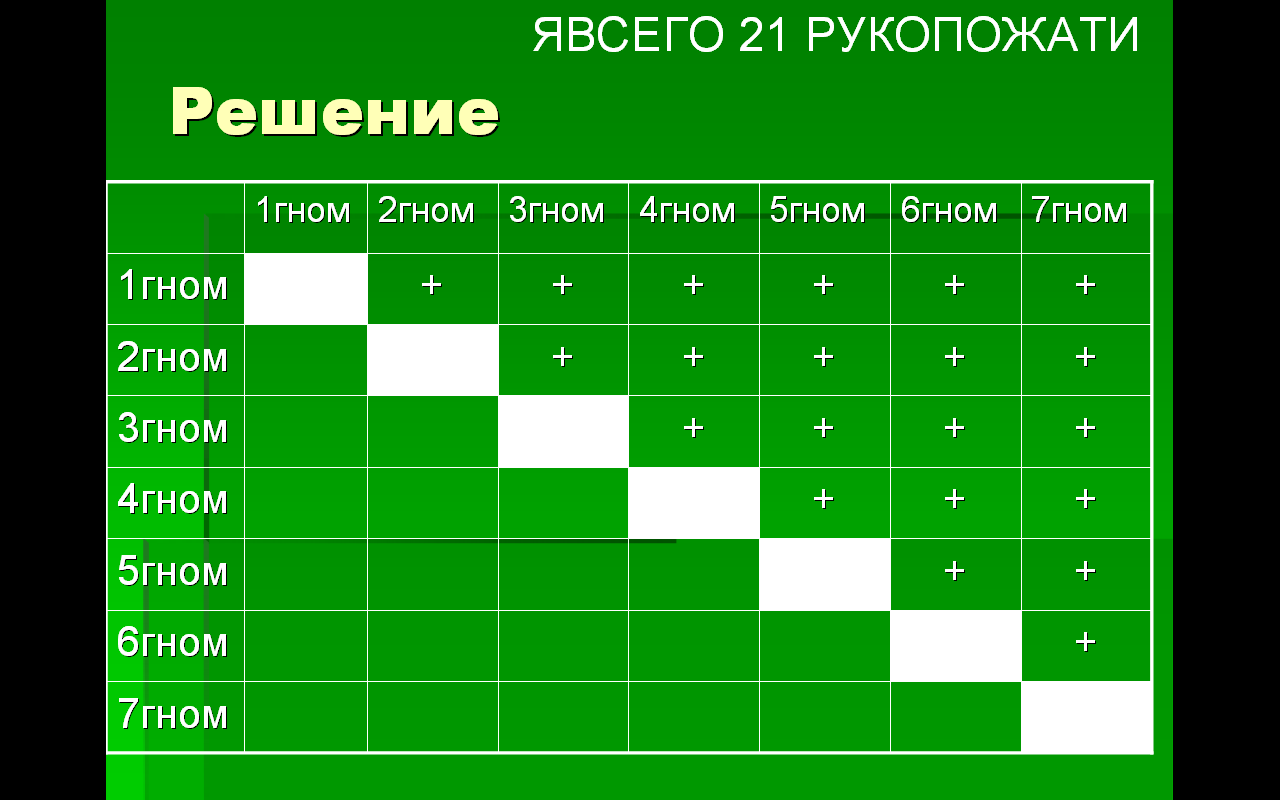
Слайд на доске с решением: б)
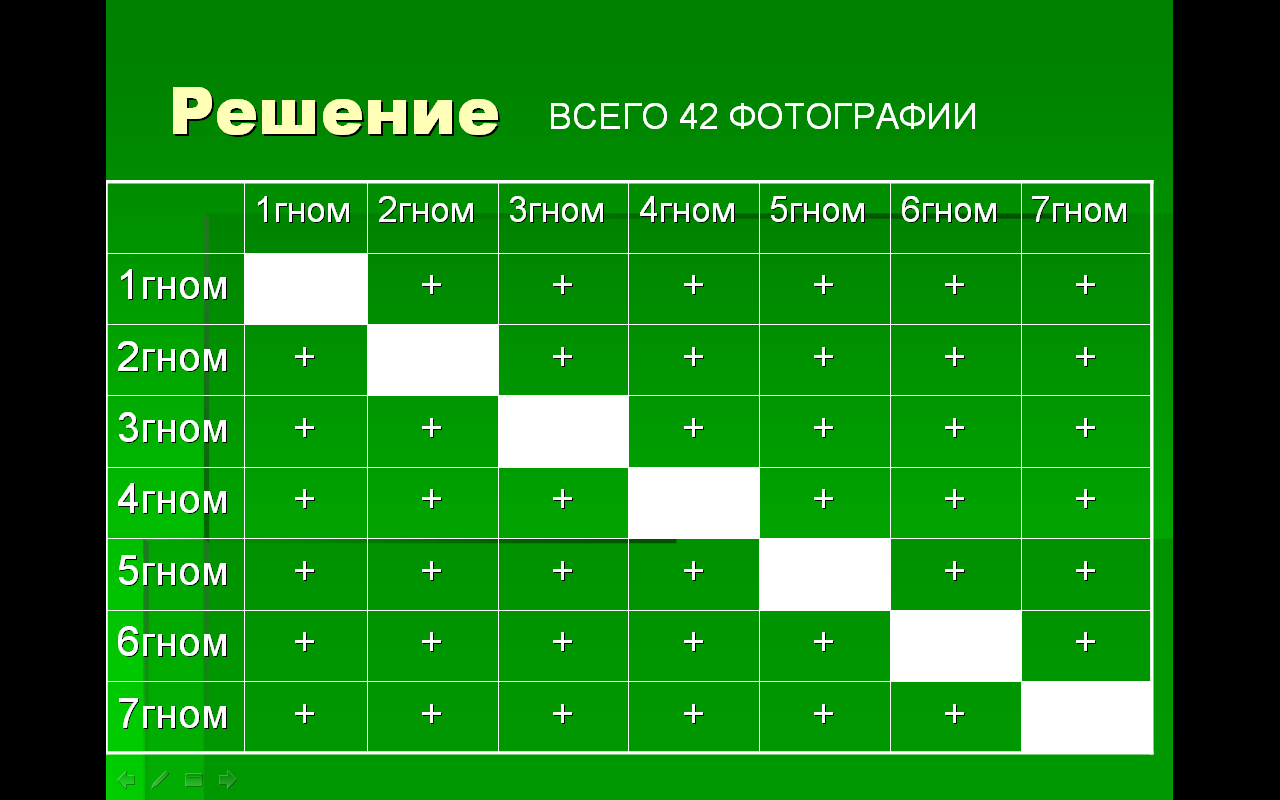
Эти две задачи очень похожи, но всё-таки они разные
При решении таких задач лучше использовать таблицу.
1)Нарисуем таблицу 8*8, первая строка и первый столбец это гномы.
2)Вычеркнем диагональ таблицы так, как гном сам с собою не может поздороваться.
3) Ячейки это кто с кем поздоровался.
4) Нижняя часть таблицы повторяет верхнюю.
Первый гном поздоровался со вторым = второй гном поздоровался с первым.
Всего 21 рукопожатие.
Задача б) отличается от а) тем, что нужно
учитывать нижнюю часть таблицы так, как
первый гном подарил фото второму, НЕРАВНО второй гном подарил фото первому.
Всего 42 фото.
Внимательно слушают, смотрят слайды, думают, анализируют, классифицируют, запоминают.
Знакомятся с моделями и схемами для решения задач в зависимости от конкретных условий.
Систематизации знаний
Систематизировать методы решений комбинаторных задач.
Слайды на доске

И следующий слайд,
Слайды решений задачи №7
Внимательно слушают, смотрят слайды, думают, анализируют, классифицируют, запоминают.
Систематизация знаний по трём
методам.
Усвоения новых знаний
Дать определе-
ние комбинаторных задачач.
Слайд на доске

Отвечают на вопрос
Установление аналогий.
Умение классифициро
вать.
Определить три метода решения задач этого типа.

Следующий слайд;
Слайд решения задачи №7
Отвечают на вопрос
Умение классифициро
вать.
Выбор наиболее эффективных способов решения задач в зависимости от конкретных решений
Сделать вывод о многовариантном решении комбинаторных задач
Слайд
Отвечают на вопрос
Создавать модели и схемы для решения задач в зависимости от конкретных условий
Рефлек
сии
Провести самостоятельную работу в группах, в малых группах, индиви- дуально.
На парте у каждого лист (формата А4) с семью задачами (приложение№1)
Слайд с ответами
Таблица на доске (ответы команд)
Коман-
да №1
Коман-
да №2
1
2
3
4
5
6
7 а
7 б
Выполняют самостоятельную работу в коллективе, в парах, индивидуально.
Сочетание индивидуальной самостоятельной работы и сотрудничество в коллективе
Объяснения домашнего задания
Обеспече
ние понимания детьми цели, содержания и способов выполне
ния домашнего задания.
Саморегуля
ция, развитие самосознания, ответствен
ного отношения
В столовой на завтрак можно выбрать булочку, пирожок с капустой, пирожок с картошкой, бутерброд, а запить их можно чаем, компотом. Из скольких вариантов завтрака можно выбирать?
Из страны «Математика» в страну «Литература» ведут четыре дороги, а из страны «Литература» в страну «Физкультура» — пять дорог. Сколькими способами можно попасть из страны «Математика» в
страну «Физкультура» через страну «Литература»?
Шифр сейфа составляют из букв и цифр, причём на первом месте ставится буква (например А7). Сколько различных вариантов шифра можно составить, используя буквы А, M, F и цифры 1, 4, 6, 9?
Несколько стран в качестве символа своего государства решили использовать флаг в виде четырёх горизонтальных полос одинаковых по ширине, но разных по цвету: белый, синий, красный, зелёный. Сколько стран могут использовать такую символику при условии, что у каждой страны свой, отличный от других, флаг?
В семье 5 человек, и за столом в кухне стоят 5 стульев. В семье решили каждый вечер, ужиная, рассаживаться на эти 5 стульев по новому. Сколько дней члены семьи смогут делать это без повторений?
Вася решил пойти на новогодний карнавал в костюме мушкетёра. В ателье проката ему предложили на выбор: четыре вида брюк, два камзола, две шляпы. Сколько различных карнавальных костюмов можно составить из этих предметов?
При встрече 4 гнома обменялись рукопожатиями. Сколько всего было сделано рукопожатий?
Пять гномов решили обменяться фотографиями. Сколько нужно фотографий?
В столовой на завтрак можно выбрать пиццу, плюшку, бутерброд, а запить их можно чаем, соком. Из скольких вариантов завтрака можно выбирать?
Из страны «Математика» в страну «Литература» ведут три дороги, а из страны «Литература» в страну «Физкультура» — четыре дороги. Сколькими способами можно попасть из страны «Математика» в
страну «Физкультура» через страну «Литература»?
Шифр сейфа составляют из букв и цифр, причём на первом месте ставится буква (например А7). Сколько различных вариантов шифра можно составить, используя буквы А, В, С и цифры 3, 7, 9?
Несколько стран в качестве символа своего государства решили использовать флаг в виде трёх горизонтальных полос одинаковых по ширине, но разных по цвету: белый, синий, красный. Сколько стран могут использовать такую символику при условии, что у каждой страны свой, отличный от других , флаг?
В семье 4 человек, и за столом в кухне стоят 4 стула. В семье решили каждый вечер, ужиная, рассаживаться на эти 4 стула по новому. Сколько дней члены семьи смогут делать это без повторений?
На первый стул может сесть любой из четырёх, на второй – только трое, на третий – двое, на четвёртый – один. 4*3*2*1=24 разных вариантов
В семье 4 человек, и за столом в кухне стоят 4 стула. В семье решили каждый вечер, ужиная, рассаживаться на эти 4 стула по новому. Сколько дней члены семьи смогут делать это без повторений?
карнавал в костюме мушкетёра. В ателье проката ему предложили на выбор: три вида брюк, два камзола, три шляпы. Сколько различных карнавальных костюмов можно составить из этих предметов?
При встрече 7 гномов обменялись рукопожатиями. Сколько всего было сделано рукопожатий?
Семь гномов решили обменяться фотографиями. Сколько нужно фотографий?
infourok.ru
| № | Ход урока Действия учителя |
Действия ученика |
| 1 | Организационный момент Учитель приветствует учащихся |
Приветствуют учителя |
| 2 | Актуализация знаний | |
| Устная работа (слайд 1 и 2). Презентация. В ходе устной работы учащиеся вспоминают правила рационального счета, замечают закономерности и решают две несложные комбинаторные задачи. Переход к следующему слайду – гиперссылка в нижнем правом углу. |
Работают устно | |
| Учитель (слайд 3): В последних двух задачах нам пришлось перебрать все возможные варианты, как обычно говорят в этих случаях – все возможные КОМБИНАЦИИ. Такие задачи называют комбинаторными, а раздел математики, в котором рассматриваются данные задачи, называется – комбинаторикой. Переход к следующему слайду – гиперссылка. |
Слушают учителя | |
| Учитель предлагает решить задачу:
(слайд 4) Мистер Холмс обращается к миссис Хадсон: “Уважаемая миссис Хадсон к нам придут гости. В качестве вторых блюд приготовьте мясо, котлеты и рыбу. На сладкое – мороженое, фрукты и пирог. Гость выбирает одно второе блюдо и одно блюдо на десерт. Подсчитайте, сколько будет гостей, и поставьте необходимое количество стульев. Очень вас прошу, чтобы количество стульев соответствовало количеству приглашенных”. Помогите миссис Хадсон. Учитель: Эта задача сложнее, чем задачи, предложенные в начале урока и для того, чтобы помочь Миссис Хадсон, чему мы должны научиться? |
Читают задачу (Приложение3), выдвигают гипотезы. | |
| Учитель: То есть изучить способы решения таких задач. Как вы думаете, о чем пойдет речь на сегодняшнем уроке? |
Предполагаемый ответ: о способах решения комбинаторных задач. | |
| 3 | Изучение методов решения комбинаторных задач | |
| Уточняет тему урока: “Методы решения
комбинаторных задач” (слайд 5) Переход к следующему слайду – гиперссылка. |
Открывают тетради, записывают число и тему урока. | |
| Историческая справка из истории
развития комбинаторики (слайд 6) Переход к следующему слайду – гиперссылка. |
Слушают учителя) | |
| Слайд 7 Методы решения комбинаторных задач. Учитель Предлагает учащимся использовать Приложение 2 Решаем первую задачу: Сколько трехзначных чисел можно составить из цифр 1, 3, 5 используя в записи числа каждую из них не больше одного раза? Слайд содержит три гиперссылки. 1-я гиперссылка – (переход к слайду 8) метод “Дерево возможных вариантов”. Разбирает с учащимися решение задачи и переходим к слайду11. |
Работают с Приложением 2 1 метод – Дерево возможных вариантов. Заполняют с учителем схему |
|
| Учитель Предлагает учащимся самостоятельно решить задачу Приложение2(№2): Постройте все слова, которые можно получить из слова ТОК перестановками его букв. Сколько из них имеет смысл? (слово ТОК не считаем). Проверяет решение задачи. Возвращаемся к слайду 7. Переход к слайду – гиперссылка. |
Работают с Приложением 2 Задача 2 Заполняют схему. Отвечают на вопрос задачи. |
|
| Слайд 7 Учитель Предлагает решить первую задачу вторым способом – “Перебор возможных вариантов”. 2-я гиперссылка – (переход к слайду 9) метод “Перебор возможных вариантов”. Разбирает с учащимися решение задачи и переходим к слайду10. Переход к следующему слайду – гиперссылка. |
Работают с Приложением 2 2 метод Заполняют с учителем таблицу |
|
| Слайд 10. Учитель предлагает учащимся из полос, лежащих на парте, составить макет Российского Флага. Затем по щелчку на слайде появляется Российский Флаг. Учитель: Что означает каждый цвет нашего флага? Историческая справка о Российском Флаге (Приложение 5). Учитель: В каких странах флаг состоит из такого же набора цветных полос? Предлагает решить задачу с флагами: Сколько флагов можно составить с помощью полос данных цветов (красный, синий, белый), если полосы располагать горизонтально? Эту задачу учащиеся решают самостоятельно, можно обозначить цвета флага – белый(Б), синий(С), красный(К). Учитель: Какой будет ответ в задаче, если не указать, как располагать полосы? Возвращаемся к слайду 7. Переход к слайду – гиперссылка. |
Составляют макет флага. Отвечают на вопрос. Отвечают на вопрос.
Работают с Приложением 2 Задача 3 Заполняют таблицу. Отвечают на вопрос задачи. Отвечают на дополнительный вопрос. |
|
| Слайд 7. 3-я гиперссылка – переход к слайду -13 физкультминутка. С помощью гиперссылки переходим к слайду 12. Следует ли брать задачу на 12 слайде, решает учитель, ориентируясь на время. Если нет, то сразу переходим на 14 слайд щелчком мыши. |
Отдыхают | |
| 4 | Физкультминутка для глаз слайд 13 Переход к следующему слайду – гиперссылка. |
|
| 5 | Слайд 12. Задача-сказка. В некотором царстве в некотором государстве жил-был Иван-царевич и была у него невеста Елена-прекрасная. Похитил его невесту Кощей бессмертный. Отправился Иван-царевич выручать Елена-прекрасную. Сначала его путь лежал через болото, где жила Кикимора-болотная. Туда вели две дороги. Кикимора указала дорогу к Бабе-яге, которая поможет Ивану-царевичу победить Кощея бессмертного, к ней ведут три дороги. Сколькими способами Иван-царевич может добраться до Бабы-яги? Переход к следующему слайду – гиперссылка. |
Решают задачу устно. Отвечают на вопрос задачи. |
| Слайд 14. Учитель Мы с вами изучили методы решения комбинаторных задач. Сможете вы теперь помочь Миссис Хадсон? Предлагает учащимся воспользоваться Для осуществления дифференцированного подхода в приложении есть дополнительные задачи — №2, №3, №4. Проверяется решение задачи. Гиперссылка. Переход к слайду 17. Проверяет ответы дополнительных задач. №2 – слайд 18. Переход к следующему слайду – гиперссылка. |
Отвечают на вопрос. Предполагаемый ответ: Да сможем. Выбирают один из способов и решают самостоятельно задачу. Кто успевает решают дополнительные задачи. |
|
| Рефлексия содержания учебного
материала. На слайде 15 появляется первый вопрос автоматически следующие два по щелчку. Учитель предлагает учащимся ответить на вопросы. |
Отвечают на вопросы | |
| Самостоятельная работа (два варианта). Приложение 4. | Выполняют самостоятельную работу. | |
| 7 | Слайд 15 – рефлексия учебной
деятельности на уроке. По щелчку на слайде появляются рисунки.
Желтый цвет – ничего не понял. |
Анализируют свою работу на уроке. После этого учащиеся и учитель видят результат урока. |
| 8 | Подводит итоги урока, выставляет
оценки. Благодарит учащихся за урок. Домашнее задание. |
Записывают д/з. |
urok.1sept.ru
Урок математики. 5-й класс. Комбинаторные задачи
Цели:
Обучающая:
- Познакомить с комбинаторными задачами,
- Научить решать простейшие задачи с помощью схем.
Развивающая:
- Развивать логику.
Воспитывающая
- Воспитывать интерес к предмету.
Ход урока
- Орг. момент — 2-3 мин.
- Устная работа — 7-8 мин.
- Объяснение нового материала — 15 мин.
- Закрепление — 15 мин
- Подведение итогов и постановка д/з — 5 мин.
I . Орг. момент.
Проверить готовность класса к уроку, собрать тетради .
Эпиграф урока.
Учитесь думать, объяснять,
Учитесь мыслить, рассуждать,
Ведь в математике, друзья,
Без логики никак нельзя!
II. Устная работа.
1. Вычислите устно
15*6 100-19 60-11 :8 :3 :7 *19 +23 *15 +6 *4 -25 ? ? ?
2. Вместо некоторых цифр поставлены *. Можно ли сравнить числа?
а) 32** и 31** в) **** и *** б) *1** и 8** г) *5* и 1 **
3. Подумайте, по какому правилу составлен ряд чисел и найдите три следующих числа
а) 20, 22, 24:
б) 2, 4, 8, 16:
в) 1, 4, 9, 16:
III. Объяснение нового материала
Сегодня мы познакомимся с новыми задачами - комбинаторными.
Живут эти задачи в особом разделе математики, который называется комбинаторика.
Комбинаторика — раздел математики, в котором изучаются вопросы о том, сколько различных комбинаций, подчиненных тем или иным условиям можно составить.
Рассмотрим задачу.
Задача 1.
Запишите все трёхзначные числа, для записи которых употребляются только цифры 1 и 2.
Решение.
В записи числа на первом месте (в разряде сотен) может стоять цифра 1 или 2
Или
На втором месте (в разряде десятков) в каждом случае также может стоять одна из двух цифр 1 или 2
На третьем месте (в разряде единиц) в каждом из полученных четырех случаев также можно записать либо 1, либо 2
Получим восемь чисел:
111; 112; 121; 122; 211; 212; 221; 222.
Задача 2.
В правлении фирмы входят 5 человек. Из своего состава правление должно выбрать президента и вице-президента. Сколькими способами можно это сделать?
Решение.
Президентом фирмы можно избрать одного из пяти человек:
Президент:
После того как президент избран, вице-президентом можно выбрать одного из четырёх оставшихся членов правления:
Значит, выбрать президента можно 5-ю способами и для каждого из выбранного президента 4-мя способами можно выбрать вице-президента.
Т.о. общее число способов
5 * 4=20.
IV. Закрепление.
Задача 3.
Запишите все трёхзначные числа, для записи которых употребляются только цифры о и 7 . Найдите сумму этих чисел и разделите её на 211.
Решение (коллективная работа).
- Какая цифра может стоять на первом месте? (выполняется схема на доске)
- На втором месте?
- На третьем?
700; 707;
770; 777;
(700 + 707+ 770+ 777) : 211 = 14.
Задача 4.(решить самостоятельно, используя схему)
Запишите все трёхзначные числа, для записи которых употребляются только цифры 5 и 7.
Ответ: 555; 557; 575; 577; 755; 757; 775; 777.
Задача 5.
В футбольной команде 5-го класса 7 человек. Члены команды выбирают капитана и вратаря.сколькими способами это можно сделать?
Решение.
- Сколько человек в команде?
- Какие варианты существуют? (капитан может быть вратарем и не может)
- Рассмотрим вариант, когда вратарь не может быть капитаном.
- Сколько вариантов выбора капитана существует? (7)
- Сколько существует вариантов выбора вратаря для выбранного капитана?(6)
- Сколькими способами можно выбрать капитана и
вратаря?
7 * 6 = 42. - Как изменится решение задачи, если вратарь может быть капитаном?
- Сколько способов выбора существует при этом
условии?
7 * 7 = 49.
V. Подведение итогов и постановка д/з.
С каким разделом математики мы сегодня познакомились?
Что такое комбинаторика?
Домашнее задание (раздается в распечатанном виде)
Сколько двузначных чисел можно составить из цифр 0; 2; 4; 6; если цифры в записи числа не повторяются? Запишите все эти числа.
Для того чтобы открыть дверь подъезда, нужно набрать трёхзначный код замка. Сколькими способами можно выбрать код замка, если все его цифры должны быть различными?
Исторические сведения.
Комбинаторика — ветвь математики, изучающая комбинации и перестановки предметов, возникла в XVII веке. Долгое время комбинаторика лежала вне основного русла развития математики. Положение дел резко изменилось после появления быстродействующих вычислительных машин. В настоящее время комбинаторные методы применяются в теории случайных процессов, статистике, математическом программировании, вычислительной математике и др.
С задачами, которых приходилось выбирать те или иные предметы, располагать их в определенном порядке и отыскивать среди разных расположений наилучшие, люди столкнулись ещё в доисторическую эпоху, выбирая наилучшее положение охотников во время охоты, воинов — во время битвы, инструментов — во время работы. Комбинаторные навыки оказались полезными в часы досуга. Со временем появились различные игры: нарды, шашки, шахматы, карты. В каждой из этих игр проходилось рассматривать различные сочетания фигур, и выигрывал тот, кто их лучше изучил, знал выигрышные комбинации и умел избегать проигрышных.
Но не только азартные игры давали пищу для комбинаторных размышлений математиков. Ещё с давних пор дипломаты. Стремясь к тайне переписки, изобретали сложные шифры, а секретные службы других стран пытались эти шифры разгадать. Позднее стали применять шифры, основанные на комбинаторных принципах.
Задачи, в которых идёт речь о тех или иных комбинациях объектов, называют комбинаторными.
Комбинаторика как наука стала развиваться параллельно с возникновением теории вероятностей, т.к. для решения вероятностных задач необходимо было подсчитать число различных комбинаций элементов. Первые научные исследования по комбинаторике принадлежат итальянским ученым Дж. Кардано, Н. Тарталье (ок.1499-1557), Г. Галилею(1564-1642) и французским ученым Б. Паскалю (1623-1662) и П. Ферма. Комбинаторику как самостоятельный раздел математики первым стал рассматривать немецкий ученый Г. Лейбниц в своей работе «Об искусстве комбинаторики», опубликованной в 1666 году. Он же впервые ввел термин «комбинаторика». Значительный вклад в развитие комбинаторики внес JI. Эйлер.
В современном обществе с развитием вычислительной техники комбинаторика добилась новых успехов. Так, с помощью ЭВМ была решена комбинаторная задача, известная под названием «проблема четыpex красок»: удалось доказать, что любую карту можно раскрасить в четыре цвета так, что никакие две страницы, имеющие общую границу, не будут окрашены в один и тот же цвет.
Литература.
- Н.Я.Виленкин, В.И.Жохов, А.С.Чесноков, С.И.Шварцбурд. Математика. Учебник для 5 класса общеобразовательных учреждений. М.:Мнемозина.
- Л.П.Попова. Поурочные разработки по математике к ученому комплекту Н.Я.Виленкина 5 класс. Москва «Вако».2009
urok.1sept.ru
Олимпиадные задания по алгебре (5 класс) на тему: Комбинаторные задачи
Комбинаторные задачи
Задача
Сколькими способами можно выбрать гласную и согласную буквы слова «полка»?
Решение: в этом слове две гласные буквы (о, а) и три согласные (п, л, к). Каждый искомый выбор задается картежом (а(1), а(2)), где а(1) – гласная буква, а(2) – согласная. Так как а(1) можно выбрать двумя способами, а а(2) тремя способами, то кортеж (а(1), а(2)) можно по правилу произведения выбрать 2*3=6 способами. Ответ: 6 способов.
Задача
Продают две игральные кости (каждая кость – кубик с отмеченным на его гранях точками). Одной до шести, причем на различных гранях разное число точек. Сколько различных пар точек может появиться на верхних гранях костей?
Решение: Для каждого случая составим таблицу вариантов:N = 3*3 =9 N = 3*4 = 12 Ответ: 1) N = 9; 2) N = 12.
Правило произведения.
Задача
Андрей, Борис, Виктор и Григорий играли в шахматы. Каждый сыграл с каждым по одной партии. Сколько партий было сыграно?
Решение: Решим задачу с помощью полного графа с четырьмя вершинами А,Б,В,Г. Обозначенными первыми буквами имени каждого из мальчиков. В полном графе проводятся всевозможные ребра. В данном случае отрезки ребер обозначают органные шахматные партии. Из рисунка видно, что граф имеет 6 ребер, значит, и партий было сыграно 6. Ответ: 6 партий.
Задача
Антон, Борис, Василий купили 3 билета на 1,2,3 места первого ряда на футбольный мачт. Сколькими способами они могут занять имеющиеся места?
Решение: на 1-е место может сесть любой из трех друзей, на 2 любой их двух оставшихся, а на 3 последний. Сказанное изобразим с помощью дерева, помещая в вершины графа первые буквы А,Б и В: 1 место 2 место 3 место упорядочная тройка друзей. Ответ: 6.
Задача
Из города А в город В ведут 5 дорог, а из города В в город С – 3 дороги. Сколько путей, проходящих через В, ведут из АВС?
Решение: Каждый путь школою видов задается картежом (а(1), а(2)), где а(1) – один из путей, соединяющих В и С. Так как по условию а(1) можно выбрать 5 способами, а(2) – 3способами, то картеж (а(1), а (2)) можно по правилу произведения составить 5*3 = 15 способами. Ответ: 15 путей.
Задача
Имеется 6 перчаток различных размеров. Сколькими способами можно выбрать из них одну перчатку на левую руку так, чтобы эти перчатки были различных размеров?
Решение: Эту задачу тоже можно решить по правилу произведения. Перчатка на левую руку может быть выбрана 6 способами. После того как она выбрана, перчатку на правую руку можно выбрать лишь 5 способами. (Размеры перчаток должны быть разными). Поэтому всего имеет 6*5= 30 способов. Ответ: 30 способов.
Задача
сколькими способами могут быть распределены золотая и серебренная медали по итогам первенства по футболу, если число команд 12. Решение: На золотую медаль претендуют 12 команд, на серебренную 11 команд. (одна получит золотую медаль). По правилу произведения получаем 12 * 11 = 132 способа. Ответ: 132 способа.
Задачи, на перебор вариантов происходящих событий.
Задача
В школьной столовой на первое можно заказать борщ, солянку, грибной суп, на второе – мясо с макаронами, рыбу с картошкой, курицу с рисом, а на третье – чай и компот. Сколько различных обедов можно составить из указанных блюд?
1 способ: Перечислим возможные варианты.
2 способ: Дерево возможностей
3 способ: Правило умножения заключается в том, что для того, чтобы найти число всех возможных исходов независимого проведения двух испытаний А и В, следует перемножить число всех исходов испытания А и число всех исходов испытания В, т.е. в нашей задаче имеется 3 элемента: первое, можно выбрать 3 раза, второе – 3 раза и третье – 2раза, получаем: 3х3х2=18.Ответ: 18.
Задача
Мисс Марпл, расследуя убийство, заметила отъезжающее от дома мистера Дэвидсона такси. Она запомнила первую цифру «2». В городке номера машин были трехзначные и состояли из цифр 1, 2, 3, 4 и 5. скольких водителей, в худшем случае, ей придется опросить, чтобы найти настоящего убийцу?
Используя правило умножения, получаем: 5*5=25.Ответ: 25 водителей.
Задача
Сколько трехзначных чисел можно составить из цифр 1, 2, 3, 5, 7, используя в записи числа каждую из них не более одного раза?
Реш. Первую цифру трехзначного числа можно выбрать четырьмя способами, т.к. после выбора остается три, то вторую цифру можно выбрать из оставшихся цифр уже тремя способами. Наконец, третью цифру можно выбрать двумя способами. Следовательно, общее число искомых трехзначных чисел равно произведению 4 * 3 * 2=24.Ответ: 24.
Задача
Сколько четных двузначных чисел можно составить из цифр 0, 2, 3, 6, 7, 9? Используя правило умножения, получаем: 5*3=15 Ответ: 15
Задача
Свете на день рождения подарили 4 плюшевых игрушки, 2 мяча и 5 кукол. Мама положила все игрушки в большую коробку. Сколькими способами Света сможет достать из коробки 1 плюшевую игрушку, 1 мяч и 1 куклу?Используя правило умножения, получаем: 2*4*5=40.Ответ:40.
Задачи на перестановки.
Перестановкой из n элементов называется каждое расположение этих элементов в определенном порядке. Число перестановок из n элементов обозначается символом Рn (Р из n элементов). Например.
Задача
в книжном шкафу на полке стоят 3 книги, как эти книги можно переставить?
Р3= 3*2*1= 6 = 3!
Задача
Саша, Петя, Денис, Оля, Настя часто ходят в кафе. Каждый раз, обедая там, они рассаживаются по-разному. Сколько дней друзья смогут это сделать без повторения?
Р5 = 5! = 5*4*3*2*1 = 120.
Задача
Сколькими способами могут быть расставлены 8 участниц, финального забега, на восьми беговых дорожках?
Число способов равно числу перестановок из 8 элементов. По формуле числа перестановок находим, что Р8=8! = 1*2*3*4*5*6*7*8 = 40320.
Задача
Сколько различных четырехзначных чисел, в которых цифры не повторяются, можно составить из цифр 0,2,4,6?
Решение: из цифр 0,2,4,6 можно получить Р4 перестановок. Из этого числа надо исключить те перестановки, которые начинаются с 0, т.к. натуральное число не может начинаться с цифры 0. Число таких перестановок равно Р3. значит, искомое число четырехзначных чисел равно Р4-Р3 = 4!-3! = 24 – 6= 18.
Задачи на размещения.
Размещением из n элементов по k (k меньше или равно n) называется любое множество, состоящее из любых k элементов, взятых в определенном порядке из данных n элементов. Обозначение: ( читают: «А из n по k).
Например : Пусть имеется три шара и две пустых ячейки. В пустые ячейки можно разместить по два шара.
Решение: из трех элементов по два будут наборы (1,2), (2,1), (1,3), (3,1), (2,3), (3,2).Размещения считаются различными, если они отличаются самими элементами или порядком их расположения. Например: (1,2), (2,1), (1,3), (3,1) в нашем примере.Число размещений можно найти не выписывая сами размещения. Будем рассуждать так: первый элемент можно выбрать тремя способами, т.к. им может быть любой из трех, для каждого выбранного первого элемента можно двумя способами выбрать второй.В результате получаем: = 3*2 = 6.
Задача
Учащиеся второго класса изучают 8 предметов. Сколькими способами можно составить расписание на один день, чтобы в нем было 4 различных предмета?
Решение: = 8*7*6*5 = 1680.
Задача
В классе десять предметов и пять уроков в день. Сколькими способами можно составить расписание на один день?
Решение: А105=10*9*8*7*6 = 30240 способов.
Задача
В 9 классе 15 предметов. Завучу школы нужно составить расписание на субботу, если в этот день 5 уроков. Сколько различных вариантов расписания можно составить, если все уроки различны?
Решение: из 15 предметов 5 любых можно выбрать А155= 15*14*13*12*11= 360360.
Задача
Сколькими способами можно составить трехцветный флаг из полос разной ширины, если имеются материи из 8 тканей?
Решение: А83=8*7*6 = 336.
Задачи на сочетания.
Сочетанием из n элементов по k называется любое множество, составленное из k элементов, выбранных из данных n элементов. Обозначение: (читают С из n по k).
Задача
Пусть имеется три шара разного цвета. Нужно рассмотреть все возможные способы составления шаров, в которых сочетаются два цвета из данных трех.
Решение: из трех элементов (1;2;3) по два будут наборы (1,2),(1,3),(2,3). В отличии от размещений в сочетаниях не имеет значения, в каком порядке указаны элементы. Два сочетания различны, если отличаются друг от друга хотя бы одним элементом. Например: (1,2),(1,3). В нашем примере, в каждом сочетании выполнимы все перестановки. Число таких перестановок равно Р2. В результате получим все возможные комбинации из 3 элементов по 2, которые отличаются либо самими элементами, либо порядком элементов, т.е. все размещения из 3 элементов по 2. всего мы получим размещений. Значит если количество размещений разделить на количество перестановок, получим количество сочетаний из трех элементов по два. Отсюда .
Задача
из 15 членов туристической группы надо выбрать трех дежурных. Сколькими способами можно сделать этот выбор?
Решение: если, каждый выбор отличается от другого хотя бы одним дежурным, значит, здесь речь идет о сочетаниях из 15 элементов по 3: .
Задача
На родительском собрании присутствует 20 человек. Сколько существует различных вариантов состава родительского комитета, если в него должны войти 5 человек?
Решение: В этой задаче нас не интересует порядок фамилий в списке комитета. Если в результате в его составе окажутся одни и те же люди, то по смыслу для нас это один и тот же вариант. Поэтому мы можем воспользоваться формулой для подсчета числа сочетаний из 20 элементов по 5. В каждом сочетании выполнимы 5 перестановок т.е.Р5= 1*2*3*4*5, в результате получим все возможные комбинации из 20 элементов по 5: А205=20*19*18*17*16.
nsportal.ru
Конспект урока «Решение комбинаторных задач» (5 класс)
АНО ПО “ШКОЛА КЛАССИЧЕСКОГО ТАНЦА”
«Решение комбинаторных задач»
в 5 классе
Подготовила: преподаватель математики
Иофик Татьяна Александровна
г. Москва
Дата: 01.10.2018 г.
Тип урока: урок изучения и первичного закрепления новых знаний
Цель урока: начать формировать умение решать простейшие комбинаторные задачи перебором, с помощью «дерева возможных вариантов», с помощью правила умножения.
Оборудование: компьютер, экран, проектор, презентация к уроку,
Задачи:
Образовательные:
К концу урока учащиеся должны уметь:
выделять комбинаторные задачи из ряда предложенных задач;
решать простейшие комбинаторные задачи;
выработать умение применять математическую теорию в конкретных ситуациях.
Воспитательные:
Способствовать:
формированию познавательного интереса к предмету; мировоззрения учащихся,
воспитанию чувства патриотизма; ответственности за качество и результат выполняемой работы.
Развивающие:
Способствовать:
совершенствованию операций умственной деятельности: анализ, синтез, классификация, способность наблюдать и делать выводы, выделять существенные признаки.
ХОД УРОКА
I. Организационный момент
Проверка готовности учащихся к уроку.
II. Актуализация знаний.
(слайд 1)
— В старинных русских сказаниях повествуется, как богатырь, доехав до распутья, читает на камне: “Прямо поедешь – голову сложишь, направо поедешь – коня потеряешь, налево поедешь – меча лишишься”. Ребята, с какой проблемой сталкивается добрый молодец на перепутье? (с проблемой выбора дальнейшего пути движения)
— Верно! А дальше уже говорится, как он выходит из того положения, в которое попал в результате выбора. Но выбирать разные пути или варианты приходится и современному человеку.
Приведите примеры, когда нам приходится делать выбор? (слайд 2)
Оказывается, существует целый раздел математики, который занят поисками ответов на эти вопросы. А вот называется он — комбинаторика. (слайд 3)
— А как вы понимаете, что такое комбинаторика? (ответы учащихся)
Комбинаторика – это раздел математики, в котором изучается, сколько различных комбинаций, подчиненных тем или иным условиям, можно составить из заданных объектов.
— Тема нашего урока называется «Решение комбинаторных задач». Откройте тетради, запишите число и тему урока.
II. Изучение нового материала.
— Задачи, которые мы сегодня будем решать, помогут вам творить, думать необычно, оригинально, смело, видеть то, мимо чего вы часто проходили не замечая, любить неизвестное, новое; преодолевать трудности.
— И еще сегодня в очередной раз убедимся, что наш мир полон математики, и продолжим исследование на предмет выявления математики вокруг нас.
Задача №1. Несколько стран решили использовать для своего государственного флага символику в виде трех горизонтальных полос одинаковой ширины разных цветов – белого, синего, красного. Сколько стран могут использовать такую символику при условии, что у каждой страны – свой флаг?
Дети рисуют флаги, используя белый, синий и красный цвета.
Итак, сколько вариантов у вас получилось? (Считаем)
— Обычный вопрос в комбинаторных задачах – это «Сколькими способами…?» или «Сколько вариантов…?»
Давайте еще раз вернемся к задаче о флагах, решим ее, используя перебор возможных вариантов:
КБС КСБ
БСК БКС
СБК СКБ
Ответ: 6 вариантов.
Итак, при решении этой задачи мы искали способ перебора возможных вариантов. Во многих случаях оказывается полезным прием построения картинки – схемы перебора вариантов. Это, во – первых, наглядно, во- вторых, позволяет нам все учесть, ничего не пропустить (слайд 4).
Решение
Флаг
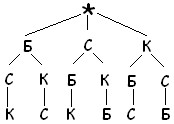
Варианты БСК, БКС, СБК, СКБ, КБС, КСБ. Этот метод называется “Дерево возможных вариантов”.
Ответ: 6 вариантов.
Вопрос, ответ на который должны знать все: “ Какой из представленных вариантов флагов – государственный флаг РФ?” Что означает каждый цвет нашего флага?
Белый цвет означает мир, чистоту, непорочность, совершенство; синий — цвет
веры и верности, постоянства; красный цвет символизирует энергию, силу, кровь,
пролитую за Отечество. (слайд 5)
Оказывается, не только флаг России имеет эти три цвета. Есть государства, флаги которых, имеют такие же цвета.
КБС – Люксембург и Нидерланды.
Найдем правило решения таких задач путем логического рассуждения.
Разберем на примере цветных полосок. Возьмем белую полоску – её можно переставить 3 раза, возьмем синюю полоску – её можно переставить только 2 раза, т.к. одно из мест уже занято белой, возьмем красную полоску – её можно положить только 1 раз.
ИТОГО: 3 х 2 х 1=6
Правило умножения: если первый элемент в комбинации можно выбрать а способами, после чего второй элемент – b способами, то общее число комбинаций будет равно а х b.
Физкультминутка для глаз.
Нарисовать глазами квадрат, круг, треугольник, овал, ромб по часовой стрелке, а затем – против часовой стрелки. (Фигуры можно нарисовать на доске)
Откроем учебник на стр. 43 и рассмотрим задачу 1 с дополнением первым после неё. Обратить внимание на логику перебора. Решить задачи №№ 137, 138, 141 методом перебора.
— Придя в школу, повесив одежду, вы очень часто отправляетесь к расписанию, посмотреть порядок уроков на день. А представьте на миг, что бы стало в школе, если бы не было расписания. Наверное, хаос: никто бы не знал, куда идти.
В помощь тому, кто составляет расписание, решим задачу:
Задача №2. В 5 классе во вторник 5 уроков: физкультура, русский язык, литература, история и математика. Сколько можно составить вариантов расписания на день, зная точно, что математика – первый урок?
Фронтальная работа
— Как бы вы предложили решить эту задачу? (ответы детей)
— Предлагаю вам закодировать названия предметов их начальной буквой: Ф – физкультура, Р – русский язык, Л – литература, И – история, М – математика.
— С какого урока мы начнем составлять расписание? (с математики)
Какие способы решения этой задачи вы знаете? (перебор, дерево, произведение). А какой вариант здесь самый удобный?
Сколько возможных вариантов расписания уроков у вас получилось? Подсчитайте. (24 варианта)
-А если бы в задаче не было условия, что математика – первый урок, что бы изменилось? (ответ, вариантов расписания было бы намного больше.- Сколько?- 120)
— Да, трудно придется тому, кто забудет порядок уроков и, не посмотрев в расписание, захочет правильно заполнить дневник.
IV. Закрепление изученного
— Настало время перекусить. Мы идем в школьную столовую
Задача№3. Сколько различных завтраков, состоящих из 1 напитка и 1 вида выпечки, можно составить из чая (ч), кофе (к), булочки (б), печенья (п) и вафель (в)?
Заполните схему дерева возможных вариантов в соответствии с условием задачи.
Напитки
Выпечка
— Обменяйтесь тетрадями с соседом по парте. Проверьте друг друга. Сколько завтраков у вас должно получиться? (6 завтраков) — Если ваш сосед выполнил задание верно, поставьте «плюс», иначе – «минус». Верните друг другу тетради.
Работа по учебнику.
Разбор решения задачи № 2, стр. 43.
Решение задач из учебника №№ 145, 146 методом «дерева возможных вариантов».
Внимание, перед вами лежат листочки с текстом отрывка из одного известного произведения. Прочитайте его.
Проказница Мартышка,
Осел,
Козел,
Да косолапый Мишка
Затеяли сыграть в …
Ударили в смычки, дерут, а толку нет.
………………..
«Стой, братцы, стой!» — кричит Мартышка —
Погодите.
Как музыке идти? Ведь Вы не так сидите!
— Из какого произведения данный отрывок и кто автор? (басня Ивана Андреевича Крылова «Квартет») (слайд 6)
— Какую задачу можно решить в этой басне? Каким способом? (ответы детей). Можно дать задание первому варианту (и первому ученику у доски) записать решение методом перебора, второму – методом «дерева вариантов», третьему – способом умножения.
V. Подведение итогов
— С чем вы познакомились сегодня на уроке? (с комбинаторными задачами)
— Какими способами вы научились решать такие задачи? (перебор, дерево, умножение)
— Итак, ученику приходится встречаться с математикой, практически, постоянно. В частности, вы просчитываете различные комбинации – когда? (обсуждение с детьми):
когда выбираете меню в столовой,
формулируете свой ответ на уроках,
составляете график дежурства по классу,
планируете, как провести свои выходные или каникулы и так далее.
VI. Домашнее задание
— Запишите в тетрадь домашнее задание:
1. №№ 139, 140 из учебника.
2. Шестеро детей выбирает роли согласно известной считалке «На златом крыльце сидели…» (слайд 7). Сколько вариантов выбора роли у каждого ребенка и сколько вариантов распределения ролей существует?
3. Придумать свою комбинаторную задачу практического характера.
VII. Рефлексия
— Ребята, нарисуйте дерево возможных эмоций (слайд 8), которые можно испытывать во время урока, в виде различных смайликов. Закрасьте тот смайлик, который соответствовал вашему настроению на уроке.
И С П О Л Ь З О В А Н Н Ы Е Р Е С У Р С Ы :
Математика. 5 класс. Дорофеев Г.В., Шарыгин И.Ф., Суворова С.Б. и др. М., «Просвещение», 2017.
https://clck.ru/EZjcE
https://yandex.ru/collections/card/5b1bcde3f03d153c20f867cd/
http://ru.fanpop.com/clubs/homer-simpson/images/10030107/title/homer-wallpaper
http://fb2.booksgid.com/content/16/luchano-malmuzi-neandertalskiy-malchik-v-shkole-i-doma/3.html
http://blog.geneticslab.emory.edu/hubfs/Exome-1.jpg?t=1517074552427
https://ru-static.z-dn.net/files/d65/b5b697993adf15b4b23c95761ef7535d.jpg
https://cf.ppt-online.org/files/slide/y/YVqXDeSM7OZdB3Qvknr4PtpzxwNI8yu1EoCcGj/slide-14.jpg
http://www.speakrus.ru/articles/babycnt.htm#golden1
infourok.ru
Решение комбинаторных задач. 5-й класс
Тип урока: формирование и совершенствование умений и навыков.
Цели урока:
- Образовательные: закрепить умение решения комбинаторных задач на примере составления многозначных чисел из предложенных цифр с помощью перечисления комбинаций (дерева возможных вариантов), подсчет общего числа комбинаций по правилу умножения.
- Развивающие: развитие математического мышления; развитие познавательного интереса учащихся; развитие умения самостоятельно выбирать способ решения и умения обосновать выбор;
- Воспитательные: формирование навыков самоконтроля, воспитание самостоятельности и настойчивости в достижении цели.
Оборудование: карточки с заданиями для индивидуальной работы, карточки с решением задач для самопроверки, карточки-«подсказки» для решения задач.
Структура урока:
- Организационный момент
- Актуализация опорных знаний и умений учащихся (устный опрос)
- Формирование и закрепление знаний и умений:
- Коллективная работа над задачами
- Индивидуальная работа над задачами
- Подведение итогов урока
- Домашнее задание
Показатель реального результата достижения цели урока: самостоятельное выполнение заданий на составление многозначных чисел с применением дерева возможных вариантов и подсчет общего числа комбинаций по правилу умножения в знакомой и измененной ситуациях.
ХОД УРОКА
1. Устный опрос
2. Натуральные числа
– Какие числа называются
натуральными? (Числа, используемые при счете
предметов)
– С помощью каких «знаков» можно
написать любое натуральное число? (С помощью
цифр: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9)
– Как называется группа из трех цифр в
записи числа, считая справа налево? (Класс)
– Как называется место, занимаемое
цифрой в записи числа? (Разряд)
– Сколько разрядов в каждом классе? (Три)
– Что обозначает цифра 0 в десятичной
записи числа? (Отсутствие единиц данного
разряда)
– Какая цифра не может стоять в старшем
разряде числа? (0)
3. Комбинаторные задачи
– Какие задачи называются
комбинаторными? (Задачи, в которых идет речь о
тех или иных комбинациях объектов)
– Что такое комбинаторика? (Раздел
математики, в котором изучаются вопросы о том,
сколько различных комбинаций, подчиненных тем
или иным условиям, можно составить)
– Какими способами мы умеем решать
комбинаторные задачи? (С помощью правила
умножения и с помощью дерева возможных
вариантов)
– В чем заключается правило
умножения? (Если первый элемент в
комбинации можно выбрать а способами,
после чего второй элемент b способами, то общее
число комбинаций из двух элементов будет a .
b).
– В чем заключается правило решения
задач с помощью дерева вариантов?
4. Работа по теме урока:
1 этап. Коллективная работа над задачами
№ 1
Запишите все трехзначные числа, для записи которых употребляются только цифры 1 и 2.
– Какая цифра может стоять в разряде
сотен? (1 или 2)
– Какая цифра может стоять в разряде
десятков в каждом из полученных двух случаев? (1
или 2)
– Какая цифра может стоять в разряде
единиц в каждом из полученных четырех случаев? (1
или 2)
По ходу рассуждений выполняется схема на доске
Получили 8 чисел: 111, 112, 121, 122, 211, 212, 221, 222
№ 2
Сколько трехзначных чисел можно составить из цифр 2, 4, 6, 8, если цифры в записи числа не повторяются?
– Сколько цифр дано? (Четыре)
– Какое условие поставлено? (Цифры не
должны повторяться)
– Какая цифра может стоять на первом
месте? (Любая)
– Если цифру поставили на первое место,
может она занимать второе, третье место? (Нет)
Первой цифрой числа может быть любая из четырех
данных цифр, второй – любая из трех других. А
третьей – любая из двух оставшихся. Всего из
данных цифр можно составить
4 . 3 . 2 = 24
трехзначных числа.
Ответ: 24 числа.
Вывод: для удобства перечисления всех возможных вариантов мы пользовались деревом вариантов. При большом количестве комбинаций дерево быстро ветвится и становится необозримым. Поэтому для подсчета количества комбинаций, если не требуется перечислить все комбинации, лучше пользоваться правилом умножения.
2 этап. Индивидуальная работа над задачами
Индивидуальная работа над задачами состоит из двух шагов:
Шаг 1 задачи № 3 и № 4. Задачи решаются
самостоятельно с последующей самопроверкой по
карточке с решением, выданным учителем. (Приложение 1)
Если учащиеся справились с решением задач № 3 и №
4, то им предлагаются задачи № 5, № 6, № 7
Если учащийся не справился с задачами № 3 и № 4,
ему предлагаются аналогичные задачи № 3.1 и №
4.1. Если учащийся справляется с задачами № 3.1 и
№ 4.1, он решет № 5, № 6, № 7.
В случае, если учащиеся затрудняются в решении
задач № 3.1, № 4.1, № 5, № 6, № 7 им выдаются
карточки-«подсказки». (Приложение
2)
№ 3
Запишите все трехзначные числа, для записи которых используются цифры 5 и 7.
№ 4
Запишите все трехзначные числа, для записи которых используются цифры 0, 2, 5, если цифры в записи не повторяются.
№ 3.1
Запишите все трехзначные числа, для записи которых используются цифры 2 и 9
№ 4.1
Запишите все трехзначные числа, в записи которых используются цифры 0, 3, 7. Если цифры в записи не повторяются.
№ 5
Сколько двухзначных чисел можно составить из цифр 0, 2, 4, 6, если цифры в записи числа не повторяются? Запишите все эти числа.
№ 6
Сколько трехзначных чисел можно составить из нечетных цифр, если цифры в записи числа не повторяются? Запишите первые 12 чисел, если составленные числа расположены в порядке возрастания.
№ 7
Сколько существует трехзначных чисел, в записи которых нет цифры 3?
Ответы:
№ 3.1 222, 229, 292, 299,
922, 929, 992, 999
№ 4.1 307, 370, 703, 730
№ 5 3 .
3 = 9 чисел 20, 24, 26, 40, 42, 46, 60, 62, 64
№ 6 5 .
4 . 3 = 60 чисел 135, 137, 139, 153, 157, 159, 173, 175,
179, 193, 195, 197
№ 7 8 .
9 . 9 = 648 чисел
5. Итог урока
– Чем удобно пользоваться при
перечислении всех возможных комбинаций?
– Почему при большом количестве
комбинаций неудобно пользоваться деревом
вариантов?
– Какое правило вы знаете для подсчета
количества комбинаций? Сформулируйте его.
6. Рефлексия. Что нового узнали на уроке? Что уже было знакомо ранее? Какие задачи вызвали наибольшее затруднение? Какая задача понравилась больше остальных?
7. Оценивание работы на уроке каждого учащегося в соответствии с количеством и номерами решенных задач и взятых подсказок.
8. Задание на дом
– Составить и решить две комбинаторных задачи на составление многозначных чисел из предложенных цифр.
urok.1sept.ru
Исследовательская работа на тему «Комбинаторные задачи» 5 класс
VII ГОРОДСКАЯ НАУЧНО-ПРАКТИЧЕСКАЯ КОНФЕРЕНЦИЯ УЧАЩИХСЯ
5-8 классов по математике, физике, информатике «ОБЫКНОВЕННОЕ ЧУДО»
Муниципальное автономное образовательное учреждение
«Физико-математическая школа №56» г. Улан-Удэ
Исследовательская работа по математике:
Комбинаторные задачи
Выполнила: Шагдурова Адиса, ученица 5а класса МАОУ «ФМШ № 56»
Руководитель: Петинова Наталья Исаевна, учитель математики высшей категории МАОУ «ФМШ № 56»
Улан–Удэ
2019
Оглавление.
Введение …………………………………………………………………………………….2
Глава I. Историческая страница…………………………………………………3
Глава II. Комбинаторные задачи ………………………………….…………. 4
Глава III. Банк комбинаторных задач……………………………………….. 8
Заключение……………………………………………………………………………….. 9
Список литературы……………………………………………………………………10
Введение
Одним из важных разделов математики является комбинаторика. Обладать «комбинаторным искусством» должен каждый человек. Люди, владеющие техникой решения комбинаторных задач, а следовательно, умеющие рассуждать, перебирать различные варианты решений, часто находят выход , казалось бы, из самой безвыходной ситуации.
Актуальность выбранной мной темы исследования обусловлена тем, что комбинаторные задачи могут дать ответ на многие вопросы, связанные с практической деятельность людей, решение задач помогает развивать умственные способности, логическое мышление, вычислительные навыки. Умение решать комбинаторные задачим необходимы представителям самых разный специальностей.
Цель работы — выявить общие подходы к решению комбинаторных задач при обилии их различных типов и многообразии приемов и методов решения, овладение методами решения задач, составить банк задач для учащихся 5 класса.
Для реализации поставленной цели необходимо решить следующие задачи исследования:
Задачи:
Познакомиться с историей возникновения науки комбинаторики;
Поиск способов решения комбинаторных задач;
Поработать с ресурсами Internet;
Расширить и углубить представление о практическом значении математики в жизни;
Уметь работать с научно-познавательной литературой, анализировать, делать выводы;
Работать над созданием банка комбинаторных задач .
В ходе решения поставленных задач использовались следующие методы исследования:
1)изучение и анализ учебно–методической литературы по проблеме исследования;
2)методы сравнения, обобщения и классификации;
3)обобщение и анализ теоретико-методического материала.
Объект исследования: комбинаторные задачи
Предмет исследования: изучение способов решения комбинаторных задач.
Данное исследование поможет по-другому посмотреть на окружающий мир. Изучив его, я смогу объективно оценивать некоторые вещи, опираясь на математические подсчеты.
Глава I. Историческая страница
Термин «комбинаторика» происходит от латинского слова «combina», что в переводе на русский означает – «сочетать», «соединять».
Комбинаторика возникла в XVII веке. Тогда широко были распространены лотереи, игры в карты и кости. И первые комбинаторные задачи касались именно азартных игр, так как возникало много вопросов, сколькими способами можно выбросить данное число очков, бросая две или три кости, или сколькими способами можно получить двух королей в данной карточной игре.
Со временем появились различные игры (нарды, карты, шашки, шахматы и т.д.). В каждой из этих игр приходилось рассматривать различные сочетания фигур, и выигрывал тот, кто их лучше изучил, знал выигрышные комбинации и умел избегать проигрышных.
Не только азартные игры давали пищу для комбинаторных размышлений математиков. Но и дипломаты, стремясь к тайне переписки, изобретали сложные шифры, а секретные службы других государств пытались эти шифры разгадать. Стали применять шифры, основанные на комбинаторных принципах, например, на различных перестановках букв, заменах букв с использованием ключевых слов и т.д.
Комбинаторика как наука стала развиваться в XIII веке параллельно с возникновением теории вероятностей, так как для решения вероятностных задач необходимо было подсчитать число различных комбинаций элементов. Первые научные исследования по комбинаторике принадлежат итальянским ученым Дж. Кардано, Н. Тарталье (1499-1557), Г. Галилею (1564-1642) и французским ученым Б. Паскалю (1623-1662) и П. Ферма. Комбинаторику как самостоятельный раздел математики первым стал рассматривать немецкий ученый Г. Лейбниц в своей работе «Об искусстве комбинаторики», опубликованной в 1666 году. Он также впервые ввел термин «комбинаторика». Значительный вклад в развитие комбинаторики внес Л.Эйлер.
Глава II. Комбинаторные задачи
Перебор возможных вариантов.
Перед нами нередко возникают проблемы, которые имеют не одно, а несколько различных решений. Обычно одни из них нас устраивают, а другие нет. Методы решения комбинаторных задач очень сильно отличаются друг от друга, но все они могут быть использованы для получения ответа. Одним из самых простых, но в то же время и самых долгих способов является перебор. При нем необходимо просто перебрать все возможные варианты решения, не составляя каких-либо схем и таблиц.
Задача 1. Сколько двузначных чисел можно составить из цифр: 1, 4 и 7. (9)
Решение: для того, чтобы не пропустить и не повторить ни одно из чисел, будем записывать их в порядке возрастания. Сначала запишем числа, начинающиеся с цифры 1, затем с цифры 4, и, наконец, с цифры 7:
11, 14, 17, 41, 44, 47, 71, 74, 77.
Задача 2. Одноклассницы Оля, Валя, и Катя дежурят по школе. Сколькими способами классный руководитель может расставить девочек по одной на каждом из трех этажей школы?
Решение: Предположим, что Олю назначили дежурить на третьем этаже. Тогда на втором этаже может дежурить Валя или Катя, а на первом – соответственно Катя или Валя. Получим два способа распределения дежурства(девочки обозначены первыми буквами их имен). Пусть теперь дежурной на третьем этаже назначили Валю. Тогда на втором этаже может дежурить Оля или Катя, а на первом – соответственно Катя или Оля. Получим еще два способа распределения дежурства. И наконец, предположим, что дежурной на третьем этаже назначили Катю. Получим еще два способа распределения дежурства. Таким образом получилось шесть способов распределения дежурства:
3-й этажО
О
В
В
К
К
2-й этаж
В
К
О
К
В
О
1-й этаж
К
В
К
О
О
В
Ответ: 6 способов
Дерево возможных вариантов.
При решении комбинаторных задач важно рассмотреть (перебрать ) все случаи. Поэтому процесс перебора желательно сделать удобным и наглядным. Например, можно проиллюстрировать с помощью схемы, которая называется деревом возможных вариантов.
Задача 1. Петя, Коля и Вася решили съесть мороженое. У мальчиков было одно клубничное, одно шоколадное, одно малиновое и одно вишнёвое мороженое. Сколько вариантов выбора мороженого было у мальчиков?
Решение: Решим эту задачу с помощью дерева возможных вариантов. Обозначим клубничное мороженое буковой «к», шоколадное – «ш», малиновое – «м», вишнёвое – «в».Поскольку мы учтём все возможные варианты, то нам всё равно, в каком порядке мальчики будут выбирать мороженое. Сначала проиллюстрируем все возможные варианты выбора Пети, затем Коли и Васи:
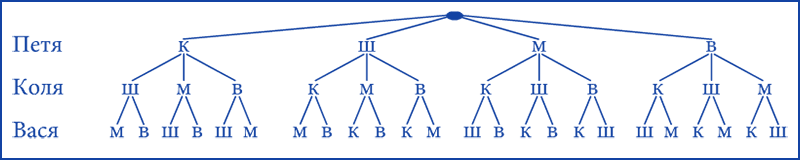
Мы перебрали все возможные варианты. Полученная схема и называется деревом возможных вариантов. Осталось определить количество этих вариантов. Для этого нужно посчитать количество вариантов в последней строке. Получилось 24 варианта.
Ответ: 24 варианта.
Задача 2. Сколько можно составить различных букетов из трех роз, если в продаже имеются белые и красные розы?
Решение:
. 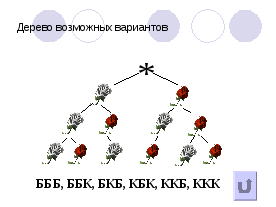
Ответ: 6 букетов.
В основе решения большинства комбинаторных задач лежит два правила: правило суммы и правило произведения.
Правило сложения
Если некоторый объект А можно выбрать m способами, а другой объект В можно выбрать n способами, то выбор «либо А, либо В» можно осуществить m+n способами.
Задача 1. На тарелке лежат 5 яблок и 4 апельсина. Сколькими способами можно выбрать один плод?
Решение: По условию задачи яблоко можно выбрать пятью способами, апельсин – четырьмя. Так как в задаче речь идет о выборе «либо яблоко, либо апельсин», то его, согласно правилу сложения, можно осуществить 5+4=9 способами
Задача2.Туриста заинтересовали 5 маршрутов в Карелии и 7 маршрутов на Кавказе. Сколькими способами он может организовать свой отпуск, имея время на один маршрут?
Решение: Поскольку имеется 5+7=12 различных маршрутов, то один из них можно выбрать 12 способами.
Ответ: 12 способов
Правило умножения
Если объект А можно выбрать m способами и если после каждого такого выбора объект В можно выбрать п способами, то выбор пары (А, В) в указанном порядке можно осуществить m∙п способами.
Для того чтобы найти число всех возможных вариантов (переборов), следует перемножить число всех исходов одного варианта и число всех исходов другого варианта. Оно прекрасно подходит в том случае, когда по условию не нужно перечислять все возможные варианты решения, необходимо просто найти их максимальное количество.
Задача 1. Сколько трехзначных чисел можно составить из цифр 1,3,5,7, используя в записи числа каждую из них не более одного раза?
Решение: Рассуждать будем так. Первую цифру трехзначного числа можно выбрать четырьмя способами. Так как после выбора первой цифры останутся три, то вторую цифру можно выбрать из оставшихся цифр уже тремя способами. Наконец, третью цифру можно выбрать (из оставшихся двух) двумя способами. Следовательно, общее число искомых трехзначных чисел равно произведению 4∙3∙2, т.е. 24.
Ответ: 24
Задача 2. Из города А в город В ведут две дороги, из города В в город С – три дороги, из города С до пристани – две дороги. Туристы хотят проехать из города А через города В и С к пристани. Сколькими способами они могут выбрать маршрут?
Решение: Пусть из города А в В туристы могут выбрать двумя способами. Далее в каждом случае они могут проехать из В в С тремя способами. Значит, имеется 2∙3 вариантов маршрута из А в С. Так как из города С на пристань можно попасть двумя способами, то всего существует 2∙3∙2=12 способов выбора туристами маршрута из города А к пристани.
Ответ: 12
Глава III. Банк задач.
1.Сколько двузначных чисел можно составить из цифр 1,2,5,7,9?
2. Сколько двузначных чисел можно составить из цифр 1,2,5,7,9 при условии, что цифры недолжны повторяться?
3.В 5а классе в понедельник 4 урока: математика, история, английский язык, русский язык. Сколько можно составить вариантов расписания на вторник?
4.Из города А в город В ведут две дороги, из города В в город С – три дороги, из города С до пристани – две дороги. Туристы хотят проехать из города А через города В и С к пристани. Сколькими способами они могут выбрать маршрут?
5. В школьной столовой имеются три первых блюда, пять вторых блюд и два третьих.
Сколькими способами ученик может выбрать обед, состоящий из первого, второго и третьего блюд?
6.В кружке художественного слова занимаются 9 девочек и 8 мальчиков. Сколько есть способов выбора пары ведущих школьного концерта, состоящий из девочки и мальчика?
7.Из класса ,в котором 28 человек , надо выбрать трех дежурных по одному на каждом этаже. Каким количеством это можно сделать?
8.В футбольном турнире участвуют несколько команд, Оказалось. Что все они использовали для трусов и футболок два разных цвета из пяти возможных: белый, красный, синий, зелены, желтый. Выяснилось, что были использованы все возможные варианты. Сколько команд участвовало в турнире?
9. Из пункта А в пункт В можно попасть десятью путями, а из пункта В в пункт С – девятью путями. Сколько имеется маршрутов из пункта А в пункт С через пункт В?
Заключение.
Моя работа заключалась в том, чтобы узнать подробнее об одном из разделов математики — комбинаторике. Я постаралась выяснить, какие методы применяются для их решения. Научилась составлять и решать комбинаторные задачи. Комбинаторных задач включены в олимпиадные задания, ГИА и ЕГЭ. Поэтому мне захотелось помочь учителям и ребятам в изучении данной темы. Я надеюсь продолжить работу над этой темой, разработать уже задачи для учащихся старших классов. Самое главное я считаю, что своей работой я заинтересовала и учащихся нашей школы, и учителей. Ведь придумывая самостоятельно задачи, ребята будут развивать в себе еще логическое мышление и творческие способности.
Список литературы:
Гнеденко Б. В., Журбенко, И. Г. Теория вероятностей и комбинаторика //Математика в школе. – 2007. — №6. – с. 67-70.
Гусев В. А. Внеклассная работа по математике в 5-8 классах. /Под. ред. С. И. Шварцбурга. — М.: Просвещение, 1977. – 288с.
Дихтярь М., Эргле Е. Исторические комбинаторные задачи и комбинаторные модели //Математика. – 2007. — №14. – с. 23-24.
Математика: Учебник для 5 кл. общеобразоват. учреждений / А.Г.Мерзляк, В.Б.Полонский,М.С, Якира. – 2-е изд.перераб. — М.: Вентана — Граф, 2017. – 304с.
Овсянникова Л.В. Факультативный курс по математике //Начальная школа. – 2005. — №9. – с. 29-33.
Виленкин Н. Я. Комбинаторика. – М.: Наука, 1969. – 328с.
Перельман Я. И. Занимательные задачи и опыты. — Д.: ВАП, 1994. – 527с.
Цыганов Ш. Комбинаторика от А до Я //Математика. – 2001. — №26. – с. 9-23.
http://combinatorica.narod.ru/second.htm
http://festival.1september.ru/articles/211057/
http://www.brsu.brest.by/pages/centr_pmo/au5.html
http://ro-che.info/docs/funceq.pdf
http://olympiads.mccme.ru/lktg/2006/3/3-3ru.pdf
infourok.ru