Комбинированные задачи — методическая рекомендация. Химия, 8–9 класс.

1.	Вычисление количества продукта по массе раствора и массовой доле реагента	2 вид — интерпретация	среднее	3 Б.	Задача на вычисление химического количества продукта реакции по известной массе раствора реагирующего вещества и его массовой доле.
2.	Вычисление массы продукта по массе раствора и массовой доле реагента	2 вид — интерпретация	среднее	3 Б.	Задача на определение массы одного из продуктов реакции по известной массе раствора и массовой доле реагирующего вещества.
3.	Вычисление объёма продукта по массе раствора и массовой доле реагента	2 вид — интерпретация	среднее	3 Б.	Задача на определение объёма одного из продуктов реакции по известной массе раствора и массовой доле реагирующего вещества.
4.	Вычисление массы раствора реагента по количеству продукта реакции	3 вид — анализ	сложное	4 Б.	Задача на вычисление массы раствора реагирующего вещества с известной массовой долей по количеству продукта реакции.
5.	Вычисление массы раствора реагента по массе второго реагента	3 вид — анализ	сложное	4 Б.	Задача на вычисление массы раствора реагирующего вещества с известной массовой долей по известной массе второго реагента.
6.	Вычисли массу раствора	3 вид — анализ	среднее	5 Б.	Задача на вычисление массы раствора реагента с определённой массовой долей, если известна масса раствора и массовая доля второго реагента.

Урок химии в 11 классе «Решение комбинированных задач».

Урок химии в 11 классе в контексте подготовки к ЕГЭ

«Решение комбинированных задач».

Цель урока:   отработать навыки решения основных типов задач, показать пути решения комбинированных задач как разновидности задания контрольно-измерительных материалов ЕГЭ.

Задачи урока:

1. Образовательная:

• приобрести навык решения подобных заданий

• акцентировать внимание на правильном оформлении результатов работы

2. Развивающая:

• развитие логического, абстрактного мышления

• развитие навыков быстрого счета

• развитие способности концентрироваться при выполнении ответственного задания

3. Воспитательная:

Дидактический материал: распечатанный раздаточный материал с заданиями.

Мотивационная модель. Учащиеся решают задачи.

Уровень подготовленности учащихся выясняется в процессе решения.

Этапы урока:

1. Организационный момент.

2. Вводное слово учителя.

3. Алгоритм решения задач.

4. Подробный разбор задачи.

5. Отработка навыка решения подобных задач.

6. Самостоятельная работа.

7. Домашнее задание.

Пояснение к уроку. Длительность урока 45 минут. На всех этапах урока учитель контролирует выполнение задач. Во время урока приобретаются навыки решения задач определенного типа. Используется соревновательный элемент: кто решит задачу быстрее отвечающего у доски.

Ход урока.

1. Организационный момент.

2. Разминка (Повторение и обобщение пройденного).

Учитель. Сегодня на уроке мы продолжим решать расчетные задачи. На прошлом уроке мы вспомнили основные типы расчетных задач. Поэтому, я не буду долго останавливаться на них и в качестве разминки я предлагаю вашему вниманию следующие задачи.

(Задачи написаны на доске ).

Вас же попрошу предложить логическую схему решение данных задач. И определить к какому типу они относятся.

Задача 1. Какой объем газа (н. у.) получается при разложение 8г оксида меди(2).

2CuO=2Cu + O2.

Ответ уч-ся: m(Cu)→ n(Cu)→ n(O2)→V(O2)

Тип: нахождения объёма (массы и кол-ва вещества ) одного вещества по известной массе, объёму или количеству вещества другого вещества.

3. Решение комбинированных задач из части В.

Учитель. А теперь я предлагаю перейти к решению более сложных, так называемых комбинированных задач. Тексты задач находятся у вас на столах.

Задача 2. (на листочках уч-ся). Масса метилового эфира масляной кислоты, полученного при взаимодействии 48г метилового спирта и 100г 44%раствора масляной кислоты, равна___г.

Учитель: А кто помнит, запах чего имеет данный эфир и где используется?

Учащиеся: Запах яблок, используется как ароматизатор в пищевой и парфюмерной промышленности.

Учитель. Хорошо. А знаете ли вы, что первыми стали получать и использовать душистые вещества арабы, а в Европе греки и римляне ещё в античные времена.После античных времён духи снова появились только в эпоху возрождения.При дворе французского короля дамы в изобилии расходовали благовония, чтобы заглушить неприятный запах, исходящий от тела. В те времена не принято было мыться: считалось, что частые омовения тела вредны для здоровья. Известно, что король Франции Людовик 04 за 78 лет жизни мылся всего … четыре раза.

А теперь продолжим решения задач и попытаемся решить ещё более сложную задачу. 4. Решение комбинированной задачи.

Задача 3 . Рассчитайте массовую долю серной кислоты в растворе, полученном при пропускании 2,24л (н. у.).сероводорода через 250г 10% раствора сульфата меди

Учащийся у доски записывает условие задачи и приступает к решению.

V(h3S)=2,24л СuSO4+h3S = CuS↓+h3SO4

mр-ра(СuSO₄)=250г 1моль 1моль 1моль

ω%(СuSO₄)=10% V(H₂S)→n(H₂S)

n(H₂SO₄)→m(H₂SO₄)→ω%(H₂SO₄)

 mр-ра(CuSO₄)→m(CuSO₄)→n (CuSO₄)

ω%(H₂SO₄)-?

n(H₂S)=2,24/22,4=0,1моль

m(CuSO₄)=250•10/100=25г

n (CuSO₄)=m/M=25/160=0,156моль-избыток

M(CuSO₄)=160г/моль

n (H₂SO₄)=n(h3S)=0,1моль

m (H

2SO₄)=n•M = 0,1•98=9,8г

M(H₂SO₄)=98г/моль

ω% (H₂SO₄)=m(H₂SO₄)/mр-ра•100%

mр-ра₂=mр-ра(H₂SO₄)+m(H₂S)-m(CuS)

n(CuS)=n(H₂S)=0,1моль

m(СuS)=0,1•96=9,6г

M(CuS)=96г/моль

m(H₂S)=n•M=0.1•34=3,4г

mр-ра₂=250+3,4-9,6=243,8г

ω% (H₂SO₄)=9,8/243,8=4%

Ответ: ω% (H₂SO₄)= 4%

 5. Решение задач с использованием алгебраических уравнений.

Речь идет об одновременно происходящих реакциях, с реагентом (реагентами) взаимодействуют все компоненты смеси. Для определения порций отдельных компонентов придется использовать алгебраический алгоритм. Поскольку в дальнейшем предстоят расчеты по уравнениям реакций, в качестве неизвестной величины лучше всего выбрать количество вещества.

Алгоритм 1. Решение через систему уравнений с двумя неизвестными

(подходит для любой задачи такого типа)

1. Составить уравнения реакций.

2. Количества веществ (ν) в исходной смеси обозначить через х, у моль и, согласно молярным соотношениям по уравнениям реакций, выразить через х, у моль количества веществ в

образовавшейся смеси.

3. Составить математические уравнения. Для этого следует выразить массу (или объем)

веществ через х, у и молярную массу (молярный объем) по формулам:

m = ν*M; V = ν*VМ.

4. Составить систему уравнений и решить ее.

5. Далее решать согласно условиям задачи

Задача 4. Пластинку из магниево-алюминиевого сплава массой 3,9 г поместили

в раствор соляной кислоты. Пластинка растворилась, и выделилось 4,48 л газа. Найти массовые доли металлов в сплаве.

Решение

1) Запишем уравнения реакции:

Mg + 2HCl = MgCl₂ +H₂↑

1моль 1моль

2Al+ 6HCl = 2AlCl₃ +3H₂↑

2моль 3моль

2) Обозначим количества веществ:

ν(Mg) = x моль; ν(Н₂) = х моль;

ν(Al) = y моль; ν(Н₂) = 1,5 у моль.

3) Составим математические уравнения: найдем массы магния, алюминия и их смеси, а также ко-

личество вещества выделившегося водорода:

m(Mg) = 24x,

m(Al) = 27y,

m(смеси) = 24х + 27y;

ν(Н₂) = V/VM = 4,48 (л) / 22,4 (л/моль) = 0,2 моль.

4) Составим систему уравнений и решим ее:

24x+ 27y=3,9

x + 1,5y = 0, 2 .

х = 0,2 — 1,5у,

24(0,2 — 1,5у) + 27у = 3,9,

у = 0,1;

х = 0,2 — 1,5*0,1 = 0,05.

5) Найдем массы магния и алюминия и их массовые доли в смеси:

m(Mg) = 0,05 (моль) * 24 (г /моль) = 1,2 г,

m(Al) = 0,1 (моль) * 27 (г /моль) = 2,7 г,

ω(Mg) = m(Mg) / m(см.) = 1,2 (г) / 3,9 (г) = 0,3077,

ω(Al) = m(Al) / m(см.) = 2,7 / 3,9 = 0,6923.

Ответ. ω(Mg) = 30,77 %; ω(Al) = 69,23 %.

Задача 5. К раствору, содержащему 5,48 г смеси сульфата и силиката натрия, прибавили избыток хлорида бария, в результате образовалось 9,12 г осадка. Найти массы солей в исходной смеси.

5.Подведение итогов урока, проверка решения задач по карточкам, выставление оценок.

Домашнее задание: составить обратную задачу к одной из предложенных и решить её.

Уроки по комбинаторике. Урок 2. Решение комбинаторных задач (конспект урока + презентация)

Тема урока: «Решение комбинаторных задач. Сочетания»

Место урока в учебном плане: «Комбинаторика. Случайные события» урок 2/8.

Тип урока: комбинированный

Цели урока:

Образовательные:

• ознакомить с типами задач на сочетания их решения;

• сформировать умения решать задачи на сочетания различными методами,

• продолжить формирование навыков решения задач на перестановки.

Развивающие:

познавательного интереса учащихся,

памяти, внимания,

умения сравнивать и анализировать,

Воспитательные:

трудолюбия,

культуры учебного труда,

культуры речи, самостоятельности,

умения работать в коллективе.

Методы обучения: объяснительно-иллюстративный, частично-поисковый,.

Формы познавательной деятельности учащихся: фронтальная, индивидуальная.

УМК: Математика: учебник для 6 кл. под редакцией Г.В.Дорофеева, И.Ф.Шарыгина и др., изд-во «Просвещение», 2008 г.; Математика, 5-6 : кн. для учителя / [С. Б. Суворова, [ Л. В. Кузнецова, С. С. Минаева, Л. О. Рослова]. — М. : Просвещение, 2006.

Оборудование: ПК или ноутбук, проектор, экран, презентация к уроку..

Программное обеспечение: ОС Windows, MS Power Point, презентация к уроку.

Дидактический материал: карточки для самостоятельной работы, карточки для работы на доске.

Литература:

1. Математика : учеб. для 6 кл. общеобразоват. учреждений/ Г. В. Дорофеев, И. Ф. Шарыгин, С. Б. Суворова и др.]; под ред. Г. В. Дорофеева, И. Ф. Шарыгина; Рос. акад. наук, Рос. акад. образования, изд-во «Просвещение». — 10-е изд. — М. : Просвещение, 2008.—302 с.: ил. — (Академический школь­ный учебник).

2. Математика, 5—б : кн. для учителя / [С. Б. Суворова, Л. В. Кузнецова, С. С. Минаева, Л. О. Рослова]. — М. : Просвещение, 2006. — 191 с. : ил.

3. Математика. 6 класс: поурочные планы по учебнику Г. В, Дорофеева, С. Б. Суворовой, И. Ф. Шарыгина и др. Часть II / авт.-сост. Т. Ю. Дюмина. — Волгоград: Учитель, 2006. — 247 с.

4. Решение задач по статистике, комбинаторике и теории вероятностей. 7—9 классы. / авт.- сост. В. Н. Студенецкая. Изд. 2-е, испр. — Волгоград: Учитель, 2006. -428 с.

5. Уроки математики с применением информационных технологий. 5-10 классы. Методическое- пособие с электронным приложением / Л.И. Горохова и др. 2-е изд., стереотип. -М.: Издательство «Глобус», 2010. — 266 с. (Coвременная школа).

6. Преподавание математики в современной школе. Методические рекомендации. Владивосток: Издательство ПИППКРО, 2003.

7. Автор-составитель — Р.И. Махиня, главный методист ПИППКРО, заслуженный учитель РФ, Рецензенты: Г.К. Пак, кандидат физико-математических наук ДВГУ; Е.А. Ланкина, кандидат физико-математических наук ДВГУ.

8. http://mmmf.math.msu.su/

9. http://portfolio.1september.ru/

10. http://combinatorica.narod.ru/

План урока:

1. Оргмомент

2. Проверка домашнего задания

3. Актуализация знаний

   • устная работа

   • решение задач у доски по карточкам и самостоятельно с проверкой (условия и ответы на слайдах)

4. Объяснение нового материала.

5. Физкультминутка.

6. Формирование умений и навыков решения задач на сочетания всеми приемлемыми способами.

7. Итоги урока

8. Домашнее задание.

Ход урока

1. Оргмомент

2. Проверка дом. задания (фронтально) и сверить ответы с решениями

(Слайды 2-4)

3. Актуализация знаний. Устная работа

(Слайд 5)

Вызвать к доске 4 учащихся – решение задач по карточкам.

Карточка № 1.

Сколько двузначных чисел можно составить, используя цифры 1, 2, 3, 4?

Реши задачу удобным способом.

Карточка № 2.

Миша решил в воскресенье навестить дедушку, своего друга Петю и старшего брата Володю. В каком порядке он может организовать визиты? Сколько вариантов получилось? Решить с помощью дерева вариантов.

Карточка № 3.

В одной деревне по сложившейся традиции мужчин называют каким-либо из следующих имен: Иван, Петр, Василий и Михаил. Проживают в этой деревне 15 мужчин. Может ли оказаться так, что в деревне нет мужчин с одинаковым именем и отчеством?

Реши задачу, составив таблицу.

Карточка № 3.

В пятницу в 4 классе должно быть четыре урока: математика, русский язык, физкультура и рисование. Сколько вариантов у завуча школы, который должен составить расписание занятий на пятницу для 4 класса.

Реши задачу удобным способом.

Учащиеся в тетрадях решают самостоятельно решают задачи.

(Слайды 6,7)

Ответы к задачам самостоятельной работы

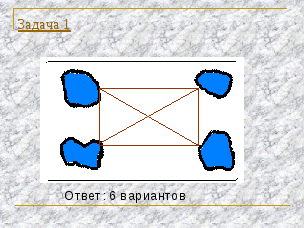
(Слайды 9,10)

Способ решения первой задачи называется методом графов.

4. Объяснение нового материала

Учитель. Запищите в тетрадь тему урока.

На прошлом уроке вы познакомились с комбинаторными задачами на перестановки. Сегодня мы рассмотрим другой вид задачи. Чтобы понять их особенности, решим две задачи.

(Слайды 12-14)

Таким образом, выбрать двух школьников из четырех можно шестью

способами.(Обратите внимание, что числа расположены в виде треугольника.)

Задача 2 (рассмотреть задачу 2 из школьного учебника).

(Слайд 16)

Каждый из языков обозначим его первой буквой, и тогда каж­дый словарь будет «словом» из двух букв: например, АН — это ан­гло-немецкий словарь, а НА — немецко-английский.

Выпишем эти «слова» в алфавитном порядке, причем для удобства подсчета вариантов каждую группу «слов», начинающихся с одной и той же буквы, расположим в отдельной строке.

Сначала фиксируем букву А и добавляем к ней все остальные буквы, кроме, естественно, самой буквы А. Так мы получим пер­вую строку: АН, АР, АФ. Затем фиксируем букву Н и, добавляя к ней остальные буквы, получаем вторую строку и т. д. В резуль­тате получим 12 «слов»:

(Слайд 17)

Таким образом, переводчику понадобится 12 словарей.

Задача № 3.

(Слайд 18)

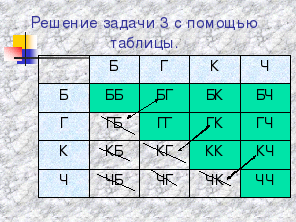
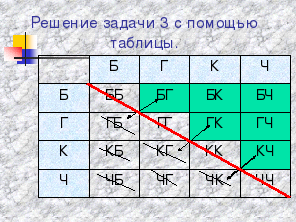
(Слайды 19,20)

Учитель: — Что общего в рассмотренных задачах? (В рассмотренных задачах из четырех элементов нужно было выбрать всевозможными способами два.)

— Почему в первой задаче мы получили 6 способов, а во второй 12? (В первой задаче коды 12 и 21 считались одинаковыми, а во второй АН и НА — разными.)

Учитель. Таким образом, в обеих задачах нужно было, как говорят в математике, составить сочетания из четырех элементов по два.

В первой задаче нам был не важен порядок этих сочетаний, то есть выбор двух школь­ников был равноправен.

А во второй задаче при работе с двумя языками, например русским и английским, нужны два словаря: англо-русский и рус­ско-английский. Поэтому порядок сочетаний был важен, и именно поэтому в результате получилось ровно в два раза больше вариантов.

Вопрос:

— Как можно изменить условие первой задачи, чтобы в результате полу­чилось не 6, а 12 вариантов?

Учитель.

(Слайд 21,22)

(Слайд 23)

Решаются они с помощью кодирования и подсчета кодов путем расположения их треугольником, с помощью дерева вариантов, таблиц.

Рассмотрим еще одну задачу (задача 3 из учебника).

Задача 3. При встрече 8 приятелей обменялись рукопожатиями. Сколько всего было рукопожатий?

Дадим каждому из приятелей номер — от 1 до 8. Тогда каждое рукопожатие можно закодировать двузначным числом. Например, двузначное число 47 — это рукопожатие между приятелями под номерами 4 и 7.

Ясно, что среди кодов рукопожатий у нас не появится, напри­мер, 33 — это означало бы, что один из друзей пожал руку сам себе. Кроме того, такие коды, как, например, числа 68 и 86, оз­начают одно и то же рукопожатие, а значит, учитывать надо толь­ко одно из них. Договоримся, что из чисел, кодирующих одно и то же рукопожатие, мы всегда будем учитывать меньшее. Поэтому из чисел 68 и 86 надо выбрать 68.

Коды рукопожатий естественно выписывать в порядке возрас­тания. Для подсчета их удобно расположить треугольником:

12, 13, 14, 15, 16, 17, 18,

23, 24, 25, 26, 27, 28,

34, 35, 36, 37, 38,

45, 46, 47, 48,

56, 57, 58,

67, 68,

78.

Число кодов равно: 7 + 6 + 5 + 4 + 3 + 2 + 1 = 28. Таким образом, всего было сделано 28 рукопожатий.

Как вы думаете, можно решить эту задачу методом графов или таблицы? (Да)

5. Физкультминутка. (Слайд 24)

6.Формирование знаний и умений.

Решение задач на сочетания из учебника № 868, 869 на доске и в тетрадях. (Слайд 25)

№ 868. Выпишите все возможные двузначные и трехзначные числа, которые мож­но составить из цифр 0, 1,2, 3, используя каждую цифру в записи толь­ко один раз.

Проверка решения задачи:

(Слайд 26)

869. а) На соревнование по легкой атлетике нужно отправить двух мальчиков из пяти лучших спортсменов среди шестиклассников — Антона, Петра, Бо­риса, Володи, Коли. Перечислите все варианты выбора участников сорев­нования. Сколько этих вариантов?

б) Для участия в эстафете 2×100 м нужно выбрать двух мальчиков из пя­ти, обязательно указав, кто побежит первым, а кто — вторым. Перечисли­те все варианты выбора участников соревнования в этом случае. Сколько этих вариантов?

Проверка решения задачи:

(Слайд 27)

№ 870 самостоятельно с проверкой на слайде.

870. На районной олимпиаде по математике оказалось шесть победителей. Од­нако на областную олимпиаду можно отправить только двоих.

а) Сколько существует вариантов выбора двух кандидатов? Указание. Дайте каждому победителю номер — от 1 до 6.

б) Сколько существует вариантов, если один из шести ребят признан луч­шим и он обязательно будет участвовать в областной олимпиаде?

(Слайд 28)

Самостоятельная работа

Самостоятельно решить в тетрадях следующие задачи. Затем поменяться тетрадью с соседом и взаимообразно проверить решения соседа и оценить.

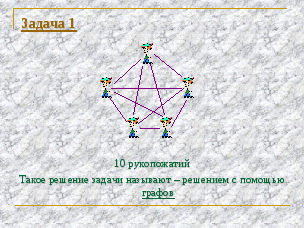
(Слайд 29,30)

Проверка решения задач:

(Слайд 31,32)

(Слайд 33, 34)

7. Итоги урока

Вопросы учащимся:

— В чем состоит особенность задач на сочетания?

— Какие два вида таких задач существуют? В чем состоит их отличие?

— Если нужно выбрать всевозможными способами из п элементов т эле­ментов, то в каком случае получится больше вариантов: когда порядок важен или когда порядок не важен? (Слайд 35)

8. Домашнее задание. (Слайд 36)

№ 875, стр.207 № 4. инд.№ 884.

Придумать по 2 задачи сочетание.

Спасибо за урок. (Слайд 37)

Консультация по физике (9 класс) на тему: Комбинированные задачи

Комбинированные задачи.

      К комбинированным задачам в текстах  ГИА относятся задания третьей части под номерами 26 и 27.Они относятся к заданиям высокого уровня сложности и проверяют умение использовать законы физики в изменённой или новой ситуации при решении задач.

       При оформлении необходимо записать полное решение, которое включает запись краткого условия задачи (Дано), запись формул, применение которых необходимо и достаточно для решения задачи, а также математические преобразования и расчёты, приводящие к числовому ответу.

       Рассмотрим несколько примеров решения таких заданий.

№1

С какой скоростью должна лететь свинцовая пуля, чтобы при ударе о стенку она расплавилась? Температура пули перед ударом равна 570С, температура плавления свинца равна 3270С. Считать, что на тепловые процессы пошла вся механическая энергия пули.

Дано:                           Решение:

t1=570С                       По закону сохранения и превращения энергии для пули:

t2=3270С                     Екин=Q

c=130Дж/кг·0С          Екин=mƲ2/2

ƛ=2,5·104 Дж/кг        Q=cm(t2 – t1)+mƛ

Ʋ — ?                             mƲ2/2= cm(t2 – t1)+mƛ   => Ʋ2/2== c(t2 – t1)+ƛ  => Ʋ=     2[c(t2 – t1)+ƛ ]

                                     [ Ʋ]=        · 0С+   =     =     =          =      м2/с2   = м/с

                                      Ʋ=    2·(130·270)+25000  =347 (м/с)

Ответ: Ʋ =347м/с

№2                            

Определите КПД электрического чайника, имеющего мощность 0,6кВт, в котором за 17,5мин 1,5л воды нагревается от 200С до 1000С.

Дано:                                    СИ:               Решение:

Рз=0,6кВт                              600Вт          

 τ=17,5мин                          1050с         η=Ап/Аз

V=1,5л                                  1,5·10-3м3       Ап=Q=c ρV(t2 — t1)

t1=200C                                                        Аз= Рз· τ

t2=1000C                                                         η= c ρV(t2 — t1)/ Рз· τ                                                                                                                      

c=4200130Дж/кг·0С                                  [η]=··м3· 0С /Вт·с=Дж/ = 1

ρ=103 кг/м3                                                 

                                                                η=4200·103·1,5·10-3·80/600·1050=0,8

 η — ?                                                     Ответ: η =0,8                                                                                             

задачи для самостоятельного решения

26.Камень брошен вертикально вверх со скоростью 10м/с. На какой высоте кинетическая энергия камня равна его потенциальной энергии? Сопротивление воздуха пренебрежимо мало.

27.Троллейбус движется равномерно по горизонтальному участку пути со скоростью 36км/ч. Сила сопротивления, действующая на троллейбус, равна 2,2кН. Найдите силу тока в обмотке двигателя, если напряжение на клеммах двигателя 550В, а КПД равен80%.

26.Автомобиль массой 1т разгоняется из состояния покоя на прямолинейном участке дороги с постоянным ускорением 2,5м/с2.Найдите работу силы сопротивления движению за первые 10секунд движения, если известно, что сила тяги двигателя равна 3,25кН.

26.Стальной осколок, падая с высоты 470м, нагрелся на 0,50С в результате совершения работы сил сопротивления воздуха. Чему равна скорость осколка у поверхности земли.

26.Два свинцовых шара массами m1=100г и m2=200г движутся навстречу друг другу со скоростями Ʋ1=4м/с и Ʋ2=5м/с. Какую кинетическую энергию будет иметь второй шар после их неупругого соударения?

27. При прохождении электрического тока 5,5А через спираль нагревателя, изготовленную из никелиновой проволоки площадью поперечного сечения 0,84мм2, за 10 мин выделилось количество теплоты 726кДж.Чему равна длина проволоки, из которой изготовлена спираль?

Лекция 4. Этапы обучения решению комбинаторных задач.

Лекция 4. Этапы обучения решению комбинаторных задач.

Цель лекции: раскрыть этапы решения комбинаторных задач в начальной школе как одного из эффективных способов обучения задач повышенной трудности.

Список литературы по теме:

1. Менцисс Я.Я. Содержательный смысл математической модели.// Начальная школа. – 1989. — № 10 – 11. – с. 67 – 69.

2. Фонина Д.С. Моделирование как важное средство обучению решению задач.// Начальная школа. – 1990. — № 3. – С. 33 – 37.

3. Белокурова Е.Е. Методика обучению решению комбинированных задач.// Начальная школа. – 1994. — № 12. – С. 43-47.

4. Белокурова Е.Е. Характеристика комбинированных задач.// Начальная школа. – 1994. — № 1. – С. 34-38.

Этапы обучения решению комбинаторных задач в начальной школе.

        В обучении школьников решению комбинаторных задач соблюдается этапность.

        Первый этап – подготовительный.  На этом этапе учащиеся приобретают опыт образования объектов из отдельных элементов. Новые объекты ученики составляют, осуществляя хаотичный перебор, и от них не требуется найти все возможные варианты в данной задаче.

        Пример задачи. Составьте из трех одинаковых по размеру кубиков красного, желтого и синего цвета несколько отличающихся друг от друга построек.

        Способ решения задачи на данном этапе. В процессе решения задачи учащиеся перебирают все возможные варианты решения и фиксируют их в виде рисунка.

        Второй этап. Обучение школьников решению задач с использованием систематического перебора.

        По сложности осуществления перебора задачи повышенной трудности делятся на следующие группы:

1. Задачи, в которых нужно произвести полный перебор во всех возможных вариантах.

        Пример задачи. Расставьте знаки «+» и «-» между данными числами 9…2…4, составьте все возможные выражения.

        Способ решения задачи – проводится полный перебор вариантов (используется прием полной индукции).

        Варианты решения. 9+2+4, 9-2-4, 9-2+4, 9+2-4.

2. Задачи, в которых производится сокращенный перебор вариантов из-за нецелесообразности выполнения полного перебора.

        Пример задачи. Четыре фигуры нарисованы в ряд: большой и маленький квадраты, большой и маленький круги так, что на первом месте находится круг и одинаковые по форме фигуры не стоят рядом. Отгадайте последовательность рассматриваемых фигур.

        Способ решения задачи – всего существует 24 различных вариантов расположения этих фигур и составлять их все, а потом выбирать соответствующие данному условию нецелесообразно, поэтому проводится сокращенный перебор вариантов, удовлетворяющих условию задачи.

        Варианты решения:

Большой круг – большой квадрат – маленький круг – маленький квадрат.

Большой круг – маленький квадрат – маленький круг – большой квадрат.

Маленький круг – большой квадрат – большой круг – маленький квадрат.

Маленький круг – маленький квадрат – большой круг – большой квадрат.

3. Задачи, в которых операция перебора производится несколько раз, но по отношению к разного рода объектам.

        Пример задачи. Три компаньона одной фирмы хранят ценные бумаги в сейфе, на котором три замка. Компаньоны хотят распределить между собой ключи от замков так, чтобы сейф мог открываться в присутствии двух компаньонов, но не одного. Как это можно сделать?

        Способ решения задачи. Сначала перебираются все возможные случаи распределения ключей. Каждому компаньону можно дать по 1 ключу или по 2 ключа, или по 3 ключа. Потом выбранный вариант проверяется в разных ситуациях.

        Варианты решения. Для записи решения задачи можно выбрать различные способы обозначения ключей (заместителей реальных предметов).

        При отборе комбинаторных задач важно учитывать следующие условия:

1. Совокупность задач должна удовлетворять принципу полноты.

        С этой точки зрения необходимо в работе над комбинаторными задачами использовать следующие основные виды комбинаторных задач:

— на упорядочение элементов множества,

— на выбор подмножеств и их упорядочение,

— на выбор подмножеств.

2. Необходимо учитывать характер содержащегося в них требования.

        С этой точки зрения можно выделить следующие группы задач:

— Задачи, в которых требуется найти и сосчитать, сколько всего можно составить различных вариантов;

— Задачи, в которых требуется выяснить, существует ли определенная конфигурация, отвечающая поставленным условиям;

— Задачи, в которых нужно найти и выбрать наилучший вариант по определенным критериям.

        Задача на упорядочение предметов (по кругу), среди которых есть одинаковые. 

        Нарисуй, какие различные колечки можно сделать из 5 одинаковых маленьких бусинок и 2 одинаковых больших бусинок.

        Задача на выбор подмножеств и их упорядочение (слева направо) при наличии дополнительных условий.

        Запиши все двузначные числа, которые можно составить из цифр 2, 4, 7 так, чтобы число десятков было больше числа единиц.

        Задача на выбор подмножеств и их подсчет их элементов.

        Красная шапочка несла бабушке 14 пирожков: с мясом, с грибами и с капустой. Пирожков с капустой было наибольшее количество. Причем их вдвое больше, чем пирожков с мясом. Сколько пирожков с грибами?

        Задача, в которой требуется найти и сосчитать, сколько всего можно составить различных вариантов.

        Площадь прямоугольника равна 12 кв. см. Длины его сторон выражена целыми числами. Сколько различных прямоугольников можно построить согласно этим условиям?

        Задача, в которой нужно найти один наилучший вариант, соответствующий определенным условиям.

        В трехзначном нечетном числе сумма цифр равна 3. Известно, что все цифры различные. Найди это число.

        Рассмотрение комбинаторных задач и различных возможностей их решения обеспечивают ученику выбор путей и средств решения в соответствии с индивидуальными особенностями.

        Третий этап. Обучение школьников решению задач с использованием систематического перебора с использованием средств организации перебора.

        К средствам организации систематического перебора относятся таблицы и графы.

        Работа с графическими средствами отнесена на третий этап, так как, во-первых, при решении задач с небольшим числом элементов нет необходимости их использования, во-вторых, «язык» графов и таблиц не совсем прост и понятен детям, вследствие чего требуется специальное ознакомление с ними.

        Прием графического и предметного моделирования является важным средством решения задач повышенной трудности.

        Моделирование в широком смысле этого слова – замена действий с реальными предметами и действия с их образцами, моделями, муляжами, макетами, а также с графическими заменителями: рисунками, чертежами (с соблюдением масштаба), схемами (без точного соблюдения масштаба).

        Предметное и графическое моделирование математической ситуации при решении задач давно применяется в школьной практике. Значение наглядности как средства развития более сложных форм конкретного мышления и формирования математических понятий состоит в том, что, как отмечает Л.Ш. Левенберг, «рисунки, схемы и чертежи не только помогают учащимся в сознательном выявлении скрытых зависимостей между величинами, но и побуждают активно мыслить, искать более рациональные пути решения задач, помогают не только усваивать знания, но и овладевать умением применять их».

        Таблица – это тоже модель задачи, но более абстрактная, чем схематический рисунок или чертеж.

        Моделирование условия задачи повышенной трудности является одним из эффективных путей решения поиска решения, отражает глубину и полноту анализа связей, данных в задаче и, следовательно. Помогает ученикам успешно решить ее.

        Обучение моделированию условия задачи включает ряд этапов:

1. Первоначально текст задачи повышенной трудности выписывается на доске и коллективно анализируется. Каждое предложение детей обсуждается и доказывается. В результате чего получается графическое изображение задачи.
2. Использование  моделирования условий задач при работе с текстами задач разного вида сначала коллективно, а затем индивидуально.
3. Ознакомление учеников с разными способами моделирование, предоставление право выбора способа.
4. Обучение самостоятельному решения задач на основе выбранного ребенком самостоятельно способа решения.

Задание для самопроверки:

Определите последовательность этапов обучения решению комбинаторных задач.

1 — обучение школьников решению задач с использованием систематического перебора с использованием средств организации перебора.

2 —  использование хаотичного перебора, который не требуется найти все возможные варианты в данной задаче.

3 — обучение решению задач с использованием систематического перебора.

Ответ на задание для самопроверки:

Последовательность этапов следующая:

2, 3, 1.