План-конспект урока на тему: План урока Цилиндр
Государственное бюджетное профессиональное образовательное учреждение
Краснодарского края
«Курганинский аграрно-технологический техникум»
Конспект открытого урока
по математике
Разработка
преподавателя математики
Приходько
Эльвиры Александровны
г. Курганинск, х. Красное поле, 2015
Урок по теме
«Цилиндр»
Цели:
Образовательные:
- ввести определение цилиндра и его элементов;
- формирование навыков самостоятельного применения знаний для решения задач на нахождение элементов цилиндра.
Воспитательные:
- формировать умение оценивать свой уровень знаний и стремление его повышать;
- воспитывать у учащихся интерес к математике.
Развивающие: развивать умение анализировать и систематизировать
имеющуюся информацию.
Оборудование:
- раздаточный материал;
- модели цилиндров;
- справочный материал с основными формулами;
- компьютер и проектор, мультимедийная презентация.
Ход урока.
I . Организационный момент.
Учитель сообщает тему урока, его цель, структуру урока, необходимость его проведения.
II. Историческая справка:
Обучающиеся сообщают исторические сведения, подготовленные к уроку .
- Цицерон утверждал, что эту могилу он смог найти по данному знаку. Это предположительно гробница Архимеда. Предание гласит, что Архимед завещал вырезать на своем надгробном памятнике рисунок, сделанный его собственной рукой. По завещанию мыслителя, математика, физика на могильном камне был вырезали символ его геометрического открытия, которым он очень гордился: Цилиндр, описанный вокруг шара.
- Другой великий ученый математик, механик, физик, философ; по происхождению швейцар, но прожил половину жизни в России, захоронен в Петербурге, полное собрание сочинений которого не умещается в 60 больших томах. Уже будучи слепым он написал математические работы, связанные с исследованиями поверхностей, которые можно развернуть на плоскости и о их кривизне. Одна из поверхностей – цилиндр.
-Вот и мы сегодня попытаемся понять красоту тела вращения Цилиндра, предлагаю построить изучение по следующим вопросам:
- Цилиндр, его основания, образующие и их свойства
- Виды цилиндра и его поверхность
- Радиус и высота, ось цилиндра
- Сечения цилиндра плоскостями
- Решение базовых задач
III. Изучение нового материала.
Ставиться проблема и обучающиеся, с помощью моделей и презентации отвечают на вопросы.
Слово «цилиндр» произошло от греческого слова «кюлиндрос», означающего «валик», «каток». На рубеже XVIII – XIX веков мужчины многих стран носили твёрдые шляпы с небольшими полями, которые так и назывались цилиндрами из-за большого сходства с геометрической фигурой цилиндром.
— Рассмотрим варианты получения цилиндра.
Преподаватель предлагает ввести понятие цилиндрической поверхности,
рассмотрев различные предметы окружающей обстановки, дающие представление о цилиндре: круговой карандаш, стакан, монетку, кастрюлю, кусок трубы, мензурку и т.д. (Представленные цилиндры должны иметь разные соотношения между высотой и диаметром). После этого даётся
изображение цилиндра, показывается его ось, высота, радиус, образующие, основания.
Цилиндр – геометрическое тело, ограниченное цилиндрической поверхностью (боковой) и основаниями.
— Что из себя представляют основания цилиндра? (круги)
— Что вы можете сказать о размерах этих кругов? (одинаковые, т.е. радиусы этих кругов равны)
— Что из себя представляет боковая поверхность? Если затрудняются ответь, то подводим к ответу: Возьмём бумажный цилиндр, разрежем его следующим образом (показываю) и развернём.
— Так что же представляет собой боковая поверхность? (прямоугольник)
Что ещё нужно знать о цилиндре?
Вводятся понятия прямого и наклонного цилиндров. Демонстрируются слайды.
Высота цилиндра — это расстояние между основаниями,
радиус цилиндра — радиус круга, являющегося основанием цилиндра.
Выясняется совместно с обучающимися, что цилиндр получается путем вращения прямоугольника вокруг одной из его сторон. На данном примере – прямоугольника АВСД вокруг стороны АВ.
Развертка цилиндра:
Развертка цилиндра выглядит следующим образом (показать на модели):
— Понятие осевого сечения цилиндра. Свойства осевого сечения. Равносторонний цилиндр. Сечения равностороннего цилиндра.
Даётся понятие осевого сечения, как сечения цилиндра плоскостью, проходящей через ось цилиндра. Осевое сечение представляет собой прямоугольник, две стороны которого – образующие, а две другие – диаметры цилиндра. Предлагается рассмотреть два любых осевых сечения и сравнить их. Обучающиеся приходят к выводу, что любые осевые сечения равны между собой. Вводится понятие равностороннего цилиндра, осевым сечением которого является квадрат. Рассматривается сечение цилиндра плоскостью, параллельной оси цилиндра и плоскостью, перпендикулярной оси цилиндра.
Составить опорный конспект по теме «Цилиндр», отобразив в нем знания, приобретенные на уроке.
Цилиндр-это фигура, состоящая из двух кругов, совмещаемых параллельным переносом и всех отрезков, соединяющих соответствующие точки этих кругов. Свойства: 1. Основания равны и параллельны (из опр.). 2. Образующие равны и параллельны (из свойств параллельного переноса, по свойству параллельных плоскостей). | |||||
Цилиндр называется прямым, если образующие перпендикулярны основанию. В прямом цилиндре: ось=высота=образующая. | Прямой цилиндр наглядно можно представить как тело, которое описывает прямоугольник при вращении его около стороны как оси. | ||||
Сечения | |||||
прямоугольник | осевое | ||||
VI . Закрепление изученного материала.
Преподаватель предлагает обучающимся устно ответить на вопросы:
1. Укажите в природе, технике, архитектуре, среди окружающих вас предметов объекты, имеющие цилиндрическую форму.
2. Объясните, что называют цилиндром, круговым цилиндром. Назовите основные элементы цилиндра и дайте им определение.
3. Дайте определение прямого цилиндра.
4. Что такое осевое сечение цилиндра?
5. Сколько осевых сечений цилиндра проходит через каждую его образующую?
6. Определите вид осевого сечения. Ответ обоснуйте.
7. Может ли осевое сечение цилиндра быть прямоугольником, квадратом, трапецией? Ответ подтвердите чертежами.
8. Имеет ли цилиндр центр симметрии? Ось симметрии? Плоскость симметрии? Укажите их в каждом случае, объясните, сколько их.
9. Какое из следующих утверждений является верным. Ответ обоснуйте.
а). Любое сечение цилиндра плоскостью, перпендикулярной оси, есть окружность, равная окружности основания.
б). Любое сечение цилиндра плоскостью есть окружность, равная окружности основания.
в). Плоскость, перпендикулярная оси цилиндра, пересекает его по кругу, равному основанию цилиндра.
г). Сечением цилиндра плоскостью могут быть круг, прямоугольник и эллипс.
После подробного разбора ответов на вопросы обучающиеся приступают к решению задач из учебника.
Решение задач.
№ 1. Найти высоту цилиндра, если радиус основания равен 4. (по рисунку)
№ 2. (№ 529. Л.С.Атанасян)
Ответ: 64 см².
№ 3. (№ 523. Л.С.Атанасян)
Ответ: 10 см, 50π см².
Итог урока.
Преподаватель предлагает вспомнить основные моменты урока, основные понятия и свойства, оценивает работу учащихся на уроке, комментируя оценки, обращает внимание на ошибки, допущенные при решении задач, благодарит за работу.
Домашнее задание.
Учебник: Башмаков М.И. Математика
Стр. 149, занятие 4,
изобразить развертку равностороннего цилиндра.
Конспект урока на тему «Цилиндр»
Тема урока: Цилиндр.
Цели урока:
Обучающие:
Ввести понятие цилиндра, его элементов;
Закрепить понятия с помощью выполнения заданий.
Развивающие:
Развивать пространственное воображение;
Развивать умение правильно излагать мысли;
Развивать умения анализировать, выделять главное, обобщать и делать выводы.
Воспитательные:
Воспитывать внимание, аккуратность, дисциплинированность;
Воспитывать уважительное отношение к одноклассникам и чувства собственного достоинства;
Воспитывать интерес к предмету, способствовать формированию представления о математике, как о части общечеловеческой культуры.
Задачи урока:
Познакомить учащихся с новым геометрическим телом, научить решать задачи по данной теме.
Развивать пространственное мышление учащихся, умения анализировать и систематизировать материал.
Воспитывать трудолюбие, графическую культуру учащихся.
Тип урока: урок изучения нового материала.
Форма урока: комбинированный урок
Продолжительность урока : 80 минут.
Оборудование урока: наглядность по теме урока, макет цилиндра, классная доска, чертежные инструменты.
План урока
Устная работа.
Изучение нового материала.
Закрепление, решение задач.
Итог урока.
Ход урока
I. Организационный момент
Здравствуйте ребята. Садитесь. Сегодня у нас на уроке присутствуют гости, покажем себя эрудированными, активными, учениками.
А теперь переходим к изучению новой темы..
II. Введение в тему:
Историческая справка.
С этим геометрическим телом человек знаком давно. Этому способствовали виды стволов деревьев, из которых со временем начали изготавливать балки для строительства жилищ, мостов и других сооружений. Ещё 3–4 тысячи лет назад люди научились украшать храмы и дворцы высокими колоннами, для чего из каменных глыб вытёсывали это. Древний термин названия этого происходит от греческого слова “килиндро” – вращаю, катаю. “Килиндрос” – свиток, валик. Евклид, указывая на способ образования этого, говорит, что если прямоугольник, вращающийся около одной из сторон, снова вернётся в то же самое положение, из которого он начал двигаться, то описанная фигура и будет этим геометрическим телом.
Как вы думаете, о чём идёт речь?
(Учащиеся предлагают варианты ответов)
Вот и поговорим сегодня о геометрическом теле, о цилиндре.
III. Объяснение нового материала.
Вводится понятие цилиндрической поверхности и цилиндра, даются определения боковой поверхности, оснований, образующей. Вводятся основные формулы.
Цилиндр — это тело вращения, которое получается при вращении прямоугольника вокруг его стороны.
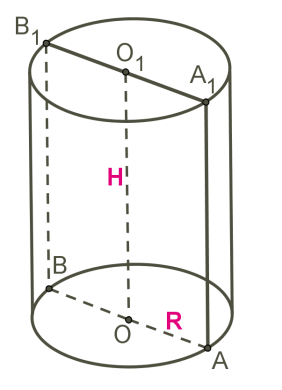
Прямоугольник AOO1A1 вращается вокруг стороны OO1.
OO1 — ось симметрии цилиндра и высота цилиндра.
AA1 — образующая цилиндра, длина которой равна длине высоты цилиндра.
AO — радиус цилиндра.
Полученная цилиндрическая поверхность называется боковой поверхностью цилиндра, а круги —
основаниями цилиндра.
Осевое сечение цилиндра — это сечение цилиндра плоскостью, которая проходит через ось цилиндра. Это сечение является прямоугольником.
При сечении цилиндра плоскостью, параллельной оси цилиндра (т.е. перпендикулярной основанию), также получается прямоугольник.
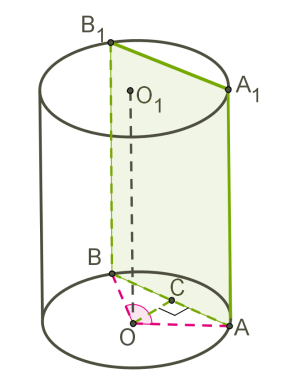
На рисунке изображён цилиндр, пересечённый плоскостью, которая параллельна оси цилиндра OO1.
ABB1A1 — прямоугольник.
OA=OB=R — радиусы.
OC — расстояние от оси цилиндра до плоскости сечения.
Дуга AB равна центральному углу AOB.
При сечении цилиндра плоскостью, параллельной основанию, в сечении получаем круг, равный основаниям цилиндра.
Если представить, что боковая цилиндрическая поверхность разрезана по образующей AA1 и развёрнута, получаем прямоугольник.

Сторона AA1 равна высоте H, а другую сторону образует развёрнутая окружность основания длиной 2πR.
Так как развёртка — прямоугольник, то боковая поверхность определяется по формуле:
Sбок.=2πR⋅H
Основания цилиндра — два круга с общей площадью 2⋅πR2.
Полная поверхность цилиндра определяется по формуле:
Sполн.=2πRH+2πR2=2πR⋅(H+R)
IV. Закрепление нового материала.
Перейдем к решению задач.
Задача 1.
Дано: Концы отрезка АВ = 13 дм лежат на окружностях оснований цилиндра. Радиус цилиндра равен 10 дм, а расстояние между прямой АВ и осью цилиндра равно 8 дм. Найти: высоту H цилиндра (см. рис. 1).
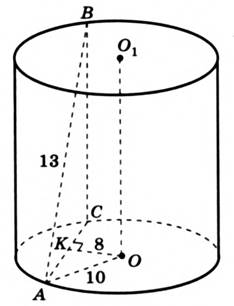
Рис. 1.
Решение: Проведем образующую ВС: Так как 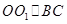 , то
, то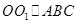 .
.
Проведем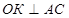 . Так как
. Так как 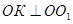 и
и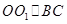 , то
, то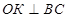 .
.
Таким образом, прямая ОК перпендикулярна к двум пересекающимся прямым АС и BC плоскости АВС. Следовательно, 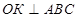
Рассмотрим ∆АКО – прямоугольный, по теореме Пифагора: 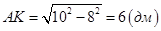 , АС=2AK=12 дм.
, АС=2AK=12 дм.
Рассмотрим 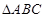 — прямоугольный, по теореме Пифагора:
— прямоугольный, по теореме Пифагора: 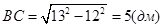 .
.
BC – образующая цилиндра, и она равна высоте цилиндра.
Ответ: H=5 дм.
Задача 2.
Дано: Через образующую АА1, цилиндра проведены две секущие плоскости, одна из которых проходит через ось цилиндра, угол между плоскостями равен φ. Найти: отношение площадей сечений цилиндра этими плоскостями.
Решение: Нарисуем плоскости α – ABB1A1 и β — AA1C1C в цилиндре. Построим угол между плоскостями на рисунке (см. рис. 2).
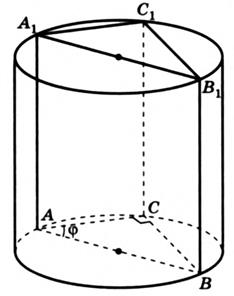
Рис. 2.
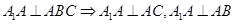 . Значит, угол
. Значит, угол 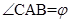 .
.
Теперь найдем отношение площадей, которое спрашивается: 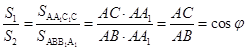 . (Угол C в треугольнике ABC – прямой, так как он опирается на диаметр нижнего основания цилиндра).
. (Угол C в треугольнике ABC – прямой, так как он опирается на диаметр нижнего основания цилиндра).
Ответ: 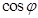 .
.
Задача 3.
Дано: Угол между образующей цилиндра и диагональю осевого сечения равен φ, Площадь основания цилиндра равна 8. Найти: площадь боковой поверхности цилиндра.
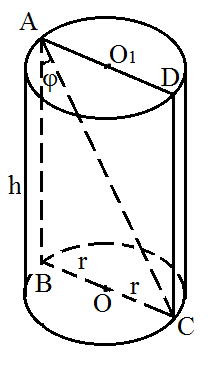
Рис. 3.
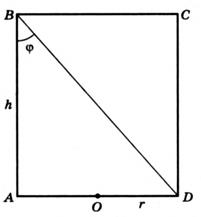
Решение: Обозначим на рисунке АВСD — осевое сечение, диагональ осевого сечения – AC, угол CAB=φ. (см. рис. 3).
Для более удобной подстановки в формулу обозначим, что BC=2r, AB=h.
Из треугольника ABC, 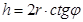 .
.
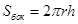
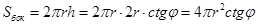 .
. В полученном выражении πr2=Sосн – по условию. Значит, 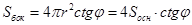 .
.
Ответ: 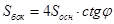 .
.
В данной задаче 3, можно воспользоваться только рисунком №4, не рисуя полностью весь цилиндр.
V. Подведение итога урока (фронтальный опрос).
Конспект урока по геометрии по теме Цилиндр»
Геометрия 11 класс
Решение задач по теме
«Цилиндр».
Учитель математики
____Зайнутдинова Р.К.
__________2018-2019 уч.год_________
Тема : Цилиндр
Форма урока: комбинированный
Цель:
1. Закрепить у учащихся знания о теле вращения – цилиндре (определение, элементы цилиндра, сечение цилиндра, формулы площади боковой и полной поверхности цилиндра).
2. Сформировать навыки решения типовых задач.
2. Развивать пространственные представления на примере круглых тел.
3. Продолжить формирование логических и графических умений
Задачи:
1. Научить учащихся строить сечение цилиндра плоскостью параллельной оси цилиндра и перпендикулярной оси цилиндра.
2. Научить учащихся применять формулы полной и боковой поверхностей цилиндра при решении задач.
Ожидаемый результат:
Учащиеся должны уметь изображать цилиндр и его сечения .
Учащиеся должны уметь применять формулы для вычисления площадей полной и боковой поверхностей при решении задач.
Учащиеся должны уметь решать простейшие геометрические задачи, связанные с цилиндром и сечениями цилиндра.
Этапы урока:
Организационный момент.
Повторение ранее изученного материала.
Закрепление.
Обучающая самостоятельная работа.
Итог урока.
Ход урока
1. Организационный момент.
2. Повторение ранее изученного материала.
Учащимся предлагается заполнить лист с заданиями.
Карточка.
1. Нанесите на рисунок основные элементы цилиндра.
2.Изобразите а) осевое сечение цилиндра; б) сечение цилиндра плоскостью, проходящей перпендикулярно оси цилиндра; в) сечение цилиндра плоскостью, проходящей параллельно оси цилиндра. Какая фигура получается в каждом случае?
3 Запишите формулы для вычисления площади поверхности цилиндра.
Что можно найти по этим формулам? Что должно быть известно в этих случаях?
Фронтальный опрос (с целью обобщения знаний и проверки выполненной работы)
Цилиндр – это геометрическое тело, состоящее из двух равных кругов, расположенных в параллельных плоскостях и множества отрезков, соединяющих соответственные точки этих кругов.
Цилиндр можно получить вращением прямоугольника вокруг одной из его сторон.
Наклонные цилиндры, прямые цилиндры, цилиндрические поверхности
Основания цилиндра – равные круги, расположенные в параллельных плоскостях
Высота цилиндра — это расстояние между плоскостями его оснований.
Радиус цилиндра – это радиус его основания.
Ось цилиндра – это прямая, проходящая через центры основания цилиндра (ось цилиндра является осью вращения цилиндра).
Образующая цилиндра — это отрезок соединяющий точку окружности верхнего основания с соответственной точкой окружности нижнего основания. Все образующие параллельны оси вращения и имеют одинаковую длину, равную высоте цилиндра.
Образующая цилиндра при вращении вокруг оси образует боковую (цилиндрическую) поверхность цилиндра.
Разверткой боковой поверхности цилиндра является прямоугольник со сторонами H и C, где H – высота цилиндра, а C – длина окружности основания.
Sб = H · C = 2πRH
Sп = Sб + 2S = 2πR(R + H).
Осевое сечение цилиндра – сечение цилиндра плоскостью, проходящей через ось цилиндра (осевое сечение цилиндра является плоскостью симметрии цилиндра). Все осевые сечения цилиндра – равные прямоугольники
Сечение плоскостью, параллельной оси цилиндра. В сечении – прямоугольники.
Сечение плоскостью перпендикулярной оси цилиндра. В сечении круги, равные основанию.
Цилиндрическая гастрономия. Цилиндрическая архитектура. Цилиндры фараона
3. Закрепление материала. Решение задач.
Ученики видят список задач для классной работы. По желанию учащиеся имеют возможность решать с опережением на оценку.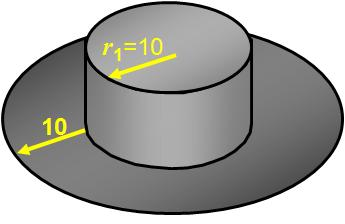
№1. (задача с практическим содержанием).
Найдите площадь поверхности (внешней и внутренней) шляпы, размеры которой (в см) указаны на рисунке.
№2 (523). Осевое сечение цилиндра – квадрат, диагональ которого равна 20 см. Найдите: а) высоту цилиндра; б) So цилиндра.
№3 (525). Площадь осевого сечения цилиндра равна 10 м2, а площадь основания – 5 м2. Найдите высоту цилиндра.
№4 (527). Концы отрезка АВ лежат на разных основаниях цилиндра. Радиус цилиндра равен r, его высота – h, расстояние между прямой АВ и осью цилиндра равно d. Найдите: a) высоту, если r = 10, d = 8, AB = 13.
№5* (532). Через образующую АА1 цилиндра проведены две секущие плоскости, одна из которых проходит через ось цилиндра. Найдите отношение площадей сечений цилиндра этими плоскостями, если угол между ними равен j.
4. Обучающая самостоятельная работа
Самостоятельная работа по вариантам. (Возможна организация парной работы).
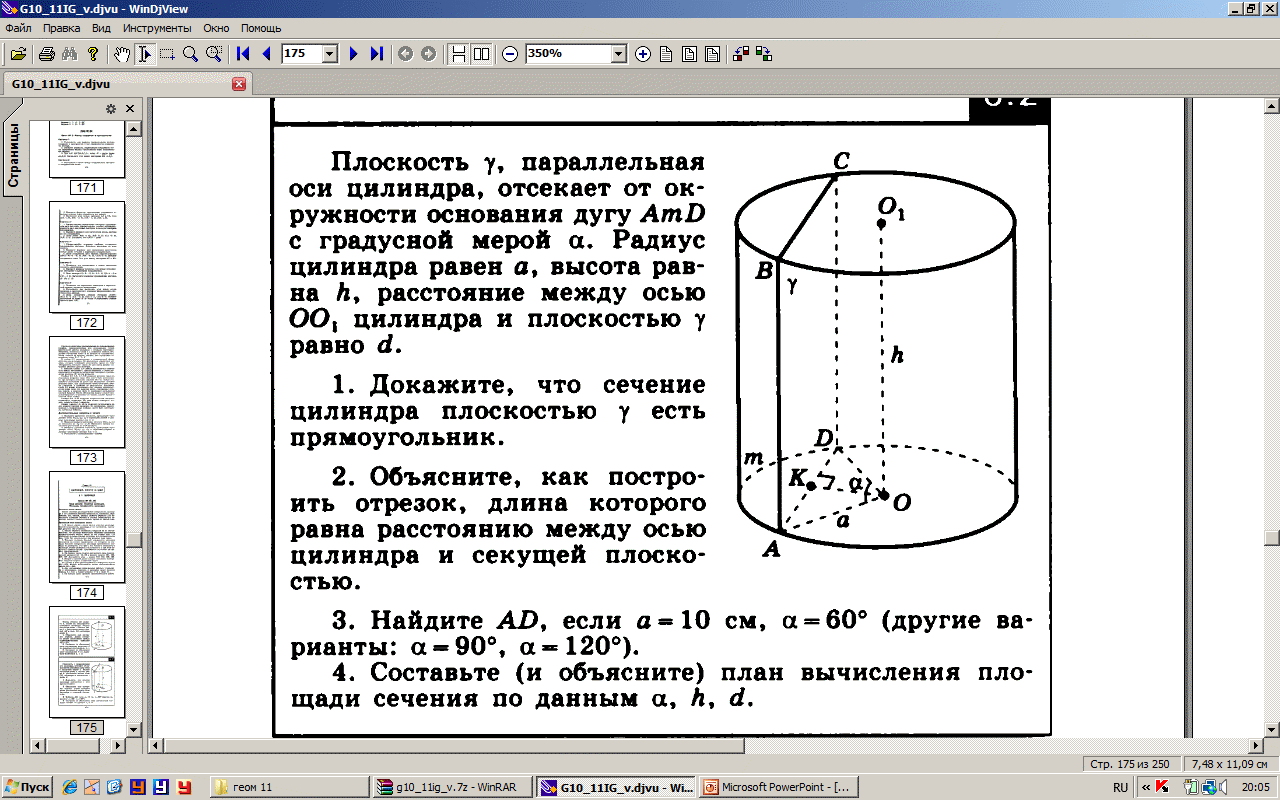
Плоскость g, параллельная оси цилиндра, отсекает от окружности основания дугу AmD с градусной мерой a. Радиус цилиндра равен a, высота равна h, расстояние между осью цилиндра ОО1 и плоскостью g равно d.
Вариант 1.
1) Докажите, что сечение цилиндра плоскостью g есть прямоугольник.
2) Найдите AD, если a =10 см, a = 60°.
Вариант 2.
1) Составьте план вычисления площади сечения по данным a, h, d.
2) Найдите AD, если a =8 см, a = 120°.
5. Подведение итогов урока.
1) Домашнее задание.
Повторить стр.130-132, гл. 1, п.59-60, №530, № 537.
2) Выставление оценок за работу на уроке.
3) Рефлексия.
Что нового вы узнали на уроке?
Чему вы научились?
Какое у вас настроение в конце урока?
Можете ли вы объяснить решение данных задач однокласснику, пропустившему урок сегодня?
Использованные источники
1. Изучение геометрии в 10-11 классах: кн. Для учителя/С.М. Саакян, В.Ф. Бутузов. – 4-е издание, М.: Просвещение, 2010.
2. Рабочая тетрадь к учебнику «Геометрия 10-11 класс» Л.С. Атанасян, М.: Просвещение, 2010
3. СD «Виртуальная школа Кирилла и Мефодия: Геометрия-11 класс»
4. http://www.220store.ru/images/produce/6518.jpeg (термос)
5. http://www.kupi-lastik.ru/goods_images/big/930050.jpg (банка кофе)
6. http://www.roxi.ru/media/user/2201/img_1255598698_940x720.jpg (банка сгущенки)
7. http://nikolife.info/images/fullnntn4nq10l80r0rfc.jpg (нарезка)
8. http://s44.radikal.ru/i105/1002/75/3471657e4528.jpg (консервы)
9. http://i.smiles2k.net/big_smiles/big_smiles_163.gif (смайлик)
10. http://content.foto.mail.ru/mail/fortuna1959/231/i-243.jpg (Пизанская башня)
11. http://www.jazztour.ru/pictures/denmark/copenhagen/sights/roundt/page4085s-107-1-rUb6NYTe-big.jpg (башня)
Конспект урока по теме «Цилиндр» , геометрия , 11 класс
Конспект урока: Решение задач по теме «Цилиндр».
Предмет: геометрия 11 класс
Учебник: «Геометрия 10-11», Л.С. Атанасян, В.Ф. Бутузов, С.Б. Кадомцева и др., 2009г
Форма урока: комбинированный
Цель:
1. Закрепить у учащихся знания о теле вращения – цилиндре (определение, элементы цилиндра, сечение цилиндра, формулы площади боковой и полной поверхности цилиндра).
2. Сформировать навыки решения типовых задач.
2. Развивать пространственные представления на примере круглых тел.
3. Продолжить формирование логических и графических умений
Задачи:
1. Научить учащихся строить сечение цилиндра плоскостью параллельной оси цилиндра и перпендикулярной оси цилиндра.
2. Научить учащихся применять формулы полной и боковой поверхностей цилиндра при решении задач.
Ожидаемый результат:
Учащиеся должны уметь изображать цилиндр и его сечения .
Учащиеся должны уметь применять формулы для вычисления площадей полной и боковой поверхностей при решении задач.
Учащиеся должны уметь решать простейшие геометрические задачи, связанные с цилиндром и сечениями цилиндра.
Этапы урока:
Организационный момент.
Повторение ранее изученного материала.
Закрепление.
Обучающая самостоятельная работа.
Итог урока.
Ход урока
1. Организационный момент.
2. Повторение ранее изученного материала.
Учащимся предлагается заполнить лист с заданиями.
Карточка.
1. Нанесите на рисунок основные элементы цилиндра.
2.Изобразите а) осевое сечение цилиндра; б) сечение цилиндра плоскостью, проходящей перпендикулярно оси цилиндра; в) сечение цилиндра плоскостью, проходящей параллельно оси цилиндра. Какая фигура получается в каждом случае?
3 Запишите формулы для вычисления площади поверхности цилиндра.
Что можно найти по этим формулам? Что должно быть известно в этих случаях?
Фронтальный опрос (с целью обобщения знаний и проверки выполненной работы)
Цилиндр – это геометрическое тело, состоящее из двух равных кругов, расположенных в параллельных плоскостях и множества отрезков, соединяющих соответственные точки этих кругов.
Цилиндр можно получить вращением прямоугольника вокруг одной из его сторон.
Наклонные цилиндры, прямые цилиндры, цилиндрические поверхности
Основания цилиндра – равные круги, расположенные в параллельных плоскостях
Высота цилиндра — это расстояние между плоскостями его оснований.
Радиус цилиндра – это радиус его основания.
Ось цилиндра – это прямая, проходящая через центры основания цилиндра (ось цилиндра является осью вращения цилиндра).
Образующая цилиндра — это отрезок соединяющий точку окружности верхнего основания с соответственной точкой окружности нижнего основания. Все образующие параллельны оси вращения и имеют одинаковую длину, равную высоте цилиндра.
Образующая цилиндра при вращении вокруг оси образует боковую (цилиндрическую) поверхность цилиндра.
Разверткой боковой поверхности цилиндра является прямоугольник со сторонами H и C, где H – высота цилиндра, а C – длина окружности основания.
Sб = H · C = 2πRH
Sп = Sб + 2S = 2πR(R + H).
Осевое сечение цилиндра – сечение цилиндра плоскостью, проходящей через ось цилиндра (осевое сечение цилиндра является плоскостью симметрии цилиндра). Все осевые сечения цилиндра – равные прямоугольники
Сечение плоскостью, параллельной оси цилиндра. В сечении – прямоугольники.
Сечение плоскостью перпендикулярной оси цилиндра. В сечении круги, равные основанию.
Цилиндрическая гастрономия. Цилиндрическая архитектура. Цилиндры фараона
3. Закрепление материала. Решение задач.
Ученики видят список задач для классной работы. По желанию учащиеся имеют возможность решать с опережением на оценку.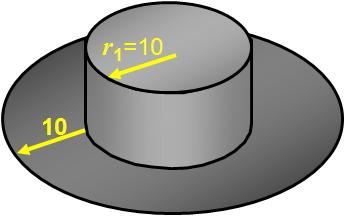
№1. (задача с практическим содержанием).
Найдите площадь поверхности (внешней и внутренней) шляпы, размеры которой (в см) указаны на рисунке.
№2 (523). Осевое сечение цилиндра – квадрат, диагональ которого равна 20 см. Найдите: а) высоту цилиндра; б) So цилиндра.
№3 (525). Площадь осевого сечения цилиндра равна 10 м2, а площадь основания – 5 м2. Найдите высоту цилиндра.
№4 (527). Концы отрезка АВ лежат на разных основаниях цилиндра. Радиус цилиндра равен r, его высота – h, расстояние между прямой АВ и осью цилиндра равно d. Найдите: a) высоту, если r = 10, d = 8, AB = 13.
№5* (532). Через образующую АА1 цилиндра проведены две секущие плоскости, одна из которых проходит через ось цилиндра. Найдите отношение площадей сечений цилиндра этими плоскостями, если угол между ними равен j.
4. Обучающая самостоятельная работа
Самостоятельная работа по вариантам. (Возможна организация парной работы).
Плоскость g, параллельная оси цилиндра, отсекает от окружности основания дугу AmD с градусной мерой a. Радиус цилиндра равен a, высота равна h, расстояние между осью цилиндра ОО1 и плоскостью g равно d.
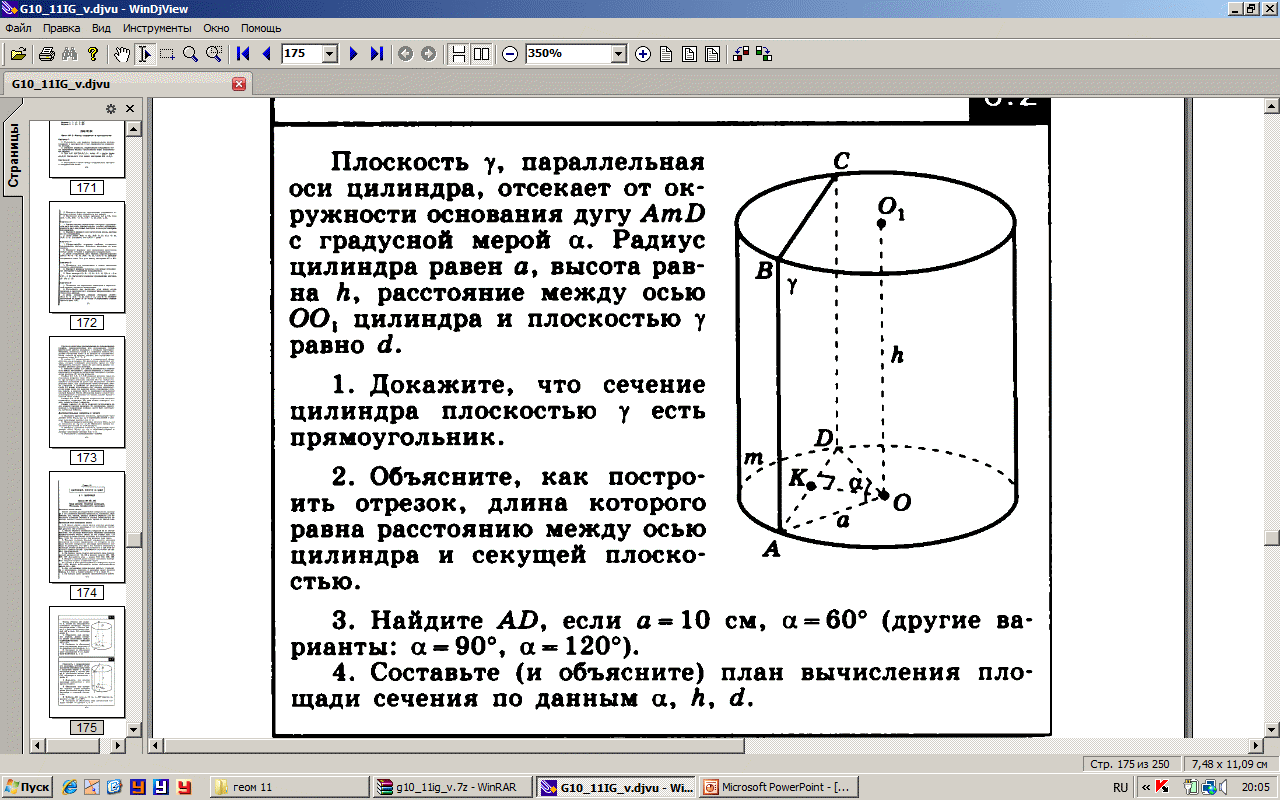
Вариант 1.
1) Докажите, что сечение цилиндра плоскостью g есть прямоугольник.
2) Найдите AD, если a =10 см, a = 60°.
Вариант 2.
1) Составьте план вычисления площади сечения по данным a, h, d.
2) Найдите AD, если a =8 см, a = 120°.
5. Подведение итогов урока.
1) Домашнее задание.
Повторить стр.130-132, гл. 1, п.59-60, №530, № 537.
2) Выставление оценок за работу на уроке.
3) Рефлексия.
Что нового вы узнали на уроке?
Чему вы научились?
Какое у вас настроение в конце урока?
Можете ли вы объяснить решение данных задач однокласснику, пропустившему урок сегодня?
Использованные источники
1. Изучение геометрии в 10-11 классах: кн. Для учителя/С.М. Саакян, В.Ф. Бутузов. – 4-е издание, М.: Просвещение, 2010.
2. Рабочая тетрадь к учебнику «Геометрия 10-11 класс» Л.С. Атанасян, М.: Просвещение, 2010
3. СD «Виртуальная школа Кирилла и Мефодия: Геометрия-11 класс»
4. http://www.220store.ru/images/produce/6518.jpeg (термос)
5. http://www.kupi-lastik.ru/goods_images/big/930050.jpg (банка кофе)
6. http://www.roxi.ru/media/user/2201/img_1255598698_940x720.jpg (банка сгущенки)
7. http://nikolife.info/images/fullnntn4nq10l80r0rfc.jpg (нарезка)
8. http://s44.radikal.ru/i105/1002/75/3471657e4528.jpg (консервы)
9. http://i.smiles2k.net/big_smiles/big_smiles_163.gif (смайлик)
10. http://content.foto.mail.ru/mail/fortuna1959/231/i-243.jpg (Пизанская башня)
11. http://www.jazztour.ru/pictures/denmark/copenhagen/sights/roundt/page4085s-107-1-rUb6NYTe-big.jpg (башня)
ОПОРНЫЙ КОНСПЕКТ ПО ТЕМЕ «ЦИЛИНДР»


























ЦИЛИНДР
►Цилиндр – фигура, полученная вращением прямоугольника вокруг оси, содержащей его сторону.
2 равных круга — основания
N OO1 – ось цилиндра
C H = |OO1| — высота
O1 AB=CD=KM=NL=l – образующие
M AO=DO=BO1=CO1=R – радиус
B ABCD – осевое сечение
KMHL – сечение, параллельно оси цилиндра
►Если ABCD – квадрат, то цилиндр называется
H равносторонним. H = 2R, l = 2R
l L
D
R
K O
A
►Ось цилиндра – прямая, проходящая через центры оснований.
►Высота цилиндра – расстояние между плоскостями его оснований.
►Образующие цилиндра – отрезки, соединяющие точки окружностей оснований ( образующие цилиндра параллельны и равны ).
►Радиус цилиндра – радиус его основания.
►Осевое сечение цилиндра – сечение плоскостью, проходящей через ось цилиндра (прямоугольник).
Площадь поверхности цилиндра.
πR2 Sосн = πR2
Sбок = 2πRH
H
2πR Т.о., Sбок = 2πRH Sполн = 2πR ( R + H )
πR2
Объём цилиндра.
Теорема. Объём цилиндра равен произведению площади основания на высоту : V = Sосн H = πR2H.
y 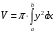 , a=0, b=H, y=R
, a=0, b=H, y=R
y = R 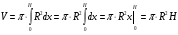
R
0 H x Т.о., V = πR2H
Сечения цилиндра плоскостями.
Сечение цилиндра плоскостью, параллель- Сечение цилиндра плоскостью, перпенди-
ной оси цилиндра – прямоугольник кулярной оси цилиндра – круг, равный
основанию
Сечение – эллипс Сечение – часть эллипса
Сечение конуса плоскостями.
Сечение конуса плоскостью, Сечение конуса плоскостью,
проходящей через его вершину, представ- перпендикулярной оси конуса – круг.
ляет собой равнобедренный треугольник,
у которого боковые стороны — образующие
конуса.
Разработка урока по геометрии по теме «Цилиндр» (11 класс)
Разработка урока по геометрии в 11 классе по учебнику Л.С. Атанасян. Тема урока «Цилиндр». На уроке вводится понятие цилиндра, цилиндрической поверхности, элементов цилиндра, виды сечений, выводятся формулы для нахождения площадей боковой и полной поверхностей цилиндра. Для закрепления материала решаются задачи из учебника, так же учащиеся знакомятся с заданиями ЕГЭ по данной теме.
Автор: учитель физики и математики: Кирьянова Светлана Павловна МБОУ «Малокалмашинская СОШ»
Тема урока: Цилиндр.
Цели:
Введение понятия цилиндрической поверхности, цилиндра, его элементов; рассмотрение различных видов сечения цилиндра плоскостью; выведение формул для вычисления площадей боковой и полной поверхностей цилиндра;
Формирование у учащихся внимательности, наблюдательности, самостоятельности, умения применять полученные знания на практике.
Задачи:
Повторить формулы длины окружности, площади круга и прямоугольника, теорему Пифагора
Познакомить учащихся с новым геометрическим телом,
Научить решать задачи по данной теме, в том числе заданий ЕГЭ
Развивать пространственное мышление учащихся, умения анализировать и систематизировать материал.
Воспитывать трудолюбие, культуру учащихся.
Тип урока: урок изучения нового материала
Методы обучения: словесный, практическая деятельность, работа с книгой, проблемный.
Оборудование: цилиндр, развертки цилиндра, шляпа-цилиндр из бумаги, набор вращение (оборудование кабинета физики), доска, карточки, рисунки сечений.
Деятельностьучащихся
1.
Организационный
Психологический настрой: Сегодня на моем демонстрационном столе шляпа. Такие шляпы носили в качестве повседневного убора мужчины 19 века. Известная женская привычка присваивать мужские элементы гардероба добралась и до шляп. Такие шляпы стали носить и женщины. Как называется эта шляпа и почему я ее принесла на урок геометрии?
(Приложение 1).
Слушают, отвечают на вопросы учителя.
Целеполагание: Действительно мы сегодня будем изучать цилиндр, его элементы, виды сечения и выведем формулы для расчета площади боковой и полной поверхностей.
Учащиеся записывают число и тему урока «Цилиндр».
2.
Получение и закрепление новых знаний: цилиндр, его элементы, виды сечения
Организует работу с учебником: для начала вы поработаете с учебником. Вам необходимо прочитать п.59., стр. 130, записать определение цилиндра и выполнить задание 1 на карточках. (Приложение 2).
Фронтальная беседа: Что называется цилиндром, основанием, высотой, радиусом, осью, образующей цилиндра? В ходе беседы учитель показывает эти элементы на модели.
Почему цилиндр называют телом вращения? Демонстрация вращения прямоугольника около одной его стороны. (Приложение 3)
Учащиеся читают учебник и работают с карточкой.
Отвечают на вопросы учителя.
Проводит связь изучаемой темы с жизнью: назовите по три примера цилиндров и цилиндрических поверхностей.
Получают карточки: Цилиндрическая гастрономия. Цилиндрическая архитектура. Цилиндрическая косметика.
Цилиндры в технике. Приводят примеры.
Какие виды сечений вы встретили при чтении учебника? Вывешивает на доску виды сечений. (Приложение 4)
Учащиеся продолжают работу с карточкой задание 2.
Решаем №522
Один ученик на доске, остальные в тетради решают № 522
Получение и закрепление новых знаний: формулы для расчета площади боковой и полной поверхностей.
Вернемся к шляпе. Чтоб она выглядела стильно ее можно покрасить или обтянуть материалом. Что для этого необходимо знать? Для этого надо знать площадь поверхности.
Предлагают свои варианты ответов.
Разрежем боковую поверхность и получим развертку — прямоугольник. Как найти площадь прямоугольника? Что является шириной и длиной этого прямоугольника?
Полная поверхность состоит из боковой поверхности и двух кругов.
Один ученик записывает на доске формулу площади прямоугольника S=ab,
выводит формулы
Sбок = h · C = 2πrh , Sцил = Sбок + 2S = 2πr(r + h).
Решаем №540.
Один ученик на доске, остальные в тетради решают № 540
3.
Д/з
Давайте остановимся, остальные номера мы будем решать на следующем уроке. а сейчас запишем д/з: Учить записи, № 539, узнать каково происхождение названия «Цилиндр».
Записывают Д/з
4.
Тема на ЕГЭ.
Сегодняшняя тема встречается на ЕГЭ в 8 задании. Я вам предлагаю решить 7 заданий с самопроверкой. Выдаются карточки с ответами на обратной стороне. Решаем с самопроверкой. (Приложение 5)
Решают задания ЕГЭ, проверяют.
5.
Рефлексия
Сложные задания или нет? Сколько решили? Все ли правильно?
Отвечают на поставлены е вопросы.
6.
Планы на последующие уроки.
Вернемся к нашей шляпе. Поднимаю шляпу, а там конус. Что это значит?
Следующее геометрическое тело для изучения будет конус.
Литература:
Геометрия: Учеб. Для 10-11 кл. общеобразоват. учреждений / Л. С. Атанасян, В.Ф. Бутузов, С.Б. Кадомцев и др.
Поурочные разработки по геометрии 10 класс./Сост. В. А. Яровенко. – М: ВАКО, 2016
Интернет – ресурсы:
https://ru.wikipedia.org
https://ege.sdamgia.ru
Яндекс.Картинки›рисунки сечения цилиндра
ПРИЛОЖЕНИЕ 1

ПРИЛОЖЕНИЕ 2
Цилиндр – это геометрическое тело, ограниченнее ___________________________ и двумя _________.
Цилиндр можно получить вращением прямоугольника вокруг _____________________________
1. Нанесите на рисунок основные элементы цилиндра.
2.Изобразите а) осевое сечение цилиндра; б) сечение цилиндра плоскостью, проходящей параллельно оси цилиндра, в) сечение цилиндра плоскостью, проходящей перпендикулярно оси цилиндра; г) под углом к оси.
ПРИЛОЖЕНИЕ 3

ПРИЛОЖЕНИЕ 4
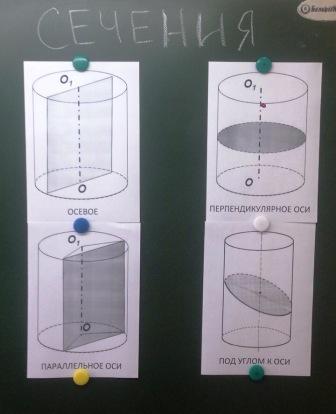
ПРИЛОЖЕНИЕ 5
Задание ЕГЭ №8 (профильный)
Радиус основания цилиндра равен 7, высота равна 10. Найдите площадь боковой поверхности цилиндра, деленную на

Длина окружности основания цилиндра равна 5, высота равна 2. Найдите площадь боковой поверхности цилиндра.
Площадь осевого сечения цилиндра равна 14. Найдите площадь боковой поверхности цилиндра, деленную на

Длина окружности основания цилиндра равна 14. Площадь боковой поверхности равна 182. Найдите высоту цилиндра.
Площадь боковой поверхности цилиндра равна 9
 , а диаметр основания равен 3. Найдите высоту цилиндра.
, а диаметр основания равен 3. Найдите высоту цилиндра.Площадь боковой поверхности цилиндра равна
 , а высота — 8. Найдите диаметр основания.
, а высота — 8. Найдите диаметр основания.Радиус основания цилиндра равен 15, а его образующая равна 14. Сечение, параллельное оси цилиндра, удалено от неё на расстояние, равное 12. Найдите площадь этого сечения.
Конспект урока геометрии на тему «Объем цилиндра» (11 класс)
Муниципальное бюджетное общеобразовательное учреждение
Платоновская средняя общеобразовательная школа
Конспект урока геометрии в 11 классе по теме
«Объём цилиндра»
Филонова Л.И., учитель математики муниципального бюджетного общеобразовательного учреждения Платоновской средней общеобразовательной школы Рассказовского района
Тема: Объем цилиндра
Класс: 11класс.
Продолжительность урока: 45 минут.
Технологии: проблемного и развивающего обучения, групповой деятельности.
Цели урока:
Образовательные:
— продолжить изучение тел вращения в ходе решения задач на вычисление объемов цилиндров;
— повторить понятие усвоения понятия цилиндра: прямого, наклонного, его оснований, боковой поверхности, сечений;
— научить видеть и показывать элементы цилиндра на модели и в изображении.
Развивающие:
— работать над развитием пространственного изображения учащихся;
— продолжить формирование логических и пространственных умений.
Воспитательные:
— работать над развитием познавательной активности и интереса к предмету.
Ход урока:
Организационный этап
Этап проверки домашнего задания
а) Проверка домашнего задания у доски. Письменно решается задача:
Насос, подающий воду в паровой котел, имеет два водяных цилиндра. Диаметры цилиндров 80 мм, а ход поршня 150 мм. Чему равна часовая производительность насоса, если каждый поршень делает 50 рабочих ходов в минуту?
б) Устная работа с классом:
— Найдите объем шахтного ствола диаметром 8 м, если его глубина 500 м.
— В цилиндрический сосуд, внутренний диаметр которого 20 см, опущена деталь. При этом уровень жидкости в сосуде поднялся на 10 см. Чему равен объем детали? Ответ обоснуйте.
— (Задание по готовому чертежу) Сформулируйте условие задачи для определения объема части цилиндра, изображенного на рисунке, и решите ее.
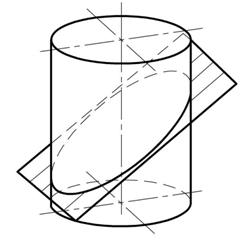
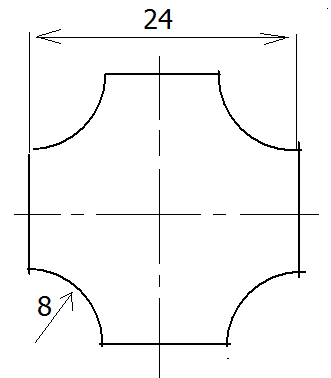
— Найдите объем п-метрового прута, форма и размеры сечения которого изображены на рисунке
В это время один учен готовит ответ у доски по карточке:
— Дайте определение цилиндра как тела вращения. Назовите элементы цилиндра. Назовите виды сечений цилиндра.
— Сформулируйте и докажите теорему об объеме цилиндра.
Учитель следит за правильностью ответов учащихся, активизирует мыслительную деятельность, зрительную память.
Организационный этап.
Выполнение практической части (индивидуальная работа)
— Вычислите объем цилиндра (работа с моделями цилиндров), вычислить площадь осевого сечения, параллельного основаниям.
Решение задач
— индивидуальные задания на карточках (выполняются в тетрадях), проверяются по истечению определенного времени на доске (решение заранее подготовлено учителем)
Сечение цилиндра плоскостно, параллельно его оси – квадрат, отсекающий от окружности основания радиуса R дугу В. Найдите объем цилиндра.
— индивидуальные задания на карточках (выполняются на доске учащимися)
1) В цилиндр вписаны правильная треугольная призма, а в призму вписан цилиндр. Найдите отношение объемов цилиндров.
2) Сколько квадратных метров бумаги в рулоне, высота которого 85 см, а радиусы 45 см и 2 см? Толщина бумаги 0,1 мм.
— задания для коллективного решения:
Развертка боковой поверхности цилиндра — квадрат со стороной 2 дм. Найдите объем цилиндра.
Этап всесторонней проверки знаний.
Самостоятельная работа (5 минут)
Вариант 1.
Во сколько раз нужно увеличить высоту цилиндра, чтобы его объем увеличился в п раз? (не менее основания)
25 м медной проволоки имеют массу 100,7 г. Найдите диаметр проволоки. (плотность меди 8,94 г/см3)
Вариант 2.
Во сколько раз нужно увеличить радиус основания цилиндра, не меняя высоту, чтобы его объем увеличился в п раз?
В цилиндрическом сосуде уровень жидкости достигает 16 дм. На какой высоте будет находиться уровень жидкости, если ее перелить во второй сосуд, диаметр которого в 2 раза больше первого.
Подведение итогов. Задание на дом.
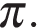
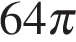 , а высота — 8. Найдите диаметр основания.
, а высота — 8. Найдите диаметр основания.