Конспект урока » Относительность движения,сложение скоростей.Мгновенная и средняя скорость.»10 класс
Класс | 10А | 10Б | 10В |
Дата |
Тема: Относительность движения,сложение скоростей.Мгновенная и средняя скорость.
Цель:
Обучающая : объяснить понятие об относительности движения. Научить определять относительную скорость
Развивающая : развивать научность мышления , уметь применять знания .
Воспитывающая: формировать добросовестное отношение к учебному труду.
Ход урока.
Ι.Организационный момент.
ΙΙ. Повторение изученного материала.
Сам. работа (20 мин)
ΙΙI. Изучение новой темы.
1.Относительность движения.
Всякое движение относительно. Это означает, что одно и то же тело одновременно и движется, и покоится. Движется относительно одних тел и одновременно покоится относительно других. Мы все, земляне, можем покоиться относительно своего письменного стола и одновременно всегда движемся относительно Солнца.
В задачах на относительность движения часто приходится пользоваться правилом сложения скоростей. Правило сложения скоростей:
скорость тела относительно неподвижной системы отсчета равна сумме скорости тела относительно подвижной системы отсчета и скорости самой подвижной системы относительно неподвижной, где
скорость тела относительно НСОскорость тела относительно ПСО
скорость ПСО относительно НС
Это правило применимо только к классическим скоростям, т.е. скоростям, значительно меньшим скорости света в вакууме (т.е. к скоростям порядка 10 6 м/с и меньше).
1) Если система отсчета и тело в ней движутся в одном направлении, то
Например, если поезд движется со скоростью 16 м/с относительно вокзала, а пассажир по ходу поезда бежит со скоростью 2 м/с относительно полок вагона, то скорость пассажира относительно вокзала равна 18 м/с.
2) Если система отсчета и тело в ней движутся в противоположных направлениях, то
Например, если в предыдущем примере пассажир будет бежать навстречу ходу поезда, то скорость, с которой он будет удаляться от вокзала, будет равна 14 м/с
3) Если в подвижной системе отсчета, движущейся со скоростью относительно неподвижной системы, тело станет двигаться со скоростью относительно подвижной системы под углом к направлению ее движения, то для определения модуля скорости тела относительно неподвижной системы придется применить теорему Пифагора или теорему косинусов — в зависимости от величины угла (рис. 10 а и б).
Например, если скорость течения v0 =1 м/с, а лодка переплывает реку со скоростью v1 = 2 м/с относительно воды перпендикулярно берегу (рис. 10), то скорость лодки относительно берега будет, согласно теореме Пифагора, равна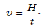
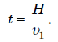

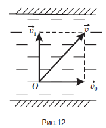
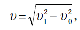
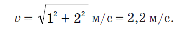
!!! Если в условии сказано, что лодка переплывает реку по кратчайшему пути, значит, ее скорость относительно берега направлена перпендикулярно берегу, а скорость лодки относительно водынаправлена под тупым углом к вектору скорости течения (рис. 11). В таком случае скорость лодки относительно берега можно определить по теореме Пифагора:
а время t, за которое лодка переплывет реку шириной Н, двигаясь с этой скоростью, можно найти как отношение этой ширины к скорости лодки относительно берега:
Если говорится о минимальном времени, за которое лодка переплывет реку, то теперь перпендикулярно берегу надо направить вектор скорости лодки относительно воды под прямым углом к течению, как на рис. 12. В этом случае минимальное время t будет равно отношению ширины реки к скорости лодки относительно течения:Таким образом, если вам нужно переплыть реку как можно быстрее, значит, надо грести перпендикулярно течению.
4) Если два тела сближаются или удаляются друг от друга, т.е. движутся в противоположных направлениях со скоростями v1 и v2 относительно неподвижных объектов, то их скорость v относительно друг друга будет по модулю равна сумме их скоростей относительно неподвижных объектов:
5) Если два тела обгоняют друг друга, т.е. движутся в одном направлении со скоростями v1 и v2 относительно неподвижных объектов, то их скорость v относительно друг друга по модулю будет равна разности их скоростей относительно неподвижных объектов:
Например, если два поезда едут по параллельным рельсам навстречу друг другу со скоростями 36 км/ч и 74 км/ч относительно вокзала, то скорость их взаимного сближения, т.е. скорость первого поезда относительно второго по модулю равна скорости второго относительно первого и равна:36 км/ч + 74 км/ч = 110 км/ч.
А если они движутся по параллельным рельсам в одном направлении, т.е., например, если второй поезд, скорость которого равна 72 км/ч, обгоняет первый, скорость которого 36 км/ч, то скорость первого поезда относительно второго
72 км/ч – 36 км/ч = 36 км/ч,
а скорость второго поезда относительно первого равна скорости
первого поезда минус скорость второго:36 км/ч – 72 км/ч = –36 км/ч.
6) Если два тела движутся со скоростями v1 и v2 относительно неподвижных объектов и векторы этих скоростей направлены под углом друг к другу, то, чтобы найти скорость второго тела относительно первого, надо найти векторную разность (рис. 13, а), а чтобы найти скорость первого тела относительно второго, надо найти векторную разность (рис. 13, б).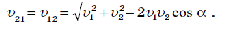
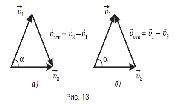
Для нахождения модуля относительной скорости можно применить теорему косинусов:
Если = 900, то удобно применить теорему Пифагора: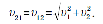
Если сказано, что два поезда длиной L1 и L2 каждый движутся навстречу друг другу со скоростями v1 и v2 относительно неподвижных объектов (деревьев, домов), то время t, в течение которого они будут проезжать мимо друг друга, можно найти, разделив сумму их длин на их скорость относительно друг друга, которая при встречном движении поездов равна сумме их скоростей: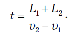
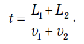
А если эти поезда обгоняют друг друга, двигаясь в одном направлении, то время обгона равно:
2.Средняя и мгновенная скорости.
1. Какой простейший вид движения вам известен? (равномерное движение)
2. Как найти скорость при равномерном движении? (перемещение разделить на время v= s / t)? Равномерное движение встречается нечасто.
Обычно механическое движение — это движение с изменяющейся скоростью. Движение, при котором скорость тела с течением времени изменяется, называют неравномерным.
Например, неравномерно движется транспорт. Автобус, начиная движение, увеличивает свою скорость; при торможении его скорость уменьшается. Падающие на поверхность Земли тела также движутся неравномерно: их скорость с течением времени возрастает.
3. Как найти скорость при неравномерном движении
? Как она называется? (Средняя скорость, vср = s/ t)На практике при определении средней скорости пользуются величиной, равной отношению пути s ко времени t, за которое этот путь пройден: vср = s/t. Ее часто называют средней путевой скоростью.
4. Какие особенности есть у средней скорости? ( Средняя скорость является векторной величиной. Для определения модуля средней скорости в практических целях этой формулой можно воспользоваться лишь в том случае, когда тело движется вдоль прямой в одну сторону. Во всех остальных случаях эта формула непригодна ).
5. Что такое мгновенная скорость? Как направлен вектор мгновенной скорости? ( Мгновенная скорость – это скорость тела в данный момент времени или в данной точке траектории. Вектор мгновенной скорости в каждой точке совпадает с направлением движения в данной точке.)
6. Чем отличается мгновенная скорость при равномерном прямолинейном движении от мгновенной скорости при неравномерном движении?
7. Можно ли определить положение тела в любой момент времени зная среднюю скорость его движения на каком-либо участке траектории? (нельзя определить его положение в любой момент времени).
Самое главное, что нужно помнить, при нахождении средней скорости — это то, что она средняя, а не средняя арифметическая скорость. Конечно, услышав задачу, сразу хочется сложить скорости и разделить на 2.Это самая распространенная ошибка.
Средняя скорость равна среднему арифметическому от скоростей тела во время движения только в том случае, когда тело с этими скоростями проходит весь путь за одинаковые промежутки времени.
ΙV . Закрепление пройденного материала.
Вода в реке движется со скоростью 3 м/с. по реке плывет плот. Чему равна скорость плота относительно берега? 1. 0 2. 3 м/с 3. 6 м/с 4. 1,5 м/с 2) Человек спускается вниз по эскалатору со скоростью 1 м/с. скорость эскалатора 4 м/с. чему равна скорость человека относительно неподвижного наблюдателя, стоящего внизу? 1. 5 м/с 2. 3 м/с 3. 0 4. Недостаточно данных 3) Какова траектория движения любой точки винта , поднимающего вверх вертолет, для наблюдателя, стоящего внизу? 1. Прямая линия 2. Винтовая линия 3. Окружность 4. Парабола
V . Домашнее задание. §
infourok.ru
Сложение скоростей
Ещё в младших классах вы сталкивались с тем, что иногда необходимо складывать скорости. Например, если две машины едут навстречу друг другу, то скорость их сближения — это сумма скоростей первой и второй машины.

Если же они двигаются в одном направлении, то скорость их сближения (или удаления) будет определяться разностью скоростей. Как мы уже говорили, решающее значение имеет выбор системы отсчёта.

Закон сложения скоростей:
если тело двигается со скоростью  в системе отсчёта
в системе отсчёта  а система отсчёта
а система отсчёта  двигается со
скоростью
двигается со
скоростью  в
системе отсчёта
в
системе отсчёта  ,
то скорость движения тела, относительно системы
,
то скорость движения тела, относительно системы  равна:
равна:

Напомним, что скорость — это векторная величина, поэтому, скорости складываются геометрически.
Пример решения задач.
Лодка двигается по реке с собственной скоростью 8 м/с, так, как показано на рисунке. Скорость течения реки составляет 1 м/с. Определите скорость лодки относительно берега.

Расположим оси координат
так, чтобы направление оси х совпадало с направлением течения реки.
Тогда проекция скорости на ось х будет равна  , т.к. на рисунке нам
указан угол между направлением течения и скоростью лодки. Обратите внимание,
что эта проекция будет отрицательной. В этом можно убедиться при построении
проекции, да и чисто логически ясно, что лодка плывет против течения, а значит,
одну из скоростей нужно обозначить за отрицательную. Проекция скорости течения
на ось х, конечно же, будет равна 1 м/с, поскольку направление течение
совпадает с направлением оси х. Тогда скорость движения лодки по оси х
относительно берега равна:
, т.к. на рисунке нам
указан угол между направлением течения и скоростью лодки. Обратите внимание,
что эта проекция будет отрицательной. В этом можно убедиться при построении
проекции, да и чисто логически ясно, что лодка плывет против течения, а значит,
одну из скоростей нужно обозначить за отрицательную. Проекция скорости течения
на ось х, конечно же, будет равна 1 м/с, поскольку направление течение
совпадает с направлением оси х. Тогда скорость движения лодки по оси х
относительно берега равна: 
Проекция вектора
скорости лодки на ось у равна 
Разумеется, проекция скорости течения на ось у будет равна нулю, потому что вектор скорости течения перпендикулярен этой оси. С помощью геометрической суммы проекций мы можем найти модуль скорости лодки, относительно берега:

Давайте рассмотрим теперь пример, который научит вас складывать какие угодно скорости.

Найдём скорость машины,
относительно самолёта в заданной системе координат. Сначала найдем проекции
скорости машины на оси х и у. Точно так же, как и в предыдущем
примере, проекция на ось х равна:  , а проекция на ось у
равна
, а проекция на ось у
равна  .
Точно так же находим проекции скорости самолёта на координатные оси:
.
Точно так же находим проекции скорости самолёта на координатные оси:


Напомним, что проекции являются скалярными величинами, поэтому их мы складываем алгебраически:


Теперь, когда мы нашли проекции скорости машины относительно самолёта на оси х и у, мы можем найти модуль скорости с помощью геометрической суммы:



Таким образом, мы получили расчётную формулу для вычисления модуля скорости одного движущегося тела, относительно другого движущегося тела. Эта формула справедлива для тех случаев, когда оба тела двигаются в одной плоскости.
Заметим, что закон сложения скоростей справедлив и для неравномерного движения. В этом случае нужно складывать мгновенные скорости.
Пример решения задачи.
Задача. Мяч катится с постоянной скоростью 10 м/с. Ему наперерез бежит футболист со скоростью 7 м/с, так, как показано на рисунке. Через какое время футболист поймает мяч, если изначально между футболистом и мячом было 40 метров?

Начнём с того, что когда футболист поймает мяч, они будут находиться в одной точке. Расположим систему координат так, чтобы направление движения футболиста совпадало с направлением оси х. Тогда, скорость мяча будет направлена под углом 45о градусов к оси х. Сделаем проекции скорости мяча на оси х и у.


videouroki.net
10 класс Урок№4 _________ Тема урока: «Мгновенная скорость. Сложение скоростей». Цели и задачи: • обеспечить восприятие, осмысление и первичное запоминание учащимися понятий мгновенная скорость, прямолинейное равноускоренное движение, ускорение; • организовать деятельность учащихся по воспроизведению изученного материала; • обобщить знания о понятии «прямолинейное равноускоренное движение»; • проверить применение на практике изученного материала; • развивать познавательную самостоятельность и творческие способности учащихся; • воспитывать навыки творческого усвоения и применения знаний; • развивать коммуникативные способности учащихся; • развивать устную речь учащихся; Ход урока
Проверка домашнего задания • Обзор тетрадей с целью выяснения наличия решения учащимися задач, которые были заданы домой. II. Мотивация, сообщение темы и цели урока |
Ни одно тело не может двигаться все время с постоянной скоростью. Трогаясь с места, велосипедист увеличивает свою скорость. Далее в течение какого-то промежутка времени он движется с постоянной или почти постоянной скоростью, но все же когда-нибудь ему придется остановиться. Для этого велосипедист тормозит – уменьшает скорость движения до нуля. При этом за одинаковые промежутки времени он перемещается на различные расстояния, то есть движется неравномерно. В каждой точке траектории значения скорости велосипедиста разные. |
Скорость тела в данной точке траектории или в данный момент называют мгновенной скоростью. Необходимо уметь рассчитывать мгновенную скорость в данный момент времени для того, чтобы задать неравномерное движение. |
Чтобы понять, что же такое мгновенная скорость, представим себе, что велосипедист, трогаясь с места, ускоряется в течение 20 секунд. Если найти отношение перемещения велосипедиста во время разгона к времени разгона, мы получим среднюю скорость на этом участке пути. Но это не значит, что в каждый момент времени реальная скорость велосипедиста была именно такой. Напротив, в начале пути скорость была равна нулю, а в конце разгона скорость была гораздо больше полученной средней скорости. |
Если разделить все время разгона на 20 равных частей и вычислить средние скорости для каждого участка, то мы получим значения средних скоростей для каждого участка. Эти значения будут еще точнее характеризовать движение. Чем меньше будут эти временные промежутки, тем меньше будет отличие между скоростями соседних участков и тем точнее будут значения этих скоростей. Если устремить промежуток времени к нулю, то отношение малого перемещения к малому промежутку времени, в течение которого это перемещение произошло, будет стремиться к определенному значению. Это и есть мгновенная скорость точки в данный момент времени. |
Мгновенная скорость точки – это предел отношения перемещения точки к промежутку времени, в течение которого это перемещение произошло, при устремлении промежутка времени к нулю. |
Мгновенная скорость всегда направлена по касательной к траектории движения. В этом можно наглядно убедиться, посмотрев на любые отделяющиеся от вращающегося тела части. К примеру, грязь, вылетающая из-под колес автомобиля, она отделяется от колеса и летит вдоль линии, касательной к поверхности колеса, так как кусочки грязи в момент отрыва имеют скорость равную скорости поверхности колеса. Аналогичным примером может служить процесс заточки ножа при помощи точильного круга. Вылетающие искры будут двигаться по касательной к поверхности круга. |
Понятие мгновенной скорости относится к точке. В дальнейшем, когда мы будем говорить о скорости движения тела, будем иметь в виду скорость какой-либо точки этого тела. |
Механическое движение относительно: тело вполне может покоиться в одной системе отсчета и при этом двигаться в другой системе отсчета с одной скоростью, а в третьей системе с другой скоростью. Траектория движения одного и того же тела в разных системах отсчета также будет различной. Рассмотрим пример, человек лежит в поезде, который в свою очередь движется относительно Земли. В этом примере человек относительно поезда имеет нулевую скорость, а относительно Земли будет двигаться со скоростью движения поезда. Некоторая точка, находящаяся на пропеллере летящего вертолета, описывает окружность в системе отсчета, связанной с вертолетом, а в системе отсчета, связанной с посадочной площадкой, находящейся на поверхности Земли, та же самая точка будет описывать уже не окружность, а винтовую линию. Перемещение тела, пройденный им путь, а также его скорость тоже изменяются, если мы переходим от одной системы отсчета к другой. Пассажир поезда неподвижен относительно движущегося поезда, перемещение и путь человека по отношению к поезду равны нулю. Но по отношению к деревьям или зданиям, расположенным вдоль железной дороги, они имеют некоторые ненулевые значения. |
Решая практические задачи, достаточно часто требуется вычислить перемещение либо скорость тела в некоторой системе отсчета, если значения этих величин уже известны, но относительно другой системы отсчета. Рассмотрим пример. Для того чтобы составить расписание движения теплохода, необходимо знать его скорость в системе отсчета, связанной с берегом и скорость течения реки тоже относительно берега. Предположим, что теплоход, плывущий по реке, имеет определенную собственную скорость. Тогда в системе отсчета, связанной с берегом, при движении теплохода вниз по течению реки модуль его скорости будет больше, а при движении вверх против течения – меньше собственной скорости теплохода. |
Скорость течения реки относительно берега измерить достаточно просто, вычислить скорость теплохода относительно воды тоже не составит труда. Теперь зная все необходимые величины, мы можем вычислить скорость движения теплохода относительно берега. Так как скорость является величиной векторной, скорость теплохода относительно берега будет равна векторной сумме вектора скорости движения теплохода в системе отсчета, связанной с водой в реке и вектором скорости течения воды. Если теплоход движется по течению, то векторы скорости теплохода относительно воды и воды относительно берега сонаправлены. Соответственно проекции этих векторов будут иметь одинаковые знаки, поэтому модуль вектора суммы векторов будет больше модуля вектора скорости теплохода относительно воды в реке. Если же теплоход идет против течения реки, то вектор скорости теплохода относительно воды будет направлен противоположно вектору скорости течения воды. Проекции этих векторов будут иметь противоположные знаки, значит, модуль вектора суммы векторов будет меньше модуля вектора собственной скорости теплохода. Это подтверждается нашими наблюдениями: что теплоход, идущий по течению, движется относительно берега значительно быстрее, такого же теплохода, движущегося против течения воды в реке. |
Эти рассуждения можно распространить на любое тело, движущееся в подвижной системе отсчета. Если тело движется в системе отсчета К1, которая сама движется относительно другой системы отсчета К2, то скорость движения этого тела относительно системы К2 равна геометрической сумме скорости тела в системе К1 и скорости движения системы отсчета К1 относительно системы отсчета К2. Это и есть закон сложения скоростей. |
Закон сложения скоростей можно получить и по-другому. Мы уже изучали закон сложения перемещений. В нем говорится о том, что перемещение тела в подвижной системе отсчета относительно неподвижной системы отсчета равно геометрической сумме перемещения тела относительно подвижной системы отсчета и перемещения подвижной системы отсчета относительно неподвижной. |
Разделим обе части этого уравнения на промежуток времени, в течение которого происходило перемещение. В результате имеем, что отношение перемещения тела относительно неподвижной системы отсчета к промежутку времени равно отношению перемещения тела относительно подвижной системы отсчета к промежутку времени плюс отношению перемещения самой подвижной системы относительно неподвижной к тому же промежутку времени. |
Согласно определению, отношение перемещения к промежутку времени, в течение которого оно произошло, равно скорости тела. Отсюда следует, что скорость тела, движущегося в подвижной системе отсчета относительно неподвижной, равна геометрической сумме скорости подвижной системы отсчета относительно неподвижной и скорости тела в подвижной системе отсчета. |
Как любое векторное уравнение, закон сложения скоростей для движения на плоскости можно записать как два уравнения для сложения проекций скоростей. Проекция вектора скорости тела на ось Х относительно системы отсчета К2 равна сумме проекции на ось Х вектора скорости тела относительно системы К1 и проекции на ось Х скорости системы отсчета К1 относительно системы отсчета К2. Проекция вектора скорости тела на ось Y относительно системы отсчета К2 равна сумме проекции на ось Y вектора скорости тела относительно системы К1 и проекции на ось Y скорости системы отсчета К1 относительно системы отсчета К2. Проекции скоростей складываются алгебраически. |
infourok.ru
План-конспект урока по физике (10 класс) на тему: «Средняя скорость. Мгновенная скорость. Относительная скорость. Сложение скоростей».
ПЛАН – КОНСПЕКТ УРОКА ПО ФИЗИКЕ В 10 КЛАССЕ
Тема урока:
«Средняя скорость. Мгновенная скорость. Относительная скорость. Сложение скоростей».
Цели урока: ввести понятие мгновенной скорости; научить определять относительную скорость движения; научить применять физические законы при решении задач
Ход урока.
- Организационный момент.
- Проверка домашнего задания
Решение задачи.
Что определяет закон движения?
Произойдет ли столкновение кораблей, если траектории их движения пересекаются?
- Изучение нового материала.
Изменение положения в пространстве движущегося тела характеризуют путь и перемещение. Но эти величины не говорят, как быстро произошло изменение. Скорость является пространственно – временной характеристикой движения тела.
Скорость – физическая величина, показывающая, какое перемещение совершило тело за единицу времени [м/с].
Если тело прошло путь 500м за время 20с, то можно предположить, что тело за каждую секунду проезжало 25 метров. Но реально это не так. Тело могло первые 5 минут двигаться, потом стоять, потом снова двигаться. Поэтому путь, пройденный телом, характеризуется средней скоростью.
Средняя скорость – физическая величина, равная отношению всего пройденного пути ко всему времени.
Средняя скорость является достаточно приближенной характеристикой движения. Проезжая по городу 20 км за 30 минут водитель на спидометре каждый раз видит мгновенную скорость.
Мгновенная скорость – физическая величина, равная отношении. Очень малого перемещения к промежутку времени, в течение которого оно было совершено.
Рассмотрим задачу в учебнике на стр.25 рис 1.20 и 1.21.
v1 – скорость лодки относительно воды
v2 – скорость лодки относительно берега
v – скорость течения реки
k1 — С.К., движется вместе с водой
k2 – С.К., связанная с берегом
— перемещение лодки относительно берега
— перемещение воды
— перемещение лодки относительно воды
Поделим на Δt.
Закон сложения скоростей: Если тело движется относительного некоторой С.О.K1 со скоростью v1 и сама С.О. K1 движется относительно другой С.О.К2 со скоростью v, то скорость тела относительно второй системы отсчета равна геометрической сумме скоростей v1 и v2.
- Решение задач
- Домашнее задание
§9-10, стр.27 упр.2 (1,2)
nsportal.ru
План-конспект урока по физике (10 класс) по теме: конспекты по физике по разделу механика 10 класс
ПЛАН – КОНСПЕКТ УРОКА ПО ФИЗИКЕ В 10 КЛАССЕ
Тема урока:
«Движение точки и тела. Положение точки в пространстве. Способы описания движения. Системы отсчета. Перемещение».
Цели урока: объяснить необходимость изучения механики; ввести понятия «траектория», «перемещение», «путь», «система отсчета».
Программное обеспечение: Microsoft Power Point.
Ход урока.
- Организационный момент.
- Изучение нового материала.
Механическое движение – изменение с течением времени положения тела по отношению к другим телам.
- Двигаетесь ли вы, находясь в классе? (В классе Вы находитесь относительно Земли, но движетесь вместе с ним вокруг Солнца)
Говорят, тело принимаем за материальную точку.
Материальная точка – тело, размерами и формой которого можно пренебречь в условиях данной задачи.
Если траектория прямая, движение называется прямолинейным, если кривая- криволинейным. Траектория движения указывает все положения, которые занимала точка. Но ничего нельзя сказать о том, быстро или медленно проходила точка отдельные участки .Чтобы получит полное описание, необходимо знать, в какой момент точка занимала то или ниое положение на траектории.
А
В
- Описать движение можно:С помощью таблиц;
- Графически;
- Аналитически.
Траектория
Линия, вдоль которой движется тело
Путь
Расстояние, которое прошло тело по траектории
S, [м]
Перемещение
Вектор, соединяющий начальную и конечную
точку траектории
S
По траектории точек
Тела
- Поступательное
- Вращательное
Колебательное
По траектории
- Прямолинейное
- Криволинейное
По пройденному пути
- Равномерное
- Неравномерное
Виды движения
Положение материальной точки в пространстве в произвольный момент времени можно определить, если ввести систему отсчета.
Система отсчета (С.О.) – совокупность тела отсчета, системы координат и часов.
- Какие системы координат вы знаете?(одномерная, двухмерная, трехмерная)
О
А
х
(шоссе)
одномерная С.К.
х
y
А
(самолет)
трехмерная С.К.
(корабль в море)
двумерная С.К.
y
О
z
А
Совокупность x(t) и y(t) в момент времени t определяет закон движения материальной точки в координатной форме.
Положение материальной точки зададим вектором r.
Радиус — вектор – вектор, соединяющий начало отсчета с положением точки в произвольный момент времени.
y
x
O
r1
r2
Δr
ry
rx
М
α
x=r cosα
y=r sinα
r=rx+ry
Δr= r2 — r1
Δr – перемещение.
- Закрепление изученного
- Какую систему координат следует выбрать?
- Трактор в поле
- Вертолет
- Поезд
- Люстра в комнате
- Подводная лодка
- Зачем введено понятие материальной точки? Когда тело можно считать материальной точкой?
- В чем отличие пути от перемещения?
- Домашнее задание
§3-6, вопросы устно в конце параграфа.
nsportal.ru
Конспект урока » Относительность движения,сложение скоростей.Мгновенная и средняя скорость.»10 класс
Класс
10Б
10В
Дата
Тема урока: Графики скорости. Решение задач.
Образовательная цель: получение учащихся, усвоивших основные знания в данной теме:
механическое движение – это изменение положения тела в пространстве относительно других тел с течением времени;
основная задача механики – определение положения тела в любой момент времени;
траектория движения – линия, вдоль которой движется тело;
путь – физическая величина, равная длине траектории, пройденной телом за некоторый промежуток времени;
перемещение – отрезок соединяющий начальное и конечное положение;
при равномерном движении путь прямо пропорционален времени движения;
график прямой пропорциональности – прямая, проходящая через начало координат;
скорость равномерного движения – это физическая величина, характеризующая быстроту движения тела; она определяется отношением пути, пройденного телом, к отрезку времени, за которое был пройден этот путь.
Цель по развитию учащихся: подготовка учащихся, овладевших следующими видами деятельности:
получать понятие “механическое движение”;
получать понятие о физических величинах “путь”, “перемещение”, “координата”, “скорость”;
получать график прямо пропорциональной зависимости пути от времени, координаты от времени с учетом погрешности;
строить графики зависимости пути от времени, координаты от времени и скорости равномерного движения от времени;
вычислять скорость, путь, перемещение и координату равномерного движения.
Задачи урока:
повторить основные понятия и физические величины прямолинейного равномерного движения;
создать условия для развития личности учеников в процессе их деятельности;
способствовать развитию практических навыков и умений;
научить выделять главное, сравнивать, развивать способности к обобщению, систематизации полученных знаний.
Ход урока
I. Актуализация раннее усвоенных знаний. (Решение качественных задач. Они позволяют учителю понять, как учащиеся усвоили теоретический материал по данной теме.)
1. Туристы перешли с одного берега озера, где располагалась их база, на другой и, посмотрев на часы, решили устроить краткий отдых. Стояла тихая погода, и им были хорошо слышны передачи радиоузла базы; поэтому последние известия они смогли прослушать, выключив свой транзистор. После этого один из туристов заявил, что расстояние до базы – почти 3 км. Каким образом он определил это расстояние? (Турист знал, что скорость звука воздухе при 20oС 340м/с. Он заметил, что сигналы точного времени, передаваемые по радио, слышны вначале из радиоприемника, а спусти некоторое время – с базы. Определив время запаздывания, он по формуле s = vзвt рассчитал расстояние до базы.)
2. Выехав рано утром из города на ровное и пустынное шоссе, шофер решил устроить первую остановку ровно через час. Как ему выполнить свое намерение, не смотря на часы? Радиоприёмник в автомобиле отсутствует. (В любом автомобиле есть счетчик пути и спидометр. Поэтому шофер должен поддерживать постоянной взятую скорость движения и дождаться увеличение километража пробега на величину, численно равную этой скорости.)
3. “Мировой рекорд” по прыжкам в высоту среди животных принадлежит маленькой южноафриканской антилопе. На какую высоту прыгнет антилопа, если она отталкивается от земли вверх со скоростью 12 м/с? (7,2 м.)
4. Человек, плывущий по реке на лодке, держится середины реки, если плывет по течению, и старается держаться около берега, если плывет против течения. Почему он так делает? (В первом случае скорость его перемещения возрастает благодаря значительной помощи течения, у которого скорость на середине реки наибольшая. Во втором случае течение реки будет мало мешать движению, поскольку у берегов скорость воды в реке всегда меньше, чем на середине.)
II. Решение задач
1. Даны уравнения движения трех различных тел, заданные в одной и той же системе координат: x1 = -20 +5t; x2 = 10 -4t; x3 = 2t. Все данные указаны в СИ.
Определите начальные координаты и проекции скоростей для каждого тела. Постройте графики зависимости координаты и проекции скорости от времени для каждого из движущихся тел.
Алгоритм решения:Запишите значения начальных координат для каждого из тел.
Запишите значения проекций скоростей для каждого из тел с учетом знака проекций.
Заполните таблицы значений координат тел для двух выбранных моментов времени.
Изобразите на графике координаты, которые занесены в таблицы для каждого из тел. Проведите через построенные точки графики зависимости координаты от времени для каждого из тел.
Пользуясь результатами нахождения проекций скоростей, изобразите точки, соответствующие проекциям скоростей тел и постойте графики для каждого из тел.
Задача 2 Движение двух велосипедистов заданы уравнениями x1 = 5t (м) и x2 = 60 – 10t (м). Определите время и координату встречи велосипедистов.
ДАНО: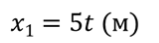
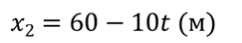
РЕШЕНИЕ:
Сравним уравнения, которыми описываются их движения с кинематическим уравнением равномерного движения
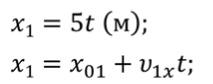
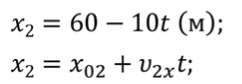
Из данных уравнений следует, что для первого велосипедиста
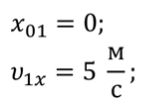
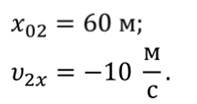
Для второго велосипедиста.Значит, оба велосипедиста участвуют в равномерном прямолинейном движении. Свяжем систему отсчета с Землей, ось «О икс» направим в сторону движения первого велосипедиста, а за начало отсчета координаты выберем точку «О», то есть положение первого велосипедиста в начальный момент времени.

Два тела встречаются тогда, когда их координаты в этот момент времени совпадают, то есть равны.
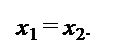
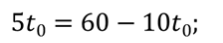
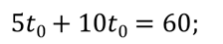
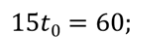
Время встречи равно
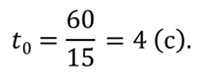
Координата встречи равна
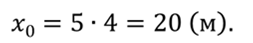
Графический метод:
Ранее было выяснено, что велосипедисты движутся равномерно и прямолинейно. Поэтому графиком движения каждого из них будет являться прямая линия. Из курса математики вы должны знать, что для построения прямой линии достаточно найти какие-либо две ее точки.
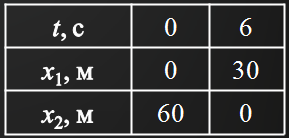
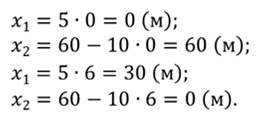
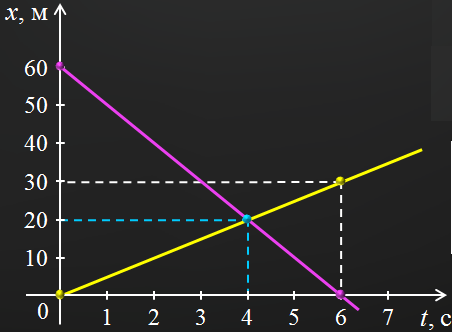
На графике хорошо видно, что прямые пересеклись в одной точке — в точке места встречи. Для того чтобы определить ее координаты, опустим из этой точки два перпендикуляра — один на ось времени, а другой на ось координат
Ответ: t0 = 4 с; х0 = 20 м.
Задача 3. Самолет взлетает с аэродрома под углом 30о к горизонту со скоростью 216 км/ч. Какой высоты самолет достигнет через 12 с и на какое расстояние в горизонтальном направлении он удалится от места взлета? Считать, что самолет в горизонтальном и вертикальном направлении движется с постоянной по модулю скоростью.
ДАНО: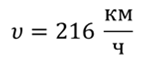
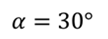
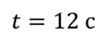
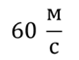
РЕШЕНИЕ:
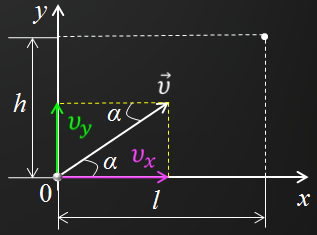
Запишем кинематические уравнения движения для каждого из случаев
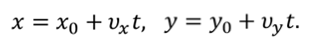
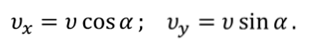
В момент времени t:
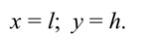
Тогда
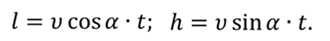
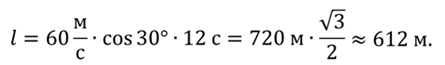
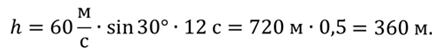
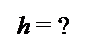
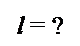
Ответ: l = 612 м; h = 360 м.
1 = 15 м/с. Найти среднюю скорость на всем пути. Доказать, что средняя скорость меньше среднего арифметического значений v1и v2. Решение задачи:дано:
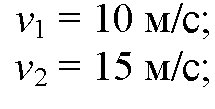
найти: vср
решение
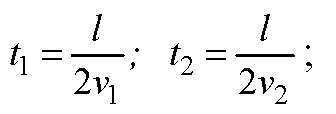
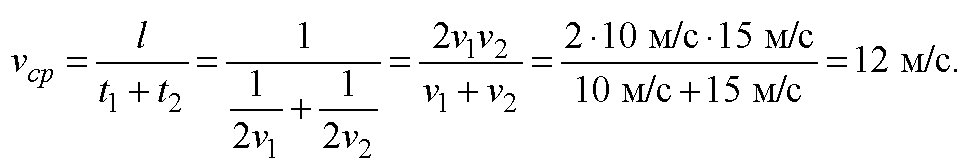
ответ:
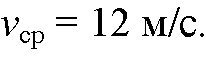
Задача 5 (Рымкевич
Решение задачи: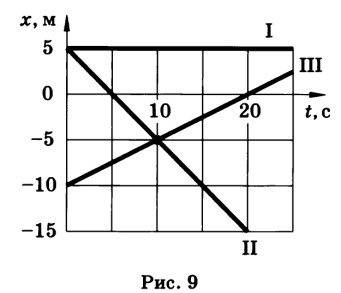
по графику видно, что начальные координаты i тела : 5 м, ii: 5 м,
iii: — 10 м. скорости движения i:
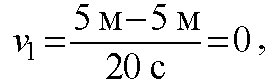
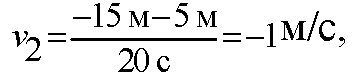
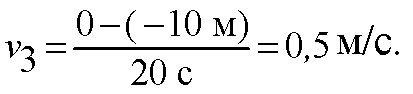
уравнения движения:
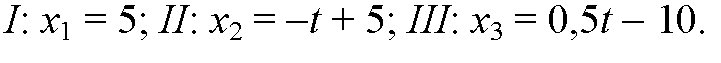
т.к. движение равномерное вдоль оси х, то найденные нами скорости v1, v2, v3 являются проекциями на ось х.
по графикам уравнения движения тел ii и iii видно, что они пересекутся в точке х = — 5 м в момент времени t = 10 с. найдем это из уравнений движения.
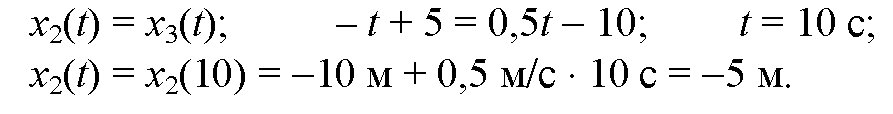
№32. Скорость велосипедиста 36 км/ч, а скорость ветра 4 м/с. Какова скорость ветра в системе отсчета, связанной с велосипедистом, при: а) встречном ветре; б) попутном ветре?
Решение задачи:дано:
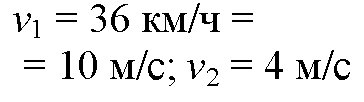
найти: v2‘, v2» .
решение.
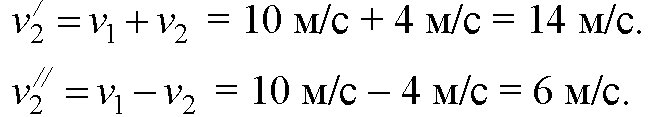
ответ:
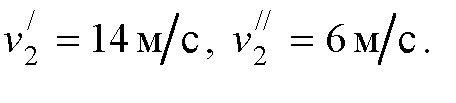 Решение задачи:
Решение задачи:дано:
v1 = 72 км/ч = 20 м/с; v2 = 54 км/ч = 15 м/с; t = 14 с.
найти l.
решение.

infourok.ru
Физика Мгновенная скорость. Сложение скоростей
Описание видеоурока
Ни одно тело не может двигаться все время с постоянной скоростью. Трогаясь с места, велосипедист увеличивает свою скорость. Далее в течение какого-то промежутка времени он движется с постоянной или почти постоянной скоростью, но все же когда-нибудь ему придется остановиться. Для этого велосипедист тормозит – уменьшает скорость движения до нуля. При этом за одинаковые промежутки времени он перемещается на различные расстояния, то есть движется неравномерно. В каждой точке траектории значения скорости велосипедиста разные.
Скорость тела в данной точке траектории или в данный момент называют мгновенной скоростью. Необходимо уметь рассчитывать мгновенную скорость в данный момент времени для того, чтобы задать неравномерное движение.
Чтобы понять, что же такое мгновенная скорость, представим себе, что велосипедист, трогаясь с места, ускоряется в течение 20 секунд. Если найти отношение перемещения велосипедиста во время разгона к времени разгона, мы получим среднюю скорость на этом участке пути. Но это не значит, что в каждый момент времени реальная скорость велосипедиста была именно такой. Напротив, в начале пути скорость была равна нулю, а в конце разгона скорость была гораздо больше полученной средней скорости.
Если же мы разделим участок пути, на котором скорость увеличивалась, на две равные по времени части и вычислим среднюю скорость для каждого участка отдельно, то мы получим совершенно разные значения средней скорости для каждого участка. Средняя скорость на первом участке будет меньше, чем на втором.
Если разделить все время разгона на 10 равных частей и вычислить средние скорости для каждого участка отдельно, то мы получим, что средняя скорость на первом участке совсем невелика, на втором – больше, на третьем – еще больше. А на десятом участке средняя скорость будет самая большая. Это и понятно – ведь велосипедист разгоняется. Такие значения скоростей будут гораздо точнее характеризовать неравномерное движение, чем средняя скорость на всем участке.
Но все же скорость на каждом из десяти участков в любой момент времени будет равна средней скорости на этом участке лишь приближенно. Реальная скорость в начале участка будет меньше средней, а в конце участка больше.
Если разделить все время разгона на 20 равных частей и вычислить средние скорости для каждого участка, то мы получим значения средних скоростей для каждого участка. Эти значения будут еще точнее характеризовать движение.
Чем меньше будут эти временные промежутки, тем меньше будет отличие между скоростями соседних участков и тем точнее будут значения этих скоростей.
Если устремить промежуток времени к нулю, то отношение малого перемещения к малому промежутку времени, в течение которого это перемещение произошло, будет стремиться к определенному значению. Это и есть мгновенная скорость точки в данный момент времени.
Мгновенная скорость точки – это предел отношения перемещения точки к промежутку времени, в течение которого это перемещение произошло, при устремлении промежутка времени к нулю.
Мгновенная скорость всегда направлена по касательной к траектории движения. В этом можно наглядно убедиться, посмотрев на любые отделяющиеся от вращающегося тела части. К примеру, грязь, вылетающая из-под колес автомобиля, она отделяется от колеса и летит вдоль линии, касательной к поверхности колеса, так как кусочки грязи в момент отрыва имеют скорость равную скорости поверхности колеса. Аналогичным примером может служить процесс заточки ножа при помощи точильного круга. Вылетающие искры будут двигаться по касательной к поверхности круга.
Понятие мгновенной скорости относится к точке. В дальнейшем, когда мы будем говорить о скорости движения тела, будем иметь в виду скорость какой-либо точки этого тела.
Механическое движение относительно: тело вполне может покоиться в одной системе отсчета и при этом двигаться в другой системе отсчета с одной скоростью, а в третьей системе с другой скоростью. Траектория движения одного и того же тела в разных системах отсчета также будет различной. Рассмотрим пример, человек лежит в поезде, который в свою очередь движется относительно Земли. В этом примере человек относительно поезда имеет нулевую скорость, а относительно Земли будет двигаться со скоростью движения поезда. Некоторая точка, находящаяся на пропеллере летящего вертолета, описывает окружность в системе отсчета, связанной с вертолетом, а в системе отсчета, связанной с посадочной площадкой, находящейся на поверхности Земли, та же самая точка будет описывать уже не окружность, а винтовую линию.
Перемещение тела, пройденный им путь, а также его скорость тоже изменяются, если мы переходим от одной системы отсчета к другой. Пассажир поезда неподвижен относительно движущегося поезда, перемещение и путь человека по отношению к поезду равны нулю. Но по отношению к деревьям или зданиям, расположенным вдоль железной дороги, они имеют некоторые ненулевые значения.
Решая практические задачи, достаточно часто требуется вычислить перемещение либо скорость тела в некоторой системе отсчета, если значения этих величин уже известны, но относительно другой системы отсчета. Рассмотрим пример. Для того чтобы составить расписание движения теплохода, необходимо знать его скорость в системе отсчета, связанной с берегом и скорость течения реки тоже относительно берега. Предположим, что теплоход, плывущий по реке, имеет определенную собственную скорость. Тогда в системе отсчета, связанной с берегом, при движении теплохода вниз по течению реки модуль его скорости будет больше, а при движении вверх против течения – меньше собственной скорости теплохода.
Скорость течения реки относительно берега измерить достаточно просто, вычислить скорость теплохода относительно воды тоже не составит труда. Теперь зная все необходимые величины, мы можем вычислить скорость движения теплохода относительно берега. Так как скорость является величиной векторной, скорость теплохода относительно берега будет равна векторной сумме вектора скорости движения теплохода в системе отсчета, связанной с водой в реке и вектором скорости течения воды. Если теплоход движется по течению, то векторы скорости теплохода относительно воды и воды относительно берега сонаправлены. Соответственно проекции этих векторов будут иметь одинаковые знаки, поэтому модуль вектора суммы векторов будет больше модуля вектора скорости теплохода относительно воды в реке. Если же теплоход идет против течения реки, то вектор скорости теплохода относительно воды будет направлен противоположно вектору скорости течения воды. Проекции этих векторов будут иметь противоположные знаки, значит, модуль вектора суммы векторов будет меньше модуля вектора собственной скорости теплохода.
Это подтверждается нашими наблюдениями: что теплоход, идущий по течению, движется относительно берега значительно быстрее, такого же теплохода, движущегося против течения воды в реке.
Эти рассуждения можно распространить на любое тело, движущееся в подвижной системе отсчета. Если тело движется в системе отсчета К1, которая сама движется относительно другой системы отсчета К2, то скорость движения этого тела относительно системы К2 равна геометрической сумме скорости тела в системе К1 и скорости движения системы отсчета К1 относительно системы отсчета К2. Это и есть закон сложения скоростей.
Закон сложения скоростей можно получить и по-другому. Мы уже изучали закон сложения перемещений. В нем говорится о том, что перемещение тела в подвижной системе отсчета относительно неподвижной системы отсчета равно геометрической сумме перемещения тела относительно подвижной системы отсчета и перемещения подвижной системы отсчета относительно неподвижной.
Разделим обе части этого уравнения на промежуток времени, в течение которого происходило перемещение. В результате имеем, что отношение перемещения тела относительно неподвижной системы отсчета к промежутку времени равно отношению перемещения тела относительно подвижной системы отсчета к промежутку времени плюс отношению перемещения самой подвижной системы относительно неподвижной к тому же промежутку времени.
Согласно определению, отношение перемещения к промежутку времени, в течение которого оно произошло, равно скорости тела. Отсюда следует, что скорость тела, движущегося в подвижной системе отсчета относительно неподвижной, равна геометрической сумме скорости подвижной системы отсчета относительно неподвижной и скорости тела в подвижной системе отсчета.
Как любое векторное уравнение, закон сложения скоростей для движения на плоскости можно записать как два уравнения для сложения проекций скоростей. Проекция вектора скорости тела на ось Х относительно системы отсчета К2 равна сумме проекции на ось Х вектора скорости тела относительно системы К1 и проекции на ось Х скорости системы отсчета К1 относительно системы отсчета К2. Проекция вектора скорости тела на ось Y относительно системы отсчета К2 равна сумме проекции на ось Y вектора скорости тела относительно системы К1 и проекции на ось Y скорости системы отсчета К1 относительно системы отсчета К2.
Проекции скоростей складываются алгебраически.
infourok.ru