Урок 16. арифметический корень натуральной степени — Алгебра и начала математического анализа — 10 класс
Алгебра и начала математического анализа, 10 класс
Урок №16 Название темы: Арифметический корень натуральной степени.
Перечень тем, рассматриваемых на уроке:
- преобразование и вычисление арифметических корней,
- свойства арифметического корня натуральной степени,
- корень нечетной степени из отрицательного числа,
- какими свойствами обладает арифметический корень натуральной степени.
Глоссарий
- Квадратным корнем из числа a называют такое число, квадрат которого будет равен a.
- Арифметическим квадратным корнем из числа а называют неотрицательное число, квадрат которого равен а.
- Кубический корень из а— это такое число, которое при возведении в третью степень дает число а.
- Корнем n-ой степени из числа a называют такое число, n-ая степень которого будет равна a.
- Арифметическим корнем натуральной степени, где n ≥ 2, из неотрицательного числа a называется неотрицательное число, n-я степень которого равна a.
Основная литература:
Колягин Ю.М., Ткачева М.В., Федорова Н.Е. и др., под ред. Жижченко А.Б. Учебно-методический комплект: Алгебра и начала математического анализа (базовый и профильный уровни). 10 кл.– М.: Просвещение, 2014.
- Сканави М. И., Зайцев В. В., Рыжков В. В. «Элементарная математика». – Книга по требованию, 2012.
- Семенова А.Л., Ященко И.В. ЕГЭ 3000 задач с ответами, математика под редакцией Москва, 2017.
- Ященко И. В. ЕГЭ 3300 задач с ответами, математика профильный уровень под редакцией Москва, 2017.
Объяснение темы «Арифметический корень натуральной степени»
Решим задачу.
Площадь квадрата S=16 м².
Обозначим сторону квадрата а, м.

Тогда, а² = 16.
Решим данное уравнение:
a=4 и а= –4.
Проверим решение:
4² = 16;
(–4)² = 16.
Ответ: длина стороны квадрата равна 4 м.
Определение:
Квадратным корнем из числа a называют такое число, квадрат которого будет равен a.
Определение:
Арифметическим квадратным корнем из числа а называют неотрицательное число, квадрат которого равен а.
Обозначение:  .
.
Определение:
Кубический корень из а— это такое число, которое при возведении в третью степень дает число а.
Обозначение: 
Например:
 .
.
 .
.
 .
.
На основании определений квадратного и кубического корней, можно сформулировать определения корня n-ой степени и арифметического корня n-ой степени.
Определение:
Корнем n-ой степени из числа a называют такое число, n-ая степень которого будет равна a.
Определение:
Арифметическим корнем натуральной степени, где n≥2, из неотрицательного числа a называется неотрицательное число, n-я степень которого равна a.
Обозначение:  – корень n-й степени, где
– корень n-й степени, где
n–степень арифметического корня;
а– подкоренное выражение.
Давайте рассмотрим такой пример:  .
.
Мы знаем, что (–4)³ = –64, следовательно,  .
.
Еще один пример: 
Мы знаем, что (–3)5 = –243, следовательно,  .
.
На основании этих примеров, можно сделать вывод:
 , при условии, что n –нечетное число.
, при условии, что n –нечетное число.
Свойства арифметического корня натуральной степени:
Если а ≥ 0, b ≥ 0 и n, m – натуральные числа, причем n ≥ 2, m ≥ 2, то справедливо следующее:
 .
.
Примеры:

 .
.
 .
.
Примеры:
 .
.
 .
.
 .
.
Пример:

 .
.
Пример:
 .
.
- Для любогоа справедливо равенство:

Пример:
Найдите значение выражения  , при 3 <x< 6.
, при 3 <x< 6.
Степени заданных арифметических корней 4 и 2, четные числа, следовательно, мы можем применить свойство №5:
 =|x – 3| = х – 3, т.к. х>3;
=|x – 3| = х – 3, т.к. х>3;
 =|x – 6|=6 – x, т.к. х<6.
=|x – 6|=6 – x, т.к. х<6.
Получаем: х – 3 + 6 – х= 3.
Примеры заданий.
Первый пример.
Задача:
Выберите верные утверждения:




Разбор задания.
Применим определение арифметического корня: Арифметическим корнем натуральной степени из неотрицательного числа a называется неотрицательное число, n-я степень которого равна a. Следовательно, верными могут быть только неотрицательные выражения.
Ответ: 
 ;
; 
Второй пример.
Задача:
Выделите самое маленькое число:
Разбор задания:
Корень из отрицательного числа будет отрицательным числом, следовательно, наименьшее число – 
Ответ: 4. 
resh.edu.ru
Арифметический корень натуральной степени
С понятием квадратного корня из числа а вы уже знакомы: это такое число, квадрат которого равен а.
 ,
,
 ,
,
 ,
,

Аналогично
определяется корень  -й
степени из числа а, где
-й
степени из числа а, где –
произвольное натуральное число.
–
произвольное натуральное число.
А теперь давайте решим такое уравнение:

Итак,
это уравнение мы можем переписать в таком виде:  .
Или
.
Или  .
.
Тогда
наше уравнение равносильно совокупности уравнений:  .
.
Понятно,
что уравнение  не
имеет решения на множестве действительных чисел. Значит, остаётся решить
уравнение
не
имеет решения на множестве действительных чисел. Значит, остаётся решить
уравнение






Итак,
наше уравнение  имеет
два действительных корня 5 и –5. Их называют корнями четвёртой степени
из числа 625. В свою очередь,
положительный корень (число 5) называют арифметическим корнем четвёртой
степени из числа 625. Обозначают его так:
имеет
два действительных корня 5 и –5. Их называют корнями четвёртой степени
из числа 625. В свою очередь,
положительный корень (число 5) называют арифметическим корнем четвёртой
степени из числа 625. Обозначают его так:  .
Таким образом,
.
Таким образом,  .
.
Запомните! Арифметическим
корнем натуральной степени  из
неотрицательного числа а называется неотрицательное число,
из
неотрицательного числа а называется неотрицательное число,  -я
степень которого равна а.
-я
степень которого равна а.
Арифметический
корень  —ой
степени из числа а обозначают так:
—ой
степени из числа а обозначают так:  .
Символ
.
Символ  называют
знаком арифметического квадратного корня или радикалом
(от латинского слова «радикс» – корень), число
называют
знаком арифметического квадратного корня или радикалом
(от латинского слова «радикс» – корень), число  называется
показателем корня, а число а, стоящее под знаком
корня, – подкоренным выражением.
называется
показателем корня, а число а, стоящее под знаком
корня, – подкоренным выражением.
Вам
хорошо известен такой частный случай арифметического корня  -й
степени, как корень второй степени, или квадратный корень из числа, то
есть когда
-й
степени, как корень второй степени, или квадратный корень из числа, то
есть когда 
В
этом случае показатель корня не пишут, а пишут просто .
.
Ещё
одним частным случаем является
 мы
привыкли называть его корнем кубическим.
мы
привыкли называть его корнем кубическим.
Как
правило, когда ясно, что речь идёт об арифметическом корне  -й
степени, слово «арифметический» не произносят, а говорят кратко: «корень
энной степени».
-й
степени, слово «арифметический» не произносят, а говорят кратко: «корень
энной степени».
Действие,
посредством которого отыскивается корень  -й
степени, называется извлечением корня
-й
степени, называется извлечением корня  -й степени.
Это действие является обратным действию возведения в
-й степени.
Это действие является обратным действию возведения в  -й
степень.
-й
степень.
Равенство
 при
при
 верно,
когда выполняются два условия:
верно,
когда выполняются два условия: ;
второе —
;
второе — .
.
Например, .
.
Число ;
;
 .
.
Видим,
что оба условия выполняются. Значит верно.
верно.
Из
определения арифметического корня следует, что если ,
то
,
то .
.
Например,

А
теперь давайте решим следующие уравнения:  и
и
 .
Итак, первое уравнение
.
Итак, первое уравнение

Перепишем
это уравнение в виде:  .
.
Преобразуем
наше уравнение, применяя формулу разности кубов. Имеем:







Перейдём к уравнению 2:

Перепишем
это уравнение в виде:  .
.
Преобразуем наше уравнение, применяя
формулу разности кубов. Имеем: .
.




Так
как  ,
то число –4 является корнем из числа –64. Однако это число не является
арифметическим корнем по определению. Число
,
то число –4 является корнем из числа –64. Однако это число не является
арифметическим корнем по определению. Число  называют
корнем кубическим из числа
называют
корнем кубическим из числа  и
обозначают так:
и
обозначают так:
Вообще,
для любого нечётного натурального числа ,
уравнение
,
уравнение ,
при
,
при  имеет
только один корень, причём отрицательный. Этот корень обозначается, как и
арифметический корень, символом
имеет
только один корень, причём отрицательный. Этот корень обозначается, как и
арифметический корень, символом .
.
И называют его корнем нечётной степени из отрицательного числа.
Запомните!
При нечётном  существует
существует ,
и притом только один. Для корней нечётной степени справедливо равенство
,
и притом только один. Для корней нечётной степени справедливо равенство 
Например,


Корень
нечётной степени из отрицательного числа а связан с арифметическим корнем из
числа  следующим
равенством:
следующим
равенством:
Например,

Арифметический
корень  -й
степени обладает несколькими свойствами. Перечислим их. Итак, при условии, что
-й
степени обладает несколькими свойствами. Перечислим их. Итак, при условии, что ,
,
 ,
а
,
а ,
,
 и
и
 –
натуральные числа, причём
–
натуральные числа, причём ,
,
 ,
справедливы равенства:
,
справедливы равенства:
1.
 .
.
2.
 .
.
3.
 .
.
4.
 .
.
5.
 .
.
Обратите
внимание, что в первом свойстве число  может
также быть равным
может
также быть равным  ;
в третьем свойстве число
;
в третьем свойстве число  может
быть любым целым, если
может
быть любым целым, если  .
.
Докажем справедливость этих свойств. Итак, первое свойство.
1.
 .
.
По
определению арифметического корня  –
это такое неотрицательное число,
–
это такое неотрицательное число,  -я
степень которого равна произведению
-я
степень которого равна произведению  .
.
 ;
;
 .
.

2.
 .
.
 ;
;
3.
 .
.
 ;
;
 .
.
4.
 .
.
 ;
;
 .
.
5.
 .
.
 ;
;
 .
.
А теперь давайте приступим к практической части нашего урока.
Задание
1.
Найдите значения выражений а)  ;
б)
;
б)  ;
в)
;
в)  .
.
Решение.
а)
 ;
б)
;
б)  ;
в)
;
в)  .
.
 ;
;
 ;
;
 ;
;
 ;
;
Задание
2.
Преобразуйте выражения: а)  ;
б)
;
б)  ;
в)
;
в)  ;
г)
;
г)  .
.
Решение.
а)
 ;
;
б)


 ;
;
в)
 ;
;
г)
 .
.
videouroki.net
Лекция по теме «Понятие действительного числа. Арифметический корень натуральной степени»
Лекция по теме «Понятие действительного числа. Арифметический корень натуральной степени»
С понятием квадратного корня из числа а вы уже знакомы: это такое число, квадрат которого равен а.
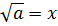 ,
, 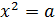 ,
, 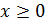 ,
, 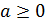
Аналогично определяется корень n-й степени из числа а, где n – произвольное натуральное число.
А теперь давайте решим такое уравнение:
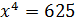
Итак, это уравнение мы можем переписать в таком виде: 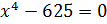 . Или
. Или 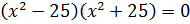 .
.
Тогда наше уравнение равносильно совокупности уравнений: 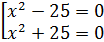 .
.
Понятно, что уравнение 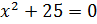 не имеет решения на множестве действительных чисел. Значит, остаётся решить уравнение
не имеет решения на множестве действительных чисел. Значит, остаётся решить уравнение
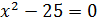
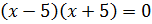
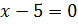
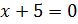
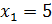
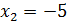
Итак, наше уравнение 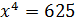 имеет два действительных корня 5 и –5. Их называют корнями четвёртой степени из числа 625. В свою очередь, положительный корень (число 5) называют арифметическим корнем четвёртой степени из числа 625. Обозначают его так:
имеет два действительных корня 5 и –5. Их называют корнями четвёртой степени из числа 625. В свою очередь, положительный корень (число 5) называют арифметическим корнем четвёртой степени из числа 625. Обозначают его так: 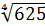 . Таким образом,
. Таким образом, 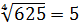 .
.
Запомните! Арифметическим корнем натуральной степени 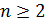 из неотрицательного числа а называется неотрицательное число,
из неотрицательного числа а называется неотрицательное число, 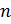 -я степень которого равна а.
-я степень которого равна а.
Арифметический корень 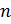 —ой степени из числа а обозначают так:
—ой степени из числа а обозначают так: 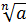 . Символ
. Символ 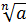 называют знаком арифметического квадратного корня или радикалом (от латинского слова «радикс» – корень), число
называют знаком арифметического квадратного корня или радикалом (от латинского слова «радикс» – корень), число 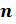 называется показателем корня, а число а, стоящее под знаком корня, – подкоренным выражением. Вам хорошо известен такой частный случай арифметического корня
называется показателем корня, а число а, стоящее под знаком корня, – подкоренным выражением. Вам хорошо известен такой частный случай арифметического корня 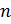 -й степени, как корень второй степени, или квадратный корень из числа, то есть когда
-й степени, как корень второй степени, или квадратный корень из числа, то есть когда 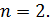
В этом случае показатель корня не пишут, а пишут просто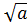 .
.
Ещё одним частным случаем является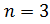
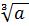 мы привыкли называть его корнем кубическим.
мы привыкли называть его корнем кубическим.
Как правило, когда ясно, что речь идёт об арифметическом корне 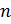 -й степени, слово «арифметический» не произносят, а говорят кратко: «корень энной степени».
-й степени, слово «арифметический» не произносят, а говорят кратко: «корень энной степени».
Действие, посредством которого отыскивается корень 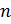 -й степени, называется извлечением корня
-й степени, называется извлечением корня 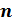 -й степени. Это действие является обратным действию возведения в
-й степени. Это действие является обратным действию возведения в 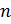 -й степень.
-й степень.
Равенство 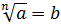 при
при 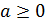 верно, когда выполняются два условия:
верно, когда выполняются два условия: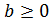 ; второе —
; второе —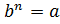 .
.
Например,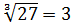 .
.
Число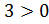 ;
;
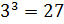 .
.
Видим, что оба условия выполняются. Значит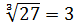 верно.
верно.
Из определения арифметического корня следует, что если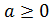 , то
, то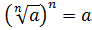 .
.
Например,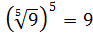
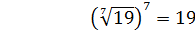
А теперь давайте решим следующие уравнения: 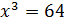 и
и 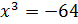 . Итак, первое уравнение
. Итак, первое уравнение
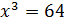
Перепишем это уравнение в виде: 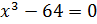 .
.
Преобразуем наше уравнение, применяя формулу разности кубов. Имеем:
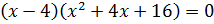
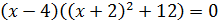
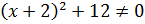
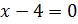
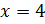
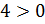
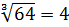
Перейдём к уравнению 2:
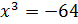
Перепишем это уравнение в виде: 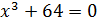 .
.
Преобразуем наше уравнение, применяя формулу разности кубов. Имеем: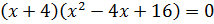 .
.
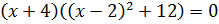
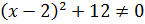
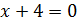
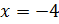
Так как 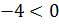 , то число –4 является корнем из числа –64. Однако это число не является арифметическим корнем по определению. Число
, то число –4 является корнем из числа –64. Однако это число не является арифметическим корнем по определению. Число 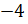 называют корнем кубическим из числа
называют корнем кубическим из числа 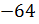 и обозначают так:
и обозначают так: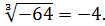
Вообще, для любого нечётного натурального числа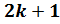 , уравнение
, уравнение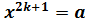 , при
, при 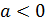 имеет только один корень, причём отрицательный. Этот корень обозначается, как и арифметический корень, символом
имеет только один корень, причём отрицательный. Этот корень обозначается, как и арифметический корень, символом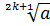 .
.
И называют его корнем нечётной степени из отрицательного числа.
Запомните! При нечётном 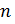 существует
существует , и притом только один. Для корней нечётной степени справедливо равенство
, и притом только один. Для корней нечётной степени справедливо равенство 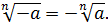
Например,
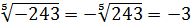
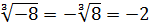
Корень нечётной степени из отрицательного числа а связан с арифметическим корнем из числа 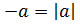 следующим равенством:
следующим равенством: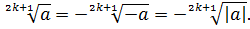
Например, 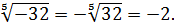
Арифметический корень 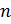 -й степени обладает несколькими свойствами. Перечислим их. Итак, при условии, что
-й степени обладает несколькими свойствами. Перечислим их. Итак, при условии, что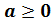 ,
, 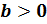 , а
, а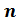 ,
, 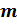 и
и 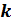 – натуральные числа, причём
– натуральные числа, причём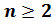 ,
, 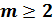 , справедливы равенства:
, справедливы равенства:
1. 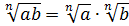 .
.
2. 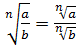 .
.
3. 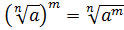 .
.
4. 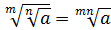 .
.
5. 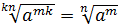 .
.
Обратите внимание, что в первом свойстве число 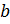 может также быть равным
может также быть равным 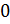 ; в третьем свойстве число
; в третьем свойстве число 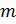 может быть любым целым, если
может быть любым целым, если 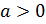 .
.
Докажем справедливость этих свойств. Итак, первое свойство.
1. 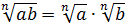 .
.
По определению арифметического корня 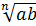 – это такое неотрицательное число,
– это такое неотрицательное число, 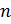 -я степень которого равна произведению
-я степень которого равна произведению 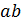 .
.
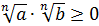 ;
;
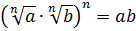 .
.
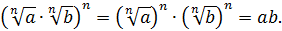
2. 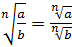 .
.
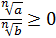 ;
;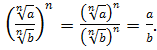
3. 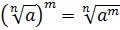 .
.
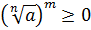 ;
;
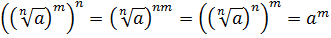 .
.
4. 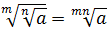 .
.
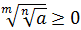 ;
;
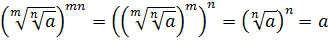 .
.
5. 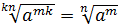 .
.
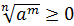 ;
;
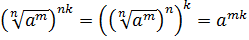 .
.
А теперь давайте приступим к практической части нашего урока.
Задание 1. Найдите значения выражений а) 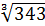 ; б)
; б) 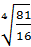 ; в)
; в) 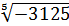 .
.
Решение.
а) 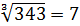 ; б)
; б) 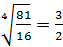 ; в)
; в) 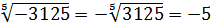 .
.
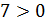 ;
; 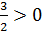 ;
;
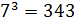 ;
; 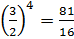 ;
;
Задание 2. Преобразуйте выражения: а) 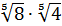 ; б)
; б) 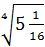 ; в)
; в) 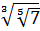 ; г)
; г) 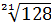 .
.
Решение.
а) 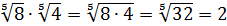 ;
;
б) 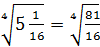
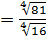
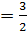 ;
;
в) 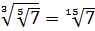 ;
;
г)  .
.
infourok.ru
Конспект урока «Арифметический корень натуральной степени»
Тема: « Корни натуральной степени из числа».
Цели:
Образовательная: обучение преобразованию выражений, содержащих корни натуральной степени, формировать навыки применения свойств корней при решении задач;
Воспитательная: воспитывать познавательную активность, аккуратности, ответственности
Развивающая: развивать логическое мышление, память, математическую речь, умение анализировать и сравнивать;
План :
1. Повторение арифметического квадратного корня .
2. Арифметический корень третьей степени( кубический корень).
3. Корень n степени.
4. Таблица корней.
5. Закрепление ( решение примеров).
6. Домашнее задание
Степенью называется выражение вида: 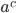 , где:
, где:
Степень с натуральным показателем {1, 2, 3,…}
Определим понятие степени, показатель которой — натуральное число (т.е. целое и положительное).
По определению:
 .
.Возвести число в квадрат — значит умножить его само на себя:

Возвести число в куб — значит умножить его само на себя три раза:
 .
.
Возвести число в натуральную степень 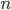 — значит умножить число само на себя
— значит умножить число само на себя 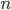 раз:
раз:
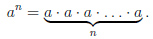
Степень с целым показателем {0, ±1, ±2,…}
Если показателем степени является целое положительное число:
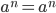 , n > 0
, n > 0
Возведение в нулевую степень:
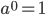 , a ≠ 0
, a ≠ 0
Если показателем степени является целое отрицательное число:
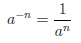 , a ≠ 0
, a ≠ 0
Прим: выражение 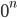 не определено, в случае n ≤ 0. Если n > 0, то
не определено, в случае n ≤ 0. Если n > 0, то 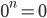
Пример 1.
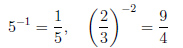
Степень с рациональным показателем
Если:
Тогда:
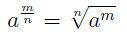
Пример 2.
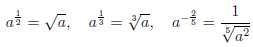
Свойства степеней
Произведение степеней
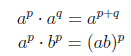
Деление степеней
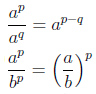
Возведение степени в степень
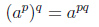
Пример 3.
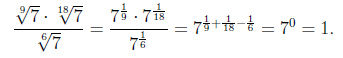
Корень
Арифметический квадратный корень
Уравнение 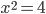 имеет два решения: x=2 и x=-2. Это числа, квадрат которых равен 4.
имеет два решения: x=2 и x=-2. Это числа, квадрат которых равен 4.
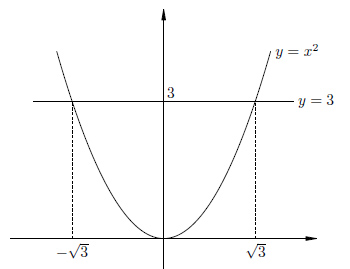
Рассмотрим уравнение 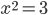 . Нарисуем график функции
. Нарисуем график функции 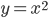 и увидим, что и у этого уравнения два решения, одно положительное, другое отрицательное.
и увидим, что и у этого уравнения два решения, одно положительное, другое отрицательное.
Но в данному случае решения не являются целыми числами. Более того, они не являются рациональными. Для того, чтобы записать эти иррациональные решения, мы вводим специальный символ квадратного корня.
Арифметический квадратный корень 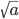 — это неотрицательное число, квадрат которого равен
— это неотрицательное число, квадрат которого равен 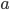 , a ≥ 0. При a < 0 — выражение
, a ≥ 0. При a < 0 — выражение 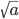 не определено, т.к. нет такого действительного числа, квадрат которого равен отрицательному числу
не определено, т.к. нет такого действительного числа, квадрат которого равен отрицательному числу 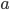 .
.
Корень из квадрата
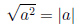
Например, 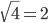 . А решения уравнения
. А решения уравнения 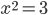 соответственно
соответственно 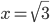 и
и 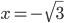
Кубический корень
Кубический корень из числа 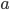 — это число, куб которого равен
— это число, куб которого равен 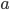 . Кубический корень определен для всех
. Кубический корень определен для всех 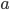 . Его можно извлечь из любого числа:
. Его можно извлечь из любого числа: 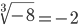 .
.
Корень n-ой степени
Корень 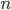 -й степени из числа
-й степени из числа 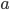 — это число,
— это число, 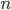 -я степень которого равна
-я степень которого равна 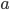 .
.
Если 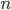 — чётно.
— чётно.
Тогда, если a < 0 корень n-ой степени из a не определен.
Или если a ≥ 0, то неотрицательный корень уравнения
 называется арифметическим корнем n-ой степени из a и обозначается
называется арифметическим корнем n-ой степени из a и обозначается 
Если 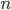 — нечётно.
— нечётно.
Пример 4.
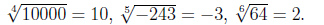
Таблица корней
Корень третьей степени (3)
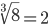
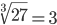
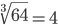
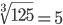
Корень седьмой степени (7)
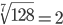
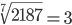
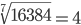
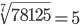
Корень четвертой степени (4)
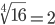
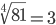
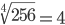
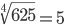
Корень восьмой степени (8)
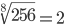
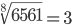
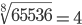
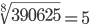
Корень пятой степени (5)
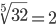
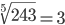
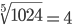
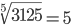
Корень девятой степени (9)
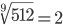
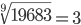
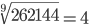
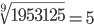
Корень шестой степени (6)
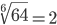
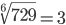
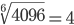
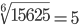
Корень десятой степени (10)
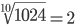
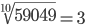
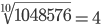
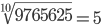
1.
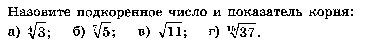
2.
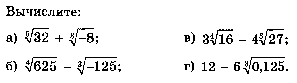
3.

4.
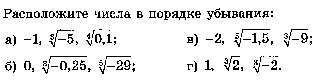
5.

6.
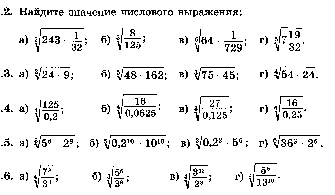
7.
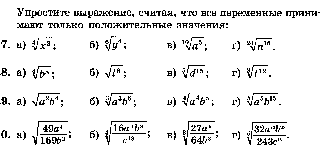
8.
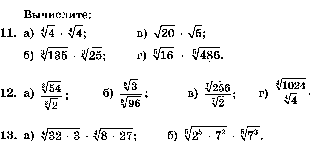
9.
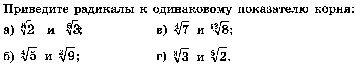
10
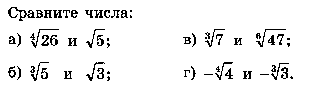
11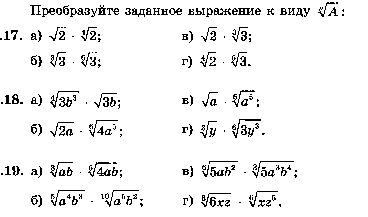
12

13. 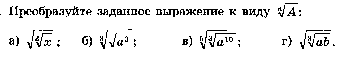
14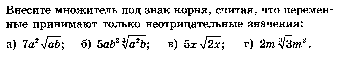
15
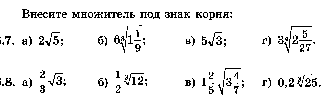
16
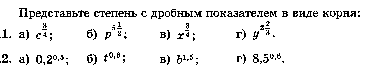
17
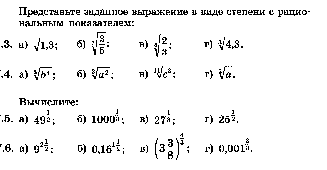
18
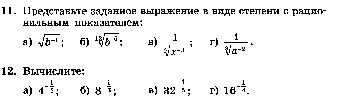
19
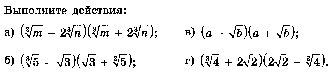
20

infourok.ru
 .
. .
. .
. .
.




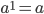 .
.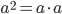
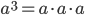 .
.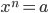 называется арифметическим корнем n-ой степени из a и обозначается
называется арифметическим корнем n-ой степени из a и обозначается