Сложение корней с разными степенями. Сложение и вычитание корней, примеры. Что такое квадратный корень
Квадратным корнем из числа X называется число A , которое в процессе умножения самого на себя (A * A ) может дать число X .
Т.е. A * A = A 2 = X , и √X = A .
Над квадратными корнями (√x ), как и над другими числами, можно выполнять такие арифметические операции, как вычитание и сложение. Для вычитания и сложения корней их нужно соединить посредством знаков, соответствующих этим действиям (например √x — √y ).
А потом привести корни к их простейшей форме — если между ними окажутся подобные, необходимо сделать приведение. Оно заключается в том, что берутся коэффициенты подобных членов со знаками соответствующих членов, далее заключаются в скобки и выводится общий корень за скобками множителя. Коэффициент, который мы получили, упрощается по обычным правилам.
Шаг 1. Извлечение квадратных корней
Во-первых, для сложения квадратных корней сначала нужно эти корни извлечь.
Все, пример решен. Но так просто бывает далеко не всегда.
Шаг 2. Вынесение множителя числа из-под корня
Если полных квадратов нет под знаком корня, можно попробовать вынести множитель числа из-под знака корня. Для примера возьмём выражение √24 + √54 .
Раскладываем числа на множители:
24 = 2 * 2 * 2 * 3 ,
54 = 2 * 3 * 3 * 3 .
В числе 24 мы имеем множитель 4 , его можно вынести из-под знака квадратного корня. В числе 54 мы имеем множитель 9 .
Получаем равенство:
√24 + √54 = √(4 * 6) + √(9 * 6) = 2 * √6 + 3 * √6 = 5 * √6 .
Рассматривая данный пример, мы получаем вынос множителя из-под знака корня, тем самым упрощая заданное выражение.
Шаг 3. Сокращение знаменателя
Рассмотрим следующую ситуацию: сумма двух квадратных корней — это знаменатель дроби, например, A / (√a + √b) .
Теперь перед нами стоит задача «избавиться от иррациональности в знаменателе».
Воспользуемся следующим способом: умножаем числитель и знаменатель дроби на выражение √a — √b .
Формулу сокращённого умножения мы теперь получаем в знаменателе:
(√a + √b) * (√a — √b) = a — b .
Аналогично, если в знаменателе имеется разность корней: √a — √b , числитель и знаменатель дроби умножаем на выражение √a + √b .
Возьмём для примера дробь:
4 / (√3 + √5) = 4 * (√3 — √5) / ((√3 + √5) * (√3 — √5)) = 4 * (√3 — √5) / (-2) = 2 * (√5 — √3) .
Пример сложного сокращения знаменателя
Теперь будем рассматривать достаточно сложный пример избавления от иррациональности в знаменателе.
Для примера берём дробь: 12 / (√2 + √3 + √5) .
Нужно взять её числитель и знаменатель и перемножить на выражение √2 + √3 — √5 .
Получаем:
12 / (√2 + √3 + √5) = 12 * (√2 + √3 — √5) / (2 * √6) = 2 * √3 + 3 * √2 — √30.
Шаг 4. Вычисление приблизительного значения на калькуляторе
Если вам требуется только приблизительное значение, это можно сделать на калькуляторе путём подсчёта значения квадратных корней. Отдельно для каждого числа вычисляется значение и записывается с необходимой точностью, которая определяется количеством знаков после запятой. Далее совершаются все требуемые операции, как с обычными числами.
Пример вычисления приблизительного значения
Необходимо вычислить приблизительное значение данного выражения √7 + √5 .
В итоге получаем:
√7 + √5 ≈ 2,65 + 2,24 = 4,89 .
Обратите внимание: ни при каких условиях не следует производить сложение квадратных корней, как простых чисел, это совершенно недопустимо. То есть, если сложить квадратный корень из пяти и из трёх, у нас не может получиться квадратный корень из восьми.
Полезный совет: если вы решили разложить число на множители, для того, чтобы вывести квадрат из-под знака корня, вам необходимо сделать обратную проверку, то есть перемножить все множители, которые получились в результате вычислений, и в конечном результате этого математического расчёта должно получиться число, которое нам было задано первоначально.
В наше время современных электронных вычислительных машин вычисление корня из числа не представляется сложной задачей. Например, √2704=52, это вам подсчитает любой калькулятор. К счастью, калькулятор есть не только в Windows, но и в обычном, даже самом простеньком, телефоне. Правда если вдруг (с малой долей вероятности, вычисление которой, между прочим, включает в себя сложение корней) вы окажитесь без доступных средств, то, увы, придется рассчитывать только на свои мозги.
Тренировка ума никогда не помещает. Особенно для тех, кто не так часто работает с цифрами, а уж тем более с корнями. Сложение и вычитание корней — хорошая разминка для скучающего ума. А еще я покажу поэтапно сложение корней. Примеры выражений могут быть следующие.
Уравнение, которое нужно упростить:
√2+3√48-4×√27+√128
Это иррациональное выражение. Для того чтобы его упростить нужно привести все подкоренные выражения к общему виду. Делаем поэтапно:
Первое число упростить уже нельзя. 2×2)
2×2)
Переписываем выражение с упрощенными слагаемыми:
√2+12×√3-12×√3+8×√2
Теперь складываем числа одним и тем же подкоренным выражением. Нельзя складывать или вычитать выражения с разными подкоренными выражениями. Сложение корней требует соблюдение этого правила.
Ответ получаем следующий:
√2+12√3-12√3+8√2=9√2
√2=1×√2 — надеюсь, то, что в алгебре принято опускать подобные элементы, не станет для вас новостью.
Выражения могут быть представлены не только квадратным корнем, но так же и с кубическим или корнем n-ной степени.
Сложение и вычитание корней с разными показателями степени, но с равнозначным подкоренным выражением, происходит следующим образом:
Если мы имеем выражение вида √a+∛b+∜b, то мы можем упростить это выражение так:
∛b+∜b=12×√b4 +12×√b3
12√b4 +12×√b3=12×√b4 + b3
Мы привели два подобных члена к общему показателю корня. Здесь использовалось свойство корней, которое гласит: если число степени подкоренного выражения и число показателя корня умножить на одно и то же число, то его вычисление останется неизменным.
На заметку: показатели степени складываются только при умножении.
Рассмотрим пример, когда в выражении присутствуют дроби.
5√8-4×√(1/4)+√72-4×√2
Будем решать по этапам:
5√8=5*2√2 — мы выносим из-под корня извлекаемую часть.
4√(1/4)=-4 √1/(√4)= — 4 *1/2= — 2
Если в тело корня представлено дробью, то часто этой дроби не измениться, если извлечь квадратный корень из делимого и делителя. В итоге мы получили описанное выше равенство.
√72-4√2=√(36×2)- 4√2=2√2
10√2+2√2-2=12√2-2
Вот и получился ответ.
Главное помнить, что из отрицательных чисел не извлекается корень с четным показателем степени. Если четной степени подкоренное выражение является отрицательным, то выражение является нерешаемым.
Сложение корней возможно только при совпадении подкоренных выражений, так как они являются подобными слагаемыми. То же самое относиться и к разности.
Сложение корней с разными числовыми показателями степени производиться посредством приведения к общей корневой степени обоих слагаемых.
Если в подкоренном выражении имеется число, возведенное в степень, то это выражение можно упростить при условии, что между показателем корня и степени существует общий знаменатель.
В математике корни могут быть квадратными, кубическими или иметь любой другой показатель (степень), который пишется слева над знаком корня. Выражение, стоящее под знаком корня, называется подкоренным выражением. Сложение корней похоже на сложение членов алгебраического выражения, то есть требует определения подобных корней.
Шаги
Часть 1 из 2: Определение корнейОбозначение корней. Выражение под знаком корня () означает, что из этого выражения необходимо извлечь корень определенной степени.
- Корень обозначают знаком.
- Показатель (степень) корня пишется слева над знаком корня. Например, кубический корень из 27 записывается так: (27)
- Если показатель (степень) корня отсутствует, то показатель считается равным 2, то есть это квадратный корень (или корень второй степени).

- Число, записанное перед знаком корня, называется множителем (то есть это число умножается на корень), например 5 (2)
- Если множителя перед корнем нет, то он равен 1 (напомним, что любое число, умноженное на 1, равняется самому себе).
- Если вы впервые работаете с корнями, сделайте соответствующие пометки над множителем и показателем корня, чтобы не запутаться и лучше понять их назначение.
Запомните, какие корни можно складывать, а какие нельзя. Так же, как нельзя складывать разные члены выражения, например, 2а + 2b 4ab, вы не можете складывать разные корни.

Определите и сгруппируйте подобные корни. Подобные корни – корни, у которых одинаковые показатели и одинаковые подкоренные выражения. Например, рассмотрим выражение:
2 (3) + (81) + 2 (50) + (32) + 6 (3)
- Во-первых, перепишите выражение так, чтобы корни с одинаковым показателем располагались последовательно.
- Затем перепишите выражение так, чтобы корни с одинаковым показателем и с одинаковым подкоренным выражением располагались последовательно.
2 (50) + (32) + 2 (3) + 6 (3) + (81)
Упростите корни. Для этого разложите (где возможно) подкоренные выражения на два множителя, один из которых вынесите из-под корня. В этом случае вынесенное число и множитель корня перемножаются.
 Таким образом, вы получите упрощенное выражение: 10 (2) + 4 (2) + 2 (3) + 6 (3) + (81)
Таким образом, вы получите упрощенное выражение: 10 (2) + 4 (2) + 2 (3) + 6 (3) + (81)Сложите множители подобных корней. В нашем примере есть подобные квадратные корни из 2 (их можно сложить) и подобные квадратные корни из 3 (их тоже можно сложить). У кубического корня из 3 подобных корней нет.
- Не существует общепринятых правил порядка записи корней в выражении. Потому вы можете записывать корни в порядке возрастания их показателей и в порядке возрастания подкоренных выражений.
Внимание, только СЕГОДНЯ!
Все интересное
Число, которое находится под знаком корня, часто мешает решению уравнения, с ним неудобно работать. Даже если оно возведено в степень, дробно или не может быть представлено в виде целого числа в определенной степени, можно попытаться вывести его из…
Даже если оно возведено в степень, дробно или не может быть представлено в виде целого числа в определенной степени, можно попытаться вывести его из…
Корнем из числа x называется такое число, которое при возведении в степень корня будет равно x. Множителем называется умножаемое число. То есть, в выражении вида x*ª-&radic-y нужно внести x под корень. Инструкция 1Определите степень…
Если подкоренное выражение содержит набор математических действий с переменными, то иногда в результате его упрощения есть возможность получить относительно простое значение, часть которого можно вынести из под корня. Бывает полезно такое упрощение…
Арифметические действия с корнями различной степени могут значительно упростить расчеты в физике и технике и сделать их более точными. При умножении и делении удобнее не извлекать корень из каждого сомножителя или делимого и делителя, а сначала…
Квадратным корнем из числа x называют число a, которое при умножении само на себя дает число x: a * a = a^2 = x, x = a. Как и над любыми числами, над квадратными корнями можно выполнять арифметические операции сложения и вычитания. Инструкция …
Как и над любыми числами, над квадратными корнями можно выполнять арифметические операции сложения и вычитания. Инструкция …
Корень в математике может иметь два значения: это арифметическое действие и каждое из решений уравнения, алгебраического, параметрического, дифференциального или любого другого. Инструкция 1Корень n-ной степени из числа a — это такое число, что…
При выполнении различных арифметических действий с корнями часто бывает необходимо умение преобразовывать подкоренные выражения. Для упрощения расчетов может понадобиться вынести множитель за знак радикала или внести под него. Это действие можно…
Корнем называют значок, обозначающий математическую операцию нахождения такого числа, возведение которого в указанную перед знаком корня степень должно дать число, указанное под этим самым знаком. Часто для решения задач, в которых присутствуют…
Знаком корня в математических науках называется условное обозначение для корней. Число, находящееся под знаком корня, называется подкоренным выражением. n = a. Корни нечетной степени существуют для отрицательных и положительных чисел, а корни четной степени — только для положительных.…
n = a. Корни нечетной степени существуют для отрицательных и положительных чисел, а корни четной степени — только для положительных.…
Приветствую, котаны! В прошлый раз мы подробно разобрали, что такое корни (если не помните, рекомендую почитать). Главный вывод того урока: существует лишь одно универсальное определение корней, которое вам и нужно знать. Остальное — брехня и пустая трата времени.
Сегодня мы идём дальше. Будем учиться умножать корни, изучим некоторые проблемы, связанные с умножением (если эти проблемы не решить, то на экзамене они могут стать фатальными) и как следует потренируемся. Поэтому запасайтесь попкорном, устраивайтесь поудобнее — и мы начинаем.:)
Вы ведь тоже ещё не вкурили?
Урок получился довольно большим, поэтому я разделил его на две части:
- Сначала мы разберём правила умножения. Кэп как бы намекает: это когда есть два корня, между ними стоит знак «умножить» — и мы хотим что-то с этим сделать.
- Затем разберём обратную ситуацию: есть один большой корень, а нам приспичило представить его в виде произведения двух корней попроще.
 С какого перепугу это бывает нужно — вопрос отдельный. Мы разберём лишь алгоритм.
С какого перепугу это бывает нужно — вопрос отдельный. Мы разберём лишь алгоритм.
Тем, кому не терпится сразу перейти ко второй части — милости прошу. С остальными начнём по порядку.
Основное правило умножения
Начнём с самого простого — классических квадратных корней. Тех самых, которые обозначаются $\sqrt{a}$ и $\sqrt{b}$. Для них всё вообще очевидно:
Правило умножения. Чтобы умножить один квадратный корень на другой, нужно просто перемножить их подкоренные выражения, а результат записать под общим радикалом:
\[\sqrt{a}\cdot \sqrt{b}=\sqrt{a\cdot b}\]
Никаких дополнительных ограничений на числа, стоящие справа или слева, не накладывается: если корни-множители существуют, то и произведение тоже существует.
Примеры. Рассмотрим сразу четыре примера с числами:
\[\begin{align} & \sqrt{25}\cdot \sqrt{4}=\sqrt{25\cdot 4}=\sqrt{100}=10; \\ & \sqrt{32}\cdot \sqrt{2}=\sqrt{32\cdot 2}=\sqrt{64}=8; \\ & \sqrt{54}\cdot \sqrt{6}=\sqrt{54\cdot 6}=\sqrt{324}=18; \\ & \sqrt{\frac{3}{17}}\cdot \sqrt{\frac{17}{27}}=\sqrt{\frac{3}{17}\cdot \frac{17}{27}}=\sqrt{\frac{1}{9}}=\frac{1}{3}.
\\ \end{align}\]
Как видите, основной смысл этого правила — упрощение иррациональных выражений. И если в первом примере мы бы и сами извлекли корни из 25 и 4 без всяких новых правил, то дальше начинается жесть: $\sqrt{32}$ и $\sqrt{2}$ сами по себе не считаются, но их произведение оказывается точным квадратом, поэтому корень из него равен рациональному числу .
Отдельно хотел бы отметить последнюю строчку. Там оба подкоренных выражения представляют собой дроби. Благодаря произведению многие множители сокращаются, а всё выражение превращается в адекватное число.
Конечно, не всегда всё будет так красиво. Иногда под корнями будет стоять полная лажа — непонятно, что с ней делать и как преобразовывать после умножения. Чуть позже, когда начнёте изучать иррациональные уравнения и неравенства, там вообще будут всякие переменные и функции. И очень часто составители задач как раз и рассчитывают на то, что вы обнаружите какие-то сокращающиеся слагаемые или множители, после чего задача многократно упростится.
Кроме того, совсем необязательно перемножать именно два корня. Можно умножить сразу три, четыре — да хоть десять! Правило от этого не поменяется. Взгляните:
\[\begin{align} & \sqrt{2}\cdot \sqrt{3}\cdot \sqrt{6}=\sqrt{2\cdot 3\cdot 6}=\sqrt{36}=6; \\ & \sqrt{5}\cdot \sqrt{2}\cdot \sqrt{0,001}=\sqrt{5\cdot 2\cdot 0,001}= \\ & =\sqrt{10\cdot \frac{1}{1000}}=\sqrt{\frac{1}{100}}=\frac{1}{10}. \\ \end{align}\]
И опять небольшое замечание по второму примеру. Как видите, в третьем множителе под корнем стоит десятичная дробь — в процессе вычислений мы заменяем её обычной, после чего всё легко сокращается. Так вот: очень рекомендую избавляться от десятичных дробей в любых иррациональных выражениях (т.е. содержащих хотя бы один значок радикала). В будущем это сэкономит вам кучу времени и нервов.
Но это было лирическое отступление. Теперь рассмотрим более общий случай — когда в показателе корня стоит произвольное число $n$, а не только «классическая» двойка. {2n}}}=\left| a \right|. \\ \end{align}\]
{2n}}}=\left| a \right|. \\ \end{align}\]
Подобные «махинации» могут здорово сэкономить вам время на экзамене или контрольной работе, поэтому запомните:
Не спешите перемножать числа в подкоренном выражении. Сначала проверьте: вдруг там «зашифрована» точная степень какого-либо выражения?
При всей очевидности этого замечания должен признать, что большинство неподготовленных учеников в упор не видят точные степени. Вместо этого они перемножают всё напролом, а затем удивляются: почему это получились такие зверские числа?:)
Впрочем, всё это детский лепет по сравнению с тем, что мы изучим сейчас.
Умножение корней с разными показателями
Ну хорошо, теперь мы умеем перемножать корни с одинаковыми показателями. А что, если показатели разные? Скажем, как умножить обычный $\sqrt{2}$ на какую-нибудь хрень типа $\sqrt{23}$? Можно ли вообще это делать?
Да конечно можно. Всё делается вот по этой формуле:
Правило умножения корней.
{2}}}=\sqrt{5}. \\ \end{align}\]
Но тогда получается какая-то хрень:
\[\sqrt{-5}=\sqrt{5}\]
Этого не может быть, потому что $\sqrt{-5} \lt 0$, а $\sqrt{5} \gt 0$. Значит, для чётных степеней и отрицательных чисел наша формула уже не работает. После чего у нас есть два варианта:
- Убиться об стену констатировать, что математика — это дурацкая наука, где «есть какие-то правила, но это неточно»;
- Ввести дополнительные ограничения, при которых формула станет рабочей на 100%.
В первом варианте нам придётся постоянно вылавливать «неработающие» случаи — это трудно, долго и вообще фу. Поэтому математики предпочли второй вариант.:)
Но не переживайте! На практике это ограничение никак не влияет на вычисления, потому что все описанные проблемы касаются лишь корней нечётной степени, а из них можно выносить минусы.
Поэтому сформулируем ещё одно правило, которое распространяется вообще на все действия с корнями:
Прежде чем перемножать корни, сделайте так, чтобы подкоренные выражения были неотрицательны.
2 = x, ?x = a. Как и над всякими числами, над квадратными корнями дозволено исполнять арифметические операции сложения и вычитания.
Инструкция
1. Во-первых, при сложении квадратных корней испробуйте извлечь эти корни. Это будет допустимо, если числа под знаком корня являются полными квадратами. Скажем, пускай задано выражение?4 + ?9. Первое число 4 – это квадрат числа 2. Второе число 9 – это квадрат числа 3. Таким образом получается, что: ?4 + ?9 = 2 + 3 = 5.
2. Если под знаком корня нет полных квадратов, то испробуйте перенести из под знака корня множитель числа. Скажем, пускай дано выражение?24 + ?54. Разложите числа на множители: 24 = 2 * 2 * 2 * 3, 54 = 2 * 3 * 3 * 3. В числе 24 имеется множитель 4, тот, что дозволено перенести из под знака квадратного корня. В числе 54 – множитель 9. Таким образом, получается что: ?24 + ?54 = ?(4 * 6) + ?(9 * 6) = 2 * ?6 + 3 * ?6 = 5 * ?6. В данном примере в итоге выноса множителя из под знака корня получилось упростить заданное выражение.
3. Пускай сумма 2-х квадратных корней является знаменателем дроби, скажем, A / (?a + ?b). И пускай перед вами стоит задача «избавиться от иррациональности в знаменателе». Тогда дозволено воспользоваться дальнейшим методом. Умножьте числитель и знаменатель дроби на выражение?a – ?b. Таким образом в знаменателе получится формула сокращенного умножения: (?a + ?b) * (?a – ?b) = a – b. По аналогии, если в знаменателе дана разность корней: ?a – ?b, то числитель и знаменатель дроби нужно умножить на выражение?a + ?b. Для примера, пускай дана дробь 4 / (?3 + ?5) = 4 * (?3 – ?5) / ((?3 + ?5) * (?3 – ?5)) = 4 * (?3 – ?5) / (-2) = 2 * (?5 – ?3).
4. Разглядите больше непростой пример избавления от иррациональности в знаменателе. Пускай дана дробь 12 / (?2 + ?3 + ?5). Нужно умножить числитель и знаменатель дроби на выражение?2 + ?3 – ?5:12 / (?2 + ?3 + ?5) = 12 * (?2 + ?3 – ?5) / ((?2 + ?3 + ?5) * (?2 + ?3 – ?5)) = 12 * (?2 + ?3 – ?5) / (2 * ?6) = ?6 * (?2 + ?3 – ?5) = 2 * ?3 + 3 * ?2 – ?30.
5. И наконец, если вам нужно только примерное значение, то дозволено посчитать значения квадратных корней на калькуляторе. Вычислите значения отдельно для всего числа и запишите с нужной точностью (скажем, два знака позже запятой). А после этого совершите требуемые арифметические операции, как с обыкновенными числами. Скажем, пускай нужно узнать примерное значение выражения?7 + ?5 ? 2,65 + 2,24 = 4,89.
Видео по теме
Обратите внимание!
Квадратные корни ни в коем случае невозможно складывать как примитивные числа, т.е. ?3 + ?2 ? ?5!!!Полезный совет
Если вы раскладываете число на множители, дабы перенести квадрат из под знака корня, то совершите обратную проверку – перемножьте все получившиеся множители и получите изначальное число.Умножение корней
Приветствую, котаны! В прошлый раз мы подробно разобрали, что такое корни (если не помните, рекомендую почитать).
Главный вывод того урока: существует лишь одно универсальное определение корней, которое вам и нужно знать. Остальное — брехня и пустая трата времени.
Сегодня мы идём дальше. Будем учиться умножать корни, изучим некоторые проблемы, связанные с умножением (если эти проблемы не решить, то на экзамене они могут стать фатальными) и как следует потренируемся. Поэтому запасайтесь попкорном, устраивайтесь поудобнее — и мы начинаем.:)
Вы ведь тоже ещё не вкурили?Урок получился довольно большим, поэтому я разделил его на две части:
- Сначала мы разберём правила умножения. Кэп как бы намекает: это когда есть два корня, между ними стоит знак «умножить» — и мы хотим что-то с этим сделать.
- Затем разберём обратную ситуацию: есть один большой корень, а нам приспичило представить его в виде произведения двух корней попроще. С какого перепугу это бывает нужно — вопрос отдельный. Мы разберём лишь алгоритм.
Тем, кому не терпится сразу перейти ко второй части — милости прошу.
С остальными начнём по порядку.
Основное правило умножения
Начнём с самого простого — классических квадратных корней. Тех самых, которые обозначаются $\sqrt{a}$ и $\sqrt{b}$. Для них всё вообще очевидно:
Правило умножения. Чтобы умножить один квадратный корень на другой, нужно просто перемножить их подкоренные выражения, а результат записать под общим радикалом:
\[\sqrt{a}\cdot \sqrt{b}=\sqrt{a\cdot b}\]
Никаких дополнительных ограничений на числа, стоящие справа или слева, не накладывается: если корни-множители существуют, то и произведение тоже существует.
Примеры. Рассмотрим сразу четыре примера с числами:
\[\begin{align} & \sqrt{25}\cdot \sqrt{4}=\sqrt{25\cdot 4}=\sqrt{100}=10; \\ & \sqrt{32}\cdot \sqrt{2}=\sqrt{32\cdot 2}=\sqrt{64}=8; \\ & \sqrt{54}\cdot \sqrt{6}=\sqrt{54\cdot 6}=\sqrt{324}=18; \\ & \sqrt{\frac{3}{17}}\cdot \sqrt{\frac{17}{27}}=\sqrt{\frac{3}{17}\cdot \frac{17}{27}}=\sqrt{\frac{1}{9}}=\frac{1}{3}.
\\ \end{align}\]
Как видите, основной смысл этого правила — упрощение иррациональных выражений. И если в первом примере мы бы и сами извлекли корни из 25 и 4 без всяких новых правил, то дальше начинается жесть: $\sqrt{32}$ и $\sqrt{2}$ сами по себе не считаются, но их произведение оказывается точным квадратом, поэтому корень из него равен рациональному числу.
Отдельно хотел бы отметить последнюю строчку. Там оба подкоренных выражения представляют собой дроби. Благодаря произведению многие множители сокращаются, а всё выражение превращается в адекватное число.
Конечно, не всегда всё будет так красиво. Иногда под корнями будет стоять полная лажа — непонятно, что с ней делать и как преобразовывать после умножения. Чуть позже, когда начнёте изучать иррациональные уравнения и неравенства, там вообще будут всякие переменные и функции. И очень часто составители задач как раз и рассчитывают на то, что вы обнаружите какие-то сокращающиеся слагаемые или множители, после чего задача многократно упростится.
Кроме того, совсем необязательно перемножать именно два корня. Можно умножить сразу три, четыре — да хоть десять! Правило от этого не поменяется. Взгляните:
Примеры.
\[\begin{align} & \sqrt{2}\cdot \sqrt{3}\cdot \sqrt{6}=\sqrt{2\cdot 3\cdot 6}=\sqrt{36}=6; \\ & \sqrt{5}\cdot \sqrt{2}\cdot \sqrt{0,001}=\sqrt{5\cdot 2\cdot 0,001}= \\ & =\sqrt{10\cdot \frac{1}{1000}}=\sqrt{\frac{1}{100}}=\frac{1}{10}. \\ \end{align}\]
И опять небольшое замечание по второму примеру. Как видите, в третьем множителе под корнем стоит десятичная дробь — в процессе вычислений мы заменяем её обычной, после чего всё легко сокращается. Так вот: очень рекомендую избавляться от десятичных дробей в любых иррациональных выражениях (т.е. содержащих хотя бы один значок радикала). В будущем это сэкономит вам кучу времени и нервов.
Но это было лирическое отступление. Теперь рассмотрим более общий случай — когда в показателе корня стоит произвольное число $n$, а не только «классическая» двойка.
{2n}}}=\left| a \right|. \\ \end{align}\]
Подобные «махинации» могут здорово сэкономить вам время на экзамене или контрольной работе, поэтому запомните:
Не спешите перемножать числа в подкоренном выражении. Сначала проверьте: вдруг там «зашифрована» точная степень какого-либо выражения?
При всей очевидности этого замечания должен признать, что большинство неподготовленных учеников в упор не видят точные степени. Вместо этого они перемножают всё напролом, а затем удивляются: почему это получились такие зверские числа?:)
Впрочем, всё это детский лепет по сравнению с тем, что мы изучим сейчас.
Умножение корней с разными показателями
Ну хорошо, теперь мы умеем перемножать корни с одинаковыми показателями. А что, если показатели разные? Скажем, как умножить обычный $\sqrt{2}$ на какую-нибудь хрень типа $\sqrt[7]{23}$? Можно ли вообще это делать?
Да конечно можно. Всё делается вот по этой формуле:
Правило умножения корней.
{2}}}=\sqrt[3]{5}. \\ \end{align}\]
Но тогда получается какая-то хрень:
\[\sqrt[3]{-5}=\sqrt[3]{5}\]
Этого не может быть, потому что $\sqrt[3]{-5} \lt 0$, а $\sqrt[3]{5} \gt 0$. Значит, для чётных степеней и отрицательных чисел наша формула уже не работает. После чего у нас есть два варианта:
Убиться об стенуконстатировать, что математика — это дурацкая наука, где «есть какие-то правила, но это неточно»;- Ввести дополнительные ограничения, при которых формула станет рабочей на 100%.
В первом варианте нам придётся постоянно вылавливать «неработающие» случаи — это трудно, долго и вообще фу. Поэтому математики предпочли второй вариант.:)
Но не переживайте! На практике это ограничение никак не влияет на вычисления, потому что все описанные проблемы касаются лишь корней нечётной степени, а из них можно выносить минусы.
Поэтому сформулируем ещё одно правило, которое распространяется вообще на все действия с корнями:
Прежде чем перемножать корни, сделайте так, чтобы подкоренные выражения были неотрицательны.
{2}}}=\sqrt[4]{75}. \end{align}\]
Ну что ж, с умножением корней разобрались. Теперь рассмотрим обратную операцию: что делать, когда под корнем стоит произведение?
Смотрите также:
- Свойства арифметического квадратного корня
- Корень степени N
- Решение задач B12: №440—447
- Материалы для подготовки к ЕГЭ по математике
- Тест по задачам B14: средний уровень, 1 вариант
- B15: Линейные функции и производная частного
Правила действий со степенями и корнями, примеры.
Адрес этой страницы (вложенность) в справочнике dpva.ru: главная страница / / Техническая информация / / Математический справочник / / Таблицы логарифмов и основные формулы. Десятичные и натуральные логарифмы. Степени, корни. / / Правила действий со степенями и корнями, примеры.
Поделиться:
Поиск в инженерном справочнике DPVA. Введите свой запрос:
Правила действий со степенями и корнями, примеры.
Поиск в инженерном справочнике DPVA. Введите свой запрос: Дополнительная информация от Инженерного cправочника DPVA, а именно — другие подразделы данного раздела:
Таблицы Брадиса. Вы сейчас здесь: Правила действий со степенями и корнями, примеры. Степенные функции y=xn и y=x1/n, n∈Z. Свойства, графики. Квадратичная функция. Свойства степеней. Свойства арифметических корней. Формулы сокращенного умножения. Примеры значения степенных функций Основные формулы логарифмов. Десятичные (lg) и натуральные логарифмы (ln). Решение показательных уравнений. Решение логарифмических уравнений. Примеры значений логарифмических и показательных функций.
Таблица. Мантиссы (дробные части) десятичных логарифмов. Таблица. Натуральные логарифмы. Таблица и формула для перехода от натуральных логарифмов к десятичным. Таблица и формула для перехода от десятичных логарифмов к натуральным. Чиcло ln π, lg π, πe, eπ, e-π, e1/(2π) , ii , e-1/(2π) и др. Численные значения числа e, 1/e, e2, lg e, ln 10, ln π, lg π, πe, eπ, e-π, e1/(2π), ii , e-1/(2π) Постоянная Эйлера γ, золотое сечение (золотая пропорция) φ, ln γ, eγ, 1/φ и др. Если Вы не обнаружили себя в списке поставщиков, заметили ошибку, или у Вас есть дополнительные численные данные для коллег по теме, сообщите , пожалуйста. 
Вложите в письмо ссылку на страницу с ошибкой, пожалуйста.Коды баннеров проекта DPVA.ru
Начинка: KJR PublisiersКонсультации и техническая
поддержка сайта: Zavarka TeamПроект является некоммерческим. Информация, представленная на сайте, не является официальной и предоставлена только в целях ознакомления. Владельцы сайта www.dpva.ru не несут никакой ответственности за риски, связанные с использованием информации, полученной с этого интернет-ресурса. Free xml sitemap generator калькулятор корней со степенями, корень н-ой степени
Нам нужно посчитать на калькуляторе онлайн корень н-ой степени из числа! У нас есть калькулятор, который мы постепенно обучаем и в том числе уже научили его считать корни н-ой степени! Для наглядной иллюстрации, как работает калькулятор по извлечению корня н-ой степени – возьмем для примера корень третьей степени.Как извлечь корень третьей степени на калькуляторе ? 1. Для того, чтобы начать считать корень н-ой степени, набираем число, из которого этот корень нам нужно извлечь! Пусть это будет число 125. 2. Для набора степени нам потребуется отдельная кнопка – без неё никак, программа же должна понимать, что вы даете её! Нажимаем кнопку «P» 3. Набираем степень, если корень третьей степени, то набираем 1/3. 4. Нажимаем равно… Друзья! Для вас ликбез: Корень н-ой степени = число в дробной степени. Например: корень третьей степени числа = число в дробной степени √x = x1/2 ³√x = x1/3 А степени мы уже проходили…
Калькулятор корней со степенями онлайн
Для набора корней со степенями, полная инструкция показана на примере корня третьей степени из числа.Корень четвертой степени калькулятор
Корень четвертой степени на калькуляторе вычисляется аналогично, что и корень третьей степени, лишь с той разницей, что вместо 3 надо поставить 4.Калькулятор корень 5 степени
Корень 5 степени на калькуляторе вычисляется аналогично, что и корень третьей степени, лишь с той разницей, что вместо 3 надо поставить 5.Корень 6 степени калькулятор
Корень 6 степени на калькуляторе вычисляется аналогично, что и корень третьей степени, лишь с той разницей, что вместо 3 надо поставить 6.Корень n ой степени калькулятор
Корень н-ой степени вычисляется аналогично, вместо нежный части дроби – знаменателя выбираем вашу н-ую степень.Калькулятор корней с буквами и степенями
Калькулятор корней с буквами и степенями – боюсь предположить, что это… Как может калькулятор вычислить из буквы, корень, степени или другие математические действия! Любо буквы в степенях и корнях!? Единственный случай – это когда применяют объяснения, как считать – но на калькуляторе буквы не применятся в расчетах… Это как масло и вода – разные субстанции…Калькулятор корень 7 степени
Корень 7 степени на калькуляторе вычисляется аналогично, что и корень третьей степени, лишь с той разницей, что вместо 3 надо поставить 7.Калькулятор корней онлайн со степенями с решением
Калькулятор корней онлайн со степенями с решением – какое вы решение собираетесь увидеть на калькуляторе… √4 = 2 3√8 = 2 4√16 = 2 5√32 = 2 И т.д… с другими цифрами… Или в обратную сторону.. 22 = 2*2 = 4 23 = 2*2*2 = 8 24 = 2*2*2*2 = 16Корень восьмой степени онлайн калькулятор
Корень восьмой степени на калькуляторе вычисляется аналогично, что и корень третьей степени, лишь с той разницей, что вместо 3 надо поставить восьмую.Калькулятор примеров с корнями и степенями
Примеры см. вышеНаписать что-нибудь…
калькулятор корней со степенями , калькулятор корень 3 степени, калькулятор с корнями и степенями , корень 3 степени онлайн калькулятор , онлайн калькулятор корней в степени , корень третий степени калькулятор , корень 4 степени онлайн калькулятор , корень третьей степени онлайн калькулятор , корень третий степени онлайн калькулятор , корень степени n калькулятор , как записать степень корня в калькуляторе , калькулятор корней со степенями онлайн , корень четвертой степени калькулятор , калькулятор дробей с корнями и степенями , калькулятор корень 5 степени , корень в 4 степени калькулятор , корень 3 степени как записать в калькулятор , корень 3 степени онлайн калькулятор как записать , корень 5 степени онлайн калькулятор , корень степени из числа калькулятор , калькулятор корней со степенями и дробями , корень в третьей степени калькулятор , калькулятор степеней и корней с решением , калькулятор дробей с корнями и степенями онлайн , корень н степени калькулятор , корень 6 степени калькулятор , корень пятой степени калькулятор , как посчитать степень корня на калькуляторе , корень 4 степени как записать в калькулятор , калькулятор корней со степенями с решением , корень n ой степени калькулятор , калькулятор корней без степеней , калькулятор корней n степени онлайн , корень 6 степени онлайн калькулятор , калькулятор выражений с корнями и степенями , корень четвертой степени онлайн калькулятор , калькулятор корней с буквами и степенями , калькулятор корень 7 степени , калькулятор корней онлайн со степенями с решением , корень пятой степени онлайн калькулятор , калькулятор квадратных корней в степени , калькулятор корня 2 степени , калькулятор корней со степенями онлайн дроби , как в калькуляторе написать корень 3 степени , степень из под корня калькулятор , корень восьмой степени онлайн калькулятор , калькулятор корней со степенями и буквами , возведение корней в степень калькулятор , корень 7 степени онлайн калькулятор , калькулятор примеров с корнями и степенямиМатематика: Степени и корни
Степени и корни
Тема степеней и квадратных корней тесно связана друг с другом.
Чтобы понять суть этих двух терминов, нужно разобраться в истории их возникновения, терминологии и главном смысле.
Математика: Степени и корни
История степени числа
Еще в Древнем Египте люди заметили, что не всегда удобно умножать одно число много раз. Ведь по правилам оформления записей требовалось описывать все действия с математическими числами. Вот и приходилось жрецам прописывать одно и то же число десять, а то и двадцать раз. Со временем записи стали понемногу упрощать, пока один из мудрецов, по имени Диофант Александрийский. Количество раз, умноженные на одно и то же число, стали записывать в правом верхнем углу, как это принято и по сей день.
Далее, француз по имени Никола Шюке ввел термин не только положительной, но и отрицательной степени. Спустя некоторое время он же добавил ко всем своим многолетним трудам нулевой показатель степени.
История квадратного корня
История этого простого символа началась еще пять веков назад! Какими только символами его не обозначали.
Лишь 1626 году он обрел близкое к сегодняшнему обозначение в виде буквы V. Это произошло благодаря ученому из Нидерланд А. Жирар. Палочку над подкоренным выражением писали отдельно от буквы несколько десятилетий. И лишь спустя некоторое время Рене Декарт преобразовал символ, соединив букву с чертой. И только к концу семнадцатого века запись выражения с корнем приобрела вид, который сохранился на сегодняшний день.
Математическое обозначение квадратного корня и степени числа
Степень числа имеет следующую запись: n², где n – это повторяющееся число, называемое основанием степени и ² — число, показывающее, сколько раз повторяется умножение основания степени, оно называется показателем степени.
Корень записывается следующим символом: √. Корень состоит из символа и подкоренного выражения, записанного под горизонтальной чертой справа.
Теория степени числа
Вычисление значения выражения, содержащего степень, называется возведением в степень.
Некоторые из показателей степеней имеют свои собственные названия. Для остальных цифровых значений используются обычные названия.
Если вы имеете дело с отрицательным показателем степени, то для этого случая существует следующее правило:
Степень с нулевым показателем имеет одно необычное свойство. Вот оно: число в нулевой степени равняется единице.
Если показатель степени равен единице, то для него существует следующее правило: если показатель степени равен единице, то число равно само себе.
Для удобства пользования математики разработали таблицу квадратов натуральных чисел, в которую вошли числа от 1 до 100. Чтобы не выискивать и не просчитывать каждый раз это на калькуляторе или в справочнике, можно распечатать таблицу и носить при себе, в книге, учебнике или расположить на столе.
Теория квадратного корняСамым простым является арифметический корень. Его можно вычислить из простого положительного числа и сам является положительным числом.
Квадратным корнем называется число, если после вычислений получается то же самое число, которое возводили в квадрат.
Корень энной степени равен числу, из которого энная степень равна числу a.
Кстати, некоторые вместо слова корень, произносят радикал. Это не является ошибкой, так как это просто-напросто устаревшее слово, использовавшееся ранее для обозначения данного действия.
Степени и корни
Упражнения
по теме
«Степени и корни»
СОДЕРЖАНИЕ
1.
Аннотация
2. Основной теоретический материал
3. Система упражнений по теме « Степени и корни»
Аннотация
В данной разработке предложен материал, касающийся степеней и корней. Даны основные определения, сформулированы свойства.
Приведены примеры заданий различной сложности: арифметические задания на вычисление значений выражений с корнями и степенями, алгебраические задания на преобразование выражений, решение уравнений и неравенств.
Рассматриваемые вопросы широко применяются в алгебре и часто используются при подготовке к итоговой государственной аттестации.
Данная тема не является самой сложной в курсе алгебры. Однако при выполнении заданий встречается много ошибок.
Использование данных упражнений поможет закрепить умения и углубить знания по данной теме.
Основные определения и теоремы.
Истоки понятия степени находятся в глубокой древности; дошедшие до нас глиняные плитки древних вавилонян содержат записи таблиц квадратов, кубов и их обратных значений.
Первоначально под степенью понимали произведение нескольких одинаковых сомножителей. Способы записи степеней и связанных с ними обратных величин – корней из числа менялись с течением времени, пока не приняли современную форму.
Дальнейшее развитие науки вызвало необходимость расширения степени. В XIV в. Французский епископ города Лизье в Нормандии Н. Орем (1323-1382гг.) впервые стал заменять в отдельных случаях корни из чисел дробными показателями степени и ввёл символические обозначения степени с дробными показателями.
Например, 8 как 41,5. Показатели, введённые Оремом, по существу выступают в виде логарифмов чисел. Орем словесно сформулировал правила для выполнения различных операций со степенями.
Значительно позднее бухгалтер из Брюгге, а впоследствии военный инженер С. Стевин (1548-1620) вновь открыл дробные показатели и указал в более общем виде, что корень энной степени из числа а можно выразить как а1/n, где а>0.
Степенью с нулевым показателем первым стал пользоваться самаркандский учёный ал-Каши в начале XV в. Независимо от него Н. Шюке в работе «Наука о числах в трёх книгах» в 1484 г. применял нулевой и отрицательный показатели.
Завершили введение современного изображения степени англичане Джон Валлис и Исаак Ньютон.
Обобщение понятия степени аn, где n- любое действительное число, позволило рассматривать показательную функцию (y=ax) на множестве действительных чисел и степенную функцию (y=xn) на множестве положительных чисел, а при целых n степенная функция определена и для x<0.
Теоретический материал
Пусть дано положительное число а и произвольное действительное число п. Число ап называется степенью,
число а – основанием степени, число п – показателем степени.
По определению полагают: а1 = а,
а0 = 1,
а-п = , п R
Если а – положительное число, т – целое число, а п – натуральное число и п2, то = .
Свойства степени. Если а и в – положительные числа, х и у – любые действительные числа, то справедливы
следующие свойства: ах ау = а х + у,
ах : ау = а х — у,
(а х) у = а х у,
ах в х = (а в) х,
= ( )х.
Пусть п – натуральное число, отличное от единицы, а – неотрицательное число.
Арифметическим корнем п –й степени из неотрицательного числа а называется неотрицательное число, п – я степень которого равна а.
Для арифметического корня п- й степени из неотрицательного числа а используется обозначение . Если п=2, пишут . По определению
( )п = а.
Для любых, в том числе отрицательных, значений, а справедлива формула = /а/, в частности,
= /а/ и 2 = /а – в/.
Свойства арифметического корня.
Если а и в – неотрицательные числа, п и к – натуральные числа, отличные
от единицы, т –целое число, то имеют место следующие соотношения:
= ( ),
= ,
= , b неравно 0,
= ,
= ,
: = .
Степень с дробным показателем.
Если а – положительное число, т – целое число, а п – натуральное число и
п 2, то = = (m.
Управжнения.
Вычислить:
1) ; 5) ;
2) ; 6) ;
3) ; 7) , если , ;
4) ; 8) , если , .
Упростить:
1) ; 3) ;
2) ; 4) .
Решить графически уравнения:
1) ; 3) ;
2) ; 4) .
Извлечь арифметический корень:
1) ; 4) ;
2) ; 5) ;
3) ; 6) .
Вычислите степени с рациональным показателем:
a
b
c
d
e
f
g
h
1
34
43
24
53
25
33
50
23
2
3
6-2
2-4
3-3
5-1
3-4
2-3
7-2
4-1
4
5
6
7
8
Вычислите:
, , , , ,
2 — + , ,
1,70+ 32:3-1 – 251/2 , 163/4 – 71,7:7-0,3 + 430,
— 0,430,4-252 +160,5, ( )21,4 + 1251/3 – ( )-1,
811/49-1/2 + 13,40 –(52)-1 , 641/3:90,5 – 35,2 3— 6,2 +5,20,
(641/3 272/3 2432/5 128 3/7 )1/
(62,5 36 -1)4 — ( 51/4253/8)sin П/ 2.

Найдите значение выражения:
, + — — , 0,3 -0,1, + , , : , , .
Найдите значение выражения:
, при п = 8,
46Р4 -4Р , при р = ,
— , при х = 7,
, при х =16,
+ , при р = 49,
— , при р =16, q = 9,
+ , при х = 16, у = 25,
— , при х = 9, у = 49,
+ , при а = 625, в = 16,
— 2 , при а = 9, в =16.

Решить иррациональные уравнения и системы иррациональных уравнений
Решите уравнения:
1) =6; 2); 3)
4) ; 5) ; 6)
Решить систему уравнений.
Задания по решению уравнений:
75х+6 = 49, ()0,5х – 1 = 4, ( )1 – 3х = 9,
2-х = ( )1-х, 3х = ( )1 + х, 10-х = ,
3х2 -5х+1 = 81, = 0,125 х-7 , 53х-123х-1 = 0,1 ,
2 х+2 – 2 х = 96, 57 х-1 + 43 х + 3 х+1 — 27 х = 0, 4 х — 102 х-1 = 24,
9 х – 3 х-1 = 6, 4 х + 36 х – 49 х = 0, 2 х-1 + 2 –х-1 = 1.

Задания по решению неравенств:
16 2 х+3, 2 5х+7 8 х, 2 х— ,
5 х , 24 х+12 –х -1 , 39 х+1 3 – х – 1
9 х — 93 –х 0, 7 х — 77 – х -2 0, ( ) х — 82 – х 0,
х+1, ( )х+2+4/ х , 2 х+1 + 32 х 10,
9 х – 3 х+1 4, 2 х – 2 1-х 1, 9х — 5 6х — 6 4 х 0.

Пускаем корни — Popmath
Скажите, какого это — ощущать себя обманутым, покинутым, преданным теми, кому больше всего доверял? Как справиться с этой пожирающей изнутри экзистенциальной бездной? Только не надо говорить, что вам такое не известно, так как до сих пор личная жизнь была образцовой — дело вовсе не в этом. Предателя нужно искать не в воспоминаниях и выцветших телефонных книгах, а в наших статьях. И этот предатель — мы. В прошлый раз, говоря о степенях, мы сознательно, с циничным и холодным расчётом умолчали о целом типе степеней, без которого разобраться в полном курсе математики вряд ли получится.
В принципе, это можно было заметить сразу. Говоря о том, как возводить в степень различные дроби, мы не упомянули обратную ситуацию — а что если сама степень является дробной? В таком случае привычная логика (это в которой можно использовать кубики) даёт нехилый сбой — умножить число само на себя неполное число раз едва ли получится, тем более представить всё это через сложение.
Наверное, пора тянуться к справочникам, наизусть заучивать определения и десяток-другой не самых симпатичных формул? Не стоит отчаиваться, давайте разрешим эту задачу так же, как и все другие — последовательно, мудро и с неизменным юмором.
Начнём с простого. Вот, допустим, перед нами возникло что-то вроде , как с этим быть? Сходу, как уже сказали, сделать ничего не получится, а направления, в котором следует мыслить, нам никто ещё не подсказал. Выхода не остаётся, кроме как исходить из уже известного. А что известно-то? Вроде как это бессмыслица. Но нами было установлено, что при умножении элементов с одинаковыми основаниями показатели степеней складываются. Так же было замечено, что любое число в первой степени это оно само и есть. Значит, можно сказать, что . Что из этого следует?
А следует, что это такое число, которое при умножении само на себя (т.е. возведении в квадрат) даёт двойку. Опираясь на прошлые рисунки, сразу скажем, что тут мы выполняем обратную задачу. Если раньше у нас были какие-то числа и мы строили на их основе квадраты, то теперь наоборот, у нас уже есть некий квадрат с заданный площадью, а нам нужно найти его сторону.
Число в центре здесь указывает на общую площадь фигуры, а числа около сторон — на их длины:
Записывается это следующим образом: и читается как «квадратный корень из двух». Нелепый знак называется «радикал», а операция, которую он обозначает — «извлечением арифметического корня».
Эм…Шеф, не гони лошадей. Почему корень квадратный-то, да и только? Ведь указанная нами выше логика работает и для всех остальных показателей. В том смысле, что можно определить степень , по которой и так далее, вплоть до степени .
Подмечено верно, корни могут быть не только квадратными, также они могут быть и кубическими (то есть, когда степень корня это тройка), и хоть пятой, хоть любой другой степени. Записывается это всё путём указания верхнего индекса для корня, к примеру это «корень третьей степени из двойки», ну а это «корень степени из «.
А как так вообще вдруг получилось, что степень это квадрат, а — это куб? Ой, да мы же это проходили уже! Квадрат это значит, что мы такой квадратик нарисовать можем.
А в третьей степени, это значит, что кубик с похожими сторонами можно найти везде, хоть бы и в магазине игрушек. А вот со всем, что больше, ну или меньше, такого ясного-понятного не представить и с реальными предметами не проделать. Печаль-тоска-огорчение…
Надо признать, что сама по себе запись может оказаться достаточно путаной. В частности, тут есть место извечной людской неаккуратности — знак корня постоянно забывают ясно закрыть, по итогам чего совершенно невозможно понять, что является реальным подкоренным выражением, а что стоит совершенно независимо. Подкоренное выражение — это то, что и заносится под знак корня, между прочим. Вообще, если что-то когда-то кажется недостаточно понятным и удобным (например, какое-то объяснение в учебнике), то скорее всего оно так и есть, первое впечатление не обманывает.
Если уж говорить о путаности, то надо заметить, что нами был упущен ещё один важный момент, всё ещё касающийся дробных степеней. Как видите, эта тема — просто-таки непаханое поле для всяких затруднений и неприятностей.
Со свойственным нашему изложению изяществу мы показали, что , но что делать, если наша степень такова, что у неё в числителе стоит не единица? Например, как понимать запись вида ? Для ответа на этот вопрос следует прибегнуть к уже знакомой нам логике — будем отталкиваться от единицы.
Мы знаем, что , этого должно быть достаточно. Помня о сложении степеней при умножении, имеем . Следовательно, для нахождения искомого значения нам надо разделить на , иначе говоря, получить дробь вида . Собственно, это верно не только для , а вообще для любого случая:
Отлично, с задачей мы справились, можно идти дальше!.. Как это не справились? Вот же формула, всё выведено, измерено, что не так? А… Вам интуитивность какая-то ещё нужна, наглядность… Ну хорошо, давайте попробуем. Для этого воспользуемся подходящим примером, например, взяв в качестве опытного материала восьмёрку. Чему равна ? Согласно нашей инструкции, нужно разделить на , что мы и сделаем, попутно обнаружив, что кубический корень восьмёрки равен , т.
к. . Итак, считаем:
Обратим внимание, что , то есть, мы извлекли корень в той степени, на которую указывал в выражении знаменатель, а полученный результат возвели в степень, на которую указывал числитель. Совпадение? Не думаем!
Смотрите, давайте рассмотрим это явление подробнее, только подберём пример посложнее, например, . Как понимать вот это всё? Да очень просто, мы всего лишь представляем это слабо понятное месиво в более привычном для нас виде .
Видите? В этом нет ничего сложного, ведь если разложим любую дробную степень на сумму степеней с числителем равным единице (то есть, на корни в степени знаменателя), то смысл этого числителя станет понятным — он указывает нам на то, сколько раз была перемножена сама на себя исходная степень. Идея это достаточно простая, но давайте ещё раз проговорим. Вот у нас , что это? Это корень степени , возведённый в -ю степень. Почему? Потому что выше мы показали, что данное выражение раскладывается на множителей, где у каждого в числителе степени стоит единица.
А сколько будет, если пять единиц сложить друг с другом? То-то же!
Давайте наконец жирно подчеркнём то, что с таким трудом узнали:
Знаменатель — это корень. Числитель — это степень. Если забыли, просто вспомните, что квадратный корень это степень , а уж у него-то понятно, что обозначает знаменатель. И да — в степень возводится весь корень, а не подкоренное выражение. Это надо запомнить лучше, чем пароль от платного аккаунта на pornhub. Хотя минуточку… вдруг запоминание подобной ерунды как-то помешает по памяти воспроизвести сам пароль? Давайте-ка убедимся, что это действительно необходимо.
Допустим, что у нас есть всё то же , которое, как только что установлено, равно . А чему тогда будет равно ? Давайте посмотрим. У нас есть , из которого извлекается корень степени , то есть наше возводится в степень , при возведении одной степени в другую показатели перемножаются, значит, получаем:
Чудны дела твои, Господи!
А-ха-ха, это опять шутка, ведь никакого бога нет.
Тем не менее, результат примечателен — в силу специфики указанной операции нет разницы, имеем мы дело со степенью выражения с корнем в своём составе, или со степенью подкоренного выражения как такового. А знаете, как это легко запомнить? Вообще не приплетая корни, ведь без этих обозначений никакой неразберихи нет вообще, так как мы точно знаем какие переменные в каких отношениях друг с другом находятся, ну и где у них там все степени стоят.
При кажущейся простоте всего упомянутого следует помнить, что большой проблемой здесь выступает отсутствие внятной иллюстрации происходящего. Конечно, в случае с уже разобранным примером вы сначала можете найти площадь квадрата , затем использовать эти данные для нахождения площади квадрата со сторонами в , ну а потом уже найти финальную площадь прямоугольника , однако согласитесь, что это скорее усложняет дело, чем его упрощает.
Во всём этом проявляется одно интересное, даже удивительное свойство математического мышления — оторванность от «реальных примеров».
Уяснив на конкретной иллюстрации в чём смысл той или иной операции, мы можем бесконечно её усложнять, в том числе и до таких случаев, когда обычное, ничем не расширенное человеческое мышление представить каких-то визуальных воплощений оказывается не в силах. Собственно, если бы не эта особенность, то весь изучаемый материал ограничивался бы… ну… примерно тем, чем он и ограничивается в школе и вузах…
Да нет, опять шутим, конечно, даже в базовом школьном материале содержится куда больше идей, чем те, которые можно получить, чертя многоугольники на песке.
Теперь, когда мы не только раскрыли секрет непонятных степеней, но и снабдили всё это небольшим философским комментарием, перейдём к свойствам операций с арифметическим корнем. Именно к тем свойствам, которые по несколько вечеров в неделю заучивают и повторяют девочки-отличницы, и которых почти не помнят их ровесники-мальчики, больше увлечённые вопросами собственного полового созревания. Именно к тем свойствам, без знания которых у вас не получится нормально написать почти ни одну контрольную, не говоря уже о сдаче итоговых экзаменов.
Короче говоря, именно к важным, обязательным для успешного понимания всего, что только можно, свойствам.
Свойства эти… как бы вам помягче сказать… они отсутствуют. Их нет. Серьёзно, на этот раз без шуток. Нет никаких особенных свойств операций с корнями, которые надо было бы запоминать, записывать на бедре под колготками, проносить на шпаргалках в рукаве. Почему? Да потому что абсолютно все «свойства операций с арифметическим корнем» это уже до боли (приятной) знакомые свойства операций со степенями! Несмотря на простоту этого факта, он почему-то часто ускользает от внимания не столько учеников и студентов, сколько уважаемых педагогов с многолетним опытом и общественным признанием.
Повторяем, это не шутка, всё очень серьёзно. Покажем свою правоту, пройдясь по каждому из этих «уникальных свойств» в отдельности.
Начнём с того, что часто называют «правилом вынесения и внесения под корень» и с чем гарантированно хоть раз путался любой, кто с этим сталкивался. Как выносить и вносить, да и причём тут степени? Внимание на экран:
Таким образом, «вынесение из под корня» это обычная формула для степени произведения, которую мы детально препарировали в предыдущем материале.
Для большей очевидности поясним всё это на примере. Вот у нас есть и от нас требуется «вынести множитель из под знака корня», как нам поступить?
А так, что мы вообще забываем про какие-то корни и имеем дело только со степенями. . Иными словами, мы делим подкоренное выражение на две (или больше) части, извлекаем корень оттуда, откуда можно, и записываем итоговое произведение.
Аналогично решается и задача с «внесением под корень»: . То есть, мы просто ищем изначально заданное число, от которого и была вычислена степень . Запись имеет ровно такой смысл, ведь степени при такой операции перемножаются, т.е. взаимно сокращаются, оставляя .
Э-э-э!! Не выношу вообще тех, которые мутят что-то, если на деле ситуация и так ясная совершенно. Зачем вилять, ерунду городить, когда напрямую сказать можно? Не надо ни про какие «корни» думать, есть просто дробные степени — вот это всё, закрыли ситуацию. Попадись такие умники моему дяде Агабеку…
Чего там ещё осталось? Например, нахождение корней от дроби.
Типа, стоит такая запись , и что с ней делать? Эх, сложно это всё, придётся ручку доставать, заучивать, повторять. Хотя нет, нам ничего этого делать никогда не придётся. Почему? Ответ такой же, как и в случае последних вопросов — мы знаем про операции со степенями. Не станем скрывать свои знания:
Да-да, посмотрите на это хорошенько, не отводите взгляд. Тут ровно то, что мы пристально разглядели раньше — возведение дроби в степень. Кто бы мог подумать, что благодаря этому мы больше никогда не запутаемся во всех этих корнях? Повторяйте за нами: «больше никогда не запутаемся».
Остаётся совсем немного. Например, как не указать на такой необычный факт, что при умножении чисел на дробь возможны сокращения? Правда-правда, вы только не пугайтесь, но всё именно так и есть. Вот как эта истина выглядит на величественном языке арифметических корней:
Не впечатляет? Это всё потому, что вы слишком испорчены пониманием того, что корни это сокращённый вариант записи степеней (это мы не устанем повторять, совсем как ваша мама, умоляющая надеть шапку при температуре на улице меньше градусов).
Не знай вы этого обстоятельства, то перед очередным зачётом могли бы не одну ночь развлекали себя мыслью «разве это всё кто-нибудь может запомнить?».
Совсем уж напоследок упомянем и особый случай. Особый случай это когда люди, составляющие задания для школьных и студенческих учебников, по какой-то причине не очень довольны своей жизнью. Печально, зато у них в руках есть какая-никакая, а власть. Что надо с властью делать? Правильно, использовать её, чтобы отомстить тем, чья жизнь ещё полна радостей и перспектив — проклятым молодым поколениям. Как этого добиться? Путём составления излишне сложных и неприятных задач, решение которых ничуть не приближает к пониманию сути производимых операций, да и вообще едва ли когда либо ещё пригодится.
Почётное место в списке таких упражнений занимают всевозможные «лесенки». Когда одно нагромождается на другое, тем более с учётом низкого качества типографии, достигается главная цель — морально унизить и потрясти читателя, создать ощущение вала информации, тотальной неразберихи и обречённости на поражение.
Есть лесенки и применительно к корням. Давайте их сейчас уничтожим (раз добраться до авторов-составителей всё равно не получится):
По мере просмотра этого упрощения у вас может возникнуть закономерный вопрос — если итоговое выражение достаточно простое, то зачем в самом начале записывать его таким чудовищным образом? А затем, читатель, чтобы ты подольше мучался, пытаясь привести его в удобоваримый вид.
Вообще, по итогам прочтения статьи у вас могло сложиться мнение, что сама манера обозначения арифметических корней нам не нравится. Что они неуинтуитивны, в них легко запутаться, а при записи от руки они требуют идеальной точности, либо велик риск по мере вычисления возвращаться на действий назад снова и снова. Что ж… это всё так и есть. В случае небольшого количества элементов использование корней и правда придаёт некоторую узнаваемость происходящему. А вот во всех остальных случаях от них стоит воздержаться. Если воздержание оказалось неудачным, то следует помнить главную максиму нашего изложения: корни — это степени.
Думаете, про степени уже знаете всё? Как бы ни так, ведь совсем по-близости уже рыскает в темноте очередная статья…
4. Корни полиномиального уравнения
Вот три важные теоремы, касающиеся корней полиномиального уравнения:
(a) Многочлен n -й степени можно разложить на n линейных множителей.
(b) Полиномиальное уравнение степени n имеет ровно n корней.
(c) Если `(x − r)` является множителем многочлена, то `x = r` является корнем соответствующего уравнения полинома.
Давайте посмотрим на несколько примеров, чтобы понять, что это значит.
Пример 1
Кубический полиномиальный F ( x ) = 4 x 3 — 3 x 2 — 6 имеет степень `3` (поскольку самая высокая мощность х , который появляется, это `3`).
Мы обсуждали этот пример в разделе 3. Как разложить полиномы на множители и нашли следующие множители:
4 x 3 — 3 x 2 — 25 x — 6 = ( x — 3) (4 x + 1) ( x + 2)
Вспомним, что многочлен 3-й степени имеет 3 корня.
Соответствующее полиномиальное уравнение формируется путем установки полинома равным нулю:
f ( х ) = 4 х 3 − 3 х 2 − 25 х
0 = 0 0 0 6 0 0 3 0В факторизованной форме это:
`(х — 3)(4х + 1)(х + 2) = 0`
Мы видим из выражений в скобках и используя 3-ю теорему сверху, что есть 3 корня, `x = 3`, `x=-1/4` и `x= −2`.
В этом примере все 3 корня нашего полиномиального уравнения степени 3 действительны.
Поскольку `(x − 3)` является множителем, то `x = 3` является корнем.
Поскольку `(4x + 1)` является множителем, то `x=-1/4` является корнем.
Так как `(x + 2)` является множителем, то `x = −2` является корнем.
Вот график нашего полинома, показывающий x -пересечений , которые являются корнями:
График f ( x ) = 4 x 3 — 3 x 2 — 25 x — 6
Пример 2
Уравнение x 5 — 4 x 4 — 7 x 3 + 14 x 2 — 44 x + 120 = 0 могут быть учтены (используя Wolfram |Alpha) и записывается как:
( х — 2)( х — 5)( х + 3)( х 2 + 4) = 0
Мы видим, что существует 3 действительных корней `x = 2, 5, -3` и 2 комплексных корней `x = ±2j` (где `j = sqrt(-1)`).
Таким образом, наше уравнение 5-й степени имеет всего 5 корней, как и ожидалось.
На графике мы видим только три действительных корня:
графика y = x 5 — 4 x 4 — 7 x 3 + 14 x 2 — 44 x + 120
[Вам нужна проверка комплексных чисел? Перейти к комплексным числам.]
Пример 3
В предыдущем разделе 2.2−5x−6 = 0`.
Чтобы проверить это, подставьте `x = -1` в многочлен. Если это корень, то при подстановке вы должны получить значение `0`.
Еще один способ увидеть, что происходит, — построить график полинома.
График y = x 3 + 2 x 2 − 5 x − 6
На графике показаны два других корня, −3 и 2.
Пример 4
Следующее полиномиальное уравнение довольно сложно решить с помощью теорем об остатках и множителях.
Будем решать с помощью Wolfram|Alpha:
х 4 + 0,4 х 3 — 6,49 х 2 + 7,244 х — 0,1920 = 3
Ответить
Результат Wolfram|Alpha:
Решить: х 4 + 0,4 х 3 − 6,49 х 2 + 7,244 х 00030 2 = 9, 030 − 2,11
Решение: {`x = -3,2`}, {`x = 1,2`}, {`x = 0.5`}, {`x = 1,1`}
Вот график:
графика y = x 4 + 0,4 x 3 — 6,49 x 2 + 7.244 x — 2.112
Три положительных корня трудно увидеть. Вот еще раз эта часть, увеличенная для более четкого просмотра:
График y = x 4 + 0,4 x 3 − 6,49 x 2 + 7.244 х − 2,112
Примечание: Полиномиальные уравнения не всегда имеют «хорошие» решения! (Под «хорошими решениями» я подразумеваю решения, которые представляют собой целые числа или простые дроби.
) Вот почему я считаю, что теоремы об остатках и множителях следует рассматривать как исторический подход, потому что вы можете использовать их только в том случае, если хотя бы некоторые из решений являются целыми числами. или простые дроби.
Если вы используете систему компьютерной алгебры (например, Wolfram | Alpha, чтобы решить их, вы можете сделать это за секунды и перейти к чему-то более значимому, например, к приложениям.
Пример 5
Решите следующее полиномиальное уравнение, используя систему компьютерной алгебры:
3 x 3 − x 2 − x + 4 = 0,
Ответить
3 x 3 − x 2 − x + 4 }
Мы видим, что есть одно действительное решение и 2 комплексных решения.
Проверяя это графически, мы имеем:
График y = 3 x 3 − x 2 − x + 4
Мы видим, что есть только один (действительный) корень, около `x = -1`, как и ожидалось.
Использование системы компьютерной алгебры для поиска корней
Мы использовали технологию, чтобы найти большинство корней выше. Это лучше, чем пытаться угадать решения, а затем делить многочлены. Используя компьютер, мы можем быстро найти корни либо графически, либо с помощью встроенного средства поиска корней, если оно доступно.
Используя график, мы можем легко найти корни полиномиальных уравнений, которые не имеют «хороших» корней, например:
x 5 + 8.5 x 4 + 10 x 3 — 37,5 x 2 — 36 x + 54 = 0,
Корнями уравнения являются просто точки пересечения x (т. е. где функция имеет значение `0`). Вот график функции:
График у = х 5 + 8.5 x 4 + 10 x 3 − 37,5 x 2 − 36 x + 54.
Мы видим решения `x=-6`, `x=-3`, `x=-2`, `x=1` и `x=1.
5`. (Увеличение масштаба вблизи этих корней на графике подтверждает эти значения.)
Сложные корни
В отношении комплексных корней применима следующая теорема:
Если коэффициенты уравнения `f(x)=0` действительны, а `a + bj` является комплексным корнем, то его сопряженное `a − bj` также является корнем.
Подробнее о комплексных числах см.: Комплексные числа
.Пример 6
В приведенном выше примере (2) у нас было 3 действительных корня и 2 комплексных корня. Эти комплексные корни образуют комплексно-сопряженную пару,
x = 0 − 2 j и x = 0 + 2 j
Пример 7
Множители многочлена x 3 + 7 x 2 + 17 x + 15 находятся с помощью системы компьютерной алгебры следующим образом:
x 3 + 7 x 2 + 17 x + 15 = ( x + 3) ( x + 2 — j ) ( x + 2 + j )
Таким образом, корни равны
.`х = −3`
`x = −2 + j` и`х = −2 − j`
Имеется один действительный корень, а остальные 2 корня образуют комплексно-сопряженную пару.
Составление полиномиальных уравнений с корнями — видео и расшифровка урока
Пример #1
Запишем полиномиальное уравнение с корнями 2, 3 и -1.
Сначала берем корни. Мы знаем, что x равны тем значениям, когда y = 0. Это означает, что мы можем переписать это уравнение так, чтобы оно равнялось 0, что дает нам множители многочлена. множителей многочлена — это члены, которые можно перемножить, чтобы получить многочлен.Если х = 2, то ( х — 2) является фактором многочлена.
Множители имеют противоположные знаки корней.
Затем запишем множители многочлена вместе и перемножим:
( x — 2)( x — 3)( x + 1)
Чтобы умножить двучленов ,9078 ,9078 ,9078 многочлены, которые имеют два члена, мы должны обязательно умножить каждый член в первом множителе на каждый член во втором множителе.
Начнем сразу с двух факторов. Мы используем коробку, чтобы помочь организовать умножение:
Обратите внимание, два красных члена похожи на члены , что означает, что они имеют одни и те же переменные с одинаковыми показателями степени. Поскольку они похожи на термы, мы объединяем их, добавляя -2 x и -3 x , чтобы получить -5 x .
Теперь, когда мы перемножили два множителя, возьмем результат и умножим его на третий множитель.Опять же, мы будем использовать прямоугольник для организации умножения, потому что это может привести к путанице при определении того, что у нас есть, а что нет.
Когда мы умножаем, мы получаем одинаковые члены. В этом случае у нас есть два набора подобных терминов. Оба синих термина имеют размер x 2, поэтому мы складываем их вместе. Оба красных термина имеют размер x в первой степени, поэтому мы их тоже добавляем.
Ответ является результатом этого умножения.Обратите внимание, что поскольку мы начали с трех корней, наш ответ имеет степень (наибольшую степень) 3.
Пример #2
Далее, давайте напишем полиномиальное уравнение, которое имеет корни 2, 2 и -3.
Этот пример содержит кратный корень из 2, поскольку он встречается дважды. Как и в предыдущем примере, у нас есть три корня, а это значит, что в итоге мы получим многочлен со степенью 3.
Сначала перепишем корни как множители. Поскольку двойки положительны, они станут отрицательными в множителе.Поскольку число 3 отрицательное, оно станет положительным в множителе.
Когда вы освоитесь, этот шаг можно пропустить и сразу перейти к написанию коэффициентов.
( x — 2)( x — 2)( x + 3)
Теперь умножим. Опять же, мы хотим начать только с двух факторов. Обычно проще начать с двух одинаковых.
Обратите внимание, что мы объединили одинаковые члены, и -2 x плюс -2 x равно -4 x .
Наконец, нам нужно умножить только что полученный результат на последний коэффициент ( x + 3).
Опять же, у нас есть два набора одинаковых членов для объединения. -4 x 2 плюс 3 x 2 равно — x 2. 4x плюс -12x равно -8 x .
Наш окончательный ответ — многочлен третьей степени.
Пример #3
Наконец, давайте напишем полиномиальное уравнение с корнями -1, 1, 4 и -4.
У этого многочлена четыре корня. Какова должна быть степень многочлена? Поскольку оно имеет четыре корня, его наибольший показатель будет равен 4.
Сначала мы начнем с записи корней в виде множителей. Поскольку все, что нам нужно сделать, это изменить знаки, мы получаем следующие множители.
( х + 1)( х — 1)( х — 4)( х + 4)
Далее нам нужно умножить. Легче всего будет умножать биномы с одинаковыми числами.Начнем с 1с.
Обратите внимание, что одинаковые члены сокращаются, потому что -1 плюс 1 равно 0. Это означает, что эти множители являются идеальными квадратами.
Далее мы умножим 4.
Опять же, подобные члены отменяются, потому что это идеальные квадраты. Вот почему мы решили сначала умножить 1 и 4. Обратите внимание, что мы не ошиблись бы, если бы сначала умножили любой из двух других факторов; просто так проще.
Теперь мы перемножим оба результата, чтобы получить окончательный ответ:
В этом случае нам нужно объединить подобные термины.
Обратите внимание, что старший показатель степени равен 4, и у нас было четыре корня. Таким образом, степень равна четырем.
Краткий обзор урока
Полиномиальные уравнения — это уравнения, содержащие несколько членов, состоящих из чисел и переменных.
степень является наивысшим показателем полинома. степень говорит нам, сколько корней находится в полиномиальном уравнении. корней полиномиального уравнения являются значениями x , где y = 0.
множитель в скобках
Умножьте пары корней вместе, используя прямоугольник для организации умножения Убедитесь, что каждый фактор был умножен на все остальные факторы, и Проверьте ответ, убедившись, что степень многочлена совпадает с числом заданных корней Объяснение урока: Действительные и комплексные корни многочленов
В этом объяснении мы научимся понимать отношения между степенью многочлена, его коэффициенты и его корни и как применять эти знания для решения задач.
Мы начнем с рассмотрения двух важных теорем о полиномах.
Основная теорема алгебры
Многочлен 𝑝(𝑥) степени 𝑛 с комплексными коэффициентами имеет, когда посчитано с кратностью, ровно 𝑛 корней.
Утверждение «при счете с кратностью» означает, что мы должны считать повторяющиеся корни по их множественность, т. количество раз, когда они повторяются. Например, в уравнении (𝑥−3)(𝑥+3)=0, мы имеем полином четвертой степени.Однако мы учитываем только два различных действительных корня. Это потому, что корень в 𝑥=3 является кратным корень кратности три; следовательно, общее количество корней, если считать с кратностью, равно четырем, как теорема состояния. Обратите внимание, что эта теорема применима к полиномам с действительными коэффициентами. потому что действительные числа — это просто комплексные числа с мнимой частью нуля.
Доказательство этой теоремы выходит за рамки этого объяснения и требует более сложных математических понятий, таких как полноты, тогда как понимание этой теоремы и ее следствий имеет большое значение и будет в центре внимания этого объяснения.
Пример 1. Количество корней многочлена
Сколько корней имеет многочлен 3𝑥−1𝑥+4𝑥−2?
Ответ
Используя основную теорему алгебры, число корней равно степени многочлена.
В данном случае нам дано многочлен в факторизованной форме. Чтобы найти степень, мы могли бы раскрыть круглые скобки, чтобы найти термин с наивысшей степенью. В качестве альтернативы, мы могли бы сэкономить себе часть работы, просто ища термины наивысшей степени в каждой паре круглых скобок; тогда степень многочлена будет степенью их произведения.В первом наборе скобок термин высшей степени равен 3𝑥 степени два. Во втором наборе скобок термин высшей степени равен 𝑥, которая имеет степень три. Следовательно, произведение этих двух членов будет иметь степень 5. что и будет степенью многочлена. Следовательно, многочлен имеет 5 корней.
Теперь рассмотрим следующую важную теорему о природе корней многочленов.
Теорема о сопряженных корнях
Пусть 𝑝 — полином с действительными коэффициентами.Если комплексное число 𝑧=𝑎+𝑏𝑖 (где 𝑎,𝑏∈ℝ) — корень из 𝑝, тогда его сопряженное 𝑧=𝑎−𝑏𝑖∗ также является корнем.
Используя свойства комплексного сопряжения, мы можем доказать эту теорему, как мы покажем.
Пусть 𝑝 — многочлен: 𝑝(𝑥)=𝑎+𝑎𝑥+𝑎𝑥+⋯+𝑎𝑥, где 𝑎,𝑎,…,𝑎 — действительные числа. Кроме того, пусть 𝑧=𝑎+𝑏𝑖 будет корнем 𝑝; то есть 𝑝(𝑧)=0. Рассмотрим значение 𝑝(𝑧)∗: 𝑝(𝑧)=𝑎+𝑎𝑧+𝑎(𝑧)+⋯+𝑎(𝑧).∗∗∗∗
Используя свойство комплексно-сопряженных чисел, что (𝑧)=(𝑧)∗ ∗, мы можем переписать это как 𝑝(𝑧)=𝑎+𝑎𝑧+𝑎𝑧+⋯+𝑎(𝑧).∗∗∗∗
Поскольку 𝑎 для 𝑘=0,1,…,𝑛 — действительные числа, мы знаем, что 𝑎=𝑎∗; следовательно, 𝑝(𝑧)=𝑎+𝑎𝑧+𝑎𝑧+⋯+𝑎(𝑧).∗∗∗∗∗∗∗∗
Используя свойство мультипликативности комплексно-сопряженных чисел, ∗∗∗, мы можем переписать это как 𝑝(𝑧)=𝑎+(𝑎𝑧)+𝑎𝑧+⋯+(𝑎𝑧).∗∗∗∗∗
Используя аддитивные свойства комплексно-сопряженных чисел 𝑧+𝑤=(𝑤) ∗∗∗, имеем 𝑝(𝑧)=𝑎+𝑎𝑧+𝑎𝑧+⋯+𝑎𝑧=(𝑝(𝑧)).∗∗∗
Поскольку 𝑧 является корнем 𝑧, мы знаем, что 𝑧 является корнем 𝑧) =0; следовательно, 𝑝(𝑧)=0=0,∗∗ что показывает, что 𝑧∗ также является корнем 𝑝.
Пример 2: Природа корней многочленов
Может ли многочлен с вещественными коэффициентами иметь ровно 3 недействительных корня?
Ответ
Теорема о сопряженных корнях говорит нам, что для каждого невещественного корня 𝑧=𝑎+𝑏𝑖 многочлена с действительными коэффициентами его сопряженное тоже является корнем.
Следовательно, если многочлен 𝑝 имел ровно 3 невещественных корня, 𝛼, 𝛽 и 𝛾, то для альфы мы знаем, что 𝛼∗ тоже невещественный корень. Следовательно, 𝛼∗ равно либо 𝛽, либо 𝛾.Без ограничения общности положим 𝛼=𝛽∗. Теперь мы также знаем, что, поскольку 𝛾 — невещественный корень, 𝛾∗ также будет невещественным корнем. Следовательно, он будет равен одному из 𝛼 или 𝛽. Если 𝛾=𝛼∗, то, взяв комплексные сопряжения, мы имеем
, откуда следует 𝛾=𝛽. Аналогичные рассуждения показывают, что если 𝛾=𝛽∗, 𝛾=𝛼. Следовательно, у нас есть противоречие с идеей о том, что у нас есть три различных невещественных корня, что означает, что невозможно иметь ровно 3 невещественных корня.
Теперь мы рассмотрим следствия этих теорем для квадратичных, кубических и квартик с действительными коэффициентами.Начиная с квадратичных, из основной теоремы алгебры мы знаем, что любое квадратное число будет иметь два корня. Из теоремы о сопряженных корнях мы знаем, что если многочлен имеет действительные коэффициенты, то если он имеет какой-либо невещественный корень, его корни будут комплексно-сопряженной парой.
Если оно имеет действительные корни, оно может иметь либо два различных действительных корня, либо один повторяющийся корень. Чтобы различать эти три разных случая, у нас есть понятие дискриминанта уравнения.
Дискриминант
Дискриминант квадратного уравнения 𝑎𝑥+𝑏𝑥+𝑐=0 определяется как 𝑏−4𝑎𝑐. Часто Δ используется для обозначения дискриминанта.
Используя дискриминант, мы идентифицируем три различных случая квадратных уравнений следующим образом:
- Положительный дискриминант: 𝑏−4𝑎𝑐>0, два действительных корня;
- Нулевой дискриминант: 𝑏−4𝑎𝑐=0, один повторяющийся действительный корень;
- Отрицательный дискриминант: 𝑏−4𝑎𝑐0, комплексно-сопряженные корни.
На графиках ниже показан каждый случай.
Используя дискриминант, мы можем определить природу корней квадратного уравнения.
Пример 3: Природа корней квадратичных чисел
Определите тип корней уравнения 𝑥+4𝑥+1=3.
Ответ
Начнем с преобразования уравнения в стандартную квадратную форму.
Данный 𝑥+4𝑥+1=3, мы умножаем на 𝑥+1, что дает 𝑥(𝑥+1)+4=3(𝑥+1).
Раскрывая скобки, имеем 𝑥+𝑥+4=3𝑥+3.
Вычитание 3𝑥+3 с обеих сторон дает 𝑥−2𝑥+1=0.
Простым осмотром мы можем разложить это уравнение на (𝑥−1)=0, из которого мы можем видеть, что есть один повторяющийся действительный корень. Не всегда возможно просто факторизовать уравнение, поэтому более общий метод нам нужно вычислить дискриминант 𝑏−4𝑎𝑐. Для этого уравнения имеем 𝑎=1, 𝑏=−2 и 𝑐=1. Следовательно, 𝑏−4𝑎𝑐=(−2)−4×1×1=4−4=0.
Поскольку дискриминант равен нулю, мы знаем, что уравнение имеет один повторяющийся действительный корень.
Обращаясь к кубическим уравнениям, основная теорема алгебры говорит нам, что каждое кубическое уравнение будет иметь три корня. Если у него также есть действительные коэффициенты, мы знаем, что для любых невещественных корней их комплексно-сопряженное тоже является корнем.
Таким образом, мы по существу имеем два возможных случая:
- один действительный корень и комплексно-сопряженная пара невещественных корней,
- три действительных корня.
В случае трех действительных корней возможно наличие повторяющихся корней.Мы могли бы иметь один повторяющийся действительный корень с кратностью три; например, (𝑥−5)=0. В качестве альтернативы мы могли бы иметь два действительных корня, один из которых повторяется с кратностью два; например, (𝑥+4)(𝑥+10)=0.
Один из интересных результатов фундаментальной теоремы алгебры и теоремы о сопряженных корнях состоит в том, что кубика с действительными коэффициентами всегда имеет хотя бы один действительный корень. Фактически эти теоремы показывают, что любой многочлен нечетной степени имеет хотя бы один действительный корень.
Идея дискриминанта может быть распространена на общие многочлены. Однако он быстро становится вычислительно сложны и обычно лучше всего оцениваются с помощью системы компьютерной алгебры.
Следующий пример продемонстрирует, как теорема о сопряженных корнях может помочь нам решить кубические уравнения.
Пример 4. Корни кубических чисел
Учитывая, что 𝑖 является одним из корней уравнения 𝑥−5𝑥+𝑥−5=0, найдите два других корня.
Ответ
Поскольку 𝑖 является корнем 𝑥−5𝑥+𝑥−5=0, мы знаем, что 𝑥−𝑖 является делителем из 𝑥−5𝑥+𝑥−5.Мы могли бы используйте это, чтобы вынести 𝑥−𝑖, а затем решить полученное квадратное уравнение с комплексными коэффициентами. Однако это будет гораздо проще чтобы сначала применить теорему о сопряженных корнях, которая говорит нам, что −𝑖 также будет корнем. Следовательно, (𝑥−𝑖)(𝑥+𝑖)=𝑥+1 является множителем 𝑥−5𝑥+𝑥−5. Следовательно, мы можем написать 𝑥−5𝑥+𝑥−5=𝑥+1(𝑥+𝛼).
Раскрывая скобки, имеем 𝑥−5𝑥+𝑥−5=𝑥+𝛼𝑥+𝑥+𝛼.
Приравнивая коэффициенты, видим, что 𝛼=−5.Следовательно, 𝑥=5 также является корнем уравнения. Следовательно, корни уравнения равны 5, −𝑖 и 𝑖.
Наконец, обратим внимание на уравнения четвертой степени. Напомним, что уравнение четвертой степени – это уравнение вида 𝑎𝑥+𝑏𝑥+𝑐𝑥+𝑑𝑥+𝑒=0,
Еще раз, применяя фундаментальную теорему алгебры, мы знаем, что уравнение четвертой степени будет иметь четыре корня. Точно так же теорема о сопряженных корнях подразумевает, что для квартики с действительными коэффициентами у нас по существу есть три возможных случая:
- все четыре корня вещественные,
- два корня вещественные, а два других образуют невещественный комплекс сопряженная пара,
- все корни недействительны и образованы двумя комплексно-сопряженными парами.
В случае квартик также возможно наличие повторяющихся корней; мы можем иметь повторяющиеся действительные корни или даже повторяющиеся комплексные корни.
Используя теорему о сопряженных корнях, мы можем решать уравнения четвертой степени с действительными коэффициентами, если нам дан единственный недействительный корень, как продемонстрирует последний пример.
Пример 5. Корни квартик
Учитывая, что 2+𝑖√3 является корнем из 𝑥−12𝑥+55𝑥−120𝑥+112=0, найдите все корни.
Ответ
Начнем с применения теоремы о сопряженных корнях для нахождения второго корня уравнения.С 𝑥−12𝑥+55𝑥−120𝑥+112 — многочлен с действительными коэффициентами, а 2 + 𝑖√3 — невещественный корень по теореме о сопряженных корнях, 2−𝑖√3 будет корнем уравнения. Следовательно, 𝑥−2−𝑖√3𝑥−2+𝑖√3=𝑥−4𝑥+7 является множителем 𝑥−12𝑥+55𝑥−120𝑥+112. Следовательно, 𝑥−12𝑥+55𝑥−120𝑥+112=𝑥−4𝑥+7𝑥+𝑏𝑥+𝑐.
Раскрывая скобки правой части, имеем 𝑥-12𝑥 + 55𝑥-120𝑥 + 112 = 𝑥 + 𝑏𝑥 + 𝑐𝑥-4𝑥-4𝑏𝑥-4𝑐𝑥 + 7𝑥 + 7𝑏𝑥 + 7𝑐.
Сбор подобных условий, мы получаем 𝑥−12𝑥+55𝑥−120𝑥+112=𝑥+(𝑏−4)𝑥+(𝑐−4𝑏+7)𝑥+(7𝑏−4𝑐)𝑥+7𝑐.
Мы можем найти 𝑏 и 𝑐, приравняв коэффициенты. От постоянного члена, у нас есть 7𝑐=112, что дает 𝑐=16. Из коэффициента 𝑥, у нас есть 𝑏−4=−12, что дает 𝑏=−8.
Используя эти значения 𝑏 и 𝑐, мы можем проверить равенство других наших коэффициентов. Это будет гарантировать, что мы сделали наши расчеты правильно. Замена 𝑏 и 𝑐 обратно в наше уравнение, мы имеем 0=𝑥−12𝑥+55𝑥−120𝑥+112=𝑥−4𝑥+7𝑥−8𝑥+16.
Проверив, мы видим, что 𝑥−8𝑥+16=(𝑥−4 ).Следовательно, 𝑥=4 является повторяющимся корнем. Следовательно, корни уравнения равны 𝑥=4, 2+𝑖√3 и 2−𝑖√3.
Ключевые моменты
- Основная теорема алгебры говорит нам, что многочлен степени 𝑛 будет иметь, если считать с кратностью, 𝑛 корни.
- Теорема о сопряженных корнях говорит нам, что невещественные корни многочленов с действительными коэффициентами встречаются в комплексно-сопряженных парах.
- В результате этих двух теорем мы можем классифицировать природу корней многочленов.
- Мы можем использовать сопряженный корень, чтобы решить уравнения кубической и четвертой степени с действительными коэффициентами.
- Все многочлены нечетной степени с действительными коэффициентами имеют хотя бы один действительный корень.
Многочлены с комплексными корнями
То Основная теорема алгебры уверяет нас, что любой многочлен с участием настоящий номер коэффициенты можно полностью разложить по полю комплексные числа .
В случае квадратичные многочлены , корни комплексные, когда дискриминант отрицательный.
Пример 1:
Фактор полностью, используя комплексные числа.
Икс 3 + 10 Икс 2 + 169 Икс
Во-первых, Икс .
Икс 3 + 10 Икс 2 + 169 Икс знак равно Икс ( Икс 2 + 10 Икс + 169 )
Теперь используйте квадратичная формула для выражения в скобках, чтобы найти значения Икс для которого Икс 2 + 10 Икс + 169 знак равно 0 .
Здесь а знак равно 1 , б знак равно 10 и с знак равно 169 .
Икс знак равно − б ± б 2 − 4 а с 2 а
Икс знак равно − 10 ± 10 2 − 4 ( 1 ) ( 169 ) 2 ( 1 ) знак равно − 10 ± 100 − 676 2 знак равно − 10 ± − 576 2
Запишите квадратный корень, используя мнимые числа.
Икс знак равно − 10 ± 24 я 2 знак равно − 5 ± 12 я
Теперь мы знаем, что значения Икс для которого выражение
Икс 2 + 10 Икс + 169
равно 0 являются Икс знак равно − 5 + 12 я и Икс знак равно − 5 − 12 я .
Таким образом, исходный многочлен можно представить как
Икс 3 + 10 Икс 2 + 169 Икс знак равно Икс ( Икс − [ − 5 + 12 я ] ) ( Икс − [ − 5 − 12 я ] )
Вы можете убедиться в этом, используя ФОЛЬГА .
Иногда вы можете разложить многочлен на множители, используя комплексные числа, не используя квадратную формулу. Например, разница квадратов правило:
Икс 2 − а 2 знак равно ( Икс + а ) ( Икс − а )
Это также может быть использовано с комплексными числами, когда а 2 отрицательно, следующим образом:
Икс 2 + 25 знак равно ( Икс + 5 я ) ( Икс − 5 я )
Пример 2:
Фактор полностью, используя комплексные числа.
9 Икс 2 у + 64 у
Во-первых, исключить у .
9 Икс 2 у + 64 у знак равно у ( 9 Икс 2 + 64 )
Теперь используйте разность правила квадратов, чтобы разложить 9 Икс 2 + 64 .
9 Икс 2 + 64 знак равно 9 Икс 2 − ( − 64 ) знак равно ( 3 Икс ) 2 − ( 8 я ) 2 знак равно ( 3 Икс + 8 я ) ( 3 Икс − 8 я )
Следовательно, 9 Икс 2 у + 64 у знак равно у ( 3 Икс + 8 я ) ( 3 Икс − 8 я ) .
Построение полиномов высокой степени с поиском корней
В предыдущем посте рассматривалось нахождение ожидаемого числа действительных нулей многочленов высокой степени. Если вы хотите узнать, сколько действительных корней имеет конкретный многочлен высокой степени, вы столкнетесь с рядом трудностей.
Если вы используете что-то вроде правила знаков Декарта, вы, вероятно, сильно переоцените количество корней. Было бы проще построить функцию и найти корни.Но это порождает еще пару проблем.
Во-первых, какой диапазон вы должны построить? Как бы далеко вы ни рисовали, откуда вы знаете, что за пределами вашего графика нет другого нуля?
Во-вторых, полином высокой степени может изменяться на много порядков, что делает невозможным рассмотрение графика в одном масштабе.
Первую трудность можно преодолеть с помощью теоремы Лагранжа [1], утверждающей, что все нули многочлена n -й степени содержатся в круге радиуса
с центром в начале сложной плоскости.
Здесь a i есть коэффициент x i .
Вторую трудность можно преодолеть, построив преобразование полинома, а не сам полином. Функция гиперболического тангенса работает хорошо, потому что она отображает 0 в 0 и потому что она сжимает реальную прямую в интервал (-1, 1). Это даст искаженную картину многочлена, но сохранит нули.
Мы проиллюстрируем все это на примере кода Python.
Мы можем вычислить наш полином из массива коэффициентов, используя метод Хорнера.
по определению поли(коэффициент, х): р = 0,0 для c в обратном (коэфф): р *= х р += с вернуть рДалее мы генерируем коэффициенты случайного многочлена 100-й степени.
импортировать scipy как sp из нормы импорта scipy.stats sp.random.seed(20201228) # сегодняшняя дата степень = 100 коэфф = норма.rvs (размер = степень + 1)Теперь найдем оценки Лагранжа на корнях.
m = max(1, sum(abs(coeff[:-2]/coeff[-1])))Теперь мы можем построить тангенс нашего многочлена
импортировать numpy как np импортировать matplotlib.pyplot как plt х = np.linspace (-м, м, 1000) у = поли (коэффициент, х) z = np.tanh(y) plt.plot(x, z)Это создает график, который в основном представляет собой просто всплеск. Оценка Лагранжа в этом случае очень широкая, но, по крайней мере, мы знаем, что для начала просмотрели достаточно широко.если мы увеличим масштаб шипа, мы получим следующее.
Если бы мы не взяли танх, наш график изменился бы более чем на 80 порядков.
Мы можем немного увеличить масштаб, чтобы лучше видеть нули.
[1] Другая граница нулей по Коши равна
.В этом примере оценка Коши более точная. Вы всегда можете вычислить обе границы и взять меньшую границу.
Положение корней полиномиального уравнения
Положение корней полиномиального уравненияНекоторые результаты о корнях уравнения: Ниже приведены результаты о корнях полиномиального уравнения с рациональными коэффициентами:
- Уравнение степени n имеет n корней, действительных или мнимых.
- Мнимые корни всегда встречаются парами, т. е. если 2 – 3i является корнем уравнения, то 2 + 3i также является его корнем. Точно так же, если 2 + √3 является корнем данного уравнения, то 2 – √3 также является его корнем.
- Уравнение нечетной степени имеет по крайней мере один действительный корень, знак которого противоположен этому коэффициенту знаку последнего члена, при условии, что коэффициент старшего члена положителен.
- Каждое уравнение четной степени, постоянный член которого отрицателен, а коэффициент при старшей степени положителен, имеет по крайней мере два действительных корня, один положительный и один отрицательный.
Положение корней полиномиального уравнения: Если f(x) = 0 — уравнение, а a, b — два действительных числа, такие что f(a) f(b) < 0, то f(x) = 0 имеет хотя бы один действительный корень или нечетное число действительных корней между a и b. если f(a) и f(b) одного знака, то между a и b либо нет действительных корней, либо четное число, либо действительные корни f(x) = 0.
Вычеты:
- Каждое уравнение нечетной степени имеет хотя бы один действительный корень, знак которого противоположен знаку его последнего члена, если коэффициент при первом члене положителен.
- Каждое уравнение четной степени, последний член которого отрицателен, а коэффициент перед первым членом положителен, имеет по крайней мере два действительных корня, один положительный и один отрицательный.
- Если уравнение имеет только одну смену знака, оно имеет один положительный корень и не более.
- Если все члены уравнения положительны и уравнение не содержит нечетных степеней x, то все его корни комплексные.
Пример: Если a, b, c, d ϵ R такие, что a < b < c < d, то покажите, что корни уравнения (x -a) (x - c) + 2(x - b ) (x – d) = 0 вещественны и различны.
Решение: Пусть f(x) = (x – a) (x – c) + 2(x – b) (x – d)
Затем
f (a) = 2(a – b) (a – d) > 0 [∵ a – b < 0 и a – d < 0]
f (b) = (b – a) (b – c) < 0 [∵ b – a > 0 и b – c < 0]
f (d) = (d – a) (d – c) > 0 [∵ d – a > 0 и d – c > 0]
Итак, корень f(x) = 0 лежит между a и b, вещественны и различны.
Использование корней для построения грубых графиков полиномов
Мы идем прямо на Полиномиальную гору с нашими проводниками, полиномами.Что эти сумасшедшие маленькие парни делают сейчас? Похоже, они рисуют волнистые линии на песке.Подождите. Они пишут свои имена или рисуют себя? Вот и все. Если мы внимательно присмотримся, то увидим, что они использовали свои корни, чтобы рисовать автопортреты на песке. Мы даже можем видеть закономерности в зависимости от их степени.
Можем ли мы использовать то, что открыли на планете многочленов, чтобы сделать собственные наброски наших полиномиальных друзей?
Да. Мы думаем, что готовы построить несколько грубых набросков этих парней.Из нашего предыдущего визита на эту планету мы уже знаем, как строить графики полиномов первой и второй степени (также известных как линейные и квадратичные функции). Теперь мы рассмотрим, как использовать их корни для построения грубых графиков многочленов более высокого порядка.
Мы можем использовать теорему об остатках, чтобы проверить наличие корней, а затем использовать синтетическое деление и разложение на множители, чтобы найти остальные.
Давайте спросим наших инопланетных друзей о некоторых маленьких хитростях и подсказках, которые облегчат задачу.
Во-первых, корней , также называемых нулями , наших многочленов являются точками пересечения оси x .
Во-вторых, мы можем иметь общее представление о том, как будет выглядеть наш график, исходя из степени многочлена.
Два конца полиномиального графа четной степени либо «вверх» на обоих концах, либо «вниз» на обоих концах. Вот так:
Граф полиномов нечетной степени с одним концом «вверх» и одним концом «вниз».
Все это мы называем конечным поведением полинома . Полиномы не видят никакой разницы между внешним и внутренним поведением, что объясняет, почему иногда с ними бывает так трудно ладить.
Последний намек на форму нашего графика — это степень многочлена. У этой подсказки есть официальное название — Теорема о поворотном моменте, но нам не о чем беспокоиться.
Основная идея состоит в том, что граф всегда имеет меньше поворотных точек, чем степень его многочлена.
График полинома второй степени имеет не более 1 витка, а полинома третьей степени — не более 2 витков. Точка поворота — это место, где полином меняет направление (движется вверх или вниз).
Лучший способ увидеть, как все это происходит, — начать строить график.
Пример задачи
График y = x 3 – 7 x + 6.
Сначала мы найдем возможные корни, рассмотрев множители константы 6. Они равны ±6, ±3, ±2 и ±1. Нет ничего проще, чем вставить 1, так что мы сделаем это в первую очередь.
P (1) = (1) 3 – 7(1) + 6
= 1 – 7 + 6
= 0
Эффективность это или лень, с результатами спорить не будем: мы знаем, что х – 1 должно быть делителем нашего многочлена, и один из его корней равен х = 1.
Теперь мы используем эту 1 в нашем синтетическом делении, чтобы найти все множители многочлена.
Второй множитель равен х 2 + х – 6. Разложение снова дает нам ( х + 3)( х – 2). Смешайте все наши факторы вместе, чтобы найти корни.
P ( x ) = ( x – 1)( x + 3)( x – 2)
Приравнивание каждой части к нулю дает нам корни из x x -3 и 2.Это означает, что все точки (1, 0), (-3, 0) и (2, 0) отображаются на нашем графике.
Обратите внимание, что график должен касаться оси x в этих трех точках и, возможно, пересекаться. Не в смысле «теперь мы мертвы», а в смысле «теперь наш знак противоположный».
Наш многочлен имеет степень 3 (из-за x 3 ), и это нечетно. Нет ничего необычного; просто странно. Его конечное поведение будет иметь один конец, указывающий вверх, и один конец, указывающий вниз.
Нам понадобится хотя бы еще одна точка в каждой части графика, чтобы получить общую форму.Что такое разделы? По одному с каждой стороны каждого корня.
Мы просто выберем несколько значений x , каждое из разных частей графика.
P (-5) = (-5) 3 – 7(-5) + 6 = -84 → (-5, -84)
P (0) = (0) 3 – 7(0) + 6 = 6 → (0, 6)
P (1,5) = (1,5) 3 – 7(1,5) + 6 = -1,125 → (1,5, -1,125)
P (5) = (5) 3 – 7(5) + 6 = 96 → (5, 96)
Теперь у нас достаточно точек, чтобы построить грубый график нашего многочлена, нанеся эти дополнительные четыре точки и соединив их плавной кривой.Мы можем позволить себе быть немного распущенными с нашим рисунком. Мы просто хотим получить общее поведение полинома.
Теперь мы можем видеть, что графики поворачиваются дважды, между x = -3 и 1 и между x = 1 и 2. Этот красивый график поворачивает точки и головы.
Проблема образца
графика F ( x ) = x 3 + x 2 — 22 x 9003 — 40.
Первое правило графических полиномов — это, «Дон» Не будем говорить о построении графиков полиномов.» Упс, это мы уже нарушили. Второе правило: «Найди возможные корни, глядя на множители константы». Следовать одному из двух правил не так уж и плохо, верно?
Множители 40 равны ± 40, ± 20, ± 10, ± 8, ± 5, ± 4, ± 2 и ± 1. Это много факторов. Копайте. ) 2 – 22(1) – 40
= 1 + 1 – 62
= -60
Нет, это не фактор.Попробуем 2.
f (2) = (2) 3 + (2) 2 – 22(2) – 40
= 8 + 4 – 44 – 40
= -72 9000 Замах и промах. Может -2?
f (-2) = (-2) 3 + (-2) 2 – 22(-2) – 40
= -8 + 4 + 44 – 40
= 0
3 Дин, дин, дин, у нас есть победитель. Наш первый корень равен x = -2, поэтому наш первый делитель равен x + 2.
Мы прогоняем это -2 через раунд синтетического деления, чтобы найти другие наши корни.
Наш многочлен:
F ( x ) = ( x + 2) ( x 2 — x — 20)
Это факторы до:
f ( x ) = ( x + 2)( x + 4)( x – 5)
Наши корни, дамы и господа: x = -2, -4 и 5 Поаплодируйте им, когда они займут свои места на графике.
Однако нам нужно больше очков.Мы выберем еще несколько значений x , чтобы попробовать, по одному из каждого раздела. Подойдут и другие номера, но мы хотим, чтобы они были небольшими и управляемыми.
f (-5) = (-5) 3 + (-5) 2 – 22(-5) – 40 = -30 → (-5, -30)
f ( -3) = (-3) 3 + (-3) 2 – 22(-3) – 40 = 8 → (-3, 8)
f (0) = (0) 3 + (0) 2 – 22(0) – 40 = -40 → (0, -40)
f (6) = (6) 3 + (6) 2 – 22( 6) – 40 = 80 → (6, 80)
Теперь у нас достаточно точек, чтобы получить грубый график нашего многочлена.
Однако нам понадобится еще больше очков, если мы хотим попасть в списки лидеров.
Степень многочлена нечетная, поэтому два его конца будут направлены в противоположные стороны.
Вот это отмеченный наградами график. За какую награду, мы не уверены. Может быть, награда за самый последний график.
Это не громкое одобрение, не так ли? Давайте попробуем другой.
Пример задачи
График y = x 5 .
Мм, кажется, мы уже нашли ноль. Это ноль.
P (0) = (0) 5 = 0
Степень 5 нечетна, поэтому мы знаем, что у конечного поведения один конец «вверх», а другой «вниз». Все, что посередине, как-то туманно.
У нас нет подходящих участков для выбора точек, поэтому мы составим таблицу и посчитаем несколько значений, чтобы получить упорядоченные пары.
Трех чисел в каждом направлении должно быть достаточно, чтобы иметь приблизительное представление о том, как выглядит график, а приблизительное представление — это все, что нам нужно.
Хорошо, это был наш третий странный график подряд. Нам нужно что-то поменять, а потом мы взорвем эту стойку с эскимо.
Пример задачи
График f ( x ) = x 4 – 9 x 2 .
Несмотря на то, что мы использовали теорему об остатках для нахождения множителей и корней, мы можем забыть, что иногда проще просто разложить полином на множители напрямую.
x 4 — 9 x 2 = 0
x 2 ( x 2 — 9) = 0
Наши корни здесь x = 0 х = ± 3.Видеть? Простой. Не работайте на математику, если можете этого избежать. Заставьте математику работать на вас.
Полиномы четной степени имеют поведение концов, когда оба конца указывают вверх или оба конца вниз. Его степень равна 4, поэтому может иметь не более 3 витков. Кроме того, это последняя задача раздела, и мы устали, так что это не может быть слишком сложно.

 С какого перепугу это бывает нужно — вопрос отдельный. Мы разберём лишь алгоритм.
С какого перепугу это бывает нужно — вопрос отдельный. Мы разберём лишь алгоритм. \\ \end{align}\]
\\ \end{align}\] {2}}}=\sqrt{5}. \\ \end{align}\]
{2}}}=\sqrt{5}. \\ \end{align}\] 2 = x, ?x = a. Как и над всякими числами, над квадратными корнями дозволено исполнять арифметические операции сложения и вычитания.
2 = x, ?x = a. Как и над всякими числами, над квадратными корнями дозволено исполнять арифметические операции сложения и вычитания.

 Главный вывод того урока: существует лишь одно универсальное определение корней, которое вам и нужно знать. Остальное — брехня и пустая трата времени.
Главный вывод того урока: существует лишь одно универсальное определение корней, которое вам и нужно знать. Остальное — брехня и пустая трата времени.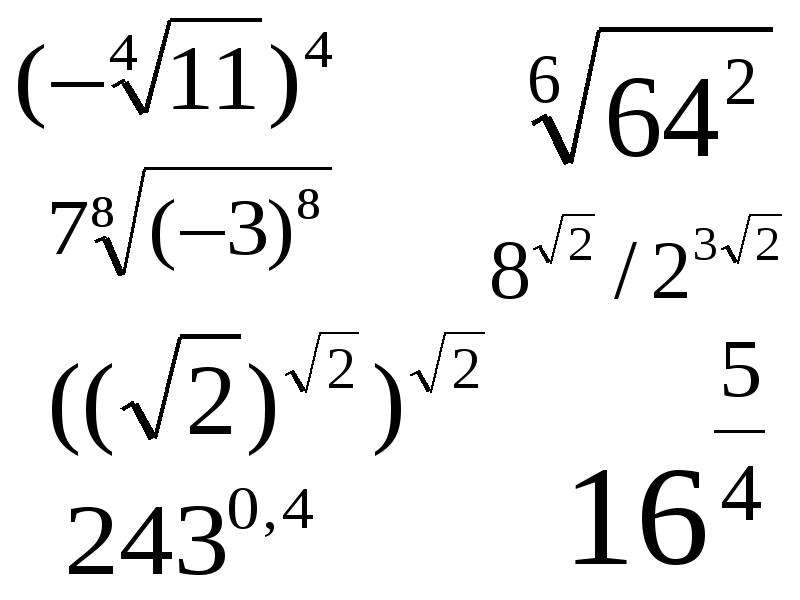 С остальными начнём по порядку.
С остальными начнём по порядку. \\ \end{align}\]
\\ \end{align}\]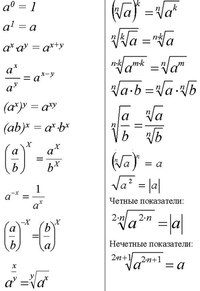
 {2n}}}=\left| a \right|. \\ \end{align}\]
{2n}}}=\left| a \right|. \\ \end{align}\] {2}}}=\sqrt[3]{5}. \\ \end{align}\]
{2}}}=\sqrt[3]{5}. \\ \end{align}\] {2}}}=\sqrt[4]{75}. \end{align}\]
{2}}}=\sqrt[4]{75}. \end{align}\] Десятичные и натуральные логарифмы. Степени, корни. / / Правила действий со степенями и корнями, примеры.
Десятичные и натуральные логарифмы. Степени, корни. / / Правила действий со степенями и корнями, примеры. Примеры значений логарифмических и показательных функций.
Примеры значений логарифмических и показательных функций.
 Как извлечь корень третьей степени на калькуляторе ?
1.
Для того, чтобы начать считать корень н-ой степени, набираем число, из которого этот корень нам нужно извлечь! Пусть это будет число 125.
2.
Для набора степени нам потребуется отдельная кнопка – без неё никак, программа же должна понимать, что вы даете её! Нажимаем кнопку «P»
3.
Набираем степень, если корень третьей степени, то набираем 1/3.
4.
Нажимаем равно… Друзья! Для вас ликбез:
Корень н-ой степени = число в дробной степени.
Например: корень третьей степени числа = число в дробной степени
√x = x1/2 ³√x = x1/3 А степени мы уже проходили…
Как извлечь корень третьей степени на калькуляторе ?
1.
Для того, чтобы начать считать корень н-ой степени, набираем число, из которого этот корень нам нужно извлечь! Пусть это будет число 125.
2.
Для набора степени нам потребуется отдельная кнопка – без неё никак, программа же должна понимать, что вы даете её! Нажимаем кнопку «P»
3.
Набираем степень, если корень третьей степени, то набираем 1/3.
4.
Нажимаем равно… Друзья! Для вас ликбез:
Корень н-ой степени = число в дробной степени.
Например: корень третьей степени числа = число в дробной степени
√x = x1/2 ³√x = x1/3 А степени мы уже проходили…

 Чтобы понять суть этих двух терминов, нужно разобраться в истории их возникновения, терминологии и главном смысле.
Чтобы понять суть этих двух терминов, нужно разобраться в истории их возникновения, терминологии и главном смысле. Лишь 1626 году он обрел близкое к сегодняшнему обозначение в виде буквы V. Это произошло благодаря ученому из Нидерланд А. Жирар. Палочку над подкоренным выражением писали отдельно от буквы несколько десятилетий. И лишь спустя некоторое время Рене Декарт преобразовал символ, соединив букву с чертой. И только к концу семнадцатого века запись выражения с корнем приобрела вид, который сохранился на сегодняшний день.
Лишь 1626 году он обрел близкое к сегодняшнему обозначение в виде буквы V. Это произошло благодаря ученому из Нидерланд А. Жирар. Палочку над подкоренным выражением писали отдельно от буквы несколько десятилетий. И лишь спустя некоторое время Рене Декарт преобразовал символ, соединив букву с чертой. И только к концу семнадцатого века запись выражения с корнем приобрела вид, который сохранился на сегодняшний день. Некоторые из показателей степеней имеют свои собственные названия. Для остальных цифровых значений используются обычные названия.
Некоторые из показателей степеней имеют свои собственные названия. Для остальных цифровых значений используются обычные названия.
 Аннотация
Аннотация
 Например, 8 как 41,5.
Показатели, введённые Оремом, по существу выступают в виде логарифмов чисел.
Орем словесно сформулировал правила для выполнения различных операций со
степенями.
Например, 8 как 41,5.
Показатели, введённые Оремом, по существу выступают в виде логарифмов чисел.
Орем словесно сформулировал правила для выполнения различных операций со
степенями.







 Наверное, пора тянуться к справочникам, наизусть заучивать определения и десяток-другой не самых симпатичных формул? Не стоит отчаиваться, давайте разрешим эту задачу так же, как и все другие — последовательно, мудро и с неизменным юмором.
Наверное, пора тянуться к справочникам, наизусть заучивать определения и десяток-другой не самых симпатичных формул? Не стоит отчаиваться, давайте разрешим эту задачу так же, как и все другие — последовательно, мудро и с неизменным юмором. Число в центре здесь указывает на общую площадь фигуры, а числа около сторон — на их длины:
Число в центре здесь указывает на общую площадь фигуры, а числа около сторон — на их длины: А в третьей степени, это значит, что кубик с похожими сторонами можно найти везде, хоть бы и в магазине игрушек. А вот со всем, что больше, ну или меньше, такого ясного-понятного не представить и с реальными предметами не проделать. Печаль-тоска-огорчение…
А в третьей степени, это значит, что кубик с похожими сторонами можно найти везде, хоть бы и в магазине игрушек. А вот со всем, что больше, ну или меньше, такого ясного-понятного не представить и с реальными предметами не проделать. Печаль-тоска-огорчение… Со свойственным нашему изложению изяществу мы показали, что , но что делать, если наша степень такова, что у неё в числителе стоит не единица? Например, как понимать запись вида ? Для ответа на этот вопрос следует прибегнуть к уже знакомой нам логике — будем отталкиваться от единицы.
Со свойственным нашему изложению изяществу мы показали, что , но что делать, если наша степень такова, что у неё в числителе стоит не единица? Например, как понимать запись вида ? Для ответа на этот вопрос следует прибегнуть к уже знакомой нам логике — будем отталкиваться от единицы. к. . Итак, считаем:
к. . Итак, считаем: А сколько будет, если пять единиц сложить друг с другом? То-то же!
А сколько будет, если пять единиц сложить друг с другом? То-то же! Тем не менее, результат примечателен — в силу специфики указанной операции нет разницы, имеем мы дело со степенью выражения с корнем в своём составе, или со степенью подкоренного выражения как такового. А знаете, как это легко запомнить? Вообще не приплетая корни, ведь без этих обозначений никакой неразберихи нет вообще, так как мы точно знаем какие переменные в каких отношениях друг с другом находятся, ну и где у них там все степени стоят.
Тем не менее, результат примечателен — в силу специфики указанной операции нет разницы, имеем мы дело со степенью выражения с корнем в своём составе, или со степенью подкоренного выражения как такового. А знаете, как это легко запомнить? Вообще не приплетая корни, ведь без этих обозначений никакой неразберихи нет вообще, так как мы точно знаем какие переменные в каких отношениях друг с другом находятся, ну и где у них там все степени стоят. Уяснив на конкретной иллюстрации в чём смысл той или иной операции, мы можем бесконечно её усложнять, в том числе и до таких случаев, когда обычное, ничем не расширенное человеческое мышление представить каких-то визуальных воплощений оказывается не в силах. Собственно, если бы не эта особенность, то весь изучаемый материал ограничивался бы… ну… примерно тем, чем он и ограничивается в школе и вузах…
Уяснив на конкретной иллюстрации в чём смысл той или иной операции, мы можем бесконечно её усложнять, в том числе и до таких случаев, когда обычное, ничем не расширенное человеческое мышление представить каких-то визуальных воплощений оказывается не в силах. Собственно, если бы не эта особенность, то весь изучаемый материал ограничивался бы… ну… примерно тем, чем он и ограничивается в школе и вузах… Короче говоря, именно к важным, обязательным для успешного понимания всего, что только можно, свойствам.
Короче говоря, именно к важным, обязательным для успешного понимания всего, что только можно, свойствам. Для большей очевидности поясним всё это на примере. Вот у нас есть и от нас требуется «вынести множитель из под знака корня», как нам поступить?
Для большей очевидности поясним всё это на примере. Вот у нас есть и от нас требуется «вынести множитель из под знака корня», как нам поступить? Типа, стоит такая запись , и что с ней делать? Эх, сложно это всё, придётся ручку доставать, заучивать, повторять. Хотя нет, нам ничего этого делать никогда не придётся. Почему? Ответ такой же, как и в случае последних вопросов — мы знаем про операции со степенями. Не станем скрывать свои знания:
Типа, стоит такая запись , и что с ней делать? Эх, сложно это всё, придётся ручку доставать, заучивать, повторять. Хотя нет, нам ничего этого делать никогда не придётся. Почему? Ответ такой же, как и в случае последних вопросов — мы знаем про операции со степенями. Не станем скрывать свои знания: Не знай вы этого обстоятельства, то перед очередным зачётом могли бы не одну ночь развлекали себя мыслью «разве это всё кто-нибудь может запомнить?».
Не знай вы этого обстоятельства, то перед очередным зачётом могли бы не одну ночь развлекали себя мыслью «разве это всё кто-нибудь может запомнить?».




 Будем решать с помощью Wolfram|Alpha:
Будем решать с помощью Wolfram|Alpha: ) Вот почему я считаю, что теоремы об остатках и множителях следует рассматривать как исторический подход, потому что вы можете использовать их только в том случае, если хотя бы некоторые из решений являются целыми числами. или простые дроби.
) Вот почему я считаю, что теоремы об остатках и множителях следует рассматривать как исторический подход, потому что вы можете использовать их только в том случае, если хотя бы некоторые из решений являются целыми числами. или простые дроби.
 5`. (Увеличение масштаба вблизи этих корней на графике подтверждает эти значения.)
5`. (Увеличение масштаба вблизи этих корней на графике подтверждает эти значения.)
 Начнем сразу с двух факторов. Мы используем коробку, чтобы помочь организовать умножение:
Начнем сразу с двух факторов. Мы используем коробку, чтобы помочь организовать умножение: Ответ является результатом этого умножения.Обратите внимание, что поскольку мы начали с трех корней, наш ответ имеет степень (наибольшую степень) 3.
Ответ является результатом этого умножения.Обратите внимание, что поскольку мы начали с трех корней, наш ответ имеет степень (наибольшую степень) 3.

 степень является наивысшим показателем полинома. степень говорит нам, сколько корней находится в полиномиальном уравнении. корней полиномиального уравнения являются значениями x , где y = 0.
степень является наивысшим показателем полинома. степень говорит нам, сколько корней находится в полиномиальном уравнении. корней полиномиального уравнения являются значениями x , где y = 0.
 В данном случае нам дано
многочлен в факторизованной форме. Чтобы найти степень, мы могли бы раскрыть круглые скобки, чтобы найти термин с наивысшей степенью. В качестве альтернативы, мы могли бы сэкономить себе часть работы, просто ища термины наивысшей степени в каждой паре круглых скобок;
тогда степень многочлена будет степенью их произведения.В первом наборе скобок термин высшей степени равен
3𝑥 степени два. Во втором наборе скобок термин высшей степени равен
𝑥, которая имеет степень три. Следовательно, произведение этих двух членов будет иметь степень 5.
что и будет степенью многочлена. Следовательно, многочлен имеет 5 корней.
В данном случае нам дано
многочлен в факторизованной форме. Чтобы найти степень, мы могли бы раскрыть круглые скобки, чтобы найти термин с наивысшей степенью. В качестве альтернативы, мы могли бы сэкономить себе часть работы, просто ища термины наивысшей степени в каждой паре круглых скобок;
тогда степень многочлена будет степенью их произведения.В первом наборе скобок термин высшей степени равен
3𝑥 степени два. Во втором наборе скобок термин высшей степени равен
𝑥, которая имеет степень три. Следовательно, произведение этих двух членов будет иметь степень 5.
что и будет степенью многочлена. Следовательно, многочлен имеет 5 корней. Пусть 𝑝 — многочлен:
𝑝(𝑥)=𝑎+𝑎𝑥+𝑎𝑥+⋯+𝑎𝑥,
где 𝑎,𝑎,…,𝑎 — действительные числа. Кроме того, пусть 𝑧=𝑎+𝑏𝑖 будет корнем 𝑝;
то есть 𝑝(𝑧)=0. Рассмотрим значение 𝑝(𝑧)∗:
𝑝(𝑧)=𝑎+𝑎𝑧+𝑎(𝑧)+⋯+𝑎(𝑧).∗∗∗∗
Пусть 𝑝 — многочлен:
𝑝(𝑥)=𝑎+𝑎𝑥+𝑎𝑥+⋯+𝑎𝑥,
где 𝑎,𝑎,…,𝑎 — действительные числа. Кроме того, пусть 𝑧=𝑎+𝑏𝑖 будет корнем 𝑝;
то есть 𝑝(𝑧)=0. Рассмотрим значение 𝑝(𝑧)∗:
𝑝(𝑧)=𝑎+𝑎𝑧+𝑎(𝑧)+⋯+𝑎(𝑧).∗∗∗∗ Следовательно, если многочлен 𝑝
имел ровно 3 невещественных корня, 𝛼, 𝛽 и 𝛾, то для альфы мы знаем, что 𝛼∗
тоже невещественный корень. Следовательно, 𝛼∗ равно либо 𝛽, либо 𝛾.Без ограничения общности положим 𝛼=𝛽∗. Теперь мы также знаем, что, поскольку 𝛾
— невещественный корень, 𝛾∗ также будет невещественным корнем. Следовательно, он будет равен одному из 𝛼 или 𝛽. Если 𝛾=𝛼∗, то, взяв комплексные сопряжения, мы имеем
Следовательно, если многочлен 𝑝
имел ровно 3 невещественных корня, 𝛼, 𝛽 и 𝛾, то для альфы мы знаем, что 𝛼∗
тоже невещественный корень. Следовательно, 𝛼∗ равно либо 𝛽, либо 𝛾.Без ограничения общности положим 𝛼=𝛽∗. Теперь мы также знаем, что, поскольку 𝛾
— невещественный корень, 𝛾∗ также будет невещественным корнем. Следовательно, он будет равен одному из 𝛼 или 𝛽. Если 𝛾=𝛼∗, то, взяв комплексные сопряжения, мы имеем Если оно имеет действительные корни, оно может иметь либо два различных действительных корня, либо один повторяющийся корень. Чтобы различать эти три разных случая,
у нас есть понятие дискриминанта уравнения.
Если оно имеет действительные корни, оно может иметь либо два различных действительных корня, либо один повторяющийся корень. Чтобы различать эти три разных случая,
у нас есть понятие дискриминанта уравнения. Данный
𝑥+4𝑥+1=3,
мы умножаем на 𝑥+1, что дает
𝑥(𝑥+1)+4=3(𝑥+1).
Данный
𝑥+4𝑥+1=3,
мы умножаем на 𝑥+1, что дает
𝑥(𝑥+1)+4=3(𝑥+1). Таким образом, мы по существу имеем два возможных случая:
Таким образом, мы по существу имеем два возможных случая:


 Используя эти значения 𝑏 и 𝑐,
мы можем проверить равенство других наших коэффициентов. Это будет гарантировать, что мы сделали наши расчеты правильно. Замена 𝑏 и 𝑐
обратно в наше уравнение, мы имеем
0=𝑥−12𝑥+55𝑥−120𝑥+112=𝑥−4𝑥+7𝑥−8𝑥+16.
Используя эти значения 𝑏 и 𝑐,
мы можем проверить равенство других наших коэффициентов. Это будет гарантировать, что мы сделали наши расчеты правильно. Замена 𝑏 и 𝑐
обратно в наше уравнение, мы имеем
0=𝑥−12𝑥+55𝑥−120𝑥+112=𝑥−4𝑥+7𝑥−8𝑥+16.




 Здесь a i есть коэффициент x i .
Здесь a i есть коэффициент x i .



 Мы можем использовать теорему об остатках, чтобы проверить наличие корней, а затем использовать синтетическое деление и разложение на множители, чтобы найти остальные.
Мы можем использовать теорему об остатках, чтобы проверить наличие корней, а затем использовать синтетическое деление и разложение на множители, чтобы найти остальные.
 Теперь мы используем эту 1 в нашем синтетическом делении, чтобы найти все множители многочлена.
Теперь мы используем эту 1 в нашем синтетическом делении, чтобы найти все множители многочлена.


 Однако нам понадобится еще больше очков, если мы хотим попасть в списки лидеров.
Однако нам понадобится еще больше очков, если мы хотим попасть в списки лидеров.
