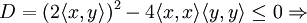6.3. Евклидовы пространства. Неравенство Коши-Буняковского.
Вещественное линейное пространство
называется евклидовым, если в нем
определена операция скалярного
произведения, по которому любым двум
векторам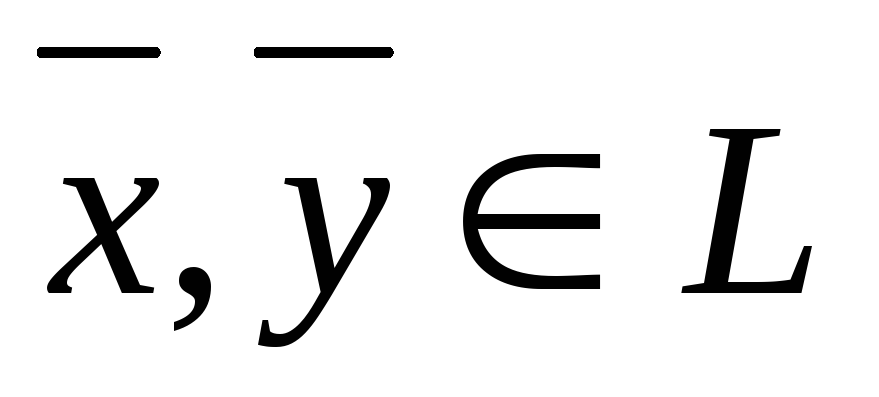 ставится в соответствие действительное
число, обозначаемое (
ставится в соответствие действительное
число, обозначаемое ( ),
и эта операция подчиняется следующим
аксиомам:
),
и эта операция подчиняется следующим
аксиомам:
1) ( )=(
)=( ),
),
2) 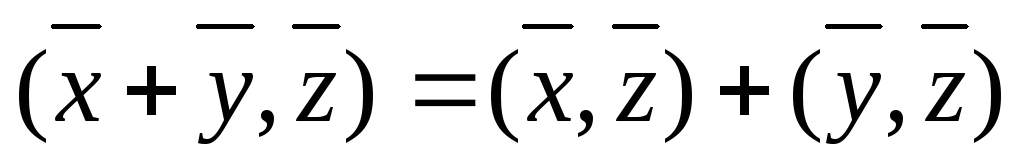 ,
,
3) 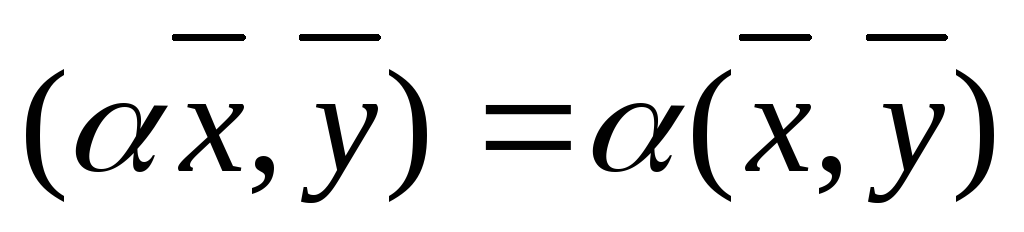
4) 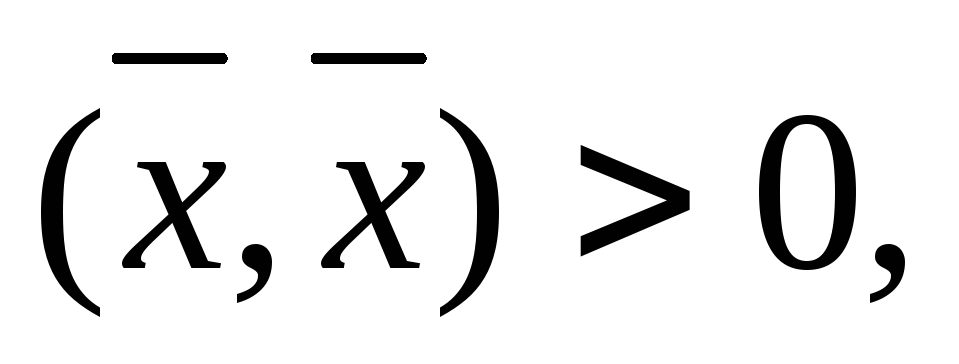 если
если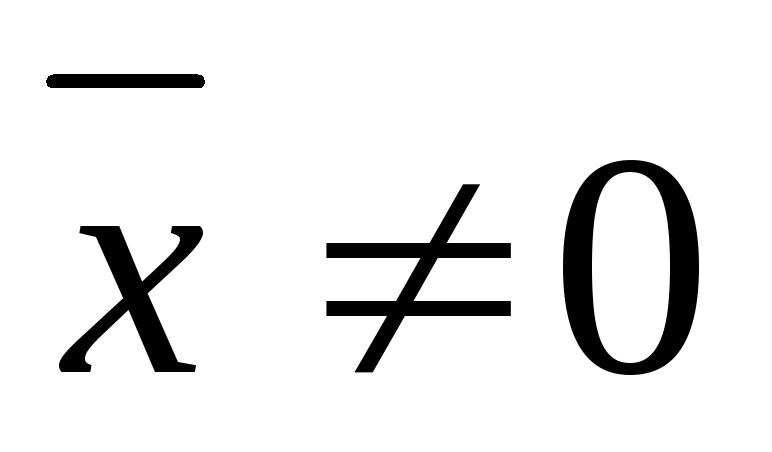 и
и ,
если
,
если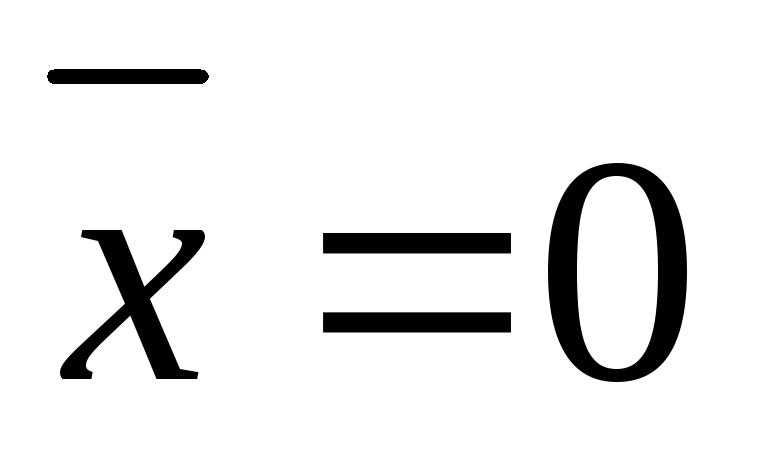 .
.
Длиной вектора 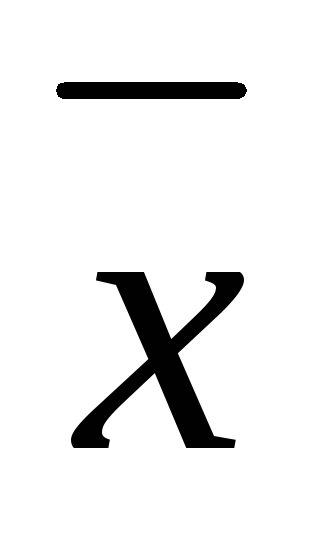 называется число |
называется число |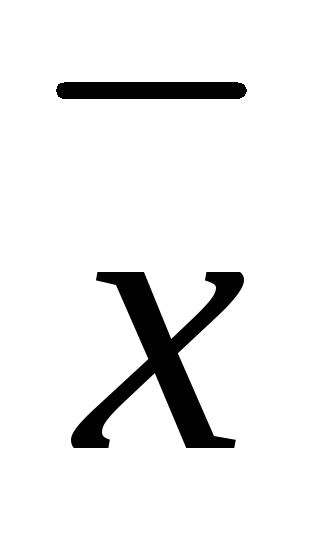 |=
|= (модуль вектора
(модуль вектора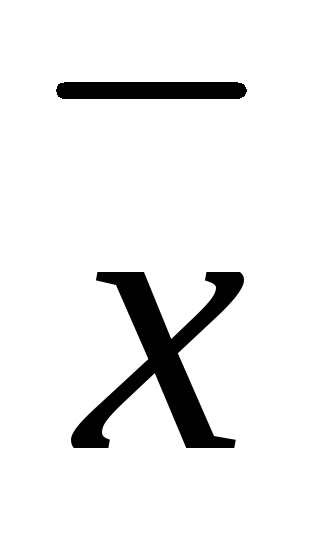 ).
|
).
|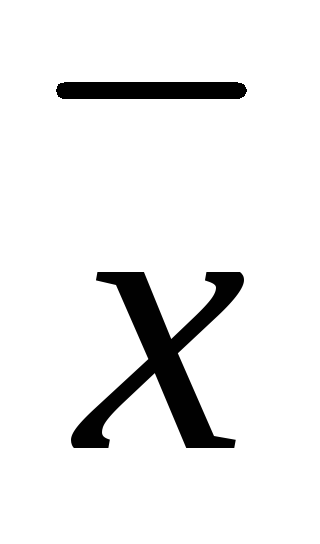 |>0,
если
|>0,
если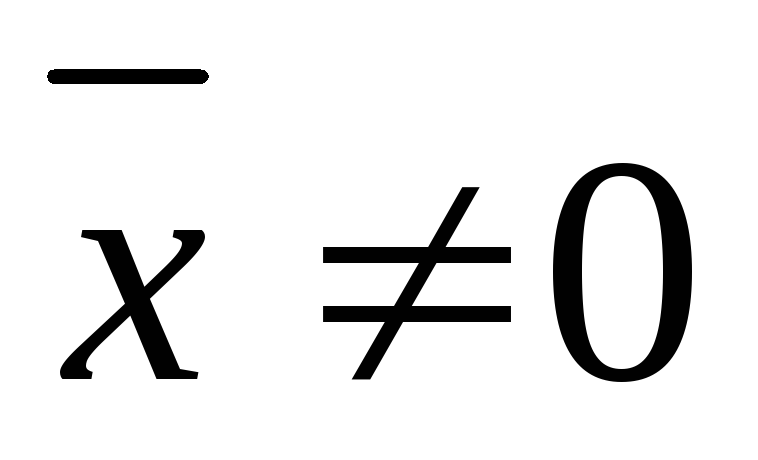
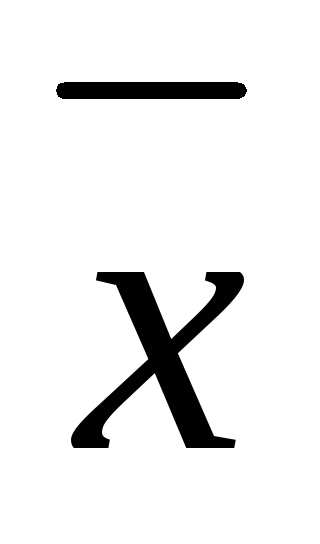 |=0,
если
|=0,
если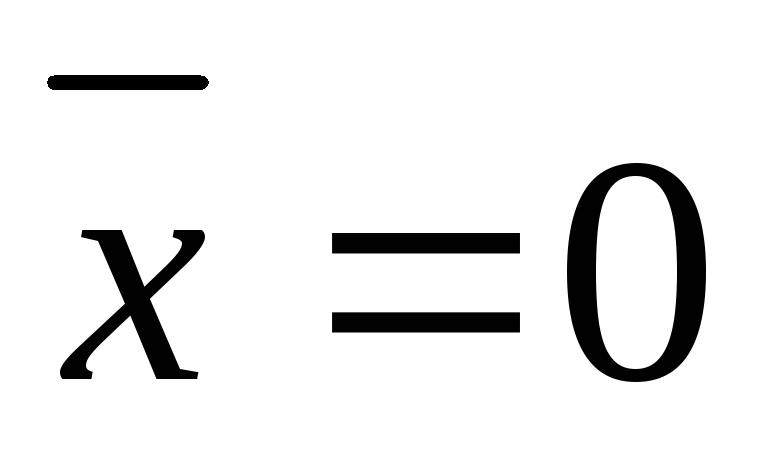 .Углом между векторами
.Углом между векторами и
и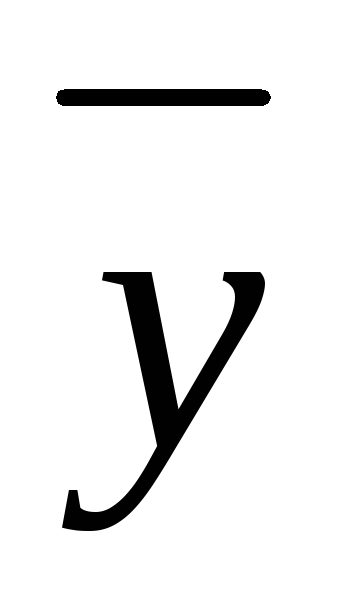 называется число
называется число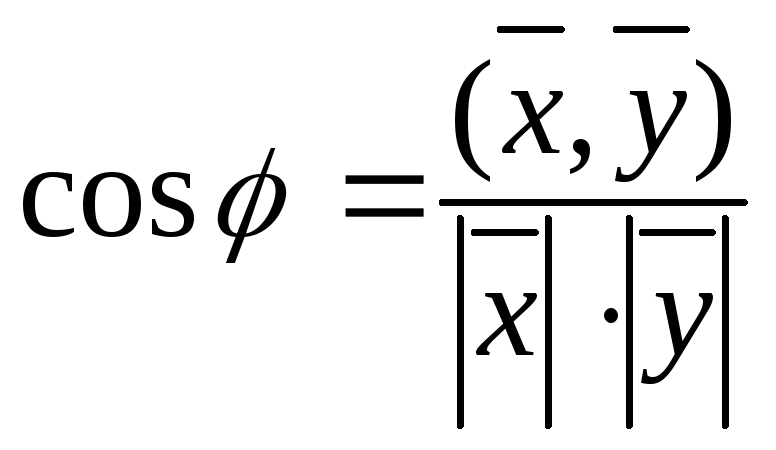 .
Если один из векторов нулевой, то угол
не определен.Расстоянием между
векторами
.
Если один из векторов нулевой, то угол
не определен.Расстоянием между
векторами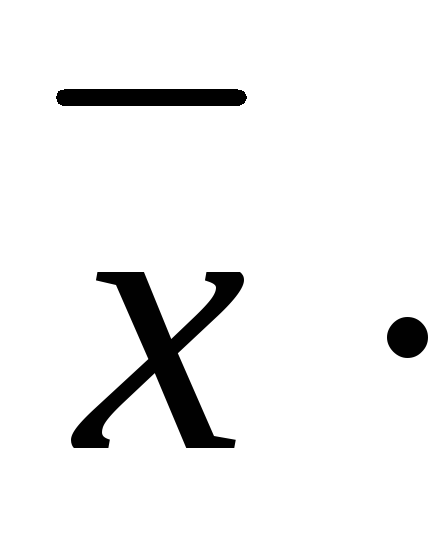 и
и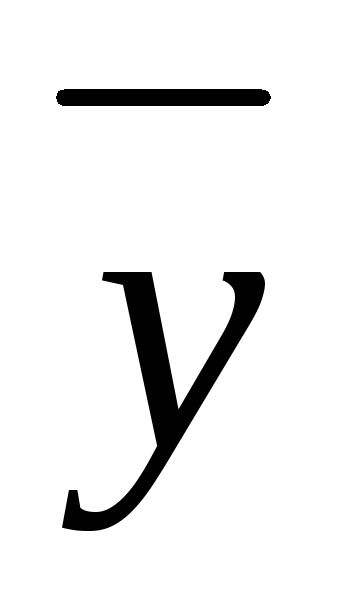 евклидова пространства называется
неотрицательное число
евклидова пространства называется
неотрицательное число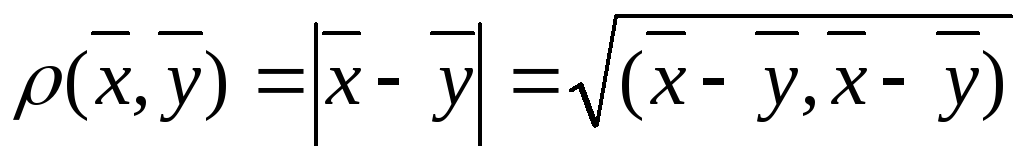
Теорема 1:Для любых двух векторов
евклидова пространства справедливо
неравенство Коши-Буняковского: .
.
Доказательство:Рассмотрим вектор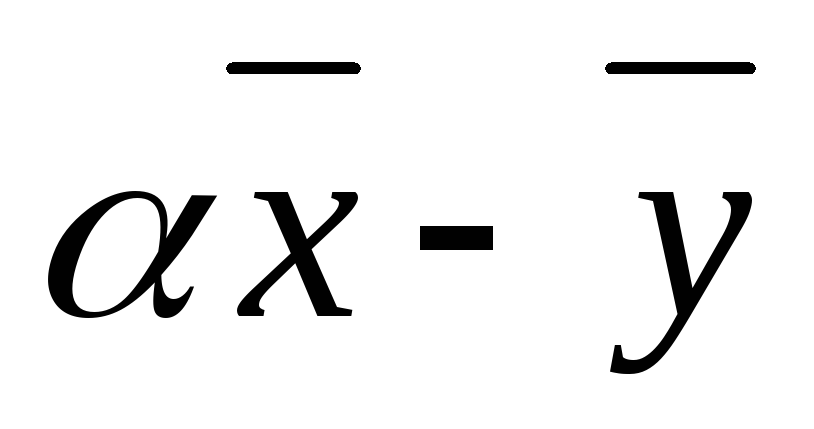 .
Из 4) следует
.
Из 4) следует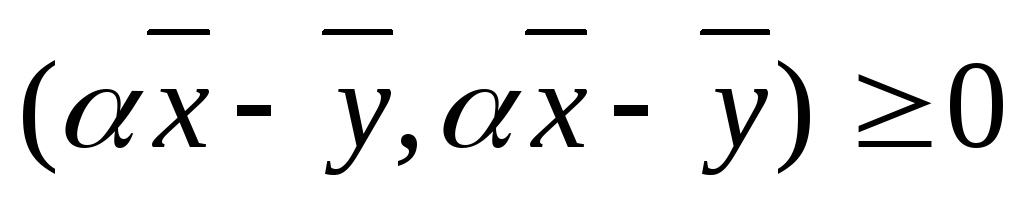 (действительное число).
(действительное число).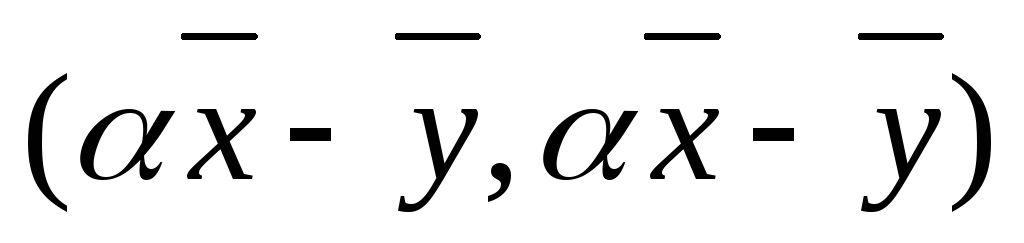 =
=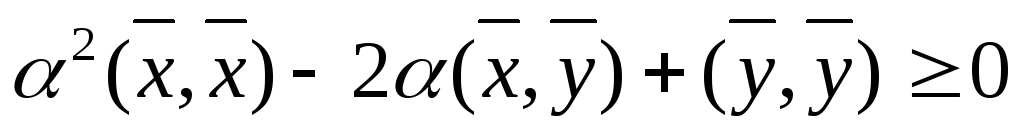 .
Это неравенство второй степени
относительносправедливо для любых
.
Это неравенство второй степени
относительносправедливо для любых и
и .
.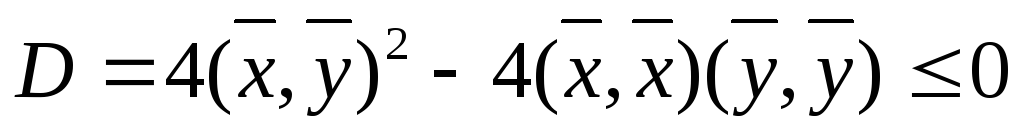
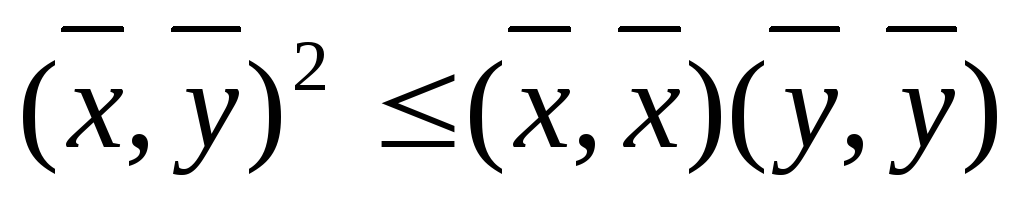 .
(Так как квадратный трехчлен относительнопринимает
неотрицательные значения при любомтогда и только тогда, когда
.
(Так как квадратный трехчлен относительнопринимает
неотрицательные значения при любомтогда и только тогда, когда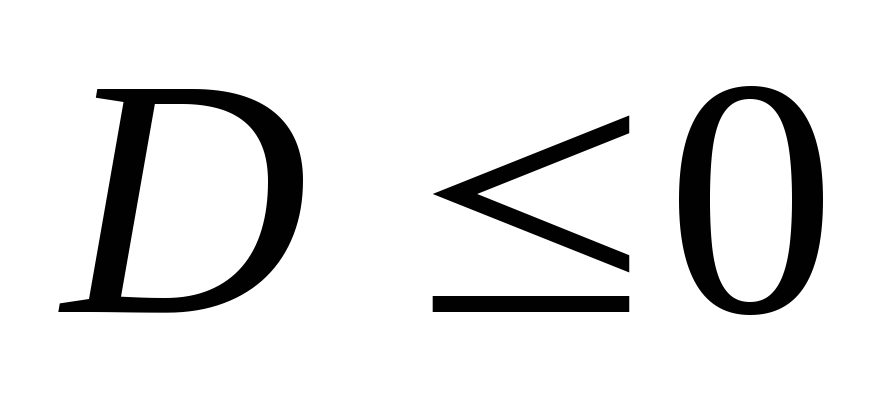 ).
). Следствие: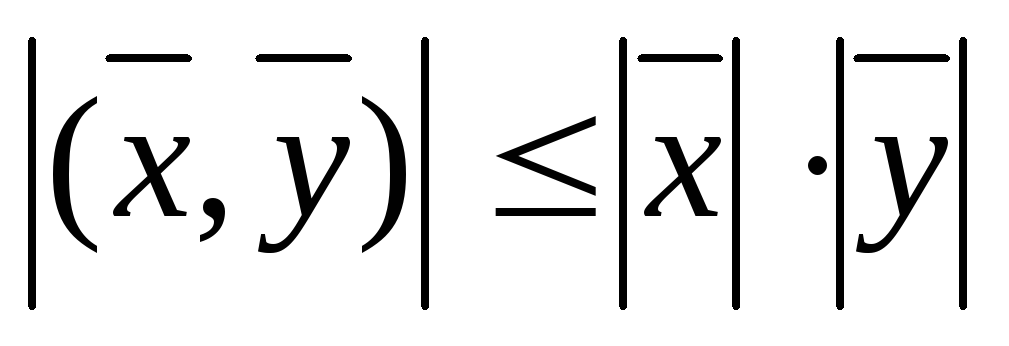
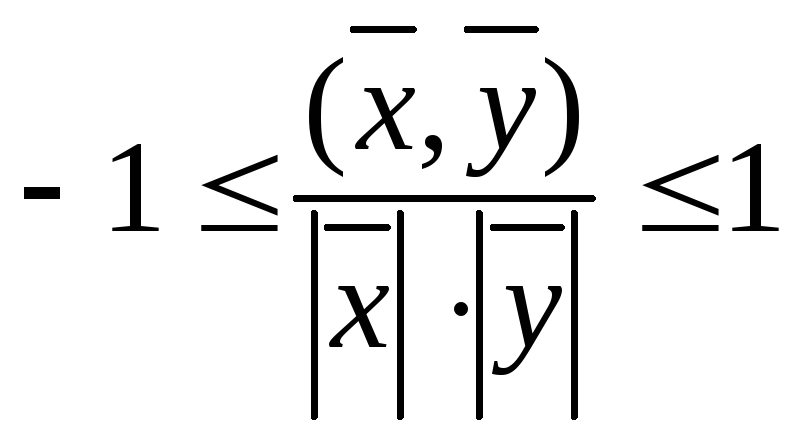
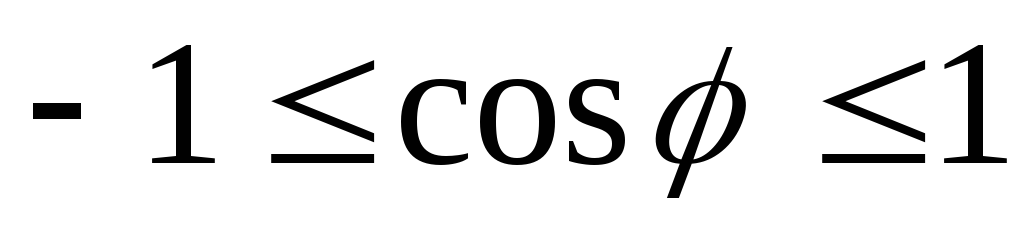 .
.
Два вектора  и
и
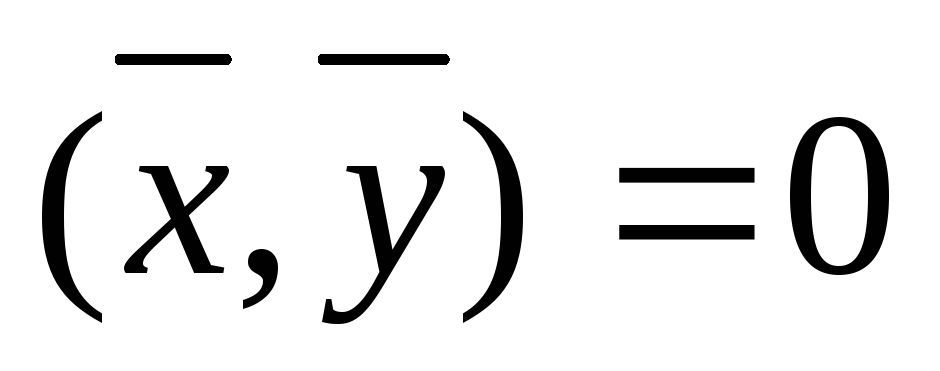 .
Обозначение.
Нулевой вектор ортогонален любому
вектору пространства.Система векторовназываетсяортогональной, если все
векторы этой системы попарно ортогональны
между собой.
.
Обозначение.
Нулевой вектор ортогонален любому
вектору пространства.Система векторовназываетсяортогональной, если все
векторы этой системы попарно ортогональны
между собой. Базис 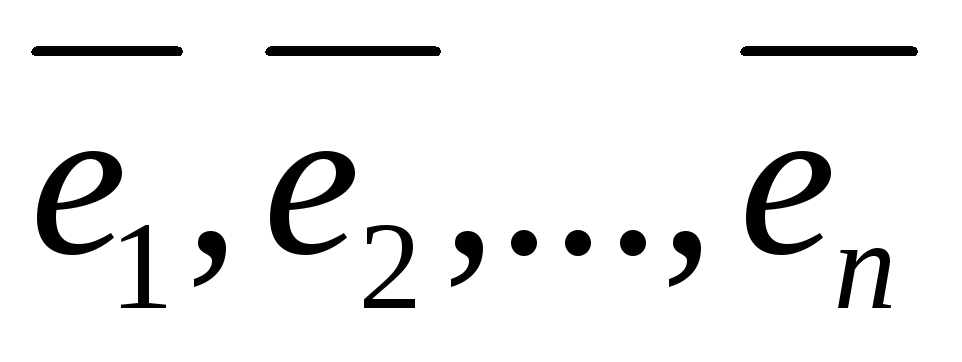 евклидова пространства называетсяортонормированным, если
евклидова пространства называетсяортонормированным, если
 и
и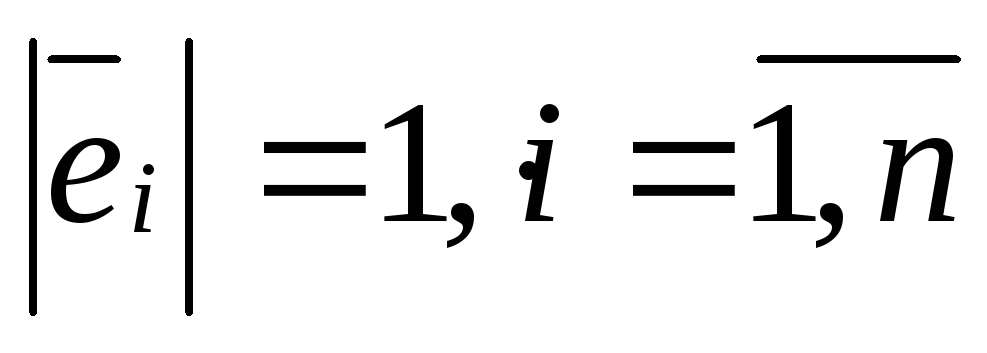 .
.
Любой вектор  в евклидовом пространстве, заданный в
ортонормированном базисе, может быть
представлен единственным образом
в евклидовом пространстве, заданный в
ортонормированном базисе, может быть
представлен единственным образом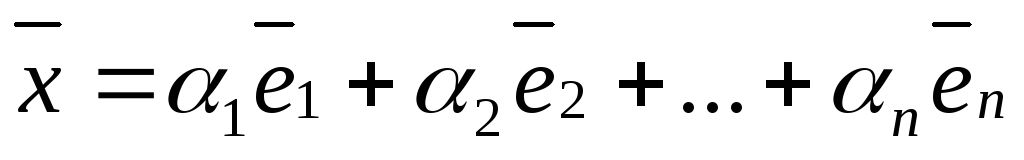
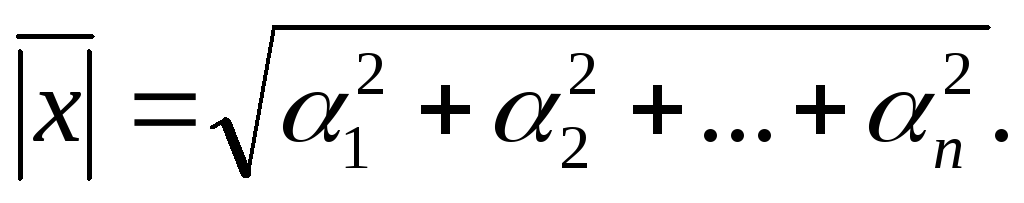 Вектор евклидова пространства называетсянормированным, если его длина равна
1, обозначается
Вектор евклидова пространства называетсянормированным, если его длина равна
1, обозначается его
координаты равны
его
координаты равны =
= .
. Пусть даны два вектора 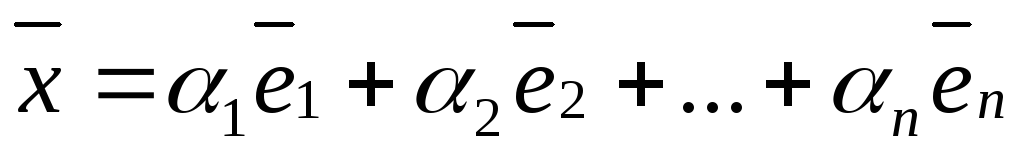 и
и в евклидовом ортонормированном
пространстве. Тогда:
в евклидовом ортонормированном
пространстве. Тогда:
1) ,
2) 
3) 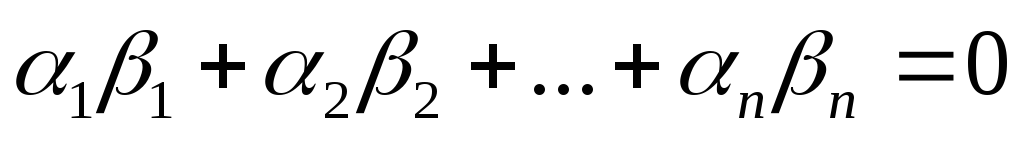 условие ортогональности
векторов,
условие ортогональности
векторов,
4) 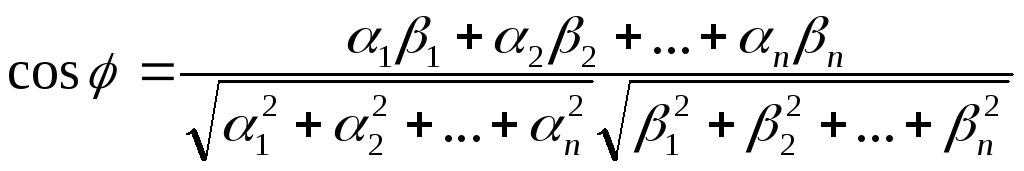
Пример 1: Система координатXOYповернута относительно начала координат
на угол. Обозначим
новую систему черезX1OY1и выразим координаты вектора в новой системе через его координаты
в новой системе через его координаты в
старой системе. Проекция вектора
в
старой системе. Проекция вектора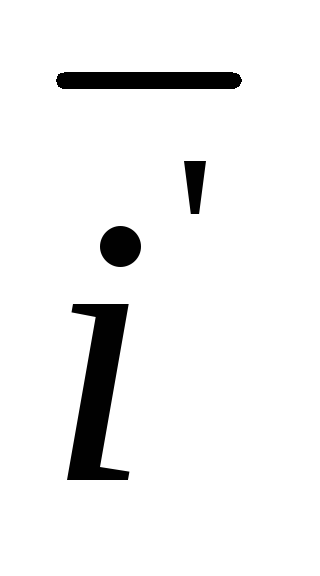 на ось ОXравнаcos,
на ось ОY–sin.
на ось ОXравнаcos,
на ось ОY–sin.
Пример: 1)
2)
2 Неравенство Коши-Буняковского
Теорема:скалярное произведение в Евклидовом или унитарном пространстве удовлетворяет следующему неравенству:|<x,y>|<=||x||y||
модуль скалярного произведения не превосходит произведения нормы каждого сомножителя.
(|<x,y>|2<=<x,x><y,y>)
Доказательство:
а) Евклидово пространство
0<=<x+ty,x+ty>=<x,x+ty>+t<y,x+ty>=<x,x>+t<x,y>+t<x,y>+t2<y,y>=<x,x>+2t<x,y>+t2<y,y>
квадратный трехчлен от t>=0, когда его D<0
D/4 = (<x,y>)2 — <x,y><y,y> <=0, получаем:
(<x,y>)2
возможно тогда и только тогда, когда:
<x+ty,x+ty>=0 когдаx+ty,x+ty — ^B
x+ty = 0 x = -ty — колинеарны.
б) Унитарное пространство:
0<=<x+ty,x+ty> = <x,x>+t<x,y>+t<y,x>+t2<y,y> = <x,x>+t(<x,y>+<y,x>)+t2<y,y> = <x,x>+2tRe<x,y>+t2<y,y>
D/4 = (Re<x,y>)2-<x,x><y,y> <= 0
Рассмотрим скалярное произведение <x,y>=ei|<x,y>| | ei|
Рассмотрим вектор x1= e-ix, тогда
< x1,y>=< e-ix,y>= ei<x,y>= e-iei|<x,y>|=|<x,y>|
(*) неравенство верно для любыхx
(Re<x,y>)2<=<x1,x1><y,y>
<x1,y>=|<x,y>| то следовательно
Re<x,y>=|<x,y>|
<x1,x1>=< eix ,eix>= ei e-i<x,x>=<x,x>
сопряжением
ei — выносим
<x,y>=< >=
>= =
= =
=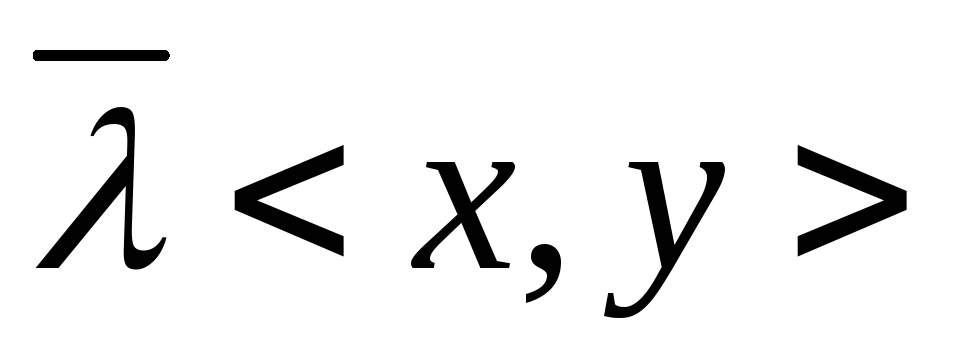
полулинейность по второму аргументу
|<x,y>|2<=<x,x><y,y>
для унитарного.
3 Матрица Грама и ее изменение при смене базиса.
(E,U ) e1,e2…en – базис, выберем в нем базис со скалярным произведением, это означает, что:
1
.
x=1e1+…+nen = (e1…en)( . ) = (e)Xe
.
n
пусть естьy=(e)Ye тогда их скалярное произведение
<x,y>=<iei , jej> = (будем считать что пространствоE) =
i<ei , jej> = i,jij<ei,ej>
Если просранство U, тосопряженное.
Пусть:
Ge = (gij) gij=<ei , ej>
Такая матрица называется матрицей Грама
<x,y>= tXeGeYe в унитарном пр-веY сопряженное.
Если задана матрица Грама, то скалярное произведение вычислятся с помощью этих двух формул, при смене базиса, меняется матрица Грама.
Изменение матрицы грама при смене базиса линейного пространства.
fn , bn bn – матрица перехода.
Xe=Cef Xf Ye= Cef Yf
E: <x,y> = tXf tCef GeCef Yf
U: — || — || — ||- || — CefYf – сопряженные.
где tCef GeCef – новая матрица Грама. (в унитарном, Cef сопряженное)
4 Ортонормированные базисы и ортогональные матрицы.
Опр: базис в Е или U пространстве называется ортонормированым, если выполнены соотношения:
<ei , ej> = ij = {1,еслиi=j and 0, еслиi<>j}
Декартов базис например.
Пусть есть два ортонормированных базиса вЕ:
e1…en
f1…fn
Cef – матрица перехода.
Ge = En 1…0
01..0
00..1
Gf = En
Gf = En = tCefGeCef = tCefCef
Матрицы вида Cef и tCef называются ортогональными. (в унитарном она сопряженная)
Матрица Cef невырожденна.
1) E | Cef | = ? |E| = 1 = | tCef | | Cef | = | Cef |2
| Cef | = (+/-)1
U
|E|=1=| tCef | |Cef | = | tCef | |tCef | = ||Cef||2
|Cef|=1
Задача: Доказать, что матрица обратная ортогональной – ортогональна, а обратная унитарной – унитарна.
Ортогональное дополнение линейного подпространсва.
Определение:пустьL пространство со скалярным произведением, есть подпространствоMLортогональное дополнение подпространстваM (Мt) – это множество всех векторов из пространстваL которые ортогональны каждому вектору из М.
Mt = {yL| <y,x>=0 xM}
Пример:
L=R3 и рассмотрим плоскостьxОy, М – плоскостьxОy. Тогда ортогональное дополнение к М – это прямые параллельные OZ.
Mt = {} (к — вектор)
2. [] Z{1, cosx, sinx, … ,cosmx, sinmx} dimZ 2m+1
M=Z{1} <b,g>=
Mt = Z{cosx, sinx, … ,cosmx, sinmx}
Свойства ортогональных дополнений:
Ортогональное дополнение подпространства – это подпространство. Мt –подпр.
Пространство L – это прямая сумма любого своего подпространства и его ортогонального дополнения.
L=MMt
Каждый вектор представлен в виде суммы из M иMt.
Их пересечение состоит из {0}
Пусть x
e1, e2, … ,ek – базис в пространствеM, тогдаx=1e1+2e2+…+kek
x – перпендикулярен каждому вектору из М.
x перендикуляренyМx перендикуляренe1, e2, … ,ek
<x,ei>=0 i
<x,x> = <1e1+2e2+…+kek , x> = 1<e1,x>+…+k<ek , x> = 0.
тоесть = 0;
xL пустьe1,…,en – ортонормированый базис пространства М. Построим вектор x1 = <x,e1>e1+…+<x,ek>ek M
x = x1+(x-x1) = x2 надо показать чтоx-x1Mt т.е. х2ортогонален нашему базисному пространству М.
<ei , x2> = <ei , x-x1> = <ei , x> — <ei , x1> — <ei , x> — <ei ,<x1, e1 >e1 +…+<x1 , ek>ek> = <ei , x> — <ei , <x , ei>ei> = <ei , x> — <ei , x><ei , ei> = 0 отлично от 0 только произведение. еi на<x , ei>ei
видно, что х2ортогонален каждому еi т.е.x2Mt. Т.е. х представим в виде суммы один из М, другой изMt.
Если Mt – это подщпространство, то мы можем у него рассмотреть ортогональное дополнение, надо доказать (Mt)t = M, еслиLM L – конечномерное пространствоdimL < oo
Связь с ситемами Линейных Уравнений.
Пространство столбцов:
( 1 ) ( 1 )
( 0 ) ( . )
Rm e=( . ) ei=( 1 )
( 0 ) ( 0 )
(ak1)
M=Z{a1, … ,a2} ak= (ak2)
( . )
(akm)
рассмотрим:
(a11a12 … a1m)
(a21 … a2m)
А= ( … )
(ak1 … akm)
тогда СЛУ AX=0 такая системазадает ортоганальное дополнение пространства М.
Алгоритм ортогонализации Грама – Шмидта.
По данному:
a1 … ak – линейно независим.
Построить новый
b1 … b1 1) все новые вектора попарно ортогональны<bi , bj>=0 [ i<>j ]
2) Z{a1, … , as} = Z{b1, … ,bs}
52(2 Листа). Понятие евклидова пространства.Аксиомы. Неравенство Коши-Буняковского
Если
каждой паре векторов  из
линейного пространстваE поставлено
в соответствие действительное число
из
линейного пространстваE поставлено
в соответствие действительное число  ,
так, что для любых
,
так, что для любых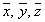 изE
и любого действительного числа
изE
и любого действительного числа  справедливы
следующие равенства:
справедливы
следующие равенства:



 при
при  ,
, ,
, —
нулевой вектор,
—
нулевой вектор,
то
говорят, что в линейном пространстве
определено скалярное
произведение  .
.
Определение. Линейное пространство E называется евклидовым,если в нем определено скалярное произведение.
16.3. Неравенство Коши — Буняковского.
Теорема.
Для любых векторов  и
и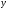 справедливо неравенство
справедливо неравенство
 .
.
Доказательство. Так как скалярное произведение является положительно определенной формой, то
 .
.
При
фиксированных векторах  и
и мы имеем квадратный трехчлен от
мы имеем квадратный трехчлен от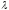 ,
дискриминант которого отрицательный
или равен нулю:
,
дискриминант которого отрицательный
или равен нулю:
 .
.
Отсюда 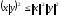 или
или .
Теорема доказана.
.
Теорема доказана.
Следствие
(неравенство треугольника). Для любых
векторов  и
и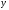 справедливо неравенство
справедливо неравенство
 .
.
Доказательство.
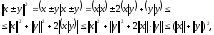
следовательно,  .
.
Пусть
дано линейное пространство L со скалярным произведением 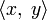 .
Пусть
.
Пусть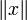 —
норма, порождённая скалярным произведением,
то есть
—
норма, порождённая скалярным произведением,
то есть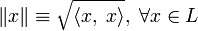 .
Тогда для любых
.
Тогда для любых имеем:
имеем:

Евклидово пространство(в математике), пространство, свойства которого описываются аксиомамиевклидовой геометрии. В более общем смысле Е. п. называетсяn-мepноевекторное пространство, в котором возможно ввести некоторые специальные координаты (декартовы) так, что метрика его будет определена следующим образом: если точкаМимеет координаты (х1, х2,…, xn), а точкаМ*— координаты (x1*, x2*,…,xn*), то расстояние между этими точками

От всякой точки до всякой точки можно провести прямую.
Ограниченную прямую можно непрерывно продолжать по прямой.
Из всякого центра всяким раствором может быть описан круг.
Все прямые углы равны между собой.
Если прямая, пересекающая две прямые, образует внутренние односторонние углы, меньшие двух прямых, то, продолженные неограниченно, эти две прямые встретятся с той стороны, где углы меньше двух прямых.
53. Евклидово пространства: Примеры, неравенство треугольника\
Наглядными примерами евклидовых пространств могут служить пространства:
 размерности
1 (вещественная прямая)
размерности
1 (вещественная прямая) размерности
2 (евклидова плоскость)
размерности
2 (евклидова плоскость) размерности
3 (евклидово трехмерное пространство)
размерности
3 (евклидово трехмерное пространство)Евклидово пространство можно считать современной интерпретацией и обобщением (так как оно допускает размерности больше трех) классической (Евклидовой) геометрии.
Можно привести и несколько более абстрактные примеры:
пространство вещественных многочленовстепени, не превосходящейn, со скалярным произведением, определенным как интеграл произведения по конечному отрезку (или по всей прямой, но с быстро спадающей весовой функцией)
вообще пространство всех линейных комбинаций конечного набора вещественных функций
пространство состояний конечномерной квантовой системы (или конечномерное подпространство полного пространства состояний) в вещественном представлении.
Следствие (неравенство треугольника). Для любых векторов
 и
и справедливо неравенство
справедливо неравенство .
.Доказательство.

следовательно,
 .
.
54. Ортогональность векторов. Процесс ортогонализации Шмидта. Существование ортонормированного базиса в Евклидовом пространстве
Определение. Векторы  и
и называются ортогональными, если угол
между ними равен
называются ортогональными, если угол
между ними равен ,
т.е.
,
т.е. .
.
Нулевой вектор ортогонален любому вектору.
Заметим,
что из ортогональности векторов  и
и следует теорема Пифагора:
следует теорема Пифагора:
 .
.
Эту теорему можно обобщить на любое число попарно ортогональных векторов:
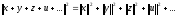
Процесс:
Процесс
Грама (англ.)
― Шмидта ― наиболее
известный алгоритм ортогонализации,
при котором полинейно
независимойсистеме строитсяортогональная
система
строитсяортогональная
система такая,
что каждый векторbi линейно выражается через
такая,
что каждый векторbi линейно выражается через  ,
то естьматрица
переходаот{ai}
к {bi}
― верхнетреугольная
матрица. При этом можно добиться того,
чтобы система{bi}
была ортонормированной и чтобы
диагональные элементы матрицы перехода
были положительны; этими условиями
система {bi}
и матрица перехода определяются
однозначно.
,
то естьматрица
переходаот{ai}
к {bi}
― верхнетреугольная
матрица. При этом можно добиться того,
чтобы система{bi}
была ортонормированной и чтобы
диагональные элементы матрицы перехода
были положительны; этими условиями
система {bi}
и матрица перехода определяются
однозначно.
16.6.
Процесс ортогонализации Грама – Шмидта. Пусть  — произвольный базис евклидова
пространства. Мы будем строить новый –
ортонормированный – базис пространства
— произвольный базис евклидова
пространства. Мы будем строить новый –
ортонормированный – базис пространства .
.
В
качестве первого вектора нового базиса
возьмем вектор 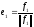 .
Таким образом, длина вектора
.
Таким образом, длина вектора равна 1. Прежде, чем построить второй
вектор нового базиса, построим вектор
равна 1. Прежде, чем построить второй
вектор нового базиса, построим вектор :
:
 .
.
Вектор  не может быть нулевым, поскольку векторы
не может быть нулевым, поскольку векторы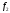 и
и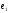 линейно независимы. Заметим, что векторы
линейно независимы. Заметим, что векторы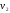 и
и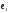 ортогональны. В качестве второго
базисного вектора возьмем вектор
ортогональны. В качестве второго
базисного вектора возьмем вектор .
Теперь будем строить третий базисный
вектор. Сначала возьмем вектор
.
Теперь будем строить третий базисный
вектор. Сначала возьмем вектор
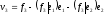 .
.
Этот
вектор – ненулевой, так как векторы  линейно независимы,- ортогонален
векторам
линейно независимы,- ортогонален
векторам и
и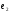 .
Остается только нормировать его:
.
Остается только нормировать его: .
Алгоритм ясен: имея
.
Алгоритм ясен: имея вектор нового базиса, мы построим
сначала вектор
вектор нового базиса, мы построим
сначала вектор
 .
.
Этот
вектор ненулевой и ортогональный
векторам  .
Нормировав его, получаем
.
Нормировав его, получаем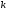 -й
вектор нового базиса
-й
вектор нового базиса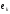 .
.
Теорема. В произвольном n-мерном евклидовом пространстве существует ортонормированный базис.
55. Ортонормированные базисы и их свойства
Определение. Базис называется ортонормированным, если его векторы попарно ортогональны и равны единице.
Определение. Декартова система координат, базис которой ортонормирован называется декартовой прямоугольной системой координат.
Теорема. В любом конечномерном пространстве существует ортонормированный базис.
Доказательство
теоремы немедленно следует из того, что
существует базис 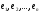 ,
в котором квадратичная форма,
соответствующая скалярному произведению,
имеет канонический вид
,
в котором квадратичная форма,
соответствующая скалярному произведению,
имеет канонический вид
 ,
,
(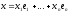 ).
В этом базисе скалярное произведение
векторов
).
В этом базисе скалярное произведение
векторов и
и задается формулой
задается формулой .
Но это и означает, что базис
.
Но это и означает, что базис ортонормированный.
ортонормированный.
Свойства:
в ортонормированном базисе скалярное произведение векторов равно сумме произведений одноименных координат этих векторов.
Любую ортонормированную систему векторов конечномерного евклидова пространства можно дополнить до ортонормированного базиса.
56.Квадратичные
формы. Приведение квадратичной формы
к каноническому виду методом Лангаржа. 


57. Положительно определенные квадратичные формы. Критерий Сильвестра
Критерий Сильвестраопределяет, является лисимметричнаяквадратнаяматрицаположительно (отрицательно, неотрицательно) определённой.
Пусть квадратичная формаимеет в каком-тобазисематрицу

Тогда эта форма положительно определена, если и только если все её главные (угловые) минорыΔiположительны. Форма отрицательно определена, если и только если знаки Δiчередуются, причём Δ1< 0. Здесьглавнымиминорами матрицыAназываются определители вида
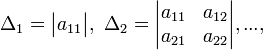

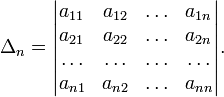
Для неотрицательно определённыхматриц критерий действует только в одну сторону: если форма неотрицательно определена, то главные миноры неотрицательны. Обратное неверно. Например, матрица

не является неотрицательно определённой — так как, например, (Mv,v) = − 2 дляv= (0,1, − 1). В то же время все её главные миноры равны 0, то есть неотрицательны.
Квадратичная форма является положительно определенной, тогда и только тогда, когда все угловые минорыеё матрицы строго положительны.
58.Кривые второго порядка: Канонические уравнения и форма:
Эллипс
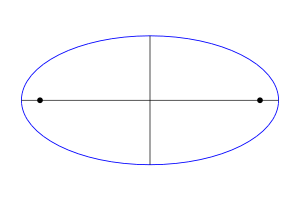

Эллипс, его фокусы и главные оси
Гипербола
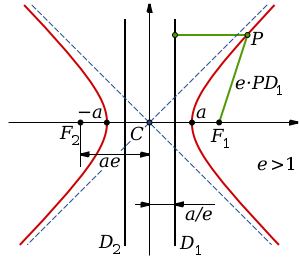
Асимптотыгиперболы (красные кривые), показанные голубым пунктиром, пересекаются в центре гиперболы,C. Два фокуса гиперболы обозначены как F1 и F2. Директрисыгиперболы обозначены линиями двойной толщины и обозначеныD1 и D2. Эксцентриситет ε равен отношению расстояний точки P на гиперболе до фокуса и до соответствующей директрисы (показаны зеленым). Вершины гиперболы обозначены как ±a.
Парабола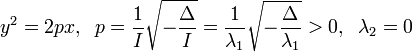

59. Поверхности второго порядка
Эллиптический
цилиндр: 
Параболический
цилиндр: 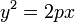

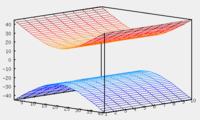
Гиперболический
цилиндр: 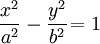
Эллипсоид:
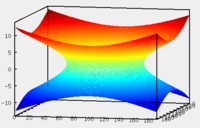
Однополостной

гиперболоид: 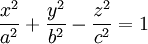
Двуполостной
гиперболоид: 
 Эллиптическийпараболоид:
Эллиптическийпараболоид:

60. Комплексные числа: Сложение, вычитание, умножение и деление в алгебраической форме
1.
Понятие комплексного числа. Из школьного курса математики известно,
что действительных чисел недостаточно
для решения квадратных уравнений.
Простейшее из квадратных уравнений 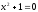 не имеет корней среди действительных
чисел. Попробуем расширить систему
действительных чисел до такой системы
чисел, чтобы это уравнение имело решение.
не имеет корней среди действительных
чисел. Попробуем расширить систему
действительных чисел до такой системы
чисел, чтобы это уравнение имело решение.
Выберем
на плоскости прямоугольную систему
координат с осью абсцисс  и осью ординат
и осью ординат .
Будем обозначать
.
Будем обозначать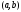 точку с абсциссой
точку с абсциссой и ординатой
и ординатой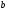 .
Определим на множестве точек плоскости
(другими словами, на упорядоченных парах
действительных чисел) операции сложения
и умножения следующим образом:
.
Определим на множестве точек плоскости
(другими словами, на упорядоченных парах
действительных чисел) операции сложения
и умножения следующим образом:

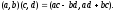
Заметим, что
 ,
,

Поэтому
точки, лежащие на оси 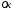 можно считать точками действительной
оси, и мы не будем различать точку
можно считать точками действительной
оси, и мы не будем различать точку и действительное число
и действительное число .
.
Кроме того,

Традиционно эту точку обозначают буквой .
Учитывая,
что для  R
R  и
и получаем:
получаем:

В этой записи операции сложения и умножения выглядят так:

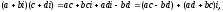
т.е.
эти операции выполняются как с обычными
двучленами с учетом равенства 
Пусть
дано число  .
Назовем число
.
Назовем число сопряженным числу
сопряженным числу .
Заметим, что
.
Заметим, что

Определив операции сложения и умножения, естественно ввести обратные операции вычитания и деления:

Последняя формула довольно громоздка, и запоминать ее не стоит. Следует только знать, что для вычисления дроби нужно числитель и знаменатель умножить на сопряженное знаменателю число.
Итак, построенная система чисел с алгебраическими операциями называется множеством комплексных чисел и обозначается С.
Ко́мпле́ксные[1] чи́сла— расширение множествавещественных
чисел. обычно обозначается .
Каждое комплексное числоzпредставляет
собой суммуx+iy, гдеxиyвещественные, аiэто так называемая
мнимая единица, являющейся корнем
уравненияi2= − 1
.
Каждое комплексное числоzпредставляет
собой суммуx+iy, гдеxиyвещественные, аiэто так называемая
мнимая единица, являющейся корнем
уравненияi2= − 1
Множество
комплексных чисел обозначается в
литературе как  (ажурное),
а иногда какC(простое),
(ажурное),
а иногда какC(простое), (полужирное).
(полужирное).
Неравенство Коши-Буняковского — это… Что такое Неравенство Коши-Буняковского?
- Неравенство Коши-Буняковского
Неравенство Коши́ — Буняко́вского связывает норму и скалярное произведение векторов в линейном пространстве. Это неравенство эквивалентно неравенству треугольника для нормы в пространстве со скалярным произведением.
Неравенство Коши — Буняковского иногда, особенно в иностранной литературе, называют неравенством Шварца, хотя работы Шварца (нем.) на эту тему появились только спустя 25 лет после работ Буняковского[1]. Конечномерный случай этого неравенства называется неравенством Коши и был доказан Коши в 1821 году.
Формулировка
Пусть дано линейное пространство L со скалярным произведением
 . Пусть
. Пусть  — норма, порождённая скалярным произведением, то есть
— норма, порождённая скалярным произведением, то есть  . Тогда для любых
. Тогда для любых  имеем
имеем ,
,
причём равенство достигается тогда и только тогда, когда векторы x и y пропорциональны (коллинеарны).
Комментарии
В конечномерном случае можно заметить, что
 , где S(x,y) — площадь параллелограмма, натянутого на векторы x и y.
, где S(x,y) — площадь параллелограмма, натянутого на векторы x и y.В общем случае

Примеры
 ,
,
- где
 обозначает комплексное сопряжение yk.
обозначает комплексное сопряжение yk.
 .
.
![\mathrm{cov}^2(X,Y) \le \mathrm{D}[X] \cdot \mathrm{D}[Y]](//xn--90abjbtjdof1b8dvb.xn--p1ai/wp-content/plugins/a3-lazy-load/assets/images/lazy_placeholder.gif) ,
,
- где cov обозначает ковариацию, а D дисперсию.
Доказательство
Значит дискриминант многочлена
 неположительный, то есть
неположительный, то есть
 .
.
Литература
- ↑ Bounjakowsky W., «Mémoires de l’Académie des sciences de St-Pétersbourg. 7 série», 1859, t. 1, № 9.
Wikimedia Foundation. 2010.
- Неравенство Джексона-Стечкина
- Неравенство Крамера-Рао
Смотреть что такое «Неравенство Коши-Буняковского» в других словарях:
Неравенство Коши — Буняковского — Неравенство Коши Буняковского связывает норму и скалярное произведение векторов в линейном пространстве. Это неравенство эквивалентно неравенству треугольника для нормы в пространстве со скалярным произведением. Неравенство Коши … … Википедия
Неравенство Коши—Буняковского — связывает норму и скалярное произведение векторов в линейном пространстве. Это неравенство эквивалентно неравенству треугольника для нормы в пространстве со скалярным произведением. Неравенство Коши Буняковского иногда, особенно в иностранной… … Википедия
Неравенство Коши — Неравенство Коши Буняковского связывает норму и скалярное произведение векторов в евклидовом пространстве. Это неравенство эквивалентно неравенству треугольника для нормы. Неравенство Коши Буняковского иногда, особенно в иностранной… … Википедия
Буняковского неравенство — Неравенство Коши Буняковского связывает норму и скалярное произведение векторов в линейном пространстве. Это неравенство эквивалентно неравенству треугольника для нормы в пространстве со скалярным произведением. Неравенство Коши Буняковского… … Википедия
Неравенство Буняковского — Неравенство Коши Буняковского связывает норму и скалярное произведение векторов в линейном пространстве. Это неравенство эквивалентно неравенству треугольника для нормы в пространстве со скалярным произведением. Неравенство Коши Буняковского… … Википедия
Неравенство Шварца — Неравенство Коши Буняковского связывает норму и скалярное произведение векторов в линейном пространстве. Это неравенство эквивалентно неравенству треугольника для нормы в пространстве со скалярным произведением. Неравенство Коши Буняковского… … Википедия
Неравенство Гёльдера — в функциональном анализе и смежных дисциплинах это фундаментальное свойство пространств . Содержание 1 Формулировка 2 Доказательство … Википедия
Неравенство Гельдера — Неравенство Гёльдера в функциональном анализе и смежных дисциплинах это фундаментальное свойство пространств Lp. Содержание 1 Формулировка 2 Частные случаи 2.1 Неравен … Википедия
Коши, Огюстен Луи — Огюстен Луи Коши Augustin Louis Cauchy … Википедия
Коши, Огюстен — Огюстен Луи Коши Огюстен Луи Коши (фр. Augustin Louis Cauchy; 21 августа 1789, Париж 23 мая 1857, Со (О де Сен)) французский математик, член Парижской академии наук, разработал фундамент математического анализа и сам внёс огромный вклад в анализ … Википедия
Неравенство Коши-Буняковского-Шварца. Ковариация
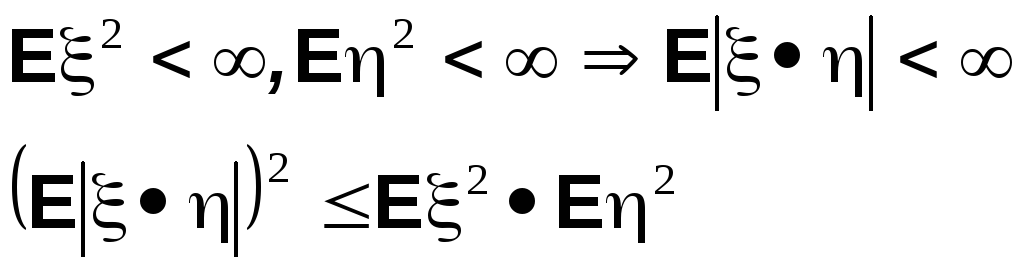
Доказательство. Если

то
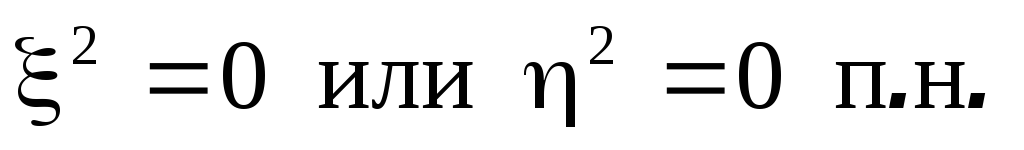
и неравенство превращается в равенство.
Если

то, используя очевидное неравенство
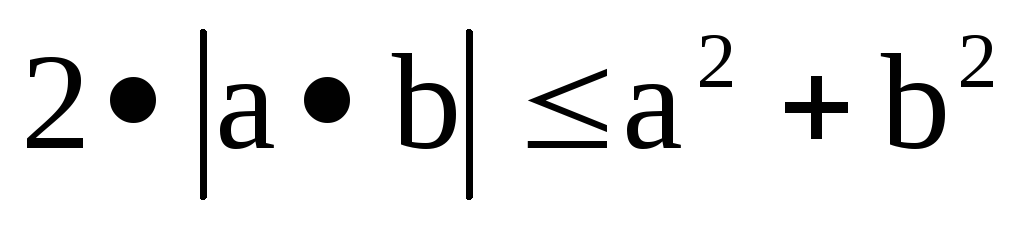
получаем

что эквивалентно доказываемому неравенству.
Применяя неравенство КБШ к случайным величинам
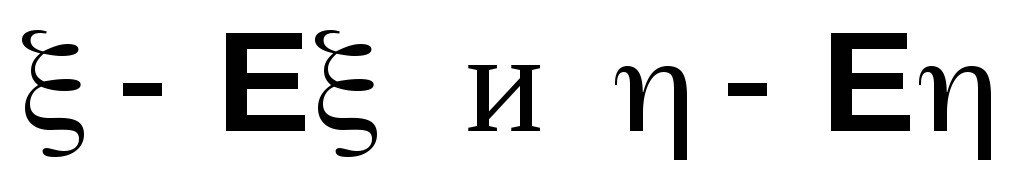
получаем
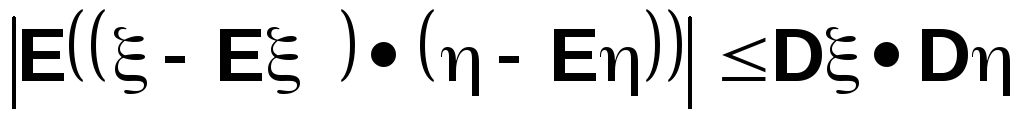
Величина

называется ковариация случайных величин

и, как мы увидим в дальнейшем, является естественной мерой связи этих случайных величин между собой.
Величина

называется коэффициент корреляции случайных величин

Из неравенства КБШ следует, что
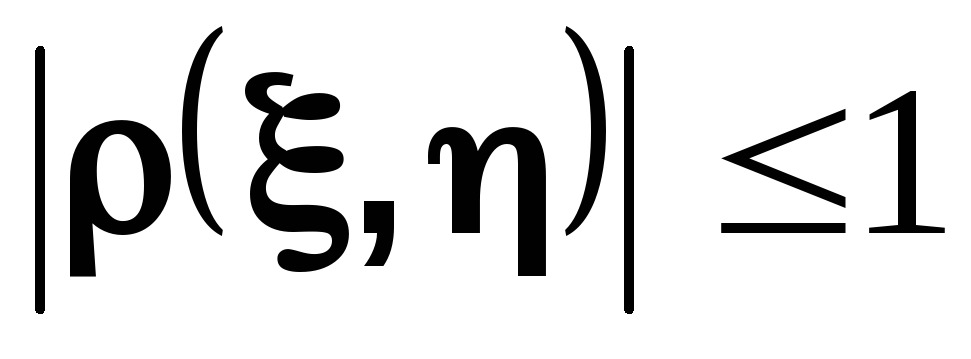
и если
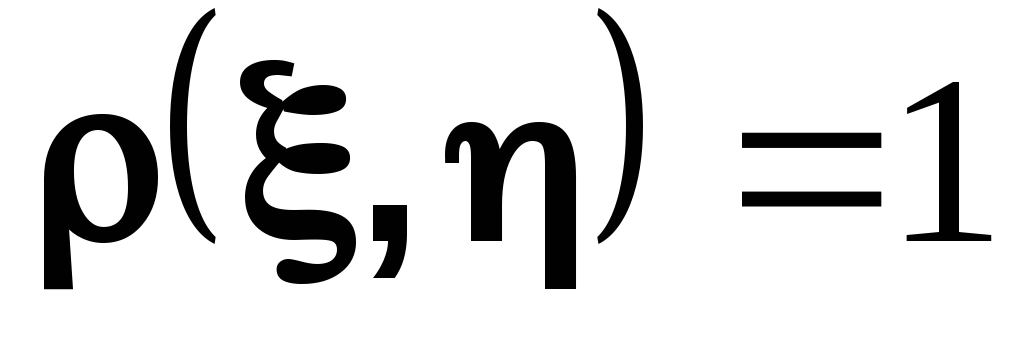
то между этими случайными величинами существует (почти наверное) линейная зависимость

с положительным коэффициентом a. В этом случае говорят, что случайные величины положительно коррелированы. Если
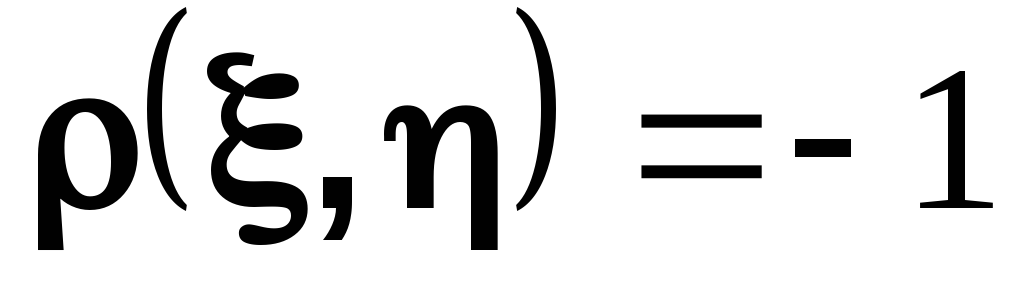
то коэффициент a отрицателен и случайные величины отрицательно коррелированы. Коэффициент корреляции используют как меру зависимости случайных величин.
Неравенство Йенсена.Выпуклые функции
Функция f(x)
называется выпуклой (как 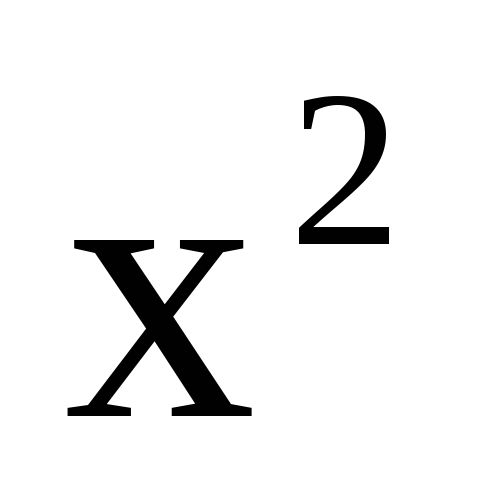 ),
если
),
если

Например,
функции  ,
exp(x) выпуклы.
,
exp(x) выпуклы.
Для выпуклых функций справедливо неравенство Йенсена

Доказательство следует из определения выпуклой функции, если в нем положить
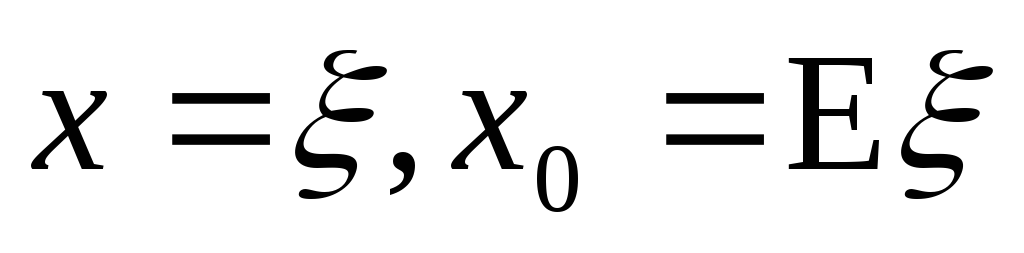
и воспользоваться свойствами 1) 2) 3) математического ожидания.
Моменты
Величина

называется к-тый момент (к-тый начальный момент) случайной величины.
Величина
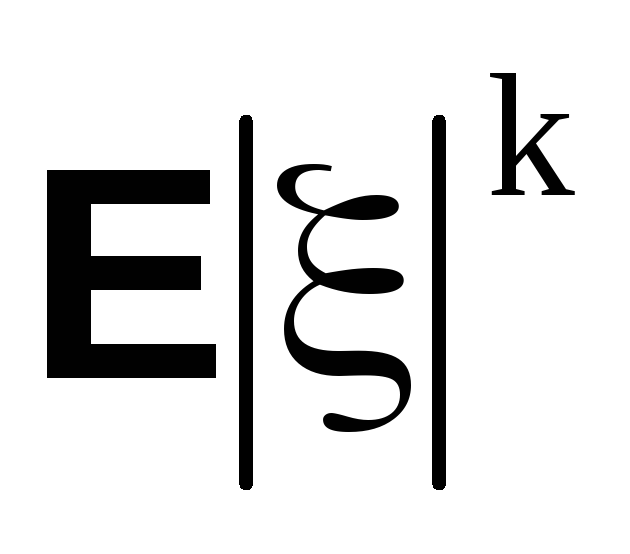
называется к-тый абсолютный момент случайной величины.
Величина
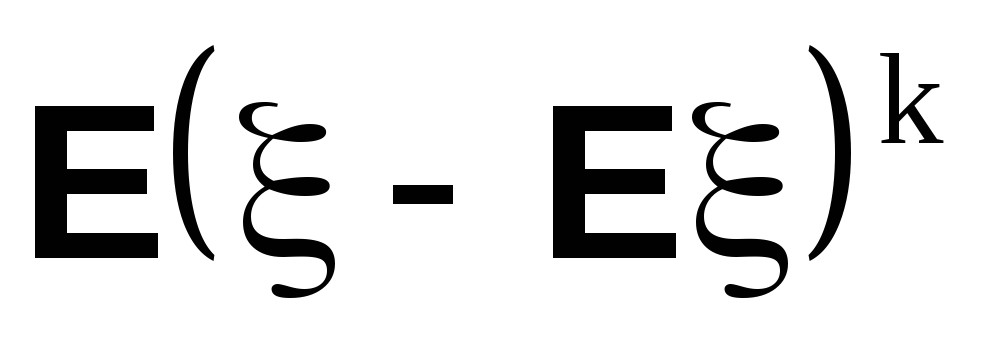
называется к-тый центральный момент случайной величины.
Ясно, что математическое ожидание это первый момент, а дисперсия второй центральный момент. Моменты часто используются в качестве дополнительных характеристик случайных величин.
Вычисление математического ожидания.
Если случайная величина простая, то ее математическое ожидание вычисляется непосредственно по определению. Например, если все значения
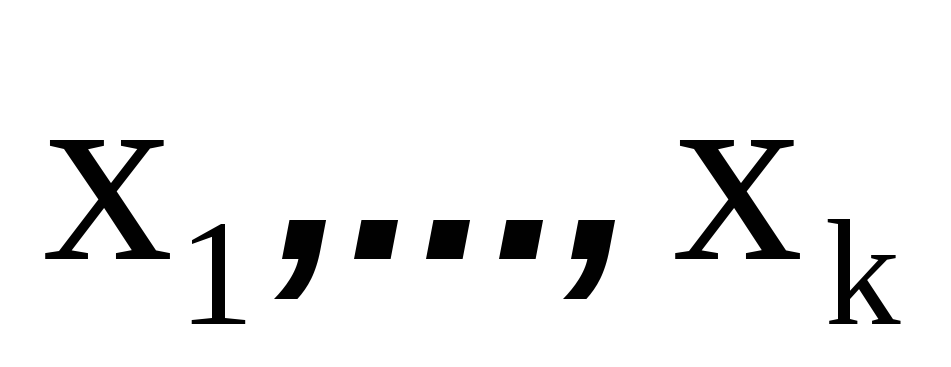
случайной величины

равновероятны, то ее математическое ожидание равно среднему арифметическому этих значений

Заметим , что у простой случайной величины математическое ожидание всегда конечно.
Для дискретной случайной величины, принимающей счетное число различных значений, имеем (приближая ее снизу последовательностью простых случайных величин)

Этот ряд не всегда сходится, и поэтому существуют дискретные случайные величины, не имеющие конечного математического ожидания. Простым достаточным условием конечности математического ожидания является ограниченность модуля случайной величины сверху (константой или другой случайной величиной, имеющей конечное математическое ожидание).
Заметим, что для вычисления математического ожидания дискретной случайной величины нам достаточно знать только ее распределение. Этот факт справедлив и в общем случае, что показывает следующая теорема.
Теорема Лебега о замене переменных
Пусть

случайная величина и g(x) – борелевская функция
Тогда
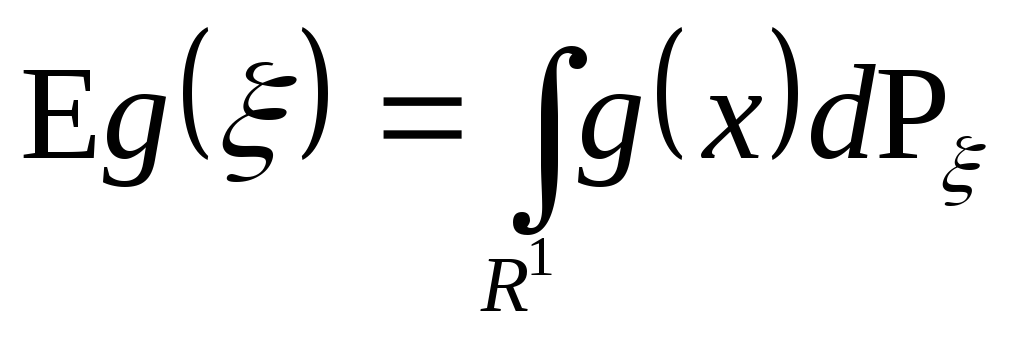
если хотя бы один из этих интегралов существует.
Вычисление интеграла Лебега на прямой.
Так как на распределение на прямой однозначно определяется функцией распределения

то интеграл Лебега часто обозначают так
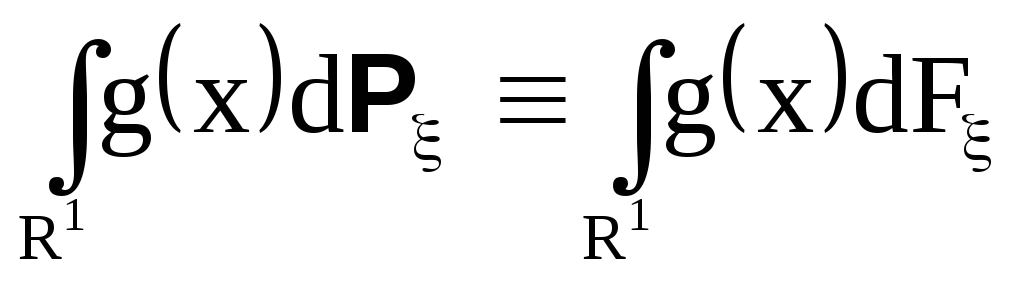
и называют интегралом Лебега-Стильтьеса от функции g по функции F.
Если функция распределения имеет плотность

то предыдущий интеграл интеграл превращается в интеграл

где

мера Лебега на прямой.
Можно показать, что
если функция g (x) интегрируема по Риману, то

где последний интеграл понимается в смысле Римана.
Таким образом,
в практически важных случаях вычисление
интеграла Лебега сводится к вычислению
конечной суммы, ряда или интеграла
Римана (или их комбинаций). В дальнейшем
для интегралов по мере Лебега будем
опускать символ  и использовать такое же обозначение
как и для интегралов Римана.
и использовать такое же обозначение
как и для интегралов Римана.
Неравенство Шварца-Буняковского — Национальная библиотека им. Н. Э. Баумана
Материал из Национальной библиотеки им. Н. Э. Баумана
Последнее изменение этой страницы: 18:20, 5 декабря 2016.
Неравенство Коши́ — Буняко́вского связывает норму и скалярное произведение векторов в линейном пространстве. Это неравенство эквивалентно неравенству треугольника для нормы в пространстве со скалярным произведением.
Неравенство Коши — Буняковского иногда, особенно в иностранной литературе, называют неравенством Шварца и неравенством Коши — Буняковского — Шварца, хотя работы Шварца на эту тему появились только спустя 25 лет после работ Буняковского[1]. Конечномерный случай этого неравенства называется неравенством Коши и был доказан Коши в 1821 году.
Формулировка
Пусть дано линейное пространство L{\displaystyle L\,\!} со скалярным произведением ⟨x,y⟩{\displaystyle \langle x,\;y\rangle }. Пусть ∥x∥{\displaystyle \|x\| \,\!} — норма, порождённая скалярным произведением, то есть ∥x∥≡⟨x,x⟩,∀x∈L{\displaystyle \|x\|\equiv {\sqrt {\langle x,\;x\rangle }},\;\forall x\in L}. Тогда для любых x,y∈L{\displaystyle x,\;y\in L} имеем:
|⟨x,y⟩|⩽∥x∥⋅∥y∥,{\displaystyle |\langle x,\;y\rangle |\leqslant \|x\|\cdot \|y\|,}причём равенство достигается тогда и только тогда, когда векторы x{\displaystyle x\,\!} и y{\displaystyle y\,\!} пропорциональны (коллинеарны).
Комментарии
В конечномерном случае можно заметить, что ∥x∥2∥y∥2−⟨x,y⟩2=S(x,y)2{\displaystyle \|x\|^{2}\|y\|^{2}-\langle x,\;y\rangle ^{2}=S(x,\;y)^{2}}
- где S(x,y){\displaystyle S(x,\;y)} — площадь параллелограмма, натянутого на векторы x{\displaystyle x\,\!} и y{\displaystyle y\,\!}.
В общем случае:
∥x∥2−⟨x,y⟩2∥y∥2=∥x−⟨x,y⟩∥y∥2y∥2.{\displaystyle \|x\|^{2}-{\frac {\langle x,\;y\rangle ^{2}}{\|y\|^{2}}}=\left\|x-{\frac {\langle x,\;y\rangle }{\|y\|^{2}}}y\right\|^{2}.\,\!}Примеры
- В пространстве комплекснозначных квадратично суммируемых последовательностей l2{\displaystyle l^{2}\,\!} неравенство Коши — Буняковского имеет вид:
- |∑k=1∞xky¯k|2⩽(∑k=1∞|xk|2)⋅(∑k=1∞|yk|2),{\displaystyle \left|\sum \limits _{k=1}^{\infty }x_{k}{\bar {y}}_{k}\right|^{2}\leqslant \left(\sum _{k=1}^{\infty }|x_{k}|^{2}\right)\cdot \left(\sum _{k=1}^{\infty }|y_{k}|^{2}\right),}
- где y¯k{\displaystyle {\bar {y}}_{k}} обозначает комплексное сопряжение yk{\displaystyle y_{k}\,\!}.
- В пространстве комплексных квадратично интегрируемых функций L2(X,F,μ){\displaystyle L^{2}(X,\;{\mathcal {F}},\;\mu )} неравенство Коши — Буняковского имеет вид:
- |∫Xf(x)g(x)¯μ(dx)|2⩽(∫X|f(x)|2μ(dx))⋅(∫X|g(x)|2μ(dx)).{\displaystyle \left|\int \limits _{X}f(x){\overline {g(x)}}\,\mu (dx)\right|^{2}\leqslant \left(\int \limits _{X}\left|f(x)\right|^{2}\,\mu (dx)\right)\cdot \left(\int \limits _{X}\left|g(x)\right|^{2}\,\mu (dx)\right).}
- В пространстве случайных величин с конечным вторым моментом L2(Ω,F,P){\displaystyle L^{2}(\Omega ,\;{\mathcal {F}},\;\mathbb {P} )} неравенство Коши — Буняковского имеет вид:
- cov2(X,Y)⩽D[X]⋅D[Y],{\displaystyle \mathrm {cov} ^{2}(X,\;Y)\leqslant \mathrm {D} [X]\cdot \mathrm {D} [Y],}
- где cov{\displaystyle \mathrm {cov} \,\!} обозначает ковариацию, а D{\displaystyle \mathrm {D} \,\!} — дисперсию.
Доказательство
- 0⩽⟨λx+y,λx+y⟩=λ2⟨x,x⟩+2λ⟨x,y⟩+⟨y,y⟩.{\displaystyle 0\leqslant \langle \lambda x+y,\;\lambda x+y\rangle =\lambda ^{2}\langle x,\;x\rangle +2\lambda \langle x,\;y\rangle +\langle y,\;y\rangle .}
Значит дискриминант многочлена λ2⟨x,x⟩+2λ⟨x,y⟩+⟨y,y⟩{\displaystyle \lambda ^{2}\langle x,\;x\rangle +2\lambda \langle x,\;y\rangle +\langle y,\;y\rangle } неположительный, то есть
- D=(2⟨x,y⟩)2−4⟨x,x⟩⟨y,y⟩⩽0.{\displaystyle D=(2\langle x,\;y\rangle )^{2}-4\langle x,\;x\rangle \langle y,\;y\rangle \leqslant 0.}
Следовательно,
- |⟨x,y⟩|⩽∥x∥⋅∥y∥.{\displaystyle |\langle x,\;y\rangle |\leqslant \|x\|\cdot \|y\|.}
Примечания
- ↑ Bounjakowsky W. «Mémoires de l’Académie des sciences de St-Pétersbourg. 7 série», 1859, t. 1, № 9.
Неравенство Коши — Буняковского — ПриМат
Неравенство, связывающее норму и скалярное произведение векторов векторного пространства. Эквивалентно неравенству треугольника для нормы в пространстве со скалярным произведением: . Справедливое для любых вещественных чисел
Доказательство:
Рассмотрим квадратный трехчлен: , где , , . Так как квадратный трехчлен принимает только неотрицательные значения, то его дискриминант неположителен, а именно, . Подставляя в неравенство значения коэффициентов , и , получаем неравенство Коши-Буняковского.
Доказательство «неравенства треугольника» :
Докажем неравенство Минковского: .
Используя неравенство Коши, получаем:
Извлекая из обеих частей этого неравенства квадратные корни, получаем неравенство Минковского. Полагая в неравенстве Минковского , получаем неравенство т. е. неравенство треугольника для расстояния .
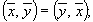


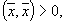 при
при  ,
, ,
, —
нулевой вектор,
—
нулевой вектор,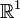 размерности
1 (вещественная прямая)
размерности
1 (вещественная прямая) размерности
2 (евклидова плоскость)
размерности
2 (евклидова плоскость) размерности
3 (евклидово трехмерное пространство)
размерности
3 (евклидово трехмерное пространство) и
и справедливо неравенство
справедливо неравенство .
.
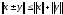 .
.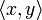 . Пусть
. Пусть 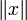 — норма, порождённая скалярным произведением, то есть
— норма, порождённая скалярным произведением, то есть  . Тогда для любых
. Тогда для любых 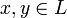 имеем
имеем ,
,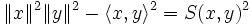 , где S(x,y) — площадь параллелограмма, натянутого на векторы x и y.
, где S(x,y) — площадь параллелограмма, натянутого на векторы x и y.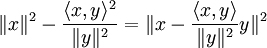
 ,
, обозначает комплексное сопряжение yk.
обозначает комплексное сопряжение yk. .
.![\mathrm{cov}^2(X,Y) \le \mathrm{D}[X] \cdot \mathrm{D}[Y]](/800/600/https/dic.academic.ru/pictures/wiki/files/50/2c7bab23479cb2caeabdbf2145b2b634.png) ,
,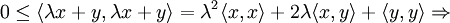
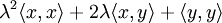 неположительный, то есть
неположительный, то есть