Урок 33. круг. окружность (центр, радиус, диаметр) — Математика — 3 класс
Математика, 3 класс
Урок №33. Круг. Окружность (центр, радиус, диаметр)
Перечень вопросов, рассматриваемых в теме:
— что такое окружность и круг?
— какие элементы имеет окружность?
— чем отличается круг от окружности?
Глоссарий по теме:
Окружность — это замкнутая кривая, все точки которой одинаково удалены от центра.
Круг – это геометрическая фигура, которая ограничена окружностью.
Радиус- это отрезок, соединяющий центр окружности с любой точкой на окружности.
Диаметр – отрезок, который соединяет две точки окружности, проходящий через центр.
Основная и дополнительная литература по теме урока:
1. Моро М. И., Бантова М. А. и др. Математика 3 класс. Учебник для общеобразовательных организаций М.; Просвещение, 2017. с. 94-96.
2. Рудницкая В. Н. Тесты по тматематике:3 класс.
3. Рудницкая В.Н. Контрольные работы по математике:3 класс. М.: Издательство»Экзамен», 2017, с. 49-54.
4. Рудницкая В. Н. КИМ ВПР. Математика .3 класс. М.: Издательство «Экзамен», 2018, с. 77-79.
Теоретический материал для самостоятельного изучения
С незапамятных времен люди используют в своей жизни круг.
1. Около 3300 года до нашей эры стали применять гончарный круг, делать круглую посуду – тарелки, вазы, кастрюли, горшки, сковородки. У посуды есть окружность (верхний край) и круг (дно).
2. Мы не можем представить свою жизнь без машин: автобус, велосипед, швейная, машинки, самолет, луноход, различные станки, подъемный кран…Они не похожи друг на друга, но присмотримся к ним повнимательнее. Есть у них у всех похожие части – детали, и одна из них – колесо. Сначала колеса были круглые и гладкие, чтобы по земле легко катились, а потом человек придумал много разных колес.
3. Круг и окружность широко применяются в архитектуре и искусстве: круглые арки, своды, купола. Круг – это форма кочевых шатров и поселений. Еще древние греки обнаружили, что с помощью циркуля и линейки можно построить множество фигур, включая шестиугольники, квадраты и другие правильные многоугольники, и создавать волшебные узоры.
Круг – это форма кочевых шатров и поселений. Еще древние греки обнаружили, что с помощью циркуля и линейки можно построить множество фигур, включая шестиугольники, квадраты и другие правильные многоугольники, и создавать волшебные узоры.
4. Необозрима сфера применения круга в математике: тригонометрический круг, круги Эйлера, задачи на построение, круговые диаграммы и т.д. Многие приборы имеют круглую шкалу, в математике таким прибором является транспортир .
5. Картинки с волшебными кругами люди используют в медицинских целях, когда на них смотришь, кажется, что они двигаются. Если смотреть на них несколько минут, то проходит головная боль.
6. Также человек использует круг, как универсальный символ, означающий целостность, непрерывность, первоначальное совершенство. Три концентрических круга символизируют прошлое, настоящее и будущее; три сферы земли: землю, воздух и воду.
Круг в жизни человека имеет очень важную роль, и без использования круглых предметов обойтись невозможно.
Окружность и круг – удивительно гармоничные, совершенные, простые фигуры. Окружность – единственная замкнутая кривая, которая может “скользить сама по себе”, вращаясь вокруг центра, поэтому колеса делают круглыми, а не квадратными или треугольными.
Круг – это колесо. Колесо – это прогресс – движение вперед. Если остановится колесо, то остановится колесо Истории. Остановятся все виды транспорта, остановятся все часы и механизмы, фабрики и заводы.
Круг – символ цикличности, повторяемости. Все движется по кругу.
Круг дает ощущение взаимосвязи с Космосом.
Сама природа выбирает эту удобную и компактную форму как шар и круг.
Сравним две фигуры.
На 1 рисунке видим замкнутую кривую линию, на которой находятся точки К и С на одинаковых расстояниях от точки О.Такая замкнутая кривая называется окружностью. Точка О — центр окружности. Все точки, поставленные на окружности, находятся на одинаковом расстоянии от центра!
Есть специальный инструмент, который позволяет чертить окружности – это циркуль.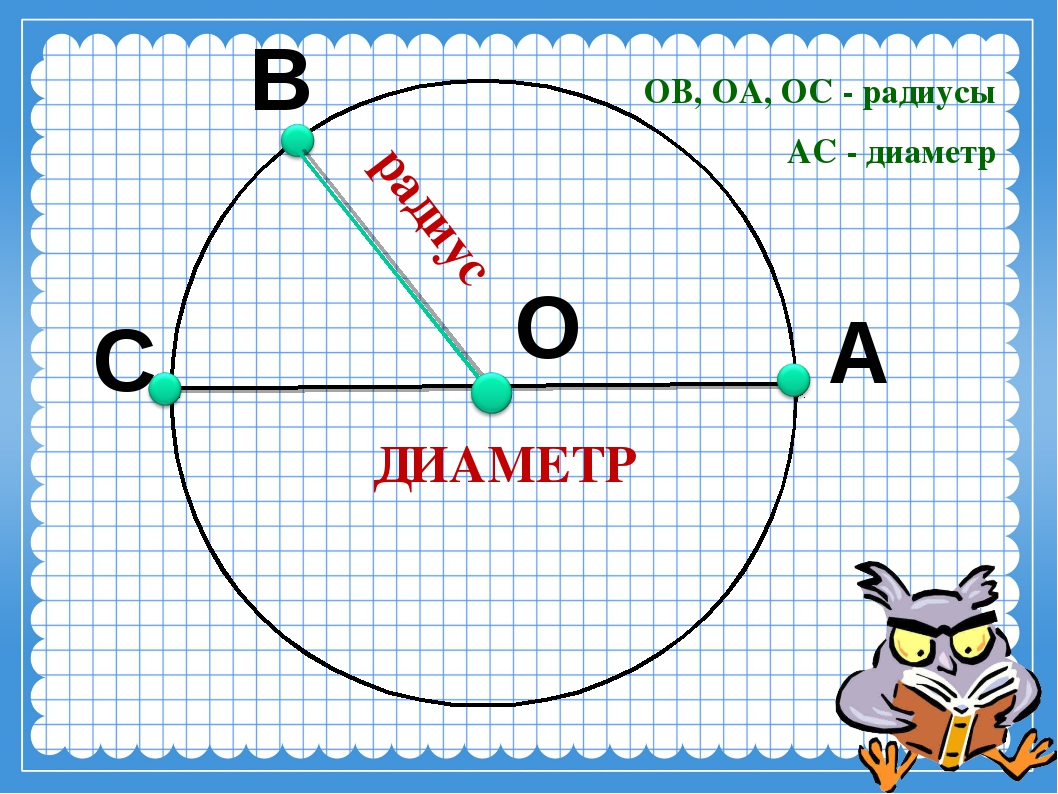
На рисунке 2 видим геометрическую фигуру, которая ограничена окружностью. Эта фигура называется круг.
Вывод: окружность — граница круга; круг — часть внутри окружности. В таблице указаны отличительные признаки круга и окружности:
Если соединить любую точку окружности с ее центром, то получится отрезок, который называется радиусом.
Если соединить 2 точки окружности, проходящих через центр, получится отрезок, который называется диаметром.
Диаметр делит круг на две равные части и все диаметры у окружности равной длины.
Задания тренировочного модуля:
1. Длина радиуса составляет 6 см. Чему равен диаметр окружности?
6см; 12 см; 3см.
Правильный ответ: 12см.
2. Заполните таблицу
радиус | 4 см | 3 см | 7 дм | 5 дм |
диаметр |
Правильный ответ:
радиус | 4 см | 3 см | 7 дм | 5 дм |
диаметр | 8 см | 6 см | 14 дм | 10 дм |
Урок 26.
 окружность и круг. сфера и шар — Математика — 5 класс
окружность и круг. сфера и шар — Математика — 5 классМатематика
5 класс
Урок №26
Окружность и круг. Сфера и шар
Переченьрассматриваемыхвопросов:
— понятия «окружность», «круг», «сфера», «шар» и их элементы;
— изображение окружности на плоскости, сферы в пространстве.
Тезаурус
Окружность – это плоская замкнутая кривая, все точки которой находятся на одинаковом расстоянии от некоторой точки – её центра.
Круг – плоская геометрическая фигура, являющаяся местом точек, расположенных на одинаковом расстоянии от некоторой точки (центра).
Центр окружности – это точка, равноудалённая от точек окружности.
Радиус окружности – это отрезок, соединяющий какую-нибудь точку этой окружности с её центром.
Хорда окружности – это отрезок, соединяющий какие-нибудь две точки окружности.
Диаметр окружности – это хорда, проходящая через центр окружности.
Шар – это геометрическое тело, совокупность всех точек пространства, находящихся от центра на расстоянии, не больше заданного.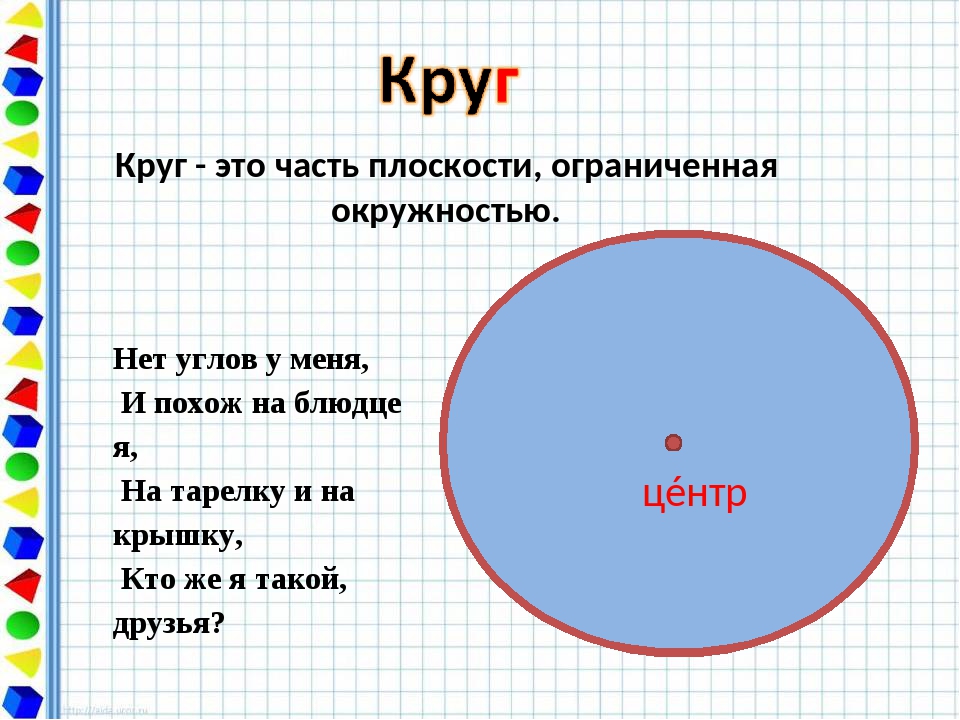
Сфера – это замкнутая поверхность, геометрическое место точек в пространстве, равноудалённых от данной точки, которую называют центром сферы.
Обязательная литература
Никольский С. М. Математика. 5 класс. Учебник для общеобразовательных учреждений.// С. М. Никольский, М. К. Потапов, Н. Н. Решетников и др. – М.: Просвещение, 2017. – 272 с.
Дополнительная литература
1. Чулков П. В. Математика: тематические тесты. 5 класс.// П. В. Чулков, Е. Ф. Шершнёв, О. Ф. Зарапина. – М.: Просвещение, 2009. – 142 с.
2. Шарыгин И. Ф. Задачи на смекалку: 5-6 классы.// И. Ф. Шарыгин, А. В. Шевкин. – М.: Просвещение, 2014. – 95 с.
Теоретический материал для самостоятельного изучения
Ещё в глубокой древности люди изобрели колесо, придумали гончарный круг, сделали украшения в виде колец, то есть создали предметы, в основе которых лежит окружность или круг. В современных устройствах эти геометрические фигуры тоже встречаются очень часто. Сегодня мы поговорим не только о том, как они используются в наше время, но и выясним их отличие друг от друга.
Итак, что же такое окружность?
Окружность – это замкнутая плоская кривая, которая состоит из всех точек на плоскости, равноудалённых от заданной точки. Эта точка называется центром окружности.
Построим окружность. Для этого поставим точку О. Возьмём циркуль и выставим с помощью линейки отрезок длиной 3 см. Поставим иголку циркуля в точку О и начертим окружность, вращая ножку циркуля с грифелем вокруг этой точки. Грифель описывает замкнутую линию, которую называют окружностью. Часть плоскости, которая лежит внутри окружности, вместе с самой окружностью, называют кругом, то есть окружность есть граница круга.
При построении окружности расстояние между ножками циркуля не меняется. Поэтому все точки окружности равно удалены от точки О. Точку O называют центром и окружности, и круга. Отметим на окружности любую точку – например, точку L. Построим отрезок, соединяющий точку L с центром окружности – точкой О.
Отрезок ОL называют радиусом окружности.
Отметим на окружности любые две точки.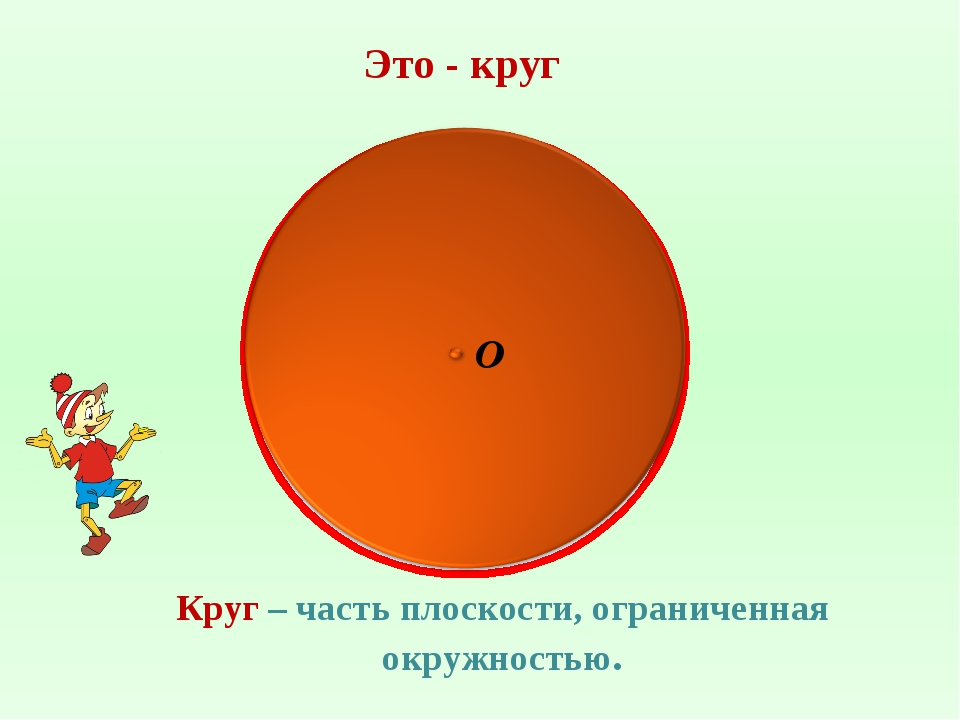 Например, C и D. Построим отрезок, соединяющий точки C и D.
Например, C и D. Построим отрезок, соединяющий точки C и D.
Отрезок CD называют хордой окружности. Некоторые хорды окружности проходят через её центр. Например, хорда AB проходит через центр окружности. Такую хорду называют диаметром окружности. То есть АВ – диаметр окружности.
Концы диаметра делят окружность на две равные части. Длина диаметра окружности равна двум радиусам. Две точки делят окружность на две части, называемые дугами. Например, CD. Обычно рассматривается одна из дуг окружности, определяемая по смыслу задачи.
Окружность разбивает плоскость на две части – внутреннюю область и внешнюю.
Давайте представим себе яблоко и воздушный шарик.
Чем они отличаются друг от друга?
Они оба имеют форму шара. Однако воздушный шарик полый внутри. Для таких предметов в математике есть название – сфера. А яблоко, с точки зрения математиков, – это шар.
Шар–это геометрическое тело, совокупность всех точек пространства, находящихся от центра на расстоянии, не больше заданного.
Отрезок, соединяющий точку поверхности шара с его центром, называется радиусом шара.
Отрезок, соединяющий две точки поверхности шара и проходящий через центр шара, называют диаметром шара.
Поверхность шара называется сферой.
Сфера – это замкнутая поверхность, геометрическое место точек в пространстве, равноудалённых от данной точки, которую называют центром сферы.
Окружность и круг являются плоскими фигурами, то есть такими, которые располагаются в пределах одной плоскости. Такие фигуры – это не что иное, как рисунки на листе бумаги. Рассмотренные на уроке сфера и шар относятся к пространственным телам. Между сферой, шаром, окружностью и кругом есть взаимосвязь. Сфера и шар образуются вращением вокруг оси окружности и круга соответственно.
Легенда о циркуле
В жизни для построений мы используем различные инструменты. Так, для того чтобы нарисовать окружность, необходим циркуль. Но как появился циркуль? Обратимся к мифам Древней Греции.
В далёкие времена в Афинах жил юноша, которого звали Талос. Он с детства был очень талантлив. В 12 лет он изобрёл гончарный круг для изготовления посуды. Также он придумал первую пилу, обратив в живой природе внимание на то, что скелет рыбы напоминает острые зубья. И наконец, Талос изобрёл устройство для построения окружностей, так называемый циркуль – инструмент в виде двух одинаковых стержней, соединённых шарниром. Так гласит легенда, а как было на самом деле, история умалчивает: известно лишь то, что на древних памятниках искусства фигуры и орнаменты из окружностей, умело выполненные древними мастерами, почти идеальны.
Он с детства был очень талантлив. В 12 лет он изобрёл гончарный круг для изготовления посуды. Также он придумал первую пилу, обратив в живой природе внимание на то, что скелет рыбы напоминает острые зубья. И наконец, Талос изобрёл устройство для построения окружностей, так называемый циркуль – инструмент в виде двух одинаковых стержней, соединённых шарниром. Так гласит легенда, а как было на самом деле, история умалчивает: известно лишь то, что на древних памятниках искусства фигуры и орнаменты из окружностей, умело выполненные древними мастерами, почти идеальны.
Тренировочные задания
№ 1. Подпишите соответствующие элементы окружности.
Вспомним определения радиуса (это отрезок, соединяющий какую-нибудь точку этой окружности с её центром), хорды (это отрезок, соединяющий какие-нибудь две точки окружности), диаметра (это хорда, проходящая через центр окружности) и ценрта окружности (это точка, равноудалённая от точек окружности).
Правильный ответ:
BO – радиус;
ВА – диаметр;
DE – хорда;
О – центр окружности.
№ 2. Выберите правильный ответ.
Рассмотрим отрезок АК, длина которого равна 8см. Построено две окружности: первая – с центром в точке A, а вторая – с центром в точке К. Их радиусы, соответственно, равны 4 см и 6 см. Сколько общих точек имеют окружности?
Решение: чтобы ответить на вопрос, изобразим отрезок и окружности.
Ответ: общих точек будет две. Они будут лежать на пересечении двух окружностей.
Урок математики -«Окружность и круг»
Урок математики в 6 классе.
Тема: Окружность, круг.
Цели урока:
- Ввести понятия окружности, круга и их элементов, изучить формулу длины окружности, применять ее при решении задач, получать значение числа в ходе выполнения практической работы;
- развивать познавательный интерес учащихся, познакомить их с историческим материалом;
-
прививать учащимся навык самостоятельности в работе, учить трудолюбию, аккуратности.

Оборудование: циркуль, карандаши, таблицы, индикаторы настроения, картинки, картонные кружки разных размеров, нитка.
Ход урока.
1.Организационный момент.
Ребята, послушайте, какая тишина!
Это в школе начались уроки.
Мы не будем тратить время зря,
И приступим все к работе.
2. Мотивация урока.
Ребята, какие геометрические фигуры мы изучили? (Прямоугольник, треугольник, квадрат…)
В канун нового года принято украшать елку и мы с вами будем этим сегодня заниматься.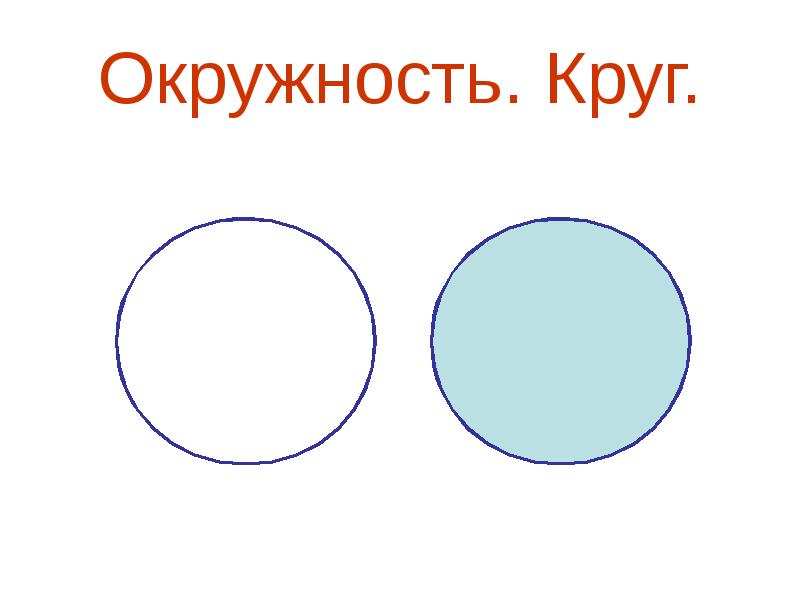 Но елка наша будет непростая, а математическая.
Но елка наша будет непростая, а математическая.
Какие фигуры мы с вами не изучали еще? Попробуйте отгадать загадку.
Нет углов у меня,
И похож на блюдце я,
На тарелку и на крышку,
На кольцо, на колесо.
Кто же я такой, друзья? (Круг)
У круга есть одна подруга,
Знакома всем ее наружность!
Она идет по краю круга
И называется -…(окружность)
Да, именно эти фигуры нам понадобятся сегодня для нашей математической елки.
Итак, тема нашего урока: «Окружность и круг».
3. Изучение нового материала.
Изучение нового материала.
Выходит девочка с моделью окружности (с ней в паре работает мальчик, который с места задает вопросы):
— А я – окружность. Внутри меня есть точка непростая.
Зовется центром, от точек всех моих он равноудален.
— В каких же отношеньях ты с прямой? — Смотря с какой.
Внутри меня, ее отрезок хордою зовут.
Чем ближе к центру, тем она длинней.
— Что будет, если хорда через центр пройдет?
— О!!! Ее диаметром геометр назовет.
— А сколько у тебя диаметров? — Ох, много…
Их бесконечность, выражаясь строго.
При том, заметьте, что из них любой
Всегда есть радиус двойной. — А радиус?
— То всякая прямая, что к центру тянется, его соединяя
С любой из точек, мне принадлежащих,
Точнее, на окружности лежащих.
Из истории.
Недаром древние греки считали окружность совершеннейшей и «самой круглой» фигурой. И в наши дни в некоторых ситуациях, когда хотят дать особую оценку, используют слово «круглый», которое считается синонимом слова «полнейший»: круглый отличник, круглый сирота и т.п.
Также считают и колесо – одно из самых замечательных изобретений человека.
Наверное, весь секрет кроется в свойствах удивительной линии – окружности.
Давайте сделаем вывод и «соберем» разбежавшиеся правила.
Начало:
Окружность – замкнутая линия без самопересечений…
Круг – это часть плоскости,…
Радиус – это отрезок, соединяющий…
Диаметр – это отрезок, соединяющий…
Хорда — это отрезок, соединяющий…
Диаметр – это хорда,…
Конец:
…все точки которой находятся на одинаковом расстоянии от центра.
…ограниченная окружностью.
…две точки окружности.
…проходящая через центр.
…соединяющий центр окружности с любой точкой на окружности.
…две точки окружности и проходящий через центр.
Назвать радиус, центр, диаметр, хорду окружности, изображенные на рисунке.
— Что изображено красным цветом? (Окружность)
— Что можно вырезать из бумаги? (Круг)
— А какая связь между ними?
Историческая справка.
Окружность – самая простая кривая линия. Радиус – происходит от латинского слова «радиус» — «спица колеса». Хорда – греческое слово и переводится – «струна». Диаметр – «диаметрос» — тоже греческое слово, переводится – «поперечник».
Хорда – греческое слово и переводится – «струна». Диаметр – «диаметрос» — тоже греческое слово, переводится – «поперечник».
Скажите, а с помощью какого инструмента мы можем построить окружность?
Загадка
Танцевальное движенье
Совершеннейшей ноги
И круги, круги, круги
Вызывают восхищенье.
Балерина создавала
Точный круг в один момент,
Подивился ей немало
Достославный геометр.
О прекрасной балерине
Вспоминал частенько он
Не по этой ли причине
… был изобретён.
(Циркуль)
Из истории возникновения циркуля.
Циркуль от латинского слова “circulus” — круг, окружность (“circa” — вокруг, кругом, то есть цирк – это круг)
Сейчас уже нельзя сказать, кто именно изобрел этот инструмент — история не сохранила для нас его имя, но легенды Древней Греции приписывают авторство Талосу, племяннику знаменитого Дедала, первого «воздухоплавателя» древности. История циркуля насчитывает уже несколько тысяч лет — судя по сохранившимся начерченным кругам, инструмент был знаком еще вавилонянам и ассирийцам (II — I века до нашей эры). На территории Франции, в галльском кургане был найден железный циркуль (I век нашей эры), во время раскопок в Помпеях было найдено много древнеримских бронзовых циркулей.
Давайте вместе построим несколько шариков для нашей математической елочки, радиусы которых равны 2см, 4см и 5см 5мм. Разукрасьте их.
Постройте на каждом из них радиус и диаметр. Измерьте, чему равен диаметр каждого шарика. Какой можно сделать вывод?
Измерьте, чему равен диаметр каждого шарика. Какой можно сделать вывод?
правильно, длина диаметра в 2 раза больше радиуса. Если обозначить r – радиус, а d – диаметр, тогда: d=2 r.
Я тоже для вас приготовила елочные шарики (картонные кружочки разных радиусов разных цветов, по 3 на одну парту).
Давайте измерим длину каждой окружности. В чем трудность? Да, к сожалению, специального прибора для измерения длины окружности нет. Но и это не останавливало человека. Предложите свой способ измерения длины окружности (обсуждение в группах).
Еще древние греки умели находить длину окружности по формуле
С = π d или С = 2πr , где d — диаметр окружности, а — радиус окружности.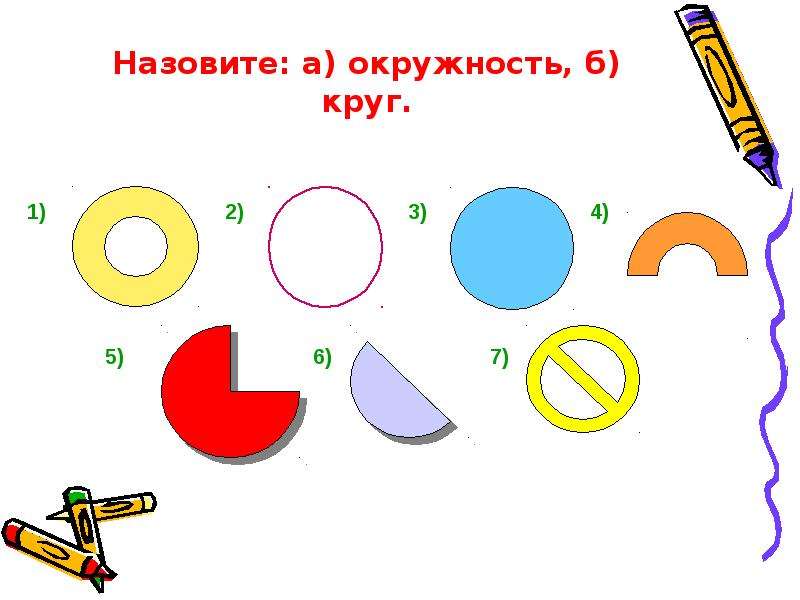
А что это за число π?
4. Первичное закрепление нового материала.
Рассмотрим на практической работе один из способов нахождения числа .
Если «опоясать» окружность ниткой, а затем ее «распрямить», то длина нитки будет приблизительно равна длине окружности. У вас имеются 3 круга различных диаметров. Измерьте длину окружности и диаметр каждого и найдите отношение длины к диаметру окружности. Результаты измерений заносятся в таблицу:
|
№ опыта |
Длина окружности (С) |
Диаметр (d) |
Значение π =С: d |
|
1 |
|
|
|
|
2 |
|
|
|
|
3 |
|
|
|
Если измерения выполнены достаточно точно, то у всех должно получиться значение π приблизительно равное 3,1-3,2.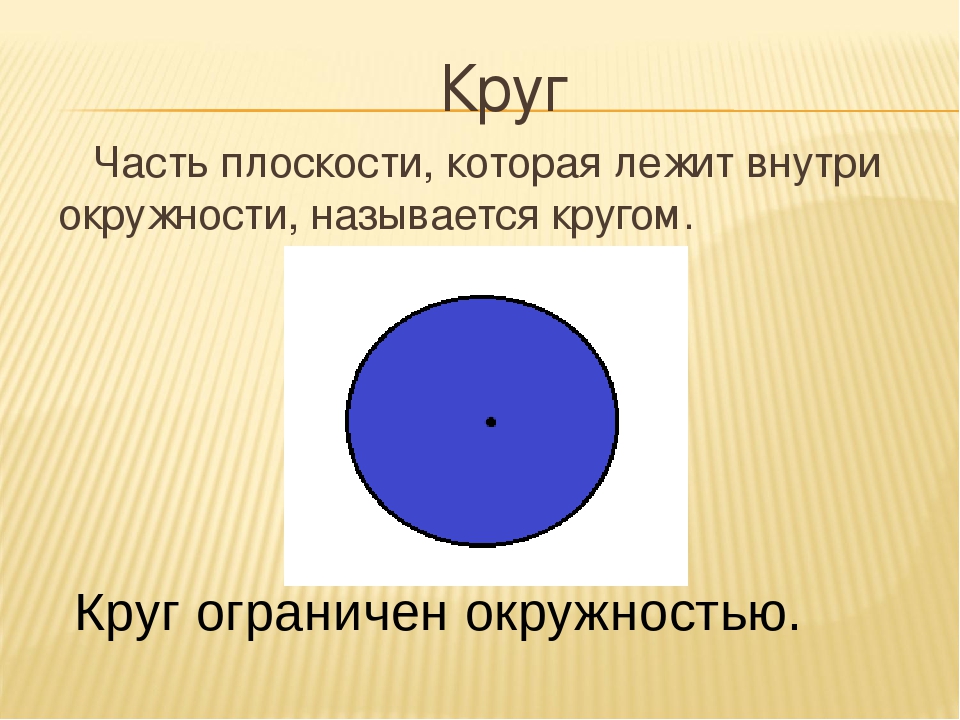
Из истории.
Еще в древности людям были известны многие геометрические фигуры, в том числе окружность и круг. Об этом свидетельствуют археологические раскопки. Еще тогда приходилось решать задачи на вычисление длины окружности. Сейчас известно, что значением числа π в разные времена считали различные числа. Так, в Древнем Египте (ок. 3500 лет назад) считали π = 3,16; древние римляне полагали, что π= 3,12. Все эти значения были определены опытным путем. Великий ученый Древней Греции Архимед определил, что значение π находится в следующих пределах 3<π<3. Легенда гласит, что когда древнегреческий город Сиракузы, где жил в своё время Архимед, захватили римляне, учёный, занимаясь научными исследованиями, чертил окружности на песке. Солдату, который пришёл убить его, он воскликнул: “Убей меня, но не тронь моих кругов”.
С помощью современных электронно – вычислительных машин число «пи» было вычислено точностью до миллиона знаков после запятой.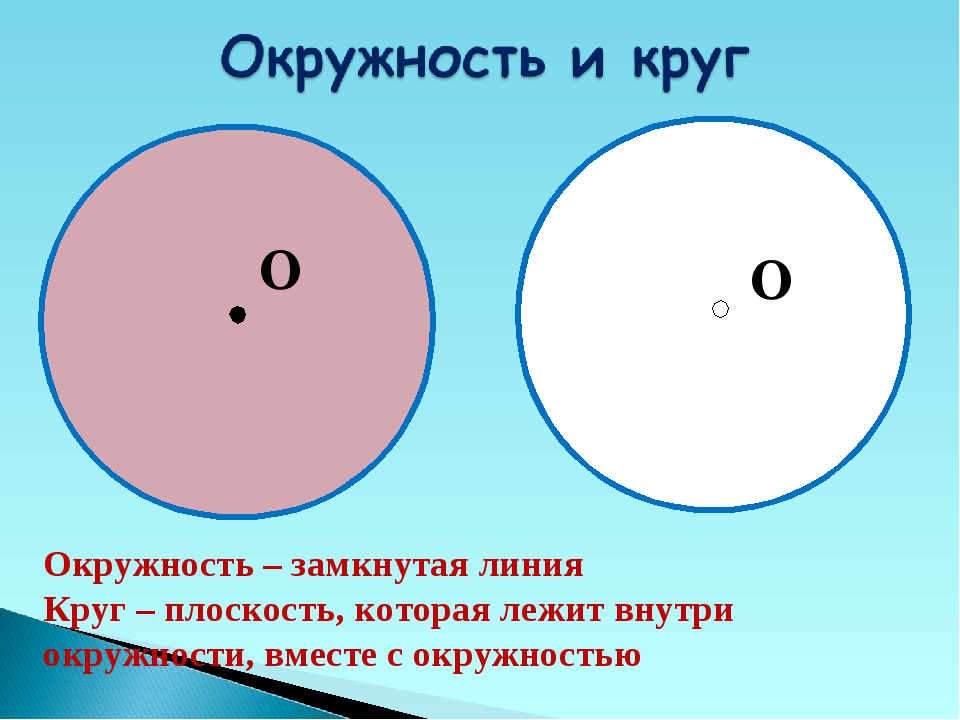 Для обозначения частного от деления длины окружности на диаметр впервые букву π использовал английский математик Джонс в 1706 г., но общепринятым это обозначение стало благодаря работам великого математика Эйлера. Он вычислил для числа я 153 десятичных знака.
Для обозначения частного от деления длины окружности на диаметр впервые букву π использовал английский математик Джонс в 1706 г., но общепринятым это обозначение стало благодаря работам великого математика Эйлера. Он вычислил для числа я 153 десятичных знака.
Для закрепления в памяти рационального выражения π – числа Архимеда (π =22/7) — может оказаться полезной шутка из учебника Магницкого:
Двадцать две совы скучали
На больших сухих суках.
Двадцать две совы мечтали
О семи больших мышах,
О мышах довольно юрких
В аккуратных серых шкурках.
Слюнки капали с усов
У огромных серых сов.
Его значение 3, 14159265358…
Желающим запомнить поможет мнемоника — придумывание стихотворных, легко запоминающихся фраз, число букв, в каждом слове которых указывает соответствующую цифру.
Мнемонические правила
Чтобы нам не ошибаться,
Надо правильно прочесть:
Три, четырнадцать, пятнадцать,
Девяносто два и шесть.
Надо только постараться
И запомнить всё как есть:
Три, четырнадцать, пятнадцать,
Девяносто два и шесть.
Три, четырнадцать, пятнадцать,
Девять, два, шесть, пять, три, пять.
Чтоб наукой заниматься,
Это каждый должен знать.
Можно просто постараться
И почаще повторять:
«Три, четырнадцать, пятнадцать,
Девять, двадцать шесть и пять».
5.Самостоятельная работа.
К нам на нашу математическую елочку пришли Колобок, Снеговик. Давайте их нарисуем и вычислим с помощью формулы С = 2πr длину окружности.
1) Рисуем колобка, окружность радиусом 4 см и разукрашиваем цветными карандашами.
2)Рисуем снеговика, радиусы окружностей которого 3 см, 4,5 см и 6 см. Затем разукрашиваем.
Из истории.
Неофициальный праздник «День числа Пи» отмечается 14 марта, которое в американском формате дат (месяц/день) записывается как 3.14, что соответствует приближённому значению числа π.
Ещё одной датой, связанной с числом π, является 22 июля, которое называется «Днём приближённого числа Пи» (англ. Pi Approximation Day), так как в европейском формате дат этот день записывается как 22/7, а значение этой дроби является приближённым значением числа π.
Памятник числу «пи» на ступенях перед зданием Музея искусств в Сиэтле.
6. Итоги урока.
Д/з.
1. Вычислите длину окружности, если r =5см.
2. Вычислите длину окружности, если d = 100 м.
3. Ученики организовали соревнования по фигурному катанию на велосипедах. В этих соревнованиях нужно было проехать четыре круга по окружности радиусом 3 м. Какое расстояние проехали велосипедисты в этом виде фигурного катания?
Творческое задание: по возможности придумать стихотворную фразу для запоминания числа π.
Рефлексия.
1. С какой геометрической фигурой мы познакомились?
2. Что надо знать, чтобы построить окружность?
3. С помощью какого инструмента мы ее строим?
4. Чему равно число π?
5. Что нового, интересного узнали?
Что нового, интересного узнали?
6. Что понравилось?
Наша математическая елка украшена, гости в сборе. Осталось только поздравить вас с наступающим Новым Годом.
Пусть Новый год вам принесет
Со снегом — смех,
С морозом — бодрость,
В делах успех,
А в духе — твердость.
Пусть все заветное свершится
И, пересилив даль дорог,
Надежда в дверь к вам постучится
И тихо ступит на порог.
Удачи вам!
Спасибо за урок!
Круг и его элементы | ЕГЭ по математике (профильной)
Круг и его элементы
Часть плоскости, ограниченная окружностью, называется кругом.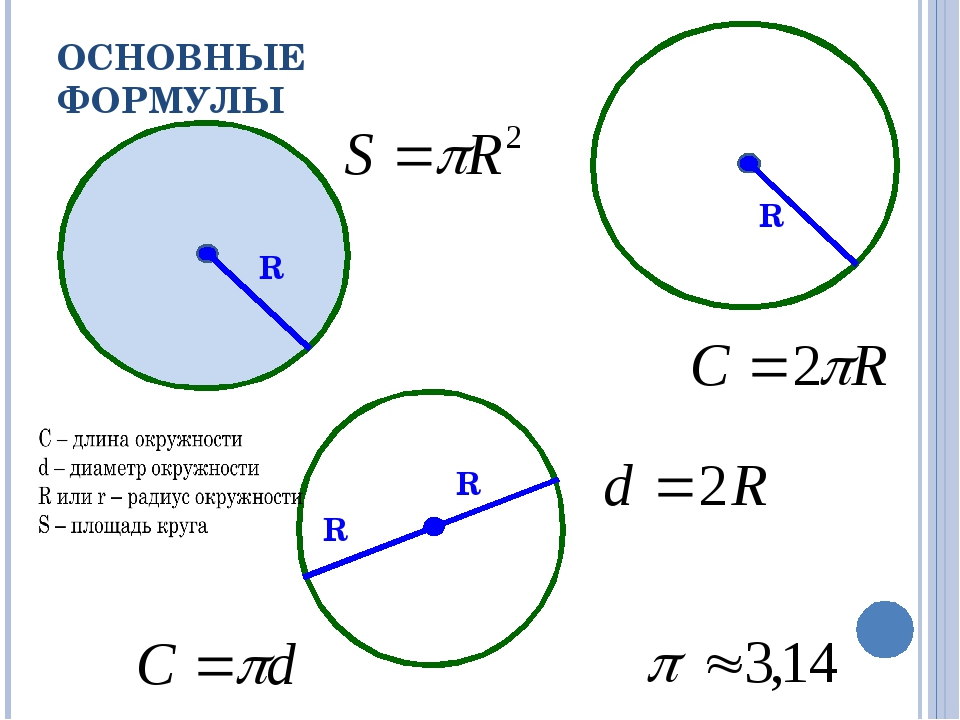
Окружность — это фигура, которая состоит из множества точек плоскости, равноудаленных от данной точки (центра).
Отрезок, соединяющий любую точку на окружности с центром окружности, называется радиусом ($R$).
$ОС=OD=OE=R$.
Отрезок, соединяющий любые две точки на окружности, называется хордой, а хорда, проходящая через центр, — диаметром ($d$).
$АВ$ и $ВС$ – хорды
$СЕ$ — диаметр
Свойства хорды и диаметра:
1. Диаметр равен двум радиусам $d=2R$;
2. Равные хорды стягивают равные дуги
Если $AB=CD$, то $∪AB=∪CD$.
3. Вся окружность составляет $360°$. Диаметр делит окружность на две полуокружности по $180°$.
4. Диаметр, проходящий через середину хорды, перпендикулярен этой хорде.
5. Диаметр, перпендикулярный хорде, делит хорду и стягиваемые ею дуги пополам.
$DC⊥AB, AM=MB, ∪AC=∪CB$
6. Хорды окружности, удаленные от центра на равные расстояния, равны.
7. Из двух хорд больше та, которая менее отдалена от центра. 2·36°}/{360°}={π·256·36°}/{360°}$
2·36°}/{360°}={π·256·36°}/{360°}$
Сокращаем полученную дробь на $36$
$S={π·256}/{10}$
Данную дробь легко перевести в десятичную дробь, необходимо просто с конца числа $256$ отделить один знак.
$S=25.6π$
В результате надо указать $S/π$, следовательно, $S/π={25.6π}/{π}=25.6$
Ответ: $25.6$
Окружность, круг, секущая и сектор
Окружность и круг — геометрические фигуры, взаимосвязанные между собой. Окружность есть граничная ломаная линия (кривая) круга,
Определение. Окружность — замкнутая кривая, каждая точка которой равноудалена от точки, называемой центром окружности.
Для построения окружности выбирается произвольная точка О, принятая за центр окружности, и с помощью циркуля проводится замкнутая линия.
Если точку О центра окружности соединить с произвольными точками на окружности, то все полученные отрезки будут между собой равны, и называются такие отрезки радиусами, сокращенно обозначаются латинской маленькой или большой буквой «эр» (r или R). Радиусов в окружности можно провести столько же, сколько точек имеет длина окружности.
Радиусов в окружности можно провести столько же, сколько точек имеет длина окружности.
Отрезок, соединяющий две точки окружности и проходящий через ее центр, называется диаметром. Диаметр состоит из двух радиусов, лежащих на одной прямой. Диаметр обозначается латинской маленькой или большой буквой «дэ» (d или D).
Правило. Диаметр окружности равен двум ее радиусам.
d = 2r
D = 2R
Длина окружности вычисляется по формуле и зависит от радиуса (диаметра) окружности. В формуле присутствует число ¶, которое показывает во сколько раз длина окружности больше, чем ее диаметр. Число ¶ имеет бесконечное число знаков после запятой. Для вычислений принято ¶ = 3,14.
Длина окружности обозначается латинской большой буквой «цэ» (C). Длина окружности пропорциональна ее диаметру. Формулы для расчета длины окружности по ее радиусу и диаметру:
C = ¶d
C = 2¶r
- Примеры
- Дано: d = 100 см.

- Длина окружности: C = 3,14 * 100 см = 314 см
- Дано: d = 25 мм.
- Длина окружности: С = 2 * 3,14 * 25 = 157 мм
Секущая окружности и дуга окружности
Всякая секущая (прямая линия) пересекает окружность в двух точках и делит ее на две дуги. Величина дуги окружности зависит от расстояния между центром и секущей и измеряется по замкнутой кривой от первой точки пересечения секущей с окружностью до второй.
Дуги окружности делятся секущей на большую и малую, если секущая не совпадает с диаметром, и на две равные дуги, если секущая проходит по диаметру окружности.
Если секущая проходит через центр окружности, то ее отрезок, расположенный между точками пересечения с окружностью, есть диаметр окружности, или самая большая хорда окружности.
Чем дальше секущая расположена от центра окружности, тем меньше градусная мера меньшей дуги окружности и больше — большей дуги окружности, а отрезок секущей, называемый хордой, уменьшается по мере удаления секущей от центра окружности.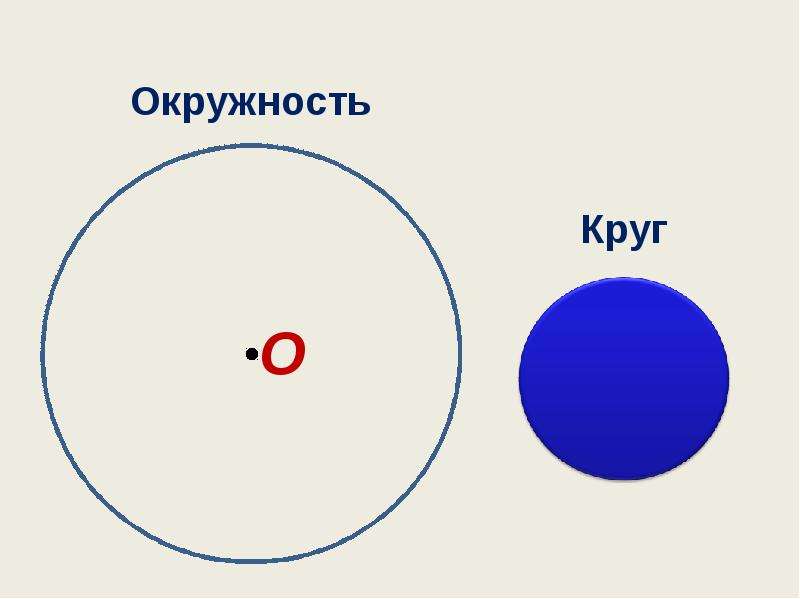
Определение. Кругом называется часть плоскости, лежащая внутри окружности.
Центр, радиус, диаметр окружности являются одновременно центром, радиусом и диаметром соответствующего круга.
Так как круг — это часть плоскости, то одним из его параметров является площадь.
Правило. Площадь круга (S) равна произведению квадрата радиуса ( r 2 ) на число ¶.
- Примеры
- Дано: r = 100 см
- Площадь круга:
- S = 3,14 * 100 см * 100 см = 31 400 см 2 ≈ 3м 2
- Дано: d = 50 мм
- Площадь круга:
- S = ¼ * 3,14 * 50 мм * 50 мм = 1 963 мм 2 ≈ 20 см 2
Если в круге провести два радиуса к разным точкам окружности, то образуется две части круга, которые называется секторами. Если в круге провести хорду, то часть плоскости между дугой и хордой называется сегментом окружности.
Определение. Сектор — это часть круга, ограниченная дугой окружности и двумя радиусами, проведенными к концам этой дуги. Сектор, образованный радиусами, расположенными под углом в 90° называется квадрантом.
Сектор — это часть круга, ограниченная дугой окружности и двумя радиусами, проведенными к концам этой дуги. Сектор, образованный радиусами, расположенными под углом в 90° называется квадрантом.
Площадь сектора составляет только часть площади круга, и ее величина пропорциональна длине дуги m или зависит от величины центрального угла a, образованного двумя радиусами с вершиной в центре круга.
Формула для вычисления площади сектора:
где S — площадь сектора; m — длина дуги; r — радиус круга; а — угловая величина дуги (и градусах).
Идеального математического круга не существует / Хабр
В точном компьютерном и физическом моделировании нуждается любой инженер, особенно если компания хочет создать самый износостойкий и прочный подшипник, его свойства окружность и параметры должны быть известны, чуть ли не до уровня атома.
Представьте, вы даёте задачу программисту найти точный процент и модель соприкосновения подшипника, и оказывается что это невозможно, так как и невозможно смоделировать точную окружность. Как и невозможно смоделировать точную площадь соприкосновения.
Как и невозможно смоделировать точную площадь соприкосновения.
Понятие круга является одним из универсальных математических понятий, дословно обобщаемым на случай произвольных метрических пространств. Но в разделе информатики, эта тема очень редко поднимается потому что до невозможности сложна.
Так что такое круг? И почему его точная математическая модель невозможна.
В научном понимании круг это правильный 65537 угольник (шестьдеся̀тпятьты̀сячпятисо̀ттридцатисемиуго́льник) — правильный многоугольник с 65 537 углами и 65 537 сторонами.
Значит для программиста круг это многоугольник с 65 537 углами — и эти углы будут соприкасаться с плоской поверхностью или такой же окружностью, и меняя равновесие всего это математического круга с 65 537 углами. Согласитесь что модель уже устарела?
Гауссом в 1796 году было доказано, что правильный n-угольник можно построить циркулем и линейкой, если нечётные простые делители n являются различными числами Ферма. В 1836 году П. Ванцель доказал, что других правильных многоугольников, которые можно построить циркулем и линейкой, не существует. Ныне это утверждение известно как теорема Гаусса — Ванцеля.
В 1836 году П. Ванцель доказал, что других правильных многоугольников, которые можно построить циркулем и линейкой, не существует. Ныне это утверждение известно как теорема Гаусса — Ванцеля.
Могу даже открыть секрет настолько узкий в отрасли подшипников, что большинство автомобильных, железнодорожных и авиа катастроф происходит именно по причине некачественных подшипников так как проверить качество и окружность порой невозможно так как наука работает в основном не с числами а «диапазонами» то и процент брака в подшипниковой индустрии из-за проблемы создания идеально ровного подшипника самый высокий.
Такую проблему мы наблюдаем и в играх
ТочностьИ эта точность очень низкая.
А 65 тысяч углов у круга это меньше миллиона.
Но даже и это не предел. Идеальный круг вообще бесконечен (имеет бесконечное количество углов). Как тогда его выразить в программировании, если любое число будет его неточной моделью? Или уже такая высокая точность будет ненужна? Ведь в любом массовом моделировании иза мельчайшей детали образуются каскадные лавинообразные эффекты которые дают разные результаты.
Спасибо за внимание.
Тригонометрический круг — материалы для подготовки к ЕГЭ по Математике
Тригонометрический круг — это самый простой способ начать осваивать тригонометрию. Он легко запоминается, и на нём есть всё необходимое.
Тригонометрический круг заменяет десяток таблиц.
- Перевод градусов в радианы и наоборот. Полный круг содержит градусов, или радиан.
- Значения синусов и косинусов основных углов. Помним, что значение косинуса угла мы находим на оси , а значение синуса — на оси .
- И синус, и косинус принимают значения от до .
- Значение тангенса угла тоже легко найти — поделив на . А чтобы найти котангенс — наоборот, косинус делим на синус.

- Знаки синуса, косинуса, тангенса и котангенса.
- Синус — функция нечётная, косинус — чётная.
- Тригонометрический круг поможет увидеть, что синус и косинус — функции периодические. Период равен .
Вот что мы видим на этом рисунке:
А теперь подробно о тригонометрическом круге:
Нарисована единичная окружность — то есть окружность с радиусом, равным единице, и с центром в начале системы координат. Той самой системы координат с осями и , в которой мы привыкли рисовать графики функций.
Мы отсчитываем углы от положительного направления оси против часовой стрелки.
Полный круг — градусов.
Точка с координатами соответствует углу ноль градусов. Точка с координатами отвечает углу в , точка с координатами — углу в . Каждому углу от нуля до градусов соответствует точка на единичной окружности.
Косинусом угла называется абсцисса (то есть координата по оси ) точки на единичной окружности, соответствущей данному углу .
Синусом угла называется ордината (то есть координата по оси ) точки на единичной окружности, соответствущей данному углу .
Например:
;
;
;
Всё это легко увидеть на нашем рисунке.
Итак, косинус и синус — координаты точки на единичной окружности, соответствующей данному углу. Косинус — абсцисса , синус — ордината . Поскольку окружность единичная, для любого угла и синус, и косинус находятся в пределах от до :
,
.
Простым следствием теоремы Пифагора является основное тригонометрическое тождество:
Для того, чтобы узнать знаки синуса и косинуса какого-либо угла, не нужно рисовать отдельных таблиц. Всё уже нарисовано! Находим на нашей окружности точку, соответствующую данному углу , смотрим, положительны или отрицательны ее координаты по (это косинус угла ) и по (это синус угла ).
Принято использовать две единицы измерения углов: градусы и радианы. Перевести градусы в радианы просто: градусов, то есть полный круг, соответствует радиан. На нашем рисунке подписаны и градусы, и радианы.
Если отсчитывать угол от нуля против часовой стрелки — он положительный. Если отсчитывать по часовой стрелке — угол будет отрицательным. Например, угол — это угол величиной в , который отложили от положительного направления оси по часовой стрелке.
Если отсчитывать по часовой стрелке — угол будет отрицательным. Например, угол — это угол величиной в , который отложили от положительного направления оси по часовой стрелке.
Легко заметить, что
,
.
Углы могут быть и больше градусов. Например, угол — это два полных оборота по часовой стрелке и еще . Поскольку, сделав несколько полных оборотов по окружности, мы возвращаемся в ту же точку с теми же координатами по и по , значения синуса и косинуса повторяются через . То есть:
,
,
где — целое число. То же самое можно записать в радианах:
,
.
Можно на том же рисунке изобразить ещё и оси тангенсов и котангенсов, но проще посчитать их значения. По определению,
,
.
В результате получим следующую таблицу.
Круг
Круг сделать легко: Нарисуйте кривую на расстоянии А так: Все точки находятся на одинаковом расстоянии от центра. |
Самостоятельно нарисовать
Вставьте булавку в доску, оберните вокруг нее веревку и вставьте в петлю карандаш.Держите веревку натянутой и нарисуйте круг!
Поиграй с ним
Попробуйте перетащить точку, чтобы увидеть, как меняются радиус и окружность.
(Посмотрите, сможете ли вы сохранить постоянный радиус!)
Радиус, диаметр и окружность
Радиус — это расстояние от центра наружу.
Диаметр проходит прямо по окружности через центр.
Окружность — это расстояние один раз по окружности.
А вот и действительно крутая вещь:
Когда мы разделим длину окружности на диаметр, мы получим 3,141592654 …
, что является числом π (Pi)
Итак, когда диаметр равен 1, длина окружности равна 3,14 1592654 … |
Можно сказать:
Окружность = π × Диаметр
Пример.
 Вы ходите по кругу диаметром 100 м. Как далеко вы прошли?
Вы ходите по кругу диаметром 100 м. Как далеко вы прошли?Пройденное расстояние = Окружность = π × 100 м
= 314м (с точностью до метра)
Также обратите внимание, что диаметр в два раза больше радиуса:
Диаметр = 2 × Радиус
Так же верно и то:
Окружность = 2 × π × Радиус
Вкратце:
| × 2 | × π |
| Радиус | Диаметр | Окружность |
Вспоминая
Длина слов может помочь вам запомнить:
- Радиус — кратчайшее слово и кратчайшая мера
- Диаметр длиннее
- Окружность самая длинная
Определение
Окружность плоская (двумерная), поэтому: |
Площадь
Площадь круга в π в раз больше квадрата радиуса, что записывается:
A = π r 2
Где
- A — это Площадь
- r — радиус
Чтобы вспомнить, подумайте «Пирог в квадрате» (хотя пироги обычно круглые):
Пример: Какова площадь круга радиусом 1.
 2 м?
2 м?Площадь = πr 2
= π × 1,2 2
= 3,14159 … × (1,2 × 1,2)
= 4,52 (до 2 знаков после запятой)
Или, используя диаметр:
A = ( π /4) × D 2
Площадьпо сравнению с площадью
Окружность составляет около 80% площади квадрата такой же ширины.
Фактическое значение (π / 4) = 0.785398 … = 78,5398 …%
И кое-что интересное для вас:
Посмотреть площадь круга по линиям
Имена
Поскольку люди изучали круги в течение тысяч лет, у них появились особые имена.
Никто не хочет говорить «линия, которая начинается на одной стороне круга, проходит через центр и заканчивается на другой стороне» , когда они могут просто сказать «Диаметр».
Итак, вот самые распространенные специальные имена:
линий
Линия, которая «просто касается» круга, когда проходит мимо, называется касательной .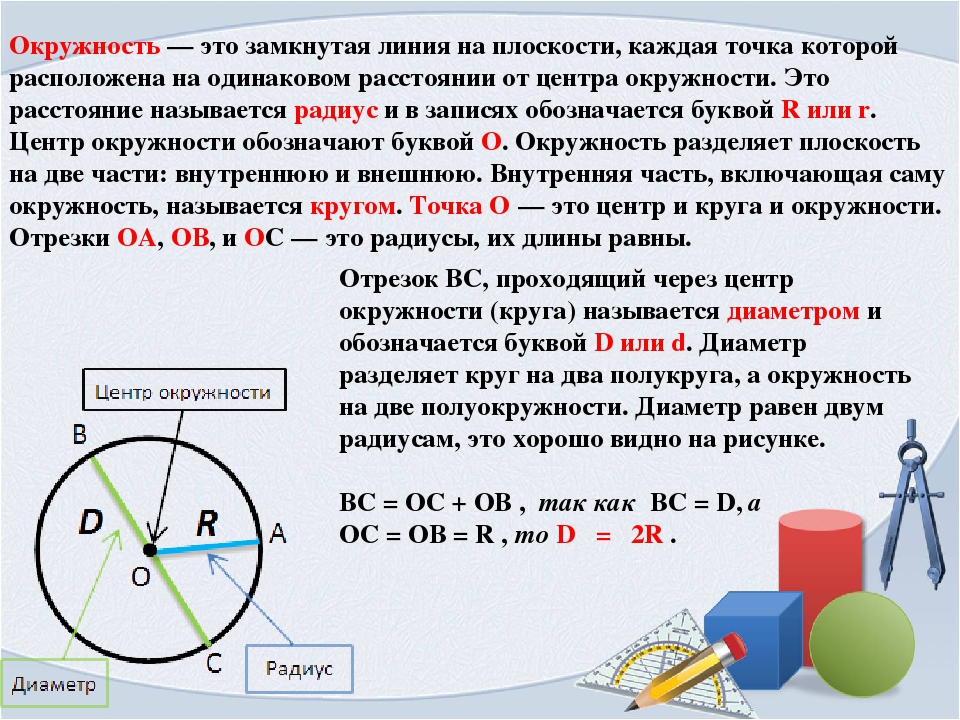
Линия, пересекающая круг в двух точках, называется секущей .
Отрезок линии, идущий от одной точки к другой на окружности круга, называется хордой .
Если он проходит через центр, он называется диаметром .
А часть окружности называется Дуга .
Ломтики
Есть два основных «кусочка» круга.
Кусочек «пиццы» называется сектором.
А отрезок, образованный аккордом, называется отрезком.
Общие сектора
Квадрант и Полукруг — это два особых типа сектора:
Четверть круга называется Квадрантом .
Полукруг называется Полукруг.
Внутри и снаружи
У круга есть внутренняя и внешняя стороны (конечно же!).Но у него также есть «включено», потому что мы можем оказаться прямо на круге.
Пример: «A» находится вне круга, «B» находится внутри круга, а «C» находится на круге.
Эллипс
Круг — это «частный случай» эллипса.
кругов
| Определение: Круг — это геометрическое место всех точек, равноудаленных от центральной точки. |
Определения, относящиеся к кругам
Диаметр = 2 x радиус окружности
arc: изогнутая линия, которая является частью окружности круг
аккорд: отрезок линии внутри круга, который касается 2 точки на окружности.
окружность: расстояние по окружности.
Диаметр : наибольшее расстояние от одного конца круга к другому.
начало: центр окружности
пи (): А число, 3,141592 .
.., равное (окружность) / (диаметр) любого круга.
радиус: расстояние от центра окружности до любой точки на Это.
сектор: похож на кусок пирога (круговой клин).
касательная к окружности: прямая, перпендикулярная радиусу касающийся ТОЛЬКО одной точки на окружности.
Окружность круга = PI x диаметр = 2 PI x радиус
где PI = = 3.141592 …
Площадь круга:
площадь = PI r 2
Длина круговой дуги: (с центральной угол)
если угол в градусов, тогда длина = x (PI / 180) x r
если угол в радиан, тогда длина = r x
Площадь сектора круга: (с центральным угол)
если угол в градусов, тогда площадь = (/ 360) x PI r 2
если угол в радианы, тогда площадь = ((/ (2PI)) x PI r 2
Уравнение окружности: (декартовы координаты)
для окружности с центром (j, k) и радиусом (r):
(x-j) ^ 2 + (y-k) ^ 2 = r ^ 2
Уравнение окружности: (полярные координаты)
для круга с центром (0, 0): r () = радиус
для круга с центром с полярными координатами: (c,) и радиус a :
r 2 — 2cr cos ( -) + с 2 = а 2
Уравнение окружности: (параметрические координаты)
для круга с началом (j, k) и радиусом r:
x (t) = r cos (t) + j y (t) = г sin (t) + к
Основная информация о кругах (геометрия, круги) — Mathplanet
Круг — это все точки в одной плоскости, которые находятся на равном расстоянии от центральной точки. Круг состоит только из точек на границе. Вы можете представить круг как обруч. Кругом являются только точки на границе. Точки внутри хула-хупа не являются частью круга и называются внутренними точками.
Круг состоит только из точек на границе. Вы можете представить круг как обруч. Кругом являются только точки на границе. Точки внутри хула-хупа не являются частью круга и называются внутренними точками.
Расстояние между средней точкой и границей круга называется радиусом. Отрезок, концы которого находятся на окружности и проходит через среднюю точку, называется диаметром. Диаметр в два раза больше радиуса. Отрезок линии, конечные точки которого находятся на круговой границе, но не проходят через среднюю точку, называется хордой.
Расстояние по окружности называется окружностью C и может быть определено с помощью радиуса r или диаметра d:
$$ \ C = 2 \ pi r $$
$$ C = \ pi d $$
Круг такой же, как 360 °. Вы можете разделить круг на более мелкие части. Часть круга называется дугой, а дуга — в соответствии с ее углом. Дуги делятся на малые дуги (0 ° Длина дуги l определяется путем подставления градуса дуги v и длины окружности C в следующую формулу: $$ l = C \ cdot \ frac {v} {360} $$ Когда диаметры пересекаются в центре круга, они образуют центральные углы. Пример Как и в случае с тортом выше, мы делим наш круг на 8 частей с одинаковым углом.Окружность круга составляет 20 единиц длины. Определите длину дуги каждой детали. Сначала нам нужно найти угол для каждой части, поскольку мы знаем, что полный круг равен 360 °, мы можем легко сказать, что каждая часть имеет угол 360/8 = 45 °. Мы подставляем эти значения в нашу формулу для длины дуг: $$ l = C \ cdot \ frac {v} {360} $$ $$ l = 20 \ cdot \ frac {45} {360} = 2,5 $$ Следовательно, длина наших дуг составляет 2,5 единицы длины. Мы могли бы еще проще сказать это, просто разделив окружность на количество частей одинакового размера: 20/8 = 2.5 Каков угол дуги окружности, если мы разделим круг на 12 частей одинакового размера Круг — это круглая фигура без углов и краев. В геометрии круг можно определить как замкнутую двумерную изогнутую форму. Вокруг нас есть несколько вещей круглой формы: автомобильная шина, настенные часы, которые показывают время, и леденец на палочке. Центр круга Центр окружности — это центральная точка окружности, от которой все расстояния до точек окружности равны. Это расстояние называется радиусом круга. Здесь точка P — центр окружности. Полукруг: Полукруг — это половина круга, образованная разрезанием всего круга вдоль отрезка прямой, проходящего через центр круга.Этот отрезок прямой называется диаметром круга. Четверть круга: Четверть круга — это четверть круга, образованная разделением круга на 4 равные части или полукруга на 2 равные части. Четверть круга также называют квадрантом. Интересные факты Шины старой желтой машины. Круглая крышка конфетной банки. Часы висят на стене. Кот играет с красным мячом. Сладкий шоколадный пончик, который я съел, И целый яблочный пирог у меня на тарелке. Блестящие пуговицы на моем платье. Какая форма? Сделать предположение. Они все круглые, как C-I-R-C-L-E. Вместо того, чтобы раздавать своим детям рабочие листы по геометрии, попросите ребенка наблюдать / определять предметы круглой формы, такие как браслет, дверная ручка или хула-хуп. Вы также можете попросить ребенка выбрать круглый предмет, например браслет или хула-хуп, и показать / определить на нем центр круга.Попросите их показать вам, как можно образовать полукруг или четверть круга. шар, площадь, периметр. Определения и формулы для радиуса круга, диаметра круга, окружности (периметра) круга, площади круга, хорды круга, дуги и дуги длина круга, сектор и площадь сектора круга Окружность = Как одна из самых основных форм на Земле — квадрат, круг и треугольник — круг был в центре внимания многих дизайнеров, иллюстраторов и художников, поскольку эта форма поддерживает структуры, которые являются как синтетическими, так и естественными. Итальянский художник Бруно Мунари исследовал визуальную историю всех трех, но круг занимал особое место. Мунари переходит к кругу, отмечая, что необходимо сразу же различать квадрат и круг, поскольку квадрат стоит по отношению к человеку, и круг , к божественному.« Древний текст говорит, что Бог — это круг, центр которого находится повсюду, но чья окружность нигде », — объясняет Мунари. Среди его многочисленных примеров — ореол, изображенный вокруг католических святых и мусульманский талисман, чтобы изобразить отчетливое отношение кругов к божественному, которое, по-видимому, даже пересекает религиозные границы. Слева — X Hour , серия кинетических арт-объектов, созданных Мунари в 1945 году. Пятьдесят пронумерованных пластин были изготовлены Данезе из Милана. Полудиски в центре каждого объекта прозрачные и вращаются по часовой стрелке, создавая геометрические фигуры, которые постоянно меняются. В «Книга кругов»: Визуализация сфер знаний Мануэль Лима дает исчерпывающее представление об истории дизайна круговой информации и дает систематизацию разновидностей круговых диаграмм, используемых сегодня дизайнерами визуализации данных. Тем не менее, рисование кругов требует некоторых базовых математических знаний. Так что давайте перейдем к этому! В основе современной математики Евклид определил круг как плоскую фигуру, содержащуюся одной линией, так что все прямые, падающие на нее из одной точки среди тех, что лежат внутри фигуры, равны одной. Другой. В более общем смысле, круг — это набор точек на плоскости, которые равноудалены от данной точки O . Расстояние r от центра называется радиусом, а точка o называется центром. Дважды радиус известен как диаметр d = 2r. Угол, под которым окружность выходит из центра, составляет полный угол, равный 360 ° или 2π радианам. Теперь предположим, что у нас есть системная ось (X, Y) , и нам нужно найти ( x (k), y (k) ) для точки K, расположенной на окружности C, с радиусом r . При визуализации некоторых данных, например круговых диаграмм, важно найти точку K. Теорема Пифагора и тригонометрия особенно полезны. Теорема Пифагора является фундаментальной и определяет отношения между тремя сторонами прямоугольного треугольника. Действительно, в нем говорится, что площадь квадрата гипотенузы равна сумме площадей квадратов двух других сторон треугольника (см. Уравнение ниже). Гипотенуза соответствует самой длинной стороне прямоугольного треугольника, противоположной прямому углу. Уравнения тригонометрии угол θ, образованный прямой линией, проведенной от центра O к точке K и оси x- или оси y- , помогают нам ориентироваться и охарактеризовать евклидово пространство, в котором это круг лежит. Имея эти уравнения и теорему, мы можем перейти к доказательству. Мы можем заменить то, что мы знаем, в приведенные выше уравнения. Другими словами, радиус r и угол θ позволяют найти как x (K) , так и y (K) .Мы можем предположить, что угол θ составляет от 1 до 360 °, и рассчитать для единичной окружности (окружности с радиусом 1). Как только мы найдем (x (K), y (K)) , на окружности C с радиусом r мы сможем найти бесконечный набор из k точек на окружности. Когда мы проводим линию между ними, мы получаем полный круг! Отлично! Но как мы можем нарисовать круг, используя часто используемые инструменты визуализации данных? Что ж, большинство инструментов обработки данных используют проверенные выше уравнения для рисования кругов.Ниже я подробно описываю, как это делается с помощью двух разных инструментов: Tableau, D3. Во-первых, Tableau позволяет довольно легко рисовать круги, используя метод создания фиктивных точек данных с помощью процесса уплотнения данных . Многочисленные сообщения в блогах сообщества Tableau объясняют этот метод, он создает дополнительные записи для недостающих данных среди k точек. Теперь, когда нам нужно нарисовать полукруг, в Таблице все, что нам нужно сделать, это вычислить набор пар {( x (k), y (k) )} примерно для 90 точек и использовать линейный график, чтобы нарисовать его.Ниже я представляю реальный пример, который основан на Таблице и уплотнении данных, где пары (x, y) — это , вычисленные для круга с радиусом 1. Во-вторых, круги рисования в D3 такие же, но используется другой синтаксис. D3 использует элемент круга SVG, который представляет собой форму, построенную с использованием четырех обязательных параметров: ( cx, cy, r ), которые являются координатой по оси x центра круга, его осью y и радиусом круга r, и элемент < path > для их рисования. Элемент < path > в SVG — один из самых мощных элементов. Он используется не только для рисования кругов, но также для рисования линий, кривых, дуг и многого другого. Элемент контура имеет только один параметр d и представляет собой список команд для рисования фигур. Действительно, существует много типов изогнутых линий, таких как: кривые Безье, гладкие формы, квадратичные кривые, которые являются более простой формой кривых Безье, и дуги, которые представляют собой части окружностей или эллипсов.D3 быстро справится со всеми этими задачами, если у вас есть четко сформулированная задача. Рисование кругов в Табло или D3, как видите, проще простого! Помимо рисования круга, важно отметить, что существует множество взаимосвязей между кругами и другими математическими понятиями в геометрии. Я привожу ниже примеры, начиная от кривых Безье, эллипсов и кончая постоянной Эйлера e . Определение: Окружность — это простая форма, состоящая из тех точек на плоскости, которые находятся на заданном расстоянии от данной точки — центра. Начало : центр круга Радиус : расстояние от центра круга до любой точки на нем. Диаметр : наибольшее расстояние от одного конца круга до другого. Диаметр = 2 × радиус (d = 2r). Окружность : расстояние по окружности. $ \ pi $ — pi : число, равное 3.141592 … или $ \ приблизительно \ frac {22} {7} $, то есть $ \ frac {\ text {окружность}} {\ text {диаметр}} $ любой окружности. Дуга : изогнутая линия, которая является частью окружности круга. Хорда : отрезок прямой внутри круга, который касается 2 точек на окружности.2 $ Если длина дуги составляет $ \ theta $ градусов или радиан, то центральный угол также измеряется в $ \ theta $ (градусах или радианах). Если вам известна длина дуги (в дюймах, ярдах, футах, сантиметрах, метрах …), вы можете найти измерение соответствующего центрального угла ($ \ theta $) по формуле: $ \ theta = 360 \ cdot \ frac {l} {P} = \ frac {360 \ cdot l} {2 \ cdot \ pi \ cdot r} = \ frac {180 \ cdot l} {\ pi \ cdot r} $ $ l $ — длина дуги.\ circ $ Случай 1: две секущие пересекают внутри окружности. Случай 2: две секущие пересекают за пределами окружности. Например, когда вы разрезаете торт, вы начинаете свои кусочки с середины.
Например, когда вы разрезаете торт, вы начинаете свои кусочки с середины.
Видеоурок Что такое круг? — [Определение, факты и пример]
Учитесь с помощью полной программы обучения математике K-5
Что такое круг? 

Давайте споем!
Давайте сделаем это!

Сопутствующий математический словарь
Геометрия кругов
Просто прокрутите вниз или щелкните то, что вы хотите, и я прокручу вниз для вас! Радиус окружности: Радиус круга — это расстояние от центра круга до внешнего края. Диаметр круга: Диаметр круга — это наибольшее расстояние по окружности.  (Диаметр проходит через центр круга. Это самое длинное расстояние.)
(Диаметр проходит через центр круга. Это самое длинное расстояние.) Окружность круга (периметр круга): Окружность круга — это периметр — расстояние по внешнему краю.
, где r = радиус окружности
и pi = 3,141592 … Хорда круга: Хорда окружности — это отрезок прямой, соединяющий одну точку на краю окружности с другой точкой на окружности.
(Диаметр — хорда — это самая длинная хорда!) математики для рисования кругов.
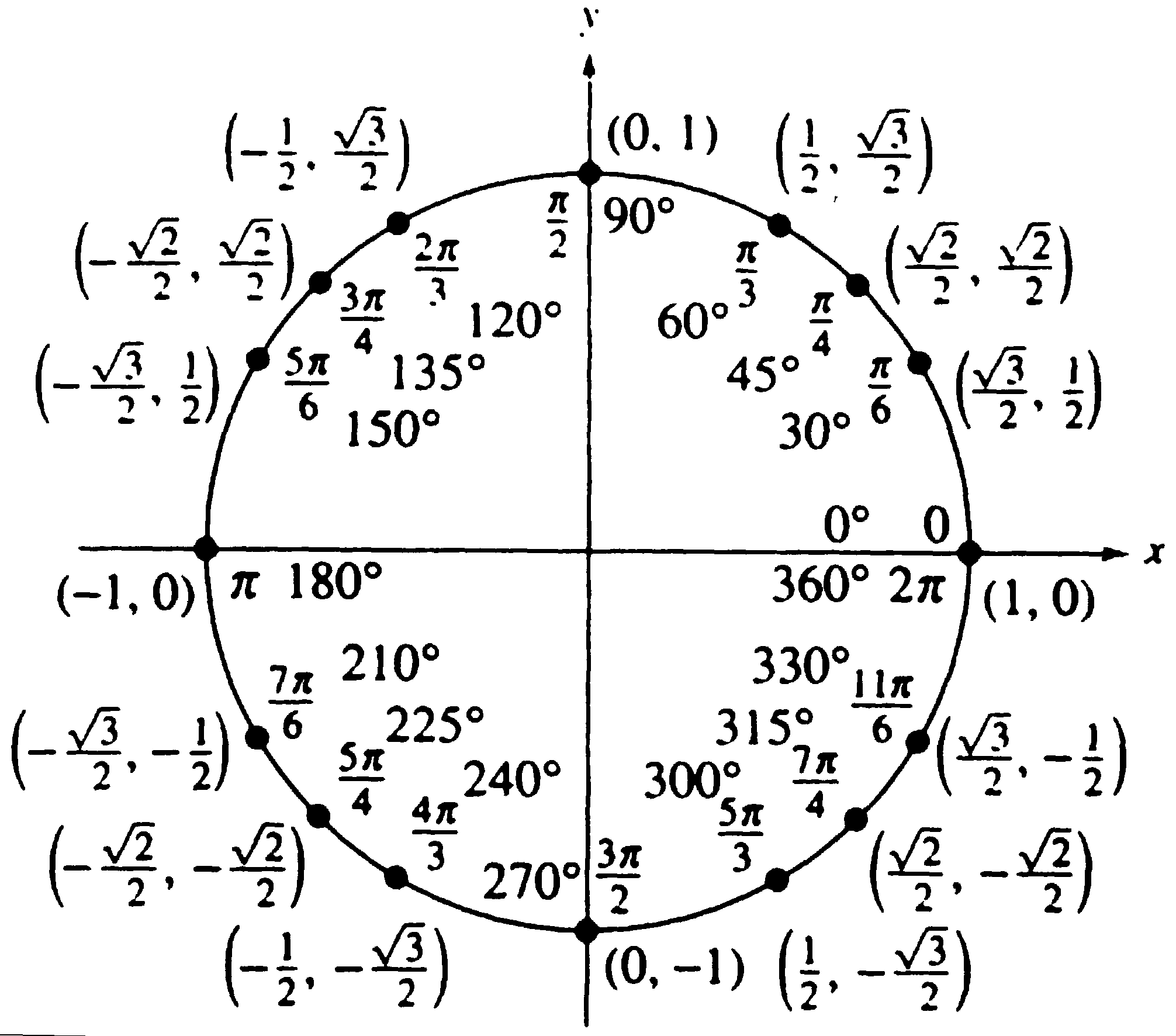 Круги — основная форма… | Марины Силивестру | Nightingale
Круги — основная форма… | Марины Силивестру | Nightingale
Tableau
D3
Окружности, начало координат, радиус, диаметр, окружность, пи, сектор, касательная
Окружность $ = \ pi \ times диаметра $.
Окружность $ = \ pi \ times d = 2 \ times \ pi \ times r $
Дуга окружности измеряется в градусах или радианах — например: 90 ° или $ \ frac {\ pi} {2} $ — четверть круга,
180 ° или $ \ pi $ — половина круг.
Дуга меньше 360 ° (или $ 2 \ pi $), потому что это весь круг. Уголки
Центральный угол
Углы между двумя секущими
На рисунке дуга AB равна 60 °, а дуга CD — 50 °.
Таким образом, угол 1 и 2 составляют ½ (60 ° + 50 °) = 55 °.



 .., равное (окружность) / (диаметр) любого круга.
.., равное (окружность) / (диаметр) любого круга.