История развития геометрии. История возникновения геометрии.
Геометрия — одна из древнейших отраслей математики. Геометрические тела были известны задолго до того, как были выведены математические принципы. Геометрия — это математическое исследование точек, линий, плоскостей, замкнутых плоских фигур и твердых тел. Используя это, можно описать или построить каждый видимый и невидимый предмет.
Геометрия происходит от слова «geo» — земля, «metria» — мера. Геометрия возникла как область знаний, занимающаяся пространственными отношениями. Геометрия одна из двух областей математики, вторая — арифметика, или алгебра.
История возникновения геометрии
Геометрия с практической точки зрения — это потребность измерять формы. Считается, что геометрия впервые стала важной, когда Египетский фараон хотел обложить налогом фермеров, которые выращивали урожай вдоль реки Нил. Чтобы вычислить правильную сумму налога, люди фараона должны были измерить количество обрабатываемой земли.
Около \(2900\) лет до нашей эры была построена первая египетская пирамида. Знание геометрии было необходимо для построения пирамид, которые состояли из квадратного основания и треугольных граней. Самая ранняя запись формулы для вычисления площади треугольника датируется \(2000\) годом до нашей эры. Египтяне и вавилоняне разработали практическую геометрию для решения повседневных проблем, но нет никаких доказательств того, что они логически выводили геометрические факты из основных принципов.
Именно греки \(600\) – \(400\) лет до нашей эры разработали принципы современной геометрии. Фалес Милетский изучил подобные треугольники и написал доказательство того, что соответствующие стороны подобных треугольников пропорциональны.
Пифагор (\(569-475\) лет до н. э.)
Следующим считается Пифагор. Пифагор был первым математиком, логически выводящим геометрические факты из основных принципов. Пифагор основал братство под названием «пифагорейцы», которые преследовали знания в математике, науке и философии. Некоторые люди считают пифагорейскую школу местом рождения разума и логической мысли. Наиболее известным и полезным вкладом пифагорейцев была теорема Пифагора. Теория гласит, что сумма квадратов катетов прямоугольного треугольника равна квадрату гипотенузы.
Евклид Александрийский (\(325-265\) лет до н. э.)
Евклид Александрийский считается “отцом современной геометрии”. Евклид ввел математическую строгость и аксиоматический метод, все еще используемый сегодня. Его книга “Начало”, написанная около 300 лет до нашей эры, считается самым влиятельным учебником всех времен и народов. Книга «Начало» была известна всем образованным людям на западе до середины 20-го века. Евклид изобрел \(23\) определения, \(5\) постулатов и \(5\) аксиом.
Аксиома — это утверждение, которое принимается без доказательств. Как только он доказал свое первое утверждение, на его основе он доказал второе, затем третье и т. д. Этот процесс известен как
Рене Декарт (\(1596-1650\))
До появления Рене Декарта в геометрии не было крупных изменений. Декарт объединил алгебру и геометрию для создания аналитической геометрии. Аналитическая геометрия, также известная как координатная геометрия, включает размещение геометрической фигуры в системе координат для иллюстрации доказательств и получения информации с использованием алгебраических уравнений.
Карл Фридрих Гаусс (\(1777-1855\))
Следующее большое развитие в геометрии пришло с развитием неевклидовой геометрии. Карл Фридрих Гаусс изобрел неевклидову геометрию, не основанную на постулатах Евклида. Параллельный постулат гласит, что через заданную точку на прямой есть одна и только одна прямая, параллельная этой линии. Неевклидова геометрия задала математическую основу для теории относительности Эйнштейна.
Больше уроков и заданий по математике вместе с преподавателями нашей онлайн-школы «Альфа». Запишитесь на пробное занятие уже сейчас!
Запишитесь на бесплатное тестирование знаний!
myalfaschool.ru
История развития геометрии
Самые первые понятия в геометрии люди приобрели еще в глубокой древности. Возникала необходимость определять площади участков земли, объемы различных сосудов и помещений и другие практические потребности. Свое начало история развития геометрии, как науки, берет в Древнем Египте около 4 тысяч лет назад. Затем знания египтян позаимствовали древние греки, которые применяли их преимущественно для того, чтобы измерять площади земельных участков. Именно с Древней Греции берет свое начало история возникновения геометрии, как науки. Древнегреческое слово «геометрия» переводится, как «землемерие».
Греческие ученые на основе открытия множества геометрических свойств смогли создать стройную систему знаний по геометрии. В основу геометрической науки были положены простейшие геометрические свойства, взятые из опыта. Остальные положения науки выводились из простейших геометрических свойств с помощью рассуждений. Вся эта система была опубликована в завершенном виде в «Началах» Евклида около 300 года до нашей эры, где он изложил не только теоретическую геометрию, но и основы теоретической арифметики. С этого источника также начинается и история развития математики.
Однако в труде Евклида ничего не сказано ни об измерении объема, ни о поверхности шара, ни об отношении длины круга к его диаметру (хотя присутствует теорема о площади круга). История развития геометрии получила продолжение в середине III века до нашей эры благодаря великому Архимеду, который смог вычислит число Пи, а также смог определить способы вычисления поверхности шара. Архимед для решения упомянутых задач применил методы, которые в дальнейшем легли в основу методов высшей математики. С их помощью он уже мог решать трудные практические задачи геометрии и механики, которые были важны для мореплавания и для строительного дела. В частности, он нашел способы определять центры тяжести и объемы многих физических тел и смог изучить вопросы равновесия тел различной формы при погружении в жидкость.
Древнегреческие ученые провели исследования свойств различных геометрических линий, важных для теории науки и практических применений. Аполлоний во II веке до нашей эры сделал много важных открытии по теории конических сечений, которые оставались непревзойденными на протяжении следующих восемнадцати веков. Апполоний применил метод координат для изучения конических сечений. Этот метод в дальнейшем смогли развить только в XVII веке ученые Ферма и Декарт. Но они применяли этот метод только для изучения плоских линий. И только в 1748 году русский академик Эйлер смог применить этот метод для изучения кривых поверхностей.
Система, разработанная Евклидом, считалась непреложной более двух тысяч лет. Однако в дальнейшем история развития геометрии получила неожиданный поворот, когда в 1826 году гениальный русский математик Н.И. Лобачевский смог создать совершенно новую геометрическую систему. Фактически основные положения его системы отличаются от положений геометрии Евклида только в одном пункте, но именно из этого пункта вытекают основные особенности системы Лобачевского. Это положение о том, что сумма углов треугольника в геометрии Лобачевского всегда меньше 180 градусов. На первый взгляд может показаться, что это утверждение неверно, однако при маленьких размерах треугольников современные средства измерения не дают правильно измерить сумму его углов.
Дальнейшая история развития геометрии доказала правильность гениальных идей Лобачевского и показала, что система Евклида просто неспособна решить многие вопросы астрономии и физики, где математики имеют дело с фигурами практически бесконечных размеров. Именно с трудами Лобачевского уже связано дальнейшее развитие геометрии, а с ней и высшей математики и астрономии.
fb.ru
История развития геометрии — от Евклида до Лобачевского :: SYL.ru
Введение
Геометрия — довольно древняя наука, родиной которой принято считать Восток. В своем становлении она прошла несколько этапов, которые включает в себя история развития математики, так как первые геометрические понятия были связаны с землемерием. И только гораздо позже произошло выделение геометрии в самостоятельную науку.

Начальный этап развития
Начальным периодом можно назвать зарождение науки в Вавилоне и Египте. Это был примерно пятый век до нашей эры, но тогда всевозможные вычисления были связаны не столько с изучением понятий, сколько с применением их для практических нужд. Строились жертвенники, измерялись земельные площади, что привело к заложению научных основ. Именно там, на Востоке, и берет свое начало история возникновения геометрии.
Второй этап в становлении геометрии
Знаменательным для развития этой науки становится седьмой век до нашей эры, когда землемерная восточная мудрость находит свое распространение в Греции. История развития геометрии делает довольно резкий скачок, так как греческие философы начинают заниматься систематическим изложением основ, доказывая любое предложение. Этот период известен теоремой Фалеса о сумме углов треугольника, открытием иррациональных чисел Пифагором, знаменитыми «Началами» Евклида. Именно последний в своем 13-томнике систематизировал геометрию как науку, где основными положениями выступали аксиомы.
История развития геометрии — третий этап
Многие греческие, индийские, арабские ученые продолжали развивать «Начала» и обогащать своими открытиями, но новый качественный рывок развитие геометрии испытывает в 17-м веке. Именно это время считается началом третьего периода, который прочно связан с именами Декарта и Ферма. Их называют создателями аналитической геометрии. Суть этой прикладной науки заключается в том, что свойства фигур начинают изучаться по их алгебраическим уравнениям, где за основу берется метод координат. Но качественное развитие геометрии не заканчивается на этом. Появляются еще две ее разновидности: дифференциальная, связанная с именами Монжа и Эйлера, и проективная, вклад в которую внесли Паскаль и Дезарг.
Четвертый этап в развитии науки о фигурах

В 19-м веке история развития геометрии ознаменована возникновением так называемой «неевклидовой» геометрии. Ее основателем принято считать Лобачевского. Именно он был родоначальником, то есть рассмотрел положение фигур, а именно параллельных прямых, в пространстве. Чуть позже еще одним ученым — Риманом — было сформулировано понятие пространства как совокупности любых однородных явлений и объектов. Здесь стоит уточнить, что ни геометрия Лобачевского, ни геометрия Римана не отрицают учения Евклида, они рассматривают свои положения с точки зрения теории пространственных отношений, но нисколько не умаляет заслуг Евклида, труды которого положены в основу школьной программы.
Заключение
Таким образом, в становлении науки четко прослеживаются ее основные вехи. Но надо сказать, что история развития геометрии не является застывшей и мертвой. Геометрическая наука постоянно в действии: расширяется круг фигур, их изучаемые свойства, меняются сами понятия об объектах.
www.syl.ru
История развития геометрии как науки (стр. 1 из 3)
Муниципальное общеобразовательное учреждение
средняя общеобразовательная школа № 6
округа Муром
Реферат
По геометрии
На тему: история развития геометрии как науки
Подготовила:
Ученица 8 «В» класса
Барскова Екатерина
Проверила:
Учитель математики
Шубина И.Н.
Г. Муром 2011 год
Содержание
1. Введение ……………………………………………………………………………. 4
2. Первый период…………………………………………………………………… 7
2.1 Геометрия Египта………………………………………………………….. 7
2.2 Геометрия Вавилона……………………………………………………… 8
2.3 Геометрия древней Греции…………………………………………… 9
3. Второй период……………………………………………………………………. 11
3.1 Труды Евклида………………………………………………………………. 11
3.2 Труды Архимеда……………………………………………………………. 12
3.3 Труды Менелая……………………………………………………………… 13
3.4 Труды Апполона……………………………………………………………. 13
4. Третий период……………………………………………………………………. 15
4.1 Труды Эйлера……………………………………………………………….. 15
5. Четвёртый период………………………………………………………… 17
6. Задачи…………………………………………………………………………………. _
6.1 Задачи древности…………………………………………………………. 18
6.2 Современные задачи……………………………………………………. 19
7. Заключение………………………………………………………………………… 20
8. Литература…………………………………………………………………………. 21
Цель работы: узнать, как развивалась наука геометрия, и сравнить решение задач в древние времена и как они решаются сейчас.
Задачи:
1. Изучить литературу об истории науки геометрии.
2. Изучить каждый этап развития.
3. Рассмотреть решение задач в древности.
4. Рассмотреть способы решения современных задач.
5. Сравнить решение задач древности и современности.
Актуальность темы: Геометрия, как и всякая наука, возникла под влиянием жизненных потребностей. Необходимость повседневного удовлетворения их ставит человека перед целым рядом вопросов о форме окружающих его предметов, вычислениях, связанных с землемерием, строительным делом и т.д. Слово «геометрия» означает «землемерие» и ясно указывает на источник его происхождения.
Введение
Геометрия возникла очень давно, это одна из самых древних наук. Геометрия (греческое, от ge — земля и metrein — измерять)— наука о пространстве, точнее — наука о формах, размерах и границах тех частей пространства, которые в нем занимают вещественные тела. Таково классическое определение геометрии, или, вернее, таково действительное значение классической геометрии. Однако современная геометрия во многих своих дисциплинах выходит далеко за пределы этого определения. Развитие геометрии принесло с собой глубоко идущую эволюцию понятия о пространстве. В том значении, в котором пространство как математический термин широко употребляется современными геометрами, оно уже не может служить первичным понятием, на котором покоится определение геометрии, а, напротив, само находит себе определение в ходе развития геометрических идей.
Важную роль играли и эстетические потребности людей: желание украсить свои жилища и одежду, рисовать картины окружающей жизни. Все это способствовало формированию и накоплению геометрических сведений. За несколько столетий до нашей эры в Вавилоне, Китае, Египте и Греции уже существовали начальные геометрические знания, которые добывались в основном опытным путем, но они не были еще систематизированы и передавались от поколения к поколению в виде правил и рецептов, например, правил нахождения площадей фигур, объемов тел, построение прямых углов и т.д. Не было еще доказательств этих правил, и их изложение не представляло собой научной теории.
Геометрия дает общее понятие о геометрической фигуре, под которой понимают не только тело, поверхность, линию или точку, но и любую их совокупность. Геометрия в первоначальном значении есть наука о фигурах, взаимном расположении и размерах их частей, а также о преобразованиях фигур. Это определение вполне согласуется с определением геометрии как науки о пространственных формах и отношениях. Действительно, фигура, как она рассматривается в геометрия, и есть пространственная форма; поэтому в геометрии говорят, например, «шар», а не «тело шарообразной формы»; расположение и размеры определяются пространственными отношениями; наконец, преобразование, как его понимают в геометрии, так же есть некоторое отношение между двумя фигурами — данной и той, в которую она преобразуется.
Измерение площадей – одна из самых первых математических задач, возникших в глубокой древности. Среди самых старых древневавилонских клинописных табличек, смысл которых удалось расшифровать, – а их возраст составляет более четырех тысяч лет, – нашлись таблички с расчетами количества зерна, которое требуется для посева в зависимости от площади поля (при заданных расстояниях между рядами и зернами в ряду). Такие расчеты тогда не казались простыми из-за громоздкого способа обозначений больших чисел, в котором особую роль играли числа 6, 10, 60 (от этой «шестидесятеричной» системы до наших дней сохранился обычай делить окружность на 360 частей и измерять углы в градусах).
Крупнейший древнегреческий историк Геродот (V век до нашей эры) оставил описание того, как египтяне после каждого разлива Нила заново размечали плодородные участки его берегов, с которых ушла вода. По Геродоту, с этого и началась геометрия.
В современном, более общем смысле, геометрия объемлет разнообразные математические теории, принадлежность которых к геометрия определяется не только сходством (хотя порой и весьма отдалённым) их предмета с обычными пространственными формами и отношениями, но также тем, что они исторически сложились и складываются на основе геометрии в первоначальном её значении и в своих построениях исходят из анализа, обобщения и видоизменения её понятий. Геометрия в этом общем смысле тесно переплетается с другими разделами математики и её границы не являются точными.
В развитии геометрии можно указать четыре основных периода, переходы между которыми обозначали качественное изменение геометрии.
Первый — период зарождения геометрия как математической науки — протекал в Древнем Египте, Вавилоне и Греции примерно до 5 в. до н. э. Первичные геометрические сведения появляются на самых ранних ступенях развития общества. Зачатками науки следует считать установление первых общих закономерностей, в данном случае — зависимостей между геометрическими величинами. Этот момент не может быть датирован. Самое раннее сочинение, содержащее зачатки геометрии, дошло до нас из Древнего Египта и относится примерно к 17 в. до н. э., но и оно, несомненно, не первое.
Геометрия, по свидетельству греческих историков, была перенесена в Грецию из Египта в 7 в. до н. э. Здесь на протяжении нескольких поколений она складывалась в стройную систему. Процесс этот происходил путём накопления новых геометрических знаний, выяснения связей между разными геометрическими фактами, выработки приёмов доказательств и, наконец, формирования понятий о фигуре, о геометрическом предложении и о доказательстве. Этот процесс привёл, наконец, к качественному скачку. Геометрия превратилась в самостоятельную математическую науку: появились систематические её изложения, где её предложения последовательно доказывались.
Геометрия Египта
Имеются вполне достоверные сведения о значительном развитии геометрических знаний в Египте более чем за две тысячи лет до нашей эры. Узкая плодородная полоса земли между пустыней и рекой Нилом ежегодно подвергалась затоплению, и каждый раз разлив смывал границы участков, принадлежавших отдельным лицам. После спада воды требовалось с возможно большей точностью восстановить эти границы, ибо каждый из участков ценился весьма высоко. Это заставило египтян заниматься вопросами измерения, то есть землемерием. Помимо этого, они вели развитую торговлю и поэтому нуждались в умении измерять емкость сосудов. Искусство кораблевождения привело их к астрономическим сведениям. Выдающиеся постройки египтян — пирамиды, которые сохранились до нашего времени, свидетельствуют, что их сооружение требовало знания пространственных форм. Все это указывает на чисто опытное происхождение геометрии.
Геометрия Вавилона
К задачам, которые вавилоняне решали алгебраическим и арифметическим методом, относятся и многие задания на определение длин, площадей при делении земельных участков, объемов земляных выемок, хозяйственных построек. Все решения, встречающиеся в клинописных текстах, ограничиваются простым перечислением этапов вычисления в виде догматических правил: «делай то — то, делай так — то». В дошедших до нас вавилонских табличках имеются задачи абстрактного характера и внешне кажущиеся не связанными с практическими нуждами. Но это не так: они возникли в результате теоретической обработки условий, первоначально порожденных потребностями практики при межевании земель, возведении стен и насыпей, при строительстве каналов, плотин, оборонительных сооружений и пр. Сохранилось немало планов земельных угодий, разделенных на участки прямоугольной, трапецеидальной или треугольной форм. Но соответствующие геометрические фигуры воспринимались ими как абстрактные, так прямоугольник они называли «то, что имеет длину и ширину», трапецию — «лбом быка», сегмент — «полем полумесяца», параллельные прямые — «двойными прямыми». У вавилонян не было таких геометрических понятий как точка, прямая, линия, поверхность, плоскость, параллельность. Измерение производилось при помощи веревки. Геометрические познания вавилонян превышали египетские.
mirznanii.com
Геометрія — Вікіпедія

Геоме́трія (від дав.-гр. γη — Земля і μετρέω — вимірюю; землеміряння) — розділ математики, наука про просторові форми, відносини і їхні узагальнення.
Геометрія — одна з найдавніших наук. Від початку вона була галуззю практичного знання, що розглядало довжини, площі, і об’єми.
Початкові поняття геометрії виникли в результаті відволікання від будь-яких властивостей і відносин тіл, крім взаємного розташування і величини. Перші виражаються в дотику або приляганні тіл один до одного, в тому, що одне тіло є частиною іншого, в розташуванні «між», «всередині» тощо. Інші виражаються в поняттях «більше», «менше», в понятті про рівність тіл.
Шляхом такого ж відволікання виникає поняття геометричного тіла. Геометричне тіло — абстракція, в якій зберігаються лише форма і розміри при повному абстрагуванні від усіх інших властивостей. При цьому геометрія, як властиво математиці взагалі, повністю абстрагується від невизначеності й рухливості реальних форм і розмірів і вважає всі досліджувані нею відносини і форми абсолютно точними і визначеними. Абстрагування від протяжності тіл призводить до понять поверхні, лінії і точки. Це явно виражене, наприклад, у визначеннях, даних Евклідом: «лінія є довжина без ширини», «поверхня є те, що має довжину і ширину». Точка без жодної протяжності — абстракція, що відображає можливість необмеженого зменшення всіх розмірів тіла, уявна межа його нескінченного розділення. Далі виникає загальне поняття про геометричну фігуру, під якою розуміють не тільки тіло, поверхню, лінію або точку, а й будь-яку їхню сукупність.
Геометрія в первинному значенні — наука про фігури, взаємне розташування і розміри їхніх частин, а також про перетворення фігур. Це визначення цілком узгоджується з визначенням геометрії як науки про просторові форми і відносини. Дійсно, фігура, як вона розглядається в геометрії, і є просторова форма; тому в геометрії говорять, наприклад, «куля», а не «тіло кулястої форми»; розташування і розміри визначаються просторовими відносинами; нарешті, перетворення, як його розуміють у геометрії, також є певне відношення між двома фігурами — даної і тієї, в яку вона перетвориться.
У сучасному, загальнішому смислі, геометрія обіймає різноманітні математичні теорії, приналежність яких до геометрії визначається не лише схожістю (хоча часом і вельми віддаленою) їхнього предмета зі звичайними просторовими формами і відносинами, але також тим, що вони історично склалися і складаються на основі геометрії в первісному її значенні, і в своїх побудовах виходять з аналізу, узагальнення і видозміни її понять. Геометрія в цьому загальному смислі тісно переплітається з іншими розділами математики та її кордони не є точними.
Узагальнення предмету геометрії[ред. | ред. код]
Можливість узагальнення і видозміни геометричних понять найлегше усвідомити на прикладі. Так, на поверхні кулі можна з’єднувати точки найкоротшими лініями — дугами великих кіл, можна вимірювати кути і площі, будувати різні фігури. Їх вивчає предмет сферичної геометрії, подібно до того, як планіметрія — геометрія на площині; геометрія на земній поверхні близька до сферичної геометрії. Закони геометрії на сфері відрізняються від законів планіметрії; наприклад, довжина кола тут не пропорційна радіусу, а зростає повільніше і досягає максимуму для екватора; сума кутів трикутника на сфері непостійна і завжди більше двох прямих. Аналогічно можна на будь-якій поверхні проводити лінії, вимірювати їхні довжини, кути між ними, визначати обмежені ними площі. Геометрія на поверхні, що будується таким чином, називається її внутрішньої геометрією (Карл Гаус, 1827). На нерівномірно вигнутій поверхні співвідношення довжин і кутів будуть різними в різних місцях, отже, вона буде геометрично неоднорідною, на відміну від площини і сфери. Можливість отримання різних геометричних співвідношень наводить на думку, що властивості реального простору можуть лише наближено описуватися звичайною геометрією. Ця ідея, вперше висловлена Миколою Лобачевським, знайшла підтвердження в загальній теорії відносності.
Ширша можливість узагальнення понять геометрії з’ясовується з наступного міркування. Звичайний реальний простір розуміють в геометрія як безперервну сукупність точок, тобто всіх можливих гранично точно визначених місць розташування гранично малого тіла. Аналогічно безперервну сукупність можливих станів будь-якої матеріальної системи, безперервну сукупність яких-небудь однорідних явищ можна трактувати як свого роду «простір». Ось один із прикладів. Відомо, що нормальний людський зір триколірний, тобто будь-яке колірне відчуття
Інший приклад. Стан газу, що перебуває в циліндрі під поршнем, визначається тиском і температурою. Тому сукупність усіх можливих станів газу можна представляти як двовимірний простір. «Точками» цього «простору» служать стани газу; «точки» розрізняються двома «координатами» — тиском і температурою, подібно до того як точки на площині розрізняються значеннями їхніх координат. Безперервна зміна стану зображується лінією в цьому просторі.
Далі можна уявити собі будь-яку матеріальну систему — механічну або фізико-хімічну. Сукупність усіх можливих станів цієї системи називають «фазовим простором». «Точками» цього простору є самі стани. Якщо стан системи визначається n величинами, то говорять, що система має n ступенів свободи. Ці величини відіграють роль координат точки-стану, як у прикладі з газом роль координат грали тиск і температура. Відповідно до цього такий фазовий простір системи називають n-мірним. Зміна стану зображується лінією в цьому просторі; окремі області станів, що виділяються з тими чи іншими ознаками, будуть областями фазового простору, а межі областей будуть поверхнями в цьому просторі. Якщо система має тільки два ступені свободи, то її стани можна зображувати точками на площині. Так, стан газу з тиском р і температурою Т відіб’ється точкою з координатами р і Т, а процеси, що відбуваються з газом, зобразити лініями на площині. Цей метод графічного зображення загальновідомий і постійно використовується у фізиці та техніці для наочного представлення процесів та їхніх закономірностей. Однак якщо число ступенів свободи більше 3, то просте графічне зображення (навіть у просторі) стає неможливим. Тоді, щоб зберегти корисні геометричні аналогії, вдаються до поняття про абстрактний фазовий простір. Так, наочні графічні методи переростають в це абстрактне уявлення. Метод фазових просторів широко застосовується в механіці, теоретичній фізиці та фізичній хімії. У механіці рух механічної системи зображують рухом точки в її фазовому просторі. У фізичній хімії особливо важливо розглядати форму і взаємне прилягання тих областей фазового простору системи з декількох речовин, які відповідають якісно різним станам. Поверхні, що розділяють ці області, суть поверхні переходів від однієї якості до іншої (плавлення, кристалізація тощо). У самій геометрії також розглядають абстрактні простори, «точками» яких служать фігури; так визначають «простори» кіл, сфер, прямих тощо. У механіці та теорії відносності вводять також абстрактний чотиривимірний простір, приєднуючи до трьох просторових координатах час як четверту координату. Це означає, що події потрібно розрізняти не тільки за положенням в просторі, але і в часі.
Таким чином, стає зрозумілим, як безперервні сукупності тих чи інших об’єктів, явищ, станів можуть підводитися під узагальнене поняття простору. У такому просторі можна проводити «лінії», що зображують безперервні послідовності явищ (станів), проводити «поверхні» і визначати відповідним чином «відстані» між «точками», даючи тим самим кількісне вираження фізичного поняття про ступінь відмінності відповідних явищ (станів) і таке подібне. Так за аналогією зі звичайною геометрією виникає «геометрія» абстрактного простору; вона може навіть мало бути схожа на звичайний простір, будучи, наприклад, неоднорідною за своїми географічним властивостях і скінченою, подібно нерівномірно викривленій замкнутій поверхні.
Предметом геометрії в узагальненому смислі виявляються не тільки просторові форми і відносини, але будь-які форми і відносини, які, будучи абстрагованими від свого змісту, виявляються подібними зі звичайними просторовими формами і відносинами. Ці просторово-подібні форми дійсності називають «просторами» і «фігурами». Простір у цьому смислі є безперервна сукупність однорідних об’єктів, явищ, станів, які грають роль точок простору, причому в цій сукупності є відносини, схожі з звичайними просторовими відносинами, як, наприклад, відстань між точками, рівність фігур тощо (фігура — взагалі частина простору). Геометрія розглядає ці форми дійсності абстраговано від конкретного змісту, вивчення ж конкретних форм і відносин у зв’язку з їхнім якісно своєрідним змістом становить предмет інших наук, а геометрія служить для них методом. Прикладом може служити будь-яке застосування абстрактної геометрія, хоча б вказане вище застосування n-мірного простору в фізичної хімії. Для геометрії характерний такий підхід до об’єкта, який полягає в узагальненні та перенесенні на нові об’єкти звичайних геометричних понять і наочних уявлень. Саме це і робиться в наведених вище прикладах простору кольорів та інших. Цей геометричний підхід зовсім не є чистою умовністю, а відповідає самій природі явищ. Проте часто одні й ті самі реальні факти можна зображувати аналітично або геометрично, як одну й ту ж залежність можна задавати рівнянням або лінією на графіку.
Не слід, однак, представляти розвиток геометрії так, що вона лише реєструє й описує геометричною мові форми і відносини, котрі вже зустрілися на практиці, подібні просторовим. В дійсності геометрія визначає широкі класи нових просторів і фігур в них, виходячи з аналізу і узагальнень даних спостережної геометрії і вже сформованих геометричних теорій. При абстрактному визначенні ці простори і фігури виступають як можливі форми дійсності. Вони, отже, не є чисто умоглядними конструкціями, а повинні служити зрештою засобом дослідження й опису реальних фактів. Микола Лобачевський, створюючи свою геометрію, вважав її можливою теорією просторових відносин. Так само, як його геометрія отримала обґрунтування в смислі її логічної спроможності і застосування до явищ природи, так і всяка абстрактна геометрична теорія проходить таку ж подвійну перевірку. Для перевірки логічної спроможності істотне значення має метод побудови математичних моделей нових просторів. Проте остаточно вкорінюються в науці тільки ті абстрактні поняття, які виправдані і побудовою штучної моделі, і застосуваннями, якщо не прямо в природознавстві і техніці, то хоча б в інших математичних теоріях, через які ці поняття так чи інакше пов’язуються з дійсністю. Легкість, з якої математики і фізики оперують тепер різними «просторами», досягнута в результаті довгого розвитку геометрії в тісному зв’язку з розвитком математики в цілому та інших точних наук. Саме внаслідок цього розвитку склалася і здобув велике значення інший бік геометрії, вказаний в загальному визначенні, даному на початку статті: включення в геометрію дослідження форм і відносин, схожих з формами і відносинами в звичайному просторі.

Геометрія — слово грецького походження. Воно означає землемірство. Однак першими «землемірами» були стародавні єгиптяни. Сільське господарство могло розвиватись лише біля річки Ніл. Щороку Ніл розливався, приносячи на землі які були залиті водою, плодючий мул. Кожен селянин мав наділ землі певної площі, однак розливи ріки не дозволяли раз і назавжди визначити межі кожного наділу, тому після чергового розливу доводилось визначати земельну ділянку заново. Це виконували землеміри — люди, що за допомогою шнура відміряли кожному селянину ділянку з площею, яка була йому приписана. Стародавні єгиптяни не знали циркуля, його винайшли греки. Однак це їм особливо не перешкоджало. Так, прямий кут вони будували мотузкою, що має довжину 12 мір. За допомогою цієї мотузки можна побудувати трикутник зі сторонами 3, 4 і 5 мір. Такий трикутник за теоремою Піфагора є прямокутним. Тому прямокутний трикутник також називають єгипетським.
 Жінка навчає дітей геометрії. Ілюстрація з паризького рукопису Евклідових «Начал», початок XIV століття
Жінка навчає дітей геометрії. Ілюстрація з паризького рукопису Евклідових «Начал», початок XIV століттяУ Стародавній Греції, починаючи з 7 століття до н. е., з часів Фалеса Мілетського, починається новий етап розвитку геометрії. Вона набуває характерного для неї абстрактного напряму, у ній виникає доведення. Грецький мислитель мілетської школи Анаксимандр здійснив першу спробу створення систематичного курсу для викладання геометрії. Перетворення це відбулося шляхом абстрагування від будь-яких властивостей тіл, крім взаємного положення і величини. Наукою геометрія стала, коли від набору рецептів перейшли до встановлення загальних закономірностей. Подальші спроби побудови систематичних курсів математики належать Гіппократу Хіоському, Феодору Кіренському, Архіту Тарентському, Евдоксу Кнідському та багатьом іншим вченим. Вони створили математичну основу для подальшого розвитку науки, теоретичного природознавства і філософії Давньої Греції. Греки склали перші систематичні і доказові праці з геометрії, великий внесок зробили Евклід, Архімед, Аполлоній Перзький.
Центральне місце серед них займають складені близько 300 до н. е. «Начала» Евкліда. Ця праця і понині залишається зразковим викладенням у дусі аксіоматичного методу: всі положення виводяться логічним шляхом з невеликого числа явно зазначених і не доводимих припущень — аксіом. Геометрія греків, звана сьогодні евклідовою, або елементарною, займалася вивченням простих форм: прямих, площин, відрізків, правильних багатокутників і багатогранників, конічних перерізів, а також куль, циліндрів, призм, пірамід і конусів. Обчислюються їхні площі і об’єми. Перетворення в основному обмежувалися геометричною подібністю.
Середньовіччя небагато дало геометрії, і наступною великою подією в її історії стало відкриття Рене Декартом (1596—1650) і П’єром Ферма (1601—1665) в XVII столітті координатного методу («Міркування про метод», 1637). Точкам зіставляються набори чисел, це дозволяє вивчати відносини між формами методами алгебри. Так з’явилася аналітична геометрія, що вивчає фігури і перетворення, які в координатах задаються алгебричними рівняннями. Приблизно одночасно з цим Блезом Паскалем і Жераром Дезаргом (1591—1661) почато дослідження властивостей плоских фігур, що не міняються при проектуванні з однієї площини на іншу. Цей розділ отримав назву проективної геометрії. Метод координат лежить з розвитком математичного аналізу ліг в основу нового підходу, що з’явився трохи пізніше, — диференціальної геометрії, де фігури і перетворення все ще задаються в координатах, але вже довільними досить гладкими функціями. Властивості цих фігур вивчаються за допомогою моці й гнучкості апарату аналізу.

Остаточне оформлення і систематичний виклад цих нових напрямів геометрії дані в XVIII — на початку XIX століття Леонардом Ейлером (1707—1783) для аналітичної геометрії (1748), Гаспаром Монжем для диференціальної геометрії (1795), Жан-Віктором Понселе для проективної геометрії (1822), причому саме вчення про геометричне зображення (у прямому зв’язку із завданнями креслення) було ще раніше (1799) розвинене і приведене в систему Монжем у вигляді нарисної геометрії. У всіх цих нових дисциплінах основи (аксіоми, початкові поняття) геометрії залишалися незмінними, коло ж фігур, що вивчаються, і їхніх властивостей, а також використаних методів розширювався.

XIX сторіччя дало два значних прориви у розвитку науки. Дослідження Миколи Лобачевського, Яноша Больяї і Карла Гауса відкрили несуперечність неевклідової геометрії, в якій знаменитий п’ятий постулат Евкліда замінений на зворотне твердження. Фелікс Клейн зв’язав всі види геометрій, згідно з ним геометрія вивчає всі ті властивості фігур, які інваріантні щодо перетворень з певної групи. При цьому кожна група задає свою геометрію. Так, ізометрії (руху) задає евклідову геометрію, група афінних перетворень — афінну геометрію, група проективних перетворень — проективну геометрію, група конформних перетворень — конформну геометрію тощо.
Двома визначними майстрами досліджень в геометрії цього часу були Бернгард Ріман, який працював переважно з інструментами математичного аналізу і ввів Ріманові поверхні, та Анрі Пуанкаре, засновник алгебричної топології і геометричної теорії динамічних систем.
Наслідком цих великих змін в геометричних поглядах концепція «простору» стала значно багатша і різноманітніша, і перетворилася на природну основу таких різних теорій, як комплексний аналіз чи класична механіка. Традиційні види геометрій були визнані як загальний однорідний простір, такий простір, який має достатню кількість симетрій, так щоб погляд з одної чи іншої точки давав той самий вид.
- Алгебра та геометрія : навч. посіб. / Д. М. Білонога, П. І. Каленюк ; М-во освіти і науки України, Нац. ун-т «Львів. політехніка». – Львів : Вид-во Львів. політехніки, 2014. – 380 с. : іл. – Бібліогр.: с. 373 (14 назв). – ISBN 978-617-607-581-3
- Д. Гильберт Основания геометрии. Перевод с немецкого под редакцией А. В. Васильева. — Л.: «Сеятель», 1923—152 с.
- Шаль М. Исторический обзор происхождения и развития геометрических методов. Москва: М. Катков, 1883. Т. 1-2.
- Александров П. С., Что такое неевклидова геометрия, М., 1950.
- Ефимов Н. В., Высшая геометрия, 4 издание. — М., 1961.
- История математики под редакцией А. П. Юшкевича — М.: Наука: Том 1. С древнейших времен до начала Нового времени. (1970); Том 2. Математика XVII столетия. (1970); Том 3. Математика XVIII столетия. (1972)
- Колмогоров А. Н., Юшкевич А. П. (ред.) Геометрия. Теория аналитических функций.[недоступне посилання з квітень 2019] // Математика XIX века. Том 2. — М.: Наука, 1981.
uk.wikipedia.org
Викторина по геометрии для 9 класса по теме «История развития геометрии как науки».
Викторина по геометрии для 9 класса по теме
«История развития геометрии как науки».
/Составлена учителем математики Краснокустовского филиала МБОУ Мучкапской СОШ Зориной Н. Н./
1 вопрос. Первые шаги культуры всюду, где она 
возникала, были связаны с необходимостью измерять расстояния и участки на земле, объемы и веса материалов, продуктов, товаров; первые значительные сооружения требовали нивелирования, выдержанной вертикали, знакомства с планом и перспективой. Необходимость измерять промежутки времени требовала систематического наблюдения над движением светил, а, следовательно, измерения углов. Всё это было неосуществимо без знакомства с элементами геометрии, и во всех странах основные геометрические представления возникали частью независимо друг от друга, частью — в порядке преемственной передачи. Так в какой из стран появилась геометрия как систематическая наука?
Ответ: Древняя Греция.Традиционно считается, что родоначальниками геометрии как систематической науки являются древние греки, перенявшие у египтян ремесло землемерия и измерения объёмов тел и превратившие его в строгую научную дисциплину. При этом античные геометры от набора рецептов перешли к установлению общих закономерностей, составили первые систематические и доказательные труды по геометрии.

Фалес
Пифагор
Евклид
Архимед

Начиная с 7 века до н. э. в Древней Греции создаются философские школы и происходит постепенный переход от практической геометрии к теоретической. Одной из первых школ была ионийская. Её основателем считается Фалес Милетский. Первым, кто начал получать новые геометрические факты при помощи рассуждений (доказательств), был древнегреческий математик Фалес (VI век до нашей эры).

Геометрия (греч. geometria, от ge — Земля и metreo — мерю), раздел математики, изучающий пространственные отношения и формы, а также другие отношений и формы, сходные с пространственными по своей структуре. С древнегреческого – «землемерие».
4 вопрос: В 5 веке до н. э. центром дальнейшего развития
математики становится Южная Италия.
Одной из самых известных школ того времени (4-5 вв.до н.э.)
являлась пифагорейская, названная так в честь своего основателя – Пифагора.
Объясняя устройства мира, пифагорейцы опирались на математику. Так, выделяя первоосновы бытия, они приписывали их атомам форму правильных многогранников: атомам огня – форму тетраэда, земли – гекаэдра (куба), воздуха – октаэдра, воды — икосаэдра. Всей Вселенной приписывалась форма додекаэдра. Сколько граней имеет додекаэдр?
Ответ: 12.
В названиях этих многогранников указывается число граней тетра — «четыре», гекса — «шесть», окта — «восемь», икоса — «двадцать», додека — «двенадцать».

5 вопрос: В 5-6 вв. до н. э. была ещё одна знаменитая школа этого 
философа. Он не был математиком, но в своих произведениях любил говорить о математике. На здании его Академии были начертаны слова: « Да не войдет сюда не искусившийся в геометрии!» Назовите имя этого философа.
Диоген
Плутарх
Аристотель
Платон
Ответ: Платон.
В трактате «Тимей» Платон изложил ученье пифагорейцев о правильных многогранниках, которые получили название «Платоновых тел».
6 вопрос:
Наибольшее влияние на всё последующее развитие геометрии оказали труды греческого учёного Евклида, жившего в Александрии в III веке до нашей эры. Этот труд более двух тысячелетий считался образцовым изложением в духе аксиоматического метода: все положения выводятся логическим путём из небольшого числа явно указанных и не доказываемых предположений — аксиом. Как называлась эта книга?
«Геометрия»
«Труд»
«Начала»
«Сборник»

Первая книга по геометрии была написана Евклидом в 280 году до н.э. и называлась «Начала». Любопытно, но именно этот учебник помогал изучать геометрию всем желающим следующие 2000 лет. Возможно, поэтому многие до сих пор величают современную геометрию Евклидовой, хотя научно доказано неактуальность некоторых его идей.
7 вопрос: Помимо Евклида выдающимся учёным эпохи эллинизма был и этот известный человек (287 -212гг. до н. э.), живший в Сиракузах, где он был советником царя Герона. Существенный вклад он внёс в математику. Ему принадлежат теоремы о площадях плоских фигур, объёмах тел. В работе «Измерение круга» он приводит вычисления приближённого значения длины окружности. В книге «О шаре и цилиндре» им дана вычисления объёма шара и площади его поверхности. Учёный, по выражению современников, был околдован геометрией, и, хотя у него было много прекрасных открытий, он просил на своей могиле изобразить цилиндр со вписанным в него шаром и указать соотношение объёмов этих тел. Позже именно по этому изображению была найдена его могила.
Архимед
Паскаль
Папп
Пифагор

Ответ: Архимед.
Широко известен открытый им закон о силе, действующей на тело,
погружённое в жидкость, которой приводится в трактате по гидростатике « О плавающих телах»; в современных школьных учебниках по физике он назван законом его имени – законом Архимеда.
8 вопрос: Аксиомы евклидовой геометрии, сформулированные в III—IV веке до н. э., составляли основу геометрии до второй половины XIX века, так как хорошо описывали физическое пространство и отождествлялись с ним. Аксиомы Евклида:
Всякие две точки можно соединить прямой линией;
Ограниченную прямую линию можно неограниченно продолжить;
Из всякого центра всяким радиусом можно описать окружность;
Все прямые углы равны между собой;
Если прямая падает на две прямые и образует внутренние односторонние углы в сумме меньше двух прямых, то при неограниченном продолжении этих двух прямых они пересекутся с той стороны, где углы меньше двух прямых.


Какое более известное название носят эти пять аксиом?
Утверждения
Теоремы
Постулаты
Высказывания
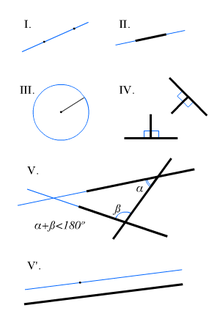
Ответ: Постулаты.
Постулаты Евклида представляют собой правила построения с помощью идеального циркуля и идеальной линейки. Самый известный из них – пятый постулат – в современном учебнике носит название Аксиомы параллельности.

9 вопрос: В рамках школьной программы в 7- 9 классах изучаются планиметрия, исследующая фигуры на плоскости, в 10-11 классах – стереометрия, в которой изучаются фигуры в пространстве. В наши дни общепринята определённая классификация различных разделов геометрии. К какому разделу относится геометрия, изучаемая в школе?
Евклидова геометрия
Начертательная геометрия
Неевклидова геометрия
Проективная геометрия

Ответ: «Евклидова геометрия»
Планиметрия и стереометрия, изучаемые в рамках школьной программы являются разделами «Евклидовой геометрии»
10 вопрос. Много веков усилия большого числа учёных были направлены на доказательство V постулата Евклида. Это объяснялось тем, что число аксиом стремились свести к минимуму. Ученые думали, что V постулат можно доказать, как теорему, опираясь на остальные аксиомы. Многовековые попытки доказательства пятого постулата Евклида привели в конце концов к появлению новой геометрии, отличающейся от евклидовой тем, что в ней V постулат не выполняется. Эту геометрию называют Неевклидовой геометрией. Эта геометрия широко используется в естествознании.
Кто из перечисленных ниже ученых не имеет отношения к открытию Неевклидовой геометрии?
Ответ: Р. Декарт.
Лобачевский предпринял попытку доказать V постулат от противного: он предположил, что через данную точку, не лежащую на данной прямой, можно провести несколько прямых, не пересекающих данную. Он попытался получить утверждение, которое противоречило бы аксиомам или полученным из них теоремам. Если бы такое утверждение удалось получить, то это означало бы, что предположение неверно. Тем самым V постулат Евклида был бы доказан. Но Лобачевский не получил противоречивых утверждений. На основании этого он пришел к выводу, что можно построить другую геометрию, отличную от геометрии Евклида. Такая геометрия теперь называется геометрией Лобачевского. Сообщение об открытии новой геометрии было сделано Лобачевским в 1826 г. К аналогичным выводам пришел венгерский математик Я. Бойяи, но свои результаты опубликовал несколько позже, в 1832 г. В рукописях немецкого математика К. Гаусса высказывались идеи, близкие к идеям Лобачевского и Гаусса. Но, опасаясь критики, он их не обнародовал.

Задача о квадратуре круга
Задача об удвоении куба с объемом в два раза большим объема данного куба
Задача о шаре, вписанном в цилиндр
Задача об измерении круга

Свое название она получила благодаря следующей легенде. В Древней Греции на острове Делосе был мор. Для его предотвращения оракул делосского храма приказал удвоить жертвенник, имеющий форму куба. Тогда бы боги смилостивились и мор прекратится. Данная задача оказалась неразрешимой, т.к. с помощью циркуля и линейки невозможно построить сторону куба, у которого объем вдвое больше данного.
12 вопрос. Геометрия играет огромную роль не только в науках, но и в искусстве. В одном из музеев находится бюст. На нем изображена Муза Геометрии. В каком из перечисленных музеев находится этот бюст? Выберете правильный ответ.

Ответ: Лувр
13 вопрос: На картине Мартина де Воса «Семь сестёр» (1590) изображены семь свободных искусств. Геометрия является пятым из семи свободных искусств по уровню обучения. Ей предшествует тривиум, состоящий из Грамматики, Риторики и Диалектики, а также Арифметика — старшая наука в квадривиуме, к которому также относятся Музыка и Астрономия. Рассмотрите внимательно картину и найдите среди семи сестёр Геометрию.
Крайняя слева девушка, в руках у которой глобус и циркуль
Рядом с первой, девушка с бумагой и карандашом
На заднем плане картины девушка, у которой на голове птица
Девушка с музыкальным инструментом

Марциал Капелла в своём трактате «Свадьба Философии и Меркурия» создал визуальные образы всех семи искусств и в том числе Геометрии. Искусства олицетворяли женщины с соответствующими атрибутами, которые сопровождались известными представителями сферы. Геометрия держит в своих руках глобус и циркуль, которым она может мерить, реже угольник, линейку или компасы.
14 вопрос: Каждая наука проходит несколько этапов становления. Это длится многие годы, даже тысячелетия. Геометрия как наука тоже имеет периоды развития, границы которых нельзя отделить какими-то определёнными годами. Каждый этап связан с именами великих математиков. Таких как Фалес, Пифагор, Евклид, Эратосфен, Декарт, Ферма и других. Сколькими периодами можно охарактеризовать развитие геометрии?
Ответ: четыре.
Первый период — период зарождения геометрии — относится ко времени примерно до V в. до н. э. и связан с развитием культуры землемерия в древнем Египте, Вавилонии и Греции.
Религиозные обряды связывались с построением жертвенников, практические потребности людей приводили к необходимости измерения площадей земельных участков, объемов (емкости) сосудов, корзин и зернохранилищ.
В VII в. до н. э. геометрические сведения были, по мнению греческих историков, перенесены из Египта и Вавилонии в Грецию. Греческие философы стали знакомиться с египетской и вавилонской мудростью. С этого времени начинается второй период развития геометрии — период систематического изложения геометрии как науки, где все предложения доказывались.
Зарождение капитализма в Европе привело к новому, третьему периоду развития геометрии — созданию в первой половине XVII в. аналитической геометрии, творцами которой были Декарт и Ферма.
Четвертый период развития геометрии знаменуется созданием неевклидовых геометрий, первой из которых является геометрия Лобачевского, созданная им при исследовании обоснования геометрии, и в частности аксиомы о параллельных прямых.
15 вопрос: Какое небесное тело носит название Геометрия?

Ответ: Астероид.
В честь геометрии назван астероид (376) Геометрия,
открытый в 1893 году.
16 вопрос: Как называется раздел геометрии, в котором геометрические фигуры и их свойства исследуются средствами алгебры?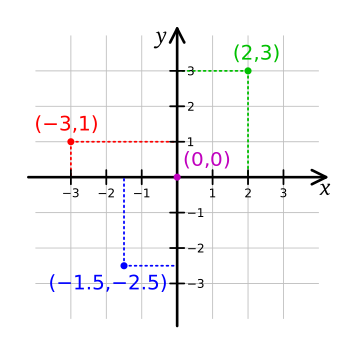
В основе этого метода лежит так называемый метод координат, впервые применённый Декартом. Каждому геометрическому соотношению этот метод ставит в соответствие некоторое уравнение, связывающее координаты фигуры или тела.
Многомерная геометрия
Сферическая геометрия
Аналитическая геометрия
Дифференциальная геометрия
Аналитическая геометрия — геометрия координатного
метода. В ней геометрические объекты описываются алгебраическими уравнениями в декартовых (иногда аффинных) координатах и затем исследуются методами алгебры и анализа.
изображением некоторой теоремы, которую доказал ученый, имеющий профессию купца, но
в свободное время занимающийся математикой.
Назовите эту теорему.
Теорема Фалеса
Теорема параллельности прямых
Теорема об углах, образованных при пересечении параллельных прямых секущей
Теорема Пифагора
Ответ: Теорема Фалеса.
Теорема Фалеса до сих пор используется в 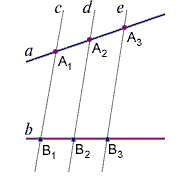
морской навигации в качестве правила о том, что столкновение судов, двигающихся с постоянной скоростью, неизбежно, если сохраняется курс судов друг на друга.
Вне русскоязычной литературы теоремой Фалеса иногда называют другую теорему планиметрии, а именно, утверждение о том, что вписанный угол, опирающийся на диаметр окружности, является прямым. Открытие этой теоремы действительно приписывается Фалесу, о чём есть свидетельство Прокла.
Они занимались перетягиванием каната
Они всегда ходили с длинной веревкой
Они измеряли земельные участки с помощью каната
Они при помощи каната строили прямые углы

В Древнем Египте для построения прямых углов применялась теорема, впоследствии получившая название теоремы Пифагора. А т.к. прямоугольный треугольник со сторонами 3,4 и 5 м строился с помощью натягивания каната на колышки, воткнутые в землю в вершинах треугольника, то древних землемеров и называли «канатонатягивателями».
19 вопрос: Архимед — один из немногих учёных античности, которого мы знаем не только по имени: сохранились некоторые сведения о его жизни и личности. Он был уникальным учёным — механиком, физиком, математиком. Основной чертой его творчества было единство теории и практики, что делает изучение его трудов интересным для ученых многих специальностей. Великий геометр древности был убит при захвате его родного города Сиракузы. Что, по преданию, сказал Архимед вражескому солдату, пришедшему его убить?«Не тронь моих кругов»
«Не мешай мне работать»

«Уйди из моего дома»
«Оставьте меня, я на пороге великого открытия»


Ответ: «Не тронь моих кругов»
По преданию, Архимед был увлечен решением геометрической задачи, чертеж которой был выполнен на песке. Солдат, убивший Архимеда, или не знал о приказе военачальника сохранить жизнь Архимеду, или не узнал Архимеда. Впоследствии этот солдат был наказан, а семья Архимеда была окружена почестями.
20 вопрос: Кто является автором самого первого учебника геометрии? Он же является однофамильцем известного греческого медика.
Асклепий

Гиппократ
Аристотель
Платон

infourok.ru
