Квадратные уравнения. Повторение теории. Задачи повышенной сложности
Тема: Квадратные уравнения
Урок: Повторение теории. Задачи повышенной сложности
Как мы с вами помним, основой теории данной темы являются формулы для вычисления корней квадратного уравнения, формула разложения квадратного трёхчлена на множители и теорема Виета.
Довольно много задач в математике сводится к решению квадратных уравнений. Некоторые примеры подобных задач мы с вами сейчас рассмотрим.
Задача №1
Решите уравнение 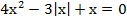 .
.
Перед нами обычное квадратное уравнение, которое, однако, имеет некоторое осложнение в виде модуля.
Для начала давайте вспомним, что такое модуль: 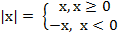 .
.
Из определения модуля следует правило решения квадратных уравнений, которые содержат модуль: при решении квадратных уравнений, в которых содержится модуль, необходимо раскрыть этот модуль на основе стандартного определения модуля.
Решение
Мы имеем уравнение 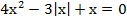 . По определению модуля, он раскрывается на 2 случая, так что теперь рассмотрим эти случаи отдельно:
. По определению модуля, он раскрывается на 2 случая, так что теперь рассмотрим эти случаи отдельно:
|
Если мод модулем у нас стоит число, больше или равное 0, то значок модуля мы можем просто выбросить, при этом не забывая про знак числа.
|
Если мод модулем у нас стоит число отрицательное, то мы убираем значок модуля, но при этом меняем знак числа, находящегося под знаком модуля.
|
После раскрытия модуля мы можем сказать, что исходное уравнение равносильно совокупности систем, полученных после раскрытия модуля, т. е.
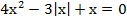 ó
ó 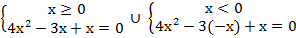 .
.
Теперь решим каждую из систем отдельно:
(а) 
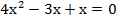
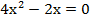
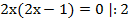
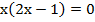
Мы помним, что произведение равно 0 тогда и только тогда, когда хотя бы один из множителей равен 0, т. е. 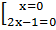 =>
=> 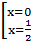 .
.
Теперь давайте вспомним, что у нас было условие, что 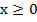 , поэтому после нахождения корней в данном случае мы должны проверить, удовлетворяют ли они нашему условию:
, поэтому после нахождения корней в данном случае мы должны проверить, удовлетворяют ли они нашему условию:
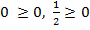 . Таким образом, мы видим, что оба корня удовлетворяют условию, поэтому мы можем сказать, что
. Таким образом, мы видим, что оба корня удовлетворяют условию, поэтому мы можем сказать, что 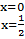 – корни заданного уравнения.
– корни заданного уравнения.
Но теперь давайте вспомним, что корней может быть и больше, т. к. есть второй вариант раскрытия модуля. Давайте решим его:
(б) 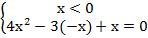
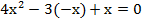
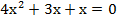

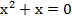
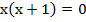
Как и в случае (а), решаем данное уравнение, получая следующие корни: 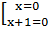 =>
=> .
.
Далее вспоминаем об условии решения данной части исходного уравнения ( ) и проверяем, удовлетворяют ли этому условию корни, которые мы получили:
) и проверяем, удовлетворяют ли этому условию корни, которые мы получили:
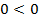 – это неправильное равенство, поэтому корень
– это неправильное равенство, поэтому корень 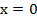 не является корнем исходного квадратного уравнения при условии, что
не является корнем исходного квадратного уравнения при условии, что  . Проверим второй корень:
. Проверим второй корень: 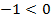 – этот корень удовлетворяет условиям, поэтому можем записать следующую систему:
– этот корень удовлетворяет условиям, поэтому можем записать следующую систему: 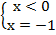 .
.
Итак, первая система (а) дала нам два корня, вторая система (б) дала один корень, поэтому теперь в ответ мы можем выписать все найденные нами корни исходного квадратного уравнения.
Ответ: 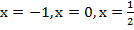 .
.
Итак, в этом примере мы решили квадратное уравнение, которое было осложнено модулем, где вместо простого решения квадратного уравнения нам пришлось решать две системы уравнений.
Задача №2
Решите уравнение 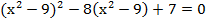 .
.
Если в данном случае мы просто «в лоб» возведём в квадрат первую скобку, то получим уравнение четвёртой степени, которое решать будет уже сложнее. Помимо этого, мы такого раньше не делали, т. е. это является для нас подсказкой к следующим действиям. Вместо этого мы воспользуемся методом «замены переменных», т. е. вместо какого-то выражения мы подставим на время другую переменную и решим исходное уравнение относительно неё.
Решение
Итак, сделаем следующую замену:  , тогда мы получим следующую систему:
, тогда мы получим следующую систему:
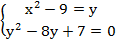
А теперь решим новое квадратное уравнение относительно y с помощью теоремы Виета:
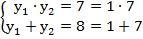 =>
=> 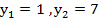 .
.
Теперь необходимо вернуться к исходной системе и сделать обратную замену: 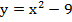
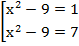
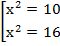

Таким образом мы получили корни исходного квадратного уравнения, используя метод замены.
Ответ: 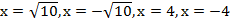 .
.
Задача №3
Решите уравнение  .
.
Мы говорили, что в предыдущем примере метод замены был довольно явно виден невооружённым глазом, в данном же случае, на первый взгляд, абсолютно не понятно, как же решать данное уравнение. Однако мы понимаем, что раскрывать скобки и приводить это уравнение к уравнению четвёртой степени – это неправильно и сложно, поэтому будем искать замену переменных.
Решение
Поскольку на первый взгляд нам не понятно, какую же делать замену, можно сделать это наугад, а можно чуть помочь себе, записав исходное уравнение следующим образом:
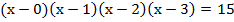 , теперь нам видно, что
, теперь нам видно, что 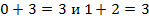 , поэтому попробуем объединить первую с четвёртой скобки и вторую с третьей.
, поэтому попробуем объединить первую с четвёртой скобки и вторую с третьей.
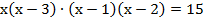
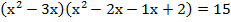
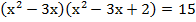
Теперь мы видим, какую же замену переменных стоит сделать:
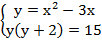
Решим новое квадратное уравнение
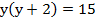
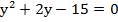
Решим полученное уравнение с помощью обратной теоремы Виета:
Не забываем, что необходимо проверить, существуют ли корни данного уравнения в принципе, для этого посчитаем дискриминант получившегося квадратного уравнения: 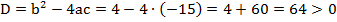 , т. е. у данного выражения корни есть.
, т. е. у данного выражения корни есть.
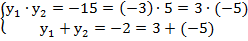 =>
=> 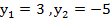
Теперь делаем обратную замену.
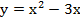
И подставляем полученные значения вместо 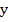 в уравнения:
в уравнения:
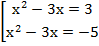

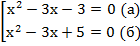
(б)
Вычислим дискриминант:
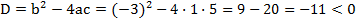 , поэтому в данном случае не существует ни одного корня.
, поэтому в данном случае не существует ни одного корня.
Т. е. в данном случае нет корней (это также можно записать символами 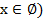 , где
, где 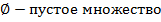 .
.
(а)
Вычислим дискриминант:
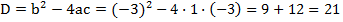 > 0, поэтому существует два различных вещественных корня. Найдём их.
> 0, поэтому существует два различных вещественных корня. Найдём их.
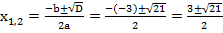 .
.
Ответ: 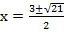 .
.
Мы рассмотрели несколько примеров, где решение уравнений осуществляется с помощью приведения их к виду обычного квадратного уравнения путём замены переменных.
Задача №4
Решите уравнение 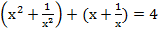 .
.
Мы видим, что первая и вторая скобки похожи, но в первой 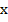 возведён в квадрат.
возведён в квадрат.
Предположительно сделаем следующую замену: 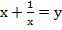
Что же нам теперь делать с первой скобкой? Необходимо тоже выразить её через y. Для этого возведём обе части в квадрат:

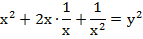
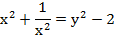
Вернёмся к исходному уравнению и запишем его использовав замену:
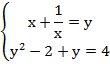
А теперь решим данную систему:
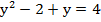
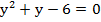
По теореме Виета находим корни:
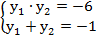 =>
=> 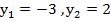
Теперь делаем обратную замену:
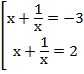
Поскольку такие уравнения решать мы умеем, то только наметим их ход решения: сведём их к квадратному, учитывая, что знаменатель не равен 0, и решим каждое в отдельности.
Решением всей задачи будет следующий ответ: 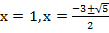 .
.
Ответ: 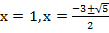 .
.
Итак, мы повторили теорию, связанную с квадратными уравнениями (основные формулы, теорему Виета и формулы разложения на множители). Затем рассмотрели более сложные задачи, а именно решение квадратных уравнений или тех, которые сводятся к квадратным, методом замены переменных.
Список литературы
- Башмаков М.И. Алгебра 8 класс. – М.: Просвещение, 2004.
- Дорофеев Г.В., Суворова С.Б., Бунимович Е.А. и др. Алгебра 8. – 5-е изд. – М.: Просвещение, 2010.
- Никольский С.М., Потапов М.А., Решетников Н.Н., Шевкин А.В. Алгебра 8 класс. Учебник для общеобразовательных учреждений. – М.: Просвещение, 2006.
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
- Фестиваль педагогический идей «Открытый урок» (Источник).
- Интернет-портал Egesdam.ru (Источник).
Домашнее задание
- Решите уравнения: а)
 ; б)
; б)  ;
; - Найдите сумму квадратов корней уравнения: а)
 ; б)
; б)  ;
; - Тест к главе 3 Дорофеев Г.В., Суворова С.Б., Бунимович Е.А. и др. Алгебра 8. – 5-е изд. – М.: Просвещение, 2010.
interneturok.ru
Примеры уравнений, приводимых к квадратным. 9-й класс
Цели:
- сформировать умение решать целые уравнения методом введения новой переменной;
- развивать познавательную активность и творческие способности учащихся;
- воспитывать навыки творческого усвоения знаний.
Оборудование: компьютер, проектор .
ХОД УРОКА
1. Сообщение темы и цели урока
2. Проверка домашнего задания
– Какие уравнения называют целыми?
– Что называют степенью уравнения?
№ 273 (2 ст.), № 274 (а) – решение представлено на
экране.
– Проверьте домашнее задание и поставьте
себе оценку в табеле.
Табель оценок
| №п/п | Виды работ на уроке |
Оценка |
| 1 | Домашнее задание | |
| 2 | Устная работа | |
| 3 | Составление алгоритма решения уравнения | |
| 4 | Работа у доски | |
| 5 | Парная работа | |
| 6 | Самостоятельная работа |
3. Устная работа
– Решим уравнения:
а) (х + 6) (х – 7) = 0 (Когда
произведение равно 0?)
б) (10 – х) (4 – х) = 0
в) х(25 + х) (2 + х) = 0
г) х2 = 25
д) х2 – 9 = 27
4. Работа по объяснению нового материала. (Создание проблемной ситуации)
– Какова степень уравнения x4 – 4х2
+ 5 = 0? (4)
– Умеем мы решать такие уравнения? (Нет)
Давайте попробуем.
– Можно переписать уравнение в таком виде: (х2)2
– 4х2 + 5 = 0?
– На какое уравнение похожа эта запись? (На
квадратное)
– Почему я выделила х2?
– Что я могу сделать с этим одночленом? (Заменить
другой переменной)
– Пусть х2 = у, тогда у2 – 4у + 5 = 0
– Что мы получили при замене переменной? (Квадратное
уравнение)
– Когда решим квадратное уравнение, значение
какой переменной мы найдём? (у)
– Это будет ответ? (Нет)
– Что мы должны сделать дальше? (Вернуться к
подстановке)
– Сколько у нас получится уравнений? (2)
– Чтобы найти значение х, мы должны решить оба
эти уравнения.
– Сколько корней имеет уравнение?
– Отчего зависит количество корней уравнения? (От
количества и знака корней уравнения с замененной
переменной)
5. Презентация решений уравнений:
х4 – 4х2 + 5 = 0 и
(х2 + х + 6)(х2 + х – 4) = 144
6. Закрепление нового материала
У доски решение с комментированием и составлением алгоритма решения.
№276(а): (2х2 + 3) – 12(2х2 + 3) + 11 = 0
№278(а): х4 – 5х2 – 36 = 0
Алгоритм решения биквадратного уравнения
Метод решения – замены переменной
1. Ввести замену переменной: пусть х2 =
y,
2. Составить квадратное уравнение с новой
переменной: аy2 + by+ с = 0 (2)
3. Решить новое квадратное уравнение (2).
4. Вернуться к замене переменной.
5. Решить получившиеся квадратные уравнения.
6. Сделать вывод о числе решений биквадратного
уравнения.
7. Записать ответ.
7. Парная работа
Самостоятельное решение с взаимопроверкой. №276(б), 278(б)
8. Самостоятельная работа
в) г) д) е) одновременное решение у доски (на 4 досках). Проверка с помощью проектора.
7. Подведение итогов. Рефлексия
– Что нового узнали на уроке?
– Какие задания были сложными? Что запомнилось?
– Как работал класс на уроке?
– Кто работал лучше всех?
Поставить оценки за урок, используя табель оценок. (Табель сдается и проверяется учителем)
8. Домашнее задание: №279(обязательно), №280 (по выбору).
urok.1sept.ru
Квадратные уравнения — примеры с решением, особенности и формулы
В современном обществе умение производить действия с уравнениями, содержащими переменную, возведённую в квадрат, может пригодиться во многих областях деятельности и широко применяется на практике в научных и технических разработках. Свидетельством тому может служить конструирование морских и речных судов, самолётов и ракет. При помощи подобных расчётов определяют траектории перемещения самых разных тел, в том числе и космических объектов. Примеры с решением квадратных уравнений находят применение не только в экономическом прогнозировании, при проектировании и строительстве зданий, но и в самых обычных житейских обстоятельствах. Они могут понадобиться в туристических походах, на спортивных состязаниях, в магазинах при совершении покупок и в других весьма распространённых ситуациях.

Разобьём выражение на составляющие множители
Степень уравнения определяется максимальным значением степени у переменной, которую содержит данное выражение. В случае, если она равна 2, то подобное уравнение как раз и называется квадратным.
Если изъясняться языком формул, то указанные выражения, как бы они ни выглядели, всегда можно привести к виду, когда левая часть выражения состоит из трёх слагаемых. Среди них: ax2 (то есть переменная, возведённая в квадрат со своим коэффициентом), bx (неизвестное без квадрата со своим коэффициентом) и c (свободная составляющая, то есть обычное число). Всё это в правой части приравнивается 0. В случае, когда у подобного многочлена отсутствует одно из его составляющих слагаемых, за исключением ax2, оно называется неполным квадратным уравнением. Примеры с решением таких задач, значение переменных в которых найти несложно, следует рассмотреть в первую очередь.
Если выражение на вид выглядит таким образом, что слагаемых у выражения в правой части два, точнее ax2 и bx, легче всего отыскать х вынесением переменной за скобки. Теперь наше уравнение будет выглядеть так: x(ax+b). Далее становится очевидно, что или х=0, или задача сводится к нахождению переменной из следующего выражения: ax+b=0. Указанное продиктовано одним из свойств умножения. Правило гласит, что произведение двух множителей даёт в результате 0, только если один из них равен нулю.
Пример
8x2 — 3x = 0
x(8x – 3) = 0
Далее действуем согласно только что описанному правилу.
x=0 или 8х – 3 = 0
В результате получаем два корня уравнения: 0 и 0,375.
Уравнения такого рода могут описывать перемещение тел под действием силы тяжести, начавших движение из определённой точки, принятой за начало координат. Здесь математическая запись принимает следующую форму: y = v0t + gt2/2. Подставив необходимые значения, приравняв правую часть 0 и найдя возможные неизвестные, можно узнать время, проходящее с момента подъёма тела до момента его падения, а также многие другие величины. Но об этом мы поговорим позднее.

Разложение выражения на множители
Описанное выше правило даёт возможность решать указанные задачи и в более сложных случаях. Рассмотрим примеры с решением квадратных уравнений такого типа.
X2 – 33x + 200 = 0
Этот квадратный трёхчлен является полным. Для начала преобразуем выражение и разложим его на множители. Их получается два: (x-8) и (x-25) = 0. В результате имеем два корня 8 и 25.
Примеры с решением квадратных уравнений в 9 классе позволяют данным методом находить переменную в выражениях не только второго, но даже третьего и четвёртого порядков.
Например: 2x3 + 2x2 – 18x – 18 = 0. При разложении правой части на множители с переменной, их получается три, то есть (x+1),(x-3) и (x+3).
В результате становится очевидно, что данное уравнение имеет три корня: -3; -1; 3.
Извлечение квадратного корня
Другим случаем неполного уравнения второго порядка является выражение, на языке букв представленное таким образом, что правая часть строится из составляющих ax2 и c. Здесь для получения значения переменной свободный член переносится в правую сторону, а после этого из обеих частей равенства извлекается квадратный корень. Следует обратить внимание, что и в данном случае корней уравнения обычно бывает два. Исключением могут служить лишь только равенства, вообще не содержащие слагаемое с, где переменная равна нулю, а также варианты выражений, когда правая часть оказывается отрицательной. В последнем случае решений вообще не существует, так как указанные выше действия невозможно производить с корнями. Примеры решений квадратных уравнений такого типа необходимо рассмотреть.
3x2— 48 = 0
3x2 = 48
В данном случае корнями уравнения окажутся числа -4 и 4.
Вычисление пощади земельного участка
Потребность в подобного рода вычислениях появилась в глубокой древности, ведь развитие математики во многом в те далёкие времена было обусловлено необходимостью определять с наибольшей точностью площади и периметры земельных участков.

Примеры с решением квадратных уравнений, составленных на основе задач такого рода, следует рассмотреть и нам.
Итак, допустим имеется прямоугольный участок земли, длина которого на 16 метров больше, чем ширина. Следует найти длину, ширину и периметр участка, если известно, что его площадь равна 612 м2.
Приступая к делу, сначала составим необходимое уравнение. Обозначим за х ширину участка, тогда его длина окажется (х+16). Из написанного следует, что площадь определяется выражением х(х+16), что, согласно условию нашей задачи, составляет 612. Это значит, что х(х+16) = 612.
Решение полных квадратных уравнений, а данное выражение является именно таковым, не может производиться прежним способом. Почему? Хотя левая часть его по-прежнему содержит два множителя, произведение их совсем не равно 0, поэтому здесь применяются другие методы.
Дискриминант
Прежде всего произведём необходимые преобразования, тогда внешний вид данного выражения будет выглядеть таким образом: x2 + 16x – 612 = 0. Это значит, мы получили выражение в форме, соответствующей указанному ранее стандарту, где a=1, b=16, c=-612.
Это может стать примером решения квадратных уравнений через дискриминант. Здесь необходимые расчёты производятся по схеме: D = b2 – 4ac. Данная вспомогательная величина не просто даёт возможность найти искомые величины в уравнении второго порядка, она определяет количество возможных вариантов. В случае, если D>0, их два; при D=0 существует один корень. В случае, если D<0, никаких шансов для решения у уравнения вообще не имеется.
О корнях и их формуле
В нашем случае дискриминант равен: 256 – 4(-612) = 2704. Это говорит о том, что ответ у нашей задачи существует. Если знать, к примеру, дискриминант, решение квадратных уравнений нужно продолжать с применением ниже приведённой формулы. Она позволяет вычислить корни.
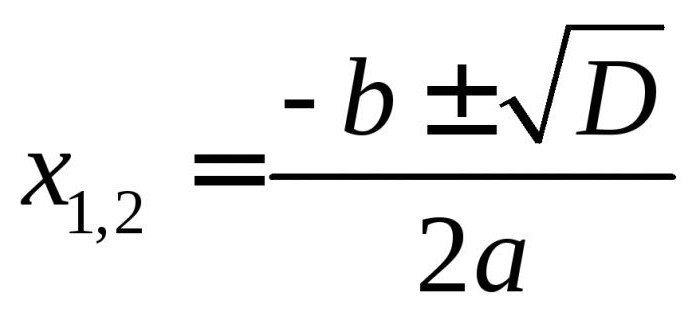
Это значит, что в представленном случае: x1=18, x2=-34. Второй вариант в данной дилемме не может являться решением, потому что размеры земельного участка не могут измеряться в отрицательных величинах, значит х (то есть ширина участка) равна 18 м. Отсюда вычисляем длину: 18+16=34, и периметр 2(34+18)=104(м2).
Примеры и задачи
Продолжаем изучение квадратных уравнений. Примеры и подробное решение нескольких из них будут приведены далее.
1) 15x2 + 20x + 5 = 12x2 + 27x + 1
Перенесём всё в левую часть равенства, сделаем преобразование, то есть получим вид уравнения, который принято именовать стандартным, и приравняем его нулю.
15x2 + 20x + 5 – 12x2 – 27x – 1 = 0
Сложив подобные, определим дискриминант: D = 49 – 48 = 1. Значит у нашего уравнения будет два корня. Вычислим их согласно приведённой выше формуле, а это значит, что первый из них буде равен 4/3, а второй 1.
2) Теперь раскроем загадки другого рода.
Выясним, есть ли вообще здесь корни x2 – 4x + 5 = 1? Для получения исчерпывающего ответа приведём многочлен к соответствующему привычному виду и вычислим дискриминант. В указанном примере решение квадратного уравнения производить не обязательно, ведь суть задачи заключается совсем не в этом. В данном случае D = 16 – 20 = -4, а значит, корней действительно нет.
Теорема Виета
Квадратные уравнения удобно решать через указанные выше формулы и дискриминант, когда из значения последнего извлекается квадратный корень. Но это бывает не всегда. Однако способов для получения значений переменных в данном случае существует множество. Пример: решения квадратных уравнений по теореме Виета. Она названа в честь Франсуа Виета, который жил в XVI веке во Франции и сделал блестящую карьеру благодаря своему математическому таланту и связям при дворе. Портрет его можно увидеть в статье.

Закономерность, которую заметил прославленный француз, заключалась в следующем. Он доказал, что корни уравнения в сумме численно равны -p=b/a, а их произведение соответствует q=c/a.
Теперь рассмотрим конкретные задачи.
3x2 + 21x – 54 = 0
Для простоты преобразуем выражение:
x2 + 7x – 18 = 0
Воспользуемся теоремой Виета, это даст нам следующее: сумма корней равна -7, а их произведение -18. Отсюда получим, что корнями уравнения являются числа -9 и 2. Сделав проверку, убедимся, что эти значения переменных действительно подходят в выражение.
График и уравнение параболы
Понятия квадратичная функция и квадратные уравнения тесно связаны. Примеры подобного уже были приведены ранее. Теперь рассмотрим некоторые математические загадки немного подробнее. Любое уравнение описываемого типа можно представить наглядно. Подобная зависимость, нарисованная в виде графика, называется параболой. Различные её виды представлены на рисунке ниже.
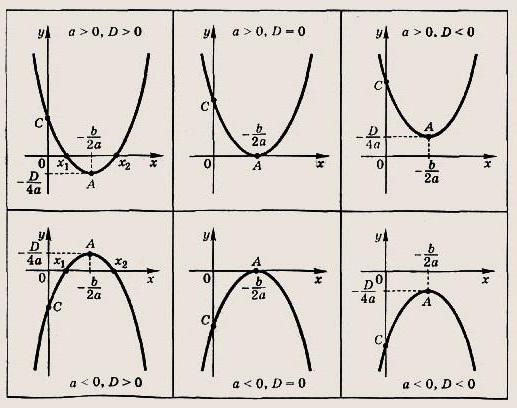
Любая парабола имеет вершину, то есть точку, из которой выходят её ветви. В случае если a>0, они уходят высоко в бесконечность, а когда a<0, они рисуются вниз. Простейшим примером подобной зависимости является функция y = x2. В данном случае в уравнении x2=0 неизвестное может принимать только одно значение, то есть х=0, а значит существует только один корень. Это неудивительно, ведь здесь D=0, потому что a=1, b=0, c=0. Выходит формула корней (точнее одного корня) квадратного уравнения запишется так: x = -b/2a.
Наглядные изображения функций помогают решать любые уравнения, в том числе и квадратные. Этот метод называется графическим. А значением переменной х является координата абсцисс в точках, где происходит пересечение линии графика с 0x. Координаты вершины можно узнать по только что приведённой формуле x0 = -b/2a. И, подставив полученное значение в изначальное уравнение функции, можно узнать y0, то есть вторую координату вершины параболы, принадлежащую оси ординат.
Пересечение ветвей параболы с осью абсцисс
Примеров с решением квадратных уравнений очень много, но существуют и общие закономерности. Рассмотрим их. Понятно, что пересечение графика с осью 0x при a>0 возможно только если у0 принимает отрицательные значения. А для a<0 координата у0 должна быть положительна. Для указанных вариантов D>0. В противном случае D<0. А когда D=0, вершина параболы расположена непосредственно на оси 0х.
По графику параболы можно определить и корни. Верно также обратное. То есть если получить наглядное изображение квадратичной функции нелегко, можно приравнять правую часть выражения к 0 и решить полученное уравнение. А зная точки пересечения с осью 0x, легче построить график.
Из истории
С помощью уравнений, содержащих переменную, возведённую в квадрат, в старину не только делали математические расчёты и определяли площади геометрических фигур. Подобные вычисления древним были нужны для грандиозных открытий в области физики и астрономии, а также для составления астрологических прогнозов.

Как предполагают современные деятели науки, одними из первых решением квадратных уравнений занялись жители Вавилона. Произошло это за четыре столетия до наступления нашей эры. Разумеется, их вычисления в корне отличались от ныне принятых и оказывались гораздо примитивней. К примеру, месопотамские математики понятия не имели о существовании отрицательных чисел. Незнакомы им были также другие тонкости из тех, которые знает любой школьник современности.
Возможно, ещё раньше учёных Вавилона решением квадратных уравнений занялся мудрец из Индии Баудхаяма. Произошло это примерно за восемь столетий до наступления эры Христа. Правда, уравнения второго порядка, способы решения которых он привёл, были самыми наипростейшими. Кроме него, подобными вопросами интересовались в старину и китайские математики. В Европе квадратные уравнения начали решать лишь в начале XIII столетия, но зато позднее их использовали в своих работах такие великие учёные, как Ньютон, Декарт и многие другие.
fb.ru
Применение формул корней квадратных уравнений. Видеоурок. Алгебра 8 Класс
В уроке внимание будет уделено применению формул решения квадратных уравнений с использованием дискриминанта и метода выделения полного квадрата. Будет рассмотрено множество разнообразных примеров.
Рассматриваем квадратное уравнение  . Вспомним, что на прошлом уроке методом выделения полного квадрата мы определили, что
. Вспомним, что на прошлом уроке методом выделения полного квадрата мы определили, что 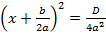 (*), из чего следовала формула корней квадратного уравнения:
(*), из чего следовала формула корней квадратного уравнения:
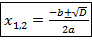 или
или 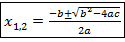 ,
,
где 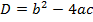 дискриминант квадратного уравнения.
дискриминант квадратного уравнения.
Для корректного применения этих формул необходимо проанализировать знак дискриминанта. Поскольку в выражении, обозначенном (*), левая часть является полным квадратом, то она всегда неотрицательна 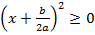 , то же самое относится и к знаменателю правой части
, то же самое относится и к знаменателю правой части 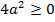 , то по знаку дискриминанта можно сделать некоторые выводы.
, то по знаку дискриминанта можно сделать некоторые выводы.
1. Если 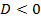 , то корней нет.
, то корней нет.
Пример 1. Решите уравнение 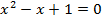 .
.
Решение.Выпишем коэффициенты этого квадратного уравнения 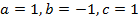 и вычислим его дискриминант
и вычислим его дискриминант  . Следовательно, корней у этого уравнения нет.
. Следовательно, корней у этого уравнения нет.
Ответ. Корней нет.
2. Если  , то уравнение имеет один корень
, то уравнение имеет один корень  , т.к. из (*) следует, что
, т.к. из (*) следует, что 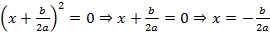 .
.
Замечание. Если говорить строго, что при  квадратное уравнение имеет два одинаковых корня, на что в школьном курсе часто не обращают внимания.
квадратное уравнение имеет два одинаковых корня, на что в школьном курсе часто не обращают внимания.
Пример 2.Решите уравнение 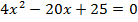 .
.
Решение. Выпишем коэффициенты этого квадратного уравнения 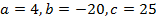 и вычислим его дискриминант
и вычислим его дискриминант  . Следовательно, корень квадратного уравнения
. Следовательно, корень квадратного уравнения 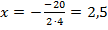 .
.
Ответ. 2,5.
Замечание. Если дискриминант квадратного уравнения нулевой, то соответствующий квадратный трехчлен можно разложить по формуле полного квадрата. Рассмотрим это на предыдущем примере.
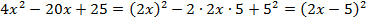
Тогда  . Получили тот же ответ. Продемонстрированный способ является одним из возможных вариантов решения, если вы сразу заметили возможность сворачивания выражения в полный квадрат.
. Получили тот же ответ. Продемонстрированный способ является одним из возможных вариантов решения, если вы сразу заметили возможность сворачивания выражения в полный квадрат.
3. Если 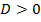 , то уравнение имеет два различных корня
, то уравнение имеет два различных корня  .
.
Пример 3. Решить уравнение 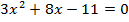 .
.
Решение. Выпишем коэффициенты квадратного уравнения 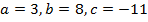 . Вычислим дискриминант
. Вычислим дискриминант 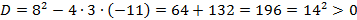 , следовательно, есть два различных корня.
, следовательно, есть два различных корня.
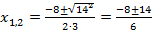 , т.е.
, т.е. 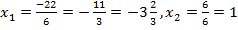 .
.
Ответ.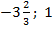 .
.
Теперь рассмотрим различные примеры.
Пример 4. Решить уравнение 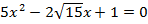 .
.
Решение. Выпишем коэффициенты квадратного уравнения  и вычислим дискриминант
и вычислим дискриминант  , таким образом, у уравнения два различных корня. В отличие от предыдущего рассмотренного случая, дискриминант не является полным квадратом, поэтому записываем его в формулу корней под корнем.
, таким образом, у уравнения два различных корня. В отличие от предыдущего рассмотренного случая, дискриминант не является полным квадратом, поэтому записываем его в формулу корней под корнем.
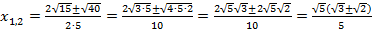 , т.е.
, т.е. 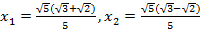 .
.
Ответ.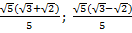 .
.
Данный пример примечателен тем, что коэффициенты квадратного уравнения и его корни содержат иррациональность, однако это не должно смущать, т.к. формула для решения универсальна для всех действительных чисел.
Пример 5. Решить уравнение 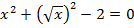 .
.
Решение. Уравнение сначала может показаться очень нестандартным, т.к. в нем присутствует корень из переменной, однако следует обратить внимание, что он в квадрате, а это позволяет упростить выражение:
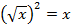 при
при 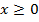 , ограничение вызвано областью определения квадратного корня. Запишем теперь уравнение в упрошенной форме с полученным ограничением (ОДЗ):
, ограничение вызвано областью определения квадратного корня. Запишем теперь уравнение в упрошенной форме с полученным ограничением (ОДЗ):
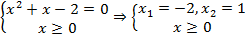 . Корни выписали из решения в предыдущем уроке, т.к. это уравнение уже рассматривалось. В данном случае обратим внимание на то, что полученное в ходе решения ограничение влияет на подходящие корни уравнения – корень
. Корни выписали из решения в предыдущем уроке, т.к. это уравнение уже рассматривалось. В данном случае обратим внимание на то, что полученное в ходе решения ограничение влияет на подходящие корни уравнения – корень 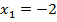 не подходит, т.к.
не подходит, т.к. 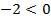 , что не удовлетворяет условию. Остается один корень уравнения
, что не удовлетворяет условию. Остается один корень уравнения 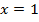 .
.
Ответ.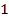 .
.
На следующем уроке мы рассмотрим алгоритм решения рациональных уравнений.
Список литературы
- Башмаков М.И. Алгебра, 8 класс. – М.: Просвещение, 2004.
- Дорофеев Г.В., Суворова С.Б., Бунимович Е.А. и др. Алгебра, 8. 5-е изд. – М.: Просвещение, 2010.
- Никольский С.М., Потапов М.А., Решетников Н.Н., Шевкин А.В. Алгебра, 8 класс. Учебник для общеобразовательных учреждений. – М.: Просвещение, 2006.
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
- School.xvatit.com (Источник).
- Ido.rudn.ru (Источник).
- Planetcalc.ru (Источник).
Домашнее задание
- № 442, 443. Дорофеев Г.В., Суворова С.Б., Бунимович Е.А. и др. Алгебра, 8. 5-е изд. – М.: Просвещение, 2010.
- При каких значениях параметра
 имеет один корень уравнение
имеет один корень уравнение  ?
? - Решите уравнение:
 .
. - *Решите уравнение:
 .
.
interneturok.ru
Биквадратные уравнения. Уравнения приводимые к квадратным
Вопросы занятия:
· повторить алгоритм решения уравнений, приводимых к квадратным;
· вспомнить, какие уравнения называются биквадратными.
Материал урока
Мы уже с вами вспоминали, какие уравнения называются квадратными и как решать квадратные уравнения с помощью дискриминанта или теоремы Виета.



Также рассматривают так называемые биквадратные уравнения. Частичка би означает два, то есть биквадратное уравнение можно понимать, как квадратное в квадратном.
Звучит не очень понятно, но на самом деле – все просто.
Определение.
Биквадратным называется уравнение вида:

Обратите внимание, здесь переменная или выражение с переменной появляются только в четвертой и второй степени, это особенность таких уравнений.
Рассмотрим пример.
Пример.

Биквадратное уравнение введением новой переменной приводится к квадратному уравнению.

Решая это уравнение, находим корни квадратного уравнения. Возвращаясь к замене, мы получим в зависимости от корней квадратного уравнения или ни одного, или одно или два квадратных уравнений. Решения этих уравнений и будут решениями исходного биквадратного уравнения.

Теперь давайте вспомним, что:

Рассмотрим пример.
Пример.

Рассмотрим ещё один пример.
Пример.

Рассмотрим ещё один пример.
Пример.

Пример.

Пример.

Рассмотрим ещё один пример.
Пример.

Итак, давайте теперь сформулируем алгоритм решения уравнений, сводящихся к квадратным в целом и решения биквадратных уравнений в частности.

Итоги урока.
Сегодня на уроке, мы рассмотрели алгоритм решения уравнений, приводимые к квадратным, вспомнили какие уравнения называются биквадратными. Рассмотрели несколько примеров.
videouroki.net
Методическая разработка по алгебре (9 класс) на тему: Решение квадратных уравнений с параметром в 9 классе
Слайд 1
Решение квадратных уравнений содержащих параметры в 9 классе.Слайд 2
При решении задач с параметрами приходится всё время производить несложные, но последовательные рассуждения, составлять для себя логическую схему решаемой задачи. Поэтому такие задачи – незаменимое средство для тренировки логического мышления. Их решение позволяет намного лучше понять обычные, без параметров, задачи. А привычка к математическим рассуждениям очень полезна при изучении высшей математики и использовании полученных знаний впоследствии.
Слайд 3
Для квадратного уравнения a в ыделяем три случая: 1. Если D= — 4 ac
Слайд 4
1. Важную роль при решении задач с параметром для квадратных уравнений играет теорема Виета . Для квадратного уравнения a , а — корни уравнения (случай D ≥0), выполнено равенство a )(х — ). Отсюда вывод теоремы Виета: + = — = .
Слайд 5
2. Второе важное замечание состоит в том, что при решении задач, сводящихся к исследованию квадратных уравнений, нужно помнить о геометрической интерпретации квадратного уравнения a , где ( ; ) – координаты вершины параболы. При а >0 ветви параболы направлены вверх, причем абсцисса вершины параболы является точкой минимума. При а
Слайд 6
Пример 1 . ( ЕГЭ, 2005, ). При каких значениях а функция у = имеет максимум при х = 4? Решение . Исходную функцию представим в виде у = . Поскольку 2>1, то данная функция монотонно возрастает и максимум данная функция достигает в той точке, что и у квадратичной функции f(x) = — + ax + 7. У этой параболы ветви направлены вниз, следовательно, максимум достигается в вершине параболы, т.е. в точке = . Согласно условию = 4, следовательно a = 8. Ответ: а = 8.
Слайд 7
Пример 2 . Решите уравнение (а – 1 ) + 2(2a + 1)x +(4a + 3) = 0. Решение . По виду это уравнение представляется квадратным. Но (внимание!) значение параметра а нам неизвестно, и оно вполне может оказаться равным 1; в этом случае коэффициент перед обращается в нуль и уравнение становится линейным. Квадратные и линейные уравнения решаются по разным алгоритмам. Итак нам надо рассмотреть два случая: а = 1 и а ≠ 1.
Слайд 8
Пусть а =1, тогда уравнение принимает вид: 0· Решив это уравнение , получаем: х = — . Частичный ответ : если а = 1, то х = — .
Слайд 9
Пусть а ≠ 1. Мы имеем квадратное уравнение (а – 1 ) + 2(2a + 1)x +(4a + 3) = 0 . Найдем его дискриминант: D =( — Итак, D = . Дальнейшие рассуждения зависят от знака дискриминанта. Если D 0 , то уравнение имеет два корня. Дискриминант обращается в нуль при а = — , положителен при а > — , отрицателен при а
Слайд 10
Пусть а — (но, напомним а ≠ 1). В этом случае дискриминант больше нуля и квадратное уравнение имеет два корня, которые мы найдем по формуле корней квадратного уравнения: = Частичный ответ : при а > — ( а ≠1) =
Слайд 11
Осталось рассмотреть случай, когда а = — . Используя формулу корней квадратного уравнения, получаем = = — . Частичный ответ : при а = — , х = — . Ответ: если а =1, то х = — если а = — , то х =- если а > — ( а ≠1 ), то = если а
Слайд 12
Пример 3. При каких значениях параметра а корни уравнения — Решение. Если а = 0, то уравнение примет вид 2 х – 2 = 0. Корень этого уравнения будет х = -1. Этот корень удовлетворяет условию x
Слайд 13
Если а ≠0, то заданное уравнение является квадратным. График функции у= f(x) , где f(x)= — 2x-3a-2 является парабола с ветвями вверх, если 2 а > 0, и ветвями вниз, если 2а 0) или на рис. 2 (для 2а
Слайд 15
Дадим аналитическое описание геометрической модели, представленной на рис.1. Во-первых, напомним, при 2 а > 0 ветви параболы направлены вверх. Во-вторых, парабола обязательно пересекается с осью Ох ( в крайнем случае касается её), иначе у квадратного уравнения не будет корней. Корни есть, значит дискриминант не отрицателен. В-третьих, в точке х =1 имеем f(1)>0. В четвертых,
Слайд 16
Итак получаем систему неравенств – аналитическую модель, дающую описание геометрической модели, представленной на рис.1.
Слайд 17
Аналогичные рассуждения позволяют составить вторую систему неравенств – аналитическую модель, дающую описание геометрической модели, представленной на рис. 2:
Слайд 18
Решим первую систему неравенств. Найдем дискриминант. D =4-4·2 а ·(-3а-2)=24 +16 a +4. Найдем f(1). f (1)=2 a · -2·1-3 a -2=- a -4. Найдем = . Так как , получаем: a Таким образом, первая система неравенств имеет следующий вид :
Слайд 19
Эта система не имеет решений, поскольку из первого её неравенства получаем а >0, а из третьего получаем а
Слайд 20
Сразу обратим внимание на то, что квадратный трехчлен имеет отрицательный дискриминант ( D= — 4·4 24 0 , а потому квадратное неравенство в данной системе неравенств можно отбросить. Далее имеем: Решением данной системы является -4
Слайд 21
Итак, мы нашли все интересующие нас значения параметра а: а=0; -4
Слайд 22
Пример 4 . Какие значения может принимать сумма квадратов действительных, различных корней уравнения +2 ax +2 — 2 – 12 =0? Решение. Квадратное уравнение имеет два различных действительных корня, когда дискриминант больше нуля. Решим неравенство D >0. -4 -2-12)>0, п олучаем а (-3;4). По теореме Виета + = -2a ; · =2 — a -12. Следовательно, + = ( -2 = 2 a +24. Т.к. a О твет :
Слайд 23
Вывод: основой для усвоения материала является здравый смысл ученика, а не только и не столько его предварительные знания. Спасибо за внимание .
nsportal.ru
Квадратные уравнения. Видеоурок. Алгебра 8 Класс
Когда вы просыпаетесь утром и слышите за окном размеренный стук капель, то сразу понимаете, что на улице идет дождь. Для этого вам даже не надо выглядывать в окно. Или мама приготовила вам с братом 5 бутербродов в школу. Увидев только 2 бутерброда, вы понимаете, что ваш брат взял с собой 3, хотя и не видели, как он это сделал.
В жизни мы часто сталкиваемся с такими ситуациями: наблюдаем одно, а на основании этих наблюдений делаем выводы о другом. Если речь идет о числовых величинах, то по результатам наблюдений мы можем составить уравнение для получения вывода – нахождения неизвестной величины.
Как измерить толщину листа бумаги? Обычная линейка не подойдет – у нее цена деления больше измеряемой величины. Но можно воспользоваться тем, что толщина у листов, обычно, практически одинаковая. Значит, если взять много листов, то толщина одного – это толщина пачки, разделенная на количество листов в ней.
Получаем метод измерения: взять пачку такой толщины, чтобы ее можно было достаточно точно измерить имеющейся линейкой, затем посчитать количество листов в ней. Если, к примеру, толщина пачки из 500 листов оказалась равной  , то получаем уравнение:
, то получаем уравнение:
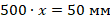
Откуда толщина одного листа:
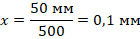
Другой пример. Вам нужно посчитать, сколько конфет лежит в пакете. Конечно, это можно сделать напрямую. Ну, а если конфет очень много? Выход есть! Если мы знаем массу одной конфеты (например, на упаковке написано: 15 г), то можем взвесить весь пакет (пусть получилось 1800 г). Обозначив количество конфет за 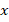 , составляем уравнение:
, составляем уравнение:
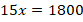
Решая уравнение, получаем ответ:
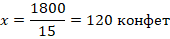
Полученные в примерах уравнения: 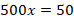 и
и 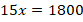 – это линейные уравнения (уравнения вида
– это линейные уравнения (уравнения вида  ). С ними и с задачами, которые ими описываются, мы уже умеем работать.
). С ними и с задачами, которые ими описываются, мы уже умеем работать.
Но в линейных уравнениях переменная всегда в первой степени (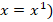 . Понятно, что так будет не всегда. Например, если мы ищем сторону квадрата с площадью
. Понятно, что так будет не всегда. Например, если мы ищем сторону квадрата с площадью 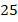 , то должны решить уравнение:
, то должны решить уравнение: 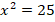 , которое уже не будет линейным (логично так и назвать его – нелинейным).
, которое уже не будет линейным (логично так и назвать его – нелинейным).
Многие задачи могут быть смоделированы нелинейными уравнениями. Например, для нахождения минимальной начальной скорости мяча 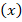 , с которой нужно его подбросить, чтобы он перелетел через забор высотой
, с которой нужно его подбросить, чтобы он перелетел через забор высотой  метра, нужно решить квадратное уравнение
метра, нужно решить квадратное уравнение 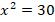 .
.
Как получилось такое уравнение?
Воспользуемся формулой из курса физики, а именно – формулой для вычисления расстояния, которое прошло тело при равноускоренном движении.
Когда мы подбрасываем мяч, то на него действует только сила тяжести, т.е. мяч движется с ускорением 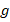 , которое направлено вниз. Пока мяч летит вверх, это ускорение замедляет его начальную скорость до
, которое направлено вниз. Пока мяч летит вверх, это ускорение замедляет его начальную скорость до 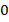 (в верхней точке), а когда он начинает падать, наоборот, разгоняет (увеличивает скорость).
(в верхней точке), а когда он начинает падать, наоборот, разгоняет (увеличивает скорость).
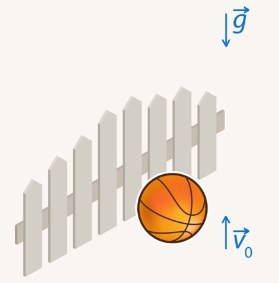
Рис. 1. Когда мяч начинает падать, ускорение увеличивает его скорость
В этом случае расстояние от земли до мяча можно вычислить по формуле:
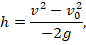
где  – начальная скорость мяча,
– начальная скорость мяча, 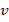 – скорость мяча на данной высоте,
– скорость мяча на данной высоте, 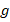 – ускорение свободного падения:
– ускорение свободного падения:
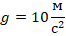
Мяч перелетит через забор, если высота его подлета станет равной высоте забора:
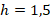 м
м
Т.к. мы ищем минимальную скорость, то достаточно, чтобы это была верхняя точка траектории, т.е. скорость мяча в ней равнялась 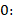
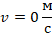
Кроме того, мы обозначили:
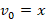
Получаем:
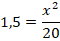
Откуда:
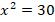
Подробнее о решении таких задач (и о том, откуда взялась использованная нами формула) вы узнаете на уроках физики в 9 классе
Рассмотрим два линейных уравнения:


Если мы их перемножим, то получим уравнение:
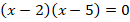
Понятно, что у этого уравнения два корня: 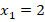 и
и 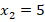 , потому что произведение равно
, потому что произведение равно 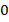 только тогда, когда хотя бы один из множителей равен
только тогда, когда хотя бы один из множителей равен 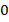 .
.
Если мы раскроем скобки в левой части, то получим уравнение:
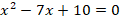
Мы получили пример простейшего нелинейного уравнения – квадратного уравнения.
Строгое определение: квадратное уравнение – это уравнение вида:
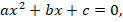
где 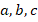 – заданные числа (коэффициенты квадратного уравнения), причем
– заданные числа (коэффициенты квадратного уравнения), причем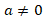 , ведь если
, ведь если 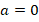 , то уравнения будет линейным
, то уравнения будет линейным 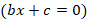 .
.
В рассмотренном нами примере квадратное уравнение 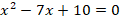 можно решить, разложив левую часть на множители:
можно решить, разложив левую часть на множители:
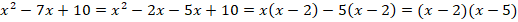
Но для любых ли 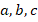 можно разложить квадратный трехчлен (так называется выражение
можно разложить квадратный трехчлен (так называется выражение  в левой части квадратного уравнения – три члена – три слагаемых, старшая степень – квадрат) на линейные множители?
в левой части квадратного уравнения – три члена – три слагаемых, старшая степень – квадрат) на линейные множители?
Например, 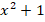 разложить на множители нам не удастся, у уравнения
разложить на множители нам не удастся, у уравнения 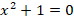 нет действительных корней (потому что, как мы знаем, квадрат действительного числа не может быть отрицательным:
нет действительных корней (потому что, как мы знаем, квадрат действительного числа не может быть отрицательным: 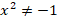 ).
).
Но можно ли как-то определить наличие или отсутствие корней квадратного уравнения по его коэффициентам? Оказывается, да. И это мы сегодня тоже научимся делать.
Итак, как решать квадратные уравнения? Один способ мы уже нашли – попытаться разложить левую часть на линейные множители, и приравнять каждый из них к 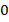 . Алгоритм будет следующий:
. Алгоритм будет следующий:
- перенести все слагаемые в одну сторону;
- разложить полученное выражение на множители;
- решить полученные линейные уравнения.
Для разложения на множители, можем использовать различные уже известные нам приемы:
- вынесение множители за скобки;
- формулы сокращенного умножения;
- метод группировки;
- выделение полного квадрата.
Повторить эти методы вы можете, посмотрев урок «Разложение многочленов на множители»
Рассмотрим несколько примеров.
Пример 1. Решить уравнение:
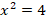
Решение.
Перенесем слагаемое из правой части уравнения в левую:
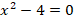
Представим число так:
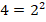
Тогда:
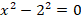
Применяем формулу разности квадратов:
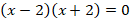
Откуда:
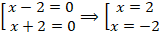
Часто в квадратных уравнениях получается 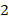 ответа, поэтому возле неизвестной ставят индексы и записывают так:
ответа, поэтому возле неизвестной ставят индексы и записывают так:

Ответ: 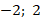 .
.
Пример 2. Решить уравнение:
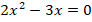
Решение.
Выносим общий множитель за скобки:

Тогда:
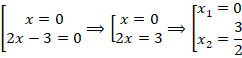
Ответ:  .
.
Рассмотренные квадратные уравнения называются неполными квадратными уравнениями. Если вы сравните их с общим видом квадратного уравнения:  , то поймете, почему.
, то поймете, почему.
Так, в уравнении 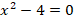 отсутствует слагаемое с
отсутствует слагаемое с 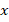 , т.е. в нем коэффициент
, т.е. в нем коэффициент 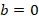 . В уравнении
. В уравнении 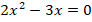 отсутствует свободный член, т.е.
отсутствует свободный член, т.е. 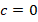 . Рассмотрим еще несколько примеров неполных квадратных уравнений.
. Рассмотрим еще несколько примеров неполных квадратных уравнений.
Пример 3. Решить уравнение:
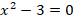
Решение.
Чтобы использовать здесь формулу разности квадратов, вспомним соотношение для квадратных корней:
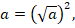
для любого неотрицательного 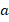 . Соответственно:
. Соответственно:
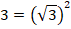
Тогда:
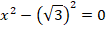
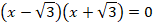
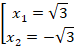
Ответ: 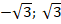 .
.
Пример 4. Решить уравнение:

Решение.
Формулы для суммы квадратов нет, поэтому мы не можем разложить левую часть уравнения на множители. В таком случае, уравнение не имеет решений. Покажем это:

Квадрат любого действительного числа всегда неотрицательная величина, значит, нельзя найти такое значение 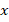 , при котором
, при котором 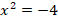 .
.
Ответ: нет действительных корней.
С примером ситуации, когда квадратное уравнение не имеет решений, можно ознакомиться ниже.
Пример задачи, которая не имеет решения
Уравнения возникают, как модели для решения некоторых задач. Понятно, что некоторые задачи могут не иметь решения, а, значит, не будет иметь решения и соответствующее уравнение.
Вернемся к примеру с мячом, который бросают вертикально вверх. Выше мы говорили о формуле для пройденного мячом расстояния:
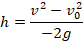
Если воспользоваться тем, что скорость при таком движении изменяется по формуле: 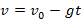 , то получим:
, то получим:
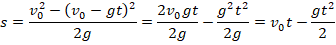
Тогда, если тело подбросили вертикально вверх со скоростью 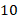 м/с, то зависимость высоты над поверхностью
м/с, то зависимость высоты над поверхностью  будет иметь вид:
будет иметь вид:
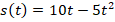
Чтобы определить время, через которое тело будет находиться на высоте 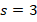 метра, нужно будет решить уравнение:
метра, нужно будет решить уравнение:

На высоте 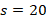 м – уравнение:
м – уравнение:

Но тело, брошенное вертикально со скоростью 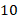 м/с, не долетит до высоты
м/с, не долетит до высоты 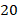 метров (максимальная высота составит
метров (максимальная высота составит 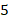 метров). Поэтому вполне естественно, что уравнение
метров). Поэтому вполне естественно, что уравнение  не будет иметь решений.
не будет иметь решений.
Когда мы говорим о том, что квадратное уравнение не будет иметь корней, то всегда будем говорить о действительных (вещественных) корнях. Мы говорили, что можно расширить такой инструмент число и ввести числа, квадрат которых может быть отрицательным (см. рис. 1):

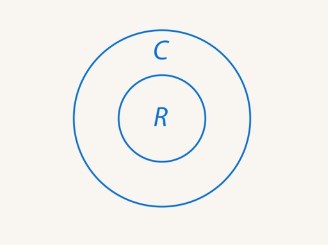
Рис. 1. Действительные и комплексные числа
Такие числа называются комплексными. Если рассматривать решение квадратного уравнения на множестве комплексных чисел, то у него всегда будет два корня. Например:
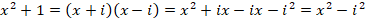
Но, если по определению:
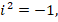
то:
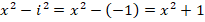
Тогда:
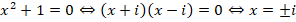
Рассмотрим еще несколько примеров квадратных уравнений.
Пример 5. Решить уравнение:
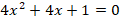
Решение.
Здесь видим формулу полного квадрата:
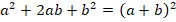
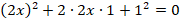
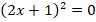
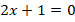
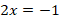

Ответ: 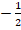 .
.
Пример 6. Решить уравнение:

Решение.
ФСУ здесь не видно, поэтому применим метод выделение полного квадрата. Квадрат первого выражения уже есть 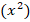 . Далее должно идти удвоенное произведение:
. Далее должно идти удвоенное произведение:  . Глядя на выражение, видим, что вместо знака вопроса должно быть
. Глядя на выражение, видим, что вместо знака вопроса должно быть  (чтобы получить
(чтобы получить 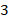 ):
):
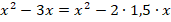
Д
interneturok.ru
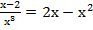 ; б)
; б) 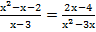 ;
;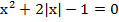 ; б)
; б) 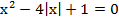 ;
;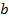 имеет один корень уравнение
имеет один корень уравнение 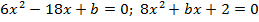 ?
?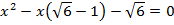 .
.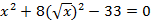 .
.