Тренажёр по алгебре (8 класс) на тему: Неполные квадратные уравнения

Самостоятельная работа по теме: «Неполные квадратные уравнения»

Вариант 1

Решить уравнения:

1. 3×2-12=0
2. 2х2+6х=0
3. 1,8х2=0
4. х2+25=0
5. х2-=0
6. х2=3х
7. х2+2х-3=2х+6
8. х2=3,6

Самостоятельная работа по теме: «Неполные квадратные уравнения»

Вариант 2

Решить уравнения:

1. 2х2-18=0

2. 3х2-12х=0

3. 2,7х2=0

4. х2+16=0

5. х2-=0

6. х2=7х

7. х2-3х-5=11-3х

8. х2=2,5

Самостоятельная работа по теме: «Неполные квадратные уравнения»

Вариант 3

Решить уравнения:

1. 3×2-1=0
2. 2х2-6х=0
3. 8х2=0
4. х2+81=0
5. х2-=0
6. х2=5х
7. х2+х-3=х+6
8. х2=8,1

Самостоятельная работа по теме: «Неполные квадратные уравнения»

Вариант 4

Решить уравнения:

1. 2х2-32=0

2. 3х2-15х=0

3. 2,4х2=0

4. х2+49=0

5. х2-=0

6. х2=х

7. х2-7х-5=11-7х

8. х2=4,9

Самостоятельная работа по теме: «Неполные квадратные уравнения»

Вариант 1

Решить уравнения:

9. 3×2-12=0
10. 2х2+6х=0
11. 1,8х2=0
12. х2+25=0
13. х2-=0
14. х2=3х
15. х2+2х-3=2х+6
16. х2=3,6

Самостоятельная работа по теме: «Неполные квадратные уравнения»

Вариант 2

Решить уравнения:

1. 2х2-18=0

2. 3х2-12х=0

3. 2,7х2=0

4. х2+16=0

5. х2-=0

6. х2=7х

7. х2-3х-5=11-3х

8. х2=2,5

Самостоятельная работа по теме: «Неполные квадратные уравнения»

Вариант 3

Решить уравнения:

9. 3×2-1=0
10. 2х2-6х=0
11. 8х2=0
12. х2+81=0
13. х2-=0
14. х2=5х
15. х2+х-3=х+6
16. х2=8,1

Самостоятельная работа по теме: «Неполные квадратные уравнения»

Вариант 4

Решить уравнения:

1. 2х2-32=0

2. 3х2-15х=0

3. 2,4х2=0

4. х2+49=0

5. х2-=0

6. х2=х

7. х2-7х-5=11-7х

8. х2=4,9

1		2		3		4
1	2;-2	1	3,-3	1	√1/3;-√1/3	1	4,-4
2	0;-3	2	0;4	2	0;3	2	0;5
3	0	3	0	3	0	3	0
4	Нет корней	4	Нет корней	4	Нет корней	4	Нет корней
5	√6;-√6	5	√5;-√5	5	√3;-√3	5	√5;-√5
6	0;3	6	0;7	6	0;5	6	0;1
7	√3;-√3	7	4;-4	7	3;-3	7	4;-4
8	0,6;-0,6	8	0,5;-0,5	8	0,9;-0,9	8	0,7;-0,7

nsportal.ru

Урок по теме «Решение квадратных уравнений». 8-й класс

Рассмотрим стандартные (изучаемые в школьном курсе математики) и нестандартные приёмы решения квадратных уравнений.

1. Разложение левой части квадратного уравнения на линейные множители.

Рассмотрим примеры:

3) х² + 10х – 24 = 0.

6(х² + х – х ) = 0 | : 6

х² + х – х – = 0;

х(х – ) + (х – ) = 0;

х(х – ) (х + ) = 0;

= ; – .

Ответ: ; – .

Для самостоятельной работы:

Решите квадратные уравнения, применяя метод разложения левой части квадратного уравнения на линейные множители.

а) х2 – х = 0; г) х2 – 81 = 0; ж) х2 + 6х + 9 = 0;

б) х2 + 2х = 0; д) 4х2 – = 0; з) х2 + 4х + 3 = 0;

в) 3х2 – 3х = 0; е) х2 – 4х + 4 = 0; и) х2 + 2х – 3 = 0.

Ответы:

а) 0; 1 г) ± 9 ж) – 3

б) -2; 0 д) з) -3; -1

в) 0; 1 е) 2 и) -3; -1

2. Метод выделения полного квадрата.

Рассмотрим примеры:

Для самостоятельной работы.

Решите квадратные уравнения, применяя метод выделения полного квадрата.

3. Решение квадратных уравнений по формуле.

ах² + вх + с = 0, (а | · 4а

4а²х² + 4ав + 4ас = 0;

2ах + 2ах·2в + в

2 – в² + 4ас = 0;

² = в² – 4ас;

= ± ;

2ах = -в ±;

х_1,2 =.

Рассмотрим примеры.

Для самостоятельной работы.

Решите квадратные уравнения, применяя формулу х_1,2 =.

4. Решение квадратных уравнений с использованием теоремы Виета (прямой и обратной)

x² + px +q = 0 – приведённое квадратное уравнение

по теореме Виета.

Если то уравнение имеет два одинаковых корня по знаку и это зависит от коэффициента .

Если p, то .

Если p, то.

Например:

Если то уравнение имеет два различных по знаку корня, причём больший по модулю корень будет , если p и будет , если p.

Например:

Для самостоятельной работы.

Не решая квадратного уравнения, по обратной теореме Виета определите знаки его корней:

Ответы:

а, б, к, л – различные корни;

в, д, з – отрицательные;

г, е, ж, и, м – положительные;

5. Решение квадратных уравнений методом “переброски”.

Для самостоятельной работы.

Решите квадратные уравнения, применяя метод “переброски”.

6. Решение квадратных уравнений с применением свойств его коэффициентов.

I. ax² + bx + c = 0, где a ⁰

1) Если а + b + с = 0, то х₁ = 1; х₂ =

Доказательство:

ax² + bx + c = 0 |: а

х² + х + = 0.

По теореме Виета

По условию а + b + с = 0, тогда b = -а – с. Далее получим

Из этого следует, что х₁ =1; х₂ = . Что и требовалось доказать.

2) Если а – b + с = 0 (или b = а +с ) , то х₁ = – 1; х₂ = –

Доказательство:

По теореме Виета

По условию а – b + с = 0 , т.е. b = а +с . Далее получим:

Поэтому х₁ = – 1; х₂ = – .

Рассмотрим примеры.

1) 345 х² – 137 х – 208 = 0.

а + b + с = 345 – 137 – 208 = 0

х_{1 =} 1; х₂ = =

Ответ: 1;

2) 132 х² – 247 х + 115 = 0.

а + b + с = 132 -247 -115 = 0.

х_{1 =} 1; х₂ = =

Ответ: 1;

Для самостоятельной работы.

Применяя свойства коэффициентов квадратного уравнения, решите уравнения

II. ax² + bx + c = 0, где a ⁰

х_1,2 = . Пусть b = 2k, т.е. чётное. Тогда получим

х_1,2 = = = =

Рассмотрим пример:

3х^{2 –} 14х + 16 = 0 .

D₁ = (-7)² – 3·16 = 49 – 48 = 1

х_{1,2 = ;}

х₁ = = 2; х_{2 =}

Ответ: 2;

Для самостоятельной работы.

а) 4х^{2 –} 36х + 77 = 0

б) 15х^{2 –} 22х – 37 = 0

в) 4х² + 20х + 25 = 0

г) 9х^{2 –} 12х + 4 = 0

Ответы:

а) 3,5; 5,5

б) -1; 2

в) -2,5

г)

III. x² + px + q = 0

х_1,2 = – ± ²– q

Рассмотрим пример:

х² – 14х – 15 = 0

х_1,2 = 7 = 7

х₁ = -1_; х₂ = 15.

Ответ: -1; 15.

Для самостоятельной работы.

а) х² – 8х – 9 = 0

б) х² + 6х – 40 = 0

в) х² + 18х + 81 = 0

г) х² – 56х + 64 = 0

Ответы:

а) -1; 9

б) -10; 4

в) –9

г) 28 18

7. Решение квадратного уравнения с помощью графиков.

Примеры.

а) х² – 3х – 4 = 0

х² = 3х + 4

Ответ: -1; 4

б) х² – 2х + 1 = 0

х² = 3х + 4

Ответ: 1

в) х² – 2х + 5 = 0

х² = 2х -5

Ответ: нет решений

Для самостоятельной работы.

Решить квадратные уравнения графически:

8. Решение квадратных уравнений с помощью циркуля и линейки.

ax² + bx + c = 0,

х² + х + = 0.

х₁ и х₂ – корни.

Пусть А(0; 1), С(0;

По теореме о секущих:

ОВ· ОД = ОА · ОС.

Поэтому имеем:

х₁ · х₂ = 1 · ОС;

ОС = х₁ х₂

К(; 0), где = —

F(0; ) = (0; ) = )

S(-; )

Итак:

1) Построим точку S(-; ) – центр окружности и точку А(0;1).

2) Проведём окружность с радиусом R = SA/

3) Абсциссы точек пересечения этой окружности с осью ох являются корнями исходного квадратного уравнения.

Возможны 3 случая:

1) R > SK (или R > ).

Окружность пересекает ось ох в точке В(х₁; 0) и D(х₂; 0), где х₁ и х₂ – корни квадратного уравнения ax² + bx + c = 0.

2) R = SK (или R = ).

Окружность касается оси ох в тоске В₁(х₁; 0), где х₁ – корень квадратного уравнения

ax² + bx + c = 0.

3) R < SK (или R < ).

Окружность не имеет общих точек с осью ох, т.е. нет решений.

Примеры.

1) x² – 2x – 3 = 0.

Центр S(-; ),т.е.

х₀ = = – = 1,

у₀ = = = – 1.

(1; – 1) – центр окружности.

Проведём окружность (S; AS), где А(0; 1).

 

Ответ: х₁ = – 1; х₂ = 3.

2) x² – 5x + 4 = 0.

х₀ = = – = 2,5; у₀ = = = 2,5.

 

Ответ: х₁ = 1; х₂ = 4.

3) x² + 4x + 4 = 0.

х₀ = = – = – 2,

у₀ = = = 2,5

Ответ: х_{= -2.}

4) x² – 2x + 3 = 0.

х₀ = = – = 1,

у₀ = = = 2.

Ответ: нет решений.

Для самостоятельной работы.

Решить следующие квадратные уравнения с помощью циркуля и линейки:

9. Решение квадратных уравнений с помощью номограммы

Для решения используют Четырёхзначные математические таблицы В.М. Брадиса (таблица XXII, стр. 83).

Номограмма позволяет, не решая квадратного уравнения x² + px + q = 0, по его коэффициентам определить корни уравнения. Например:

5) z² + 4z + 3 = 0.

Оба корня отрицательные. Поэтому сделаем замену: z₁ = – t. Получим новое уравнение:

t² – 4t + 3 = 0.

t₁ = 1 ; t₂ = 3

z₁ = – 1 ; z₂ = – 3.

Ответ: – 3; – 1

6) Если коэффициенты p и q выходят за пределы шкалы, то выполняют подстановку z = k · t и решают с помощью номограммы уравнение: z²

+ pz + q = 0.

к² t² + p· kt + q = 0. |: к²

t² + t + = 0.

к берут с расчётом, чтобы имели место неравенства:

Для самостоятельной работы.

С помощью таблицы Брадиса решить следующие квадратные уравнения:

10. Геометрический метод решения квадратных уравнений

Рассмотрим примеры, которые решаются с помощью геометрии.

Пример 1. (из “Алгебры” ал-Хорезми)

х² + 10х = 39.

10 : 4 = 2 ; · 2 = 6 .

S_ABCD = х² + 4S_пр. + 4S_кв. = х² + 4·2х + 4 · 6 = х² + 10х + 25.

Заменим х² + 10х на 39.

S_ABCD = 39 + 25 = 64 = 8².

Значит сторона АВ = 8.

х= 8 – 2 – 2 =8 – 5 = 3.

х = 3

х_{1 +} х

2 = -10,

3 + х₂ = -10,

х₂ = -13.

Ответ: – 13

Пример 2. (решение уравнения древними греками)

у² + 6у – 16 = 0.

у² + 6у = 16, |+ 9

у² + 6у + 9 = 16 + 9

(у + 3)² = 25

у + 3 = ± 5,

у₁ = 2, у₂ = -8.

Ответ: -8; 2

Для самостоятельной работы.

Решите геометрически уравнение у^{2 –} 6у – 16 = 0.

Ответ: – 2; 8.

urok.1sept.ru

Решение квадратных уравнений, формулы и примеры

Коэффициент называется старшим коэффициентом, а — свободным членом.

Если старший коэффициент , то квадратное уравнение (1) имеет вид и называется приведенным.

Чтобы квадратное уравнение (1) записать в виде (2), необходимо его левую и правую части поделить на старший коэффициент .

Решение квадратных уравнений с помощью дискриминанта

Если дискриминант , то квадратное уравнение (1) имеет два различных действительных корня:

   

Если дискриминант , то уравнение имеет два равных действительных корня (или корень кратности два)

   

Если дискриминант , то квадратное уравнение (1) действительных корней не имеет, то есть

   

Решение квадратных уравнений с помощью выделения полного квадрата

В левой части уравнения (2) выделим полный квадрат при помощи формулы сокращенного умножения «квадрат суммы/разности»:

   

Таким образом, уравнение (2) принимает вид:

   

или

   

Если выражение , то применим к левой части последнего равенства формулу «разность квадратов», в результате будем иметь:

   

Использовав тот факт, что произведение равно нулю, когда хотя бы один из сомножителей равен нулю, придем к следующей совокупности линейных уравнений:

   

Если выражение , то уравнение запишется в виде

   

Оно имеет кратный корень .

В случае, когда , то квадратное уравнение \eqref{GrindEQ__1_} действительных корней не имеет: .

Решение квадратных уравнений с помощью теоремы Виета

Если приведенное квадратное уравнение \eqref{GrindEQ__2_} имеет корни и , то

   

Следствие. Таким образом, целые решения уравнения \eqref{GrindEQ__2_} являются делителями свободного коэффициента .

Решение квадратных уравнений способом переброски коэффициентов

Умножим левую и правую части уравнения (1) на старший коэффициент :

или .

В результате старший коэффициент умножается на свободный член, то есть как бы «перебрасывается» к нему.

Делаем замену

   

В результате получаем уравнение

   

которое является равносильным заданному уравнению (1). Его корни та находим, если это возможно, по теореме Виета (если нет, то вычисляем дискриминант).

Искомые решения исходного уравнения

   

Частные случаи квадратных уравнений

Если хотя бы один из коэффициентов или равен нулю, то уравнение (1) называется \textbf{неполным}.

Если , то уравнение (1) принимает вид: , его кратный корень .

Если , то уравнение (1) запишется в виде , откуда

   

Если права часть , то уравнение имеет два корня

   

В случае же, если , то уравнение корней не имеет: .

Если , то уравнение \eqref{GrindEQ__1_} принимает вид , откуда

   

то есть

   

ru.solverbook.com

Нестандартные способы решения квадратных уравнений

Нестандартные способы решения квадратных уравнений

Сиднев А.А. 1

---

1МБОУ «Школа № 48»

Кувшинова Л.В. 1

---

1МБОУ «Школа № 48»

Текст работы размещён без изображений и формул.
Полная версия работы доступна во вкладке «Файлы работы» в формате PDF

Введение

Математическое образование, получаемое в школе, является важнейшим компонентом общего образования и общей культуры современного человека. Практически все, что окружает современного человека – это все так или иначе связано с математикой. А последние достижения в физике, технике и информационных технологиях не оставляют никакого сомнения, что и в будущем положение вещей останется прежним. Поэтому решение многих практических задач сводится к решению различных видов уравнений.

Уравнения в школьном курсе алгебры занимают ведущее место. На их изучение отводится времени больше, чем на любую другую тему школьного курса математики. Сила теории уравнений в том, что она не только имеет теоретическое значение для познания естественных законов, но и служит конкретным практическим целям.

Актуальность темы заключается в том, что на уроках алгебры, геометрии, физики мы очень часто встречаемся с решением  квадратных  уравнений. Большинство задач о пространственных формах и количественных отношениях реального мира сводится к решению различных видов уравнений. Овладевая способами их решения, люди находят ответы на различные вопросы из науки и техники (транспорт, сельское хозяйство, промышленность, связь и т. д.). Поэтому каждый ученик должен уметь верно и рационально решать  квадратные уравнения,  это также может мне  пригодится при решении более сложных задач, в том числе  в 9 классе, а также 10 и 11 и при сдаче экзаменов.

Цель: Изучить стандартные и нестандартные способы решения квадратных уравнений

Задачи

1. Изложить наиболее известные способы решения уравнений
2. Изложить нестандартные способы решения уравнений
3. Сделать вывод

Объект исследования: квадратные уравнения

Предмет исследования: способы решения квадратных уравнений

Методы исследования:

• Теоретические: изучение литературы по теме исследования; 
• Анализ: информации  полученной при изучении литературы;  результатов полученных  при решении квадратных уравнений     различными способами.
• Сравнение способов на рациональность их использования при решении квадратных уравнений.

 

Глава 1.Квадратные уравнения и стандартные способы решения

1.1.Определение квадратного уравнения

Квадратным уравнением называется уравнение вида ax² + bx + c = 0, где х – переменная, а, b и с– некоторые числа, причем, а ≠ 0.

Числа а, b и с — коэффициенты квадратного уравнения. Число а называют первым коэффициентом, число b– вторым коэффициентом и число c – свободным членом.

Полное квадратное уравнение — это квадратное уравнение, в котором присутствуют все три слагаемых т.е. коэффициенты в и с отличны от нуля.

Неполное квадратное уравнение — это уравнение, в котором хотя бы один из коэффициентов  в или, с равен нулю.

Определение 3. Корнем квадратного уравнения ах² + bх + с = 0 называют всякое значение переменной х, при котором квадратный трехчлен ах² + bх + с обращается в нуль.

Определение 4. Решить квадратное уравнение — значит найти все его

корни или установить, что корней нет.

Пример:  – 7x + 3 =0

 В каждом из уравнений вида a  + bx + c = 0, где а ≠ 0, наибольшая степень переменной x – квадрат. Отсюда и название: квадратное уравнение.

Квадратное уравнение, в котором коэффициент при х2 равен 1, называют приведенным квадратным уравнением.

 Пример

х² – 11х+30=0, х² –8х=0.

1.2.Стандартные способы решения квадратных уравнений

Решение квадратных уравнений с помощью выделения квадрата двучлена

Решение квадратного уравнения, в котором оба коэффициента при неизвестных и свободный член отличны от нуля. Такой способ решения квадратного уравнения называют выделением квадрата двучлена.

Разложение левой части уравнения на множители.

Решим уравнение х² + 10х — 24 = 0.  Разложим левую часть на множители:

х² + 10х — 24 = х² + 12х — 2х — 24 = х(х + 12) — 2(х + 12) = (х + 12)(х — 2).

Следовательно,  уравнение можно переписать так:(х + 12)(х — 2) = 0

Произведение  множителей равно нулю,  если  по крайней мере, один из его множителей равен нулю.

Ответ: -12; 2.

Решение квадратного уравнения по формуле.

Дискриминант квадратного уравнения ax² + bx + c = 0 выражение b²– 4ас = D  — по знаку которого судят о наличии у этого уравнения действительных корней.

Возможные случаи в зависимости от значения D:

1. Если D>0, то уравнение имеет два корня.
2. Если D= 0, то уравнение имеет один корень: х =
3. Если D <0, то уравнение не имеет корней.

Решение уравнений с помощью теоремы Виета.

Теорема: Сумма корней приведенного квадратного уравнения равна второму коэффициенту, взятому с противоположным знаком, а произведение корней равно свободному члену.

Приведенное квадратное уравнение имеет вид:

х² + bx + c = 0.

Обозначим второй коэффициент буквой р, а свободный член буквой q:

х² + px + q = 0, тогда

x₁ + x₂  = — p; x₁· x₂ =  q

 

 

Глава 2.Нестандартные способы решения квадратных уравнений

2.1.Решение с помощью свойств коэффициентов квадратного уравнения

Свойства коэффициентов квадратного уравнения – это такой способ решения квадратных уравнений, который поможет быстро и устно найти корни уравнения:

ax² + bx + c = 0

1. Если а+ b+c= 0, то x₁ = 1, x₂ =

Пример. Рассмотрим уравнение х² +3х – 4= 0.

a + b + c = 0, то x₁ = 1, x₂ =

1+3+(-4) = 0, тогда x₁ = 1, x₂ =  = — 4

Проверим полученные корни с помощью нахождения дискриминанта:

D= b²– 4ас=3²– 4·1·(-4) = 9+16= 25

x₁ =    =    =  =  = — 4

x₂ =  =  =  =  = 1

Следовательно, если + b +c= 0, то x₁ = 1, x₂ =

2. Если b = a + c, то x₁ = -1, x₂ =

Пример. Рассмотрим уравнение 3х² +4х +1 = 0, a=3, b=4, c=1

Если b= a + c, то x₁ = -1, x₂ =  , то 4 = 3 + 1

Корни уравнения: x₁ = -1, x₂ =  

Значит корнями этого уравнения являются –1 и . Проверим это с помощью нахождения дискриминанта:

D= b²– 4ас=4²– 4·3·1 = 16 – 12 = 4

x₁ =    =    =  =  = — 1

x₂ =  =  =  =  =  

Следовательно, b= a + c, то x₁ = -1, x₂ =

2.2.Способ «переброски»

При этом способе коэффициент а умножается на свободный член, как бы «перебрасывается» к нему, поэтому его и называют способом «переброски». Этот способ применяют, когда можно легко найти корни уравнения, используя теорему Виета и, что самое важное, когда дискриминант есть точный квадрат.

Если а±b+c≠0, то используется прием переброски:

Пример:

3х²+4х+1=0; 3+4+1 ≠ 0

Применяя способ «переброски» получаем:

 х² + 4х+3= 0

Таким образом, с помощью теоремы Виета получаем корни уравнения:

x₁ = — 3, x₂ = -1.

Однако корни уравнения необходимо поделить на 3 (то число, которое «перебрасывали»):

Значит, получаем корни: x₁ = -1, x₂ = .

Ответ:  ; — 1

2.3.Решение с помощью закономерности коэффициентов

1. Если уравнение ax² + bx + c = 0, коэффициент b= (a²+1), и коэффициент c = a, то его корни равны x₁ = — a, x₂ =

Таким образом, решаемое уравнение должно иметь вид

ax² + (а² +1)∙ х + а= 0

Пример. Рассмотрим уравнение 3х² +10х +3 = 0.

Таким образом, корни уравнения: x₁ = -3, x₂ =

Проверим данное решение с помощью дискриминанта:

D= b²– 4ас=10²– 4·3·3 = 100 – 36 = 64

x₁ =    =    =  =  = — 3

x₂ =  =  =  =  =   ; Следовательно, x₁ = — a, x₂ =

2. Если уравнение ax² — bx + c = 0, коэффициент b= (a²+1), и коэффициент c = a, то его корни равны x₁ = a, x₂ =

Таким образом, решаемое уравнение должно иметь вид

ax² —  (а² +1)∙ х+ а= 0

Пример. Рассмотрим уравнение 3х² — 10х +3 = 0.

Таким образом, корни уравнения: x₁ = 3, x₂ =

Проверим данное решение с помощью дискриминанта:

D= b²– 4ас=10²– 4·3·3 = 100 – 36 = 64

x₁ =    =    =  =  =   

x₂ =  =  =  =  = 3; Следовательно, x₁ =  a, x₂ =

3. Если уравнение ax² + bx — c = 0, коэффициент b= (a²-1), и коэффициент c = a, то его корни равны x₁ = —a, x₂ =

Таким образом, решаемое уравнение должно иметь вид

ax² +  (а² —1)∙ х — а= 0

Пример. Рассмотрим уравнение 3х² + 8х —3 = 0..

Таким образом, корни уравнения: x₁ = — 3, x₂ =

Проверим данное решение с помощью дискриминанта:

D= b²– 4ас=8²+ 4·3·3 = 64 + 36 = 100

x₁ =    =    =  =   = — 3

x₂ =  =  =  =  =  ;Следовательно, x₁ = — a, x₂ =

4. Если уравнение ax² — bx — c = 0, коэффициент b= (a²-1), и коэффициент c = a, то его корни равны x₁ = a, x₂ =

Таким образом, решаемое уравнение должно иметь вид

ax² —  (а² —1)∙ х — а= 0

Пример. Рассмотрим уравнение 3х² — 8х —3 = 0..

Таким образом, корни уравнения: x₁ = 3, x₂ = —

Проверим данное решение с помощью дискриминанта:

D= b²– 4ас=8²+ 4·3·3 = 64 + 36 = 100

x₁ =    =    =  =   = —

x₂ =  =  =  =  = 3; Следовательно, x₁ = a, x₂ = —

2.4.Решение с помощью циркуля и линейки

            Предлагаю следующий способ нахождения корней квадратного    уравнения    ах²  + bх + с = 0 с помощью циркуля и линейки (рис.6 ).

       Допустим, что искомая окружность пересекает ось

абсцисс в точках В(х₁; 0 ) и D (х₂; 0), где х₁ и х₂ — корни уравнения   ах²  + bх + с = 0,  и  проходит  через  точки

Рис.6

 

 

А(0; 1) и С(0; c/a) на  оси  ординат.  Тогда по теореме о секущих  имеем OB • OD = OA • OC, откуда OC =  = =  

Центр окружности находится в точке пересечения перпендикуляров SF и SK, восстановленных в серединах хорд AC и BD, поэтому

SK =  =  = —

SF =  =  = 

Итак:

1) построим точки S      (центр окружности) и A(0; 1);

2) проведем окружность с радиусом SA;

3) абсциссы точек пересечения этой окружности с осью Ох являются корнями исходного квадратного уравнения.

  При этом возможны три случая.

1) Радиус окружности больше ординаты центра (AS > SK, или  R > a + c/2a),  окружность пересекает ось Ох в двух точках (рис. 7а) В(х₁; 0) и D(х₂; 0), где х₁ и х₂ — корни квадратного уравнения  ах²  + bх + с = 0.

2) Радиус окружности равен ординате центра  (AS = SB, или R = a + c/2a), окружность касается оси Ох (рис.8б) в точке В(х₁; 0), где х₁ — корень квадратного уравнения.

 3) Радиус окружности меньше ординаты центра     AS<S, R<                                     

окружность не имеет общих точек с осью абсцисс (рис 7в), в этом случае уравнение не имеет решения.  

 а)AS>SB, R>           б) AS=SB, R=                в)   AS<S, R<   

   Два решения x₁ и x₂        Одно решение x₁                                  Нет решения

        

Рис.7

 Пример.

Решим уравнение  х² — 2х — 3 = 0  (рис.8).

Решение. Определим координаты  точки центра окружности по формулам:

x = —  = —  = 1,

y =  =  = -1

Проведем окружность радиуса SA, где А (0; 1).

Ответ: х₁ = — 1; х₂ = 3.

 

2.5.Геометрический способ решения квадратных  уравнений.

           В древности, когда геометрия была более развита, чем алгебра, квадратные уравнения решали не алгебраически, а геометрически. Приведу ставший знаменитым пример из «Алгебры» ал — Хорезми.

Примеры.

      1) Решим уравнение х² + 10х = 39.

      В оригинале эта задача формулируется следующим образом : «Квадрат и десять корней равны 39» (рис.9).

      Решение. Рассмотрим квадрат со стороной х, на его сторонах строятся прямоугольники  так,  что  другая  сторона   каждого   из   них    равна  2,5, следовательно,  площадь каждого равна 2,5х. Полученную фигуру дополняют затем до нового квадрата ABCD, достраивая в  углах четыре равных квадрата , сторона каждого их них 2,5, а площадь 6,25.

 

      Площадь  S  квадрата  ABCD  можно  представить  как сумму  площадей:

первоначального  квадрата   х²,  четырех  прямоугольников (4• 2,5х = 10х ) и четырех пристроенных квадратов (6,25• 4 = 25), т.е. S = х² + 10х + 25. Заменяя

х² + 10х числом 39, получим, что S =  39 + 25 = 64, откуда следует, что сторона квадрата ABCD, т.е. отрезок АВ = 8. Для искомой стороны х первоначального квадрата получим:

x = 8 — 2  — 2  = 3

2) А вот, например, как древние греки решали уравнение у² + 6у — 16 = 0.

Решение представлено на рис 10.  где

у² + 6у = 16, или  у² + 6у + 9 = 16 + 9.

Решение. Выражения  у² + 6у + 9 и 16 + 9 геометрически представляют собой

один и тот же квадрат, а исходное уравнение у² + 6у — 16 + 9 — 9 = 0 — одно и то же уравнение. Откуда и получаем, что у + 3 = ± 5, или у₁ = 2, у₂ = — 8 (рис.  .

                     рис.10

3) Решить геометрически уравнение у² —  6у — 16 = 0.

Преобразуя уравнение, получаем

у² —  6у = 16.

       На рис 11.   находим «изображения» выражения у² —  6у, т.е. из площади квадрата со стороной у два раза вычитается площадь квадрата со стороной, равной 3. Значит, если к выражению у² —  6у  прибавить 9, то получим площадь квадрата со стороной  у  — 3. Заменяя выражение у² —  6у  равным ему числом 16,

получаем: (у — 3)² = 16 + 9, т.е. у — 3 = ± √25, или у — 3 = ± 5, где у₁ = 8 и у₂ = — 2.

 

 

Заключение

В ходе выполнения своей исследовательской работы я считаю, что с поставленной целью и задачами я справился, мне удалось обобщить и систематизировать изученный материал по выше указанной теме.

Нужно отметить, что каждый способ решения квадратных уравнений по-своему уникален. Некоторые способы решения помогают сэкономить время, что немаловажно при решении заданий на контрольных работах и экзаменах.   При работе над темой я  ставил задачу, выяснить какие методы являются стандартными, а какие нестандартными.

Итак, стандартные методы (используются чаще при решении квадратных уравнений):

• Решение с помощью выделения квадрата двучлена
• Разложение левой части на множители
• Решение квадратных уравнений по формуле
• Решение с помощью теоремы Виета
• Графическое решение уравнений

Нестандартные методы:

• Свойства коэффициентов квадратного уравнения
• Решение способом переброски коэффициентов
• Решение с помощью закономерности коэффициентов
• Решение квадратных уравнений, с помощью циркуля и линейки.
• Исследование уравнения на промежутках действительной оси
• Геометрический способ

При этом следует заметить, что каждый способ обладает своими особенностями и границами применения.

Решение уравнений с использованием теоремы Виета

Достаточно легкий способ, дает возможность сразу увидеть корни уравнения, при этом легко находятся только целые корни.

Решение уравнений способом переброски

За минимальное количество действий можно найти корни уравнения, применяется совместно со способом теоремы Виета, при этом также легко найти только целые корни.

Свойства коэффициентов квадратного уравнения

Доступный метод для устного нахождения корней квадратного уравнения, но подходит только к некоторым уравнениям

Графическое решение квадратного уравнения

Наглядный способ решения квадратного уравнения, однако могут возникать погрешности  при составлении графиков

Решение квадратных уравнений с помощью циркуля и линейки

Наглядный способ решения квадратного уравнения, но также могут возникать погрешности

Геометрический способ решения квадратных уравнений

Наглядный способ, похож на способ выделения полного квадрата

Решая уравнения разными способами,  я пришел к выводу, что зная комплекс методов решения квадратных уравнений, можно решить любое уравнение, предлагаемое в процессе обучения.

При этом, следует заметить, что одним из более рациональных способов решения квадратных уравнений является способ «переброски» коэффициента. Однако самым универсальным способом можно считать стандартный способ решения уравнений по формуле, потому что данный способ позволяет решить любое квадратное уравнение, хотя иногда и за более длительное время. Также такие способы решения, как способ «переброски», свойство коэффициентов и теорема Виета помогаю сэкономить время, что очень важно при решении заданий на экзаменах и контрольных работах.

Думаю, что моя работа будет интересна учащимся 9-11 классов, а также тем, которые хотят научиться решать рационально квадратные  уравнения и хорошо подготовиться к выпускным экзаменам. Также она будет интересна и учителям математики, за счет рассмотрения истории квадратных уравнений и систематизации способов их решения.

Список литературы

1. Глейзер, Г.И. История математики в школе/ Г.И. Глейзер.-М.: Просвещение, 1982- 340с.
2. Гусев, В.А. Математика. Справочные материалы/ В.А. Гусев, А.Г. Мордкович — М.: Просвещение, 1988, 372с.
3. Ковалева Г. И., Конкина Е. В. «Функциональный метод решения уравнений и неравенств», 2014 г.
4. Кулагин Е. Д. «300 конкурсных задач по математике», 2013 г.
5. Потапов М. К. «Уравнения и неравенства. Нестандартные методы решения» М. «Дрофа», 2012 г.
6. .Барвенов С. А «Методы решения алгебраических уравнений», М. «Аверсэв», 2006 г.
7. Супрун В.П. «Нестандартные методы решения задач по математике» — Минск «Полымя», 2010г
8. Шабунин М.И. «Пособие по математике для поступающих в вузы», 2005г.
9. Башмаков М.И. Алгебра: учеб. для 8 кл. общеобразоват. учреждений. – М.: Просвещение, 2004. – 287с.
10. Шаталова С. Урок – практикум по теме «Квадратные уравнения».- 2004.

 

 

Просмотров работы: 8900

school-science.ru

РАЗЛИЧНЫЕ СПОСОБЫ РЕШЕНИЯ КВАДРАТНЫХ УРАВНЕНИЙ

Управление образования администрации Новокузнецкого муниципального района

МБОУ «Куртуковская основная общеобразовательная школа»

XIX районная научно-практическая конференция учащихся

Секция: Математика. Экономика

Различные способы решения

квадратных уравнений

Выполнил: Бажеев Владислав, 8 класс

МБОУ «Куртуковская ООШ имени В.П.Зорькина»

Руководитель: Рогачева Светлана

Александровна, учитель математики

первой категории

Куртуково

2014

Содержание

Введение 3

Квадратные уравнения и их классификация 5

Анализ способов решения квадратных уравнений 8

Заключение 16

Список использованных источников и литературы……………………………………17

Приложение 18

Введение

На уроках алгебры в 8 классе мы впервые познакомились с квадратными уравнениями и изучили формулы корней, с помощью которых можно решать любые квадратные уравнения. От учителя я узнал, что изучением квадратных уравнений люди занимались еще с древних веков, оказывается, существует множество способов их решения, которые в школьной программе не рассматриваются. Меня это заинтересовало, и я решил узнать, какие еще способы решения квадратного уравнения существуют.

Актуальность темы: в школьных учебниках дана не полная информация о квадратных уравнениях и способах их решения. Более рациональные способы решения тестовых заданий ГИА и ЕГЭ позволили бы существенно сократить время выполнения заданий.

Цель: изучение различных способов решения квадратных уравнений и приобретение навыков их рационального использования.

Задачи:

• изучение теоретического материала по теме «Различные способы решения квадратных уравнений»;

• апробация изученных способов при решении тестовых заданий ГИА 9;

• обобщение изученного материала в презентации «Способы решения квадратных уравнений».

Объект исследования: квадратные уравнения.

Предмет исследования: способы решения квадратного уравнения.

Методы исследования:

• работа с учебной и научно-популярной литературой,

• сравнение,

• анализ,

• решение задач.

Практическое значение результатов работы: изучение различных способов решения квадратных уравнений позволит мне пополнить знания по данной теме, которые пригодятся при сдаче экзаменов. Проектный продукт по исследуемой теме в форме презентации позволит использовать обобщенную и систематизированную информацию другими учениками для повышения математической грамотности и учителем для подготовки факультативных занятий.

Квадратные уравнения и их классификация

Квадратным уравнением называют уравнение вида ах² + bх + с = 0, где коэффициенты а, b, с — любые действительные числа, причем а ≠ 0. Коэффициенты а, b, с различают по названиям: а – первый или старший коэффициент, b — второй коэффициент, с — свободный член.

Данные уравнения называют квадратными потому, что наибольшая степень переменной х – квадрат. Также их называют уравнением второй степени.

Все квадратные уравнения можно условно разделить на три вида:

1. полные квадратные уравнения;

2. неполные квадратные уравнения;

3. приведенные квадратные уравнения.

Полное квадратное уравнение – это квадратное уравнение, в котором присутствуют все три слагаемых: ах² + bх + с = 0, а ≠ 0.

Неполное квадратное уравнение – это уравнение, в котором хотя бы один из коэффициентов b или с равен нулю.

Приведенное квадратное уравнение – это уравнение вида x² + px + q = 0, в котором старший коэффициент a=1, р – коэффициент при х (p = ), q – свободный член (q = ).

Корнем квадратного уравнения ах² + bх + с = 0 называют такое значение х, при котором квадратный трехчлен ах² + bх + с обращается в нуль.

Решить квадратное уравнение — значит найти все его корни или установить, что корней нет [4].

В свою очередь каждое квадратное уравнение, по количеству или отсутствию корней, можно условно отнести к одному из классов:

1. не имеют корней;

2. имеют ровно один корень;

3. имеют два различных корня.

В этом состоит важное отличие квадратных уравнений от линейных, где корень всегда существует и единственен. Определение количества корней квадратного уравнения осуществляется с помощью дискриминанта.

Способ решения квадратных уравнений через дискриминант является наиболее распространенным, так как подходит к решению квадратных уравнений любого вида.

Дискриминант в переводе с латинского — «различитель».

Формула дискриминанта: D = b² − 4ac.

Таким образом, квадратное уравнение ах² + bх + с = 0 ,

• если D > 0, то имеет два различных корня;

• если D = 0, то имеет единственный корень;

• если D < 0, то не имеет корней.

Формула корней квадратного уравнения имеет вид: , она позволяет найти корни любого квадратного уравнения (если они есть), в том числе приведенного и неполного.

Также в школьном курсе рассматриваются способы решения неполных квадратных уравнений, которые различаются от коэффициента равного нулю:

1. если с = 0, то уравнение имеет вид ах² + bх = 0. Решая уравнение такого вида, используется метод разложения на множители: х (ах + b) = 0 , значит х = 0, либо ах + b = 0. В итоге получается два корня: х₁= 0, х₂=

2. если в = 0, то уравнение имеет вид ах² + с = 0. Уравнение преобразуют к виду ах² = — с и далее . В случае, когда — отрицательное число, то уравнение не имеет корней. В случае, когда — неотрицательное число, то уравнение имеет два корня:

3. если с = 0 и b = 0, то уравнение принимает вид ах² = 0 и оно имеет один корень х = 0.

Однако, изучение дополнительной литературы показало, что помимо описанных формул существуют и другие способы решения квадратных уравнений, которые порой позволяют быстрее найти решение и более рационально использовать время на выполнение математических заданий.

В рамках данной исследовательской работы нами изучены следующие способы решения квадратных уравнений:

1. Решение квадратных уравнений по формуле.

2. Разложение левой части уравнения на множители.

3. Метод выделения полного квадрата.

4. Решение уравнений с использованием теоремы Виета.

5. Решение квадратных уравнений способом «переброски» старшего коэффициента.

6. Применение свойств коэффициентов квадратного уравнения.

7. Графическое решение квадратного уравнения.

Анализ способов решения квадратных уравнений

Рассмотрим решение квадратных уравнений различными способами и приведем примеры.

1) Решение квадратных уравнений по формуле.

Формулы корней квадратного уравнения с использованием дискриминанта приведены в предыдущей главе.

Пример 1

12х² +7х +1= 0,

D = b² − 4ac = 7² — 4·12·1 =

= 49 – 48 = 1,

х₁ = -1/3 и х₂ = — 1/4 .

Ответ: -1/3 и — 1/4

Пример 2

х² – 12х + 36 = 0,

D = b² − 4ac =

= (-12)² — 4·1·36 =

= 144 — 144 = 0,

х = 6.

Ответ: 6

Пример 3

7х² — 25х + 23 = 0,

D = b² − 4ac =

= (-25)² — 4·7·23 =

= 625 – 644 = — 19,

Ответ: корней нет

2) Разложение левой части уравнения на множители

Существует три основных способа разложения на множители:

1. вынесение общего множителя за скобки;

2. использование формул сокращенного умножения;

3. способ группировки.

С помощью 1 и 2 способов наиболее рационально решать неполные квадратные уравнения.

Пример 1

х² – 2х = 0, т.е. с = 0

х (х – 2) = 0

х = 0 или х – 2 = 0

х = 2

Ответ: 0; 2.

Пример 2

9х² – 25 = 0, т.е. b=0

(3х – 5) (3х + 5) = 0

3х – 5 = 0 или 3х + 5 = 0

х = 1 х = — 1

Ответ: — 1 ; .

Пример 3

х² – 4х + 4 = 0, разложим левую часть уравнения на множители;

х² – 2х – 2х + 4 = 0,

х ( х – 2 ) – 2 ( х – 2 ) = 0,

(х — 2)( х – 2 ) = 0, произведение равно нулю, значит хотя бы один из его множителей равен нулю

х – 2 = 0, х = 2.

Ответ: 2.

Пример 4

х² + 10х – 24 = 0,

х² + 12х – 2х – 24 = 0,

х ( х + 12 ) – 2 ( х + 12 ) = 0,

( х + 12 ) ( х – 2 ) = 0,

х + 12 = 0 или х – 2 = 0

х = — 12 х = 2.

Ответ: -12 и 2.

3) Метод выделения полного квадрата

Метод выделения полного квадрата заключается в приведении уравнения общего вида к неполному квадратному уравнению. В этом

помогают формулы сокращенного умножения, а именно, квадратов суммы и разности: (а + b)² = a² + 2ab + b²; (a – b)² = a² – 2ab + b².

Этот метод применим для любых квадратных уравнений, но не всегда удобен в использовании.

Пример 1

х² – 4х + 4 = 0, используем формулу сокращенного умножения;

(х – 2)² = 0,

х – 2 = 0,

х = 2.

Ответ: 2

Пример 2

х² + 6х – 7 = 0, выделим в левой части полный квадрат

х² + 2х · 3 + 3² – 3² – 7 = 0, первое слагаемое – квадрат числа х, а второе – удвоенное произведение х на 3, поэтому чтобы получить полный квадрат, нужно прибавить 3².

Преобразуем левую часть уравнения прибавляя к ней и вычитая 3².

( х + 3 )² – 9 – 7 = 0,

( х + 3 )² – 16 = 0, ( х + 3 )² = 16,

х + 3 = 4 или х + 3 = — 4

х = 1 х = — 7.

Ответ: 1 и -7 .

4) Решение уравнений с использованием теоремы Виета

Приведенное квадратное уравнение имеет вид х² + рх + q = 0, если х₁ и х₂ – корни уравнения, то согласно теореме Виета сумма корней приведенного квадратного уравнения равна второму коэффициенту с обратным знаком, а произведение корней равно свободному члену.

Его корни удовлетворяют теореме Виета: х₁ · х₂ = q

х₁ + х₂ = — р.

По коэффициентам можно предсказать знаки корней.

1. Если свободный член приведенного уравнения положителен, то уравнение имеет два одинаковых по знаку корня и это зависит от второго коэффициента.

Если q > 0 и р > 0 , то оба корня отрицательны.

Если q > 0 и р < 0 , то оба корня положительные.

Пример 1

х² + 10х + 9 = 0,

х₁ = — 1 и х₂ = — 9,

т.к. q = 9 > 0 и р = 10 > 0;

Пример 2

х² – 6х + 9 = 0,

х₁ = 3 и х₂ = 3,

т.к. q = 9 > 0 и р = — 6 < 0.

2. Если свободный член приведенного уравнения отрицателен, то уравнение имеет два различных по знаку корня.

Если q < 0 и р > 0 , то больший по модулю корень будет отрицателен.

Если q < 0 и р < 0, то больший по модулю корень будет положителен.

Пример 1

х² + 2х – 8 = 0,

х₁ = — 4 и х₂ = 2,

т.к. q = — 8 < 0 и р = 2 > 0 ;

Пример 2

х² – 2х – 15 = 0,

х₁ = 5 и х₂ = — 3,

т.к. q = — 15 < 0 и р = — 2 < 0.

Также справедлива теорема, обратная теореме Виета.

Если числа х₁ и х₂ таковы, что х₁ · х₂ = q

х₁ + х₂ = — р,

то х₁ и х₂ – корни квадратного уравнения x² + px + q = 0.

Пример 1

х² – 7х + 10 = 0

х₁ + х₂ = 7;

х₁ · х₂ = 10

Подбираем числа, это 2 и 5

2 + 5 = 7; 2 · 5 = 10

Ответ: 2; 5.

Пример 2

х² + px -35 = 0, один из корней равен 7.

Найти другой корень и коэффициент р.

Применим теорему Виета: х₁ + х₂ = — р; х₁ · х₂ = -35.

Пусть х₁=7 , значит: 7 · х₂ = -35; х₂ = -5.

7 + х₂ = — р; — р = 7 + (-5) = 2,

значит: р = -2.

Ответ: -5 , р = -2.

Теорема Виета позволяет находить корни квадратного уравнения без использования формулы корней, а также применять проверку корней данного уравнения.

5) Решение квадратных уравнений способом «переброски» старшего коэффициента

Умножая обе части квадратного уравнения на а, получаем уравнение

а ² х² + аb х + а с = 0.

Пусть а х = у, откуда ; тогда получим уравнение у² + bу + а с = 0,

равносильное данному. С помощью теоремы Виета найдем корни: у₁ и у₂,

где у₁ у₂ = ас и у₁ + у₂ = — b.

Окончательно получаем и .

При этом способе коэффициент а умножается на свободный член, как бы «перебрасывается» к нему, поэтому его называют способом «переброски».

Этот способ применяют, когда можно легко найти корни уравнения, используя теорему Виета и, что самое важное, когда дискриминант есть точный квадрат.

Метод хорош для квадратных уравнений с «удобными» коэффициентами. В некоторых случаях позволяет решить квадратное уравнение устно.

Пример 1

2х² – 11х + 15 = 0, «перебросим» коэффициент 2 к свободному члену:

у² – 11у + 30 = 0, согласно теореме Виета найдем корни:

у₁у₂ = 30 и у₁ + у₂ = 11,

у₁ = 5 и у₂ = 6, окончательно получим:

х₁ = 5/2 и х₂ = 6/2,

х₁ = 2,5 и х₂ = 3.

Ответ: 2,5 и 3.

Пример 2

«перебросим» коэффициент к свободному члену и получим уравнение:

у² – ( 3 + ) у + 3= 0, применим теорему Виета:

у₁у₂ = 3 и у₁ + у₂ = 3 + ,

у₁ = 3 и у₂ = ,

х₁ = /2 и х₂ = 1/3.

Ответ: /2 и 1/3.

6) Применение свойств коэффициентов квадратного уравнения

Пусть дано квадратное уравнение ах² + bх + с = 0, где а ≠ 0.

1. Если сумма коэффициентов равна нулю, т.е. а + b + с = 0, то х₁ = 1, х₂ = .

Доказательство: Разделим обе части уравнения на а, получим приведенное квадратное уравнение

Согласно теореме Виета: х₁ · х₂ = , х₁ + х₂ = — .

По условию, а + в + с = 0, тогда в = — а — с. Значит,

х₁ · х₂ = = 1 · , х₁ + х₂ = — = — = 1 + .

Получаем х₁ = 1, х₂ = , что и требовалось доказать.

Пример 1

3х² + 5х – 8 = 0,

т.к. а + b + с = 0

( 3 + 5 – 8 = 0 ), то получим

х₁ = 1, х₂ = = — .

Ответ: 1 и — .

Пример 2

1999х² – 2000х + 1 = 0,

т.к. а + b + с = 0

(1999 – 2000 + 1 = 0), значит

х₁ = 1, х₂ = = .

Ответ: 1 и .

2. Если а — b + с = 0, или b = а + с, то х₁ = -1, х₂ = — .

Доказательство аналогично.

Пример 1

11х² + 27х + 16 = 0,

Т.к. а — в + с = 0, (11 – 27 + 16 = 0), значит

х₁ = — 1, х₂ = — = — .

Ответ: -1 и —

3. Если второй коэффициент b = 2k четное число, то формулу корней можно записать в виде .

Пример 1

4х² – 36х + 77 = 0,

а = 4, b = — 36, с = 77, k = — 18;

D = k² – ас = ( — 18 )² – 4 · 77 = 324 – 308 = 16, D > 0, два различных корня;

х₁ = 5, 5 , х₂ = 3,5.

Ответ: 5,5 и 3,5.

Пример 2

х² + 18х + 81 = 0,

а = 1, b = 18, c = 81 , k = 9

D = k² – ас = 9² – 81 = 0 ,

D = 0 , значит один корень

= -9.

Ответ: — 9.

7. Графическое решение квадратного уравнения

Преобразуем уравнение х² + рх + q = 0 и получим вид: х² = — рх — q.

Построим графики зависимостей у = х² и у = — рх — q.

График первой зависимости — парабола, проходящая через начало координат.

График второй зависимости – прямая (приложение 1, рис.1).

Возможны следующие случаи:

• прямая и парабола могут пересекаться в двух точках, абсциссы точек пересечения являются корнями квадратного уравнения;

• прямая и парабола могут касаться и имеют одну общую точку, значит уравнение имеет одно решение;

• прямая и парабола не имеют общих точек, т. е. квадратное уравнение не имеет корней.

Применяя графический метод не всегда можно найти точное значение корней. Поэтому этот метод часто применяют не для нахождения корней уравнения, а для определения их количества.

Пример 1

х² – 3х – 4 = 0, запишем уравнение в виде х² = 3х + 4, рассмотрим графики зависимостей у = х² и у = 3х + 4,

Построим параболу у = х² по координатам:

Прямую у = 3х + 4 построим по двум точкам М (0; 4) и N(3; 13) (приложение 1, рис.2).

Прямая и парабола пересекаются в двух точках А и В с абсциссами х₁= -1 и х₂=4.

Ответ: — 1 и 4 .

Пример 2

х² – 2х + 1 = 0,

Построим параболу у = х² по координатам (см. таблицу выше) и прямую

у = 2х — 1 по двум точкам М(0; -1) и N(1/2; 0) (приложение 1, рис.3).

Прямая и парабола пересекаются в точке А с абсциссой х = 1.

Ответ: 1.

Пример 3

х² – 2х + 5 = 0,

Построим параболу у = х² по координатам (см. таблицу выше) и прямую

у = 2х — 5 по двум точкам М( 0; -5) и N( 2,5; 0) (приложение 1, рис.4).

Прямая и парабола не имеют точек пересечения, значит данное уравнение не имеет корней.

Ответ: нет корней.

Проектный продукт в форме презентации на тему «Различные способы решения квадратных уравнений» был апробирован на учащихся 8 класса МБОУ «Куртуковская ООШ имени В.П.Зорькина». Практическое применение изученных способов решения квадратных уравнений показало, что не все способы одинаково удобны и легки в использовании.

После небольшой практики среди одноклассников был проведен опрос на предмет сложности, рациональности и практичности применения каждого из изученных способов решения квадратных уравнений.

Результаты опроса приведены в таблице:

Способ сложный

Способ рациональный, всегда применяю

Интересный способ, буду применять

1. Решение квадратных уравнений по формуле

+

2. Разложение левой части уравнения на множители

+

3. Метод выделения полного квадрата

+

4. Решение уравнений с использованием теоремы Виета

+

5. Решение квадратных уравнений способом «переброски» старшего коэффициента

+

6. Применение свойств коэффициентов квадратного уравнения

+

7. Графическое решение квадратного уравнения

+

Результаты показали, что наиболее сложными оказались способы разложение левой части уравнения на множители, метод выделения полного квадрата и графическое решение квадратного уравнения. К рациональным и наиболее знакомым ребята отнесли методы решение квадратных уравнений по формуле и решение уравнений с использованием теоремы Виета. Интерес среди учеников вызвали способы применения свойств коэффициентов квадратного уравнения и решение квадратных уравнений способом «переброски» старшего коэффициента.

ЗАКлючение

В заключении работы хочу отметить, что все поставленные в ходе исследования задачи были выполнены. В процессе работы были найдены различные способы решения квадратных уравнений. Они были изучены и апробированы на решении конкретных уравнений.

В результате работы был создан проектный продукт по исследуемой теме в форме презентации, который позволит другим учащимся эффективно освоить различные способы решения квадратных уравнений на конкретных примерах.

Выполненная работа показывает, что использование различных способов при решении квадратных уравнений является важным звеном в изучении математики, развивает внимание и сообразительность. Школьный курс математики построен так, что наши знания по математике год от года углубляются и расширяются. Считаю, что начинать подготовку выпускника нужно заблаговременно, глубоко изучая каждую тему программы по математике. Знания различных способов решения квадратных уравнений позволяют очень быстро и рационально решать многие уравнения, в том числе тестовые задания по ГИА и ЕГЭ.

Список использованных источников и литературы

1. Алимов Ш.А. Алгебра, 6-8 классы [Текст]: учебник / Ш.А.Алимов, В.А.Ильин и др. М.: Просвещение, 1981. – 201 с.

2. Гусев В.А. Математика: Справочные материалы [Текст]: книга для учащихся / В.А. Гусев, А.Г. Мордкович. М.: Просвещение, 1988. – 416 с.

3. Дроздов В. Квадратное уравнение: варианты решения. Математика // Приложение к газете «Первое сентября» №10/1997. стр.6.

4. Макарычев Ю.Н. Алгебра. 8 класс [Текст]: учебник для общеобразоват. учреждений / Ю.Н.Макарычев, Н.Г.Миндюк, К.И.Нешков, С.Б. Суворова; под ред. С.А.Теляковского. М.: Просвещение, 2012. – 271 с.

5. Математика. Приложение к газете «Первое сентября»: № 24, 1997; №18, 1998, №21, 1998.

6. Панкратова Л. Квадратные уравнения. Математика // Приложение к газете «Первое сентября» №21/1996. стр.5-6.

7. Плужников И. Десять способов решения квадратных уравнений. Математика // Приложение к газете «Первое сентября» №40/2000. стр.24 -31.

8. Шаталова С. Способы решения квадратных уравнений // «Математика в школе» №42/2004.

Приложение 1

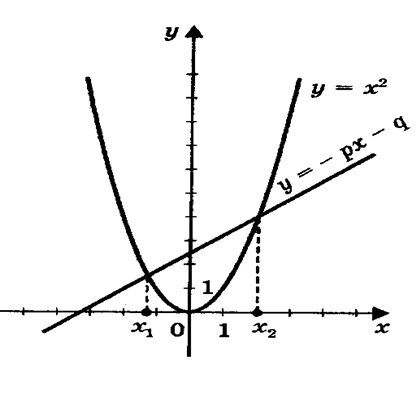
Рисунок 1

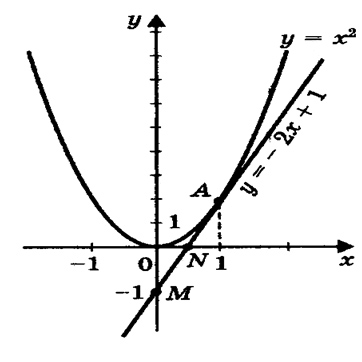
Рисунок 3

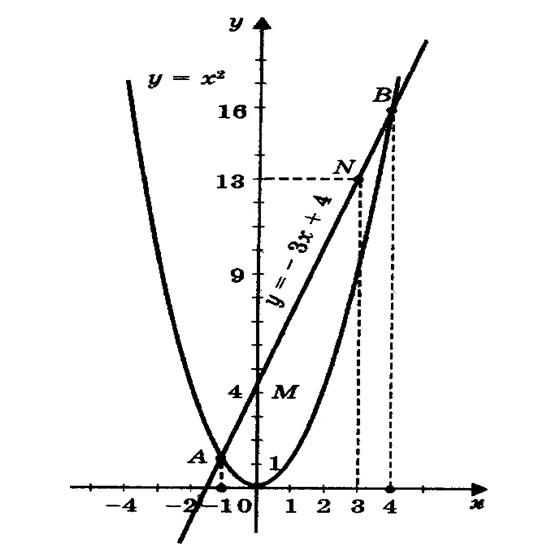
Рисунок 2

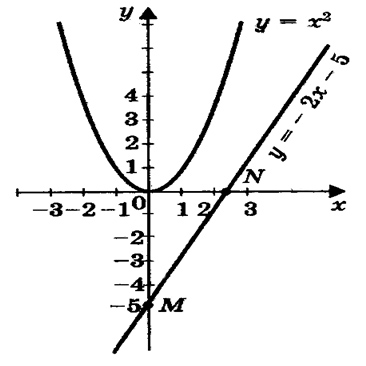
Рисунок 4

infourok.ru