Легкие задачи по геометрии – Учебно-методический материал по геометрии (7 класс) по теме: Основные задачи по геометрии 7 класс. УМК Атанасян Л.С.

Posted on by alexxlab

Содержание

Учебно-методический материал по геометрии (7 класс) по теме: Основные задачи по геометрии 7 класс. УМК Атанасян Л.С.

Задачи по геометрии за курс 7 класса (для итогового повторения).

  1. На прямой a расположены точки A, B, C, причем A B = 5см,  BC = 7 см. Какой может быть длина отрезка AC.
  2. На прямой a отмечены  точки A, B, M.   Найдите длину AM и MB, если AB =  6 см, MA + MB = 9 см.
  3. Прямой угол ADB разделен лучом DC на два угла, причем один угол на 90 больше другого. Найдите градусные меры этих углов.
  4. Угол AOB, равный 1240, лучом OC разделен на два угла, разность которых равна 340. Найдите эти углы. Чему равен угол, образованный лучом OC и биссектрисой угла AOB.
  5. Угол AOB, равный 1360, лучом OC разделен на два угла, градусные меры которых относятся как 3:1. Найдите эти углы. Чему равен угол, образованный лучом OC и биссектрисой угла AOB.
  6. Луч BM делит развернутый угол ABC в отношении 5:1, считая от луча BA. Найдите угол ABK, если BK – биссектриса угла MBC.
  7. Один из смежных углов на 500 больше другого. Найдите эти углы.
  8. Разность двух смежных углов равна 540. Найдите эти углы.
  9. Прямая ВК перпендикулярна прямым МВ и КТ. Докажите, что треугольники МВО и ОКТ равны. Найдите углы ОМВ, ВОМ, ОТК, если известно, что МВ=КТ, а угол ТОК=400. (Обязательно доказательство равенства треугольников)
  1. Отрезки АС и ВD пересекаются в точке О.  ВD = АС, ОВ=ОС.                                               а) Докажите, что  ∆ АОВ =  ∆ СОD;

            б) Найдите периметр   ∆ СОD, если АВ=9см, ВО=5см, ОD=7см.

  1. В  ∆АВС АВ = ВС, ВЕ – медиана треугольника АВС, Угол АВЕ =41˚. Найдите углы АВС и СЕВ.
  2. В  ∆АВС и ∆А1В1С1 медианы ВМ и В1М1 равны, АВ=А1В1 ,  АМ=А1М1. Докажите, что ∆АВС = ∆А1В1С1.
  3. Найдите все неразвернутые углы, образованные при пересечении двух прямых, если сумма трех из них равна 3070.
  4.  Равнобедренные треугольники ABC  и ADC имеют общее основание AC. Докажите, что BAD = BCD.
  5.  На медиане  CM равнобедренного треугольника ABC с основанием AB взята точка О.Докажите, что треугольник AOB равнобедренный.
  6. Один из внешних углов равнобедренного треугольника равен             126˚. Найдите углы треугольника.
  7. AD и CE – биссектрисы равнобедренного треугольника с основанием AC. Докажите, что  AEC =  CDA.
  8. Точки  C и D  расположены по разные стороны от прямой AB так,                     что AD = AC, BD = DC. Докажите, что AB – биссектриса угла DAC.
  9. Какими являются перечисленные углы? Обозначьте равные углы:

Углы 1 и 2 —

Углы 2 и 3 —

Углы 1 и 4 —

Углы 3 и 4 —

Углы 3 и 5 —

Углы 4 и 5 —

  1. Найдите все неразвернутые углы, образованные при пересечении двух прямых, если сумма трех из них равна 3070.
  2. Определите углы: МРО, РВО, ОВТ, ХКО, АКО, КОА, ОАК, ОАС, ВОА, РОК, если известно, что угол ОРВ=520, а угол РОВ=1020, РВ параллельно АК.
  1. Найдите все углы, образованные при пересечении двух параллельных прямых f и d секущей c, если один из углов на 50˚ больше другого.
  2. В  треугольнике АВС
  3. Один из внешних углов равнобедренного треугольника равен             126˚. Найдите углы треугольника.
  4. В треугольнике ABC угол A равен 700, внешний угол при вершине B равен  790. Найдите угол C. Ответ дайте в градусах.
  5. В треугольнике ABC угол A равен 390, АС=ВС. Найдите угол C. Ответ дайте в градусах.
  6. В треугольнике ABC угол C равен 1300,АС=ВС. Найдите угол A. Ответ дайте в градусах.
  7. В треугольнике ABC АС=ВС. Внешний угол при вершине B равен 1520. Найдите угол C. Ответ дайте в градусах.
  8. Сумма двух углов треугольника и внешнего угла к третьему равна 1200. Найдите этот третий угол. Ответ дайте в градусах.
  9. В треугольнике ABC угол C равен 900, CH — высота, угол A равен 60. Найдите угол BCH. Ответ дайте в градусах.
  10. Один острый угол прямоугольного треугольника на 420 больше другого. Найдите больший острый угол. Ответ дайте в градусах
  11. Дан прямоугольный треугольник АВС с прямым углом С. Угол В равен 300. Гипотенуза равна 12, а катет СВ равен  10. Определите периметр треугольника и угол А.
  12. В треугольнике АВС угол А больше угла В в 9 раз, а угол С меньше угла А на 100. Определите углы треугольника и укажите, каким этот треугольник является.
  13. Угол при основании равнобедренного треугольника равен 700, чему равен внешний угол при при основании треугольника, не смежный с данным углом?
  14. Внешний угол при основании равнобедренного треугольника на 200 больше одного из углов при основании треугольника. Найдите углы треугольника.
  15. В треугольнике ABC точка D лежит на стороне BC, причем AD = DC.Сумма внешних углов при вершине A равна 1600. Найдите угол C, если AD – биссектриса угла BAC.
  16. Один из углов прямоугольного треугольника равен 30˚, а сумма гипотенузы и  меньшего катета равна  12,6 см. Найдите длину гипотенузы.
  17. Дан квадрат  со стороной 16 см. Точка М лежит на стороне  и делит эту сторону в отношении 3:5 от вершины . Прямая, проходящая через точку М пересекает сторону  в точке Т, таким образом, что угол ВТМ равен 1200. Из вершины  к прямой ТМ проведен перпендикуляр . Определите длину этого перпендикуляра.
  18. Даны две параллельные прямые и секущая, которая пересекает прямые в точках А и В. Биссектрисы углов А и В пересекаются в точке О. Найдите периметр треугольника АВО, если известно, что АВ равно 8, угол ВАО в 2 раза меньше угла ОВА, а АК равно 12,6 см, где точка К – точка пересечения прямой АО и одной из параллельных прямых.
  19. Один из внешних углов прямоугольного треугольника равен 1200. Найдите большую и меньшую стороны треугольника, если их сумма равна 18 см.
  20. В прямоугольном треугольнике ABC с гипотенузой BC и углом B равным 600, проведена высота AD. Найдите DC, если DB = 2 см.
  21. В прямоугольном треугольнике ABC с гипотенузой AC, равной 12 см проведена высота BD. Найдите CD, DA если 0.

nsportal.ru

Как решать задачи по геометрии. Часть 2

Поиск верной цепочки рассуждений

Первую часть этой статьи можно прочитать здесь.

Представь, что ты идешь по улице, думаешь о каких-то своих делах и вдруг видишь воспитательницу из детского сада, в который ты ходил. Что произойдет дальше? А дальше твои мысли практически неизбежно хотя бы на несколько секунд переключатся на воспоминания о детском садике или детстве вообще. Как ты не хотел спать во время тихого часа. Или как подрался из-за игрушки в песочнице. О твоих друзьях и ненавистной (или любимой?) манной каше на завтрак. И так далее. Причем 5 минут назад ты даже и не предполагал вспоминать всё это! Но вдруг вот вспомнил. Почему? Ну, понятное дело, потому что увидел воспитательницу, образ которой вызвал у тебя определенные АССОЦИАЦИИ. Так устроен человеческий мозг и наша память – мы мысленно связываем события, явления и людей друг с другом. Скажи себе «весна» — и будет один поток образов (ручьи, голубое небо, капель и т.д.). Скажи «моя бабушка» — совсем другой. Это и называется ассоциациями.

Этот эффект замечательно работает при решении геометрических задач:

Берешь каждый компонент задачи и смотришь какие ассоциации у тебя возникают в связи с ним. После чего, рассмотрев все компоненты, ищешь логические связи или пересечения ассоциаций.

Давай поясню на примере, чтоб было понятнее.

Задача. Докажите, что если сторона одного равностороннего треугольника равна стороне другого равностороннего треугольника, то треугольники равны.

Строим чертеж и пишем известные данные.


Имеем:


Теперь давай думать. Треугольник \(ABC\) равносторонний. Что нам это дает? Что мы вообще знаем про равносторонние треугольники? Ну, во-первых, у них равны все три стороны (это следует из названия). Во-вторых, у них все углы равны между собой и градусная мера этих углов равна \(60°\). В-третьих – любая высота в них является биссектрисой и медианой. Пока всё. Ну и у треугольника \(DEF\) – аналогично.


Обрати внимание – это все новая и верная информация, которую мы получили из предыдущей. Но часть ее нам не пригодится при решении данной задачи. Поэтому пока что наносим потенциально возможные пути развития логической цепочки тонким серым цветом.

Продолжаем. Какие возможные пути нам дает информация об равенстве \(АВ\) и \(DE\)? Хм… Да пожалуй, что никаких не дает. Хорошо, значит, она пригодится в дальнейших рассуждениях сама по себе.

Всё? Нет, не всё. Мы ведь можем идти не только от исходных данных к цели, но и наоборот – от цели к исходным данным (вспоминай пример с квестом из предыдущей части статьи, там где про замок на острове). Действительно, давай зададимся вопросом – а как мы вообще можем доказать равенство треугольников? Ну, в школьном курсе есть для этого всего три признака! Помнишь их? Первый – по двум сторонам и углу между ними, второй – по стороне и двум прилежащим к ней углам, третий – по трем сторонам. Теория! Теория! Учи теорию! Без нее — никак!

Хорошо, добавляем эти данные в схему.


Теперь, пожалуй, мы выжали из условий задачи всё. Давай искать логические связи и пересечения.

Cходу бросается в глаза – равенство треугольников доказывается по трем сторонам и в каждом из треугольников есть равенство трех сторон. Плюс еще и в исходных данных есть равенство \(AB\) и \(DE\). Вот и связка!

Да, в самом деле, если \(AB = BC = CA\) и \(DE = EF = DF\), при этом известно, что \(AB = DE\), то значит все шесть сторон равны друг другу: \(BC = CA = AB = DE = EF = DF\). Таким образом, мы в треугольниках \(ABC\) и \(DEF\) имеем равенство трех пар сторон, следовательно, треугольники равны по третьему признаку. Что и требовалось доказать.

Итоговая логическая схема решения:


Итоговая запись решения:

Готово.

В более сложных задачах приходится делать большее количество промежуточных шагов при решении. Принцип их совершения такой же – каждый новый компонент полученной информации рассматриваешь на ассоциации и строишь от него «тропинки» во все стороны к новой информации. Ищешь связи и пересечения. Если не нашел, рассматриваешь дальше. И так пока не найдешь связку, цепочку от исходных данных к вопросу задачи. Как будто тропинку в лесу ищешь.

Делать это довольно интересно, надо только относиться к решению задач как к игре, а не тяжкой повинности.

Возможно, у тебя возник вопрос: «а что делать если ассоциации не появляются?». Ответ прост: «учи теорию и решай задачи!». Каждая новая теорема формирует в мозгу новые логические связи, а каждая новая задача закрепляет их.

И небольшой матхак:

Все данные из задачи должны быть использованы!

В задачах по геометрии очень редко даются лишние условия. Если ты застопорился при решении, то внимательно посмотри, что из дано ты еще не пускал в дело.

cos-cos.ru

Геометрия, 9 класс: уроки, тесты, задания

  • Векторы

    1. Понятие вектора
    2. Сложение и вычитание векторов
    3. Умножение векторов на число
    4. Применение векторов к решению задач

  • Метод координат

    1. Координаты вектора
    2. Простейшие задачи в координатах
    3. Уравнение окружности. Уравнение прямой

  • Соотношение между сторонами и углами треугольника. Скалярное произведение векторов

    1. Синус, косинус, тангенс угла
    2. Соотношения между сторонами и углами треугольника
    3. Скалярное произведение векторов

  • Длина окружности и площадь круга

    1. Правильные многоугольники
    2. Длина окружности и площадь круга

  • Движение

    1. Понятие движения. Симметрия
    2. Параллельный перенос и поворот

  • Начальные сведения о стереометрии

    1. Многогранники
    2. Тела и поверхности вращения

    • www.yaklass.ru

    Задачи по геометрии на повторение курса 7 класса

    Задачи на повторение курса геометрии в 7 классе

    1) Найдите величины смежных углов, если один из них в 5 раз больше другого. ( 30 и 50)

    2) Отрезки MN и DK пересекаются в их общей середине B. Докажите равенство треугольников MDB и NKB. (по 1 признаку)

    3) Найдите периметр равнобедренного треугольника ADC с основанием AD, если AD = 7 см, DC = 8 см.(23 )

    4) Найдите неразвернутые углы, образованные при пересечении двух прямых, если сумма двух из них равна 126°(63 и 117)

    5) Точки М, N и R лежат на одной прямой, MN = 11 см, RN = 20 см. Найдите расстояние MR.(21 или 9)

    6) Угол, противолежащий основанию равнобедренного треугольника, равен 50° . Найдите величину внешнего угла при основании.(115)

    7) Найдите углы треугольника, на которые высота разбивает равносторонний треугольник.(30, 60 и 90)

    8) Найдите все углы, образованные при пересечении двух параллельных прямых секущей, если один из них равен 42° .(42 и 138)

    9) Найдите все углы, образованные при пересечении двух параллельных прямых секущей, если один из них 126° .(126 и 54)

    10) Найдите смежные углы, если один из них на 55° больше другого.(62,5 и 117,5)

    11) Луч SR является биссектрисой угла S, а отрезки SM и SN равны. Докажите равенство треугольников SMO и SNO.(1 признак)

    12) Найдите длину отрезка AM и градусную меру угла ABK, если BM – медиана, а BK – биссектриса треугольника ABC и известно, что AC = 17 см, угол ABC равен 84°(42о и 8,5 см)

    13) Отрезки AB и CM пересекаются в точке O. Луч OK является биссектрисой угла MOB. Найдите угол MOK, если угол AOM равен 86° .(47)

    14) В треугольнике MOK 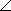hello_html_m16284583.pngO = 76°, а угол M в 3 раза меньше внешнего угла при вершине K. Найдите неизвестные углы треугольника.(38 и 114)

    15) Найдите углы при основании MР равнобедренного треугольника МОР, если MK– его биссектриса и 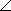hello_html_m16284583.pngOKM = 96°.(64)

    16) Найдите все углы, образованные при пересечении двух параллельных прямых секущей, если один из них равен 42°.(42 и 138)

    17) Два внешних угла треугольника при разных вершинах равны. Периметр треугольника равен 74 см, а одна из сторон равна 16 см. Найдите две другие стороны треугольника.(29 и 29)

    18) В равнобедренном треугольнике ABC с основанием ВС проведена медиана AM. Найти медиану AM, если периметр треугольника ABC равен 32 см, а периметр треугольника ABM равен 24 см.(8)

    19) Сумма накрест лежащих углов при пересечении двух параллельных прямых секущей равна 210. Найти эти углы.(110)

    20) Найти смежные углы, если один из них на 45 больше другого.(67,5 и 112,5)

    21) Один из углов прямоугольного треугольника равен 60, а сумма гипотенузы и меньшего из катетов равна 26,4 см. Найти гипотенузу треугольника.(8,8 и 17,6)

    22) Разность двух односторонних углов при пересечении двух параллельных прямых секущей равна 50 градусам. Найти эти углы.(115 и 65)

    23) Найдите неразвернутые углы, образованные при пересечении двух прямых, если сумма двух из них равна 126°.(63 и 117)

    24) Основание равнобедренного треугольника равно 8см. Медиана, проведенная к боковой стороне, разбивает треугольник на два треугольника так, что периметр одного треугольника на 2см больше периметра другого. Найти боковую сторону данного треугольника.(6 или 10)

    25) В прямоугольном треугольнике ABC с прямым углом С внешний угол при вершине А равен 120, АС+АВ=18см. Найти AC и AB.(6 и 12)

    26) Найдите все углы, образованные при пересечении двух параллельных прямых а и в секущей с , если один из углов на 700 больше другого.(105 и 65)

    infourok.ru

    Теорема Пифагора. Геометрия, 8 класс: уроки, тесты, задания.

    1. Гипотенуза прямоугольного треугольника

    Сложность: лёгкое

    		2
    2. Площадь прямоугольного треугольника

    Сложность: лёгкое

    		3
    3. Боковая сторона прямоугольной трапеции

    Сложность: лёгкое

    		3
    4. Диагональ прямоугольника

    Сложность: лёгкое

    		3
    5. Сторона ромба

    Сложность: среднее

    		3
    6. Диагональ квадрата

    Сложность: среднее

    		3
    7. Высота равнобедренного треугольника

    Сложность: среднее

    		3
    8. Катет прямоугольного треугольника

    Сложность: среднее

    		1
    9. Признак прямоугольного треугольника

    Сложность: среднее

    		2
    10. Периметр равнобедренной трапеции (подобные треугольники)

    Сложность: среднее

    		3
    11. Прикладная задача на составление уравнения

    Сложность: среднее

    		5
    12. Старинная китайская задача

    Сложность: среднее

    		5
    13. Прикладная задача на вычисление расстояния

    Сложность: среднее

    		4
    14. Текстовая задача на использование теоремы Пифагора

    Сложность: сложное

    		3
    15. Стороны прямоугольного треугольника, дана сумма катета и гипотенузы

    Сложность: сложное

    		3
    16. Расстояние между вершинами тупых углов параллелограмма

    Сложность: сложное

    		5
    17. Прикладная задача на вычисление стороны квадрата

    Сложность: сложное

    		2
    18. Общая хорда двух равных окружностей

    Сложность: сложное

    		4

    www.yaklass.ru

    Как научиться решать задачи по геометрии? — КиберПедия

    Решаем задачи по геометрии

    Решение задач

    Любой студент или школьник должен запомнить одну простую истину – можно решить любую задачу, какой бы трудной она не казалась на первый взгляд. Ведь задачи составляют для закрепления теоретических знаний и отработки определенных практических навыков, следовательно, для того, чтобы их решали, а не в целях третирования учащихся.

    Разумеется, есть такие сверхсложные варианты задач, которые пытаются разрешить столетиями. Однако их количество не так уж и велико, да и награда за найденное решение будет больше «пятерки» за контрольную работу или экзамен. Встретить нечто подобное в школьной программе невозможно.

    Следовательно, для того, что бы научиться решать задачи по геометрии необходимо иметь желание, усидчивость и тренированные мозги и воображение. Других путей освоить эту интересную область математики не существует, мы не берем в расчет решебники со 2 по 11 класс и всевозможные ГДЗ, очень сильно облегчающие жизнь студенту. Однако, получив все необходимые навыки и тщательно проштудировав теорию, можно приблизиться к пониманию того, что существует определенная методика решения задач по геометрии, способная упростить процесс решения любой задачи. Для этого необходимо всегда выполнять следующие действия:

    1. Изучив условие задачи, сразу же займитесь составление чертежа. Без толковой схемы затруднительно решить даже простую задачу, а сложную – практически невозможно. При этом не жадничайте, экономить место в тетради вы будете в другом случае. Визуализация условия задачи по геометрии требует максимально возможного объема на тетрадном листе. Чем крупнее чертеж, тем нагляднее и доступнее будут решение задачи.

    2. Построив чертеж или схему, нанесите на нее все известные данные – прямые и косвенные (которые можно получить путем промежуточных вычислений). Поверьте, решение задачи может «всплыть» сразу же после того, как вы сделаете эту нехитрую работу.

    3. Не полагайтесь во всем на интуицию и пространственное воображение, без знания теоретической базы серьезных результатов вам не достигнуть. При этом можно не забираться в дебри формулировок, а запомнить и осмыслить несколько десятков распространенных формул и правил.

    4. Помните о небольших хитростях: о задачах, которые решаются методом «первого и второго треугольника», об использовании центра окружности в соответствующих случаях (всегда соединяйте «интересные» точки вписанных и описанных фигур с центром окружности), о правилах суммы углов треугольника и прочих несложных способах вычисления промежуточных величин, которые помогут в поиске искомого значения.



    5. Всегда записывайте «полет» вашей мысли. После трех-четырех связок вы можете потерять нить рассуждений и потратить значительное время на попытки вспомнить уже принятое решение. После решения задачи обязательно проверьте себя. Это поможет избежать досадных ошибок, которые могли ускользнуть от вашего внимания, увлеченного удачными поисками варианта решения задачи.

    В заключение несколько слов о неудачах и патовых ситуациях, когда все потуги учащегося не приводят к положительным результатам. Для выхода из тупика используйте несколько простых действий:

    Во-первых, переверните схему задачи. Посмотрите на чертеж буквально «под другим углом». Вероятно, вы что-то упустили или не заметили, и решение может прийти само собой.

    Во-вторых, отложите «затруднительную» задачу в сторону, отвлекитесь на другое дело. Через десять минут мозг «перезагрузится», «накатанная» схема, которая привела вас в тупик, забудется и можно начинать искать новый путь к решению задачи.

    В-третьих, примените тактическую хитрость. Вспомните, что вы проходите по программе на данный момент. На контрольной работе вам, как правило, будут задавать задачи с четкой привязкой к изученной теории. Постарайтесь заново оценить условие с точки зрения именно «последних» теоретических материалов. Например, если вы занимались изучением хорды или биссектрисы, постарайтесь «по максимуму» заполнить чертеж именно этими элементами.

    Решаем задачи по геометрии

    Решение задач

    Любой студент или школьник должен запомнить одну простую истину – можно решить любую задачу, какой бы трудной она не казалась на первый взгляд. Ведь задачи составляют для закрепления теоретических знаний и отработки определенных практических навыков, следовательно, для того, чтобы их решали, а не в целях третирования учащихся.



    Разумеется, есть такие сверхсложные варианты задач, которые пытаются разрешить столетиями. Однако их количество не так уж и велико, да и награда за найденное решение будет больше «пятерки» за контрольную работу или экзамен. Встретить нечто подобное в школьной программе невозможно.

    Следовательно, для того, что бы научиться решать задачи по геометрии необходимо иметь желание, усидчивость и тренированные мозги и воображение. Других путей освоить эту интересную область математики не существует, мы не берем в расчет решебники со 2 по 11 класс и всевозможные ГДЗ, очень сильно облегчающие жизнь студенту. Однако, получив все необходимые навыки и тщательно проштудировав теорию, можно приблизиться к пониманию того, что существует определенная методика решения задач по геометрии, способная упростить процесс решения любой задачи. Для этого необходимо всегда выполнять следующие действия:

    1. Изучив условие задачи, сразу же займитесь составление чертежа. Без толковой схемы затруднительно решить даже простую задачу, а сложную – практически невозможно. При этом не жадничайте, экономить место в тетради вы будете в другом случае. Визуализация условия задачи по геометрии требует максимально возможного объема на тетрадном листе. Чем крупнее чертеж, тем нагляднее и доступнее будут решение задачи.

    2. Построив чертеж или схему, нанесите на нее все известные данные – прямые и косвенные (которые можно получить путем промежуточных вычислений). Поверьте, решение задачи может «всплыть» сразу же после того, как вы сделаете эту нехитрую работу.

    3. Не полагайтесь во всем на интуицию и пространственное воображение, без знания теоретической базы серьезных результатов вам не достигнуть. При этом можно не забираться в дебри формулировок, а запомнить и осмыслить несколько десятков распространенных формул и правил.

    4. Помните о небольших хитростях: о задачах, которые решаются методом «первого и второго треугольника», об использовании центра окружности в соответствующих случаях (всегда соединяйте «интересные» точки вписанных и описанных фигур с центром окружности), о правилах суммы углов треугольника и прочих несложных способах вычисления промежуточных величин, которые помогут в поиске искомого значения.

    5. Всегда записывайте «полет» вашей мысли. После трех-четырех связок вы можете потерять нить рассуждений и потратить значительное время на попытки вспомнить уже принятое решение. После решения задачи обязательно проверьте себя. Это поможет избежать досадных ошибок, которые могли ускользнуть от вашего внимания, увлеченного удачными поисками варианта решения задачи.

    В заключение несколько слов о неудачах и патовых ситуациях, когда все потуги учащегося не приводят к положительным результатам. Для выхода из тупика используйте несколько простых действий:

    Во-первых, переверните схему задачи. Посмотрите на чертеж буквально «под другим углом». Вероятно, вы что-то упустили или не заметили, и решение может прийти само собой.

    Во-вторых, отложите «затруднительную» задачу в сторону, отвлекитесь на другое дело. Через десять минут мозг «перезагрузится», «накатанная» схема, которая привела вас в тупик, забудется и можно начинать искать новый путь к решению задачи.

    В-третьих, примените тактическую хитрость. Вспомните, что вы проходите по программе на данный момент. На контрольной работе вам, как правило, будут задавать задачи с четкой привязкой к изученной теории. Постарайтесь заново оценить условие с точки зрения именно «последних» теоретических материалов. Например, если вы занимались изучением хорды или биссектрисы, постарайтесь «по максимуму» заполнить чертеж именно этими элементами.

    Как научиться решать задачи по геометрии?

    Дорогие ребята, Вы начали изучать геометрию. Это новая для вас дисциплина, и вы поначалу можете испытывать трудности в её освоении. Не пугайтесь: пройдет некоторое время, и вы научитесь с легкостью решать любые геометрические задачи. Для приобретения необходимого навыка нужно лишь приложить немного усилий. Итак, как решать задачи по геометрии?

    Вам понадобится: учебник, тетрадь, ручка, карандаш, линейка, транспортир, циркуль, ластик.

    Инструкция:

    1. Внимательно прочитайте условие задачи.
    2. Сделайте чертеж.
    3. Отметьте на чертеже то, что вам дано: длины сторон, величины углов. Если в условии задачи сказано, что какие-то отрезки равны, поставьте на них одинаковые штрихи. Равные по величине углы отмечайте одинаковыми дужками: одинарными, двойными, волнистыми. Углы разных величин выделяйтеразными
      4. дужками.
    4. Исследуйте фигуры, представленные в задаче. Вспомните их определения и свойства.
    5. Определите тему, к которой относится ваша задача. Освежите в голове теоретический материал по этой теме, повторите основные теоремы.
    6. Рассмотрите примеры решения задач по этой теме. В задачах, приводимых в учебнике в качестве примеров, часто рассматриваются принципиальные вопросы, которые вы должны знать.
    7. Если вы чувствуете себя в теме достаточно уверенно, приступайте к решению задачи. Начните с того, что требуется найти или доказать. Подумайте, каким путем это можно сделать. То есть, решайте задачу «с конца».
    8. Если вы не видите путей решения задачи, попробуйте найти хоть что-нибудь, используя имеющиеся данные. Возможно, так к вам придет идея, как решать задачу.

    Полезные советы: не увлекайтесь «устными» доказательствами. Записывайте решение задачи как можно более подробно, если не оговорено иное. Некоторые вещи могут казаться вам очевидными, но всё равно прописывайте их. Так у вас будет отрабатываться навык, вы лучше запомните идею.

    Рекомендации от учителя математики Е.В.Жалыбиной

     

     

    cyberpedia.su

    Добавить комментарий

    Ваш адрес email не будет опубликован. Обязательные поля помечены *