Линейная функция и ее график (В.А.Тарасов). Видеоурок. Алгебра 7 Класс
В предыдущих уроках мы изучали линейное уравнение с двумя переменными, это уравнение вида 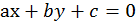 ,
,  . Мы выяснили, что графиком данного уравнения является прямая. Рассмотрим пример:
. Мы выяснили, что графиком данного уравнения является прямая. Рассмотрим пример:
Пример 1:
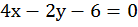 (1)
(1)
Перепишем его таким образом, чтобы у был в одной части, а все остальное в другой:
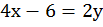
Сократим на 2:
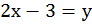
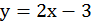 (2)
(2)
Мы получили частный случай уравнения 1, в котором 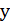 стоит обособленно в левой части, графиком обоих выражений будет одна и та же прямая, но запись 2 мы будем называть линейной функцией у от х.
стоит обособленно в левой части, графиком обоих выражений будет одна и та же прямая, но запись 2 мы будем называть линейной функцией у от х.
Построим график данной функции, для этого составим таблицу:
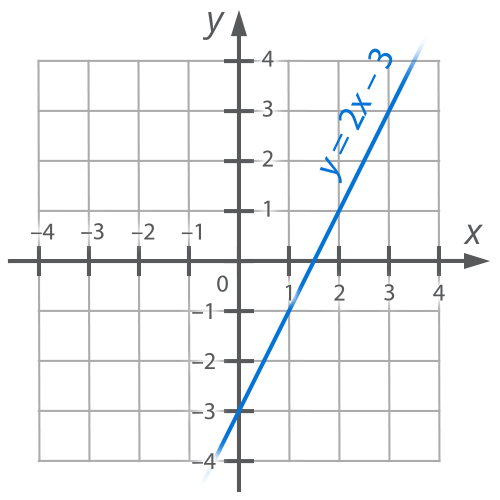
Рис. 1. График функции y=2x-3
Определим линейную функцию в общем случае из линейного уравнения с двумя переменными:
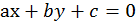

Поскольку 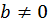 можем обе части поделить на b:
можем обе части поделить на b:
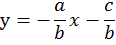
Введем более удобные обозначения:
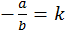 ,
, 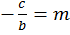
Получаем выражение:
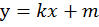 (3)
(3)
Для примера №1 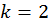
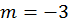
Таким образом, пара чисел k и m задают конкретну
interneturok.ru
§ 8. Линейные и квадратичные функции
Заметим, что, так как график функции y = f (x) симметричен относительно оси OY, то есть функция f (x) является четной, то отражение относительно OY не меняет вид графи-
ка. |
|
|
|
|
|
|
|
| Пример 9. Постройте график функции y = 2 |
| . | ||||
| 4 − x | ||||||
| Решение. | Запи- | |||||
шем | функцию | в виде | |||||
y = 2 |
|
| . | Следо- | |||
| − (x − 4) | ||||||
вательно, | построение | ||||||
графика | производится | ||||||
последовательным выполнением преобразований известного графика функции y = 

относительно оси OY, параллельный перенос на четыре единицы вправо и растяжение графика от оси OХ в два раза (рис. 30).
Линейная функция y = kx + b . Функция определена на всей числовой прямой, D( f ) = Ў . Множество ее изменения – также множество всех действительных чисел, E( f ) = Ў . Функция не ограничена. Она не имеет точек экстремума. При k > 0 функция является возрастающей, при
k < 0 | – | убывающей. |
При | k = 0 | функция яв- |
ляется постоянной. Графиком линейной функции является прямая.
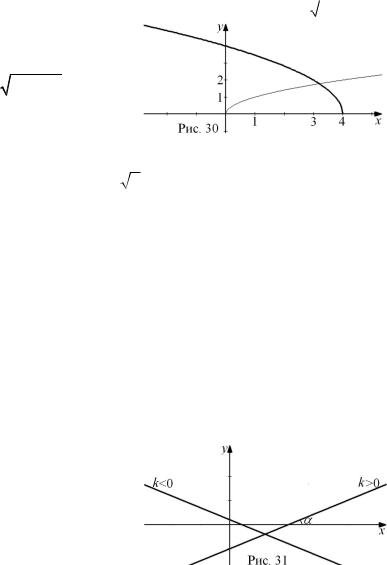
Угловой коэффициент k прямой равен тангенсу угла между
прямой | и положительным направлением оси абсцисс, |
k = tgα | (рис. 31). Из аксиом геометрии известно, что если |
две точки прямой принадлежат плоскости, то и вся прямая принадлежит плоскости. Поэтому для построения графика линейной функции достаточно задать две точки.
Квадратичная функция y = ax2 + bx + c ( a ¹ 0 ).
Функция определена на всей числовой прямой. Графиком квадратичной функции является парабола.
Для построения графика квадратичной функции целесообразно преобразовать формулу, выделив полный квадрат:
| 2 |
|
|
|
| ж |
| b ц2 | 4ac − b2 |
|
| 2 |
| |
y = ax |
| + | bx + | c | = | a з x + |
|
| ч + | 4a | = a(x − | x0 ) |
| + y0 , где |
|
|
|
| |||||||||||
|
|
|
|
|
| и | 2a ш |
|
|
|
| |||
x0 = − |
| b | , y0 = | 4ac − b2 | . Таким образом, получаем, что вер- | |||||||||
2a |
| 4a |
| |||||||||||
|
|
|
|
|
|
|
|
|
|
|
| |||
шина |
| параболы | находится | в точке с | координатами | |||||||||
x0 = − |
| b | , y0 | = | 4ac − b2 | . График квадратичной функции сим- | ||||||||
2a |
| 4a | ||||||||||||
|
|
|
|
|
|
|
|
|
|
|
| |||
метричен относительно прямой x = x0 . |
|
|
|
| ||||||||||
При a > | 0 ветви параболы направлены вверх. В точке | |||||||||||||
x0 функция имеет минимум и принимает в этой точке наименьшее значение. При x > x0 функция возрастает, при x < x0 функция убывает. В этом случае квадратичная функция ограничена снизу и не ограничена сверху.
При a < 0 ветви параболы направлены вниз. В точке x0 функция имеет максимум и принимает в этой точке наибольшее значение. При x > x0 функция убывает, при x < x0 функция возрастает. В этом случае квадратичная функция ограничена сверху и не ограничена снизу.
Если дискриминант соответствующего квадратного уравнения положителен, то парабола пересекает ось абсцисс в двух точках. Если дискриминант равен нулю, то парабола касается оси абсцисс. Если дискриминант отрицателен, то парабола расположена выше оси абсцисс, если a > 0 , и ниже оси абсцисс, если a < 0 .
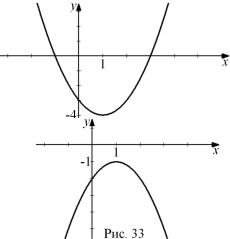
Пример 10. Постройте графики функций y = x2 − 2x − 3
и y = 2x − x2 − 2 . |
|
|
|
Решение. | Вершина | параболы y = x2 − 2x − 3 имеет | |
координаты | x0 | = 1 | и |
y0 = − 4 . Так как | старший | ||
коэффициент a = 1 положи- | |||
телен, то ветви | параболы | ||
направлены вверх. Также, | |||
решив | уравнение | ||
x2 − 2x − 3 = 0 , можно найти точки пересечения с осью абсцисс:
x1 = − 1 и x2 | = 3 (рис. 32). |
Для | параболы |
y = 2x − x2 − 2 аналогично полу- | |
чаем, что x0 | = 1 и y0 = − 1 , и ветви ее направлены вниз. Дан- |

ная парабола не имеет точек пересечения с осью абсцисс, так как дискриминант соответствующего квадратного уравнения отрицателен (рис. 33).
§ 9. Построение графиков дробно-линейных функций
Функция вида y = ax + b , где c ¹ 0 и ad ¹ bc , назы- cx + d
вается дробно-линейной. Графиком этой функции является гипербола.
Частным случаем дробно-линейной функции является функция обратной пропорциональности y = kx . График этой
функции состоит из двух ветвей, симметричных относительно начала координат. При k > 0 гипербола расположена в первой и третьей четвертях, при k < 0 – во второй и четвертой четвертях.
| Пример 11. Постройте график функции | y = | 3x + 10 . | ||||
|
|
|
|
|
| 2x + 4 | |
| Решение. | Выделим | целую | часть | дроби | ||
y = | 3x + 10 = 3x + 6 + 4 = | 1,5(2x + 4) + 4 = 1,5 + | 2 | . |
| ||
x + 2 |
| ||||||
| 2x + 4 | 2x + 4 | 2x + 4 |
|
| ||
Таким образом, уравнение, которым задается график функ-
ции, примет вид y = 1,5 + | 2 |
| . График заданной функции по- | |
x + | 2 | |||
|
|
лучается из графика функции y = 1x сдвигом на 2 единицы по
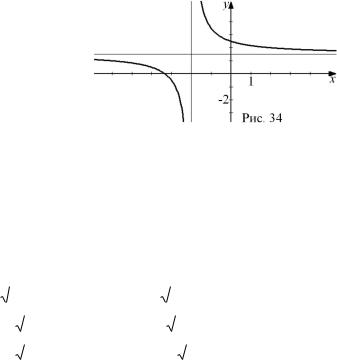
оси OX влево, растяжением вдоль оси OY в 2 раза и сдвигом на 1,5 единицы по оси OY вверх.
Заметим, что график функции не пересекает прямые x = − 2 и y = 1,5 , хотя и приближается к ним достаточно близко. Такие прямые называются асимптотами графика функции. График дробно-линейной функции имеет две асимптоты
– вертикальную x = − 2 и горизонтальную y = 1,5 . Построение графика удобно начинать именно с нахождения асимптот: для нахождения вертикальной асимптоты приравниваем знаменатель дроби нулю, а для нахождения горизонтальной асимптоты выделяем целую часть дроби (рис. 34).
Построение графика произвольной дробно-линейной
функции y = ax + b выполняется по алгоритмам, разобран- cx + d
ным в примере 11.
Упражнения
8.Постройте графики функций:
а) | y = | 2 | 3x — 1 | ; |
|
| б) y = | 4x + 10 | — 3; | |||||
в) | y = | 2 + |
|
| ; | г) y = 2 |
|
| — 3 ; | |||||
| 3- x | x + 5 | ||||||||||||
д) y = | 2 — |
|
| ; | е) y = 3- |
|
|
| . | |||||
| x + 4 |
| 2x + 9 | |||||||||||
9.Постройте графики функций:
а) | y = | 3× 2x — 1; | б) | y = | 0,52x+ 3 — 6 ; |
в) | y = | 20,5x — 4 ; | г) | y = | log2 (x + 3) — 1; |
studfile.net
| 1. |
Аргумент линейной функции
Сложность: лёгкое |
1,5 |
| 2. |
Таблица значений линейной функции
Сложность: лёгкое |
2 |
| 3. |
Точка пересечения графика линейной функции с осью Оy
Сложность: лёгкое |
1 |
| 4. |
Точка пересечения графика линейной функции с осью Ох или с осью Оy
Сложность: лёгкое |
2 |
| 5. |
График линейной функции
Сложность: среднее |
2,8 |
| 6. |
Вопросы по графику линейной функции
Сложность: среднее |
4 |
| 7. |
Нахождение по графику формулы линейной функции
Сложность: среднее |
1 |
| 8. |
Задача на составление выражения
Сложность: среднее |
3 |
| 9. |
Координаты точки пересечения графиков
Сложность: сложное |
3 |
| 10. |
Наибольшее или наименьшее значение линейной функции
Сложность: сложное |
3 |
| 11. |
Составь уравнение прямой
Сложность: сложное |
5 |
www.yaklass.ru
Линейная функция и ее график 1) Линейной функцией называется функция, которую можно задать формулой вида y = kx + b, где x – независимая переменная, k и b – некоторые числа. 2) Графиком линейной функции является прямая. 3) Алгоритм построения графика линейной функции: 1) Найти координаты двух точек графика 2)Отметить полученные точки на координатной плоскости 3)Провести через полученные точки прямую Построение графика линейной функции: ты берешь два каких-либо икса, (например, 0 и 1), подставляешь их в формулу, находишь соответствующие игреки. Затем отмечаешь эти две точки на координатной плоскости, прикладываешь линейку, и график готов. Просто и быстро, и ничего выдумывать не надо. | Линейная функция и ее график 1) Линейной функцией называется функция, которую можно задать формулой вида y = kx + b, где x – независимая переменная, k и b – некоторые числа. 2) Графиком линейной функции является прямая. 3) Алгоритм построения графика линейной функции: 1) Найти координаты двух точек графика 2)Отметить полученные точки на координатной плоскости 3)Провести через полученные точки прямую Построение графика линейной функции: ты берешь два каких-либо икса, (например, 0 и 1), подставляешь их в формулу, находишь соответствующие игреки. Затем отмечаешь эти две точки на координатной плоскости, прикладываешь линейку, и график готов. Просто и быстро, и ничего выдумывать не надо. | Линейная функция и ее график 1) Линейной функцией называется функция, которую можно задать формулой вида y = kx + b, где x – независимая переменная, k и b – некоторые числа. 2) Графиком линейной функции является прямая. 3) Алгоритм построения графика линейной функции: 1) Найти координаты двух точек графика 2)Отметить полученные точки на координатной плоскости 3)Провести через полученные точки прямую Построение графика линейной функции: ты берешь два каких-либо икса, (например, 0 и 1), подставляешь их в формулу, находишь соответствующие игреки. Затем отмечаешь эти две точки на координатной плоскости, прикладываешь линейку, и график готов. Просто и быстро, и ничего выдумывать не надо. | Линейная функция и ее график 1) Линейной функцией называется функция, которую можно задать формулой вида y = kx + b, где x – независимая переменная, k и b – некоторые числа. 2) Графиком линейной функции является прямая. 3) Алгоритм построения графика линейной функции: 1) Найти координаты двух точек графика 2)Отметить полученные точки на координатной плоскости 3)Провести через полученные точки прямую Построение графика линейной функции: ты берешь два каких-либо икса, (например, 0 и 1), подставляешь их в формулу, находишь соответствующие игреки. Затем отмечаешь эти две точки на координатной плоскости, прикладываешь линейку, и график готов. Просто и быстро, и ничего выдумывать не надо. | Линейная функция и ее график 1) Линейной функцией называется функция, которую можно задать формулой вида y = kx + b, где x – независимая переменная, k и b – некоторые числа. 2) Графиком линейной функции является прямая. 3) Алгоритм построения графика линейной функции: 1) Найти координаты двух точек графика 2)Отметить полученные точки на координатной плоскости 3)Провести через полученные точки прямую | Линейная функция и ее график 1) Линейной функцией называется функция, которую можно задать формулой вида y = kx + b, где x – независимая переменная, k и b – некоторые числа. 2) Графиком линейной функции является прямая. 3) Алгоритм построения графика линейной функции: 1) Найти координаты двух точек графика 2)Отметить полученные точки на координатной плоскости 3)Провести через полученные точки прямую |
infourok.ru
Асимптоты графика функции. График дробно-линейной функции
Асимптоты графика функции. График дробно-линейной функции.
В этой статье мы рассмотрим, что такое асимптота графика функции, и как ее находить.
Асимптота – это прямая, к которой бесконечно близко приближается график функции.
Асимптоты бывают горизонтальные, вертикальные и наклонные.
Если мы посмотрим на хорошо известный нам график функции  , то увидим, что график этой функции бесконечно близко приближается к прямой
, то увидим, что график этой функции бесконечно близко приближается к прямой  (ось ОY) — это вертикальная асимптота, и к прямой
(ось ОY) — это вертикальная асимптота, и к прямой  (ось ОХ) — это горизонтальная асимптота:
(ось ОХ) — это горизонтальная асимптота:

В общем случае горизонтальная асимптота — это прямая, параллельная оси OX. Уравнение горизонтальной асимптоты имеет вид  , где
, где  — число, к которому стремятся значения функции
— число, к которому стремятся значения функции  , когда
, когда  стремится к
стремится к  .
.
То есть  .
.
Вертикальная асимптота — это прямая, параллельная оси OY. Уравнение вертикальной асимптоты имеет вид  . Здесь
. Здесь  — значение переменной
— значение переменной  , при котором функция
, при котором функция  не определена. Как правило, это ноль знаменателя. Если значение
не определена. Как правило, это ноль знаменателя. Если значение  стремится к точке, в которой знаменатель равен нулю, то абсолютное значение дроби при этом неограниченно возрастает.
стремится к точке, в которой знаменатель равен нулю, то абсолютное значение дроби при этом неограниченно возрастает.
В некоторых случаях для построения графика функции бывает достаточно найти асимптоты графика.
Рассмотрим дробно-линейную функцию. В общем виде уравнение дробно-линейной функции имеет вид:  .
.
График дробно-линейной функции — это гипербола. Как мы знаем, гипербола имеет две асимптоты: горизонтальную и вертикальную.
Заметим, что при  знаменатель равен нулю, в этой точке функция
знаменатель равен нулю, в этой точке функция  не определена. Поэтому прямая
не определена. Поэтому прямая  — вертикальная асимптота.
— вертикальная асимптота.
Степень  в числителе дроби
в числителе дроби  равна степени
равна степени  в знаменателе. Поэтому при
в знаменателе. Поэтому при  числитель и знаменатель растут с одинаковой скоростью, и
числитель и знаменатель растут с одинаковой скоростью, и
 и уравнение горизонтальной асимптоты имеет вид
и уравнение горизонтальной асимптоты имеет вид  .
.
График дробно-линейной функции  — это гипербола, симметричная относительно точки пересечения асимптот графика. Поэтому, чтобы построить график, нам остается только выяснить его расположение относительно этой точки.
— это гипербола, симметричная относительно точки пересечения асимптот графика. Поэтому, чтобы построить график, нам остается только выяснить его расположение относительно этой точки.
Для этого достаточно найти точки пересечения графика с осями координат.
Точка пересечения с осью OX (y=o):  .
.
Точка пересечения с осью OY (x=0):  .
.
Построим график функции  . Это дробно-линейная функция и ее график — гипербола.
. Это дробно-линейная функция и ее график — гипербола.
Найдем горизонтальную и вертикальную асимптоты.
Уравнение горизонтальной асимптоты:  ;
;
уравнение вертикальной асимптоты (ноль знаменателя): 

Найдем точки пересечения с осями координат:
С осью ОХ:  ;
; 
с осью OY(x=0):  .
.

То есть график функции  выглядит как-то так:
выглядит как-то так:

И, наконец, наклонная асимптота. Наклонная асимптота — это к прямая, к кторой стремится график функции на бесконечности.
Уравнение наклонной асимптоты имеет вид  .
.
Коэффициенты  и
и  вычисляются следующим образом:
вычисляются следующим образом:


Найдем асимптоты графика функции 
1. Начнем с области определения функции. Функция  не определена в точке
не определена в точке  , следовательно прямая
, следовательно прямая  является вертикальной асимптотой.
является вертикальной асимптотой.
2. Степень числителя дроби  на единицу больше степени знаменателя, поэтому предел этого отношения при
на единицу больше степени знаменателя, поэтому предел этого отношения при  отношения равен бесконечности. Следовательно, график функции
отношения равен бесконечности. Следовательно, график функции  не имеет горизонтальной асимптоты.
не имеет горизонтальной асимптоты.
3. Попробуем найти наклонную асимптоту.

(Предел функции равен отношению коэффициентов при максимальных степенях  в числителе и знаменателе дроби).
в числителе и знаменателе дроби).



Итак, уравнение наклонной асимптоты: 

График функции  , построенный с помощью специальной программы, показывает, что асимптоты были найдены верно:
, построенный с помощью специальной программы, показывает, что асимптоты были найдены верно:


И.В. Фельдман, репетитор по математике.
ege-ok.ru
Методическая разработка по алгебре (7 класс) на тему: Презентация «Линейная функция, её график, свойства».
Слайд 1
Линейная функция, её график, свойства. Кирьянова Марина Владимировна, учитель математики МОУ СОШ №3 с. Кочубеевское Ставропольского краяСлайд 2
Укажите линейные уравнения : 1) 5y = x 2) 3y = 0 3) y 2 + 16x 2 = 0 4) + y = 4 5) x + y =4 6) y = -x + 11 7) + 0.5x – 2 = 0 8) 25d – 2m + 1 = 0 9) y = 3 – 2x 5
Слайд 3
Функция вида у = kx + b называется линейной . Графиком функции вида у = kx +b является прямая . Для построения прямой необходимы только две точки , так как через две точки проходит единственная прямая.
Слайд 4
Найти уравнения линейных функций y =-x+0,2; y= 1 2 , 4x-5,7 ; y =- 9 x- 1 8; y= 5 ,04x; y =- 5 ,04x; y=1 26 ,35+ 8 ,75x; y=x -0, 2; y=x :8; y=0, 00 5x; y=13 3 ,13 3 13 3 x; y= 3 — 1 0 , 01x ; y=2 : x ; y =-0, 004 9; y= х:6 2 .
Слайд 5
y = kx + b – линейная функция х – аргумент (независимая переменная) у – функция (зависимая переменная) k , b – числа (коэффициенты) к ≠ 0
Слайд 6
х Х 1 Х 2 Х 3 у У 1 У 2 У 3
Слайд 7
у = — 2х + 3 – линейная функция. Графиком линейной функции является прямая, для построения прямой нужно иметь две точки х – независимая переменная, поэтому её значения выберем сами ; У – зависимая переменная, её значение получится в результате подстановки выбранного значения х в функцию. Результаты запишем в таблицу: х у 0 2 Если х = 0, то у = — 2 · 0 + 3 = 3 . 3 Если х=2, то у = -2 · 2+3 = — 4+3= -1 . — 1 Точки (0;3) и (2; -1) отметим на координатной плоскости и проведем через них прямую. х у 0 1 1 У= — 2х+3 3 2 — 1 выбираем сами
Слайд 8
Построить график линейной функции у = — 2 х +3 Составим таблицу: х у 03 1 1 Построим на координатной плоскости точки ( 0 ; 3 ) и ( 1 ; 5 ) и проведем через них прямую х 1 0 1 3 у
Слайд 9
I вариант II вариант y=x-4 y =- x+4 Определить взаимосвязь коэффициентов k и b и расположения прямых Построить график линейной функции
Слайд 10
y=x-4 y=-x+4 I вариант II вариант x y 1 2 0 -4 x 1 2 0 4 y
Слайд 11
х 0 у y = kx + m (k > 0) х 0 у y = kx + m (k 0, то линейная функция у = kx + b возрастает если k
Слайд 12
С помощью графика линейной функции у = 2х — 6 ответить на вопросы: а) при каком значении х будет у = 0 ? б) при каких значениях х будет у 0 ? в) при каких значениях х будет у 0 ? 1 0 3 у 1 х -6 а) у = 0 при х = 3 б) у 0 при х 3 Если х 3 , то прямая расположена выше оси х , значит, ординаты соответствующих точек прямой положительны в) у 0 при х 3 Если х 3 , то прямая расположена ниже оси х , значит, ординаты соответствующих точек прямой отрицательны
Слайд 13
Задания для самостоятельного решения: построить графики функций (выполнять в тетради) 1. у = 2х – 2 2. у = х + 2 3. у = 4 – х 4 . у = 1 – 3х О братите внимание: точки, выбранные вами для построения прямой, могут быть другими, но расположение графиков обязательно должно совпадать
Слайд 14
Ответ к заданию 1
Слайд 15
Ответ к заданию 2
Слайд 16
Ответ к заданию 3
Слайд 17
Ответ к заданию 4
Слайд 19
На каком рисунке изображён график линейной функции y = kx ? Ответ объяснить . 1 2 3 4 5 x y x y x y x y x y
Слайд 20
Ученик допустил ошибку при построении графика функции. На каком рисунке? 1. y =х+2 2. y =1,5х 3. y =-х-1 x y 2 1 x y 3 1 x y 3 3
Слайд 21
1 2 3 4 5 x y x y y x y x y На каком рисунке коэффициент k отрицателен? x
Слайд 22
Назовите знак коэффициента k для каждой из линейных функций:
Слайд 23
На каком рисунке свободный член b в уравнении линейной функции отрицателен? 1 2 3 4 5 х y x y x y x y x y
Слайд 24
Выберите линейную функцию, график которой изображен на рисунке у = х — 2 у = х + 2 у = 2 – х у = х – 1 у = — х + 1 у = — х — 1 у = 0,5х у = х +2 у = 2х Молодец! Подумай!
Слайд 25
x y 1 2 0 1 2 3 -1 -2 -1 -2 x y 1 2 0 1 2 3 -1 -2 -1 -2 y=2x y=2x+ 1 y=2x- 1 y=-2x+ 1 y = -2x- 1 y =-2x
Слайд 26
y=-0,5x+ 2 , y=-0,5x , y=-0,5x- 2 x y 1 2 0 1 2 3 -1 -2 -1 -2 3 4 5 6 -3 x y 1 2 0 2 3 -1 -2 -1 -2 3 4 5 6 -3 1 y=0,5x+ 2 y=0,5x- 2 y=0,5x y=-0,5x+ 2 y=-0,5x y =-0,5x- 2
Слайд 27
y=x+ 1 y=x- 1 , y=x y 1 2 0 1 2 3 -1 -2 -1 -2 3 4 5 6 -3 x y 1 2 0 1 2 3 -1 -2 -1 -2 3 4 5 6 -3 x y=-x y=-x+ 3 y =-x- 3 y=x+ 1 y=x- 1 y=x
Слайд 28
Составить уравнение линейной функции по следующим условиям:
Слайд 29
подведем итог
Слайд 30
Выводы записать в тетрадь Мы узнали: *Функция вида у = kx + b называется линейной. * Графиком функции вида у = kx + b является прямая . *Для построения прямой необходимы только две точки , так как через две точки проходит единственная прямая. *Коэффициент k показывает возрастает или убывает прямая. *Коэффициент b показывает, в какой точке прямая пересекает ось OY . *Условие параллельности двух прямых.
Слайд 32
Желаю успехов!
Слайд 33
Алгебра – это слово произошло от названия сочинения Мухаммеда Аль-Хорезми «Аль- джебр и Аль- мукабала », в котором алгебра излагалась как самостоятельный предмет
Слайд 34
Роберт Рекорд – это английский математик, который в 1556г. ввёл знак равенства и объяснил свой выбор тем, что ничто не может быть более равным, чем два параллельных отрезка.
Слайд 35
Готфрид Лейбниц – немецкий математик (1646 – 1716г.г.), который первым ввёл термин «абсцисса» — в 1695г., «ордината» — в 1684г., «координаты» — в 1692г.
Слайд 36
Рене Декарт – французский философ и математик (1596 – 1650г.г.), который первым ввёл понятие «функция»
Слайд 37
Использованная литература 1.МордковичА.Г. и др. Алгебра: учебник для 7 класса общеобразовательных учреждений – М.: Просвещение,2010. 2.Звавич Л.И. и др. Дидактические материалы по алгебре для 7 класса — М.: Просвещение,2010. 3.Алгебра 7 класс, под редакцией Макарычев Ю.Н. и др., Просвещение, 2010 г. 4.Интернетресурсы: www.symbolsbook.ru/Article.aspx %…id%3D222
nsportal.ru