Рабочая программа по курсу «Решение уравнений и неравенств, содержащих модуль и параметр» (7 класс)
«Рассмотрено» Председатель МО учителей математики и информатики ________Т.Н. Барышникова Протокол № 1 от «28» августа 2014года | «Согласовано» Заместитель директора по УВР ____________ И.С.Кукина «_____» августа 2014года | «Утверждаю» Директор МОУ «ГИМНАЗИЯ №5» ______________ В.В.Киреев Приказ № 246 от « 01 » сентября 2014года |
РАБОЧАЯ ПРОГРАММА
по «Решению уравнений и неравенств, содержащих параметр и модуль»
в 7-А, 7-Б классах
учителя высшей квалификационной категории
Барышниковой Татьяны Николаевны
Рассмотрено на заседании педагогического совета.
Протокол №1
от 29 августа 2014года
г. Саратов
2014-2015 учебный год
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА
В основу положена программа по математике для классов с углубленным изучением математики в основной школе.
Обучение математике в основной школе направлено на достижение следующих целей:
1) в направлении личностного развития:
• формирование представлений о математике как части общечеловеческой культуры, о значимости математики в развитии цивилизации и современного общества;
• развитие логического и критического мышления, культуры речи, способности к умственному эксперименту;
• формирование интеллектуальной честности и объективности, способности к преодолению мыслительных стереотипов, вытекающих из обыденного опыта;
• воспитание качеств личности, обеспечивающих социальную мобильность, способность принимать самостоятельные решения;
• формирование качеств мышления, необходимых для адаптации в современном информационном обществе;
• развитие интереса к математическому творчеству и математических способностей;
2) в метапредметном направлении:
• развитие представлений о математике как форме описания и методе познания действительности, создание условий для приобретения первоначального опыта математического моделирования;
• формирование общих способов интеллектуальной деятельности, характерных для математики и являющихся основой познавательной культуры, значимой для различных сфер человеческой деятельности;
3) в предметном направлении:
• овладение математическими знаниями и умениями, необходимыми для продолжения образования, изучения смежных дисциплин, применения в повседневной жизни;
• создание фундамента для математического развития, формирования механизмов мышления, характерных для математической деятельности.
Цели курса: — развить математическое мышление, — изучение различных методов решения задач, — углубление знаний по основному курсу, — развитие интереса к математике, — формирование целостной системы решения упражнений с модулями и параметрами, — формированию навыков организации учащимися самостоятельных микроисследований.
Данный курс рассчитан на 34 часа, т.е. 1 час в неделю, предполагает четкое изложение теории вопроса, решение типовых задач, самостоятельную работу. Программа составлена на основе сборника: «Факультативные курсы. Сборник № 2, часть 1. – М.: Просвещение, 1990». В программе приводится распределение учебного времени, каждое занятие состоит из двух частей: задачи, решаемые с учителем, и задачи, для самостоятельного решения. Основными формами организации учебных занятий является: урок-лекция, урок закрепления нового материала, практическая работа, творческие задания.
В результате изучения курса учащиеся должны знать:
определение модуля и его геометрический смысл,
алгоритм раскрытия модуля,
приемы решения уравнений и неравенств с модулем,
различные способы решения уравнений с параметрами,
приемы построения графиков уравнений, содержащих модуль.
Учащиеся должны уметь:
Решать упражнения на преобразование выражений, содержащих знак модуля,
Решать уравнения и неравенства определенных видов с модулем,
Решать линейные уравнения с параметрами.
Литература
1. Изучение сложных тем курса алгебры в средней школе: Учебно-методические материалы по математике. М.: Илекса, Ставрополь: Сервисшкола, 2002
2. В.В. Локоть. Задачи с параметрами. Учебное пособие.- М.:АРКТИ, 2003
3. Ершова, А. П, и др. Тетрадь-конспект по алгебре для 7, 8 классов — М.: Илекса. 2004
4. Ершова, А. П, и др Самостоятельные и контрольные работы по алгебре для 7,8 класса — М.: Илекса. 2004.
5. Лебединская Е. А. и др. Задания для обучения и развития учащихся, М.:Интелект-центр, 2002.
6. Л.И. Звавич и др. Новые контрольные и проверочные работы по алгебре для 7, 8 класса.
7. Зив, В.А. Гольдич.. Дидактические материалы по алгебре для 7, 8 класса. — СПб: ЧеРо-на Неве, 2003.
Содержание тем учебного курса
Тема 1. Решение уравнений и неравенств, содержащих знак модуля (20 часов)
Понятие модуля, алгебраический и геометрический смысл. Раскрытие знака модуля, преобразование выражений, содержащих модуль. Некоторые свойства модуля. Решение уравнений, содержащих знак модуля. Метод интервалов решения уравнений, содержащих модуль. Построение графиков функций, содержащих знак модуля. Графическая интерпретация решения уравнений, содержащих переменную под знаком модуля. Решение неравенств, содержащих знак модуля.
Тема 2. Уравнения и неравенства с параметрами (14 часов)
Что такое параметр. Основные понятия. Линейные уравнения с параметрами. Графический способ решения уравнений с параметрами. Линейные неравенства с параметрами. Системы уравнений с параметрами. Уравнения с параметрами, содержащие переменную под знаком модуля.
Календарно-тематическое планирование учебного материала
№ урока
Тема
дата
план
факт
7»А»
7 «Б»
1
Модуль, алгебраический и геометрический смысл
06.09.14
2
Модуль, алгебраический и геометрический смысл
13.09.14
3
Раскрытие знака модуля, преобразование выражений, содержащих модуль.
20.09.14
4
Раскрытие знака модуля, преобразование выражений, содержащих модуль.
27.09.14
5
Раскрытие знака модуля, преобразование выражений, содержащих модуль.
04.10.14
6
Раскрытие знака модуля, преобразование выражений, содержащих модуль.
11.10.14
7
Некоторые свойства модуля.
18.10.14
8
Некоторые свойства модуля.
25.10.14
9
Решение уравнений с модулем.
15.11.14
10
Решение уравнений с модулем.
22.11.14
11
Метод интервалов решения уравнений, содержащих модуль
29.11.14
12
Метод интервалов решения уравнений, содержащих модуль
06.12.14
13
Построение графиков функций у = |f(x)|, y = ||f(x)| + a| .
13.12.14
14
Построение графиков функций у = |f(x)|, y = ||f(x)| + a| .
20.12.14
15
Построение графиков функций у = |f(x)|, y = ||f(x)| + a| .
27.12.14
16
Построение графиков функций y = f(|x|), y = f(|x|) + a, y = |f(|x|) + a|.
17.01.15
17
Построение графиков функций y = f(|x|), y = f(|x|) + a, y = |f(|x|) + a|.
24.01.15
18
Графическое решение уравнений с модулем.
31.01.15
19
Графическое решение уравнений с модулем.
07.02.15
20
Графическое решение уравнений с модулем.
14.02.15
21
21.02.15
22
Линейные уравнения с параметрами.
28.02.15
23
Линейные уравнения с параметрами.
07.03.15
24
Линейные уравнения с параметрами.
14.03.15
25
Графический способ решения уравнений с параметрами.
21.03.15
26
Графический способ решения уравнений с параметрами.
04.04.15
27
Линейные неравенства с параметрами.
11.04.15
28
Линейные неравенства с параметрами.
18.04.15
29
Системы линейных уравнений с параметрами
25.04.15
30
Системы линейных уравнений с параметрами
02.05.15
31
Системы линейных уравнений с параметрами08.05.15
32
Уравнения с параметрами, содержащие переменную под знаком модуля
16.05.23
33
Уравнения с параметрами, содержащие переменную под знаком модуля
23.05.15
34
Уравнения с параметрами, содержащие переменную под знаком модуля
30.05.15
Календарно-тематическое планирование по «Решение уравнений и неравенств, содержащих параметр и модуль» для 7 кл. при 1 уроке в неделю, всего 34 часа.
№ п/п
Тема
Кол-во час
Основные виды учебной деятельности
Результаты освоения образовательной программы
Вид контроля
Дата проведения
Личностные
Метапредметные
План
Факт
7 «А»
7 «Б»
1-2
Модуль, алгебраический и геометрический смысл
2
Формулировать определение модуля, его алгебраический и геометрический смысл. Выполнять вычисления выражений, содержащих модуль.
Знать определение модуля, его алгебраический и геометрический смысл. Выполнять вычисления выражений, содержащих модуль.
Развитие логического и критического мышления, культуры речи, способности к умственному эксперименту
Формирование представлений о математике как части общечеловеческой культуры, о значимости математики в развитии цивилизации и современного общества
Работа у доски, индивидуальная работа по карточкам
06.09.14
13.09.14
3-6
Раскрытие знака модуля, преобразование выражений, содержащих модуль.
4
Формулировать определение модуля, его алгебраический и геометрический смысл. Выполнять преобразования выражений, содержащих модуль, раскрывать модуль.
Знать определение модуля, его алгебраический и геометрический смысл. Выполнять преобразования выражений, содержащих модуль, раскрывать модуль.
Понимать смысл поставленной задачи, умение ясно, точно, грамотно излагать свои мысли в письменной речи; умение контролировать процесс и результат учебной математической деятельности
Понимание сущности алгоритмических предписаний и умение действовать в соответствии с предложенным алгоритмом; умение видеть математическую задачу в других дисциплинах, в окружающей жизни
Практическая работа, проблемные задания
20.09.14
27.09.14
04.10.14
11.10.14
7-8
Некоторые свойства модуля.
2
Формулировать свойства модуля, применять свойства для преобразования выражений и вычислений.
Знать свойства модуля, применять свойства для преобразования выражений и вычислений.
Воспитание качеств личности, обеспечивающих социальную мобильность, способность принимать самостоятельные решения
Формирование общих способов интеллектуальной деятельности, характерных для математики и являющихся основой познавательной культуры, значимой для различных сфер человеческой деятельности
Фронтальный опрос
18.10.14
25.10.14
9-10
Решение уравнений с модулем.
2
Решать простейшие уравнения с модулем алгебраическим и геометрическими способами.
Уметь решать простейшие уравнения с модулем алгебраическим и геометрическими способами.
Понимать смысл поставленной задачи, умение ясно, точно, грамотно излагать свои мысли в письменной речи; умение контролировать процесс и результат учебной математической деятельности
Понимание сущности алгоритмических предписаний и умение действовать в соответствии с предложенным алгоритмом; умение видеть математическую задачу в других дисциплинах, в окружающей жизни
Устный опрос, работа у доски, индивидуальная работа по карточкам
15.11.14
22.11.14
11-12
Метод интервалов решения уравнений, содержащих модуль
2
Решать уравнения, содержащие модуль методом интервалов.
Уметь решать уравнения, содержащие модуль методом интервалов.
Развитие логического и критического мышления, культуры речи, способности к умственному эксперименту
Формирование представлений о математике как части общечеловеческой культуры, о значимости математики в развитии цивилизации и современного общества
Работа у доски, индивидуальная работа по карточкам
29.11.14
06.12.14
13-15
Построение графиков функций у = |f(x)|, y = ||f(x)| + a| .
3
Строить по точкам графики, выполнять построение графиков функций, используя алгоритмы построения графиков функций у = |f(x)|, y = ||f(x)| + a| .
Знать алгоритмы построения графиков функций у = |f(x)|, y = ||f(x)| + a| , уметь строить графики.
Понимать смысл поставленной задачи, умение ясно, точно, грамотно излагать свои мысли в письменной речи; умение контролировать процесс и результат учебной математической деятельности
Понимание сущности алгоритмических предписаний и умение действовать в соответствии с предложенным алгоритмом; умение видеть математическую задачу в других дисциплинах, в окружающей жизни
Практическая работа, проблемные задания, самостоятельная работа
13.12.14
20.12.14
27.12.14
16-17
Построение графиков функций y = f(|x|), y = f(|x|) + a, y = |f(|x|) + a|.
2
Строить по точкам графики, выполнять построение графиков функций, используя алгоритмы построения графиков функций y = f(|x|), y = f(|x|) + a, y = |f(|x|) + a|.
Знать алгоритмы построения графиков функций y = f(|x|), y = f(|x|) + a, y = |f(|x|) + a|, уметь строить графики.
Понимать смысл поставленной задачи, умение ясно, точно, грамотно излагать свои мысли в письменной речи; умение контролировать процесс и результат учебной математической деятельности
Понимание сущности алгоритмических предписаний и умение действовать в соответствии с предложенным алгоритмом; умение видеть математическую задачу в других дисциплинах, в окружающей жизни
Работа у доски, индивидуальная работа по карточкам
17.01.15
24.01.15
18-20
Графическое решение уравнений с модулем.
3
Решать уравнения с модулем графическим способом
Уметь решать уравнения с модулем графическим способом
Развитие логического и критического мышления, культуры речи, способности к умственному эксперименту
Формирование представлений о математике как части общечеловеческой культуры, о значимости математики в развитии цивилизации и современного общества
Практическая работа, проблемные задания, самостоятельная работа
31.01.15
07.02.15
14.02.15
21
Что такое параметр. Основные понятия.
1
Формулировать понятие параметра, решать простейшие уравнения с параметром.
Знать, что такое параметр, и что значит решить уравнение с параметром. Уметь , решать простейшие уравнения с параметром.
Развитие логического и критического мышления, культуры речи, способности к умственному эксперименту
Формирование представлений о математике как части общечеловеческой культуры, о значимости математики в развитии цивилизации и современного общества
Фронтальный опрос
21.02.15
22-24
Линейные уравнения с параметрами.
3
Решать линейные уравнения с параметром, формулировать ответ.
Уметь решать линейные уравнения с параметром, записывать ответ.
Понимать смысл поставленной задачи, умение ясно, точно, грамотно излагать свои мысли в письменной речи; умение контролировать процесс и результат учебной математической деятельности
Понимание сущности алгоритмических предписаний и умение действовать в соответствии с предложенным алгоритмом; умение видеть математическую задачу в других дисциплинах, в окружающей жизни
Работа у доски, индивидуальная работа по карточкам
28.02.15
07.03.15
14.03.15
25-26
Графический способ решения уравнений с параметрами.
2
Решать уравнения с параметрами на основе графических представлений.
Уметь решать уравнение с параметром графическим способом.
Понимать смысл поставленной задачи, умение ясно, точно, грамотно излагать свои мысли в письменной речи; умение контролировать процесс и результат учебной математической деятельности
Понимание сущности алгоритмических предписаний и умение действовать в соответствии с предложенным алгоритмом; умение видеть математическую задачу в других дисциплинах, в окружающей жизни
Практическая работа
21.03.15
04.04.15
27-28
Линейные неравенства с параметрами.
2
Формулировать понятие неравенства с параметром, иметь представление, что значит решить неравенство с параметром.
Уметь решать линейные неравенства с параметрами
Развитие логического и критического мышления, культуры речи, способности к умственному эксперименту
Формирование представлений о математике как части общечеловеческой культуры, о значимости математики в развитии цивилизации и современного общества
Фронтальный опрос
11.04.15
18.04.15
29-31
Системы линейных уравнений с параметрами
3
Решать системы линейных уравнений с параметрами
Уметь решать системы линейных уравнений с параметрами
Понимать смысл поставленной задачи, умение ясно, точно, грамотно излагать свои мысли в письменной речи; умение контролировать процесс и результат учебной математической деятельности
Понимание сущности алгоритмических предписаний и умение действовать в соответствии с предложенным алгоритмом; умение видеть математическую задачу в других дисциплинах, в окружающей жизни
Работа у доски, индивидуальная работа по карточкам
25.04.15
02.05.15
08.05.15
32-34
Уравнения с параметрами, содержащие переменную под знаком модуля
3
Решать уравнения с параметрами, содержащие переменную под знаком модуля
Уметь решать уравнения с параметрами, содержащие переменную под знаком модуля
Развитие логического и критического мышления, культуры речи, способности к умственному эксперименту
Формирование представлений о математике как части общечеловеческой культуры, о значимости математики в развитии цивилизации и современного общества
Практическая работа, проблемные задания, самостоятельная работа
16.05.23
23.05.15
30.05.15
Занятие элективного курса по математике «Задачи с модулями и параметрами» по теме «Решение линейных уравнений с параметрами»
Занятие по теме «Линейные уравнения с параметрами», 9 класс Моргунова Н.А.
Занятие элективного курса по математике «Задачи с модулями и параметрами» по теме
«Решение линейных уравнений с параметрами»
Тема занятия: «Решение линейных уравнений с параметрами».
Цель занятия: обобщение и закрепление навыков решения линейных уравнений с параметром.
Задачи занятия:
Образовательная – закрепить алгоритм решения уравнений, формировать осознанный подход к решению уравнений с параметром;
Развивающая – способствовать развитию логического мышления, навыков исследовательской деятельности, творческих способностей, интуиции.
Воспитательная – воспитать самостоятельность, ответственность, способствовать формированию алгоритмической культуры, рациональному использованию времени.
Технологии:
развивающее обучение, проблемное обучение, проектные методы обучения, ИКТ, здоровьесберегающие технологии, обучение в сотрудничестве.
Оборудование: компьютерный класс, мультимедийный проектор.
Ход занятия:
I этап – актуализация знании и опыта ( 2 мин.)
— Здравствуйте ребята!
На протяжении нескольких занятий вы учились решать линейные уравнения с параметрами. Сегодняшнее занятие – итоговое по данной теме.
Начиная изучать элективный курс, мы решили, что каждый раздел будем завершать исследовательской работой. Тема «Решение линейных уравнений с параметрами» — не исключение.
Итак, сегодня на занятии мы познакомимся с исследовательской работой по теме; с использованием ЦОР «Виртуальная математика» выполним ряд практических заданий и с его же помощью проведем самостоятельную работу.
II этап– представление исследовательской работы учащихся( с помощью мультимедийного проектора)- 10 мин.:

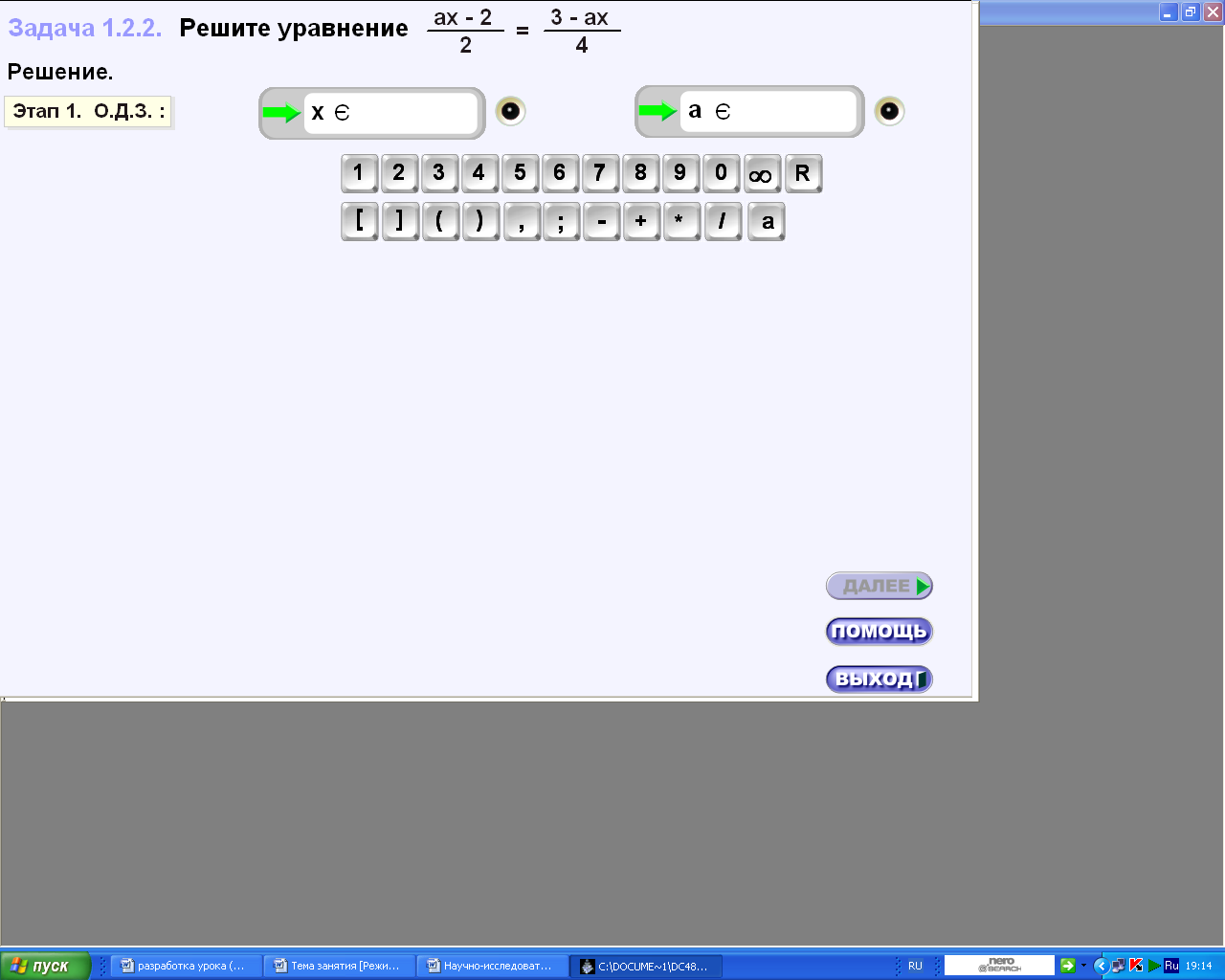
III этап – выполнение практических заданий с использованием ЦОР «Виртуальная математика» (за центральным компьютером выполняет учащийся, ход решения проецируется на экран, остальные – получают задания в виде раздаточного материала)
1. 
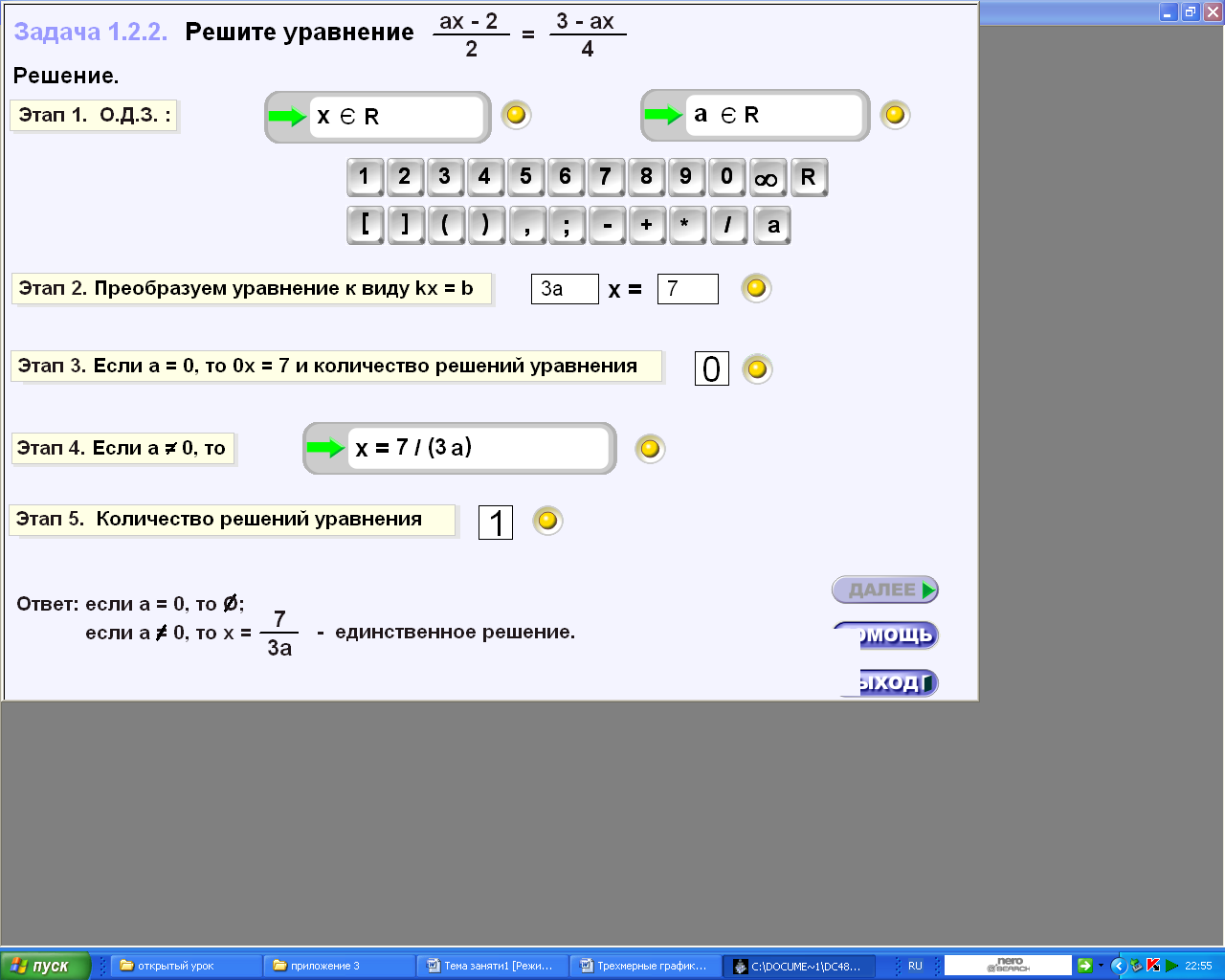
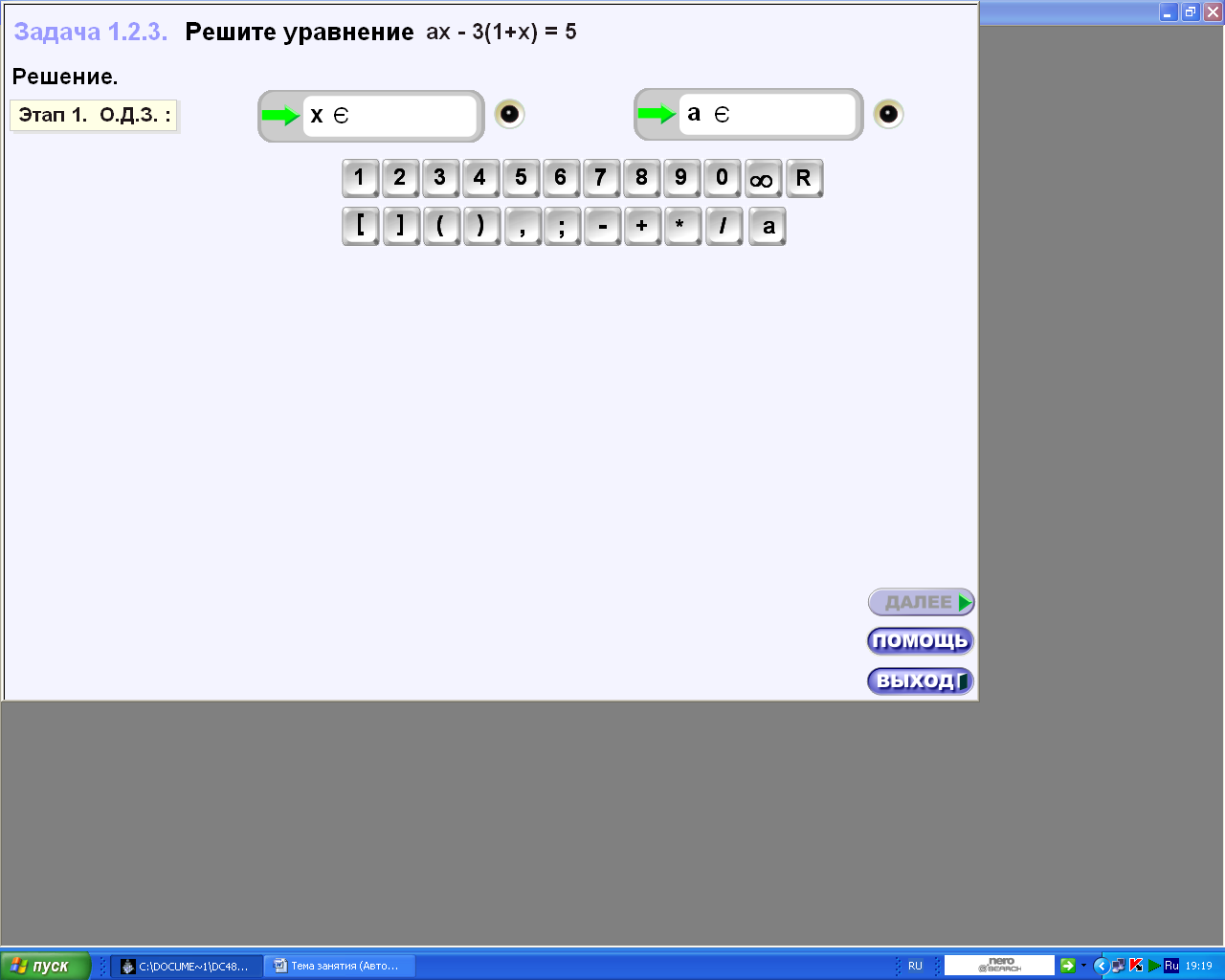
2. 
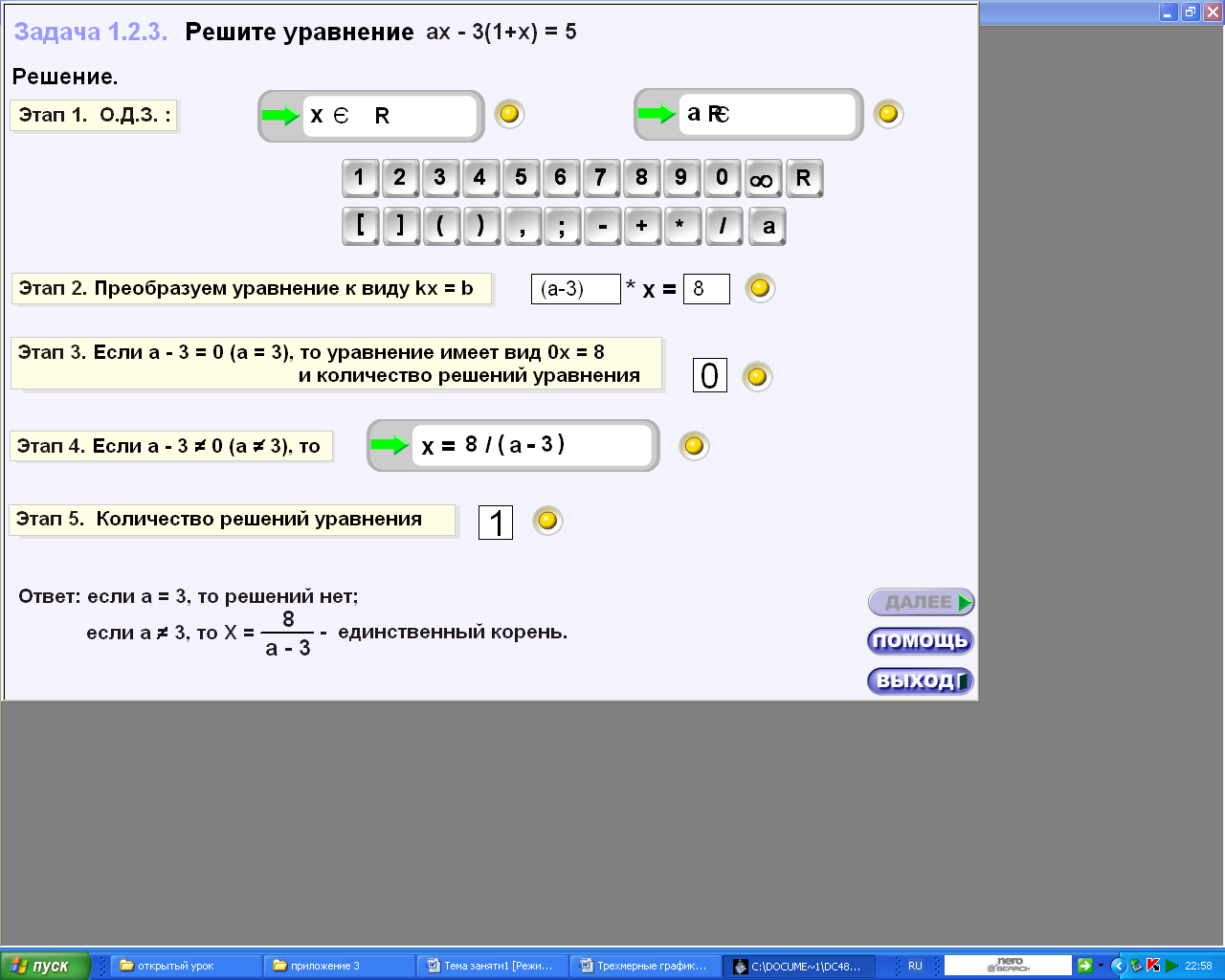
IV этап – самостоятельная работа с использованием ЦОР «Виртуальная математика»
1) Физкультминутка.
Крепко сомкнуть веки, а затем в течение нескольких секунд часто моргать.
Без усилий, но плотно сомкнуть веки и прикрыть их ладонями, чтобы на одну минуту полностью исключить воздействие на глаза света.
Сделать массаж век, легко поглаживая их указательным пальцем в направлении от носа к виску.
2) Учащиеся рассаживаются за рабочие места за компьютеры
— Вам предлагается 5 уравнений. Их можно выполнять в любом порядке. В отличии от тренировочных заданий, программа проверяет все решение сразу, а не поэтапно.
1. 
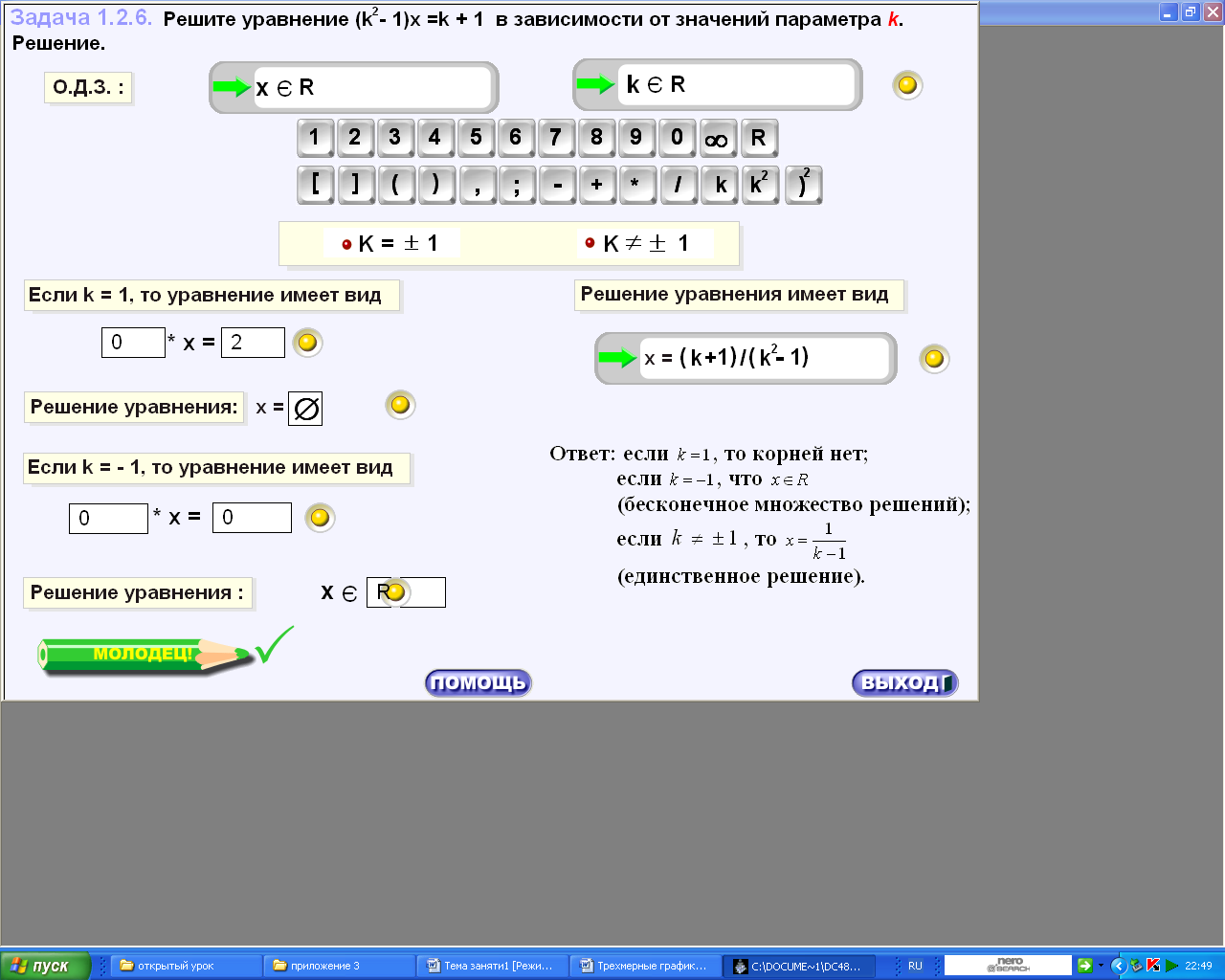
2.  3.
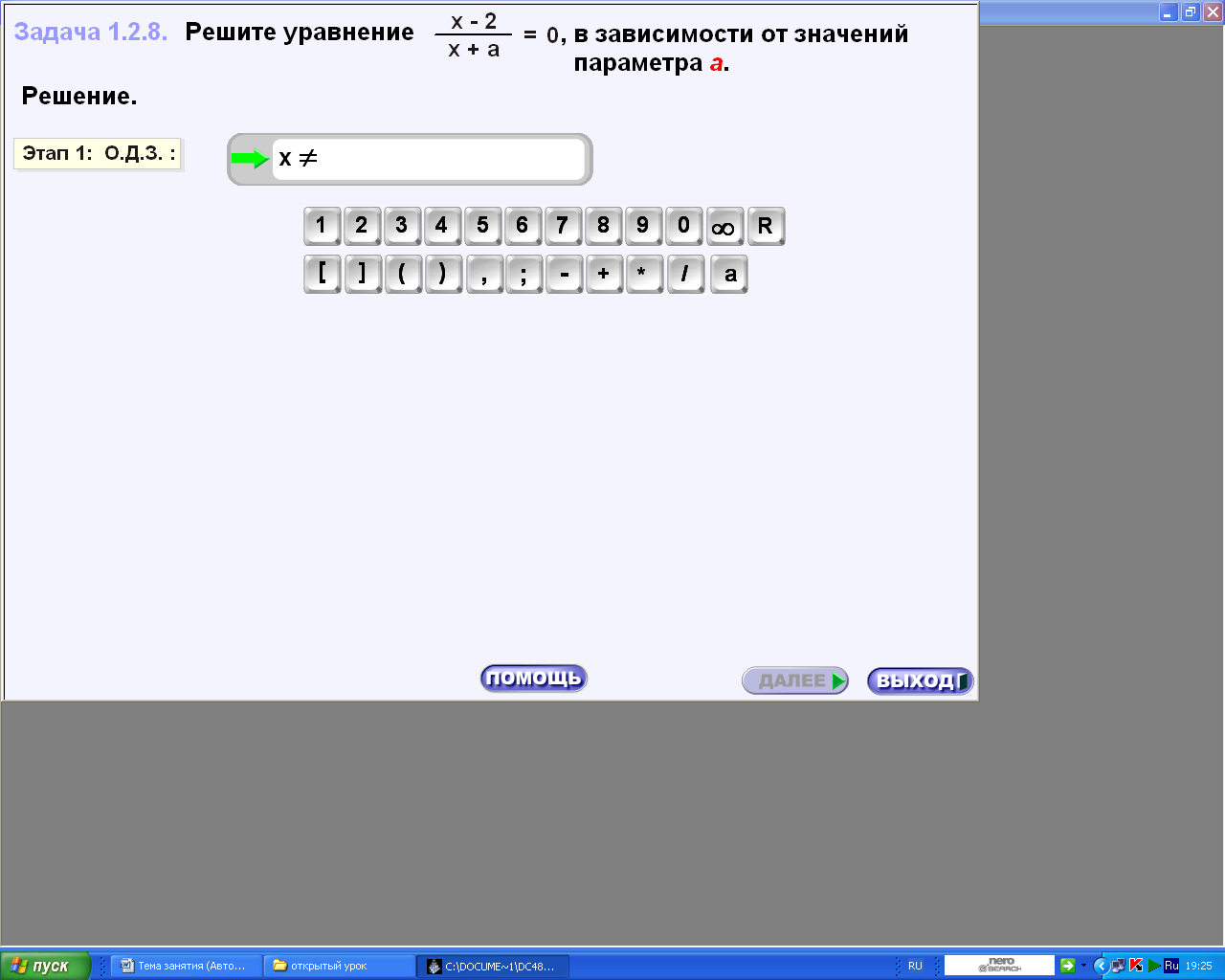
3. 
4. 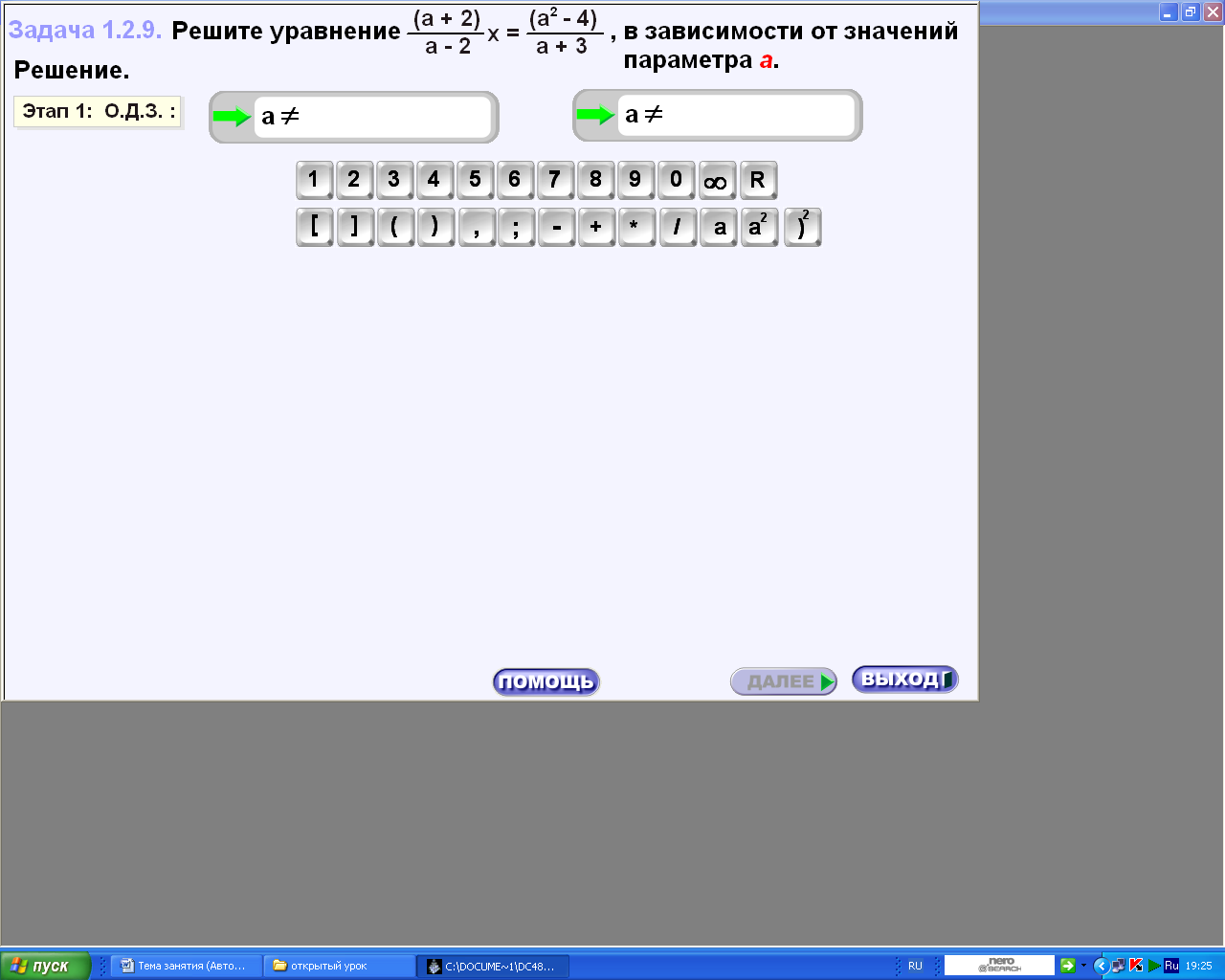 5.
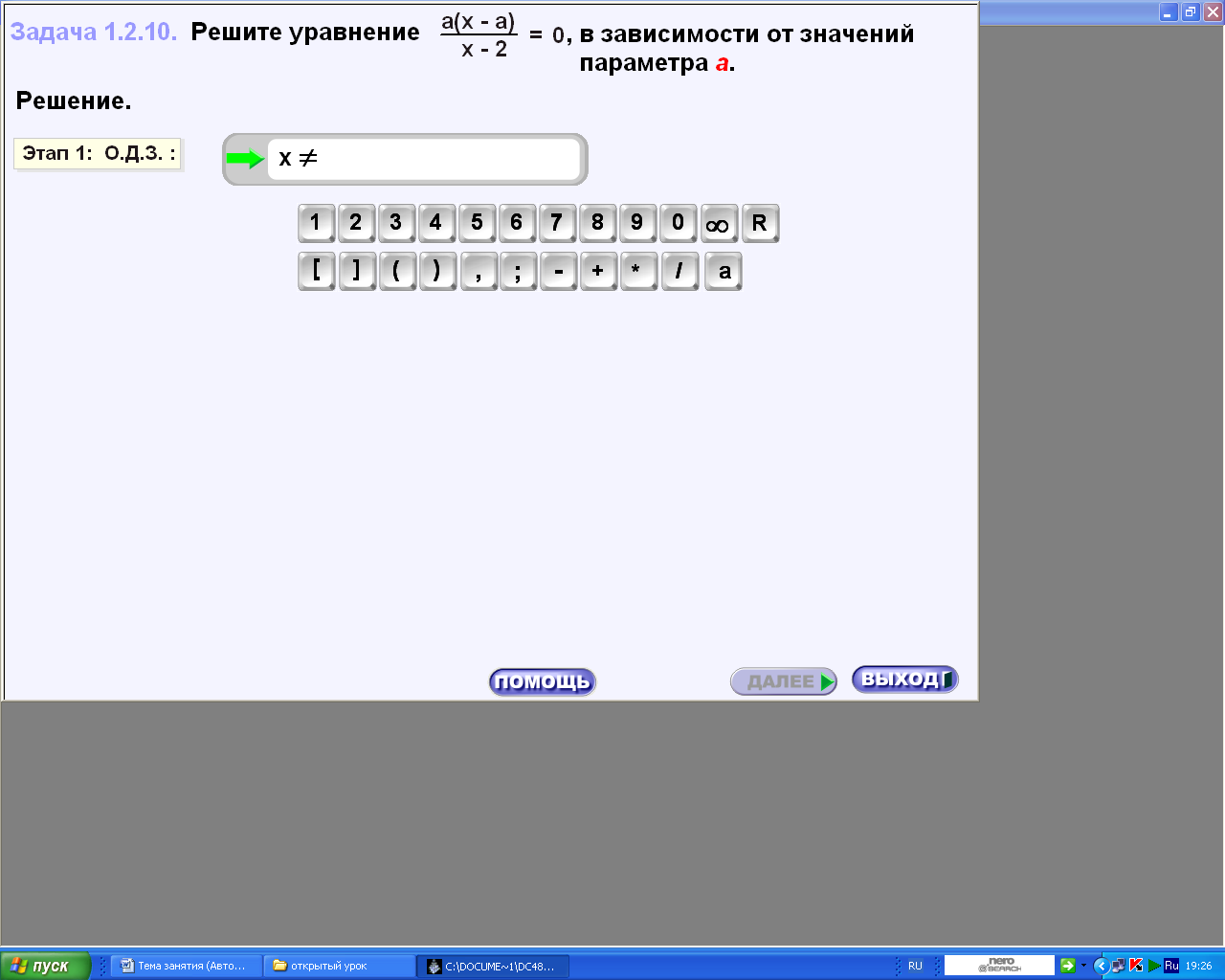
5. 
— Оцените, пожалуйста, результаты своей работы и покажите их учителю. Для этого воспользуйтесь «Таблицей оценки результатов своей работы»

V этап — Выполнение заданий на опережение (для тех учащихся, которые справились с контролем раньше остальных)
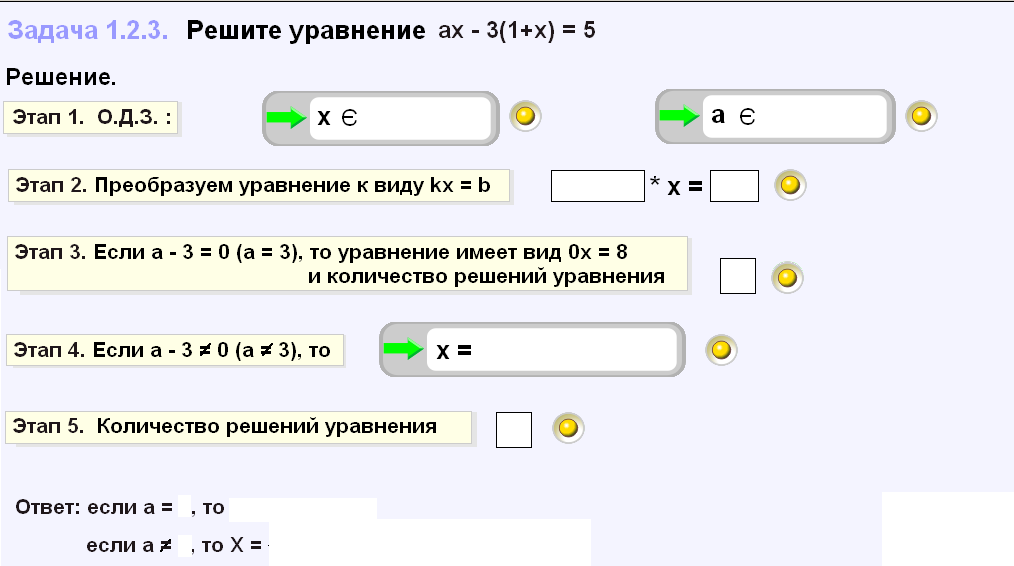
Задача 1.2.4. При каждом значении параметра а решите уравнение ах-6=4а-7х.
VI этап – подведение итогов занятия.
ЦОР взяты с сайта «Единая коллекция цифровых образовательных ресурсов»
http://school-collection.edu.ru/
http://school-collection.edu.ru/catalog/rubr/df413b15-266b-4a0a-bdb2-28fc41140ab2/?interface=pupil&class[]=51&subject[]=17
http://school-collection.edu.ru/catalog/rubr/df413b15-266b-4a0a-bdb2-28fc41140ab2/111910/?interface=pupil&class=51&subject=17
«Система линейных уравнений с параметром»
Горячева Надежда Евгеньевна, учитель математики высшей квалификационной категории МОУ СОШ №2 города Каргополя Архангельской области.
ПРОЕКТ УРОКА.
Предмет – алгебра
Класс – 8 (модуль)
Тема урока: Уравнения, содержащие переменную под знаком модуля.



 Тип урока: урок изучения нового материала.
Тип урока: урок изучения нового материала.
Система целей урока:



 Образовательные цели урока:
Образовательные цели урока:
познакомить обучающихся с разными способами решения уравнений, содержащих знак модуля;
активизировать деятельность учащихся за счет решения разноуровневых заданий.
Развивающие цели урока:
развивать и совершенствовать умение применять имеющиеся у учащихся знания в новой ситуации;
способствовать развитию умения определять черты сходства и различия в изучаемых объектах;
способствовать развитию умения делать выводы и обобщения.
Воспитательные цели урока:
способствовать выработке у школьников желания и потребности изучаемых фактов;
воспитывать самостоятельность и творчество, умение достигать поставленную цель, умение делать правильный выбор сообразно своим возможностям.
Задачи урока:
повторить определение модуля числа;
научить решать уравнения, содержащие знак модуля разными способами;
закрепить практические навыки решения уравнений, содержащих знак модуля.
Формы организации деятельности на уроке:
фронтальная
индивидуальная
Структура урока:
организационный момент;
мотивационная беседа;
актуализация знаний;
объяснение нового материала;
первичное закрепление, решение упражнений;
подведение итогов;
рефлексия.
Методы:
словесные;
наглядные;
практические.
Оборудование:
компьютер;
проектор;
учебник “Алгебра 8” под ред. Н.Я.Виленкина.
Раздаточный материал:
карточки с заданиями.
Прогнозируемый результат: закрепление умений и навыков решения уравнений, содержащих знак модуля; формирование умения планировать свою работу; достижение каждым учащимся того уровня умений и навыков, который ему необходим:
I уровень — решать простейшие уравнения, содержащие знак модуля; решать уравнения, содержащие знак модуля по заданному алгоритму;
II уровень — решать уравнения, содержащие знак модуля, самостоятельно выбирая метод решения.
Урок алгебры 8 класс
Тема урока: Уравнения, содержащие переменную под знаком модуля. Слайд 1
Цели: Сформировать знания учащихся о решении уравнений, содержащих переменную под знаком модуля. Развивать технику вычисления, логическое мышление.
Тип урока: урок изучения нового материала
Ход урока
Орг. момент
Сегодня на уроке мы познакомимся с новыми способами решения уравнений, содержащих знак модуля.
Прежде, чем перейти к решению уравнений давайте вспомним определение модуля числа
Слайд2
Определение: Модулем числа называется само число, если оно неотрицательное, и число ему противоположное, если число отрицательное.
Выполним запись определения на математическом языке:

Вспомнив определение модуля действительного числа, можно перейти к практике, решению заданий.
Слайд 3,4
Вычислите значение модуля, следующих выражений, 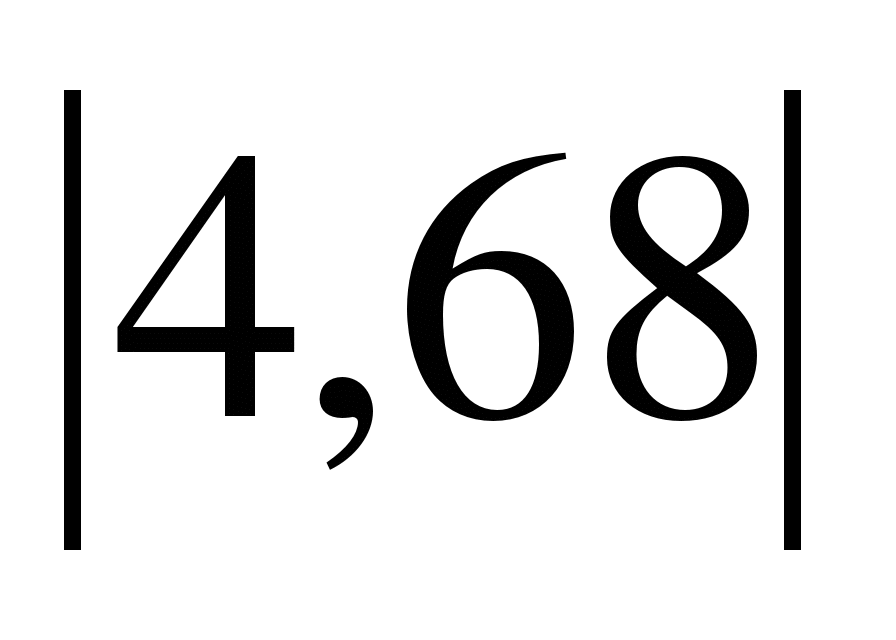 ,
,  ,
, 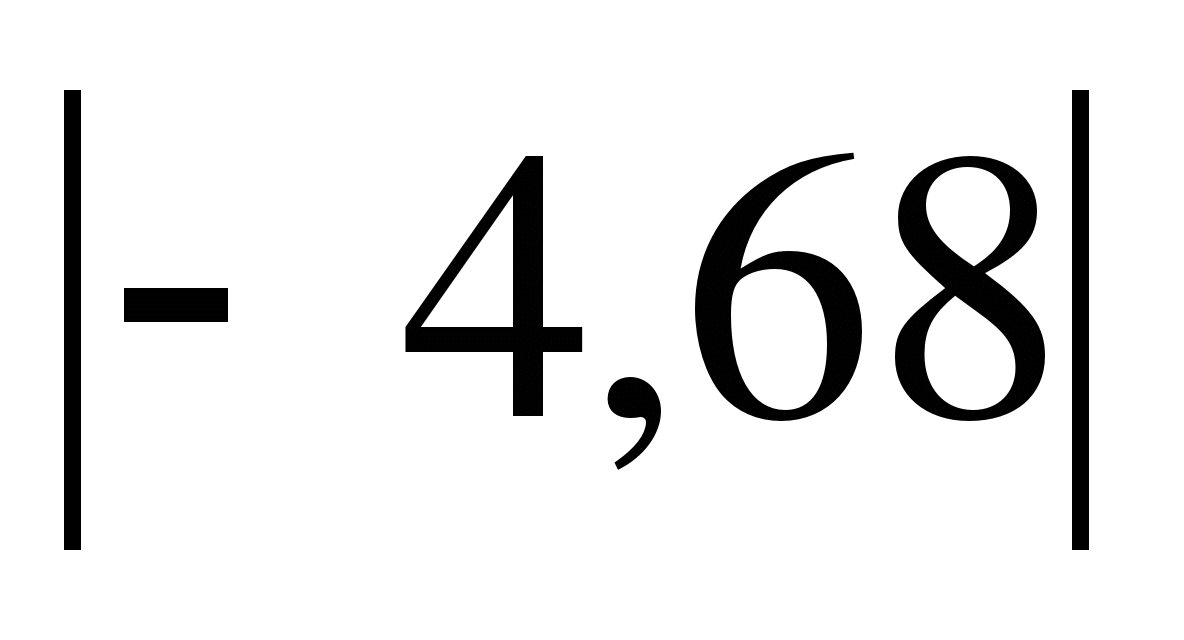 ,
,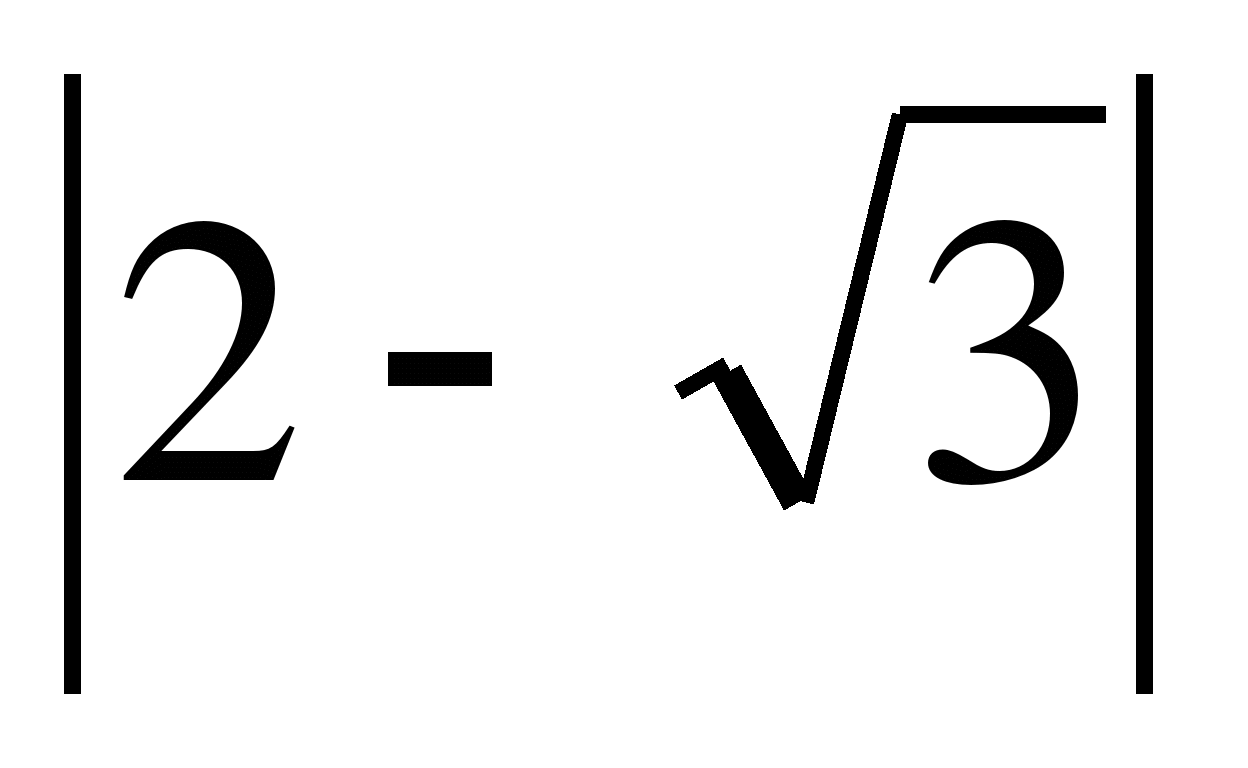 ,
,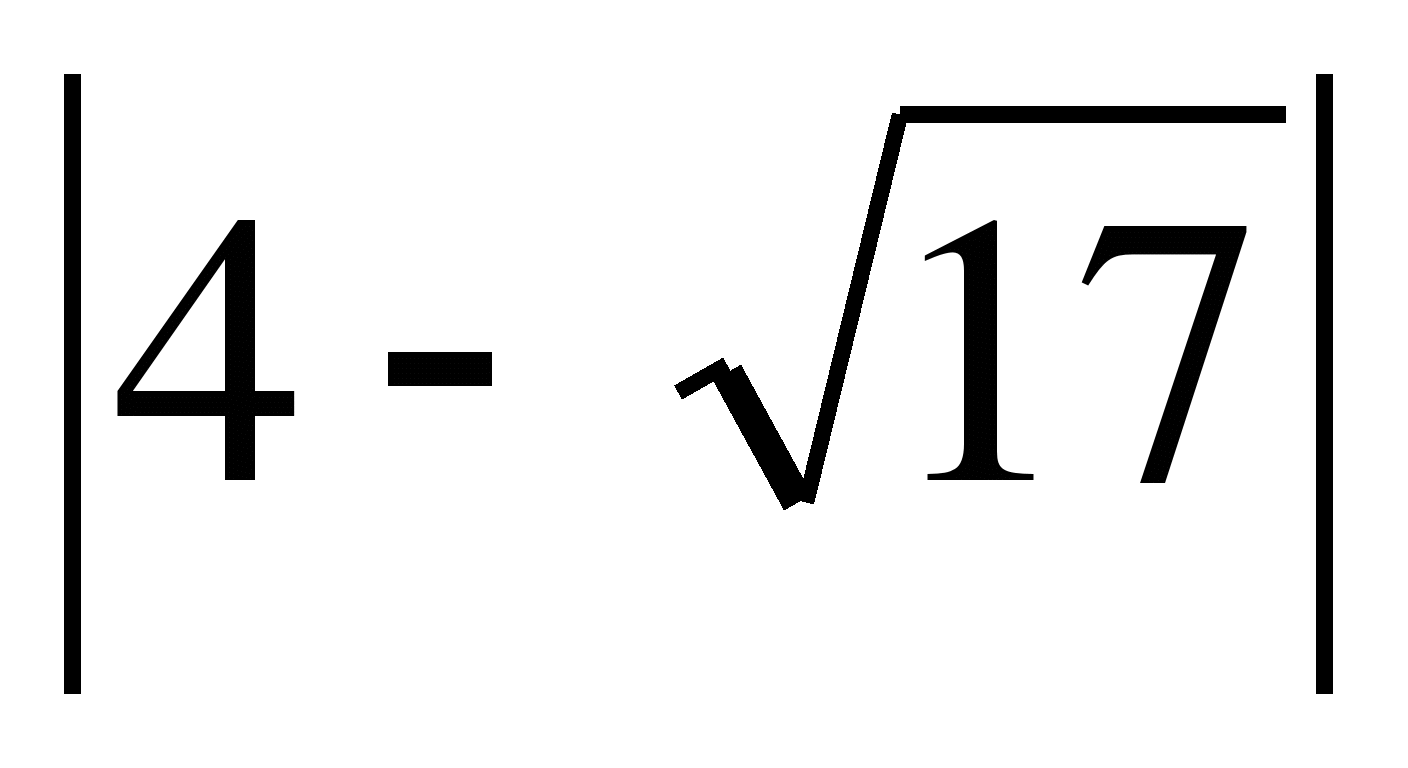 ,
, 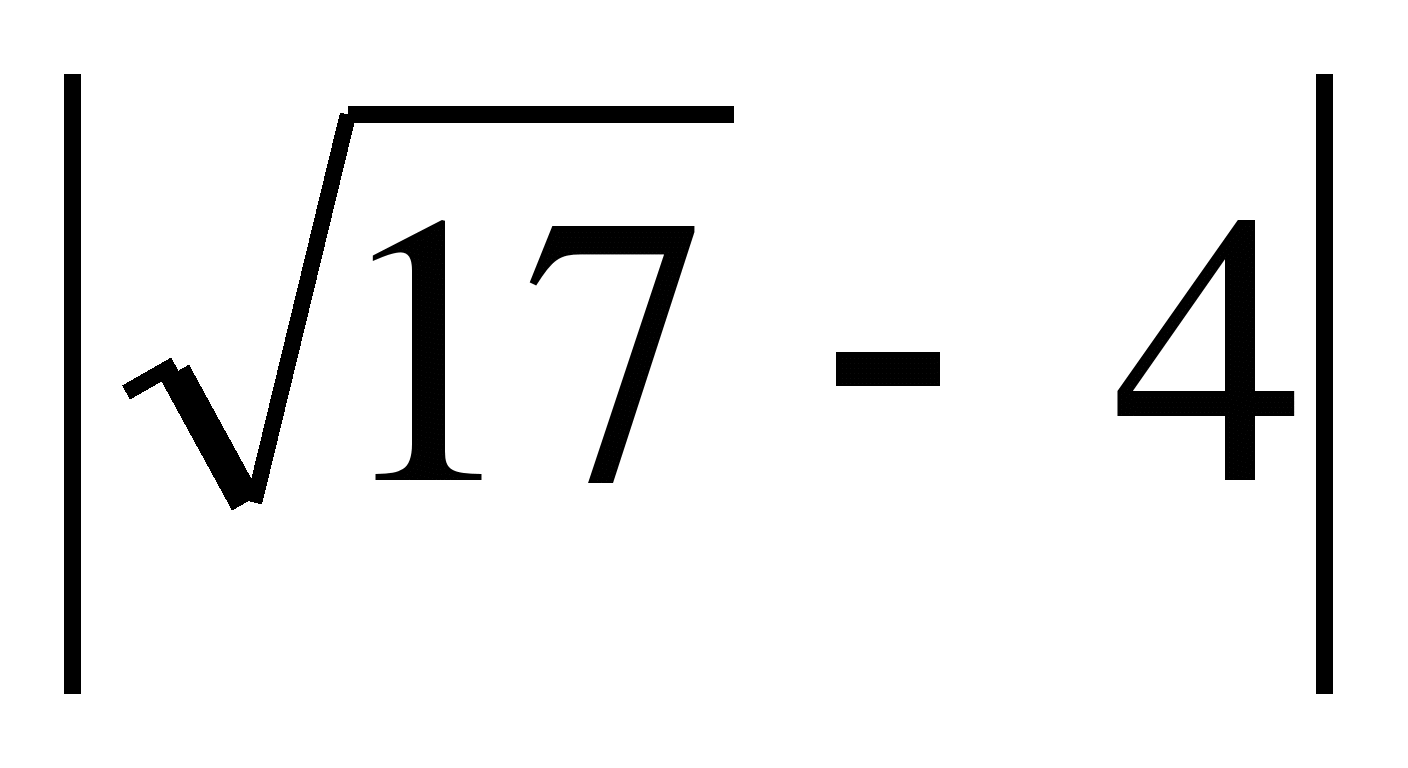 ,
,  .
.
При вычисления модуля проговариваем определение. Что можно сказать про значение модуля для любого из вычисленных выражений. (Значение модуля всегда неотрицательно)
Слайд 5
На основании определения модуля мы можем решать простейшие уравнения, содержащие знак модуля.
Определите, сколько корней имеет уравнение, и найдите эти корни.
А)  =11;
=11;
Б)  =0;
=0;
В)  = -3;
= -3;
Г)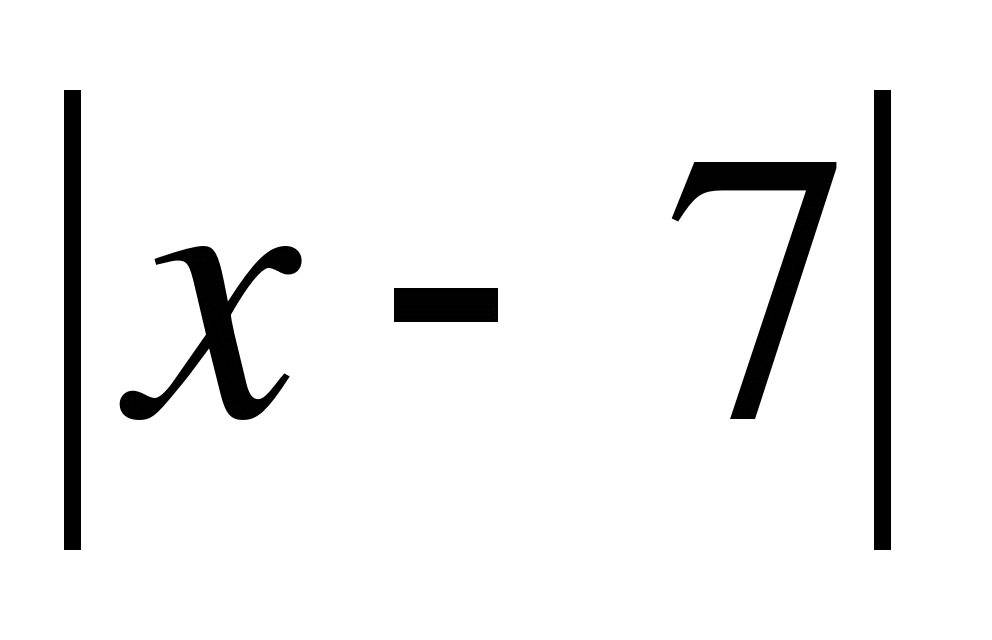 =5
=5
В каком случае 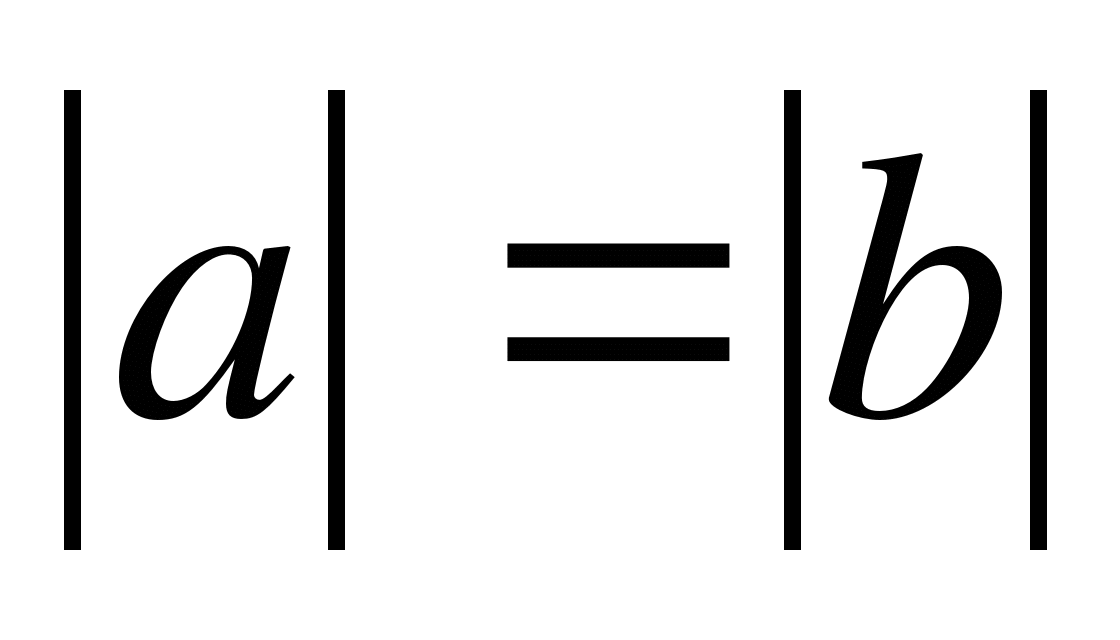
(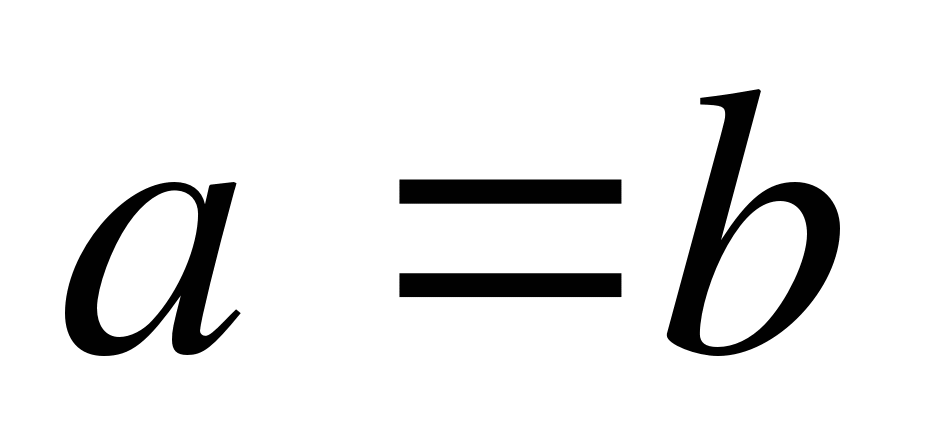 или
или 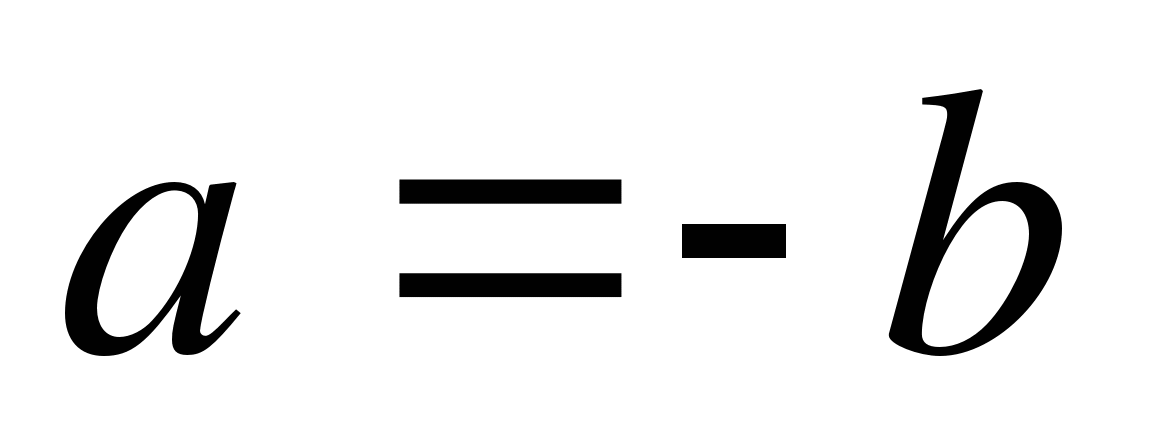 )
)
Слайд 6
Справедливо следующее замечание:
Если 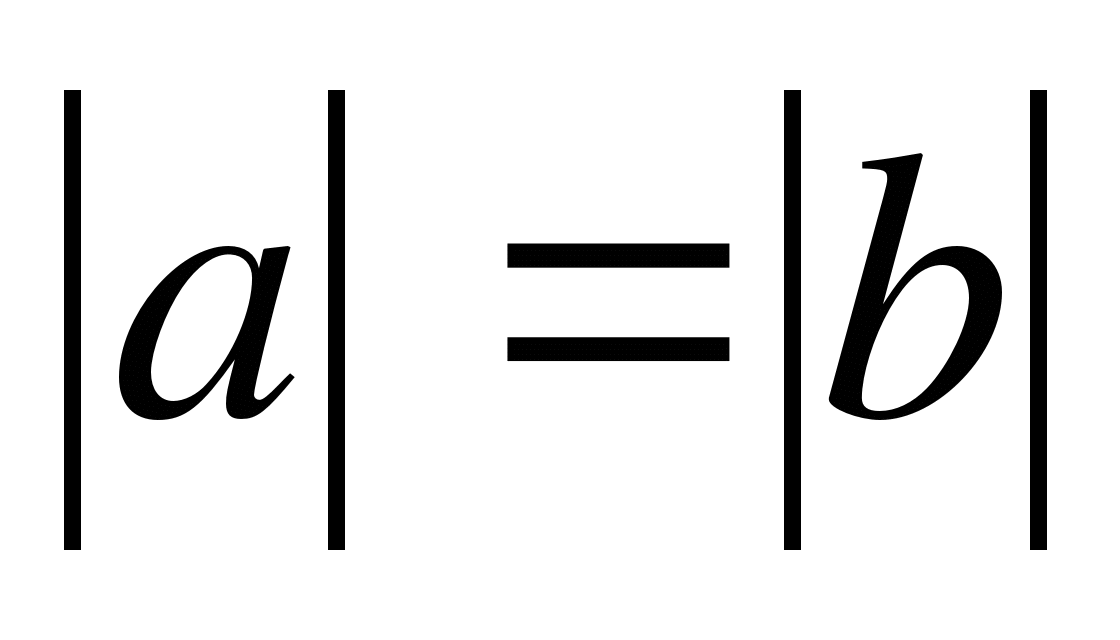 , то либо
, то либо 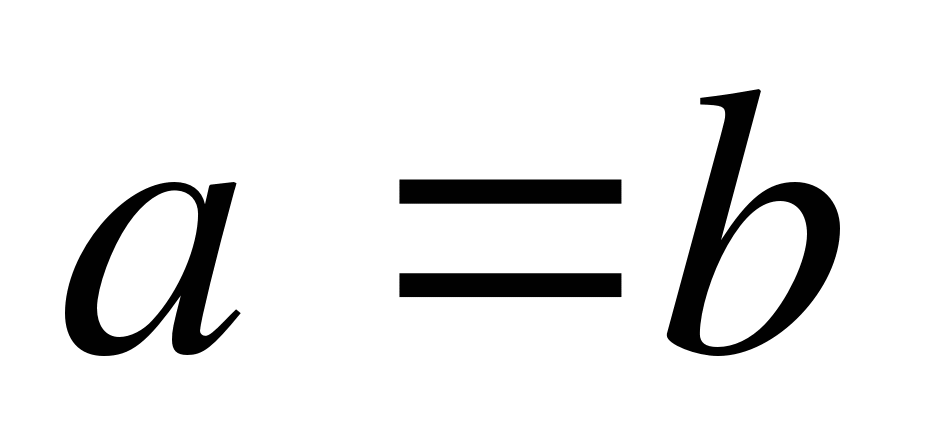 , либо
, либо 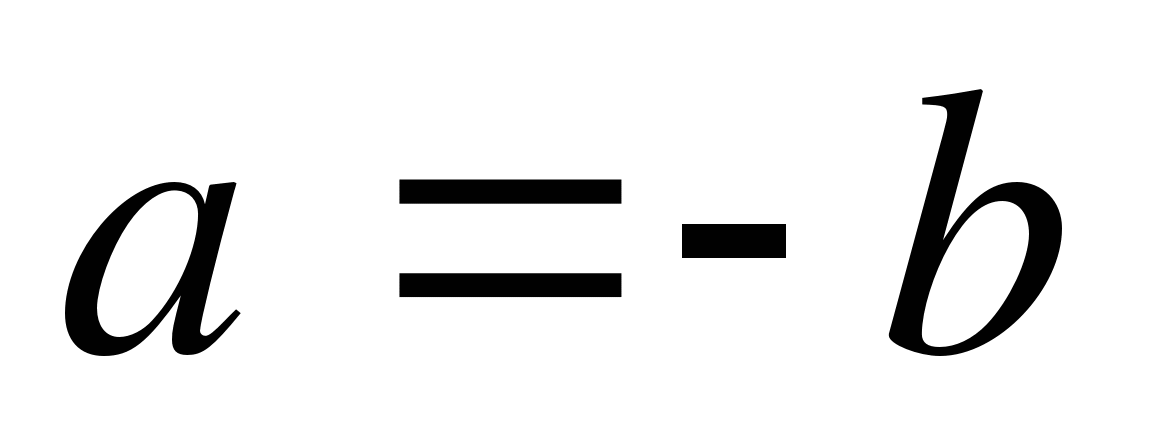 .
.
Слайд 7
Данное замечание используется для решения уравнений вида: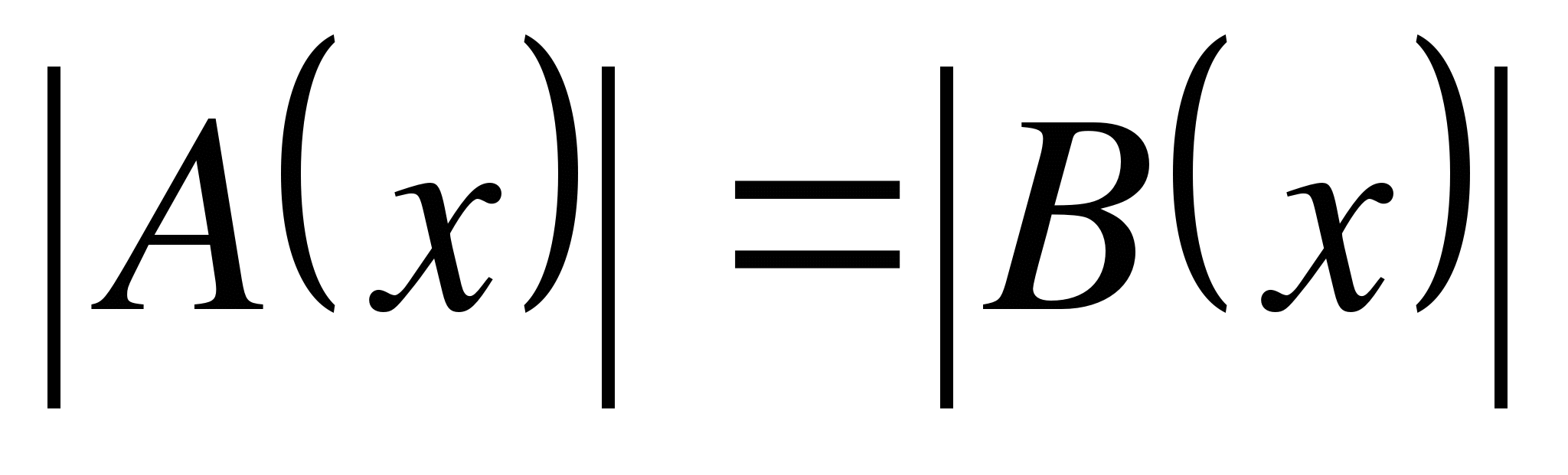 .
.
Решим уравнение 


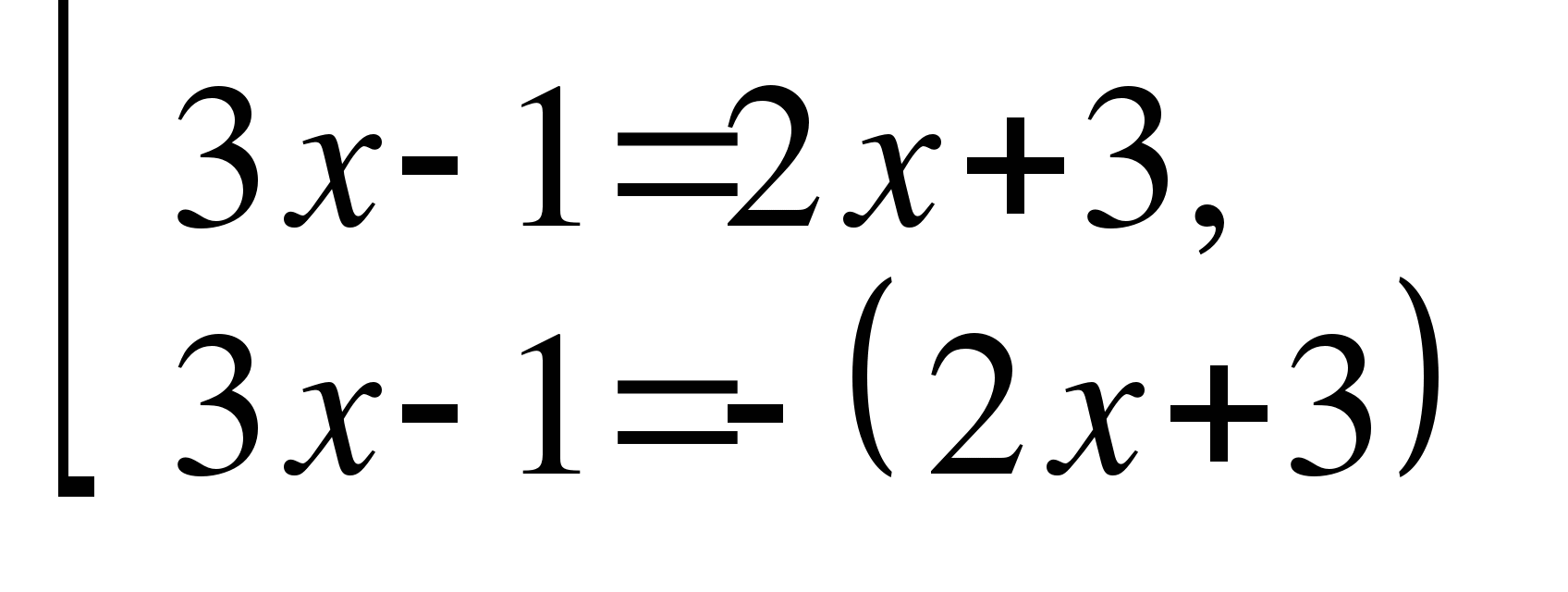
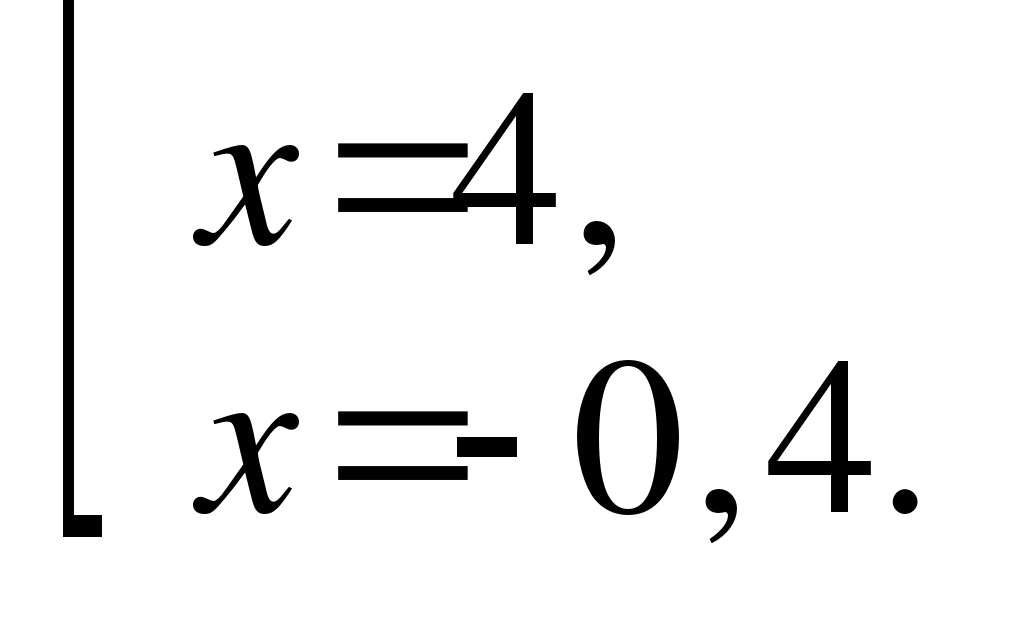
Рассмотрим уравнение 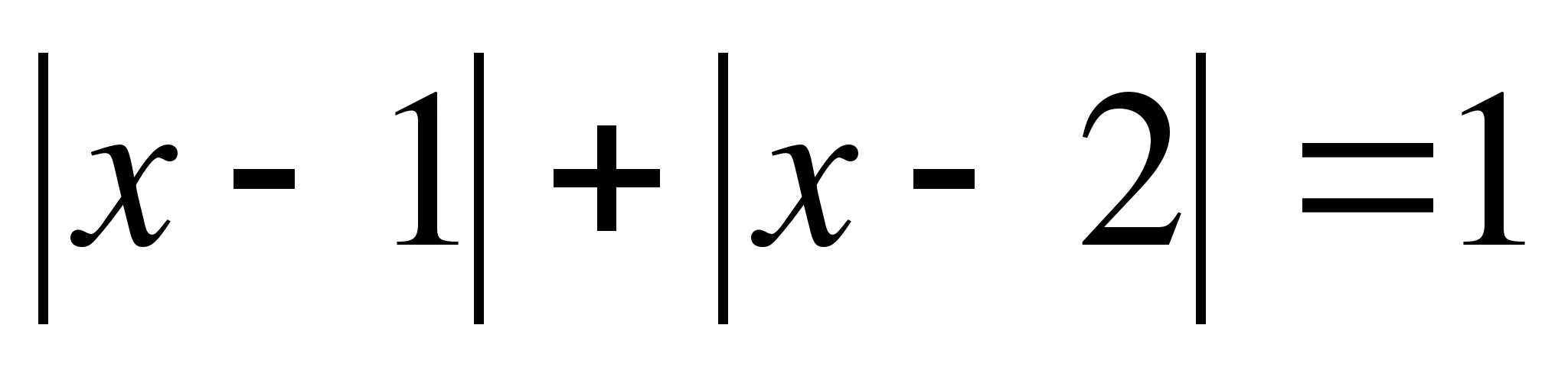
Чем отличается данное уравнение от уравнений, которые мы решали?
— в левой части стоит сумма модулей, а в правой число. Можем ли мы воспользоваться одним из ранее рассмотренных способов?
Слайд 8
Для решения уравнений такого вида мы будем использовать метод разбиения на промежутки, для этого:
Находим нули выражений, стоящих под знаком модуля
Отмечаем полученные значения на числовой оси
Данные точки разбивают числовую ось на промежутки внутри которых выражения сохраняют постоянный знак (промежутки знакопостоянства)
Определяем знаки выражений, стоящих под знаком модуля на каждом из промежутков знакопостоянства.
Используя, определение модуля раскрываем модуль на каждом из промежутков, решаем уравнение.
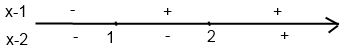 1)
1)
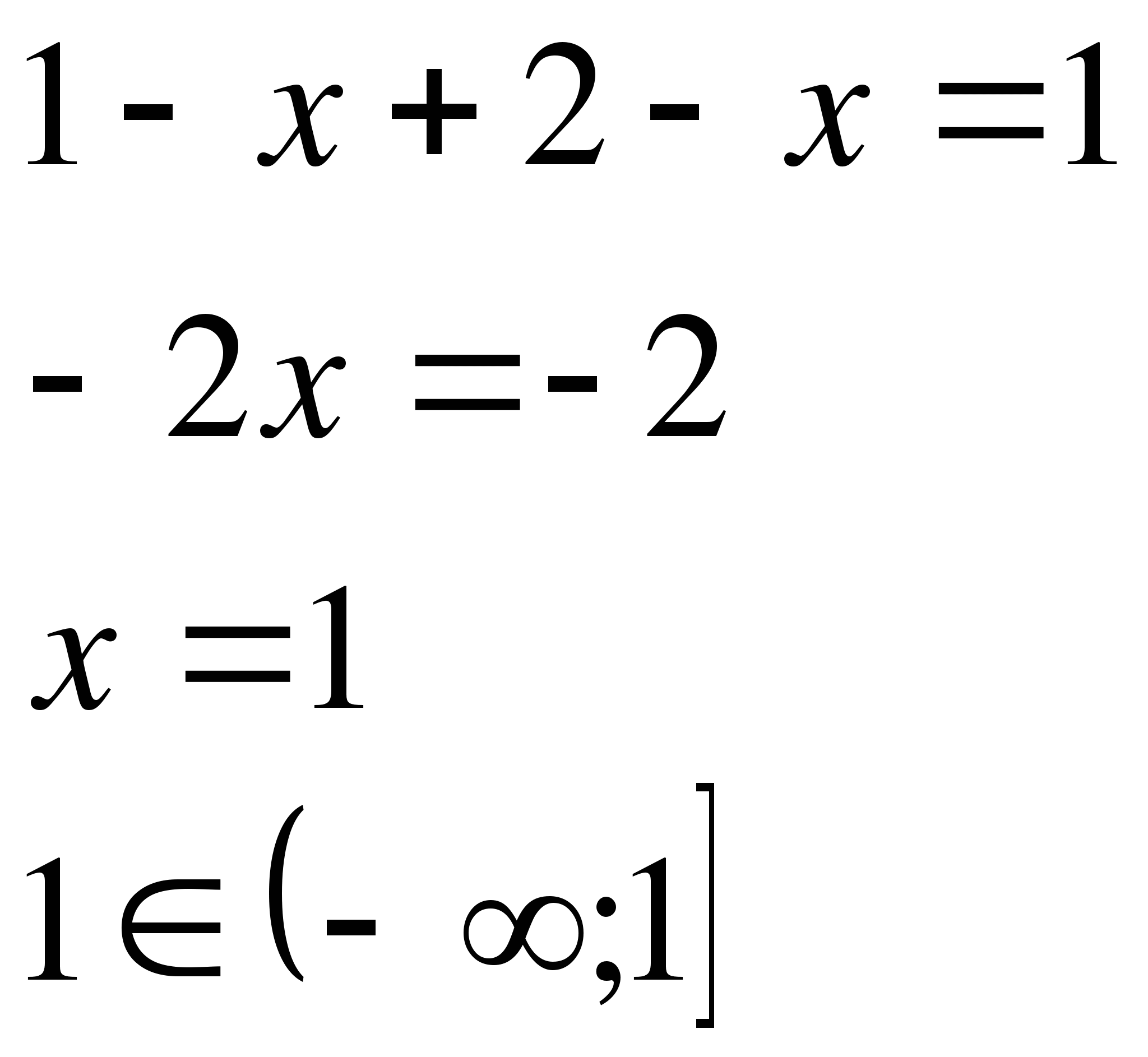
2) 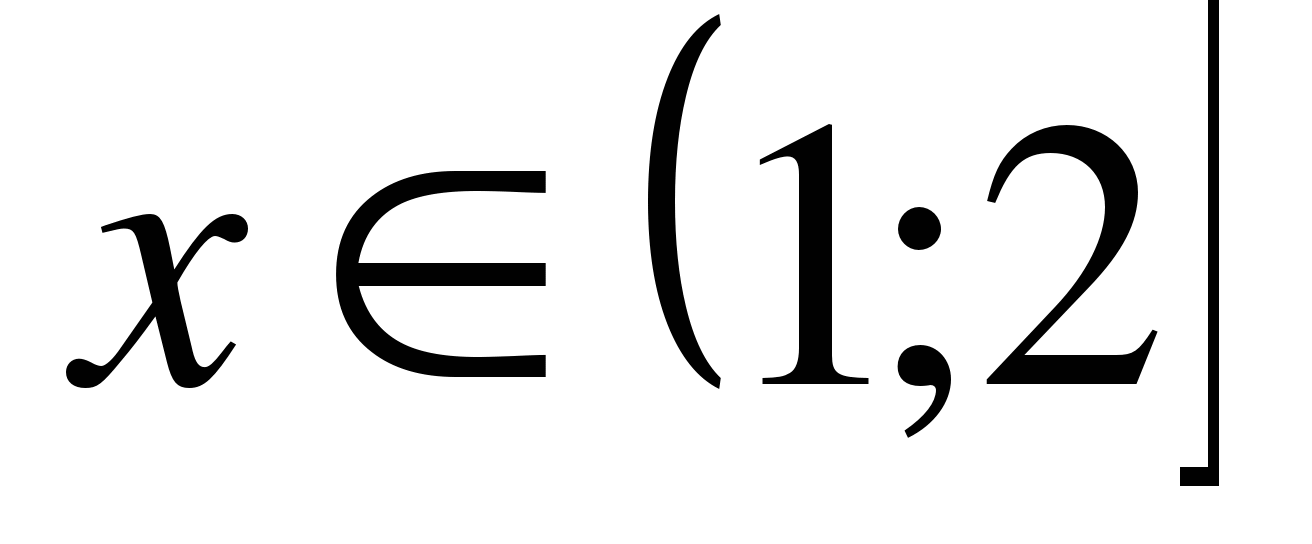
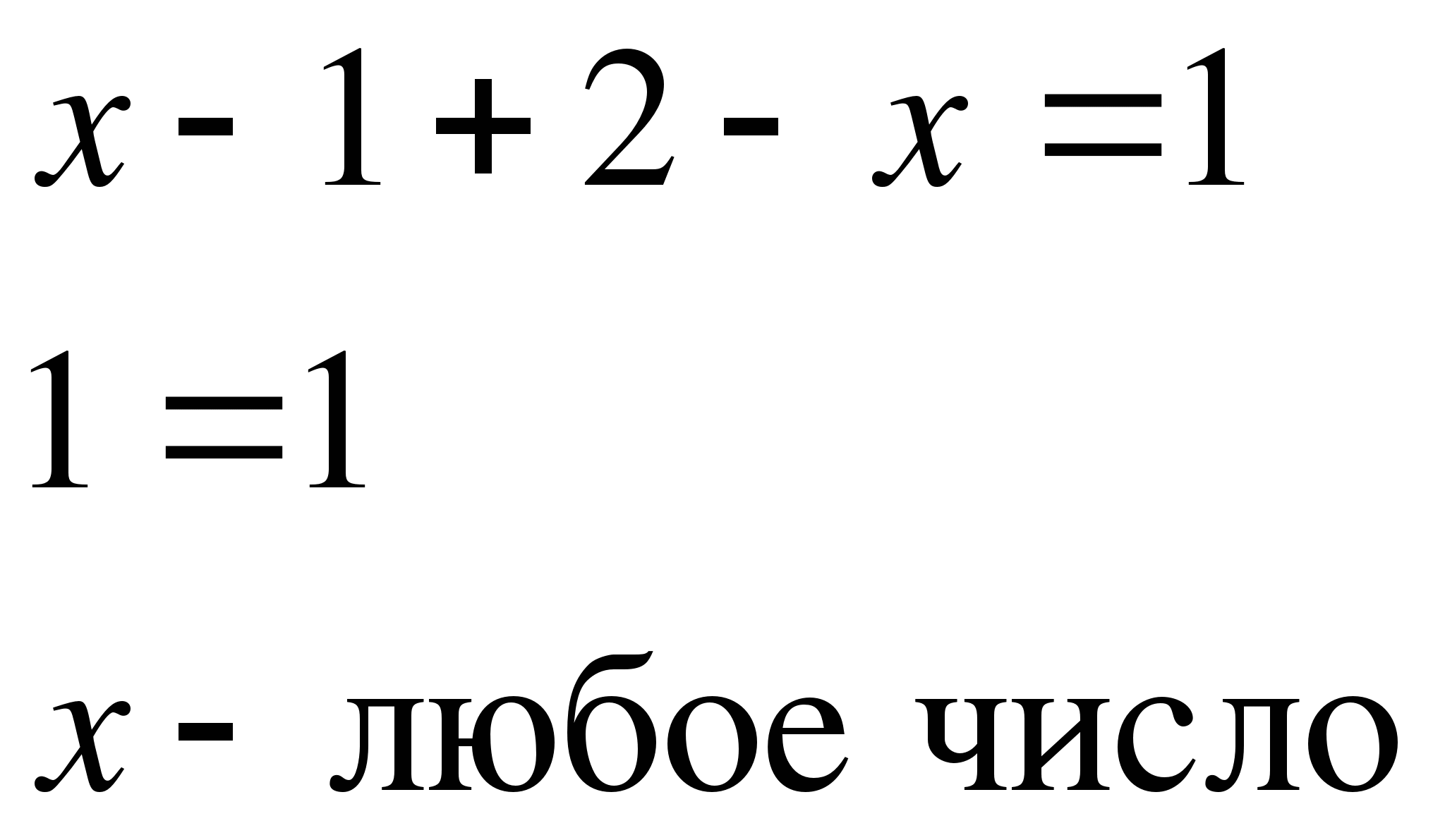
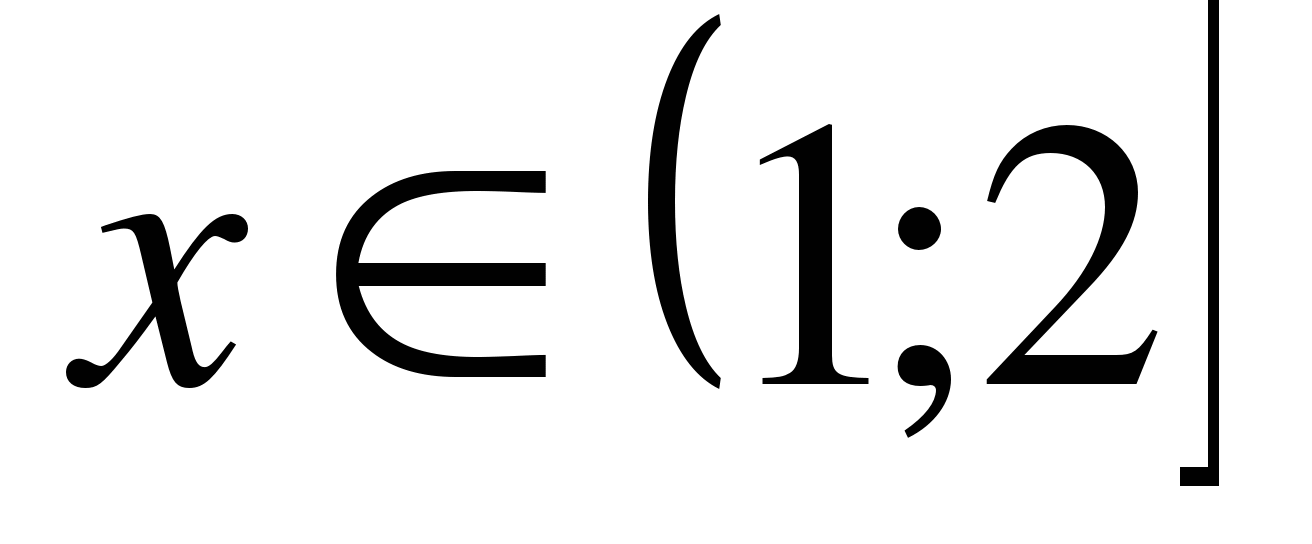
3)
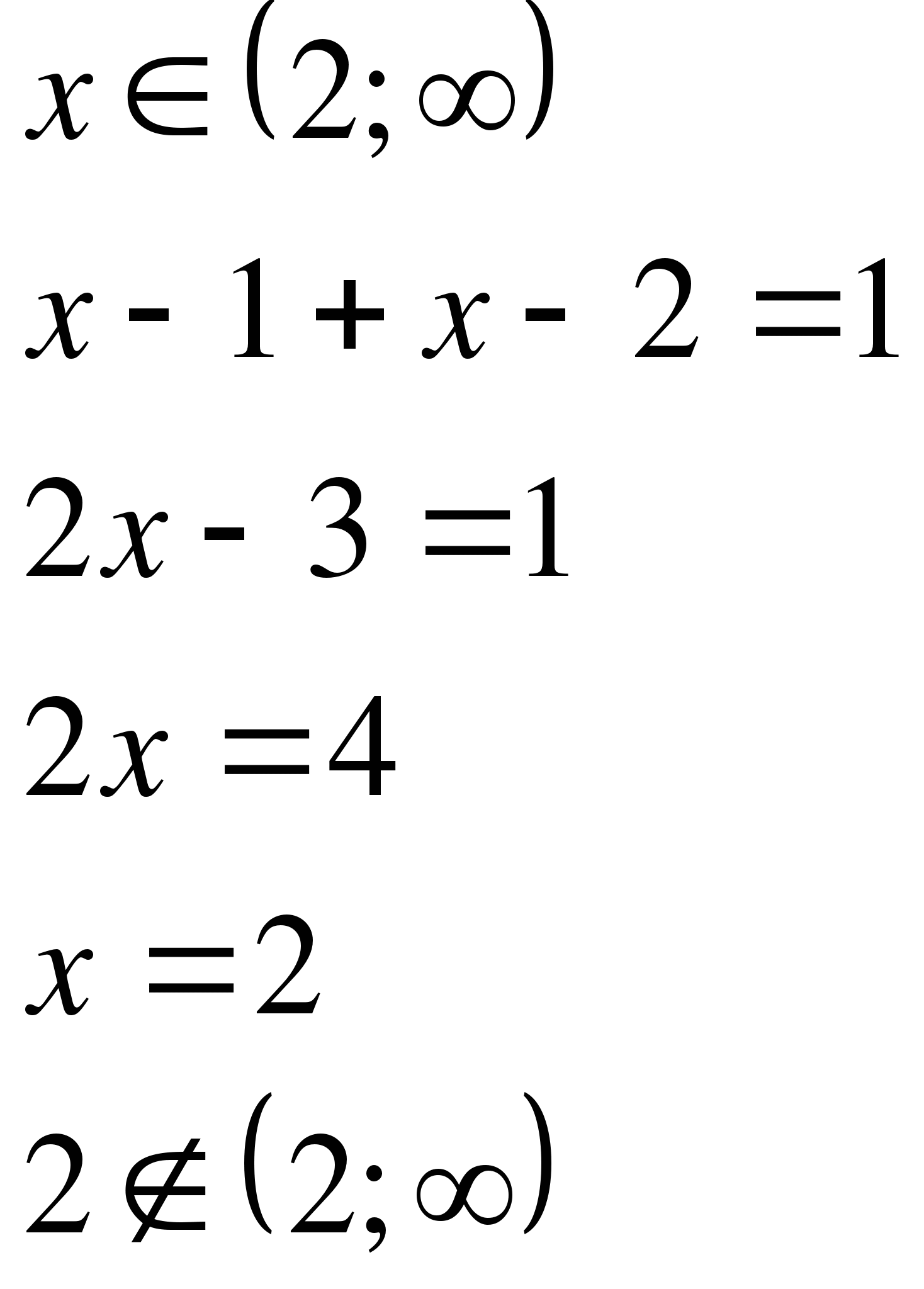
Ответ:
Упражнения на закрепление:
1) 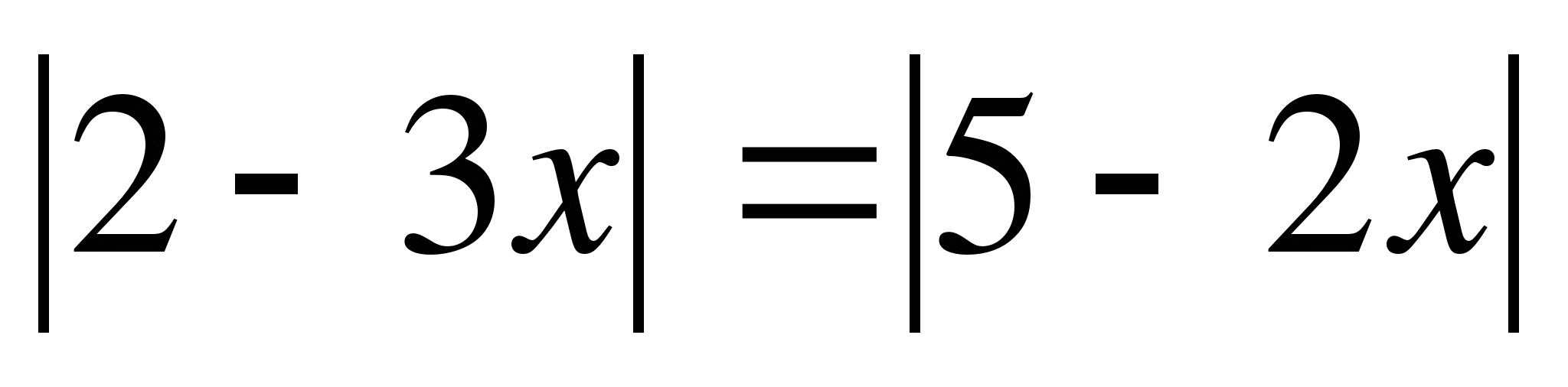 Ответ:
Ответ: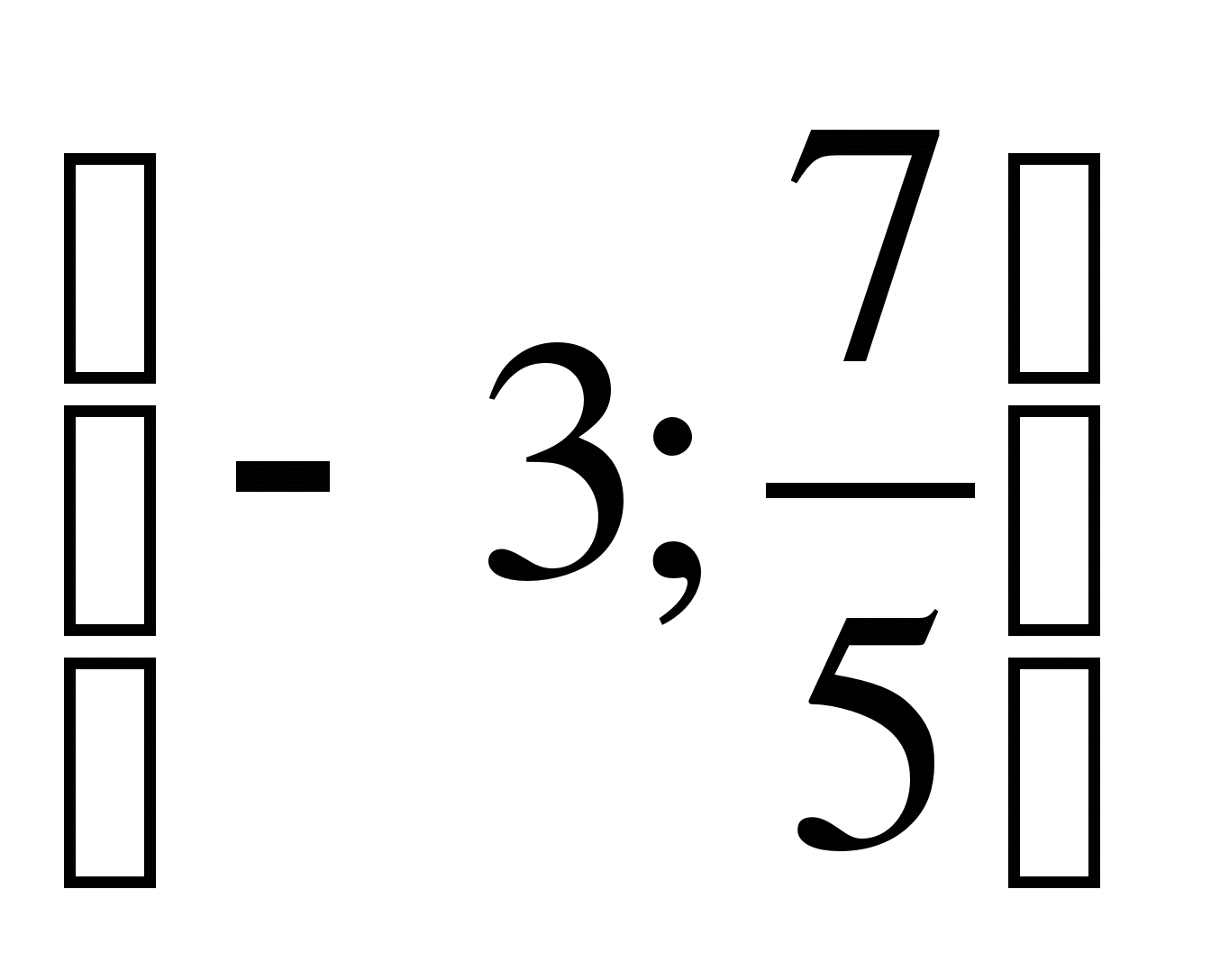
2) 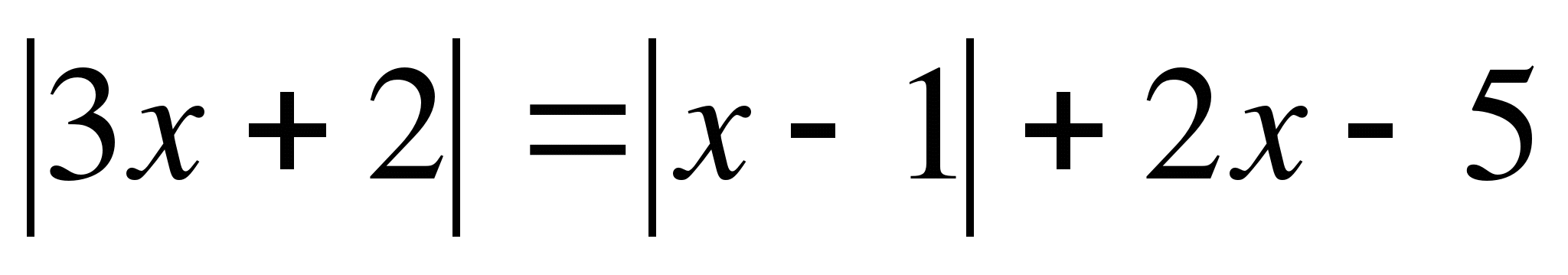 Ответ: нет корней.
Ответ: нет корней.
Итог урока:
Домашнее задание: Подберите уравнения, которые решаются каждым, из рассмотренных на уроке способом, и решите их.
Слайд 1

Слайд 2

Слайд 3
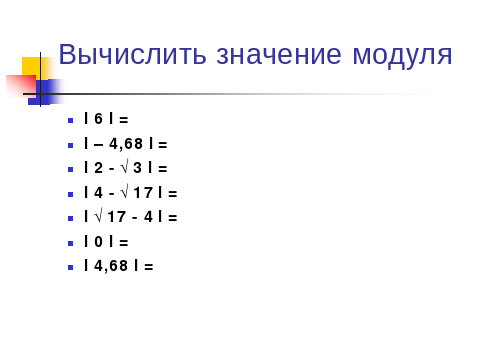
Слайд 3

Слайд 4

Слайд 5

Слайд 6

Слайд 7

Слайд 8

Онлайн урок уравнения с модулем и параметрами
Давай повторим определения, которые ты уже знаешь и которые мы будем использовать на нашем уроке.

Модулем или абсолютной величиной действительного числа a называется само это число, если a ≥ 0, и противоположное число -а, если a < 0.

Для модуля выполняются свойства, если а ⩾ 0.

Уравнение — это равенство, содержащее одну или несколько переменных, значение которых нужно найти.
Теперь установи соответствие между картинками и определениями, которые мы только что повторили.

= -x2 — 8= x2 — 8= x2 + 8= ±(x2 + 8)

= -x2 — 8= x2 + 8= ±(x2 + 8)= ±(x2 — 8)

Сегодня на уроке ты:
1. Повторишь стандартные способы решений уравнений с модулем.
2. Решишь уравнение с модулем и параметром графически.
3. Решишь 3 очень сложные задачи на уравнения и системы уравнений с модулями и параметрами.
Линейное уравнение, содержащее переменную под знаком модуля
Вопросы занятия:
· вспомнить основные понятия, связанные с уравнениями такого типа;
· применить знания в практических заданиях по данной теме.
Материал урока
Прежде чем мы приступим к решению уравнений с модулем, давайте вспомним, что такое модуль числа.
Определение.
Мы
говорили, что модулем числа а называется расстояние от начала
координат до точки  .
А обозначают его так:
.
А обозначают его так:  .
.
Например,

И в самом деле, расстояние в единичных отрезках от начала отсчёта до точки с координатой 4 равно 4. А расстояние от точки отсчёта до точки с координатой – 2 равно 2.
Поскольку модуль – это расстояние, то он не может принимать отрицательные значения.
Давайте вспомним свойства модуля действительного числа.
Первым мы запишем самое очевидное свойство: модуль числа не может быть отрицательным числом.

Модуль числа равен нулю тогда и только тогда, когда это число равно нулю.

Противоположные числа имеют равные модули.

Модуль произведения двух чисел равен произведению модулей этих чисел.

Модуль
частного от деления  на
на
 равен
частному от деления модуля числа
равен
частному от деления модуля числа  на
модуль числа
на
модуль числа  .
.

Следующее свойство модуля записывается в виде неравенства:

Это свойство говорит о том, что модуль суммы двух чисел не превосходит сумму модулей этих чисел.
Теперь перейдём к линейным уравнениям, содержащим переменную под знаком модуля.
Определение.
Итак, линейным уравнением, содержащим переменную под знаком модуля называется уравнение вида:

где
а – постоянная,  –
переменная.
–
переменная.
Давайте решим уравнение  в
общем виде.
в
общем виде.
Возможны три случая.

Задание.
Решить уравнения:
 ,
,
 ,
,
 .
.
Решение.

Задание.
Решить уравнения:
а)  ;
б)
;
б)  .
.
Решение.


Итоги урока
На этом уроке мы более подробно рассмотрели тему «лЛинейное уравнение, содержащее переменную под знаком модуля». Вспомнили основные понятия, связанные с уравнениями такого типа. А также рассмотрели некоторые задания на применение знаний по данной теме.