Линейные уравнения с параметрами и уравнения, приводимые к линейным

I введение

Тема “Решение и исследование уравнений с параметрами” присутствует в материалах Единого государственного экзамена. Не все выпускники справляются с задачей, которую в школе “не проходили”. Данная тема является одной из самых трудных в курсе алгебры. Задачи с параметрами рассматривают в школьном курсе пока крайне редко, бессистемно, поэтому при решении таких задач у учеников обычно возникают затруднения. Совершенно очевидно, что к “встрече” с такими задачами надо специально готовиться.

Данные задачи играют значительную роль в формировании логического мышления и математической культуры школьников, позволяют проверить первоначальные навыки исследовательской деятельности. Учащиеся, владеющие методами решения задач с параметрами, успешно справляются с другими задачами.

Известны различные типы уравнений и неравенств с параметрами: дробно-рациональные, иррациональные, тригонометрические, показательные, логарифмические, степенные.

Чаще всего они сводятся к следующим четырём основным видам:

1. линейные уравнения с параметром,
2. линейные неравенства с параметром,
3. квадратичные уравнения с параметром,
4. квадратичные неравенства с параметром.

Рассмотрим уравнение

Пусть, тогда уравнение примет вид

Решим его:

 

Пусть , тогда уравнение примет вид , решением которого является любое действительное значение .

Пусть , тогда уравнение примет вид . Решив его, получим, что . В этом случае уравнение не имеет решения.

Следовательно, сам факт существования решения зависит от значения параметра .

Определение. Исследовать и решить уравнение с параметром это значит :

— найти все системы значений параметров, при которых данное уравнение имеет решение;

— найти все решения для каждой найденной системы значений параметров, т.е. для неизвестного и параметра должны быть указаны свои области допустимых значений.

II  Простейшие линейные уравнения с параметром

1.

Ответ:

при корней нет,

при

2.

Ответ:

при корней нет,

при

3.

Ответ:

при корней нет,

при .

4.

Ответ:

при корней нет,

при .

5.

Ответ:

при

при

6.

Ответ:

при

при

7.

Ответ:

при

при

8.

Ответ:

при

при

9.

Ответ:

если , то корней нет

если ,

если

10.

1)

2.

3.

Ответ:

при , корней нет

если ,

при

Таким образом, при решении линейных уравнений с параметром сначала его нужно привести к виду, удобному для исследования (стандартный канонический вид линейного уравнения с параметром), выполнив ряд преобразований, потом следует определить контрольные значения параметра, т.е. те значения, при которых коэффициент при обращается в ноль. Эти значения разбивают множество значений параметра на несколько множеств, которые необходимо исследовать.

III Линейные уравнения с параметром, имеющие стандартный канонический вид

– стандартный канонический вид линейного уравнения с параметром

Примеры:

1)

Ответ:

если

если

2)

Ответ:

при

при

при

3)

Ответ:

при

при

при

IV. Уравнения, приводимые к линейным уравнениям с параметром

Схема решения уравнений, приводимых к линейным :

1. Указать и исключить все значения параметра и переменной, при которых уравнение теряет смысл
2. Умножить обе части уравнения на общий знаменатель, не равный нулю
3. Привести уравнение-следствие к виду и решить его
4. Исключить значения параметра, когда найденный корень принимает значения, при которых уравнение теряет смысл
5. Записать ответ

1.Примеры решений уравнений, содержащих параметр в знаменателе:

1)

Умножим уравнение на :

Ответ:

при

при

при

2)

Умножим уравнение на :

Ответ:

при

при

при

2.

Примеры решений уравнений, содержащих и параметр и переменную в знаменателе

Умножим уравнение на :

Исключим те a, при которых :

Ответ:

при

при

при

Линейные уравнения с параметром

К задачам с параметром можно отнести, например, поиск решения линейных и квадратных уравнений в общем виде, исследование уравнения на количество имеющихся корней в зависимости от значения параметра.

Не приводя подробных определений, в качестве примеров рассмотрим следующие уравнения:

у = kx, где x, y – переменные, k – параметр;

у = kx + b, где x, y – переменные, k и b – параметр;

аx² + bх + с = 0, где x – переменные, а, b и с – параметр.

Решить уравнение (неравенство, систему) с параметром это значит, как правило, решить бесконечное множество уравнений (неравенств, систем).

Задачи с параметром можно условно разделить на два типа:

а) в условии сказано: решить уравнение (неравенство, систему) – это значит, для всех значений параметра найти все решения. Если хотя бы один случай остался неисследованным, признать такое решение удовлетворительным нельзя.

б) требуется указать возможные значения параметра, при которых уравнение (неравенство, система) обладает определенными свойствами. Например, имеет одно решение, не имеет решений, имеет решения, принадлежащие промежутку и т. д. В таких заданиях необходимо четко указать, при каком значении параметра требуемое условие выполняется.

Параметр, являясь неизвестным фиксированным числом, имеет как бы особую двойственность. В первую очередь, необходимо учитывать, что предполагаемая известность говорит о том, что параметр необходимо воспринимать как число. Во вторую очередь, свобода обращения с параметром ограничивается его неизвестностью. Так, например, операции деления на выражение, в котором присутствует параметр или извлечения корня четной степени из подобного выражения требуют предварительных исследований.

Поэтому необходима аккуратность в обращении с параметром.

Например, чтобы сравнить два числа -6а и 3а, необходимо рассмотреть три случая:

1) -6a будет больше 3a, если а отрицательное число;

2) -6а = 3а в случае, когда а = 0;

3) -6а будет меньше, чем 3а, если а – число положительное 0.

Решение и будет являться ответом.

Линейные уравнения с параметром

Пусть дано уравнение kx = b. Это уравнение – краткая запись бесконечного множества уравнений с одной переменной.

При решении таких уравнений могут быть случаи:

1. Пусть k – любое действительное число не равное нулю и b – любое число изR, тогда x = b/k.

2. Пусть k = 0 и b ≠ 0, исходное уравнение примет вид  0 · x = b. Очевидно, что у такого уравнения решений нет.

3. Пусть k и b числа, равные нулю, тогда имеем равенство 0 · x = 0. Его решение  – любое действительное число.

Алгоритм решения такого типа уравнений:

1. Определить «контрольные» значения параметра.

2. Решить исходное уравнение относительно х при тех значениях параметра, которые были определены в первом пункте.

3. Решить исходное уравнение относительно х при значениях параметра, отличающихся от выбранных в первом пункте.

4. Записать ответ можно в следующем виде:

Ответ:

1) при … (значения параметра), уравнение имеет корни …;

2) при … (значения параметра), в уравнении корней нет.

Пример 1.

Решить уравнение с параметром |6 – x| = a.

Решение.

Легко видеть, что здесь a ≥ 0.

По правилу модуля 6 – x = ±a, выразим х:

x = 6 ± a.

Ответ: х = 6 ± a, где a ≥ 0.

Пример 2.

Решить уравнение a(х – 1) + 2(х – 1) = 0 относительно переменной х.

Решение.

Раскроем скобки: aх – а + 2х – 2 = 0

Запишем уравнение в стандартном виде: х(а + 2) = а + 2.

В случае, если выражение а + 2 не нуль , т. е. если а ≠ -2, имеем решение х = (а + 2) / (а + 2), т.е. х = 1.

В случае, если а + 2 равно нулю, т.е. а = -2, то имеем верное равенство 0 · x = 0, поэтому х – любое действительное число.

Ответ: х = 1 при а ≠ -2 и х € R при а = -2.

Пример 3.

Решить уравнение x/a + 1 = а + х относительно переменной х.

Решение.

Если а = 0, то преобразуем уравнение к виду а + х = а² + ах или (а – 1)х = -а(а – 1). Последнее уравнение при а = 1 имеет вид 0 · x = 0, следовательно, х – любое число.

Если а ≠ 1, то последнее уравнение примет вид х = -а.

Данное решение можно проиллюстрировать на координатной прямой (рис. 1)

Ответ: нет решений при а = 0; х – любое число при а = 1; х = -а при а ≠ 0 и а ≠ 1.

Графический метод

Рассмотрим еще один способ решения уравнений с параметром – графический. Этот метод применяется достаточно часто.

Пример 4.

Сколько корней в зависимости от параметра a имеет уравнение ||x| – 2| = a?

Решение.

Для решения графическим методом строим графики функций y = ||x| – 2| и y = a (рис. 2).

На чертеже наглядно видны возможные случаи расположения прямой y = a и количество корней в каждом из них.

Ответ: корней у уравнения не будет, если а < 0; два корня будет в случае, если a > 2 и а = 0; три корня уравнение будет иметь в случае а = 2; четыре корня – при 0 < a < 2.

Пример 5.

При каком а уравнение 2|x| + |x – 1| = a имеет единственный корень?

Решение.

Изобразим графики функций  y = 2|x| + |x – 1| и y = a. Для  y = 2|x| + |x – 1|, раскрыв модули методом промежутков, получим:

      {-3x + 1, при x < 0,

y = {x + 1, при  0 ≤ x ≤ 1,

      {3x – 1, при x > 1.

На рисунке 3 хорошо видно, что единственный корень уравнение будет иметь только при а = 1.

Ответ: а = 1.

Пример 6.

Определить число решений уравнения |x + 1| + |x + 2| = a в зависимости от параметра а?

Решение.

График функции  y = |x + 1| + |x + 2| будет представлять собой ломаную. Ее вершины будут располагаться в точках (-2; 1) и (-1; 1) (рисунок 4).

Ответ: если параметр a будет меньше единицы, то корней у уравнения не будет; если а = 1, то решение уравнения является бесконечное множество чисел из отрезка [-2; -1]; если значения параметра а будут больше одного, то уравнение будет иметь два корня.

 Остались вопросы? Не знаете, как решать уравнения с параметром?
Чтобы получить помощь репетитора – зарегистрируйтесь.
Первый урок – бесплатно!

Зарегистрироваться

© blog. tutoronline.ru, при полном или частичном копировании материала ссылка на первоисточник обязательна.

Презентация «Линейные уравнения с параметром»

Линейные уравнения с параметрами (7класс)

Линейное уравнение

Уравнение вида ах = в , где а и в – числа, х — переменная, называется линейным.

ах = в

а ≠ 0

а = 0

в = 0

в ≠ 0

в ≠ 0

в = 0

0 ∙ х = в

х = 0

0 ∙ х = 0

уравнение не имеет корней

х – любое число

уравнение имеет один корень

уравнение имеет один корень

:

• 1. Определить «контрольные» значения параметра.
• 2. Решить исходное уравнение относительно х при тех значениях параметра, которые были определены в первом пункте.
• 3. Решить исходное уравнение относительно х при значениях параметра, отличающихся от выбранных в первом пункте.
• 4. Записать ответ можно в следующем виде:
• Ответ:
• 1) при … (значения параметра), уравнение имеет корни …;
• 2) при … (значения параметра), в уравнении корней нет.

Линейное уравнение

Примеры:

4) 23 x = 10 — a

23 x = 10 – a

23 и 10 – числа ,

х – неизвестное число ,

a – выполняет роль известного числа.

a – называют параметром ,

уравнение – уравнением с параметром .

2

Примеры решения легкого уравнения

1)Решить уравнение 5x = a .

Ответ: x = , при любом a .

= a

Ответ: x = 2a , при любом a .

Вывод: если параметр является свободным членом в уравнении,

то уравнение всегда имеет один корень.

2) Решить уравнение 0•х = а.

Ответ: при а 0, корней нет,

при а = 0, х – любое из множества R .

Решить уравнение ( а -2)х= а -2

Решение: Найдем контрольные значения параметра для коэффициента при х ,

т.е. если а -2=0, то а =2.

• Если а =2, то а -2=0, и уравнение ( а -2)х= а -2 примет вид 0х=0, то х – любое число.
• Если а ≠2, то деление на а возможно х==1

Ответ: любое число, при а =2;

1, при а ≠2

Пример 1.

Решить уравнение с параметром |6 – x| = a.

Решение.

Легко видеть, что здесь a ≥ 0.

По правилу модуля 6 – x = ±a, выразим х:

x = 6 ± a.

Ответ: х = 6 ± a, где a ≥ 0.

Пример 2.

Решить уравнение a(х – 1) + 2(х – 1) = 0 относительно переменной х.

Решение.

• Раскроем скобки: aх – а + 2х – 2 = 0
• Запишем уравнение в стандартном виде: х(а + 2) = а + 2.
• В случае, если выражение а + 2 не нуль , т. е. если а ≠ -2, имеем решение х = (а + 2) / (а + 2), т.е. х = 1.
• В случае, если а + 2 равно нулю, т.е. а = -2, то имеем верное равенство 0 · x = 0, поэтому х – любое действительное число.

Ответ: х = 1 при а ≠ -2 и х € R при а = -2.

Пример 3. Решить уравнение x/a + 1 = а + х относительно переменной х. Решение. Если а = 0, то преобразуем уравнение к виду а + х = а 2  + ах или (а – 1)х = -а(а – 1). Последнее уравнение при а = 1 имеет вид 0 · x = 0, следовательно, х – любое число. Если а ≠ 1, то последнее уравнение примет вид х = -а.

Линейное уравнение с параметром

Уравнение ах = 2а+8 с параметром а .

Напишите уравнение, которое получится при

1) а =10 , 2) а = -3 , 3) а = 0.

I

Дано уравнение ах = 5х+4.

Найти множество корней уравнения в случае, если

1) а =5 , 2) а ≠ 5.

II

Линейное уравнение с параметром

При каких значениях параметра а уравнение ах +7 = 1+2а

• имеет единственный корень;
• имеет бесконечное множество корней;
• не имеет корней?

III

Проверь себя :

Если а≠0, то ах =2а – 6

— единственный корень .

Если а=0, то 0 ∙ х +7=1+0

0 ∙ х = -6

— корней нет.

Линейное уравнение с параметром

Решите уравнение (b-3)x=10(2b+x) с параметром b .

IV

Решение:

(b-3) x = 20b +10x

(b-13) x =20b

Случаи:

b-13≠0

если b-13=0 , то b=13 и 0∙x=260

уравнение корней не имеет

нет решения

если b-13≠0 , то b≠13 и

единственный корень

Ответ: 1) если b=13 , то корней нет,

2) если b≠13 , то уравнение имеет единственный корень

.

Вывод:

Решить уравнение с параметром b – это значит установить соответствие, с помощью которого для каждого значения параметра b указывается множество корней данного уравнения.

Алгоритм решения линейного уравнения

с параметром .

1.   Определить «контрольные» значения параметра при х в уравнении вида ах = b .

2.  Рассмотреть случаи   решения уравнения относительно х , при контрольных значениях параметра и отличных от «контрольных».

3.     Записать ответ в виде:

1) уравнение корней не имеет, при значениях параметра … .

2) уравнение имеет корни … ; при значениях параметра …

  3) уравнение имеет корни … ; при значениях параметра … .

Решите уравнение с параметром а

• (1-а) х=а-1
• (1+а) х=2а+1+а 2
• ах – 3 = х +3а

Д/З Решить уравнения

• aх = 7a-3
• 5b (b-1) x = 2
• 2ax – a =16
• n(x-1) = n+1
• * a (a-1) x = a 2 +a – 2

Рабочая программа элективного курса Решение уравнений и неравенства с параметрами ФГОС 10-11 классы

1	Понятие уравнения с параметрами.	1 ч.			Презентация «Уравнения с параметрами»	Коммуникативные: представлять конкретное содержание и сообщать его в письменной и устной форме; уметь (или развивать способность) с помощью вопросов добывать недостающую информацию. Регулятивные: ставить учебную задачу на основе соотнесения того, что уже известно и усвоено, и того, что еще неизвестно; самостоятельно формулировать познавательную цель и строить действия в соответствии с ней. Познавательные: проводить анализ способов решения уравнений с параметром
	Линейные уравнения, их системы и неравенства с параметром.	22 ч
2	Линейные уравнения с параметрами. Зависимость количества корней от значения коэффициентов aи b.	1 ч.			Презентация «Линейные уравнения с параметром»	Коммуникативные: интересоваться чужим мнением и высказывать свое; устанавливать и сравнивать разные точки зрения, прежде чем принимать решение и делать выбор; с достаточной полнотой и точностью выражать свои мысли в соответствии с задачами и условиями коммуникации. Регулятивные: проектировать траектории развития через включение в новые виды деятельности и формы сотрудничества. Познавательные: осуществлять синтез как составление целого из частей
3	Алгоритм решения линейных уравнений с параметром.	1 ч.			Схема 1. «Решение линейных уравнений»	Коммуникативные: разрешать конфликты — выявлять, идентифицировать проблемы, искать и оценивать альтернативные способы разрешения конфликта, принимать решение и реализовывать его. Регулятивные: формировать целевые установки учебной деятельности; выстраивать алгоритмы действий. Познавательные: создавать и преобразовывать модели и схемы для решения задач
4	Применение алгоритма решения линейных уравнений с параметром.	1 ч.			Схема 1. «Решение линейных уравнений»	Коммуникативные: переводить конфликтную ситуацию в логический план и разрешать ее как задачу через анализ ее условий; демонстрировать способность к эмпатии, стремление устанавливать доверительные отношения взаимопонимания. Регулятивные: определять последовательность промежуточных целей с учетом конечного результата; предвосхищать временные характеристики достижения результата (отвечать на вопрос «когда будет результат?») Познавательные: восстанавливать предметную ситуацию, описанную в задаче, путем переформулирования, упрощенного пересказа текста, с выделением только существенной информации
5	Решение линейных уравнений с параметрами.	1 ч.			Схема 1. «Решение линейных уравнений»	Коммуникативные: осуществлять совместное целеполагание и планирование общих способов работы на основе прогнозирования. Регулятивные: вносить коррективы и дополнения в способ своих действий в случае расхождения эталона, реального действия и его результата. Познавательные: выделять и формулировать познавательную цель; выражать смысл ситуации различными средствами (рисунки, символы, схемы, знаки)
6	Линейные уравнения с дополнительными условиями к корням уравнения.	1 ч.				Коммуникативные: регулировать соб­ственную деятельность, осуществлять контроль и коррекцию хода и результатов деятельности Регулятивные: оценивать достигнутый результат. Познавательные: выбирать наиболее эффективные способы решения задачи выбирать основания и критерии для сравнения, сериации, классификации объектов
7	Решение линейных уравнений с параметрами при наличии дополнительных условий с корнями уравнения.	1 ч.				Коммуникативные: осуществлять совместое целеполагание и планирование общих способов работы на основе прогнозирования. Регулятивные: формулировать познавательную цель и строить действия в соответствии с ней; использовать различные ресурсы для достижения цели. Познавательные: развивать навыки познавательной рефлексии как осознания совершаемых действий и мыслительных процессов
8	Уравнения с параметрами, приводимые к линейным.	1 ч.				Коммуникативные: слушать и слышать друг друга; уметь представлять конкретное содержание и сообщать его в письменной и устной форме. Регулятивные: принимать познавательную цель, сохранять ее при выполнении учебных действий, регулировать весь процесс их выполнения и четко выполнять требования познавательной задачи. Познавательные: выводить следствия из имеющихся в условии задачи данных
9	Решение уравнений с параметрами, приводимых к линейным.	1 ч.				Коммуникативные: организовывать и пла­нировать учебное сотрудничество с учителем и сверстниками. Регулятивные: формировать постановку учеб­ной задачи на основе соотнесения того, что уже известно и усвоено учащимися, и того, что еще неизвестно. Познавательные: уметь устанавливать аналогии
10	Классификация систем линейных уравнений по количеству решений.	1 ч.			Презентация «Системы линейных уравнений с параметрами»	Коммуникативные: уметь точно и грамотно выражать свои мысли. Регулятивные: формировать целевые установки учебной деятельности, выстраивать алго­ритм действий. Познавательные: использовать знаково-символические средства; моделирование
11	Понятие системы линейных уравнений с параметрами.	1 ч.			Схема 2. «Зависимость количества решений системы линейных уравнений от коэффициентов системы»	Коммуникативные: организовывать и пла­нировать учебное сотрудничество с учителем и сверстниками. Регулятивные: формировать целевые уста­новки учебной деятельности, выстраивать последовательность необходимых операций (алгоритм действий). Познавательные: уметь осуществлять анализ объектов с выделением существенных и несу­щественных признаков
12	Алгоритм решения систем линейных уравнений с параметрами.	1 ч.			Схема 2. «Зависимость количества решений системы линейных уравнений от коэффициентов системы»	Коммуникативные: определять цели и функ­ции участников, способы взаимодействия; планировать общие способы работы. Регулятивные: обнаруживать и формулиро­вать учебную проблему, составлять план выполнения работы. Познавательные: выбирать наиболее эффек­тивные способы решения задач
13	Применение алгоритма решения систем линейных уравнений (с двумя переменными) с параметрами.	1 ч.			Схема 2. «Зависимость количества решений системы линейных уравнений от коэффициентов системы»	Коммуникативные: воспринимать текст с уче­том поставленной учебной задачи, находить в тексте информацию, необходимую для ре­шения. Регулятивные: формировать постановку учеб­ной задачи на основе соотнесения того, что уже известно и усвоено учащимися, и того, что еще неизвестно. Познавательные: уметь осуществлять сравне­ние и классификацию по заданным критериям
14	Решение систем линейных уравнений (с двумя переменными) с параметрами.	1 ч.			Схема 2. «Зависимость количества решений системы линейных уравнений от коэффициентов системы»	Коммуникативные: формировать коммуникативные действия, направленные на структурирование информации по данной теме. Регулятивные: формировать целевые установки учебной деятельности; выстраивать последовательность необходимых операций. Познавательные: произвольно и осознанно овладевать общим приемом решения задач
15	Решение линейных уравнений и систем линейных уравнений, содержащих параметры.	1 ч.				Коммуникативные: осуществлять совместную деятельность в группах; задавать вопросы с целью получения необходимой для решения проблемы информации; осуществлять деятельность с учетом конкретных учебно-познавательных задач. Регулятивные: принимать познавательную цель, сохранять ее при выполнении учебных действий, регулировать весь процесс их выполнения и четко выполнять требования познавательной задачи. Познавательные: выделять существенную информацию из текстов разных видов
16	Тест «Линейные уравнения и системы линейных уравнений с параметрами»	1 ч.				Коммуникативные: развивать умение обме­ниваться знаниями между одноклассниками для принятия эффективных совместных ре­шений. Регулятивные: осуществлять контроль дея­тельности («что сделано») и пошаговый контроль («как выполнена каждая операция, входящая в состав учебного действия»). Познавательные: ориентироваться на разно­образие способов решения задач
17	Линейные неравенства с параметрами.	1 ч.			Презентация  «Линейные неравенства с параметрами»	Коммуникативные: определять цели и функ­ции участников, способы взаимодействия; планировать общие способы работы; обме­ниваться знаниями между членами группы для принятия эффективных совместных ре­шений. Регулятивные: самостоятельно формулировать познавательную цель и строить действия в соответствии с ней. Познавательные: устанавливать аналогии
18	Решение линейных неравенств с параметрами.	1 ч.			Схема 3. «Решение неравенства »	Коммуникативные: организовывать и пла­нировать учебное сотрудничество с учителем и сверстниками. Регулятивные: осознавать самого себя как движущую силу своего научения, к преодоле­нию препятствий. Познавательные: произвольно и осознанно владеть общим приемом решения задач
19	Решение линейных неравенств с параметрами с помощью графической интерпретации.	1 ч.				Коммуникативные: описывать содержание совершаемых действий. Регулятивные: осознавать качество и уровень усвоения; оценивать достигнутый результат. Познавательные: выбирать наиболее эффективные способы решения задачи в зависимости от конкретных условий
20	Системы линейных неравенств с одной переменной, содержащих параметры.	1 ч.				Коммуникативные: развивать умение использовать языковые средства, адекватные обсуждаемой проблеме; уметь (или развивать способность) с помощью вопросов добывать недостающую информацию. Регулятивные: определять новый уровень отношения к самому себе как субъекту деятельности. Познавательные: применять методы  информационного поиска, в том числе с помощью компьютерных средств
21	Алгоритм решения систем линейных неравенств с одной переменной, содержащих параметры.	1 ч.				Коммуникативные: стремиться устанавливать доверительные отношения взаимопонимания; использовать адекватные языковые средства для отображения своих чувств, мыслей и побуждений. Регулятивные: самостоятельно формулировать познавательную цель и строить план действия в соответствии с ней. Познавательные: использовать приобретенные знания и умения в практической деятельности и повседневной жизни
22	Решение систем неравенств с одной переменной, содержащих параметры.	1 ч.				Коммуникативные: осуществлять совместную деятельность в рабочих группах с учетом конкретных учебно- познавательных задач, задавать уточняющие вопросы; формулировать собственные мысли, высказывать и обосновывать свою точку зрения. Регулятивные: адекватно оценивать свои достижения, осознавать возникающие трудности, искать их причины и пути преодоления. Познавательные: выбирать наиболее эффективные способы решения задачи в зависимости от конкретных условий
23	Решение линейных неравенств с параметрами и систем неравенств с одной переменной, содержащих параметры.	1 ч.			Схема 3. «Решение неравенства »	Коммуникативные: с достаточной полнотой и точностью выражать свои мысли в соответствии с задачами и условиями коммуникации. Регулятивные: осознавать качество и уровень усвоения. Познавательные: выбирать наиболее эффективные способы решения задачи в зависимости от конкретных условий
	Квадратные уравнения и неравенства	11 ч
24	Понятие квадратного уравнения с параметром.	1 ч.			Презентация «Квадратное уравнение с параметром»	Коммуникативные: определять цели и функ­ции участников, способы взаимодействия; планировать общие способы работы; обмениваться знаниями для принятия эффективных совместных ре­шений. Регулятивные: составлять план последова­тельности действий; формировать способ­ность к волевому усилию в преодолении препятствий. Познавательные: уметь осуществлять срав­нение и классификацию по заданным крите­риям
25	Алгоритм решения квадратных уравнений с параметром.	1 ч.				Коммуникативные: формировать коммуника­тивные действия, направленные на структу­рирование информации по данной теме. Регулятивные: осознавать учащимся уровень и качество усвоения результата.  Познавательные: произвольно и осознанно владеть общим приемом решения задач
26	Решение квадратных уравнений с параметрами.	1 ч.				Коммуникативные: управлять поведением партнера – убеждать его, контролировать, корректировать и оценивать его действия. Регулятивные: осознавать самого себя как движущую силу своего научения, к преодолению препятствий. Познавательные: произвольно и осознанно овладевать общим приемом решения задач
27	Решение квадратных уравнений с параметром первого типа.	1 ч.				Коммуникативные: искать и оценивать альтернативные способы разрешения конфликта, принимать решение и реализовывать его. Регулятивные: проектировать траектории развития через включение в новые виды деятельности и формы сотрудничества. Познавательные: осуществлять сравнение и классификацию по заданным критериям
28	Применение теоремы Виета при решении квадратных уравнений с параметром.	1 ч.			Презентация «Теорема Виета при решении квадратных уравнений с параметром»	Коммуникативные: развивать умение обме­ниваться знаниями между одноклассниками для принятия эффективных совместных ре­шений. Регулятивные: корректировать деятельность: вносить изменения в процесс с учетом воз­никших трудностей и ошибок, намечать спо­собы их устранения. Познавательные: ориентироваться на разно­образие способов решения задач
29	Расположение корней квадратичной функции относительно заданной точки.	1 ч.				Коммуникативные: управлять своим пове­дением (контроль, самокоррекция, оценка своего действия). Регулятивные: формировать способность к мобилизации сил и энергии; способность к волевому усилию в преодолении препятствий. Познавательные: произвольно и осознанно владеть общим приемом решения задач
30	Использование теоремы Виета при решении квадратных уравнений с параметрами.	1 ч.				Коммуникативные: осуществлять совместную деятельность в группах; задавать вопросы с целью получения необходимой для решения проблемы информации; осуществлять деятельность с учетом конкретных учебно-познавательных задач. Регулятивные: принимать познавательную цель, сохранять ее при выполнении учебных действий, регулировать весь процесс их выполнения и четко выполнять требования познавательной задачи. Познавательные: выделять существенную информацию из текстов разных видов
31	Уравнения с параметрами, приводимые к квадратным.	1 ч.				Коммуникативные: развивать умение обме­ниваться знаниями между одноклассниками для принятия эффективных совместных ре­шений. Регулятивные: осуществлять контроль дея­тельности («что сделано») и пошаговый контроль («как выполнена каждая операция, входящая в состав учебного действия»). Познавательные: ориентироваться на разно­образие способов решения задач
32	Решение уравнений с параметрами, приводимых к квадратным.	1 ч.				Коммуникативные: определять цели и функ­ции участников, способы взаимодействия; планировать общие способы работы; обме­ниваться знаниями между членами группы для принятия эффективных совместных ре­шений. Регулятивные: самостоятельно формулировать познавательную цель и строить действия в соответствии с ней. Познавательные: устанавливать аналогии
33	Решение квадратных уравнений с параметрами.	1 ч.				Коммуникативные: организовывать и пла­нировать учебное сотрудничество с учителем и сверстниками. Регулятивные: осознавать самого себя как движущую силу своего научения, к преодоле­нию препятствий. Познавательные: произвольно и осознанно владеть общим приемом решения задач
34	Решение задач по теме «Квадратные уравнения с параметрами»	1 ч.				Коммуникативные: описывать содержание совершаемых действий. Регулятивные: осознавать качество и уровень усвоения; оценивать достигнутый результат. Познавательные: выбирать наиболее эффективные способы решения задачи в зависимости от конкретных условий

Задачи с параметром. Линейные уравнения и их системы | Шевкин.Ru

25.04.2017

Шевкин А.В. Задачи с параметром: Линейные уравнения и их системы. /Серия «Математика. Проверь себя». М.: ООО «Русское слово – учебная книга», 2003. – 32 с.

Дополнение. В газете «Математика» 9-10/2004 опубликована часть книги: весь теоретический материал и задания для самоконтроля. По этим материалам можно ознакомиться с содержанием книги. Задания самостоятельных работ аналогичны заданиям для самоконтроля.

Книга содержит 4 варианта самостоятельных работ по каждой из двух тем, вынесенных в название книжки. До выполнения самостоятельной работы учащиеся могут повторить основные приемы решения линейных уравнений с параметром и их систем,  выполнить работу для самоконтроля, с помощью которой можно проверить свою готовность к самостоятельной работе, исправив допущенные ошибки с помощью специальных указаний.

Предисловие для учителя

Дидактические материалы серии «Проверь себя» содержат задания для программированного самоконтроля и самостоятельные работы. В данной брошюре собраны материалы по темам, изучаемым в 9 классе:

• Линейные уравнения с параметром,
• Системы линейных уравнений с параметром.

Задачи с параметром являются наиболее сложными задачами вступительных экзаменов в вузы, поэтому познакомиться с некоторыми идеями их решения, освоить способы решения наиболее простых задач с параметром желательно как можно раньше.

Данная книжка адресована учащимся 8-9 классов, планирующим в будущем сдавать экзамен по математике при поступлении в вуз. Работая с нею, учащиеся могут на несложных примерах освоить идею решения задач с параметром, научиться решать несложные задачи и проверить свои умения с помощью имеющихся в книжке самостоятельных работ.

В книжке использованы несложные задачи конкурсных экзаменов в вузы, дающие представление о минимальных требованиях к умению решать задачи с параметром.

Идея задач с параметром разъяснена на примере линейных уравнений и их систем. Объяснение материала ведется подробно — от простого к сложному. При этом уделяется достаточно внимания предупреждению наиболее распространенных ошибок учащихся.

Таблица верных ответов приведена на с. 15-18, она изымается при проведении самостоятельных работ на отметку.

При работе с любой темой из данной брошюры учащиеся сначала должны повторить уже изученный материал, прочитав основные правила по этой теме и разобрав образцы их применения. Затем они должны выполнить задания для самоконтроля, к каждому из которых даны ответы. После ответов буквой указаны перечисленные ниже команды, с помощью которых происходит управление учебной деятельностью учащихся. В зависимости от того, какой ответ получен, дается указание «исправьте ошибку при вычислении дискриминанта» и т. п. или «верно, переходите к следующему заданию».

После того как задания для самоконтроля выполнены всеми учащимися класса, проводится самостоятельная работа, которую учащиеся выполняют на отдельных листах. При этом все решения записываются полностью.

Чтобы сразу после проведения работы учащиеся могли узнать свою предварительную отметку, они вписывают номера ответов, которые считают правильными, в специальную таблицу в правом верхнем углу своего листа и запоминают номера своих ответов. Например, так:

Петров И.

9 а класс  вариант 3

4    4

5    5

3    3

1    1

После сбора работ учитель сообщает номера верных ответов для каждого варианта и правило, по которому учащиеся могут вычислить свою отметку: за верно выполненные 4 задания ставится «5», каждый неверный ответ снижает отметку на 1 балл. Следует предупредить учащихся, что по этому правилу они узнают лишь предварительную отметку. Окончательная отметка выставляется после проверки работы учителем.

Двадцатилетний опыт применения такого способа проверки знаний и умений школьников в школе № 679 г. Москвы показывает, что в большинстве случаев предварительная отметка остается неизменной. В редких случаях она понижается, когда, например, учащийся указывает правильный ответ, не следующий из его решения. Еще реже итоговая отметка оказывается выше предварительной — если ученик получает правильный ответ, но неправильно указывает его номер.

Следует отметить, что учащимся нравится такой вид контроля, так как он предсказуем — объем самостоятельной работы и уровень ее сложности заранее известны — и есть возможность к ней подготовиться. 

Если учитель ведет рабочий журнал, то в нем сначала фиксируется факт выполнения учеником задания для самоконтроля, а после проверки самостоятельной работы отметка выставляется в колонку, соответствующую выполненному варианту работы. Отметка из рабочего журнала учителя переносится в классный журнал, что отмечается «галочкой» около перенесенной отметки в рабочем журнале. В случае необходимости учитель может дать ученику другой вариант работы для исправления отметки по теме.

 

Ниже приведены страницы 5-8 из книги, посвященные линейным уравнениям с параметром, Задания для самоконтроля. Четыре варианта заданий для самостоятельной работы аналогичны заданиям для самоконтроля. Аналогично построена работа и по второй теме.

Линейные уравнения с параметрами (7 класс)

1. Линейные уравнения с параметрами (7класс)

2. Линейное уравнение

Уравнение вида ах = в, где а и в – числа, хпеременная, называется линейным.
ах = в
а=0
в=0
в≠0
0∙х=0
0∙х=в
х – любое
число
уравнение
не имеет
корней
а≠0
в=0
в≠0
х=0
уравнение
уравнение
имеет один имеет один
корень
корень
Матчина Надежда Егоровна, школа №258, СПБ.
Линейное уравнение
Примеры:
23 x = 10 – n
1)
2)
3)
4) 23 x = 10 — n
23 и 10 – числа,
х – неизвестное
число,
n – выполняет роль
известного числа.
n – называют параметром,
уравнение – уравнение с параметром.
Матчина Надежда Егоровна, школа №258, СПБ.
Линейное уравнение с параметром
I
II
Уравнение ах = 2а+8 с параметром а.
Напишите уравнение, которое получится
при
1) а =10, 2) а = -3, 3) а = 0.
Дано уравнение ах = 5х+4.
Найти множество корней уравнения в
случае, если
1) а =5, 2) а ≠ 5.
Матчина Надежда Егоровна, школа №258, СПБ.
Линейное уравнение с параметром
III
При каких значениях параметра а
уравнение ах +7 = 1+2а
a) имеет единственный корень;
b) имеет бесконечное множество корней;
c) не имеет корней?
Проверь себя:
Если а≠0, то ах =2а – 6
— единственный корень.
Если а=0, то 0∙х +7=1+0
0∙х = -6
— корней нет.
Матчина Надежда Егоровна, школа №258, СПБ.
Линейное уравнение с параметром
IV
Решите уравнение (b-3)x=10(2b+x) с
параметром b.
Решение:
Случаи:
(b-3) x = 20b +10x
(b-13) x =20b
b-13≠0
если b-13≠0,
то b≠13 и
если b-13=0, то
b=13 и 0∙x=260
уравнение корней
не имеет
единственный
корень
Ответ: 1) если b=13, то корней нет,
2) если b≠13, то уравнение имеет единственный корень
Матчина Надежда Егоровна, школа №258, СПБ.
нет решения
.
Линейное уравнение с параметром
Вывод:
Решить уравнение с параметром b –
это значит установить соответствие, с
помощью которого для каждого
значения параметра b указывается
множество корней данного уравнения.
Матчина Надежда Егоровна, школа №258, СПБ.
Линейное уравнение с параметром
Решите уравнение с параметром а
1) (1-а) х=а-1
2) (1+а) х=2а+1+а2
3) ах – 3 = х +3а
Матчина Надежда Егоровна, школа №258, СПБ.
Линейное уравнение с параметром
Д/З Решить уравнения
1) aх = 7a-3
2) 5b (b-1) x = 2
3) 2ax – a =16
4) n(x-1) = n+1
5)
*
a (a-1) x = a2+a – 2
Матчина Надежда Егоровна, школа №258, СПБ.

Теория параметрических уравнений, задачи

Уравнение, которое кроме неизвестной величины содержит также другую дополнительную величину, которая может принимать различные значения из некоторой области, называется параметрическим. Эта дополнительная величина в уравнении называется параметр . На самом деле с каждым параметрическим уравнением может быть написано множество уравнений. Мы рассмотрим модуль параметрического уравнения и решение простых параметрических уравнений.

---

Задача 1 Решите уравнения в отношении к $x$
A) $x + a = 7$
B) $2x + 8a = 4$
C) $x + a = 2a – x$
D) $ax = 5$
E) $a – x = x + b$
F) $ax = 3a$

Решение:

A) $x + a = 7 \Leftrightarrow x = 7 – a$, то есть решение к данному уравнению найдено. 2}$ является решением уравнения.

---

Задача $4$ Для каких значений $x$ следующие выражения имеют равные значения :
A) $5x + a$ и $3ax + 4$
B) $2x — 2$ и $4x + 5a$

Решение:

Чтобы получить одинаковые значения мы должны найти решения уравнений
$5x + a = 3ax + 4$ и $2x – 2 = 4x + 5a$

A) $5x + a = 3ax + 4 \Leftrightarrow$
$5x — 3ax = 4 – a \Leftrightarrow$
$(5 — 3a)x = 4 – a$
Если $5 — 3a \neq 0$, т.e. $a \neq \frac{5}{3}$, решения есть $x = \frac{4-a}{5-3a}$
Если $5 — 3a = 0$, т.e. $a = \frac{5}{3}$, уравнение принимает вид $0\cdot x = 4 – \frac{5}{3} \Leftrightarrow$
$0\cdot x = \frac{7}{3}$, что не имеет решения

B) $2x — 2 = 4x + 5a \Leftrightarrow$
$-2 — 5a = 4x — 2x \Leftrightarrow$
$2x = — 2 — 5a \Leftrightarrow$
$x = -\frac{2+5a}{2}$

---

Задача 5 Решите параметрическое уравнение:
A) $|ax + 2| = 4$
B) $|2x + 1| = 3a$
C) $|ax + 2a| = 3$

Решение:

A) $|ax + 2| = 4 \Leftrightarrow ax + 2 = 4$ или $ax + 2 = -4 \Leftrightarrow$
$ax = 2$ или $ax = — 6$
Если $a \neq 0$, уравнения примут вид $x = \frac{2}{a}$ or $x = -\frac{6}{a}$
Если $a = 0$, уравнения не имею решения

B) Если $a Если $a > 0$, это эквивалентно $2x + 1 = 3a$
или $2x + 1 = -3a \Leftrightarrow 2x = 3a — 1 \Leftrightarrow x = \frac{3a-1}{2}$ or
$2x = -3a — 1 \Leftrightarrow x = \frac{3a-1}{2} = -\frac{3a-1}{2}$

C) $|ax + 2a| = 3 \Leftrightarrow ax + 2a = 3$ или $ax + 2a = — 3$,
и мы находим $ax = 3 — 2a$ или $ax = -3 — 2a$
Если a = 0, тогда нет решений, если $a \neq 0$
решениями есть: $x = \frac{3-2a}{a}$ и $x = -\frac{3+2a}{a}$

---

Задача 6 Решите уравнение $2 – x = 2b – 2ax$, где a и b являются действительными параметрами. Найдите, для каких значениях a уравнение имеет в качестве решения натуральное число, если $b = 7$

Решение:

Представим данное уравнение в следующем виде: $(2a — 1)x = 2(b — 1)$
Возможны следующие варианты:
Если $2a — 1 \neq 0$, т.e. $a \neq \frac{1}{2}$, уравнение имеет единственное решение
$x = \frac{2(b-1)}{2a-1}$
Если $a = \frac{1}{2}$ и $b = 1$, уравнение получает вид $0\cdot x = 0$ и любое $x$ является решением
Если $a = \frac{1}{2}$ и $b \neq 1$, мы получаем $0\cdot x = 2(b — 1)$, где $2(b — 1) \neq 0$
В этом случае уравнение не имеет решения.
Если $b = 7$ и $a \neq \frac{1}{2}$ является единственным решением
$x = \frac{2(7-1)}{2a-1} = \frac{12}{2a-1}$
Если a целое число, тогда $2a — 1$ также есть целым числом и решением есть
$x = \frac{12}{2a-1}$ является натуральным числом когда
$2a — 1$ есть положительным делителем для числа $12$.
Чтобы a было целым числом, делитель числа $12$ должен быть нечетным. Но только $1$ и $3$ являются положительными нечетными числами, на которые делится12
Поэтому $2a — 1 = 3 \Leftrightarrow a = 2$ или $2a — 1 = 1 \Leftrightarrow$
$a = 1 a = 2$ или $2a — 1 = 1 \Leftrightarrow a = 1$

---

Задача 7 Решите уравнение $|ax — 2 – a| = 4$, где a является параметром. Найдите, для каких значениях а корнями уравнения являются целые отрицательные числа.

Решение:

Из определения модуля мы получаем
$|ax — 2 – x| = 4 \Leftrightarrow ax — 2 – x = 4$ или $ax — 2 – x = — 4$
Из первого равенства мы получаем $x(a — 1) — 2 = 4 \Leftrightarrow$
$(a — 1)x = 4 + 2 \Leftrightarrow (a — 1)x = 6$
Из второго равенства мы получаем $(a — 1)x = -2$
Если $a — 1 = 0$, т.e. $a = 1$, последнее уравнение не имеет решения.
Если $a \neq 1$ мы находим, что $x = \frac{6}{a-1}$ или $x = -\frac{2}{a-1}$
Чтобы эти корни были целыми отрицательными числами, должно выполняться следующее:
Для первого равенство $a — 1$ должно быть отрицательным делителем 6, и для второго — положительным делителям 2
Тогда $a — 1 = -1; -2; -3; — 6$ или $a — 1 = 1; 2$
Мы получаем $a — 1 = -1 \Leftrightarrow a = 0; a — 1 = -2 \Leftrightarrow$
$a = -1; a — 1 = -3 \Leftrightarrow a = -2; a — 1 = -6 \Leftrightarrow a = -5$
или $a — 1 = 1 \Leftrightarrow a = 2; a — 1 = 2 \Leftrightarrow a = 3$
Тогда $a = -5; -2; -1; 0; 2; 3$ являются решениями задачи.

---

Задача 8 Решите уравнение:
A) $3ax – a = 1 – x$, где a это параметр;
B) $2ax + b = 2 + x$, где a и b являются параметрами

Решение:

A) $3ax + x = 1 + a \Leftrightarrow (3a + 1)x = 1 + a$.
Если $3a + 1 \neq 0$, т.e. $a \neq -11 /3 /3$ , решение есть
$x = \frac{1+a}{3a+1}$
Если $a = -\frac{1}{3}$ уравнение принимает вид $0\cdot x = \frac{1.1}{3}$, что не имеет решения.

B) $2ax – x = 2 – b \Leftrightarrow (2a — 1)x = 2 – b$
Если $2a — 1 \neq 0$, т.e. $a \neq \frac{1}{2}, x = \frac{2-b}{2a-1}$ является решением.
Если $a = \frac{1}{2}$ уравнение принимает вид $0.x = 2 – b$
Тогда, если $b = 2$, любое x является решением, если $b \neq 2$, уравнение не имеет решения.

---

Задача 9 Дано уравнение $6(kx — 6) + 24 = 5kx$ , где к — целое число. Найдите, для каких значений k уравнение:
A) имеет корень $-\frac{4}{3}$
B) не имеет решения;
C) имеет корень как натуральное число.

Решение:

Перепишем уравнение в виде $6kx — 36 + 24 = 5kx \Leftrightarrow kx = 12$

A) Если $x = -\frac{4}{3}$, для k мы получим уравнение $-\frac{4}{3k} = 12 \Leftrightarrow k = — 9$

B) Уравнение $kx = 12$ не имеет решения, когда $k = 0$

C) Когда $k \neq 0$ является корнем $x = \frac{12}{k}$ и это натуральное число, если k есть целым положительным числом, на которое делится 12, т. e. $k = 1, 2, 3, 4, 6, 12$

---

Задача 10 Решите уравнение:
A) $2ax + 1 = x + a$, где a является параметром;
B) $2ax + 1 = x + b$, где a и b являются параметрами.

Решение:

A) $2ax + 1 = x + a \Leftrightarrow 2ax – x = a — 1 \Leftrightarrow$
$(2a — 1)x = a — 1$
Если $2a — 1 \neq 0$, т.e. $a \neq \frac{1}{2}$, единственным решением уравнения является
$x = \frac{a-1}{2a-1}$
Если $2a — 1 = 0$, т.e. $a = \frac{1}{2}$, уравнение принимает вид
$0.x = \frac{1}{2}- 1 \Leftrightarrow 0.x = -\frac{1}{2}$, что не имеет решения

B) $2ax + 1 = x + b \Leftrightarrow$
$2ax – x = b — 1 \Leftrightarrow$
$(2a — 1)x = b — 1$
Если $2a — 1 \neq 0$, т.e. $a \neq \frac{1}{2}$, решением является
$x = \frac{b-1}{2a-1}$
Если $a = \frac{1}{2}$, уравнения эквивалентно $0.x = b — 1$
Если b = 1 любое x является решением, если $b \neq 1$ тогда нет решения.

---

Задача 11 Дано уравнение $3(ax — 4) + 4 = 2ax$, где параметром является целым числом. Найдите, для каких значений a уравнение в качестве корней имеет:
А) $\left(-\frac{2}{3}\right)$
B) целое число
C) натуральное число

Решение:

A) Если $x = -\frac{2}{3}$ есть решением уравнения, тогда должно быть истинным
$3\left[a\left(-\frac{2}{3}\right) — 4\right] + 4 = 2a\left(-\frac{2}{3}\right) \Leftrightarrow$
$-2a — 12 + 4 = -\frac{4a}{3} \Leftrightarrow$
$\frac{4a}{3} — 2a = 8 \Leftrightarrow \frac{4a-6a}{3} = 8 \Leftrightarrow$
$-\frac{2a}{3} = 8 \Leftrightarrow a = -12$

B) $3(ax — 4) + 4 = 2ax \Leftrightarrow 3ax — 2ax = 12 — 4 \Leftrightarrow ax = 8$
Если $a \neq 0$ решением является $x = \frac{8}{a}$, это целое число, если а является делимым числа $8$.
Поэтому; $±2; ±4; ±8$
Если $a=0$, уравнение не имеет решения

C) Чтобы получить натуральное (целое положительное) число для этого решения $x=\frac{8}{a}$ число должно равняться: $a=1, 2, 4, 8$

---

Задача 12 Дано уравнение $2 – x = 2b – 2ax$, где $a$ и $b$ — параметры. Найдите, для каких значений a уравнение имеет решения в виде натурального числа, если $b = 7$

Решение:

В уравнение мы подставляем $b = 7$ и получаем $2 – x = 2.7 — 2ax \Leftrightarrow$
$2ax – x = 14 – 2 \Leftrightarrow (2a — 1)x = 12$
Если $2a -1 \neq 0$, т.e. $a \neq \frac{1}{2}$, уравнение примет вид
$x = \frac{12}{2a-1}$ и это будет натуральное число, если знаменатель $2a — 1$ есть положительным делимым $12$ и кроме того, чтобы оно было целым числом, необходимо, чтобы $2a — 1$ было нечетным числом.
Поэтому $2a — 1$ может быть $1$ или $3$
Из $2a — 1 = 1 \Leftrightarrow 2a = 2 \Leftrightarrow a = 1$ и $2a — 1 = 3$
$\Leftrightarrow 2a = 4 \Leftrightarrow a = 2$

---

Задача 13 Дана функция $f(x) = (3a — 1)x — 2a + 1$, где a — параметр. Найдите, для каких значений a график функции:
А) пересекает ось абсцисс;
B) пересекает ось абсцисс

Решение:

Чтобы график функции пересёк ось абсцисс, необходимо, чтобы
$(3a — 1)\cdot x -2a + 1 = 0$ имело решения и не имело решения для непересечения оси абсцисс.
С уравнения мы получаем $(3a — 1)x = 2a — 1$
Если $3a — 1 \neq 0$, т.e. $a \neq \frac{1}{3}$, уравнение имеет решения
$x = \frac{2a-1}{3a-1}$, поэтому график функции пересекает ось абсцисс.
Если $a = \frac{1}{3}$, мы получаем $0.x = \frac{2}{3} — 1 \Leftrightarrow 0.x = -\frac{1}{3}$, что не имеет решения.
Поэтому, если $a = \frac{1}{3}$, график функций не пересекает ось абсцисс.

---

Задача 14 Решите параметрическое уравнение:
A) $|x -2| = a$
B) $|ax -1| = 3$
C) $|ax — 1| = a — 2$

Решение:

A) Если $a 0$ мы получаем:
$|x — 2| = a \Leftrightarrow x — 2 = a$ или $x — 2 = -a$
Из $x — 2 = a \Rightarrow x = a + 2$, и из
$x — 2 = -a \Rightarrow x = 2 – a$
Если $a = 0$, тогда $x — 2 = 0$ или $x = 2$

B) $|ax — 1| = 3 \Leftrightarrow ax — 1 = 3$ или $ax — 1 = -3$
откуда $ax = 4$ или $ax = — 2$
Если $a \neq 0$ решения: $x = \frac{4}{a}$ or $x = -\frac{2}{a}$
Если $a = 0$, здесь нет решения

C) Если $a — 2 Если $a — 2 > 0$, т. 2 — 4x – 0 \Leftrightarrow x(x — 4) = 0 \Leftrightarrow$
$x = 0$ или $x = 4$
С условием, что $х> 3$, поэтому только $x = 4$ есть решением. Для второго уравнения мы получаем
$ax – x = 1 — 2a \Leftrightarrow (a — 1)x = 1 — 2a$
Если $a — 1 = 0$, здесь нет решения (Почему?), если $a — 1 \neq 0$, i.e. $a \neq 1$, решением есть
$x = \frac{1-2a}{a-1}$ Эти два уравнения будут равны, если $4 = \frac{1-2a}{a-1} \Leftrightarrow$ $4(a — 1) = 1 — 2a \Leftrightarrow 4a + 2a = 1 + 4 \Leftrightarrow 6a = 5 \Leftrightarrow a = \frac{5}{6}$

Решения с использованием определителей с двумя переменными

Линейные уравнения: решения с использованием определителей с двумя переменными

Квадратный массив чисел или переменных, заключенный между вертикальными линиями, называется определителем . Определитель отличается от матрицы тем, что определитель имеет числовое значение, а матрица — нет. Следующий определитель имеет две строки и два столбца.

Значение этого определителя находится путем нахождения разницы между произведением по диагонали вниз и произведением по диагонали вверх:

Пример 1

Оцените следующий определитель.

Пример 2

Решите следующую систему с помощью определителей.

Для решения этой системы создаются три определителя. Один называется определителем знаменателя , обозначенным D; другой — x — определитель числителя , обозначенный D _x ; , а третий — y — определитель числителя , обозначенный D _y .

Определитель знаменателя, D , формируется путем взятия коэффициентов x и y из уравнений, записанных в стандартной форме.

Определитель числителя x формируется путем взятия постоянных членов из системы и помещения их в позиции коэффициентов x с сохранением коэффициентов y .

Определитель числителя y формируется путем взятия постоянных членов из системы и размещения их в позициях y -коэффициентов и сохранения коэффициентов x-.

Ответы для x и y следующие:

Чек оставлен вам.Решение: х = -5, у = -2.

Много раз поиск решений с использованием определителей упоминается как Правило Крамера по имени математика, разработавшего этот метод. Правило Крамера вряд ли можно считать «кратчайшим путем», но это довольно изящный способ решения систем уравнений с использованием определителей.

Пример 3

Используйте правило Крамера, чтобы решить эту систему.

Чек оставлен вам. Решение , .

Надежный регулятор LQ для скачкообразных линейных систем с неопределенными параметрами

1.

Басар, Т. и Бернхард, П., h2 – Оптимальное управление и связанные с ним проблемы минимаксного проектирования: динамический игровой подход , 2-е изд. , Биркхаузер: Бостон , Массачусетс, 1995.

Google Scholar

2.

Букас, Е.К., «Надежная устойчивость линейных кусочно-детерминированных систем в условиях согласования», Теория управления и передовые технологии , Vol.10, № 4, 1995.

3.

Букас Е.К. и Хаури, Х., «Управление производственным потоком и профилактическое обслуживание: стохастический подход к управлению», IEEE Trans. на АКПП , об. AC-35, No. 9, 1990.

4.

Boukas, EK, Zhu, Q. and Zhang, Q., «Кусочно-детерминированная модель марковского процесса для гибких производственных систем с профилактическим обслуживанием», Journal of Optimization Theory и Приложения , Vol. 81, № 2, стр. 259–275, 1994.

Google Scholar

5.

Букас Э.К. и Ян, Х., «Оптимальное управление производственным потоком и профилактическое обслуживание», Trans. на АКПП , об. АС–41, № 6, стр. 881–885, 1996.

Google Scholar

6.

Букас Э.К. и Ян, Х., «Надежная устойчивость нелинейных кусочно-детерминированных систем в условиях согласования», Математические проблемы в технике: теория, методы и приложения , Vol.3, стр. 203–215, 1998.

Google Scholar

7.

Де Соуза, К.Э. и Фрагозо, М.Д., «Управление H8 для линейных систем с марковскими параметрами скачка», Теория управления и передовые технологии , Vol. 1993. Т. 9. № 2. С. 457–466.

Google Scholar

8.

Ji, Y. и Chizeck, H., «Управляемость, устойчивость и линейно-квадратичное управление марковским скачком с непрерывным временем», IEEE Trans.автомат. контр. , Том. 35, 1990.

9.

Нето, А. Т., Дион, Дж. М. и Дугард, Л., «Границы надежности для регуляторов LQ», IEEE Trans. автомат. контр. , Том. 37, стр. 1373–1377, 1992.

Google Scholar

10.

Пан, З. и Басар, Т., « h2 — управление марковскими системами скачков и решения связанных с ними кусочно-детерминированных дифференциальных игр», в книге Г.Дж. Редактор Олсдера, Annals of Dynamic Games , Vol.3, pp. 61–94 1995.

11.

Wonham, WM, «Случайные дифференциальные уравнения в теории управления», Вероятностные методы в прикладной математике , Vol. 2, А.Т. Beruche-Reid, editor, NY, 1971.

12.

Yasuda, K. and Hirai, K., «Верхние и нижние оценки решения алгебраического уравнения Риккати», IEEE Trans. на АКПП , об. АС–24, № 1, стр. 83–487, 1979.

Google Scholar

13.

Чжоу, К. и Харгонекар, П.П., «Надежная стабилизация линейных систем с ограниченной по нормали изменяющейся во времени неопределенностью», Systems Control Lett. , Том. 10, стр. 17–20, 1988.

Google Scholar

Произошла ошибка при настройке пользовательского файла cookie

Произошла ошибка при настройке пользовательского файла cookie

Этот сайт использует файлы cookie для повышения производительности. Если ваш браузер не принимает файлы cookie, вы не можете просматривать этот сайт.

Настройка браузера на прием файлов cookie

Существует множество причин, по которым файл cookie не может быть установлен правильно. Ниже приведены наиболее распространенные причины:

• В вашем браузере отключены файлы cookie. Вам необходимо сбросить настройки браузера, чтобы принять файлы cookie, или спросить вас, хотите ли вы принимать файлы cookie.
• Ваш браузер спрашивает, хотите ли вы принимать файлы cookie, и вы отказались. Чтобы принять файлы cookie с этого сайта, нажмите кнопку «Назад» и примите файл cookie.
• Ваш браузер не поддерживает файлы cookie. Попробуйте другой браузер, если вы подозреваете это.
• Дата на вашем компьютере в прошлом. Если часы вашего компьютера показывают дату до 1 января 1970 г., браузер автоматически забудет файл cookie. Чтобы это исправить, установите правильное время и дату на своем компьютере.
• Вы установили приложение, которое отслеживает или блокирует установку файлов cookie.Вы должны отключить приложение при входе в систему или проконсультироваться с системным администратором.

Почему этому сайту требуются файлы cookie?

Этот сайт использует файлы cookie для повышения производительности, запоминая, что вы вошли в систему, когда переходите со страницы на страницу. Предоставить доступ без файлов cookie потребует от сайта создания нового сеанса для каждой посещаемой вами страницы, что замедляет работу системы до неприемлемого уровня.

Что сохраняется в файле cookie?

Этот сайт не хранит ничего, кроме автоматически сгенерированного идентификатора сеанса в файле cookie; никакая другая информация не фиксируется.

Как правило, в файле cookie может храниться только та информация, которую вы предоставляете, или выбор, который вы делаете при посещении веб-сайта. Например, сайт не может определить ваше имя электронной почты, если вы не решите ввести его. Разрешение веб-сайту создавать файлы cookie не дает этому или любому другому сайту доступ к остальной части вашего компьютера, и только сайт, создавший файл cookie, может его прочитать.

Решающие системы с правилом Крамера — алгебра и тригонометрия

Цели обучения

В этом разделе вы:

• Оценить  2 × 2  определителей.
• Используйте правило Крамера, чтобы решить систему уравнений с двумя переменными.
• Вычислите  3 × 3  определителей.
• Используйте правило Крамера, чтобы решить систему из трех уравнений с тремя переменными.
• Знать свойства определителей.

Мы научились решать системы уравнений с двумя переменными и тремя переменными, а также несколькими методами: подстановкой, сложением, методом исключения Гаусса, использованием обратной матрицы и построением графика.Некоторые из этих методов легче применять, чем другие, и они более подходят в определенных ситуациях. В этом разделе мы изучим еще две стратегии решения систем уравнений.

Вычисление определителя матрицы 2×2

Определитель — это действительное число, которое может быть очень полезно в математике, поскольку имеет множество применений, например, для вычисления площади, объема и других величин. Здесь мы будем использовать определители, чтобы выяснить, является ли матрица обратимой, используя элементы квадратной матрицы, чтобы определить, существует ли решение системы уравнений.Однако, возможно, одним из наиболее интересных приложений является их использование в криптографии. Защищенные сигналы или сообщения иногда отправляются закодированными в матрице. Данные могут быть расшифрованы только с помощью обратимой матрицы и определителя. Для наших целей мы сосредоточимся на определителе как признаке обратимости матрицы. Вычисление определителя матрицы включает в себя следование определенным шаблонам, описанным в этом разделе.

Нахождение определителя матрицы 2 × 2

Найдите определитель данной матрицы.

[reveal-answer q=»1408516″]Показать решение[/reveal-answer][hidden-answer a=»1408516″]

[/ скрытый ответ]

Использование правила Крамера для решения системы двух уравнений с двумя переменными

Теперь мы представим последний метод решения систем уравнений, использующий определители. Этот метод, известный как правило Крамера, восходит к середине 18 века и назван в честь его новатора, швейцарского математика Габриэля Крамера (1704–1752), который представил его в 1750 году во Введении к анализу линий алгебры.Правило Крамера — жизнеспособный и эффективный метод поиска решений систем с произвольным числом неизвестных при условии, что у нас есть такое же количество уравнений, как и неизвестных.

Правило Крамера даст нам единственное решение системы уравнений, если она существует. Однако, если система не имеет решения или имеет бесконечное число решений, на это будет указывать нулевой определитель. Чтобы выяснить, является ли система противоречивой или зависимой, придется использовать другой метод, такой как исключение.

Чтобы понять правило Крамера, давайте внимательно посмотрим, как мы решаем системы линейных уравнений, используя основные операции со строками. Рассмотрим систему двух уравнений с двумя переменными.

Мы исключаем одну переменную, используя операции со строками, и находим другую. Скажем, что мы хотим решить для Если уравнение (2) умножается на коэффициент, противоположный коэффициенту в уравнении (1), уравнение (1) умножается на коэффициент в уравнении (2), и мы складываем два уравнения, переменная будет устранено.

Теперь найдите

.

Точно так же, чтобы решить для мы исключим

Решение прощает

Обратите внимание, что знаменатель для обоих и является определителем матрицы коэффициентов.

Мы можем использовать эти формулы для решения for и , но правило Крамера также вводит новое обозначение:

Ключом к правилу Крамера является замена интересующего столбца переменных столбцом констант и вычисление определителей. Затем мы можем выразить как частное двух определителей.

Использование правила Крамера для решения системы 2 × 2

Решите следующую систему, используя правило Крамера.

Попробуйте

Используйте правило Крамера, чтобы решить систему уравнений 2 × 2.

[reveal-answer q=»fs-id1440640″]Показать решение[/reveal-answer]
[скрытый ответ = «fs-id1440640»]

[/скрытый ответ]

Вычисление определителя матрицы 3 × 3

Найти определитель матрицы 2×2 несложно, но найти определитель матрицы 3×3 сложнее.Один из методов состоит в том, чтобы дополнить матрицу 3×3 повторением первых двух столбцов, получив матрицу 3×5. Затем мы вычисляем сумму произведений записей на по каждой из трех диагоналей (слева вверху справа внизу) и вычитаем произведения записей на по каждой из трех диагоналей (слева внизу на право вверху). Это легче понять с визуальным и пример.

Найдите определитель матрицы 3×3.

1. Дополнить первыми двумя столбцами.
2. От верхнего левого угла к нижнему правому: умножьте числа по первой диагонали. Прибавьте результат к произведению записей по второй диагонали. Добавьте этот результат к произведению записей вниз по третьей диагонали.
3. Из нижнего левого угла в верхний правый: вычтите произведение записей вверх по первой диагонали. Из этого результата вычтите произведение вхождений вверх по второй диагонали. Из этого результата вычтите произведение вхождений вверх по третьей диагонали.

Алгебра выглядит следующим образом:

Нахождение определителя матрицы 3 × 3

Найдите определитель матрицы 3 × 3 по данным

[reveal-answer q=»1570002″]Показать решение[/reveal-answer][hidden-answer a=»1570002″]

Дополните матрицу первыми двумя столбцами, а затем следуйте формуле.Таким образом,

[/ скрытый ответ]

Попробуйте

Найдите определитель матрицы 3 × 3.

[reveal-answer q=»fs-id1643971″]Показать решение[/reveal-answer]
[скрытый ответ = «fs-id1643971»]

[/скрытый ответ]

Можно ли использовать тот же метод, чтобы найти определитель большей матрицы?

Нет, этот метод работает только для матриц. Для больших матриц лучше всего использовать графическую утилиту или компьютерное программное обеспечение.

Использование правила Крамера для решения системы трех уравнений с тремя переменными

Теперь, когда мы можем найти определитель матрицы 3 × 3, мы можем применить правило Крамера для решения системы трех уравнений с тремя переменными. Правило Крамера является простым и следует шаблону, согласующемуся с правилом Крамера для матриц 2 × 2. Однако по мере увеличения порядка матрицы до 3 × 3 требуется гораздо больше вычислений.

Когда мы вычисляем, что определитель равен нулю, правило Крамера не указывает, имеет ли система решение или бесконечное число решений. Чтобы выяснить это, мы должны выполнить исключение в системе.

Рассмотрим систему уравнений 3 × 3.

где

Если мы записываем определитель, мы заменяем столбец постоянным столбцом. Если мы записываем определитель, мы заменяем столбец постоянным столбцом. Если мы записываем определитель, мы заменяем столбец постоянным столбцом. Всегда проверяйте ответ.

Решение системы 3 × 3 с помощью правила Крамера

Найдите решение данной системы 3 × 3, используя правило Крамера.

[reveal-answer q=»1588465″]Показать решение[/reveal-answer][hidden-answer a=»1588465″]

Используйте правило Крамера.

Затем

Решение[/hidden-answer]

Попробуйте

Используйте правило Крамера, чтобы решить матрицу 3 × 3.

[reveal-answer q=»fs-id1405450″]Показать решение[/reveal-answer]
[скрытый ответ = «fs-id1405450»]

[/скрытый ответ]

Использование правила Крамера для решения несогласованной системы

Решите систему уравнений по правилу Крамера.

Использование правила Крамера для решения зависимой системы

Решите систему с бесконечным числом решений.

Понимание свойств определителей

Есть много свойств определителей. Здесь перечислены некоторые свойства, которые могут быть полезны при вычислении определителя матрицы.

Свойства определителей

1. Если матрица имеет форму верхнего треугольника, определитель равен произведению элементов по главной диагонали.
2. При перестановке двух строк определитель меняет знак.
3. Если две строки или два столбца идентичны, определитель равен нулю.
4. Если матрица содержит строку нулей или столбец нулей, определитель равен нулю.
5. Определитель обратной матрицы является обратной величиной определителя матрицы
6. Если какая-либо строка или столбец умножается на константу, определитель умножается на тот же коэффициент.

Иллюстрация свойств определителей

Проиллюстрируйте каждое из свойств определителей.

Использование правила Крамера и свойств определителя для решения системы

Найдите решение данной системы 3 × 3.

[reveal-answer q=»fs-id1653554″]Показать решение[/reveal-answer]
[скрытый ответ = ”fs-id1653554″]

Используя правило Крамера, мы имеем

Обратите внимание, что второй и третий столбцы идентичны. Согласно свойству 3 определитель будет равен нулю, поэтому решения либо нет, либо решений бесконечное множество. Мы должны выполнить исключение, чтобы узнать.

1. Умножьте уравнение (3) на –2 и добавьте результат к уравнению (1).

Получение утверждения, являющегося противоречием, означает, что система не имеет решения.[/hidden-answer]

Раздел Упражнения

Устный

Объясните, почему мы всегда можем вычислить определитель квадратной матрицы.

[reveal-answer q=»1405260″]Показать решение[/reveal-answer][hidden-answer a=»1405260″]

Определитель — это сумма и произведения элементов в матрице, поэтому вы всегда можете оценить это произведение, даже если оно в конечном итоге равно 0.

[/скрытый ответ]

Изучая правило Крамера, объясните, почему нет единственного решения системы, когда определитель вашей матрицы равен 0. Для простоты используйте amatrix.

Объясните, что означает в терминах обратной матрицы наличие нулевого определителя.

[reveal-answer q=»fs-id1394601″]Показать решение[/reveal-answer]
[скрытый ответ = «fs-id1394601»]

Обратное не существует.

[/скрытый ответ]

Определитель матрицы равен 3.Если вы поменяете строки и умножите первую строку на 6, а вторую строку на 2, объясните, как найти определитель, и дайте ответ.

Алгебраический

Для следующих упражнений найдите определитель.

[reveal-answer q=»fs-id1394170″]Показать решение[/reveal-answer]
[скрытый ответ = «fs-id1394170»]

[/скрытый ответ]

[reveal-answer q=»fs-id1430900″]Показать решение[/reveal-answer]
[скрытый ответ = «fs-id1430900»]

[/скрытый ответ]

[reveal-answer q=»fs-id1395220″]Показать решение[/reveal-answer]
[скрытый ответ = ”fs-id1395220″]

[/скрытый ответ]

[reveal-answer q=»fs-id1660075″]Показать решение[/reveal-answer]
[скрытый ответ = «fs-id1660075»]

[/скрытый ответ]

[reveal-answer q=»fs-id885813″]Показать решение[/reveal-answer]
[скрытый ответ = ”fs-id885813″]

[/скрытый ответ]

[reveal-answer q=»fs-id1339464″]Показать решение[/reveal-answer]
[скрытый ответ = ”fs-id1339464″]

[/скрытый ответ]

[reveal-answer q=»fs-id1601846″]Показать решение[/reveal-answer]
[скрытый ответ = «fs-id1601846»]

[/скрытый ответ]

[reveal-answer q=»fs-id1663783″]Показать решение[/reveal-answer]
[скрытый ответ = ”fs-id1663783″]

[/скрытый ответ]

[reveal-answer q=»fs-id1616218″]Показать решение[/reveal-answer]
[скрытый ответ = ”fs-id1616218″]

[/скрытый ответ]

[reveal-answer q=»fs-id1534877″]Показать решение[/reveal-answer]
[скрытый ответ = ”fs-id1534877″]

[/скрытый ответ]

Для следующих упражнений решите систему линейных уравнений, используя правило Крамера.

[reveal-answer q=»fs-id1694937″]Показать решение[/reveal-answer]
[скрытый ответ = ”fs-id1694937″]

[/скрытый ответ]

[reveal-answer q=»fs-id1433846″]Показать решение[/reveal-answer]
[скрытый ответ = ”fs-id1433846″]

[/скрытый ответ]

[reveal-answer q=»fs-id1516926″]Показать решение[/reveal-answer]
[скрытый ответ = ”fs-id1516926″]

[/скрытый ответ]

[reveal-answer q=»fs-id1615360″]Показать решение[/reveal-answer]
[скрытый ответ = ”fs-id1615360″]

[/скрытый ответ]

[reveal-answer q=»fs-id1530071″]Показать решение[/reveal-answer]
[скрытый ответ = «fs-id1530071»]

[/скрытый ответ]

Для следующих упражнений решите систему линейных уравнений, используя правило Крамера.

[reveal-answer q=»fs-id1530969″]Показать решение[/reveal-answer]
[скрытый ответ = ”fs-id1530969″]

[/скрытый ответ]

[reveal-answer q=»fs-id1699357″]Показать решение[/reveal-answer]
[скрытый ответ = ”fs-id1699357″]

[/скрытый ответ]

[reveal-answer q=»fs-id1506671″]Показать решение[/reveal-answer]
[скрытый ответ = «fs-id1506671»]

[/скрытый ответ]

[reveal-answer q=»1433664″]Показать решение[/reveal-answer][hidden-answer a=»1433664″]
[/hidden-answer]

[reveal-answer q=»fs-id1673950″]Показать решение[/reveal-answer]
[скрытый ответ = ”fs-id1673950″]

Бесконечные решения

[/скрытый ответ]

Технология

В следующих упражнениях используйте функцию определителя в графической утилите.

[reveal-answer q=»fs-id1597711″]Показать решение[/reveal-answer]
[скрытый ответ = ”fs-id1597711″]

[/скрытый ответ]

[reveal-answer q=»fs-id1

5″]Показать решение[/reveal-answer]
[скрытый ответ = ”fs-id1

5″]

[/скрытый ответ]

Реальные приложения

Для следующих упражнений создайте систему линейных уравнений для описания поведения.Затем вычислите определитель. Будет ли уникальное решение? Если да, то найти единственное решение.

Два числа в сумме дают 56. Одно число на 20 меньше другого.

[reveal-answer q=»fs-id1702584″]Показать решение[/reveal-answer]
[скрытый ответ = ”fs-id1702584″]

Да; 18, 38

[/скрытый ответ]

Два числа в сумме дают 104. Если вы дважды сложите первое число и два раза второе число, получится 208

Три числа в сумме дают 106.Первое число на 3 меньше второго. Третье число на 4 больше первого числа.

[reveal-answer q=»fs-id17

«]Показать решение[/reveal-answer]
[скрытый ответ = ”fs-id17

″]

Да; 33, 36, 37

[/скрытый ответ]

Три числа в сумме дают 216. Сумма первых двух чисел равна 112. Третье число на 8 меньше первых двух вместе взятых.

Для следующих упражнений создайте систему линейных уравнений для описания поведения.Затем решите систему для всех решений, используя правило Крамера.

Вы инвестируете 10 000 долларов на два счета, на которые начисляются 8% и 5% годовых. В конце года на ваших объединенных счетах было 10 710 долларов. Сколько было вложено в каждый счет?

[reveal-answer q=»fs-id1354932″]Показать решение[/reveal-answer]
[скрытый ответ = ”fs-id1354932″]

7000 долларов на первый счет, 3000 долларов на второй счет.

[/скрытый ответ]

Вы инвестируете 80 000 долларов США в два счета, 22 000 долларов США в один счет и 58 000 долларов США в другой счет.В конце года, при условии простых процентов, вы заработали 2470 долларов в виде процентов. Второй счет получает на полпроцента меньше, чем удвоенный процент по первому счету. Каковы процентные ставки для ваших счетов?

Кинотеатру необходимо знать, сколько билетов для взрослых и детей было продано из 1200 билетов. Если детские билеты стоят 5,95 долл. США, билеты для взрослых — 11,15 долл. США, а общая сумма выручки составила 12 756 долл. США, сколько было продано детских билетов и билетов для взрослых?

[reveal-answer q=»fs-id1584198″]Показать решение[/reveal-answer]
[скрытый ответ = ”fs-id1584198″]

120 детей, 1080 взрослых

[/скрытый ответ]

Концертный зал продает одиночные билеты по 40 долларов каждый и билеты для пар по 65 долларов.Если общий доход составил 18 090 долларов США и был продан 321 билет, то сколько было продано одиночных билетов и сколько билетов для пар?

Вы решили покрасить кухню в зеленый цвет. Вы создаете цвет краски, смешивая желтую и синюю краски. Вы не можете вспомнить, сколько галлонов каждого цвета вошло в вашу смесь, но вы знаете, что всего было 10 галлонов. Кроме того, вы сохранили квитанцию ​​и знаете, что общая потраченная сумма составила 29,50 долларов США. Если каждый галлон желтого стоит 2,59 доллара, а каждый галлон синего стоит 3 доллара.19, сколько галлонов каждого цвета входит в вашу зеленую смесь?

[reveal-answer q=»fs-id1584221″]Показать решение[/reveal-answer]
[скрытый ответ = ”fs-id1584221″]

4 галлона желтого цвета, 6 галлона синего цвета

[/скрытый ответ]

Вы продали два вида шарфов на фермерском рынке и хотели бы знать, какой из них более популярен. Всего было продано 56 шарфов, желтый шарф стоил 10 долларов, фиолетовый — 11 долларов. Если ваш общий доход составил 583 доллара, сколько желтых шарфов и сколько фиолетовых шарфов было продано?

В вашем саду выращивают два вида помидоров, зеленый и красный.Красный весит 10 унций, а зеленый весит 4 унции. У вас есть 30 помидоров общим весом 13 фунтов 14 унций. Сколько у вас помидоров каждого вида?

[reveal-answer q=»fs-id1699000″]Показать решение[/reveal-answer]
[скрытый ответ = «fs-id1699000»]

13 зеленых помидоров, 17 красных помидоров

[/скрытый ответ]

На рынке три самых популярных овоща составляют 53% продаж овощей. Продажи кукурузы на 4% выше, чем у брокколи, продажи которой на 5% выше, чем у лука.Какую долю рынка занимает каждый овощ?

На том же рынке три самых популярных фрукта составляют 37% от общего количества продаваемых фруктов. Клубники продают вдвое больше, чем апельсинов, а киви продают на один процент больше, чем апельсинов. Для каждого фрукта найдите процент от общего количества проданных фруктов.

[reveal-answer q=»fs-id1648808″]Показать решение[/reveal-answer]
[скрытый ответ = ”fs-id1648808″]

Клубника 18%, апельсины 9%, киви 10%

[/скрытый ответ]

Три группы выступили на концертной площадке.Первая группа взимала 15 долларов за билет, вторая группа взимала 45 долларов за билет, а последняя группа взимала 22 доллара за билет. Было продано 510 билетов на общую сумму 12 700 долларов. Если у первой группы было на 40 зрителей больше, чем у второй группы, сколько билетов было продано на каждую группу?

Кинотеатр продал билеты на три фильма. Билеты на первый фильм стоили 5 долларов, билеты на второй фильм — 11 долларов, а на третий фильм — 12 долларов. На первый фильм было продано 100 билетов.Общее количество проданных билетов составило 642, а общий доход составил 6 774 доллара. Сколько билетов на каждый фильм было продано?

[reveal-answer q=»fs-id1637286″]Показать решение[/reveal-answer]
[скрытый ответ = ”fs-id1637286″]

100 для фильма 1, 230 для фильма 2, 312 для фильма 3

[/скрытый ответ]

В прошлом году мужчины в возрасте 20–29, 30–39 и 40–49 лет составляли 78% заключенных в тюрьме. В этом году те же возрастные группы составили 82,08% населения. Возрастная группа 20–29 лет увеличилась на 20%, возрастная группа 30–39 лет увеличилась на 2%, а возрастная группа 40–49 лет уменьшилась по сравнению с их предыдущим населением.Первоначально в возрастной группе 30–39 лет заключенных было на 2% больше, чем в возрастной группе 20–29 лет. Определите процент заключенных для каждой возрастной группы в прошлом году.

В женской тюрьме по дороге общее число заключенных в возрасте от 20 до 49 лет составило 5525 человек. В этом году возрастная группа 20-29 лет увеличилась на 10%, возрастная группа 30-39 лет уменьшилась на 20%, а возрастная группа 40-49 лет удвоилась. Сейчас там 6040 заключенных. Первоначально в возрастной группе 30–39 лет было на 500 человек больше, чем в возрастной группе 20–29 лет. Определите количество заключенных для каждой возрастной группы в прошлом году.

[reveal-answer q=»fs-id1425394″]Показать решение[/reveal-answer]
[скрытый ответ = ”fs-id1425394″]

20–29: 2 100, 30–39: 2 600, 40–49: 825

[/скрытый ответ]

Для следующих упражнений используйте этот сценарий: Компания, заботящаяся о своем здоровье, решает приготовить пищевую смесь из миндаля, сушеной клюквы и орехов кешью в шоколаде. Информация о пищевой ценности этих продуктов показана на (Рисунок).

	Жир (г)	Белок (г)	Углеводы (г)
Миндаль (10)	6	2	3
Клюква (10)	0. 02	0	8
Кешью (10)	7	3,5	5,5

Для специальной «низкоуглеводной» трейловой смеси имеется 1000 штук смеси. Общее количество углеводов 425 г, общее количество жиров 570,2 г. Если орехов кешью на 200 штук больше, чем клюквы, сколько штук каждого предмета будет в смеси?

Для «походного» микса в миксе 1000 штук, содержащих 390.8 г жира и 165 г белка. Если миндаля столько же, сколько орехов кешью, то сколько каждого элемента содержится в смеси?

[reveal-answer q=»fs-id1647224″]Показать решение[/reveal-answer]
[скрытый ответ = ”fs-id1647224″]

300 миндаля, 400 клюквы, 300 кешью

[/скрытый ответ]

Для смеси «Энергия-бустер» в смеси 1000 штук, содержащих 145 г белка и 625 г углеводов. Если количество миндаля и кешью в сумме равно количеству клюквы, сколько каждого элемента содержится в смеси?

Обзор упражнений

Системы линейных уравнений: две переменные

В следующих упражнениях определите, является ли упорядоченная пара решением системы уравнений.

и

[reveal-answer q=»fs-id1395131″]Показать решение[/reveal-answer]
[скрытый ответ = ”fs-id1395131″]

№

[/скрытый ответ]

и

В следующих упражнениях используйте замену для решения системы уравнений.

[reveal-answer q=»fs-id1698278″]Показать решение[/reveal-answer]
[скрытый ответ = ”fs-id1698278″]

[/скрытый ответ]

[reveal-answer q=»fs-id1428954″]Показать решение[/reveal-answer]
[скрытый ответ = ”fs-id1428954″]

[/скрытый ответ]

В следующих упражнениях используйте сложение для решения системы уравнений.

[reveal-answer q=»fs-id1584732″]Показать решение[/reveal-answer]
[скрытый ответ = ”fs-id1584732″]

Решений не существует.

[/скрытый ответ]

Для следующих упражнений напишите систему уравнений для решения каждой задачи. Решите систему уравнений.

Фабрика имеет функцию затрат на производство и функцию дохода. Какова точка безубыточности?

[reveal-answer q=»fs-id1536207″]Показать решение[/reveal-answer]
[скрытый ответ = ”fs-id1536207″]

[/скрытый ответ]

Исполнитель взимает плату, где указано общее количество посетителей шоу.Заведение берет 75 долларов за билет. После того, как много людей купят билеты, место станет безубыточным, и какова общая стоимость билетов, проданных в этот момент?

[reveal-answer q=»fs-id1358367″]Показать решение[/reveal-answer]
[скрытый ответ = ”fs-id1358367″]

[/скрытый ответ]

Системы линейных уравнений: три переменные

Для следующих упражнений решите систему из трех уравнений, используя замену или сложение.

[reveal-answer q=»fs-id1513414″]Показать решение[/reveal-answer]
[скрытый ответ = ”fs-id1513414″]

[/скрытый ответ]

[reveal-answer q=»fs-id1366211″]Показать решение[/reveal-answer]
[скрытый ответ = «fs-id1366211»]

Решений не существует.

[/скрытый ответ]

[reveal-answer q=»fs-id1409562″]Показать решение[/reveal-answer]
[скрытый ответ = «fs-id1409562»]

[/скрытый ответ]

[reveal-answer q=»fs-id1417064″]Показать решение[/reveal-answer]
[скрытый ответ = ”fs-id1417064″]

[/скрытый ответ]

Для следующих упражнений напишите систему уравнений для решения каждой задачи.Решите систему уравнений.

Три нечетных числа в сумме дают 61. Меньшее число на одну треть больше, а среднее число на 16 меньше большего. Какие три числа?

[reveal-answer q=»fs-id1706459″]Показать решение[/reveal-answer]
[скрытый ответ = ”fs-id1706459″]

11, 17, 33

[/скрытый ответ]

Билеты на спектакль в местном театре распроданы. Они продают все 500 билетов на общую сумму 8 070 долларов. Билеты стоили 15 долларов для студентов, 12 долларов для детей и 18 долларов для взрослых. Если группа продала в три раза больше билетов для взрослых, чем билетов для детей, сколько билетов каждого типа было продано?

Системы нелинейных уравнений и неравенств: две переменные

Для следующих упражнений решите систему нелинейных уравнений.

[reveal-answer q=»fs-id1695047″]Показать решение[/reveal-answer]
[скрытый ответ = «fs-id1695047»]

[/скрытый ответ]

[reveal-answer q=»fs-id1403141″]Показать решение[/reveal-answer]
[скрытый ответ = ”fs-id1403141″]

Нет решения

[/скрытый ответ]

[reveal-answer q=»fs-id1513095″]Показать решение[/reveal-answer]
[скрытый ответ = «fs-id1513095»]

Нет решения

[/скрытый ответ]

Для следующих упражнений постройте график неравенства.

[reveal-answer q=»1663822″]Показать решение[/reveal-answer][hidden-answer a=»1663822″][/hidden-answer]

Для следующих упражнений постройте график системы неравенств.

[reveal-answer q=»1600811″]Показать решение[/reveal-answer][hidden-answer a=»1600811″][/hidden-answer]

Частичные дроби

Для следующих упражнений разложите на частичные дроби.

[reveal-answer q=»fs-id1530172″]Показать решение[/reveal-answer]
[скрытый ответ = ”fs-id1530172″]

[/скрытый ответ]

[reveal-answer q=»fs-id1440535″]Показать решение[/reveal-answer]
[скрытый ответ = «fs-id1440535»]

[/скрытый ответ]

[reveal-answer q=»fs-id1528465″]Показать решение[/reveal-answer]
[скрытый ответ = ”fs-id1528465″]

[/скрытый ответ]

[reveal-answer q=»fs-id1582588″]Показать решение[/reveal-answer]
[скрытый ответ = ”fs-id1582588″]

[/скрытый ответ]

Матрицы и операции с матрицами

В следующих упражнениях выполните запрошенные операции над заданными матрицами.

[reveal-answer q=»fs-id1615553″]Показать решение[/reveal-answer]
[скрытый ответ = ”fs-id1615553″]

[/скрытый ответ]

[reveal-answer q=»fs-id1706172″]Показать решение[/reveal-answer]
[скрытый ответ = ”fs-id1706172″]

не определено; размеры не соответствуют

[/скрытый ответ]

[reveal-answer q=»fs-id1650879″]Показать решение[/reveal-answer]
[скрытый ответ = ”fs-id1650879″]

не определено; внутренние размеры не соответствуют

[/скрытый ответ]

[reveal-answer q=»fs-id1647736″]Показать решение[/reveal-answer]
[скрытый ответ = ”fs-id1647736″]

[/скрытый ответ]

[reveal-answer q=»fs-id1693755″]Показать решение[/reveal-answer]
[скрытый ответ = ”fs-id1693755″]

[/скрытый ответ]

[reveal-answer q=»fs-id1700302″]Показать решение[/reveal-answer]
[скрытый ответ = «fs-id1700302»]

не определено; внутренние размеры не соответствуют

[/скрытый ответ]

Решающие системы с исключением Гаусса

Для следующих упражнений напишите систему линейных уравнений из расширенной матрицы. Укажите, будет ли единственное решение.

[reveal-answer q=»fs-id1637532″]Показать решение[/reveal-answer]
[скрытый ответ = ”fs-id1637532″]

с бесконечными решениями

[/скрытый ответ]

Для следующих упражнений напишите расширенную матрицу из системы линейных уравнений.

[reveal-answer q=»fs-id1656057″]Показать решение[/reveal-answer]
[скрытый ответ = ”fs-id1656057″]

[/скрытый ответ]

[reveal-answer q=»fs-id1528512″]Показать решение[/reveal-answer]
[скрытый ответ = ”fs-id1528512″]

[/скрытый ответ]

Для следующих упражнений решите систему линейных уравнений методом исключения Гаусса.

[reveal-answer q=»fs-id1422121″]Показать решение[/reveal-answer]
[скрытый ответ = ”fs-id1422121″]

Решений не существует.

[/скрытый ответ]

[reveal-answer q=»fs-id1455902″]Показать решение[/reveal-answer]
[скрытый ответ = ”fs-id1455902″]

Решений не существует.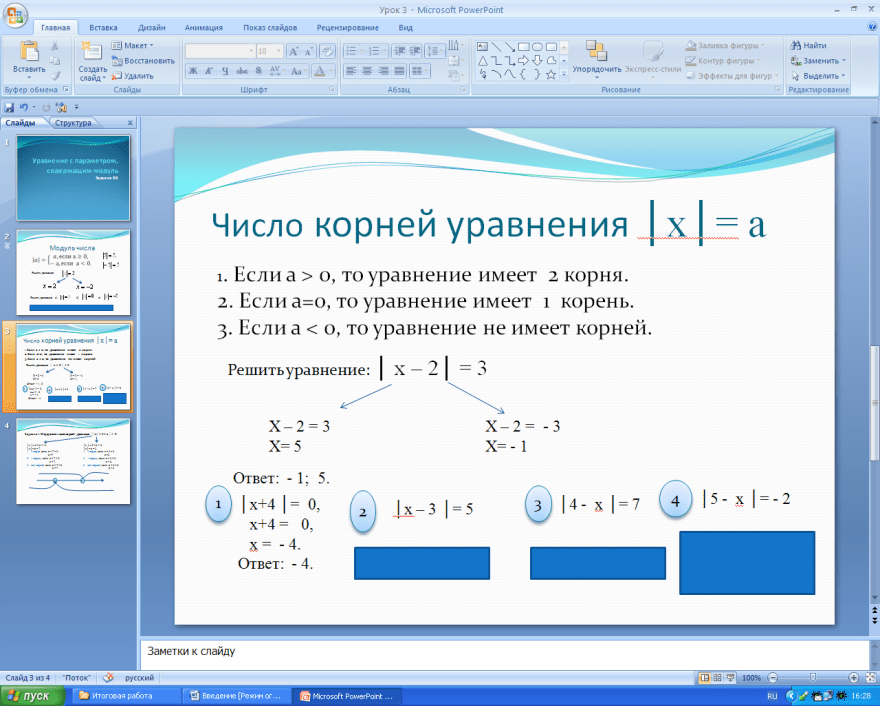

[/скрытый ответ]

Решающие системы с инверсиями

Для следующих упражнений найдите обратную матрицу.

[reveal-answer q=»fs-id1531734″]Показать решение[/reveal-answer]
[скрытый ответ = «fs-id1531734»]

[/скрытый ответ]

[reveal-answer q=»fs-id1514199″]Показать решение[/reveal-answer]
[скрытый ответ = ”fs-id1514199″]

Инверсия не существует.

[/скрытый ответ]

Для следующих упражнений найдите решения, вычислив обратную матрицу.

[reveal-answer q=»fs-id299169″]Показать решение[/reveal-answer]
[скрытый ответ = ”fs-id299169″]

[/скрытый ответ]

[reveal-answer q=»fs-id1531936″]Показать решение[/reveal-answer]
[скрытый ответ = ”fs-id1531936″]

[/скрытый ответ]

Для следующих упражнений напишите систему уравнений для решения каждой задачи. Решите систему уравнений.

Учеников попросили принести в класс свои любимые фрукты. 90% фруктов состояли из бананов, яблок и апельсинов. Если апельсины были вдвое менее популярны, чем бананы, а яблоки были на 5% популярнее бананов, каков процент каждого фрукта в отдельности?

[reveal-answer q=»fs-id1403411″]Показать решение[/reveal-answer]
[скрытый ответ = «fs-id1403411»]

17% апельсины, 34% бананы, 39% яблоки

[/скрытый ответ]

Женское общество устроило распродажу выпечки, чтобы собрать деньги, и продавало пирожные и печенье с шоколадной крошкой.Они оценили пирожные в 2 доллара, а печенье с шоколадной крошкой — в 1 доллар. Они собрали 250 долларов и продали 175 предметов. Сколько пирожных и сколько печенья было продано?

Решающие системы с правилом Крамера

Для следующих упражнений найдите определитель.

[reveal-answer q=»fs-id1504600″]Показать решение[/reveal-answer]
[скрытый ответ = «fs-id1504600»]

0

[/скрытый ответ]

[reveal-answer q=»fs-id1698281″]Показать решение[/reveal-answer]
[скрытый ответ = ”fs-id1698281″]

6

[/скрытый ответ]

В следующих упражнениях используйте правило Крамера для решения линейных систем уравнений.

[reveal-answer q=»fs-id1508832″]Показать решение[/reveal-answer]
[скрытый ответ = ”fs-id1508832″]

[/скрытый ответ]

[reveal-answer q=»fs-id1584180″]Показать решение[/reveal-answer]
[скрытый ответ = ”fs-id1584180″]

( х , 5 х + 3)

[/скрытый ответ]

[reveal-answer q=»fs-id1508865″]Показать решение[/reveal-answer]
[скрытый ответ = ”fs-id1508865″]

[/скрытый ответ]

Практический тест

Является ли следующая упорядоченная пара решением системы уравнений?

с

[reveal-answer q=»fs-id1435942″]Показать решение[/reveal-answer]
[скрытый ответ = ”fs-id1435942″]

Да

[/скрытый ответ]

Для следующих упражнений решите системы линейных и нелинейных уравнений с помощью замены или исключения.Укажите, если решения не существует.

[reveal-answer q=»fs-id1406246″]Показать решение[/reveal-answer]
[скрытый ответ = ”fs-id1406246″]

Решений не существует.

[/скрытый ответ]

[reveal-answer q=»fs-id1455840″]Показать решение[/reveal-answer]
[скрытый ответ = «fs-id1455840»]

[/скрытый ответ]

[reveal-answer q=»fs-id1615810″]Показать решение[/reveal-answer]
[скрытый ответ = ”fs-id1615810″]

[/скрытый ответ]

[reveal-answer q=»fs-id1703248″]Показать решение[/reveal-answer]
[скрытый ответ = «fs-id1703248»]

[/скрытый ответ]

Для следующих упражнений постройте график следующих неравенств.

[reveal-answer q=»1380134″]Показать решение[/reveal-answer][hidden-answer a=»1380134″][/hidden-answer]

Для следующих упражнений запишите разложение на неполные дроби.

[reveal-answer q=»fs-id1519238″]Показать решение[/reveal-answer]
[скрытый ответ = ”fs-id1519238″]

[/скрытый ответ]

Для следующих упражнений выполните заданные матричные операции.

[reveal-answer q=»fs-id1694107″]Показать решение[/reveal-answer]
[скрытый ответ = «fs-id1694107»]

[/скрытый ответ]

[reveal-answer q=»fs-id1583988″]Показать решение[/reveal-answer]
[скрытый ответ = ”fs-id1583988″]

[/скрытый ответ]

[reveal-answer q=»fs-id1295612″]Показать решение[/reveal-answer]
[скрытый ответ = «fs-id1295612»]

[/скрытый ответ]

Если бы какой был определитель, если бы вы поменяли местами строки 1 и 3, умножили бы вторую строку на 12 и взяли обратное?

Перепишите систему линейных уравнений в виде расширенной матрицы.

[reveal-answer q=»fs-id1456561″]Показать решение[/reveal-answer]
[скрытый ответ = ”fs-id1456561″]

[/скрытый ответ]

Перепишите расширенную матрицу в виде системы линейных уравнений.

В следующих упражнениях используйте метод исключения Гаусса для решения систем уравнений.

[reveal-answer q=»fs-id1518911″]Показать решение[/reveal-answer]
[скрытый ответ = ”fs-id1518911″]

Решений не существует.

[/скрытый ответ]

В следующих упражнениях используйте обратную матрицу для решения системы уравнений.

[reveal-answer q=»fs-id1440484″]Показать решение[/reveal-answer]
[скрытый ответ = «fs-id1440484»]

[/скрытый ответ]

В следующих упражнениях используйте правило Крамера для решения систем уравнений.

[reveal-answer q=»fs-id1703905″]Показать решение[/reveal-answer]
[скрытый ответ = «fs-id1703905»]

[/скрытый ответ]

Для следующих упражнений решите систему линейных уравнений.

Фабрика, производящая сотовые телефоны, имеет следующие функции затрат и доходов: и какой диапазон сотовых телефонов они должны производить каждый день, чтобы получить прибыль? Округлите до ближайшего числа, приносящего прибыль.

[reveal-answer q=»fs-id1598123″]Показать решение[/reveal-answer]
[скрытый ответ = ”fs-id1598123″]

32 и более сотовых телефона в день

[/скрытый ответ]

Небольшая ярмарка стоит 1,50 доллара для студентов, 1 доллар для детей и 2 доллара для взрослых.За один день пришло в три раза больше детей, чем взрослых. Всего было продано 800 билетов на общую сумму 1050 долларов. Сколько билетов каждого типа было продано?

Глоссарий

Правило Крамера

метод решения систем уравнений, имеющих такое же количество уравнений, что и переменных, с использованием определителей

определитель

число, рассчитанное с использованием элементов квадратной матрицы, определяющее такую ​​информацию, как наличие решения системы уравнений

уравнений — Брайан 2 2.5.0.3 документация

Уравнения используются как в NeuronGroup , так и в Synapses to:

Примечание

Модели Брайана определяются системами обыкновенного дифференциала первого порядка. уравнения, но в некоторых учебниках вы можете увидеть интегрированную форму синапсов. и документы. Подробнее о том, как это сделать, см. в разделе Преобразование из интегрированной формы в ОДУ. для преобразования между этими представлениями.

Уравнения определяются многострочными строками.

Уравнение представляет собой набор отдельных строк в строке:

1. dx/dt = f : единица (дифференциальное уравнение)

2. x = f : единица измерения (подвыражение)

3. x : единица измерения (параметр)

Каждое уравнение может быть разбито на несколько строк для улучшения форматирования.Также могут быть включены комментарии с использованием # . Субъединицы не допускаются, т. е. надо писать вольт , а не мВ . Это чтобы было понятно, что значения внутри всегда сохраняются в основных единицах, поэтому при получении не может возникнуть путаницы значения из NeuronGroup и отбрасывание единиц. Составные единицы, конечно, также разрешены (например, фарад/метр**2 ). Также можно использовать три специальных «единицы»: 1 обозначает безразмерную переменную с плавающей запятой, boolean и integer обозначают безразмерные переменные соответствующего вида.

Примечание

Для молярной концентрации базовой единицей, которая должна использоваться в уравнениях, является ммоль (или мМ ), , а не молярный . Это связано с тем, что 1 моляр равен 10³ моль/м³ в единицах СИ (т. е. имеет «шкалу» 10³), тогда как 1 миллимоляр соответствует 1 моль/м³.

Определены некоторые специальные переменные: t , dt (время) и xi (белый шум). Имена переменных, начинающиеся со знака подчеркивания, и несколько других имен, имеющих особое значение при определенных условиях. обстоятельства (т.г. имена, оканчивающиеся на _pre или _post ), запрещены.

Для стохастических уравнений с несколькими значениями xi необходимо выяснить, соответствуют ли они одному и тому же или различные шумовые экземпляры. Чтобы сделать это различие, можно использовать произвольный суффикс, например. используя xi_1 несколько раз относится к одной и той же переменной, xi_2 (или xi_inh , xi_alpha и т. д.) относится к другой. Будет выдана ошибка, если вы используете более одного простого xi .Обратите внимание, что шум всегда не зависит от нейронов, вы можете обойти это только ограничение, определив переменную шума как общий параметр и обновив ее с помощью определяемой пользователем функции (например, с помощью run_regularly ), или создайте группу, моделирующую шум, и привяжите ее переменную (см. Связанные переменные).

Строки уравнений могут использовать стандартные арифметические операции для числовых значений. значения, используя синтаксис Python 3. Поддерживаемые операции: + , - , * , / (деление с плавающей запятой), // (половое деление), % (остаток), ** (сила).Для присвоения переменных, например. в операторах сброса, также можно использовать соответствующие присвоения на месте, такие как += . Для сравнения, операции == (равенство), != (неравенство), < , <= , > и >= доступны. Значения истинности можно комбинировать с помощью и и или , или инвертировано с использованием вместо . Обратите внимание, что Брайан не поддерживает любые операции, специфичные для целых чисел, например.г. «побитовое И» или операции сдвига.

Предупреждение

Версии Brian до 2.1.3.1 не поддерживали // в качестве деления этажа оператора и потенциально использовал другую семантику для оператора / в зависимости от того, использовался ли Python 2 или 3. Чтобы правильно написать код и однозначно работает как с более новыми, так и со старыми версиями Брайана, вы можете используйте такие выражения, как 1.0*a/b для принудительного разделения с плавающей запятой (если один из операндов является числом с плавающей запятой, и Python 2, и Python 3 будут использовать деление с плавающей запятой) или floor(a/b) для принудительного разделения пола Обратите внимание, что функция floor всегда возвращает значение с плавающей запятой, если важно, чтобы результат был целочисленным значением, дополнительно оберните его с функцией int .

Брайан также поддерживает стандартные математические функции с теми же именами, что и используемые в библиотеке numpy (например, exp , sqrt , abs , clip , sin , cos , …) — полный список см. в разделе Функции по умолчанию. Обратите внимание, что поддержка для таких функций предусмотрен сам Брайан и перевод на о различных целях генерации кода заботятся автоматически.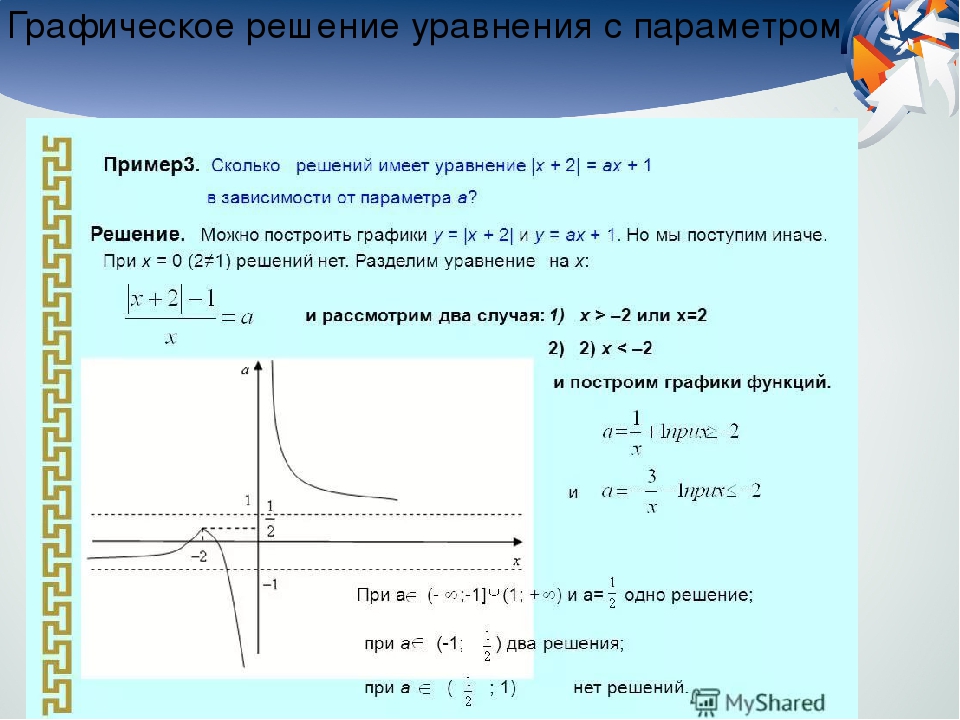 Вам следует поэтому обращайтесь к ним напрямую по имени, а не как e.г. np.sqrt или numpy.sqrt независимо от того, как вы импортированный Брайан или numpy. Это также означает, что вы не можете напрямую ссылаться на произвольные функции из numpy или других библиотек. За подробности о том, как расширить поддержку нестандартных функций, см. Пользовательские функции.

Уравнения, определяющие нейронные или синаптические уравнения, могут содержать ссылки на внешние параметры или функции. Эти ссылки просматриваются в то время что симуляция запущена.Если вы не укажете, где их искать, это будет искать в локальном/глобальном пространстве имен Python (т. е. в блоке кода, где вы вызываете run() ). Если вы хотите переопределить это, вы можете указать явный «пространство имен». Это словарь Python с ключами, являющимися именами переменных, как они появляются в уравнениях, а значения являются желаемым значением этого Переменная. Это пространство имен можно указать либо при создании группы или когда вы можете выполнить функцию run() , используя аргумент ключевого слова пространства имен .

В следующих трех примерах показаны различные способы обеспечения внешнего значения переменных, в данном случае все они имеют одинаковый эффект:

 # Явный аргумент для NeuronGroup
G = NeuronGroup(1, 'dv/dt = -v/tau: 1', namespace={'tau': 10*ms})
сеть = сеть (G)
net.run(10*мс)

# Явный аргумент функции запуска
G = NeuronGroup(1, 'dv/dt = -v/tau: 1')
сеть = сеть (G)
net.run(10*мс, namespace={'tau': 10*мс})

# Неявное пространство имен из контекста
G = NeuronGroup(1, 'dv/dt = -v/tau: 1')
сеть = сеть (G)
тау = 10*мс
сеть.запустить (10 * мс)
 

Подробнее см. Пространства имен.

Следующие темы не обязательны для новичков.

Флаг — это ключевое слово в скобках в конце строки, которое уточняет уравнения. Есть несколько ключевых слов:

управляемый событиями

используется только в синапсах и означает, что дифференциальное уравнение должно быть обновлено только во время событий. Это означает, что уравнение вынесено из непрерывного обновление состояния, и вместо этого генерируется оператор обновления состояния на основе событий, который вставляется в коды событий (до и после). Это может только квалифицировать дифференциальные уравнения синапсов. В настоящее время только одномерный линейные уравнения могут быть обработаны (см. ниже).

, если не рефрактерный

это означает, что переменная не обновляется в течение рефрактерного периода. Это может только квалифицировать дифференциальные уравнения групп нейронов.

константа

это означает, что параметр не будет изменяться во время выполнения. Это позволяет оптимизация в программах обновления состояния.Это может только уточнять параметры.

константа над dt

это означает, что подвыражение будет оцениваться только один раз в начале шага по времени. Это может быть полезно, например. аппроксимировать нелинейный член как постоянна на временном шаге, чтобы использовать линейное численное интегрирование алгоритм. Это также обязательно для подвыражений, которые ссылаются на состояние с сохранением состояния. такие функции, как rand() , чтобы убедиться, что они оцениваются только один раз (иначе эл.г. запись значения с помощью StateMonitor переоценит его и, следовательно, не записывать те же значения, которые используются в других местах). Этот может уточнять только подвыражения.

общий

это означает, что параметр или подвыражение не зависят от нейрона/синапса а скорее одно значение для всего NeuronGroup или Synapses . Общий подвыражение может ссылаться только на другие общие переменные.

linked

это означает, что параметр ссылается на параметр в другой NeuronGroup .Дополнительные сведения см. в разделе Связанные переменные.

Можно указать несколько флагов следующим образом:

 dx/dt = f : единица (флаг1,флаг2)
 

Ниже перечислены все специальные символы, которые Брайан использует в уравнения и кодовые блоки, а также их значения.

dt

Ширина временного шага

i

Индекс нейрона ( NeuronGroup ) или пресинаптического нейрона синапса ( Синапсы )

j

Индекс постсинаптического нейрона синапса

lastspike

Последний выброс нейрона (для рефрактерности)

lastupdate

Время последнего обновления синаптических переменных в управляемом событиями уравнения (определяются только при использовании управляемых событиями уравнений).

N

Количество нейронов ( NeuronGroup ) или синапсов ( Synapses ). Использовать N_pre или N_post для количества пресинаптических или постсинаптические нейроны в разрезе синапсов .

not_refractory

Логическая переменная, которая обычно имеет значение true и значение false, если нейрон в настоящее время находится в рефрактерном состоянии

т

Текущее время

t_in_timesteps

Текущее время, измеренное во временных шагах

xi, xi_*

Стохастический дифференциал в уравнениях

Уравнения, определенные как управляемые событиями, полностью игнорируются при обновлении состояния.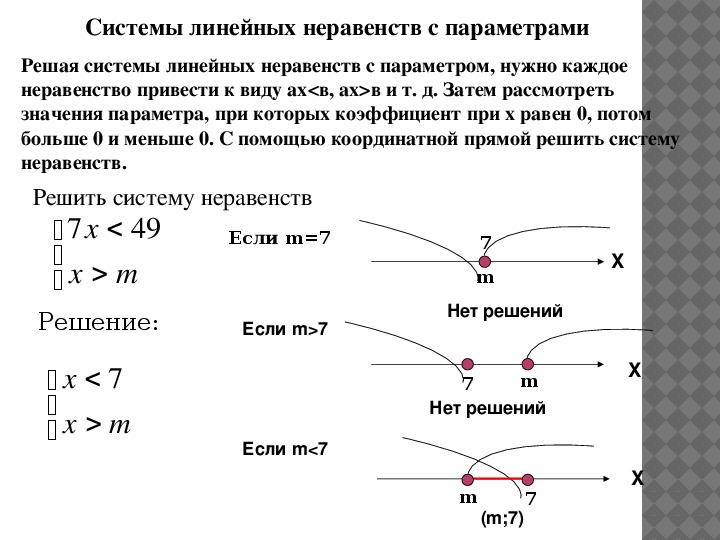 Они определены только как переменные, к которым можно получить доступ извне. Есть дополнительные ограничения:

• Переменная, управляемая событиями, не может использоваться никаким другим уравнением, кроме также событийный.

• Уравнение, управляемое событиями, не может зависеть от дифференциального уравнения, которое не управляемые событиями (напрямую или косвенно через подвыражения). Это может зависеть на постоянный параметр.

В настоящее время автоматические обновления по событиям возможны только для одномерных линейные уравнения, но это может быть расширено в будущем.

Определения модели для NeuronGroup и Synapses могут быть простыми строками или уравнения объекта. Такие объекты можно объединять с помощью оператора добавления:

 eqs = Уравнения ('dx/dt = (yx)/tau: volt')
eqs += Equations('dy/dt = -y/tau: volt')
 

Уравнения позволяют задавать значения в строках, но делают это простым замена строки, например вы можете сделать:

 eqs = Уравнения ('dx/dt = x/tau : вольт', tau=10*мс)
 

, но это точно эквивалентно:

 eqs = Уравнения ('dx/dt = x/(10*ms) : вольт')
 

Объект Equations выполняет базовую проверку синтаксиса и выдает ошибку, если два уравнения, определяющие объединяются одни и те же переменные. Однако он не выполняет модульную проверку, проверку неизвестных идентификаторов или неправильные флаги — все это будет сделано во время инстанцирования объекта NeuronGroup или Synapses .

Объединение уравнений

 >>> мембрана_eqs = Equations('dv/dt = -(v + I)/ тау : вольт')
>>> eqs1 = мембрана_eqs + Equations('''I = sin(2*pi*freq*t) : вольт
... частота: Гц''')
>>> eqs2 = мембрана_eqs + уравнения ('''I : вольт''')
>>> печать (eqs1)
I = грех (2 * пи * частота * т): В
dv/dt = -(v + I)/ тау : V
частота : Гц
>>> печать (eqs2)
dv/dt = -(v + I)/ тау : V
Я : В
 

Замена имен переменных

 >>> general_equation = 'dg/dt = -g / tau: Сименс'
>>> eqs_exc = Equations(general_equation, g='g_e', tau='tau_e')
>>> eqs_inh = уравнения (общее_уравнение, g='g_i', tau='tau_i')
>>> печать (eqs_exc)
dg_e/dt = -g_e / тау_e : S
>>> печать (eqs_inh)
dg_i/dt = -g_i / тау_i : S
 

Вставка значений

 >>> eqs = Equations('dv/dt = мю/тау + сигма/тау**.