История логарифмов — Википедия
История логарифмов как алгебраического понятия прослеживается с античных времён. Идейным источником и стимулом применения логарифмов послужил тот факт (известный ещё Архимеду[1]), что при перемножении степеней с одинаковым основанием их показатели складываются[2]: ab⋅ac=ab+c{\displaystyle a^{b}\cdot a^{c}=a^{b+c}}.
Индийский математик VIII века Вирасена[en], исследуя степенные зависимости, опубликовал таблицу целочисленных показателей (то есть, фактически, логарифмов) для оснований 2, 3, 4[3].
 Логарифмическая таблица М. Штифеля, «Arithmetica integra», 1544
Логарифмическая таблица М. Штифеля, «Arithmetica integra», 1544Решающий шаг был сделан в средневековой Европе. Потребность в сложных расчётах в XVI веке быстро росла, и значительная часть трудностей была связана с умножением и делением многозначных чисел, а также извлечением корней. В конце века нескольким математикам, почти одновременно, пришла в голову идея: заменить трудоёмкое умножение на простое сложение, сопоставив с помощью специальных таблиц геометрическую и арифметическую прогрессии, при этом геометрическая будет исходной[1]. Тогда и деление автоматически заменяется на неизмеримо более простое и надёжное вычитание, упростятся также возведение в степень и извлечение корня.
Первым эту идею опубликовал в своей книге «Arithmetica integra» (1544) Михаэль Штифель, который, впрочем, не приложил серьёзных усилий для практической реализации своей идеи[4][5]. Главной заслугой Штифеля является переход от целых показателей степени к произвольным рациональным
Джон Непер и его «удивительная таблица логарифмов»[править | править код]

В 1614 году шотландский математик-любитель Джон Непер опубликовал на латинском языке сочинение под названием «Описание удивительной таблицы логарифмов» (лат. Mirifici Logarithmorum Canonis Descriptio). В нём было краткое описание логарифмов и их свойств, а также 8-значные таблицы логарифмов синусов, косинусов и тангенсов, с шагом 1′. Термин логарифм, предложенный Непером, утвердился в науке. Теорию логарифмов Непер изложил в другой своей книге «Построение удивительной таблицы логарифмов» (лат. Mirifici Logarithmorum Canonis Constructio), изданной посмертно в 1619 году его сыном Робертом.
Судя по документам, техникой логарифмирования Непер владел уже к 1594 году[7]. Непосредственной целью её разработки было облегчить Неперу сложные астрологические расчёты[8]; именно поэтому в таблицы были включены только логарифмы тригонометрических функций.
Понятия функции тогда ещё не было, и Непер определил логарифм кинематически, сопоставив равномерное и логарифмически-замедленное движение; например, логарифм синуса он определил следующим образом[9]:
Логарифм данного синуса есть число, которое арифметически возрастало всегда с той же скоростью, с какой полный синус начал геометрически убывать.
В современных обозначениях кинематическую модель Непера можно изобразить дифференциальным уравнением[10]:
- dxx=−dyM{\displaystyle {\frac {dx}{x}}=-{\frac {dy}{M}}},
где M — масштабный множитель, введённый для того, чтобы значение получилось целым числом с нужным количеством знаков (десятичные дроби тогда ещё не нашли широкого применения). Непер взял M = 10 000 000.
Строго говоря, Непер табулировал не ту функцию, которая сейчас называется логарифмом. Если обозначить его функцию LogNap(x){\displaystyle \operatorname {LogNap} (x)}, то она связана с натуральным логарифмом следующим образом[10]:
- LogNap(x)=M⋅(ln(M)−ln(x)){\displaystyle \operatorname {LogNap} (x)=M\cdot (\ln(M)-\ln(x))}
Очевидно, LogNap(M)=0{\displaystyle \operatorname {LogNap} (M)=0}, то есть логарифм «полного синуса» (соответствующего 90°) есть нуль — этого и добивался Непер своим определением. Также он хотел, чтобы все логарифмы были положительны; нетрудно убедиться, что это условие для x<M{\displaystyle x<M} выполняется. LogNap(0)=∞{\displaystyle \operatorname {LogNap} (0)=\infty }.
Основное свойство логарифма Непера: если величины образуют геометрическую прогрессию, то их логарифмы образуют прогрессию арифметическую. Однако правила логарифмирования для неперовой функции отличались от правил для современного логарифма, например:
- LogNap(a⋅b)=LogNap(a)+LogNap(b)−LogNap(1){\displaystyle \operatorname {LogNap} (a\cdot b)=\operatorname {LogNap} (a)+\operatorname {LogNap} (b)-\operatorname {LogNap} (1)}
Как вскоре обнаружилось, из-за ошибки в алгоритме все значения таблицы Непера содержали неверные цифры после шестого знака
Спустя несколько лет после книги Непера появились логарифмические таблицы, использующие более близкое к современному понимание логарифма. Лондонский профессор Генри Бригс издал 14-значные таблицы десятичных логарифмов (1617), причём не для тригонометрических функций, а для произвольных целых чисел до 1000 (7 лет спустя Бригс увеличил количество чисел до 20000). В 1619 году лондонский учитель математики Джон Спайделл (англ. John Speidell) переиздал логарифмические таблицы Непера, исправленные и дополненные так, что они фактически стали таблицами натуральных логарифмов. У Спайделла тоже были и логарифмы самих чисел до 1000 (причём логарифм единицы, как и у Бригса, был равен нулю) — хотя масштабирование до целых чисел Спайделл сохранил
[13][14].В 1620-е годы Эдмунд Уингейт и Уильям Отред изобрели первую логарифмическую линейку, до появления карманных калькуляторов служившую незаменимым расчётным орудием инженера[15]. С помощью этого компактного инструмента можно быстро производить все алгебраические операции, в том числе с участием тригонометрических функций[16]. Точность расчётов — около 3 значащих цифр.

Вскоре выяснилось, что место логарифмов в математике не ограничивается расчётными удобствами. В 1629 году бельгийский математик Грегуар де Сен-Венсан показал, что площадь под гиперболой y=1x{\displaystyle y={\frac {1}{x}}} меняется по логарифмическому закону[17]. В 1668 году немецкий математик Николас Меркатор (Кауфман) открыл и опубликовал в своей книге Logarithmotechnia разложение логарифма в бесконечный «ряд Меркатора»[18]. По мнению многих историков, появление логарифмов оказало сильное влияние на многие математические концепции, в том числе:
- Формирование и признание общего понятия иррациональных и трансцендентных чисел[19].
- Появление показательной функции и общего понятия числовой функции, числа Эйлера, развитие теории разностных уравнений [20].
- Начало работы с бесконечными рядами[18].
- Общие методы решения дифференциальных уравнений различных типов.
- Существенное развитие теории численных методов, требуемых для вычисления точных логарифмических таблиц.
До конца XIX века общепринятого обозначения логарифма не было, основание a указывалось то левее и выше символа log, то над ним. В конечном счёте математики пришли к выводу, что наиболее удобное место для основания — ниже строки, после символа log: logab{\displaystyle \log _{a}b}. Краткие обозначения наиболее употребительных видов логарифма — lg,ln{\displaystyle \lg ,\;\ln } для десятичного и натурального — появились намного раньше сразу у нескольких авторов и закрепились окончательно также к концу XIX века[21].
Близкое к современному понимание логарифмирования — как операции, обратной возведению в степень — впервые появилось у Валлиса (1685) и Иоганна Бернулли (1694), а окончательно было узаконено Эйлером
Из свойств логарифма следует, что вместо трудоёмкого умножения многозначных чисел достаточно найти (по таблицам) и сложить их логарифмы, а потом по тем же таблицам (раздел «Антилогарифмы») выполнить потенцирование, то есть найти значение результата по его логарифму. Выполнение деления отличается только тем, что логарифмы вычитаются.
Первые таблицы логарифмов опубликовал Джон Непер (1614), и они содержали только логарифмы тригонометрических функций, причём с ошибками. Независимо от него свои таблицы опубликовал Йост Бюрги, друг Кеплера (1620). В 1617 году оксфордский профессор математики Генри Бригс опубликовал таблицы, которые уже включали десятичные логарифмы самих чисел, от 1 до 1000, с 8 (позже — с 14) знаками. Но и в таблицах Бригса обнаружились ошибки. Первое безошибочное издание на основе таблиц Георга Веги (1783) появилось только в 1857 году в Берлине (таблицы Бремикера)
[23].В России первые таблицы логарифмов были изданы в 1703 году при участии Л. Ф. Магницкого[24]. В СССР выпускались несколько сборников таблиц логарифмов[25]:
- Брадис В. М. Четырёхзначные математические таблицы. М.: Дрофа, 2010, ISBN 978-5-358-07433-0. Таблицы Брадиса, издаваемые с 1921 года, использовались в учебных заведениях и в инженерных расчётах, не требующих большой точности. Они содержали мантиссы десятичных логарифмов чисел и тригонометрических функций, натуральные логарифмы и некоторые другие полезные расчётные инструменты.
- Вега Г.
- Бремикер К. Логарифмо-тригонометрические таблицы. М.: Наука, 1962. 664 с. Классические шестизначные таблицы, удобные для расчётов с тригонометрическими функциями.
- Пятизначные таблицы натуральных значений тригонометрических величин, их логарифмов и логарифмов чисел, 6-е издание, М.: Наука, 1972.
- Таблицы натуральных логарифмов, 2-е издание, в 2 томах, М.: Наука, 1971.
- Десятизначные таблицы логарифмов комплексных чисел. М., 1952.
Расширение логарифма на комплексную область[править | править код]
Первые попытки распространить логарифмы на комплексные числа предпринимали на рубеже XVII—XVIII веков Лейбниц и Иоганн Бернулли, однако создать целостную теорию им не удалось — в первую очередь по той причине, что тогда ещё не было ясно определено само понятие логарифма[26]. Дискуссия по этому поводу велась сначала между Лейбницем и Бернулли, а в середине XVIII века — между Д’Аламбером и Эйлером. Бернулли и Д’Аламбер считали, что следует определить log(−x)=log(x){\displaystyle \log(-x)=\log(x)}, в то время как Лейбниц доказывал, что логарифм отрицательного числа есть мнимое число
[26]. Полная теория логарифмов отрицательных и комплексных чисел была опубликована Эйлером в 1747—1751 годах и по существу ничем не отличается от современной[27]. Хотя спор продолжался (Д’Аламбер отстаивал свою точку зрения и подробно аргументировал её в статье своей «Энциклопедии» и в других трудах), подход Эйлера к концу XVIII века получил всеобщее признание.В XIX веке, с развитием комплексного анализа, исследование комплексного логарифма стимулировало новые открытия. Гаусс в 1811 году разработал полную теорию многозначности логарифмической функции[28], определяемой как интеграл от 1z{\displaystyle {\frac {1}{z}}}. Риман, опираясь на уже известные факты об этой и аналогичных функциях, построил общую теорию римановых поверхностей.
Разработка теории конформных отображений показала, что меркаторская проекция в картографии, возникшая ещё до открытия логарифмов (1550), может быть описана как комплексный логарифм[29].
- Абельсон И. Б. Рождение логарифмов. — М.—Л.: Гостехиздат, 1948. — 231 с.
- Гиршвальд Л. Я. История открытия логарифмов. — Харьков: Изд-во Харьковского университета, 1952. — 33 с.
- Клейн Ф. Элементарная математика с точки зрения высшей. — М.: Наука, 1987. — Т. I. Арифметика. Алгебра. Анализ. — 432 с.
- Математика XVII столетия // История математики / Под редакцией А. П. Юшкевича, в трёх томах. — М.: Наука, 1970. — Т. II.
- Математика XVIII столетия // История математики / Под редакцией А. П. Юшкевича, в трёх томах. — М.: Наука, 1972. — Т. III.
- Колмогоров А. Н., Юшкевич А. П. (ред.). Математика XIX века. Геометрия. Теория аналитических функций. — М.: Наука, 1981. — Т. II.
- Успенский Я. В. Очерк истории логарифмов. — Петроград: Научное книгоиздательство, 1923. — 78 с.
- ↑ 1 2 Успенский Я. В. Очерк истории логарифмов, 1923, с. 9.
- ↑ Клейн Ф. Элементарная математика с точки зрения высшей, 1987, с. 206.
- ↑ Gupta, R. C. (2000), «History of Mathematics in India», in Hoiberg, Dale & Ramchandani, Students’ Britannica India: Select essays, New Delhi: Popular Prakashan, с. 329
- ↑ История математики, том II, 1970, с. 54—55.
- ↑ Vivian Shaw Groza, Susanne M. Shelley (1972), Precalculus mathematics, New York: Holt, Rinehart, Winston, с. 182, ISBN 978-0-03-077670-0, <https://books.google.com/?id=yM_lSq1eJv8C&pg=PA182&dq=%22arithmetica+integra%22+logarithm&q=stifel>
- ↑ Клейн Ф. Элементарная математика с точки зрения высшей, 1987, с. 210.
- ↑ Успенский Я. В. Очерк истории логарифмов, 1923, с. 13.
- ↑ История математики, том II, 1970, с. 56.
- ↑ Хрестоматия по истории математики. Математический анализ. Теория вероятностей / Под ред. А. П. Юшкевича. — М.: Просвещение, 1977. — С. 40. — 224 с.
- ↑ 1 2 История математики, том II, 1970, с. 59.
- ↑ 1 2 История математики, том II, 1970, с. 61.
- ↑ Успенский Я. В. Очерк истории логарифмов, 1923, с. 39.
- ↑ История математики, том II, 1970, с. 63.
- ↑ Charles Hutton. Mathematical Tables. London, 1811, p. 30.
- ↑ История математики, том II, 1970, с. 65-66.
- ↑ Березин С. И. Счётная логарифмическая линейка. — М.: Машиностроение, 1968.
- ↑ История математики, том II, 1970, с. 133.
- ↑ 1 2 Успенский Я. В. Очерк истории логарифмов, 1923, с. 52.
- ↑ Клейн Ф. Элементарная математика с точки зрения высшей, 1987, с. 51, 286, 352.
- ↑ Клейн Ф. Элементарная математика с точки зрения высшей, 1987, с. 213, 217.
- ↑ Florian Cajori. A History of Mathematics, 5th ed (неопр.). — AMS Bookstore, 1991. — С. 152. — ISBN 0821821024.
- ↑ Рыбников К. А. История математики. В двух томах. — М.: Изд. МГУ, 1963. — Т. II. — С. 25.
- ↑ История математики, том II, 1970, с. 62.
- ↑ Гнеденко Б. В. Очерки по истории математики в России, издание 2-е. — М.: КомКнига, 2005. — С. 66. — 296 с. — ISBN 5-484-00123-4.
- ↑ Логарифмические таблицы //Большая советская энциклопедия.
- ↑ 1 2 История математики, том III, 1972, с. 325-328.
- ↑ Рыбников К. А. История математики. В двух томах. — М.: Изд. МГУ, 1963. — Т. II. — С. 27, 230—231.
- ↑ Математика XIX века. Том II: Геометрия. Теория аналитических функций, 1981, с. 122-123.
- ↑ Клейн Ф. Элементарная математика с точки зрения высшей. — М.: Наука, 1987. — Т. II. Геометрия. — С. 159—161. — 416 с.
Определение логарифма | Логарифмы
Определение
Логарифм — это показатель степени, в которую надо возвести основание, чтобы получить число, стоящее под знаком логарифма.
Если логарифм b по основанию a равен c, это означает, что основание a в степени c равно числу b, стоящему под знаком логарифма:
Примеры.
так как, чтобы получить 49 (число, стоящее под знаком логарифма), основание 7 нужно возвести в квадрат.
так как, чтобы получить 81, основание 3 нужно возвести в степень 4.
так как
так как
так как
так как
так как
Запись некоторых логарифмов отличается от стандартной.
Например, вместо
пишут
Логарифм по основанию 10 называется десятичным. О нем и о свойствах логарифмов — дальше.
Комплексный логарифм — Википедия
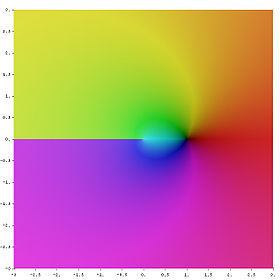 Наглядное представление функции натурального комплексного логарифма (главная ветвь). Аргумент значения функции обозначается цветом, а модуль — яркостью.
Наглядное представление функции натурального комплексного логарифма (главная ветвь). Аргумент значения функции обозначается цветом, а модуль — яркостью.Комплексный логарифм — аналитическая функция, получаемая распространением вещественного логарифма на всю комплексную плоскость (кроме нуля). Существует несколько эквивалентных способов такого распространения. Данная функция имеет широкое применение в комплексном анализе. В отличие от вещественного случая, функция комплексного логарифма многозначна.
Для комплексных чисел логарифм можно определить так же, как для вещественных, то есть как обращение показательной функции. На практике используется практически только натуральный комплексный логарифм, основание которого — число Эйлера e{\displaystyle e}: он обозначается обычно Lnz{\displaystyle \mathrm {Ln} \,z}.
Натуральный логарифм комплексного числа z{\displaystyle z} определяется[1] как решение w{\displaystyle w} уравнения ew=z.{\displaystyle e^{w}=z.} |
Другие, эквивалентные данному, варианты определения приведены ниже.
В поле комплексных чисел решение этого уравнения, в отличие от вещественного случая, не определено однозначно. Например, согласно тождеству Эйлера, eπi=−1{\displaystyle e^{\pi i}=-1}; однако также e−πi=e3πi=e5πi⋯=−1{\displaystyle e^{-\pi i}=e^{3\pi i}=e^{5\pi i}\dots =-1}. Это связано с тем, что показательная функция вдоль мнимой оси является периодической (с периодом 2π{\displaystyle 2\pi })[2], и одно и то же значение функция принимает бесконечно много раз. Таким образом, комплексная логарифмическая функция w=Lnz{\displaystyle w=\mathrm {Ln} \,z} является многозначной.
Комплексный нуль не имеет логарифма, поскольку комплексная экспонента не принимает нулевого значения. Ненулевое z{\displaystyle z} можно представить в показательной форме:
- z=r⋅ei(φ+2πk),{\displaystyle z=r\cdot e^{i(\varphi +2\pi k)}\;\;,} где k{\displaystyle k} — произвольное целое число
Тогда Lnz{\displaystyle \mathrm {Ln} \,z} находится по формуле[3]:
- Lnz=lnr+i(φ+2πk){\displaystyle \mathrm {Ln} \,z=\ln r+i\left(\varphi +2\pi k\right)}
Здесь lnr=ln|z|{\displaystyle \ln \,r=\ln \,|z|} — вещественный логарифм. Отсюда вытекает:
Комплексный логарифм Lnz{\displaystyle \mathrm {Ln} \,z} существует для любого z≠0{\displaystyle z\neq 0}, и его вещественная часть определяется однозначно, в то время как мнимая часть имеет бесконечное множество значений, различающихся на целое кратное 2π.{\displaystyle 2\pi .} |
 Вещественная часть комплексного логарифма
Вещественная часть комплексного логарифмаИз формулы видно, что у одного и только одного из значений мнимая часть находится в интервале (−π,π]{\displaystyle (-\pi ,\pi ]}. Это значение называется главным значением комплексного натурального логарифма[1]. Соответствующая (уже однозначная) функция называется главной ветвью логарифма и обозначается lnz{\displaystyle \ln \,z}. Иногда через lnz{\displaystyle \ln \,z} также обозначают значение логарифма, лежащее не на главной ветви. Если z{\displaystyle z} — вещественное число, то главное значение его логарифма совпадает с обычным вещественным логарифмом.
Из приведённой формулы также следует, что вещественная часть логарифма определяется следующим образом через компоненты аргумента:
- Re(ln(x+iy))=12ln(x2+y2){\displaystyle \operatorname {Re} (\ln(x+iy))={\frac {1}{2}}\ln(x^{2}+y^{2})}
На рисунке показано, что вещественная часть как функция компонентов центрально-симметрична и зависит только от расстояния до начала координат. Она получается вращением графика вещественного логарифма вокруг вертикальной оси. С приближением к нулю функция стремится к −∞.{\displaystyle -\infty .}
Логарифм отрицательного числа находится по формуле[3]:
- Ln(−x)=lnx+iπ(2k+1)(x>0, k=0,±1,±2…){\displaystyle \mathrm {Ln} (-x)=\ln x+i\pi (2k+1)\qquad (x>0,\ k=0,\pm 1,\pm 2\dots )}
Примеры значений комплексного логарифма[править | править код]
Приведём главное значение логарифма (ln{\displaystyle \ln }) и общее его выражение (Ln{\displaystyle \mathrm {Ln} }) для некоторых аргументов:
- ln(1)=0;Ln(1)=2kπi{\displaystyle \ln(1)=0;\;\mathrm {Ln} (1)=2k\pi i}
- ln(−1)=iπ;Ln(−1)=(2k+1)iπ{\displaystyle \ln(-1)=i\pi ;\;\mathrm {Ln} (-1)=(2k+1)i\pi }
- ln(i)=iπ2;Ln(i)=12iπ(4k+1){\displaystyle \ln(i)=i{\frac {\pi }{2}};\;\mathrm {Ln} (i)={\frac {1}{2}}i\pi (4k+1)}
Следует быть осторожным при преобразованиях комплексных логарифмов, принимая во внимание, что они многозначны, и поэтому из равенства логарифмов каких-либо выражений не следует равенство этих выражений. Пример ошибочного рассуждения:
- iπ=ln(−1)=ln((−i)2)=2ln(−i)=2(−iπ/2)=−iπ{\displaystyle i\pi =\ln(-1)=\ln((-i)^{2})=2\ln(-i)=2(-i\pi /2)=-i\pi } — явная ошибка.
Отметим, что слева стоит главное значение логарифма, а справа — значение из нижележащей ветви (k=−1{\displaystyle k=-1}). Причина ошибки — неосторожное использование свойства loga(bp)=p logab{\displaystyle \log _{a}{(b^{p})}=p~\log _{a}b}, которое, вообще говоря, подразумевает в комплексном случае весь бесконечный набор значений логарифма, а не только главное значение.
Комплексная логарифмическая функция и риманова поверхность[править | править код]
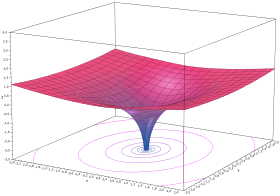
 Риманова поверхность для комплексного логарифма
Риманова поверхность для комплексного логарифмаВ комплексном анализе вместо рассмотрения многозначных функций на комплексной плоскости принято иное решение: рассматривать функцию как однозначную, но определённую не на плоскости, а на более сложном многообразии, которое называется римановой поверхностью[4]. Комплексная логарифмическая функция также относится к этой категории: её образ (см. рисунок) состоит из бесконечного числа ветвей, закрученных в виде спирали. Эта поверхность непрерывна и односвязна. Единственный нуль у функции (первого порядка) получается при z=1{\displaystyle z=1}. Особые точки: z=0{\displaystyle z=0} и z=∞{\displaystyle z=\infty } (точки разветвления бесконечного порядка)[5].
В силу односвязности риманова поверхность логарифма является универсальной накрывающей[6] для комплексной плоскости без точки 0{\displaystyle 0}.
Логарифм комплексного числа также может быть определён как аналитическое продолжение вещественного логарифма на всю комплексную плоскость. Пусть кривая Γ{\displaystyle \Gamma } начинается в единице, заканчивается в z, не проходит через нуль и не пересекает отрицательную часть вещественной оси. Тогда главное значение логарифма в конечной точке w{\displaystyle w} кривой Γ{\displaystyle \Gamma } можно определить по формуле[5]:
- lnz=∫Γduu{\displaystyle \ln z=\int \limits _{\Gamma }{du \over u}}
Если Γ{\displaystyle \Gamma } — простая кривая (без самопересечений), то для чисел, лежащих на ней, логарифмические тождества можно применять без опасений, например:
- ln(wz)=lnw+lnz, ∀z,w∈Γ:zw∈Γ{\displaystyle \ln(wz)=\ln w+\ln z,~\forall z,w\in \Gamma \colon zw\in \Gamma }
Главная ветвь логарифмической функции непрерывна и дифференцируема на всей комплексной плоскости, кроме отрицательной части вещественной оси, на которой мнимая часть скачком меняется на 2π{\displaystyle 2\pi }. Но этот факт есть следствие искусственного ограничения мнимой части главного значения интервалом (−π,π]{\displaystyle (-\pi ,\pi ]}. Если рассмотреть все ветви функции, то непрерывность имеет место во всех точках, кроме нуля, где функция не определена. Если разрешить кривой Γ{\displaystyle \Gamma } пересекать отрицательную часть вещественной оси, то первое такое пересечение переносит результат с ветви главного значения на соседнюю ветвь, а каждое следующее пересечение вызывает аналогичное смещение по ветвям логарифмической функции[5] (см. рисунок).
Из формулы аналитического продолжения следует, что на любой ветви логарифма[2]:
- ddzlnz=1z{\displaystyle {\frac {d}{dz}}\ln z={1 \over z}}
Для любой окружности S{\displaystyle S}, охватывающей точку 0{\displaystyle 0}:
- ∮Sdzz=2πi{\displaystyle \oint \limits _{S}{dz \over z}=2\pi i}
Интеграл берётся в положительном направлении (против часовой стрелки). Это тождество лежит в основе теории вычетов.
Можно также определить аналитическое продолжение комплексного логарифма с помощью версий ряда Меркатора, известных для вещественного случая:
| ln(1+x)=x−x22+x33−x44+…{\displaystyle \ln(1+x)=x-{\frac {x^{2}}{2}}+{\frac {x^{3}}{3}}-{\frac {x^{4}}{4}}+\dots } | (Ряд 1) |
| ln(1+x1−x)=2(x+x33+x55+x77+…){\displaystyle \ln \left({\frac {1+x}{1-x}}\right)=2\left(x+{\frac {x^{3}}{3}}+{\frac {x^{5}}{5}}+{\frac {x^{7}}{7}}+\dots \right)} | (Ряд 2) |
Однако из вида этих рядов следует, что в единице сумма ряда равна нулю, то есть ряд относится только к главной ветви многозначной функции комплексного логарифма. Радиус сходимости обоих рядов равен 1.
Связь с обратными тригонометрическими и гиперболическими функциями[править | править код]
Поскольку комплексные тригонометрические функции связаны с экспонентой (формула Эйлера), то комплексный логарифм как обратная к экспоненте функция связан с обратными тригонометрическими функциями[7][8]:
- Arcsinz=−iLn(iz+1−z2){\displaystyle \operatorname {Arcsin} z=-i\operatorname {Ln} (iz+{\sqrt {1-z^{2}}})}
- Arccosz=−iLn(z+i1−z2){\displaystyle \operatorname {Arccos} z=-i\operatorname {Ln} (z+i{\sqrt {1-z^{2}}})}
- Arctgz=−i2ln1+zi1−zi+kπ(z≠±i){\displaystyle \operatorname {Arctg} z=-{\frac {i}{2}}\ln {\frac {1+zi}{1-zi}}+k\pi \;(z\neq \pm i)}
- Arcctgz=−i2lnzi−1zi+1+kπ(z≠±i){\displaystyle \operatorname {Arcctg} z=-{\frac {i}{2}}\ln {\frac {zi-1}{zi+1}}+k\pi \;(z\neq \pm i)}
Гиперболические функции на комплексной плоскости можно рассматривать как тригонометрические функции мнимого аргумента, поэтому и здесь имеет место связь с логарифмом [8]:
- Arshz=Ln(z+z2+1){\displaystyle \operatorname {Arsh} z=\operatorname {Ln} (z+{\sqrt {z^{2}+1}})} — обратный гиперболический синус
- Archz=Ln(z+z2−1){\displaystyle \operatorname {Arch} z=\operatorname {Ln} \left(z+{\sqrt {z^{2}-1}}\right)} — обратный гиперболический косинус
- Arthz=12Ln(1+z1−z){\displaystyle \operatorname {Arth} z={\frac {1}{2}}\operatorname {Ln} \left({\frac {1+z}{1-z}}\right)} — обратный гиперболический тангенс
- Arcthz=12Ln(z+1z−1){\displaystyle \operatorname {Arcth} z={\frac {1}{2}}\operatorname {Ln} \left({\frac {z+1}{z-1}}\right)} — обратный гиперболический котангенс
Первые попытки распространить логарифмы на комплексные числа предпринимали на рубеже XVII—XVIII веков Лейбниц и Иоганн Бернулли, однако создать целостную теорию им не удалось — в первую очередь по той причине, что тогда ещё не было ясно определено само понятие логарифма[9]. Дискуссия по этому поводу велась сначала между Лейбницем и Бернулли, а в середине XVIII века — между Д’Аламбером и Эйлером. Бернулли и Д’Аламбер считали, что следует определить log(−x)=log(x){\displaystyle \log(-x)=\log(x)}, в то время как Лейбниц доказывал, что логарифм отрицательного числа есть мнимое число[9]. Полная теория логарифмов отрицательных и комплексных чисел была опубликована Эйлером в 1747—1751 годах и по существу ничем не отличается от современной[10]. Хотя спор продолжался (Д’Аламбер отстаивал свою точку зрения и подробно аргументировал её в статье своей «Энциклопедии» и в других трудах), подход Эйлера к концу XVIII века получил всеобщее признание.
В XIX веке, с развитием комплексного анализа, исследование комплексного логарифма стимулировало новые открытия. Гаусс в 1811 году разработал полную теорию многозначности логарифмической функции[11], определяемой как интеграл от 1z{\displaystyle {\frac {1}{z}}}. Риман, опираясь на уже известные факты об этой и аналогичных функциях, построил общую теорию римановых поверхностей.
Разработка теории конформных отображений показала, что меркаторская проекция в картографии, возникшая ещё до открытия логарифмов (1550), может быть описана как комплексный логарифм[12].
- Теория логарифмов
- История логарифмов
- Математика XVIII столетия // История математики / Под редакцией А. П. Юшкевича, в трёх томах. — М.: Наука, 1972. — Т. III.
- Колмогоров А. Н., Юшкевич А. П. (ред.). Математика XIX века. Геометрия. Теория аналитических функций. — М.: Наука, 1981. — Т. II.
- ↑ 1 2 Логарифмическая функция. // Математическая энциклопедия (в 5 томах). — М.: Советская Энциклопедия, 1982. — Т. 3.
- ↑ 1 2 Фихтенгольц Г. М. Курс дифференциального и интегрального исчисления, 1966, Том II, стр. 520-522..
- ↑ 1 2 Корн Г., Корн Т. Справочник по математике, 1973, с. 623..
- ↑ Свешников А. Г., Тихонов А. Н. Теория функций комплексной переменной, 1967, с. 92-94..
- ↑ 1 2 3 Свешников А. Г., Тихонов А. Н. Теория функций комплексной переменной, 1967, с. 45-46, 99-100..
- ↑ Болтянский В. Г., Ефремович В. А. Наглядная топология. — М.: Наука, 1982. — С. 112. — (Библиотечка Квант, выпуск 21).
- ↑ Фихтенгольц Г. М. Курс дифференциального и интегрального исчисления, 1966, Том II, стр. 522-526..
- ↑ 1 2 Корн Г., Корн Т. Справочник по математике, 1973, с. 624..
- ↑ 1 2 История математики, том III, 1972, с. 325-328..
- ↑ Рыбников К. А. История математики. В двух томах. — М.: Изд. МГУ, 1963. — Т. II. — С. 27, 230-231..
- ↑ Математика XIX века. Том II: Геометрия. Теория аналитических функций, 1981, с. 122-123..
- ↑ Клейн Ф. Элементарная математика с точки зрения высшей. — М.: Наука, 1987. — Т. II. Геометрия. — С. 159-161. — 416 с.
Логарифмы — это… Что такое Логарифмы?
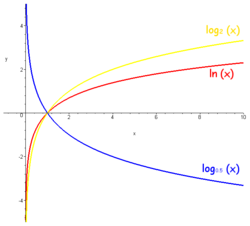
Рис. 1. Графики логарифмических функций
Логарифм числа b по основанию a определяется как показатель степени, в которую надо возвести число a, чтобы получить число b. Обозначение: 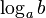 . Из определения следует, что записи
. Из определения следует, что записи 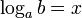 и ax = b равносильны.
и ax = b равносильны.
Пример: 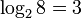 , потому что 23 = 8.
, потому что 23 = 8.
Вещественный логарифм
Логарифм вещественного числа logab имеет смысл при 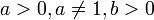 .
.
Наиболее широкое применение нашли следующие виды логарифмов.
Если рассматривать логарифмируемое число как переменную, мы получим логарифмическую функцию, например: 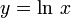 . Эта функция определена в правой части числовой прямой: x > 0, непрерывна и дифференцируема там (см. рис. 1).
. Эта функция определена в правой части числовой прямой: x > 0, непрерывна и дифференцируема там (см. рис. 1).
Свойства
Натуральные логарифмы
Для производной натурального логарифма справедлива простая формула:
По этой причине в математических исследованиях преимущественно используют именно натуральные логарифмы. Они нередко появляются при решении дифференциальных уравнений, исследовании статистических зависимостей (например, распределения простых чисел) и т. п.
При 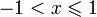 справедливо равенство
справедливо равенство
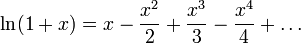 | (1) |
В частности,
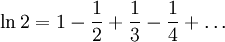 |
Формула (1) не имеет большой практической ценности из-за того, что ряд очень медленно сходится и значение x ограничено весьма узким диапазоном. Однако нетрудно получить из неё более удобную формулу:
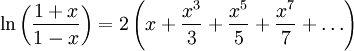 | (2) |
Этот ряд сходится быстрее, а кроме того, левая часть формулы теперь может выразить логарифм любого положительного числа.
Связь с десятичным логарифмом: 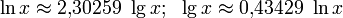 .
.
Десятичные логарифмы

Рис. 2. Логарифмическая шкала
Логарифмы по основанию 10 (обозначение: lg a) до изобретения калькуляторов широко применялись для вычислений. Неравномерная шкала десятичных логарифмов обычно наносится и на логарифмические линейки. Подобная шкала широко используется в различных областях науки, например:
Логарифмическая шкала также широко применяется для выявления показателя степени в степенных зависимостях и коэффициента в показателе экспоненты. При этом график, построенный в логарифмическом масштабе по одной или двум осям, принимает вид прямой, более простой для исследования.
Комплексный логарифм
Многозначная функция
Для комплексных чисел логарифм определяется так же, как вещественный. Начнём с натурального логарифма, который обозначим 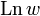 и определим как множество всех комплексных чисел z таких, что ez = w. Комплексный логарифм существует для любого
и определим как множество всех комплексных чисел z таких, что ez = w. Комплексный логарифм существует для любого 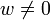 , и его вещественная часть определяется однозначно, в то время как мнимая имеет бесконечное множество значений. По этой причине его называют многозначной функцией. Если представить w в показательной форме:
, и его вещественная часть определяется однозначно, в то время как мнимая имеет бесконечное множество значений. По этой причине его называют многозначной функцией. Если представить w в показательной форме:
 ,
,
то логарифм 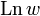 находится по формуле:
находится по формуле:
Здесь 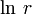 — вещественный логарифм, r = | w | , k — произвольное целое число. Значение, получаемое при k = 0, называется главным значением комплексного натурального логарифма; принято брать в нём значение аргумента
— вещественный логарифм, r = | w | , k — произвольное целое число. Значение, получаемое при k = 0, называется главным значением комплексного натурального логарифма; принято брать в нём значение аргумента 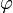 в интервале ( − π,π]. Соответствующая (уже однозначная) функция называется главной ветвью логарифма и обозначается
в интервале ( − π,π]. Соответствующая (уже однозначная) функция называется главной ветвью логарифма и обозначается 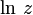 . Иногда через
. Иногда через 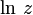 также обозначают значение логарифма, лежащее не на главной ветви.
также обозначают значение логарифма, лежащее не на главной ветви.
Из формулы следует:
- Вещественная часть логарифма определяется по формуле:
- Логарифм отрицательного числа находится по формуле:
Примеры (приведено главное значение логарифма):
- ln( − 1) = iπ


Аналогично рассматриваются комплексные логарифмы с другим основанием. Следует, однако, быть осторожным при преобразованиях комплексных логарифмов, принимая во внимание, что они многозначны, и поэтому из равенства логарифмов каких-либо выражений не следует равенство этих выражений. Пример ошибочного рассуждения:
- iπ = ln( − 1) = ln(( − i)2) = 2ln( − i) = 2( − iπ / 2) = − iπ — явная нелепость.
Отметим, что слева стоит главное значение логарифма, а справа — значение из нижележащей ветви (k = − 1). Причина ошибки — неосторожное использования свойства 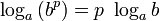 , которое, вообще говоря, подразумевает в комплексном случае весь бесконечный набор значений логарифма, а не только главное значение.
, которое, вообще говоря, подразумевает в комплексном случае весь бесконечный набор значений логарифма, а не только главное значение.
Аналитическое продолжение
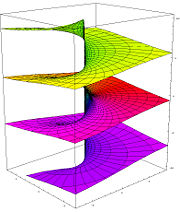
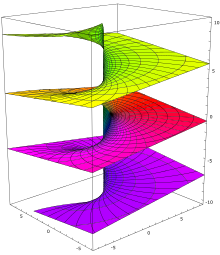
Рис. 3. Комплексный логарифм (мнимая часть)
Логарифм комплексного числа также может быть определён как аналитическое продолжение вещественного логарифма на всю комплексную плоскость. В явном виде продолжение логарифма вдоль кривой Γ, не проходящей через 0, можно осуществить по формуле (соответствующую функцию также обозначаем ln)
При этом, если Γ — простая кривая (без самопересечений), то для чисел, лежащих на ней, логарифмические тождества можно применять без опасений, например
Из формулы аналитического продолжения следует, что на любой ветви логарифма
Для любой окружности S, охватывающей точку 0:
Интеграл берётся в положительном направлении (против часовой стрелки). Это тождество лежит в основе теории вычетов.
Риманова поверхность
Комплексная логарифмическая функция — пример римановой поверхности; её мнимая часть (рис. 3) состоит из бесконечного числа ветвей, закрученных наподобие спирали. Эта поверхность односвязна; её единственный нуль (первого порядка) получается при z = 1, особые точки: z = 0 и 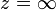 (точки разветвления бесконечного порядка).
(точки разветвления бесконечного порядка).
Риманова поверхность логарифма является универсальной накрывающей для комплексной плоскости без точки 0.
Исторический очерк
Вещественный логарифм
Потребность в сложных расчётах в XVI веке быстро росла, и значительная часть трудностей была связана с умножением и делением многозначных чисел. В конце века нескольким математикам, почти одновременно, пришла в голову идея: заменить трудоёмкое умножение на простое сложение, сопоставив с помощью специальных таблиц геометрическую и арифметическую прогрессии, при этом геометрическая будет исходной. Тогда и деление автоматически заменяется на неизмеримо более простое и надёжное вычитание. Первым эту идею опубликовал в своей книге «Arithmetica integra» Михаэль Штифель, который, впрочем, не приложил серьёзных усилий для реализации своей идеи.
В 1614 году шотландский математик-любитель Джон Непер опубликовал на латинском языке сочинение под названием «Описание удивительной таблицы логарифмов». В нём было краткое описание логарифмов и их свойств, а также 8-значные таблицы логарифмов синусов, косинусов и тангенсов, с шагом 1′. Термин логарифм, предложенный Непером, утвердился в науке.
Понятия функции тогда ещё не было, и Непер определил логарифм кинематически, сопоставив равномерное и логарифмически-замедленное движение. В современной записи модель Непера можно изобразить дифференциальным уравнением: dx/x = -dy/M, где M — масштабный множитель, введенный для того, чтобы значение получилось целым числом с нужным количеством знаков (десятичные дроби тогда ещё не нашли широкого применения). Непер взял M = 10000000.
Строго говоря, Непер табулировал не ту функцию, которая сейчас называется логарифмом. Если обозначить его функцию LogNap(x), то она связана с натуральным логарифмом следующим образом:
Очевидно, LogNap(M) = 0, то есть логарифм «полного синуса» есть нуль — этого и добивался Непер своим определением. LogNap(0) = ∞.
Основное свойство логарифма Непера: если величины образуют геометрическую прогрессию, то их логарифмы образуют прогрессию арифметическую. Однако правила логарифмирования для неперовой функции отличались от правил для современного логарифма.
Например, LogNap(ab) = LogNap(a) + LogNap(b) — LogNap(1).
К сожалению, все значения таблицы Непера содержали вычислительную ошибку после шестого знака. Однако это не помешало новой методике вычислений получить широчайшую популярность, и составлением логарифмических таблиц занялись многие европейские математики, включая Кеплера.
В 1620-е годы Эдмунд Уингейт и Уильям Отред изобрели первую логарифмическую линейку, до появления карманных калькуляторов — незаменимый инструмент инженера.
Близкое к современному понимание логарифмирования — как операции, обратной возведению в степень — впервые появилось у Валлиса и Иоганна Бернулли, а окончательно было узаконено Эйлером в XVIII веке. В книге «Введение в анализ бесконечных» (1748) Эйлер дал современные определения как показательной, так и логарифмической функций, привёл разложение их в степенные ряды, особо отметил роль натурального логарифма.
Эйлеру принадлежит и заслуга распространения логарифмической функции на комплексную область.
Комплексный логарифм
Первые попытки распространить логарифмы на комплексные числа предпринимали на рубеже XVII—XVIII веков Лейбниц и Иоганн Бернулли, однако создать целостную теорию им не удалось — в первую очередь по той причине, что тогда ещё не было ясно определено само понятие логарифма. Дискуссия по этому поводу велась сначала между Лейбницем и Бернулли, а в середине XVIII века — между Даламбером и Эйлером. Бернулли и Даламбер считали, что следует определить log(-x) = log(x). Полная теория логарифмов отрицательных и комплексных чисел была опубликована Эйлером в 1747—1751 годах и по существу ничем не отличается от современной.
Хотя спор продолжался (Даламбер отстаивал свою точку зрения и подробно аргументировал её в статье своей «Энциклопедии» и в других трудах), однако точка зрения Эйлера быстро получила всеобщее признание.
Логарифмические таблицы

Логарифмические таблицы
Из свойств логарифма следует, что вместо трудоёмкого умножения многозначных чисел достаточно найти (по таблицам) и сложить их логарифмы, а потом по тем же таблицам выполнить потенцирование, то есть найти значение результата по его логарифму. Выполнение деления отличается только тем, что логарифмы вычитаются. Лаплас говорил, что изобретение логарифмов «продлило жизнь астрономов», многократно ускорив процесс вычислений.
При переносе десятичной запятой в числе на n разрядов значение десятичного логарифма этого числа изменяется на n. Например, lg8314,63 = lg8,31463 + 3. Отсюда следует, что достаточно составить таблицу десятичных логарифмов для чисел в диапазоне от 1 до 10.
Первые таблицы логарифмов опубликовал Джон Непер (1614), и они содержали только логарифмы тригонометрических функций, причём с ошибками. Независимо от него свои таблицы опубликовал Иост Бюрги, друг Кеплера (1620). В 1617 году оксфордский профессор математики Генри Бригс опубликовал таблицы, которые уже включали десятичные логарифмы самих чисел, от 1 до 1000, с 8 (позже — с 14) знаками. Но и в таблицах Бригса обнаружились ошибки. Первое безошибочное издание на основе таблиц Вега (1783) появилось только в 1857 году в Берлине (таблицы Бремивера).
В России первые таблицы логарифмов были изданы в 1703 году при участии Л. Ф. Магницкого. В СССР выпускались несколько сборников таблиц логарифмов.
- Брадис В. М. Четырехзначные математические таблицы. 44-е издание, М., 1973.
Таблицы Брадиса (1921) использовались в учебных заведениях и в инженерных расчётах, не требующих большой точности. Они содержали мантиссы десятичных логарифмов чисел и тригонометрических функций, натуральные логарифмы и некоторые другие полезные расчётные инструменты.
- Вега Г. Таблицы семизначных логарифмов, 4-е издание, М., 1971.
Профессиональный сборник для точных вычислений.
- Пятизначные таблицы натуральных значений тригонометрических величин, их логарифмов и логарифмов чисел, 6 изд., М.: Наука, 1972.
- Таблицы натуральных логарифмов, 2-е издание, в 2 томах, М.: Наука, 1971.
См. также
Литература
Wikimedia Foundation. 2010.
Двоичный логарифм — Википедия
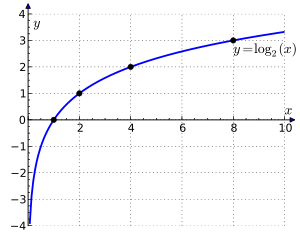 График двоичного логарифма
График двоичного логарифмаДвоичный логарифм — логарифм по основанию 2. Другими словами, двоичный логарифм числа b{\displaystyle b} есть решение уравнения 2x=b.{\displaystyle 2^{x}=b.}
Двоичный логарифм вещественного числа b{\displaystyle b} существует, если b>0.{\displaystyle b>0.} Согласно стандарту ISO 31-11, он обозначается[1]lbb,{\displaystyle \operatorname {lb} b,} lb(b){\displaystyle \operatorname {lb} (b)} или log2b{\displaystyle \log _{2}b}. Примеры:
- lb1=0;lb2=1;lb16=4{\displaystyle \operatorname {lb} 1=0;\,\operatorname {lb} 2=1;\,\operatorname {lb} 16=4}
- lb0,5=−1;lb1256=−8{\displaystyle \operatorname {lb} 0{,}5=-1;\,\operatorname {lb} {\frac {1}{256}}=-8}
Исторически двоичные логарифмы нашли своё первое применение в теории музыки, когда Леонард Эйлер установил: двоичный логарифм отношения частот двух музыкальных тонов равен количеству октав, которое отделяет один тон от другого. Эйлер также опубликовал таблицу двоичных логарифмов целых чисел от 1 до 8 с точностью до семи десятичных знаков[2][3].
С созданием информатики выяснилось, что двоичные логарифмы необходимы для определения количества битов, необходимых для кодирования сообщения. Другие области, в которых часто используется двоичный логарифм, включают комбинаторику, биоинформатику, криптографию, проведение спортивных турниров и фотографию. Стандартная функция для вычисления двоичного логарифма предусмотрена во многих распространённых системах программирования.
В нижеследующей таблице предполагается, что все значения положительны[4]:
Существует очевидное обобщение приведенных формул на случай, когда допускаются отрицательные переменные, например:
- lb|xy|=lb(|x|)+lb(|y|),{\displaystyle \operatorname {lb} |xy|=\operatorname {lb} (|x|)+\operatorname {lb} (|y|),}
- lb|xy|=lb(|x|)−lb(|y|),{\displaystyle \operatorname {lb} \!\left|{\frac {x}{y}}\right|=\operatorname {lb} (|x|)-\operatorname {lb} (|y|),}
Формула для логарифма произведения без труда обобщается на произвольное количество сомножителей:
- lb(x1x2…xn)=lb(x1)+lb(x2)+⋯+lb(xn){\displaystyle \operatorname {lb} (x_{1}x_{2}\dots x_{n})=\operatorname {lb} (x_{1})+\operatorname {lb} (x_{2})+\dots +\operatorname {lb} (x_{n})}
Связь двоичного, натурального и десятичного логарифмов:
- lbx≈1,442695lnx{\displaystyle \operatorname {lb} x\approx 1{,}442695\ln x}
- lbx≈3,321928lgx{\displaystyle \operatorname {lb} x\approx 3{,}321928\lg x}
Если рассматривать логарифмируемое число как переменную, мы получим функцию двоичного логарифма: y=lbx{\displaystyle y=\operatorname {lb} x}. Она определена при всех x>0,{\displaystyle x>0,} область значений: E(y)=(−∞;+∞){\displaystyle E(y)=(-\infty ;+\infty )}. График этой функции часто называется логарифмикой, она обратна для функции y=2x{\displaystyle y=2^{x}}. Функция монотонно возрастает, непрерывна и дифференцируема всюду, где она определена. Производная для неё даётся формулой[5]:
- ddxlbx=lbex{\displaystyle {\frac {d}{dx}}\operatorname {lb} x={\frac {\operatorname {lb} e}{x}}}
Ось ординат (x=0){\displaystyle (x=0)} является вертикальной асимптотой, поскольку:
- limx→0+0lbx=−∞{\displaystyle \lim _{x\to 0+0}\operatorname {lb} x=-\infty }
Теория информации[править | править код]
Двоичный логарифм натурального числа N{\displaystyle N} позволяет определить число цифр b(N){\displaystyle b(N)} во внутреннем компьютерном (битовом) представлении этого числа:
- b(N)=⌊lbN⌋+1{\displaystyle b(N)=\lfloor \operatorname {lb} N\rfloor +1} (скобки обозначают целую часть числа)
Информационная энтропия — мера количества информации, также основана на двоичном логарифме
Сложность рекурсивных алгоритмов[править | править код]
Оценка асимптотической сложности рекурсивных алгоритмов, основанных на принципе «разделяй и властвуй»[6] — таких, как быстрая сортировка, быстрое преобразование Фурье, двоичный поиск и т. п.
Комбинаторика[править | править код]
Если двоичное дерево содержит n{\displaystyle n} узлов, то его высота не меньше, чем log2n{\displaystyle \log _{2}n} (равенство достигается, если n{\displaystyle n} является степенью 2)[7]. Соответственно, число Стралера — Философова для речной системы с n{\displaystyle n} притоками не превышает[8]log2n+1{\displaystyle \log _{2}n+1}.
Изометрическая размерность частичного куба с n{\displaystyle n} вершинами не меньше, чем log2n.{\displaystyle \log _{2}n.} Число рёбер куба не более, чем 12nlog2n,{\displaystyle {\frac {1}{2}}n\log _{2}n,} равенство имеет место, когда частичный куб является графом гиперкуба[9].
Согласно теореме Рамсея, неориентированный граф с n{\displaystyle n} вершинами содержит либо клику, либо независимое множество, размер которого логарифмически зависит от n.{\displaystyle n.} Точный размер этого множества неизвестен, но наилучшие в настоящий момент оценки содержат двоичные логарифмы.
Другие применения[править | править код]
Число кругов игры по олимпийской системе равно двоичному логарифму от числа участников соревнований[10].
В теории музыки, чтобы решить вопрос о том, на сколько частей делить октаву, требуется отыскать рациональное приближение для log232≈0,585.{\displaystyle \log _{2}{\frac {3}{2}}\approx 0{,}585.} Если разложить это число в непрерывную дробь, то третья подходящая дробь (7/12) позволяет обосновать классическое деление октавы на 12 полутонов[11].
- ↑ Иногда, особенно в немецких изданиях, двоичный логарифм обозначается ldb{\displaystyle \operatorname {ld} b} (от лат. logarithmus dyadis), см. Bauer, Friedrich L. Origins and Foundations of Computing: In Cooperation with Heinz Nixdorf MuseumsForum (англ.). — Springer Science & Business Media, 2009. — P. 54. — ISBN 978-3-642-02991-2.
- ↑ Euler, Leonhard (1739), «Chapter VII. De Variorum Intervallorum Receptis Appelationibus», Tentamen novae theoriae musicae ex certissismis harmoniae principiis dilucide expositae, Saint Petersburg Academy, с. 102—112, <http://eulerarchive.maa.org/pages/E033.html> .
- ↑ Tegg, Thomas (1829), «Binary logarithms», London encyclopaedia; or, Universal dictionary of science, art, literature and practical mechanics: comprising a popular view of the present state of knowledge, Volume 4, с. 142–143, <https://books.google.com/books?id=E-ZTAAAAYAAJ&pg=PA142> .
- ↑ Выгодский М. Я. Справочник по элементарной математике, 1978, с. 187..
- ↑ Логарифмическая функция. // Математическая энциклопедия (в 5 томах). — М.: Советская Энциклопедия, 1982. — Т. 3.
- ↑ Harel, David; Feldman, Yishai A. Algorithmics: the spirit of computing. — New York: Addison-Wesley, 2004. — P. 143. — ISBN 978-0-321-11784-7.
- ↑ Leiss, Ernst L. (2006), A Programmer’s Companion to Algorithm Analysis, CRC Press, с. 28, ISBN 978-1-4200-1170-8, <https://books.google.com/books?id=E6BNGFQ6m_IC&pg=RA2-PA28>
- ↑ Devroye, L. & Kruszewski, P. (1996), «On the Horton–Strahler number for random tries», RAIRO Informatique Théorique et Applications Т. 30 (5): 443—456, doi:10.1051/ita/1996300504431, <https://eudml.org/doc/92635> .
- ↑ Eppstein, David (2005), «The lattice dimension of a graph», European Journal of Combinatorics Т. 26 (5): 585–592, DOI 10.1016/j.ejc.2004.05.001
- ↑ Харин А. А. Организация и проведение соревнований. Методическое пособие. — Ижевск: УдГУ, 2011. — С. 27.
- ↑ Шилов Г. Е. Простая гамма. Устройство музыкальной шкалы. М.: Физматгиз, 1963. 20 с. Серия «Популярные лекции по математике», выпуск 37.
Неперов логарифм — Википедия
Материал из Википедии — свободной энциклопедии
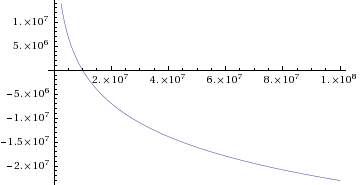 График неперова логарифма для значений аргумента от 0 до 108
График неперова логарифма для значений аргумента от 0 до 108Под неперовым логарифмом (англ. Napierian (Naperian) logarithm), как правило, понимают натуральный логарифм. Сам Джон Непер, имя которого носит функция, описал функцию, не совпадающую с современным натуральным логарифмом (см. ниже)[1]. Поэтому под неперовым логарифмом могут понимать и ту функцию, которую он использовал:
- NapLog(x)=log107xlog107107−1.{\displaystyle \mathrm {NapLog} (x)={\frac {\log {\frac {10^{7}}{x}}}{\log {\frac {10^{7}}{10^{7}-1}}}}.}
Это частное от деления логарифмов, поэтому выбор основания не принципиален. Согласно современному пониманию, это выражение не является логарифмом. Однако его можно переписать следующим образом:
- NapLog(x)=log107107−1107−log107107−1x{\displaystyle \mathrm {NapLog} (x)=\log _{\frac {10^{7}}{10^{7}-1}}10^{7}-\log _{\frac {10^{7}}{10^{7}-1}}x}
что есть линейная функция конкретного логарифма. Она обладает многими свойствами логарифма в его современном понимании, например:
- NapLog(xy)=NapLog(x)+NapLog(y)−161180950{\displaystyle \mathrm {NapLog} (xy)=\mathrm {NapLog} (x)+\mathrm {NapLog} (y)-161180950}
Неперов логарифм связан с натуральным:
- NapLog(x)≈9999999.5(16.11809565−lnx){\displaystyle \mathrm {NapLog} (x)\approx 9999999.5(16.11809565-\ln x)}
Также он связан с десятичным логарифмом:
- NapLog(x)≈23025850(7−log10x).{\displaystyle \mathrm {NapLog} (x)\approx 23025850(7-\log _{10}x).}
При этом
- 16.11809565≈7ln(10){\displaystyle 16.11809565\approx 7\ln \left(10\right)}
и
- 23025850≈107ln(10).{\displaystyle 23025850\approx 10^{7}\ln(10).}
Примечания[править | править код]
- ↑ Larson, Ron; Hostetler, Robert P.; Edwards, Bruce H. Essential Calculus Early Transcendental Functions (неопр.). — U.S.A: Richard Stratton, 2008. — С. 119. — ISBN 978-0-618-87918-2.
Источники[править | править код]
- Boyer, Carl B. & Merzbach, Uta C. (1991), A History of Mathematics, Wiley, с. 313, ISBN 978-0-471-54397-8 .
- Edwards, Charles Henry (1994), The Historical Development of the Calculus, Springer-Verlag, с. 153 .
- Phillips, George McArtney (2000), Two Millennia of Mathematics: from Archimedes to Gauss, vol. 6, CMS Books in Mathematics, Springer-Verlag, с. 61, ISBN 978-0-387-95022-8 .
Общее определение и свойства логарифмов, основные формулы и логарифмические функции, примеры решения
 По мере развития общества, усложнения производства развивалась и математика. Движение от простого к сложному. От обычного учёта методом сложения и вычитания, при их многократном повторении, пришли к понятию умножения и деления. Сокращение многократно повторяемой операции умножения стало понятием возведения в степень. Первые таблицы зависимости чисел от основания и числа возведения в степень были составлены ещё в VIII веке индийским математиком Варасена. С них и можно отсчитывать время возникновения логарифмов.
По мере развития общества, усложнения производства развивалась и математика. Движение от простого к сложному. От обычного учёта методом сложения и вычитания, при их многократном повторении, пришли к понятию умножения и деления. Сокращение многократно повторяемой операции умножения стало понятием возведения в степень. Первые таблицы зависимости чисел от основания и числа возведения в степень были составлены ещё в VIII веке индийским математиком Варасена. С них и можно отсчитывать время возникновения логарифмов.
Исторический очерк
Возрождение Европы в XVI веке стимулировало и развитие механики. Требовался большой объем вычисления, связанных с умножением и делением многозначных чисел. Древние таблицы оказали большую услугу. Они позволяли заменять сложные операции на более простые – сложение и вычитание. Большим шагом вперёд стала работа математика Михаэля Штифеля, опубликованная в 1544 году, в которой он реализовал идею многих математиков. Что позволило использовать таблицы не только для степеней в виде простых чисел, но и для произвольных рациональных.
В 1614 году шотландец Джон Непер, развивая эти идеи, впервые ввёл новый термин «логарифм числа». Были составлены новые сложные таблицы для расчёта логарифмов синусов и косинусов, а также тангенсов. Это сильно сократило труд астрономов.
Стали появляться новые таблицы, которые успешно использовались учёными на протяжении трёх веков. Прошло немало времени, прежде чем новая операция в алгебре приобрела свой законченный вид. Было дано определение логарифма, и его свойства были изучены.
Только в XX веке с появлением калькулятора и компьютера человечество отказалось от древних таблиц, успешно работавших на протяжении XIII веков.
Определение логарифма
Сегодня мы называем логарифмом b по основанию a число x, которое является степенью числа а, чтобы получилось число b. В виде формулы это записывается: x = log a(b).
Например, log 3(9) будет равен 2. Это очевидно, если следовать определению. Если 3 возвести в степень 2, то получим 9.
Так, сформулированное определение ставит только одно ограничение, числа a и b должны быть вещественными.
Разновидности логарифмов
Классическое определение носит название вещественный логарифм и фактически является решением уравнения ax = b. Вариант a = 1 является пограничным и не представляет интереса. Внимание: 1 в любой степени равно 1.
Вещественное значение логарифма определено только при основании и аргументе больше 0, при этом основание не должно равняться 1.
Особое место в области математики играют логарифмы, которые будут называться в зависимости от величины их основания:
 Двоичные с основанием a = 2, нашли своё применение во многих разделах дискретной математики, информатике, а также теории информации, записываются как lb (b).
Двоичные с основанием a = 2, нашли своё применение во многих разделах дискретной математики, информатике, а также теории информации, записываются как lb (b).- Десятичные с основанием a = 10, записываются как lg (b).
- Натуральные с основанием a = e, где математическая константа e = 2,71828 иррациональное и трансцендентное число, называемое Постоянная Эйлера, записываются как ln (b).
Правила и ограничения
Основополагающим свойством логарифмов является правило: логарифм произведения равен логарифмической сумме. log abp = lоg a(b) + log a(p).
Как вариант этого утверждения будет: log с(b/p) = lоg с(b) log с(p), функция частного равна разности функций.
Из предыдущих двух правил легко видно, что: lоg a(bp) = p * log a(b).
Среди других свойств можно выделить:
 Правило тождественности, когда aloga(b) = b, следствием этого правила является следующее утверждение: если aloga(b) = aloga(c), то b = c.
Правило тождественности, когда aloga(b) = b, следствием этого правила является следующее утверждение: если aloga(b) = aloga(c), то b = c.- Замечательные значения отражены в двух формулах: логарифм единицы всегда равен нулю log a(1) = 0 и логарифм числа, равного основанию, равен единице log a(a) = 1.
- При использовании отрицательных чисел можно применить формулу, справедливую для модуля чисел: log c|ab| = log c|a| + log c|b|.
Замечание. Не надо делать распространённую ошибку — логарифм суммы не равен сумме логарифмов.
Как найти логарифм
 Многие века операция поиска логарифма была довольно трудоёмкой задачей. Математики пользовались известной формулой логарифмической теории разложения на многочлен:
Многие века операция поиска логарифма была довольно трудоёмкой задачей. Математики пользовались известной формулой логарифмической теории разложения на многочлен:
ln (1 + x) = x (x^2)/2 + (x^3)/3 ( x^4)/4 + … + ((-1)^(n + 1))*((x^n)/n), где n — натуральное число больше 1, определяющее точность вычисления.
Логарифмы с другими основаниями вычислялись, используя теорему о переходе от одного основания к другому и свойстве логарифма произведения.
Так как этот способ очень трудоёмкий и при решении практических задач трудноосуществим, то использовали заранее составленные таблицы логарифмов, что значительно ускоряло всю работу.
В некоторых случаях использовали специально составленные графики логарифмов, что давало меньшую точность, но значительно ускоряло поиск нужного значения. Кривая функции y = log a(x), построенная по нескольким точкам, позволяет с помощью обычной линейки находить значения функции в любой другой точке. Инженеры длительное время для этих целей использовали так называемую миллиметровую бумагу.
В XVII веке появились первые вспомогательные аналоговые вычислительные условия, которые к XIX веку приобрели законченный вид. Наиболее удачное устройство получило название логарифмическая линейка. При всей простоте устройства, её появление значительно ускорило процесс всех инженерных расчётов, и это переоценить трудно. В настоящее время уже мало кто знаком с этим устройством.
Появление калькуляторов и компьютеров сделало бессмысленным использование любых других устройств.
Уравнения и неравенства
Для решения различных уравнений и неравенств с использованием логарифмов применяются следующие формулы:
- Переход от одного основания к другому: lоg a(b) = log c(b) / log c(a),
- Как следствие предыдущего варианта: lоg a(b) = 1 / log b(a).
Для решения неравенств полезно знать:
- Значение логарифма будет положительным только в том случае, когда основание и аргумент одновременно больше или меньше единицы, если хотя бы одно условие нарушено, значение логарифма будет отрицательным.
- Если функция логарифма применяется к правой и левой части неравенства, и основание логарифма больше единицы, то знак неравенства сохраняется, в противном случае он меняется.
Примеры задач
Рассмотрим несколько вариантов применения логарифмов и их свойства. Примеры с решением уравнений:
 Задача 1. Решить уравнение log 2(2x-1) = 4. Решение: по определению 2х 1 = 24 , или 2х 1 = 16, далее 2х = 17, получаем х = 8,5. Ответ: при значении х = 8,5 уравнение действительно.
Задача 1. Решить уравнение log 2(2x-1) = 4. Решение: по определению 2х 1 = 24 , или 2х 1 = 16, далее 2х = 17, получаем х = 8,5. Ответ: при значении х = 8,5 уравнение действительно.- Задача 2. Вычислить log 6(30) / log 30(6) log 6(180) / log5(6). Решение: приведём к одному основанию 6. Следующим действием раскрываем скобки и вместо логарифма 6 по основанию 6 подставляем его значение 1. Таким образом, log 6(30) * lоg 6(30) log 6(180) * log 6(5). Разложим числа на простые множители log 6(5*6) * log 6(5*6) lоg 6(5*6*6) * log 6(5) и заменяем логарифм 5 по основанию 6 на t. Тогда (t +1) * (t +1) (t +2) * t. Раскрываем скобки t2 + t + t +1 t 2 2t. Приводим подобные члены и получаем 1. Ответ: значение выражения равно 1.
Рассмотрим вариант размещения логарифма в степени:
- Задача 3. Вычислить 25^log 5(3). Решение: в условиях задачи запись аналогична следующей (5^2)^log5(3) или 5^(2 * log 5(3)). Запишем по-другому: 5^log 5(3*2), или квадрат числа в качестве аргумента функции можно записать как квадрат самой функции (5^log 5(3))^2. Используя свойства логарифмов, это выражение равно 3^2. Ответ: в результате вычисления получаем 9.
Практическое применение
Являясь исключительно математическим инструментом, кажется далёким от реальной жизни, что логарифм неожиданно приобрёл большое значение для описания объектов реального мира. Трудно найти науку, где его не применяют. Это в полной мере относится не только к естественным, но и гуманитарным областям знаний.
Логарифмические зависимости
Приведём несколько примеров числовых зависимостей:
 Число простых чисел на интервале от 1 до n приблизительно равно n / ln (n).
Число простых чисел на интервале от 1 до n приблизительно равно n / ln (n).- Для поиска k-го простого числа можно пользоваться формулой k * ln (k).
- Логарифмическое распределение часто используется для оценки вероятностных событий в генетике и физике.
- В информатике известно, что для хранения в памяти компьютера натурального числа N потребуется log 2(N) + 1 бит памяти.
Механика и физика
Исторически механика и физика всегда развивались с использованием математических методов исследования и одновременно служили стимулом для развития математики, в том числе логарифмов. Теория большинства законов физики написана языком математики. Приведём только два примера описания физических законов с использованием логарифма.
Решать задачу расчёта такой сложной величины как скорость ракеты можно, применяя формулу Циолковского, которая положила начало теории освоения космоса:
V = I * ln (M1/M2), где
- V – конечная скорость летательного аппарата.
- I – удельный импульс двигателя.
- M 1 – начальная масса ракеты.
- M 2 – конечная масса.
Другой важный пример — это использование в формуле другого великого учёного Макса Планка, которая служит для оценки равновесного состояния в термодинамике.
S = k * ln (Ω), где
- S – термодинамическое свойство.
- k – постоянная Больцмана.
- Ω – статистический вес разных состояний.
Химия
Менее очевидным будет использования формул в химии, содержащих отношение логарифмов. Приведём тоже только два примера:
- Уравнение Нернста, условие окислительно-восстановительного потенциала среды по отношению к активности веществ и константой равновесия.
- Расчёт таких констант, как показатель автопролиза и кислотность раствора тоже не обходятся без нашей функции.
Психология и биология
 И уж совсем непонятно при чём здесь психология. Оказывается, сила ощущения хорошо описывается этой функцией как обратное отношение значения интенсивности раздражителя к нижнему значению интенсивности.
И уж совсем непонятно при чём здесь психология. Оказывается, сила ощущения хорошо описывается этой функцией как обратное отношение значения интенсивности раздражителя к нижнему значению интенсивности.
После вышеприведённых примеров уже не удивляет, что и в биологии широко используется тема логарифмов. Про биологические формы, соответствующие логарифмическим спиралям, можно писать целые тома.
Другие области
Кажется, невозможно существование мира без связи с этой функцией, и она правит всеми законами. Особенно, когда законы природы связаны с геометрической прогрессией. Стоит обратиться к сайту МатПрофи, и таких примеров найдётся множество в следующих сферах деятельности:
 Теории акустики.
Теории акустики.- Радиотехнике и электросвязи.
- Астрономии.
- Сейсмологии.
- Оптике.
- Фотографии.
- Сельском хозяйстве.
- Теории управления.
Список может быть бесконечным. Освоив основные закономерности этой функции, можно окунуться в мир бесконечной мудрости.
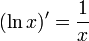
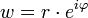 ,
,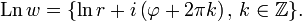
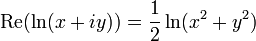

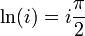
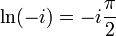
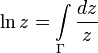
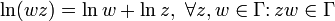
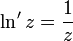
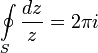
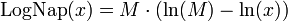
 Двоичные с основанием a = 2, нашли своё применение во многих разделах дискретной математики, информатике, а также теории информации, записываются как lb (b).
Двоичные с основанием a = 2, нашли своё применение во многих разделах дискретной математики, информатике, а также теории информации, записываются как lb (b). Правило тождественности, когда aloga(b) = b, следствием этого правила является следующее утверждение: если aloga(b) = aloga(c), то b = c.
Правило тождественности, когда aloga(b) = b, следствием этого правила является следующее утверждение: если aloga(b) = aloga(c), то b = c. Задача 1. Решить уравнение log 2(2x-1) = 4. Решение: по определению 2х 1 = 24 , или 2х 1 = 16, далее 2х = 17, получаем х = 8,5. Ответ: при значении х = 8,5 уравнение действительно.
Задача 1. Решить уравнение log 2(2x-1) = 4. Решение: по определению 2х 1 = 24 , или 2х 1 = 16, далее 2х = 17, получаем х = 8,5. Ответ: при значении х = 8,5 уравнение действительно. Число простых чисел на интервале от 1 до n приблизительно равно n / ln (n).
Число простых чисел на интервале от 1 до n приблизительно равно n / ln (n). Теории акустики.
Теории акустики.