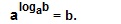11.4.3. Десятичный логарифм   математика-повторение

Логарифм по основанию 10 называют десятичным логарифмом и при написании опускают основание 10 и букву «о» в написании слова «log».

lg7=log₁₀7,        lg7 – десятичный логарифм числа 7.

Примеры. Вычислить:

lg10; lg100; lg1000; lg0,1; lg0,01; lg0,001.

1)    lg10=1,  так как 10¹=10.

2)    lg100=2, так как10²=100.

3)    lg1000=3, так как 10³=1000.

4)    lg0,1=-1, так как 10^-1=1/10=0,1.

5)    lg0,01=-2, так как 10^-2=1/10²=1/100=0,01.

6)    lg0,001=-3, так как 10^-3=1/10

3=1/1000=0,001.

Найти значение выражения: 

10^lg8;  10^lg4+10^lg3,5;  10^5lg2;  100^lg3;  10^lg5+2;  10^lg60-1.

Используем:

• основное логарифмическое тождество:

(см. предыдущий урок 11.4.2. «Примеры на основное логарифмическое тождество» здесь)

• формулу произведения степеней с одинаковыми основаниями: a^m∙aⁿ=a^m+n,
• формулу частного степеней с одинаковыми основаниями: a^m:aⁿ=
  a^{m— n}

1)    10^lg8=8

2)    10^lg4+10^lg3,5=4+3,5=7,5.

3)    10^5lg2=(10^lg2)⁵=2⁵=32.

4)    100^lg3=(10²)^lg3=(10^lg3)²=3²=9.

5)    10^lg5+2=10^lg5∙10²=5∙100=500.

6)    10^lg60-1=10^lg60:10¹=60:10=6.

Решить уравнение.

1)    lgx=10^lg30-1.

Упростим правую часть равенства как в предыдущих примерах.

lgx=10^lg30:10¹;

lgx=30:10;

lgx=3;

x=10³;

x=1000.

2)    lg (x+3)=2.

x+3=10²;

x+3=100;

x=100-3;

x=97.

3)    lg (x+5)=-1.

x+5=10^-1;

x+5=0,1;

x=0,1-5;

x=-4,9.

 

Запись имеет метки: десятичный логарифм

www.mathematics-repetition.com

Десятичный логарифм

Навигация по странице:

Определение. Логарифмом числа b по основанию a, где a > 0, a ≠ 1, b > 0, называется показатель степени, в которую нужно возвести основание a, чтоб получить число b.

Определение. Десятичный логарифм — логарифм по основанию 10.

Другими словами, десятичный логарифм числа b является решением уравнения 10^x = b.

Обозначение. Десятичный логарифм обозначается lg x или log x.

Калькулятор десятичных логарифмов

lg 2

Свойства десятичного логарифмов

Для любых x > 0 и y > 0 выполняются следующие свойства десятичных логарифмов.

1. lg x = log₁₀x — так как основание десятичного логарифма равно 10.

2. 10^{lg b} = b.

3. lg 1 = 0

4. lg 10 = 1

5. lg 10ⁿ = n

6. lg(x · y) = lg x + lg y

7. lg xy = lg x — lg y

8. lg xⁿ = n lg x

9. График функции y = lg x

10. (lg x)′ = 1x ln 10

11. ∫	lg x dx = x lg x — xln 10 + C

Пример 1. Найти значения десятичного логарифма от чисел 100, 1000, 0.1, 0.01, 0.001.

lg 100 = lg 10² = 2

lg 1000 = lg 10³ = 3

lg 0.1 = lg 10^-1 = -1

lg 0.01 = lg 10^-2 = -2

lg 0.001 = lg 10^-3 = -3

Пример 2.

Доказать равенство: a ^{lg b} = b ^{lg a}.

Запишем очевидное равенство:

lg b · lg a = lg a · lg ab

Возведем 10 в соответствующие степени

10^{lg b · lg a} = 10^{lg a · lg b}

(10^{lg b})^{lg a} = (10^{lg a})^{lg b}

b^{lg a} = a^{lg b}

Равенство доказано.

Пример 3.

Зная, что lg 2 = a, lg 3 = b, lg 5 = c, выразить lg 6; lg 30; lg 16 через a, b, c.

Используем формулы логарифма произведения и степени получим:

lg 6 = lg (2·3)= lg 2 + lg 3 = a + b;

lg 30 = lg (5·2·3)= lg 5 + lg 2 + lg 3 = a + b + c;

lg 16 = lg 2⁴= 4 · lg 2 = 4a.

Пример 4.

Вычислить log₉ 5 · log₂₅ 27.

Перейдем к основе 10:

log₉ 5 · log₂₅ 27 = lg 5lg 9 · lg 27lg 25

Используем свойство логарифма степени lg xⁿ = n lg x:

lg 5lg 9 · lg 27lg 25 = lg 5lg 3² · lg 3³lg 5² = lg 52 lg 3 · 3 lg 32 lg 5 = 34

Пример 5.

Вычислить log₃₀ 8, если lg 5 = a, lg 3 = b.

Перейдем к основе 10:

log ₃₀ 8 = lg 8lg 30 = lg 2³lg (3 · 10) =

Используем свойство логарифма степени, произведения, частного и то что 2= 105:

= 3 lg 2lg 3 + lg 10 = 3 lg 2lg 3 + 1 = 3 lg 105lg 3 + 1 = 3(lg 10 — lg 5)lg 3 + 1 = 3(1 — lg 5)lg 3 + 1 =

Подставим lg 5 = a, lg 3 = b:

= 3(1 — a)b + 1

Ответ:

log₃₀ 8 = 3(1 — a)b + 1

ru.onlinemschool.com

Десятичные и натуральные логарифмы

При решении логарифмов пока мы с вами сталкивались лишь с логарифмами, у которых были одинаковые основания.

Однако, зачастую приходится искать значения выражений, которые составлены из логарифмов по разным основаниям.

…

Заметим, что действия с логарифмами возможны только при одинаковых основаниях!

Тогда как поступают, если основания у логарифмов разные? Что нужно сделать, чтобы найти значения таких выражений? Так вот для этого вводятся десятичные и натуральные логарифмы, а также формула перехода от логарифма по одному основанию к логарифму по другому основанию.

Среди различных оснований для вычисления логарифмов чаще всего используется число

10. Логарифмы по такому основанию называют десятичными. Другими словами, десятичный логарифм числа  есть решение уравнения

 Десятичные логарифмы используются довольно часто, поэтому для них введено специальное обозначение: , читают «десятичный логарифм числа ».

Что же касается натурального логарифма числа, то так называют логарифм этого числа по основанию , где  – иррациональное число, приближённо

Натуральный логарифм также имеет особое обозначение: , читают так: «натуральный логарифм числа

».

Кстати, иррациональное число е играет важную роль в математике и её приложениях. Число е можно представить как сумму:

……           

Все свойства, которые мы рассматривали для логарифмов по произвольному основанию, справедливы для десятичного и натурального логарифмов.

1., .                                                       1., .

2. .                                                                        2. .

 3. .                                                                          3. .

4. , , .                            4. , , .

5. , , .                              5. , , .

6. , , .                                    6. , , .

7. , , .                                   7. , , .

А теперь давайте разберёмся, как вычисляют десятичный и натуральный логарифмы. Проще всего значение логарифма можно найти с помощью инженерного калькулятора.

Итак, на инженерном калькуляторе для вычисления значения десятичного логарифма есть кнопка «log», для натурального логарифма – кнопка «ln».

Давайте посмотрим, как находят значения следующих логарифмов при помощи инженерного калькулятора: ; .

Найдём значение десятичного логарифма числа .

Для этого наберём число  и нажмём кнопку «log». Видим, на табло у нас высветились следующие цифры: …

На практике, конечно, мы округлим это число до нужного разряда.

Теперь найдём значение . Для этого наберём 15 и нажмём кнопку «ln». На табло у нас высветились следующие цифры: ….

Ранее мы с вами уже говорили, что с появлением логарифмов многие учёные занялись составлением логарифмических таблиц. Так, например, первые таблицы десятичных логарифмов для чисел от 1 до 1000 опубликовал в 1617 году оксфордский профессор математики Генри Бригс, с восемью (позже — с четырнадцатью) знаками.

Давайте рассмотрим принцип использования такой таблицы на примере двузначной таблицы десятичных логарифмов. На экране вы видите таблицу, в которой указаны значения десятичных логарифмов чисел от 1 до .

 

Левый столбец таблицы отвечает за число целых, а верхняя строка – за число десятых. Давайте найдём значение .

Итак, значение этого логарифма будет расположено на пересечении строки с числом 7 целых и столбца с числом 3 десятых. Как видим, значение нашего логарифма совпало с ранее найденным нами при помощи инженерного калькулятора, оно  .

А теперь найдём значение  при помощи таблицы натуральных логарифмов российского математика Брадиса.

На экране вы видите таблицу, в которой указаны значения натуральных логарифмов чисел от 1 до 99. Здесь левый столбец таблицы отвечает за число десятков, а верхняя строка – за число единиц.

Итак, значение  будет расположено на пересечении строки с числом 1 и столбца с числом 5. Как видим, значение нашего логарифма совпало с ранее найденным нами при помощи инженерного калькулятора, оно приближённо равно .

А как же быть с вычислением логарифмов по другим основаниям? Ведь при помощи инженерного калькулятора и таблиц логарифмов мы вычисляли только значения десятичных и натуральных логарифмов. Оказывается, достаточно знать значения только десятичных и натуральных логарифмов чисел, чтобы находить логарифмы чисел по любому основанию. Для этого используют формулу перехода от логарифма по одному основанию к логарифму по другому основанию.

Сейчас мы её с вами выведем. Итак, пусть .

Перейдём к показательной форме записи этого равенства, то есть получим .

Теперь прологарифмируем это равенство по основанию с. Другими словами, найдём логарифмы с основанием  обеих частей этого равенства. Получим:.

Применим к левой части равенства свойство логарифма степени, получим  .

Теперь разделим обе части равенства на . Получим .

Так как , то имеем .

Получившееся равенство и есть формула перехода от логарифма по одному основанию к логарифму по другому основанию.

Отметим, что эта формула верна, если выполняются следующие условия:

, , , , .

Из формулы перехода от логарифма по одному основанию к логарифму по другому основанию следует формула .

Также из формулы перехода от логарифма по одному основанию к логарифму по другому основанию при  и при  получаются формулы перехода к десятичным и натуральным логарифмам.

 и

А теперь давайте приступим к практической части нашего урока.

Задание 1. Найдите значение .

Решение.

Исходя из формулы  , имеем логарифм

При помощи калькулятора вычислим значения десятичного  – оно  

и   .

Подставим найденные значения в формулу перехода. Получим, что  .

Задание 2. Пусть , . Выразите через   и   число  .

Решение.

videouroki.net

Десятичный логарифм и его свойства

Определение и формулы десятичного логарифма

Этот логарифм является решением показательного уравнения . Иногда (особенно в зарубежной литературе) десятичный логарифм обозначается еще как , хотя первые два обозначения присущи и натуральному логарифму.

Первые таблицы десятичных логарифмов были опубликованы английским математиком Генри Бригсом (1561-1630) в 1617 г. (поэтому иностранные ученые часто называют десятичные логарифмы еще бригсовыми), но эти таблицы содержали ошибки. На основе таблиц (1783 г.) словенского и австрийского математики Георга Барталомея Веги (Юрий Веха или Веховец, 1754-1802) в 1857 г. немецкий астроном и геодезист Карл Бремикер (1804-1877) опубликовал первое безошибочное издание. При участии русского математика и педагога Леонтия Филипповича Магницкого (Телятин или Теляшин, 1669-1739) в 1703 г. в России были изданы первые таблицы логарифмов. Десятичные логарифмы широко применялись для вычислений.

Свойства десятичных логарифмов

Этот логарифм обладает всеми свойствами, присущими логарифму по произвольному основанию:

1. Основное логарифмическое тождество:

   

2. .

3. .

4. .

5. .

6. .

7. Переход к новому основанию:

   

8. .

9. .

Функция десятичного логарифма — это функция . График этой кривой часто называют логарифмикой.

Свойства функции y=lg x

1) Область определения: .

2) Множество значений: .

3) Функция общего вида.

4) Функция непериодическая.

5) График функции пересекается с осью абсцисс в точке .

6) Промежутки знакопостоянства: для та для .

7) Функция возрастает на всей области определения.

8) Точек минимума/максимума нет.

9) График:

Производная логарифма натурального

   

Интеграл от натурального логарифма

   

Ряд Маклорена

   

Понравился сайт? Расскажи друзьям!

ru.solverbook.com

Подготовка школьников к ЕГЭ (Справочник по математике — Алгебра

Определение логарифма, основное логарифмическое тождество

      Рассмотрим два произвольных действительных числа   a   и   b,   удовлетворяющих условиям

(1)

      Определение. Логарифмом числа   b   по основанию   a   называют такую степень, в которую надо возвести число   a,   чтобы получить число   b.

      Другими словами, логарифм числа   b   по основанию   a   – это такое число   x,   которое является решением уравнения

      Доказательство того, что решение уравнения (2) существует и единственно, выходит за рамки школьной программы.

      Для логарифма числа   b   по основанию   a   используется обозначение:

log_a b .

      Таким образом, для всех действительных чисел   a   и   b,   удовлетворяющих условиям (1), справедливо равенство

которое часто называют основным логарифмическим тождеством.

      Замечание. Обратим особое внимание на то, что при решении уравнения (2) мы ищем показатель степени, а при решении уравнения

x ^a = b.

мы ищем основание степени, которое вычисляется по формуле

и в случае, когда   a   – натуральное число, является корнем натуральной степени из числа   b.

      Пример 1. Решить уравнение

x³ = 81 .

      Решение. Воспользовавшись понятием кубического корня и свойствами степеней, получаем

      Ответ: .

      Пример 2. Решить уравнение

3^x= 81 .

      Решение. Воспользовавшись тем, что число   81   является четвертой степенью числа   3 ,   получаем:

      Ответ:   4 .

      Задача. Доказать, что число

log₂ 3

иррационально.

      Решение. Предположим противное, т.е. предположим, что указанное число рационально. Тогда существует несократимая дробь

,

числитель и знаменатель которой являются натуральными числами и такая, что справедливо равенство:

      Из определения логарифма отсюда вытекает равенство:

следствием которого является равенство:

2^m= 3ⁿ .

      Но последнее равенство невозможно, поскольку его левая часть четное число, а правая – нечетное. Полученное противоречие доказывает требуемое в задаче утверждение.

Свойства логарифмов

      Перечисленные ниже свойства логарифмов вытекают из основного логарифмического тождества:

Использование свойств логарифмов при решении логарифмических уравнений и неравенств

      Для того, чтобы не ошибаться при решении логарифмических уравнений и неравенств, свойства логарифмов, перечисленные в предыдущем разделе, следует применять внимательно и аккуратно.

      Например, если при решении уравнения или неравенства требуется преобразовать выражение

log_a ( f (x)² ) ,

то вместо формулы

следует применять формулу

поскольку в противном случае можно потерять корни.

      По той же причине при преобразовании выражений

log_a ( f (x) g (x))    и

следует использовать формулы:

и

      Замечание. Желающим усовершенствовать свои знания и умения при решении уравнений и неравенств с логарифмами мы рекомендуем ознакомиться с нашими учебными пособиями «Решение логарифмических уравнений» и «Решение логарифмических неравенств».

Десятичные логарифмы и натуральные логарифмы

      В математике, физике и во многих других областях естествознания и технологий важное место занимают десятичные логарифмы и натуральные логарифмы.

      Десятичные логарифмы – это логарифмы с основанием   10,   а основанием натуральных логарифмов является иррациональное и трансцендентное число   e,   которое определяется по формуле

доказательство которой выходит за рамки школьной программы.

      Для десятичных и натуральных логарифмов используются соответственно обозначения:

lg b       и       ln b,

причем

lg e = 0,43429…,

ln 10 = 2,30259…

      Графики логарифмических функций представлены в разделе «Графики степенных, показательных и логарифмических функций» нашего справочника.

      На сайте можно также ознакомиться с нашими учебными материалами для подготовки к ЕГЭ и ОГЭ по математике.

www.resolventa.ru

Логарифмы. Десятичные и натуральные логарифмы

ГККП «Многопрофильный колледж» акимата г. Астаны,

преподаватель математики

Дуйкенова Лязат Сайлауовна

План учебного занятия

Преподаватель: Дуйкенова Лязат Сайлауовна

Предмет: математика

Специальность, группа 1ПОВт-117 __________________

Тема занятия: Логарифмы. Десятичные и натуральные логарифмы.

Дата __________________________

Тип занятия: урок сообщения новых знаний

Форма проведения — Коллективная, индивидуальная, творческая.

Цель занятия: Ознакомить студентов с понятием логарифма, свойствами логарифмов.

Образовательная

Ознакомить студентов с понятием логарифма числа и со свойствами логарифмов; дать понятие десятичного и натурального логарифма; научить применению свойств логарифма при решении примеров.

Развивающая

развивать самостоятельность мышления студентов при решении задач; формировать учебно-познавательные компетенции в ходе развития навыков самоконтроля.

Воспитательная

развивать у студентов исследовательскую культуру.

Методы: наглядно-иллюстративный, интерактивные методы

Оснащение занятия: мультимедийное оборудование, задания для устного счета, карточки

Межпредметные связи — физика, история, география, химия, астрономия, биология, информатика

Основная

Дополнительная

А.Абылкасымова. Алгебра и начала анализа, учебник 11 класса.

сборник задач по математике

Ход и хронометраж занятия

Этапы занятия

Содержание этапа

Время

1

Организационный момент

Приветствие, проверка отсутствующих и готовности аудитории

2мин

2

Контроль знаний Критерии оценки знаний

Фронтальный опрос

1. Проверка домашней работы (ответы)

2. Определение степени с действительным показателем.

3. Представить в виде степени и в виде корня (устный счет)

8мин

3

Метод изложения нового материала

Перечень освещаемых вопросов

1.Понятие логарифма.

2. Определение логарифма числа.

3. Свойства логарифма.

4. Применение свойств логарифма.

15мин

4

Самостоятельная работа студентов

Выполнение письменных работ

Вычислить логарифмы

8мин

5

Закрепление материала

Фронтальный опрос

1.Понятие логарифма.

2. Определение логарифма числа.

3. Свойства логарифма.

4. Применение свойств логарифма.

10 мин

6

Подведение итогов занятия

Выставление оценок с комментариями.

1 мин

7

Домашнее задание

п.13, №204, 208,

стр 92-93.

1мин

Роспись преподавателя____________________

Ход и хронометраж урока

Организационный момент

2 мин

2

Контроль знаний

8 мин

3

Метод изложения нового материала

15 мин

4

Самостоятельная работа студентов

8 мин

5

Закрепление материала

10 мин

6

Подведение итогов занятия

1 мин

7

Домашнее задание

1 мин

Тема: Логарифмы. Десятичные и натуральные логарифмы.

Цель урока: Ознакомить студентов с понятием логарифма, свойствами логарифмов.

Задачи:

Образовательная

ознакомить с понятием логарифма числа и свойствами логарифмов;

дать понятие десятичного и натурального логарифма; научить применению свойств логарифма при решении примеров

Развивающая

развивать самостоятельность мышления студентов при решении задач; формировать учебно-познавательные компетенции в ходе развития навыков самоконтроля.

Воспитательная

развивать у студентов исследовательскую культуру.

Наглядность: интерактивная доска, карточки, устный счет

Ход урока

1. Организационный момент (отсутствующие)

2. Контроль знаний обучающихся:

Фронтальный опрос

1. Проверка домашней работы (сверка ответов)

2. Карточки с заданиями.

3. Определение степени с действительным показателем.

4. Представить в виде степени и в виде корня (устно)

3. Изложение нового материала

Урок я хочу начать притчей: «Однажды молодой человек пришел к мудрецу. Каждый день по пять раз я произношу фразу: «Я принимаю радость в мою жизнь, но радости в моей жизни нет». Мудрец положил перед собой ложку, свечу и кружку и попросил: « назови, что ты выбираешь из них?». «Ложку», — ответил юноша. «Произнеси это 5 раз». И юноша послушно произнес 5 раз. «Вот видишь», — сказал мудрец, «повторяй хоть миллион раз в день, она не станет твоей. Надо…». Что же надо? Протянуть руку и взять ложку.

Тема урока: “Логарифм и его свойства”. Сегодня мы ознакомимся с понятием и определением логарифма числа, со свойствами логарифма, закрепим умения применять эти понятия при решении задач.

Есть в математике тема одна,

Логарифмической функцией называется она.

Логарифм появился, чтобы легче считать,

Логарифм – показатель, это надо знать!

Вы знакомы с шестью действиями над числами

Эти действия образуют три пары взаимно обратных действий. А для того чтобы решить уравнение а^х=в , где а>0 и а  1 придумали седьмое действие, которое называется логарифмом.

Рассмотрим уравнение 2^х = 16.

Как найти число, в которую нужно возвести число 2,

чтобы получить число 16, х =4. т.к. 2⁴ =16, это равенство можно заменить

= 4

log_а N= x ,где N>0 , а>0, а1

Сообщение из истории математики (1студент)

Совершаем небольшой экскурс в историю математики. Обучающие слушают сообщение на тему “Изобретение логарифма”. На доске записи, которые предлагаем записать в тетрадь.

Джон Непер – 1614 год – изобретение логарифма
Бригс – 1624 год – создание таблиц логарифмов.
1703 год – перевод таблиц на русский язык
Л. Магницкий – 1716 год – издание семизначных логарифмических таблиц.

Логарифмическая линейка(2студент)

Слово логарифм происходит от греческого (число) и (отношение) и переводится, следовательно, как отношение чисел. Выбор изобретателем (1594 г.) логарифмов Дж. Непером такого названия объясняется тем, что логарифмы возникли при сопоставлении двух чисел, одно из которых является членом арифметической прогрессии, а другое — геометрической.

Определение. Логарифмом положительного числа в при положительном основании а, называется показатель степени, в которую нужно возвести основание а, чтобы получить логарифмируемое число в.

=N

Формула  (где в>0, а>0 и а1) называется основным логарифмическим тождеством.

Пример:

1) log₃ 9=2 т.к. 9>0,3>0, 3=1, 3 =9.
2) log ₉ 3=0,5 т.к. 3>0, 9>0, 9=1, 9 =3

Также существуют десятичные и натуральные логарифмы.

log₁₀ x= lg x –это десятичный логарифм.
log_е x=ln x-это натуральный логарифм.

Сообщения ( студенты)

Логарифмы с основанием е ввел С п е й д е л (1619 г.), составивший первые таблицы для функции In x. Название более позднего происхождения натуральный (естественный) объясняется “естественностью” этого логарифма.

Н. Мерка т о р (1620–1687), предложивший это название, обнаружил, что

In х – это площадь под гиперболой у = . Он предлагал также название “гиперболический”.

К доске вызвать обучающегося для записи свойств степеней.

Свойство 1. log_а 1=0, пример:log₃1=0

Свойство 2. log_а а=1, пример:log₅5=1

Свойство 3. Логарифм произведения положительных чисел равен сумме логарифмов множителей log_аN₁N₂= log_а N₁ + log_в N₂

Пример:log₁₂3+ log₁₂4= log₁₂3*4= log₁₂12=1

Свойство 4. Логарифм частного двух положительных чисел равен разности логарифмов делимого и делителя. log_а = log_а N₁— log_а N₂

Пример:log₂48- log₂3= log₂= log₂16=4

Свойство 5. Логарифм степени равен произведению показателя степени на логарифм основания этой степени. log_а N^k=k log_а N.

Пример: log₂3⁴=4 log₂3

Свойство 6 . Логарифм корня п-ой степени log_a =log_aN, N0

Пример: log₅ = log₅2

Свойство 7 .Формула перехода к новому основанию log_aN= 0c1

Свойство 8. Логарифм, основание которого в степени log_a^rN= log_aN

Пример: log₂³7= log₂7

Презентация «Практическое применение логарифмов».

1.Решить примеры (у доски)

а) lg 8+ lg 125= lg 8*125= lg 1000=3;

б) log₂ 7- log₂ = log₂ = log₂ 16₌ 4

2. Вычислить логарифмы:

1. log₃ (27*81)= log₃ 27+ log₃ 81 =3+4 =7

2. log₂ (32)³ = 3 log₂ 32=3*5=15

3. lg 100= 2

4. lg 1/1000 = -3

5. log ₃ = ½

4. Самостоятельная работа студентов

1 уровень

1. Представить равенства через логарифмы

а)3⁴ = 81 б) 2³ =8

2. Проверьте равенство:

а) = 4 б) = 6

в) = -3 г) = -4

3. Найти логарифмы данных чисел

а) = б) =

4. Решить уравнения:

а) = -2 б) = -2

5. Вычислить:

а) — = б) + =

2 уровень

1. Решить уравнения:

а) = -3 б) = -2

2. Вычислить:

а) б)

3. Решить уравнения:

а) = 4 б) = 2

4. Вычислить:

а)( — )⁴ б) —

5. Вычислить:

б)

5. Закрепление нового материала.

1. Фронтальный опрос

2. Понятие логарифма.

3. Определение логарифма числа.

4. Свойства логарифма.

5. Применение свойств логарифма.

Решение задач по учебнику: №206, 209, 210, стр 93

6. Домашнее задание: п.13. № 204, 208, стр 92-93.

7. Итог урока, оценивание

Анкета для рефлексии

1.На уроке я работал

активно

пассивно

2. Своей работой на уроке я

доволен

не доволен

3. Урок для меня показался

коротким

длинным

4. За урок я

не устал

устал

5. Мое настроение

стало лучше

стало хуже

6. Материал урока мне был

полезен / бесполезен

интересен / скучен

7. Урок я бы оценил (а) на

1.На уроке я работал

активно

пассивно

2. Своей работой на уроке я

доволен

не доволен

3. Урок для меня показался

коротким

длинным

4. За урок я

не устал

устал

5. Мое настроение

стало лучше

стало хуже

6. Материал урока мне был

полезен / бесполезен

интересен / скучен

7. Урок я бы оценил (а) на

1.На уроке я работал

активно

пассивно

2. Своей работой на уроке я

доволен

не доволен

3. Урок для меня показался

коротким

длинным

4. За урок я

не устал

устал

5. Мое настроение

стало лучше

стало хуже

6. Материал урока мне был

полезен / бесполезен

интересен / скучен

7. Урок я бы оценил (а) на

Устный счет

1. Представить в виде корня

х^5/2 у^7/11 а^-1/3 в^1/5

2^4/5 р^-8/13 m^0.3 с^2/7

11^4/5 р^-0,1 m^0.5 х^-1/9

2.Представить в виде степени:

3. Вычислить:

Примеры

1.Выразить равенства через логарифмы:

3³= 27 2⁶ = 64

5³ = 125 2^-3 =

3^-4 = ( )^-2 =64

2.Найти логарифмы данных чисел:

log₂ 16 = log₃ 27 =

log_1/2 8 = log₇ =

3.Решить уравнение:

log₃ х = 2 log₅ х = -3 log_1/2 х = -4

log₃ х = 2 log₄ х = -3 log_1/4 х = -2

log_1/3 х = 3 log₅ х = 4 log_1/7 х = -2

Историческая справка

• Знания логарифмов и основных логарифмических свойств необходимы для людей многих профессий: физиков, химиков, астрономов, психологов, географов и экологии

• Логарифмы по основанию 10 до изобретения калькуляторов широко применялись для вычислений. Неравномерная шкала десятичных логарифмов обычно наносится и на логарифмические линейки

• Логарифмическая линейка хорошо знакома нашим родителям. Она позволяет выполнять умножение и деление чисел, возведение в степень и вычисление квадратных и кубических корней.

• Шкала Рихтера — классификация силы землетрясений, созданная и представленная в 1935 г. геологом Чарльзом Рихтером. Шкала основана на принципе логарифма: каждое деление увеличивается в 10 раз, и его основанием является общая энергия, выделяемая при землетрясении.

• В 1858 году немецкий физик и психолог Густав Фехнер доказал, основной психофизический закон, в котором говорится, что интенсивность воспринимаемого нами ощущения пропорциональна логарифму силы раздражения. Его формулируют так: «При изменении силы раздражителя в геометрической прогрессии, интенсивность ощущения меняется в арифметической прогрессии».

• Логарифмы применяются и в психических явлениях. «Шкала Ландау» самый яркий пример. Знаменитый физик по ней оценивал заслуги своих коллег. Шкала была логарифмическая (классу 2 отвечали достижения в 10 раз меньше, чем для класса 1). Из физиков имел класс 0,5, Бор, Дирак, Гейзенберг имели класс 1

• Астрономы измеряют «блеск» небесных светил в звездных величинах. Блеск в астрономии — величина пропорциональная логарифму светового потока. Её направление обратное: чем больше значение звездной величины, тем слабее блеск объекта.

• Xимическая шкала кислотности очень близка к шкале звездных величин. Чем выше кислотность, тем ниже значение индекса, основанием логарифма служит 10.

• Играя на рояле, пианист играет на логарифмах. Ступени темперированной хроматической гаммы представляют логарифмы этих величин

с основанием 2.

• Логарифмическая спираль часто встречается в природе. Впервые логарифмическая спираль описана Декартом, а потом была исследована Бернулли

• Паук Эпейра сплетая паутину, закручивает паутину, скручивая нити вокруг центра по логарифмической спирали

• Живые существа обычно растут во всех направлениях, сохраняя общее начертание своей формы. Раковины морских животных могут расти лишь в одном направлении. Чтобы не слишком вытягиваться в длину им приходится скручиваться.

• Многие Галактики закручены по логарифмической спирали. Солнечная система, как одна из Галактик тоже закручена по такой спирали.

Решить примеры

1.Решить примеры (у доски)

а) lg 8+ lg 125=

б) log₂ 7- log₂ =

2. Вычислить логарифмы:

1. log₃ (27*81)=

2. log₂ (32)³ =

3. lg 100=

4. lg  =

5. log ₃ =

6. log₂ 32=

7. log₅ 625 =

8. log₂ 2 =

9. log₃  =

10) log₄  =

Карточка 1

1. Представить в виде корня:

х^5/2 у^7/11

^{а-1/3 в1/5}

2. Представить в виде степени

Карточка 2

1. Представить в виде корня:

у^5/12 а^5/11

а^-1/8 в^1/4

2. Представить в виде степени:

Карточка 3

1.Представить в виде корня:

у^-5/2 х^7/15

^{а-2/3 в11/5}

2. Представить в виде степени

Карточка 4

1. Представить в виде корня:

n^5/17 m^4/13

x^-1/9 a^7/10

2. Представить в виде степени:

1 уровень

1. Представить равенства через логарифмы

а)3⁴ = 81 б) 2³ =8

2. Проверьте равенство:

а) = 4 б) = 6

в) = -3 г) = -4

3. Найти логарифмы данных чисел

а) = б) =

4. Решить уравнения:

а) = -2 б) = -2

5. Вычислить:

а) — = б) + =

2 уровень

1. Решить уравнения:

а) = -3 б) = -2

2. Вычислить:

а) б)

3. Решить уравнения:

а) = 4 б) = 2

4. Вычислить:

а)( — )⁴ б) —

5. Вычислить:

б)

infourok.ru

Серия уроков по теме «Логарифм.Свойства логарифмов»

Муниципальное общеобразовательное учреждение

«Средняя общеобразовательная школа им. генерала Захаркина И.Г.», г.Кременки, Калужская область.

Разработка урока с применением ИКТ по теме:

«Десятичные и натуральные логарифмы».

Ларешина О.А

учитель математики и информатики,

I квалификационная категория.

г. Кремёнки

2017

Алгебра и начала анализа, 10 класс.

Тема урока,

№ урока по теме

«Десятичные и натуральные логарифмы.

Урок № 2 в теме «Логарифмическая функция»

Актуальность использования средств ИКТ

Возможность самопроверки, проверки знаний с наименьшими затратами времени. Визуализация изучаемого материала. Необходимость объективного оценивания знаний и умений в более короткие сроки 

Цель урока

Повторить определение логарифма, применять основное логарифмическое тождество при решении заданий. Ввести понятие десятичного и натурального логарифма.

Сформировать знания по определению десятичных и натуральных логарифмов.  

 

 

Задачи урока

Обучающие

Развивающие

Воспитательные

Знать:

определения и обозначения десятичного и натурального логарифмов.

Формирование умений применять приемы сравнения, обобщения; выделять главное;

способствовать формированию информационной культуры;

развитие мыслительных операций посредством конкретизации, развитие зрительной памяти, потребности к самообразованию, способствовать развитию познавательных процессов.

Воспитание познавательной активности, чувства ответственности, уважения друг к другу, взаимопонимания, уверенности в себе; воспитание культуры общения.

Развитие умений оценивать себя, свои возможности, брать ответственность за принятое решение;

формирование коммуникативной культуры

Компетенции, формируемые на уроке

Общекультурные, учебно-познавательные, информационные, коммуникативные.

Вид используемых на уроке средств ИКТ (универсальные, ОЭР на CD-ROM, ресурсы сети Интернет)

Презентация в POWER POINT

Универсальные (компьютер, проектор, экран)

Необходимое аппаратное и программное обеспечение

(локальная сеть, выход в Интернет, мультимедийный компьютер, программные средства)

Мультимедийный компьютер, локальная сеть

ОРГАНИЗАЦИОННАЯ СТРУКТУРА УРОКА

ЭТАП 1

Организация начала занятия, обеспечение полной готовности к работе

Цель

Выявить уровень знаний. Актуализировать новые знания. Теоретическая разминка. ( 3 мин)

Цель

Коррекция знаний и умений учащихся (проверка домашнего задания). Постановка целей, определение задач на урок  (выполняют учащиеся) (4-6 мин)

Основной вид деятельности со средствами ИКТ

 Домашнюю работу учащиеся проверяют с помощью компьютера. Взаимопроверка. В головном компьютере находится файл с ГДЗ

Форма организации деятельности учащихся

Фронтальная

Функции преподавателя на данном этапе

Консультант

Основные виды деятельности преподавателя

 Консультирует по невыполненным заданиям из домашней работы

Промежуточный контроль

 Заполнение карточек рефлексии.

ЭТАП 2

Актуализация опорных знаний 

Основной вид деятельности со средствами ИКТ

Задания проверочной работы предложены в презентации (слайд № 2)

Форма организации деятельности учащихся

Индивидуальная (при выполнении проверочной работы), коллективная (при проверке)

Функции преподавателя на данном этапе

Организационная

Основные виды деятельности преподавателя

Координатор действий

Промежуточный контроль

Проверка результатов по презентации (слайд № 3).

Заполнение индивидуального листа-самоконтроля (бумажный вариант)

ЭТАП 3

Изучение нового материала

Цель

Обеспечение восприятия осмысления и первичного запоминания знаний

Длительность этапа

13-15 минут

Основной вид деятельности со средствами ИКТ

Демонстрация презентации (слайды 4-11)

Форма организации деятельности учащихся

Смотрят презентации, слушают учителя, записывают в тетрадь

Функции преподавателя на данном этапе

Объясняет новый материал

Основные виды деятельности преподавателя

Организует беседу, обобщает

Промежуточный контроль

Запись определений из учебника (§16), отметка о выполнении в индивидуальном листе- самоконтроле.

ЭТАП 4

Закрепление полученных знаний

Цель

Закрепить полученные знания, начать вырабатывать умения по их применению

Длительность этапа

12-14 минут

Основной вид деятельности со средствами ИКТ

Самостоятельно проверяют правильность выполнения (по компьютеру), анализируют ошибки

Форма организации деятельности учащихся

Работают в парах: выполняют задания по учебнику

Функции преподавателя на данном этапе

Консультирование, контроль

Основные виды деятельности преподавателя

Отвечает на вопросы учащихся, возникших в ходе выполнения самостоятельной работы

Промежуточный контроль

Заполнение индивидуального листа-самоконтроля (бумажный вариант)

ЭТАП 5

Подведение итогов занятия. Объяснение домашнего задания

Цель

Дать анализ и оценку успешности достижения цели. Рефлексия занятия, объяснение домашнего задания

Длительность этапа

3-5 минут

Основной вид деятельности со средствами ИКТ

Слайд № 12 презентации

Форма организации деятельности учащихся

Записывают домашнее задание

Функции преподавателя на данном этапе

Координатор

Основные виды деятельности преподавателя

Выполняет инструктаж по домашнему заданию

Промежуточный контроль

Заполнение индивидуального листа-самоконтроля (бумажный вариант).

Лист самоконтроля

«Десятичные и натуральные логарифмы».

Домашнее задание

290-2

290-4

291-2

291-4

292-2

292-4

293-2

293-4

294-2

294-4

295-2

296-2

Отметка о

выполнении

Дом. задание

296-4

296-2

296-4

297-2

297-4

298-2

298-4

299-2

299-4

300-2

Отметка о

выполнении

Проверочная работа 

1

2

3

4

5

Отметка о

выполнении

Новый материал

Отметка о

выполнении

Решение упражнений

301-1

302-1

303-1

304-1

305-1

306-1

307-1

Отметка о

выполнении

Доп. задание

259-1

259-2

259-3

259-4

Отметка о

выполнении

Итоги:

Отметка за урок

Обозначение

+

Верно

—

Не верно

+ —

Недочёт

— +

Ошибка

0

Не приступал

Примечание: учебник «Алгебра и начала анализа 10-11», авторы: Ш.А. Алимов,

Ю.М. Колягин и другие.

infourok.ru