Как решать логарифмы с одинаковыми основаниями примеры. Логарифм. Свойства логарифма (сложение и вычитание)

(от греческого λόγος — «слово», «отношение» и ἀριθμός — «число») числа b по основанию a (log α b ) называется такое число c , и b = a c , то есть записи log α b =c и b=a c эквивалентны. Логарифм имеет смысл, если a > 0, а ≠ 1, b > 0.

Говоря другими словами логарифм числа b по основанию а формулируется как показатель степени , в которую надо возвести число a , чтобы получить число b (логарифм существует только у положительных чисел).

Из данной формулировки вытекает, что вычисление x= log α b , равнозначно решению уравнения a x =b.

Например:

log 2 8 = 3 потому, что 8=2 3 .

Выделим, что указанная формулировка логарифма дает возможность сразу определить значение логарифма , когда число под знаком логарифма выступает некоторой степенью основания. И в правду, формулировка логарифма дает возможность обосновать, что если

b=a с , то логарифм числа b по основанию a равен с . Также ясно, что тема логарифмирования тесно взаимосвязана с темой степени числа .

Вычисление логарифма именуют логарифмированием . Логарифмирование — это математическая операция взятия логарифма. При логарифмировании, произведения сомножителей трансформируется в суммы членов.

Потенцирование — это математическая операция обратная логарифмированию. При потенцировании заданное основание возводится в степень выражения, над которым выполняется потенцирование. При этом суммы членов трансформируются в произведение сомножителей.

Достаточно часто используются вещественные логарифмы с основаниями 2 (двоичный), е число Эйлера e ≈ 2,718 (натуральный логарифм) и 10 (десятичный).

На данном этапе целесообразно рассмотреть образцы логарифмов log 7 2, ln√ 5, lg0.0001.

А записи lg(-3), log -3 3.2, log -1 -4.3 не имеют смысла, так как в первой из них под знаком логарифма помещено отрицательное число , во второй — отрицательное число в основании, а в третьей — и отрицательное число под знаком логарифма и единица в основании.

Условия определения логарифма.

Стоит отдельно рассмотреть условия a > 0, a ≠ 1, b > 0.при которых дается определение логарифма . Рассмотрим, почему взяты эти ограничения. В это нам поможет равенство вида x = log α b , называемое основным логарифмическим тождеством , которое напрямую следует из данного выше определения логарифма.

Возьмем условие a≠1 . Поскольку единица в любой степени равна единице, то равенство x=log α b может существовать лишь при b=1 , но при этом log 1 1 будет любым действительным числом . Для исключения этой неоднозначности и берется a≠1 .

Докажем необходимость условия a>0 . При a=0 по формулировке логарифма может существовать только при b=0 . И соответственно тогда log 0 0

может быть любым отличным от нуля действительным числом, так как нуль в любой отличной от нуля степени есть нуль. Исключить эту неоднозначность дает условие a≠0 . А при a нам бы пришлось отвергнуть разбор рациональных и иррациональных значений логарифма, поскольку степень с рациональным и иррациональным показателем определена лишь для неотрицательных оснований. Именно по этой причине и оговорено условие a>0 .

И последнее условие b>0 вытекает из неравенства a>0 , поскольку x=log α b , а значение степени с положительным основанием a всегда положительно.

Особенности логарифмов.

Логарифмы характеризуются отличительными особенностями , которые обусловили их повсеместное употребление для значительного облегчения кропотливых расчетов. При переходе «в мир логарифмов» умножение трансформируется на значительно более легкое сложение, деление — на вычитание, а возведение в степень и извлечение корня трансформируются соответствующе в умножение и деление на показатель степени.

Формулировку логарифмов и таблицу их значений (для тригонометрических функций) впервые издал в 1614 году шотландский математик Джон Непер. Логарифмические таблицы, увеличенные и детализированные прочими учеными, широко использовались при выполнении научных и инженерных вычислений, и оставались актуальными пока не стали применяться электронные калькуляторы и компьютеры.

Логарифмом числа N по основаниюа называется показатель степених , в которую нужно возвестиа , чтобы получить числоN

При условии, что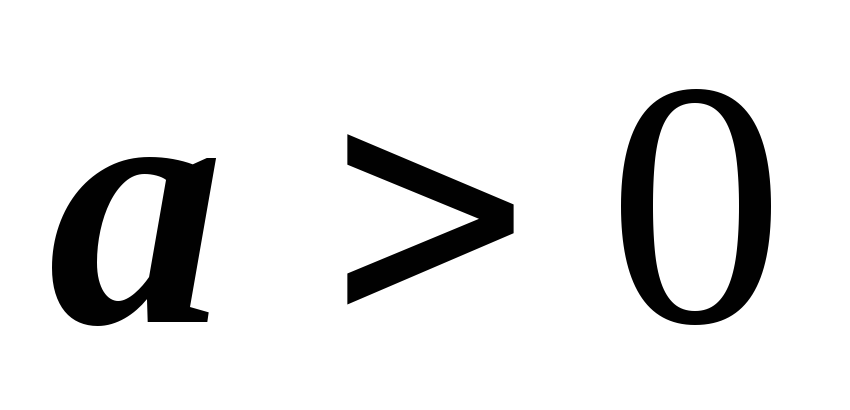
,
,

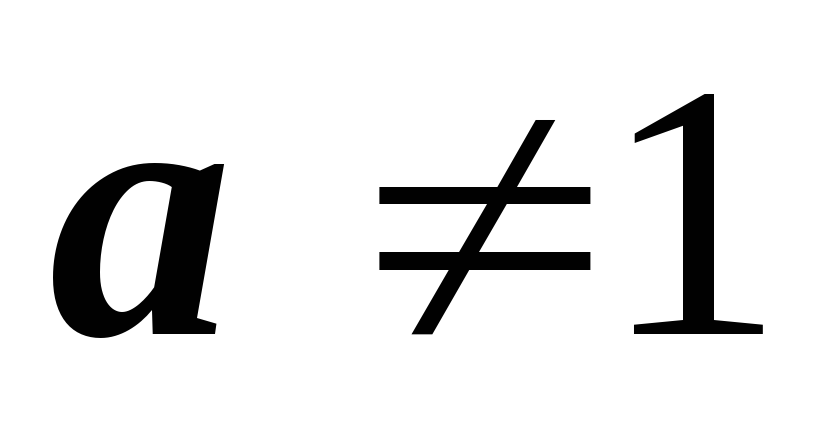maxido.ru

Умножение логарифмов, формула и примеры

Определение и формулы для умножения логарифмов

1 случай. .

Доказательство. Используя частный случай формулы перехода к новому основанию (свойство 11), будем иметь:

   

Что и требовалось доказать.

Например. .

2 случай. При умножении нескольких логарифмов с разными основаниями выражение также можно в некоторых случаях упростить, перейдя к логарифмам с одним основанием по формуле перехода

   

Примеры решения задач

3 случай. Произведение логарифмов с одинаковыми основаниями также можно иногда преобразовать, основываясь на свойствах логарифма.

Понравился сайт? Расскажи друзьям!

ru.solverbook.com

Как сравнивать логарифмы с разным основанием

Как сравнивать логарифмы с разным основанием.

При решении показательных и логарифмических неравенств нередко возникает необходимость сравнить логарифмы с разным основанием.

Рассмотрим, как это сделать.

Пример 1. Сравнить и .

Чтобы сравнить эти логарифмы, нужно найти число, которое стоит на числовой прямой между 

и .

Нетрудно увидеть, что ,

То есть , следовательно, 

 

Чаще ситуация выглядит сложнее.

 

Пример 2. Сравнить  и .

Так как , следовательно, . Аналогично, 

, следовательно, .

То есть значение обоих логарифмов — дробное число, лежащее в пределах от 1 до 2. Подобрать промежуточное число, которое стоит на числовой прямой между и  уже сложнее.

Поступим так. Предположим, в знаменателе промежуточного числа стоит 2. Умножим оба логарифма на 2, то есть сравним числа

и 

Перенесем 2 в показатель степени:

и 

и 

Теперь нетрудно увидеть, что ,  следовательно, .

Если умножение на 2 не приводит к желаемому результату, нужно попытаться умножить на 3, потом на 4  и т.д.

 

Пример 3. В некоторых случаях прежде чем сравнивать логарифмы, нужно выполнить определенные преобразования.

Сравнить  и 

Так как , мы можем преобразовать логарифм с основанием 2:

Итак, мы сравниваем числа  и .

Прибавим к обоим числам 2:

и 

Преобразуем: 

Теперь нам нужно сравнить числа

и 

Значение обоих логарифмов — дробное число, принадлежащее промежутку .

Предположим, в знаменателе промежуточного числа стоит 2. Умножим оба логарифма на 2, то есть сравним числа

и 

Перенесем 2 в показатель степени:

и 

и 

, следовательно, .

, следовательно, .

Получили, что , следовательно, .

 

Репетитор по математике Инна Владимировна Фельдман.

ege-ok.ru

Сумма логарифмов | Логарифмы

Сумма логарифмов с одинаковыми основаниями равна логарифму произведения выражений, стоящих под знаками логарифмов слагаемых:

   

(x>0, y>0).

С помощью этого свойства в некоторых случаях можно найти, чему равна сумма логарифмов, даже если логарифм каждого слагаемого не является рациональным числом.

Например,

   

   

   

   

Это свойство верно, в частности, и для десятичных и натуральных логарифмов.

Сумма десятичных логарифмов равна десятичному логарифму произведения выражений, стоящих под знаками логарифмов слагаемых:

   

Например,

   

   

   

Сумма натуральных логарифмов равна натуральному логарифму произведения выражений, которые стоят под знаками логарифмов в слагаемых:

   

Переход от суммы логарифмов к логарифму произведения верен и в случае когда количество слагаемых больше двух:

   

   

Например,

   

   

   

   

Это свойство логарифмов широко используется при упрощении выражений, в ходе решения логарифмических уравнений и неравенств.

www.logarifmy.ru

Логарифм равен логарифму | Логарифмы

Уравнения, в которых один логарифм равен другому логарифму, можно считать простейшими в случае, когда основания этих логарифмов равны:

   

При решении любого логарифмического уравнения следует определить его ОДЗ либо выполнить проверку найденных корней. В уравнениях вида «логарифм равен логарифму» нахождение ОДЗ может быть упрощено.

Под знаком логарифма должно стоять положительное число, следовательно,

ОДЗ:

   

По свойству логарифмической функции, из того что равны логарифмы по одному основанию

   

следует, что выражения, стоящие под знаками логарифмов, также равны:

   

А раз они равны между собой, если одно из выражений положительно, то другое — также положительно. Следовательно, для нахождения области допустимых значений уравнения достаточно выбрать только одно из двух условий (разумеется, выбирают то неравенство, которое проще решить).

Примеры.

   

ОДЗ:

   

   

Так как логарифмы по одинаковому основанию равны, приравниваем выражения, стоящие под знаками логарифмов:

   

   

   

   

Первый корень не входит в ОДЗ.

Ответ:2.

   

Если разность логарифмов равна нулю,  уравнение может быть представлено в виде «логарифм равен логарифму»:

   

Поэтому в ОДЗ достаточно записать лишь одно условие:

   

   

Поскольку равны логарифмы с одинаковыми основаниями, выражения, стоящие под знаками логарифмов, тоже равны:

   

   

   

   

   

   

Второй корень не входит в ОДЗ.

Ответ: 1,5.

www.logarifmy.ru