Ломаная линия / Виды линий / Справочник по математике для начальной школы

1. Главная
2. Справочники
3. Справочник по математике для начальной школы
4. Виды линий
5. Ломаная линия

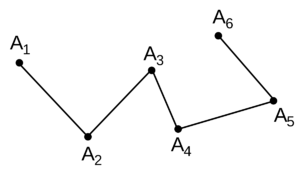
Ломаная линия состоит из отрезков — звеньев.

---

Конец одного отрезка — на­чало другого. Ни­какие два соседние звена не лежат на одной прямой.

---

 Концы каждого звена — это вершины. Их можно обозначать буквами.

---

Ломаная линия бывает незамкнутая.

---

Из незамкнутой ломаной линии можно получить замкнутую ломаную линию.

Такая замкнутая ломаная линия называется треугольником.

У нее три вершины.

---

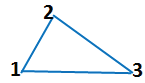
У треугольника три звена.

---

Замкнутая ломаная линия из четырёх звеньев называется четырёхугольником.

---

Замкнутая ломаная линия из пяти или шести звеньев называется многоугольником.

---

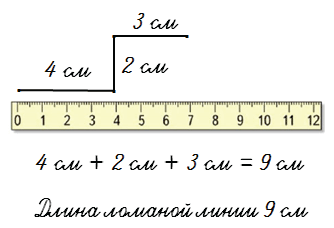
Чтобы найти длину ломаной линий нужно измерить длину каждого звена-отрезка и сложить все длины.

Например,

Поделись с друзьями в социальных сетях:

Советуем посмотреть:

Точка. Кривая. Прямая линия

Отрезок. Луч

Длиннее. Короче. Уже. Шире. Одинаковые по длине и ширине

Виды линий

Правило встречается в следующих упражнениях:

1 класс

Страница 71, Моро, Волкова, Степанова, Учебник, 1 часть

Страница 16, Моро, Волкова, Рабочая тетрадь, 1 часть

Страница 34, Моро, Волкова, Рабочая тетрадь, 1 часть

Страница 37, Моро, Волкова, Рабочая тетрадь, 1 часть

Страница 12. Вариант 1. № 3, Волкова, Проверочные работы

Страница 25, Моро, Волкова, Степанова, Учебник, 2 часть

Страница 41, Моро, Волкова, Степанова, Учебник, 2 часть

Страница 107, Моро, Волкова, Степанова, Учебник, 2 часть

Страница 32, Моро, Волкова, Рабочая тетрадь, 2 часть

Страница 36, Моро, Волкова, Рабочая тетрадь, 2 часть

2 класс

Страница 5, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 1 часть

Страница 8, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 1 часть

Страница 41, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 1 часть

Страница 52, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 1 часть

Страница 64, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 1 часть

Страница 92, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 1 часть

Страница 32. Вариант 1. № 3, Моро, Волкова, Проверочные работы

Страница 5, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть

Страница 68, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть

Страница 83, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть

3 класс

Страница 5, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 1 часть

Страница 6, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 1 часть

Страница 14, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 1 часть

Страница 19, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 1 часть

Страница 41, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 1 часть

Страница 108, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 1 часть

Страница 5, Моро, Волкова, Рабочая тетрадь, 1 часть

Страница 14, Моро, Волкова, Рабочая тетрадь, 1 часть

Страница 35, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть

Страница 7. Вариант 2. № 2, Моро, Волкова, Проверочные работы

4 класс

Страница 8, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 1 часть

---

© budu5.com, 2019

Пользовательское соглашение

Copyright

budu5.com

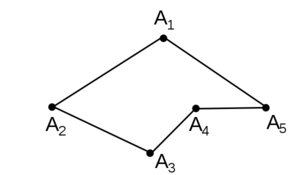
звенья, вершины, длина. Замкнутая ломаная

Ломаная линия – это геометрическая фигура, состоящая из последовательно соединённых отрезков, в которой конец одного отрезка является началом следующего. При этом соседние (имеющие общую точку) отрезки не должны лежать на одной прямой.

Отрезки, из которых состоит ломаная, называются её звеньями, а концы этих отрезков – вершинами ломаной.

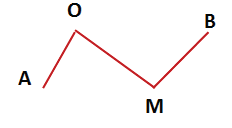
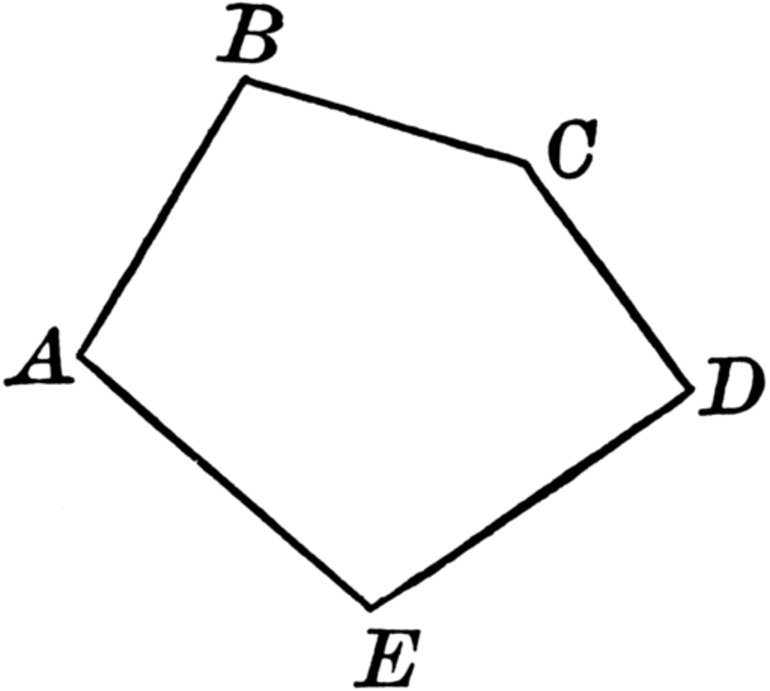
Построим ломаную из четырёх отрезков:

Отрезки AB, BC, CD и DE – это звенья ломаной. Точки A, B, C, D и E – вершины ломаной. Обозначение ломаной линии составляют из букв, стоящих при её вершинах, называя их по порядку. Например, говорят или пишут: ломаная ABCDE или ломаная EDCBA.

Замкнутая ломаная

Если концы ломаной совпадают, то такая ломаная называется замкнутой:

ломаная ABCDE.

Замкнутая ломаная линия, у которой звенья не пересекаются между собой, называется многоугольником:

многоугольник ABCED.

Длина ломаной

Длина ломаной – это сумма длин всех её звеньев.

Найдём длину ломаной, сложив длины всех её звеньев:

ABCD = AB + BC + CD = 4 см + 3 см + 2 см = 9 см.

naobumium.info

звенья, вершины и длина, разновидности

Ломаной называется особая разновидность геометрической фигуры, которая составлена из нескольких отрезков. Эти отрезки последовательно соединены между собой своими концами. Конец каждого отрезка, за исключением последнего, является начальной точкой следующего. Смежные отрезки не должны находиться на одной прямой линии.

…

Вконтакте

Facebook

Twitter

Google+

Мой мир

Существует и другое определение того, что такое ломаная фигура. Согласно ему это геометрический объект, который представляет собой непрямую линию и состоит из череды отрезков, последовательно соединенных между собой. Эти отрезки могут образовывать углы различной величины. Даже если угол между ними будет минимальным, он все равно будет ломать линию и ее уже можно считать ломаной. В этом и заключается ее основное отличие от прямой.

Это интересно: разность чисел — что это, как ее найти?

Ломаную линию следует отличать от кривой. Основное отличие заключается в том, что отрезки ломаной являются прямыми линиями, а отрезки кривой — нет. Эти понятия подробно объяснит школьная программа по математике за 8 класс.

Звенья, вершины и длина

Чтобы полностью усвоить сущность и свойства этого понятия, рассмотрим, что такое звенья ломаной линии в математике, а также что представляют собой ее вершины и длина:

1. Отдельные отрезки, составляющие такую линию, называются ее звеньями. Каждая такая линия может состоять как минимум из двух звеньев. Максимальное количество звеньев при этом не ограничено.
2. Точки соединения концов этих отрезков называются вершинами.
3. Если концы ломаной соединяются в одной точке, такая фигура носит название замкнутой. Ее звенья могут иметь взаимные пересечения.
4. Если же звенья одной замкнутой линии не пересекаются между собой, она называется многоугольником.
5. Геометрическое понятие длины ломаной включает в себя сумму длин всех ее звеньев.

Интересно знать: что такое выпуклый четырехугольник, его особенности и признаки.

Обозначение ее составляется из заглавных латинских букв, которые стоят на вершинах:

1. Каждая вершина на рисунке обозначается одной буквой (например: A, B, C, D или E).
2. Звено принято обозначать двумя буквами (концы соответствующего отрезка, например: AB, BC, CD, DE).

В целом такую совокупность принято называть ABCDE или EDCBA.

Обратите внимание: что такое луч в геометрии.

Разновидности

В геометрии принято различать несколько разновидностей по структуре:

1. Замкнутые самопересекающиеся.
2. Незамкнутые самопересекающиеся.
3. Замкнутые без самопересечений.
4. Незамкнутые без самопересечений.

Как уже было описано выше, замкнутая непересекающаяся фигура получила название многоугольника.

Если звенья фигуры имеют пересечения между собой — она называется самопересекающейся.

Многоугольники

Многоугольник — это геометрическая фигура, которая характеризуется количеством углов и звеньев. Углы составлены парами звеньев замкнутой ломаной, сходящимися в одной точке. Звенья называются еще сторонами многоугольника. Общие точки двух отрезков называют вершинами многоугольника.

Количество звеньев или сторон в каждом многоугольнике соответствует количеству углов в нем же. Замкнутая ломаная из трех отрезков называется треугольником. Ломаная из четырех звеньев получила название четырехугольника. Фигура из пяти отрезков — пятиугольник и т. д.

Часть плоскости, которая ограничена замкнутой ломаной, называется плоским многоугольником. Другое ее название — многоугольная область.

Свойства

Ниже приведены основные свойства, общие для всех многоугольников:

1. Если вершины многоугольника служат концами одной стороны, их называют соседними. Если же вершины не прилежат к одной стороне, они несоседние.
2. Наименьшее количество сторон у многоугольника равняется трем. Однако треугольники, находясь рядом друг с другом, могут образовывать новые фигуры.
3. Если отрезок соединяет между собой несоседние вершины, он носит название диагонали.
4. Если фигура лежит относительно одной прямой в любой полуплоскости, она называется выпуклой. При этом прямая содержит в себе одну сторону фигуры и сама принадлежит полуплоскости.
5. Угол, смежный внутреннему углу многоугольника при некоторой вершине, называется внешним.
6. Если все стороны и углы многоугольника равны, он называется правильным.

Треугольники

Треугольником в математике принято называть плоскую геометрическую фигуру, которая состоит из трех точек, не располагающихся на одной прямой. Эти точки соединены тремя отрезками.

Точки представляют собой вершины или треугольника, а отрезки — его стороны. Возле каждой из вершин образуется угол треугольника. Таким образом эта фигура имеет три угла, что видно из ее названия.

Различают следующие виды треугольников:

1. Равносторонние — все стороны их равны по длине.
2. Разносторонние — все стороны различаются по длине.
3. Равнобедренные — две стороны из трех имеют одинаковую длину.
4. Остроугольные — если все углы острые.
5. Прямоугольные — если имеется прямой угол.
6. Тупоугольные — если есть один тупой угол.

Четырехугольники

Плоская геометрическая фигура, имеющая четыре угла и четыре стороны, называется четырехугольником.

Если все углы у четырехугольника прямые — это прямоугольник.

Правильный четырехугольник носит название квадрата.

Существуют и другие разновидности четырехугольников — ромб, трапеция, параллелограмм и пр. Все они подчиняются общим правилам, описанным выше.

obrazovanie.guru

Замкнутая ломаная линия — как она выглядит, и что такое вершины ломаной

Ломаной линией в геометрии принято называть геометрическую фигуру, которая состоит из двух или нескольких отрезков. Конец одного отрезка является началом другого. Обязательное условие, которому подчиняется любая ломаная, — соседние отрезки не должны располагаться на одной прямой.

Эти геометрические фигуры находят самое широкое применение в разных областях науки и практики:

1. Картография — для построения изображений улиц и схем маршрутов.
2. Архитектура — очертания зданий и строений.
3. Ландшафтный дизайн — декоративное оформление и расположение тропинок.
4. Химия — молекулярная структура сложных полимерных соединений.
5. Медицина — мониторы для контроля функционального состояния органов и систем.

Типы ломаных линий

Рассматриваемые геометрические фигуры могут быть выстроены самыми разнообразными способами — они могут быть незамкнутыми и замкнутыми, пересекающимися и непересекающимися.

Замкнутая ломаная соответствует определенной геометрической фигуре — многоугольнику.

Если отрезки одной такой фигуры имеют точки пересечения друг с другом — эта линия называется самопересекающейся.

Всего существует 4 типа подобных линий по своей структуре:

1. Замкнутые, которые не имеют пересечений.
2. Незамкнутые, которые не имеют пересечений.
3. Незамкнутые самопересекающиеся.
4. Замкнутые, имеющие самопересечения.

Разновидностью такой геометрической фигуры может считаться зигзаг, у которого последовательные отрезки образуют прямой угол и параллельны друг другу через один. Зигзагами широко пользуются в обиходе — в портновском мастерстве, декоративном искусстве, оформлении предметов обихода.

Особенности замкнутых линий

Рассмотрим подробнее составляющие части этой геометрической фигуры.

1. Один отрезок из тех, что составляют описываемую фигуру, называется ее звеном. Ломаной может считаться такая линия, которую составляют как минимум два отрезка — звена. Если звено одно — это просто единичный отрезок.
2. Существует также понятие вершины ломаной. Этим термином принято называть точку, в которой соединяются концы двух звеньев. Такие точки в геометрии принято обозначать с помощью заглавных латинских букв. Сама ломаная называется сочетанием обозначений этих вершин. Например, названием такой линии может послужить сочетание ABCDEF.
3. Если концы крайних звеньев этого геометрического объекта соединяются в одной точке, такая линия называется замкнутой.
4. Ломаная линия может пересекать саму себя.
5. Конечные вершины такой фигуры в геометрии принято называть черными точками.

Как уже было сказано выше, эта разновидность линий может иметь самопересечения. Наиболее популярным примером замкнутой линии, имеющей самопересечения, является пятиконечная звезда.

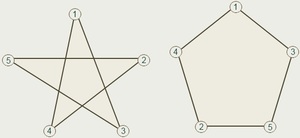
Многоугольник как разновидность замкнутой ломаной

Разновидностью описываемой геометрической фигуры является многоугольник. Точками в многоугольнике являются его вершины, а отрезки называются сторонами.

1. Если вершины принадлежат одной и той же стороне многоугольника — они носят название смежных.
2. Если отрезок соединяет две любых вершины, не являющиеся смежными, он называется диагональю.
3. Если у многоугольника имеется n вершин — он называется n-угольником. У такой фигуры имеется количество сторон, равное n.
4. Такая ломаная делит плоскость на 2 части — внешнюю и внутреннюю.
5. Если точки многоугольника лежат по одну сторону от прямой и проходят через 2 соседние вершины — его принято называть выпуклым.
6. Угол выпуклого многоугольника при данной вершине — это угол, который образован двумя его сторонами, для которых эта вершина является общей.
7. Внешний угол выпуклого многоугольника при определенной вершине — это угол, смежный с внутренним углом многоугольника при этой же самой вершине.

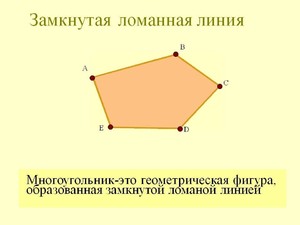
Примерами многоугольников являются четырехугольники, треугольники, пятиугольники. Рассмотрим подробнее отличительные черты этих фигур.

Треугольник — это геометрическая фигура, которая состоит из трех точек, расположенных не на одной прямой. Эти точки попарно соединяются между собой отрезками.

Четырехугольником в геометрии называется фигура, которая имеет четыре угла и четыре стороны. Четырехугольники встречаются самые разнообразные — это могут быть трапеции, квадраты, параллелограммы, ромбы.

У трапеции параллельны две стороны, которые называются основаниями. Остальные две стороны не параллельны. У параллелограмма между собой параллельны две противоположные стороны.

Отличительной чертой прямоугольника является то, что все его углы прямые. У квадрата являются равными все четыре стороны. Кроме того, все углы у квадрата являются прямыми.

Если у многоугольника все стороны и углы равны, он называется правильным. Такой многоугольник всегда будет выпуклым.

liveposts.ru

Урок по математике на тему «Отрезок. Ломаная» (1 класс)

Раздел: Геометрические фигуры.

Тема: Отрезок. Ломаная

Школа: КГУ «Средняя школа № 6» акимата г. Усть — Каменогорска

Дата: 13.10.2016г

Имя учителя: Шахова В.Р.

КЛАСС: 1 «Б»

Количество присутствующих:

отсутствуют:

Цель(и) обучения, к которой(ым) стремится данный урок

1.3.1.1. -распознавать и называть геометрические фигуры: точку, прямую, кривую, ломаную, замкнутую и незамкнутую линии, отрезок, луч, угол.

Цели урока

Все учащиеся смогут:

различать отрезок, ломаную;

Большинство учащихся смогут:

видеть отрезки и ломаные в предметах окружающего мира, строить их при помощи линейки

Некоторые учащиеся смогут:

построить отрезок и ломаную линии с помощью линейки и на основе алгоритма

Языковые цели

Учащиеся могут:

узнать что такое ломаная линия, из чего она состоит, чем отличается от отрезка, луча, прямой линии, кривой линии

Ключевые слова и фразы:

Отрезок, ломаная

Речь, используемая для диалога/письма на уроке:

Вопросы для обсуждения:

– Что такое отрезок?

— Что такое ломаная?

— Как построить отрезок?

Письмо:

Задания на построение отрезка и ломаной.

Предыдущее обучение

Знание последовательности чисел от 0 до 10, числовой луч. Состав чисел 2-10. Классификация предметов по их признакам. Точка. Линия. Луч.

План

Время

Запланированные задания

Ресурсы

0-1 мин

Вот звенел для нас звонок – начинается урок. Ровно встали, подтянулись и друг другу улыбнулись.

2-5 мин

Актуализация знаний. Постановка учебной задачи. (Г,И,П)

• На что похожа веревка у меня в руках? (на линию)

• Какую линию можно сделать из этой веревки? (прямую незамкнутую линию, замкнутую линию).

• Растяните веревку, чтобы образовалась прямая незамкнутая линия.

• А теперь встаньте в круг и, держась за веревку, создать замкнутую линию — «круг радости», в котором дети могут пожелать друг другу хорошего дня и новых открытий на уроке.

• Чтобы пожелания исполнились, нужно забрать с собой часть этой веревки.

• Как это можно сделать?

• Давайте отрежем веревку при помощи ножниц. (Отрежьте часть веревки с двух сторон).

• Что получилось?

• Ребята, часть веревки называется отрезком.

• Встречались ли вы с отрезком в жизни? Приведите примеры. (отрезок дороги, отрезок времени).

• Чем отрезок отличается от прямой?

• У прямой линии нет начала и конца, она бесконечна, а отрезок имеет начало и конец.

— Объединитесь в группы по четыре человека и соедините свои отрезки. Что у вас получилось?

— Посмотрите, одна группа выложила отрезки по одной прямой, а другая, в виде ломаной линии.

— С прямой линией мы уже знакомы. Давайте теперь познакомимся с ломаной линией.

— Как вы думаете, почему она так называется?

— Ломаная линия состоит из отрезков, не лежащих на одной прямой. Конец одного отрезка является началом другого отрезка.

— Поэкспериментируйте в группах, в создании ломаной линии.

— Найдите среди окружающих предметов отрезки и ломаные. Приведите доказательства того, что найденный предмет является отрезком или ломаной.

бельевая веревка длиной 5 м, ножницы

5-13 мин

Работа по учебнику.

Научись строить отрезок.

— Как можно изобразить отрезок?

— Давайте откроем учебник на с. 50 и ознакомимся с алгоритмом изображения отрезка.

-Постройте отрезки на отдельных листах, следуя по шагам алгоритма. Обменяйтесь листами и осуществите взаимопроверку в парах.

Найди отрезок.

— Рассмотрите изображение в учебнике и назовите только отрезки.

— Как вы отличаете отрезки от линий?

(П)Построй ломаную.

— Помогите Ластику и Линейке построить на бумаге ломаную из 4 звеньев. Образец построения фигуры приведен в учебнике.

— Опишите порядок построения ломаной.

Попробуй.

— Ребята сравните отрезки по длине.

— Длину каких отрезков сравнить не удалось? Почему? (Затруднение может возникнуть при сравнении оранжевых отрезков, так как они изображены перпендикулярно друг другу.)

— Главное правило, которому следует следовать при сравнении, — совместить концы двух отрезков.

Учебник. Ламинированный картон

14-15 мин

Динамическая пауза

Дружно все ребятки встали,(дети встают из-за парт),

На носочки поднялись, (поднимаются на носочки),

И подняли ручки ввысь, (руки поднимают над головой)

Мы до солнышка достанем,

И совсем большими станем.(пытаются дотянуться выше, шевелят пальчиками)

Пусть нам светит солнышко,(делают круговое движение руками, опуская руки вниз)

Луч стремится вниз,(дети наклоняются, руки расслаблены)

Детки очень умные в классе собрались!(дети распрямляют спинки, плечи, гладят себя по голове)

16- 18 мин

Работа по учебнику.

Реши.

— Рассмотрите в учебнике на с. 51 иллюстрацию и определите, сколько отрезков на ней изображено? (7 отрезков)

— Попробуйте визуально определить, по какой дорожке ежик быстрее доберется до своего домика. (Самой короткой является дорожка, состоящая из одного отрезка.)

— Как называется верхняя дорожка?

— Из скольких отрезков входит в состав ломаной? (6 отрезков)

Развитие языковых компетенций

Проведите игру. Используйте отрезки веревки, которые ребята получили в начале урока. По команде ведущего: «Отрезок!» они демонстрируют свои фрагменты веревки, подняв их вверх. При команде ведущего: «Ломаная!» дети объединяются в группы и составляют из своих фрагментов ломаные линии. После этого можно подсчитать, сколько отрезков составляют ломаные.

Учебник, отрезки веревки

19-23 мин

Построй отрезки МК и МН.

— Для построения отрезков пользуйтесь линейкой, а для аккуратного выполнения работы в тетради необходим остро заточенный карандаш.

— Какая линия у вас получилась?

— Сколько в ней звеньев?

— Дополни чертеж таким образом, чтобы в ломаной было 4 звена.

— При помощи линейки измерьте длину отрезков и запишите над ними их числовое значение.

Чертеж.

— Рассмотрите чертеж. Сколько на нем отрезков?

— Запишите их названия

Реши примеры.

— Ответы запишите в пустые окошки.

Рабочая тетрадь:

рабочий лист 47, линейка, простой карандаш

23-24 мин

Пальчиковая гимнастика

25-32 мин

Измерь длину змейки.

— Посчитайте количество звеньев. Результат запишите в пустые окошки.

— Попробуйте измерить змейку при помощи линейки. Сложив числовое значение каждого звена ломаной линии, вы узнаете ее длину.

— Постройте при помощи линейки и простого карандаша ломаную такой же длины что и змейка. Помни, что одно звено змейки, равно одной клетке.

Вставь пропущенные числа.

— Вставьте в клетки пропущенные числа и решите примеры.

Рабочая тетрадь: рабочий лист 48, линейка, простой карандаш

33-35 мин

Рефлексия

• Что такое отрезок?

• Что такое ломаная?

• Как построить отрезок?

• Какие линии удобно изображать при помощи линейки? Чем луч отличается от прямой линии?

Изображения линий и точек.

Лестница успеха

Дополнительная информация

Дифференциация

Задание «Построй змейку». Те ребята, которые не умеют складывать числа, могут откладывать по линейке или по клеткам в тетради длину каждого звена ломаной. Это задание дано для ребят, умеющих считать до 20

Оценивание

Наблюдая за работой учащихся в группе, их самостоятельной работой.

Задавая вопросы по ходу урока.

Просматривая работы учащихся в тетради (задания).

Анализируя результаты ученической рефлексии. Ступеньки успеха

Межпредметные связи

Рефлексия для учителя

Важные вопросы по уроку:

Комментарии по проведенному уроку

Итоговая оценка (с точки зрения преподавания и обучения)

Какие два момента были наиболее успешны?

Какие два момента улучшили урок?

Что узнал из урока о классе и отдельных людях, что я расскажу на следующем уроке?

infourok.ru

Ломаная линия ℹ️ определение, виды, теоремы, примеры построения замкнутых и незамкнутых геометрических фигур, вершины и звенья

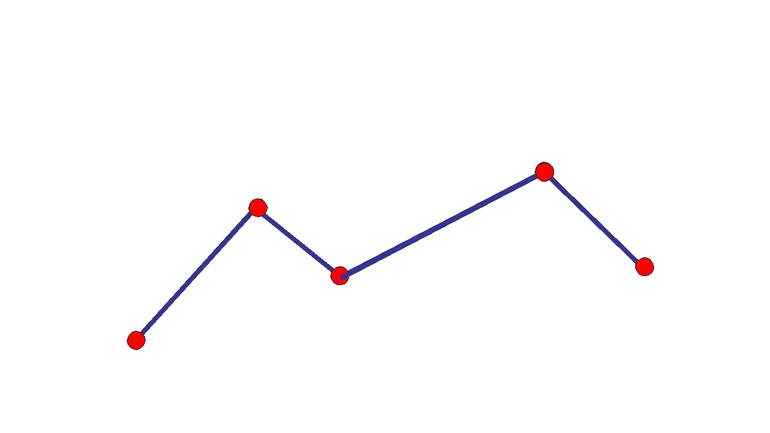
Краткое описание

Специалисты называют ломаной ту геометрическую фигуру, которая представляет собой непрямую линию, состоящую исключительно из многочисленных соединённых отрезков. Учащимся нужно запомнить, что все эти фрагменты могут сходиться под абсолютно разными углами. Проще говоря, если есть даже самый маленький угол между двумя соединёнными отрезками, то это линия своеобразного ломаного типа.

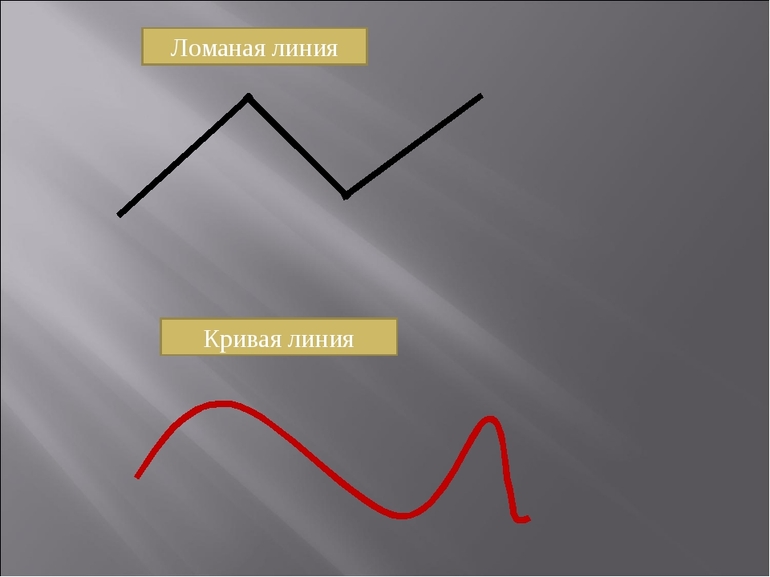
Прямая тоже может состоять сразу из нескольких геометрических фрагментов, но угол их соединения приравнивается к нулю. Для избежания грубых математических ошибок нужно помнить, что ломаная линия отличается от кривой, так как отдельные отрезки представляют собой прямую линию, чего нельзя сказать о кривой.

В некоторых случаях пространственная ломаная может образовывать замкнутую фигуру. Но такая ситуация возможна только тогда, когда концы крайних отрезков совпадают, а также пересекают самих себя. Рассматриваемая в математике фигура состоит из вершин и отрезков, которые и соединяют эти вершины. Но в этом случае действует правило — два последних отрезка не должны лежать на одной прямой.

Сторонами или звеньями изогнутой линии принято называть составные отрезки. Минимальное количество звеньев — два. Специалисты привыкли называть чёрными точками конечные вершины ломаной линии. Чтобы графически всё выглядело правильно, необходимо использовать обозначения в соответствии с названиями задействованных вершин.

Если конечные вершины совпадают, тогда речь касается изогнутой замкнутой линии. В качестве примера можно рассмотреть многоугольник. Эта фигура представляет собой плоскую замкнутую ломаную, которая лишена каких-либо самопересечений. Вершины ломаной линии и её звенья относятся к многоугольнику. Если речь касается фигуры с тремя сторонами и вершинами, то это треугольник.

Немного сложнее разобраться с замкнутой ломаной и её четырьмя сторонами, так как это может быть прямоугольник, квадрат, параллелограмм, ромб и даже трапеция. Если фигура имеет пять или более сторон, то она называется n-угольником. Символ n указывает на точное число вершин.

Некоторые математические примеры касаются изогнутой линии с самопересечениями (пятиконечная звезда). К этой категории также можно отнести зигзаг, в котором каждый второй отрезок параллелен другому, а последние формируют одинаковый угол.

Математическое определение

Ломанной принято называть ту геометрическую фигуру, которая состоит из обычных отрезков (R1, R2, R3 и R4, Rn-1 Rn). Вершинами изогнутой принято называть точки R1…Rn, а вот все остальные отрезки — это неотъемлемые звенья. Если для любого w действует формула {1, 2, n — 2}, а отрезки не расположены на одной прямой, то такая ломанная будет называться невырожденной. В противном случае придётся иметь дело с вырожденным примером.

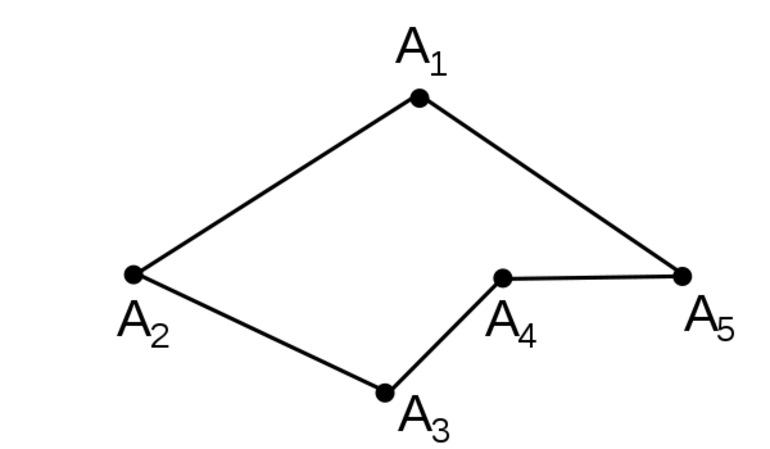
Для лучшего усвоения этой темы следует рассмотреть несколько примеров. Изогнутая может иметь самопересечение, но это возможно только в том случае, если минимум два отрезка обладают общей точкой (за исключением вершины).

В математике часто можно встретить фигуру, которая является обычной ломаной линией. В этом случае практикуется применение следующей записи: R1R2R3R4R5R6. Если ученику предстоит разобраться со всеми нюансами построения замкнутой ломаной из трёх звеньев и более, тогда ему понадобятся вспомогательные отрезки (к примеру: R1, R2, а также Rn -1 Rn, которые не должны лежать на одной прямой).

Замкнутую плоскую ломаную линию принято называть многоугольником. Если рассматривать многогранники, то все стороны фигуры будут называться рёбрами. Учителя России предпочитают создавать краткосрочное планирование по этой теме, так как в этом случае можно донести больше полезной информации до учеников.

Гораздо проще разобраться с изгибами зигзага, так как они используются в швейном деле, в распространённом декоративном оформлении предметов обихода в качестве орнамента. Стоит отметить, что изогнутая линия нашла широкое применение в различных отраслях:

1. Архитектура. Изогнутые линии позволяют сооружать интересные номера.
2. Картография (тщательное проектирование маршрутов и подробное схематическое изображение всех улиц).
3. Химическая отрасль (различные соединения и своеобразные молекулярные структуры).
4. Востребованный дизайн ландшафтов (утончённое оформление, расположение дорожек).
5. Медицина (мониторы для наблюдения за сердечным ритмом).
6. Метод освоения каллиграфических навыков в китайском языке.

Изучение этой темы в математике является обязательным, так как от этого зависит качество усвоения материала учеником.

Основные разновидности ломаных

Геометрическая фигура может быть построена совершенно по любому из действующих методов. Специалисты выделяют замкнутую, а также незамкнутую ломанную. Повышенное внимание уделяют самопересекающимся, непересекающимся линиям. Классическая замкнутая ломаная является многоугольником. В математике самопересекающейся принято называть ту линию, отрезки которой имеют минимум одно пересечение. По своей структуре ломаная может быть весьма разнообразной, из-за чего нужно внимательно относиться ко всем аспектам.

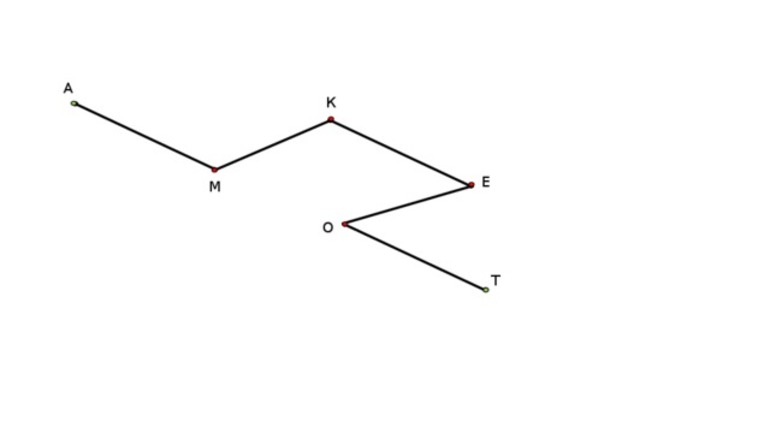
В начальных классах школы принято рассматривать следующий пример: ломаная включает в себя сразу пять звеньев либо сторон: ZX, XC, CV, VB, BN. Та точка, где неизбежно соединяются два звена, называется вершиной. В этом случае имеется сразу четыре вершины: X, С, V, B.

Повышенное внимание нужно уделить изучению звена ломаной. Звеньями эксперты привыкли называть стороны либо отрезки, из которых образована линия. Всего одно такое звено может быть рассмотрено только в качестве отрезка. А вот для построения ломаной необходимо задействовать как минимум два звена. Вершины — это классические точки, которые представляют собой концы одних отрезков ломаной. Обозначить точки можно только латинскими буквами.

Пример замкнутой, а также традиционной незамкнутой ломаной линии, которую часто можно встретить в геометрии и алгебре:

Если необходимо определить точную длину ломаной, то для этого следует поочерёдно сложить все известные данные задействованных звеньев (ZX + XC + CV + VB + BN).

Базовые понятия

Чтобы гарантировано освоить все правила, которые касаются использования изогнутой линии в математике, необходимо разобраться со звеньями. Существует ряд нюансов, которые можно сопоставить с элементарной геометрической конструкцией. Линию формируют отдельные отрезки, которые в математике называются звеньями. Если все концы ломаной соединяются в одной точке, то такая фигура будет называться замкнутой.

Все задействованные звенья могут обладать взаимными пересечениями. Вершинами специалисты привыкли называть точки соединения отрезков. О многоугольнике можно говорить только в том случае, если звенья не пересекаются между собой. Звено обозначают сразу двумя латинскими буквами. Каждая вершина изогнутой линии может обозначаться только одной буквой. Только тщательное изучение всех правил и нюансов позволит правильно решать математические задачи.

Особенности построения многоугольников

В этом случае речь касается геометрической фигуры, отличающейся итоговым количеством звеньев, углов. Последние могут быть сформированы только несколькими звеньями замкнутой ломаной, которые сходятся в одной точке. Задействованные звенья также могут носить логическое название сторон многоугольника. Общие точки двух отрезков называются вершинами. Стоит учесть, что количество сторон либо звеньев в каждой такой фигуре в точности соответствует количеству углов. Если задействовать замкнутую ломаную из трёх отрезков, то в итоге получится треугольник.

Абсолютно все многоугольники обладают одинаковыми свойствами. Самая маленькая фигура включает в себя всего три стороны. Но расположенные в непосредственной близости треугольники могут формировать совершенно новые фигуры. Если имеющиеся вершины изучаемого многоугольника являются своеобразным дополнением одной стороны, то их всегда называют соседними.

Когда многоугольник был расположен относительно одной прямой в любой плоскости, то она называется выпуклой. А вот прямая может содержать в себе одну сторону фигуры и принадлежать полуплоскости. Если отрезок соединяет не соседние вершины, то он называется диагональю. Смежный внутренний угол при некоторой вершине называется внешним.

Следует отметить тот факт, что когда все имеющиеся углы и стороны многоугольника равны между собой, то речь касается правильных отрезков. Каждая геометрическая фигура обладает определёнными параметрами. Треугольниками в алгебре принято называть обычную плоскую фигуру, которая состоит из трёх точек, не расположенных на одной прямой. Для соединения используются обычные отрезки. Точки выступают в роли вершин треугольника. Такая фигура имеет всего три угла. Специалисты различают 6 разновидностей треугольников:

1. Элементарные разносторонние. В этом случае каждая следующая сторона отличается своей длиной.
2. Равносторонние. Абсолютно все стороны обладают идентичной длиной.
3. Специфические остроугольные. Сформированные углы имеют острую форму.
4. Универсальные равнобедренные. Сразу две стороны из трёх существующих обладают одинаковой длиной.
5. Тупоугольные. Фигура обладает одним тупым углом.
6. Традиционные прямоугольные. Нарисованная фигура должна иметь минимум один прямой угол.

Четырёхугольником называют ту конструкцию, которая обладает четырьмя сторонами и четырьмя сторонами. Использование таких геометрических фигур обладает определёнными нюансами.

Ключевые нюансы

Существует две линии SWT и SFT одинаковой толщины, которые соединяют свободные концы одной прямой ST. В итоге образуется ломаная. Изогнутая SFT именуется внутренней ломаной, а вот SWT внешней. В качестве примера лучше всего рассмотреть фигуру, которая соответствует математической теореме, что внешняя изогнутая превышает внутреннюю.

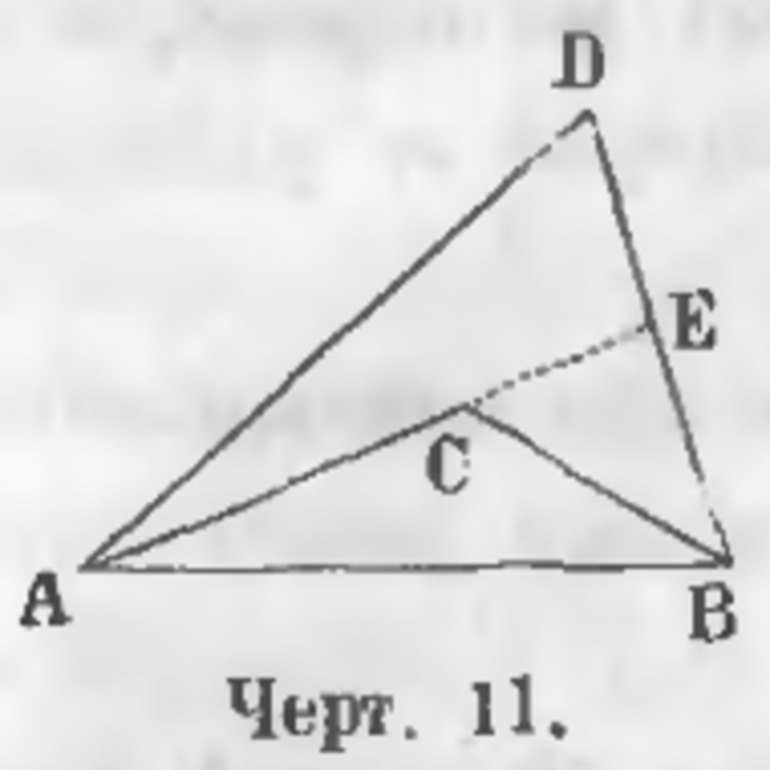
По условиям задачи были даны две ломаные: внутренняя SFT и внешняя SWT. Необходимо доказать, что SWT больше SFT. Для решения этой задачи нужно продолжить линию SF до пересечения с отрезком WT в точке Е. Линия SWE как ломаная гораздо больше прямой SE. Ломанная FET больше имеющейся прямой FT. Если сложить между собой все эти неравенства, то в итоге можно получить: SW+ WE + FE + ET > SF + FE + FT.

Для получения достоверного результата нужно вычесть из обеих частей неравенства по СЕ:

• SW+ WE + ET > SF + FT.
• WE + ET = WT.

Необходимо рассмотреть и вторую теорему, в соответствии с которой итоговая сумма пересекающихся изогнутых линий больше не пересекающихся. По условиям задачи были даны обычные пересекающиеся ломаные HLK и HRK, а также HR, LK и пересекающиеся части. Решение выглядит следующим образом: неравенства отрезков вытекают из того, что ломаная HEL гораздо больше прямой HL, а вот координаты KER превышают KR.

Нелишним также будет научиться находить общую меру сразу двух линий при помощи линейки. Это правило обязательно осваивают в начальных классах. Для поиска неизвестной общей меры обязательно нужно на большую линию наложить меньшую, потом первый остаток на меньший отрезок, а второй остаток на первый. Все эти манипуляции повторяют ровно до тех пор, пока самый последний остаток максимально не уложится в предпоследнем выполненном действии. Измерение линий всегда означает то, что учащемуся необходимо отыскать её отношение к другим отрезкам, принятым за единицу. Полученное значение называют длиной этой линии, которая может выражаться исключительно в каких-нибудь единицах.

Изучение ломаных линий очень важно, так как они окружают человека повсюду. Речь касается прямых линий, которые меняют своё первоначальное направление, замыкаются, а также пересекаются.

nauka.club

Урок математики «Отрезок. Ломаная линия.»

Урок по математике

Тема: «Отрезок. Ломаная линия»

1 класс

учитель начальных классов:

Уголкова С.Н.

Тип урока: Изучение и первичное закрепление нового материала.

Цель: Ввести понятия «отрезок» и «ломаная», «звено ломаной», «вершины ломаной», «замкнутая ломаная» и «незамкнутая ломаная ». Познакомить с ломаной линией и ее компонентами.

Задачи урока:

1) Образовательная:

• познакомить учащихся с ломаной линией и её видами; усвоение понятий «ломаная», «звено ломаной линии», «вершина ломаной»;

• повторить понятия: отрезок, линия; луч;

• совершенствование вычислительных умений и навыков.

2) Развивающие:

• развивать логическое мышление, пространственное воображение, внимание, память, фантазию;

• совершенствовать уровень развития математической речи ;

3) Воспитывающие:

Материалы и оборудование:

Мультимедийная презентация.

Компьютер, проектор, экран.

Спагетти, кусочек пластилина.

Учебники, тетради.

Ожидаемый результат:

• знать что такое ломаная линия, из чего она состоит, чем отличается от отрезка, луча, прямой линии, кривой линии

• расширение знаний о геометрическом материале

• повышение активности учащихся на уроках

• использование учащимися приобретённых знаний и умений в практической деятельности

• обогащение словарного запаса

Ход урока

1. Орг. момент.

Учитель. Вот звонок нам дал сигнал:
Поработать час настал.
Так что время не теряем,
И работать начинаем.

– Руки? – На месте!
– Ноги? – На месте!
– Локти? – У края!
– Спина? – Прямая

-Сегодня на уроке, ребята, вас ожидает много интересных заданий, новых открытий, а помощниками вам будут: внимание, находчивость, смекалка.

— В конце урока вас ждет сюрприз.( На доске конверт)

2.Актуализация знаний учащихся. Постановка цели и задач урока. Мотивация учебной деятельности учащихся.

Учитель — Проверим наш багаж знаний. Проведем небольшую разминку.

Игра «Молчанка» (Задачи в стихах.)

Шесть грибов нашёл Вадим,

А потом ещё один.

Вы ответьте на вопрос:

Сколько он грибов принёс? 7

Майским вечером к пеструшке

На блины пришли подружки.

3 несушки, 3 клохтушки.

Сколько курочек в избушке? 6

В гнезде у синичек лежат семь яичек.

Мама-синичка положила ещё два яичка.

Сколько яичек в гнезде у синичек? 9

Потеряла крольчиха крольчат,

А крольчата лежат и молчат.

Один — за ветлой,

Двое — за метлой,

Один — под листком,

Двое — под кустом.

Притаились они и молчат

Сколько вы насчитали крольчат? 6

-Какая цифра пропущена?

2+ =4 3+ =5 5- =4 3- =1

-Сегодня мы с вами вновь отправляемся в путешествие. А куда, вы должны отгадать. Разложите цифры в порядке возрастания и прочитайте слово.

8 6 5 7 1 3 4 2 9

И т е р г о м е я ( геометрия) слайд 1

— Кто живет в этой стране?

— Какие геометрические фигуры на рисунке?

— Сколько прямых линий? 3

-Что вы знаете о прямой? ( Линия, у которой нет начала и конца .Она бесконечна, не имеет границ, т.е. её можно продолжить в любую сторону).

— А сколько прямых можно провести через 2 точки?

-А сколько кривых линий на рисунке? 5

— Что вы знаете о кривой?

Слайд 2

— Найдите луч, отрезок , прямую. Объясните свой выбор.

Учитель: Все линии назвали?

Д.- Нет. Учитель. Почему?

Д.- Не знаем название одной линии.

Учитель: А что бы вы хотели узнать про эту линию?

Д. (Предположения детей).

-Как называется?

-Как начертить?

-Из чего состоит?

-Как сконструировать?

-Где можно увидеть?

Учитель: Сегодня на уроке мы исследуем такие линии, и, надеюсь, ответим на многие ваши вопросы.

3.«Открытие» нового знания.

(Исследование ломаной линии путём практической работы.

Наблюдение . Анализ. Сравнение.

1. Практическая работа. (Работа в парах)

-Посмотрите, что у меня в руках? (Вермишель спагетти)

-Какую геометрическую фигуру она вам напоминает? (Прямую линию)

-Возьмите в руки спагетти. Как из прямой линии получить отрезок? Ответы учащихся.

-Переломите в середине, а затем каждую часть ещё раз переломите пополам.

-Какие геометрические фигуры вам напоминают? (Отрезки, их получилось 4)

-Соедините их кусочками пластилина между собой. Можно ли теперь назвать полученную фигуру прямой линией? (Нет)

Учитель: Обсудите в паре и приготовьтесь ответить на вопрос: Какое название вы бы дали этой линии?

Учитель: Что интересного заметили, моделируя линию?

……………….. В процессе наблюдения выясняем:

— части линии – отрезки (Как можно назвать части линии?)

— соединяются концами (Как соединяются отрезки?)

— идут друг за другом (Как следуют?) Последовательно.

— Как бы вы назвали такую геометрическую фигуру? (Поломанная линия)

— Я должна немного поправить вас, она называется «ломаная» линия.

Слайд 3

— Каждая ломаная линия состоит из нескольких отрезков — звеньев. Сколько звеньев в этой ломаной? 6

— Звенья ломаной не лежат на одной прямой. Конец одного звена является началом другого. Место, где соединяются два звена, называется вершиной.

— Сколько вершин у данной ломаной линии? 5

— Кроме того, у ломаной линии есть 2 конца.

Физкультминутка.

4.Первичное закрепление

Учитель открывает на доске таблицу № 1:

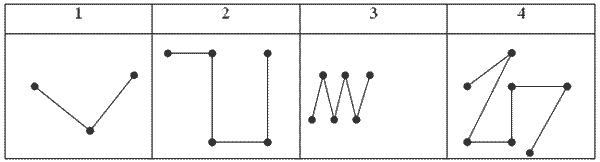
— Какие фигуры изображены в таблице? (ломаные линии)

— У какой ломаной больше всего звеньев? 4

— У какой ломаной меньше всего звеньев? 1

— Какая ломаная имеет три вершины? 2

— Какая ломаная имеет пять вершин? 4

Учитель открывает на доске таблицу №2:

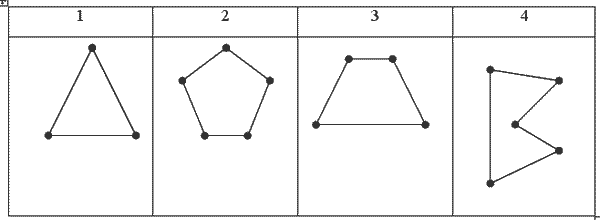
— Это тоже ломаные линии. Чем они отличаются от ломаных линий на первой таблице? (Все звенья соединены между собой)

— Такие ломаные линии называют «замкнутыми», а линии на первой таблице — «незамкнутыми» линиями.

— Назовите замкнутую ломаную линию, которая имеет меньше всего звеньев. 1

— Верно, а может ли быть замкнутая линия из двух звеньев, подумайте. Давайте построим такую ломаную линию. (Нет, чтобы «замкнуть» линию нужно третье звено)

Работа со счетными палочками. Составление ломаных линий из 2,3,4 звеньев. Замкнутые и незамкнутые линии.

5.Упражнение в применении знаний.

— Хотелось бы вам самим начертить ломаную?

— Откройте тетради. Расскажите, как начертить отрезок? Поставить точку. Соединить точки. Как соединить точки?

Д.- Линейкой. (Отрезки можно начертить только по линейке. Ломаную линию так же).

— Теперь начертим ломаную из двух звеньев.

— Как будем соединять точки? Д.- Последовательно. (Друг за другом). Работаем аккуратно и точно. Проверка.

6.Подведение итога урока

— С какой геометрической фигурой познакомились? (ломаной линией)

— Из каких элементов состоит ломаная линия? (Из звеньев и вершин)

— Какие бывают ломаные линии? (Замкнутые и незамкнутые)

7. Рефлексия.

Учитель: — Кому на уроке было трудно?

— Что было самым трудным?

— Кто справился с работой легко?

— мы очень хорошо работали, но остался конверт с сюрпризом. (на доске с начала урока закрытый конверт)

В нём ваша награда за хорошую работу (орден – звёздочки)

— Что он напоминает?

— Молодцы!

infourok.ru